Презентация. Построение сечения пирамиды по трём точкам, лежащим на гранях
Построение сечений довольно трудоёмкая заадча, с которой справляются далеко не все ученики.
Представляю Вашему внимани работу моего ученика, который успешно строит пирамиды по трём
точкам, лежащим на гранях
Просмотр содержимого документа
«Презентация. Построение сечения пирамиды по трём точкам, лежащим на гранях»

Построение сечения пирамиды по 3-ём точкам, лежащим на гранях.
Презентацию подготовил Овчаренко В. В.
10 «А» класс

Дано:
Точки P,Q,R, лежащие на гранях ABM, AEM, DEM соответственно.

1
Проведём MP до пересечения с ребром AB в точке P1, аналогично и для оставшихся точек.

2
Проведём RQ и R1Q1 до их пересечения в точке T2

3
Повторим шаг 2 для RP и R1P1, получим точку T1

4
Соединим Т1 и Т2, получим прямую.( Эта прямая есть пересечение плоскости искомого сечения и плоскости основания)

5
AE∩T1T2=S1. Проведем прямую S1Q.
S1Q∩AM=K, S1Q∩ME=L.

Построим отрезок КР, продлим его до пересечения с ребром ВМ в точке F.
Аналогично для точек L и R, получим точку G.

7
Продлим ВС до пересечения с зелёной (в данном случае) прямой, через полученную точку и F проведём отрезок, продлим его до пересечения с ребром СМ в точке N

8
Соединим N и G, KLGNF и есть искомое сечение, заштрихуем или закрасим его.
Построение сечения пирамиды по 3 -ём точкам лежащим

 Дано: Точки P, Q, R, лежащие на гранях ABM, AEM, DEM соответственно.
Дано: Точки P, Q, R, лежащие на гранях ABM, AEM, DEM соответственно.
 1 Проведём MP до пересечения с ребром AB в точке P 1, аналогично и для оставшихся точек.
1 Проведём MP до пересечения с ребром AB в точке P 1, аналогично и для оставшихся точек.
 2 Проведём RQ и R 1 Q 1 до их пересечения в точке T 2
2 Проведём RQ и R 1 Q 1 до их пересечения в точке T 2
 3 Повторим шаг 2 для RP и R 1 P 1, получим точку T 1
3 Повторим шаг 2 для RP и R 1 P 1, получим точку T 1
 4 Соединим Т 1 и Т 2, получим прямую. ( Эта прямая есть пересечение плоскости искомого сечения и плоскости основания)
4 Соединим Т 1 и Т 2, получим прямую. ( Эта прямая есть пересечение плоскости искомого сечения и плоскости основания)
 5 AE∩T 1 T 2=S 1. Проведем прямую S 1 Q∩AM=K, S 1 Q∩ME=L.
5 AE∩T 1 T 2=S 1. Проведем прямую S 1 Q∩AM=K, S 1 Q∩ME=L.
 6 Построим отрезок КР, продлим его до пересечения с ребром ВМ в точке F. Аналогично для точек L и R, получим точку G.
6 Построим отрезок КР, продлим его до пересечения с ребром ВМ в точке F. Аналогично для точек L и R, получим точку G.

 8 Соединим N и G, KLGNF и есть искомое сечение, заштрихуем или закрасим его.
8 Соединим N и G, KLGNF и есть искомое сечение, заштрихуем или закрасим его.
5.3.4 Сечения куба, призмы, пирамиды
Видеоурок: Задачи на построение сечений
Лекция: Сечения куба, призмы, пирамиды
 Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды
Для решения практически всех задач из раздела стереометрии необходимы знания и навыки в построении сечения объемных тел. Именно об этом мы сейчас с вами и поговорим.
Для начала давайте вспомним, что нам необходимо для построения плоскости. Построить плоскость можно:
с помощью трёх точек;
с помощью двух пересекающихся прямых;
с помощью прямой и точки, которая не лежит на прямой;
а также с помощью двух параллельных прямых.
Что такое секущие плоскости?
Секущей плоскостью пирамиды, призмы или куба называется такая плоскость, по обе стороны которой будут иметься точки объемного тела.
Сечение пирамиды, куба или призмы – это многоугольник, который состоит из точек, принадлежащих объемному телу.
 Построение сечения
Построение сечения
Чтобы построить сечение, необходимо выделить минимум три точки, в которых секущая плоскость пересекает объемное тело, а затем соединить их.
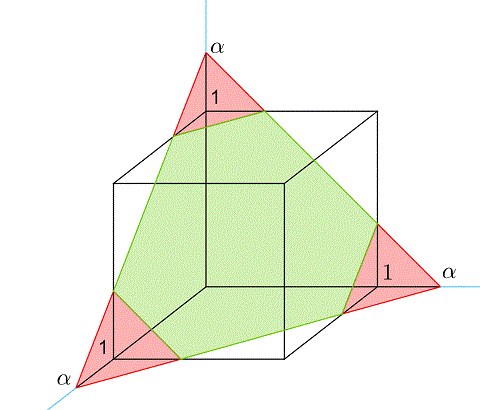
Например, на рисунке показан куб, внутри которого находится секущая плоскость, которая пересекла грани куба в 6 точках. Это значит, что сечением данной фигуры будет шестиугольник.
Чтобы построить сечение объемной фигуры, необходимо решить две задачи:
- Найти линии, по которым пересекаются две плоскости.
Для этого необходимо рассмотреть секущую плоскость и плоскость грани объемной фигуры. Найти хотя бы две точки, в которых эти плоскости пересекаются. После этого точки необходимо соединить прямой. Аналогичные построения выполнить со всеми гранями, которые пересекаются с секущей плоскостью.
- Найти точку, в которой некоторая прямая пересекает плоскость.
Данная задача сводится к обратному. Рассматриваем грани объемной фигуры, находим точки, в которых данные грани пересекают секущую плоскость, и ставим на этом месте точки. После нахождения всех точек пересечения, соединяем их последовательно.
Метод внутреннего проецирования
Всем привет, давайте поработаем? Освоим метод внутреннего проецирования при построении сечений различных объемных фигур. Вообще построить сечение можно следующими методами: аксиоматическим, методом следов, методом внутреннего проецирования.
Аксиоматический метод применяется чаще всего, когда плоскость задана неявно (например, одной точкой или одной прямой и условием: построить плоскость через данную точку (прямую) параллельно или перпендикулярно какому-либо ребру, прямой, плоскости). Метод следов применяется при явном задании плоскости (тремя точками или прямой и точкой, пересекающимися прямыми, параллельными прямыми), и при возможности построить след секущей плоскости (когда проекция прямой и сама прямая пересекаются в пределах чертежа, то есть секущая плоскость не параллельна основанию многогранника). Наконец, метод внутреннего проецирования применяется, когда секущая плоскость параллельна или почти параллельна основанию, и построить след невозможно.
Задача 1. Построить сечение прямой призмы плоскостью, проходящей через точки .
Задача 1. Дано.
Шаг 1. Проведем прямые и – прямые, по которым плоскость рассечет грани и призмы.
Задача 1. Шаг 1.
Шаг 2. Проведем прямую секущей плоскости и ее проекцию в плоскости основания.
Задача 1. Шаг 2.
Шаг 3. Проведем прямую – это проекция будущей прямой секущей плоскости, которую мы пытаемся восстановить, получив недостающую точку этой прямой (и секущей плоскости). Построенная нами проекция пересечет проекцию в точке .
Задача 1. Шаг 3.
Шаг 4. Из точки построим перпендикуляр к основанию, и доведем его до пересечения с прямой , получив, таким образом, точку , принадлежащую сечению.
Задача 1. Шаг 4.
Шаг 5. Через точки и секущей плоскости проведем прямую до пересечения ею ребра . Таким образом получим последнюю точку искомого многоугольника сечения.
Задача 1. Шаг 5.
Шаг 6. Строим сечение.
Соединяем точки и , и -и готово!
Задача 1. Шаг 6.
Задача 2. Построить сечение правильной пятиугольной призмы плоскостью, проходящей через точки методом внутреннего проецирования.
На первом рисунке показаны уже линии, по которым плоскость рассечет грани и .
Задача 2. Дано.
Шаг 1. Проведем прямую секущей плоскости и ее проекцию в плоскости основания .
Задача 2. Шаг 1.
Шаг 2. Проводим проекции будущих прямых секущей плоскости и – просто соединяем вершины основания. Находим точки пересечения этих прямых с – Точки и .
Задача 2. Шаг 2.
Шаг 3. Из точек и восставим перпендикуляры к плоскости основания, и определим точки их пересечения с прямой – это точки прокола секущей плоскости перпендикулярами. Точки и принадлежат плоскости.
Задача 2. Шаг 3. Шаг 4.
Шаг 4. Проводим прямые и . Эти прямые принадлежат секущей плоскости и пересекут ребра призмы в точках и – это последние нужные нам точки, чтобы мы могли полностью восстановить сечение.
Окончательный вид сечения
Задача 3. Построим сечение шестиугольной правильной призмы плоскостью, проходящей через точки методом внутреннего проецирования.
Задача 3. Дано.
Шаг 1. Проведем прямую и ее проекцию в плоскости основания .
Задача 3. Шаг 1.
Шаг 2. Проводим аналогично прямую секущей плоскости и ее проекцию .
Задача 3. Шаг 2.
Шаг 3. То же проделываем с точками и : проводим прямую и ее проекцию в плоскости основания.
Задача 3. Шаг 3.
Шаг 4. Проводим проекцию будущей прямой секущей плоскости – . Находим точки пересечения с проекциями и – и .
Шаг 5. Из полученных точек и поднимаем перпендикуляры до пересечения с соответствующими прямыми плоскости сечения: из точки – до пересечения с , из точки – до пересечения с прямой – получим точки и .
Задача 3. Шаг 4.
Задача 3. Шаг 5.
Шаг 6. Аналогично соединяем вершины и , получаем проекцию будущей прямой секущей плоскости. Находим точки пересечения с проекциями и – и .
Шаг 7. Из точки поднимаем перпендикуляр до пересечения с прямой – точка .
Шаг 8. Из точки поднимаем перпендикуляр до пересечения с прямой – точка  .
.
Задача 3. Шаги 6-8
Шаг 9. Проводим прямую , находим точку пересечения этой прямой с ребром -точку .
Шаг 10. Проводим прямую , находим точку ее пересечения с ребром – точку .
Задача 3. Шаги 9-10.
Шаг 11. Проводим прямые , , , .
Шаг 12. Продлеваем ребро вверх до пересечения с прямой – нужно получить их пересечение, точку .
Шаги 13-14. Проводим прямые и . Находим точки и , в которых эти прямые пересекут ребра и  соответственно.
соответственно.
Задача 3. Шаги 11-14.
Шаг 15. Проводим , завершая сечение.
Задача 3. Шаг 15.
Окончательный вид сечения:
Задача 3. Завершение построения
Невозможно освоить метод внутреннего проецирования, не научившись работать с пирамидами, ведь их боковые грани наклонены к основанию. Поэтому при построении сечений пирамид метод внутреннего проецирования имеет свои особенности.
Задача 4. Построить сечение правильной шестиугольной пирамиды методом внутреннего проецирования. Плоскость сечения провести через точки .
Задача 4. Дано
Шаг 1. Проводим сразу же отрезок , по этой прямой плоскость рассечет грань . Проведем прямую плоскости, и ее проекцию в плоскости основания.
Задача 4. Шаг 1.
Шаг 2. Соединяем вершину с вершиной , а вершину с вершиной , получая проекции будущих прямых искомой плоскости сечения. Прямая пересекает в точке , прямая пересекает в точке .
Задача 4. Шаг 2.
Шаг 3. Вот здесь как раз проявят себя особенности построения: так как боковые грани имеют наклон к основанию, то из полученных точек неверно восстанавливать перпендикуляры. Необходимо соединить точки и с вершиной пирамиды. Тогда пересечение прямой с прямой плоскости – точка – будет принадлежать сечению. Аналогично, пересечение прямой и прямой даст нам точку сечения.
Задача 4. Шаг 3
Шаг 4. Получим аналогичным образом точку . Проведем BE, пересечение и даст нам основание высоты пирамиды – точку .
Задача 4. Шаг 4.
Шаг 5. Определим место пересечения высоты пирамиды с прямой – точку  .
.
Шаг 6. Проводим прямую . Так как обе точки принадлежат плоскости, то вся прямая принадлежит плоскости и пересечет противоположное ребро в точке .
Задача 4. Шаги 5-6.
Шаг 7. Проводим прямую секущей плоскости . Ее пересечение с ребром – точка .
Задача 4. Шаг 7
Шаг 8. Проводим прямую секущей плоскости . Ее пересечение с ребром – точка .
Задача 4. Шаг 8.
Шаг 9. Теперь у нас есть все точки, в которых сечение пересечет ребра пирамиды. Просто соединим их.
Задача 4. Шаг 9.
Окончательный вид сечения:
Задача 4. Сечение
Задача 5. Построить сечение правильной четырехугольной призмы методом внутреннего проецирования. Две из трех точек, через которые надо провести сечение, лежат в гранях пирамиды. Чтобы четко показать это, я провела через данные точки сечения и вершину пирамиды прямые и .
Задача 5. Дано.
Шаг 1. Проведем прямую через точки секущей плоскости и . Через точки и проведем проекцию . Важно, что прямые и принадлежат одной плоскости.
Задача 5. Шаг 1.
Шаг 2. Соединяем вершины и . Это проекция будущей прямой секущей плоскости – . Проекция пересечет проекцию в точке . Соединим точку с вершиной пирамиды. Полученная прямая пересечет прямую в точке .
Задача 5. Шаг 2.
Шаг 3. Точка принадлежит плоскости , так как принадлежит прямой этой плоскости . Также вследствие принадлежности прямой точка принадлежит искомому сечению. Поэтому можем соединить точки и . Полученная прямая пересечет ребро в точке .
Задача 5. Шаг 3.
Шаг 4. Дальнейшее построение очевидно, и не требует пояснений:
Задача 5. Шаг 4.
Шаг 5.
Задача 5. Шаг 5
Окончательный вид полученного сечения:
Окончание построения
Презентация. Построение сечения пирамиды по трём точкам, лежащим на гранях
Построение сечений довольно трудоёмкая заадча, с которой справляются далеко не все ученики.
Представляю Вашему внимани работу моего ученика, который успешно строит пирамиды по трём
точкам, лежащим на гранях
Просмотр содержимого документа
«Презентация. Построение сечения пирамиды по трём точкам, лежащим на гранях»

Построение сечения пирамиды по 3-ём точкам, лежащим на гранях.
Презентацию подготовил Овчаренко В. В.
10 «А» класс

Дано:
Точки P,Q,R, лежащие на гранях ABM, AEM, DEM соответственно.

1
Проведём MP до пересечения с ребром AB в точке P1, аналогично и для оставшихся точек.

2
Проведём RQ и R1Q1 до их пересечения в точке T2

3
Повторим шаг 2 для RP и R1P1, получим точку T1

4
Соединим Т1 и Т2, получим прямую.( Эта прямая есть пересечение плоскости искомого сечения и плоскости основания)

5
AE∩T1T2=S1. Проведем прямую S1Q.
S1Q∩AM=K, S1Q∩ME=L.

6
Построим отрезок КР, продлим его до пересечения с ребром ВМ в точке F.
Аналогично для точек L и R, получим точку G.

7
Продлим ВС до пересечения с зелёной (в данном случае) прямой, через полученную точку и F проведём отрезок, продлим его до пересечения с ребром СМ в точке N

8
Соединим N и G, KLGNF и есть искомое сечение, заштрихуем или закрасим его.