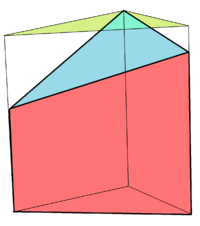
Треугольная призма все формулы и примеры задач
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Элементы треугольной призмы
Треугольники ABC и A1B1C1 являются основаниями призмы.
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы.
Стороны граней являются ребрами призмы (A1B1, A1
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
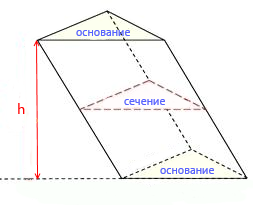
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
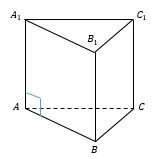
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
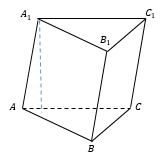
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
или
V=Sосн . h
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
или
S
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
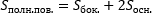
так как Sбок=Pосн.h, то получим:
Sполн.пов.=Pосн.h+2Sосн
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы:
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см2, то высота должна быть выражена в сантиметрах, а объем — в см 3 . Если площадь основания в мм2, то высота должна быть выражена в мм, а объем в мм3 и т. д.
Пример призмы
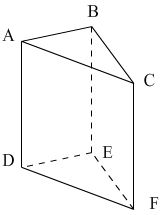
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
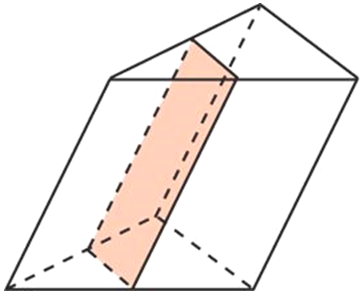
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S 2 = S1k2 = S122 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Призма. Формулы и свойства призмы
Определение.
Призма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) — параллелограммы, что имеют общие стороны с этими многоугольниками.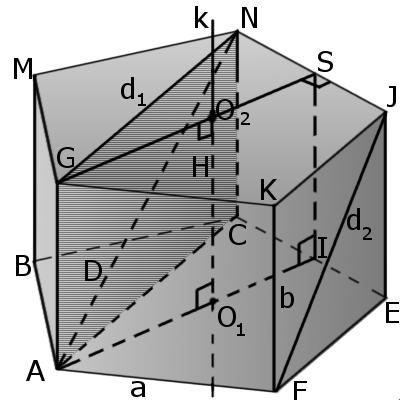 |
 | |
| Рис.1 | Рис.2 |
Определение. Основы призмы — две грани, которые являются равными параллельными плоскими многоугольниками (ABCEF, GMNJK).
Определение. Боковые грани призмы — все остальные грани за исключением основ.
Определение. Боковая поверхность призмы — совокупность всех боковых граней призмы.
Определение. Поверхность призмы — это совокупность поверхностей двух оснований и боковой поверхности.
Определение. Боковое ребро призмы — общая сторона двух боковых граней.
Определение. Высота — это перпендикуляр, который соединяет две основы призмы под прямым углом.
Определение. Диагональ основания призмы — это отрезок, соединяющий две не соседние вершины, принадлежащие этой же основе.
Определение. Диагональ боковой грани призмы
— это отрезок, соединяющий две противоположные вершины, лежащие на одной боковой грани однако принадлежат различным основам.Определение. Диагональ призмы (AN) — это отрезок, соединяющий две вершины, лежащие на разных основаниях, но не лежат на одной боковой стороне.
Определение. Диагональное сечение — это пересечение призмы плоскостью, проходящей через диагональ основания призмы и боковое ребро. Треугольная призма (в основе призмы треугольники) не имеет диагональных сечений.
Определение. Перпендикулярное сечение — это пересечение призмы плоскостью, пересекающей боковые ребра призмы под прямым углом.
Определение. Прямая призма — это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.
Определение. Наклонная призма — это призма, в которой боковые грани не перпендикулярны к основанию.
Определение. Усечённая призма — это призма, в которой две основы не параллельны (рис. 2). Усечённая призма может быть, как прямой, так наклонной.
Объём призмы
Формула. Объём призмы через площадь основания и высоту:V = SоснH
Формула. Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра:V = SпL
Формула. Объём правильной прямой призмы через высоту (h), длину стороны (a) и количество сторон (n):Площадь поверхности призмы
Формула. Площадь боковой поверхности призмы через периметр основания и высоту:Sb = P·h
Формула. Площадь поверхности призмы через площадь основания, периметр основания и высоту:S = 2Soсн + P·h
Формула. Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):Основные свойства призмы
Основы призмы — равные многоугольники.
Боковые грани призмы — параллелограммы.
Боковые ребра призмы параллельны и равны между собой.
Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
Высота прямой призмы равна длине бокового ребра.
Высота наклонной призмы всегда меньше длины ребра.
В прямой призме гранями могут быть прямоугольниками или квадратами.
Треугольная призма — Википедия
Материал из Википедии — свободной энциклопедии
Треугольная призма — призма с тремя боковыми гранями. Этот многогранник имеет в качестве граней треугольное основание, его копию, полученную в результате параллельного переноса и 3 грани, соединяющие соответствующие стороны[en]. Прямая треугольная призма имеет прямоугольные боковые стороны, в противном случае призма называется косой
Однородная треугольная призма — это прямая треугольная призма с равносторонним основанием и квадратными боковыми сторонами.
Призма является пятигранником, у которого две грани параллельны, в то время как нормали трёх других лежат в одной плоскости (которая не обязательно параллельна основаниям). Эти три грани являются параллелограммами. Все сечения, параллельные основаниям, являются одинаковыми треугольниками.
Полуправильный (однородный) многогранник[править | править код]
Прямая треугольная призма является полуправильным многогранником или, более обще, однородным многогранником, если основание является правильным треугольником, а боковые стороны — квадратами.
Этот многогранник можно рассматривать как усечённый треугольный осоэдр, представленный символом Шлефли t{2,3}. Его также можно рассматривать как прямое произведение треугольника на отрезок, что представляется как {3}x{}. Двойственным многогранником треугольной призмы является треугольная бипирамида.
Группой симметрии прямой призмы с треугольным основанием является D3h порядка 12. Группой вращения служит D3 с порядком 6. Группа симметрии не содержит центральную симметрию.
Объём любой призмы равен произведению площади основания на расстояние между основаниями. В нашем случае, когда основание треугольно, нужно просто вычислить площадь треугольника и умножить на длину призмы:
V=12bhl{\displaystyle V={\frac {1}{2}}bhl} где b — длина стороны основания, h равна высоте треугольника, а l равна расстоянию между треугольниками.
Усечённая прямая треугольная призма имеет одну усечённую треугольную грань[1].
Имеется полная D2h симметрия гранений[en] (удаление части многогранника, не создавая новые вершины, пересечение рёбер новоё вершиной не считается) треугольной призмы. Получающиеся многогранники имеются многогранники с 6 гранями в виде равнобедренного треугольника, один многогранник сохраняет исходные верхний и нижний треугольники, и один сохраняет исходные квадраты. Две симметрии гранения C3v имеют один базовый треугольник, 3 грани в виде боковых самопересекающихся квадратов и 3 грани в виде равнобедренных треугольников.
Варианты симметрии[править | править код]
Этот многогранник топологически является частью последовательности однородных усечённых многогранников с вершинными конфигурациями (3.2n.2n) и имеющими симметрию [n,3] группы Коксетера.
| Варианты симметрии *n32 усечённых мозаик: 3.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *n32 [n,3] | Сферическая | Евклидова[en]* | Компактная гиперболич. | Параком- пактная | Некомпактная гиперболич. | ||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]… | *∞32 [∞,3] | [12i,3] | [9i,3] | [6i,3] | |
| Усечённые фигуры |  |  |  |  |  | ||||||
| Конфигурация[en]* | 3.4.4 | 3.6.6 | 3.8.8 | 3.10.10 | 3.12.12[en] | 3.14.14[en] | 3.16.16[en] | 3.∞.∞[en] | 3.24i.24i | 3.18i.18i | 3.12i.12i |
| Разделённые фигуры |  |  |  |  |  |  |  |  | |||
| Конфигурация[en]* | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12[en] | V3.14.14[en] | V3.16.16 | V3.∞.∞ | |||
Этот многогранник топологически является частью последовательности рёберно усечённых[en] многогранников с вершинной фигурой (3.4.n.4), которая продолжается как умощения гиперболической плоскости. Эти вершинно-транзитивные[en] фигуры имеют зеркальную симметрию[en] (*n32).
Составные тела[править | править код]
Имеется 4 однородных составных тела из треугольных призм:
Соты[править | править код]
Существует 9 однородных сот, которые включают треугольные призмы:
Связанные многогранники[править | править код]
Треугольная призма является первой в пространственной серии полуправильных многогранников[en]. Каждый последующий однородный многогранник имеет в качестве вершинной фигуры предыдущий многогранник. Торольд Госсет[en] обнаружил эту серию в 1900 году как содержащую все виды граней правильных многомерных многогранников, содержащую все симплексы и ортоплексы (правильные треугольники и квадраты в случае треугольной призмы). В нотации Коксетера[en] треугольной призме соответствует символ −121.
| k21[en] в пространстве размерности n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Пространство | Конечное | Евклидово | Гиперболическое | ||||||||
| En[en] | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Группа Коксетера | E₃=A₂A₁ | E₄=A₄ | E₅=D₅ | E₆ | E₇[en] | E₈ | E₉ = Ẽ₈ = E₈+ | E₁₀ = T₈ = E₈++ | |||
| Диаграмма Коксетера |      |      |        |          |            |              |                |                  | |||
| Симметрия[en] | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Порядок | 12 | 120 | 192 | 51 840 | 2 903 040 | 696 729 600 | ∞ | ||||
| Граф |  |  |  |  |  |  | — | — | |||
| Обозначение | −121 | 021 | 121 | 221[en] | 321[en] | 421[en] | 521[en] | 621[en] | |||
Четырёхмерное пространство[править | править код]
Треугольная призма существует как ячейка в большом числе четырёхмерных однородных четырёхмерных многогранников[en], включая:
Правильная треугольная призма | Банк ЕГЭ
Правильная треугольная призма — призма, в основаниях которой лежат два правильных треугольника, а все боковые грани строго перпендикулярны этим основаниям.Обозначения
- $ABCA_1B_1C_1$ — правильная треугольная призма
- $a$ — длина стороны основания призмы
- $h$ — длина бокового ребра призмы
- $S_{\text{осн.}}$ — площадь основания призмы
- $V_{\text{призмы}}$ — объем призмы
Площадь оснований призмы
В основании правильной треугольной призмы лежит правильный треугольник со стороной $a$. По свойствам правильного треугольника $$ S_{\text{осн.}}=\frac{\sqrt{3}}{4}\cdot a^2 $$ Таким образом, получается, что $S_{ABC}=S_{A_1B_1C_1}=\frac{\sqrt{3}}{4}\cdot a^2$.Объем призмы
Объем призмы вычисляется как произведение площади ее основания на ее высоту. Высотой правильной призмы является любое из ее боковых ребер, например, ребро $AA_1$. В основании правильной треугольной призмы находится правильный треугольник, площадь которого нам известна. Получаем $$ V_{\text{призмы}}=S_{\text{осн.}}\cdot AA_1=\frac{\sqrt{3}}{4}\cdot a^2 \cdot h $$Находим BD
BD является высотой правильного треугольника со стороной $a$, лежащего в основании призмы. По свойствам правильного треугольника $$ BD=\frac{\sqrt{3}}{2}\cdot a $$ Аналогичным образом, приходим к заключению, что длины всех остальных диагоналей оснований призмы равны $\frac{\sqrt{3}}{2}\cdot a$.Находим $BD_1$
В треугольнике $DBD_1$:- $DB=\frac{\sqrt{3}}{2}\cdot a$ — как мы только что выяснили
- $DD_1=h$
- $\angle BDD_1=90^{\circ}$ — потому что прямая $DD_1$ перпендикулярна плоскости $ABC$
Находим $BC_1$
В треугольнике $CBC_1$:- $CB=a$
- $CC_1=h$
- $\angle BCC_1=90^{\circ}$ — потому что прямая $CC_1$ перпендикулярна плоскости $ABC$
Нахождение площади сечения треугольной призмы — «Шпаргалка ЕГЭ»
Решение задачи
В данном уроке показано решение геометрической задачи, которое можно использовать в качестве примера при решении задач С2 при подготовке к ЕГЭ по математике.
Прежде всего, условие задачи изображается схематически на рисунке. Далее выполняется построение сечения. Боковая грань — прямая, по которой плоскость пересекает основание призмы . Так как верхнее основание параллельно нижнему основанию, то прямые, по которым плоскость пересекает данные плоскости, будут параллельны. Так как параллельно , то четырехугольник по определению — трапеция. Площадь трапеции определяется по формуле: . Далее утверждается, что является средней линией и при этом она равна половине стороны . Высота определяется из треугольника . При этом применяется свойство высоты равностороннего треугольника , где — сторона треугольника, а также теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Таким образом, подставив найденные значения в формулу площади трапеции, определяется искомое значение площади сечения.