Введение в стереометрию. Построение сечений
Цели:
- Научить применять полученные знания на практике, по образцу, алгоритму, с подсказкой.
- Закрепить умения построения сечений, используя аксиомы стереометрии.
- Развивать пространственное мышление учащихся.
Ход урока.
I. Организационная часть.
II. Разбор домашнего задания.
Домашнее задание было по трём уровням сложности
Задача 1 и 2 — первый уровень
Задача 3 и 4 – второй уровень
Задача 5 и 6 – третий уровень
Задача 1. АВСА1С1 – треугольная призма, точка F – середина ребра АВ, точка О лежит на продолжении ребра ВС так, что С расположена между В и О. Постройте сечение призмы плоскостью
Задача 2. Точка О – середина ребра DD1 куба ABCDA1B1C1D1. Постройте точки пересечения прямых A1O и C1O с плоскостью основания ABCD и вычислите расстояние между ними, если длина ребра куба 2 см.
Задача 3. Дана треугольная пирамида SABC Точки Р и R лежат на ребрах SA и ВС, точка F лежит на продолжении ребра АС так, что точка С лежит между точками А и F. Постройте сечение пирамиды плоскостью PRF
Задача 4. SABCD — четырехугольная пирамида. Точка Р лежит в грани SCD, а точка F на продолжении ребра DC так, что точка D лежит между F и С. Постройте сечение пирамиды плоскостью PFB.
Задача 5. DABC — правильный тетраэдр, длина ребра которого равна 4 см. Точка О — середина ребра DB. Точка F лежит на продолжении ребра ВС так, что С — середина отрезка BF, точка Т лежит на продолжении ребра АС так, что С — середина отрезка AT. Постройте сечение тетраэдра плоскостью FTO и вычислите его периметр.
Задача 6. DABC — треугольная пирамида Точка F лежит на ребре DB, точка Т лежит на продолжении ребра АВ так, что точка А расположена между точками Т и В, а точка R лежит на продолжении ребра CD так, что точка С лежит между точками D и R. Постройте сечение пирамиды плоскостью TFR.
III. Работа по готовым чертежам.
Каждой группе предлагаются задачи в зависимости от уровня сложности. Учащиеся выполняют данные задания, а затем коллективное обсуждение хода решения.
Условие: являются ли закрашенные фигуры сечениями изображённых многогранников плоскостью
PQR? В тех случаях, когда сечение показано неправильно, найдите правильное решение.На рисунках изображены правильные параллелепипеды.
Задание первого уровня:
Задание второго уровня:
Задание третьего уровня:
IV. Практическая работа.
Каждой группе даётся основное задание и дополнительное. В дополнительном задании на рисунках изображены треугольные призмы (1 и 2 уровень) и треугольная пирамида (3 уровень).
Работа оценивается учителем с последующей отметкой в журнал.
Задание первого уровня:
- В треугольной пирамиде DABC точка О —
точка пересечения медиан грани
- Дополнительное задание: являются ли закрашенные фигуры сечениями изображённых многогранников плоскостью PQR? В тех случаях, когда сечение показано неправильно, найдите правильное решение.
Задание второго уровня:
- АВСА1В1С1 — треугольная призма. Точка О лежит на ребре A1C1,. Точка F лежит на продолжении ребра АС так, что С лежит между А и F. Точка К лежит на продолжении ребра АВ так, что В расположена между А и К. Постройте сечение призмы плоскостью OKF.
- Дополнительное задание: являются ли закрашенные фигуры сечениями изображённых многогранников плоскостью PQR? В тех случаях, когда сечение показано неправильно, найдите правильное решение.
Задание третьего уровня:
- Основание прямоугольного параллелепипеда ABCDAlB1C1D1
— квадрат, длина стороны которого равна 2 см.
Точка О — середина бокового ребра
- Дополнительное задание: являются ли закрашенные фигуры сечениями изображённых многогранников плоскостью PQR? В тех случаях, когда сечение показано неправильно, найдите правильное решение.
V. Домашнее задание.
Учащиеся выбирают соответствующий уровень сложности.
Задание для первого уровня сложности:
Задание для второго уровня сложности:Задание для третьего уровня сложности:
VI. Рефлексия. Подведение итогов урока.
urok.1sept.ru
Стереометрия. Площадь сечения через площадь проекции сечения.
Если сечение сложной формы, то не стоит пытаться найти его площадь “в лоб”. Умный гору обойдет… И мы обойдем: определим площадь проекции сечения (обычно это очень просто) и угол наклона плоскости сечения к плоскости основания. Потом воспользуемся известной формулой. Но об этом – дальше.
Задача 1. В прямоугольном параллелепипеде  с ребрами
с ребрами 
 и
и  точки
точки  и
и  -середины ребер
-середины ребер  и
и  соответственно. Плоскость
соответственно. Плоскость  пересекает ребро
пересекает ребро  в точке
в точке  .
.а) Докажите, что  ;
;
б) Найдите площадь сечения этого параллелепипеда плоскостью 

Рисунок 1 – к задаче 1
Построим сечение. Построим прямую  – ведь точки
– ведь точки  и
и  принадлежат одной грани. Построим прямую
принадлежат одной грани. Построим прямую  и найдем точку пересечения прямой
и найдем точку пересечения прямой  и прямой
и прямой  – точку
– точку  .
.

Рисунок 2 – к задаче 1
Эта точка принадлежит как плоскости грани  , так и плоскости грани
, так и плоскости грани  . Проведем прямую
. Проведем прямую  и определим точку пересечения этой прямой с ребром
и определим точку пересечения этой прямой с ребром  – точку
– точку  .
.

Рисунок 3 – к задаче 1
Построим линии, по которым сечение «режет» грани параллелепипеда:  .
.

Рисунок 4 – к задаче 1
Теперь построим прямую  и определим точку ее пересечения с прямой
и определим точку ее пересечения с прямой  – точка
– точка  пересечения лежит в плоскости верхней грани, и это позволяет соединить ее с точкой
пересечения лежит в плоскости верхней грани, и это позволяет соединить ее с точкой  . Теперь найдем место пересечения отрезка
. Теперь найдем место пересечения отрезка  с ребром
с ребром  – точку
– точку  , и можно обводить и штриховать сечение:
, и можно обводить и штриховать сечение:

Рисунок 5 – к задаче 1
Докажем пункт а). Рассмотрим треугольники  и
и  . Они подобны, так как образованы параллельными прямыми:
. Они подобны, так как образованы параллельными прямыми:  . Так как
. Так как  , то коэффициент подобия этих треугольников –
, то коэффициент подобия этих треугольников –  . Тогда
. Тогда  . Так как треугольники
. Так как треугольники  и
и  также подобны с коэффициентом
также подобны с коэффициентом  , то
, то  . Но треугольники
. Но треугольники  и
и  равны по 2 признаку, следовательно,
равны по 2 признаку, следовательно,  , или
, или  , то есть
, то есть  .
.
б) Определим площадь сечения. Для этого можно определить площадь проекции этого сечения, и косинус угла между плоскостью и основанием параллелепипеда. Сначала найдем площадь проекции. Отрежем два треугольника от основания параллелепипеда, тогда оставшееся – и есть площадь проекции (многоугольник  – выделено голубым цветом).
– выделено голубым цветом).

Рисунок 6 – к задаче 1
Площадь основания параллелепипеда равна 12, отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,
![Rendered by QuickLaTeX.com \[S_{PB_1W}=\frac{PB_1 \cdot B_1W}{2}=2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e500f37b29fc9ea32a615adb82a44f17_l3.png)
Отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,
![Rendered by QuickLaTeX.com \[S_{ A_1ZD_1}=\frac{PB_1 \cdot B_1W}{2}=4,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7e5715aed483eb873473ad79595ce25d_l3.png)
Тогда площадь проекции равна
![Rendered by QuickLaTeX.com \[S_{pr}=12-2-4,5=5,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-56b4492c779fa7b63845b1fac2cd18bc_l3.png)
Теперь найдем угол наклона плоскости сечения к плоскости основания, вернее, его косинус. Нужно найти косинус угла – или любую другую тригонометрическую функцию – угла  . Рассмотрим треугольник
. Рассмотрим треугольник  . Он прямоугольный, катет
. Он прямоугольный, катет  (равен высоте параллелепипеда). Длина отрезка
(равен высоте параллелепипеда). Длина отрезка  может быть найдена из треугольника
может быть найдена из треугольника  :
:
![Rendered by QuickLaTeX.com \[WZ^2=WC_1^2+C_1Z^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1b51f95bf16337ee62b98a49ec7b10f3_l3.png)
По ранее доказанному  ,
,  .
.
![Rendered by QuickLaTeX.com \[WZ=\sqrt{ WC_1^2+C_1Z^2}=\sqrt{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e18d00edb018e66fabe4924ece37ee59_l3.png)
![Rendered by QuickLaTeX.com \[WY^2=WZ^2+ZY^2=2^2+2=6\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8f43c3b60546b5c5d9fa003f92b85278_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[\cos{\angle YWZ}=\frac{WZ}{WY}=\frac{\sqrt{2}}{\sqrt{6}}=\frac{1}{\sqrt{3}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c7e9281d78d127677bf013e94b840058_l3.png)
Площадь сечения равна
![Rendered by QuickLaTeX.com \[S=\frac{ S_{pr}}{\cos{\angle YWZ}}=5,5\sqrt{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c5ca612bc136fd767348208423dc3d32_l3.png)
Ответ:  .
.
Задача 2. В правильной четырехугольной призме  сторона
сторона  основания равна 6, а боковое ребро
основания равна 6, а боковое ребро  равно
равно  . На ребрах
. На ребрах  и
и  отмечены точки
отмечены точки  и
и  соответственно, причем
соответственно, причем  .
.
а) Пусть  – точка пересечения плоскости
– точка пересечения плоскости  с ребром
с ребром  . Докажите, что
. Докажите, что  – квадрат;
– квадрат;
б) Найдите площадь сечения призмы плоскостью  .
.

Рисунок 1 – к задаче 2
Проведем прямую  и через точку
и через точку  – параллельную ей прямую, так как плоскость сечет противоположные грани параллелепипеда (прямой призмы) по параллельным прямым:
– параллельную ей прямую, так как плоскость сечет противоположные грани параллелепипеда (прямой призмы) по параллельным прямым:

Рисунок 2 – к задаче 2
Найдем точку пересечения прямой  и
и  – точку
– точку  . Эта точка принадлежит плоскости грани
. Эта точка принадлежит плоскости грани  . Поэтому ее можно соединить с точкой
. Поэтому ее можно соединить с точкой  отрезком, который пересечет ребро
отрезком, который пересечет ребро  в точке
в точке  . Найдем точку пересечения прямой
. Найдем точку пересечения прямой  и
и  – точку
– точку  . Эта точка принадлежит плоскости грани
. Эта точка принадлежит плоскости грани  . Поэтому ее можно соединить с точкой
. Поэтому ее можно соединить с точкой  отрезком, который пересечет ребро
отрезком, который пересечет ребро  в точке
в точке  .
.

Рисунок 3 – к задаче 2

Рисунок 4 – к задаче 2
Соединяя точки  ,
,  ,
,  ,
,  ,
,  ,
,  , получим искомое сечение.
, получим искомое сечение.
Докажем, что  – квадрат.
– квадрат.

Рисунок 5 – к задаче 2
Так как отрезки  и
и  принадлежат одной плоскости (плоскости сечения) и одновременно параллельным плоскостям верхнего и нижнего оснований призмы, то они параллельны. Также
принадлежат одной плоскости (плоскости сечения) и одновременно параллельным плоскостям верхнего и нижнего оснований призмы, то они параллельны. Также  .
.
 и
и  – диагонали прямых правильных призм со стороной основания 1 и высотой
– диагонали прямых правильных призм со стороной основания 1 и высотой  . Тогда
. Тогда
![Rendered by QuickLaTeX.com \[MN=LK=\sqrt{AM^2+A_1N^2+AA_1^2}=\sqrt{1^2+1^2+(4\sqrt{3})^2}=\sqrt{50}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2bebedee840fd6682ed52c3800fda563_l3.png)
Получается,  – как минимум, ромб. И по признаку параллелограмма, так как противоположные стороны попарно равны, то
– как минимум, ромб. И по признаку параллелограмма, так как противоположные стороны попарно равны, то  – квадрат.
– квадрат.
б) Определим площадь сечения. Для этого можно определить площадь проекции этого сечения, и косинус угла между плоскостью и основанием параллелепипеда. Сначала найдем площадь проекции. Отрежем два треугольника от основания параллелепипеда, тогда оставшееся – и есть площадь проекции (многоугольник  – выделено фиолетовым цветом).
– выделено фиолетовым цветом).

Рисунок 6 – к задаче 2
Площадь основания призмы равна 36, отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,
![Rendered by QuickLaTeX.com \[S_{PB_1W}=\frac{KD_1\cdot D_1N}{2}=12,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a23402f6db84ccffa0607fcb7a51c2d2_l3.png)
Отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,
![Rendered by QuickLaTeX.com \[S_{ JB_1I}=\frac{JB_1 \cdot B_1I}{2}=12,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0f3dd84da6a5af3eba3d7d0840a7a768_l3.png)
Тогда площадь проекции равна
![Rendered by QuickLaTeX.com \[S_{pr}=36-12,5-12,5=11\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a1ff5b78930b7b0bd59ceded65b4df9e_l3.png)
Теперь найдем угол наклона плоскости сечения к плоскости основания, вернее, его косинус. Нужно найти косинус угла – или любую другую тригонометрическую функцию – угла  . Рассмотрим треугольник
. Рассмотрим треугольник  . Он прямоугольный, катет
. Он прямоугольный, катет  (равен высоте параллелепипеда). Длина отрезка
(равен высоте параллелепипеда). Длина отрезка  может быть найдена из треугольника
может быть найдена из треугольника  :
:
![Rendered by QuickLaTeX.com \[IK^2=IC_1^2+C_1K^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f08e78c92bee4b30a563242f8229c31b_l3.png)
По ранее доказанному  ,
,  .
.
![Rendered by QuickLaTeX.com \[IK=\sqrt{ IC_1^2+C_1K^2}=\sqrt{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b228ea31ba3130b3696b8d8a94ab0378_l3.png)
![Rendered by QuickLaTeX.com \[LK^2=IL^2+IK^2=(4\sqrt{3})^2+2=50\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-32bf54cd0e5cd62b7bd8f988e4915f0f_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[\cos{\angle LKI}=\frac{KI}{LK}=\frac{\sqrt{2}}{\sqrt{50}}=\frac{1}{5}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aca71a2522e4bda3e21502325a3b58ca_l3.png)
Площадь сечения равна
![Rendered by QuickLaTeX.com \[S=\frac{ S_{pr}}{\cos{\angle LKI}}=55\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7ca6c29dfe3472317ca11a0c0869b652_l3.png)
Ответ:  .
.
easy-physic.ru
Объекты в стереометрии. Базовый уровень. Видеоурок. Геометрия 10 Класс
В планиметрии мы изучали свойства плоских фигур. Хотя в природе их не найдешь – любой объект объёмный. Почему же мы так много времени уделили плоским фигурам, которых не существует в окружающем мире?
Есть природа, а есть модели природных объектов, которые у нас получается исследовать – отрезки, углы, фигуры. Они, в свою очередь, являются элементами объёмных тел. Изучив подробно свойства плоских фигур, теперь мы сможем применять полученные знания для исследования тел в пространстве.
Кирпич имеет форму параллелепипеда, а его грани – форму прямоугольника. Бревно имеет форму цилиндра, а спил (сечение) – форму круга, если спил сделан перпендикулярно оси бревна, и эллипса, если под углом.
То есть переход от планиметрии к стереометрии – это расширение математической модели, а не замена одной на другую.
В планиметрии с изображением фигур было все просто: лист бумаги, по сути, представлял плоскость, и изобразить на нём плоскую фигуру (например, квадрат со стороной а) не составляло труда.
В стереометрии мы будем объёмные фигуры изображать на плоскости, что потребует от нас определенных навыков.
Особенности нашего зрения
Мы привыкли доверять своим глазам и не задаемся вопросом, почему один и тот же объект вблизи выглядит крупнее, чем вдали? Или почему разные по величине предметы порой кажутся одного размера? Механизмы зрения довольно сложны, однако некоторые его особенности можно объяснить на основе геометрических представлений.
Всякий предмет имеет линейные размеры: длину, ширину и высоту. Но как только он попадает в наше поле зрения, то приобретает еще один размер – угловой. Давайте разберемся, что это означает. Когда мы смотрим на предмет, то через каждую его точку можно провести от глаза луч, называемый лучом зрения. Понятно, что их будет бесконечно много. Любые два луча зрения образуют угол зрения (см. рис. 1).

Рис. 1. Угол зрения
Тот угол зрения, под которым предмет виден целиком, и принято называть угловым размером предмета. Как и всякий плоский угол, он измеряется в градусах, минутах, секундах или в радианах.
Угловой размер предмета – величина не постоянная и зависит от расстояния предмета от глаза: чем предмет дальше, тем меньше угол зрения, под которым он виден.
Чтобы понять причину этого явления, вспомним, что на сетчатке глаза изображение предмета получается обратным и уменьшенным. При удалении предмета его изображение на сетчатке становится меньше, поэтому он и кажется нам уменьшающимся (см. рис. 2). При сокращении расстояния изображение, напротив, увеличивается, и предмет кажется увеличивающимся (см. рис. 3).
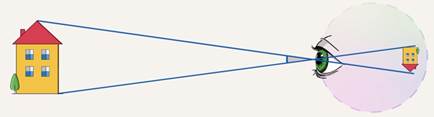
Рис. 2. Предмет кажется уменьшающимся при его удалении

Рис. 3. Предмет кажется увеличивающимся при его приближении
Теперь легко объяснить, почему две «убегающие» вдаль параллельные линии (железнодорожные рельсы, края прямолинейного шоссе) кажутся «сходящимися» в одной точке (см. рис. 4). Такое же впечатление создают ряды телеграфных столбов или деревьев вдоль дороги. Это лишь иллюзия, которая возникает из-за видимого уменьшения расстояния между прямыми по мере их удаления.

Рис. 4. Железнодорожные рельсы кажутся «сходящимися» в одной точке
Часто приходится сталкиваться и с другой ситуацией. Если рассматривать предметы одинаковой формы, но разных линейных размеров под одним и тем же углом зрения, то кажется, что их размеры равны. Поэтому мы можем закрыть монеткой Луну или Солнце.
А при полном солнечном затмении лунный диск в точности заслоняет солнечный (см. рис. 5). В этот момент наблюдатель с Земли видит оба небесных тела под одним углом зрения.

Рис. 5. При полном солнечном затмении лунный диск в точности заслоняет солнечный
Увидеть такое уникальное явление было бы невозможно, если бы линейные размеры Солнца и Луны, а также расстояния от них до Земли не состояли в определенной математической зависимости: диаметры Солнца и Луны (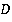 и
и 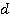 ) и расстояния от этих тел до Земли (
) и расстояния от этих тел до Земли ( и
и  ) связаны пропорцией:
) связаны пропорцией:

Исходя из указанных особенностей нашего зрения, важно научиться правильно изображать объекты, чтобы избежать оптического обмана и искажения восприятия.
Работая с такими фигурами, необходимо научиться изображать их на бумаге. Для этого нужно следовать двум соображениям:
- При изображении дли́ны отрезков и величи́ны углов могут меняться, т.е. длинный отрезок вполне может быть изображен коротким, а прямой угол острым или тупым;
- Параллельность отрезков сохраняется всегда. Длины параллельных отрезков меняются в одинаковой степени, т.е. параллельные равные отрезки всегда будут изображены тоже как параллельные и равные.
Пока мы будем использовать эти утверждения без доказательства, так как у нас не хватает теоретической базы. Но скоро мы сможем это сделать. А пока потренируемся изображать различные тела.
Начнем с куба. Попробуйте взять любой предмет в виде куба, поставить его на стол и нарисовать его границы, глядя под таким углом (см. рис. 1). После этого сравните с тем, что мы сейчас нарисуем, используя геометрические свойства.

Рис. 1. Куб под определенным углом
Все грани куба являются квадратами. Противоположные стороны квадратов параллельны и равны. Это свойство сохранится при изображении.
Изобразим ближнюю к нам грань в виде квадрата, верхнюю грань – в виде произвольного параллелограмма (см. рис. 2). Мы получили уже три ребра, исходящих из одной точки. Все остальные ребра будут изображены параллельными и равными одному из них, т.е. дальше все получится автоматически.

Рис. 2. Ближняя и верхняя грани куба
Изображаем правую грань, сохраняя параллельность соответствующих ребер.
Остальные ребра при рассматривании куба с этой точки нам не видны. Их изображают пунктирами (см. рис. 3).

Рис. 3. Куб
Итак, еще раз, самое главное:
- Параллельные ребра куба должны быть параллельны и равны друг другу на изображении;
- Все ребра куба равны, но непараллельные ребра на рисунке могут быть неравными;
- Все углы граней куба прямые. Но на рисунке некоторые остались прямыми, другие изображены острыми или тупыми.
Зная, как нарисовать куб, несложно понять, как нарисовать прямоугольный параллелепипед – достаточно заменить квадрат передней грани на прямоугольник и дальше пропорционально изменить длины соответствующих ребер (см. рис. 4).
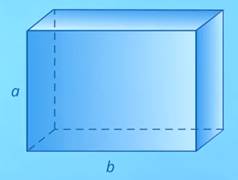
Рис. 4. Параллелепипед
Изобразим теперь произвольную призму. Верхнее и нижнее основания призмы – равные многоугольники. Причем соответствующие стороны у них параллельны.
Изображаем два равных многоугольника ровно один над другим, если призма прямая, и со сдвигом, если призма наклонная (см. рис. 5).

Рис. 5. Верхние и нижние основания прямой и наклонная призм
Верхнее основание нам видно целиком, поэтому мы изображаем его целиком сплошными линиями. Невидимые боковые ребра и стороны нижнего основания изображаем пунктиром. Все боковые ребра призмы параллельны друг другу, это должно выполняться и для рисунка (см. рис. 6).

Рис. 6. Прямая и наклонная призмы
Перейдем теперь к пирамидам и начнем с треугольной. В основании пирамиды лежит треугольник. В треугольнике нет параллельных сторон, поэтому основание можно изобразить любым треугольником. В качестве вершины можно выбрать любую точку сверху и соединить её с вершинами треугольника в основании. Невидимое ребро делаем пунктирным. Чаще всего основание пирамиды располагают к нам вершиной, но иногда и наоборот (см. рис. 7). Главное не повернуть пирамиду таким образом, чтобы два ребра оказались очень близко или вообще совпали.
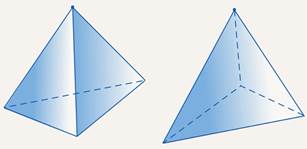
Рис. 7. Треугольные пирамиды
В четырехугольной пирамиде нужно учитывать, что если в основании есть параллельные стороны, то на рисунке они должны остаться параллельными. Так, если в основании квадрат, то мы изображаем параллелограмм. При этом, глядя на уже готовый рисунок, нам не удастся понять, что на самом деле лежит в основании – квадрат, прямоугольник, ромб или произвольный параллелограмм (см. рис. 8). Поэтому в описании фигуры нужно делать соответствующее пояснение.

Рис. 8. Четырехугольная пирамида (основание – квадрат)
Для изображения непараллельных отрезков верно аналогичное утверждение. Непараллельные отрезки изображаются непараллельными. Таким образом, если в основании пирамиды лежит трапеция, то изображена она должна быть в виде именно трапеции – две стороны параллельны, а две – нет (см. рис. 9). Причем, трапеция на рисунке будет не совсем произвольная: отношение длин оснований должно сохраниться.
Это общее правило при изображении пространственных фигур на плоскости: пропорции параллельных отрезков должны сохраняться.
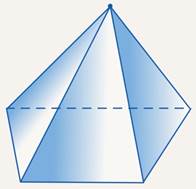
Рис. 9. Четырехугольная пирамида (основание – трапеция)
Кроме многогранников, нужно уметь изображать также тела вращения, границами которых являются кривые линии. Речь идет о конусе, цилиндре и шаре.
С какой бы стороны мы не глядели на шар, мы увидим круг (см. рис. 10). Поэтому рисуем окружность.
Рис. 10. Круг
Чтобы показать трехмерность фигуры, изображаем большой круг – сечение шара плоскостью, проходящей через центр (см. рис. 11).

Рис. 11. Сечение шара плоскостью, проходящей через центр
Если на круг смотреть под углом, мы увидим его как эллипс. Именно так и изображаем большой круг. Ближняя часть большого круга видима, дальняя – нет (см. рис. 12).

interneturok.ru
Элективный курс Сечение в стереометрии
Краснодарский край, г. Славянск-на-Кубани
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 3
имени полководца А. В. Суворова
города Славянска-на-Кубани
муниципального образования Славянский район
УТВЕРЖДЕНОрешением педагогического совета
от 31.08.2017 года протокол № 1
Председатель
________________ Т.Я. Кириллова
РАБОЧАЯ ПРОГРАММА
курса
«Сечения в школьном курсе стереометрии»
Уровень образования (класс): среднее общее образование, 10 — 11классах
Количество часов: 34 часа в 10 классе
34 часа в 11 классе
ИТОГО: 68 часов
Учитель: Контора Евгения Владимировна
Программа разработана на основе: авторской программы элективного курса Дегтяревой З. А. «Сечение в школьном курсе геометрии» 10 класса (Сборник программ и элективных курсов №13. Физико-математический блок. Краснодар, 2006).
Пояснительная записка
Нормативными документами для составления рабочей программы являются:
Авторская программа элективного курса Дегтяревой З. А. «Сечение в школьном курсе геометрии» (Сборник программ и элективных курсов №13. Физико-математический блок. Краснодар, 2006).
Федеральный Закон от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации».
ООП ООО МБОУ СОШ №3 (пр. № 405 от 1.09.2015г.)
Цели курса заключаются в создании условий и возможностей:
уточнить готовность и способность осваивать данный материал на повышенном уровне;
максимально развить познавательные способности учащихся;
расширить представления о методах построения сечения многогранников и способах изображения пространственных фигур на плоскости;
научить ориентироваться в простейших геометрических ситуациях и обнаруживать образы в окружающей обстановке;
Задачи курса:
повышать уровень пространственного воображения учащихся;
показывать геометрию во всей ее многогранности;
развивать творческие способности учащихся.
Общая характеристика учебного предмета
Решение геометрических задач вызывает трудности у многих учащихся. Это объясняется, прежде всего, тем, что редко какая либо задача по геометрии может быть решена с использованием определённой теоремы или формулы. Методы решения геометрических задач обладают некоторыми особенностями, а именно:
большое разнообразие, трудность формального описания;
взаимозаменяемость;
отсутствие чётких границ области применения.
Большинство задач требует применения разнообразных теоретических знаний, доказательства утверждений, справедливых лишь при определенном расположении фигуры, применение различных формул. Приобрести навыки в решении задач можно, лишь решив достаточно большое их количество, ознакомившись с различными методами, приёмами и подходами. Программа для общеобразовательных школ по геометрии не акцентирует внимание на методах решения задач, особенно на их частные случаи. Искусство же решать задачи основывается на хорошем знании теоретической части курса, знании достаточного количества геометрических фактов, в овладении определённым арсеналом приёмов и методов решения геометрических задач.
При изучении стереометрии в 10-11-х классах общеобразовательной школы практически ежеурочно приходится строить чертежи, т. е. изображать на плоскости различные пространственные фигуры, строить сечения. Каждая задача при решении требует определенного навыка со стороны ученика в построении «читаемого» чертежа. На первых этапах изучения стереометрии ученик не умеет читать чертеж «изнутри», не видит взаимосвязи между отдельными элементами той или иной фигуры. Это представляет определенные трудности, как со стороны учителя, так и со стороны ученика. Отдельные учащиеся, оканчивая школу, и поступая в высшие учебные заведения, испытывают трудности при изучении начертательной геометрии, технического черчения и других наук.
Задачам на изображение пространственных фигур на плоскости и построение сечений в школьном курсе геометрии уделяется недостаточное внимание. Поскольку данные задачи составляют базу для работы, развивающей навыки построения, способствующей формированию умения читать и понимать чертеж, устанавливать связи между его частями, то недостаточность этой системы обуславливает недостаточное развитие пространственного мышления ученика, низкий уровень его графической культуры.
Поэтому так важно выработать практические навыки в решении задач на построение. В этом прагматическая функция предлагаемого старшеклассникам курса по выбору. Но по содержанию материала и методам работы с ними, налицо и его развивающая функция.
В процессе геометрических построений учащиеся в практическом плане знакомятся со свойствами фигур и отношений, учатся пользоваться чертежными инструментами, приобретают графические навыки. Так же в процессе построений ученики убеждаются в правильности многих математических утверждений.
Описание места учебного предмета в учебном плане
Учебный курс
Количество часов в неделю
10 класс
2015 – 2016
учебный год
11 класс
2016–2017
учебный год
Сечения в школьном курсе стереометрии
1
1
ИТОГО за год
34
34
Содержание учебного курса
1. Задачи на построение сечения. Вычисление элементов сечения и его площади.
Нахождение точки пересечения прямой с плоскостью Построение линии пересечения двух плоскостей. Сечения тетраэдра. Построение сечений многогранников методом следов. Построение сечений многогранников методом внутреннего проектирования Построение сечений многогранников с помощью теорем стереометрии. Нахождение площади сечений в многогранниках. Использование свойств подобных треугольников.
2. Вычисление расстояний и углов в пространстве.
Понятие расстояния в пространстве. Расстояние от точки до прямой, от точки до плоскости. Расстояние между перпендикулярными, скрещивающимися прямыми.
Основные этапы построения расстояния между скрещивающимися прямыми. Теорема о трех косинусах.
Угол между лучами, между прямыми. Угол между скрещивающимися прямыми. Построение. Вычисление. Применение формулы о трех косинусах. Угол между прямой и плоскостью, между плоскостями. Двугранный угол.
Прием достраивания пирамиды до параллелепипеда при решении задач на вычисление углов и расстояний в пространстве]. Геометрическое место точек пространства, равноудаленных от вершин многоугольника, от сторон многоугольника.
Место доказательства в решении стереометрических задач на вычисление углов и расстояний в пространстве. Правила выполнения выносных чертежей при вычислении углов и расстояний в пространстве. Определение минимального базиса при решении задачи на вычисление расстояний и углов в пространстве.
3. Комбинации тел.
Понятие комбинации тел. Цилиндры, вписанные и описанные около призм. Конусы, вписанные и описанные около пирамид. Комбинации цилиндра и тетраэдра, конуса и призмы.
Сферы, вписанные и описанные около прямых призмы, правильных пирамид. Сферы, вписанные и описанные около произвольных пирамид. Произвольные комбинации сферы с многогранниками. Комбинации серы и правильных многогранников. Каркасные многогранники. Комбинации круглых тел. Выполнение выносных чертежей в решении задач, связанных с комбинациями тел.
4. Объемы и поверхности тел. Избранные вопросы стереометрии.
Высоты тетраэдра. Ортоцентрический тетраэдр. Середины ребер куба. Пирамида. Объем тетраэдра с попарно перпендикулярными боковыми ребрами. Объем тетраэдра по площади двух его граней, их общего ребра и двугранного угла, образованного этими гранями. Об отношении объемов тетраэдров, имеющих по равному трехгранному углу. Прием достраивания тетраэдра до параллелепипеда при вычислении объемов. Задачи на сравнение площадей поверхностей и объемов многогранников. [Теорема Менелая]. Геометрические задачи на отыскание наибольшего и наименьшего значения. Применение тригонометрии в решении стереометрических задач.
Тематическое планирование
Содержание учебного материала10 класс
11 класс
Задачи на построение сечения. Вычисление элементов сечения и его площади.
10
5
Нахождение точки пересечения прямой с плоскостью. Построение линии пересечения двух плоскостей. Сечения тетраэдра. Построение сечений многогранников методом следов. Построение сечений многогранников методом внутреннего проектирования Построение сечений многогранников с помощью теорем стереометрии. Нахождение площади сечений в многогранниках. Использование свойств подобных треугольников.
Вычисление расстояний и углов в пространстве.
5+15
7
Построение и вычисления расстояния от точки до плоскости как длины перпендикуляра, проведенного из этой точки к плоскости.
Расстояние от точки до плоскости как длина перпендикуляра, проведенного из этой точки к плоскости.
Расстояния от точки до плоскости как расстояние от проходящей через данную точку А прямой параллельной данной.
Решение задач по теме: «Расстояние от точки до плоскости».
Решение задач по теме: «Расстояние от точки до плоскости».
Расстояние между перпендикулярными скрещивающимися прямыми.
Построение и вычисление расстояния между скрещивающимися прямыми, если они перпендикулярны.
Расстояние между скрещивающимися прямыми как расстояние между параллельными плоскостями, проходящими через эти прямые
Построение общего перпендикуляра к двум скрещивающимся прямым.
Основные этапы построения расстояния между скрещивающимися прямыми.
Основные этапы построения расстояния между скрещивающимися прямыми
Теорема о трех косинусах
Угол между лучами, между прямыми. Угол между скрещивающимися прямыми. Построение. Вычисление. Применение формулы о трех косинусах. Угол между прямой и плоскостью. Угол между плоскостями. Двугранный угол.
Прием достраивания пирамиды до параллелепипеда при решении задач на вычисление углов и расстояний в пространстве
Место доказательства в решении стереометрических задач на вычисление углов и расстояний в пространстве. Правила выполнения выносных чертежей при вычислении углов и расстояний в пространстве. Определение минимального базиса при решении задачи на вычисление расстояний и углов в пространстве.
Комбинации тел.
11
Понятие комбинации тел. Цилиндры, вписанные и описанные около призм. Конусы, вписанные и описанные около пирамид. Комбинации цилиндра и тетраэдра, конуса и призмы.
Сферы, вписанные и описанные около прямых призмы, правильных пирамид. Сферы, вписанные и описанные около произвольных пирамид. Произвольные комбинации сферы с многогранниками. Комбинации сферы и правильных многогранников. Каркасные многогранники. Комбинации круглых тел. Выполнение выносных чертежей в решении задач, связанных с комбинациями тел.
Объемы и поверхности тел.
Избранные вопросы стереометрии.
4
11
Высоты тетраэдра. Ортоцентрический тетраэдр. Середины ребер куба. Пирамида. Объем тетраэдра с попарно перпендикулярными боковыми ребрами. Объем тетраэдра по площади двух его граней, их общего ребра и двугранного угла, образованного этими гранями. Об отношении объемов тетраэдров, имеющих по равному трехгранному углу. Прием достраивания тетраэдра до параллелепипеда при вычислении объемов. Задачи на сравнение площадей поверхностей и объемов многогранников. [Теорема Менелая]. Геометрические задачи на отыскание наибольшего и наименьшего значения. Применение тригонометрии в решении стереометрических задач
Описание учебно-методического и материально-технического обеспечения образовательной деятельности
Веннинджер М. «Модели многогранников» Издательство «Мир» Москва 1974г.
Литвиненко В. Н. «Задачи на развитие пространственных представлений» Москва
Просвещение 1991г.Углы и расстояния в школьном курсе стереометрии: Методические рекомендации. – Краснодар: Краснодарский экспериментальный центр развития образования, 1991г.
Четвертухин Н. Ф. Стереометрические задачи на проекционном чертеже. М.: Учпедгиз, 1952г.
Семенов А.В. и др. Оптимальный банк заданий для подготовки учащихся. Единый государственный экзамен. Математика. Учебное пособие. / А. В. Семенов, Л. С. Трепалин, И. П. Ященко, П. И. Захаров; под ред. И. В. Ященко; Московский Центр непрерывного математического образования. — М.: Интеллект-Центр, 2015. — 80 с.
Математика. Решение задач повышенной сложности . Как получить максимальный балл на ЕГЭ. А.В. Семенов и др. «Интеллект-Центр», 2015 -128с.
ЕГЭ . Математика. 30 вариантов типовых тестовых заданий и 800 заданий части 2(С). Под ред. Семенова А.Л., Ященко И.В. — М.: 2013 — 216 стр.
Учебно-тренировочные тесты ЕГЭ под редакцией Ф.Ф. Лысенко. Ростов-на-Дону. Издательство «Легион» .2014-2015г.
Классная доска;
Интерактивная доска;
Персональный компьютер;
Мультимедийный проектор;
Интернет-ресурсы:
http://urokimatematiki.ru
http://pedsovet.su/load/18
http://www.fipi.ru
http://festival.1september.ru
http://school—collection.edu.ru
www.reshuege.ru
www.alexlarin.net
Планируемые результаты изучения учебного предмета:
Учащиеся должны иметь представление:
о структуре и содержании курса и его месте в общеобразовательной программе;
о способах построения изображения пространственных фигур на плоскости;
о различных методах построения сечений;
о практическом применении данных задач.
Учащиеся должны знать:
Учащиеся должны уметь:
классифицировать предложенные задачи по методам их решения;
различать заданные элементы и их характеристики;
анализировать и исследовать решения задач.
Учащиеся должны владеть:
СОГЛАСОВАНОПротокол № 1 заседания ШМО учителей
естественно-математического цикла
от «___» августа 2017 г.
_________________
СОГЛАСОВАНО
Заместитель директора по УВР
____________ Л.Г.Беленко
«_____» августа 2017 г.
Раздел№ урока
Тема урока
Даты проведения
Оборудова
ние
план
факт
1. Вычисление расстояний и углов в пространстве.
Построение и вычисления расстояния от точки до плоскости как длины перпендикуляра, проведенного из этой точки к плоскости.
Расстояние от точки до плоскости как длина перпендикуляра, проведенного из этой точки к плоскости.
Расстояния от точки до плоскости как расстояние от проходящей через данную точку А прямой параллельной данной.
Решение задач по теме: «Расстояние от точки до плоскости».
Решение задач по теме: «Расстояние от точки до плоскости».
2. Задачи на построение сечения. Вычисление элементов сечения и его площади.
Нахождение точки пересечения прямой с плоскостью
Построение линии пересечения двух плоскостей.
Сечения тетраэдра.
Построение сечений многогранников методом следов.
Построение сечений многогранников методом внутреннего проектирования
Построение сечений многогранников методом внутреннего проектирования (центральное).
Построение сечений многогранников с помощью теорем стереометрии.
Нахождение площади сечений в многогранниках.
Использование свойств подобных треугольников.
Контрольная работа №1 по теме «Сечения».
1. Вычисление расстояний и углов в пространстве.
Анализ К/Р. Расстояние между перпендикулярными скрещивающимися прямыми.
Построение и вычисление расстояния между скрещивающимися прямыми, если они перпендикулярны.
Расстояние между скрещивающимися прямыми как расстояние между параллельными плоскостями, проходящими через эти прямые.
Построение общего перпендикуляра к двум скрещивающимся прямым.
Основные этапы построения расстояния между скрещивающимися прямыми.
Основные этапы построения расстояния между скрещивающимися прямыми.
Теорема о трех косинусах.
Контрольная работа №2 по теме «Расстояния».
Анализ КР. Угол между лучами, между прямыми.
Угол между скрещивающимися прямыми. Построение. Вычисление.
Угол между скрещивающимися прямыми. Построение. Вычисление.
Применение формулы о трех косинусах. Угол между прямой и плоскостью.
Угол между плоскостями. Двугранный угол.
Решение задач по теме: «Угол между плоскостями. Двугранный угол».
Контрольная работа №3 по теме «Углы».
4. Объемы и поверхности тел. Избранные вопросы стереометрии.
Анализ КР. Высоты тетраэдра. Ортоцентрический тетраэдр. Решение задач.
Середины ребер куба. Решение задач.
Пирамида. Решение задач.
Решение задач ЕГЭ: С-2.
Итого:
34
Практическая часть:
- виды работ
1 чет.
2чет.
3чет.
4чет.
Итого за год
Контрольные работы
0
1
1
1
3
№ урока
Тема урока
Даты проведения
Оборудова
ние
план
факт
2. Задачи на построение сечения. Вычисление элементов сечения и его площади.
Решение задач на построение сечений многогранников с условиями параллельности.
01.09
Решение задач на построение сечений многогранников с условиями перпендикулярности.
08.09
Решение задач на построение сечений
15.09
Приемы вычисления элементов сечения, его периметра и площади.
22.09
Вычисление периметра и площади сечения. Решение задач.
29.09
1. Вычисление
расстояний и
углов в пространстве
Вычисление расстояний в пространстве
06.10
Вычисление углов в пространстве
13.10
Прием достраивания пирамиды до параллелепипеда при решении задач на вычисление углов и расстояний в пространстве
20.10
Место доказательства в решении стереометрических задач на вычисление углов и расстояний в пространстве
27.10
Правила выполнения выносных чертежей при вычислении углов и расстояний в пространстве.
10.11
Определение минимального базиса при решении задачи на вычисление расстояний и углов в пространстве.
17.11
Контрольная работа №1 по теме: «Вычисление элементов сечений. Расстояний и углов в пространстве»
24.11
3.Комбинации тел.
Анализ контрольной работы.
Понятие комбинации тел.
01.12
Цилиндры, вписанные и описанные около призм.
08.12
Конусы, вписанные и описанные около пирамид.
15.12
Комбинации цилиндра и тетраэдра, конуса и призмы.
22.12
Сферы, вписанные и описанные около прямых призмы, правильных пирамид.
12.01
Сферы, вписанные и описанные около произвольных пирамид.
19.01
Произвольные комбинации сферы с многогранниками.
26.01
Комбинации сферы и правильных многогранников.
02.02
Каркасные многогранники. Комбинации круглых тел.
09.02
Выполнение выносных чертежей в решении задач, связанных с комбинациями тел.
16.02
Контрольная работа №2 по теме: «Комбинации тел.»
23.02
4. Объемы и поверхности тел. Избранные вопросы стереометрии
Анализ контрольной работы. Пирамида.
01.03
Объем тетраэдра с попарно перпендикулярными боковыми ребрами.
08.03
Объем тетраэдра по площади двух его граней, их общего ребра и двугранного угла, образованного
15.03
Об отношении объемов тетраэдров, имеющих по равному трехгранному углу.
29.03
Прием достраивания тетраэдра до параллелепипеда при вычислении объемов.
05.04
Задачи на сравнение площадей поверхностей и объемов многогранников.
12.04
Геометрические задачи на отыскание наибольшего и наименьшего значения.
19.04
Применение тригонометрии в решении стереометрических задач.
26.04
Контрольная работа №3 по теме: «Объемы и поверхности тел. Избранные вопросы стереометрии»
03.05.
Анализ контрольной работы.
Решение задач ЕГЭ № 17
10.05
Решение задач ЕГЭ № 17
17.05
Итого:
34
Практическая часть:
- виды работ
1 чет.
2чет.
3чет.
4чет.
Итого за год
Контрольные работы
0
1
1
1
3
infourok.ru
Объекты в стереометрии. Профильный уровень. Видеоурок. Геометрия 10 Класс
В планиметрии мы изучали свойства плоских фигур. Хотя в природе их не найдешь – любой объект объёмный. Почему же мы так много времени уделили плоским фигурам, которых не существует в окружающем мире?
Есть природа, а есть модели природных объектов, которые у нас получается исследовать – отрезки, углы, фигуры. Они, в свою очередь, являются элементами объёмных тел. Изучив подробно свойства плоских фигур, теперь мы сможем применять полученные знания для исследования тел в пространстве.
Кирпич имеет форму параллелепипеда, а его грани – форму прямоугольника. Бревно имеет форму цилиндра, а спил (сечение) – форму круга, если спил сделан перпендикулярно оси бревна, и эллипса, если под углом.
То есть переход от планиметрии к стереометрии – это расширение математической модели, а не замена одной на другую.
В планиметрии с изображением фигур было все просто: лист бумаги, по сути, представлял плоскость, и изобразить на нём плоскую фигуру (например, квадрат со стороной а) не составляло труда.
В стереометрии мы будем объёмные фигуры изображать на плоскости, что потребует от нас определенных навыков.
Особенности нашего зрения
Мы привыкли доверять своим глазам и не задаемся вопросом, почему один и тот же объект вблизи выглядит крупнее, чем вдали? Или почему разные по величине предметы порой кажутся одного размера? Механизмы зрения довольно сложны, однако некоторые его особенности можно объяснить на основе геометрических представлений.
Всякий предмет имеет линейные размеры: длину, ширину и высоту. Но как только он попадает в наше поле зрения, то приобретает еще один размер – угловой. Давайте разберемся, что это означает. Когда мы смотрим на предмет, то через каждую его точку можно провести от глаза луч, называемый лучом зрения. Понятно, что их будет бесконечно много. Любые два луча зрения образуют угол зрения (см. рис. 1).

Рис. 1. Угол зрения
Тот угол зрения, под которым предмет виден целиком, и принято называть угловым размером предмета. Как и всякий плоский угол, он измеряется в градусах, минутах, секундах или в радианах.
Угловой размер предмета – величина не постоянная и зависит от расстояния предмета от глаза: чем предмет дальше, тем меньше угол зрения, под которым он виден.
Чтобы понять причину этого явления, вспомним, что на сетчатке глаза изображение предмета получается обратным и уменьшенным. При удалении предмета его изображение на сетчатке становится меньше, поэтому он и кажется нам уменьшающимся (см. рис. 2). При сокращении расстояния изображение, напротив, увеличивается, и предмет кажется увеличивающимся (см. рис. 3).

Рис. 2. Предмет кажется уменьшающимся при его удалении

Рис. 3. Предмет кажется увеличивающимся при его приближении
Теперь легко объяснить, почему две «убегающие» вдаль параллельные линии (железнодорожные рельсы, края прямолинейного шоссе) кажутся «сходящимися» в одной точке (см. рис. 4). Такое же впечатление создают ряды телеграфных столбов или деревьев вдоль дороги. Это лишь иллюзия, которая возникает из-за видимого уменьшения расстояния между прямыми по мере их удаления.

Рис. 4. Железнодорожные рельсы кажутся «сходящимися» в одной точк
interneturok.ru
ЭОР «Построение сечений в многогранниках методом следов». Геометрия. 10 класс
Учитель математики: Романова Т.А.
МОУ Надеждинская сош Кошкинского района
17 ноября 2009г.
Цели урока:
Формирование у учащихся навыков решения задач на построение сечений методом следов.
Формирование и развитие у учащихся пространственного воображения.
Развитие графической культуры и математической речи.
Обучающая цель: формирование умений и навыков построения сечений методом следов.
Воспитывающая цель: воспитывать чувство сплоченности, взаимопомощи, воспитывать умения работать индивидуально над задачей.
Тип урока: урок формирования и совершенствования знаний.
Формы организации учебной деятельности: индивидуальная, коллективная.
Техническое обеспечение урока: компьютер, мультимедийный проектор, набор геометрических тел (куб, параллелепипед, пирамида).
Структура урока:

Ход урока
Организационный момент.
Слово учителя. Ребята, я предлагаю вам повторить и вспомнить некоторые геометрические понятия и определения.
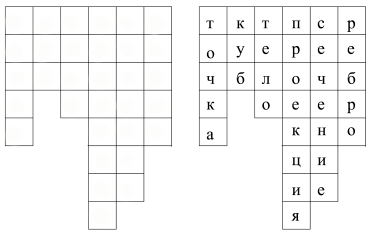
Основное понятие геометрии – место пересечения двух прямых, не имеющее измерения.
Геометрическая фигура, состоящая из шести квадратных граней.
Отдельный предмет в пространстве.
Способ изображения пространственных фигур на плоскость.
Плоская фигура, образуемая пересечением тела плоскостью.
Сторона грани многогранника.
Многогранник, поверхность которого состоит из четырех треугольников.
Ответы:
1. Точка 2. Куб 3. Тело 4. Проекция 5. Сечение 6. Ребро 7. Тетраэдр
Слово учителя: А теперь давайте все вместе назовем тему нашего урока!…. Правильно! Тема нашего урока: «Построение сечений» . А еще конкретнее, « Построение сеченийв многогранниках методом следов»
Слово учителя: Вы изучили аксиомы стереометрии, следствия из аксиом, теоремы о параллельности прямых и плоскостей в пространстве. При решении многих стереометрических задач используют сечение многогранника плоскостью. Существует несколько методов построения сечений многогранника плоскостью: метод следов, метод внутреннего проектирования и комбинированный метод. Мы изучим метод следов.
На уроках черчения вы пользовались определением: Сечение – это изображение фигуры, которая получается при мысленном рассечении тела плоскостью. Вот таким определением мы и будем пользоваться сегодня на уроке. (См. слайды 3, 4)

В тетраэдре сечениями могут быть только треугольники или четырехугольники, а в параллелепипеде – треугольники, четырехугольники, пятиугольники или шестиугольники.
Метод следов включает три важных пункта:
Строится линия пересечения (след) секущей плоскости с плоскостью основания многогранника.
Находим точки пересечения секущей плоскости с ребрами многогранника.
Строим и заштриховываем сечение.
Рассмотрим пример (мультимедийный проектор).

Решить задачу № 79 из учебника.
Рассмотреть по слайдам еще 2 примера построения сечений тетраэдра
Задание №1 Построить сечение тетраэдра плоскостью, проходящей через точки K, M, N
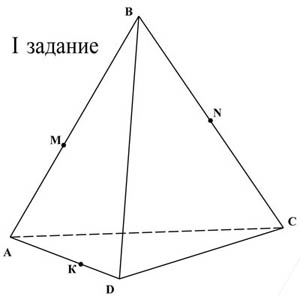

Ответ
Слово учителя: Ребята, перед вами пример неправильного построения сечения куба АBCDA1B1C1D1 плоскостью, проходящей через заданные точки N, C, D1. А рядом сечение построено верно.
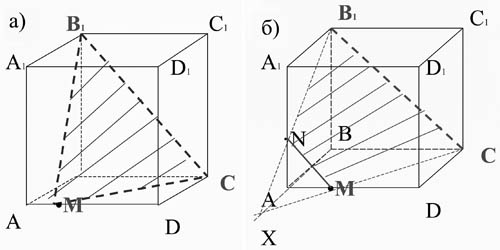
Задание № 2 : Построить сечение куба, проходящее через точки М, N, L.
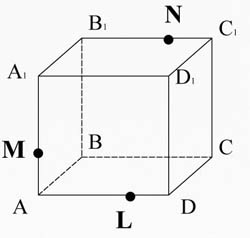
Алгоритм построения
1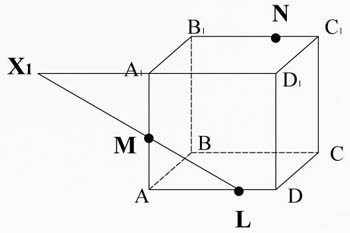
2)
)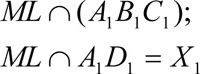
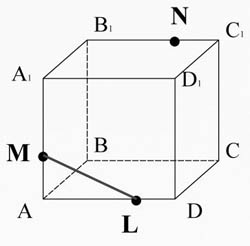
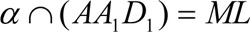
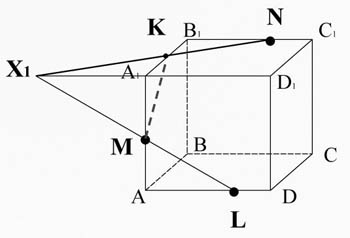
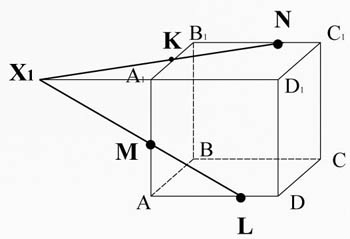
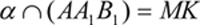
3)
4)
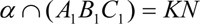
5)
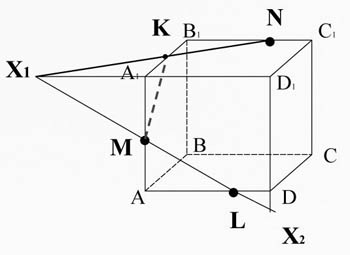
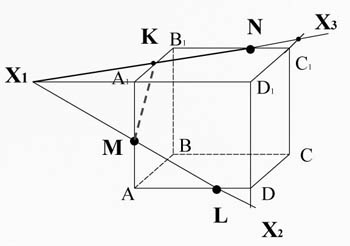
6)
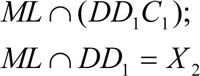
7)
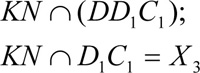
7)
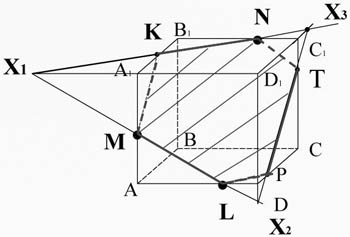
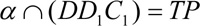
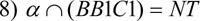
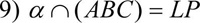
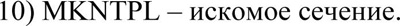
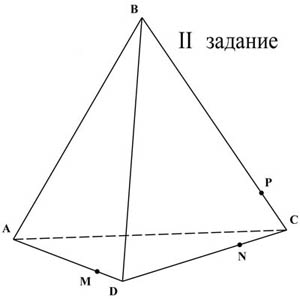 Домашнее задание:
Домашнее задание:
п.14, № 80 и задание № 2
(построить на полученных листочках сечение тетраэдра)
Подвести итог урока.
Что называется сечением?
Что может получится в результате сечения тетраэдра?
— параллелепипеда?
Как построить сечение методом следов?
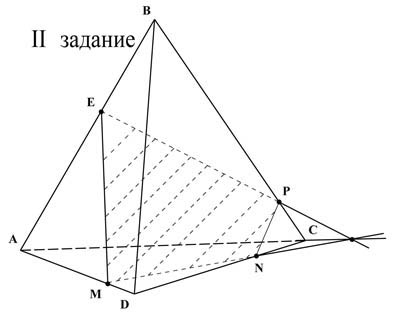
Ответ
infourok.ru