Первый закон Ньютона. Инерциальные системы отсчета. Видеоурок. Физика 10 Класс
В кинематике мы рассматривали, как движется то или иное тело, могли рассчитать ускорение автомобиля, время перемещения грузика, но мы никогда не задумывались – а почему движется тело тем или иным образом? Раздел физики, который изучает причину движения тела, называется динамика. Тема урока: «Первый закон Ньютона».
Динамика изучает причины, по которым тело начинает двигаться, начинает изменять свою скорость. А при каких же состояниях тело находится в состоянии покоя, когда его скорость равна нулю? Какие условия необходимы для равномерного прямолинейного движения, когда скорость постоянна?
Нарисуем схематически тело, находящееся в состоянии покоя (рис. 1).

Рис. 1. Тело находится в состоянии покоя
Тело подвешено на нити к штативу, тело находится в состоянии покоя, то есть его скорость равна нулю. Какие тела действуют на этот шарик? Это Земля – притяжение Земли и натяжение нити. Получается, что притяжение Земли и натяжение нити взаимно компенсируют друг друга, 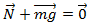 , то есть тело находится в состоянии покоя, если действие на него других тел скомпенсировано.
, то есть тело находится в состоянии покоя, если действие на него других тел скомпенсировано.
Если бы шарик находился в состоянии покоя в безвоздушном пространстве, в вакууме, где на него вообще ничего не действует, то он бы тоже находился в состоянии покоя.
Тело находится в состоянии покоя, если действия на него других сил скомпенсированы или на него ничего не действует.
Перейдем к состоянию равномерного прямолинейного движения. При каких же условиях скорость тела остается константой?
Рассмотрим случай, в котором тело движется по абсолютно гладкой поверхности и полностью отсутствует сопротивление воздуха (рис. 2).
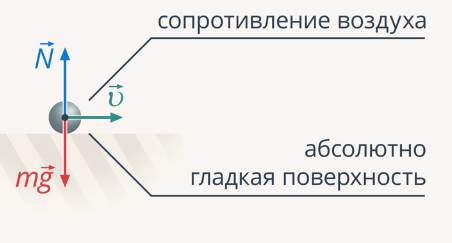
Рис. 2. Равномерное прямолинейное движение
При отсутствии сопротивления воздуха и сил трения тело никогда не остановится, его скорость будет оставаться постоянной. Это значит, что тело находится в состоянии равномерного прямолинейного движения, на тело действует только Земля и сила реакции опоры, но на движение тела в горизонтальном направлении они никакого влияния не оказывают.
Аристотель считал, что для того, чтобы тело двигалось с постоянной скоростью, необходимо на него оказать действие другими телами. Действие других тел на исследуемое тело – это причина наличия у него скорости, считал Аристотель. Галилей впервые указал, что действие на тело других тел – это не причина наличия у тела скорости, а причина изменения скорости, то есть появление у тела ускорения.
Для того чтобы тело находилось в состоянии покоя или двигалось равномерно и прямолинейно, необходимо выполнение одинаковых условий: либо на тело ничего не действует, либо действие на него других тел скомпенсировано.
Движение – это понятие относительное. Во всех ли системах отсчета справедливо утверждение про состояние покоя и равномерное прямолинейное движение?
Рассмотрим следующую ситуацию. Петр стоит на улице и наблюдает за движением железнодорожного вагона. В вагоне сидит Степан и смотрит на яблоко, которое лежит на столе. В какой-то момент вагон начинает разгоняться, то есть его скорость возрастает (появляется ускорение). В этот момент яблоко по инерции покатится назад (рис. 3).

Рис. 3. Иллюстрация к примеру
В системе отсчета Петра яблоко движется также в сторону движения поезда, только чуть медленнее, чем сам поезд, под действием силы трения, возникающей между столом и яблоком. По инерции оно стремится сохранить состояние покоя. Если вагон разгоняется плавно, так что Степан не замечает этого, то для него произошло чудо и яблоко покатилось без причины. Хотя речь идет об одинаковых явлениях. Отсюда можно понять, что сделанные ранее выводы справедливы не для всех систем отсчета. СО наподобие СО, связанной с Петром, называются инерциальными, а наподобие СО, связанной со Степаном, – неинерциальными.
Инерциальная система отсчета – СО, в которой тело находится в состоянии покоя или движется равномерно и прямолинейно. Сформулируем первый закон Ньютона.
Существуют такие системы отсчета, в которых тело находится в состоянии покоя или равномерного и прямолинейного движения, если на это тело не действуют другие тела или их действие взаимно скомпенсировано.
Ветка. Точка зрения Аристотеля на причину движения
Инерциальная система отсчета – это очень удобная модель для описания движения тела и причин, которые вызывают такое движение. Физика не всегда пользовалась понятием «инерциальная система отсчета», впервые это понятие появилось благодаря Исааку Ньютону. Древние греки представляли себе движение совсем по-иному.
Согласно Аристотелю, существует единственная инерциальная система отсчета, эта система отсчета связана с Землей. Все остальные системы отсчета второстепенны. Соответственно, все движения, которые получает тело, относительно Земли называются

Рис. 4. Принудительное движение по Аристотелю
Пока лошадь прилагает силу, телега движется, как только лошадь остановилась, то останавливается и телега – нет силы, нет и скорости. Согласно Аристотелю, именно сила объясняет у тела наличие скорости. Казалось бы, все настолько очевидно, что никаких вопросов быть не должно. Однако были и критики, которые предлагали проделать некие эксперименты. Если взять в руку указку, а затем ее отпустить, то она упадет точно под тем местом где мы ее отпустили. Но если бомбардировщик сбрасывает бомбу, то она упадет немного дальше то того места, где ее сбросили (рис. 5). Но ведь это естественное движение, которое сообщилось Землей. Что же заставляет эту бомбу перемещаться немного вперед?

Рис. 5. Пример критики Аристотеля
На что Аристотель отвечал, что при падении бомбы она увлекается потоками воздуха, которые толкают ее немного вперед. Тогда у критиков возник еще один вопрос: «Что же будет если откачать воздух? Упадет и тогда бомба четко под местом выброса?». На данный вопрос Аристотель отвечал, что при отсутствии воздуха такое возможно, но в природе не бывает пустоты (вакуума не существует).[М1]
Галилео Галилей сформулировал принцип инерции: причина изменения скорости – это действие на тело других тел. Если на тело не действуют другие тела или это действие скомпенсировано, то скорость тела меняться не будет. Предпочтительным состоянием тела является не только покой, но и равномерное прямолинейное движение.
Ветка. Почему Земля – неинерциальная система отсчета. Маятник Фуко
Во многих задачах мы рассматриваем движение тела относительно Земли, негласно мы считаем, что Земля – инерциальная система отсчета. Так ли это на самом деле? Оказывается, не всегда. Если рассматривать движение Земли относительно своей оси или движение Земли относительно звезд, то это движение совершается с некоторым ускорением. Система отсчета, которая движется с некоторым ускорением, не может считаться инерциальной в полном смысле. Что же это за ускорение, которое появляется у Земли при вращении вокруг своей оси, так ли оно велико, и можно ли считать Землю инерциальной системой отсчета?
Земля вращается вокруг своей оси, значит, все точки, лежащие на ее поверхности, непрерывно меняют направление своей скорости (рис. 6).

Рис. 6. Направление скорости точек поверхности Земли при ее вращении
Скорость – это вектор, и, если его направление меняется, значит, у нас появляется некое ускорение. Значит, Земля условно должна быть выведена из состава инерциальных систем отсчета. Если подсчитать это ускорение для точек, находящихся на экваторе, а это точки, обладающие максимальным ускорением по сравнению с точками, находящимися ближе к полюсу, то его значение получится:  .
.
Индекс «с» говорит о том, что это ускорение центростремительное. Сравним с ускорением свободного падения:  .
.
Разница в несколько сотен раз, конечно же, этим ускорением в принципе можно пренебрегать и считать Землю инерциальной системой отсчета. Однако при длительных наблюдениях забывать о вращении Земли, конечно же, нельзя. Убедительно это доказал французский ученый Жан Бернар Леон Фуко.
Маятник Фуко представляет собой массивный груз, подвешенный на очень длинной нити. Выведем такой груз из положения равновесия и посмотрим, как он будет колебаться в течение долгого времени, какую траекторию будет описывать (рис. 7).

Рис. 7. Траектория колебаний маятника Фуко, вид сверху
Траектория колебания маятника не будет прямой, она будет смещаться, это смещение маятника обусловлено вращением Земли, смещение траектории колебаний груза, подвешенного на длинной нити.
Ветка. К вопросу о формулировке первого закона Ньютона
Иногда можно столкнуться с формулировкой первого закона Ньютона:
Если на тело не действуют никакие тела либо их действие взаимно уравновешено (скомпенсировано), то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно, то есть сохранять свою скорость.
Всегда ли это выражение корректно? Рассмотрим следующую ситуацию (рис. 8).

Рис. 8. Инерциальная и неинерциальная системы отсчета
Вагон поезда, у которого занавешены все окна, то есть пассажир поезда не видит, движется поезд относительно тел, находящихся на улице или нет. У нас две системы отсчета – система отсчета пассажира Володи и система отсчета наблюдателя на земле Кати. Поезд начинает ускоряться, то есть скорость его увеличивается. Что произойдет с яблоком, которое лежит на столике поезда? Яблоко по инерции покатится в противоположную сторону. Володя не видит, что поезд начал разгоняться, и вдруг яблоко, которое находилось в состоянии покоя, начинает на него катиться. Он в недоумении, ведь на яблоко не действовали никакие силы. У Володи возникает вопрос: может, механика Ньютона несправедлива, ведь яблоко находилось в состоянии покоя? У Кати такого вопроса не возникает, ведь тело движется по инерции. Поэтому мы можем сформулировать первый закон Ньютона более корректно:
Существуют такие системы отсчета, в которых тело сохраняет состояние покоя либо будет двигаться равномерно и прямолинейно, если на него не действуют другие тела или действие других тел скомпенсировано.
Эта формулировка позволяет избежать коллизии между Володей и Катей; не обязательно быть в системе, в которой такая ситуация наблюдается: Володя находится в системе, в которой эта ситуация не сохраняется, значит, он находится в неинерциальной системе отсчета. Катя находится в инерциальной системе отсчета – коллизия разрешена.
Вращением Земли обусловлен еще ряд интересных факторов: в реках северного полушария правый берег более крутой, а левый более пологий. В реках южного полушария наоборот.
В большинстве случаев мы будем считать Землю инерциальной системой отсчета, применять в ней законы Ньютона и выяснять, почему же движется тело.
Список литературы
Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Мнемозина, 2014.
Кикоин И.К., Кикоин А.К. Физика – 9, Москва, Просвещение, 1990.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Интернет-портал Fizika.in (Источник).
Интернет-портал Shpargalka.kz (Источник).
Интернет-портал Reftrend.ru (Источник).
Домашнее задание
Дать определение первому закону Ньютона.
Какие системы отсчета существуют?
[М1]У меня вопрос, как мог Аристотель отвечать про бомбу? В Древней Греции не было бомбардировщиков. Эта параллель некорректна.
Первый закон Ньютона ℹ️ определение для инерциальных систем отсчета, формула и формулировка, условия применения, примеры действия правила

Общая информация
В физике всего три закона, или правила, Ньютона, которые являются основой классической механики. Они используются для описания более сложных процессов, а также решения задач. Учащимся требуется знать кратко три закона Ньютона:

- Первый связан с инерциальными системами отсчета.
- Второй утверждает зависимость ускорения от силы воздействия на физическое тело.
- Третий определяет взаимосвязь сил, действующих на объект.
Правила были впервые сформулированы ученым Исааком Ньютоном в XVII веке. Классическая механика являлась основной парадигмой до XX века, пока Альберт Эйнштейн не сформулировал положения релятивистской динамики.
Положения трех законов были выведены опытным путем. Они применяются для объектов, скорости которых намного меньше, чем 3*108 м/с. Перед изучением законов Ньютона нужно ознакомиться с основными положениями динамики.
Основные положения
Тело двигается равномерно, равноускоренно, прямолинейно или находится в состоянии покоя (находится в одной точке). При равномерном и прямолинейном движении скорость объекта является постоянной величиной в пространстве, т. е. не изменяется с течением времени. Если скорость меняется, то тело движется равноускоренно. Когда тело без движения, на него действуют силы, равные по модулю и противоположны по направлению.
Динамика — раздел физики, который изучает правила и законы взаимодействия объектов в целом. В этом случае не рассматривается такие взаимодействия:
- Атомарные.
- Молекулярные.
- Субатомные.
Они не влияют на динамику движения объекта, поскольку силы, действующие на тело, настолько малы, что ими можно пренебречь. Далее следует рассмотреть законы И. Ньютона и формулы.
Первый закон
Чтобы понять назначение и применение I закона Ньютона, следует представить тело, находящееся в состоянии покоя, т. е. на него не действуют другие объекты. Этот пример является простейшей системой механического типа. Если предположить существование другого объекта, который движется под воздействием внешних сил, относительно искомого тела.
Центром системы отсчета для движущегося объекта является тело, скорость которого равна 0 (v = 0). Первый закон Ньютона формулируется следующим образом: в инерциальных системах отсчета (ИСО) тела двигаются равномерно и прямолинейно, а также могут находиться в состоянии покоя, когда они не взаимодействуют с другими телами или на них не действуют внешние силы (их действие может быть скомпенсировано).

У I правила Ньютона существует другое название — закон инерции. Системы отсчета, находящиеся у поверхности Земного шара, являются инерциальными. При проведении экспериментов следует учитывать различные отклонения от I закона Ньютона. Они связаны с ее вращением вокруг оси.
За ИСО можно принять гелиоцентрическую систему, начальные координаты которой помещены в центр Солнца. Ее И. Ньютон использовал для открытия закона Всемирного тяготения. Кроме того, автобус, который движется равномерно и прямолинейно, также является ИСО. Чтобы новичкам было понятно, нужно руководствоваться таким правилом: любая система считается инерциальной, когда ее центр движется равномерно и прямолинейно или ее v = 0.
Однако скорость тела изменяется, поскольку оно может взаимодействовать с другими телами, передавая им кинетическую энергию. Для описания этого процесса нужно разобрать влияние массы и силы на изменение величины скорости объекта.
Понятие массы
Основная формулировка массы имеет такой вид: физическая величина, которая является мерой инертности физического тела. Она обладает скалярностью и аддитивностью. В первом случае выражается одним действительным неотрицательным числом. Второй термин означает следующее: общая масса тела (m), состоящего из нескольких частей с массами m1, m2, m3 и m4, эквивалентна их сумме. Формула записывается следующим образом: m = m1 + m2 + m3 + m4.
При большей массе инертность физического объекта возрастает. Например, пластмассовую машинку легче остановить, чем груженый грузовик или легковую машину, т. е. инертность последних намного больше первой. Единица измерения массы — кг.

При взаимодействии тела приобретают некоторые физические величины, называемые ускорением. Массы обратно пропорциональны ускорениям. Для понимания процесса нужно разобрать следующий пример: машина с массой m1 столкнулась с объектом, масса которого m2. В результате этого появляются ускорения a1 и a2 для первого и второго объектов. Это можно записать таким образом: m1 * m2 = — a2 * a1. Минус перед ускорениями означает направленность по разным направлениям.
Величина силы
Сила — векторная величина, действующая на физическое тело и влияющая на скорость его перемещения в пространстве. Обозначается она буквой F и измеряется в ньютонах (Н) при помощи специального прибора — динамометра. Последний состоит из пружины, связанной со стрелочным указателем. Если пружину растянуть, то произойдет отклонение стрелки, которая указывает количественную характеристику F.
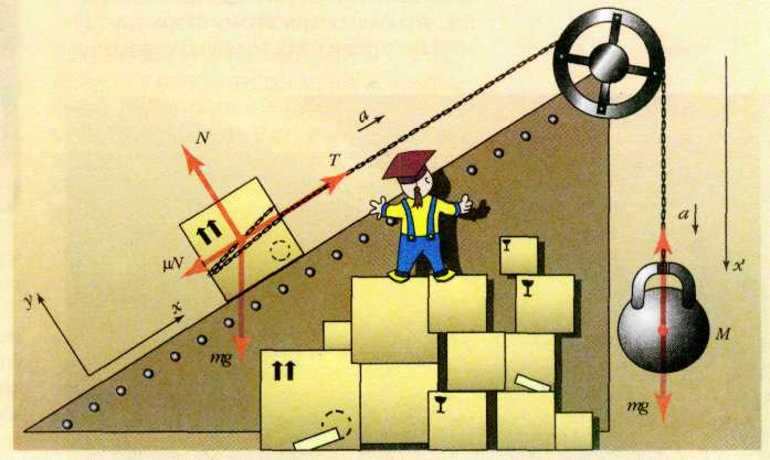
Следует отметить, что на объект может действовать несколько сил, которые учитываются при решении задач и исследовании некоторых процессов. Они имеют важную особенность — природу возникновения. Например, на автомобиль действует F, состоящая из следующих элементов (сил):
- Тяги (Fтяг = m * a), направленной в сторону движения.
- Трения (Fтр = a * m * g, а — коэффициент трения и g — ускорение свободного падения 9,81 м/с 2 ) — противоположно относительно Fт.
- Реакция опоры (N = m * g) — вверх, относительно дороги.
- Тяжести (Fт = m * g) — вниз.
В литературе по физике используется термин «равнодействующая сила». Он означает значение векторной суммы всех составляющих, действующих на объект.
Таким образом, I закон Ньютона применяется при исследовании движения и взаимодействия физических тел, а также для расчета инерциальных составляющих посредством разделения силы на составляющие элементы.
Законы Ньютона: кратко и понятно о формулах и формулировках на конкретных примерах
В школьном курсе физики изучаются три закона Ньютона, являющиеся основой классической механики. Сегодня с ними знаком каждый школьник, но во времена великого ученого подобные открытия считались революционными. Законы Ньютона, кратко и понятно будут описаны ниже, они помогают не только понять основу механики и взаимодействия объектов, но и помогают записать данные в качестве уравнения.
Вводная информация
Впервые три закона Иссак Ньютон описал в труде «Математические начала натуральной философии» (1867 год), в котором были подробно изложены не только собственные выводы ученого, но все знания по этой теме открытые другими философами и математиками. Таким образом, труд стал фундаментальным в истории механики, а позднее и физики. В нем рассмотрены перемещение и взаимодействие массивных тел.
Интересно знать! Исаак Ньютон был не только талантливым физиком, математиком и астрономом, но и считался гением в механике. Занимал должность президента королевского общества Лондона.
 Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).
Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).
Именно это упрощение позволило проигнорировать естественные физические явления: воздушное сопротивление, трение, температуру или другие физические показатели объекта.
Полученные данные могли быть описаны только по времени, массе или длине. Именно из-за этого формулировки Ньютона обеспечивают лишь подходящие, но приближенные значения, которые нельзя использовать для описания точной реакции крупных или изменяемых по форме объектов.
Перемещение массивных предметов, которые участвуют в определениях, принято исчислять в инерциальной системе отсчета, представленной в виде системы координат из трех измерений, и при этом она не увеличивает свою скорость и не оборачивается вокруг своей оси.
Ее часто называют системой отсчета Ньютона, но при этом ученый никогда не создавал и не использовал подобной системы, а использовал нерациональную. Именно в этой системе тела могут двигаться так, как описывает это Ньютон.
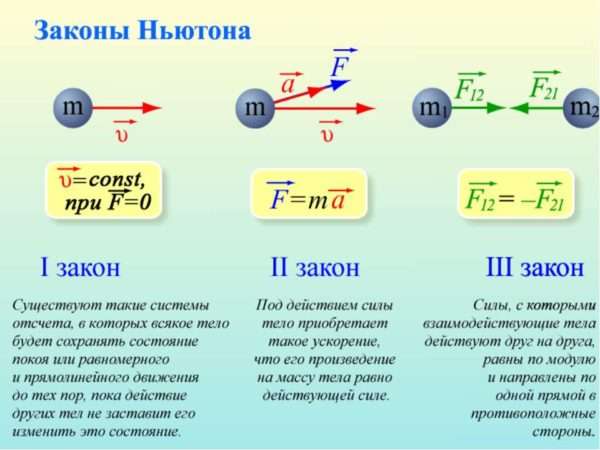
Первый закон
Называется законом инерции. Не существует его практической формулы, зато есть несколько формулировок. В учебниках по физике предлагается следующая формулировка первого закона Ньютона: есть инерциальные системы отсчета, в отношении которых объект, если он свободен от воздействия любых сил (или же они моментально компенсируется), находиться в полном покое или же двигается по прямой и с одинаковой скоростью. Что означает данное определение и как его понять?
Простыми словами первый закон Ньютона объясняется так: любое тело, если его не трогать и никоим образом не воздействовать на него, будет оставаться постоянно в состоянии покоя, то есть бесконечно стоять на месте. То же самое происходит и при его движении: оно будет равномерно двигаться по заданной траектории бесконечно, пока на него не воздействует что-либо.
Подобное утверждение озвучивал Галилео Галилей, но не смог уточнить и точно описать это явление. В этой формулировке важно правильно понять, что такое инерциальные системы отсчета. Если сказать совсем простыми словами, то это система, в которой выполняется действие данного определения.
Это интересно! Изучаем термины: энтропия – что же это такое простыми словами
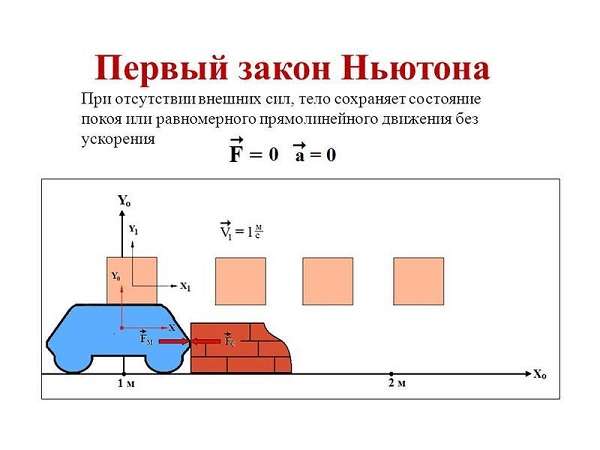 Первый закон Ньютона
Первый закон Ньютона
В мире можно увидеть огромное множество подобных систем, если понаблюдать за движением:
- поезда на заданном участке с одинаковой скоростью,
- Луны вокруг Земли,
- колеса обозрения в парке.
Это интересно! Как правильно перевести МПА атмосферы
В качестве примера рассмотрим некоего парашютиста, который уже раскрыл парашют и движется прямолинейно и при этом равномерно по отношению к поверхности Земли. Движение человека не прекратиться до тех пор, пока земное притяжение будет компенсироваться движением и сопротивлением воздуха. Как только это сопротивление уменьшится, то притяжение увеличится, что приведет к изменению скорости парашютиста – его движение станет прямолинейным и равноускоренным.
Именно в отношении этой формулировки существует яблочная легенда: Исаак отдыхал в саду под яблоней и размышлял о физических явлениях, когда с дерева сорвалось спелое яблоко и упало в траву. Именно ровное падение заставило ученого изучить этот вопрос и выдать в итоге научное объяснение движению предмета в некой системе отсчета.
Интересно знать! Помимо трех явлений в механике, Исаак Ньютон также объяснил движение Луны как спутника Земли, создал корпускулярную теорию света и разложил радугу на 7 цветов.
Второй закон
 Данное научное обоснование касается не просто движения предметов в пространстве, а взаимодействия их с другими объектами и результатов этого процесса.
Данное научное обоснование касается не просто движения предметов в пространстве, а взаимодействия их с другими объектами и результатов этого процесса.
Закон гласит: увеличение скорости объекта с некоторой постоянной массой в инерциальной системе отсчета прямо пропорционально силе воздействия и обратно пропорционально постоянной массе движущегося предмета.
Проще говоря, если существует некое движущиеся тело, масса которого не изменяется, и на него вдруг начнет воздействовать посторонняя сила, то оно начнет ускоряться. А вот скорость ускорения будет прямо зависеть от воздействия и обратно пропорционально зависеть от массы движущегося предмета.
Для примера можно рассмотреть снеговой шар, который катиться с горы. Если шар толкать по ходу движения, то ускорения шара будет зависеть от мощности воздействия: чем она больше, тем больше ускорение. Но, чем больше масса данного шара, тем меньше будет ускорение. Данное явление описывается формулой, в которой учитывается ускорение, или «a», равнодействующая масса всех воздействующих сил, или «F», а также масса самого предмета, или «m»:
а = F/m
Следует уточнить, что данная формула может существовать только в том случае, если равнодействующая всех сил не меньше и не равна нулю. Применяется закон только относительно тел, которые двигаются со скоростью меньше световой.
Это интересно! Квантовые постулаты Нильса Бора: кратко об основных положениях
Полезное видео: первый и второй законы Ньютона
Третий закон
 Многие слышали выражение: «На каждое действие есть свое противодействие». Его часто используют не только в общеобразовательных целях, но и воспитательных, объясняя, что на каждую силу найдется большая.
Многие слышали выражение: «На каждое действие есть свое противодействие». Его часто используют не только в общеобразовательных целях, но и воспитательных, объясняя, что на каждую силу найдется большая.
Эта формулировка пошла от очередного научного утверждения Исаака Ньютона, а точнее его третьего закона, который объясняет взаимодействие различных сил в природе относительно какого-либо тела.
Третий закон Ньютона определение имеет такое: предметы оказывают воздействие друг на друга с силами одинаковой природы (соединяющей массы предметов и направлены вдоль прямой), которые равны по своим модулям и при этом направлены в разные стороны. Данная формулировка звучит достаточно сложно, но простыми словами объяснить закон легко: каждая сила имеет свое противодействие или равную силу, направленную в обратную сторону.
Гораздо проще будет понять смысл закона, если в качестве примера взять пушку, из которой стреляют ядрами. Пушка воздействует на снаряд с той же силой, с которой снаряд воздействует на пушку. Подтверждением этого будет небольшое движение пушки назад во время выстрела, что подтвердит воздействие ядра на орудие. Если взять как пример тоже самое яблоко, которое падает на землю, то станет понятно, что яблоко и земля воздействуют друг на друга с равной силой.
Это интересно! В чем заключается принцип теории Гюйгенса Френеля
Закон имеет также математическое определение, в котором используется сила первого тела (F1) и второго (F2):
F1 = -F2
Знак минуса сообщает о том, что векторы сил двух разных тел направлены в противоположные стороны. При этом важно помнить, что данные силы не компенсируют друг друга, поскольку направлены относительно двух тел, а не одного.
Полезное видео: 3 закона Ньютона на примере велосипеда
Вывод
Данные законы Ньютона кратко и четко необходимо знать каждому взрослому человеку, поскольку они являются основой механики и действуют в повседневной жизни, несмотря на то, что не при всех условиях данные закономерности соблюдаются. Они стали аксиомами в классической механике, и на основе их были созданы уравнения движения и энергии (сохранение импульса и сохранение механической энергии).
Законы Ньютона — это… Что такое Законы Ньютона?
Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год).
Первый закон Ньютона
Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.
Современная формулировка
В современной физике первый закон Ньютона принято формулировать в следующем виде[1]:
Закон верен также в ситуации, когда внешние воздействия присутствуют, но взаимно компенсируются (это следует из 2-го закона Ньютона, так как скомпенсированные силы сообщают телу нулевое суммарное ускорение).
Историческая формулировка
Ньютон в своей книге «Математические начала натуральной философии» сформулировал первый закон механики в следующем виде:
Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. |
С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает. С другой стороны, в произвольной (скажем, вращающейся) системе отсчёта закон инерции неверен. Поэтому ньютоновская формулировка нуждается в уточнениях.
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
Современная формулировка
В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. |
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
где — ускорение материальной точки;
— сила, приложенная к материальной точке;
— масса материальной точки.
Или в более известном виде:
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил. |
где — импульс точки,
- где — скорость точки;
— время;
— производная импульса по времени.
Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:
или
Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности.
Нельзя рассматривать частный случай (при ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.
Историческая формулировка
Исходная формулировка Ньютона:
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. |
Интересно, что если добавить требование инерциальной системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.
Третий закон Ньютона
Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой , а второе — на первое с силой . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
Современная формулировка
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: |
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.
Историческая формулировка
Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга равны и направлены в противоположные стороны. |
Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость[2].
Выводы
Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, если потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел , то возникает закон сохранения суммарной механической энергии взаимодействующих тел:
Законы Ньютона являются основными законами механики. Из них могут быть выведены уравнения движения механических систем. Однако не все законы механики можно вывести из законов Ньютона. Например, закон всемирного тяготения или закон Гука не являются следствиями трёх законов Ньютона.
Комментарии к законам Ньютона
Сила инерции
Законы Ньютона справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона: , где — это ускорение, наблюдаемое в рассматриваемой системе отсчёта, и — ускорение данной точки этой неинерциальной системы отсчёта относительно любой инерциальной системы отсчёта. Однако часто, для упрощения рассмотрения, вводят фиктивную «силу инерции» , и тогда эти уравнения движения переписываются в виде, идентичном второму закону Ньютона. Математически здесь всё корректно (правильно), но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального воздействия на тело. Ещё раз подчеркнём: «сила инерции» — это лишь удобная параметризация того, как отличается движение в инерциальной и неинерциальной системах отсчета.
Законы Ньютона и Лагранжева механика
Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках Лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), и из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами). Более того, в рамках Лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.
Решение уравнений движения
Уравнение является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию(перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.
Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
Исторический очерк
 Страница «Начал» Ньютона с аксиомами механики
Страница «Начал» Ньютона с аксиомами механикиОсновные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде.
|
Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов этот принцип является прямым следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».
Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта) и сила. Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств (ранее физики пользовались понятием вес).
Завершили математизацию механики Эйлер и Лагранж.