 2x=1
синус квадрат икс равен единице как решается?
2x=1
синус квадрат икс равен единице как решается? Плиз решите срочно только правильно даю 20 баллов!!!!!
Пожалуйста, помогите с вариантом по дифференциалам, срочно (100 баллов)
деление двузначных трехзначных четырехзначных чисел на одно число. 72:6 488:4. 666:6. 666:3. 3000:1000.
1. Выразите из уравнения y через x. Найдите три каких-либо решения уравнения. а) 2x+y=5 б) 3x-y=2,5
основания BC и AD равнобедренной трапеции ABCD равны 28 и 12 соответственно, а одна из боковых сторон равно 4 корня из 13 . Найти площадь это трапеции
−21−1,7y=45,3+3,4y. пжпжпжпжпж 21 балл
Капитан купил у аборигенов песочные часы, которые отсчитывают ровно одну минуту. Долгими вечерами во время плавания капитан коротал время, переворачив
… ая эти часы и наблюдая за падающими песчинками.
Он заметил, что, какой промежуток времени ни выбери, за предыдущий такой же промежуток на дно падает на столько же больше песка, на сколько меньше песка падает на дно за следующий. Например, если за некоторый десяток секунд на дно падает на унцию песка меньше, чем за предыдущий десяток, то за следующий десяток секунд на дно упадёт ещё на унцию песка меньше.
Следующий промежуток — такой, начало которого совпадает с концом текущего.
Известно, что за первые 10 секунд на дно упал 21 грамм песка. А с 21 по 30 секунду включительно — 14 грамм песка.
Сколько грамм песка в песочных часах?
Например, если за некоторый десяток секунд на дно падает на унцию песка меньше, чем за предыдущий десяток, то за следующий десяток секунд на дно упадёт ещё на унцию песка меньше.
Следующий промежуток — такой, начало которого совпадает с концом текущего.
Известно, что за первые 10 секунд на дно упал 21 грамм песка. А с 21 по 30 секунду включительно — 14 грамм песка.
Сколько грамм песка в песочных часах?
Помогите с математикой пожалуйста (с решением)
ПОМОГИТЕ ПОЖАЛУЙСТА Запишіть рiвняння прямої, яка симетрична прямій 2х + у — 8 = 0 відносно початку координат.
Капитан купил у аборигенов песочные часы, которые отсчитывают ровно одну минуту. Долгими вечерами во время плавания капитан коротал время, переворачив
… ая эти часы и наблюдая за падающими песчинками.
Он заметил, что, какой промежуток времени ни выбери, за предыдущий такой же промежуток на дно падает на столько же больше песка, на сколько меньше песка падает на дно за следующий.
Например, если за некоторый десяток секунд на дно падает на унцию песка меньше, чем за предыдущий десяток, то за следующий десяток секунд на дно упадёт ещё на унцию песка меньше.
Косинус квадрат и синус квадрат
Разбираемся с простыми понятиями:
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).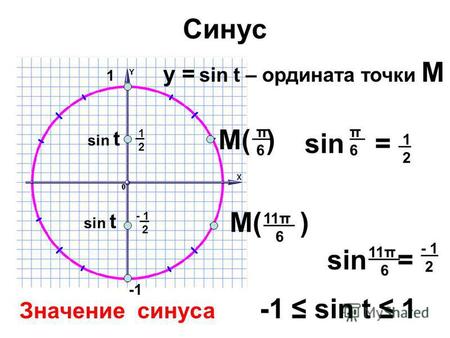
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin2α = 1 — cos2α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin2α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos2α = 1 — sin2α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos2α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или заданиеДобавить интересную новость
Таблица синусов, таблица значений синусов, в помощь студентам таблица синусов.
Содержание:
Таблица синусов — это посчитанные значения синусов от 0° до 360°. Когда нет рядом калькулятора таблица синусов просто незаменима. Для того, чтобы узнать чему равен синус от нужного Вам угла достаточно найти его в таблице и все. Таблица синусов — это основно материал тригонометрии, который необходимо знать или, как минимум, понимать. Пользуйтесь на здоровье таблицей значений синусов. Если Вы изучаете тригонометрические функции Вам может понадобиться перечень тригонометрических формулы.
Таблица синусов 0° — 180°
|
|
|
|
Таблица синусов 180° — 360°
|
|
|
|
На нашем сайте представлено много теоретического материала по тригонометрии. Здесь Вы можете найти таблицы тригонометрических функций: таблицу синусов, таблицу косинусов, таблицу тангенсов и таблицу котангенсов. Также специально для улучшения понимания материала по тригонометрии мы добавили тригонометрические формулы, чтобы решение тригонометрических задач по математике вызывало меньше затруднений. Пользуйтесь нашим сайтом и таблицей синусов на здоровье.
Слишком сложно?
Таблица синусов, таблица значений синусов не по зубам? Тебе ответит эксперт через 10 минут!
формулы cos, sin, tg, ctg
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями.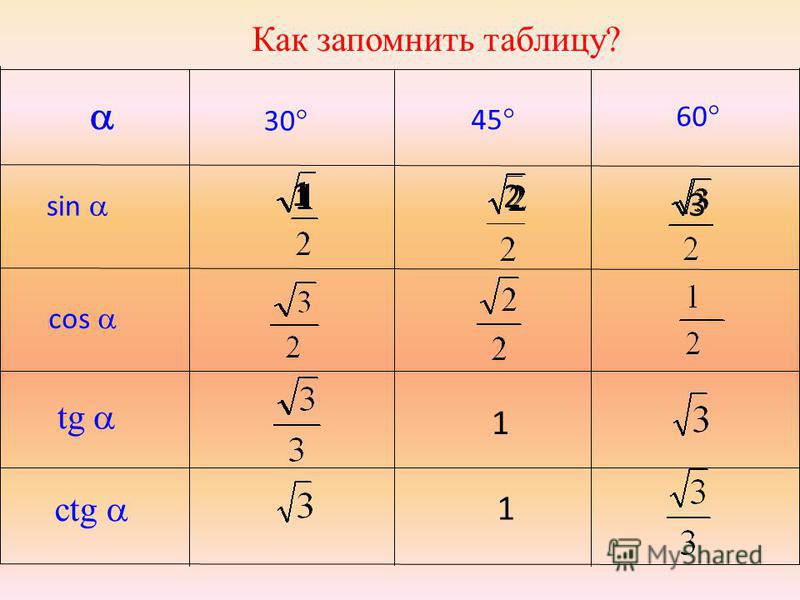 Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Тригонометрические тождестваsin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложенияsinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ
На основе формул сложения выводятся тригонометрические формулы кратного угла.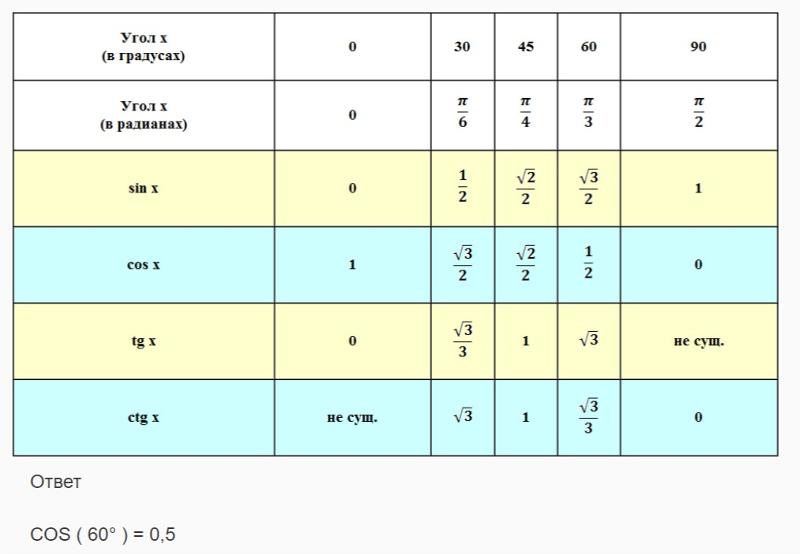
Формулы кратного угла: двойного, тройного и т.д.
Формулы двойного и тройного углаsin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеФормулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного углаsin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα
Формулы понижения степени
Формулы понижения степениsin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8
Часто при расчетах действовать с громоздктми степенями неудобно.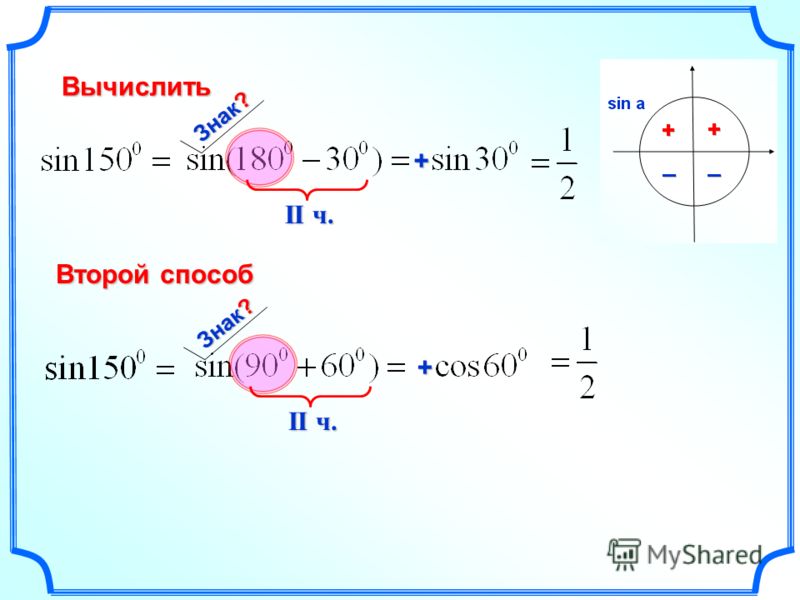 Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
для четных n
sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)
для нечетных n
sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функцийsinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функцийsinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановкаsinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2
3Тригонометрические идентичности
Возможно, вам сначала захочется прочитать о тригонометрии!
Прямой треугольник
Тригонометрические идентичности — это уравнения, которые верны для прямоугольных треугольников. (Если это не прямоугольный треугольник, перейдите на страницу «Треугольники».)
Каждая сторона прямоугольного треугольника имеет имя:
Соседний всегда находится рядом с углом
И Напротив находится напротив угла
Мы скоро будем играть со всеми видами функций, но помните, что все возвращается к этому простому треугольнику с:
- Угол θ
- Гипотенуза
- Соседний
- напротив
Синус, косинус и тангенс
Три основных функции в тригонометрии — это синус, косинус и тангенс.
Это всего лишь длина одной стороны разделить на другой
Для прямоугольного треугольника с углом θ :
Функция синуса: | sin ( θ ) = Противоположно / Гипотенуза |
Функция косинуса: | cos ( θ ) = Соседний / Гипотенуза |
Касательная функция: | tan ( θ ) = противоположный / смежный |
Для данного угла θ каждое отношение остается неизменным
независимо от того, насколько большой или малый треугольник
Когда мы разделим синус на косинус, получим:
sin (θ) cos (θ) = Противоположный / Гипотенуза Соседний / Гипотенуза = Противоположный Соседний = tan (θ)
Итак, мы можем сказать:
Это наша первая тригонометрическая идентификация .
Косеканс, секанс и котангенс
Мы также можем разделить «наоборот» (например, Соседний / Противоположный вместо Противоположный / Соседний ):
Косекансная функция: | csc ( θ ) = Гипотенуза / Напротив |
Секущая функция: | сек ( θ ) = Гипотенуза / Соседний |
Котангенс Функция: | детская кроватка ( θ ) = рядом / напротив |
Пример: когда Противоположность = 2 и Гипотенуза = 4, тогда
sin (θ) = 2/4 и csc (θ) = 4/2
Учитывая все, что мы можем сказать:
грех (θ) = 1 / csc (θ)
cos (θ) = 1 / сек (θ)
загар (θ) = 1 / детская кроватка (θ)
И наоборот:
csc (θ) = 1 / sin (θ)
сек (θ) = 1 / cos (θ)
детская кроватка (θ) = 1 / tan (θ)
А еще у нас есть:
детская кроватка (θ) = cos (θ) / sin (θ)
Теорема Пифагора
Следующие тригонометрические тождества мы начнем с теоремы Пифагора:
Теорема Пифагора гласит, что в прямоугольном треугольнике, квадрат a плюс квадрат b равен квадрату c: a 2 + b 2 = c 2 |
Деление на c 2 дает
а 2 с 2 + б 2 с 2 знак равно с 2 с 2
Это можно упростить до:
( a с ) 2 + ( б с ) 2 = 1
Теперь, a / c — это Противоположно / Гипотенуза , что составляет sin (θ)
И b / c — это Соседний / Гипотенуза , что составляет cos (θ)
Итак (a / c) 2 + (b / c) 2 = 1 также можно записать:
Примечание:- sin 2 θ означает найти синус θ, затем возвести результат в квадрат и
- sin θ 2 означает возведение θ в квадрат, , затем выполнить синусоидальную функцию
Пример: 32 °
Использование только 4 десятичных разряда :
- sin (32 °) = 0.5299 …
- cos (32 °) = 0,8480 …
Теперь посчитаем sin 2 θ + cos 2 θ :
0,5299 2 + 0,8480 2
= 0,2808 … + 0,7191 …
= 0,9999 …
Мы очень близки к 1, используя всего 4 десятичных знака. Попробуйте его на на своем калькуляторе , возможно, вы получите лучшие результаты!
Связанные идентификаторы включают:
sin 2 θ = 1 — cos 2 θ
cos 2 θ = 1 — sin 2 θ
tan 2 θ + 1 = sec 2 θ
tan 2 θ = sec 2 θ — 1
детская кроватка 2 θ + 1 = csc 2 θ
детская кроватка 2 θ = csc 2 θ — 1
Как вы их помните? Упомянутые до сих пор личности можно запомнить |
Но подождите… Это еще не все!
Есть еще много идентификаторов … вот некоторые из наиболее полезных:
Противоположные углы
грех (-θ) = -sin (θ)
cos (−θ) = cos (θ)
загар (-θ) = -тан (θ)
Double Angle Identities
Полуугловые идентификаторы
Обратите внимание, что «±» означает, что это может быть или один , в зависимости от значения θ / 2
Тождества суммы углов и разностей
Обратите внимание, что это означает, что вы можете использовать плюс или минус, а средство — использовать противоположный знак.
sin (A B) = sin (A) cos (B) cos (A) sin (B)
cos (A B) = cos (A) cos (B) sin (A) sin (B)
загар (A B) = загар (A) загар (B) 1 загар (A) загар (B)
детская кроватка (A B) = детская кроватка (A) детская кроватка (B) 1 детская кроватка (B) детская кроватка (A)
Треугольники
Существуют также идентичности треугольников, которые применяются ко всем треугольникам (а не только к прямоугольным треугольникам).
Тригонометрические тождества.Темы по тригонометрии.
Темы | Дом
20
Взаимные идентичности
Тангенс и котангенс
Пифагорейские тождества
Формулы суммы и разности
Формулы двойного угла
Формулы полууглов
Изделий суммами
Суммы как произведения
ИДЕНТИЧНОСТЬ — ЭТО РАВЕНСТВО, которое истинно для любого значения переменной.(Уравнение — это равенство, которое верно только для определенных значений переменной.)
В алгебре, например, у нас есть это тождество:
( x + 5) ( x -5) = x 2 — 25.
Значение идентичности состоит в том, что при вычислении мы можем заменить любой член другим. Мы используем идентичность, чтобы придать выражению более удобную форму. В исчислении и во всех его приложениях центральное значение имеют тригонометрические тождества.
На этой странице мы представим основные идентичности. У студента не будет лучшего способа практиковать алгебру, чем доказывать их. Ссылки на доказательства приведены ниже.
Взаимные идентичности
| sin θ | = | 1 csc θ | csc θ | = | 1 sin θ | |
| cos θ | = | 1 сек θ | сек θ | = | 1 cos θ | |
| tan θ | = | 1 детская кроватка θ | детская кроватка θ | = | 1 тангенс угла θ | |
Проба
Опять же, при вычислении мы можем заменить любой член идентичности другим.Итак, если мы видим «sin θ», то при желании можем заменить
| это с « | » 1 csc θ | «; и симметрично, если мы увидим» | 1 csc θ | «, |
, тогда мы можем заменить его на «sin θ».
Проблема 1. Что означает утверждение, что csc θ является обратной величиной
sin θ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Это означает, что их продукт 1.
sin θ csc θ = 1.
Урок 5 алгебры.
Задача 2. Оценить
tan 30 ° csc 30 ° cot 30 °.
| желто-коричневый 30 ° csc 30 ° cot 30 ° | = | желто-коричневый 30 ° cot 30 ° csc 30 ° |
| = | 1 · csc 30 ° | |
| = | 2. | |
Тема 4.
Тангенс и котангенс
| тангенс угла θ = | sin θ cos θ | детская кроватка θ = | cos θ sin θ |
Проба
Пример 1. Покажите: tan θ cos θ = sin θ.
Решение: Проблема означает, что мы должны написать левую часть, а затем показать с помощью подстановок и алгебры, что мы можем преобразовать ее, чтобы она выглядела как правая часть.
Начинаем:
Мы подошли к правой стороне.
Пифагорейские тождества
| а) | sin 2 θ + cos 2 θ | = | 1. |
| б) | 1 + загар 2 θ | = | сек 2 θ |
| c) | 1 + детская кроватка 2 θ | = | csc 2 θ |
| a ‘) | грех 2 θ | = | 1 — cos 2 θ. |
| cos 2 θ | = | 1 — грех 2 θ. | |
Они называются тождествами Пифагора, потому что, как мы увидим в их доказательстве, они являются тригонометрической версией теоремы Пифагора.
Два идентификатора, помеченные как ‘) — «простое число» — просто разные версии а).Первый показывает, как мы можем выразить sin θ через cos θ; второй показывает, как мы можем выразить cos θ через sin θ.
Примечание: sin 2 θ — «синус-квадрат тета» — означает (sin θ) 2 .
Задача 3. Треугольник 3-4-5 прямоугольный.
а) Почему?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Он удовлетворяет теореме Пифагора.
б) Оцените следующее:
| sin 2 θ | = | 16 25 | cos 2 θ | = | 9 25 | sin 2 θ + cos 2 θ | = | 1. |
Пример 2. Показать:
Это то, что мы хотели показать.
Формулы суммы и разности
| sin (α + β) | = | sin α cos β + cos α sin β |
| sin (α — β) | = | sin α cos β — cos α sin β |
| cos (α + β) | = | cos α cos β — sin α sin β |
| cos (α — β) | = | cos α cos β + sin α sin β |
Примечание: В формулах синуса + или — слева также + или — справа.Но в формулах косинуса + слева становится — справа; и наоборот.
Поскольку эти тождества доказываются непосредственно из геометрии, от студента обычно не требуется усваивать доказательство. Однако все последующие тождества основаны на этих формулах суммы и разности. Студент обязательно должен их знать.
Вот доказательство формул суммы.
Пример 3. Оценить sin 15 °.
| Решение. | грех 15 ° | |||
| Формулы | ||||
| Темы 4 и 5 | ||||
Пример 4.Доказательство:
Это то, что мы хотели доказать.
Формулы двойного угла
Проба
Существует три версии cos 2α. Первый — с точки зрения обоих cos α и sin α. Второй — только по cos α. Третий — только с точки зрения sin α
| Пример 5. Показать: sin 2α |
Это то, что мы хотели доказать.
| Пример 6. Показать: |
| Решение. | грех x |
— согласно предыдущему тождеству с α =.
Формулы полууглов
Следующие формулы половинного угла являются инверсией формул двойного угла, поскольку α составляет половину от 2α.
Знак плюс или минус будет зависеть от квадранта. Под корнем косинус имеет знак +; синус, знак -.
Проба
| Пример 7. Вычислить cos | . π 8 | . |
| Пример 8. Вывести идентификатор для tan | . α 2 | . |
при делении числителя и знаменателя на cos α.
Изделий суммами
| а) | sin α cos β | = | ½ [грех (α + β) + грех (α — β)] | |
| б) | cos α sin β | = | ½ [sin (α + β) — sin (α — β)] | |
| c) | cos α cos β | = | ½ [cos (α + β) + cos (α — β)] | |
| г) | грех α sin β | = | −½ [cos (α + β) — cos (α — β)] | |
Проба
Суммы как произведения
| д) | грех A + грех B | = | 2 sin ½ ( A + B ) cos ½ ( A — B ) |
| е) | грех A — грех B | = | 2 sin ½ ( A — B ) cos ½ ( A + B ) |
| г) | cos A + cos B | = | 2 cos ½ ( A + B ) cos ½ ( A — B ) |
| ч) | cos A — cos B | = | −2 sin ½ ( A + B ) sin ½ ( A — B ) |
В доказательствах ученик увидит, что тождества с e) по h) являются обращениями от a) до d) соответственно, которые доказываются в первую очередь.Тождество f) используется для доказательства одной из основных теорем исчисления, а именно о производной sin x .
Учащийся не должен пытаться запомнить эти личности. Достаточно попрактиковаться в их доказательствах — и увидеть, что они исходят из формул суммы и разности.
Темы | Дом
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: themathpage @ яндекс.com
Малоугловая аппроксимация | Блестящая вики по математике и науке
Приближение малых углов повсеместно используется во всех областях физики, включая механику, волны и оптику, электромагнетизм, астрономию и многое другое. Ниже мы рассмотрим несколько хорошо известных примеров, чтобы проиллюстрировать, почему малоугловое приближение полезно в физике.
Простой маятник
Малые колебания простого маятника лучше всего моделировать в малоугловом приближении.2 \ ddot {\ theta} \ подразумевает \ ddot {\ theta} + \ frac {g} {\ ell} \ sin \ theta = 0, τ = Iα⟹ − ℓmgsinθ = mℓ2θ¨⟹θ¨ + ℓg sinθ = 0 ,
где θ \ thetaθ — угол между струной и вертикалью.
Решения этого уравнения движения можно найти в терминах функций, называемых эллиптическими интегралами, с которыми трудно работать вручную. Однако, используя малоугловое приближение,
θ¨ + gℓsinθ = 0 ⟹ θ¨ + gℓθ = 0. \ Ddot {\ theta} + \ frac {g} {\ ell} \ sin \ theta = 0 \ подразумевает \ ddot {\ theta} + \ frac {g} {\ ell} \ theta = 0.θ¨ + ℓg sinθ = 0⟹θ¨ + ℓg θ = 0.
Новое дифференциальное уравнение легко разрешимо. Решения имеют вид θ (t) = Acos (gℓt) + Bsin (gℓt) \ theta (t) = A \ cos \ left (\ sqrt {\ frac {g} {\ ell}} t \ right) + B \ sin \ left (\ sqrt {\ frac {g} {\ ell}} t \ right) θ (t) = Acos (ℓg t) + Bsin (ℓg t) для констант AAA и BBB в зависимости от начальные условия, успешно воспроизводящие колебательное поведение маятника.
Угловое расстояние в астрономии
Размер или расстояние между небесными телами в астрономии обычно записывается в терминах углового диаметра или видимого размера , т.е.е. угол θ \ thetaθ между двумя телами, если смотреть с Земли. Если расстояние между двумя удаленными точками равно ddd, а средняя точка между ними находится на расстоянии DDD от Земли, то этот угол подчиняется соотношению
tanθ2 = d2D. \ Tan \ frac {\ theta} {2} = \ frac {d} {2D} .tan2θ = 2Dd.
Диаграмма, соответствующая этой формуле, ниже:
Угловое разделение двух далеких звезд, вид с Земли
Используя малоугловое приближение, угловое расстояние можно переписать как
θ = dD.\ theta = \ frac {d} {D} .θ = Dd.
Приближение полезно, потому что обычно угловое расстояние легче всего измерить в астрономии, а разница между углами настолько мала, что сам угол более полезен, чем синус.
В градусе 60 угловых минут, а угловой диаметр Солнца составляет приблизительно 323232 угловых минуты. Зная, что Солнце находится на расстоянии около 888 световых минут от Земли, оцените диаметр Солнца. 58.8 \ text {m} 3,7 × 108 м от Земли. Что из следующего является наилучшим приближением диаметра Луны в метрах?
Дифракция на одной щели
При дифракции с одной щелью, свет, проходящий через барьер с щелью, превышающей одну длину волны света, имеет профиль интенсивности, измеренный за барьером, который показывает характерный рисунок пиков и впадин. Условие минимума в этом распределении интенсивности:
dsinθ = mλ, d \ sin \ theta = m \ lambda, dsinθ = mλ,
, где ddd — ширина щели, θ \ thetaθ — угол к точке измерения от центра щели, λ \ lambdaλ — длина волны света, а mmm — ненулевое целое число.
Это условие можно переписать с точки зрения вертикального расстояния от центра экрана измерений, yyy, как показано на диаграмме выше. Предположим, что экран измерения находится на расстоянии DDD от барьера. Обычно считается, что DDD намного больше, чем ddd, и можно использовать малоугловое приближение для θ \ thetaθ. Тогда формула для минимумов интенсивности принимает вид
y = mλDd, y = \ frac {m \ lambda D} {d}, y = dmλD,
— удобное выражение для длины волны света, ширины щели и расстояния от барьера до экрана.
λad \ frac {\ lambda a} {d} dλa 2λda \ frac {2 \ lambda d} {a} a2λd 2λad \ frac {2 \ lambda a} {d} d2λa λda \ frac {\ lambda d} {a} aλdВ эксперименте по дифракции с одной щелью с шириной щели aaa, расстоянием ddd между барьером и измерительным экраном и светом с длиной волны λ \ lambdaλ, какова ширина центрального максимального пика?
График квадрата синуса (x)
График квадрата синуса (x) | математикатестподготовка.ком назад к вопрос и ответ по математике
- Шаг 1. Найдите выражение греха 2 x
- Использование формул двойного угла: cos 2x = cos 2 x — sin 2 x, обозначьте его как уравнение (1)
- Использование тождеств Пифагора: sin 2 x + cos 2 x = 1
- Подставьте cos 2 x = 1 — sin 2 x в уравнение (1), затем
- cos 2x = 1 — sin 2 x — sin 2 x
- cos 2x = 1 — 2sin 2 x.
- Выразите sin 2 x в левой части уравнения, тогда
- 2sin 2 x = 1 — cos 2x, разделим коэффициент 2 в каждом элементе уравнения
- sin 2 x = 1/2 — (1/2) cos 2x
- , таким образом, получаем выражение sin 2 x
- Шаг 2: Постройте график y = (1/2) cos 2x
- Примечание: для функции периода y = A cos (Bx + C) ее амплитуда равна A.период T = 2 pi / B и фазовый сдвиг C.
- В данном случае его амплитуда A = 1/2, период T = 2 pi / 2 = pi и фазовый сдвиг C = 0
- Шаг 3. Постройте график y = — (1/2) cos 2x
- Отразите график y = (1/2) cos2x по оси x, чтобы получить график y = — (1/2) cos2x
- Шаг 4: Нарисуйте два графика, например y 1 = 1/2 и y 2 = — (1/2) cos2x, чтобы сложить их.
- Когда x = 0, y = 1/2 + (-1/2) cos2x = 1/2 + (- 1/2) = 0
- Когда x = pi / 4, y = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
- Когда x = pi / 2, y = 1/2 + (-1/2) cos2x = 1/2 + 1/2 = 1
- Когда x = 3pi / 4, y = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
- Когда x = pi, y = 1/2 + (-1/2) cos2x = 1/2 + (- 1/2) = 0
- Когда x = 5pi / 4, y = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
- Когда x = 3pi / 2, y = 1/2 + (-1/2) cos2x = 1/2 + 1/2 = 1
- Когда x = 7pi / 4.у = 1/2 + (-1/2) cos2x = 1/2 + 0 = 1/2
- Когда x = 2pi, y = 1/2 + (-1/2) cos2x = 1/2 + (- 1/2) = 0
- Следовательно, график y = 1/2 + [- (1/2) cos 2x] равен:
- Сводка:
- График y = sin 2 x является суммой графика y = 1/2 и графика y = (-1/2) cos2x
- Сумма графика y = 1/2 и графика y = (-1/2) cos2x является графиком y = (-1/2) cos2x, перемещающимся на 1/2 единицы.
4.E: Тригонометрические тождества и уравнения (упражнения)
Упражнение \ (\ PageIndex {1} \)
Используйте графическую утилиту для построения графика каждой стороны данного уравнения. Если уравнение идентично, докажите это. Если уравнение не совпадает с тождеством, продемонстрируйте один вход, на котором две стороны уравнения имеют разные значения. Помните, что при подтверждении идентичности постарайтесь преобразовать одну часть уравнения в другую, используя известные личности.{2} = 4 \]
Упражнение \ (\ PageIndex {2} \)
Студент утверждает, что \ (\ cos (\ theta) + \ sin (\ theta) = 1 \) является тождеством, потому что \ (\ cos (0) + \ sin (0) = 1 + 0 = 0 \). Как бы вы отреагировали на этого студента?
Упражнение \ (\ PageIndex {3} \)
Если тригонометрическое уравнение имеет одно решение, то периодичность тригонометрических функций означает, что уравнение будет иметь бесконечно много решений. Предположим, у нас есть тригонометрическое уравнение, для которого обе части уравнения равны при бесконечном множестве различных входов.\ circ \).
Упражнение \ (\ PageIndex {6} \)
Рентгеновская кристаллография — важный инструмент в химии. Одним из применений рентгеновской кристаллографии является обнаружение макромолекул атомной структуры. Например, двойная спиральная структура ДНК была обнаружена с помощью рентгеновской кристаллографии.
Основная идея рентгеновской кристаллографии заключается в следующем: два рентгеновских луча с одинаковой длиной волны \ (\ lambda \) и фазой направлены под углом \ (\ theta \) к кристаллу, состоящему из атомов, расположенных в решетке. в плоскостях, разделенных расстоянием \ (d \), как показано на рисунке 4.5.1. Лучи отражаются от различных атомов (обозначенных как \ (P \) и \ (Q \) на рисунке 4.5) внутри кристалла. Один рентгеновский луч (нижний, как показано на рисунке 4.5) должен проходить большее расстояние, чем другой. При отражении рентгеновские лучи объединяются, но из-за фазового сдвига нижнего луча комбинация может иметь небольшую или большую амплитуду. Закон Брэгга гласит, что сумма отраженных лучей будет иметь максимальную амплитуду, когда дополнительная длина, которую должен пройти более длинный луч, равна целому кратному длине волны \ (\ lambda \) излучения.Другими словами, \ [n \ lambda = 2d \ sin (\ theta), \]
для некоторого положительного целого числа \ (n \). Предположим, что \ (\ lambda = 1.54 \) ангстрема и \ (d = 2.06 \) ангстрема. Примерно с двумя десятичными знаками наименьшее значение \ (\ theta \) (в градусах), для которого \ (n = 1 \).
Рисунок \ (\ PageIndex {1} \): Рентгеновские лучи, отраженные от атомов кристалла.
Упражнение \ (\ PageIndex {7} \)
Используйте соответствующую сумму или разность идентичности, чтобы найти точное значение каждого из следующих.\ circ) = \ dfrac {\ sqrt {2}} {2} \).
\ (\ cos (\ dfrac {7 \ pi} {9} + \ dfrac {2 \ pi} {9}) = \ cos (\ pi) = -1 \) Упражнение \ (\ PageIndex {8} \)
Углы \ (A \) и \ (B \) находятся в стандартном положении и \ (\ sin (\ dfrac {1} {2}, \ cos (A)> 0) \), \ (\ cos (B) = \ dfrac {3} {4} \) и \ (\ sin (B) <0 \). Нарисуйте на плоскости углы \ (A \) и \ (B \), а затем найдите каждый из следующих элементов.
- \ (\ cos (A + B) \)
- \ (\ cos (A — B) \)
- \ (\ sin (A + B) \)
- \ (\ sin (A — B) \)
- \ (\ загар (A + B) \)
- \ (\ tan (A — B) \)
- Ответ
Сначала мы используем тождество Пифагора, чтобы определить \ (\ cos (A) \) и \ (\ sin (B) \).Отсюда получаем \ [\ cos (A) = \ dfrac {\ sqrt {3}} {2} \] и \ [\ sin (B) = — \ dfrac {\ sqrt {7}} {4} \ ]
(a) \ [\ cos (A + B) = \ cos (A) \ cos (B) — \ sin (A) \ sin (B) = \ dfrac {\ sqrt {3}} {2} \ cdot \ dfrac {3} {4} — \ dfrac {1} {2} \ cdot (- \ dfrac {\ sqrt {7}} {4}) = \ dfrac {3 \ sqrt {3} + \ sqrt {7} } {8} \]
Упражнение \ (\ PageIndex {9} \)
Определите углы \ (A \) и \ (B \), при которых нам известны значения косинуса и синуса, чтобы можно было использовать тождество суммы или разности для вычисления точного значения данной величины.\ circ) \) и результат в части (a).
Упражнение \ (\ PageIndex {10} \)
Проверьте тождество суммы и разницы для касательной:
\ [\ tan (A — B) = \ dfrac {\ tan (A) — \ tan (B)} {1 + \ tan (A) \ tan (B)} \] и
\ [\ tan (A + B) = \ dfrac {\ tan (A) + \ tan (B)} {1 — \ tan (A) \ tan (B)} \]Упражнение \ (\ PageIndex {11} \)
Подтвердите идентификационные данные совместных функций
- \ (\ cot (\ dfrac {\ pi} {2} — x) = \ tan (x) \)
- \ (\ sec (\ dfrac {\ pi} {2} — x) = \ csc (x) \)
- \ (\ csc (\ dfrac {\ pi} {2} — x) = \ sec (x) \)
- Ответ
(a) \ [\ cot (\ dfrac {\ pi} {2} — x) = \ dfrac {\ cos (\ dfrac {\ pi} {2} — x)} {\ sin (\ dfrac {\ pi } {2} — x)} = \ dfrac {\ sin (x)} {\ cos (x)} = \ tan (x) \]
Упражнение \ (\ PageIndex {12} \)
Нарисуйте графики, чтобы определить, является ли данное уравнение идентичностью.\ circ) = \ dfrac {1} {2} \)
\ (\ соз (2х) \ соз (х) = \ грех (2х) \ грех (х) = -1 \) Упражнение \ (\ PageIndex {15} \)
- Используйте графическое устройство, чтобы нарисовать график \ (f (x) = \ sin (x) + \ cos (x) \), используя \ (- \ pi \ leq x \ leq 2 \ pi \) и \ ( -2 \ leq y \ leq 2 \). Кажется ли график этой функции синусоидой? Если это так, приблизьте амплитуду и фазовый сдвиг синусоиды. Какой период у этой синусоиды.
- Используйте одно из тождеств суммы, чтобы переписать выражение \ (\ sin (x + \ dfrac {\ pi} {4}) \).Затем используйте значения \ (\ sin (\ dfrac {\ pi} {4}) \) и \ (\ cos (\ dfrac {\ pi} {4}) \) для дальнейшей перезаписи выражения.
- Используйте результат из части (b), чтобы показать, что функция \ (f (x) = \ sin (x) + \ cos (x) \) действительно является синусоидальной функцией. Каковы его амплитуда, фазовый сдвиг и период?
Упражнение \ (\ PageIndex {16} \)
- Используйте графическое устройство, чтобы нарисовать график \ (g (x) = \ sin (x) + \ sqrt {3} \ cos (x) \), используя \ (- \ pi \ leq x \ leq 2 \ pi \) и \ (- 2,5 \ leq y \ leq 2.5 \). Кажется ли график этой функции синусоидой? Если это так, приблизьте амплитуду и фазовый сдвиг синусоиды. Какой период у этой синусоиды.
- Используйте одно из тождеств суммы, чтобы переписать выражение \ (\ sin (x + \ dfrac {\ pi} {3}) \). Затем используйте значения \ (\ sin (\ dfrac {\ pi} {3}) \) и \ (\ cos (\ dfrac {\ pi} {3}) \) для дальнейшей перезаписи выражения.
- Используйте результат из части (b), чтобы показать, что функция \ (g (x) = \ sin (x) + \ sqrt {3} \ cos (x) \) действительно является синусоидальной функцией.Каковы его амплитуда, фазовый сдвиг и период?
Упражнение \ (\ PageIndex {17} \)
Когда на цепь подается два напряжения, результирующее напряжение в цепи будет суммой отдельных напряжений. Предположим, что два напряжения \ (V_ {1} (t) = 30 \ sin (120 \ pi t) \) и \ (V_ {2} (t) = 40 \ cos (120 \ pi t) \) приложены к схема. График суммы \ (V (t) = V_ {1} (t) + V_ {2} (t) \) показан на рисунке 4.8.
- Используйте график для оценки значений \ (C \) так, чтобы \ [y = 50 \ sin (120 \ pi (t — c)) \] соответствовало графику \ (V \).
- Используйте тождество разности синусов, чтобы переписать \ (50 \ sin (120 \ pi (t — c)) \) как выражение формы \ (50 \ sin (A) \ cos (B) — 50 \ cos (A ) \ sin (B) \), где \ (A \) и \ (B \) включают \ (t \) и / или \ (C \). Исходя из этого, определите значение C, которое сделает
\ [30 \ sin (120 \ pi t) + 40 \ cos (120 \ pi t) = 50 \ sin (120 \ pi (t — c)) \]. Сравните это значение \ (C \) с тот, который вы оценили в части (а).
Рисунок \ (\ PageIndex {2} \): График \ (V (t) = V_ {1} (t) + V_ {2} (t) \).{2} (\ theta) = \ dfrac {5} {9} \). Поскольку \ (\ sin (\ theta) <0 \), мы видим, что \ (\ sin (\ theta) = - \ dfrac {\ sqrt {5}} {3} \). Теперь используйте соответствующие тождества с двойным углом, чтобы получить \ [\ sin (2 \ theta) = - \ dfrac {4 \ sqrt {5}} {9} \] \ [\ cos (2 \ theta) = - \ dfrac {1} {9} \]
Затем используйте \ (\ tan (2 \ theta) = \ dfrac {\ sin (2 \ theta)} {\ cos (2 \ theta)} = 4 \ sqrt {5} \). {2} (x)} \)
- Ответ
(а) Это личность.Начните с левой части уравнения и используйте \ (\ cot (t) = \ dfrac {\ cos (t)} {\ sin (t)} \) и \ (\ sin (2t) = 2 \ sin (t )\Стоимость)\).
Упражнение \ (\ PageIndex {21} \)
Найдите более простую формулу для \ (\ cos (\ pi + x) \) через \ (\ cos (x) \). Проиллюстрируйте графиком.
Упражнение \ (\ PageIndex {22} \)
Одноклассник делится своим решением задачи решения \ (\ sin (2x) = 2 \ cos (x) \) на интервале \ ([0, 2 \ pi) \). Он написал
\ [\ sin (2x) = 2 \ cos (x) \]
\ [\ dfrac {\ sin (2x)} {2} = \ cos (x) \]
\ [\ sin (x) = \ cos (x) \]
\ [\ tan (x) = 1 \], поэтому \ (x = \ dfrac {\ pi} {4} \) или \ (x = \ dfrac {5 \ pi} {4} \)
- Нарисуйте графики \ (\ sin (2x) \) и \ (2 \ cos (x) \) и объясните, почему это одноклассники
- Найдите ошибку в аргументе этого одноклассника.\ circ) = — \ sqrt {\ dfrac {1 + \ dfrac {\ sqrt {3}} {2}} {2}} = — \ dfrac {1} {2} \ sqrt {2 + \ sqrt {3} } \)
Упражнение \ (\ PageIndex {24} \)
Определите точное значение каждого из следующих значений:
- \ (\ sin (\ dfrac {3 \ pi} {8}) \)
- \ (\ cos (\ dfrac {3 \ pi} {8}) \)
- \ (\ tan (\ dfrac {3 \ pi} {8}) \)
- \ (\ sin (\ dfrac {5 \ pi} {8}) \)
- \ (\ cos (\ dfrac {5 \ pi} {8}) \)
- \ (\ tan (\ dfrac {5 \ pi} {8}) \)
- \ (\ sin (\ dfrac {11 \ pi} {12}) \)
- \ (\ cos (\ dfrac {11 \ pi} {12}) \)
- \ (\ tan (\ dfrac {11 \ pi} {12}) \)
- Ответ
(a) \ (\ sin (\ dfrac {3 \ pi} {8}) = \ sqrt {\ dfrac {1 + \ dfrac {\ sqrt {2}} {2}} {2}} = \ dfrac { 1} {2} \ sqrt {2 + \ sqrt {2}} \)
(c) \ (\ tan (\ dfrac {3 \ pi} {8}) = \ sqrt {\ dfrac {2 + \ sqrt { 2}} {2 — \ sqrt {2}}} = \ sqrt {3 + 2 \ sqrt {2}} \)
(h) \ (\ cos (\ dfrac {11 \ pi} {12}) = — \ sqrt {\ dfrac {1 + \ dfrac {\ sqrt {3}} {2}} {2}} = — \ dfrac {1} {2} \ sqrt {2 + \ sqrt {3}} \)Упражнение \ (\ PageIndex {25} \)
Если \ (\ cos (x) = \ dfrac {2} {3} \) и \ (\ sin (x) <0 \) и \ (0 \ leq x \ leq 2 \ pi \), определите точное значение каждого из следующих элементов:
- \ (\ cos (\ dfrac {x} {2}) \)
- \ (\ sin (\ dfrac {x} {2}) \)
- \ (\ tan (\ dfrac {x} {2}) \)
- Ответ
(a) Отметим, что, поскольку \ (\ dfrac {3 \ pi} {2} \ leq x \ leq 2 \ pi, \ dfrac {3 \ pi} {4} \ leq \ dfrac {x} {2} \ лек \ пи \).
\ [\ sin (\ dfrac {x} {2}) = \ sqrt {\ dfrac {1 — \ dfrac {2} {3}} {2}} = \ dfrac {1} {\ sqrt {6}} \]
Упражнение \ (\ PageIndex {26} \)
Если \ (\ sin (x) = \ dfrac {2} {5} \) и \ (\ cos (x) <0 \) и \ (0 \ leq x \ leq 2 \ pi \), определите точное значение каждого из следующих элементов:
- \ (\ cos (\ dfrac {x} {2}) \)
- \ (\ sin (\ dfrac {x} {2}) \)
- \ (\ tan (\ dfrac {x} {2}) \)
Упражнение \ (\ PageIndex {27} \)
Прямоугольник вписан в полукруг радиусом \ (r \), как показано на схеме, как показано ниже.{3} (x)] \] следующим образом.
- Напишите s \ [\ sin (4x) = \ sin (2 (2x)) \] и используйте тождество двойного угла для синуса, чтобы переписать эту формулу.
- Теперь используйте идентичность двойного угла для синуса и одну из идентичностей двойного угла для косинуса, чтобы переписать выражение из части (а).
- Алгебраически перепишите выражение из части (b), чтобы получить желаемую формулу для \ (\ sin (4x) \).
Упражнение \ (\ PageIndex {30} \)
Запишите каждое из следующих выражений как сумму значений тригонометрических функций.\ circ) \)
(e) \ (\ cos (\ dfrac {7 \ pi} {12}) + \ cos (\ dfrac {\ pi} {12}) = 2 \ cos (\ dfrac {\ pi} {3}) \ cos (\ dfrac {\ pi} {4}) = \ dfrac {\ sqrt {2}} {2} \)
Упражнение \ (\ PageIndex {32} \)
Найдите все решения данного уравнения. Используйте графическую утилиту, чтобы построить график каждой стороны данного уравнения, чтобы проверить свои решения.
- \ [\ sin (2x) + \ sin (x) = 0 \]
- \ [\ sin (x) \ cos (x) = \ dfrac {1} {4} \]
- \ [\ cos (2x) + \ cos (x) = 0 \]
- Ответ
(а) \ [\ sin (2x) + \ sin (x) = 0 \]
\ [2 \ sin (\ dfrac {3x} {2}) \ cos (\ dfrac {x} {2}) = 0 \]
Итак, \ [\ sin (\ dfrac {3x} {2}) = 0 \] или \ [\ cos (\ dfrac {x} {2}) = 0 \].Это дает \ [x = k \ pi \] или \ [x = \ dfrac {2 \ pi} {3} + k (2 \ pi) \] или \ [x = \ dfrac {4 \ pi} {3} + k (2 \ pi) \], где \ (k \) — целое число.
KryssTal: тригонометрические уравнения
KryssTal: тригонометрические уравнения
В алгебре мы рассматривали решение простых уравнений, таких как 5X — 2 = 0 и квадратные уравнения типа Х 2 — 3X + 1 = 0 . В тригонометрии мы ввели тригонометрические функции (синусы, косинусы и касательные).В этом эссе мы объединим тригонометрическую функцию в уравнения, которые можно решить.
Начнем с напоминания о тригонометрических соотношениях: Sin X / Cos X = Желто-коричневый X Sin 2 X + Cos 2 X = 1 Кроме того, существуют отношения, называемые двойных углов : Sin 2X = 2 Sin X Cos X Cos 2X = Cos 2 X — Sin 2 X Поскольку Sin 2 X + Cos 2 X = 1, это последнее соотношение также можно записать как: Cos 2X = 1-2 Sin 2 X Cos 2X = 2 Cos 2 X — 1
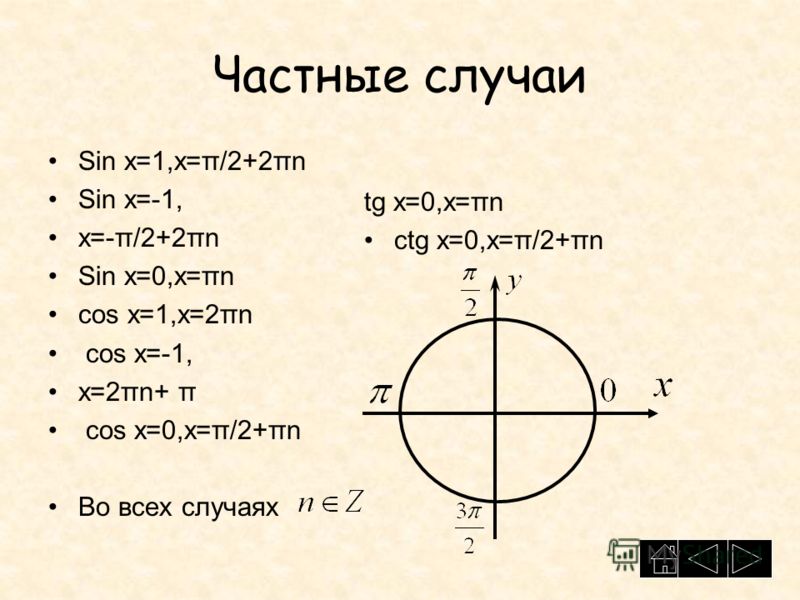
Прежде чем мы сможем решить сложные тригонометрические уравнения, мы должны посмотреть, как изменяются синусы и косинусы.Ниже приведен график Y = Sin X. X измеряется в радианах. Синусы периодические. Они колеблются между 1 и -1 на протяжении 360 o (2 π радиан), начиная с 0 и заканчивая 0,. Ниже приведен график Y = Cos X. Это похоже, но в другой фазе.
Косинусы также колеблются между 1 и -1 на протяжении 360 o (2 π радиан), начиная с 1 и заканчивая 1.В таблице ниже обобщена информация как для синусов, так и для косинусов между 0 o и 360 o (от 0 до 2 π радиан).Эта информация будет использоваться при решении тригонометрических уравнений.
Угол
( o )Угол
(рад)Синус Косинус 0 0 0 1 30 π / 6 1/2 √3 / 2 45 π / 4 1 / √2 1 / √2 60 π / 3 √3 / 2 1/2 90 π / 2 1 0 120 2π / 3 √3 / 2 -1 / 2 135 3π / 4 1 / √2 -1 / √2 150 5π / 6 1/2 -√3 / 2 180 π 0 -1 210 7π / 6 -1 / 2 -√3 / 2 225 5π / 4 -1 / √2 -1 / √2 240 4π / 3 -√3 / 2 -1 / 2 270 3π / 2 –1 0 300 5π / 3 -√3 / 2 1/2 315 7π / 4 -1 / √2 1 / √2 330 11π / 6 -1 / 2 √3 / 2 360 2π 0 1
Используя таблицу или графики выше и некоторую алгебру, решите следующие уравнения для значений от 0 o до 360 o . Sin X = 1/2Используя таблицу, легко увидеть, что X имеет два значения в требуемом диапазоне. Это:
X = 30 o и X = 150 o .
Cos X + 1/2 = 0Изменив уравнение (чтобы получить Cos X с одной стороны и числа с другой стороны) дает:
Cos X = -1 / 2
Используя таблицу, мы видим, что X имеет два значения в требуемом диапазоне.Это:
X = 120 o и X = 240 o .
Cos X Tan X = 1 / √2Использование идентичности для замены Tan X дает:
Cos X (Sin X / Cos X) = 1 / √2
Косинусы сокращаются, чтобы дать:
Sin X = 1 / √2
Это дает два значения X:
X = 45 o и X = 135 o .
2 Cos 2X + 1 = 0Переставьте уравнение:
Cos 2X = — 1/2
Следовательно, 2X = 120 o и 240 o , что дает:
X = 60 o и X = 120 o .
Sin X — Cos 2X = 0Используя тождество двойного угла, замените Cos 2X на (1-2 Sin 2 X):
Грех X — (1-2 Sin 2 X) = 0
Sin X — 1 + 2 Sin 2 X = 0
который преобразуется в квадратное уравнение в Sin 2 X:
2 Sin 2 X + Sin X — 1 = 0
Это можно решить путем факторизации:
(2 Sin X — 1) (Sin X + 1) = 0
Это уравнение дает 0, если либо 2 Sin X — 1 = 0, либо Sin X + 1 = 0.Другими словами:
Sin X = 1/2 или Sin X = -1
Первое уравнение дает два значения (X = 30 o , X = 150 o ), второе уравнение дает одно значение (270 o ). Таким образом, решение исходного уравнения:
X = 30 o , X = 150 o и X = 270 o .
2 Cos 2 X + Sin 2X = 0Используя идентичность двойного угла, Sin 2X можно заменить на 2 Sin X Cos X:
2 Cos 2 X + 2 Sin X Cos X = 0
2 Cos X является общим для обоих терминов, поэтому его можно переписать:
2 Cos X (Cos X + Sin X) = 0
Это уравнение дает 0, если либо 2 Cos X = 0, либо Cos X + Sin X = 0.Другими словами:
Cos X = 0 или Sin X = -Cos X
Первое уравнение дает два значения (X = 90 o , X = 270 o ). Второе уравнение также дает два значения (135 o и 315 o — проверьте эти цифры в таблице). Таким образом, решение исходного уравнения:
X = 90 o , X = 135 o , X = 270 o и 315 o .
© 2000, 2009 KryssTal
Введение в алгебру и способы решения простых, одновременных и квадратных уравнений. Прямоугольные треугольники, синусы, косинусы, касательные. Использование тригонометрических функций, рядов и формул. Графы — это способ визуализации алгебраических функций. Декартова система координат вводится вместе с описанием построения графика из первых принципов.Есть примеры разных типов графиков. Индекс и база. Определены логарифмы. База 10 и база e. Использование логарифмов в расчетах. Ряды для логарифмов. Сферическая тригонометрия — это тригонометрия треугольников, нарисованных на сфере. .
 1736
1736 5592
5592 8387
8387 9877
9877 9703
9703 7986
7986 515
515 1392
1392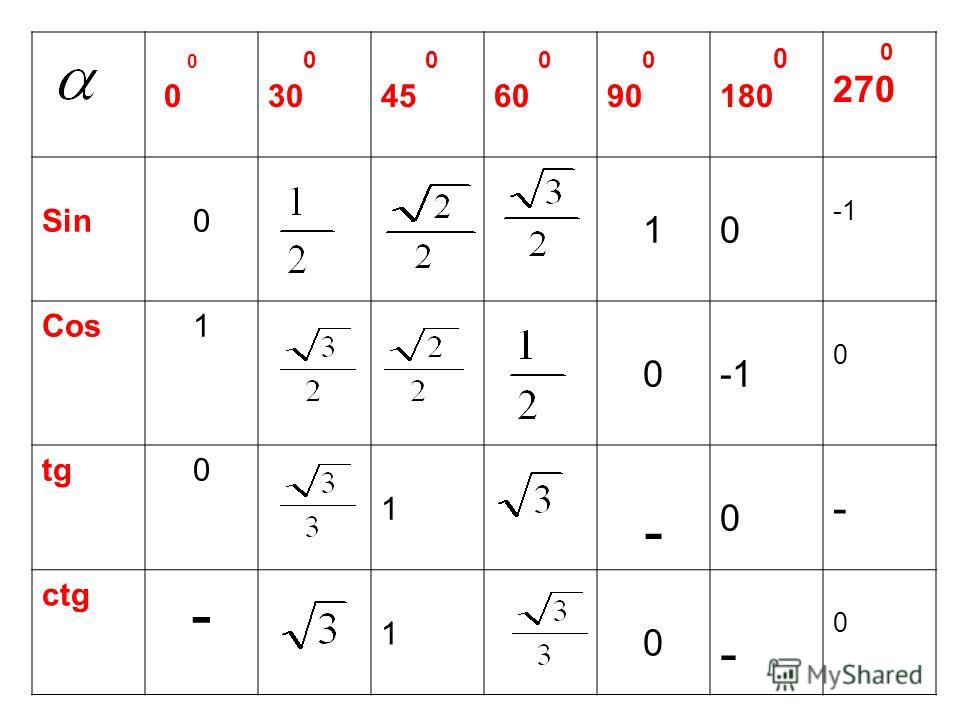 225
225 5878
5878 848
848 9877
9877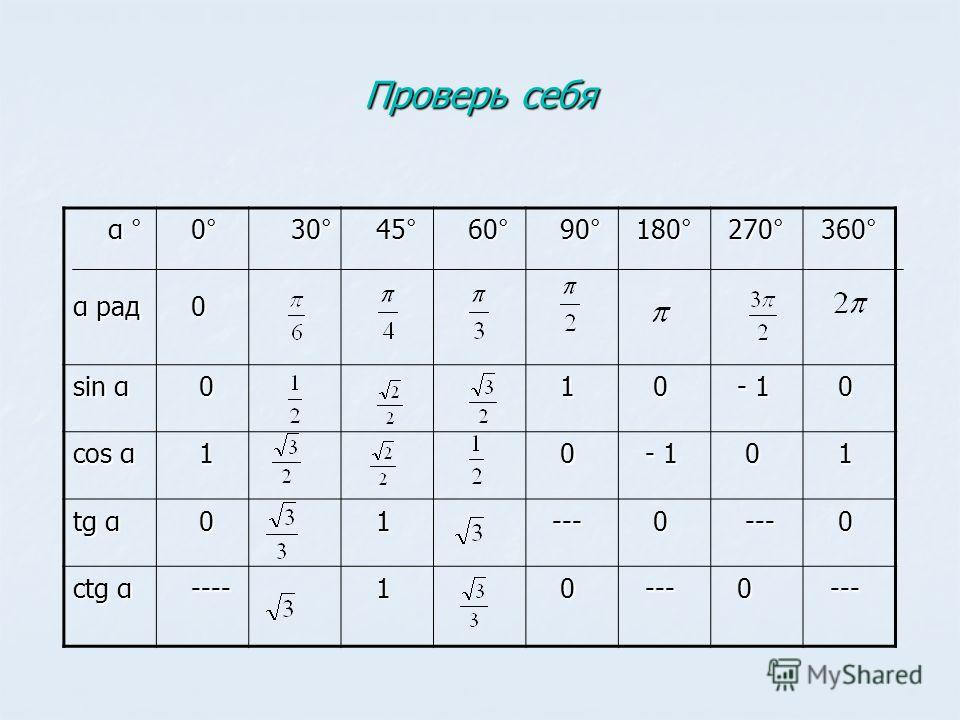 9744
9744 809
809 5299
5299 1564
1564