Тригонометрический круг со всеми значениями, числовая окружность синус косинус тангенс котангенс, как пользоваться тригонометрическим кругом

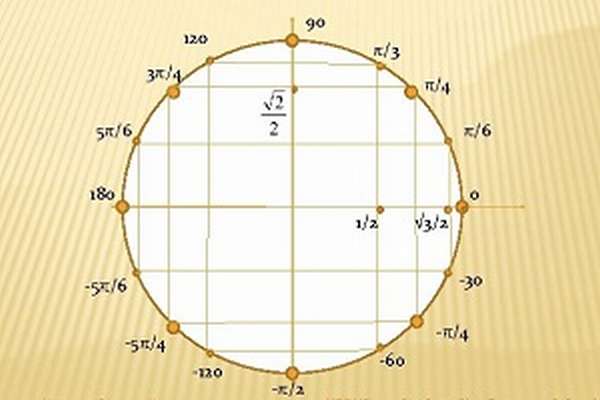
Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.

Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.

Тригонометрическая окружность

Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.

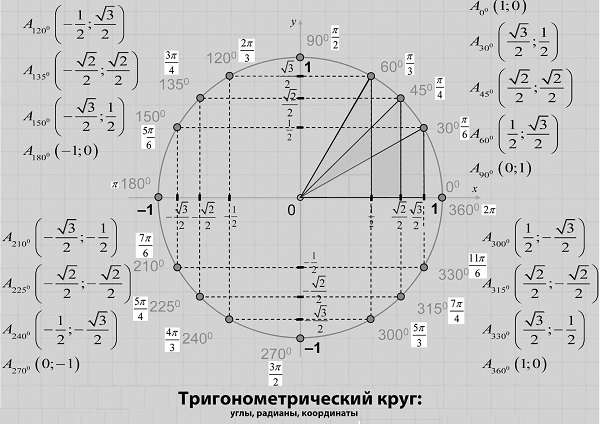
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.

Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике

Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.

Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.

Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).

Построение единичной окружности

Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.

Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.

Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.

Углы на тригонометрическом круге

Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.

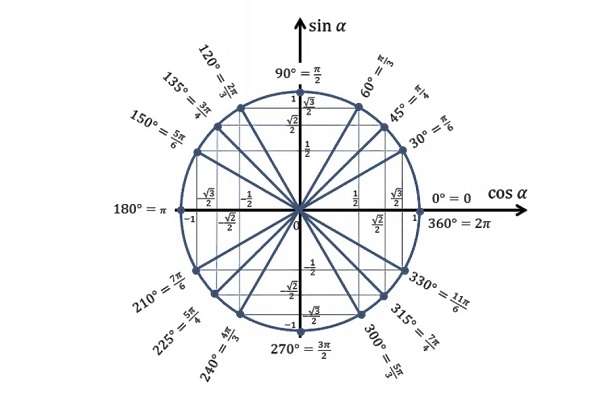
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?

Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.

Измеряются углы в радианах:

• от 0 до 90° значения углов от 0 до ∏/2,
• от 90 до 180° значения углов от ∏/2 до ∏,
• от 180 до 270° от ∏ до 3*∏/2,
• последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.

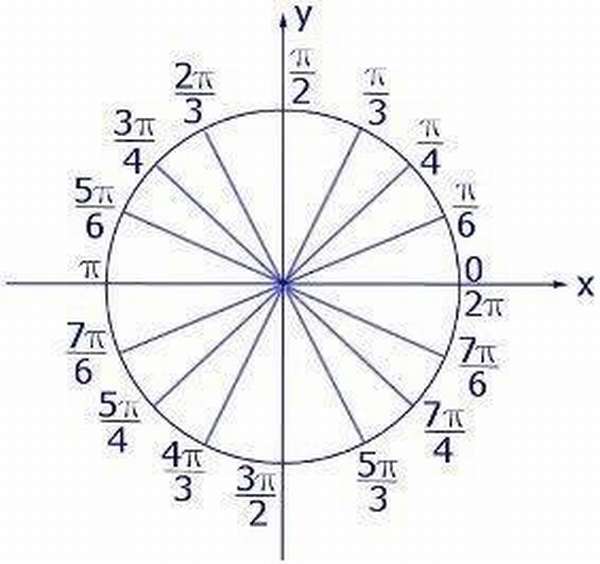
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.

Перевод углов из градусов в радианы

Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.

Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:

1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956

В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:

1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

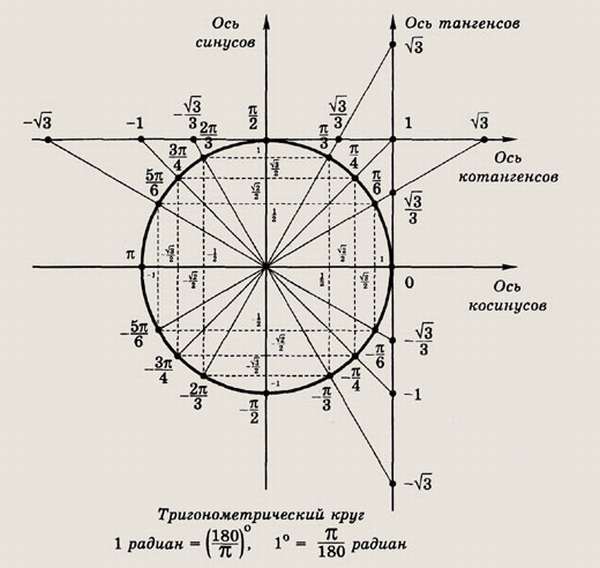
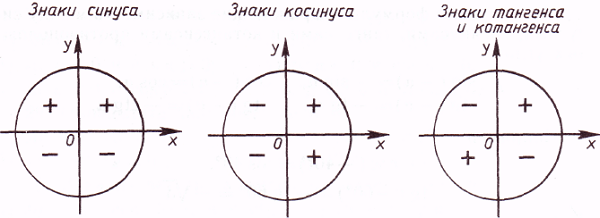
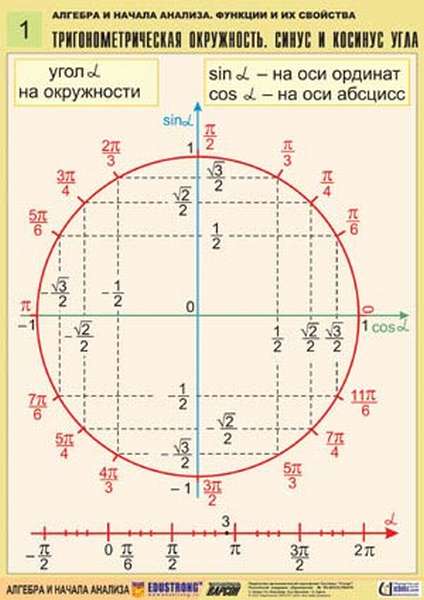
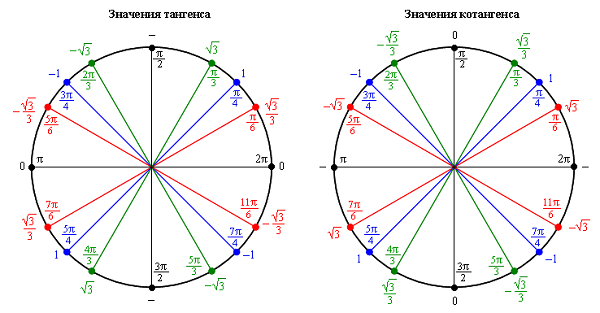
Косинус, синус, тангенс, котангенс на тригонометрической окружности

Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.

Заключение

В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.

Тригонометрия окружность со всеми значениями: ось синусов

Тригонометрический круг. Единичная окружность. Числовая окружность. Что это такое?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.

Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…» )

 

Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.

Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.

Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику. Сходите по ссылке, кто ещё не был. Тогда и здесь всё ясно будет.

Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность. Это я расскажу прямо здесь и сейчас.

Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов. Это будет в следующих уроках.

Всё. Разобравшись с этими тремя китами, получим надёжную, безотказную и совершенно законную шпаргалку для всей тригонометрии сразу.

А то в школьных учебниках с этой самым тригонометрическим кругом как-то не очень…

Начнём, помаленьку.

В предыдущем уроке вы усвоили, что синус, косинус, тангенс и котангенс (т.е.

тригонометрические функции) зависят только от угла. И не зависят от длин сторон в прямоугольном треугольнике. Отсюда интересный вопрос. Пусть у нас есть вот такой угол. Назовём его угол β. Буква красивая.)

Раз есть угол, у него должны быть тригонометрические функции! Синус, скажем, или котангенс… А где их взять? Нет ни гипотенузы, ни катетов…

Как определить тригонометрические функции угла без прямоугольного треугольника? Задачка… Придётся опять лезть в сокровищницу мировых знаний. К средневековым людям. Те всё умели…

Первым делом возьмём координатную плоскость. Это самые обычные координатные оси, ОХ – по горизонтали, ОY – по вертикали. И… прибьём одну сторону угла к положительной полуоси ОХ. Вершина угла, естественно, в точке О. Крепко прибьём, чтобы не оторвать! Вторую сторону оставим подвижной, чтобы угол менять можно было. Раздвижной у нас угол будет. Конец неприбитой стороны угла обозначим точкой А. Получим вот такую картинку:

 

 

Так, угол пристроили. А где его синус, где косинус? Спокойно! Сейчас всё будет.

Отметим координаты точки А на осях. Наведите курсор мышки на картинку и всё увидите. На ОХ это будет точка В, на ОY — точка С. Понятно, что В и С — это какие-то числа. Координаты точки А.

Так вот, число В будет косинусом угла β, а число С – его синусом!

С чего бы это? Древние люди учили нас, что синус и косинус – это отношения сторон! Которые от длин сторон не зависят. А мы тут координаты точки придумали… Но! Посмотрите на треугольник

ОАВ. Прямоугольный, кстати… По древнему определению косинус угла β равен отношению прилежащего катета к гипотенузе. Т.е. ОВ/ОА. Ладно, не возражаем. Причём косинус и синус не зависят от длин сторон.

Синус, косинус, тангенс и котангенс. Тригонометрический круг

А это вообще отлично! Это значит, что длины сторон можно брать какие угодно. Имеем полное право взять длину ОА за единицу! Неважно чего. Хоть метр, хоть километр, всё равно синус не меняется. А в этом случае

Вот так. Если провести такие же рассуждения для синуса, получим, что синус угла β равен АВ. Но АБ = ОС. Следовательно,

Можно сказать совсем просто. Синусом угла β будет игрековая

координата точки А, а косинусом – иксовая. Слова нестандартные, но тем лучше. Запоминается надёжнее! А запомнить это надо. Железно запомнить. Косинус – по иксу, синус – по игреку.

Нет, не обидели средневековые люди древних! Сберегли наследие! И отношение сторон сохранили, и возможности расширили чрезвычайно!

Однако, а где тригонометрический круг!? Где единичная окружность!? Ни слова про круги не было!

Верно. Но осталось всего ничего. Взять подвижную сторону ОА и повернуть её вокруг точки О на полный оборот. Как вы думаете, какую фигуру нарисует при этом точка А? Совершенно верно! Окружность! Вот она.

Вот это и будет тригонометрический круг.

Вот так. А почему круг — тригонометрический? Круг и круг… Вопрос резонный. Поясняю. Каждой точке окружности соответствуют два числа. Координата этой точки по Х и координата этой точки по Y. А координаты у нас что? Наведите курсор на рисунок. Координаты у нас — точки В и С. Т.е.

косинус и синус угла β. Т.е. тригонометрические функции. Поэтому круг и называется тригонометрическим.

Вспомнив, что ОА = 1, а ОА – радиус, сообразим, что это же – и единичная окружность тоже.

А так как синус и косинус — просто какие-то числа — этот тригонометрический круг будет ещё и числовой окружностью.

Три термина в одном флаконе.)

В данной теме эти понятия: тригонометрический круг, единичная окружность и числовая окружность – одно и то же. В более широком смысле, единичная окружность – это любая окружность с радиусом, равным единице. Тригонометрический круг – практический термин, как раз для работы с единичной окружностью в тригонометрии. Чем мы сейчас и позанимаемся. Работой с тригонометрическим кругом.

Первую половину работы мы уже выполнили. Нарисовали тригонометрический круг с помощью угла (классно звучит, правда?).

Теперь выполним вторую половину работы. Сделаем то же самое, только наоборот. Пройдём путь от тригонометрического круга к углу.

Пусть нам дана единичная окружность. Т.е. просто окружность, нарисованная на координатной плоскости, с радиусом, равным единице. Возьмём произвольно точку А на окружности. Отметим её координаты точками В и С на осях. Как нам помнится, её координаты — это cosβ (по иксу) и sinβ (по игреку). И синус с косинусом отметим. Получим вот такую картинку:

Всё понятно? Внимание, вопрос!

Где β!? Где угол β, без которого синуса и косинуса не бывает!?

Наводим курсор на картинку, и… вот он, вот он угол β! Именно его синус и косинус являются координатами точки А.

Кстати, здесь не нарисована прибитая сторона угла. Она и в предыдущих рисунках не нужна, только так, для понимания… Угол всегда отсчитывается от положительного направления оси ОХ. От направления стрелки.

А если точку А взять в другом месте? Окружность — она круглая… Да пожалуйста! Где угодно! Поместим, к примеру, точку А во вторую четверть, отметим её координаты, синус, косинус, как полагается. Вот так:

Самые наблюдательные заметят, что синус угла β – положительный (точка С – на положительной полуоси OY), а вот косинус – отрицательный! Точка В лежит на отрицательной полуоси ОХ.

Наводим курсор на картинку и видим угол β. Угол β здесь – тупой. Чего, кстати, решительно не бывет в прямоугольном треугольнике. А зря, что ли, мы возможности расширяли?

Уловили суть тригонометрического круга? Если взять точку в любом месте окружности, её координатами будут косинус и синус угла. Угол отсчитывается от положительного направления оси ОХ и до прямой, соединяющей центр координат с этой самой точкой на окружности.

Вот и всё. Проще хотелось бы, да некуда. Кстати, мой вам совет. Работая с тригонометрическим кругом, рисуйте не только точки на окружности,

но и сам угол! Как на этих рисунках. Понятнее будет.

Рисовать вам этот круг в тригонометрии постоянно придётся. Это не обязаловка, это и есть та легальная шпаргалка, которой пользуются умные люди. Сомневаетсь? Тогда назовите мне по памяти знаки вот таких выражений, к примеру: sin130⁰, cos150⁰, sin250⁰, cos330⁰? Я уж не спрашиваю про cos1050⁰ или sin(-145⁰)… Про такие углы в следующем уроке написано.

И нигде-то вы подсказку не найдёте. Только на тригонометрическом круге. Рисуем примерный угол в правильной четверти и сразу видим, куда попадают его синус и косинус. На положительные полуоси, или отрицательные. Кстати, определение знаков тригонометрических функций постоянно требуется в самых различных заданиях…

Или ещё, чисто для примера… Надо вам, например, узнать, что больше, sin130⁰, или sin155⁰? Попробуй-ка, сообрази просто так…

А мы умные, мы нарисуем тригонометрический круг. И нарисуем на нём угол

примерно 130 градусов. Исходя только из того, что он больше 90 и меньше 180 градусов. Ориентируемся на угол, а не на окружность! Уж где пересечёт подвижная сторона угла окружность, там и пересечёт. Отмечаем игрековую координату точки пересечения. Это будет sin130⁰. Как на этом рисунке:

А затем, здесь же, нарисуем угол 155 градусов. Примерно нарисуем, зная, что он больше 130 градусов. И меньше 180. Отметим и его синус. Наведите курсор на картинку, всё увидите. Ну и что, какой синус больше? Тут уж совсем трудно ошибиться! Конечно sin130⁰ больше, чем sin155⁰!

Долго? Да ну?! Никто не требует от вас тщательно прорисовывать картину и обеспечивать мультипликацию! Поработаете с этим сайтом, и по этой задаче будете за 10 секунд рисовать вот такую картинку:

Другой и не сообразит, что это за каракули, да… А вы спокойно и уверенно дадите правильный ответ! Хотя, аккуратность и не мешает… А то можно такую «окружность» нарисовать, что ответ обратный получится…

Эта задачка — только один пример широких возможностей тригонометрического круга. Освоить эти возможности вполне реально. Чем мы и займёмся далее.

Чаще всего вам придётся иметь с тригонометрическими функциями в обычной, алгебраической записи. Типа sin45⁰, tg(-3), cos(x+y) и так далее. Безо всяких картинок и тригонометрических кругов! Рисовать этот самый круг надо самим. Руками. Если, конечно, хотите легко и правильно решать задания по тригонометрии. В том числе и самые продвинутые. Но особо не волнуйтесь. Уж на этом сайте, в тригонометрии, я вам обеспечу рисование кругов! И вы освоите этот крайне полезный приём. Однозначно.

Подведём итоги урока.

В этой теме мы плавно перешли от тригонометрических функций угла в прямоугольном треугольнике к тригонометрическим функциям любого угла. Для этого нам понадобилось освоить понятия «тригонометрический круг, единичная окружность, числовая окружность». Это очень полезно.)

Здесь я рассказывал о тригонометрическом круге в применении к синусу и косинусу. Но тангенс и котангенс тоже можно увидеть на круге! Одно движение ручкой, и вы легко и правильно определяете знак тангенса — котангенса любого угла, решаете тригонометрические неравенства и вообще потрясаете окружающих своими тригонометрическими способностями.)

Если вас интересуют такие перспективы — можно посетить урок «Тангенс и котангенс на тригонометрическом круге» в Особом разделе 555.

Далее мы разберёмся со следующими вопросами.

Как выглядят углы в 1000 градусов? Как выглядят отрицательные углы? Что за загадочное число «Пи», на которое неизбежно наталкиваешься в любом разделе тригонометрии? И каким боком это «Пи» к углам пристраивается? Всё это – в следующих уроках.

---

Тригонометрический круг (окружность)

ОПРЕДЕЛЕНИЕ

Тригонометрический круг (окружность) – круг радиуса один (единичная окружность), с центром в начале координат (рисунок 1).

За нулевое положение радиуса, принимается его положение на положительном направлении оси Ox. Угол поворота радиуса отсчитывается от положительного направления оси Ox: с плюсом – против часовой стрелки, с минусом – по часовой стрелке. Полный круг – это . Каждому углу от до соответствует точка на единичной окружности.

Синусом угла есть ордината точки , а косинусом угла есть абсцисса точки .

Рис. 1

Примеры решения задач

ПРИМЕР 1

Задание	Используя единичную окружность, определить синус и косинус угла .
Решение	Отложим на единичной окружности угол равный (рис. 1), ему будет соответствовать точка A окружности. Найдем синус заданного угла. Для этого найдем проекцию точки A на ось Oy, ею будет точка . Значит, ордината точки A равна и значение . Для нахождения косинуса заданного угла, найдем проекцию точки A на ось Ox. Ею будет точка , тогда абсцисса точка A равна и, соответственно, .
Ответ

Единицы измерения углов

Углы обычно измеряются либо в градусах, либо в радианах. Перевести градусы в радианы просто: 360 градусов (полный круг) соответствует радиан.

ПРИМЕР 2

Задание	Перевести: 1) угол в градусы; 2) угол в радианы.
Решение	1) Для того чтобы перевести угол из радиан в градусы, умножим данный угол на . Получим     2) Для того чтобы перевести заданный угол из градусов в радианы, умножим его на . Получим
Ответ

На единичной окружности также можно находить углы, которые больше 360 градусов. Поскольку, значения синуса и косинуса на тригонометрическом круге повторяются каждые .

ПРИМЕР 3

Задание	Найти с помощью единичной окружности синус угла .
Решение	Представим данный угол следующим образом     Таким образом, необходимо сделать два полных обхода окружности, а затем остановиться в точке соответствующей углу в (рис. 1). Синусу соответствует ордината этой точки, то есть .
Ответ

Читайте также:

Тригонометрические функции

Тригонометрические уравнения и их решение

Косинус 45 градусов

Основное тригонометрическое тождество

Обратные тригонометрические функции

Синус угла

Тригонометрическая единичная окружность. Функция синуса. Функция косинуса.

Возьмем ось \(x\) и ось \(y\) , и пусть \(0\)-начало координат. Круг с центром в точке \(0\) и радиусом \(1\) называется тригонометрической окружностью или единичной окружностью.

Единичная окружность

Если \(P\)- точка на окружности, а \(A\)-угол между отрезком \(PO\) и \(x\), то:

 

 

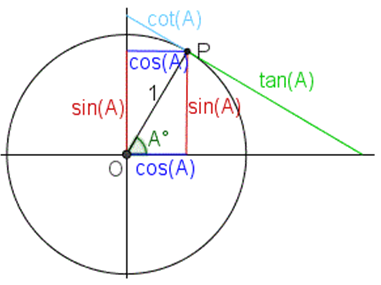
• \(x\)-координата \(P\) называется косинусом \(A\). мы пишем \(cos (A)\) или \(cos A\);
• \(y\)-координата \(P\) называется синусом \(A\). Мы пишем \(sin (A)\) или \(sin A\);

число \(\frac{sin (A)} { cos (A)}\) называется касательной \(A\) , мы пишем \(tg (A)\) ;

 

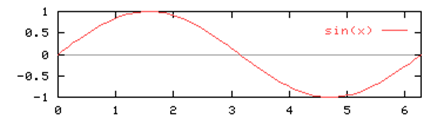
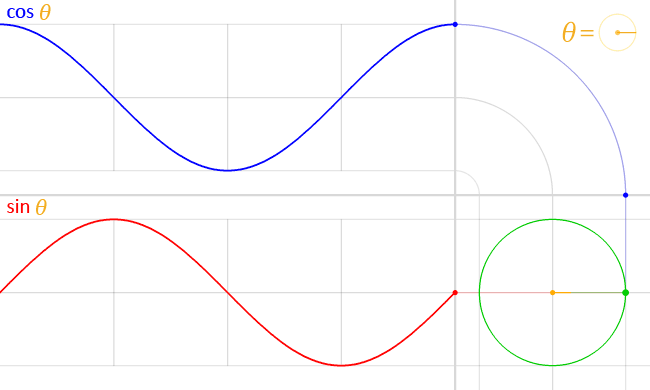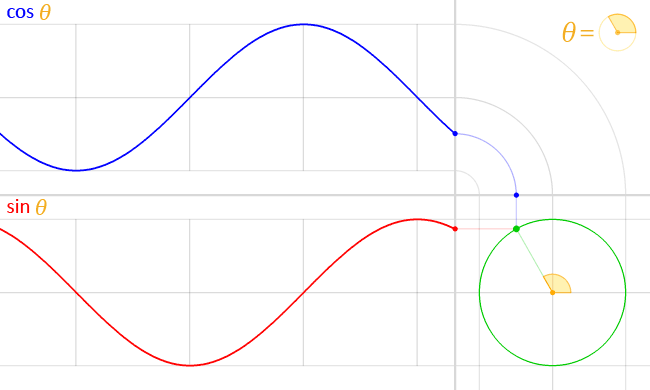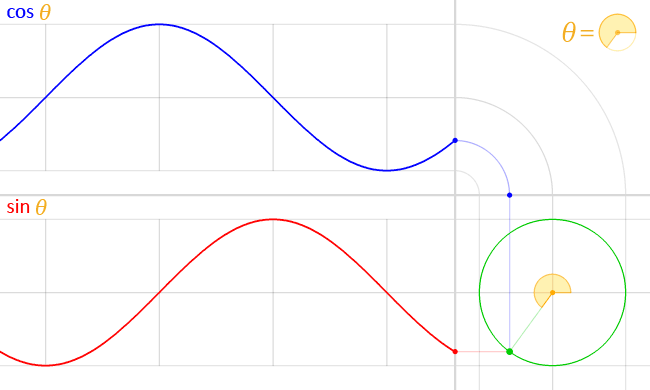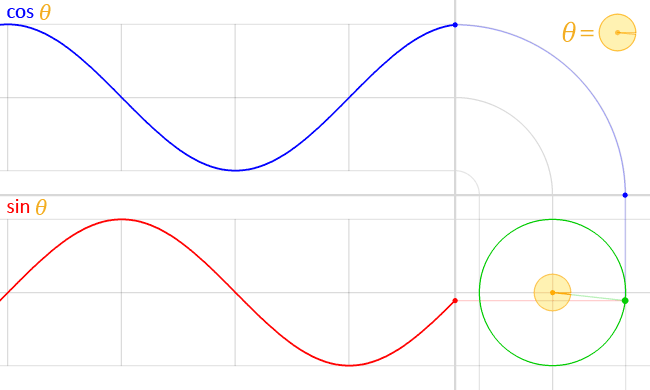
Функция синуса
\(sin: R — > [-1;1]\)

Все тригонометрические функции являются периодическими c периодом \( 2π.\)
Диапазон функции равен \([-1,1]\).

 

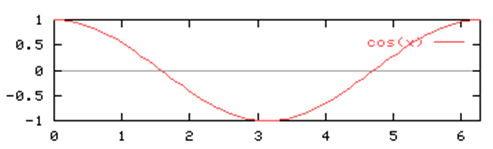
Функция косинуса
\(cos: R — > [-1;1]\)

Период \(2π\).
Диапазон функции также равен \( [-1,1]\) .

 

Функция тангенса
\(tan: R — > R\)
Период диапазона \(π\) функции \(R\) не определен при \( x = \frac{π}{2} + kn, k=0,1,2,…\)
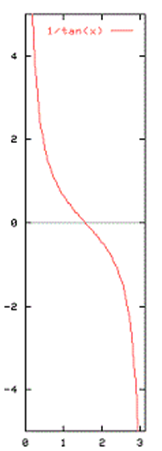
График функции тангенса на интервале \(0 — π\)

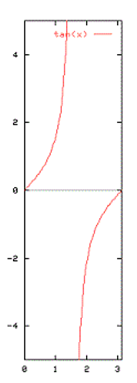
Функция котангенс 
\(ctg: R — > R\)
Диапазон функции \(R\). период \(π\) и что функция не определена при \( x = kn, k=0,1,2,…\)

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(60)
4	Найти точное значение	sin(30 град. )
5	Найти точное значение	sin(60 град. )
6	Найти точное значение	tan(30 град. )
7	Найти точное значение	arcsin(-1)
8	Найти точное значение	sin(pi/6)
9	Найти точное значение	cos(pi/4)
10	Найти точное значение	sin(45 град. )
11	Найти точное значение	sin(pi/3)
12	Найти точное значение	arctan(-1)
13	Найти точное значение	cos(45 град. )
14	Найти точное значение	cos(30 град. )
15	Найти точное значение	tan(60)
16	Найти точное значение	csc(45 град. )
17	Найти точное значение	tan(60 град. )
18	Найти точное значение	sec(30 град. )
19	Преобразовать из радианов в градусы	(3pi)/4
20	График	y=sin(x)
21	Преобразовать из радианов в градусы	pi/6
22	Найти точное значение	cos(60 град. )
23	Найти точное значение	cos(150)
24	Найти точное значение	tan(45)
25	Найти точное значение	sin(30)
26	Найти точное значение	sin(60)
27	Найти точное значение	cos(pi/2)
28	Найти точное значение	tan(45 град. )
29	График	y=sin(x)
30	Найти точное значение	arctan(- квадратный корень 3)
31	Найти точное значение	csc(60 град. )
32	Найти точное значение	sec(45 град. )
33	Найти точное значение	csc(30 град. )
34	Найти точное значение	sin(0)
35	Найти точное значение	sin(120)
36	Найти точное значение	cos(90)
37	Преобразовать из радианов в градусы	pi/3
38	Найти точное значение	sin(45)
39	Найти точное значение	tan(30)
40	Преобразовать из градусов в радианы	45
41	Найти точное значение	tan(60)
42	Упростить	квадратный корень x^2
43	Найти точное значение	cos(45)
44	Упростить	sin(theta)^2+cos(theta)^2
45	Преобразовать из радианов в градусы	pi/6
46	Найти точное значение	cot(30 град. )
47	Найти точное значение	arccos(-1)
48	Найти точное значение	arctan(0)
49	График	y=cos(x)
50	Найти точное значение	cot(60 град. )
51	Преобразовать из градусов в радианы	30
52	Упростить	( квадратный корень x+ квадратный корень 2)^2
53	Преобразовать из радианов в градусы	(2pi)/3
54	Найти точное значение	sin((5pi)/3)
55	Упростить	1/( кубический корень от x^4)
56	Найти точное значение	sin((3pi)/4)
57	Найти точное значение	tan(pi/2)
58	Найти угол А	tri{}{90}{}{}{}{}	
59	Найти точное значение	sin(300)
60	Найти точное значение	cos(30)
61	Найти точное значение	cos(60)
62	Найти точное значение	cos(0)
63	Найти точное значение	arctan( квадратный корень 3)
64	Найти точное значение	cos(135)
65	Найти точное значение	cos((5pi)/3)
66	Найти точное значение	cos(210)
67	Найти точное значение	sec(60 град. )
68	Найти точное значение	sin(300 град. )
69	Преобразовать из градусов в радианы	135
70	Преобразовать из градусов в радианы	150
71	Преобразовать из радианов в градусы	(5pi)/6
72	Преобразовать из радианов в градусы	(5pi)/3
73	Преобразовать из градусов в радианы	89 град.
74	Преобразовать из градусов в радианы	60
75	Найти точное значение	sin(135 град. )
76	Найти точное значение	sin(150)
77	Найти точное значение	sin(240 град. )
78	Найти точное значение	cot(45 град. )
79	Преобразовать из радианов в градусы	(5pi)/4
80	Упростить	1/( кубический корень от x^8)
81	Найти точное значение	sin(225)
82	Найти точное значение	sin(240)
83	Найти точное значение	cos(150 град. )
84	Найти точное значение	tan(45)
85	Вычислить	sin(30 град. )
86	Найти точное значение	sec(0)
87	Упростить	arcsin(-( квадратный корень 2)/2)
88	Найти точное значение	cos((5pi)/6)
89	Найти точное значение	csc(30)
90	Найти точное значение	arcsin(( квадратный корень 2)/2)
91	Найти точное значение	tan((5pi)/3)
92	Найти точное значение	tan(0)
93	Вычислить	sin(60 град. )
94	Найти точное значение	arctan(-( квадратный корень 3)/3)
95	Преобразовать из радианов в градусы	(3pi)/4
96	Вычислить	arcsin(-1)
97	Найти точное значение	sin((7pi)/4)
98	Найти точное значение	arcsin(-1/2)
99	Найти точное значение	sin((4pi)/3)
100	Найти точное значение	csc(45)