Внеклассный урок — Формулы двойного аргумента
Формулы двойного аргумента (двойного угла)Выражения sin 2x, cos 2x, tg 2x можно выразить через sin x, cos x, tg x. Эти преобразующие формулы называются формулами двойного аргумента (или двойного угла).
Логику преобразования можно понять на примере выражения sin 2x.
Представим это выражение в виде sin (x + x).
Тогда мы легко можем применить формулу синуса суммы аргументов:
sin (x + x) = sin x cos x + cos x sin x = 2 sin x cos x.
Мы получили первую из формул двойного аргумента. А вот все формулы:
sin 2x = 2 sin x cos x cos 2x = cos2x – sin2x cos 2x = 1 – 2 sin2x 2 tg x |
В первых строках мы показали, как была получена первая формула из таблицы.
Вычислим остальные три.
2) cos 2x = cos2x – sin2x.
Здесь так же представляем 2х в виде х + х и применяем формулу косинуса сложения аргументов:
cos 2x = cos (x + x) = cos x cos x – sin x sin x = cos2x – sin2x.
3) cos 2x = 1 – 2 sin2x.
Здесь мы просто продолжим преобразовывать предыдущую формулу.
Используем для этого основное тригонометрическое тождество cos2x + sin2x = 1.
Из этого тождества следует, что cos2x = 1 – sin2x. Итак, выпишем предыдущую формулу, вставим значение cos2x, сведем подобные члены и получим результат:
cos 2x = cos2x – sin2x = 1 – sin2x – sin2x = 1 – 2sin2x.
2 tg x
4) tg 2x = ————
1 – tg2x
Способов, как прийти к такому тождеству, два.
Первый способ. Здесь нам поможет формула тангенса сложения аргументов. Для этого представим tg 2x в виде tg (x + х). Итак:
tg х + tg х 2 tg х
tg 2x = tg (x + х) = —————— = —————
1 – tg х tg х 1 – tg2х
Второй способ. Он сложнее. Сначала применяем формулы синуса и косинуса сложения аргументов:
sin (x + х) sin x cos х + cos x sin х
tg 2x = tg (x + х) = —————— = ———————————
cos (x + х) cos x cos х – sin x sin х
Теперь, чтобы упростить выражение, делим все его части на cos x cos х, сокращаем подобные члены и приходим к решению:
sin x cos х cos x sin х 2 sin х
————— + ————— —————
cos x cos х cos x cos х 2 cos х 2 tg x
———————————— = ——————— = —————
cos x cos x sin x sin х sin2x 1 – tg2x
————— – ————— 1 – ————
cos x cos x cos x cos х cos2x
ПРИМЕЧАНИЕ:
При решении конкретных задач важно помнить, что задача имеет смысл лишь в том случае, если в процессе решения знаменатели нигде не оказываются равны нулю.
Теперь для наглядности решим несколько примеров по теме.
Пример 1. Упростить выражение:
sin 2α
———
sin α
Решение:
sin 2α 2 sin α cos α
——— = —————— = 2 cos α
sin α sin α
Пример 2. Пусть tg α = 3/4 и 180º < α < 270º.
Найти sin 2α.
Решение.
В первую очередь, отмечаем, что угол находится в третьей четверти. Значит, синус будет со знаком минус.
1
1) Значение синуса мы могли бы найти через формулу 1 + ctg2 α = ———.
sin2 α
Значит, нам надо сначала вычислить значение котангенса. Мы знаем, что tg α · ctg α = 1. Следовательно:
1 1 4
ctg α = —— = —— = ——
tg α 3/4 3
2) Теперь находим значение синуса:
1 1 1 1 9
sin2 α = ————— = ————— = ———— = —— = ——
1 + ctg2 α 1 + (4/3)2 1 + 16/9 25/9 25
3
sin α = – ——
5
3) Мы знаем, что sin 2α = 2 sin α cos α.
Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:
9 16
cos2 α = 1 – sin2 α = 1 – —— = ——
25 25
4
cos α = – ——
5
4) Осталось применить формулу двойного угла:
3 4 2 · 3 · 4 24
sin 2α = 2 · (– ——) · (– ——) = ———— = —— = 0,96.
5 5 5 · 5 25
Пример решен.
Пример 3: Вычислить
π π
cos2 — – sin2 —
8 8
Решение.
Это выражение соответствует правой части формулы косинуса двойного
аргумента (cos 2x = cos2x – sin2x).
Значит, просто приравняем его к левой части. Для этого замечаем, что
π
х = —
8
Остается ввести в формулу это значение х и решить уравнение:
π π π 2π π √2
cos2 —— – sin2 —— = cos 2 ∙ —— = cos —— = cos —— = —— .
8 8 8 8 4 2
Пример решен.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) |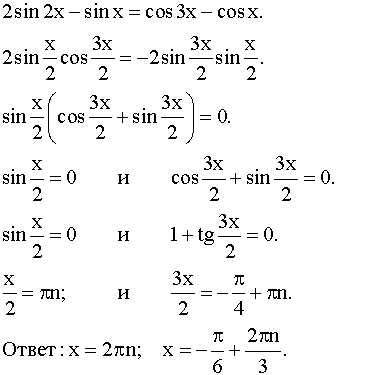
|
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | sin(pi/6) | ||
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) |
|
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | ||
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) |
|
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| (1) | Основное тригонометрическое тождество | sin2(α) + cos2(α) = 1 | ||
| (2) | Основное тождество через тангенс и косинус | 1 + tg2(α) = 1/cos2(α) | ||
| (3) | Основное тождество через котангенс и синус | 1 + ctg2(α) = 1/sin2(α) | ||
| (4) | Соотношение между тангенсом и котангенсом | tg(α)ctg(α) = 1 | ||
| (5) | Синус двойного угла | sin(2α) = 2sin(α)cos(α) | ||
| (6) | Косинус двойного угла | cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α) | ||
| (7) | Тангенс двойного угла |
| ||
| (8) | Котангенс двойного угла |
| ||
| (9) | Синус тройного угла | sin(3α) = 3sin(α)cos2(α) – sin3(α) | ||
| (10) | Косинус тройного угла | cos(3α) = cos3(α) – 3cos(α)sin2(α) | ||
| (11) | Косинус суммы/разности | cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β) | ||
| (12) | Синус суммы/разности | sin(α±β) = sin(α)cos(β) ± cos(α)sin(β) | ||
| (13) | Тангенс суммы/разности | tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β)) | ||
| (14) | Котангенс суммы/разности | ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β)) | ||
| (15) | Произведение синусов | sin(α)sin(β) = ½(cos(α–β) – cos(α+β)) | ||
| (16) | Произведение косинусов | cos(α)cos(β) = ½(cos(α+β) + cos(α–β)) | ||
| (17) | Произведение синуса на косинус | sin(α)cos(β) = ½(sin(α+β) + sin(α–β)) | ||
| (18) | Сумма/разность синусов | sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β)) | ||
| (19) | Сумма косинусов | cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β)) | ||
| (20) | Разность косинусов | cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β)) | ||
| (21) | Сумма/разность тангенсов | tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β) | ||
| (22) | Формула понижения степени синуса | sin2(α) = ½(1 – cos(2α)) | ||
| (23) | Формула понижения степени косинуса | cos2(α) = ½(1 + cos(2α)) | ||
| (24) | Сумма/разность синуса и косинуса | sin(α) ± cos(α) = &sqrt;2sin(α±π/4) | ||
| (25) | Сумма/разность синуса и косинуса с коэффициентами | Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²))) | ||
| (26) | Основное соотношение арксинуса и арккосинуса | arcsin(x) + arccos(x) = π/2 | ||
| (27) | Основное соотношение арктангенса и арккотангенса | arctg(x) + arcctg(x) = π/2 |
Математика (при поддержке «Ветвистого древа») 2009—2021Чему равен sin 2x. Основные формулы тригонометрии
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла.
Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов.
Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов.
Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Универсальная тригонометрическая подстановка
Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки .
Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве.
Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у
= sin x .
Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов.
На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д).
у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.
Итак, нам нужны косинус двойного угла и тригонометрическая единица:
Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:
и подставить его в косинус двойного угла, то получим:
Это — еще одна формула косинуса двойного угла:
Эта формула — ключ к получению формулы понижения степени:
Итак, формула понижения степени синуса:
Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:
Теперь из тригонометрической единицы выразим синус:
Подставим это выражение в формулу косинуса двойного угла:
Получили еще одну формулу косинуса двойного угла:
Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.
Таким образом, формула понижения степени косинуса:
Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:
Так как тангенс — отношение синуса к косинусу то формула для тангенса:
Котангенс — отношение косинуса к синусу.
Поэтому формула для котангенса:
Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.
Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.
Урок алгебры в 10-м классе по теме «Формулы двойного аргумента»
Цели урока:
Образовательные – вывести формулы тригонометрии, позволяющие выразить sin 2x, cos 2x, tg 2x через sinx, cosx, tgx, показать многообразие их применения.
Развивающие – вырабатывать навыки и
умения использовать полученные формулы в
тригонометрических преобразованиях, развивать
математическое мышление учащихся, умение видеть
и применить изученные тождества, развивать
умения самостоятельной учебно-познавательной
деятельности, развивать культуру речи и
любознательность.
Воспитательные – побуждать учащихся к преодолению трудностей в процессе умственной деятельности, к самоконтролю и самоанализу.
Ожидаемый результат: Каждый учащийся должен знать вывод формул двойного аргумента и уметь применять их для преобразований тригонометрических выражений на уровне обязательных результатов обучения.
Тип урока: Урок ознакомления с новым материалом.
План урока:
- Организационно-мотивационный этап.
- Актуализация имеющихся знаний и личного опыта учащихся (устная работа).
- Изучение нового материала.
- Домашнее задание.
- Итог урока.
- Закрепление изученного материала (контрольный срез).
Ход урока
Презентация.
1. Организационно-мотивационный этап.
Сегодня на уроке мы выведем формулы тригонометрии – формулы двойного аргумента и рассмотрим многообразие их применения. Эпиграфом нашего урока будут слова Бернардо Больцано “Формула подчас кажется более мудрой, чем выдумавший ее человек”.
2. Актуализация имеющихся знаний и личного опыта учащихся (устная работа).
Вспомним формулу синус суммы, косинус суммы и тангенс суммы аргументов. Вызываются 3 учащихся, которые на 3 досках записывают отдельно эти формулы:
sin(x +y) = sinxcosy + cosxsiny;
cos(x+y) = cosxcosy – sinxsiny;
tg(x+y) = .
Далее учащиеся устно работают с места.
№1 Упростить:
а)
б)
в)
г)
№2 Вычислить:
а)
б)
в)
г)
д)
3. Изучение нового материала.
Сейчас мы выведем с вами тригонометрические формулы двойного аргумента и рассмотрим многообразие их применения.
Если положить в формулах, записанных вами в начале урока на доске x= y, то получаем:
1)
sin(x+y) = sinxcosy + cosxsiny
sin2x = sinxcosx + sinxcosx = 2sinxcosx
2)
cos(x+y) = cosxcosy – sinxsiny
cos2x = cosxcox – sinxsinx = cos2x – sin2x
3)
tg(x+y) =
tg2x =
Каждую из 3-х формул выводит 1 ученик.
Рассмотреть варианты применения данных формул.
- sin10x = 2sin5x*cos5x
- sin
- cos(8x – 14y) = cos2(4x – 7y) – sin2(4x – 7y)
- tg
- 2sin7xcos7x = sin14x
- cos23,5t — sin23,5t = cos7t
А теперь докажем два тождества, используя доказанную в начале урока формулу cos 2x = cos 2x – sin2x
1.
Доказать тождество:
cos2x = 1 – 2sin2x
cos2x = cos2x – sin2x = (1 — sin2x) — sin2x
= 1 — 2 sin2x
cos2x = 1 — 2 sin2x
2. Доказать тождество:
cos2x = 2cos2x – 1
cos2x = cos2x – sin2x = cos2x – (1 — cos2x)
= 2cos2x – 1
cos2x = 2cos2x – 1
3. Выразить sin2x из равенства:
cos2x = 1 — 2sin2x
2 sin2x = 1 – cos2x
sin2x =
4. Выразить cos2x из равенства:
cos2x = 2cos2x – 1
cos2x+1 = 2cos2x
2cos2x = cos2x+1
cos2x =
Итак, выполняя №1 и №2, мы получили еще два варианта формулы двойного аргумента, а выполняя №3 и №4, вывели формулы понижения степени.
4. Домашнее задание.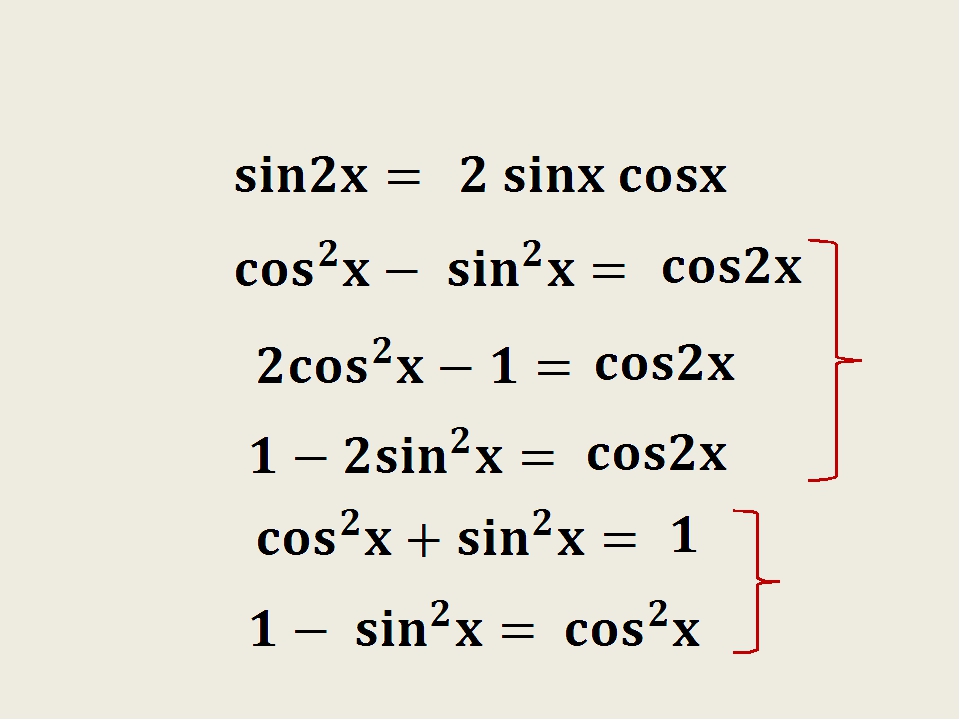
- §21
- №21.1 – 21.6 (а)
- №21.9 (а)
5. Итог урока.
- Что нового узнали на уроке?
- Довольны ли вы своей работой на уроке?
6. Закрепление изученного материала. Контрольный срез.
Учащиеся выполняют работу на карточках с дифференцированными заданиями по теме урока (самопроверка).
1 вариант.
№1 Упростите, продолжив решение, и выберите правильный ответ:
а)
Ответ:
1) 4/3;
2) 4/3cosx;
3) 2/3;
4) 4/3ctgx.
б)
Ответ:
1) cos20;
2) 2cos20;
3) ctg20;
4) другой ответ.
№2 Упростите и выберите правильный ответ:
а)
Ответ:
1) 3tgx;
2) 3sinx;
3) 1.
5sinx;
4) 3tg2x.
б) cos2t – cos2t =
Ответ:
1) sin2t;
2) -sin2 t;
3) 2cos2 t+sin2 t;
4) другой ответ.
2 вариант.
№1 Упростите, продолжив решение, и выберите правильный ответ:
а)
Ответ:
1) -3tg2x;
2) 3sin2 x;
3) 6 tgx;
4) 3tg2 x.
б)
Ответ:
1) 3/2;
2) 2/3;
3) 2/3sin2x;
4) другой ответ.
№2 Упростите и выберите правильный ответ:
а)
Ответ:
1) tg2x;
2) 2sinx;
3) 1/2sinx;
4) 1/2 + tgx.
б) cos2t + sin2t =
Ответ:
1) cos2t;
2) 2sint;
3) cost-sint;
4) другой ответ.
Проверяются верные ответы.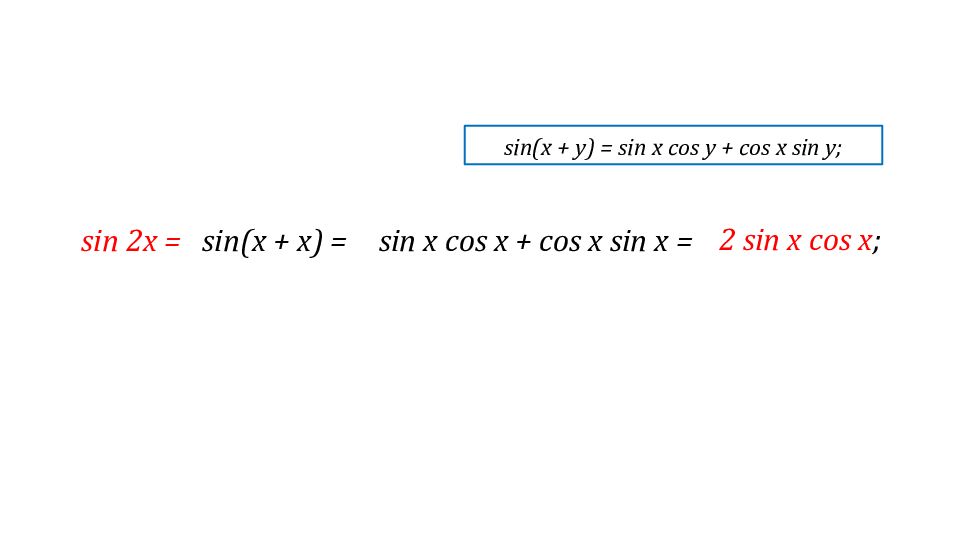
1 вариант:
№1 а) 1; б) 2.
№2 а) 2;б) 1.
2 вариант:
№1 а) 4; б) 2.
№2 а) 3; б) 1.
Учащиеся поднимают руку, кто при выполнении работы сделал 2 ошибки, затем – кто одну ошибку и, наконец, кто не сделал ни одной ошибки, выполнил всё полностью и верно.
Молодцы ребята, отлично поработали.
Ученики сдают карточки на проверку учителю.
На следующих двух уроках мы с вами продолжим изучение применения формул двойного аргумента в тригонометрических преобразованиях.
Спасибо всем за урок!
Урок решить уравнение синус 2х 1 2. Тригонометрические уравнения — формулы, решения, примеры. можно познакомиться с функциями и производными
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A .
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках.
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности.
На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
как вывести забытую тригонометрическую формулу?
На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии.
Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.
Будем опираться на следующие формулы:
- Основное тригонометрическое тождество: sin2a+cos2a = 1
- Определение тангенса:
- Определение котангенса:
- Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
- Формула косинуса суммы: cos(a+b) = cosacosb—sinasinb
Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:
- Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb—cosasinb
- Косинус разности: cos(a-b) = cosacos(-b)—sinasin(-b) = cosacosb+sinasinb
Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:
- Синус двойного угла: sin2a = sin(a+a) = sinacosa+cosasina = 2sinacosa
- Косинус двойного угла: cos2a = cos(a+a) = cosacosa—sinasina = cos2a—sin2a
Аналогично получаются и формулы других кратных углов:
- Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos2a—sin2a)sina = 2sinacos2a+sinacos2a—sin3a = 3sinacos2a—sin3a = 3sina(1-sin2a)-sin3a = 3sina-4sin3a
- Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa—sin2asina = (cos2a—sin2a)cosa-(2sinacosa)sina = cos3a-sin2acosa-2sin2acosa = cos3a-3sin2acosa = cos3a-3(1-cos2a)cosa = 4cos3a-3cosa
Прежде чем двигаться дальше, рассмотрим одну задачу.
Дано: угол — острый.
Найти его косинус, если
Решение, данное одним учеником:
Т.к. , то sina = 3,а cosa = 4.
(Из математического юмора)Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin2a+cos2a = 1 и разделим его на cos2a. Получим:
- Связь тангенса и косинуса:
Так что решением этой задачи будет:
(Т.к. угол острый, при извлечении корня берётся знак +)- Аналогично получаем связь котангенса и синуса:
Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию.
Выведем её так:- Формула тангенса суммы: . Разделив числитель и знаменатель на произведение косинусов, получим:
Сразу выводится и
- Формула тангенса двойного угла:
Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла:
cos2a = cos2a—sin2a
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos2a+1 = cos2a—sin2a+cos2a+sin2a
2cos2a = cos2a+1
Выражая cosa через cos2a и выполняя замену переменных, получаем:- Косинус половинного угла:
Знак берётся в зависимости от квадранта.
Аналогично, отняв от левой части равенства единицу, а от правой — сумму квадратов синуса и косинуса, получим:
cos2a-1 = cos2a—sin2a—cos2a—sin2a
2sin2a = 1-cos2a- Cинус половинного угла:
И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, b+x-y. Тогда
sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosxsiny+sinxcosy-cosxsiny = 2sinxcosy. Выразим теперь x и y через a и b.Поскольку a = x+y, b = x-y, то . Поэтому
- Представление суммы синусов в виде произведения:
Сразу же можно вывести
- Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))
Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.
Sin2x — Формула, Тождества, Примеры, Доказательство
Формула Sin2x — одна из формул двойного угла в тригонометрии.
Используя эту формулу, мы можем найти синус угла, значение которого увеличивается в два раза. Мы знаем, что грех — это одно из основных тригонометрических соотношений, которое определяется как отношение длины противоположной стороны (угла) к длине гипотенузы в прямоугольном треугольнике. Существуют различные формулы, связанные с sin2x, и их можно проверить, используя основные тригонометрические формулы.2x с точки зрения различных тригонометрических функций с использованием разных тригонометрических формул и, следовательно, вывести формулы.Что такое Sin2x?
Sin2x — это тригонометрическая формула в тригонометрии, которая используется для решения различных тригонометрических задач, задач интегрирования и дифференцирования. Он используется для упрощения различных тригонометрических выражений. Формула Sin2x может быть выражена в различных формах с использованием различных формул тригонометрии. Наиболее часто используемая формула sin2x представляет собой удвоенное произведение функции синуса и функции косинуса, которое математически определяется выражением sin2x = 2 sinx cosx.
Мы также можем выразить sin2x через функцию тангенса.Sin2x Формула
Формула sin2x представляет собой тождество двойного угла, используемое для функции синуса в тригонометрии. Тригонометрия — это раздел математики, изучающий взаимосвязь между углами и сторонами прямоугольного треугольника. Есть две основные формулы для sin2x:
- sin2x = 2 sin x cos x (в терминах sin и cos)
- sin2x = (2tan x)/(1 + tan 2 x) (относительно тангенса)
Это основные формулы sin2x.Но мы можем записать эту формулу только в терминах sin x (или) cos x, используя тригонометрическое тождество sin 2 x + cos 2 x = 1. Используя это тригонометрическое тождество, мы можем написать sinx = √(1 — cos 2 х) и cosx = √(1 — sin 2 х). Отсюда формулы sin2x через cos и sin:
- sin2x = 2 √(1 — cos 2 x) cos x (формула sin2x через cos)
- sin2x = 2 sin x √(1 — sin 2 x) (формула sin2x через sin)
Происхождение Sin 2x Identity
Чтобы получить формулу для sin2x, можно использовать формулу суммы углов sin.
Формула суммы sin: sin(A + B) = sin A cos B + sin B cos A. Давайте посмотрим на вывод sin2x шаг за шагом:Подставьте A = B = x в формулу sin(A + B) = sin A cos B + sin B cos A,
sin(x + x) = sin x cos x + sin x cos x
⇒ sin2x = 2 sin x cos x
Таким образом, мы получили формулу sin2x.
Формула Sin2x для загара
Мы можем записать формулу sin2x только в терминах функции тангенса или тангенса.Для этого начнем с формулы sin2x.
sin2x = 2 sin x cos x
Умножьте и разделите приведенное выше уравнение на cos x. Затем
sin2x = (2 sin x cos 2 x)/(cos x)
= 2 (sin x/cosx) × (cos 2 x)
Мы знаем, что sin x/cos x = tan x и cos x = 1/(sec x). Итак,
sin2x = 2 тангенс x × (1/сек 2 x)
Используя одно из тригонометрических тождеств Пифагора, сек 2 х = 1 + тангенс 2 х.2x = (1 — cos2x)/2
- Формула Sin2x называется формулой двойного угла функции синуса.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.
Выведем её так:
Выразим теперь x и y через a и b.
Используя эту формулу, мы можем найти синус угла, значение которого увеличивается в два раза. Мы знаем, что грех — это одно из основных тригонометрических соотношений, которое определяется как отношение длины противоположной стороны (угла) к длине гипотенузы в прямоугольном треугольнике. Существуют различные формулы, связанные с sin2x, и их можно проверить, используя основные тригонометрические формулы.2x с точки зрения различных тригонометрических функций с использованием разных тригонометрических формул и, следовательно, вывести формулы.
Мы также можем выразить sin2x через функцию тангенса.
Формула суммы sin: sin(A + B) = sin A cos B + sin B cos A. Давайте посмотрим на вывод sin2x шаг за шагом:
☛ Похожие темы:
Часто задаваемые вопросы о Sin2x Formula
Что такое формула Sin2x?
Формула Sin2x представляет собой формулу двойного угла функции синуса, а sin 2x = 2 sin x cos x является наиболее часто используемой формулой. Но sin2x с точки зрения тангенса равен sin 2x = 2tan(x)/(1 + tan 2 (x)).
Каков период Sin2x?
Период sin bx в общем случае равен (2π)/b.Таким образом, период sin2x равен (2π)/2 = π, что означает, что значение sin2x повторяется через каждые π радиан.
Что такое Sin2A с точки зрения Cos?
Общая формула sin2A: sin2A = 2 sin A cos A. Используя sin 2 A + cos 2 A = 1, мы получаем sin A = √(1 — cos 2 A). Подставляя это в данную формулу, sin2A = 2 √(1 — cos 2 A) cos A. Эта формула выражается только в терминах функции косинуса или косинуса.
Как доказать формулу Sin 2x?
Из формулы суммы sin мы имеем sin (A + B) = sin A cos B + cos A sin B.
Подставив здесь A = B = x, мы получим sin 2x = 2 sin x cos x.
Что такое Sin2A с точки зрения греха?
Общая формула sin 2A: sin 2A = 2 sin A cos A. Используя sin 2 A + cos 2 A = 1, мы получаем cos A = √(1 — sin 2 A). Подставив это в приведенную выше формулу, sin2A = 2 sin A √(1 — sin 2 A). Эта формула представлена только в терминах функции sin или синуса.
Sin2x равен 2 Sin x?
Нет, sin2x не равно 2 sin x.2x = (1 — cos2x)/2.
Формула Sin2x. Получение, использование, примеры и часто задаваемые вопросы
Тригонометрия — занимательный и фундаментальный раздел математики. Мы изучаем ряд формул, теорем и уравнений тригонометрии, которые широко используются в науке. В этой статье мы увидим часть этой широкой области, которая включает функцию греха, формулу двойного угла и, в частности, формулу двойного угла для функции греха. Мы увидим его вывод, пример и использование всех формул sin2x.
Формулы и тождества для sin 2x, cos 2x, tan 2x, cot 2x, sec 2x и cosec 2x известны как формулы двойного угла, потому что они имеют угол в два раза больше, чем угол, присутствующий в их формулах.
Формула Sin 2x
Формула Sin 2x равна 2sinxcosx.
[Изображение будет загружено в ближайшее время]
Sin 2x =2 sinx cosx
Вывод формулы Sin2x
Прежде чем приступить к фактическому доказательству, сначала давайте взглянем на саму формулу.
Sin 2x = 2 sinx cosx
Обратите внимание, что формула sin2x является произведением sinx и cosx.Мы начнем с использования известной формулы, в которой sin и cos кратны друг другу. Этот подход приводит к формуле, известной нам как формула суммы углов греха.
Sin(a+b) = Sin a Cos b + Cos a Sin b
, где a и b — углы.
Мы можем заменить a и b как x, что дает нам
Sin(x+x) = Sin x Cos x + Cos x Sin x
, что можно записать как
Sin(2x)= 2Sin x Cos x
Отсюда доказано.
Использование формулы Sin2x All
Эти формулы двойного угла, а точнее формулы cos 2x и sin 2x, используются в больших задачах интегрирования и дифференцирования.Помимо чистой математики, они также используются в реальных задачах высоты и расстояния. Упрощение больших проблем облегчит нам их решение. Это упрощение осуществляется с помощью формул двойного угла cos 2x и формулы sin 2x.
Примеры, основанные на формуле sin2x
Вопрос: Найдите формулу 2sinx sin2x через Cos
Ответ: Мы можем упростить данное выражение, подставив значение sin 2x. Поскольку мы знаем, что
Sin (2x) = 2Sin x Cos x
При подстановке полученного значения,
2sin x sin2x = 2sinx 2sinxcosx
2sinxsin2x = 4sin 10024 2 xcos 905, чтобы получить в этом выражении 2 x05 потому что мы можем использовать тождество Sin 2 θ + Cos 2 θ = 1.
2 = альтернативный способ выражения 1+sin2x -> если это то, что вы искали.
Все еще ищете помощь? Получите правильный ответ, быстро.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ – — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° − ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ е ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А А Â Ã Ä Å Æ Ç Э Э Ê Ë Я Я Я Я Ð С Ò О Ô Õ О Ø О Ш Ù Ú Û О Ý Ÿ Þ а а â г ä å æ ç э э э ë я я я я ð с ò о ô х ö ø œ ш ù ú û ü ý þ ÿ А В Г Δ Е Ζ Η Θ я Κ Λ М N Ξ О Π Р Σ Т Υ Φ Χ Ψ Ом α β γ дельта ε ζ η θ я κ λ мю ν ξ о π р ς о т υ ф х ψ ю ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊
тригонометрических тождеств
| Тригонометрические тождества |
| (Математика | Триггер | удостоверения) |
| sin(theta) = a / c | csc(тета) = 1/sin(тета) = с/а |
| потому что (тета) = б / с | сек(тета) = 1/cos(тета) = c/b |
| tan(тета) = sin(тета) / cos(тета) = a / b | кроватка(тета) = 1/ загар(тета) = б/а |
sin(-x) = -sin(x)
csc(-x) = -csc(x)
cos(-x) = cos(x)
sec(-x) = sec(x)
tan(-x) ) = -загар(х)
раскладушка(-х) = -раскладушка(х)
| sin ^2 (x) + cos ^2 (x) = 1 | тангенс ^2 (x) + 1 = сек ^2 (x) | детская кроватка ^2 (x) + 1 = csc ^2 (x) | |
| грех(х у) = sin x cos y cos х грех у | |||
| cos(xy) = cos x уютный грех х грех у | |||
тангенс(х у) = (тангенс х тангенс у) / (1 загар х загар у)
sin(2x) = 2 sin x cos x
cos(2x) = cos ^2 (x) — sin ^2 (x) = 2 cos ^2 (x) — 1 = 1 — 2 sin ^2 (х)
тангенс (2x) = 2 тангенс (x) / (1 — тангенс ^ 2 (x))
sin ^2 (x) = 1/2 — 1/2 cos(2x)
cos ^2 (x) = 1/2 + 1/2 cos(2x)
sin x — sin y = 2 sin( (x — y)/2) cos( (x + y)/2)
cos x — cos y = -2 sin( (x — y)/2 ) sin( (x + y)/2 )
| уголок | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| грех ^2 (а) | 0/4 | 1/4 | 2/4 | 3/4 | 4/4 |
| соз ^2 (а) | 4/4 | 3/4 | 2/4 | 1/4 | 0/4 |
| рыжевато-коричневый ^2 (а) | 0/4 | 1/3 | 2/2 | 3/1 | 4/0 |
Дан треугольник abc с углами A,B,C; а напротив А, б напротив Б, в напротив С:
a/sin(A) = b/sin(B) = c/sin(C) (Закон Синус)
| (закон косинусов) |
(a — b)/(a + b) = tan [(A-B)/2] / tan [(A+B)/2] (Закон касательных)
Какова формула 1 sin2x? — Ответы на все
Какова формула 1 sin2x?
1+sin2x = 1+2sinxcosx = sin^2x + cos^2x + 2sinxcosx = (sinx + cosx)^2 = альтернативный способ выражения 1+sin2x -> если это то, что вы искали.
2(x) в этих точках равно 1,
Как найти диапазон sin2x?
числа (синус определяется для любой меры угла),
- т. е. −∞
- Диапазон равен −1≤y≤1or[−1.1] , как максимум, так и минимум.
- Домен: −∞
- Диапазон: −1≤y≤1or[−1,1]
Как найти диапазон синуса?
Объяснение: Область определения функции тангенса не включает никаких значений x, которые являются нечетными кратными π/2 . Диапазон функции синуса от [-1, 1].2 x является «квадратом синуса от x», что является функцией, отличной от функции синуса. Sin 2x означает Sin угла ‘2x’.
Является ли sin2x 2sinx?
Sin 2x — это не то же самое, что 2 sin x. Синус удвоенного угла (x) равен удвоенному синусу x cos x.
Как найти cos 2x?
1 ответ
- Для cos2x имеем:
- cos2x=cos2x-sin2x. cos2x=2cos2x−1.
- sinx=√24. cos2x=1−2sin2x.
- Мы можем использовать приведенное выше, чтобы найти cos2x:
- Используйте выбранное нами тождество: cos2x=1−2sin2x.
- Измените обозначение, чтобы упростить манипулирование:
- Замените sinx на √24 :
- Возведение в квадрат числителя и знаменателя дроби:
Как решать тождества с двойным углом?
Двуугольные тождества – Тригонометрические тождества
- Использование отношения синусов для вычисления углов и сторон (Sin = o h \frac{o}{h} h o )
- Используйте отношение косинуса для вычисления углов и сторон (Cos = a h \frac{a}{h} h a )
- Использовать отношение тангенсов для вычисления углов и сторон (Tan = o a \frac{o}{a} a o )
Как упростить cos4x?
Ответ.2 раза по требованию.
Sin2X Формула
Тригонометрия — интересный и важный раздел математики. У него много тождеств, которые очень полезны для изучения и вывода многих уравнений и формул в науке. В этой статье будут рассмотрены некоторые конкретные виды тригонометрических формул, которые популярны как формулы двойного угла.
Эти формулы возможны со всеми 6 видами тригонометрических соотношений. Здесь мы увидим формулу Sin 2X с концепцией, выводом и примерами.Такие формулы популярны, так как в них используются тригонометрические функции двойных углов. Давайте учиться этому!
Концепция греха 2x
Возьмем прямоугольный треугольник. В этом треугольнике у нас есть три стороны, а именно – гипотенуза, противоположная сторона (перпендикуляр) и прилежащая сторона (высота). Наибольшая сторона — это гипотенуза, сторона, лежащая против угла, является противоположной, а сторона, на которую опираются и гипотенуза, и противоположная сторона, является прилежащей стороной. В основе тригонометрии лежат шесть основных соотношений.Это,
- Синус (sin)
- Косинус (cos)
- Тангенс (тангенс)
- Секанс (сек)
- Косеканс (csc)
- Котангенс (кроватка)
Тождества и формулы с двойным углом полезны для решения определенных задач интеграции, где двойная формула может значительно упростить решение.
Поэтому в математике, как и в физике, такие формулы полезны для вывода многих важных тождеств.
Тригонометрические формулы, такие как Sin2x, Cos 2x, Tan 2x, популярны как формулы двойного угла, потому что в их тригонометрических функциях есть двойные углы.Для решения многих задач мы можем использовать их широко.
Формула Sin 2x:
Sin2x=2sinxcosx
Где х угол.
Источник: en.wikipedia.org
Вывод формулы
Понятно, что значение Sin для двойного угла находится в виде произведения значений sin и Cos одиночного угла. Мы можем легко вывести эту формулу, используя формулу сложения углов Sin.
Мы знаем, что формула сложения греха имеет вид:
.Грех(Х+Y)=SinXCosY+CosXSinY,
Где X и Y — два угла.
В приведенной выше формуле замените Y на X, при условии, что оба угла X и Y равны. Таким образом,
Грех(Х+Х)=SinXCosX+CosXSinY
Следовательно, Sin 2x = 2 Sin x Cos x
.Решенные примеры для Sin 2x Formula
Q.
1: Найдите значение Рассчитать sin75∘sin15∘.
Решение: Как дано,
sin75∘sin15∘
=sin(90∘−15∘)sin15∘
=cos15∘sin15∘[as cosx=sin(90∘−x)]
т. е. =12sin30∘[применяя формулу двойного угла sin2x=2sinxcosx]
Итак, =12 × 12[as sin30∘=12]=14
Таким образом, sin75∘sin15∘ будет равно 14
.В.2: Найдите значение sin90∘, используя формулу двойного угла.
Решение. Мы знаем, что формула двойного угла для sin: Sin2x=2SinxCosx
.Положим x=45∘
Sin(2×45∘)=2 Sin45∘Cos45∘
Поскольку Sin45∘=12√
Cos45∘=12√
Следовательно, путем подстановки получаем:
Sin90∘=2×12√×12√
=2×12=1
Таким образом, значение Sin90∘1.
Двухугольные и полуугольные тождества
Двухугольные и полуугольные удостоверения
Особые случаи формул суммы и разности для синуса и косинуса дают то, что известно как тождеств двойного угла и тождеств половинного угла .
Во-первых, используя тождество суммы для синуса,
грех 2α = грех (α + α)
sin 2α = sin α cos α + cos α sin α
sin 2α = 2 sin α cos α
Аналогично для косинуса,
Используя тождество Пифагора, sin 2 α+cos 2 α=1, можно вывести два дополнительных тождества косинуса.
и
Тождества половинного угла для синуса и косинуса получены из двух тождеств косинуса, описанных ранее.
Знак двух предыдущих функций зависит от квадранта, в котором находится результирующий угол.
Пример 1: Найдите точное значение sin 105°, используя тождество половинного угла.
При следующей проверке помните, что 105° находится во втором квадранте, а синусоидальные функции во втором квадранте положительны. Кроме того, 210 ° находится в третьем квадранте, а функции косинуса в третьем квадранте отрицательны. На рисунке 1 эталонный треугольник 210° в третьем квадранте представляет собой треугольник 30°–60°–90°.
Следовательно, cos 210° = −cos 30°.
Рисунок 1
Чертеж для примера 1.
Использование тождества половины угла для синуса,
Пример 2: Найдите точное значение cos 165°, используя тождество половинного угла.
При следующей проверке помните, что 165° находится во втором квадранте, а функции косинуса во втором квадранте отрицательны. Кроме того, 330 ° находится в четвертом квадранте, а функции косинуса в четвертом квадранте положительны.На рисунке 2 эталонный треугольник 330° в четвертом квадранте представляет собой треугольник 30°–60°–90°. Следовательно, cos 330° = cos 30°.
Рисунок 2
Чертеж для примера 2.
Используя тождество половины угла для косинуса,
Пример 3: Используйте тождество двойного угла, чтобы найти точное значение cos 2 x при условии, что sin x = .