Тригонометрические выражения и тригонометрические формулы [wiki.eduVdom.com]
subjects:mathematics:тригонометрические_выражения_и_формулы
Отметим на координатной оси Ох справа от точки О точку А и построим окружность с центром в точке О и радиусом ОА (так называемым начальным радиусом).
Окружность с центром в точке О и радиусом ОА
Рис.1
Пусть при повороте на угол a против часовой стрелки начальный радиус ОА переходит в радиус ОВ.
Тогда:
Синусом (sin α) угла α называется отношение ординаты точки В к длине радиуса.
Косинусом (cos α) угла α называется отношение абсциссы точки В к длине радиуса.
Тангенсом (tg α) угла α называется отношение ординаты точки В к ее абсциссе.
Котангенсом (ctg α) угла α называется отношение абсциссы точки В к ее ординате.

Секанс определяется как sec α = 1/(cos α)
Косеканс определяется как cosec α = 1/(sin α)
В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x
Если координаты точки В равны x и y, то:
$$\sin{\alpha} = \frac{y}{R}\;;\; \cos{\alpha} = \frac{x}{R}\;;\; {\rm tg}\, \alpha = \frac{y}{x}\;;\; {\rm ctg}\, \alpha = \frac{x}{y}$$
Таблица значений sin α, cos α, tg α, ctg α
Приведем таблицу значений тригонометрических функций некоторых углов (прочерк сделан, когда выражение не имеет смысла):
| Таблица значений sin α, cos α, tg α, ctg α | ||||||||
| 0º | 30º | 45º | 60º | 90º | 180º | 270º | 360º | |
|---|---|---|---|---|---|---|---|---|
| 0 рад | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ | $\frac{3\pi}{2}$ | $2\pi$ | |
| $\sin \alpha$ | 0 | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | 1 | 0 | -1 | 0 |
| $\cos \alpha$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | 0 | -1 | 0 | 1 |
| $\textrm{tg}\, \alpha$ | 0 | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | — | 0 | — | 0 |
| $\textrm{ctg}\, \alpha$ | — | $\sqrt{3}$ | 1 | $\frac{1}{\sqrt{3}}$ | 0 | — | 0 | — |
Свойства sin, cos, tg и ctg
Свойства синуса (sin), косинуса (cos), тангенса(tg) и котангенса(ctg):
Определение знака
Если α-угол I или II координатной четверти, то sin α > 0;
Если α-угол III или IV координатной четверти, то sin α < 0;
Если α-угол I или IV координатной четверти, то cos α > 0;
Если α-угол II или III координатной четверти, то cos α < 0;
Если α-угол I или III координатной четверти, то tg α > 0 и ctg α > 0;
Если α-угол II или IV координатной четверти, то tg α < 0 и ctg α < 0.

Синус, тангенс и котангенс — нечетные функции; косинус — четная функция.
Для чётной функции справедливо равенство: y(-x) = y(x). Примеры чётных функций: y = cos(x), y = x2.
Для НЕчётной функции справедливо равенство: y(-x) = -y(x). Примеры НЕчётных функций: y = sin(x), y = x.
При изменении угла на целое число оборотов значения тригонометрических функций не меняются.
1 радиан — это мера центрального угла, которому соответствует длина дуги, равная длине радиуса окружности.
Связь радианов с градусами: $1° =\frac{\pi}{180}\text{рад; 1 рад }=\frac{180°}{\pi}$.
Основные тригонометрические тождества
Формулы приведения
| X | $\frac{\pi}{2}-\alpha$ | $\frac{\pi}{2}+\alpha$ | $\pi-\alpha$ | $\pi+\alpha$ | $\frac{3\pi}{2}-\alpha$ | $\frac{3\pi}{2}+\alpha$ | $2\pi-\alpha$ | $2\pi+\alpha$ |
|---|---|---|---|---|---|---|---|---|
| sin x | cos α | cos α | sin α | -sin α | -cos α | -cos α | -sin α | sin α |
| cos x | sin α | -sin α | -cos α | -cos α | -sin α | sin α | cos α | cos α |
| tg x | ctg α | -ctg α | -tg α | tg α | ctg α | -ctg α | -tg α | tg α |
| ctg x | tg α | -tg α | -ctg α | ctg α | tg α | -tg α | -ctg α | ctg α |
Формулы сложения
Формулы двойного угла
Формулы двойного угла или двойного аргумента:
Формулы половинного аргумента
Формулы половинного аргумента (для sin и cos — формулы понижения степени):
Формулы суммы и разности
Формулы произведения
Соотношения между sin x, cos x и tg(x/2)
Один из способов использования: свести всё к tg(x/2) и путём замены получить обычное алгебраическое выражение.
Простейшие тригонометрические уравнения
Дополнительно
subjects/mathematics/тригонометрические_выражения_и_формулы.txt · Последние изменения: 2021/03/24 18:37 — ¶
SIN (функция SIN) — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.
Описание
Возвращает синус заданного угла.
Синтаксис
SIN(число)
Аргументы функции SIN описаны ниже.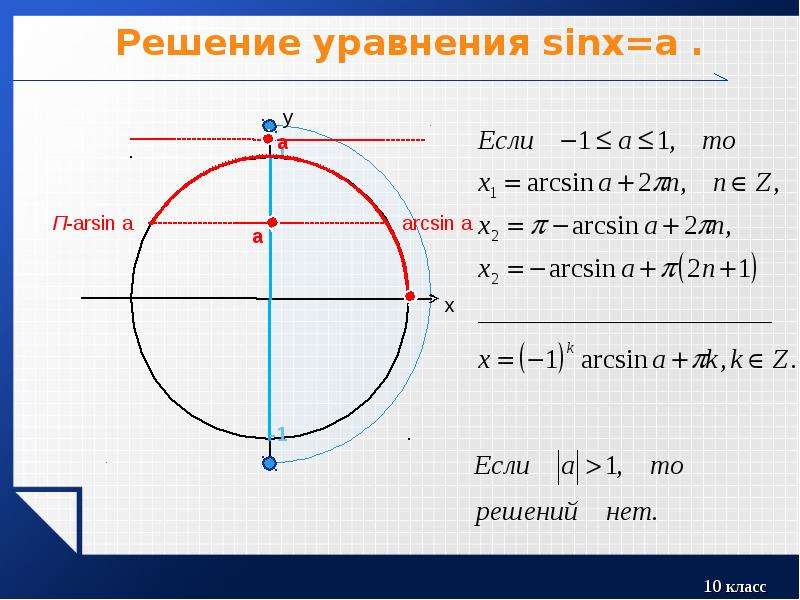
Замечание
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=SIN(ПИ()) |
Синус пи радиан (0, приблизительно). |
0,0 |
|
=SIN(ПИ()/2) |
Синус пи/2 радиан. |
1,0 |
|
=SIN(30*ПИ()/180) |
Синус угла 30 градусов. |
0,5 |
|
=SIN(РАДИАНЫ(30)) |
Синус 30 градусов. |
0,5 |
3.1.10. Тригонометрические уравнения
Глава 3. Решение уравнений и неравенств
3.1.
3.
 1.10.
1.10.
Найдём условие, при котором будут равны синусы двух углов. Пусть sin a = sin b. Тогда sin a – sin b = 0, и по известной формуле разности синусов имеем
Рассмотрим решение простейшего уравнения sin x = a. Если |a| > 1, то решений нет, если |a| ≤ 1, то в силу периодичности синуса решений будет бесконечно много. По определению обратных тригонометрических функций, одно из решений − это arcsin a. Следовательно, наше уравнение можно переписать в виде sin x = sin (arcsin a). Тогда либо x – arcsin a = 2πn, либо x + arcsin a = 2(n + 1)π, Оба эти равенства могут быть объединены в одно:

Аналогично можно показать, что формула общего решения уравнения cos x = a при |a| ≤ 1 имеет вид
| x = arctg a + πn, |
Формула общего решения уравнения ctg x = a при любом действительном a имеет вид
| x = arcctg a + πn, |
Рассмотренные уравнения называются простейшими тригонометрическими уравнениями.
|
Модель 3.5. Простейшие тригонометрические уравнения |
Решите уравнение sin 2x = cos 3x.
Пример 2
Решите уравнение sin x – 2 cos x = 0.
|
Преобразуем уравнение sin x = 2 cos x. Рассмотрим те x, для которых cos x = 0. Для этих x sin x = ±1. Следовательно, эти x не являются корнями исходного уравнения, так как при их подстановке получается неверное числовое равенство 0 = ±1. Значит, cos x ≠ 0. Разделим обе части уравнения на cos x ≠ 0, имеем tg x = 2, x = arctg 2 + πn, Ответ. x = arctg 2 + πn, |
Пример 3
Решите уравнение sin2 x – 6 sin x cos x + 5 cos2 x = 0.
Только что рассмотренные уравнения называются однородными уравнениями соответственно 1-го и 2-го порядка. Вспомним определение многочлена n-ной степени, данное в § 2.1.1. Однородным многочленом n-ного порядка относительно переменных u и v называется многочлен, у которого сумма степеней переменных постоянна у всех членов.
Аналогично, уравнения au + bu = 0 и au2 + bvu + cv2 = 0 также называются однородными уравнениями 1-го и 2-го порядка. В нашем случае было u = sin x и v = cos x.
Уравнение 1-го порядка делением на v сводится к линейному относительно новой переменной Уравнения 2-го порядка делением на сводятся к квадратному относительно
Уравнения с обратными тригонометрическими функциями, как правило, удаётся решить, применяя одну и ту же тригонометрическую функцию к обеим частям данного уравнения.
Пример 4Решите уравнение arccos x = arctg x.
sin | cos | tg | ctg | ||||
I | + | + | + | + | |||
II | + | | | | |||
III | | | + | + | |||
IY | | + | | + | – | /2 | | 3/2 | 2 – |
sin | -sin | cos | +sin | — cos | — sin | ||
cos | cos | +sin | — cos | sin | cos | ||
tg | — tg | + ctg | tg | + ctg | — tg | ||
ctg | — ctg | + tg | ctg | + tg | -ctg | 0 | 30 | 45 | 60 | 90 | 180 | 270 |
/ 6 | /4 | /3 | /2 | | 3/2 | ||
sin | 0 | Ѕ | 2 / 2 | 3 / 2 | 1 | 0 | – 1 |
cos | 1 | 3 / 2 | 2 / 2 | Ѕ | 0 | 1 | 0 |
tg | 0 | 3 / 3 | 1 | 3 | | 0 | |
ctg | – | 3 | 1 | 3 / 3 | 0 | | 0 |
Запишите формулу корней уравнения a)sinx=a b)tgx=a
На підставі вихідних даних визначити виробничу потужність цеху та коефіцієнт її використання. Кількість однотипних верстатів у цеху на початок року 70
… од., з 1 березня встановлено ще 6 од., з 1 липня вибуло 10 од., число робочих днів у році – 252, режим роботи двозмінний, тривалість зміни – 8 годин, регламентований відсоток простоїв устаткування на ремонтах – 5%, продуктивність одного верстата – 8 деталей за годину; фактичний випуск продукції за рік – 1,9 млн. деталей.
Кількість однотипних верстатів у цеху на початок року 70
… од., з 1 березня встановлено ще 6 од., з 1 липня вибуло 10 од., число робочих днів у році – 252, режим роботи двозмінний, тривалість зміни – 8 годин, регламентований відсоток простоїв устаткування на ремонтах – 5%, продуктивність одного верстата – 8 деталей за годину; фактичний випуск продукції за рік – 1,9 млн. деталей.
ПОМОГИТЕ СРОЧНО! Постройте сечение параллелепипеда `ABCDA_1B_1C_1D_1` плоскостью, проходящей через следующие точки:
а) середины рёбер `AB`, `AD` и `A
… A_1`;
б) `B`, `C` и середину ребра `A_1B_1`;
в) `A`, `C` и середину ребра `A_1B_1`;
г) середины рёбер `A A_1`, `AD` и центр грани `B B_1C_1C`;
д) центры граней `ABCD`, `A A_1B_1B` и `B B_1C_1C`;
е) середины рёбер `AB`, `BC` и `D D_1`;
ж) середины рёбер `A_1B_1`, `C C_1` и вершину `A`;
з) середину ребра `C C_1` и точки `K`, `L`, лежащие на рёбрах `AB` и `A_1B_1`, если `BK:KA=A_1L:LB_1=1:2`;
и) середину ребра `A_1B_1` вершину `A` и точку `M` на ребре `B_1C_1`, если `B_1M:MC_1=1:3`;
к) середины рёбер `AD`, `CD` и `A_1B_1`;
л) середины рёбер `AB`, `BC` и `C C_1`;
м) вершину `B_1`, центр грани `ABCD` и середину ребра `A A_1`;
н) середины рёбер `CD`, `BC` и точку `M`, лежащую на продолжении ребра `A A_1` за точку `A_1`, если `MA_1=1/2 A A_1`;
o) середины рёбер `AD`, `C C_1` и `A_1B_1`.
Срочно помогите!!!
В растворе содержится 40 % соли. Если добавить 120 г соли, то в растворе будет содержаться 70 % соли. Какова первоначальная масса раствора? Сколько гр … аммов соли было в растворе первоначально? решить уравнением
Знайдіть кут між векторами m i n якщо (m+3n)(m-n)=11, |m|=2, |n|=3
Помогите пожалуйста срочно очень!!!!
решите срочно пожалуйста через два часа экзамен
Найдите плошадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
найти область определения функции y=1/x-3, и можете досканально объяснить
найти область определения функции y=1/x-3, и можете досканально объяснить как вы получили данный ответ
Формулы понижения степени в тригонометрии
Тригонометрические формулы обладают рядом свойств, одно из которых это применение формул понижения степени. Они способствуют упрощению выражений при помощи уменьшения степени.
Они способствуют упрощению выражений при помощи уменьшения степени.
Формулы понижения работают по принципу выражения степени синуса и косинуса через синус и косинус первой степени, но кратного угла. При упрощении формула становится удобной для вычислений, причем повышается кратность угла от α до nα.
Формулы понижения степени, их доказательство
Ниже приводится таблица формул понижения степени со 2 по 4 для sin и cos угла. После ознакомления с ними зададим общую формулу для всех степеней.
sin2α=1-cos 2α2cos2α=1+cos 2α2sin3=3·sin α-sin 3α4sin4=3-4·cos 2α+cos 4α8cos4 α=3+4·cos 2α+cos 4α8
Данные формулы предназначены для понижения степени.
Существует формулы двойного угла у косинуса и синуса, из которых и следуют формулы понижения степени cos2α=1-2·sin2α и cos2α=2·cos2α-1. Равенства разрешаются относительно квадрата синуса и косинуса, которые предоставляются как sin2α=1-cos2α2 и cos2α=1+cos2α2.
Формулы понижения степеней тригонометрических функций перекликаются с формулами синуса и косинуса половинного угла.
Имеет место применение формулы тройного угла sin3α=3·sinα-4·sin3αи cos3α=-3·cosα+4·cos3α.
Если решать равенство относительно синуса и косинуса в кубе, получим формулы понижения степеней для синуса и косинуса:
sin3α=3-4·cos2α+cos4α8 и cos3α=3·cosα+cos3α4.
Формулы четвертой степени тригонометрических функций выглядят так: sin4α=3-4·cos2α+cos4α8 и cos4α=3+4·cos2α+cos4α8.
Чтобы понизить степени эти выражений, можно действовать в 2 этапа, то есть дважды понижать, тогда это выглядит таким образом:
sin4α =(sin2α)2=(1-cos2α2)2=1-2·cos2α+cos22α4==1-2·cos2α+1+cos4α24=3-4·cos2α+cos4α8;cos4α=(cos2α)2=(1+cos2α2)2=1+2·cos2α+cos22α4===1+2·cos2α+1+cos4α24=3+4·cos2α+cos4α8
Методом подстановки мы упростили сложное выражение. Для того, чтобы записать общий вид формул понижения степени разделим их на с наличием четных и нечетных показателей. Четные показатели, где n=2, 4, 6…, выражение имеет вид sinnα=Cn2n2n+12n-1·∑(-1)n2-kk=0n2-1·Ckn·cos((n-2·k)α) и cosnα=Cn2n2n+12n-1∑(-1)n2-kk=0n2-1·Ckn·cos((n-2·k)α).
Нечетные показатели, где n=3, 5, 7…, выражение имеет вид
sinnα=12n-1·∑(-1)n-12-kk=0n-12·Ckn·cos((n-2·k)α) и cosnα=12n-1∑(-1)n-12-kk=0n-12·Ckn·cos((n-2·k)α).
Cpq=p!q!·(p-q)! — это число сочетаний из p элементов по q.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеФормулы понижения степени общего вида используются на любого выражения с высокой степенью для его упрощения. Рассмотрим пример для понижения кубического синуса. Третья степень нечетная, значит воспользуемся формулой sinnα=12n-1·∑(-1)n-22-kk=0n-12-k·Ckn·sin((n-2·k)α) где значение n присвоим 3. Подставляя n=3 в выражение, получим
sin3α=123-1·∑(-1)3-12-kk=03-12-k·Ck3·sin((3-2·k)α)==14·∑(-1)1-kk=01·Ck3·sin((3-2·k)α)==14·((-1)1-0·C03·sin((3-2·0)α) +(1)1-1·C13·sin((3-2·1)α))==14·((-1)1·3!0!·3!·sin3α+(-1)0·3!1!·(3-1)!·sinα)==14·(-sin3α+3·sinα)=3·sinα-sin3α4
Примеры применения формул понижения степени
Чтобы закрепить материал, необходимо детально разобрать его на примерах с использованием формулы понижения степени. Таким образом будет понятен принцип решения, подстановка и весь алгоритм.
Таким образом будет понятен принцип решения, подстановка и весь алгоритм.
Справедлива ли формула вида cos4α=3+4·cos2α+cos4α8 при α=α6.
Решение
Для того, чтобы данная формула прошла проверку на возможность понижения степени с заданным значением угла α, необходимо посчитать левую и правую стороны. По условию имеем, что α=π6, тогда 2α=π3, следовательно 4α=2π3.
По таблице тригонометрических функций имеем, что cosα=cosπ6=32, тогда cos2α=cosπ3=12.
Для подробного уяснения необходимо проштудировать статью значения синуса, косинуса, тангенса и котангенса. Подставляя в формулу, получим cos4α=(cosπ6)4=(32)4=916 и 3+4cos2α+cos4α8=3+4cosπ3+cos2π38=3+4·12+(-12)8=916
Отсюда видим, что левая и правая части равенства верны при α=π6, значит, выражение справедливо при значении заданного угла. Если угол отличен от α, формула понижения степени одинаково применима.
Пример 2При помощи формулы понижения степени преобразовать выражение sin32β5.
Решение
Кубический синус для угла α имеет формулу вида sin3α=3·sinα-sin3α4. В данном случае необходимо выполнить замену α на 2β5 и подставить в формулу, тогда получаем выражение вида sin32β5=3·sin2β5-sin(3·2β5)4.
Это выражение равно равенству sin32β5=3·sin2β5-sin6β54.
Ответ: sin32β5=3·sin2β5-sin6β54.
Для решения сложных тригонометрических уравнений применяют формулы понижения степени. Они способны упростить выражение и сделать его намного удобным для вычислений или подстановки числовых значений.
Интеграл синуса
Согласно формулам интегрирования интеграл от синуса sin (x) равен косинусу, причем со знаком минус. Многие часто допускает ошибки потому что не может запомнить, что производная от синуса равна минус косинусу, а от косинуса — синусу со знаком плюс.
Те кто изучает первоначальную должны помнить что к правой стороне следует добавить постоянную
Ету постоянную определяют с дополнительной условия.
График синуса имеет вид
Синус нечетная, а косинус — четная функция, поэтому при интегрировании появляется знак минус. В начале всем кажется все простым и понятным. Но рано или поздно наступает время усложнять интеграл, то есть интегрировать синус двойного угла, тройного аргумента и т.д. И во многих возникают трудности с интегрированием. Для вывода формулы интеграла для sin (k*x) проведем все выкладки сначала. Для того чтобы свести интеграл к табличной формулы надо внести коэффициент под дифференциал, но это изменит сам интеграл. Поэтому одновременно делим на коэффициент
Зная эту формулу, интеграл от синуса двойного угла записываем одной строкой
Далее можем проинтегрировать синус тройного угла
и т.д.
int(sin(k*x)=-1/k*cos(k*x).
По такой же формуле выводят интеграл от синуса половины угла, который равен минус 2 косинус половины угла.
Интеграл от синуса одной третьей х равен
Распространенные примеры интегрирования синуса
Пример 1. Найти интеграл от sin(4*x).
Найти интеграл от sin(4*x).
Решение: По формуле интегрирования находим
Пример 2. Вычислить интеграл от sin(5*x).
Решение: Выполняем интегрирования
Пример 3. Проинтегрировать выражение sin(7*x).
Решение: Находим неопределенный интеграл
Пример 4. Найти интеграл функции y=sin(x/5).
Решение: Находим неопределенный интеграл
Как только Вы научитесь вычислять простые интегралы от синуса можете переходить к определенному интегралу
Пример 5. Найти первоначальную от sin(x) которая в нуле равна 2.
Решение: Вычисляем первоначальную
Из условия на первоначальную находим постоянную
-cos(0)+C=2;
C=2+cos(0)=3.
Возвращаемся к первоначальной и подставляем найденную постоянную
Это и есть ответ к задаче.
Пример 7. Проинтегрировать синус двойного угла y=sin(2*x) от 0 до 45 градусов.
Решение: Записываем интеграл от синуса и подставляем пределы интегрирования
По физическому содержанию определенный интеграл равен площади фигуры ограниченной функцией sin (x) и осью абсцисс.
Но определенный интеграл и площадь, это не одно и то же. Интеграл может быть отрицательным, а площадь нет. Если функция большую площадь имеет под осью абсцисс, то ее определенный интеграл отрицательный.
Площадь криволинейной трапеции равна интегралу от разницы уравнения верхней кривой и нижней.
В данном случае верхняя кривая это ось абсцисс или y = 0. Нижняя — это график синуса. Поэтому формула площади синус функции равна 1, или определенному интегралу по модулю.
Если функция антисимметрична относительно оси абсцисс то ее интеграл равен нулю, а площадь равна двойному интегралу графика над осью абсцисс. Например, интеграл синуса двойного угла от -45 до 45 градусов равен нулю
В то же время площадь заштрихованной фигуры равна единице.
На графике это будет выглядеть.
Из следующих материалов Вы узнаете, как найти интеграл от функции вида
какие формулы свертки и замены переменных при этом следует использовать. Также Вы овладеете методикой вычисления интегралов вида полином умноженый на синус функцию
где — полином от переменной. В таких случаях применяют интегрирования по частям, но об этом пойдет речь позже.
В таких случаях применяют интегрирования по частям, но об этом пойдет речь позже.
На этом знакомство с интегрированием синуса завершается. Интегралы от других тригонометрических и обратных к ним функций Вы найдете на страницах категории «Интегрирование функций».
Тригонометрические тождества и формулы
Ниже приведены некоторые из наиболее важных определений, тождеств и формул в тригонометрии.
Тригонометрические функции острых углов
грех X = opp / hyp = a / c, csc X = hyp / opp = c / a
загар X = opp / adj = a / b, детская кроватка X = adj / opp = b / a
cos X = adj / hyp = b / c, сек X = hyp / adj = c / b,Тригонометрические функции произвольных углов
грех X = b / r, csc X = r / b
tan X = b / a, детская кроватка X = a / b
cos X = a / r, сек X = r / aОсобые треугольники
С помощью специальных треугольников можно найти тригонометрические функции специальных углов: 30, 45 и 60 градусов.
Синус и косинус в треугольниках
В любом треугольнике мы имеем:
1 — Синус-закон
грех A / a = грех B / b = грех C / c
2 — Законы косинусов
a 2 = b 2 + c 2 — 2 b c cos A
b 2 = a 2 + c 2 — 2 a c cos B
c 2 = a 2 + b 2 — 2 a b cos CОтношения между тригонометрическими функциями
cscX = 1 / sinX
sinX = 1 / cscX
сек X = 1 / cos X
cosX = 1 / секX
tanX = 1 / cotX
cotX = 1 / tanX
tanX = sinX / cosX
cotX = cosX / sinXПифагорейские тождества
sin 2 X + cos 2 X = 1
1 + загар 2 X = сек 2 X
1 + детская кроватка 2 X = csc 2 XИдентификаторы с отрицательным углом
sin (-X) = — sinX, нечетная функция
csc (-X) = — cscX, нечетная функция
cos (-X) = cosX, четная функция
сек (-X) = секX, четная функция
tan (-X) = — tanX, нечетная функция
cot (-X) = — cotX, нечетная функцияCofunctions Identities
sin (π / 2 — X) = cosX
cos (π / 2 — X) = sinX
загар (π / 2 — X) = cotX
детская кроватка (π / 2 — X) = tanX
сек (π / 2 — X) = cscX
csc (π / 2 — X) = secXФормулы сложения
cos (X + Y) = cosX cosy — sinX sinY
cos (X — Y) = cosX cosy + sinX sinY
sin (X + Y) = sinX cosy + cosX sinY
sin (X — Y) = sinX уютно — cosX sinY
tan (X + Y) = [tanX + tanY] / [1 — tanX tanY]
tan (X — Y) = [tanX — tanY] / [1 + tanX tanY]
детская кроватка (X + Y) = [cotX cotY — 1] / [cotX + cotY]
детская кроватка (X — Y) = [cotX cotY + 1] / [cotY — cotX]Формулы суммы к произведению
cosX + cosy = 2cos [(X + Y) / 2] cos [(X — Y) / 2]
sinX + sinY = 2sin [(X + Y) / 2] cos [(X — Y) / 2]Отличие от формул продукта
cosX — cosy = — 2sin [(X + Y) / 2] sin [(X — Y) / 2]
sinX — sinY = 2cos [(X + Y) / 2] sin [(X — Y) / 2]Формулы произведения суммы / разности
cosX cosy = (1/2) [cos (X — Y) + cos (X + Y)]
sinX cosy = (1/2) [sin (X + Y) + sin (X — Y)]
cosX sinY = (1/2) [sin (X + Y) — sin [(X — Y)]
sinX sinY = (1/2) [cos (X — Y) — cos (X + Y)]Формула разности квадратов
sin 2 X — грех 2 Y = sin (X + Y) sin (X — Y)
cos 2 X — cos 2 Y = — sin (X + Y) sin (X — Y)
cos 2 X — sin 2 Y = cos (X + Y) cos (X — Y)Формулы двойных углов
грех (2X) = 2 sinX cosX
cos (2X) = 1-2sin 2 X = 2cos 2 X — 1
загар (2X) = 2tanX / [1 — загар 2 X]Формулы множественных углов
sin (3X) = 3sinX — 4sin 3 X
cos (3X) = 4cos 3 X — 3cosX
sin (4X) = 4sinXcosX — 8sin 3 XcosX
cos (4X) = 8cos 4 X — 8cos 2 X + 1Формулы полууглов
sin (X / 2) = + или — √ ((1 — cosX) / 2)
cos (X / 2) = + или — √ ((1 + cosX) / 2)
tan (X / 2) = + или — √ ((1 — cosX) / (1 + cosX))
= sinX / (1 + cosX) = (1 — cosX) / sinXФормулы снижения мощности
sin 2 X = 1/2 — (1/2) cos (2X))
cos 2 X = 1/2 + (1/2) cos (2X))
sin 3 X = (3/4) sinX — (1/4) sin (3X)
cos 3 X = (3/4) cosX + (1/4) cos (3X)
sin 4 X = (3/8) — (1/2) cos (2X) + (1/8) cos (4X)
cos 4 X = (3/8) + (1/2) cos (2X) + (1/8) cos (4X)
sin 5 X = (5/8) sinX — (5/16) sin (3X) + (1/16) sin (5X)
cos 5 X = (5/8) cosX + (5/16) cos (3X) + (1/16) cos (5X)
sin 6 X = 5/16 — (15/32) cos (2X) + (6/32) cos (4X) — (1/32) cos (6X)
cos 6 X = 5/16 + (15/32) cos (2X) + (6/32) cos (4X) + (1/32) cos (6X)Периодичность тригонометрических функций
sin (X + 2π) = sin X, период 2π
cos (X + 2π) = cos X, период 2π
сек (X + 2π) = сек X, период 2π
csc (X + 2π) = csc X, период 2π
tan (X + π) = tan X, период π
детская кроватка (X + π) = детская кроватка X, период π- Тригонометрические таблицы.

- Свойства шести тригонометрических функций. График, область, диапазон, асимптоты (если есть), симметрия, пересечения по осям x и y, а также точки максимума и минимума каждой из 6 тригонометрических функций.
Дополнительные ссылки и ссылки по тригонометрии
Тригонометрия.Решите задачи тригонометрии.
Бесплатные вопросы по тригонометрии с ответами. пожаловаться на это объявление
Производная sin x — подход к исчислению
12
Производная sin x
Производная cos x
Производная от tan x
Производная от детской кроватки x
Производная sec x
Производная от csc x
ПРОИЗВОДНАЯ sin x равна cos x .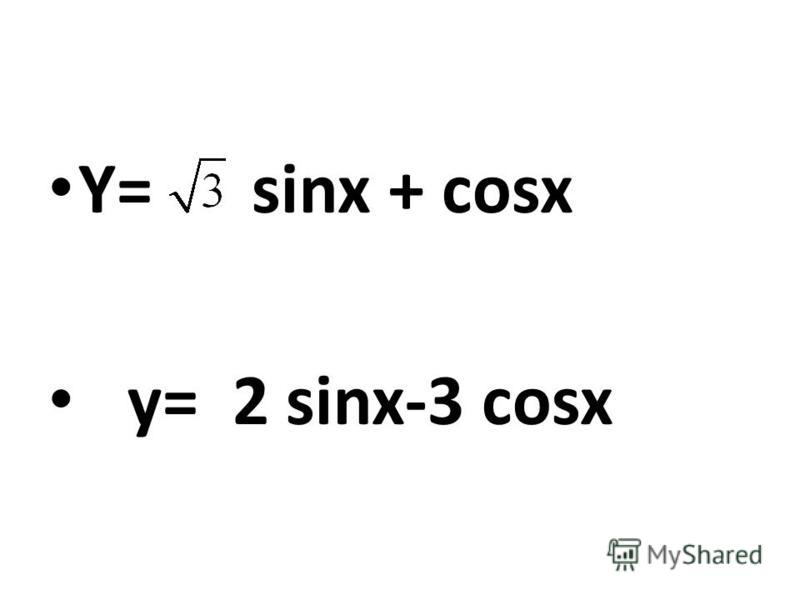 Чтобы доказать это, мы будем использовать следующий идентификатор:
Чтобы доказать это, мы будем использовать следующий идентификатор:
sin A — sin B = 2 cos ½ ( A + B ) sin ½ ( A — B ).
(Тема 20 Тригонометрии.)
Проблема 1. Используйте это удостоверение, чтобы показать:
| sin ( x + h ) — sin x | = |
Чтобы увидеть доказательство, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| sin ( x + h ) — sin x | = | 2 cos ½ ( x + h + x ) sin ½ ( x + h — x ) |
| = | 2 cos ½ (2 x + h ) sin ½ h | |
| = | ||
Однако, прежде чем перейти к производной sin x , мы должны доказать лемму; что является предварительной вспомогательной теоремой, необходимой для доказательства основной теоремы. Эта лемма требует следующего тождества:
Эта лемма требует следующего тождества:
Задача 2. Докажите, что tan θ, разделенный на sin θ, равен.
| tan θ sin θ | = | 1 cos θ | . |
(См. Раздел 20 Тригонометрии.)
| tan θ sin θ | = | тан θ · | 1 sin θ | = | sin θ cos θ | · | 1 sin θ | = | 1 cos θ |
Лемма, которую мы должны доказать, обсуждается в теме 14 Тригонометрии.(Взгляните на это.) Вот он:
ЛЕММА. Когда θ измеряется в радианах, тогда
Доказательство. Это невозможно доказать, применяя обычные теоремы о пределах (Урок 2). Мы должны перейти к геометрии и к значениям sin θ и радианной меры.
Пусть O будет центром единичной окружности, то есть окружности радиуса 1;
, и пусть θ будет центральным углом BOA первого квадранта, измеренным в радианах.
Тогда, поскольку длина дуги s = r θ и r = 1, дуга BA равна θ. (Тема 14 Тригонометрии.)
Угол вытяжки B’OA равен углу θ, в результате дуга AB ‘ равна дуге BA ;
нарисуйте прямую BB ‘, разрезая AO на P ;
и нарисуйте прямые BC, B’C , касательные к окружности.
Затем
BB ‘ BAB’ BC + CB ‘.
Теперь, в этом единичном круге, BP = PB ‘ = sin θ, (Тема 17 Тригонометрии),
, так что BB ‘ = 2 sin θ;
| и BC = CB ‘ = tan θ. (Для tg θ = | BC OB | = | BC 1 | = до н. э. .) э. .) |
Таким образом, продолжающееся неравенство, приведенное выше, становится:
2 грех θ θ θ.
При делении каждого члена на 2 sin θ:
| 1 | θ sin θ | 1 cos θ | . |
(Задача 2.) И принимая обратные, меняя таким образом смысл:
| 1> | грех θ θ | > cos θ. |
(Урок 11 по алгебре, теорема 5.)
При смене знаков снова меняется смысл:
| -1 | sin θ θ | −cos θ, |
(Урок 11 алгебры, теорема 4),
и если мы добавим 1 к каждому члену:
| 0 | 1 — | грех θ θ | 1 — cos θ. |
Теперь, когда θ становится очень близким к 0 (θ 0), cos θ становится очень близким к 1; следовательно, 1 — cos θ становится очень близким к 0. Выражение в середине, будучи меньше , чем 1 — cos θ, становится еще ближе к 0 (а слева ограничено 0), поэтому выражение в середине точно приблизится к нулю. Это означает:
Выражение в середине, будучи меньше , чем 1 — cos θ, становится еще ближе к 0 (а слева ограничено 0), поэтому выражение в середине точно приблизится к нулю. Это означает:
Это то, что мы хотели доказать.
Учащийся должен помнить, что для того, чтобы переменная «приближалась» к нулю или какому-либо пределу (Определение 2.1), не означает, что переменная когда-либо равна этому пределу.
Производная sin x
| d dx | грех x | = cos x |
Чтобы доказать это, мы применим определение производной (Урок 5). Сначала мы рассчитаем коэффициент разницы.
| = | , проблема 1, | ||
| = | , при делении числителя и знаменателя на 2, | ||
| = | |||
Теперь возьмем предел как h 0. Но предел продукта равен произведению пределов. (Урок 2.) Множитель справа имеет вид sin θ / θ. Следовательно, согласно лемме при h 0 его предел равен 1. Следовательно,
Но предел продукта равен произведению пределов. (Урок 2.) Множитель справа имеет вид sin θ / θ. Следовательно, согласно лемме при h 0 его предел равен 1. Следовательно,
| d dx | грех x | = cos x . |
Мы разработали формулу.
Производная cos x
| d dx | cos x | = −sin x |
Для этого мы будем использовать следующий идентификатор:
| cos x = sin ( | π 2 | — х ). |
Функция любого угла равна совместной функции его дополнения.
(Тема 3 тригонометрии).
Следовательно, при применении цепного правила:
Мы установили формулу.
Производная от tan x
| Теперь загар x = | sin x cos x | .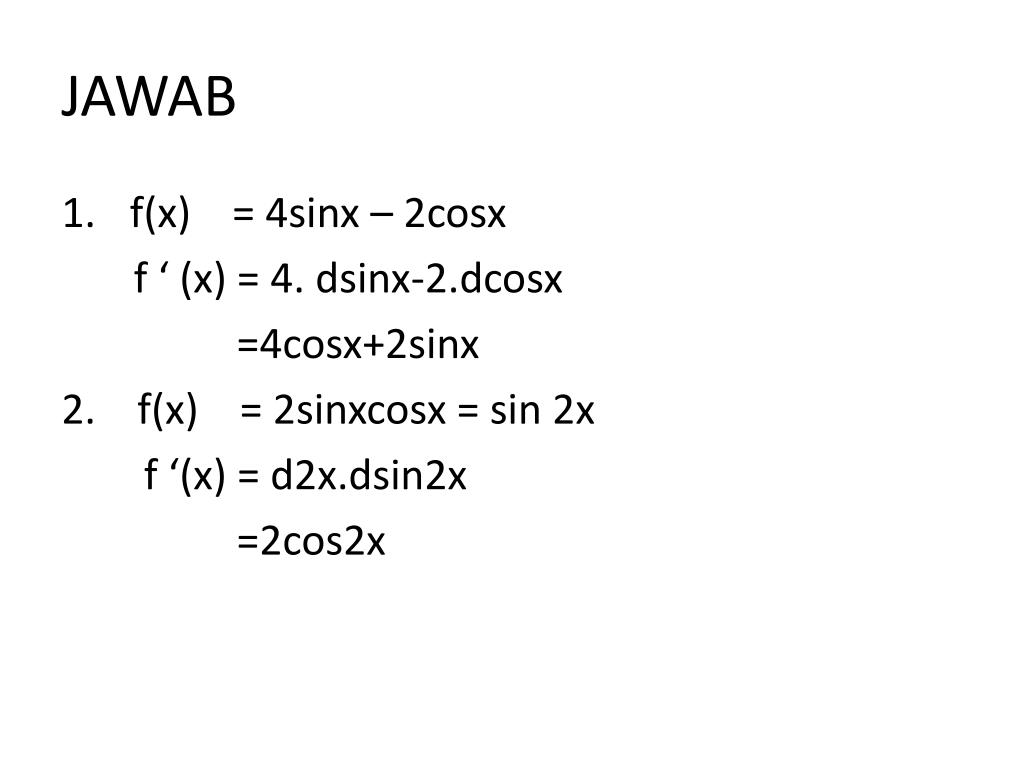 | (Тема 20 Тригонометрии.) |
Следовательно, согласно правилу частного:
| d dx | желто-коричневый x | = | d dx | sin x cos x | = | cos x · cos x — sin x (−sin x ) cos 2 x | ||
| = | cos 2 x + sin 2 x cos 2 x | |||||||
| = | 1 cos 2 x | |||||||
| = | сек 2 x . | |||||||
Мы разработали формулу.
Задача 3. Производная от детской кроватки х . Доказательство:
| d dx | детская кроватка x = −csc 2 x |
| d dx | детская кроватка x | = | d dx | cos x sin x | ||||
| = | sin x (−sin x ) — cos x · cos x sin 2 x | |||||||
| = | — (sin 2 x + cos 2 x ) sin 2 x | |||||||
| = | – | 1 sin 2 x | ||||||
| = | −csc 2 x .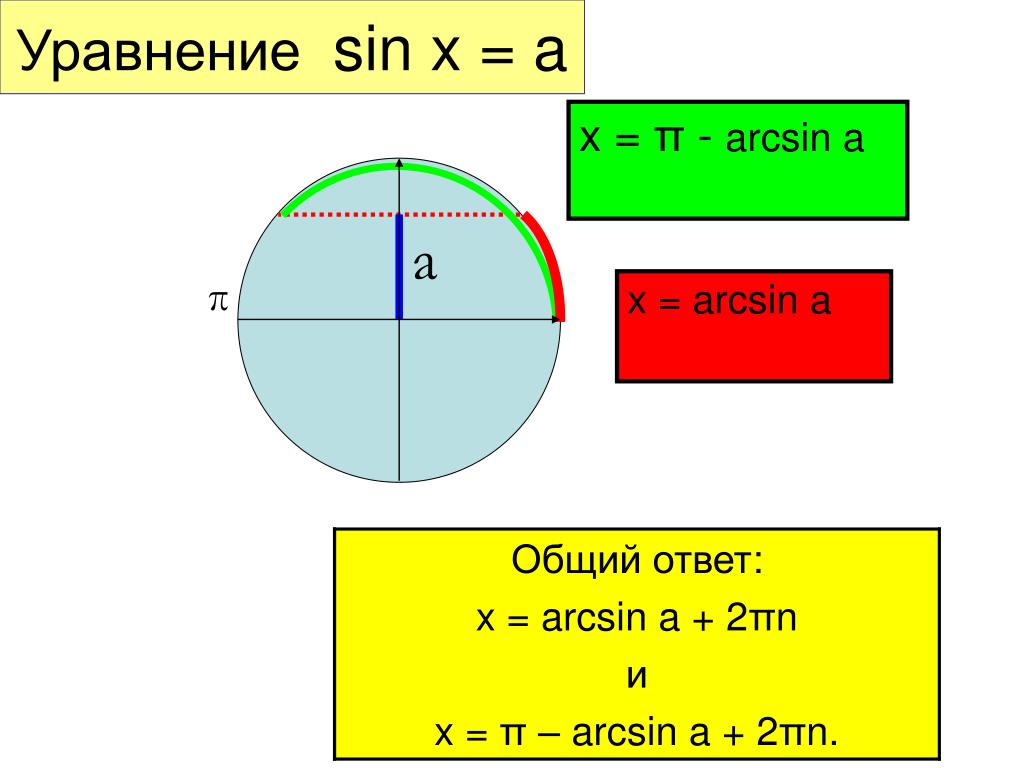 | |||||||
Производная sec x
| d dx | сек x | = сек x желто-коричневый x |
| Так как sec x = | 1 cos x | = | (cos x ) -1 | , |
, затем при использовании цепного правила и общего правила мощности:
Мы установили формулу.
Задача 4. Производная от csc x . Доказательство:
| d dx | csc x | = | −csc x детская кроватка x |
Пример. Вычислить производную sin ax 2 .
Решение . При применении цепного правила,
| d dx | грех топор 2 | = | cos ax 2 · | d dx | топор 2 | = | cos ax 2 · | 2 топор | = | 2 ax cos ax 2 . |
Задача 5. Вычислить эти производные.
| а) | d dx | грех 5 x | = | 5 cos 5 x |
| б) | d dx | ½ sin 2 x | = | sin x cos x |
| в) | d dx | 2 cos 3 x | = | −6 sin 3 x |
| г) | d dx | x cos x | = | cos x — x sin x |
| д) | d dx | sin 2 x cos x | = | 2 cos 2 x cos x — sin 2 x sin x |
| е) | d dx | желто-коричневый (3 x ) 2 | = | 18 x сек 2 (3 x ) 2 |
| г) | d dx | 2 детская кроватка | x 2 | = | — csc 2 | x 2 |
| h) | d dx | сек 4 x | = | 4 секунды 4 x желто-коричневый 4 x |
| i) | d dx | a csc bx | = | — ab csc bx детская кроватка bx |
| j) | = |
Проблема 6. ABC — прямой угол, а прямая AD вращается на
ABC — прямой угол, а прямая AD вращается на
, так что угол θ увеличивается в положительное направление. С какой скоростью — сколько радиан в секунду — он увеличивается, если BC постоянен на уровне 3 см, а AB (назовем его x ) уменьшается со скоростью −3 см / с, а его длина составляет 6 см. ?
Следующий урок: Производные обратных тригонометрических функций
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
4. Формулы полуугловых
М. Борна
Мы разработаем формулы для синуса, косинуса и тангенса половинного угла.
Формула полуугла — синус
Начнем с формулы косинуса двойного угла, с которой мы познакомились в предыдущем разделе. 2 (α / 2) = (1 — cos α) / 2`
2 (α / 2) = (1 — cos α) / 2`
Решение дает нам следующий синус для тождества полуугла :
`sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2`
Знак (положительный или отрицательный) для `sin (alpha / 2)` зависит от квадранта в котором лежит `α / 2`.
Если α / 2 находится в первом или втором квадранте , в формуле используется положительный регистр:
`sin (альфа / 2) = sqrt (1-cos alpha) / 2`
Если α / 2 находится в третьем или четвертом квадранте , в формуле используется отрицательный регистр:
`sin (alpha / 2) = — sqrt (1-cos alpha) / 2`
Формула полуугла — косинус
Используя аналогичный процесс, с той же заменой `theta = alpha / 2` (таким образом, 2 θ = α ) мы подставляем в личность
cos 2 θ = 2cos 2 θ — 1 (см.2 (альфа / 2) = (1 + cos alpha) / 2`
Решая относительно cos (α / 2), получаем:
`cos (альфа / 2) = + — sqrt ((1 + cos alpha) / 2`
Как и раньше, нужный нам знак зависит от квадранта.
Если α / 2 находится в первом или четвертом квадранте , в формуле используется положительный регистр:
`cos (альфа / 2) = sqrt ((1 + cos alpha) / 2`
Если α / 2 находится во втором или третьем квадранте , в формуле используется отрицательный регистр:
`cos (альфа / 2) = — sqrt ((1 + cos alpha) / 2`
Формула полуугла — касательная
Тангенс половины угла определяется по формуле:
`tan (alpha / 2) = (1-cos alpha) / (sin alpha)`
Проба
Сначала напомним «tan x = (sin x) / (cos x)».2а)) `
Затем находим квадратный корень:
`= (1-cos a) / (sin a)`
Конечно, нам нужно будет делать поправку на положительные и отрицательные знаки, в зависимости от рассматриваемого квадранта. @`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) `
@`, используя соотношение половинного угла синуса, приведенное выше.(текст (o))) / 2) `
`= + — sqrt (((1 + 0.866)) / 2)`
`= 0,9659`
Первый квадрант, значит положительный.
2. Найдите значение sin (alpha / 2), если cos alpha = 12/13, где 0 ° < α <90 °.
Ответ
`sin (альфа / 2) = + — sqrt ((1-cos alpha) / 2)`
`= sqrt ((1-12 / 13) / 2)`
`= sqrt ((1/13) / 2)`
`= sqrt (1/26)`
`= 0,1961`
Мы выбираем позитив, потому что находимся в первом квадранте.п / (п!) + … #
Мы сразу видим, что члены в синусоидальном ряду очень похожи на члены в экспоненциальном ряду — они того же размера, что и существуют, но часто имеют противоположный знак, и половина из них отсутствует.
Вспоминая, что степени # i # изменяются в периодическом четырехэтапном шаблоне, который имеет два последовательных знака плюс и два последовательных знака минус, мы задаемся вопросом, может ли изменение # x # на # ix # в экспоненциальном ряду помочь нашей проблеме знаков. 3 / (3!) +.(-x)) #
3 / (3!) +.(-x)) #
Гиперболические функции — это набор функций, тесно связанных с этими формулами с тригонометрическими функциями. По мере того, как вы продвигаетесь к дифференциальным уравнениям, вы столкнетесь с ситуациями, когда простая смена знака на коэффициент делает разницу между поиском решений триггерной и гиперболической функции. Связь между двумя наборами функций очень важна.
Тригонометрические формулы и идентичности — Полный список
Последнее обновление: фев.6 августа 2019 г. по адресу Teachoo
Изучите все концепции главы 2, отношения и функции класса 11 — БЕСПЛАТНО. Проверка — Тригонометрия Класс 11 — Все концепции
В формулах тригонометрии мы узнаем
Основные формулы
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Знак греха, cos, tan в разных квандрантах
Радианы
Отрицательные углы (четно-нечетные тождества)
Значение sin, cos, tan повторяется через 2π
Угол сдвига на π / 2, π, 3π / 2 (тождества ко-функции или тождества периодичности)
Сумма углов и тождества разностей
Формулы двойного угла
Формулы тройного угла
Половинные углы (формулы уменьшения мощности)
Сумма идентичностей (сумма идентичностей продуктов)
Идентичности продукта (продукт для суммирования идентичностей)
Закон синуса
Закон косинуса
Что такое функции обратной тригонометрии?
Область и диапазон функций обратной тригонометрии
Обратные тригонометрические формулы
- Замены обратной тригонометрии
sin, cos tan при 0, 30, 45, 60 градусах
Пифагорейские тождества
Признаки греха, кос, загар в разных квадрантах
Чтобы узнать знак греха, cos, tan в разных квадрантах,
мы помним
А дд → S угар → Т o → C штраф
Представляя в виде таблицы
Квадрант я | Квадрант II | Квадрант III | Квадрант IV | |
грех | + | + | — | — |
потому что | + | — | — | — |
загар | + | — | + | — |
Радианы
Радианная мера = π / 180 × мера степени
Также,
1 градус = 60 минут
я. е. 1 ° = 60 ’
е. 1 ° = 60 ’
1 минута = 60 секунд
т.е. 1 ’= 60’ ’
Отрицательные углы (четно-нечетные тождества)
sin (–x) = — sin x
cos (–x) = cos x
tan (–x) = — tan x
сек (–x) = сек x
cosec (–x) = — cosec x
детская кроватка (–x) = — детская кроватка x
Значение sin, cos, tan повторяется через 2π
грех (2π + х) = грех х
cos (2π + x) = cos x
загар (2π + х) = загар х
Угол сдвига на π / 2, π, 3π / 2 (тождества ко-функции или тождества периодичности)
sin (π / 2 — x) = cos x | cos (π / 2 — x) = sin x |
sin (π / 2 + x) = cos x | cos (π / 2 + x) = — sin x |
sin (3π / 2 — x) = — cos x | cos (3π / 2 — x) = — sin x |
sin (3π / 2 + x) = — cos x | cos (3π / 2 + x) = sin x |
грех (π — х) = грех х | cos (π — x) = — cos x |
sin (π + x) = — грех x | cos (π + x) = — cos x |
sin (2π — x) = — грех x | cos (2π — x) = cos x |
грех (2π + х) = грех х | cos (2π + x) = cos x |
Сумма углов и тождества разностей
Формулы двойного угла
Формулы тройного угла
Половинные углы (формулы уменьшения мощности)
Сумма идентичностей (сумма идентичностей продуктов)
Идентичности продукта (продукт для суммирования идентичностей)
Продукт суммировать идентичности
2 cosx cosy = cos (x + y) + cos (x — y)
-2 sinx siny = cos (x + y) — cos (x — y)
2 sinx cosy = sin (x + y) + sin (x — y)
2 cosx siny = sin (x + y) — sin (x — y)
Закон синуса
Здесь
- A, B, C — вершины ∆ ABC
- a — сторона, противоположная A i.
 е. до н.э
е. до н.э - b — сторона, противоположная B, т. е. AC
- c — сторона, противоположная C, т.е. AB
Закон косинуса
Так же, как закон синуса, у нас есть закон косинуса
Что такое обратные тригонометрические функции
Если sin θ = x
Затем положив грех на правильную сторону
θ = грех -1 Икс
грех -1 х = θ
Итак, угол, обратный греху, — это угол.
Точно так же все функции тригонометрии обратны углу.
Примечание : Здесь угол измеряется в радианах, а не в градусах.
Итак, у нас есть
грех -1 Икс
потому что -1 Икс
загар -1 Икс
Cosec -1 Икс
сек -1 Икс
загар -1 Икс
Область и диапазон обратных тригонометрических функций
Домен | Диапазон | |
грех -1 | [–1, 1] | [-π / 2, π / 2] |
потому что -1 | [–1, 1] | [0, π] |
загар -1 | р | (-π / 2, π / 2) |
Cosec -1 | р — (–1, 1) | [π / 2, π / 2] — {0} |
сек -1 | р — (–1, 1) | [0, π] — {π / 2} |
детская кроватка -1 | р | (0, π) |
Формулы обратной тригонометрии
Некоторые формулы обратной тригонометрии:
грех –1 (–X) = — грех -1 Икс
потому что –1 (–X) = π — sin -1 Икс
загар –1 (–X) = — загар -1 Икс
Cosec –1 (–X) = — cosec -1 Икс
сек –1 (–X) = — сек -1 Икс
детская кроватка –1 (–X) = π — детская кроватка -1 Икс
Подстановка обратной тригонометрии
Тригонометрических идентичностей
| Тригонометрические идентичности |
| (Математика | Триггер | Личности) |
| sin (тета) = кондиционер | csc (theta) = 1 / sin (theta) = c / a |
| cos (тета) = b / c | сек (тета) = 1 / cos (тета) = c / b |
| загар (тета) = грех (тета) / соз (тета) = а / б | кроватка (тета) = 1 / загар (тета) = b / a |
sin (-x) = -sin (x)
csc (-x) = -csc (x)
cos (-x) = cos (x)
sec (-x) = sec (x)
tan (-x ) = -тан (x)
детская кроватка (-x) = -колыбельная (x)
| sin ^ 2 (x) + cos ^ 2 (x) = 1 | загар ^ 2 (x) + 1 = сек ^ 2 (x) | детская кроватка ^ 2 (x) + 1 = csc ^ 2 (x) | |
| sin (x y) = sin x cos y cos х грех у | |||
| cos (x y) = cos x уютный грех х грех у | |||
загар (x y) = (загар х загар у) / (1 загар х загар у)
sin (2x) = 2 sin x cos x
cos (2x) = cos ^ 2 (x) — sin ^ 2 (x) = 2 cos ^ 2 (x) — 1 = 1-2 грех ^ 2 (x)
загар (2x) = 2 загар (x) / (1 — загар ^ 2 (x))
sin ^ 2 (x) = 1/2 — 1/2 cos (2x)
cos ^ 2 (x) = 1/2 + 1/2 cos (2x)
sin x — грех y = 2 sin ((x — y) / 2) cos ((x + y) / 2)
cos x — cos y = -2 sin ((x — y) / 2) sin ((x + y) / 2)
| угол | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| грех ^ 2 (а) | 0/4 | 1/4 | 2/4 | 3/4 | 4/4 |
| cos ^ 2 (а) | 4/4 | 3/4 | 2/4 | 1/4 | 0/4 |
| желто-коричневый ^ 2 (а) | 0/4 | 1/3 | 2/2 | 3/1 | 4/0 |
Данный треугольник abc с углами A, B, C; a противоположно A, b напротив B, c напротив C:
a / sin (A) = b / sin (B) = c / sin (C) (Закон Синусов)
| (Закон косинусов) |
(a — b) / (a + b) = tan [(A-B) / 2] / tan [(A + B) / 2] (Закон касательных)
Лекция 127: Формула полууглового доказательства: sin (x / 2)
1: Что такое единичный круг? 2: Единичный круг и угол (Часть 1 из 2) 3: Единичный круг и угол (Часть 2 из 2) 4: Единичный круг и угол (30 и 60 градусов) 5: Единичный круг и знаки x и y 6: функция тригонометрии: объяснение синуса 7: функция тригонометрии: объяснение косинуса 8: функция тригонометрии: объяснение тангета 9: функция тригонометрии: объяснение котангета 10: функция тригонометрии: объяснение секант 11: тригонометрия Функция: объяснение косеканса 12: Что такое отрицательные углы? 13: Как преобразовать углы больше 360? 14: Что такое четные и нечетные функции? 15: Основные триггерные идентификации16: Использование единичной окружности для оценки триггерных функций 17: Использование единичной окружности для оценки Триггерные функции 18: Использование единичного круга для оценки триггерных функций 19: Формула сокращения (1 из 4) Сложение / вычитание 2 pi20: Формула сокращения (2 из 4) Сложение / вычитание pi21: Формула сокращения (3 из 4) Добавить pi / 222: Формула сокращения (4 из 4) Вычтем pi / 223: график y = sin (theta) (1 из 2) 24 : График y = sin (theta) (2 из 2) и единичный круг 25: график y = cos (theta) 26: график y = tan (theta) 27: период графиков синуса и косинуса 28: общее уравнение для синуса и Косинус 29: Общее уравнение для синуса и косинуса: Амплитуда 30: Общее уравнение для синуса и косинуса: Период 31: Общее уравнение для синуса и косинуса: Сдвиг влево / вправо 32: Общее уравнение для синуса и косинуса: Сдвиг вверх / вниз 33: Графическая сумма функций тригонометрии (1 из 2) 34: Графическая сумма функций тригонометрии (2 из 2) 35: График отрицательной функции триггера 36: Графическое изображение произведения тригонометрической функции (без калькуляторов!) 37: Графическое изображение произведения триггера Функция (без калькуляторов!) 38: Построение графика произведения триггерной функции (без калькуляторов!) 39: Построение графика функции y = — (1/2) sinx40: Построение графика функции y = 2 + 2cosx41: определение амплитуды, периода, и график y = -3sin3x42: найти амплитуду, период и график y = 4cos [(1/2) x] 43: найти амплитуду, период и график y = cos [x- (pi / 2)] 44: Найдите амплитуду Pe riod и График y = 3sin [(2x / 3) — (pi / 6)] 45: Найдите амплитуду, период и график y = 2cos [3x + (pi / 4)] — 146: Найдите амплитуду, период, Фазовый угол и напишите уравнение 47: Найдите амплитуду, период, фазовый угол и запишите уравнение 48: Найдите амплитуду, период, фазовый угол и запишите уравнение49: График y = tan4x50: График y = csc2x51: Функция обратной синусоиды52: Функция обратного косинуса53 : Функция обратной касательной 54: функция обратной тригонометрии: не запутайтесь! 55: угол в радианах 56: длина дуги (окружность) 57: площадь сектора (окружность) 58: основы тригонометрии 59: основы тригонометрии: пример 60: основы тригонометрии : Упражнение 161: Основы тригонометрии: Упражнение 262: Основы тригонометрии: Упражнение 363: Основы тригонометрии: Упражнение 464: Функции обратного триггера: Найти угол 65: Функции обратного триггера: Упр. 166: Обратные триггерные функции: Пример. 267: Обратные триггерные функции: Сводка 68: Найти все неизвестные (Adj =? Opp =?) 69: Найти все неизвестные (Adj =? Hyp =?) 70: Найти все неизвестные (Adj =? Angle =?) 71: Задача Задача № 172: Задача № 273: Задача № 374: Задача № 475: Высота флага =? 76: Расстояние до ближайшей звезды =? 77: Высота здания =? 78: Расстояние между Венерой и Солнцем =? 79: Окружность планеты =? 80: Угол геосинхронного спутника =? 81: Определение закона синуса 82: Доказанный закон синуса 83: Пример SSA (сторона-сторона-угол) 84: Пример AAS (угол-угол-сторона ) 85: Осторожно: НЕТ случаев решения с законом синуса 86: множественные решения с законом синуса 87: определение высоты спутника 88: определение высоты горы 89: что такое закон косинусов? 90: поиск трех углов с учетом трех сторон91: Доказанный закон косинусов92: Найдите расстояние и пеленг самолета93: Найдите расстояние между кораблями94: Формула Герона: Введение95: Доказанная формула Герона96: Каковы основные тригонометрические тождества? 97: Cofunction Trigonometric Identities98: Упростить тригонометрическое выражение: 199: Упростить тригонометрическое выражение: 2100: Проверить идентичность: 1101: Подтвердить идентичность: 2102: Проверить идентичность: 3103: Подтвердить идентичность: 4104: Формулы сложения и вычитания 105: Доказательство сложения Формула (косинус) 106: доказательство формулы вычитания (косинус) 107: доказательство идентичности кофункции 108: доказательство формулы сложения (синус) 109: доказательство формулы вычитания (синус) 110: доказательство формулы сложения (касательная) 111: доказательство Формула вычитания (касательная) 112: Найдите sin75 ,.
166: Обратные триггерные функции: Пример. 267: Обратные триггерные функции: Сводка 68: Найти все неизвестные (Adj =? Opp =?) 69: Найти все неизвестные (Adj =? Hyp =?) 70: Найти все неизвестные (Adj =? Angle =?) 71: Задача Задача № 172: Задача № 273: Задача № 374: Задача № 475: Высота флага =? 76: Расстояние до ближайшей звезды =? 77: Высота здания =? 78: Расстояние между Венерой и Солнцем =? 79: Окружность планеты =? 80: Угол геосинхронного спутника =? 81: Определение закона синуса 82: Доказанный закон синуса 83: Пример SSA (сторона-сторона-угол) 84: Пример AAS (угол-угол-сторона ) 85: Осторожно: НЕТ случаев решения с законом синуса 86: множественные решения с законом синуса 87: определение высоты спутника 88: определение высоты горы 89: что такое закон косинусов? 90: поиск трех углов с учетом трех сторон91: Доказанный закон косинусов92: Найдите расстояние и пеленг самолета93: Найдите расстояние между кораблями94: Формула Герона: Введение95: Доказанная формула Герона96: Каковы основные тригонометрические тождества? 97: Cofunction Trigonometric Identities98: Упростить тригонометрическое выражение: 199: Упростить тригонометрическое выражение: 2100: Проверить идентичность: 1101: Подтвердить идентичность: 2102: Проверить идентичность: 3103: Подтвердить идентичность: 4104: Формулы сложения и вычитания 105: Доказательство сложения Формула (косинус) 106: доказательство формулы вычитания (косинус) 107: доказательство идентичности кофункции 108: доказательство формулы сложения (синус) 109: доказательство формулы вычитания (синус) 110: доказательство формулы сложения (касательная) 111: доказательство Формула вычитания (касательная) 112: Найдите sin75 ,.





 2 (альфа / 2) = (1 + cos alpha) / 2`
2 (альфа / 2) = (1 + cos alpha) / 2` е. до н.э
е. до н.э