Системы линейных уравнений с двумя переменными
Муниципальное бюджетное общеобразовательное
учреждение «Баклановская средняя
общеобразовательная школа» Сорочинского района
Оренбургской области
Урок по алгебре в 7 классе.
Решение систем линейных уравнений
с двумя переменными.
Учитель математики
Козлова Юлия Александровна
Урок «Решение систем линейных уравнений с двумя переменными». 7-й класс
Цели:
Образовательная: закрепление, систематизация и обобщение знаний о методах решения и исследования системы уравнений, формирование знаний и умений в решении систем уравнений, используя возможности программы «живая геометрия».
Развивающая: формирование навыков самостоятельной деятельности, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного, развитию математического кругозора, мышления и речи, внимания и памяти.
Воспитательная: привитие интереса к изучаемому предмету; воспитание активности, организованности и взаимопомощи через работу в парах.
Оборудование: проектор, интерактивная доска, презентация, раздаточный материал.
Тип урока: урок закрепления, обобщения и систематизации знаний
ХОД УРОКА
Организационный момент
– Здравствуйте, ребята! Прошу занять свои места. На этом уроке мы должны закрепить основные способы решения систем уравнений, проверить свое умение самостоятельно применять полученные знания, способствовать развитию логического мышления и грамотной математической речи.
– Я тоже надеюсь, что нам всем вместе удастся добиться успеха.
Итак, записываем в тетради число, классная работа, тема урока.
Рефлексия настроения (слайд 2)
1. , если нет — (слайд 4).
, если нет — (слайд 4).
Верно ли утверждение?
Линейное уравнение с двумя переменными имеет вид: ах2 + вх = с (–)
Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно (+).
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство (+)
Существуют только два способа решения систем: способ подстановки и способ сложения (–)
Решить систему уравнений – это значит найти все её решения или установить, что их нет (+)
Если в уравнении перенести слагаемое из одной части в другую, то получится уравнение, равносильное данному уравнению (–)
Взаимопроверка. Ребята поменяйтесь тетрадями и сравните полученную кривую с кривой, изображенной на слайде, и оцените работу соседа. (Слайд 3)
(Слайд 3)
А теперь давайте вспомним, что называется решением линейного уравнения, решением системы линейных уравнений с двумя переменными. И давайте мы с вами проверим в ходе выполнения устных заданий. (Слайд 5)
Вычислить устно:
Найдите пару чисел, которая является решением уравнения
а) (1; 7) б) (-5; 1) в) (-9; 7) г) (0; 2)
2. Укажите пару чисел, которая является решением системы уравнений
а) (0; -4) б) (10; 0) в) (-6; -12) г) (3; 4)
Обобщение и систематизации знаний.
Решение систем уравнений различными способами. (Слайд 6)
Ну а теперь давайте вспомним способы решения систем линейных уравнений с двумя переменными. Я вам раздам листы с заданиями на 4 варианта. Кто решит первый, выйдет на доске запишет пару чисел, которая является решением системы. По полученному решению в координатной плоскости найдем букву. Из букв составим слово, а ученик познакомит со сведениями из истории математики.
(Приложение 1)
(1;0)
(4;1)
(5;5)
(2;1)
(Приложение 2)
(1;-2)
(2;3)
(4;1)
Историческая справка:
ЕГИПЕТ. (Слайд 8) Первые задачи на составление и решение систем уравнений с несколькими переменными встречаются в египетских и вавилонских текстах второго тысячелетия до нашей эры, а также в трудах древнегреческих и индийских ученых. Решались они различными искусственными способами, единого алгоритма не было.
КИТАЙ. Алгоритм решения систем линейных уравнений был напечатан в Китае в труде “Математика в девяти книгах” (206 г. до н.э.), где рассматривались системы и давились правила их решения. При этом все изложение словесно. Коэффициенты системы располагались на счетной доске в виде таблицы. При повторных действиях было замечено, что следует поступать по одному и тому же правилу систематически.
Системы линейных уравнений [wiki.
 eduVdom.com]
eduVdom.com]Линейное уравнение с двумя переменными — это уравнение вида ах + by = с, где х и у — переменные, a, b и с — некоторые числа. Решение уравнения с двумя переменными (не обязательно линейного) — это пара значений переменных, при подстановке которых в уравнение оно обращается в верное равенство.
Общий вид системы линейных уравнений с двумя переменными: $$ \left\{\begin{matrix} ax + by = c \\ dx + ey = f \end{matrix}\right. $$
Решение системы уравнений с двумя переменными (не обязательно линейных) — это пара значений переменных, при подстановке которых в уравнение системы каждое из них обращается в верное равенство.
Алгоритм решения системы линейных уравнений с двумя переменными методом подстановки:
выразить из какого-нибудь уравнения системы одну переменную через другую;
подставить в другое уравнение системы вместо этой переменной полученное выражение;
решить полученное уравнение с одной переменной;
найти соответствующее значение второй переменной и выписать решение системы.

Алгоритм решения системы линейных уравнений с двумя переменными
умножить почленно уравнения системы, подобрав множители таким образом, чтобы коэффициенты при одной из переменных стали противоположны;
сложить почленно левые и правые части уравнений системы;
решить полученное уравнение с одной переменной;
найти соответствующее значение второй переменной и выписать решение системы.
Пример 1. Решите систему уравнений $$ \left\{\begin{matrix} \frac{x}{2} — \frac{y}{3} = 1 \\ 2x — 3y = 2 \end{matrix}\right. $$
Решение: Из второго уравнения системы: $x = \frac{2+3y}{2}$
Подставим получившееся выражение в первое уравнение вместо х: $$ \frac{2+3y}{4} — \frac{y}{3} = 1 \\ \frac{6+9y-4y}{12} = 1 \\ 5y+6 = 12 \\ 5y = 6 \\ y = \frac{5}{6} $$
Найдём x: $$ x = \frac{2+3\cdot\frac{6}{5}}{2} \\ x = \frac{14}{5} $$
Ответ: (2,8; 1,2)
Пример 2. Решите систему уравнений
$$
\left\{\begin{matrix}
\frac{x}{2} — \frac{y}{4} = 2
\\ 2x + 3y = 5
\end{matrix}\right.
$$
Решите систему уравнений
$$
\left\{\begin{matrix}
\frac{x}{2} — \frac{y}{4} = 2
\\ 2x + 3y = 5
\end{matrix}\right.
$$
Решение: Умножив первое уравнение на (-4), получим систему: $$ \left\{\begin{matrix} -2x + y = -8 \\ 2x + 3y = 5 \end{matrix}\right. $$
Отсюда: $$ 4y = -3 \\ y = -\frac{3}{4} \\ x = \frac{5-3y}{2} \\ x = \frac{5 — 3\cdot(-\frac{3}{4})}{2} \\ x = \frac{29}{8} $$
Ответ: $(\frac{29}{8};-\frac{3}{4})$
subjects/mathematics/системы_линейных_уравнений.txt · Последние изменения: 2013/02/02 18:12 — ¶
Различные способы решения систем двух линейных уравнений с двумя переменными
Тип урока: систематизации и обобщения изученного.
Цель урока:
- Обобщить изученный материал по теме;
- Проконтролировать степень усвоения знаний и умений по изученной теме;
- Показать рациональность применения различных способов решения для конкретной системы;
- Развивать коммуникативные навыки.

Ход урока
Организационный момент (2 мин.)
Работа проходит в группах по 5-6 человек, всего класс разделен на 5 групп.
Актуализация знаний (10 мин.)
Учитель: Мы с вами продолжаем заниматься решением систем двух линейных уравнений с двумя переменными различными способами.
- Давайте вспомним, что называется системой?
- Что означает решить систему уравнений?
- Сколько решений может иметь система уравнений?
- Как называется система уравнений, имеющая хотя бы одно решение? Не имеющая решений?
- Что является графиком линейной функции?
- Система состоит из двух линейных уравнений. А каким может быть взаимное расположение двух прямых на плоскости?
- Сколько общих точек имеют прямые в каждом из этих случаев?
- Сколько решений может иметь система в зависимости от взаимного расположения прямых на плоскости?
- Как узнать, совместна ли система, т.
 е. имеет ли
она решение?
е. имеет ли
она решение? - Какие способы для нахождения решения системы линейных уравнений существуют?
Учащиеся называют способы решения, на доске появляется следующие записи:
- способ сложения;
- способ подстановки;
- способ сравнения;
- графический способ;
- формулы Крамера.
Практическое применение всех способов решения (10мин.)
Для решения систем линейных уравнений нам известно пять способов решения. Предлагаю применить каждый из этих способов для решения следующей системы
.
Выберем самый рациональный способ для данной системы, но не забудем отметить достоинства остальных методов.
У доски по одному представителю от
каждой группы решают заданную систему своим
способом, который определен с помощью жеребьевки
(отрывают лепестки от ромашки, на которых
написаны названия способов решения).
Обсуждение решения (3мин)
Подведем итог нашей работы (этап рефлексии).
- Понравилось ли вам решать систему предложенным вам способом?
- Что вы чувствовали во время решения?
- Было ли вам комфортно?
- Какой из данных методов наиболее оптимален для данной системы уравнений?
- Во всех ли случаях решения мы получили одинаковый ответ?
- Почему это произошло?
Практическая работа по выбору рационального способа решения системы линейных уравнений (15 мин)
Однако нельзя хвалить один способ и
использовать его при решении всех систем
уравнений, а другой считать ненужным,
неправильным. Если математики придумали столько
различных способов решения, и все они до сих пор
применяются на практике, то можно сделать вывод,
что для любой системы найдется наиболее
рациональный способ. И, наша с вами задача
научиться делать этот выбор.
И, наша с вами задача
научиться делать этот выбор.
Предлагаю вашему вниманию пять систем. Вам необходимо для каждой из них определить рациональный способ решения и обосновать свой выбор.
Можно предложить следующее соответствие между заданными системами уравнений и способами решения:
а) Способ подстановки;
б) Графический способ;
в) способ сравнения;
г) формулы Крамера;
д) способ сложения.
Учащимся предлагается обосновать такой выбор или внести коррективы. Представители от каждой группы у доски решают ту систему, которая им досталась в результате жеребьевки. Остальные обучающиеся работают на местах.
Подведение итогов урока, рефлексия (5 мин)
Какой же вывод можно вынести из проделанной работы? (учащиеся предлагают свои варианты) Хочется надеяться, что теперь прежде чем решать систему своим любимым способом задумаетесь “ А может быть другой метод решения более удобен, рационален в данной ситуации?”
Домашнее задание: подобрать по две
системы линейных уравнений на каждый способ
решения.
Решение систем линейных уравнений с двумя переменными
1. Решение систем линейных уравнений с двумя переменными.
МБОУ лицей №82 п.Каменоломни Ростовской области.
Решение систем линейных
уравнений с двумя переменными.
Алгебра 7 класс.
Подготовила учитель математики
Бобер Е.В.
2012год.
2. Цели урока:
Повторить определения уравнения,системы уравнений, их решений;
Повторить алгоритмы решения систем
уравнений;
Восстановить и отработать навыки
решения систем линейных уравнений с
двумя переменными
3. Задание № 1
Решите линейные уравнения , ответырасположите в порядке возрастания.
3У+ 7 = 13
Н5
х – 1= -4
13 – 3У = 1
7х = 7
5
Р6
Д
Ф
2
Т
11
7
Г
( у + 5)∙ 2 = 0
2х – 1 = 9
2х –11 =-8
11
О
1
Е
-3
А
4
И
у
15
Диофант Александрийский,
древнегреческий математик, ок.
 3
3века н.э. «Арифметика» из 13 книг, 6
сохранились до наших дней.
В 5 книгах содержатся методы
решения неопределенных уравнений.
Задача. В клетке сидят кролики и фазаны
вместе у них 18 ног. Узнайте сколько в
клетке тех и других.
Решение.
Пусть: Х- число кроликов
У- число фазанов
Тогда 4х + 2у = 18.
2х + у = 9
у = 9 — 2х
Методом перебора: (1;7), (2;5), (3;3), (4;1).
Уравнение 4х+2у=18 называют
неопределенным или диофантовым
уравнением (уравнение в целых или
натуральных числах)
5. Система уравнений и её решение
ОпределениеСистемой уравнений называется некоторое количество уравнений,
объединенных фигурной скобкой
(система уравнений –это конъюнкция нескольких уравнений)
Решением системы уравнений с двумя переменными называется пара значений
переменных, обращающая каждое уравнение системы в верное равенство
(решение системы уравнений – это пересечение решений всех уравнений,
входящих в систему)
Решить систему уравнений — это значит найти все её решения или установить,
что их нет
6.
 Решение системы графическим способом у — х=2,
Решение системы графическим способом у — х=2,у+х=10;
Выразим у
через х
y
10
у=х+2,
у=10-х;
Построим график
первого уравнения
y=x+2
6
у=х+2
х 0
у 2
y=10 — x
-2
2
0
Построим график
второго уравнения
1
-2
0 1
у=10 — х
х 0
у 10
10
0
Ответ: (4; 6)
4
10
x
7. Решение системы способом сложения
Решениесистемы
способом
Уравняем
модули
сложения
коэффициентов
перед уравнением
х=3,
7·3+2у=1;
7х+2у=1, ||·(-3)
17х+6у=-9;
Сложим уравнех=3,
ния почленно
21+2у=1;
-21х-6у=-3,
+ 17х+6у=-9;
____________
Решим
х=3,
уравнение
2у=-20;
— 4х = — 12,
7х+2у=1;
х=3,
Подставим
у=-10.
х=3,
7х+2у=1;
Ответ: (3; — 10)
Решим
уравнение
8. Решение системы способом подстановки
Решение системы способомВыразим у
подстановки
через х
Подстави
мх и
найдем у
-х+у=1,
2х+у=4;
У = х + 1,
2х+у=4;
____________
2х + х + 1= 4,
3х =4 – 1,
3х = 3
Х = 1;
Подставим
полученное
выражение в другое
уравнение
х=1,
— 1+у=1;
х=1,
у=2;
Решим
уравнение
Ответ: (1; 2)
9.
 Проверочная работа 1 вариант
Проверочная работа 1 вариантРешите задачу: Сумма двух чисел равна
33, а их разность равна7. Найдите эти
числа.
2 вариант
Решите задачу: Разность чисел равна 8, а
их сумма равна 22. Найдите эти числа.
10. Проверка:
1вариантх+у=33
+ х – у = 7.
2х = 40
х=20.
20+у=33
у=13.
Ответ: ( 20;13)
2 вариант
х — у=8
+ х + у =22.
2х = 30
х=15.
15- у=8
у=7.
Ответ: ( 15;7)
11. Домашняя работа
Составить три системы уравнений ирешить их разными способами
Успехов
в домашней работе
Система линейных уравнений с 2 переменными
Система линейных уравнений с 2 переменными
«Математику нельзя изучать, наблюдая как это делает сосед»
2x-y=1
Что записано на экране?
2x-y=1
Что записано на экране?
Ответ: Линейное уравнение с двумя переменными.
2x-y=1
Что называется решением уравнения с двумя переменными?
2x-y=1
Что называется решением уравнения с двумя переменными?
Ответ. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Что называется графиком уравнения двумя переменными?
Что называется графиком уравнения с двумя переменными?
Ответ: Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Что является графиком линейного уравнения с двумя переменными?
Что является графиком линейного уравнения с двумя переменными?
Ответ: Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая .
2x-y=1
Как узнать будет ли пара (1;1), (1;5) решением уравнения?
2x-y=1
Как узнать будет ли пара (1;1), (1;5) решением уравнения?
Ответ:
2 ·1-1=1 верно
Пара (1;1) является решением уравнения
2x-y=1
Как узнать будет ли пара (1;1), (1;5) решением уравнения?
Ответ:
2 ·1-1=1 верно
Пара (1;1) является решением уравнения
2·1-5=1 неверно
Пара (1;5) не является решением уравнения
2x-y=1
Найти три решения данного уравнения.
Выразить переменную y через переменную x.
а) x + y = 4;
б) 2x – y = 2;
в) x + 2y = 4;
г) x – y = 0.
Выразить переменную y через переменную x.
а) x + y = 4; y = 4 — x
б) 2x – y = 2; y = 2x — 2
в) x + 2y = 4; y = 2 – 0,5x
г) x – y = 0. y = x
При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8
При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8
Ответ: при k= -6 и b ≠8
При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8
Ответ: при k= -6 и b ≠8
б) пересекает график функции y= -6x+8
При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8
Ответ: при k= -6 и b ≠8
б) пересекает график функции y= -6x+8
Ответ: при к ≠ -6
При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8
Ответ: при k= -6 и b ≠8
б) пересекает график функции y= -6x+8
Ответ: при к ≠ -6
в) совпадает с графиком функции y=-6x+8
При каких k и b график линейной функции y = kx + b
а) параллелен графику функции y= -6x+8
Ответ: при k= -6 и b ≠8
б) пересекает график функции y= -6x+8
Ответ: при к ≠ -6
в) совпадает с графиком функции y=-6x+8
Ответ: при k= -6 и b=8
Задача. Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.
Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.
Задача. Сумма двух чисел равна 12, а их разность равна 2. Найдите эти числа.
Обозначим первое число буквой x, а второе буквой y.
По условию задачи сумма чисел равна 12, т.е.
x+y=12.
Так как разность чисел равна 2, то
x – y =2.
Система уравнений — это
несколько уравнений, в которых одни и те же буквы обозначают одни и те же числа.
Или – несколько уравнений, для которых надо найти общие решения.
Решение системы уравнений с двумя переменными — это
пара значений переменных, обращающая каждое уравнение системы в верное равенство.
Что называют системой уравнений?
Рассмотрим два линейных уравнения:
Y=-x+3 и Y=2x-3
Найдём такую пару значений (x;y) , которая
одновременно является решением
и первого и второго уравнения
При x=2 и y=1 и первое и второе уравнения превращаются в верные равенства.
1 = -2+3 и 1 = 2∙2 -3
То, есть пара (2; 1) является общим решением этих
уравнений.
Решить систему уравнений — это найти их общие решения
Поиск общего решения нескольких уравнений называют решением системы уравнений .
Уравнения записывают друг под другом и обозначают фигурной скобкой
y=-x+3
y=2x-3 А ответ записывают в виде пары (x;y)
Ответ: (2;1)
Графический метод решения системы y=-x+3 y=2x-3
Y=-x+3
x
y
A(0;3)
D(3;3)
3
0
0
3
M(2;1)
Y=1
B(3;0)
X=2
Y=2x-3
y
x
0
-3
C(0;-3)
3
3
Ответ: (2;1)
Правило решения системы графическим способом:
- Построить график каждого из уравнений системы;
2) Найти координаты точки пересечения построенных прямых (если они пересекаются)
Y=0,5x+2
x
y
B(2;3)
0
2
2
A(0;2)
3
D(2;0)
C(0;-1)
Y=0,5x-1
Графики функций параллельны и не пересекаются.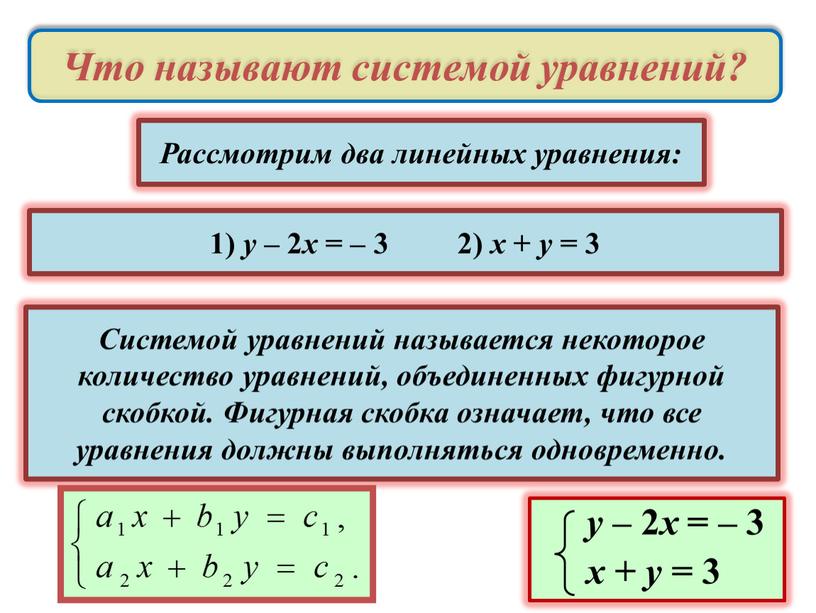
y
x
0
-1
0
2
Говорят, что система несовместна.
Решим систему уравнений: Y= 0,5x+2 Y= 0,5x-1
Ответ: Система не имеет решений.
Y=x+3
D(1;4)
y
x
Система
Y=x+3
Y=x+3
A(0;3)
0
3
C(-1;2)
0
-3
B(-3;0)
Y=x+3
Графики функций совпадают.
y
x
4
1
2
-1
Говорят, что система неопределенна
Ответ: система имеет бесконечное множество решений
Алгоритм нахождения количества системы уравнений с 2 переменными
1) Из каждого уравнения выразить y через х.
2)
Если
к1 к2
Если к1=к2,
b 1 b 2
Графики
пересекаются
Система имеет единственное решение
Графики параллельны
Если к1=к2,
b1=b2
Система не имеет решений
Графики совпадают
Система имеет бесконечно много решений
Является ли пара чисел решением системы
(3;1)
(2;2)
верно
верно
неверно
верно
(3;1) не является решением
(2;2) является решением
Решите в тетрадях систему уравнений: Y= -0,5x +3 Y= 0,5x -3
Y= — 0,5x+3
x
y
0
3
B(2;2)
2
2
A(0;3)
M(6;0)
Y= 0,5x-3
y
x
C(0;-3)
0
-3
D(2;-2)
-2
2
Ответ: система имеет 1 решение (6;0)
Алгоритм нахождения количества системы уравнений с 2 переменными
1) Из каждого уравнения выразить y через х.
2)
Если
к1 к2
Если к1=к2,
b 1 b 2
Графики
пересекаются
Система имеет единственное решение
Графики параллельны
Если к1=к2,
b1=b2
Система не имеет решений
Графики совпадают
Система имеет бесконечно много решений
Выяснить, сколько решений имеет система.
1 вариант 2 вариант
Проверка 1 варианта
к1 = к2= — 0,5
b1 b2
к1 к2
Система не имеет решений
Система имеет единственное
решение
Проверка 2 варианта
к1=к2,
b1=b2
к1 к2
Система имеет единственное
решение
Система имеет бесконечно
много решений
Домашнее задание:
п.42 (определение, примеры)
№ 1058, № 1061
№ 1063, №1067(а)
Система линейных уравнений с 2 переменными
k1 = -1
k2 = 1
Урок по алгебре на тему «Решение систем линейных уравнений с двумя переменными способом сложения».

Открытый урок по алгебре на тему
«Решение систем линейных уравнений с двумя переменными способом сложения».
Учитель Попкова Людмила Григорьевна
Цели
образовательная: освоить еще один способ решения систем уравнений – способ сложения, закрепление, систематизация и обобщение знаний о методах решения и исследования системы уравнений, контроль за усвоением ЗУН;
воспитательная: привитие интереса к изучаемому предмету;
развивающая: формирование навыков самостоятельной деятельности, выработка внимания, наблюдательности и сообразительности.
выработать критерии оценки своей работы, умение анализировать проделанную работу и адекватно её оценивать.
Ход урока.
1. Организационный момент.
Представим себе, что сегодня наш класс – научно-исследовательский институт. А вы, ученики, — сотрудники этого института.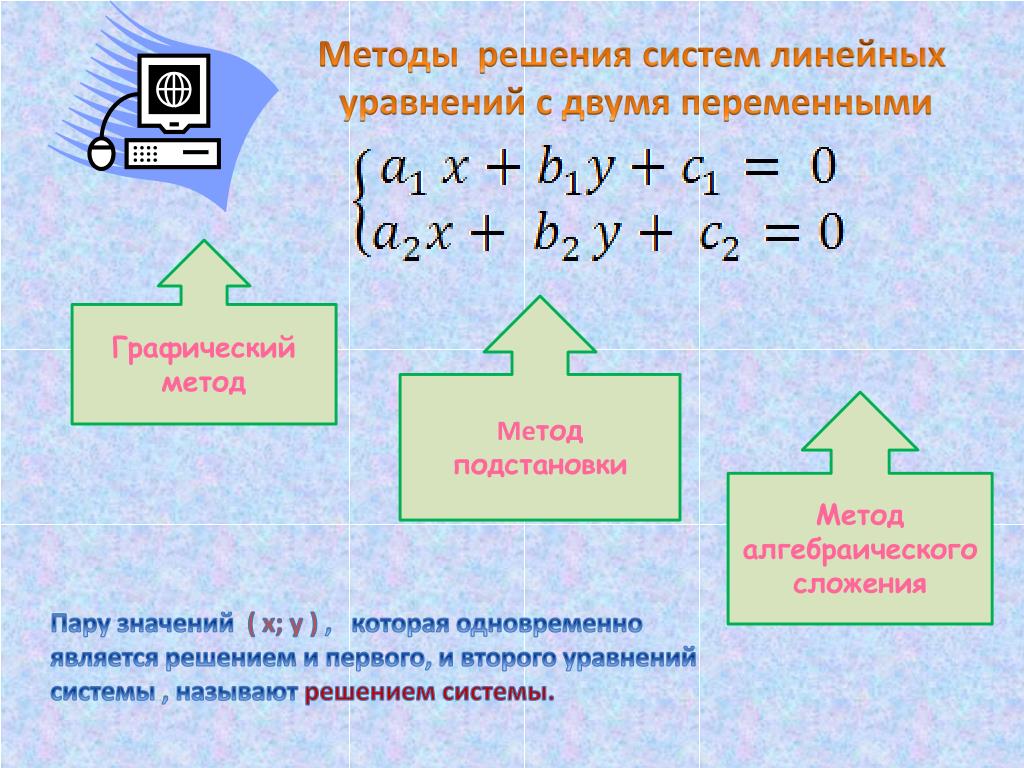 А именно, сотрудники различных лабораторий по проблемам математики. Вас всех пригласили принять участие в заседании учёного совета этого НИИ, чтобы обсудить с вами тему «Решение систем линейных уравнений с двумя переменными». В процессе работы в НИИ вы должны: закрепить изученный материал, показать уровень усвоения темы, рассмотреть еще один способ решения систем линейных уравнений, проконтролировать и оценить свои знания. Девизом нашего заседания является лозунг: «Дорогу осилит идущий, а математику мыслящий». Но прежде, чем войти в лаборатории НИИ, вам необходимо пройти испытание, которое будет пропуском в эти лаборатории.
А именно, сотрудники различных лабораторий по проблемам математики. Вас всех пригласили принять участие в заседании учёного совета этого НИИ, чтобы обсудить с вами тему «Решение систем линейных уравнений с двумя переменными». В процессе работы в НИИ вы должны: закрепить изученный материал, показать уровень усвоения темы, рассмотреть еще один способ решения систем линейных уравнений, проконтролировать и оценить свои знания. Девизом нашего заседания является лозунг: «Дорогу осилит идущий, а математику мыслящий». Но прежде, чем войти в лаборатории НИИ, вам необходимо пройти испытание, которое будет пропуском в эти лаборатории.
Устный счет “ одним взглядом ”
Вывод: система линейных уравнений может иметь одно решение, не иметь решений, иметь множество решений.
Итак, мы получили пропуск в лаборатории. Перед нами лаборатория теоретиков.
2. Повторение и проверка домашнего задания
Лаборатория теоретиков и исследований.
Давайте примем участие в работе этих лабораторий.
Сейчас два наших сотрудника пройдут в лабораторию исследований и выполнят задания
У доски 2 ученика решают домашние системы 2-мя способами 3х – у = 2,
х – 3у =6, х + 2у = 10 (графически),
2у — 5х = -4( способом подстановки),
А с остальными мы пройдем в лабораторию теоретиков
В лаборатории теоретиков много правил, по которым мы работаем.
проводится фронтальный опрос по теме урока:
Какие уравнения с двумя переменными называются линейными?
Что является графиком линейного уравнения с двумя переменными?
Из уравнения 3х-5у=7 выразить каждую переменную через другую.
Что называется решением системы линейных уравнений с двумя переменными?
Что значит решить уравнение с двумя переменными?
Перечислить известные способы решения систем линейных уравнений с двумя неизвестными.
В чем достоинство и недостаток графического способа решения систем линейных уравнений с двумя неизвестными?
Сформулировать алгоритм решения систем линейных уравнений с двумя неизвестными графическим способом и способом подстановки.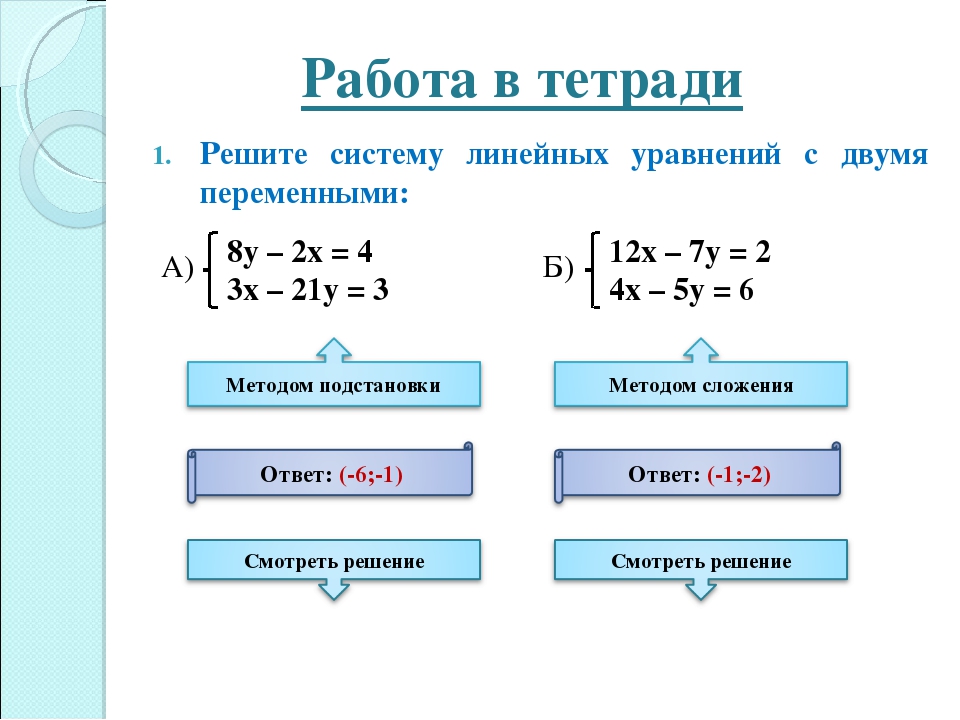
Какой из них вам показался более удобным?
Владение математикой – это умение решать задачи, причём не только стандартные, но и требующие оригинальности, изобретательности, смекалки, находчивости.
Лаборатория исследований.
3. Изучение нового материала. 2х -7у = 3,
3х + 7у = 7
Поступило задание: Решить систему уравнений:
Каким способом удобно решить? Заметим, что в уравнениях системы коэффициенты при переменной у являются противоположными числами. Сложим почленно уравнения системы:2х+3х-7у+7у=3+7. Получим линейное уравнение с одной переменной у, а именно 5х=10. Заменим одно из уравнений системы полученным уравнением, получим равносильную систему:
5х=10,
3х +7у=7. (2)
Из первого уравнения находим: х=2
Подставим это значение во второе уравнение системы и получим линейное уравнение с переменной х: 3*2+7у=7, откуда: у=1/7. Пара чисел(2;1/7) является решением системы(2),а, следовательно, и равносильной системы(1). В равносильности этих систем можно убедиться графически.
В равносильности этих систем можно убедиться графически.
Из разобранного примера видно, что при сложении уравнений системы получилось уравнение только с одной переменной. В качестве второго уравнения системы можно выбрать любое уравнение данной системы. В результате таких преобразований была получена система, равносильная данной. В этом и состоит суть метода сложения.
Поступило еще одно задание:
Пример 2. Решить систему уравнений способом сложения:
3а — 5b = 9,
2a — 7b = 17.
В отличие от предыдущего примера в это случае коэффициенты при a, а также и при b не являются противоположными числами. Поэтому сложение уравнений не позволит получить уравнение с одной переменной. Следовательно, необходимо добиться того, чтобы в уравнениях коэффициенты при любой переменной, например, при b стали противоположными числами.
Коэффициенты при b являются простыми числами 5 и 7. Поэтому умножим все члены первого уравнения на число 7, а второе уравнение на -5. При этом уравнения будут равносильными и система также равносильна данной 21a – 35b = 63,
При этом уравнения будут равносильными и система также равносильна данной 21a – 35b = 63,
-10a + 35b = -85
В данной системе коэффициенты при b – противоположные числа. Поэтому сложим уравнения системы и получим линейное уравнение с одной переменной: 21a-35b-10a+35b=63-85 или 11a = -22.
Запишем систему, равносильную данной. В качестве первого уравнения выберем полученное уравнение, в качестве второго уравнения – например, первое уравнение данной системы. Имеем, 11a = -22,
3a – 5b = 9.
Из первого уравнения найдем a=-2 и подставим это значение во второе уравнение. Получаем линейное уравнение с одной переменной: 3(-2)-5b=9,
-6-5b=9,
-5b=9+6,
-5b=15,
b=-3.
Итак, данная система уравнений имеет единственное решение a=-2, b=-3.
Уважаемые сотрудники, уточните тему нашего урока. Какое название можно дать рассмотренному способу решения систем уравнений с 2-мя переменными?
Давайте сформулируем алгоритм решения систем уравнений способом сложения:
Итак, при решении систем линейных уравнений методом сложения:
1. умножают уравнения системы подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами
умножают уравнения системы подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами
2.складывают почленно левые и правые части уравнений системы
3.решают полученное уравнение с одной переменной
4.находят соответствующее значение второй переменной.
Отметим, что если в уравнениях системы коэффициенты при одной из переменных являются противоположными числами, то при решении пункт 1 пропускают и начинают сразу с пункта 2.
Производственная гимнастика
Наступило время производственной гимнастики (кулачками, кошачьи лапки, вращение плеч, глазами и поморгали).
4. Закрепление полученных знаний.
Лаборатория систем линейных уравнений.
Перед нами лаборатория систем линейных уравнений. Давайте примем участие в исследованиях этой лаборатории.
Выдающийся физик Альберт Эйнштейн – основоположник теории относительности — говорил так: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Вот и займёмся решением систем линейных уравнений. Попробуем применить известный алгоритм к решению систем уравнений.
Задания из учебника №№1082(а, в), 1083(а, в), 1085(б, г).
2х+11у=15, 4х-7у=30, х-6у=17, 3х+2у=-5, 7х+2у=1, 4х+7у=90,
10х-11у=9 4х-5у=90 5х+6у=13(с/п) -5х+2у=45 17х+6у=-9 5х-6у=20.
5. Обучающая самостоятельная работа.
6. Подведение итогов.
Итак, уважаемые сотрудники, мы заканчиваем наше исследование. Вы сегодня хорошо потрудились. Вспомним алгоритм решения систем уравнений с двумя переменными способом сложения.
Запишите домашнее задание: п.44,№№1082(б, г), 1083(б, г).
7.Притча:
Шёл мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил «Что ты делал целый день? И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил «А что ты делал целый день?» и тот ответил «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма»
Мудрец остановился и задал каждому по вопросу. У первого спросил «Что ты делал целый день? И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил «А что ты делал целый день?» и тот ответил «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма»
Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.
Кто возил камни? (приклейте жёлтый жетон)
Кто добросовестно работал? (приклейте синий жетон)
Кто строил храм? (приклейте красный жетон)
8. В конце урока выставляются оценки.
Вариант 1 Вариант 2 Вариант 3
a + b = 2, х + у = 5, a – b = 1,
a – b = 6. х – у = 7 a + b = -5
Вариант 4 Вариант 5 Вариант 6
2х + у = 5, a + b = 4, 3х – у = 5,
3х — 5у = 1 3a — 5b = 20 2х + 7у = 11
Вариант 7 Вариант 8 Вариант 9
3у — 2х = 12, 2х — 3у= -1, 2х + 3у= -1,
4у + 3х = -1 3х + 4у = 7 3х + 5у = -2
Вариант 1 Вариант 2 Вариант 3
a + b = 2, х + у = 5, a – b = 1,
a – b = 6. х – у = 7 a + b = -5
х – у = 7 a + b = -5
Вариант 4 Вариант 5 Вариант 6
2х + у = 5, a + b = 4, 3х – у = 5,
3х — 5у = 1 3a — 5b = 20 2х + 7у = 11
Вариант 7 Вариант 8 Вариант 9
3у — 2х = 12, 2х — 3у= -1, 2х + 3у= -1,
4у + 3х = -1 3х + 4у = 7 3х + 5у = -2
Вариант 1 Вариант 2 Вариант 3
a + b = 2, х + у = 5, a – b = 1,
a – b = 6. х – у = 7 a + b = -5
Вариант 4 Вариант 5 Вариант 6
2х + у = 5, a + b = 4, 3х – у = 5,
3х — 5у = 1 3a — 5b = 20 2х + 7у = 11
Вариант 7 Вариант 8 Вариант 9
3у — 2х = 12, 2х — 3у= -1, 2х + 3у= -1,
4у + 3х = -1 3х + 4у = 7 3х + 5у = -2
Решение системы линейных уравнений с двумя переменными — концепция
Система линейных уравнений — это два или более уравнений, содержащих одни и те же переменные. Решения системы уравнений — это точка пересечения линий. Существует четыре метода решения систем линейных уравнений : построение графиков, подстановка, исключение и матрицы. Решение систем уравнений сначала появляется в алгебре I, но более сложные приложения встречаются в алгебре II.
Решение систем уравнений сначала появляется в алгебре I, но более сложные приложения встречаются в алгебре II.
Решение системы линейных уравнений с двумя переменными, поэтому, если вы помните, линейное уравнение — это в основном просто уравнение для линии, и когда мы решаем систему, мы смотрим на два уравнения, поэтому у нас есть две линии, и мы пытаемся выяснить, где пересекаются эти две линии, и если они вообще пересекаются, хорошо, значит, это может произойти тремя способами, хорошо? У нас есть две линии, которые могут пересекаться в одной точке, что означает, что у нас будет один ответ, который будет координатной точкой xy, скажем, 2, -4, что-то в этом роде.
Другая ситуация, которая может произойти, эти линии могут быть параллельны, что означает, что у них не будет никакого пересечения этих линий, у них не будет никакого решения, где эти две линии равны друг другу и, наконец, эти два уравнения может быть для одной и той же точной линии, что означает, что у нас будет бесконечное количество точек, лежащих на любой из этих линий, которые дадут нам решение, хорошо, и поэтому мы собираемся поговорить о каждой из этих .
Существует несколько различных способов решения этих проблем, вы можете решить их графически, и в Алгебре 2 мы обычно не делаем слишком много этого решения графически. это, и вы увидите, где они пересекаются, хорошо, поэтому мы знаем, как это сделать, но на самом деле это не даст нам математического ответа, мы не сможем найти эту точку, если наши графики не будут полностью точными, что является своего рода трата времени, поэтому мы можем сделать это алгебраически, и в нашем распоряжении есть два способа: подстановка, когда мы решаем переменную и вставляем ее, или исключение, когда мы складываем или вычитаем два уравнения в надежде избавиться от одной из переменных so.
Системы линейных уравнений, в основном касающиеся того, как линии пересекаются или не пересекаются, и у нас есть несколько способов сделать это, а именно замена или исключение.
Цели обучения
Введение
Учебник
Практические задачи
|
Линейные уравнения
Обзор
Линейное уравнение определяется как алгебраическое уравнение, в котором каждый член является либо константой, либо произведением переменной и константы, причем переменная ограничивается первой степенью.Другими словами, у вас может быть переменная, такая как x (= x 1 ), но не x 2 или x 3 , или любая другая более высокая степень. Кроме того, линейные уравнения могут не включать члены, которые представляют собой произведение двух переменных (например, xy ). Линейные уравнения могут иметь одну или несколько переменных, хотя наиболее часто встречаются, вероятно, уравнения с двумя переменными. Эти переменные часто обозначаются как x и y .Вы часто будете видеть линейное уравнение с двумя переменными, записанное в форме:
y = mx + b
Это обозначение называется формой пересечения наклона . График линейного уравнения представляет собой прямую линию (отсюда и название linear ). Константа м будет определять наклон линии (т.е. насколько круто она поднимается слева направо или наоборот).Константа b определяет точку пересечения оси y (точка, в которой линия пересекает ось y ). Линейные уравнения иногда называют уравнениями прямой . Возможно, более важно отметить тот факт, что форму уравнения с пересечением наклона иногда записывают с использованием разных меток для констант, в зависимости от того, в какой части мира вы находитесь. В Австралии, например, это записывается как y = м x + c .Не позволяйте этому сбить вас с толку, поскольку это то же самое уравнение. Обратите внимание, что форму пересечения наклона нельзя использовать для описания вертикальных линий, поскольку для такой линии наклон не определен. Однако он может описывать горизонтальных линий ( м становится нулевым , и поэтому y фактически является константой с тем же значением, что и b для любого значения x ). Вот график для линейного уравнения y = 0,5x + 1:
График линейного уравнения y = 0.5 х + 1
Обратите внимание, что уравнение y = 0,5 x + 1 находится в форме пересечения наклона, поэтому константа м здесь принимает значение 0,5. Для любого уравнения в этом формате, которое имеет положительное значение м , наклон линии будет положительным (т.е. линия будет наклоняться вверх слева направо). Если м принимает отрицательное значение, уклон будет отрицательным (т.е.е. линия будет наклоняться вниз слева направо). Если наклон равен нуль , линия будет горизонтальной . В том же уравнении значение b равно на (1), что означает, что точка, в которой линия пересекает ось y (точка пересечения оси y ), находится в точке y = 1. Если у нас есть график в виде прямой линии, и мы хотим вывести уравнение в форме пересечения наклона ( y = mx + b ), мы можем получить значение b , просто найдя значение y в точке, где линия пересекает ось y .Значение м можно найти, получив координаты x и y любых двух точек на линии и применив следующую формулу:
| м = | Δ y | = | y 2 — y 1 |
| Δ x | x 9308 x 9302 930 x 930 1 |
Треугольный символ здесь (Δ) для тех, кто не знаком с ним, является заглавной формой греческой буквы Дельта , которая используется в математике для обозначения разницы (как в разнице значений для y , или разница в значениях x между двумя точками на линии).Если линия горизонтальная, y 2 — y 1 (Δ y ) будет равно нулю, и, следовательно, м также будет равно нулю. Уравнение y = mx + b тогда будет описывать линию, параллельную оси x на расстоянии b над ней (если b положительно) или под ней (если b отрицательно). Если у нас есть значения для м (наклон графика) и b (интервал y ), мы можем вычислить интервал x (точка, где линия пересекает ось x ): переупорядочивая форму пересечения наклона уравнения пересечения наклона, чтобы найти значение x , для которого y равно нулю.Для уравнения y = 0,5x + 1 это будет выглядеть следующим образом:
0,5 x + 1 = y ⇒ 0,5 x + 1 = 0 ⇒ x + 2 = 0 ⇒ x = 0 — 2 = -2
Что мы сделали здесь, так это перегруппировали уравнение, чтобы получить y в правой части, заменить 0 на y , умножить обе части на два, чтобы избавиться от рационального числа (0.5), а затем снова переставьте уравнение, чтобы получить x самостоятельно в левой части. Если вы посмотрите еще раз на график, вы увидите, что ответ правильный. Конечно, мы могли бы найти точку пересечения x , проверив, где линия пересекает ось x на графике, но если нам заданы значения для m и b в уравнении, мы всегда можем вычислить x — перехват. Это, вероятно, приведет к более точному ответу в тех случаях, когда значения m и b не являются целыми числами просто потому, что точность, с которой мы можем точно сказать, где линия пересекает ось, может варьироваться.
Общий вид уравнения прямой записывается следующим образом:
топор + по + c = 0
В общей форме уравнения a , b и c являются целыми числами. Либо a , либо b могут равняться нулю, но не оба сразу. По соглашению принимает значение, равное или большее нуля.Мало того, что график этого уравнения представляет собой прямую линию, но и любая прямая линия (включая горизонтальные и вертикальные варианты) может быть представлена уравнением в этой форме. Можно показать, что для графика уравнения в этой форме, если b не равно нулю, наклон графика будет равен — ( a / b ), а y -перехват будет равен — ( c / b ). Положительные или отрицательные эти значения будут зависеть от того, являются ли значения a , b и c положительными или отрицательными.Хотя y обычно является зависимой переменной в линейных уравнениях, мы можем манипулировать уравнением, чтобы вместо этого получить x в левой части:
| ax + по + c = 0 ⇒ ax = — ( по + c ) ⇒ x = — | по + c | 51 |
| 51 | ||
Если b равно нулю, уравнение сводится к следующему:
Если мы построим график этого уравнения, мы получим вертикальную линию на расстоянии — ( c / a ) единиц от оси y .Таким образом, общая форма уравнения прямой ( ax + на + c = 0), в отличие от формы пересечения наклона ( y = mx + b ), может представляют собой случай вертикальной линии. Мы также можем посмотреть, что происходит, когда y является зависимой переменной.
| топор + по + c = 0 ⇒ по = — ( ax + c ) ⇒ y = — | ax + c | 51 |
Если a равно нулю, уравнение сводится к:
Если мы построим график этого уравнения, мы получим горизонтальную линию на расстоянии — ( c / b ) единиц от оси x .Таким образом, общая форма уравнения прямой линии может также представлять случай горизонтальной линии. Если a не равно нулю, интервал x будет равен — ( c / a ). Вот пример линейного уравнения, записанного в общем виде:
3 x + 4 y — 12 = 0
В этом уравнении a равно три ( a = 3), b равно четыре ( b = 4) и c равно минус двенадцать ( c = -12).Поскольку x и y находятся на одной стороне уравнения, любая переменная может быть зависимой переменной или независимой переменной. Мы могли бы переставить уравнение, чтобы преобразовать x в функцию x или наоборот. Однако из того, что мы установили об общей форме уравнения линии, мы можем определить наклон , пересечение по оси x и пересечение по оси линии (любые два из которых позволят нам нарисовать график) следующим образом:
Наклон = — ( a / b ) = — 3 / 4
y -intercept = — ( c / b 930 -12 / 4 ) = 3
x -intercept = — ( c / a ) = — (-12 / 3 ) = 4
В форме пересечения уклона уравнение выглядит следующим образом:
y = -0.75 х + 3
Вот график:
График линейного уравнения (в общем виде) 3 x + 4 y — 12 = 0
Одновременные линейные уравнения
В системе двух или более линейных уравнений (иногда называемой линейной системой ) уравнения связаны друг с другом общими переменными.Хотя каждое уравнение может отличаться, любая переменная, которая появляется более чем в одном уравнении, будет иметь одинаковое значение в каждом из них. Более того, уравнения согласуются друг с другом в том смысле, что все они могут быть истинными одновременно . В одной из простейших линейных систем нас обычно просят найти решения для двух уравнений с двумя переменными. В качестве примера возьмем следующую пару уравнений:
2 x + 3 y = 6 [1]
4 x + 9 y = 15 [2]
Принимая любое из этих уравнений отдельно, мы могли бы найти любое количество значений для x и y , которые удовлетворяли бы этому уравнению.Однако мы хотим найти пару значений, которые удовлетворят и уравнениям. Один из возможных вариантов решения — решить уравнение [1] для x через y . Затем мы можем подставить этот производный член для x в уравнение [2]. Пересмотренная версия второго уравнения будет иметь только одну переменную и должна быть достаточно простой для решения с использованием стандартных методов, описанных на странице «Решение алгебраических уравнений». Посмотрим, как это работает:
2 x + 3 y = 6 ⇒ 2 x = 6-3 y ⇒ x = 3-1.5 y
Здесь мы вычли 3 y из обеих частей уравнения, а затем разделили обе части уравнения на два , чтобы получить x собственно в левой части. Теперь мы можем заменить член 3 — 1,5y на x в уравнении [2] следующим образом:
4 (3 — 1,5 y ) + 9 y = 15 ⇒ 12-6 лет + 9 y = 15 ⇒ 12 + 3 y = 15
⇒ 3 y = 15-12 ⇒ 3 y = 3 ⇒ y = 1
Теперь у нас есть значение y ( y = 1), которое мы можем подставить в уравнение [1]:
2 x + 3 = 6 ⇒ 2 x = 6-3 ⇒ 2 x = 3 ⇒ x = 1.5
Вы можете проверить правильность решения, подставив значения x и y в оба уравнения и проверив, что они оба являются идентичностями (т.е. что они оба являются математически правильными утверждениями):
2 x + 3 y = 6 ⇒ 3 + 3 = 6
4 x + 9 y = 15 ⇒ 6 + 9 = 15
Мы также могли бы попробовать несколько иной подход к решению этой линейной системы.Идея этого второго подхода состоит в том, чтобы изолировать члены, включающие одну из двух переменных на одной стороне уравнения, а затем манипулировать одним или обоими уравнениями до тех пор, пока левая или правая часть обоих уравнений не станет идентичной. Вот снова два уравнения:
2 x + 3 y = 6 [1]
4 x + 9 y = 15 [2]
Мы можем легко переписать оба уравнения, чтобы выделить выражения, содержащие x в левой части обоих уравнений, следующим образом:
2 x = 6–3 y [3]
4 x = 15–9 y [4]
Если теперь умножить уравнение [3] на два, мы получим два уравнения, в которых левая часть уравнений идентична:
4 x = 12–6 y [5]
4 x = 15–9 y [4]
Поскольку по определению обе части уравнения равны, то, если левые части уравнений [4] и [5] равны, правые части также должны быть равны.Следовательно, мы можем вывести новое уравнение только с одной переменной ( y ) следующим образом:
12 — 6 y = 15 — 9 y
Собирая одинаковые термины вместе, мы получаем:
3 y = 3 ⇒ y = 1
Теперь мы можем подставить полученное значение y в любое из исходных уравнений, чтобы получить значение x .Принимая уравнение [1], как и раньше, получаем:
2 x + 3 = 6 ⇒ 2 x = 6 — 3 ⇒ 2 x = 3 ⇒ x = 1,5
Используя этот второй подход, мы получаем точно такое же решение, что и раньше, поэтому нет необходимости снова проверять правильность решений. Из вышеизложенного может показаться, что существует только одно решение для этой конкретной системы линейных уравнений, но это не всегда так для линейной системы из двух уравнений.Фактически существует три варианта такой системы:
- решений нет
- есть ровно одно решение
- есть бесконечное количество решений
Лучше всего это можно проиллюстрировать, посмотрев на графическое представление линейной системы. Мы можем представить систему, нарисовав график обоих уравнений на одной и той же паре осей. Если решения нет, мы должны увидеть пару параллельных линий (т.е. линии, которые никогда не встретятся). Если есть одно решение, мы ищем две линии, пересекающиеся в одной точке. Координаты x и y этой точки будут значениями x и y , которые удовлетворяют обоим уравнениям одновременно . Если существует бесконечное количество решений, два уравнения будут давать ту же строку (два уравнения фактически эквивалентны ), и каждая точка на линии будет иметь координаты x и y со значениями, которые удовлетворяют оба уравнения.Вот график для уравнений [1] и [2] в приведенном выше примере:
Графики линейных уравнений 2 x + 3 y = 6 и 4 x + 9 y = 15
Из графиков видно, что две линии действительно пересекаются в координатах x = 1,5, y = 1, так что есть единственное решение для этой конкретной линейной системы.Другой способ выразить это — сказать, что набор решений (набор всех возможных решений) состоит из единственной точки, определяемой координатами {1.5, 1}). Теперь рассмотрим следующую пару линейных уравнений:
3 x + 2 y = 6 [1]
3 x + 2 y = 12 [2]
Если линейная система имеет единственное решение, которое работает для всех уравнений в ней, то говорят, что уравнения согласованы друг с другом.В уравнениях [1] и [2] выше левая часть уравнения в обоих случаях равна 3 x + 2 y , что означает, что правая часть обоих уравнений также должна быть равна для другого. Если бы уравнения согласовывались друг с другом, было бы верно следующее утверждение:
6 = 12
Ясно, что здесь есть проблема, поскольку шесть не равно двенадцати.Эти два уравнения явно не согласованы друг с другом, что означает, что у этой конкретной линейной системы нет решения. В этом случае мы ожидаем увидеть, что, когда мы рисуем график обоих уравнений на одной и той же паре осей, результирующие линии будут параллельны. Вот графики для уравнений [1] и [2]:
Графики линейных уравнений 3 x + 2 y = 6 и 3 x + 2 y = 12
Системы с тремя уравнениями и двумя переменными
Предположим на мгновение, что нас попросили решить трех уравнений с двумя переменными ( x и y ) одновременно.На первый взгляд, это сложнее, чем решение двух уравнений, но все не всегда так, как кажется. Мы ищем значения x и y , которые удовлетворяют всем трем уравнениям одновременно, как и раньше. С точки зрения графики, система будет иметь решение только в том случае, если графики всех трех уравнений пересекаются друг с другом в общей точке. Однако, если подумать, нам нужны только два уравнения, чтобы найти значения для x и y . Мы начнем с рассмотрения линейной системы, включающей три уравнения с двумя переменными, имеет ли решение, а затем исследуем систему, в которой его нет.Рассмотрим следующие уравнения:
x — 2 y = -1 [1]
3 x + 5 y = 8 [2]
4 x + 3 y = 7 [3]
Глядя на любые два этих уравнений по отдельности, мы можем сказать, что они независимы друг от друга, потому что одно уравнение не может быть выведено из другого алгебраически.Однако обратите внимание, что уравнение [3] на самом деле является суммой уравнений [1] и [2], что означает, что любое одно уравнение в этой линейной системе может быть получено из двух других с помощью сложения или вычитания. Факт остается фактом: если существует единственное решение линейной системы, включающей три уравнения с двумя переменными, мы всегда можем найти его, используя только два уравнения, хотя необходимо будет обеспечить, чтобы значения x и y Найденное также будет удовлетворять третьему уравнению.Если они этого не сделают, значит, у системы нет решения. Чтобы решить указанную выше линейную систему с использованием уравнений [1] и [2], мы начнем с переписывания уравнения [1], чтобы получить выражение, которое мы можем заменить на x в уравнении [2]:
x = -1 + 2 y
Теперь перепишем уравнение [2], подставив вместо x :
3 (-1 + 2 y ) + 5 y = 8
Теперь умножьте скобки и соберите похожие термины:
-3 + 6 y + 5 y = 8 ⇒ 11 y = 11 ⇒ y = 1
Теперь замените y в уравнении [2]:
3 x + 5 = 8 ⇒ 3 x = 8-5 = 3 ⇒ x = 1
Чтобы проверить, удовлетворяется ли уравнение [3] значениями, которые мы получили для x и y , подставьте эти значения ( x = 1, y = 1) в уравнение [3]:
4 + 3 = 7
Поскольку «четыре плюс три равно семи» является математически правильным утверждением (в математических терминах, тождество ), мы нашли набор решений.Это единственная точка, определяемая координатами x = 1, y = 1. Чтобы подчеркнуть этот результат, вот графики всех трех уравнений, нарисованные на общем наборе осей:
Графики линейных уравнений x — 2 y = -1, 3 x + 5 y = 8 и 4 x + 3 y = 7
Теперь рассмотрим следующую систему уравнений:
x + y = 1 [1]
2 x + y = 1 [2]
3 x + 2 y = 3 [3]
Линейная система, определяемая уравнениями [1], [2] и [3], здесь не имеет решения.Кажется очевидным несоответствие между уравнениями [1] и [2], поскольку x + y и 2 x + y оба равны одному , но имейте в виду, что это факт возможен, если x равно ноль . Если мы сложим уравнения [1] и [2] вместе, мы получим следующее:
3 x + 2 y = 2 [4]
Если теперь вычесть уравнение [4] из уравнения [3], мы получим:
0 = 1
Ясно, что это утверждение не может быть верным (с математической точки зрения, это не тождество ).Поэтому говорят, что линейная система несовместима с и не имеет решения. Чтобы доказать свою точку зрения, мы представляем ниже графики всех трех уравнений, начерченные на общей оси. Есть одно решение для каждой пары уравнений, но нет решения для системы в целом.
Графики линейных уравнений x + y = 1, 2 x + y = 1 и 3 x + 2 y = 3
Системы с тремя уравнениями и тремя переменными
Здесь мы рассмотрим решение систем линейных уравнений, включающих три уравнения и три переменные ( x , y и z ).Линейные системы могут включать большое количество уравнений, а система, состоящая из четырех уравнений, может быть решена одновременно с использованием ручных методов. Кроме того, обычно требуется помощь компьютера. Эта страница предназначена для базового введения в линейные уравнения, поэтому мы не будем рассматривать линейные системы, включающие более трех линейных уравнений или трех переменных (однако следует отметить, что довольно сложные системы, включающие нелинейных уравнений часто можно моделировать с помощью систем линейных уравнений).Предположим, у нас есть три линейных уравнения, каждое из которых включает переменные x , y и z . Наша цель — найти значения x , y и z , которые удовлетворяют всем трем уравнениям одновременно. Рассмотрим следующие уравнения:
x + y — z = 4 [1]
x — 2 y + 3 z = -6 [2]
2 x + 3 y + z = 7 [3]
Наша основная цель должна заключаться в уменьшении сложности проблемы за счет уменьшения количества уравнений и количества переменных до тех пор, пока мы не получим одно линейное уравнение, которое мы сможем решить стандартными методами.Обычно мы можем достичь этого путем исключения. Выбор того, с чего начать, часто бывает несколько произвольным, поскольку обычно существует несколько возможностей. В этом случае мы можем заметить, что в уравнении [1] мы имеем — z , а в уравнении [3] мы имеем + z . Таким образом, мы можем исключить переменную z из этих уравнений, просто сложив их вместе, чтобы получить:
3 x + 4 y = 11 [4]
Мы можем снова использовать уравнение [1], на этот раз, чтобы исключить z из уравнения [2].Во-первых, мы должны умножить уравнение [1] на три, чтобы получить:
3 x + 3 y — 3 z = 12 [1a]
Мы обозначили это уравнение [1a], потому что оно получено из уравнения [1] и по существу эквивалентно ему. Теперь мы можем сложить уравнение [2] и уравнение [1a] вместе, чтобы получить:
4 x + y = 6 [5]
Теперь у нас есть два уравнения вместо исходных трех, и мы удалили переменную z .Теперь мы можем исключить y из уравнений [4] и [5]. Сначала нам нужно умножить уравнение [5] на минус четыре (-4), чтобы получить:
-16 x + -4 y = -24 [5a]
Затем мы складываем уравнение [4] и уравнение [5a] вместе, чтобы избавиться от y :
-13 x = -13 ⇒ x = 1
Теперь мы можем решить уравнение [4] для y , подставив одно вместо x :
3 + 4 y = 11 ⇒ 4 y = 11 — 3 = 8 ⇒ y = 2
Теперь у нас есть значения x и y ( x = 1, y = 2), поэтому мы можем решить для z , подставив эти значения в одно из исходных уравнений.Просто потому, что это первое уравнение в списке и ни по какой другой причине, мы будем использовать уравнение [1]:
x + y — z = 4 ⇒ 1 + 2 — z = 4 ⇒ — z = 4 — 3 ⇒ z = -1
Таким образом, набор решений равен x = 1, y = 2, z = -1. Однако, поскольку у нас есть три переменных, мы не можем представить графики трех уравнений на двухмерной плоскости.Каждый из трехмерных графиков уравнений будет описывать различных плоскостей , а решением линейной системы будут координаты x , y и z точки, в которой пересекаются все три плоскости. На иллюстрации ниже показано трехмерное представление плоскостей и точки, в которой они пересекаются (обратите внимание, что плоскости, описывающие три уравнения, могут быть расширены до бесконечности, но мы ограничили представление здесь плюс и минус десять единиц по всем осям) .Обратите внимание, что пересечение любых двух плоскостей будет прямой линией. Также обратите внимание, что любые две плоскости, если их удлинить, в конечном итоге пересекут друг друга, если они не параллельны друг другу.
Графики линейных уравнений x + y — z = 4, x — 2 y + 3 z = -6 и 2 x + 3 y + z = 7
Решите одновременный набор двух линейных уравнений
Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные числа, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочленов, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Упрощение, Упрощение, Пример Правые треугольники, Ветер, рисунок
Система линейных уравнений — линейная алгебра с приложениями
Практические задачи во многих областях науки, таких как биология, бизнес, химия, информатика, экономика, электроника, инженерия, физика и социальные науки, часто можно свести к решению системы линейных уравнений.Линейная алгебра возникла в результате попыток найти систематические методы решения этих систем, поэтому естественно начать эту книгу с изучения линейных уравнений.
Если, и — действительные числа, график уравнения вида
— прямая линия (если и не равны нулю), поэтому такое уравнение называется линейным уравнением в переменных и. Однако часто удобно записывать переменные как, особенно когда задействовано более двух переменных.Уравнение вида
называется линейным уравнением в переменных. Здесь обозначают действительные числа (называемые коэффициентами соответственно), а также число (называемое постоянным членом уравнения). Конечный набор линейных уравнений в переменных называется системой линейных уравнений в этих переменных. Следовательно,
— линейное уравнение; коэффициенты при, и равны, и, а постоянный член равен.Обратите внимание, что каждая переменная в линейном уравнении встречается только в первой степени.
Для линейного уравнения последовательность чисел называется решением уравнения, если
, то есть, если уравнение удовлетворяется при выполнении замен. Последовательность чисел называется решением системы уравнений, если она является решением каждого уравнения в системе.
Система может вообще не иметь решения, или она может иметь уникальное решение, или она может иметь бесконечное семейство решений.Например, система не имеет решения, потому что сумма двух чисел не может быть одновременно 2 и 3. Система, у которой нет решения, называется несогласованной ; система с хотя бы одним решением называется согласованная .
Покажите, что для произвольных значений и
— это решение системы
Просто подставьте эти значения,, и в каждое уравнение.
Поскольку оба уравнения удовлетворяются, это решение для всех вариантов и.
Величины и в этом примере называются параметрами , а набор решений, описанный таким образом, считается заданным в параметрической форме и называется общим решением для системы. Оказывается, что решения каждой систем уравнений (если — это решений) могут быть даны в параметрической форме (то есть, переменные, задаются в терминах новых независимых переменных и т. Д. .).
Когда задействованы только две переменные, решения систем линейных уравнений могут быть описаны геометрически, потому что график линейного уравнения представляет собой прямую линию, если оба они не равны нулю. Более того, точка с координатами и лежит на прямой тогда и только тогда, когда — то есть когда, является решением уравнения. Следовательно, решения системы линейных уравнений соответствуют точкам, которые лежат на всех рассматриваемых линиях.
В частности, если система состоит только из одного уравнения, должно быть бесконечно много решений, потому что на прямой бесконечно много точек. Если система имеет два уравнения, есть три возможности для соответствующих прямых:
- Линии пересекаются в одной точке. Тогда в системе будет уникального решения , соответствующего этой точке.
- Линии параллельны (и четкие) и не пересекаются. Тогда в системе нет решения .
- Строки идентичны. Тогда в системе будет бесконечно много решений — по одному на каждую точку на (общей) прямой.
С тремя переменными график уравнения может быть показан как плоскость и, таким образом, снова дает «картину» множества решений. Однако у этого графического метода есть свои ограничения: когда задействовано более трех переменных, физическое изображение графов (называемых гиперплоскостями) невозможно. Необходимо обратиться к более «алгебраическому» методу решения.
Перед описанием метода мы вводим понятие, упрощающее вычисления. Рассмотрим следующую систему
трех уравнений с четырьмя переменными. Массив чисел
, встречающееся в системе, называется расширенной матрицей системы. Каждая строка матрицы состоит из коэффициентов переменных (по порядку) из соответствующего уравнения вместе с постоянным членом. Для наглядности константы разделены вертикальной линией.Расширенная матрица — это просто другой способ описания системы уравнений. Массив коэффициентов при переменных
называется матрицей коэффициентов системы, а
называется постоянной матрицей системы.
Элементарные операции
Алгебраический метод решения систем линейных уравнений описывается следующим образом. Две такие системы называются эквивалентными , если они имеют одинаковый набор решений.Система решается путем написания серии систем, одна за другой, каждая из которых эквивалентна предыдущей системе. Каждая из этих систем имеет тот же набор решений, что и исходная; цель состоит в том, чтобы получить систему, которую легко решить. Каждая система в серии получается из предыдущей системы простой манипуляцией, выбранной так, чтобы она не меняла набор решений.
В качестве иллюстрации мы решаем систему таким образом. На каждом этапе отображается соответствующая расширенная матрица.Исходная система —
Сначала вычтите дважды первое уравнение из второго. В результате получается система
., что эквивалентно оригиналу. На этом этапе мы получаем, умножив второе уравнение на. В результате получается эквивалентная система
.Наконец, мы дважды вычитаем второе уравнение из первого, чтобы получить другую эквивалентную систему.
Теперь Эту систему легко решить! И поскольку он эквивалентен исходной системе, он обеспечивает решение этой системы.
Обратите внимание, что на каждом этапе в системе (и, следовательно, в расширенной матрице) выполняется определенная операция для создания эквивалентной системы.
Следующие операции, называемые элементарными операциями , могут в обычном порядке выполняться над системами линейных уравнений для получения эквивалентных систем.
- Поменяйте местами два уравнения.
- Умножьте одно уравнение на ненулевое число.
- Добавьте одно уравнение, кратное одному, к другому уравнению.
Предположим, что последовательность элементарных операций выполняется над системой линейных уравнений. Тогда полученная система имеет тот же набор решений, что и исходная, поэтому две системы эквивалентны.
Элементарные операции, выполняемые над системой уравнений, производят соответствующие манипуляции с строками расширенной матрицы. Таким образом, умножение строки матрицы на число означает умножение каждой записи строки на.Добавление одной строки к другой означает добавление каждой записи этой строки к соответствующей записи другой строки. Аналогично выполняется вычитание двух строк. Обратите внимание, что мы считаем две строки равными, если соответствующие записи совпадают.
В ручных вычислениях (и в компьютерных программах) мы манипулируем строками расширенной матрицы, а не уравнениями. По этой причине мы переформулируем эти элементарные операции для матриц.
Следующие операции называются элементарными операциями со строками матрицы.
- Поменять местами два ряда.
- Умножить одну строку на ненулевое число.
- Добавить кратное одной строки в другую строку.
На иллюстрации выше серия таких операций привела к матрице вида
, где звездочки обозначают произвольные числа. В случае трех уравнений с тремя переменными цель состоит в том, чтобы получить матрицу вида
Это не всегда происходит, как мы увидим в следующем разделе.Вот пример, в котором это действительно происходит.
Решение:
Расширенная матрица исходной системы —
Чтобы создать в верхнем левом углу, мы можем умножить строку с 1 на. Однако можно получить без введения дробей, вычтя строку 2 из строки 1. Результат:
Верхний левый угол теперь используется для «очистки» первого столбца, то есть для создания нулей в других позициях в этом столбце.Сначала отнимите строку 1 от строки 2, чтобы получить
.Далее вычтите строку 1 из строки 3. Результат:
.Это завершает работу над столбцом 1. Теперь мы используем во второй позиции второй строки, чтобы очистить второй столбец, вычитая строку 2 из строки 1 и затем добавляя строку 2 к строке 3. Для удобства обе операции со строками сделано за один шаг. Результат
Обратите внимание, что две последние манипуляции не повлияли на первый столбец (во второй строке там стоит ноль), поэтому наши предыдущие усилия там не были подорваны.Наконец, мы очищаем третий столбец. Начните с умножения строки 3 на, чтобы получить
.Теперь вычтите временную строку 3 из строки 1, а затем прибавьте умноженную строку 3 к строке 2, чтобы получить
.Соответствующие уравнения:, и, которые дают (единственное) решение.
Алгебраический метод, представленный в предыдущем разделе, можно резюмировать следующим образом: Для данной системы линейных уравнений используйте последовательность элементарных операций со строками, чтобы преобразовать расширенную матрицу в «красивую» матрицу (что означает, что соответствующие уравнения легко решить. ).В примере 1.1.3 эта красивая матрица приняла вид
.Следующие определения идентифицируют хорошие матрицы, возникающие в этом процессе.
Матрица, как говорят, находится в форме рядов (и будет называться матрицей рядов , если она удовлетворяет следующим трем условиям:
- Все нулевых строк (полностью состоящие из нулей) находятся внизу.
- Первая ненулевая запись слева в каждой ненулевой строке — это a, называемая ведущей для этой строки.
- Каждый ведущий находится справа от всех ведущих в строках над ним.
Матрица строка-эшелон называется сокращенной формой строки-эшелона (и будет называться сокращенной матрицей строки-эшелон, если, кроме того, она удовлетворяет следующему условию:
4. Каждый ведущий элемент — это единственная ненулевая запись в своем столбце.
Матрицы «строка-эшелон» имеют форму «лестницы», как показано в следующем примере (звездочки указывают произвольные числа).
Ведущие идут «вниз и вправо» через матрицу. Записи выше и справа от ведущих s произвольны, но все записи ниже и слева от них равны нулю. Следовательно, матрица в виде эшелона строк находится в сокращенной форме, если, кроме того, все элементы непосредственно над каждым ведущим равны нулю. Обратите внимание, что матрица в форме эшелона строк может с помощью нескольких дополнительных операций со строками быть приведена к сокращенной форме (используйте операции со строками, чтобы последовательно создавать нули над каждой ведущей единицей, начиная справа).
Важность матриц строка-эшелон вытекает из следующей теоремы.
Каждая матрица может быть приведена к (сокращенной) форме строки-эшелона последовательностью элементарных операций со строками.
Фактически, мы можем дать пошаговую процедуру для фактического нахождения матрицы ряда строк. Обратите внимание: несмотря на то, что существует множество последовательностей операций со строками, которые приведут матрицу к форме ряда строк, та, которую мы используем, является систематической и ее легко программировать на компьютере. Обратите внимание, что алгоритм имеет дело с матрицами в целом, возможно, со столбцами нулей.
Шаг 1. Если матрица полностью состоит из нулей, остановитесь — она уже в виде эшелона строк.
Шаг 2. В противном случае найдите первый столбец слева, содержащий ненулевую запись (назовите его), и переместите строку, содержащую эту запись, в верхнюю позицию.
Шаг 3. Теперь умножьте новую верхнюю строку на, чтобы создать интерлиньяж.
Шаг 4. Вычитая числа, кратные этой строке, из строк под ней, сделайте каждую запись ниже начального нуля. Это завершает первую строку, и все дальнейшие операции со строками выполняются с оставшимися строками.
Шаг 5. Повторите шаги 1–4 для матрицы, состоящей из оставшихся строк.
Процесс останавливается, когда либо на шаге 5 не остается строк, либо оставшиеся строки состоят полностью из нулей.
Обратите внимание на то, что алгоритм Гаусса является рекурсивным: после получения первого интервала процедура повторяется для оставшихся строк матрицы. Это упрощает использование алгоритма на компьютере. Обратите внимание, что в решении примера 1.1.3 не использовался гауссовский алгоритм в том виде, в каком он был написан, потому что первый ведущий не был создан путем деления строки 1 на.Причина этого в том, что он избегает дробей. Однако общий шаблон ясен: создайте ведущие слева направо, используя каждый из них по очереди, чтобы создать нули под ним. Вот один пример.
Решение:
Соответствующая расширенная матрица —
Создайте первую ведущую, поменяв местами строки 1 и 2
Теперь вычтите умноженную строку 1 из строки 2 и вычтите умноженную строку 1 из строки 3.Результат
Теперь вычтите строку 2 из строки 3, чтобы получить
.Это означает, что следующая сокращенная система уравнений
эквивалентен исходной системе. Другими словами, у них одинаковые решения. Но эта последняя система явно не имеет решения (последнее уравнение требует этого и удовлетворяет, а таких чисел не существует). Следовательно, исходная система не имеет решения.
Для решения линейной системы расширенная матрица преобразуется в сокращенную форму строки-эшелон, а переменные, соответствующие ведущим, называются ведущими переменными .Поскольку матрица представлена в сокращенной форме, каждая ведущая переменная встречается ровно в одном уравнении, поэтому это уравнение может быть решено для получения формулы для ведущей переменной в терминах не ведущих переменных. Принято называть нелидирующие переменные «свободными» переменными и маркировать их новыми переменными, называемыми параметрами . Каждый выбор этих параметров приводит к решению системы, и каждое решение возникает таким образом. Эта процедура в целом работает и получила название
.Для решения системы линейных уравнений выполните следующие действия:
- Перенести расширенную матрицу \ index {расширенная матрица} \ index {матрица! Расширенная матрица} в сокращенную матрицу «строка-эшелон», используя элементарные операции со строками.
- Если возникает строка, система несовместима.
- В противном случае присвойте не ведущие переменные (если они есть) в качестве параметров и используйте уравнения, соответствующие сокращенной матрице строки-эшелон, чтобы найти ведущие переменные в терминах параметров.
Существует вариант этой процедуры, в котором расширенная матрица переносится только в строчно-эшелонированную форму. Не ведущие переменные назначаются как параметры, как и раньше. Затем последнее уравнение (соответствующее форме строки-эшелона) используется для решения последней ведущей переменной в терминах параметров.Эта последняя ведущая переменная затем подставляется во все предыдущие уравнения. Затем второе последнее уравнение дает вторую последнюю ведущую переменную, которая также подставляется обратно. Процесс продолжает давать общее решение. Эта процедура называется обратной заменой . Можно показать, что эта процедура численно более эффективна и поэтому важна при решении очень больших систем.
Рейтинг
Можно доказать, что уменьшенная строка-эшелонированная форма матрицы однозначно определяется.То есть, независимо от того, какая серия операций со строками используется для переноса в сокращенную матрицу с эшелонированием строк, результатом всегда будет одна и та же матрица. Напротив, это неверно для матриц ряда строк: разные серии операций со строками могут переносить одну и ту же матрицу в разные матрицы ряда строк. В самом деле, матрица может быть перенесена (с помощью одной строковой операции) в матрицу-эшелон строк, а затем с помощью другой строковой операции в (сокращенную) матрицу-эшелон. Тем не менее, — это , правда, что количество ведущих единиц должно быть одинаковым в каждой из этих матриц эшелонов строк (это будет доказано позже).Следовательно, количество зависит только от того, каким образом приведено в строй.
Ранг матрицы — это количество ведущих s в любой матрице строка-эшелон, в которую могут быть перенесены операции со строками. Вычислить ранг.Решение:
Приведение к строительной форме
Так как эта матрица эшелонов строк имеет два ведущих s, rank.
Предположим, что ранг, где — матрица со строками и столбцами.Тогда потому что ведущие s лежат в разных строках, и потому что ведущие s лежат в разных столбцах. Кроме того, у ранга есть полезное приложение к уравнениям. Напомним, что система линейных уравнений называется непротиворечивой, если она имеет хотя бы одно решение.
Проба:
Тот факт, что ранг расширенной матрицы равен, означает, что есть ровно ведущие переменные и, следовательно, точно не ведущие переменные. Все эти нелидирующие переменные назначаются как параметры в гауссовском алгоритме, поэтому набор решений включает в себя именно параметры.Следовательно, если существует хотя бы один параметр, а значит, и решений бесконечно много. Если нет параметров и поэтому единственное решение.
Теорема 1.2.2 показывает, что для любой системы линейных уравнений существуют ровно три возможности:
- Нет решения . Это происходит, когда ряд встречается в форме эшелона строк. Это тот случай, когда система непоследовательна.
- Уникальное решение . Это происходит, когда каждая переменная является ведущей переменной.
- Бесконечно много решений . Это происходит, когда система согласована и есть хотя бы одна не ведущая переменная, поэтому задействован хотя бы один параметр.
https://www.geogebra.org/m/cwQ9uYCZ
Пожалуйста, ответьте на эти вопросы после открытия веб-страницы:
1. Для данной линейной системы, что представляет каждая из них?
2. Что можно сказать о решениях, исходя из графика? Есть ли у системы одно решение, нет решения или бесконечно много решений? Почему
3.Измените постоянный член в каждом уравнении на 0, что изменилось на графике?
4. Для следующей линейной системы:
Можете ли вы решить это методом исключения Гаусса? Что вы наблюдаете, глядя на график?
Многие важные проблемы включают линейных неравенств , а не линейных уравнений Например, условие для переменных может принимать форму неравенства, а не равенства.Существует метод (называемый симплексным алгоритмом ) для поиска решений системы таких неравенств, который максимизирует функцию вида где и — фиксированные константы.
Система уравнений с переменными называется однородной , если все постоянные члены равны нулю, то есть если каждое уравнение системы имеет вид
Очевидно, решение такой системы; это называется тривиальным решением .Любое решение, в котором хотя бы одна переменная имеет ненулевое значение, называется нетривиальным решением .
Наша главная цель в этом разделе — дать полезное условие, при котором однородная система имеет нетривиальные решения. Следующий пример поучителен.
Решение:
Приведение расширенной матрицы к сокращенной форме эшелона строк описано ниже.
Ведущими переменными являются,, и, например, назначается в качестве параметра.Тогда общее решение:,,,. Следовательно, взяв (скажем), мы получим нетривиальное решение:,,,.
Существование нетривиального решения в примере 1.3.1 обеспечивается наличием в решении параметра. Это связано с тем, что существует не ведущая переменная (в данном случае). Но здесь должно быть не ведущей переменной, потому что здесь четыре переменные и только три уравнения (и, следовательно, не более три ведущие переменные).Это обсуждение обобщает доказательство следующей основной теоремы.
Если однородная система линейных уравнений имеет больше переменных, чем уравнений, то она имеет нетривиальное решение (фактически бесконечно много).
Проба:
Предположим, что есть уравнения в переменных, где, и пусть обозначают сокращенную строчно-эшелонированную форму расширенной матрицы. Если есть ведущие переменные, есть не ведущие переменные и, следовательно, параметры. Следовательно, достаточно показать это.Но потому что имеет ведущие единицы и строки, и по гипотезе. Итак, что дает.
Обратите внимание, что обратное утверждение теоремы 1.3.1 неверно: если однородная система имеет нетривиальные решения, у нее не должно быть больше переменных, чем у уравнений (система имеет нетривиальные решения, но.)
Теорема 1.3.1 очень полезна в приложениях. В следующем примере представлена иллюстрация из геометрии.
Мы называем график уравнения коникой , если не все числа, и равны нулю.Покажите, что есть хотя бы одна коника, проходящая через любые пять точек на плоскости, которые не все лежат на одной прямой.Решение:
Пусть координаты пяти точек будут,,, и. График проходов if
Это дает пять уравнений, по одному для каждого, линейных по шести переменным,,,,, и. Следовательно, по теореме 1.1.3 существует нетривиальное решение. Если все пять точек лежат на линии с уравнением, вопреки предположению. Следовательно, один из « отличен от нуля.
Линейные комбинации и базовые решения
Что касается строк, два столбца считаются равными , если они имеют одинаковое количество записей и соответствующие записи одинаковы. Позвольте и быть столбцами с одинаковым количеством записей. Что касается операций с элементарными строками, их сумма получается путем сложения соответствующих записей, и, если это число, скалярное произведение определяется путем умножения каждой записи на. Точнее:
Сумма скалярных кратных нескольких столбцов называется линейной комбинацией этих столбцов.Например, это линейная комбинация и для любого выбора чисел и.
Решение:
Для, мы должны определить, существуют ли числа, и такие, что, то есть
Приравнивание соответствующих элементов дает систему линейных уравнений,, и для,, и. Путем исключения Гаусса решение есть, и где — параметр. Взяв, мы видим, что это линейная комбинация, и.
Обращаясь к, снова ищем, и такие, что; то есть
, что приводит к уравнениям,, и для действительных чисел, и.Но на этот раз существует , нет решения, которое читатель может проверить, так что , а не , является линейной комбинацией, и.
Наш интерес к линейным комбинациям проистекает из того факта, что они предоставляют один из лучших способов описания общего решения однородной системы линейных уравнений. Когда
решает такую систему с переменными, запишите переменные в виде матрицы столбцов:. Обозначается тривиальное решение. В качестве иллюстрации, общее решение в
Пример 1.3.1 — это,, и, где — параметр, и теперь мы могли бы выразить это как
, говоря, что общее решение -, где произвольно.
Теперь пусть и — два решения однородной системы с переменными. Тогда любая линейная комбинация этих решений снова оказывается решением системы. В более общем плане:
Фактически, предположим, что типичное уравнение в системе есть, и предположим, что
, являются решениями. Потом и
.
Следовательно, это тоже решение, потому что
Аналогичный аргумент показывает, что Утверждение 1.1 верно для линейных комбинаций более двух решений.
Примечательно то, что каждые решений однородной системы представляет собой линейную комбинацию определенных частных решений, и, фактически, эти решения легко вычисляются с использованием гауссовского алгоритма. Вот пример.
Решить однородную систему с матрицей коэффициентовРешение:
Приведение дополненной матрицы к уменьшенной форме —
, поэтому решениями являются,, и методом исключения Гаусса.Следовательно, мы можем записать общее решение в матричной форме
Вот и частные решения, определяемые гауссовским алгоритмом.
Решения и в примере 1.3.5 обозначены следующим образом:
Алгоритм Гаусса систематически выдает решения для любой однородной линейной системы, называемые базовыми решениями , по одному для каждого параметра.
Кроме того, алгоритм дает стандартный способ выразить каждые решений как линейную комбинацию базовых решений, как в Примере 1.3.5, где общее решение принимает вид
Следовательно, вводя новый параметр, мы можем умножить исходное базовое решение на 5 и таким образом исключить дроби.
По этой причине:
Любое ненулевое скалярное кратное базового решения будет по-прежнему называться базовым решением.
Таким же образом гауссовский алгоритм производит базовые решения для в каждой однородной системе, по одному для каждого параметра (есть нет базовых решений, если система имеет только тривиальное решение).Более того, каждое решение задается алгоритмом как линейная комбинация
этих базовых решений (как в Примере 1.3.5). Если имеет ранг, теорема 1.2.2 показывает, что есть ровно параметры, а значит, и базовые решения. Это доказывает:
Решение:
Приведение расширенной матрицы к сокращенной строчно-эшелонированной форме —
, поэтому общее решение:,,,, и где, и — параметры.В матричной форме это
Отсюда базовые решения —
Система линейных уравнений | Нет уникального решения | GMAT Math Practice Questions
Приведенный ниже примерный вопрос GMAT в количественном выражении представляет собой вопрос о линейных уравнениях и проверяет концепции, связанные с типами решений для системы линейных уравнений. Эта концепция обычно проверяется в GMAT как вопрос о достаточности данных, а не как вопрос для решения проблемы.Практический вопрос GMAT уровня ниже 600 в системе линейных уравнений.
Вопрос 3 : Для каких значений ‘k’ пара уравнений 3x + 4y = 12 и kx + 12y = 30 НЕ будет иметь единственное решение?
- 9
- 12
- 3
- 7,5
- 2,5
Достичь Q51 в GMAT Quant
Онлайн-курс GMAT
@ INR 3500
Видео Объяснение
Онлайн-классы GMAT
Начало вт, 27 апреля 2021 г.
Пояснительный ответ
Условие однозначного решения линейных уравнений
Система линейных уравнений ax + by + c = 0 и dx + ey + g = 0 будет иметь уникальное решение, если две линии, представленные уравнениями ax + by + c = 0 и dx + ey + g = 0 пересекаются в точке.
то есть, если две линии не параллельны и не совпадают.
По сути, наклон двух линий должен быть разным.
Что это означает?
ax + by + c = 0 и dx + ey + g = 0 будут пересекаться в одной точке, если их наклоны различны.
Выразите оба уравнения в стандартизированном формате y = mx + c, где m — наклон линии, а c — точка пересечения с y.
ax + by + c = 0 можно записать как y = \ — \ frac {a} {b} x — \ frac {c} {a} \\)
И dx + ey + g = 0 можно записать как y = \ — \ frac {d} {e} x — \ frac {g} {e} \\)
Наклон первой линии равен \ — \ frac {a} {b} \\), а наклон вторая строка — \ — \ frac {d} {e} \\)
Для уникального решения наклон линий должен быть другим.
∴ \ — \ frac {a} {b} \ neq — \ frac {d} {e} \\)
или \\ frac {a} {d} \ neq \ frac {b} {e} \\)
Условие, чтобы уравнения НЕ имели единственного решения
Наклоны должны быть равны
Или \\ frac {a} {d} = \ frac {b} {e} \\)
Примените условие в данном уравнения для нахождения k
В приведенном выше вопросе a = 3, b = 4, d = k и e = 12.
Следовательно, \\ frac {3} {k} = \ frac {4} {12} \ \)
Или «k» должно быть равно 9, чтобы система линейных уравнений НЕ имела единственного решения.
Вопрос: «Какое значение k?»
Когда k = 9, система уравнений будет представлять собой пару параллельных линий (их пересечения по оси Y разные). Таким образом, этого НЕТ решения. система линейных уравнений с двумя переменными.
Правильный ответ — вариант A.
Система линейных уравнений Facts for Kids
Линейная система с тремя переменными определяет набор плоскостей (по одной плоскости для каждого уравнения).Точка пересечения — это решение.В математике система линейных уравнений (или линейная система ) представляет собой набор линейных уравнений, включающих один и тот же набор переменных.
Описание
Математики показывают взаимосвязь между различными факторами в форме уравнений. «Линейные уравнения» означают, что переменная появляется только один раз в каждом уравнении без возведения в степень. «Система» линейных уравнений означает, что все уравнения верны одновременно.Итак, человек, решающий систему уравнений, ищет значения каждой переменной, которые сделают все уравнения истинными одновременно. Если никакие такие значения не могут удовлетворить все уравнения в системе, то уравнения называются «несовместимыми».
Например,
— это система трех уравнений с тремя переменными,,. «Решение» линейной системы — это присвоение чисел переменным таким образом, чтобы все уравнения выполнялись одновременно.Решение системы выше дается
, поскольку он делает все три уравнения действительными:
В математике теория линейных систем — это раздел линейной алгебры, предмет, который является фундаментальным для современной математики. Компьютерные алгоритмы нахождения решений являются важной частью численной линейной алгебры, и такие методы играют важную роль в инженерии, физике, химии, информатике и экономике.Система нелинейных уравнений часто может быть аппроксимирована линейной системой (см. Линеаризация), что является полезным методом при создании математической модели, компьютерной модели или компьютерного моделирования относительно сложной системы. Для сложных систем существует множество уравнений и много переменных, а не только две или три. Во многих случаях количество уравнений и переменных в системе одинаково. В некоторых случаях переменных больше, чем уравнений, и решение будет представлять собой диапазон различных значений, а не одно точное решение.
Простой пример
Простейшая линейная система включает два уравнения и две переменные:
Один из методов решения такой системы заключается в следующем. Сначала решите верхнее уравнение относительно:
Теперь подставьте это выражение для x в нижнее уравнение:
В результате получается одно уравнение, включающее только переменную. Решение дает и подставляет это обратно в уравнение для урожайности:
Этот метод распространяется на системы с дополнительными переменными.
Использование матриц
Очень часто все коэффициенты записываются в виде матрицы A, которая называется матрицей коэффициентов.
Примерно так же переменные можно записать в виде вектора:
- .
Это позволяет записать
- .
Математически определенный выше вектор представляет собой матрицу размером 1 на n. Затем система уравнений может быть решена с помощью операции умножения, определенной для матриц.A, x и b — все части одного алгебраического поля.
Решение системы линейных уравнений
При поиске решений системы линейных уравнений возможны три случая:
- Нет решения
- Есть ровно одно решение
- Есть много решений; точное количество зависит от свойств поля. Во многих случаях решений будет бесконечное количество.
Существует две категории методов решения системы линейных уравнений.Итерационные методы используют много шагов для получения решения, прямые методы требуют только одного шага:
- Примером прямого метода является решение системы для одной переменной; эту переменную можно исключить и заменить выражением, в котором используются только другие переменные, или числом. Выполнение этого для всех переменных уравнения приведет к решению системы, если оно существует.
- Другой метод — преобразовать два уравнения так, чтобы одна из сторон уравнений была одинаковой в обоих случаях; тогда можно написать другое уравнение, которое заменяет два уравнения и сокращает количество уравнений на одно.
- Исключение по Гауссу
- QR-разложение
- Разложение Холецкого
- Правило Крамера
Примеры итерационных методов:
- Релаксация, включая методы Гаусса-Зейделя и Якоби
- Многосеточный метод
- Метод Крылова
Есть примеры, такие как геодезия, где измерений намного больше, чем неизвестных. Такая система почти всегда переопределена и не имеет точного решения.Каждое измерение обычно неточно и включает некоторую погрешность. Поскольку измерения неточны, невозможно получить точное решение системы линейных уравнений; такие методы, как наименьшие квадраты, могут использоваться для вычисления решения, которое наилучшим образом соответствует переопределенной системе. Это решение методом наименьших квадратов часто можно использовать в качестве замены для точного решения.
Решение системы линейных уравнений имеет сложность не более O (n 3 ). Для решения общей системы из n линейных уравнений необходимо не менее n 2 операций.Лучший алгоритм, известный на сегодняшний день, был разработан Доном Копперсмитом и Шмуэлем Виноградом и датируется 1990 годом. Его сложность n 2.376 К сожалению, практического применения он не имеет.
использует
Использование компьютеров для решения систем линейных уравнений используется каждый день.


 е. имеет ли
она решение?
е. имеет ли
она решение?


 и два неизвестных
у которого есть одно решение:
и два неизвестных
у которого есть одно решение:  и два неизвестных
без решения:
и два неизвестных
без решения:  и два неизвестных
имеющий бесконечное количество решений:
и два неизвестных
имеющий бесконечное количество решений: 

 (0, -1) НЕ является решением второго уравнения 4 x — 2 y = 10.
(0, -1) НЕ является решением второго уравнения 4 x — 2 y = 10.  Если вам нужен обзор линий графика,
не стесняйтесь вернуться к Урок 27: Графические линии.
Если вам нужен обзор линий графика,
не стесняйтесь вернуться к Урок 27: Графические линии. 



 2
2