Решение систем неравенств первой степени
Решение систем неравенств первой степени
Ключевые слова: решение систем неравенств первой степени, двойные неравенства, примеры решения задач. Раздел ОГЭ по математике: 3.2.4. Системы линейных неравенств.
Неравенства с одной переменной решают почти так же, как и уравнения. Значение переменной, при подстановке которой в неравенство получается верное числовое неравенство, называется решением неравенства. Решить неравенство – это значит найти все его решения или показать, что их нет.
Решение неравенств первой степени было рассмотрено ранее. В данном конспекте — решение систем неравенств первой степени.
Когда требуется найти множество значений переменной, удовлетворяющих одновременно двум или нескольким неравенствам, говорят, что надо решить систему неравенств. Общий приём решения системы неравенств состоит в следующем: сначала решаем каждое неравенство отдельно, a затем находим множество их общих решений. При нахождении множества общих решений целесообразно пользоваться координатной прямой как опорным образом
Примеры решения задач
Пример 1. Решим систему неравенств
Решив первое неравенство, получим, что х > –0,5, решив второе неравенство, получим, что х > –1. Изобразим на координатной прямой множество решений каждого неравенства.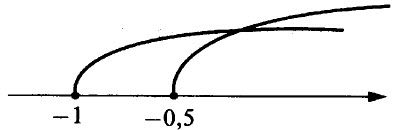
Из рисунка видно, что общей частью этих двух лучей служит множество чисел, больших –0,5.
Ответ: (–0,5; +оо).
Пример 2. Найдём множество решений двойного неравенства –2 < 4 – 3х < 10.
Решить двойное неравенство –2 < 4 – 3х < 10 – это то же самое, что решить систему неравенств

Вы можете сделать это самостоятельно. Но можно вести запись решения и с помощью двойных неравенств:
–2 < 4 – 3х < 10, –2 – 4 < –3х < 10 – 4,
–6 < –3х < 6, 6 > 3х > –6,
–6 < 3х < 6, –2 < х < 2.
Ответ: (–2; 2).
Пример 3. Решим задачу: «Боковая сторона равнобедренного треугольника равна 13 см, a его периметр больше 44 см. Какую длину может иметь основание треугольника?»
Для решения составим по условию задачи систему неравенств, используя неравенство треугольника. Пусть длина основания треугольника равна х см. Тогда периметр треугольника равен (х + 26) см и в соответствии с условием х + 26 > 44.
Длина каждой стороны треугольника меньше суммы длин двух других сторон. Поэтому можно составить ещё два неравенства, которым должны удовлетворять искомые величины: х < 26; 13 < х + 13. Получаем систему неравенств:

Решив её, получим, что 18 < х < 26.
Ответ: (18; 26).
Это конспект по алгебре на тему «Решение неравенств первой степени». Выберите дальнейшие действия:
uchitel.pro
Система неравенств — решение. Система линейных неравенств
Неравенства и системы неравенств — это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту «натаскивают» своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.
Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию «система неравенств». Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой — какие-то моменты остаются в «тени», не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого «наложения» зачастую случаются ошибки.
Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия. Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Виды неравенств
Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй — это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 — 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») либо меньше или равна другой величине (знак «≤»). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются «простыми». Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций. Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения:
- Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t1 ≤ t2, то t2 ≥ t1).
- Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t1 ≤ t2, то t1 + число ≤ t2 + число).
- Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t1≥ t2, t3≥ t4, то t1 + t3≥ t2 + t4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t1 ≤ t2 и число ≤ 0, то число · t1 ≥ число · t2).
- Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t1 ≤ t2, t3 ≤ t4, t1, t2, t3, t4 ≥ 0 то t1 · t3 ≤ t2 · t4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t1 ≤ t2 и число ≤ 0, то число · t1 ≥ число · t2).
- Все неравенства обладают свойством транзитивности (например, если t1 ≤ t2 и t2 ≤ t3, то t1 ≤ t3).

Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Общие сведения. Способы решения
Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств — это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется. В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
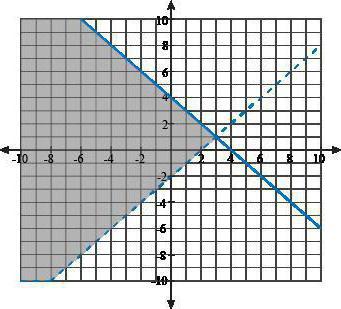
Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак «больше», либо только знак «меньше» и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный. Он применяется в двух этапах.
Первый включает себя действия по избавлению от одной из неизвестных переменных. Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется «сокращение») во время складывания неравенств. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Способ подстановки
Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х4 — х2 — 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: «Пусть t = х2«, далее модель переписывают в новом виде. В нашем случае получится t2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым. Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
- Неравенства выписываются отдельно, определяется решение каждого из них.
- Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.
Какой способ использовать?
Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Если что-то не получается
Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.

Решебник?
А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с поставленной задачей, а затем попытаться выполнить подобное в самостоятельном порядке.
Выводы
Алгебра — это один из самых сложных предметов в школе. Ну что же тут поделать? Математика всегда была такой: кому-то она даётся легко, а кому-то с затруднением. Но в любом случае следует помнить, что общеобразовательная программа построена так, что с ней может справиться любой ученик. К тому же, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
fb.ru
система неравенств — это… Что такое система неравенств?
- система неравенств
simultaneous inequalities
Англо-русский словарь технических терминов.
2005.
- система непродольного профилирования
- система несегментной записи
Смотреть что такое «система неравенств» в других словарях:
Система уравнений — У этого термина существуют и другие значения, см. Система (значения). Система уравнений это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных. Формальная запись общего вида… … Википедия
Солнечная система — Истинное понятие о С. системе, как о совокупности планет и других небесных тел, движущихся по известным законам вокруг Солнца, составилось лишь благодаря работам Кеплера и Ньютона. Движение же С. системы в пространстве, ее соотношение с другими… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ЗАМКНУТАЯ СИСТЕМА — элементов, замкнутая система функций, система элементов jn некоторого линейного нормированного пространства Нтакая, что любой элемент можно сколь угодно точно приблизить в метрике пространства Нконечной линейной комбинацией элементов из этой… … Математическая энциклопедия
Квантовая система — Квантовая механика Принцип неопределённости Введение … Математическая формулировка … Основа … Википедия
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории чисел, в к ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в … Математическая энциклопедия
ДИОФАНТОВЫХ ПРИБЛИЖЕНИЙ МЕТРИЧЕСКАЯ ТЕОРИЯ — раздел теории чисел, изучающий метрич. свойства чисел, обладающих определенными свойствами аппроксимации (см. Диофантовы приближения, Метрическая теория чисел). Одной из первых теорем Д. п. м. т. является теорема Хинчина (см. [1], [2]), в… … Математическая энциклопедия
СМЕШАННЫХ ОБЪЕМОВ ТЕОРИЯ — раздел теории выпуклых тел, изучающий функционалы, возникающие при рассмотрении линейных комбинаций тел (см. Сложение множеств). Объем Vлинейной комбинации выпуклых тел К i в евклидовом пространстве с коэффициентами является однородным… … Математическая энциклопедия
ПРОБОЙ МАГНИТНЫЙ — туннельный переход эл нов проводимости в металле с одной классич. орбиты в магн. поле на другую (см. ТУННЕЛЬНЫЙ ЭФФЕКТ). П. м. приводит к изменению энергетич. спектра металла в магн. поле. Наблюдается при низких (гелиевых) темп рах в чистых… … Физическая энциклопедия
МИНКОВСКОГО ТЕОРЕМА — 1) М … Математическая энциклопедия
ИСКЛЮЧЕНИЯ ТЕОРИЯ — теория исключения неизвестных из системы алгебраич. уравнений. Более точно, пусть имеется система уравнений где fi многочлены с коэффициентами из заданного поля Р. Задача исключения неизвестных х 1 ,…, х k из системы (1) (неоднородная задача… … Математическая энциклопедия
НЕЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА — численные методы решения методы, заменяющие решение краевой задачи решением дискретной задачи (см. Линейная краевая задача;численные методы решения и Нелинейное уравнение;численные методы решения). Во многих случаях, особенно при рассмотрении… … Математическая энциклопедия
dic.academic.ru
StudyPort.Ru — Система неравенств. Решения системы
Системой неравенств называется совокупность неравенств, для которых нужно найти значения неизвестных, удовлетворяющие одновременно всем неравенствам системы.
Значения неизвестных, удовлетворяющие одновременно всем уравнением системы называются решениями системы.
Примеры систем неравенств:
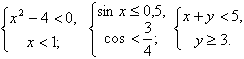
Системы неравенств могут состоять из двух и более неравенств и содержать одну и более переменных. Система неравенств может не иметь решений, иметь несколько решений, иметь бесконечное множество решений.
В школьной программе изучаются системы, содержащие одну переменную.
Для решения различных видов систем разработано много различных методов решения, но в рамках школьного курса рассматривается один самый простой метод. Он заключается в том, что мы решаем каждое неравенство в отдельности, а затем все полученные решения пересекаем на координатной оси.
Примеры решения систем неравенств.
1. Решить систему неравенств 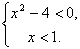
Решим первое неравенство:
x2-4 < 0;
(x-2)(x+2) < 0.
Решим это неравенство методом интервалов.
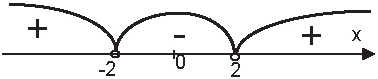
Решением этого неравенства будет промежуток (-2;2).
Второе неравенство уже решено — пересекаем решения первого и второго неравенства.
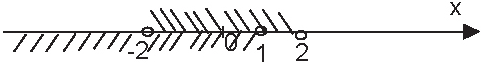
Итак, решением системы неравенств будет промежуток (-2;1).
Ответ: (-2;1).
2. Решить систему неравенств 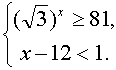
Решим первое неравенство:
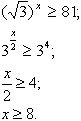
Решим второе неравенство:
x-12 < 1;
x < 13.
Пересекаем решения первого и второго неравенства.

Итак, решение системы неравенств — промежуток [8;13).
Ответ: [8;13).
studyport.ru
система неравенств — это… Что такое система неравенств?
- система неравенств
- set of inequalities
Большой англо-русский и русско-английский словарь. 2001.
- система непродольных наблюдений
- система несегментной записи
Смотреть что такое «система неравенств» в других словарях:
Система уравнений — У этого термина существуют и другие значения, см. Система (значения). Система уравнений это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных. Формальная запись общего вида… … Википедия
Солнечная система — Истинное понятие о С. системе, как о совокупности планет и других небесных тел, движущихся по известным законам вокруг Солнца, составилось лишь благодаря работам Кеплера и Ньютона. Движение же С. системы в пространстве, ее соотношение с другими… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ЗАМКНУТАЯ СИСТЕМА — элементов, замкнутая система функций, система элементов jn некоторого линейного нормированного пространства Нтакая, что любой элемент можно сколь угодно точно приблизить в метрике пространства Нконечной линейной комбинацией элементов из этой… … Математическая энциклопедия
Квантовая система — Квантовая механика Принцип неопределённости Введение … Математическая формулировка … Основа … Википедия
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории чисел, в к ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в … Математическая энциклопедия
ДИОФАНТОВЫХ ПРИБЛИЖЕНИЙ МЕТРИЧЕСКАЯ ТЕОРИЯ — раздел теории чисел, изучающий метрич. свойства чисел, обладающих определенными свойствами аппроксимации (см. Диофантовы приближения, Метрическая теория чисел). Одной из первых теорем Д. п. м. т. является теорема Хинчина (см. [1], [2]), в… … Математическая энциклопедия
СМЕШАННЫХ ОБЪЕМОВ ТЕОРИЯ — раздел теории выпуклых тел, изучающий функционалы, возникающие при рассмотрении линейных комбинаций тел (см. Сложение множеств). Объем Vлинейной комбинации выпуклых тел К i в евклидовом пространстве с коэффициентами является однородным… … Математическая энциклопедия
ПРОБОЙ МАГНИТНЫЙ — туннельный переход эл нов проводимости в металле с одной классич. орбиты в магн. поле на другую (см. ТУННЕЛЬНЫЙ ЭФФЕКТ). П. м. приводит к изменению энергетич. спектра металла в магн. поле. Наблюдается при низких (гелиевых) темп рах в чистых… … Физическая энциклопедия
МИНКОВСКОГО ТЕОРЕМА — 1) М … Математическая энциклопедия
ИСКЛЮЧЕНИЯ ТЕОРИЯ — теория исключения неизвестных из системы алгебраич. уравнений. Более точно, пусть имеется система уравнений где fi многочлены с коэффициентами из заданного поля Р. Задача исключения неизвестных х 1 ,…, х k из системы (1) (неоднородная задача… … Математическая энциклопедия
НЕЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА — численные методы решения методы, заменяющие решение краевой задачи решением дискретной задачи (см. Линейная краевая задача;численные методы решения и Нелинейное уравнение;численные методы решения). Во многих случаях, особенно при рассмотрении… … Математическая энциклопедия
dic.academic.ru