Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Определение 1Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.
Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Определение 3Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x
Решение системы линейных неравенств с одной переменной
Тема урока: Решение системы линейных неравенств с одной переменнойДата: _______________
Класс: 6а, 6б, 6в
Тип урока: изучение нового материала и первичное закрепление.
Дидактическая цель: создать условия для осознания и осмысления блока новой учебной информации.
Цели: 1) Образовательная: ввести понятия: решение систем неравенств, равносильные системы неравенств и их свойства; научить применять эти понятия при решении простейших систем неравенств с одной переменной.
2) Развивающая: способствовать развитию элементов творческой, самостоятельной деятельности учащихся; развивать речь, умение мыслить, анализировать, обобщать, высказывать свои мысли четко, лаконично.
3) Воспитательная: воспитание уважительного отношения друг к другу и ответственного отношения к учебному труду.
Задачи:
повторить теорию по теме числовые неравенства и числовые промежутки;
привести пример задачи, которая решается системой неравенств;
рассмотреть примеры решения систем неравенств;
выполнить самостоятельную работу.
Формы организации учебной деятельности: — фронтальная – коллективная — индивидуальная.
Методы: объяснительно – иллюстративный.
План урока:
1. Организационный момент, мотивация, постановка цели
2. Актуализация изучения темы
3. Изучение нового материала
4. Первичное закрепление и применение нового материала
5. Выполнение самостоятельной работы
6. Домашнее задание и рекомендации по его выполнению
7. Подведение итогов урока. Рефлексия.
Ход урока:
1. Организационный момент
Неравенство может быть хорошим помощником. Только надо знать, когда к нему необходимо обратиться за помощью. На языке неравенств нередко формулируется постановка задач во многих приложениях математики. Например, многие экономические задачи сводятся к исследованию систем линейных неравенств. Поэтому важно уметь решать системы неравенств. А что же значит – «решить систему неравенств»? Это мы и разберем сегодня на уроке.
2. Актуализация знаний.
Устная работа с классом, три ученика работают по индивидуальным карточкам.
Для повторения теории темы «Неравенства и их свойства», проведем тестирование с последующей проверкой и беседой по теории данной темы. Каждое задание теста предполагает ответ «Да» — фигура 
В результате выполнения теста должна получиться какая-то фигура.
Верно ли утверждение: если х>2 и у>14, то х+у >16?
Верно ли утверждение: если х>2 и у>14, то х·у<28?
Является ли число 0 решением неравенства 3х-1<11?
Является ли неравенство 3х+ 12>2х – 2 строгим?
Существует ли целое число, принадлежащее промежутку
 ?
?Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства не меняется?
(ответ:  ).
).
Установить соответствие между неравенством и числовым промежутком
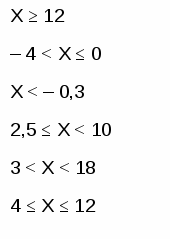
1. (– ; – 0,3)
2. (3; 18)
3. [12; + )
4. (– 4; 0]
5. [4; 12]
6. [2,5; 10)
«
 Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните, почему допущена ошибка, запишите в тетрадь правильное решение.
Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните, почему допущена ошибка, запишите в тетрадь правильное решение.
2х<8-6
х>-1
3. Изучение нового материала.
— Как вы думаете, что называется решением системы неравенств?
(Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы)
— Что значит « Решить систему неравенств»?
(Решить систему неравенств– значит найти все её решения или доказать, что решений нет)
— Что надо сделать, чтобы ответить на вопрос « является ли заданное число
решением системы неравенств?»
(Подставить это число в оба неравенства системы, если получатся верные неравенства, то заданное число является решением системы неравенств, если получатся неверные неравенства, то заданное число не является решение системы неравенств)
Сформулировать алгоритм решения систем неравенств
1. Решить каждое неравенство системы.
2. Изобразить графически решения каждого неравенства на координатной прямой.
3. Найти пересечение решений неравенств на координатной прямой.
4. Записать ответ в виде числового промежутка.
Рассмотреть примеры:
 Ответ:
Ответ: 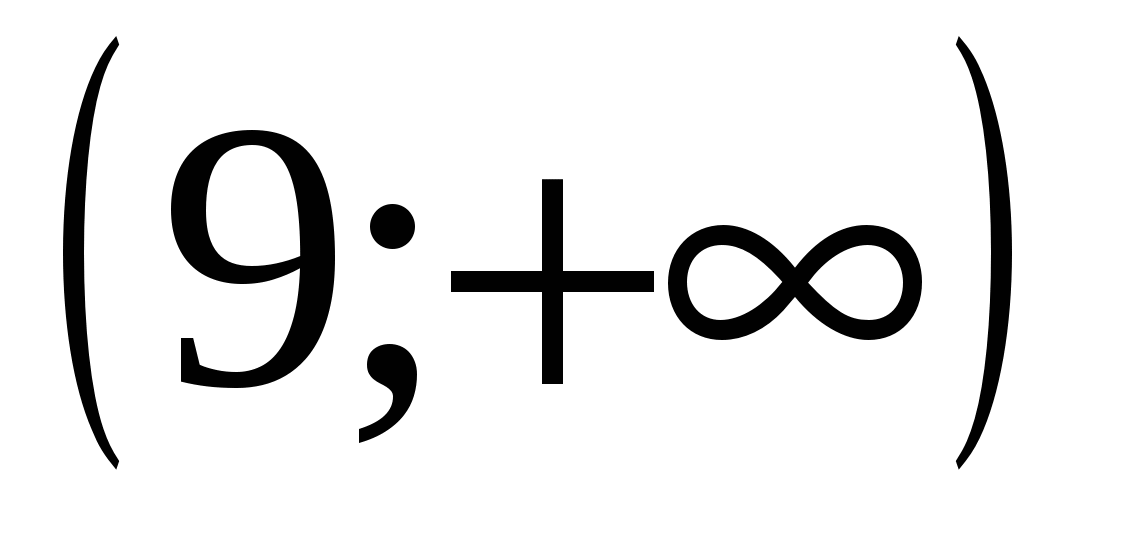
 Ответ: нет решений
Ответ: нет решений
4. Закрепление темы.
Работа с учебником № 1016, № 1018, № 1022
5. Самостоятельная работа по вариантам (Карточки- задания для учащихся на столах)
Самостоятельная работа
Вариант 1
Решите систему неравенств:

а) х + 3 > 2,
2x  5;
5;

б) х -4 > 5 – 2x,
3 – 2x < 7 + x;
Вариант 2
Решите систему неравенств:

а) х — 1 < 0,
2x  1;
1;

б) х -3 > 3x — 5,
2x + 7 > 3;
6. Домашнее задание: с. 221 п. 39 читать, № 1017, №1019 доп. №1023
7. Подведение итогов урока (выставляются оценки)
— Проанализируйте свою работу на уроке и поставьте себе оценку «5» — все понимаю; «4»- понимаю, но есть вопросы; «?» -затрудняюсь решать системы неравенств.
Рефлексия: — Какую тему рассмотрели сегодня на уроке?
— В чем испытали затруднения?
— Над чем необходимо еще поработать?
Линейное неравенство — Википедия
- < — меньше
- > — больше
- ⩽{\displaystyle \leqslant } — меньше либо равно
- ⩾{\displaystyle \geqslant } — больше либо равно
- ≠{\displaystyle \neq } — не равно
а также (формально)
Линейное неравенство выглядит точно также, как линейное уравнение, но вместо знака равно ставится знак неравенства.
Линейные неравенства вещественных чисел[править | править код]
Двумерные линейные неравенства[править | править код]
 График линейного неравенства:
График линейного неравенства:x + 3y < 9
Двумерные линейные неравенства — это выражения вида:
- ax+by<c{\displaystyle ax+by<c} и ax+by⩾c,{\displaystyle ax+by\geqslant c,}
где неравенства могут быть строгими или не строгими. Множество решений такого неравенства можно графически представить как полуплоскость (все точки с «одной стороны» от фиксированной прямой) евклидовой плоскости[2]. Прямая, определяющая полуплоскость (ax + by = c) не включается в решение, если неравенство строгое. Простая процедура определения, какая из полуплоскостей является решением — вычисление значения функции ax + by в точке (x0, y0), не находящейся на прямой, и проверке, удовлетворяет ли эта точка неравенству.
Например[3], чтобы нарисовать решение x + 3y < 9, сначала проводим прямую с уравнением x + 3y = 9 (пунктирная линия), чтобы показать, что прямая не принадлежит области решений, поскольку неравенство строгое. Затем выбираем удобную точку не на прямой, такую как (0,0). Поскольку 0 + 3(0) = 0 < 9, эта точка принадлежит множеству решений неравенства и полуплоскость, содержащая эту точку, (полуплоскость «ниже» прямой) является множеством решений линейного неравенства.
Линейные неравенства в пространствах более высокой размерности[править | править код]
В пространстве Rn линейные неравенства — это выражения, которые можно записать в виде
- f(x¯)<b{\displaystyle f({\bar {x}})<b} или f(x¯)⩽b,{\displaystyle f({\bar {x}})\leqslant b,}
где f — линейная форма, x¯=(x1,x2,…,xn){\displaystyle {\bar {x}}=(x_{1},x_{2},\ldots ,x_{n})}, а b — постоянная вещественная величина.
Более конкретно, это можно записать как
- a1x1+a2x2+⋯+anxn<b{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}<b}
или
- a1x1+a2x2+⋯+anxn⩽b.{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}\leqslant b.}
Здесь x1,x2,…,xn{\displaystyle x_{1},x_{2},…,x_{n}} называются неизвестными, а a1,a2,…,an{\displaystyle a_{1},a_{2},…,a_{n}} называются коэффициентами.
Альтернативно, то же самое можно записать как
- g(x)<0{\displaystyle g(x)<0\,} или g(x)⩽0,{\displaystyle g(x)\leqslant 0,}
где g — аффинная функция[4]
То есть
- a0+a1x1+a2x2+⋯+anxn<0{\displaystyle a_{0}+a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}<0}
или
- a0+a1x1+a2x2+⋯+anxn⩽0.{\displaystyle a_{0}+a_{1}x_{1}+a_{2}x_{2}+\cdots +a_{n}x_{n}\leqslant 0.}
Заметим, что любое неравенство, содержащее знаки «больше» или «больше либо равно» можно переписать на неравенство со знаками «меньше» или «меньше либо равно», так что нет необходимости определять линейные неравенства с этими знаками.
Системы линейных неравенств[править | править код]
Система линейных неравенств — это набор неравенств с одними и теми же переменными:
- a11x1+a12x2+⋯+a1nxn⩽b1a21x1+a22x2+⋯+a2nxn⩽b2⋮⋮⋮⋮am1x1+am2x2+⋯+amnxn⩽bm{\displaystyle {\begin{alignedat}{7}a_{11}x_{1}&&\;+\;&&a_{12}x_{2}&&\;+\cdots +\;&&a_{1n}x_{n}&&\;\leqslant \;&&&b_{1}\\a_{21}x_{1}&&\;+\;&&a_{22}x_{2}&&\;+\cdots +\;&&a_{2n}x_{n}&&\;\leqslant \;&&&b_{2}\\\vdots \;\;\;&&&&\vdots \;\;\;&&&&\vdots \;\;\;&&&&&\;\vdots \\a_{m1}x_{1}&&\;+\;&&a_{m2}x_{2}&&\;+\cdots +\;&&a_{mn}x_{n}&&\;\leqslant \;&&&b_{m}\\\end{alignedat}}}
Здесь x1, x2,…,xn{\displaystyle x_{1},\ x_{2},…,x_{n}} — переменные, a11, a12,…, amn{\displaystyle a_{11},\ a_{12},…,\ a_{mn}} — коэффициенты системы, а b1, b2,…,bm{\displaystyle b_{1},\ b_{2},…,b_{m}} — константные члены.
Кратко это можно записать как матричное неравенство
- Ax⩽b,{\displaystyle Ax\leqslant b,}
где A — матрица m×n, x — n×1 вектор-столбец[en] переменных, а b — m×1 вектор-столбец констант.
В описанных выше системах могут использоваться как строгие, так и нестрогие неравенства.
- Не все системы линейных неравенств имеют решение.
Приложения[править | править код]
Многогранники[править | править код]
Множество решений вещественного неравенства образует полупространство n-мерного вещественного пространства, одно из двух полупространств, определённых соответствующим линейным уравнением.
Множество решений системы линейных неравенств соответствует пересечению полупространств, определённых индивидуальными неравенствами. Оно является выпуклым множеством, поскольку полупространства являются выпуклыми множествами, а пересечение множества выпуклых множеств является также выпуклым множеством. В невырожденных случаях это выпуклое множество является выпуклым многогранником (возможно, неограниченным, к примеру, полупространство, пластина между двумя параллельными полупространствами или выпуклый конус). Оно может быть также пустым или выпуклым многогранником меньшей размерности, ограниченным аффинным подпространством n-мерного пространства Rn.
Линейное программирование[править | править код]
Задача линейного программирования ищет оптимум (максимальное или минимальное значение) функции (называемой целевой функцией) при некотором наборе ограничений на переменные, которые, в общем случае, являются линейными неравенствами[5]. Список этих ограничений составляет систему линейных неравенств.
Выше данное определение требует вполне определённых операций сложения, умножения и сравнения. Поэтому понятие линейного неравенства может быть распространено на упорядоченные кольца и, в частности, на упорядоченные поля. Обобщения такого типа представляют лишь теоретический интерес пока приложения этих обобщений не станут очевидными.
- ↑ Miller, Heeren, 1986, с. 355.
- ↑ Технически, такое утверждение корректно, когда a и b одновременно нулю не равны. В случае равенства нулю решением является пустое множество, либо вся плоскость.
- ↑ Angel, Porter, 1989, с. 310.
- ↑ В случае 2-мерного пространства как линейная форма, так и аффинная функция исторически называются линейными функциями поскольку их графики — прямые линии. В других размерностях ни одна из этих функций не имеет прямую в качестве графика, так что обобщение линейной функции в более высокие размерности делается в смысле алгебраических свойств и это приводит к разделению на два вида функций. Однако, разница в этих функциях — просто добавленная константа.
- ↑ Angel, Porter, 1989, с. 373.
Системы линейных неравенств с одной переменной
Вопросы занятия:
· вспомнить, что такое числовое неравенство, неравенство с переменными, линейное неравенство с одной и двумя переменными;
· повторить способы решения линейных неравенств.
Материал урока
Определение.
Говорят, что задана система двух неравенств с одной переменной, если требуется найти все значения переменной, при которых оба неравенства системы обращаются в верные числовые неравенства.
Определение.
Если каждое из этих неравенств является линейным неравенством, то говорят, что задана система линейных неравенств с одной переменной.
Определение.
Решением системы неравенств называют такое значение переменной, при котором неравенства системы преобразуются в верные числовые неравенства.
Определение.
Решить систему неравенств – найти все её решения или доказать, что решений нет.
Алгоритм решения систем линейных неравенств довольно прост.

Но прежде чем мы приступим к решению систем, давайте вспомним, что такое пересечение и объединение числовых промежутков.
Как связаны числовые неравенства с промежутками числовой прямой, мы знаем.

Рассмотрим множество, которое состоит из нескольких интервалов на числовой оси.

Говорят, что это множество состоит из объединения числовых промежутков.
Записывают это так

Теперь давайте найдём пересечение и объединение двух числовых множеств.
Изобразим эти множества на одной числовой прямой. Для удобства, первое множество мы изобразим сверху, а второе множество изобразим снизу.

В объединение промежутков входят все промежутки, на которых штриховка есть или снизу или сверху или и там и там.
В пересечение множеств войдут те промежутки, на которых есть штриховка снизу и сверху одновременно.

Пересечение множеств может быть пустым множеством. Например, если мы попробуем найти пересечение этих множеств, то увидим, что нет таких значений, которые входят в каждое из этих множеств. Тогда говорят, что пересечением этих множеств является пустое множество.
Решениями систем неравенств будет пересечение множеств, которые будут решениями каждого из неравенств системы.
Пример.

Пример.

Пример.

Наравне с системами неравенств рассматривают совокупности неравенств.
Определение.
Говорят, что задана совокупность двух неравенств с одной переменной, если требуется найти все такие значения переменной, при каждом из которых хотя бы одно из неравенств совокупности, обращается в верное числовое неравенство.
Определение.
Решением совокупности неравенств называют значение переменной, при котором хотя бы одно неравенство совокупности обращается в верное числовое неравенство.
Теперь давайте попробуем решить рассмотренные нами примеры, но знак системы заменим на знак совокупности.
Вернёмся к первому примеру.

Перейдём ко второму примеру.

Перейдём к последнему примеру.

К решению систем неравенств прибегают и тогда, когда надо решить двойное неравенство.
Пример.

Итоги урока
Сегодня мы вспомнили, что такое системы линейных неравенств с одной переменной, совокупности линейных неравенств с одной переменной.
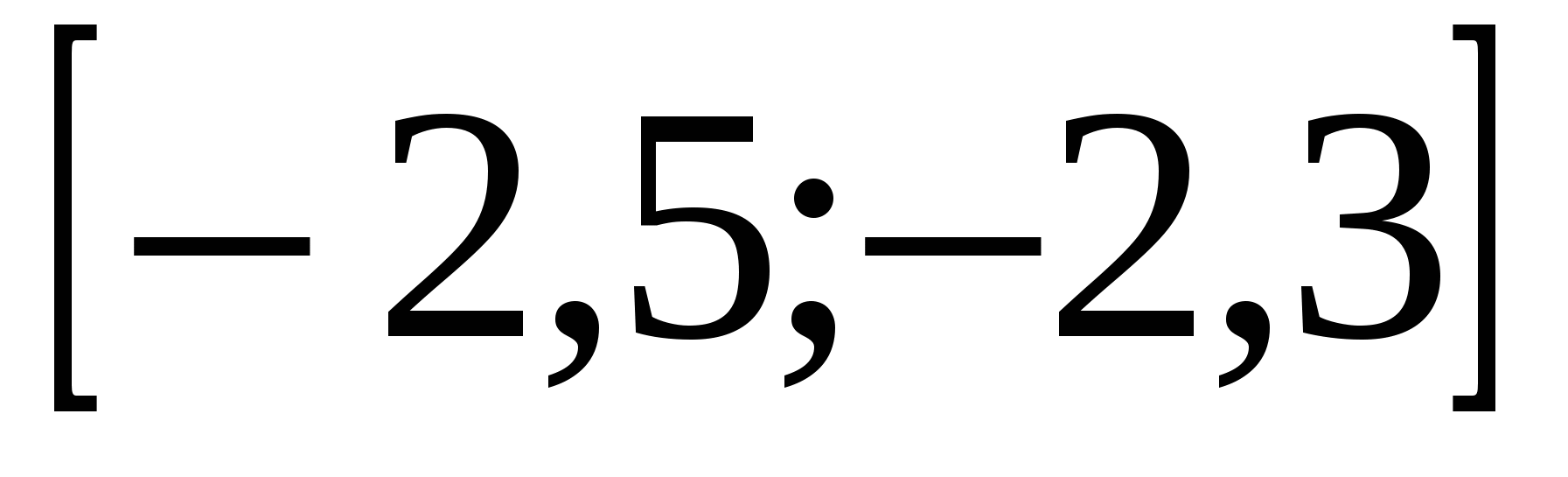 ?
?