Сколько система имеет решений: Как найти сколько решений имеет система уравнений? Плииииз помогите:) — Детская игровая комната «Волшебный лес»

Posted on 15.02.197010.06.2021 by alexxlab

Содержание

Системы линейных уравнений (Лекция №14)

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных

x₁,…,x_n.

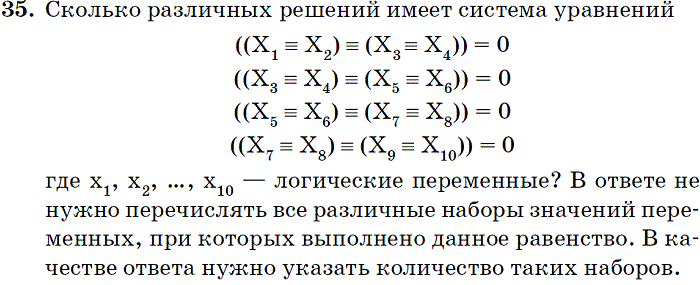
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система может иметь единственное решение.
Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

т. е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1

, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A^-1B.

Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

,

Таким образом, x = 3, y = – 1.
Итак, х₁=4,х₂=3,х
3=5.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.

Найдем матрицу А^-1.

Проверка:
Решите матричное уравнение AX+B=C, где
Из уравнения получаем .

Следовательно,

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т. е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

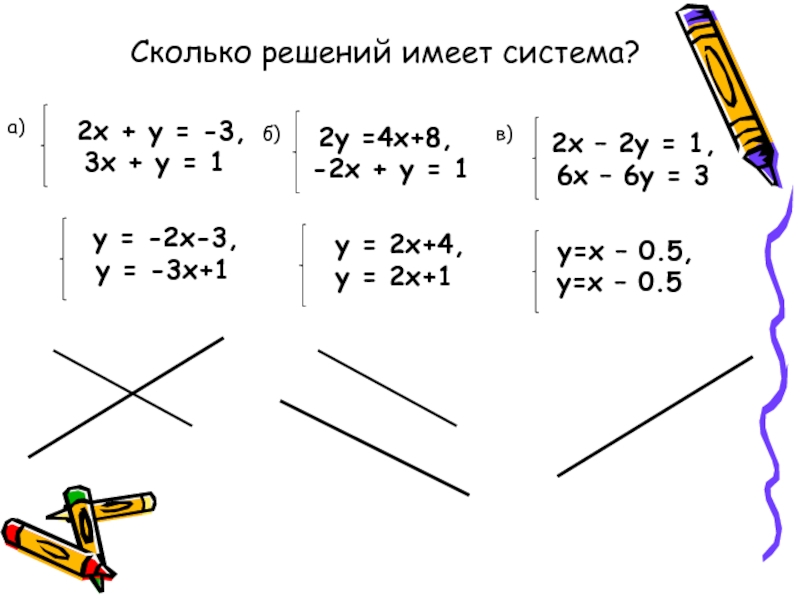
Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

Итак, х=1, у=2, z=3.
Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.

. Поэтому .
1. При
2. При p = 30 получаем систему уравнений которая не имеет решений.
3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y, yÎR.

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

перестановка строк или столбцов;

умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

Вернемся к системе уравнений.

Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Метод Крамера решения систем линейных уравнений

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение

. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Формулы Крамера для нахождения неизвестных:

Найти значения и возможно только при условии, если

Этот вывод следует из следующей теоремы.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

. (2)

Согласно теореме Крамера имеем:

Итак, решение системы (2):

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Как явствует из теоремы Крамера, при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Условия:

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

Условия:

* ,

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Условия:

** .

Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Пусть дана система

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет.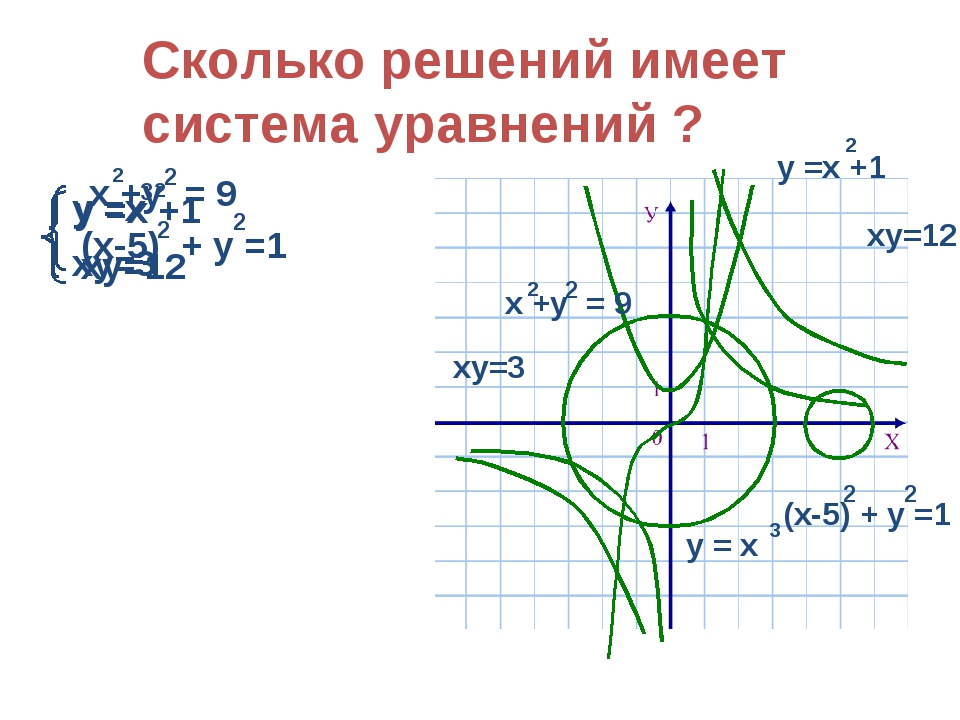 Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Пример 7. Решить систему линейных уравнений методом Крамера:

Здесь a — некоторое вещественное число. Решение. Находим определитель системы:

Находим определители при неизвестных

По формулам Крамера находим:

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

По формулам Крамера находим:

И, наконец, система четырёх уравнений с четырьмя неизвестными.

Пример 9. Решить систему линейных уравнений методом Крамера:

Внимание! Методы вычисления определителей четвёртого порядка здесь объясняться не будут. За этим — на соответствующий раздел сайта. Но небольшие комментарии будут. Решение. Находим определитель системы:

Небольшой комментарий. В первоначальном определителе из элементов второй строки были вычтены элементы четвёртой строки, из элементов третьей строки — элементы четвёртой строки, умноженной на 2, из элементов четвёртой строки — элементы первой строки, умноженной на 2. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Находим определители при неизвестных

Для преобразований определителя при четвёртом неизвестном из элементов первой строки были вычтены элементы четвёртой строки.

По формулам Крамера находим:

Итак, решение системы — (1; 1; -1; -1).

Самые внимательные, наверное, заметили, что в статье не было примеров решения неопределённых систем линейных уравнений. А всё потому, что методом Крамера решить такие системы невозможно, можно лишь констатировать, что система неопределённа. Решения таких систем даёт метод Гаусса.

Другое по теме «Системы уравнений и неравенств»

Начало темы «Линейная алгебра»

Поделиться с друзьями

Метод отображения Задание 1. Сколько решений имеет система:

Решение системы логических уравнений

Решение системы логических уравнений . Сколько решений имеет уравнение A BB C C D = 0 Количество наборов переменных равно =. Можно составить таблицу истинности и проверить, сколько наборов соответствуют

Подробнее Линейная алгебра Вариант 4
Линейная алгебра Вариант Задание. Систему уравнений привести к равносильной разрешенной системе, включив в набор разрешенных неизвестных,,. Записать общее решение, найти соответствующее базисное решение:
Подробнее 5. Исчисление высказываний и предикатов
5. Исчисление высказываний и предикатов Пусть дано непустое множество простых предложений Q. Расширим это множество, присоединив к нему все те предложения, которые можно образовать с использованием сентенциональных
Подробнее АЛГОРИТМ СИМПЛЕКС-МЕТОДА
АЛГОРИТМ СИМПЛЕКС-МЕТОДА Прежде всего нужно знать, что симплекс-метод является универсальным методом решения задач линейного программирования (ЗЛП) в том смысле, что он позволяет решать ЗЛП с любым количеством
Подробнее Иррациональные уравнения
Иррациональные уравнения Уравнения, в которых переменная содержится под знаком корня, называются иррациональными.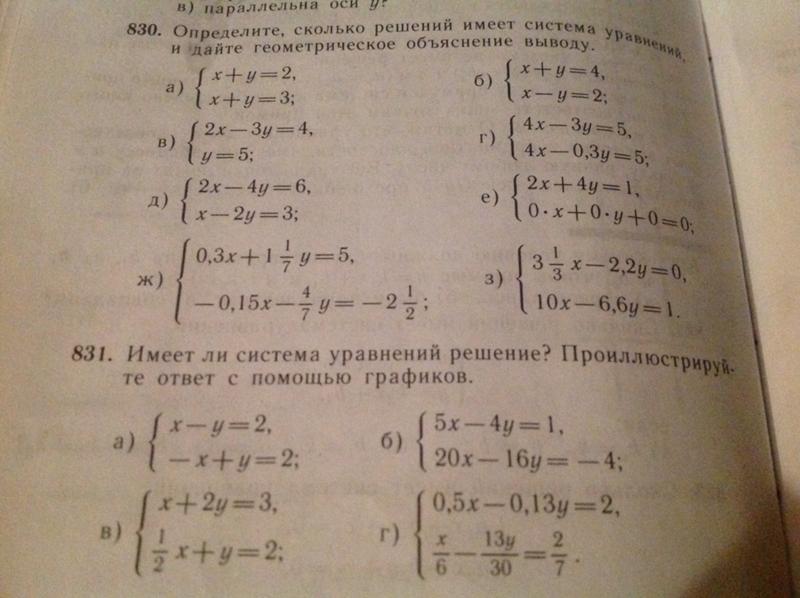 Решение иррациональных уравнений сводится к переходу от иррационального к рациональному
Подробнее ПЕРВЫЕ ШАГИ НА ПУТИ К ОЛИМПУ
УДК 51 ПЕРВЫЕ ШАГИ НА ПУТИ К ОЛИМПУ Соколова В.В., Мандров Г. научные руководители учитель математики старших классов Новикова О.В., учитель информатика старших классов Мясникова И.С. Муниципальное общеобразовательное
Подробнее Умножение числа на 10.»
Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа 2 Урок математики в 3 классе «Сочетательное свойство умножения. Умножение числа на 10.» Учитель: Гурьянова Е.С. г. Навашино
Подробнее Иррациональные неравенства
Иррациональные неравенства Неравенства, в которых переменная содержится под знаком корня, называются иррациональными Основным методом решения иррациональных неравенств является метод сведения исходного
Подробнее Тема 5 Рациональные системы уравнений
Тема 5 Рациональные системы уравнений F ( x, x,.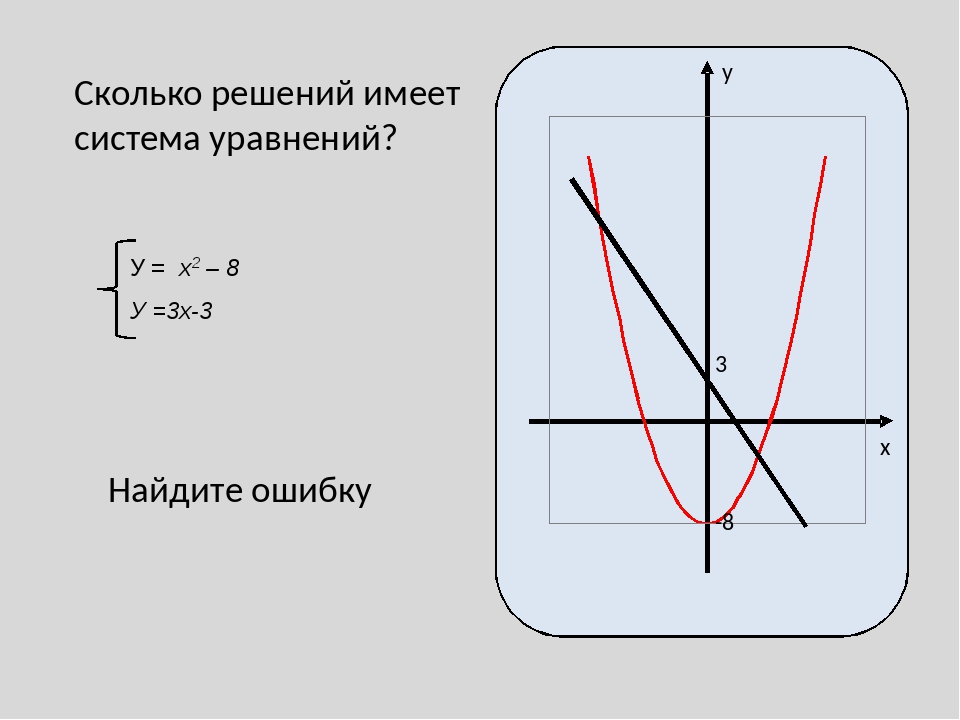 .., ) 0, F ( x, x,…, ) 0, Система уравнений вида где… Fk ( x, x,…, ) 0, F i( x, x,…, ), i,…, k, некоторые многочлены, называется системой рациональных
Подробнее Формула крюков. Первые примеры
Формула крюков Что для нас головоломка, духом тайны разум будит очевидно, для потомка просто школьным курсом будет. И. Губерман Первые примеры На рисунке показаны все существующие способов так заполнить
Подробнее 16 (повышенный уровень, время 2 мин)
16 (повышенный уровень, время мин) Тема: Кодирование чисел. Системы счисления. Что нужно знать: принципы кодирования чисел в позиционных системах счисления чтобы перевести число, скажем, 15, из системы
Подробнее Алгебраические уравнения
Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0,,, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами
Подробнее Затем дробную часть числа 0,
Арифметические основы компьютерной техники. Пример. Даны два числа: 76.54 и 5.7 Задание Перевести числа в двоичную, восьмеричную и шестнадцатеричную системы счисления. Затем перевести числа в восьмеричной
Подробнее Тема: Системы счисления
Коротко о главном Тема: Системы счисления Системы счисления — это способ представления чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, который существовали раньше
Подробнее B13 (повышенный уровень, время 7 мин)
B3 (повышенный уровень, время 7 мин) Тема: динамическое программирование. Что нужно знать: динамическое программирование это способ решения сложных задач путем сведения их к более простым задачам того
Подробнее Поиск кратчайших расстояний в графе
Поиск кратчайших расстояний в графе 1 Алгоритм Дейкстры поиск кратчайших расстояний от одной вершины до всех остальных. Дан граф, на ребрах графа указаны числа, их можно называть «весами» ребер. Расстояние
Подробнее УРАВНЕНИЯ В ЦЕЛЫХ ЧИСЛАХ
УРАВНЕНИЯ В ЦЕЛЫХ ЧИСЛАХ 1. Разложение на множители a) ( x 1)( y+ ) 9. б) x(y 98). в) x + y= xy. г) x + 4xy 7y. д) 19x yz 995, решить в простых числах. Делимость чисел а) y = 5x + 6. б) в) г) д) x + 1=
Подробнее Задача 5 «Кольцевая линия»
Задача 5 «Кольцевая линия» Полное решение этой задаче основано на следующем наблюдении. Пусть Андрей и Борис живут на различных станциях, причем при движении от Андрея к Борису по и против часовой стрелки
Подробнее СПРАВОЧНИК ПО МАТЕМАТИКЕ. 5 9 классы
СПРАВОЧНИК ПО МАТЕМАТИКЕ 5 9 классы МОСКВА «ВАКО» 201 УДК 32.851 ББК 4.262.22 С4 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ
Подробнее Тестовые задания и диктанты
Глава4 Уравнения 1 Тестовые задания и диктанты Т-01 Решение линейного уравнения Т-02 Решение уравнений разложением на множители Т-03 Рациональные уравнения, сводящиеся к линейным Т-04 Замена неизвестного
Подробнее ПЕРЕСТАНОВКИ.
Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.
ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
Подробнее г. Классная работа.
5.0. 014 г. Классная работа. Уравнения и системы уравнений с параметрами. Опыт вступительных экзаменов в вузы показывает, что решение уравнений и неравенств, содержащих параметры, вызывает большие затруднения
Подробнее Симметрия в задачах с параметрами
И. В. Яковлев Материалы по математике MathUs.ru Симметрия в задачах с параметрами Симметрия одно из ключевых понятий математики и физики. Вы знакомы с геометрической симметрией фигур и вообще различных
Подробнее 22 (повышенный уровень, время 7 мин)
К. Поляков, 09-6 22 (повышенный уровень, время 7 мин) Тема: динамическое программирование. Что нужно знать: динамическое программирование это способ решения сложных задач путем сведения их к более простым
Подробнее Решение Задачи об N ферзях
Решение Задачи об N ферзях Андрея Борисовича Скрыпника (Эл.почта — [email protected]) 2017 год Содержание 1 Формулировка Задачи об N ферзях 1 2 Алгоритм решения Задачи об N ферзях 2 2.1 Первая детализация
Подробнее Решение уравнений в целых числах
Решение уравнений в целых числах Линейные уравнения. Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.
Подробнее Одномерные массивы. Лабораторная работа 9
Лабораторная работа 9 Одномерные массивы Массивы. Ссылочные типы и null. Часто в программах требуется завести большое количество переменных одного и того же типа. Можно, конечно, написать большое количество
Подробнее Задания С6 ЕГЭ олимпиадного характера
Задания С6 ЕГЭ олимпиадного характера 1. Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 11 раз больше, либо в 11 раз
Подробнее Символ N O P Q R S T U V W X Y Z Код символа
Открытая олимпиада школьников «Информационные технологии» 2017-18 Решения заданий заключительного этапа для 7 и 8 класса 1. Системы счисления (1 балл) [Торрент] Петя решил скачать файл используя торрент-клиент.
Подробнее Однородные СЛАУ. Фундаментальная система решений
Задание. Найти общее решение и ФСР однородной системы $\left\{\begin{array}{l} x_{1}+x_{2}-3 x_{4}-x_{5}=0 \\ x_{1}-x_{2}+2 x_{3}-x_{4}=0 \\ 4 x_{1}-2 x_{2}+6 x_{3}+3 x_{4}-4 x_{5}=0 \\ 2 x_{1}+4 x_{2}-2 x_{3}+4 x_{4}-7 x_{5}=0 \end{array}\right.$
Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):
$$A=\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 1 & -2 & 2 & -1 & 0 \\ 4 & -2 & 6 & 3 & -4 \\ 2 & 4 & -2 & 4 & -7 \end{array}\right)$$
с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & -6 & 6 & 15 & 0 \\ 0 & 2 & -2 & 10 & -5 \end{array}\right)$$
Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 9 & -3 \\ 0 & 0 & 0 & 12 & -4 \end{array}\right)$$
От четвертой строки отнимем $\frac{4}{3}$ третьей и третью строку умножим на $\frac{1}{3}$ :
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right)$$
Нулевые строки можно далее не рассматривать, тогда получаем, что
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \end{array}\right)$$
Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -6 & 0 \\ 0 & -2 & 2 & 5 & 0 \\ 0 & 0 & 0 & 3 & -1 \end{array}\right)$$
то есть получаем систему, соответствующую данной матрице:
$$\left\{\begin{array}{l} x_{1}+x_{2}-6 x_{4}=0 \\ -2 x_{2}+2 x_{3}+5 x_{4}=0 \\ 3 x_{4}-x_{5}=0 \end{array}\right. $$
Или, выразив одни переменные через другие, будем иметь:
$$\left\{\begin{array}{l} x_{1}=-x_{2}+6 x_{4} \\ x_{2}=x_{2} \\ x_{3}=x_{2}-\frac{5}{2} x_{4} \\ x_{4}=x_{4} \\ x_{5}=3 x_{4} \end{array}\right.$$
Здесь $x_{2}, x_{4}$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1}, x_{3}, x_{5}$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$
Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3=2$ (для проверки, это число должно равняться количеству свободных переменных).
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
$$\left\{\begin{array}{l} x_{1}=-x_{2}+6 x_{4} \\ x_{3}=x_{2}-\frac{5}{2} x_{4} \\ x_{5}=3 x_{4} \end{array}\right.$$
Тогда придавая в первом случае, например, независимым переменным значения $x_{2}=1$ , $x_{4}=0$ получаем, что $\left\{\begin{array}{l} x_{1}=-1+6 \cdot 0=-1 \\ x_{3}=1-\frac{5}{2} \cdot 0=1 \\ x_{5}=3 \cdot 0=0 \end{array}\right.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что {x_{1}=12, x_{3}=-5, x_{5}=6} , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
$$X_{1}=\left(\begin{array}{r} -1 \\ 1 \\ 1 \\ 0 \\ 0 \end{array}\right), X_{2}=\left(\begin{array}{r} 12 \\ 0 \\ -5 \\ 2 \\ 6 \end{array}\right)$$
Общее решение является линейной комбинацией частных решений:
$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}\left(\begin{array}{r} -1 \\ 1 \\ 1 \\ 0 \\ 0 \end{array}\right)+C_{2}\left(\begin{array}{r} 12 \\ 0 \\ -5 \\ 2 \\ 6 \end{array}\right)$$
где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:
$\left\{\begin{array}{l} x_{1}=-C_{1}+12 C_{2} \\ x_{2}=C_{1} \\ x_{3}=C_{1}-5 C_{2} \\ x_{4}=2 C_{2} \\ x_{5}=6 C_{2} \end{array}\right.$ $C_{1}, C_{2} \neq 0$
Придавая константам $C_{1}, C_{2}$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.
Системы уравнений. Способы решения систем уравнений
Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
x — 4y = 2
3x — 2y = 16
Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.
Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.
Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Рассмотрим решение системы уравнений:
x — 4y = 2
3x — 2y = 16
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
x — 4y = 2;
x = 2 + 4y.
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
3x — 2y = 16;
3(2 + 4y) — 2y = 16.
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
3(2 + 4y) — 2y = 16;
6 + 12y — 2y = 16;
6 + 10y = 16;
10y = 16 — 6;
10y = 10;
y = 10 : 10;
y = 1.
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Ответ: x = 6, y = 1.
Способ сравнения
Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.
Например, для решение системы:
x — 4y = 2
3x — 2y = 16
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
x — 4y = 2 3x — 2y = 16
-4y = 2 — x -2y = 16 — 3x
y = (2 — x) : — 4 y = (16 — 3x) : -2
Составляем из полученных выражений уравнение:
Решаем уравнение, чтобы узнать значение x:

2 — x · (-4) = 16 — 3x · (-4)
-4 -2
2 — x = 32 — 6x
—x + 6x = 32 — 2
5x = 30
x = 30 : 5
x = 6
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
x — 4y = 2 3x — 2y = 16
6 — 4y = 2 3 · 6 — 2y = 16
-4y = 2 — 6 -2y = 16 — 18
-4y = -4 -2y = -2
y = 1 y = 1
Ответ: x = 6, y = 1.
Способ сложения или вычитания
Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.
Рассмотрим систему:
x — 4y = 2
3x — 2y = 16
Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:
(3x — 2y) · -2 = 16 · -2
-6x + 4y = -32
Получим:
x — 4y = 2
-6x + 4y = -32
Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:
+ x — 4y = 2
-6x + 4y = -32
-5x = -30
Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.
Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:
(x — 4y) · 3 = 2 · 3
3x — 12y = 6
Получим:
3x — 12y = 6
3x — 2y = 16
Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:
— 3x — 12y = 6
3x — 2y = 16
-10y = -10
Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
3x — 2y = 16
3x — 2 · 1 = 16
3x — 2 = 16
3x = 16 + 2
3x = 18
x = 18 : 3
x = 6
Ответ: x = 6, y = 1.
Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:
Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.
Графический способ решения систем уравнений
1. Графический способ решения систем уравнений
2. Цели урока
• Закрепить навыки построения графиков
функций
• Ввести уравнение окружности
• Использовать графический метод для
решения систем уравнений
• Применить графический метод при
решении заданий с параметрами
Повторение
1.Что является графиком уравнения ху=9 ?
гипербола
2. Что является графиком уравнения х+у=9 ?
прямая
2
2
3. Что является графиком уравнения х+у =9 ?
окружность
2
4. Что является графиком уравнения х + у =9
парабола
4.
Установите соответствие между графиком функции и формулой у= х
у= х
2
у=кх+в
у= к/х
у= х
3
у=х
5. Построить график уравнения
2
2
х + у =25
X -5
y
0
-4
-3
0
3
3 4 5 4
4
3
5
0
6. Графиком уравнения (х-а) +(у-b) =r является окружность с центром в точке О (а,b) и радиусом r.
Графиком уравнения
2
2
2
(х-а) +(у-b) =r является
окружность с центром в
точке О (а,b) и радиусом r.
r
а
b
( x 6)2 ( y 8)2 9
8
( x 10)2 y 2 16
x2 y 2 4
-9
-6
10
-5
x2 ( y 5)2 1
( x 9Написать
)2 ( y 5)2 16
уравнение окружности
8. Построить график уравнения
2
2
(х+4) + (у-4) =16
2
2
(х- 5) + у = 4
5.18(г)
2
х –у = 4
2х + у = -1
5
2
х –у = 4
2
х –у = 4
2
у = х- 4
Графиком уравнения
является парабола,
ветви направлены
вверх, вершина (0;-4)
2х + у = -1
Графиком уравнения
является прямая
х
0
2
у -1 — 5
-3
-3
2х + у = -1
Т. 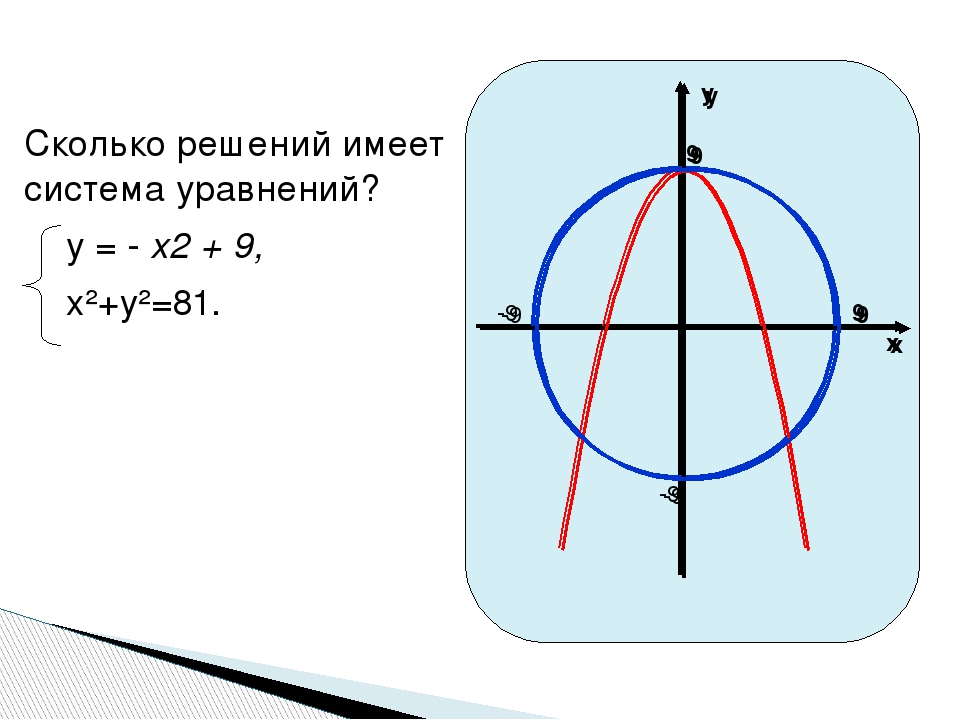к. графики пересекаются в двух точках ,
то система уравнений имеет два решения
(1;-3), (-3;5)
5.19(г)
ху = 6,
3х-2у=0.
ху=6,
у=6/х
Графиком данного уравнения
является гипербола,
ветви которой находятся
в I и III четвертях
3х-2у=0
ху=6
х 1 2 3 6
у 6 3 2 1
3х-2у=0 Графиком данного уравнения
является прямая
х 0 2
у 0 3
Т.к. графики пересекаются в двух точках
система имеет два решения (-2;-3) и(2;3).
5.20 (г)
2
2
(х+2) +(у-2) =1
у = х+1
2
2
2
(х+2) +(у-2) =1
у = х+1
2
(х+2) +(у-2) =1
Графиком уравнения является
окружность с центром
в точке (-2;2) радиуса 1
График уравнения у = х+1
получается из графика у= х
параллельным переносом вдоль оси ОХ на 1 влево
Т.к. графики уравнений не пересекаются,
то система не имеет решений
Сколько решений имеет
система уравнений ?
2
у =х +1
2
+у+1= 9
ух=х
2
2
(х-5) + у =1
ху=3
ху=12
2
32
ху=12
2
х +у2 = 9
ху=3
2
у=х
3
2
(х-5) + у =1
5. 37 (а)
2
у- х = 4
у + рх =4
2
у- х = 4
2
у=х+4
При каких р система уравнений
Имеет одно решение?
Графиком данного уравнения
является парабола,
вершина (0;4),
ветви направлены вверх
у + рх =4 Графиком данного
у = -рх+4 уравнения
является прямая
Ответ: Система имеет одно решение при р=0
2
2
2
2
х + у2 = 4
у –х = р
5.38
х +у =4
Графиком уравнения является
окружность, с центром
в точке (0;0) радиуса 2
у –х2 = р
2
у=х+р
Графиком уравнения является парабола
ветви направлены вверх, вершина (0;р)
Ответ: Система имеет три решения при р=-2 и
одно решение при р =2
15. Сколько решений имеет система уравнений?
2
х + у =25
2
2
у- х = 0
Решений нет
одно
два
три
четыре
показать рисунок
17. Сколько решений имеет система уравнений?
2
х + у =25
2
2
у- х = 5
Решений нет
одно
два
три
четыре
Показать рисунок
19.
Сколько решений имеет система уравнений? 2
х + у =25
2
2
у- х = -5
Решений нет
одно
два
три
четыре
Показать рисунок
21. Сколько решений имеет система уравнений?
2
х + у =25
2
2
у- х = -7
Решений нет
одно
два
три
четыре
Показать рисунок
23. Сколько решений имеет система уравнений?
2
х + у = 25
2
2
у- х = 7
Решений нет
одно
два
три
четыре
Показать рисунок
25. Вопросы рефлексии
• Каковы мои главные результаты сегодня?
• Какие трудности встретились во время
выполнения заданий? Как я их
преодолевал?
• Что я узнал нового на уроке?
• Что вызвало интерес?
Урок 49. решение задач при помощи систем уравнений первой степени — Алгебра — 7 класс
Алгебра
7 класс
Урок № 49
Решение задач при помощи систем уравнений первой степени
Перечень рассматриваемых вопросов:
• Решение задач.
• Система уравнений.
• Решение системы уравнений.
Тезаурус:
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Решить систему – это значит найти все её решения.
Алгебраический способ состоит в получении ответа на вопрос задачи с помощью составления уравнения или системы уравнений и последующего решения уравнения или системы.
Основная литература:
Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Рассмотрим задачу. Сошлись два пастуха, Иван и Пётр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?
Мы не знаем, сколько овец у Ивана, и сколько у Петра.
Обозначим за х число овец у Ивана, а за у – число овец у Петра.
Мысленно разделим условие задачи на две независимые части:
1. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!»
2. А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!»
Для каждой из частей составим уравнение с двумя неизвестными.
Начнем с первой части.
Если бы Пётр отдал Ивану одну овцу, то у Петра осталось бы (у – 1) овец.
А у Ивана стало бы (х + 1) овец.
Но тогда у Ивана было бы вдвое больше овец, чем у Петра.
Можем составить уравнение x + 1 = 2(y – 1).
Составим уравнение с двумя неизвестными для второй части. Если бы Иван отдал Петру 1 овцу, то у Ивана осталось бы (x – 1) овец. А у Петра стало бы (y + 1) овец, и тогда они имели бы овец поровну. Можем составить уравнение: x – 1 = y + 1
Мы составили два уравнения.
И в первом и во втором уравнении х обозначает число овец у Ивана, а у – число овец у Петра. Другими словами, каждое неизвестное число обозначает одно и то же в обоих уравнениях. Значит, эти уравнения можно рассматривать совместно, то есть объединить их в систему уравнений:
Решим эту систему способом подстановки.
Раскроем скобки в правой части первого уравнения.
Выразим х через у.
Подставим (2у – 3) вместо х во второе уравнение системы. Получим уравнение с одним неизвестным у.
Решим его. Упростим левую часть уравнения.
Перенесем неизвестные в левую часть. уравнения, а числа – в правую.
Подставим у = 5 в первое уравнение.
Получим х = 7.
Система имеет единственное решение: х = 7, у = 5.
Вернемся к исходным обозначениям.
Получаем, что у Ивана было 7 овец, а у Петра 5 овец.
Таким образом, мы решили задачу при помощи системы уравнений первой степени.
Задачи с помощью системы уравнений можно решать по следующей схеме.
Сначала вводим обозначения неизвестных.
Мысленно разделив условие задачи на две части, составляем 2 уравнения и объединяем их в систему.
Решаем полученную систему уравнений.
Возвращаемся к условию задачи и использованным обозначениям.
Отбираем решения и записываем ответ.
Разбор заданий из тренировочного модуля.
1. Решим задачу алгебраическим способом.
Задача.
Даны 3 числа, сумма которых равна 23. Если к удвоенному первому числу прибавить второе число и вычесть третье, то получится 32. А если из первого числа вычесть удвоенное второе и прибавить третье, то получится 8.
В задаче 3 неизвестные, поэтому введем следующие обозначения:
Пусть х – первое число, у – второе число, z – третье число.
Мысленно разделим условие задачи на 3 части, по каждой из которых составим уравнение с тремя неизвестными:
Вернёмся к условию задачи: первое число 15, второе число 5, третье число 3.
Ответ: 15, 5, 3.
Составим систему уравнений по условию задачи.
В трех сосудах 54л воды. Если из первого перелить во второй сосуд 4л, то в обоих сосудах будет воды поровну, а если из третьего сосуда перелить во второй 17л, то во втором сосуде окажется в 4 раза больше воды, чем в третьем. Сколько воды в каждом сосуде?
Пусть x л воды было в первом сосуде, y л воды – во втором, z воды – в третьем. Значит, всего в трёх сосудах было x + y + z л воды, что равно 54 л. Составим уравнение: x + y + z = 54.
Когда из первого сосуда перелили 4 л воды во второй сосуд, то во втором сосуде стало y + 4 л воды, а в первом сосуде x – 4 л воды. По условию задачи воды стало в сосудах поровну. Составляем уравнение:
y + 4 = x – 4.
Если из третьего сосуда перелить во второй 17 л, то в третьем останется z – 17 л, а во втором станет y + 17 л. По условию задачи во втором сосуде окажется в 4 раза больше воды, чем в третьем. Можем составить уравнение: y + 17 = 4(z – 17).
Записываем систему уравнений:
2. Система уравнений по условию задачи.
Составим систему уравнений по условию задачи: 5% одного числа и 4% другого вместе составляют 46, а 4% первого числа и 5% второго вместе составляют 44. Найдите эти числа.
систем линейных уравнений, примеры решений, рисунки и практические задачи. Система просто ..
Что такое система уравнений?
Отвечать
Система уравнений просто означает «более одного уравнения». Система линейных уравнений — это не более 1 строки, см. Рисунок:
Хорошо, так что же такое
решение системы уравнений? Отвечать
Решение — это место, где уравнения «встречаются» или пересекаются.Красная точка — это решение системы.
Сколько решений могут иметь системы линейных уравнений?
Отвечать
Может быть нулевое решение, одно решение или бесконечное количество решений — каждый случай подробно описан ниже. Примечание. Хотя системы линейных уравнений могут иметь 3 или более уравнений, мы собираемся обратиться к наиболее распространенному случаю — стержню с ровно 2 линиями.
Вариант I: 1 Решение
Это наиболее распространенная ситуация, когда линии пересекаются ровно в одной точке.
Дело 2: Нет решений
Это происходит только тогда, когда линии параллельны. Как видите, параллельные линии никогда не встретятся.
Пример стержня, у которого нет решения:
Строка 1: $$ y = 5x + 13 $$
Строка 2: $$ y = 5x + 12 $$
Вариант III: Бесконечные решения
Это самый редкий случай, и он возникает только тогда, когда у вас есть та же строка
Рассмотрим, например, две строки ниже (y = 2x + 1 и 2y = 4x + 2).Эти два уравнения — одна и та же линия.
Пример системы с бесконечным числом решений:
Строка 1: y = 2x + 1
Строка 2: 2y = 4x + 2
Как мы можем найти решения систем уравнений?
Найти решение систем линейных уравнений можно любым из следующих способов:
Графики и решения систем линейных уравнений
Результаты обучения
Графические системы уравнений
Постройте систему двух линейных уравнений
Постройте систему двух линейных неравенств
Оценить заказанные пары как решения для систем
Определить, является ли упорядоченная пара решением системы линейных уравнений
Определить, является ли упорядоченная пара решением системы линейных неравенств
Классифицируйте решения по системам
Определите, какой тип решения будет иметь система, на основе ее графика
Путь течения реки зависит от многих переменных, включая размер реки, количество воды в ней, какие предметы плавают в реке, идет ли дождь или нет, и так далее.Если вы хотите лучше всего описать его поток, вы должны принять во внимание эти другие переменные. В этом может помочь система линейных уравнений.
Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Вы найдете системы уравнений во всех приложениях математики. Они являются полезным инструментом для обнаружения и описания взаимосвязи поведения или процессов.Например, редко можно найти схему транспортного потока, на которую влияет только погода. Несчастные случаи, время суток и крупные спортивные события — это лишь некоторые из других переменных, которые могут повлиять на движение транспорта в городе. В этом разделе мы исследуем некоторые основные принципы построения графиков и описания пересечения двух линий, составляющих систему уравнений.
Построение системы линейных уравнений
В этом разделе мы рассмотрим системы линейных уравнений и неравенств с двумя переменными.Сначала мы попрактикуемся в построении графиков двух уравнений на одном и том же наборе осей, а затем изучим различные соображения, которые необходимо учитывать при построении графиков двух линейных неравенств на одном и том же наборе осей. Для построения графика системы линейных уравнений используются те же методы, что и для построения графиков отдельных линейных уравнений. Мы можем использовать таблицы значений, наклона и интервала y или интерцептов x и y , чтобы построить обе линии на одном и том же наборе осей.
Например, рассмотрим следующую систему линейных уравнений с двумя переменными.
[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]
Давайте изобразим их, используя форму пересечения наклона на одном и том же наборе осей. Помните, что форма пересечения наклона выглядит как [latex] y = mx + b [/ latex], поэтому мы захотим решить оба уравнения для [latex] y [/ latex].
Сначала найдите y в [latex] 2x + y = -8 [/ latex]
[латекс] \ begin {array} {c} 2x + y = -8 \\ y = -2x — 8 \ end {array} [/ latex]
Во-вторых, решите относительно y в [latex] x-y = -1 [/ latex]
[латекс] \ begin {array} {r} x-y = -1 \, \, \, \, \, \\ y = x + 1 \ end {array} [/ latex]
Теперь система записывается как
[латекс] \ begin {array} {c} y = -2x — 8 \\ y = x + 1 \ end {array} [/ latex]
Теперь вы можете построить оба уравнения, используя их наклоны и точки пересечения на одном и том же наборе осей, как показано на рисунке ниже.Обратите внимание на то, что графики имеют одну общую точку. Это их точка пересечения, точка, которая лежит на обеих линиях. В следующем разделе мы убедимся, что эта точка является решением системы.
В следующем примере вам будет предоставлена система для построения графика, состоящая из двух параллельных линий.
Пример
Постройте график системы [латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex], используя наклоны и пересечения линий по оси Y.
Показать решение
Во-первых, график [латекс] y = 2x + 1 [/ latex], используя наклон m = 2 и точку пересечения по оси y (0,1)
Затем добавьте [латекс] y = 2x-3 [/ latex], используя наклон m = 2 и точку пересечения оси y (0, -3)
Обратите внимание на то, что это параллельные линии, и они не пересекаются.В следующем разделе мы обсудим, как не существует решений системы уравнений, представляющих собой параллельные прямые.
В следующем примере вам будет предоставлена система, уравнения которой выглядят по-разному, но после построения графика оказываются той же линией.
Пример
Изобразите систему [латекс] \ begin {array} {c} y = \ frac {1} {2} x + 2 \\ 2y-x = 4 \ end {array} [/ latex], используя x — и y -перехватывает.
Показать решение
Сначала найдите точки пересечения по осям x и y [latex] y = \ frac {1} {2} x + 2 [/ latex]
Пересечение x будет иметь значение 0 для y, поэтому подставьте y = 0 в уравнение и выделите переменную x.
[латекс] \ begin {array} {c} 0 = \ frac {1} {2} x + 2 \\\ подчеркивание {\, \, \, \, \, \, \, \, — 2 \, \, \, \, \, \, — 2} \\ — 2 = \ frac {1} {2} x \\\ left (2 \ right) \ left (-2 \ right) = \ left (2 \ справа) \ frac {1} {2} x \\ — 4 = x \ end {array} [/ latex]
Х-точка пересечения [latex] y = \ frac {1} {2} x + 2 [/ latex] равна [latex] \ left (-4,0 \ right) [/ latex].
Пересечение оси Y легче найти, поскольку это уравнение имеет форму точки пересечения с угловым коэффициентом. Y-точка пересечения равна (2,0).
Теперь мы можем построить [latex] y = \ frac {1} {2} x + 2 [/ latex], используя точки пересечения
Теперь найдите перехваты [latex] 2y-x = 4 [/ latex]
Подставьте y = 0 в уравнение, чтобы найти точку пересечения с x.
[латекс] \ begin {array} {c} 2y-x = 4 \\ 2 \ left (0 \ right) -x = 4 \\ x = -4 \ end {array} [/ latex]
Перехватчик x [latex] 2y-x = 4 [/ latex] равен [latex] \ left (-4,0 \ right) [/ latex].
Теперь подставьте x = 0 в уравнение, чтобы найти точку пересечения оси y.
[латекс] \ begin {array} {c} 2y-x = 4 \\ 2y-0 = 4 \\ 2y = 4 \\ y = 2 \ end {array} [/ latex]
Y-пересечение [latex] 2y-x = 4 [/ latex] равно [latex] \ left (0,2 \ right) [/ latex].
ПОДОЖДИТЕ, это те же самые перехваты, что и [latex] y = \ frac {1} {2} x + 2 [/ latex]! Фактически, [latex] y = \ frac {1} {2} x + 2 [/ latex] и [latex] 2y-x = 4 [/ latex] на самом деле являются одним и тем же уравнением, выраженным по-разному.Если бы вы записали их оба в форме пересечения наклона, вы бы увидели, что это одно и то же уравнение.
На графике они представляют собой одну и ту же линию. В следующем разделе мы увидим, что системы с двумя одинаковыми уравнениями в них имеют бесконечное число решений.

Построение графика системы линейных уравнений состоит из выбора метода построения графиков, который вы хотите использовать, и построения графиков обоих уравнений на одном и том же наборе осей. Когда вы строите график системы линейных неравенств на одном и том же наборе осей, вам необходимо учесть еще несколько вещей.
Постройте систему двух неравенств
Помните из модуля по построению графиков, что график одного линейного неравенства разбивает координатную плоскость на две области. По одну сторону лежат все решения неравенства. С другой стороны, решений нет. Рассмотрим график неравенства [латекс] y <2x + 5 [/ latex].
Пунктирная линия [латекс] y = 2x + 5 [/ latex]. Каждая упорядоченная пара в заштрихованной области под линией является решением [latex] y <2x + 5 [/ latex], поскольку все точки под линией делают неравенство истинным.Если вы сомневаетесь в этом, попробуйте подставить координаты x и y точек A и B в неравенство — вы увидите, что они работают. Итак, заштрихованной областью показаны все решения этого неравенства.
Граничная линия делит координатную плоскость пополам. В этом случае он показан пунктирной линией, поскольку точки на линии не удовлетворяют неравенству. Если бы неравенство было [латекс] y \ leq2x + 5 [/ латекс], то граница была бы сплошной.
Изобразим еще одно неравенство: [latex] y> −x [/ latex].Вы можете проверить пару точек, чтобы определить, какую сторону границы нужно заштриховать. Контрольные точки M и N дают верные утверждения. Итак, заштриховываем область над линией. Линия пунктирна, поскольку точки на линии не соответствуют действительности.
Чтобы создать систему неравенств, вам необходимо построить график двух или более неравенств вместе. Давайте использовать [latex] y <2x + 5 [/ latex] и [latex] y> −x [/ latex], поскольку мы уже изобразили каждый из них.
Фиолетовая область показывает, где перекрываются решения двух неравенств.Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [latex] y> −x [/ latex], так и для [latex] y <2x + 5 [/ latex].
В следующем примере вам дана система двух неравенств, граничные линии которых параллельны друг другу.
Примеры
Изобразите систему [latex] \ begin {array} {c} y \ ge2x + 1 \\ y \ lt2x-3 \ end {array} [/ latex]
Показать решение
Границы для этой системы такие же, как и для системы уравнений из предыдущего примера:
[латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex]
Построение граничных линий будет аналогичным, за исключением того, что неравенство [латекс] y \ lt2x-3 [/ latex] требует, чтобы мы нарисовали пунктирную линию, а неравенство [латекс] y \ ge2x + 1 [/ латекс] потребует сплошная линия.Графики будут выглядеть так:
Теперь нам нужно добавить регионы, представляющие неравенства. Для неравенства [латекс] y \ ge2x + 1 [/ latex] мы можем проверить точку по обе стороны от линии, чтобы увидеть, какую область закрасить. Давайте проверим [латекс] \ left (0,0 \ right) [/ latex], чтобы упростить задачу.
Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ ge2x + 1 [/ latex]
[латекс] \ begin {array} {c} y \ ge2x + 1 \\ 0 \ ge2 \ left (0 \ right) +1 \\ 0 \ ge {1} \ end {array} [/ latex]
Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ ge2x + 1 [/ latex].График теперь будет выглядеть так:
Теперь закрасим область, которая показывает решения неравенства [латекс] y \ lt2x-3 [/ latex]. Опять же, мы можем выбрать [latex] \ left (0,0 \ right) [/ latex] для тестирования, потому что это упрощает алгебру.
Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ lt2x-3 [/ latex]
[латекс] \ begin {array} {c} y \ lt2x-3 \\ 0 \ lt2 \ left (0, \ right) x-3 \\ 0 \ lt {-3} \ end {array} [/ latex ]
Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ lt2x-3 [/ latex].График теперь будет выглядеть так:
У этой системы неравенства нет общих черт.
Как бы выглядел график, если бы система выглядела так?
[латекс] \ begin {массив} {c} y \ ge2x + 1 \\ y \ gt2x-3 \ end {array} [/ latex].
Проверка точки [latex] \ left (0,0 \ right) [/ latex] вернет положительный результат для неравенства [latex] y \ gt2x-3 [/ latex], и тогда график будет выглядеть следующим образом:
Фиолетовая область — это область перекрытия обоих неравенств.

В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Проверим алгебраически, является ли точка решением линейного уравнения или неравенства.
Определить, является ли упорядоченная пара решением системы линейных уравнений
Линии на графике выше определены как
[латекс] \ begin {массив} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex].
Они пересекаются в том, что выглядит как [латекс] \ left (-3, -2 \ right) [/ latex].
Используя алгебру, мы можем проверить, что эта общая точка на самом деле [latex] \ left (-3, -2 \ right) [/ latex], а не [latex] \ left (-2.999, -1.999 \ right) [/ latex ]. Подставляя значения x и y упорядоченной пары в уравнение каждой линии, вы можете проверить, находится ли точка на обеих линиях. Если подстановка приводит к истинному утверждению, значит, вы нашли решение системы уравнений!
Поскольку решение системы должно быть решением всех уравнений в системе, вам нужно будет проверить точку в каждом уравнении.В следующем примере мы заменим -3 на x и -2 на y в каждом уравнении, чтобы проверить, действительно ли это решение.
Пример
[латекс] \ left (-3, -2 \ right) [/ latex] решение системы
[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]
Показать решение Сначала проверьте [латекс] 2x + y = -8 [/ latex]:
[латекс] \ begin {массив} {r} 2 (-3) + (- 2) = -8 \\ — 8 = -8 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Теперь проверьте [латекс] x-y = -1 [/ latex].
[латекс] \ begin {array} {r} (- 3) — (- 2) = -1 \\ — 1 = -1 \\\ text {TRUE} \ end {array} [/ latex]
[латекс] \ left (-3, -2 \ right) [/ latex] является решением [латекса] x-y = -1 [/ latex]
Поскольку [latex] \ left (-3, -2 \ right) [/ latex] является решением каждого из уравнений в системе, [latex] \ left (-3, -2 \ right) [/ latex] это решение системы.
Ответ
[латекс] \ left (-3, -2 \ right) [/ latex] — это решение системы.
Пример
— это (3, 9) решение системы
[латекс] \ begin {array} {r} y = 3x \\ 2x – y = 6 \ end {array} [/ latex]
Показать решение Поскольку решение системы должно быть решением всех уравнений в системе, отметьте точку в каждом уравнении.
Замените 3 на x и 9 на y в каждом уравнении.
[латекс] \ begin {массив} {l} y = 3x \\ 9 = 3 \ left (3 \ right) \\\ text {TRUE} \ end {array} [/ latex]
(3, 9) представляет собой раствор [латекс] y = 3x [/ латекс].
[латекс] \ begin {array} {r} 2x – y = 6 \\ 2 \ left (3 \ right) –9 = 6 \\ 6–9 = 6 \\ — 3 = 6 \ text {FALSE } \ end {array} [/ latex]
(3, 9) — это , а не раствор [латекса] 2x – y = 6 [/ латекс].
Поскольку (3, 9) не является решением одного из уравнений системы, оно не может быть решением системы.
Ответ
(3, 9) не является решением системы.
Подумай об этом
[латекс] (- 2,4) [/ латекс] решение для системы
[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]
Прежде чем производить какие-либо вычисления, посмотрите на заданную точку и первое уравнение в системе. Можете ли вы предсказать ответ на вопрос, не занимаясь алгеброй?
Показать решение
Подставьте -2 вместо x и 4 вместо y в первое уравнение:
[латекс] \ begin {array} {l} y = 2x \\ 4 = 2 \ left (-2 \ right) \\ 4 = -4 \\\ text {FALSE} \ end {array} [/ latex]
Вы можете остановить тестирование, потому что точка, которая является решением системы, будет решением обоих уравнений в системе.
[latex] (- 2,4) [/ latex] НЕ является решением для системы
[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]

Помните, что для решения системы уравнений значения точки должны быть решением обоих уравнений. Как только вы найдете одно уравнение, для которого точка неверна, вы определили, что оно не является решением системы.
Мы можем использовать тот же метод, чтобы определить, является ли точка решением системы линейных неравенств.
Определить, является ли упорядоченная пара решением системы линейных неравенств
На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, потому что их координаты делают оба неравенства истинными.
Напротив, точки M и A лежат за пределами области решения (фиолетовый). Хотя точка M является решением неравенства [latex] y> −x [/ latex], а точка A является решением неравенства [latex] y <2x + 5 [/ latex], ни одна из точек не является решением для система .В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.
Пример
Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex]?
Показать решение Проверьте суть каждого неравенства. Замените 2 на x и 1 на y . Является ли дело решением обоих неравенств?
[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] x + y> 1 [/ latex].
[латекс] \ begin {array} {r} 2x + y <8 \\ 2 \ left (2 \ right) +1 <8 \\ 4 + 1 <8 \\ 5 <8 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] 2x + y <8. [/ Latex]
Поскольку (2, 1) является решением каждого неравенства, оно также является решением системы.
Ответ
Точка (2, 1) является решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex].
Вот график системы в приведенном выше примере. Обратите внимание, что (2, 1) находится в фиолетовой области, которая является областью перекрытия для двух неравенств.
Пример
Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex]?
Показать решение
Отметьте точку с каждым неравенством. Замените 2 на x и 1 на y . Является ли дело решением обоих неравенств?
[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] x + y> 1 [/ latex].
[латекс] \ begin {array} {r} 3x + y <4 \\ 3 \ left (2 \ right) +1 <4 \\ 6 + 1 <4 \\ 7 <4 \\\ text {FALSE} \ end {array} [/ latex]
(2, 1) — это , а не как решение для [латекса] 3x + y <4 [/ latex].
Поскольку (2, 1) — это , а не как решение одного из неравенств, это не решение системы.
Ответ
Точка (2, 1) не является решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex].
Вот график этой системы. Обратите внимание, что (2, 1) не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).
Как показано выше, нахождение решений системы неравенств может быть выполнено путем графического отображения каждого неравенства и определения области, в которой они находятся. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графике для системы двух линейных неравенств. Общие шаги описаны ниже:
Изобразите каждое неравенство в виде линии и определите, будет ли оно сплошным или пунктирным.
Определите, с какой стороны каждой граничной линии представлены решения неравенства, проверив точку на каждой стороне
Заштрихуйте область, которая представляет решения для обоих неравенств
Пример
Закрасьте область графика, которая представляет решения для обоих неравенств.[латекс] x + y \ geq1 [/ латекс] и [латекс] y – x \ geq5 [/ латекс].
Показать решение Изобразите одно неравенство. Сначала нарисуйте граничную линию, используя таблицу значений, пересечений или любой другой метод, который вы предпочитаете. Граница для [латекса] x + y \ geq1 [/ latex] — это [латекс] x + y = 1 [/ latex] или [латекс] y = −x + 1 [/ latex]. Поскольку знак равенства стоит вместе со знаком «больше», граница будет сплошной.
Найдите упорядоченную пару по обе стороны от ограничивающей линии. Вставьте значения x и y в неравенство [latex] x + y \ geq1 [/ latex] и посмотрите, какая упорядоченная пара дает истинное утверждение.
[латекс] \ begin {array} {r} \ text {Test} 1: \ left (−3,0 \ right) \\ x + y \ geq1 \\ — 3 + 0 \ geq1 \\ — 3 \ geq1 \\\ text {FALSE} \\\\\ text {Test} 2: \ left (4,1 \ right) \\ x + y \ geq1 \\ 4 + 1 \ geq1 \\ 5 \ geq1 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Поскольку (4, 1) приводит к истинному утверждению, область, которая включает (4, 1), должна быть заштрихована.
Проделайте то же самое со вторым неравенством. Постройте граничную линию, затем проверьте точки, чтобы определить, какая область является решением неравенства. В этом случае граница [латекс] y – x = 5 \ left (\ text {или} y = x + 5 \ right) [/ latex] сплошная.Контрольная точка (−3, 0) не является решением [latex] y – x \ geq5 [/ latex], а контрольная точка (0, 6) является решением.
Ответ
Фиолетовая область на этом графике показывает набор всех решений системы.

В этом разделе мы увидели, что решения систем линейных уравнений и неравенств могут быть упорядоченными парами. В следующем разделе мы будем работать с системами, у которых нет решений или есть бесконечно много решений.
Используйте график для классификации решений для систем
Напомним, что линейное уравнение отображается в виде линии, что означает, что все точки на линии являются решениями этого линейного уравнения.Есть бесконечное количество решений. Как мы видели в предыдущем разделе, если у вас есть система линейных уравнений, пересекающихся в одной точке, эта точка является решением системы. Что произойдет, если линии никогда не пересекаются, как в случае с параллельными линиями? Как бы вы описали решения для такой системы? В этом разделе мы рассмотрим три возможных результата решения системы линейных уравнений.
Три возможных исхода решений систем уравнений
Напомним, что решение системы уравнений — это значение или значения, которые верны для всех уравнений в системе.Есть три возможных исхода решений систем линейных уравнений. Графики уравнений внутри системы могут сказать вам, сколько решений существует для этой системы. Посмотрите на изображения ниже. На каждой показаны две линии, составляющие систему уравнений.
Одно решение Нет решений Бесконечные решения
Если графики уравнений пересекаются, то существует одно решение, истинное для обоих уравнений. Если графики уравнений не пересекаются (например, если они параллельны), то для обоих уравнений нет истинных решений. Если графики уравнений одинаковы, то существует бесконечное количество решений, которые верны для обоих уравнений.
Одно решение: Когда система уравнений пересекается в упорядоченной паре, система имеет одно решение.
Бесконечные решения: Иногда два уравнения отображаются в виде одной линии, и в этом случае у нас есть бесконечное количество решений.
Нет решения: Когда линии, составляющие систему, параллельны, решений нет, потому что эти две линии не имеют общих точек.
Пример
Используя график [latex] \ begin {array} {r} y = x \\ x + 2y = 6 \ end {array} [/ latex], показанный ниже, определите, сколько решений есть в системе.
Показать решение Линии пересекаются в одной точке. Таким образом, у этих двух линий есть только одна общая точка, есть только одно решение системы.
Ответ
Есть одно решение этой системы.
Пример (расширенный)
Используя график [latex] \ begin {array} {r} y = 3,5x + 0,25 \\ 14x – 4y = -4,5 \ end {array} [/ latex], показанный ниже, определите, сколько решений имеет система. .
Показать решение Линии параллельны, то есть не пересекаются. Решения по системе нет.
Ответ
Нет решений по системе.
Пример
Сколько решений имеет система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex]?
Показать решение Сначала изобразите оба уравнения на одних и тех же осях.
Два уравнения изображены на одной линии. Таким образом, каждая точка на этой линии является решением системы уравнений.
Ответ
Система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex] имеет бесконечное количество решений.

В следующем разделе мы изучим некоторые алгебраические методы нахождения решений систем уравнений. Напомним, что линейные уравнения с одной переменной могут иметь одно решение, без решения или много решений, и мы можем проверить это алгебраически.Мы будем использовать те же идеи для алгебраической классификации решений систем с двумя переменными.
Систем уравнений с двумя переменными
Введение в системы уравнений
Система уравнений состоит из двух или более уравнений с двумя или более переменными, где любое решение должно одновременно удовлетворять всем уравнениям в системе.
Цели обучения
Объясните, какие системы уравнений могут представлять
Основные выводы
Ключевые моменты
Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.
Чтобы линейная система имела единственное решение, должно быть как минимум столько же уравнений, сколько переменных.
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара [латекс] (x, y) [/ latex], которая удовлетворяет каждому уравнению независимо. Графически решения — это точки пересечения линий.
Ключевые термины
система линейных уравнений : Набор из двух или более уравнений, состоящих из двух или более переменных, которые рассматриваются одновременно.
зависимая система : система линейных уравнений, в которой два уравнения представляют
одну и ту же линию; существует бесконечное количество решений зависимой системы.
несовместимая система : Система линейных уравнений без общего решения, потому что они
представляют собой параллельные линии, которые не имеют общих точек или прямых.
независимая система : Система линейных уравнений с ровно одной парой решений [latex] (x, y) [/ latex].
Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям системы одновременно.Некоторые линейные системы могут не иметь решения, в то время как другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных. Даже в этом случае это не гарантирует уникального решения.
В этом разделе мы сосредоточимся в первую очередь на системах линейных уравнений, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными:
[латекс] 2x + y = 15 \ 3x — y = 5 [/ латекс]
Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо.В этом примере упорядоченная пара (4, 7) является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
[латекс] 2 (4) + 7 = 15 \\ 3 (4) — 7 = 5 [/ латекс]
Оба эти утверждения верны, поэтому [latex] (4, 7) [/ latex] действительно является решением системы уравнений.
Обратите внимание, что система линейных уравнений может содержать более двух уравнений и более двух переменных.Например,
[латекс] 3x + 2y — z = 12 \\ x — 2y + 4z = -2 \\ -x + 12y -z = 0 [/ латекс]
— это система трех уравнений с тремя переменными [латекс] x, y, z [/ latex]. Решение системы выше дается
[латекс] x = 1 \ y = -2 \ z = — 2 [/ латекс]
, поскольку он делает все три уравнения действительными.
Типы линейных систем и их решения
В общем, линейная система может вести себя одним из трех возможных способов:
Система имеет единственное уникальное решение .
В системе нет решения .
В системе бесконечно много решений .
Каждая из этих возможностей представляет собой определенный тип системы линейных уравнений с двумя переменными. Каждый из них может отображаться графически, как показано ниже. Обратите внимание, что решение системы линейных уравнений — это любая точка, в которой линии пересекаются.
Системы линейных уравнений: Графические представления трех типов систем.
Независимая система имеет ровно одну пару решений [latex] (x, y) [/ latex]. Точка пересечения двух линий — единственное решение.
Непоследовательная система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекутся.
У зависимой системы бесконечно много решений. Линии точно такие же, поэтому каждая пара координат на линии является решением обоих уравнений.
Графическое решение систем
Простой способ решить систему уравнений — это найти точку или точки пересечения уравнений.Это графический метод.
Цели обучения
Графическое решение системы уравнений с двумя переменными
Основные выводы
Ключевые моменты
Чтобы решить систему уравнений графически, нарисуйте уравнения и укажите точки пересечения как решения. У системы уравнений может быть несколько решений.
Система линейных уравнений будет иметь одну точку пересечения или одно решение.
Чтобы построить график системы уравнений, записанных в стандартной форме, вы должны переписать уравнения в форме пересечения углов наклона.
Ключевые термины
Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Графический метод : способ визуального нахождения набора значений, который решает систему уравнений.
Система уравнений (также известная как одновременные уравнения) — это система уравнений с несколькими переменными, которая решается, когда значения всех переменных одновременно удовлетворяют всем уравнениям.Наиболее распространенные способы решения системы уравнений:
Графический метод
Метод замещения
Метод исключения
Здесь мы обратимся к графическому методу.
Графическое решение систем
Некоторые системы имеют только один набор правильных ответов, в то время как другие имеют несколько наборов, которые удовлетворяют всем уравнениям. Графически показано, что набор уравнений, решенных только с одним набором ответов, будет иметь только одну точку пересечения, как показано ниже.Эта точка считается решением системы уравнений. В наборе линейных уравнений (например, на изображении ниже) есть только одно решение.
Система линейных уравнений с двумя переменными : На этом графике показана система уравнений с двумя переменными и только один набор ответов, который удовлетворяет обоим уравнениям.
Система с двумя наборами ответов, которые удовлетворяют обоим уравнениям, имеет две точки пересечения (таким образом, два решения системы), как показано на изображении ниже.
Система уравнений с несколькими ответами: Это пример системы уравнений, показанной графически, которая имеет два набора ответов, которые удовлетворяют обоим уравнениям в системе.
Преобразование в форму пересечения уклона
Прежде чем успешно решить систему графически, необходимо понять, как графически отображать уравнения, записанные в стандартной форме, или [latex] Ax + By = C [/ latex]. Вы всегда можете использовать графический калькулятор для графического представления уравнений, но полезно знать, как самостоятельно формулировать такие уравнения.
Для этого необходимо преобразовать уравнения в форму пересечения наклона или [латекс] y = mx + b [/ latex], где м = наклон и b = пересечение по оси y.
Лучший способ преобразовать уравнение в форму пересечения наклона — сначала выделить переменную y , а затем разделить правую часть на B , как показано ниже.
[латекс] \ begin {align} \ displaystyle Ax + By & = C \\ By & = — Ax + C \\ y & = \ frac {-Ax + C} {B} \\ y & = — \ frac {A} { B} x + \ frac {C} {B} \ end {align} [/ latex]
Теперь [latex] \ displaystyle — \ frac {A} {B} [/ latex] — это уклон м, и [latex] \ displaystyle \ frac {C} {B} [/ latex] — точка пересечения по оси Y б .
Определение решений на графике
После того, как вы преобразовали уравнения в форму с пересечением наклона, вы можете нанести их на график. Чтобы определить решения системы уравнений, определите точки пересечения между графическими уравнениями. Упорядоченная пара, которая представляет собой пересечение (я), представляет собой решение (я) системы уравнений.
Метод замещения
Метод подстановки — это способ решения системы уравнений путем выражения уравнений только с помощью одной переменной.
Цели обучения
Решите системы уравнений с двумя переменными с помощью подстановки
Основные выводы
Ключевые моменты
Система уравнений — это система уравнений, которая может быть решена с использованием определенного набора значений.
Метод подстановки работает, выражая одну из переменных через другую, затем подставляя ее обратно в исходное уравнение и упрощая его.
Очень важно проверить свою работу после того, как вы нашли набор значений для переменных.Сделайте это, подставив найденные вами значения обратно в исходные уравнения.
Решение системы уравнений можно записать в виде упорядоченной пары ( x , y ).
Ключевые термины
метод подстановки : Метод решения системы уравнений путем выражения уравнения только одной переменной
Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Метод подстановки для решения систем уравнений — это способ упростить систему уравнений, выразив одну переменную через другую, тем самым удалив одну переменную из уравнения. Когда полученное упрощенное уравнение имеет только одну переменную, с которой можно работать, уравнение становится разрешимым.
Метод замещения состоит из следующих шагов:
В первом уравнении решите одну из переменных через другие.
Подставьте это выражение в остальные уравнения.
Продолжайте, пока не сведете систему к одному линейному уравнению.
Решите это уравнение, а затем выполняйте обратную замену, пока решение не будет найдено.
Решение методом подстановки
Попрактикуемся в этом, решив следующую систему уравнений:
[латекс] x-y = -1 [/ латекс]
[латекс] x + 2y = -4 [/ латекс]
Начнем с решения первого уравнения, чтобы выразить x через y .
[латекс] \ begin {align} \ displaystyle x-y & = — 1 \\ x & = y-1 \ end {align} [/ latex]
Затем мы заменим наше новое определение x во второе уравнение:
[латекс] \ displaystyle \ begin {align} x + 2y & = — 4 \\ (y-1) + 2y & = — 4 \ end {align} [/ latex]
Обратите внимание, что теперь это уравнение имеет только одну переменную (y). Затем мы можем упростить это уравнение и решить относительно y :
[латекс] \ displaystyle \ begin {align} (y-1) + 2y & = — 4 \\ 3y-1 & = — 4 \\ 3y & = — 3 \\ y & = — 1 \ end {align} [/ latex]
Теперь, когда мы знаем значение y , мы можем использовать его, чтобы найти значение другой переменной, x. Для этого подставьте значение y в первое уравнение и решите относительно x .
[латекс] \ displaystyle \ begin {align} x-y & = — 1 \\ x — (- 1) & = — 1 \\ x + 1 & = — 1 \\ x & = — 1-1 \\ x & = — 2 \ end {align} [/ latex]
Таким образом, решение системы: [latex] (- 2, -1) [/ latex], то есть точка, где две функции графически пересекаются. Проверьте решение, подставив значения в одно из уравнений.
[латекс] \ displaystyle \ begin {align} x-y & = — 1 \\ (- 2) — (- 1) & = — 1 \\ — 2 + 1 & = — 1 \\ — 1 & = — 1 \ end {align} [/ латекс]
Метод исключения
Метод исключения используется для исключения переменной, чтобы упростить поиск оставшейся переменной (переменных) в системе уравнений.
Цели обучения
Решите системы уравнений с двумя переменными методом исключения
Основные выводы
Ключевые моменты
Этапы метода исключения следующие: (1) составить уравнения так, чтобы переменные выровнялись, (2) изменить одно уравнение, чтобы оба уравнения использовали согласованную переменную, которую можно исключить, (3) сложить уравнения, чтобы исключить переменную, (4) решить и (5) выполнить обратную замену для поиска другой переменной.
Всегда проверяйте ответ.Это делается путем включения обоих значений в одно или оба исходных уравнения.
Ключевые термины
метод исключения : Процесс решения системы уравнений путем исключения одной переменной для более простого решения оставшейся переменной.
Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Метод исключения для решения систем уравнений, также известный как исключение добавлением , представляет собой способ исключения одной из переменных в системе, чтобы более просто оценить оставшуюся переменную.После успешного нахождения значений остальных переменных они подставляются в исходное уравнение, чтобы найти правильное значение для другой переменной.
Метод исключения включает следующие шаги:
Перепишите уравнения так, чтобы переменные выровнялись.
Измените одно уравнение так, чтобы оба уравнения имели переменную, которая компенсировалась бы при сложении уравнений.
Добавьте уравнения и удалите переменную.
Найдите оставшуюся переменную.
Обратно подставить и решить для другой переменной.
Решение методом исключения
Метод исключения можно продемонстрировать на простом примере:
[латекс] \ displaystyle 4x + y = 8 \\ 2y + x = 9 [/ латекс]
Сначала выровняйте переменные, чтобы уравнения можно было легко сложить на более позднем этапе:
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ x + 2y & = 9 \ end {align} [/ latex]
Затем посмотрите, не настроены ли уже какие-либо переменные таким образом, что их сложение приведет к их исключению из системы.Если нет, умножьте одно уравнение на число, позволяющее компенсировать переменные. В этом примере переменную y можно исключить, если мы умножим верхнее уравнение на [латекс] -2 [/ латекс], а затем сложим уравнения.
Шаг умножения:
[латекс] \ displaystyle \ begin {align} -2 (4x + y & = 8) \\ x + 2y & = 9 \ end {align} [/ latex]
Результат:
[латекс] \ displaystyle \ begin {align} -8x-2y & = — 16 \\ x + 2y & = 9 \ end {align} [/ latex]
Теперь добавьте уравнения, чтобы исключить переменную y .
[латекс] \ displaystyle \ begin {align} -8x + x-2y + 2y & = — 16 + 9 \\ — 7x & = — 7 \ end {align} [/ latex]
Наконец, найдите переменную x .
[латекс] \ displaystyle \ begin {align} -7x & = — 7 \\ x & = \ frac {-7} {- 7} \\ x & = 1 \ end {align} [/ latex]
Затем вернитесь к одному из исходных уравнений и замените найденное нами значение на x . Проще всего выбрать простейшее уравнение, но подойдет любое уравнение.
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ 4 (1) + y & = 8 \\ 4 + y & = 8 \\ y & = 4 \ end {align} [/ latex]
Следовательно, решение уравнения (1,4).Всегда важно проверить ответ, подставив оба этих значения вместо соответствующих переменных в одно из уравнений.
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ 4 (1) + 4 & = 8 \\ 4 + 4 & = 8 \\ 8 & = 8 \ end {align} [/ latex]
Несогласованные и зависимые системы с двумя переменными
Для линейных уравнений с двумя переменными несовместные системы не имеют решений, а зависимые системы имеют бесконечно много решений.
Цели обучения
Объясните, когда системы уравнений с двумя переменными несовместимы или зависимы как графически, так и алгебраически.
Основные выводы
Ключевые моменты
Графически уравнения в зависимой системе представляют собой одну и ту же линию. Уравнения в противоречивой системе представляют собой параллельные линии, которые никогда не пересекаются.
Мы можем использовать методы решения систем уравнений для определения зависимых и несовместимых систем: Зависимые системы имеют бесконечное количество решений. Применение методов решения систем уравнений приведет к истинному тождеству, например [латекс] 0 = 0 [/ латекс].Несогласованные системы не имеют решений. Применение методов решения систем уравнений приведет к противоречию, например к утверждению [латекс] 0 = 1 [/ латекс].
Ключевые термины
несовместимая система : Система линейных уравнений без общего решения, потому что они
представляют собой параллельные линии, которые не имеют общих точек или прямых.
независимая система : Система линейных уравнений с ровно одной парой решений.
зависимая система : система линейных уравнений, в которой два уравнения представляют
одну и ту же линию; существует бесконечное количество решений зависимой системы.
Напомним, что линейная система может вести себя одним из трех возможных способов:
Система имеет единственное уникальное решение.
В системе нет решения.
В системе бесконечно много решений.
Также напомним, что каждая из этих возможностей соответствует типу системы линейных уравнений с двумя переменными. Независимая система уравнений имеет ровно одно решение [latex] (x, y) [/ latex]. Несогласованная система не имеет решения, а зависимая система имеет бесконечное количество решений.
В предыдущих модулях обсуждалось, как найти решение для независимой системы уравнений. Теперь мы сосредоточимся на выявлении зависимых и несовместимых систем линейных уравнений.
Зависимые системы
Уравнения линейной системы независимы , если ни одно из уравнений не может быть получено алгебраически из других. Когда уравнения независимы, каждое уравнение содержит новую информацию о переменных, и удаление любого из уравнений увеличивает размер набора решений.Системы, которые не являются независимыми, по определению зависимые . Уравнения в зависимой системе могут выводиться друг из друга; они описывают одну и ту же линию. Они не добавляют новую информацию о переменных, и потеря уравнения из зависимой системы не изменяет размер набора решений.
Мы можем применять методы замены или исключения для решения систем уравнений, чтобы идентифицировать зависимые системы. Зависимые системы имеют бесконечное количество решений, потому что все точки на одной линии также находятся на другой линии.После использования замены или добавления результирующее уравнение будет идентичным, например [латекс] 0 = 0 [/ латекс].
Например, рассмотрим два уравнения
[латекс] 3x + 2y = 6 \ 6x + 4y = 12 [/ латекс]
Мы можем применить метод исключения для их оценки. Если бы мы умножили первое уравнение на коэффициент [латекс] -2 [/ латекс], мы получили бы:
[латекс] \ displaystyle \ begin {align} -2 (3x + 2y & = 6) \\ — 6x-4y & = — 12 \ end {align} [/ latex]
Добавление этого ко второму уравнению даст [латекс] 0 = 0 [/ латекс].Таким образом, две линии зависимы. Также обратите внимание, что это одно и то же уравнение, увеличенное в два раза; другими словами, второе уравнение может быть получено из первого.
На графике два уравнения образуют идентичные линии, как показано ниже.
Зависимая система : Уравнения [латекс] 3x + 2y = 6 [/ latex] и [latex] 6x + 4y = 12 [/ latex] являются зависимыми, и при отображении на графике они образуют одну и ту же линию.
Обратите внимание, что существует бесконечное количество решений для зависимой системы, и эти решения относятся к общей линии.
Несогласованные системы
Линейная система непротиворечива, если у нее есть решение, и непоследовательна в противном случае. Напомним, что графическое представление несовместимой системы состоит из параллельных линий, которые имеют одинаковый наклон, но разные точки пересечения [latex] y [/ latex]. Они никогда не пересекутся.
Мы также можем применять методы решения систем уравнений для выявления несовместимых систем. Когда система несовместима, можно вывести противоречие из уравнений, например, утверждение [латекс] 0 = 1 [/ латекс].
Рассмотрим следующие два уравнения:
[латекс] 3x + 2y = 6 \ 3x + 2y = 12 [/ латекс]
Мы можем применить метод исключения, чтобы попытаться решить эту систему. Вычитая первое уравнение из второго, обе переменные удаляются, и мы получаем [латекс] 0 = 6 [/ латекс]. Это противоречие, и мы можем определить, что это несовместимая система. Графики этих уравнений на плоскости [latex] xy [/ latex] представляют собой пару параллельных линий.
Несогласованная система: Уравнения [латекс] 3x + 2y = 6 [/ латекс] и [латекс] 3x + 2y = 12 [/ латекс] несовместимы.
В общем случае несоответствия возникают, если левые части уравнений в системе линейно зависимы, а постоянные члены не удовлетворяют соотношению зависимости. Система уравнений, левые части которой линейно независимы, всегда непротиворечива.
Приложения систем уравнений
Системы уравнений могут использоваться для решения многих реальных задач, в которых для одних и тех же переменных используется несколько ограничений.
Цели обучения
Применение систем уравнений с двумя переменными к реальным примерам
Основные выводы
Ключевые моменты
Если у вас есть проблема, которая включает несколько переменных, вы можете решить ее, создав систему уравнений.
После определения переменных определите отношения между ними и запишите их в виде уравнений.
Ключевые термины
Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Системы уравнений в реальном мире
Система уравнений, также известная как одновременные уравнения, представляет собой набор уравнений с несколькими переменными. Ответ на систему уравнений — это набор значений, который удовлетворяет всем уравнениям в системе, и таких ответов может быть много для любой данной системы.Ответы обычно записываются в виде упорядоченной пары: [латекс] \ left (x, y \ right) [/ latex]. Подходы к решению системы уравнений включают замену и исключение, а также графические методы.
Существует несколько практических приложений систем уравнений. Они подробно показаны ниже.
Планирование мероприятия
Система уравнений может использоваться для решения задачи планирования, в которой необходимо учитывать несколько ограничений:
Эмили устраивает большую вечеринку после школы.Принципал наложил два ограничения. Во-первых, общее количество людей (учителей и студентов, вместе взятых) должно составлять [латекс] 56 [/ латекс]. Во-вторых, на каждые семь учеников должен приходиться один учитель. Итак, сколько учеников и сколько учителей приглашено на вечеринку?
Во-первых, нам нужно идентифицировать и назвать наши переменные. В данном случае нашими переменными являются учителя и ученики. Количество учителей будет [латекс] Т [/ латекс], а количество учеников — [латекс] S [/ латекс].
Теперь нам нужно составить наши уравнения.Существует ограничение, ограничивающее общее количество людей [латекс] 56 [/ латекс], поэтому:
[латекс] T + S = 56 [/ латекс]
На каждые семь учеников должен приходиться один учитель, поэтому:
[латекс] \ frac {S} {7} = T [/ латекс]
Теперь у нас есть система уравнений, которую можно решить с помощью замены, исключения или графически. Решение системы: [латекс] S = 49 [/ латекс] и [латекс] T = 7 [/ латекс].
Поиск неизвестных количеств
Этот следующий пример показывает, как системы уравнений используются для нахождения величин.
Группа студентов и учителей [латекс] 75 [/ латекс] в поле собирает сладкий картофель для нуждающихся. Кейси собирает в три раза больше сладкого картофеля, чем Дэвис, а затем, возвращаясь к машине, берет еще пять! Глядя на ее недавно увеличившуюся кучу, Дэвис замечает: «Ух ты, у тебя [латекса] 29 [/ латекса] картофеля больше, чем у меня!» Сколько сладкого картофеля собрали Кейси и Дэвис каждый?
Чтобы решить, мы сначала определяем наши переменные. Количество сладкого картофеля, которое собирает Кейси, — [латекс] K [/ латекс], а количество сладкого картофеля, которое собирает Дэвис, — [латекс] D [/ латекс].
Теперь мы можем писать уравнения на основе ситуации:
[латекс] K-5 = 3D [/ латекс]
[латекс] D + 29 = K [/ латекс]
Отсюда замена, исключение или построение графика покажут, что [латекс] K = 41 [/ латекс] и [латекс] D = 12 [/ латекс].
Важно всегда проверять свои ответы. Хороший способ проверить решения системы уравнений — это посмотреть на функции графически, а затем увидеть, где пересекаются графики. Или вы можете подставить свои ответы в каждое уравнение и убедиться, что они приводят к точным решениям.
Другие приложения
Существует множество других приложений для систем уравнений, таких как определение того, какой ландшафтный дизайнер предлагает лучшее предложение, сколько разные операторы сотовой связи берут за минуту, или сравнение информации о питании в рецептах.
Qalaxia — это бесплатный сайт вопросов и ответов для классных комнат. В Калаксии:
Студенты просят помочь с домашним заданием на онлайн-форумах по домашнему заданию и получают помощь от экспертов и студентов-волонтеров
Студенты задают вопросы и получают ответы от экспертов отрасли
Студенты получают вознаграждение за то, что задают вопросы и отвечают на них
Студенты зарабатывают часы волонтерской работы, помогая другим студентам, не выходя из дома
Студенты заинтересованы в том, чтобы задавать вопросы и отвечать на вопросы экспертов
Учителя имеют доступ к библиотеке вопросов с участием учителей и отраслевых экспертов
Студенты наслаждаются индивидуальным обучением с помощью механизма рекомендаций, который адаптируется к успеваемости студентов, и индивидуальной помощи экспертов
Qalaxia будет готова к использованию в апреле 2017 года.Пожалуйста, подпишитесь здесь для получения обновлений
Лучшие вопросы и ответы. От специалистов для учебных заведений.
Qalaxia — это награждаемый сайт вопросов и ответов для учителей, студентов и экспертов, где эксперты делятся своими мыслями и знаниями с классами.
Эксперты любят Qalaxia за то, что они могут помогать студентам в свободное и удобное время, отвечая на них и задавая вопросы.
Студенты любят Qalaxia, поскольку они зарабатывают вознаграждение за правильные ответы на вопросы викторины и за размещение хороших вопросов, на которые могут ответить эксперты. Qalaxia стимулирует и предоставляет студентам необходимую помощь для своевременного выполнения домашних заданий и удовлетворения их любопытства.
Учителя любят Qalaxia, потому что она не только помогает своим ученикам закончить домашнее задание и удовлетворить их любопытство, но также дает учителям полную прозрачность в отношении того, сколько усилий учеников и экспертной помощи было вложено в каждый вопрос домашнего задания.
Мир, в котором ни один вопрос студента не остается без ответа или без ответа
Мы пробуждаем и укрепляем вопрошающего в каждом ребенке и наставника в каждом отдельном человеке
Qalaxia — это платформа вопросов и ответов, созданная для воспитания в каждом ученике исследователя, ищущего и исследователя.Qalaxia поощряет студентов получать знания не только от учителей, но и от удаленных экспертов-волонтеров.
Искусственный интеллект и опытный помощник преподавателя в каждом классе
Актуальная помощь для студентов
Замечательный учитель рядом с каждым учеником, когда это необходимо
Увлечен образованием
Эксперты в области искусственного интеллекта и программного обеспечения
Имеют опыт академической и профессиональной подготовки
Сколько решений имеет система линейных уравнений? — IVY Lounge Test Prep
Теперь вот сумасшедший ярлык, который я использую:
Когда я пишу свои линейные уравнения в стандартной форме, например:
Ax + By = C
и
Dx + Ey = F
наклоны определяются коэффициентами переменных (A, B, D и E), а пересечения по оси Y определяются B, E, C и F.
Итак, вот самый большой трюк:
наклоны одинаковы, если A и D пропорциональны B и E!
Другими словами, если у меня есть эти…
2x + 5y = 9
4x + 10y = 15
… Я могу сделать пропорцию 2/4 = 5/10, уменьшить обе стороны, чтобы понять, что они обе равны 1⁄2 и, следовательно, одинаковы, и осознаем, что эти два уравнения имеют одинаковый наклон !
Итак, если у них одинаковый наклон, они либо параллельны и НЕ имеют решения, либо они одинаковы и имеют БЕСКОНЕЧНЫЕ решения.
Как узнать, какой именно? Простой! Посмотрите, пропорциональны ли B и E также C и F! Давайте проверим …
5/9 = 10/15
… НЕТ! Не равный! Так что их точки пересечения по оси Y разные. Это означает, что они параллельны. Это означает, что для этой системы НЕТ решений.
Видите? На самом деле не так уж и сложно. А возможность увидеть, сколько решений вы ищете в системе линейных уравнений, принесет вам баллы
и , сэкономив ваше время на SAT. Счет!
Итак, теперь вы понимаете все хитрые способы тестирования на линиях и системах линейных уравнений.Вы знаете все способы представления линии. Вы знаете, что числа в уравнениях на самом деле ЗНАЧИТ в реальных сценариях. Вы знаете, какие ситуации дают вам СИСТЕМУ линейных уравнений, и вы также знаете, сколько решений будет у этой системы! Это на самом деле ОЧЕНЬ МНОГО! Особенно на SAT!
Но есть пара тем из «детской алгебры», которые мои ученики склонны игнорировать, потому что они кажутся неважными, — а потом они их пропускают! Так что следите за обновлениями, и на следующей неделе я полностью обновлю ваше понимание забытых пасынков алгебры: неравенства и абсолютной ценности!
Сколько решений имеет система уравнений? Совет для учителей
На этой неделе мы узнали отличный способ различать различные варианты того, сколько решений существует при работе с двумя уравнениями в системе уравнений.Я работал с группой студентов, которые изо всех сил пытались понять, что они пытались сделать, определяя, сколько решений возможно. Они просто не понимали, что значит для системы уравнений одно решение против отсутствия решений против бесконечного числа решений. Итак, мы начали добавлять стратегию жестов рук, и это действительно помогло некоторым из них по-другому понять эту тему.
Одно серьезное заблуждение, которое я увидел, заключалось в том, что ученики продолжали думать, что если наклон другой, то решения не должно быть.Я думаю, они путали термин «решение» с «ответом». Мне нужно было заставить их понять, что когда есть одно решение, тогда да, линии не равны — они отличаются друг от друга. Но есть — это , решение вопроса, где пересекаются эти линии? У этих двух линий есть одна общая черта, а и — это то, что мы пытаемся выяснить.
Супер простой совет для обучения, сколько решений в системе уравнений
Я начал использовать жесты рук каждый раз, когда нам предлагали новую систему уравнений, чтобы поговорить о том, как они будут выглядеть, а затем поговорить о том, сколько пар координат будет одинаковым для обеих линий.Это была простая стратегия, но она могла быстро и четко показать, что происходит:
Нет решений
Одно решение
Бесконечные решения
Привлечение студентов
И потом я вспомнил, что обучение на практике намного мощнее, чем обучение на основе видения. Я попросил студентов использовать свои руки, чтобы проиллюстрировать взаимосвязь в системах уравнений.Каждую систему уравнений, которую мы видели, они должны были использовать свои руки, чтобы проиллюстрировать, как эти две линии будут связаны друг с другом.
Когда ученики использовали руки для представления двух линий, это был способ объяснить свое мышление. Это было действительно мощно и заставило всех объяснить каждую систему — так что было много математических «разговоров» без использования слов. Они должны были показать, как будут выглядеть эти линии, а затем сказать, сколько решений, по их мнению, может быть найдено.
Разве вам не нравятся быстрые (и бесплатные!) Стратегии, которые действительно помогают студентам понять это ?! Хотите, чтобы бесплатные увлекательные задания по математике были доставлены прямо в ваш почтовый ящик? Присоединяйтесь к клубу «Лабиринт месяца», чтобы получить бесплатные математические лабиринты, которые дают учащимся необходимую им математическую практику.
Да! Запишитесь в клуб «Лабиринт месяца»!
Не могу дождаться встречи с вами!
Чтобы получить еще больше советов по системам уравнений, ознакомьтесь с 9 заданиями «Сколько решений» и «15 упражнениями по системам уравнений для вашего класса». Спасибо за прочтение. До скорого!
Связанные
Решения систем линейных уравнений
В этом уроке будут рассмотрены 3 типа решений систем линейных уравнений.Система линейных уравнений может иметь одно решение, не иметь решения или бесконечно много решений. Наклоны и точки пересечения линий по оси y определят тип решения, которое будет иметь система.
Решения систем линейных уравнений: 1 решение

Система линейных уравнений имеет одно решение, если линии имеют разный наклон независимо от значений их пересечений по оси Y.
Например, следующие системы линейных уравнений будут иметь одно решение.Мы показываем уклоны для каждой системы синим цветом. Обратите внимание, как различаются уклоны.
1. y = (-2 /9 ) x + 6
y = 2x + — 3
2. y = -8x + 6
y = 8x + -10
3. y = 0,5x + 3
y = 6x + 3
Когда система двух линейных уравнений имеет разные наклоны, они будут встречаться в пространстве в одной точке. Точка пересечения — это решение.
Если мы построим график для первой системы слева, вы увидите решение или точку пересечения с оранжевой точкой. Если вы не понимаете, как мы построили линии ниже, перейдите к урокам по построению графика уклона.
у = (-2/9) х + 6
у = 2х + -3
Решения систем линейных уравнений: нет решения

Система линейных уравнений не имеет решения, если линии имеют одинаковый наклон, но разные точки пересечения по оси Y.
Например, следующие системы линейных уравнений не будут иметь решения.Мы показываем наклоны для каждой системы красным цветом, а точки пересечения по оси Y — синим. Обратите внимание, что наклон такой же, но пересечения по оси Y разные.
4. y = -2x + 1
y = -2x — 2
5. y = 3x + 5
y = 3x + -8
6. y = (2/5) х + -6
у = (2/5) х + 1
Когда система двух линейных уравнений имеет одинаковый наклон, но разные точки пересечения по оси Y, они никогда не встречаются в пространстве.Поскольку они никогда не встречаются, решений нет.
Построив график четвертой системы, вы увидите, что линии параллельны.
y = -2x + 1
y = -2x — 2
Решения систем линейных уравнений: бесконечно много решений.

Система линейных уравнений имеет бесконечно много решений, если прямые имеют одинаковый наклон и одинаковую точку пересечения по оси y.
Например, следующие системы линейных уравнений будут иметь бесконечно много решений. Обратите внимание, как одинаковый наклон и как такая же точка пересечения по оси Y.
7. y = 2x + 1
y = 2x + 1
8. y = -4x + 1/2
y = -4x + 1/2
9. y = (3/4) x + 8
у = (3/4) х + 8
Когда система двух линейных уравнений имеет одинаковый наклон и одинаковую точку пересечения по оси Y, они встречаются повсюду. Так как они встречаются повсюду, решений бесконечно много
После построения графиков седьмой системы мы видим, что два графика встречаются повсюду.
y = 2x + 1
y = 2x + 1 .