Сложение и вычитание степеней ⬅️
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
где
a — основание степени
n — показатель степени
Соответственно, an= a·a·a·a…·a
Читается такое выражение, как a в степени n.
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя. А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например число 2, то решается она довольно просто:
2 — основание степени
3 — показатель степени
Действия, конечно, можно выполнять и в
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).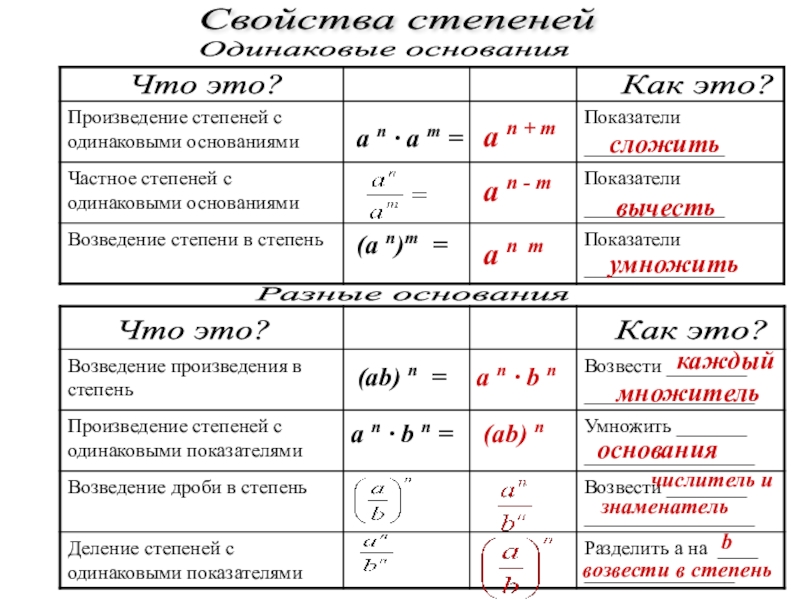
Число | Вторая степень | Третья степень |
1 | 1 | 1 |
2 | 4 | 8 |
3 | 9 | 27 |
4 | 16 | 64 |
5 | 25 | 125 |
6 | 36 | 216 |
7 | 49 | 343 |
8 | 64 | 512 |
9 | 81 | 729 |
10 | 100 | 1000 |
Свойства степеней: когда складывать, а когда вычитать
Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — давайте их рассмотрим.
Всего их пять штук — давайте их рассмотрим.
Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
a — основание степени (не равное нулю)
m, n — показатели степени, натуральное число
Свойство 4: степень возведения
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Затем полученные результаты перемножаются.
a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Сложение и вычитание степеней
Как складывать числа со степенями и как вычитать степени — очень просто. Основной принцип такой: выполняется сначала возведение в степень, а уже потом действия сложения и вычитания. Примеры:
- 23+ 34= 8 + 81= 89
- 63— 33= 216 — 27 = 189
И еще несколько правил:
|
Сложение степеней с разными показателями
В таком случае действуем согласно общему правилу: сначала выполняем возведение в степень каждого числа, затем — производим сложение.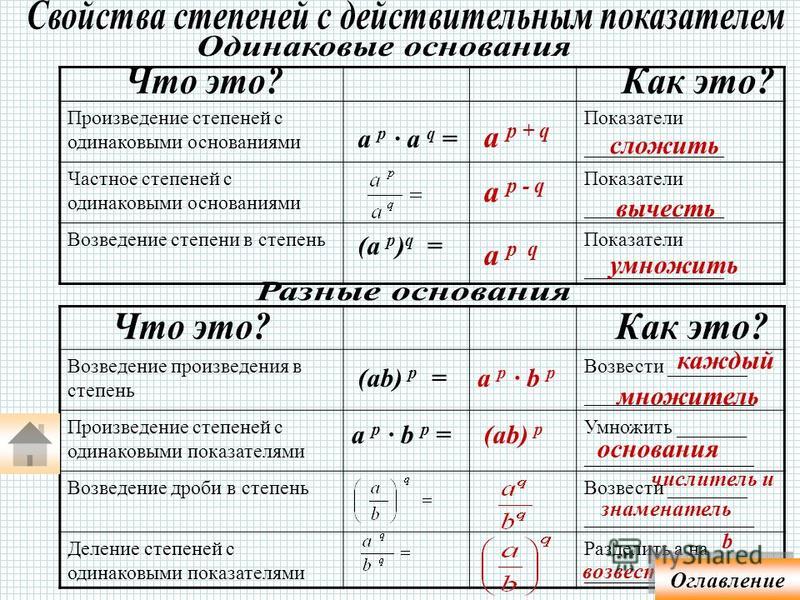
Сложение степеней с разными основаниями
В целом, это ничем не отличается от предыдущего пункта. Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим сложение.
- 34+ 54=81 + 625 = 706
- 14+ 72= 1+ 49 = 50
Как складывать числа с одинаковыми степенями
Точно также, как и в предыдущем примере. Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень.
Сначала возводим каждое число в степень и затем выполняем сложение.
В уравнениях это будет происходить немного иначе. Если показатель и основание степени одинаковые (тогда это называется переменная, a2, например) — их коэффициенты можно складывать. Коэффициент — это число перед переменной a 2.
2, 3, 5 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Вычитание степеней с одинаковым основанием
Здесь принцип тот же, что и со сложением: возводим в степень числа и только потом вычитаем их.
Вычитание степеней с разными основаниями
Могут быть разные основания, но одинаковые степени. А могут быть и разные основания, и разные показатели. Поэтому сначала выполняем возведение в степень каждого числа, затем — производим вычитание.
- 54— 44= 625 — 256 = 369
- 74— 32= 2401 — 9 = 2392
Вычитание чисел с одинаковыми степенями
Все точно также, как и со сложением. Если степени одинаковые, а основания разные, то нельзя вычесть основания и затем эту разницу возводить в степень. Сначала возводим каждое число в степень и затем выполняем вычитание.
И та же история с коэффициентами: если показатель степени и основание степени одинаковые (тогда это называется переменная, a
6 и 3 — коэффициенты
a2 — переменная
Если перед переменной в уравнении нет коэффициента, это значит, что он равен 1.
Как умножать степень числа разным основанием. Как умножать степени, умножение степеней с разными показателями
В прошлом видеоуроке мы узнали, что степенью некоего основания называется такое выражение, которое представляет собой произведение основания на самого себя, взятого в количестве, равном показателю степени. Изучим теперь некоторые важнейшие свойства и операции степеней.
Например, умножим две разные степени с одинаковым основанием:
Представим это произведение в полном виде:
(2) 3 * (2) 2 = (2)*(2)*(2)*(2)*(2) = 32
Вычислив значение этого выражения, мы получим число 32. С другой стороны, как видно из этого же примера, 32 можно представить в виде произведения одного и того же основания (двойки), взятого в количестве 5 раз. И действительно, если пересчитать, то:
Таким образом, можно с уверенностью прийти к выводу, что:
(2) 3 * (2) 2 = (2) 5
Подобное правило успешно работает для любых показателей и любых оснований. Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.
Это свойство умножения степени вытекает из правила сохранности значения выражений при преобразованиях в произведении. При любом основании а произведение двух выражений (а)х и (а)у равно а(х + у). Иначе говоря, при произведении любых выражений с одинаковым основанием, итоговый одночлен имеет суммарную степень, образующуюся сложением степени первого и второго выражений.
Представляемое правило прекрасно работает и при умножении нескольких выражений. Главное условие — что бы основания у всех были одинаковыми. Например:
(2) 1 * (2) 3 * (2) 4 = (2) 8
Нельзя складывать степени, да и вообще проводить какие-либо степенные совместные действия с двумя элементами выражения, если основания у них являются разными.
Как показывает наше видео, в силу схожести процессов умножения и деления правила сложения степеней при произведении прекрасно передаются и на процедуру деления. Рассмотрим такой пример:
Произведем почленное преобразование выражения в полный вид и сократим одинаковые элементы в делимом и делителе:
(2)*(2)*(2)*(2)*(2)*(2) / (2)*(2)*(2)*(2) = (2)(2) = (2) 2 = 4
Конечный результат этого примера не так интересен, ведь уже в ходе его решения ясно, что значение выражения равно квадрату двойки. И именно двойка получается при вычитании степени второго выражения из степени первого.
И именно двойка получается при вычитании степени второго выражения из степени первого.
Чтобы определить степень частного необходимо из степени делимого вычесть степень делителя. Правило работает при одинаковом основании для всех его значений и для всех натуральных степеней. В виде абстракции имеем:
(а) х / (а) у = (а) х — у
Из правила деления одинаковых оснований со степенями вытекает определение для нулевой степени. Очевидно, что следующее выражение имеет вид:
(а) х / (а) х = (а) (х — х) = (а) 0
С другой стороны, если мы произведем деление более наглядным способом, то получим:
(а) 2 / (а) 2 = (а) (а) / (а) (а) = 1
При сокращении всех видимых элементов дроби всегда получается выражение 1/1, то есть, единица. Поэтому принято считать, что любое основание, возведенное в нулевую степень, равно единице:
Вне зависимости от значения а.
Однако будет абсурдно, если 0 (при любых перемножениях дающий все равно 0) будет каким-то образом равен единице, поэтому выражение вида (0) 0 (ноль в нулевой степени) просто не имеет смысла, а к формуле (а) 0 = 1 добавляют условие: «если а не равно 0».
Решим упражнение. Найдем значение выражения:
(34) 7 * (34) 4 / (34) 11
Так как основание везде одинаково и равно 34, то итоговое значение будет иметь такое же основание со степенью (согласно вышеуказанных правил):
Иначе говоря:
(34) 7 * (34) 4 / (34) 11 = (34) 0 = 1
Ответ: выражение равно единице.
Если умножаются (или делятся) две степени, у которых разные основания, но одинаковые показатели, то их основания можно перемножить (или поделить), а показатель степени у результата оставить таким же как у множителей (или делимого и делителя).
В общем виде на математическом языке эти правила записываются так:
a m × b m = (ab) m
a m ÷ b m = (a/b) m
При делении b не может быть равно 0, то есть второе правило надо дополнить условием b ≠ 0.
Примеры:
2 3 × 3 3 = (2 × 3) 3 = 63 = 36 × 6 = 180 + 36 = 216
6 5 ÷ 3 5 = (6 ÷ 3) 5 = 2 5 = 32
Теперь на этих конкретных примерах докажем, что правила-свойства степеней с одинаковыми показателями верны. Решим данные примеры так, как будто мы не знаем о свойствах степеней:
Решим данные примеры так, как будто мы не знаем о свойствах степеней:
2 3 × 3 3 = (2 × 2 × 2) × (3 × 3 × 3) = 2 × 2 × 2 × 3 × 3 × 3 = 8 × 27 = 160 + 56 = 216
65 ÷ 35 = (6 × 6 × 6 × 6 × 6) ÷ (3 × 3 × 3 × 3 × 3) == 2 × 2 × 2 × 2 × 2 = 32
Как мы видим, ответы совпали с теми, которые были получены, когда использовались правила. Знание этих правил позволяет упростить вычисления.
Обратите внимание, что выражение 2 × 2 × 2 × 3 × 3 × 3 можно представить в таком виде:
(2 × 3) × (2 × 3) × (2 × 3).
Это выражение в свою очередь есть нечто иное как (2 × 3) 3. то есть 6 3 .
Рассмотренные свойства степеней с одинаковыми показателями могут быть использованы в обратную сторону. Например, сколько будет 18 2 ?
18 2 = (3 × 3 × 2) 2 = 3 2 × 3 2 × 2 2 = 9 × 9 × 4 = 81 × 4 = 320 + 4 = 324
Свойства степеней также используются при решении примеров:
= 2 4 × 3 6 = 2 4 × 3 4 × 3 × 3 = 6 4 × 3 2 = 6 2 × 6 2 × 3 2 = (6 × 6 × 3) 2 = 108 2 = 108 × 108 = 108 (100 + 8) = 10800 + 864 = 11664
Правило деления степеней. При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. Примеры:
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя. Примеры:
Слайд 11 из презентации «Деление и умножение степеней» к урокам алгебры на тему «Степень»
Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке алгебры, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Деление и умножение степеней.ppt» можно в zip-архиве размером 1313 КБ.
«Деление и умножение степеней» — a2 a3 = a2+3 = a5. a3 = a · a · a. Найдем произведение a2 и a3. 100. 2+3. 5 раз. 64 = 144 = 1 0000 =. Умножение и деление степеней. 3 раза. a2 a3 =.
«Степени двойки» — 1024+. Правила перевода из одной системы счисления в другую. Гусельникова Е.В. Школа №130. Содержание. Таблица степеней двойки. Переведём число 1998 из десятичной в двоичную систему. Кислых В.Н. 11Э Зинько К.О. 11Э. Преподаватель: Выполнили: Рассмотрим схему преобразования на примере.
«Степень с отрицательным показателем» — Степень с отрицательным показателем. 5 12?3 (27?3). -2. -1. Вычислите: -3.
«Степень с рациональным показателем» — по теме: «Степень с рациональным показателем». Цели урока: I. Организационная часть. Проверка домашнего задания 1.Математический диктант 2. Взаимопроверка III.Самостоятельная работа IV. Обобщающий урок. Ход урока. Подготовка к контрольной работе V. Подведение итогов урока VI. II.
«Степень с целым показателем» — Представьте выражение в виде степени. X-12. Расположите в порядке убывания. Представьте выражение x-12 в виде произведения двух степеней с основанием x, если один множитель известен. Вычислите. Упростите.
«Свойства степени» — Обобщение знаний и умений по применению свойств степени с натуральным показателем. Вычислительная пауза. Свойства степени с натуральным показателем. Проверь себя! Применение знаний для решения различных по сложности задач. Тест. Физминутка. Развитие настойчивости, мыслительной активности и творческой деятельности.
Правило деление степеней
1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):
(abc…) n = a n b n c n …
Пример 1. (7 2 10) 2 = 7 2 2 2 10 2 = 49 4 100 = 19600. Пример 2. (x 2 –a 2) 3 = [(x +a)(x — a)] 3 =(x +a) 3 (x — a) 3
Практически более важно обратное преобразование:
a n b n c n … = (abc…) n
т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.
Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2) 2 =[(a +b)(a 2 – ab +b 2)] 2 =(a 3 +b 3) 2
2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:
Пример 5. Пример 6.
Обратное преобразование:. Пример 7.. Пример 8..
3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:
Пример 9.2 2 2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .
4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого
Пример 11. 12 5:12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3:(x-y) 2 =x-y.
5. При возведении степени в степень показатели степеней перемножаются:
Пример 13. (2 3) 2 =2 6 =64. Пример 14.
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 . 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Алгебра – 7 класс.
 n$.
n$. mathematics-tests.com
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.

П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т. e. 1 = 1, откуда следует,
e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
- Правила техники безопасности при работе утюгом Правила техники безопасности при работе утюгом. 1.Перед включением утюга в электросеть нужно проверить изоляцию шнура и положение утюга на подставке. 2.Включение и […]
- Проблемы водного налога Состояние, анализ и проблемы совершенствования водного налога При заборе воды сверх установленных квартальных (годовых) лимитов водопользования налоговые ставки в части такого превышения […]
- как составить приказ о переходе с 223фз на 44 фз Сергей Антонов 30 Ответ написан год назад Профессор 455 Ответ написан год назад Например: приказ об отмене применения положения о закупках. Оценка ответа: 0 Добавить […]
- Деление отрицательных чисел Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению. Если « a » и « b » положительные числа, то разделить число « a » на число « […]
- Разрешения D1, 960Н, 720Р, 960Р, 1080Р
Системы видеонаблюдения получают все большее распространение по всему миру.
 Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […]
Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […] - Конституционное право Российской Федерации. Баглай М.В. 6-е изд., изм. и доп. — М.: Норма, 200 7 . — 7 84 с. Настоящий учебник, представляющий собой шестое, измененное и дополненное, издание, написан известным […]
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .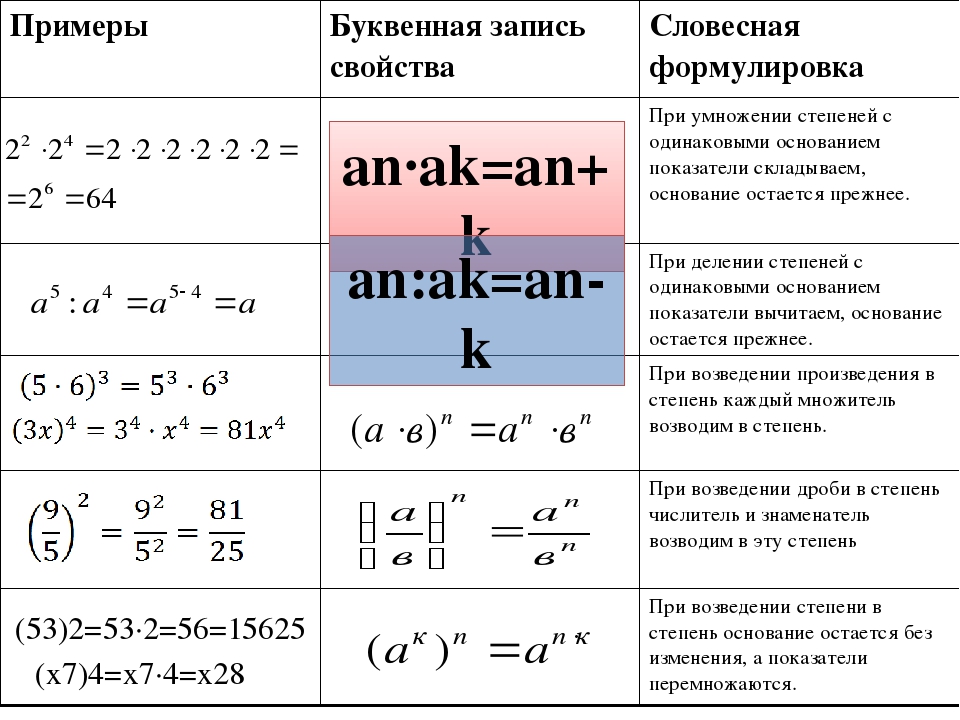
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а . 3 = 8
.
3 = 8
.
Примеры для решения:
Возведение в степень презентация
Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
среда, 4 июля 2018 г.
Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.
Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.
Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.
Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.
Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».
воскресенье, 18 марта 2018 г.
Сумма цифр числа — это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.
Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.
1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.
2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки — это не математическое действие.
3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.
Это не математическое действие.
4. Складываем полученные числа. Вот это уже математика.
Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё.
С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.
Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.
Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.
Ой! А это разве не женский туалет?
— Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?
Какой еще туалет?
Женский… Нимб сверху и стрелочка вниз — это мужской.
Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,
Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:
Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
1А — это не «минус четыре градуса» или «один а». Это «какающий человек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.
Со школы всем нам известно правило о возведении в степень: любое число с показателем N равно результату перемножения данного числа на самого себя N-ное количество раз. Иными словами, 7 в степени 3 — это 7, умноженное на себя три раза, то есть 343. Еще одно правило — возведение любой величины в степень 0 дает единицу, а возведение отрицательной величины представляет собой результат обычного возведения в степень, если она четная, и такой же результат со знаком «минус», если она нечетная.
Иными словами, 7 в степени 3 — это 7, умноженное на себя три раза, то есть 343. Еще одно правило — возведение любой величины в степень 0 дает единицу, а возведение отрицательной величины представляет собой результат обычного возведения в степень, если она четная, и такой же результат со знаком «минус», если она нечетная.
Правила же дают и ответ, как возводить число в отрицательную степень. Для этого нужно возвести обычным способом нужную величину на модуль показателя, а потом единицу поделить на результат.
Из этих правил становится понятно, что выполнение реальных задач с оперированием большими величинами потребует наличия технических средств. Вручную получится перемножить на самого себя максимум диапазон чисел до двадцати-тридцати, и то не более трех-четырех раз. Это не говоря уж о том, чтобы потом еще и единицу разделить на результат. Поэтому тем, у кого нет под рукой специального инженерного калькулятора, мы расскажем, как возвести число в отрицательную степень в Excel.
Решение задач в Excel
Для разрешения задач с возведением в степень Excel позволяет пользоваться одним из двух вариантов. -C2.
-C2.
Второй вариант — использование готовой функции «Степень», принимающей два обязательных аргумента — число и показатель. Чтобы приступить к ее использованию, достаточно в любой свободной ячейке поставить знак «равно» (=), указывающий на начало формулы, и ввести вышеприведенные слова. Осталось выбрать две ячейки, которые будут участвовать в операции (или указать конкретные числа вручную), и нажать на клавишу Enter. Посмотрим на нескольких простых примерах.
Формула | Результат | |||
СТЕПЕНЬ(B2;C2) | ||||
СТЕПЕНЬ(B3;C3) |
Как видим, нет ничего сложного в том, как возводить число в отрицательную степень и в обычную с помощью Excel. Ведь для решения данной задачи можно пользоваться как привычным всем символом «крышечка», так и удобной для запоминания встроенной функцией программы. Это несомненный плюс!
Ведь для решения данной задачи можно пользоваться как привычным всем символом «крышечка», так и удобной для запоминания встроенной функцией программы. Это несомненный плюс!
Перейдем к более сложным примерам. Вспомним правило о том, как возводить число в отрицательную степень дробного характера, и увидим, что эта задача очень просто решается в Excel.
Дробные показатели
Если кратко, то алгоритм вычисления числа с дробным показателем следующий.
- Преобразовать дробный показатель в правильную или неправильную дробь.
- Возвести наше число в числитель полученной преобразованной дроби.
- Из полученного в предыдущем пункте числа вычислить корень, с условием, что показателем корня будет знаменатель дроби, полученной на первом этапе.
Согласитесь, что даже при оперировании малыми числами и правильными дробями подобные вычисления могут занять немало времени. Хорошо, что табличному процессору Excel без разницы, какое число и в какую степень возводить. C$3».
C$3».
Число / Степень | |||||
Обратите внимание, что положительные числа (даже нецелые) без проблем вычисляются при любых показателях. {a}ix=cosax+isinax}
, где i = (− 1) {\displaystyle i={\sqrt {(}}-1)}
; е — константа, примерно равная 2,7; а — произвольная постоянная. Доказательство этого равенства можно найти в любом учебнике по высшей математике.
{a}ix=cosax+isinax}
, где i = (− 1) {\displaystyle i={\sqrt {(}}-1)}
; е — константа, примерно равная 2,7; а — произвольная постоянная. Доказательство этого равенства можно найти в любом учебнике по высшей математике.
Предупреждения
- При увеличении показателя степени ее значение сильно возрастает. Поэтому если ответ кажется вам неправильным, на самом деле он может оказаться верным. Вы можете проверить это, построив график любой показательной функции, например, 2 x .
Сложение и вычитание чисел с разными степенями. Правило умножение степеней с разными основаниями
Урок на тему: «Правила умножения и деления степеней с одинаковыми и разными показателями. Примеры»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой. 3=8$.
3=8$.
Деление степеней с одинаковым основанием. Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями.
3.a-3 есть a0 = 1, второй числитель. В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. Теперь рассмотрим их на конкретных примерах и попробуем доказать.
Таким образом мы доказали, что при делении двух степеней с одинаковыми основаниями, их показатели надо вычитать. После того как определена степень числа, логично поговорить про свойства степени.
Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Приведем пример, подтверждающий основное свойство степени. Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке.
Свойства степеней с натуральными показателями
Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями. Для наглядности покажем это свойство на примере. Например, для любых натуральных чисел p, q, r и s справедливо равенство. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
Сложение и вычитание одночленов
Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. Достаточно очевидно, что для любого натурального n при a=0 степень an есть нуль. Действительно, 0n=0·0·…·0=0. К примеру, 03=0 и 0762=0. Переходим к отрицательным основаниям степени. Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m, где m — натуральное.
Переходим к доказательству этого свойства. Докажем, что при m>n и 0Осталось доказать вторую часть свойства. Следовательно, am−an>0 и am>an, что и требовалось доказать. Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами.
Если p=0, то имеем (a0)q=1q=1 и a0·q=a0=1, откуда (a0)q=a0·q. По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно.
При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Эти неравенства по свойствам корней можно переписать соответственно как и. А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно.
Основные свойства логарифмов
Вычисление значения степени называют действием возведения в степень. 1. Если Вы теперь аккуратно воспользуетесь свойствами степеней (при возведении степени в степень показатели…
1. Если Вы теперь аккуратно воспользуетесь свойствами степеней (при возведении степени в степень показатели…
То есть показатели степени действительно вычитаются, но, поскольку в знаменателе у степени показатель отрицательный, при вычитании минус на минус даёт плюс, и показатели складываются. Вспомним, что называется одночленом, и какие операции можно делать с одночленами. Напомним, что для приведения одночлена к стандартному виду необходимо вначале получить численный коэффициент, перемножив все численные множители, а после этого перемножить соответствующие степени.
Переход к новому основанию
То есть, мы должны научиться различать подобные и не подобные одночлены. Сделаем вывод: подобные одночлены имеют одинаковую буквенную часть, и такие одночлены можно складывать и вычитать.
Спасибо Вам за отзыв. Если наш проект вам понравился и вы готовы помочь или принять участие в нём, перешлите информацию о проекте знакомым и коллегам. В предыдущем видео говорилось,что в примерах с одночленами может быть только умножение:»Найдем отличие этих выражений от предыдущих.
Само понятие одночлена как математической единицы подразумевает только умножение чисел и переменных, если есть другие операции, выражение уже не будет одночленом. Но вместе с тем между собой одночлены можно складывать, вычитать, делить… Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают! Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
То есть, свойство натуральной степени n произведения k множителей записывается как (a1·a2·…·ak)n=a1n·a2n·…·akn. Правил относительно сложения и вычитания степеней с одинаковыми основаниями не существует. Основание и аргумент первого логарифма — точные степени. 4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю.
Основание и аргумент первого логарифма — точные степени. 4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю.
Каждая арифметическая операция порою становится слишком громоздкой для записи и её стараются упростить. Когда-то так было и с операцией сложения. Людям было необходимо проводить многократное однотипное сложение, например, посчитать стоимость ста персидских ковров, стоимость которого составляет 3 золотые монеты за каждый. 3+3+3+…+3 = 300. Из-за громоздкости было придумано сократить запись до 3 * 100 = 300. Фактически, запись «три умножить на сто» означает, что нужно взять сто троек и сложить между собой. Умножение прижилось, обрело общую популярность. Но мир не стоит на месте, и в средних веках возникла необходимость проводить многократное однотипное умножение. Вспоминается старая индийская загадка о мудреце, попросившем в награду за выполненную работу пшеничные зёрна в следующем количестве: за первую клетку шахматной доски он просил одно зерно, за вторую – два, третью – четыре, пятую – восемь и так далее. 3. В остальном, когда различные основания и показатели, произвести полное умножение нельзя. Иногда можно частично упростить или прибегнуть к помощи вычислительной техники.
3. В остальном, когда различные основания и показатели, произвести полное умножение нельзя. Иногда можно частично упростить или прибегнуть к помощи вычислительной техники.
Степень с отрицательным показателем. Деление степеней с одинаковым основанием. 4. Уменьшите показатели степеней 2a4/5a3 и 2/a4 и приведите к общему знаменателю. Основание и аргумент первого логарифма — точные степени. Данное свойство распространяется на степень произведения трех и большего количества множителей. Следовательно, am−an>0 и am>an, что и требовалось доказать. Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке. То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным. Вычисление значения степени называют действием возведения в степень. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).
После того как определена степень числа, логично поговорить про свойства степени. В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров. Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами.
Приведем пример, подтверждающий основное свойство степени. Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Основное свойство дроби позволяет записать равенство am−n·an=a(m−n)+n=am.
Переход к новому основанию
То есть, свойство натуральной степени n произведения k множителей записывается как (a1·a2·…·ak)n=a1n·a2n·…·akn. Для наглядности покажем это свойство на примере. Доказательство можно провести, используя предыдущее свойство. Например, для любых натуральных чисел p, q, r и s справедливо равенство. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
Доказательство можно провести, используя предыдущее свойство. Например, для любых натуральных чисел p, q, r и s справедливо равенство. Для большей ясности приведем пример с конкретными числами: (((5,2)3)2)5=(5,2)3+2+5=(5,2)10.
Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. Достаточно очевидно, что для любого натурального n при a=0 степень an есть нуль. Действительно, 0n=0·0·…·0=0. К примеру, 03=0 и 0762=0. Переходим к отрицательным основаниям степени. Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m, где m — натуральное.
Переходим к доказательству этого свойства. Докажем, что при m>n и 0По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При этом условию p>q будет соответствовать условие m1>m2, что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями.
Операции с корнями. Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем;нодействиясостепенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения. Если мы хотим, чтобы формула a m: a n=a m — nбыла справедлива при m = n,нам необходимо определение нулевой степени. Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать.
Вынесение показателя степени из логарифма
Если основания разные, эти правила не работают! Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств. Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами. Часто в процессе решения требуется представить число как логарифм по заданному основанию.
Часто в процессе решения требуется представить число как логарифм по заданному основанию.
Свойства степеней, формулировки, доказательства, примеры.
Число n может быть абсолютно любым, ведь это просто значение логарифма. Она так и называется: основное логарифмическое тождество. Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением. В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма.
Примеры решения примеров с дробями, содержащими числа со степенями
Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице. 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения. Вот и все свойства. Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Логарифмическая единица и логарифмический ноль
2. a-4 есть a-2 первый числитель. В этом случае советуем поступать следующим образом. Это действие третьей ступени. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0n=0, а при знакомстве с делением мы условились, что на нуль делить нельзя. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями.
a-4 есть a-2 первый числитель. В этом случае советуем поступать следующим образом. Это действие третьей ступени. Например, основное свойство дроби am·an=am+n при упрощении выражений часто применяется в виде am+n=am·an. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0n=0, а при знакомстве с делением мы условились, что на нуль делить нельзя. Из полученного равенства am−n·an=am и из связи умножения с делением следует, что am−n является частным степеней am и an. Этим доказано свойство частного степеней с одинаковыми основаниями.
Аналогично, если q=0, то (ap)0=1 и ap·0=a0=1, откуда (ap)0=ap·0. В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. Эти неравенства по свойствам корней можно переписать соответственно как и. А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно.
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби. 5}$. Ответ: $\frac{2x}{1}$ или 2x.
5}$. Ответ: $\frac{2x}{1}$ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.
Умножение и деление степеней, алгебра, 7 класс
Дата публикации: .
Урок на тему: «Правила умножения и деления степеней с одинаковыми и разными показателями. Примеры»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. 3=8$.
3=8$.
Как перемножить разные числа с одинаковыми степенями. Формулы степеней и корней
Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно — разность квадратов! Получаем:
Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило.
Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.
Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках.
Но важно запомнить: меняются все знаки одновременно !
Вернемся к примеру:
И снова формула:
Целыми мы называем натуральные числа, противоположные им (то есть взятые со знаком « ») и число.
целое положительное число , а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе.
А теперь давайте рассмотрим новые случаи. Начнем с показателя, равного.
Любое число в нулевой степени равно единице :
Как всегда, зададимся вопросом: почему это так?
Рассмотрим какую-нибудь степень с основанием. Возьмем, например, и домножим на:
Итак, мы умножили число на, и получили то же, что и было — . А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на. Значит.
Можем проделать то же самое уже с произвольным числом:
Повторим правило:
Любое число в нулевой степени равно единице.
Но из многих правил есть исключения. И здесь оно тоже есть — это число (в качестве основания).
С одной стороны, в любой степени должен равняться — сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, как и любое число в нулевой степени, должен равняться. Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.
Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.
Поехали дальше. Кроме натуральных чисел и числа к целым относятся отрицательные числа. Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:
Отсюда уже несложно выразить искомое:
Теперь распространим полученное правило на произвольную степень:
Итак, сформулируем правило:
Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: (т.к. на делить нельзя).
Подведем итоги:
I. Выражение не определено в случае. Если, то.
II. Любое число в нулевой степени равно единице: .
III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: .
Ну и, как обычно, примеры для самостоятельного решения:
Разбор задач для самостоятельного решения:Знаю-знаю, числа страшные, но на ЕГЭ надо быть готовым ко всему! Реши эти примеры или разбери их решение, если не смог решить и ты научишься легко справляться с ними на экзамене!
Продолжим расширять круг чисел, «пригодных» в качестве показателя степени.
Теперь рассмотрим рациональные числа. Какие числа называются рациональными?
Ответ: все, которые можно представить в виде дроби, где и — целые числа, причем.
Чтобы понять, что такое «дробная степень» , рассмотрим дробь:
Возведем обе части уравнения в степень:
Теперь вспомним правило про «степень в степени» :
Какое число надо возвести в степень, чтобы получить?
Эта формулировка — определение корня -ой степени.
Напомню: корнем -ой степени числа () называется число, которое при возведении в степень равно.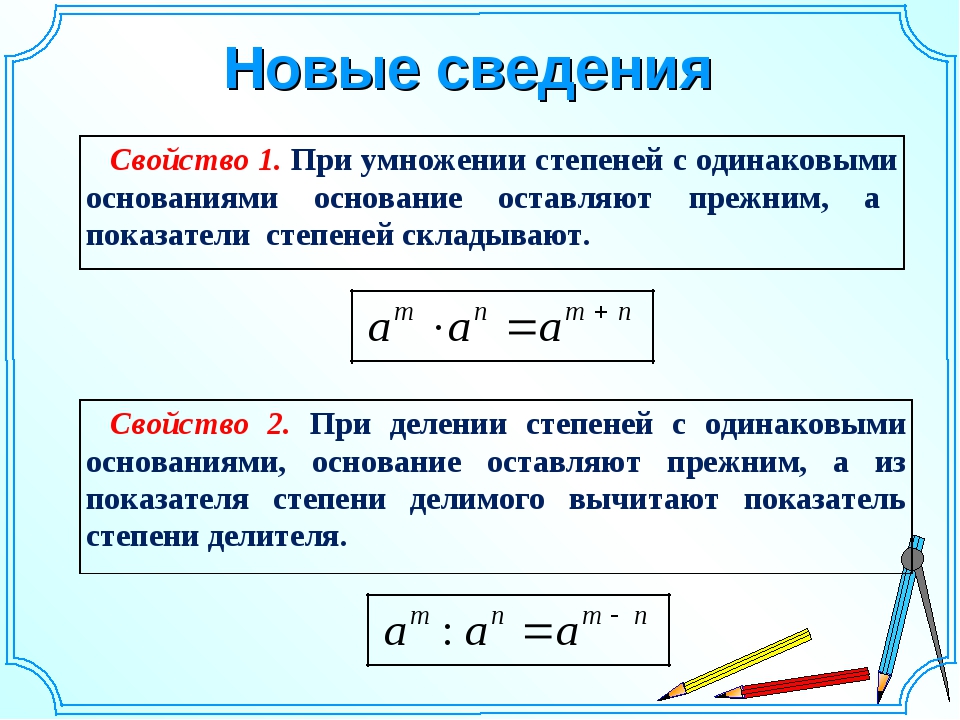
То есть, корень -ой степени — это операция, обратная возведению в степень: .
Получается, что. Очевидно, этот частный случай можно расширить: .
Теперь добавляем числитель: что такое? Ответ легко получить с помощью правила «степень в степени»:
Но может ли основание быть любым числом? Ведь корень можно извлекать не из всех чисел.
Никакое!
Вспоминаем правило: любое число, возведенное в четную степень — число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!
А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение не имеет смысла.
А что насчет выражения?
Но тут возникает проблема.
Число можно представить в виде дргих, сократимых дробей, например, или.
И получается, что существует, но не существует, а ведь это просто две разные записи одного и того же числа.
Или другой пример: раз, то можно записать. Но стоит нам по-другому записать показатель, и снова получим неприятность: (то есть, получили совсем другой результат!).
Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем .
Итак, если:
- — натуральное число;
- — целое число;
Примеры:
Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:
5 примеров для тренировкиРазбор 5 примеров для тренировки
1. Не забываем об обычных свойствах степеней:
2. . Здесь вспоминаем, что забыли выучить таблицу степеней:
ведь — это или. Решение находится автоматически: .
Ну а теперь — самое сложное. Сейчас мы разберем степень с иррациональным показателем .
Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением
Ведь по определению иррациональные числа — это числа, которые невозможно представить в виде дроби, где и — целые числа (то есть, иррациональные числа — это все действительные числа кроме рациональных).
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.
Например, степень с натуральным показателем — это число, несколько раз умноженное само на себя;
…число в нулевой степени — это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось — поэтому результатом является только некая «заготовка числа», а именно число;
…степень с целым отрицательным показателем — это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число.
Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
КУДА МЫ УВЕРЕНЫ ТЫ ПОСТУПИШЬ! (если научишься решать такие примеры:))
Например:
Реши самостоятельно: Разбор решений:1. Начнем с уже обычного для нас правила возведения степени в степень:
Начнем с уже обычного для нас правила возведения степени в степень:
Теперь посмотри на показатель. Ничего он тебе не напоминает? Вспоминаем формулу сокращенного умножения разность квадратов:
В данном случае,
Получается, что:
Ответ: .
2. Приводим дроби в показателях степеней к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например:
Ответ: 16
3. Ничего особенного, применяем обычные свойства степеней:
ПРОДВИНУТЫЙ УРОВЕНЬ
Определение степени
Степенью называется выражение вида: , где:
- — основание степени;
- — показатель степени.
Степень с натуральным показателем {n = 1, 2, 3,…}
Возвести число в натуральную степень n — значит умножить число само на себя раз:
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
Возведение в нулевую степень :
Выражение неопределенное, т. к., с одной стороны, в любой степени — это, а с другой — любое число в -ой степени — это.
к., с одной стороны, в любой степени — это, а с другой — любое число в -ой степени — это.
Если показателем степени является целое отрицательное число:
(т.к. на делить нельзя).
Еще раз о нулях: выражение не определено в случае. Если, то.
Примеры:
Степень с рациональным показателем
- — натуральное число;
- — целое число;
Примеры:
Свойства степеней
Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.
Посмотрим: что такое и?
По определению:
Итак, в правой части этого выражения получается такое произведение:
Но по определению это степень числа с показателем, то есть:
Что и требовалось доказать.
Пример : Упростите выражение.
Решение : .
Пример : Упростите выражение.
Решение : Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием мы объединяем, а остается отдельным множителем:
Поэтому степени с основанием мы объединяем, а остается отдельным множителем:
Еще одно важное замечание: это правило — только для произведения степеней !
Ни в коем случае нелья написать, что.
Так же, как и с предыдущим свойством, обратимся к определению степени:
Перегруппируем это произведение так:
Получается, что выражение умножается само на себя раз, то есть, согласно определению, это и есть -я степень числа:
По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: !
Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать? Но это неверно, ведь.
Степень с отрицательным основанием.До этого момента мы обсуждали только то, каким должен быть показатель степени. Но каким должно быть основание? В степенях с натуральным показателем основание может быть любым числом .
И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже. Давайте подумаем, какие знаки (« » или « ») будут иметь степени положительных и отрицательных чисел?
Давайте подумаем, какие знаки (« » или « ») будут иметь степени положительных и отрицательных чисел?
Например, положительным или отрицательным будет число? А? ?
С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.
Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть, или. Но если мы умножим на (), получится — .
И так до бесконечности: при каждом следующем умножении знак будет меняться. Можно сформулировать такие простые правила:
- четную степень, — число положительное .
- Отрицательное число, возведенное в нечетную степень, — число отрицательное .
- Положительное число в любой степени — число положительное.
- Ноль в любой степени равен нулю.
Определи самостоятельно, какой знак будут иметь следующие выражения:
Справился? Вот ответы:
1) ; 2) ; 3) ; 4) ; 5) ; 6) .
В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.
В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание — степень четная, а значит, результат всегда будет положительным. Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Очевидно нет, так как (потому что).
Пример 6) уже не так прост. Тут нужно узнать, что меньше: или? Если вспомнить, что, становится ясно, что, а значит, основание меньше нуля. То есть, применяем правило 2: результат будет отрицательным.
И снова используем определение степени:
Все как обычно — записываем определение степеней и, делим их друг на друга, разбиваем на пары и получаем:
Прежде чем разобрать последнее правило, решим несколько примеров.
Вычисли значения выражений:
Решения :
Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно — разность квадратов!
Итак, вспомнили? Это формула сокращенного умножения, а именно — разность квадратов!
Получаем:
Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило 3. Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.
Если домножить его на, ничего не поменяется, верно? Но теперь получается следующее:
Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках. Но важно запомнить: меняются все знаки одновременно! Нельзя заменить на, изменив только один неугодный нам минус!
Вернемся к примеру:
И снова формула:
Итак, теперь последнее правило:
Как будем доказывать? Конечно, как обычно: раскроем понятие степени и упростим:
Ну а теперь раскроем скобки. Сколько всего получится букв? раз по множителей — что это напоминает? Это не что иное, как определение операции умножения : всего там оказалось множителей. То есть, это, по определению, степень числа с показателем:
То есть, это, по определению, степень числа с показателем:
Пример:
Степень с иррациональным показателем
В дополнение к информации о степенях для среднего уровня, разберем степень с иррациональным показателем. Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением — ведь по определению иррациональные числа — это числа, которые невозможно представить в виде дроби, где и — целые числа (то есть, иррациональные числа — это все действительные числа, кроме рациональных).
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах. Например, степень с натуральным показателем — это число, несколько раз умноженное само на себя; число в нулевой степени — это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось — поэтому результатом является только некая «заготовка числа», а именно число; степень с целым отрицательным показателем — это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)
Например:
Реши самостоятельно:
Ответы:
- Вспоминаем формулу разность квадратов. Ответ: .
- Приводим дроби к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например: .
- Ничего особенного, применяем обычные свойства степеней:
КРАТКОЕ ИЗЛОЖЕНИЕ РАЗДЕЛА И ОСНОВНЫЕ ФОРМУЛЫ
Степенью называется выражение вида: , где:
Степень с целым показателем
степень, показатель которой — натуральное число (т. е. целое и положительное).
е. целое и положительное).
Степень с рациональным показателем
степень, показатель которой — отрицательные и дробные числа.
Степень с иррациональным показателем
степень, показатель которой — бесконечная десятичная дробь или корень.
Свойства степеней
Особенности степеней.
- Отрицательное число, возведенное в четную степень, — число положительное .
- Отрицательное число, возведенное в нечетную степень, — число отрицательное .
- Положительное число в любой степени — число положительное.
- Ноль в любой степени равен.
- Любое число в нулевой степени равно.
ТЕПЕРЬ ТЕБЕ СЛОВО…
Как тебе статья? Напиши внизу в комментариях понравилась или нет.
Расскажи о своем опыте использования свойств степеней.
Возможно у тебя есть вопросы. Или предложения.
Напиши в комментариях.
И удачи на экзаменах!
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом:
a n = a * a * a * …a n .
Например:
- 2 3 = 2 в третьей степ.
 = 2 * 2 * 2 = 8;
= 2 * 2 * 2 = 8; - 4 2 = 4 в степ. два = 4 * 4 = 16;
- 5 4 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
- 10 5 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
- 10 4 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- a n * a m = (a) (n+m) ;
- a n: a m = (a) (n-m) ;
- (a b) m =(a) (b*m) .
Проверим на примерах:
2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично: 2 3: 2 2 = 8 / 4 =2. Иначе 2 3-2 = 2 1 =2.
(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.
А как же быть со сложением и вычитанием ? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 3 3 + 2 4 = 27 + 16 = 43;
- 5 2 – 3 2 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3) 2 = 2 2 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3) 3 = 8 3 = 512.
Как производить вычисления в более сложных случаях ? Порядок тот же:
- при наличии скобок – начинать нужно с них;
- затем возведение в степень;
- потом выполнять действия умножения, деления;
- после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: a m / n .
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b) n = a n * b n .
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?
Исходя из свойств 4 и 5 (смотри пункт выше), получается :
A (- n) = 1 / A n , 5 (-2) = 1 / 5 2 = 1 / 25.
И наоборот:
1 / A (- n) = A n , 1 / 2 (-3) = 2 3 = 8.
А если дробь?
(A / B) (- n) = (B / A) n , (3 / 5) (-2) = (5 / 3) 2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1…и т. д.
A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3…и т. д.
Кроме того, если (-a) 2 n +2 , n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.
Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: A m / n . Читается как: корень n-ой степени из числа A в степени m.
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;
А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 – рациональные числа;
В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
r 1 – в этом случае равно 3;
r 2 – будет равно 4.
Тогда, при А = 1, 1 π = 1.
А = 2, то 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16.
А = 1/2, то (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?
В алгебре найти произведение степеней можно в двух случаях:
1) если степени имеют одинаковые основания;
2) если степени имеют одинаковые показатели.
При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:
При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:
Рассмотрим, как умножать степени, на конкретных примерах.
Единицу в показателе степени не пишут, но при умножении степеней — учитывают:
При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:
В выражениях возведение в степень выполняется в первую очередь.
Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:
www.algebraclass.ru
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .
Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Так, сумма 2a 2 и 3a 2 равна 5a 2 .
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.
Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .
Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.
Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .
Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.
Так, a n .a m = a m+n .
Для a n , a берётся как множитель столько раз, сколько равна степень n;
И a m , берётся как множитель столько раз, сколько равна степень m;
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .
Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1
Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).
Это правило справедливо и для чисел, показатели степени которых — отрицательные .
1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.
2. y -n .y -m = y -n-m .
3. a -n .a m = a m-n .
Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.
Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
Таким образом a 3 b 2 делённое на b 2 , равно a 3 .
Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел.
При делении степеней с одинаковым основанием их показатели вычитаются. .
Так, y 3:y 2 = y 3-2 = y 1 . То есть, $\frac = y$.
И a n+1:a = a n+1-1 = a n . То есть $\frac = a^n$. 3$
3$
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.
2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.
3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .
4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .
5. Умножьте (a 3 + b)/b 4 на (a — b)/3.
6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).
7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .
8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2
Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.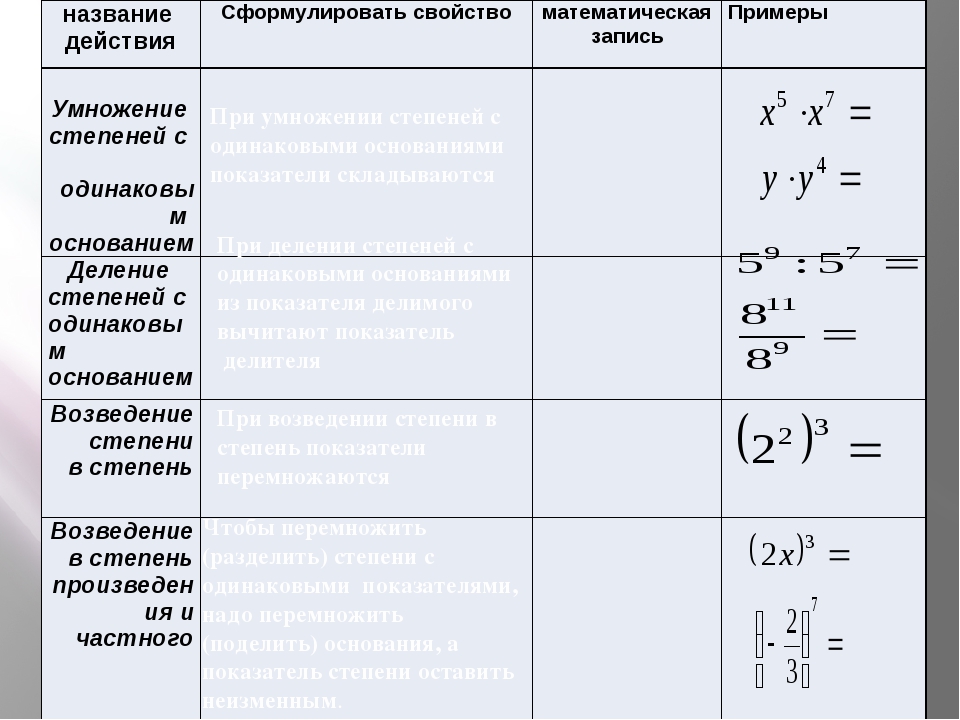
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3
Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5
Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.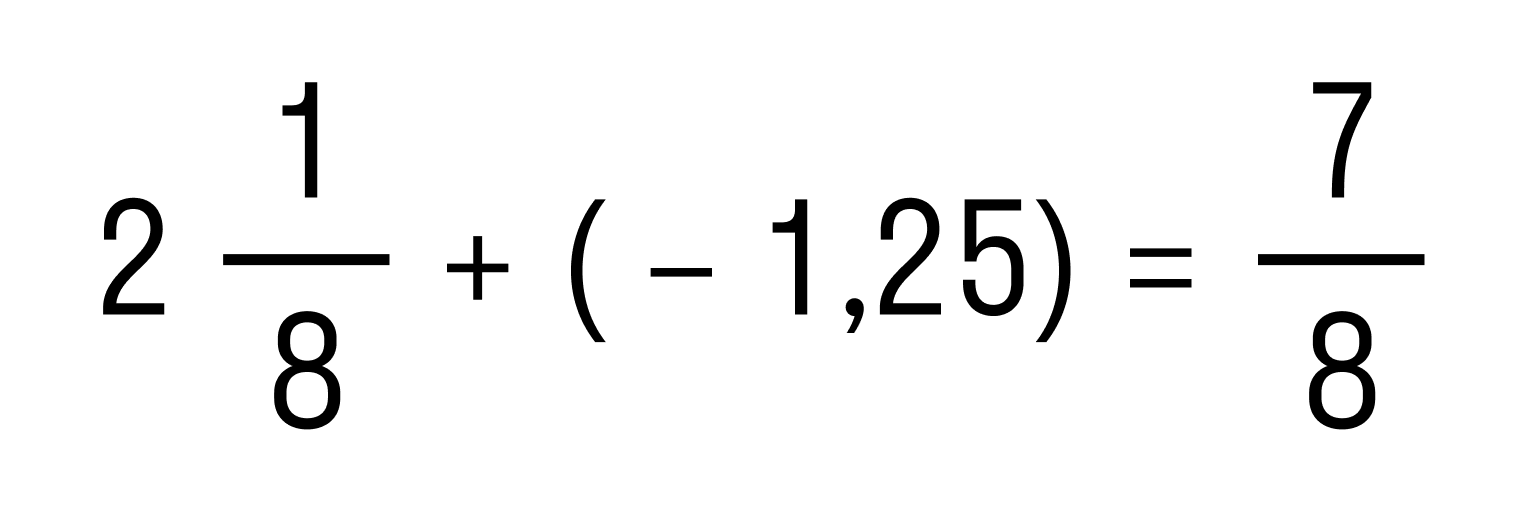
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
Правила умножения степеней с разным основанием
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§ 69. Умножение и деление степеней с одинаковыми основаниями
Умножение и деление степеней с одинаковыми основаниями
Теорема 1. Чтобы перемножить степени с одинаковыми основаниями, достаточно показатели степеней сложить, а основание оставить прежним , то есть
Доказательство. По определению степени
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
Мы рассмотрели произведение двух степеней. На самом же деле доказанное свойство верно для любого числа степеней с одинаковыми основаниями.
Теорема 2. Чтобы разделить степени с одинаковыми основаниями, когда показатель делимого больше показателя делителя, достаточно из показателя делимого вычесть показатель делителя, а основание оставить прежним, то есть при т > п
(a =/= 0)
Доказательство. Напомним, что частным от деления одного числа на другое называется число, которое при умножении на делитель дает делимое. Поэтому доказать формулу , где a =/= 0, это все равно, что доказать формулу
Если т > п , то число т — п будет натуральным; следовательно, по теореме 1
Теорема 2 доказана.
Следует обратить внимание на то, что формула
доказана нами лишь в предположении, что т > п . Поэтому из доказанного пока нельзя делать, например, таких выводов:
К тому же степени с отрицательными показателями нами еще не рассматривались и мы пока что не знаем, какой смысл можно придать выражению 3 — 2 .
Теорема 3. Чтобы возвести степень в степень, достаточно перемножить показатели, оставив основание степени прежним , то есть
Доказательство. Используя определение степени и теорему 1 этого параграфа, получаем:
что и требовалось доказать.
Например, (2 3) 2 = 2 6 = 64;
518 (Устно.) Определить х из уравнений:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;
2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .
519. (У с т н о. ) Упростить:
) Упростить:
520. (У с т н о.) Упростить:
521. Данные выражения представить в виде степеней с одинаковыми основаниями:
1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;
2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n
.
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
В предыдущей статье мы рассказали, что из себя представляют одночлены. В этом материале разберем, как решать примеры и задачи, в которых они применяются. Здесь будут рассмотрены такие действия, как вычитание, сложение, умножение, деление одночленов и возведение их в степень с натуральным показателем. Мы покажем, как определяются такие операции, обозначим основные правила их выполнения и то, что должно получится в результате.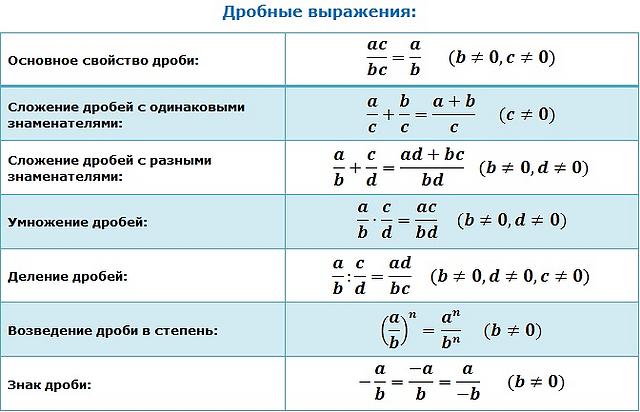 Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.
Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.
Удобнее всего работать со стандартной записью одночленов, поэтому все выражения, которые будут использованы в статье, мы приводим в стандартном виде. Если изначально они заданы иначе, рекомендуется сначала привести их к общепринятой форме.
Правила сложения и вычитания одночленов
Наиболее простые действия, которые можно проводить с одночленами – это вычитание и сложение. В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).
Когда мы складываем или вычитаем одночлены, сначала записываем в общепринятой форме соответствующую сумму и разность, после чего упрощаем получившееся выражение. Если есть подобные слагаемые, их нужно привести, скобки – раскрыть. Поясним на примере.
Пример 1
Условие: выполните сложение одночленов − 3 · x и 2 , 72 · x 3 · y 5 · z .
Решение
Запишем сумму исходных выражений.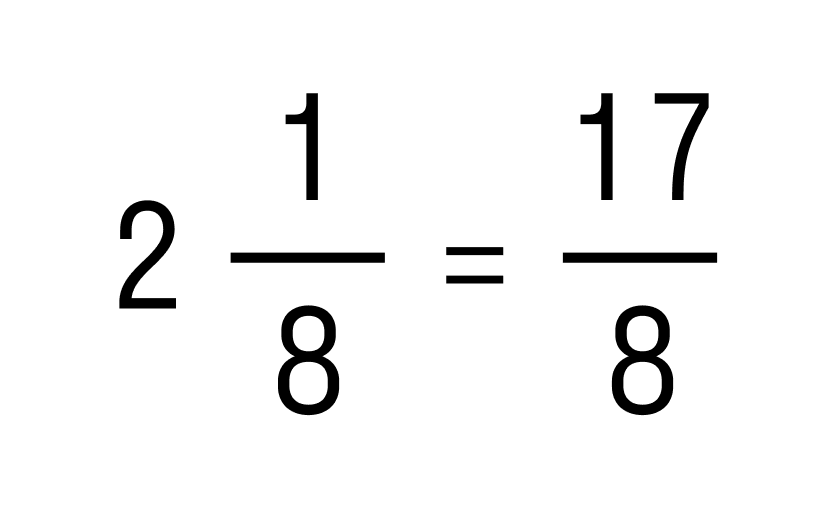 Добавим скобки и поставим между ними плюс. У нас получится следующее:
Добавим скобки и поставим между ними плюс. У нас получится следующее:
(− 3 · x) + (2 , 72 · x 3 · y 5 · z)
Когда мы выполним раскрытие скобок, получится — 3 · x + 2 , 72 · x 3 · y 5 · z . Это многочлен, записанный в стандартной форме, который и будет результатом сложения данных одночленов.
Ответ: (− 3 · x) + (2 , 72 · x 3 · y 5 · z) = − 3 · x + 2 , 72 · x 3 · y 5 · z .
Если у нас задано три, четыре и больше слагаемых, мы осуществляем это действие точно так же.
Пример 2
Условие: проведите в правильном порядке указанные действия с многочленами
3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c
Решение
Начнем с раскрытия скобок.
3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c
Мы видим, что полученное выражение можно упростить путем приведения подобных слагаемых:
3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = = (3 · a 2 + a 2 — 7 · a 2) + 4 · a · c — 2 2 3 · a · c + 4 9 = = — 3 · a 2 + 1 1 3 · a · c + 4 9
У нас получился многочлен, который и будет результатом данного действия.
Ответ: 3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = — 3 · a 2 + 1 1 3 · a · c + 4 9
В принципе, мы можем выполнить сложение и вычитание двух одночленов с некоторыми ограничениями так, чтобы получить в итоге одночлен. Для этого нужно соблюсти некоторые условия, касающиеся слагаемых и вычитаемых одночленов. О том, как это делается, мы расскажем в отдельной статье.
Правила умножения одночленов
Действие умножения не налагает никаких ограничений на множители. Умножаемые одночлены не должны соответствовать никаким дополнительным условиям, чтобы в результате получится одночлен.
Чтобы выполнить умножение одночленов, нужно выполнить следующие шаги:
- Правильно записать произведение.
- Раскрыть скобки в полученном выражении.
- Сгруппировать по возможности множители с одинаковыми переменными и числовые множители отдельно.
- Выполнить необходимые действия с числами и применить к оставшимся множителям свойство умножения степеней с одинаковыми основаниями.

Посмотрим, как это делается на практике.
Пример 3
Условие: выполните умножение одночленов 2 · x 4 · y · z и — 7 16 · t 2 · x 2 · z 11 .
Решение
Начнем с составления произведения.
Раскрываем в нем скобки и получаем следующее:
2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11
2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11
Все, что нам осталось сделать – это умножить числа в первых скобках и применить свойство степеней для вторых. В итоге получим следующее:
2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11 = — 7 8 · t 2 · x 4 + 2 · y · z 3 + 11 = = — 7 8 · t 2 · x 6 · y · z 14
Ответ: 2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11 = — 7 8 · t 2 · x 6 · y · z 14 .
Если у нас в условии стоят три многочлена и больше, мы умножаем их по точно такому же алгоритму. Более подробно вопрос умножения одночленов мы рассмотрим в рамках отдельного материала.
Правила возведения одночлена в степень
Мы знаем, что степенью с натуральным показателем называют произведение некоторого числа одинаковых множителей. На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.
На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.
Пример 4
Условие: выполните возведение одночлена − 2 · a · b 4 в степень 3 .
Решение
Мы можем заменить возведение в степень на умножение 3 -х одночленов − 2 · a · b 4 . Запишем и получим нужный ответ:
(− 2 · a · b 4) 3 = (− 2 · a · b 4) · (− 2 · a · b 4) · (− 2 · a · b 4) = = ((− 2) · (− 2) · (− 2)) · (a · a · a) · (b 4 · b 4 · b 4) = − 8 · a 3 · b 12
Ответ: (− 2 · a · b 4) 3 = − 8 · a 3 · b 12 .
А как быть в том случае, когда степень имеет большой показатель? Записывать большое количество множителей неудобно. Тогда для решения такой задачи нам надо применить свойства степени, а именно свойство степени произведения и свойство степени в степени.
Решим задачу, которую мы привели выше, указанным способом.
Пример 5
Условие: выполните возведение − 2 · a · b 4 в третью степень.
Решение
Зная свойство степени в степени, мы можем перейти к выражению следующего вида:
(− 2 · a · b 4) 3 = (− 2) 3 · a 3 · (b 4) 3 .
После этого мы возводим в степень — 2 и применяем свойство степени в степени:
(− 2) 3 · (a) 3 · (b 4) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .
Ответ: − 2 · a · b 4 = − 8 · a 3 · b 12 .
Возведению одночлена в степень мы также посвятили отдельную статью.
Правила деления одночленов
Последнее действие с одночленами, которое мы разберем в данном материале, – деление одночлена на одночлен. В результате мы должны получить рациональную (алгебраическую) дробь (в некоторых случаях возможно получение одночлена). Сразу уточним, что деление на нулевой одночлен не определяется, поскольку не определяется деление на 0.
Для выполнения деления нам нужно записать указанные одночлены в форме дроби и сократить ее, если есть такая возможность.
Пример 6
Условие: выполните деление одночлена − 9 · x 4 · y 3 · z 7 на − 6 · p 3 · t 5 · x 2 · y 2 .
Решение
Начнем с записи одночленов в форме дроби.
9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2
Эту дробь можно сократить. После выполнения этого действия получим:
3 · x 2 · y · z 7 2 · p 3 · t 5
Ответ: — 9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2 = 3 · x 2 · y · z 7 2 · p 3 · t 5 .
Условия, при которых в результате деления одночленов мы получим одночлен, приводятся в отдельной статье.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Сложение ⚠️ корней, вычитание корней с одинаковыми и разными показателями
ОпределениеДействие сложения и вычитания квадратных корней возможно лишь при условии одинаковости подкоренных выражений слагаемых.
Сложение корней, формулы
Складывать подобные квадратные корни, то есть иррациональные выражения с одинаковым основанием, очень просто. Для этого суммируют множители слагаемых, а подкоренное число остается неизменным:
Для этого суммируют множители слагаемых, а подкоренное число остается неизменным:
\(m\sqrt a+n\sqrt a=\left(m+n\right)\sqrt a\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В случае со сложением корней с разными подкоренными значениями нужно привести их к подобию. Упрощение корневых чисел выполняют по следующему алгоритму:
- Раскладывание подкоренного числа на два множителя так, чтобы один из них являлся числом, из которого извлекается целый квадратный корень.
- Извлечение корня из квадратного числа, запись ответа перед символом корня. Второй множитель остается под знаком корня.
- Упрощенные корни с одинаковым основанием можно складывать как подобные.
Пример
\(3\sqrt{50}+2\sqrt8+\sqrt{12}\)
\(3\sqrt{50}=3\sqrt{25\times2}=3\times5\sqrt2=15\sqrt2\)
\(2\sqrt8=2\sqrt{4\times2}=2\times2\sqrt2=4\sqrt2\)
\(\sqrt{12}\;=\sqrt{4\times3}=2\times1\sqrt2=2\sqrt2\)
После упрощения исходное выражение приобретает вид:
\(15\sqrt2+4\sqrt2+2\sqrt2=21\sqrt2\)
ПримечаниеПодкоренные выражения между собой не суммируются и не вычитаются. При этом выражения под одним корнем складываются и вычитаются как обычные числа.
При этом выражения под одним корнем складываются и вычитаются как обычные числа.
Вычитание корней, формулы
При вычитании подобных корней вычитаются их множители, а подкоренное выражение не меняется:
\(m\sqrt a-n\sqrt a=\left(m-n\right)\sqrt a\)
Чтобы узнать разность иррациональных чисел с разным основанием, нужно привести уменьшаемое и вычитаемое к единому образцу. Для этого используют тот же алгоритм, что и перед сложением.
Пример
\(4\sqrt{75}-3\sqrt{24}\)
\(4\sqrt{75}=4\sqrt{25\times3}=4\times5\sqrt3=20\sqrt3\)
\(3\sqrt{12}=3\sqrt{4\times3}=3\times2\sqrt3=6\sqrt3\)
Упростив, получаем:
\(20\sqrt3-6\sqrt3=14\sqrt3\)
Сложение корней со степенями
Складывание и вычитание корней с разными степенями, но одинаковым основанием имеет следующую последовательность:
Допустим, надо решить данное выражение:
\(\sqrt[3]а+\sqrt[4]а\)
Для начала проведем процедуру упрощения:
\(\sqrt[3]а+\sqrt[4]а=12\times\sqrt a^4+12\times\sqrt a^3\)
\(12\times\sqrt a^4+12\times\sqrt a^3=12\times\sqrt{a^4+a^3}\)
При приведении двух подобных членов к общему показателю корневого числа применяется одно из свойств корней. 2}=\left|а-2\right|+\left|а-4\right|\)
2}=\left|а-2\right|+\left|а-4\right|\)
Раскроем модули в промежутке \(2\leq а\leq4\):
\(\vert а-2\vert=а-2,\;т.к.\;а-2\geq0\)
\(\vert а-4\vert=4-а,\;т.к.\;а-4\leq0\)
Следовательно, \(\vert а-2\vert+\vert а-4\vert=а-2+4-а=2\)
Ответ: 2.
Сложение и вычитание с экспонентами [Видео и практика]
Привет, ребята! Добро пожаловать в этот видеоролик о сложении и вычитании с экспонентами.
Для начала, чтобы мы все были на одной странице, я собираюсь определить экспонентов , а также несколько других вещей, чтобы в дальнейшем, надеюсь, не было такой путаницы.
Итак, я начну с базы (или в данном случае переменной базы). Основание — это число, которое возводится в степень чего-либо, и это число называется показателем .3 \)
Итак, чтобы упростить этот процесс, мы должны искать две вещи. Во-первых, одинаковы ли наши базы (или переменные); и во-вторых, наши экспоненты такие же? Обе вещи должны быть правдой, чтобы мы могли сложить эти два термина вместе. Тот же самый процесс сложения и вычитания с показателями также называется объединением подобных терминов, что может показаться вам более знакомым. Что ж, это одно и то же.
Тот же самый процесс сложения и вычитания с показателями также называется объединением подобных терминов, что может показаться вам более знакомым. Что ж, это одно и то же.
Хорошо, оглядываясь назад на нашу проблему, мы видим, что наши базы совпадают, и наши показатели такие же.2 + 5 \)
На этом этапе все подобные термины были объединены, и мы не можем сделать никакого дальнейшего упрощения. Итак, мы закончили.
Надеюсь, это видео было полезным.
Увидимся в следующий раз!
Сложение экспонент — методы и примеры
Алгебра — один из основных курсов математики. Чтобы понять алгебру, важно знать, как использовать показатели и радикалы. Добавление показателей является частью учебной программы по алгебре, и по этой причине для учащихся важно иметь более прочную основу в математике.
Многие студенты часто путают сложение показателей степени со сложением чисел и, следовательно, в конечном итоге совершают ошибки. Эти недоразумения обычно влекут за собой различие в значении таких терминов, как возведение в степень и экспоненты.
Эти недоразумения обычно влекут за собой различие в значении таких терминов, как возведение в степень и экспоненты.
Прежде чем углубляться в советы о том, как добавлять показатели, давайте начнем с определения терминов для показателей. Начнем с того, что показатель степени — это просто многократное умножение числа на само себя. В математике эта операция называется возведением в степень.Следовательно, возведение в степень — это операция, включающая числа в форме b n , где b упоминается как основание, а число n — это показатель степени, или индекс, или степень . Например, x 4 содержит 4 в качестве показателя степени, а x называется базой.
Показатели иногда называют степенями чисел. Показатель показывает, сколько раз число должно быть умножено само на себя. Например, x 4 = x × x × x × x.
Как складывать экспоненты?
Для сложения показателей степени и переменные должны быть одинаковыми. Вы добавляете коэффициенты переменных, оставляя показатели без изменений. Добавляются только термины с одинаковыми переменными и полномочиями. Это правило согласуется также с умножением и делением экспонент.
Вы добавляете коэффициенты переменных, оставляя показатели без изменений. Добавляются только термины с одинаковыми переменными и полномочиями. Это правило согласуется также с умножением и делением экспонент.
Ниже приведены шаги для сложения показателей степени:
- Проверьте термины, если они имеют одинаковое основание и показатель степени
Например, 4 2 +4 2 , эти термины имеют одинаковое основание 4 и показатель степени 2.
- Вычисляйте каждый член по отдельности, если они имеют разное основание или показатель степени
Например, 3 2 + 4 3 , эти члены имеют разные показатели степени и основания.
- Сложите результаты.
Сложение показателей с разными показателями степени и основаниями
Сложение показателей осуществляется путем вычисления сначала каждого показателя, а затем добавления: Общая форма таких показателей: a n + b m .
Пример 1
- 4 2 + 2 5 = 4⋅4 + 2⋅2⋅2⋅2 = 16 + 32 = 48
- 8 3 + 9 2 = (8) (8) (8) + (9) (9) = 512 + 81 = 593
- 3 2 + 5 3 = (3) (3) + (5) (5) ) (5) = 9 + 125 = 134
- 6 2 + 6 3 = 252.
- 3 4 + 3 6 = 81 + 729 = 810.
Сложение показателей с одинаковыми основаниями и показателями
Общая формула имеет следующий вид:
b n + b n = 2b n
Пример 2
- 4 2 + 4 2 = 2⋅4 2 = 2⋅4⋅4 = 32
- 8 3 + 8 3 + 8 3 = 3 (8 3 ) = 3 * 512 = 1536
- 3 2 + 3 2 = 2 (3 2 ) = 2 * 9 = 18
- 5 2 + 5 2 = 2 (5 2 ) = 2 * 25 = 50.

Как складывать отрицательные экспоненты с разными основаниями?
Добавление отрицательных показателей осуществляется путем вычисления каждого показателя отдельно и последующего добавления:
a -n + b -m = 1 / a n + 1 / b m
Пример 3
4 -2 + 2 -5 = 1/4 2 + 1/2 5 = 1 / (4⋅4) + 1 / (2⋅2⋅2⋅2⋅2) = 1/16 + 1/32 = 0,09375
Как сложить дробную с разными основаниями и показателями?
Добавление дробных показателей выполняется путем вычисления каждого показателя отдельно, а затем добавления:
a n / m + b k / j .
Пример 4
3 3/2 + 2 5/2 = √ (3 3 ) + √ (2 5 ) = √ (27) + √ (32 ) = 5,196 + 5,657 = 10,853
Как сложить дробные показатели с одинаковыми основаниями и одинаковыми дробными показателями?
b н / м + b н / м = 2b н / м
Пример 5
4 2/3 + 4 2/3 = 2⋅4 2/3 = 2 ⋅ 3 √ (4 2 ) = 5. 04
04
Как складывать переменные с разными показателями степени?
Сложение показателей осуществляется путем вычисления каждого показателя по отдельности и последующего добавления:
x n + x m
Как складывать переменные с одинаковыми показателями?
x n + x n = 2x n
Пример 6
x 2 + x 2 = 2 x 2
Пример 7
(4 -1 + 8 -1 ) ÷ (2/3) -1
= (1/4 + 1/8) ÷ (3/2)
= ( 2 + 1) / 8 ÷ 3/2
= (3/8 ÷ 3/2)
= (3/8 ÷ 2/3)
= ¼
Пример 8
Упростить: (1 / 2) -2 + (1/3) -2 + (1/4) -2
Решение:
(1/2) -2 + (1/3) -2 + (1/4) -2
= (2/1) 2 + (3/1) 2 + (4/1) 2
= (2 2 + 3 2 + 4 2 )
= (4 + 9 + 16)
= 29
4 простых способа умножения экспонент [+ действия]
Что общего у землетрясений, фондового рынка, информатики и ядерной физики?
Все они включают показателей умножения .
Показатели являются неотъемлемой частью алгебры, полиномиальных уравнений и математических курсов более высокого уровня, но многим студентам сложно понять, как с ними работать. Вы ознакомились с правилами экспоненты со своим классом, и теперь пора применить их.
Давайте рассмотрим: правила экспоненты
Прежде чем вы начнете учить своих учеников умножению экспоненты, вы можете провести с ними быстрый обзор основ работы показателей.
Показатели (также называемые степенями ) регулируются правилами, как и все остальное в математическом классе.Вот краткое резюме:
Показатель степени — это способ выражения повторного умножения . Например, 35 представляет собой три, умноженные на себя пять раз:
35 = 3 × 3 × 3 × 3 × 3 = 243
35 = 243
Первое число называется основанием . Представляет собой число, которое умножается.
Второе меньшее число — это показатель степени . Он представляет собой количество раз, когда основание умножается само на себя.
Он представляет собой количество раз, когда основание умножается само на себя.
Существует семь правил экспоненты :
- Правило произведения степеней : сложение степеней при умножении подобных оснований
- Правило соотношения степеней : вычитание степеней при делении подобных оснований
- Правило силы полномочий : Умножение степеней вместе при увеличении степени на другой показатель
- Степень произведения rul e: Распределение мощности на каждую базу при возведении нескольких переменных в степень
- Степень правила частного : Распределение мощности на все значения в частное
- Правило нулевой степени : Любое основание, возведенное в степень нуля, становится единицей
- Правило отрицательной экспоненты : Чтобы изменить отрицательную экспоненту на положительную, переверните ее в обратную
Понятно? Тогда давай продолжим.
Как умножить экспоненты 4 способами
Помните, что все эти стратегии — просто ярлыки, помогающие упростить более сложные уравнения. Чтобы найти фактическое значение показателя степени, учащиеся должны сначала понять, что это означает: повторное умножение .
Познакомьте студентов с основами, такими как выражение показателей в виде произведений, прежде чем переходить к умножению показателей.
Когда они освоятся с концепцией, пора начинать.
1. Умножение степеней с одинаковым основанием
Когда вы умножаете экспоненты, используйте первое правило: складывайте степени при умножении одинаковых оснований.
52 × 56 =?
Основания уравнения остаются неизменными, а значения показателей складываются.
52 × 56 = 58
Но почему это работает? Давайте посмотрим немного внимательнее:
Сложение экспонент — это всего лишь быстрый путь к ответу. Когда мы складываем экспоненты, мы увеличиваем количество раз, когда основание умножается само на себя.
Это правило остается неизменным, независимо от сложности вопроса. Вот более сложный пример с переменными:
(2𝒙8) (3𝒙5) =?
Сначала умножьте числа (2 и 3) вместе, поскольку они представляют собой коэффициентов , а не основание. (Коэффициент — это число, умноженное на переменную, например 𝒙.)
Затем сложите показатели степени.
(2𝒙8) (3𝒙5) = 6𝒙13
2. Умножение степеней с разными основаниями
Можно умножать экспоненты с разными основаниями, но есть одна важная загвоздка: экспоненты должны быть одинаковыми.
Вот как это сделать:
54 × 24 =?
Сначала умножьте основания вместе. Затем добавьте показатель степени. Вместо того, чтобы складывать два показателя вместе, оставьте то же самое.
54 × 24 = 104
Вот почему это работает:
Это из-за правила четвертой степени: распределяет мощность на каждую базу при возведении нескольких переменных в степень . Это уравнение также можно записать как (5 × 2) 4, что означает, что показатель степени распределяется между 5 и 2.
Это уравнение также можно записать как (5 × 2) 4, что означает, что показатель степени распределяется между 5 и 2.
А теперь попробуем умножить переменные на показатели.
(3y3) (4y3) =?
Помните, правило остается в силе до тех пор, пока , поскольку показатели степени и переменные равны (потому что переменные 𝒙 и y не могут быть объединены).
(3y3) (4y3) = 12y3
3. Умножение показателей степени с разными основаниями и показателями
Что происходит, когда вы хотите умножить разные показатели степени с разными основаниями?
Короткий ответ: вы не можете. В отличие от приведенных выше примеров, здесь нет ярлыка.
Например:
Поскольку 24 и 32 не имеют ничего общего, чтобы их можно было объединить, ответ не может быть упрощен до одного показателя степени и должен быть выражен как обычное число.
4. Умножение отрицательных показателей
Это может показаться сложным, но умножение показателей показателей на отрицательные числа в точности совпадает с умножением показателей показателей на неотрицательные числа.
Начните с изучения свойств отрицательных чисел. В частности, просмотрите, как их складывать и умножать.Ваши ученики должны чувствовать себя комфортно, работая с отрицательными числами, прежде чем они перейдут к отрицательным показателям.
Затем запомните правило седьмого показателя степени: , чтобы изменить отрицательный показатель степени на положительный, переверните его на обратное значение .
То же основание, разные степени:
4-3 × 42 =?
Помните — складывайте экспоненты с одинаковыми основаниями.
4-3 × 42 = 4-1
Чтобы решить эту экспоненту, переверните отрицательную экспоненту в обратную.
4-1 = ¼ = 0.25
Другое основание, но одинаковые показатели:
2-5 × 3-5 =?
Как и выше, умножьте основания и оставьте степень без изменений.
2-5 × 3-5 = 6-5
Чтобы решить, переверните отрицательный показатель степени в обратную величину.
6-5 = ⅙5
Если показатели степени не имеют ничего общего, решите уравнение напрямую:
2-3 × 32
Сначала преобразуйте отрицательные показатели степени в обратные, затем вычислите.
При умножении показателей степени напомните учащимся:
- Сложить показатели , если основания одинаковые
- Умножить основания , если показатели одинаковые
- Если ничего не одинаково , просто решите это
Практика умножения на экспоненты
1.Prodigy
Повышение уровня владения математикой — важная часть уверенности учащихся в курсах математики в средней школе и колледже. Студенты могут практиковать умножение показателей и другие математические концепции с Prodigy, в то время как вы задаете индивидуальные вопросы в игре, основанные на содержании урока.
Ваш класс будет исследовать мир, наполненный увлекательными заданиями, экзотическими домашними животными и изучением математики. Вы сможете выбрать, на какие вопросы они будут отвечать, и в режиме реального времени получать данные о том, что они усвоили, над чем работают и где им может потребоваться дополнительная помощь.
Обладая 1400 навыками, вы сможете предоставить материалов, соответствующих учебной программе, по любой теме, которую вы изучаете, включая умножение показателей.
2. Exponent War
Education.comКлассическая карточная игра, но с невероятно интересным поворотом!
Ученики работают в группах по двое и соревнуются друг с другом. Раздайте каждой команде колоду карт (с вынутыми дамами, валетами и королями) и попросите каждого игрока вытащить две карты.Первая карта — это база, а вторая карта — экспонента.
Каждой паре предстоит соревноваться, чтобы решить свое уравнение и найти продукт. Побеждает команда с наибольшим ответом. Установите таймер для класса и посмотрите, кто наберет больше очков.
Пока ученики играют, пройдитесь по классу и убедитесь, что они не пропустили ни одной ступеньки. Если вы видите много ошибок или затруднений у учащихся, примите это как знак того, что вам, возможно, придется сделать некоторый обзор.
3. Exponent Scavenger Hunt
Дайте вашим ученикам возможность искать сокровища и исследовать класс с помощью экспоненциальной охоты за мусорщиками.
Разделите ваш класс на группы по три или четыре человека. В зависимости от количества групп, сделайте несколько разных наборов карточек. Начинайте каждый набор с карточки, на которой есть проблема. Напишите ответ на проблему на следующей карточке, а другую задачу на обратной стороне. Продолжайте, пока не получите три или четыре набора задач (или больше).
Начиная с первой карточки, каждая группа должна решить задачу и найти правильный ответ где-нибудь еще в классе .Найдя правильную карточку для ответов, они могут перевернуть ее и решить следующую задачу. Раздайте учащимся записки для решения и позвольте им начать поиск ответов. Какая бы команда ни финишировала первой, становится победителем!
4. Exponent Jeopardy
Каждый ученик любит классическую игру Jeopardy. Используя настраиваемый шаблон, замените мелочи вопросами, которые дают студентам возможность попрактиковаться в умножении показателей, и разделите класс на две команды.
Вот несколько советов, которые помогут обеспечить бесперебойную работу игры:
- Если у вас большой класс, подумайте о том, чтобы разделить класс на несколько игр, чтобы у каждого ученика была возможность участвовать.
- Чтобы объединить математические и компьютерные навыки, Предложите учащимся сделать игру самостоятельно.Дайте им шаблон (или пусть более продвинутые ученики начнут с нуля) и попросите их сделать небольшую игру.
- Используйте его в качестве конечного упражнения перед тестом и комбинируйте более важные вопросы с более сложными ответами
5. Рабочие листы для умножения показателей
Рабочие листы — это проверенный метод развития математики свободное владение определенным набором навыков. Они также могут быть индикатором понимания учащимся, когда используются как часть стратегии формирующего оценивания.Вот некоторые из наших фаворитов:
Если вы ищете рабочий лист, который охватывает больше, чем просто умножение экспонент, ознакомьтесь с нашей таблицей правил экспонент (с ключом ответа).
Чтобы добиться чего-то более уникального, попробуйте это упражнение с умножением полиномов. Как и в обычном рабочем листе, в нем есть вопросы, на которые студенты должны ответить, но он также содержит «банк ответов» для студентов. Вырежьте прилагаемые полоски и перемешайте их. Попросите учащихся сопоставить ответы с правильным разделом на своем листе после решения уравнения и демонстрации своей работы.
Показатели умножения: давайте рассмотрим
Если ваши ученики помнят только три вещи, убедитесь, что это следующие концепции:
- Сложите степени при умножении как основание
- Умножьте основания при умножении как показателях
- Показатели — это произведение многократного умножения
Если они запомнят эти три правила, у них будет прочный фундамент, построенный еще до первого урока алгебры в старшей школе.
Как всегда, делайте это медленно и убедитесь, что учащиеся понимают основы, прежде чем все усложняется. Это может показаться сложной идеей для преподавания, но придерживайтесь шагов и продвигайтесь в логическом порядке, чтобы увидеть, как знания ваших учеников растут.
Это может показаться сложной идеей для преподавания, но придерживайтесь шагов и продвигайтесь в логическом порядке, чтобы увидеть, как знания ваших учеников растут.
Создайте или войдите в свою учетную запись учителя на Prodigy — увлекательной игровой платформе для обучения математике, которую легко использовать как преподавателям, так и ученикам. Программа Prodigy, согласованная с общими учебными программами во многих англоязычных странах, используется миллионами учителей и студентов по всему миру.Зарегистрируйтесь сейчас
Добавление экспонентов — определение, шаги, метод, примеры
Сложение показателей относится к простому сложению чисел, но в форме показателей степени или степени. Другими словами, добавление основания и показателя степени добавляет степени. Показатель также называется степенью числа, и он показывает, сколько раз число умножается само на себя. В общем, x n означает, что x умножается на себя n раз. Добавление показателей выполняется в разных типах, давайте посмотрим, что это за типы, и решим несколько примеров, чтобы лучше понять эту концепцию.
Что такое сложение экспонентов?
Сложение показателей — это процесс сложения показателей или степеней числа независимо от того, одинаковое основание или нет. Экспоненты также можно назвать степенью чисел, поскольку они представляют, сколько раз число умножается само на себя. Например, 3 2 = 3 × 3, где 3 — основание, а 2 — показатель степени.
Здесь в члене x n ,
- х называется базой
- n называется экспонентой или степенью
- x n читается как x в степени n (или) x, возведенной в n
При сложении показателей следует помнить одно главное правило: основание и показатель степени должны быть одинаковыми, а сложение выполняется над коэффициентом.Комбинируемые переменные имеют одинаковую базу и одинаковую мощность. Это правило применимо и ко всем другим формам показателей степени, то есть к вычитанию, умножению и делению.
Шаги сложения экспонент
Сложение показателей степени может быть выполнено, если основание и показатель степени совпадают. Бывают случаи, когда основание и показатель степени отличаются, но мы все равно можем выполнить сложение для этих выражений. Давайте посмотрим на этапы добавления показателей.
Бывают случаи, когда основание и показатель степени отличаются, но мы все равно можем выполнить сложение для этих выражений. Давайте посмотрим на этапы добавления показателей.
- Шаг 1. Проверьте термины в выражении, если они имеют одинаковое основание и одинаковые показатели.Например, 2 2 + 2 2 . Как мы видим, и основание, и экспонента равны 2.
- Шаг 2: Если основание и показатель степени отличаются, вычислите выражение с отдельными членами. Например, 5 3 + 4 2 . База и показатель степени разные.
- Шаг 3. Сложите результаты.
Методы сложения экспонент
Сложение экспонент может производиться разными способами.Основное правило при добавлении показателей степени состоит в том, что основание и показатель степени должны быть одинаковыми. Однако иногда основание и показатель степени могут не совпадать, поэтому для вычисления выражения нам нужно рассчитывать члены по отдельности. Давайте посмотрим на разные методы.
Давайте посмотрим на разные методы.
Метод 1: сложение показателей с одинаковым основанием и экспонентами
Добавление показателей степени, когда основание и показатель степени совпадают, выполняется очень простым способом. Общая форма сложения показателей с одинаковым основанием и показателями: n + n = 2a n .Давайте посмотрим на пример, чтобы лучше понять это. Например: 4 3 + 4 3 = 2 (4 3 ) = 2 × 4 × 4 × 4 = 128.
Метод 2: сложение показателей с разным основанием и показателями
Если основание и показатель степени имеют разные значения, мы сначала добавляем каждый показатель степени, а затем вычисляем все выражение. Общая форма вычисления различных оснований и экспонент: n + b m . Давайте посмотрим на пример, чтобы лучше понять это.Например: 3 3 + 5 2 = 3 × 3 × 3 + 5 × 5 = 27 + 25 = 52.
Метод 3. Сложение отрицательных экспонент с разными основаниями
Добавление отрицательных показателей осуществляется путем вычисления каждого члена индивидуально с последующим сложением суммы. Термины записываются в дробной форме, а затем складываются. Общая форма вычисления отрицательных показателей с разными основаниями: -n + b -m = 1 / a n + 1 / b m . Давайте применим общую форму на примере, чтобы лучше понять это.Например: 6 -2 + 3 -3 = 1/6 2 + 1/3 3 = 1/36 + 1/27 = 0,0648.
Термины записываются в дробной форме, а затем складываются. Общая форма вычисления отрицательных показателей с разными основаниями: -n + b -m = 1 / a n + 1 / b m . Давайте применим общую форму на примере, чтобы лучше понять это.Например: 6 -2 + 3 -3 = 1/6 2 + 1/3 3 = 1/36 + 1/27 = 0,0648.
Метод 4: сложение дробных показателей с одинаковым основанием и показателями
Показатели степени также могут быть выражены в виде дроби. Таким образом, сложение этих дробей в форме показателей степени может быть выполнено с использованием этой общей формы, a n / m + a n / m = 2a n / m . Для дробей мы можем преобразовать дробные показатели в форму корня i.е. корень квадратный или кубический в зависимости от дроби. Давайте применим эту общую форму к примеру для лучшего понимания. Например: 4 1/2 + 4 1/2 = 2 (4 1/2 ) = 2 × √4 = 2 × 2 = 4.
Метод 5: Сложение дробных показателей с разными основаниями и показателями
Показатели, записанные в дробной форме с разным основанием и разными показателями, выражаются в общем виде как n / m + b d / c .Здесь сначала вычисляется каждый член, а затем вычисляется весь результат. Дробная форма преобразуется в ее корень, а затем вычисляется. Давайте посмотрим на пример, 27 1/3 + 4 1/2 = 3 √27 + √4 = 3 + 2 = 5.
Метод 6. Добавление переменной с одинаковыми показателями
Это похоже на метод сложения показателей с одинаковым основанием и одинаковыми показателями. Общая форма: x n + x n = 2x n . Давайте посмотрим на пример: 7 2 + 7 2 = 2 (7 2 ) = 2 × 7 × 7 = 98.
Метод 7. Добавление переменной с разными показателями
Общая форма для вычисления переменных с разными показателями: x n + x m . Давайте посмотрим на пример: 4 2 + 4 3 = 4 2 × 3 = 4 6 = 4096.
Давайте посмотрим на пример: 4 2 + 4 3 = 4 2 × 3 = 4 6 = 4096.
Связанные темы
Ниже перечислены несколько интересных тем, связанных с добавлением показателей степени. Посмотри.
Часто задаваемые вопросы о добавлении экспонентов
Что означает сложение экспонентов?
Сложение показателей — это процесс сложения членов с одинаковым основанием и показателем степени.Сложение может происходить только в том случае, если основание и показатель степени совпадают. Бывают случаи, когда это не так, это можно решить, посмотрев, одинаковы ли показатели двух членов или одинаковы ли основания двух членов. В противном случае добавление экспонентов невозможно.
Каковы шаги для сложения экспонент?
Добавление показателей степени выполняется в 3 простых шага, это:
- Проверьте термины в выражении, если они имеют одинаковое основание и одинаковые показатели.

- Если основание и показатель степени разные, вычислить выражение с отдельными членами.
- Сложите результаты.
Какое правило сложения экспонент?
Самым важным правилом сложения показателей является то, что основание и показатель степени терминов, добавляемых для сложения, должны быть одинаковыми. Если они одинаковы, коэффициенты будут сложены, а основание и показатель степени будут одинаковыми.
Можно ли складывать числа с разными показателями?
Нет, возможно сложение чисел с разными показателями, так как правило сложения показателей состоит в том, что основание и показатель степени должны быть одинаковыми.Хотя что-то основание и экспонента могут быть разными, но одно отличие не применимо.
Вы добавляете экспоненты при сложении?
Для сложения экспонент основание и экспонента должны быть одинаковыми. Коэффициент переменной добавляется без изменения показателя степени. В выражение добавлены члены с такими же переменными и степенями. Это правило применяется как для умножения, так и для деления.
Это правило применяется как для умножения, так и для деления.
Как сложить мономы с показателями степени?
Добавляя два или более одинаковых одночлена, мы сначала складываем коэффициенты, в то время как переменные и показатели переменной совпадают.Мы можем получить результат, добавив подобные одночлены.
Умножение экспонент — правила, объяснения и примеры
Умножение двух выражений с показателями степени называется умножением показателей степени. Умножение показателей включает определенные правила, зависящие от основания и степени. Иногда учащимся трудно понять из-за разных оснований, отрицательных показателей и нецелых показателей. Давайте узнаем больше об умножении показателей в этой статье.
Что такое экспоненты умножения?
Прежде чем исследовать концепцию умножения показателей, напомним значение показателей. Показатель может быть определен как количество раз, когда величина умножается сама на себя. Например, когда 2 умножается на себя трижды, это выражается как 2 × 2 × 2 = 2 3 . Здесь 2 — это основание , а 3 — это степень или показатель степени . Читается как «2 в степени 3».
Здесь 2 — это основание , а 3 — это степень или показатель степени . Читается как «2 в степени 3».
Теперь давайте обсудим, что означает умножение показателя степени. Когда любые два выражения с показателями умножаются, это называется умножением показателей. Давайте рассмотрим различные случаи с помощью примеров, чтобы лучше понять концепцию.
Правила умножения экспонент с одинаковым основанием
Рассмотрим два выражения с одинаковым основанием, то есть n и m . Здесь база — «а». Когда члены с одинаковым основанием умножаются, степени складываются, т.е.е., a м × a n = a {m + n}
Давайте рассмотрим несколько примеров, чтобы понять, как складываются полномочия.
Пример 1: Умножение 2 4 × 2 2
Решение: Здесь база такая же, то есть 2. По правилу сложим степени, 2 4 × 2 2 = 2 (4 + 2) = 2 6 = 64,
По правилу сложим степени, 2 4 × 2 2 = 2 (4 + 2) = 2 6 = 64,
Проверим ответ.2 4 × 2 2 = (2 × 2 × 2 × 2) × (2 × 2) = 2 × 2 × 2 × 2 × 2 × 2 = 2 6 = 64
Пример 2: Найдите произведение 10 45 и 10 39
Решение: В данном вопросе база такая же, то есть 10. По правилу складываем степени, 10 45 × 10 39 = 10 (45 + 39) = 10 84 .
Будет ли правило оставаться прежним, если базы разные? Давайте посмотрим на это в следующем разделе.
Правила умножения экспонент с различным основанием
Когда два числа или переменные имеют разные основания, мы можем умножать выражения, следуя некоторым основным правилам экспонент. Здесь у нас есть два сценария:
Когда базы разные и силы одинаковые.
Рассмотрим два выражения с разным основанием и одинаковой мощностью a n и b n . Здесь основания — это a и b, а степень — n. При умножении степеней с разными основаниями и одинаковыми степенями сначала умножаются основания. Математически это можно записать как n × b n = (a × b) n .
Здесь основания — это a и b, а степень — n. При умножении степеней с разными основаниями и одинаковыми степенями сначала умножаются основания. Математически это можно записать как n × b n = (a × b) n .
Пример: Найдите произведение 5 2 и 8 2 .
Решение: Здесь базы разные, но силы те же. Итак, применяя правило, мы сначала умножим основания, то есть 5 2 × 8 2 = (5 × 8) 2 = 40 2 = 1600.
Когда базы и силы разные.
Рассмотрим два выражения с разными основаниями и степенями a n и b m . Здесь основания — это a и b. Степени равны n и m. Когда выражения с разными основаниями и разными степенями умножаются, каждое выражение оценивается отдельно, а затем умножается. Математически это можно записать как a n × b m = (a n ) × (b m )
.
Пример: Умножьте выражения: 10 3 × 7 2 .
Решение: Здесь базы и мощности разные. Поэтому каждый термин будет решаться отдельно. 10 3 × 7 2 = 1000 × 49 = 49000.
Напомним правила умножения показателей с одинаковым основанием и с разными основаниями на следующем рисунке.
Правила умножения отрицательных экспонент
Отрицательные экспоненты говорят нам, сколько раз нам нужно умножить величину, обратную основанию.Другими словами, мы можем преобразовать отрицательную экспоненту в положительную, записав обратную величину данного выражения, а затем решить ее как положительное выражение. Например, 2 -3 можно записать как 1/2 3 . Для умножения отрицательных показателей нам необходимо соблюдать определенные правила, которые приведены в следующей таблице.
| Ящики | Правила |
|---|---|
Когда базы одинаковые. | a -n × a -m = a — (n + m) = 1 / a {n + m} |
| Когда основания разные, а отрицательные силы одинаковы. | a -n × b -n = (a × b) -n = 1 / (a × b) n |
| Когда основания и отрицательная сила разные. | a -n × b -m = (a -n ) × (b -m ) |
Теперь давайте разберемся с этими правилами с помощью следующих примеров.
Пример 1: Найдите произведение 2 -3 и 2 -9
Решение: Здесь база такая же, то есть 2.Силы отрицательные и разные. Таким образом, 2 -3 × 2 -9 = 2 — (3 + 9) = 2 -12 = 1/2 12 = 1/4096 ≈ 0,000244
Пример 2: Умножение 6 -3 × 3 -3
Решение: Здесь основания разные, а отрицательные степени такие же.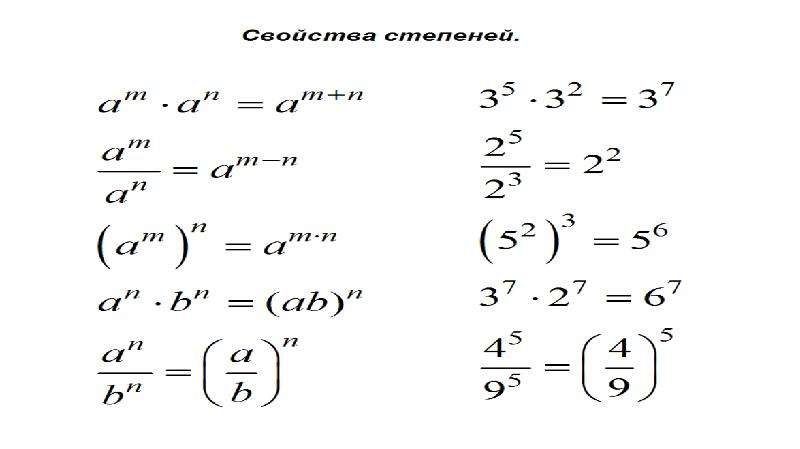 Таким образом, 6 -3 × 3 -3 = (6 × 3) -3 = 18 -3 = 1/18 3 = 1/5832 ≈ 0,0001715
Таким образом, 6 -3 × 3 -3 = (6 × 3) -3 = 18 -3 = 1/18 3 = 1/5832 ≈ 0,0001715
Пример 3: Умножение 7 -2 × 6 -3
Решение: Здесь разные основания и отрицательные степени.Таким образом, 7 -2 × 6 -3 = 1/7 2 × 1/6 3 = 1 / (7 2 × 6 3 ) ≈ 9,45 × 10 -5
Правила умножения экспонент с переменными
Если основанием выражения является переменная, мы используем те же правила умножения экспоненты, которые используются для чисел.
Если базисы переменных одинаковы, степени складываются.
Пример: Найдите произведение 4 и 10
Решение: База переменных та же, то есть «a».Итак, мы добавим экспоненты: 4 × 10 = 4 + 10 = 14
Если основания переменных различны, а степени одинаковы, сначала умножаются основания.
Пример: Умножить a 17 × b 17
Решение: Базы переменных разные, а степени одинаковые, то есть a 17 × b 17 = (a × b) 17 = (ab) 17
Если основания переменных и степени различны, члены оцениваются отдельно, а затем умножаются.
Пример: Найдите произведение x 8 и y 9 .
Решение: Базы и степени переменных различны, то есть x 8 × y 9 = x 8 y 9
Умножение экспоненты с квадратным корнем
В этом разделе мы исследуем умножение экспонент, когда основания имеют квадратный корень. Следует отметить, что правила экспоненты остаются неизменными, если основания являются квадратными корнями.
Помимо этого, следует помнить об одном важном моменте: мы можем преобразовывать радикалы в рациональные показатели, а затем умножать полученные выражения. Например, квадратный корень из положительного числа √a можно выразить как рациональную экспоненту следующим образом. √a = a 1/2 . Теперь, когда нам нужно переписать данный экспоненциальный член как рациональную экспоненту, мы умножаем существующую степень на 1/2. Например, если нам нужно перезаписать √5 3 как рациональную экспоненту, мы сначала преобразуем радикал √5 в 5 1/2 , а затем умножим степень 3 на 1/2, что делает это 3/2.Теперь радикал √5 3 преобразован в рациональную экспоненту и записывается как 5 3/2 .
Например, квадратный корень из положительного числа √a можно выразить как рациональную экспоненту следующим образом. √a = a 1/2 . Теперь, когда нам нужно переписать данный экспоненциальный член как рациональную экспоненту, мы умножаем существующую степень на 1/2. Например, если нам нужно перезаписать √5 3 как рациональную экспоненту, мы сначала преобразуем радикал √5 в 5 1/2 , а затем умножим степень 3 на 1/2, что делает это 3/2.Теперь радикал √5 3 преобразован в рациональную экспоненту и записывается как 5 3/2 .
Правила умножения экспонент с квадратным корнем
Теперь давайте воспользуемся правилами умножения экспонент, которые применимы к выражениям, в которых основаниями являются квадратные корни.
Когда основания квадратного корня одинаковы, степени складываются.
Пример: Найдите произведение (√5) 2 и (√5) 7 .
Решение: Основания квадратного корня такие же. Таким образом, (√5) 2 × (√5) 7 = (√5) 2 + 7 = (√5) 9 = (5) 9/2 .
Когда основания квадратного корня различны и степени одинаковы, сначала умножаются основания.
Пример: Умножение (√5) 3 × (√7) 3
Решение: Основания квадратного корня различны, а степени одинаковы.Таким образом, (√5) 3 и (√7) 3 = (√5 × √7) 3 = [√ (5 × 7)] 3 = (√35) 3 = ( 35) 3/2
Если основания квадратного корня и степени различны, показатели степени оцениваются отдельно, а затем умножаются.
Пример: Рассмотрим произведение (√5) 3 и (√7) 4 .
Решение: Основания квадратного корня и степени различны. Таким образом, (√5) 3 × (√7) 4 = 11.18 × 49 ≈ 547,82
Таким образом, (√5) 3 × (√7) 4 = 11.18 × 49 ≈ 547,82
Правила умножения экспонент на дроби
Если основанием выражения является дробь, возведенная в степень, мы используем те же правила экспоненты, которые используются для оснований, являющихся целыми числами. Изучите следующую таблицу, чтобы увидеть различные сценарии.
| Ящики | Правила |
|---|---|
| Когда дробные основания одинаковы. | (a / b) n × (a / b) м = (a / b) n + m |
| Когда дробные основания различны, но степени одинаковы. | (a / b) n × (c / d) n = (a / b × c / d) n |
| Когда дробные основания и степени различны. | (a / b) n × (c / d) м = (a n × c м ) / (b n × d м ) |
Давайте рассмотрим несколько решенных примеров, чтобы лучше понять это.
Пример 1: Найдите произведение (2/3) 2 и (15/8) 2
Решение: Здесь дробные основания разные, но степени те же.Таким образом, применяя приведенное выше правило, (2/3) 2 × (15/8) 2 = (2/3 × 15/8) 2 = (5/4) 2 = 5 2 /4 2 = 25/16.
Пример 2: Умножение (2/3) 2 × (2/3) 5
Решение: Здесь дробное основание такое же. (2/3) 2 × (2/3) 5 = (2/3) 2 + 5 = Таким образом, (2/3) 7 = 2 7 /3 7 = 128/2187.
Пример 3: Умножение (3/4) 2 × (2/3) 3
Решение: Здесь дробные основания и степени различны.Итак, сначала мы решим каждый член отдельно, а затем двинемся дальше. (3/4) 2 × (2/3) 3 = Таким образом, (3 2 × 2 3 ) / (4 2 × 3 3 ) = (9 × 8) / (16 × 27) = 1/6.
Как умножить дробные экспоненты?
Когда член имеет дробную степень, он называется дробной степенью. Например, 2 3/5 — это дробная экспонента. Давайте разберемся с правилами, которые применяются для умножения дробных показателей с помощью следующей таблицы.
| Ящики | Правила |
|---|---|
| Когда базы одинаковые. | a н / м × a k / j = a н / м + k / j |
| Когда основания разные, но дробные степени одинаковы. | a н / м × b н / м = (a × b) н / м |
| Когда основания и дробные степени различны. | a н / м × b k / j = (a н / м ) × (b k / j ) |
Давайте разберемся с этими правилами с помощью следующих примеров.
Пример 1: Умножение 2 1/2 и 2 3/2
Решение: Здесь базы такие же. Таким образом, 2 1/2 × 2 3/2 = 2 1/2 + 3/2 = 2 4/2 = 2 2 = 4.
Таким образом, 2 1/2 × 2 3/2 = 2 1/2 + 3/2 = 2 4/2 = 2 2 = 4.
Пример 2: Найдите произведение 2 1/2 и 3 1/2
Решение: Здесь основания разные, но дробные степени такие же.Таким образом, 2 1/2 × 3 1/2 = (2 × 3) 1/2 = 6 1/2 = √6.
Пример 3: Умножение 4 2/3 × 2 1/3
Решение: Здесь основания и дробные степени разные. Таким образом, 4 2/3 × 2 1/3 ≈ 2,52 × 1,26 = 3,1752
Советы по умножению экспонент:
- Ноль в любой степени (кроме 0) равен 0.
- Любое число в нулевой степени равно 1.
- Показатель степени — это способ выражения многократного умножения.
☛ Связанные темы
Часто задаваемые вопросы по умножению экспонент
Как работает умножение экспонент?
Умножение показателей степени означает нахождение произведения двух выражений с показателями степени. Поскольку существуют разные сценарии, такие как разные основания или разные показатели, для их решения применяются разные правила экспоненты.Есть несколько основных правил, которые используются практически во всех случаях. Например,
Поскольку существуют разные сценарии, такие как разные основания или разные показатели, для их решения применяются разные правила экспоненты.Есть несколько основных правил, которые используются практически во всех случаях. Например,
- Когда выражения с одинаковым основанием умножаются, степени складываются, т. Е. m × a n = a (m + n)
- Чтобы умножить выражения с разными основаниями и одинаковыми степенями, сначала умножаются основания. Математически это можно записать как n × b n = (a × b) n .
- Когда выражения с разным основанием и разной степенью умножаются, каждый член оценивается отдельно, а затем перемножается.Математически это можно записать как n × b m = (a n ) × (b m ).
Можно ли перемножить экспоненты с разными коэффициентами?
Да, выражения с разными коэффициентами можно перемножать. Коэффициенты умножаются отдельно, как показано в примере. Например, 3a 2 × 4a 3 = (3 × 4) × (a 2 × a 3 ) = 12a 5 .
Например, 3a 2 × 4a 3 = (3 × 4) × (a 2 × a 3 ) = 12a 5 .
Вы складываете степени при умножении экспонент?
Когда показатели с одинаковыми основаниями умножаются, степени складываются.Например, 3 4 × 3 5 = 3 ( 4 + 5) = 3 9 .
Как умножить экспоненты с разными основаниями?
Чтобы умножить показатели с разными основаниями и одинаковыми степенями, основания умножаются, а степень записывается вне скобок. a n × b n = (a × b) n . Например, 2 2 × 3 2 = (2 × 3) 2 = 6 2 = 36. Однако, когда мы умножаем экспоненты с разными основаниями и разными степенями, каждый показатель степени решается отдельно, а затем они умножаются.a n × b m = (a n ) × (b m ). Например, 2 2 × 5 4 = (2) 2 × (5) 4 = 4 × 625 = 2500.
Что означает умножение экспонент с одинаковым основанием?
Умножение показателей степени на одно и то же основание означает, что основания одинаковы, а показатели степени различны. В этом случае база остается общей и добавляются разные мощности, то есть m × a n = a (m + n) .Например, 2 3 × 2 4 = 2 (3 + 4) = 2 7 = 128
Как умножить экспоненты на круглые скобки?
При умножении показателей степени в круглых скобках степень за пределами скобок умножается на каждую степень внутри скобок. Например, (2a 2 b 3 ) 2 = 2 2 × a (2 × 2) × b (3 × 2) = 4a 4 b 6 .
Каковы правила умножения экспонент?
Существуют разные правила умножения экспонент.Основные правила умножения показателей приведены ниже.
- Когда выражения с одинаковым основанием умножаются, степени складываются, т.
 Е. m × a n = a (m + n)
Е. m × a n = a (m + n) - Когда выражения с разными основаниями и одинаковыми степенями умножаются, то общая степень записывается вне скобок, то есть a n × b n = (a × b) n .
- Когда выражения с разными основаниями и разными степенями умножаются, каждый член оценивается отдельно, а затем умножается, т.е.е., a n × b m = (a n ) × (b m ).
Как умножить экспоненты с отрицательными степенями?
Умножение показателя степени на отрицательную степень подчиняется тому же набору правил, что и умножение показателя степени положительной степени. Единственная разница здесь в том, что мы должны быть осторожны при сложении и вычитании целых чисел. Например, 2 -3 × 2 -9 = 2 — (3 + 9) = 2 -12 = 1/2 12 = 1/4096 ≈ 0.000244
Как умножить экспоненты с переменными?
Для умножения показателей степени на переменные мы используем те же правила, что и для чисел. Например, умножим y 5 × y 3 . Согласно правилу экспоненты для умножения с одинаковым основанием, мы просто складываем степени. Это означает, что это будет y 5 × y 3 = y 5 + 3 = y 8 .
Сложение и вычитание с экспонентами — Видео и стенограмма урока
Основы экспоненты
Так же, как супергерои, экспоненты обладают особыми способностями.Они могут упростить многократное умножение, чтобы мы могли сэкономить место! Хорошо, может быть, их способности не так уж интересны, но они, безусловно, полезны в математике и естественных науках. Мы можем выполнять все виды различных математических вычислений с показателями, но в этом уроке мы сосредоточимся только на двух: сложении и вычитании с показателями.
Прежде чем приступить к сложению и вычитанию с показателями степени, мы должны обсудить несколько вещей. Что такое показатель степени? Показатели или степени соответствуют количеству раз, когда основание используется в качестве множителя.5
Это выражение имеет коэффициент 8, основание x и показатель степени 5.
Кстати, если перед переменной или символом нет числа, то коэффициент будет 1. То же верно, если вы не видите экспоненту. Следовательно, член y будет иметь коэффициент 1 и показатель степени 1; их просто не нужно писать, что немного упрощает. Вот еще один пример: 2 x будет означать коэффициент 2, основание x и показатель степени 1.
Понял? Теперь мы можем перейти к некоторым простым правилам, чтобы, наконец, начать складывать и вычитать члены с показателями.
Добавление показателей — примеры и методы
Добавление показателей : Алгебра входит в число основных учебных курсов по математике. Чтобы понять алгебру, важно понимать, как использовать защитники и радикалы. Добавление спонсоров является частью учебной программы по алгебре и, следовательно, жизненно важно для студентов, чтобы иметь более устойчивую структуру по математике.
Многие студенты часто путают добавление спонсоров с добавлением чисел и, следовательно, совершают ошибки. Эти недоразумения обычно влекут за собой различие в определении таких терминов, как возведение в степень, а также показатели степени.
Прежде чем углубляться в указатели того, как именно добавлять показатели, давайте начнем с определения терминов для спонсоров. Начнем с того, что спонсор — это просто дублированное умножение числа само по себе. В математике эта процедура называется возведением в степень.По этой причине возведение в степень представляет собой операцию, влекущую за собой числа в форме b n, где b описывается как основание, а число n является показателем степени, индексом или степенью. Например, x4 состоит из 4 в качестве показателя степени, а x называется основанием.
Показатели иногда называют степенями чисел. Сторонник означает, что число может увеличиваться само по себе. Например, x4 = x × x × x × x.
Читайте также: Формула линейной интерполяции
Как складывать экспоненты?Чтобы добавить спонсоров, должны быть сопоставлены и спонсоры, и переменные.Продолжайте и добавляйте коэффициенты переменных, оставляя экспоненты без изменений. Включены только термины с одинаковыми переменными и полномочиями. Это правило также соответствует делению и умножению показателей.
Ниже приведены шаги для добавления спонсоров:
Убедитесь, что вы проверили условия, если у них одинаковые базы и спонсоры.
Например, 42 +42, эти члены имеют одно и то же основание четыре и показатель степени 2.
Рассчитайте каждый член по отдельности, если они имеют различное основание или показатель степени
Например, 32 + 43, у этих условий есть как разные сторонники, так и основания.
Сложите результаты друг с другом.
Читайте также: Как рассчитать формулу угловой скорости
Сложение показателей с различными основаниями и показателямиВключение покровителей осуществляется путем вычисления сначала каждого спонсора, а затем добавления: Общая форма таких покровителей: a n + b m.
Пример 1
83+ 92 = (8) (8) (8) + (9) (9) = 512 + 81 = 593
42+ 25 = 4 ⋅ 4 +2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 16 +32 = 48
62+ 63 = 252.
34+ 36 = 81 + 729 = 810.
32+ 53 = (3) (3) + (5) (5) (5) = 9 + 125 = 134
Сложение экспонент с одинаковыми показателями и основаниемОбщая формула:
млрд + b n = 2b n
Пример 2
83+ 83+ 83 = 3 (83) = 3 * 512 = 1536
52+ 52 = 2 (52) = 2 * 25 = 50
32+ 32 = 2 (32) = 2 * 9 = 18
42+ 42 = 2⋅42 = 2⋅4⋅4 = 32
Добавление переменных с разными показателямиНачните вычислять каждую экспоненту отдельно, а затем выполните сложение: xn + x m
. Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […]
Оборудование постоянно совершенствуется, и данная сфера постоянно развивается. Как и в любой […] = 2 * 2 * 2 = 8;
= 2 * 2 * 2 = 8;


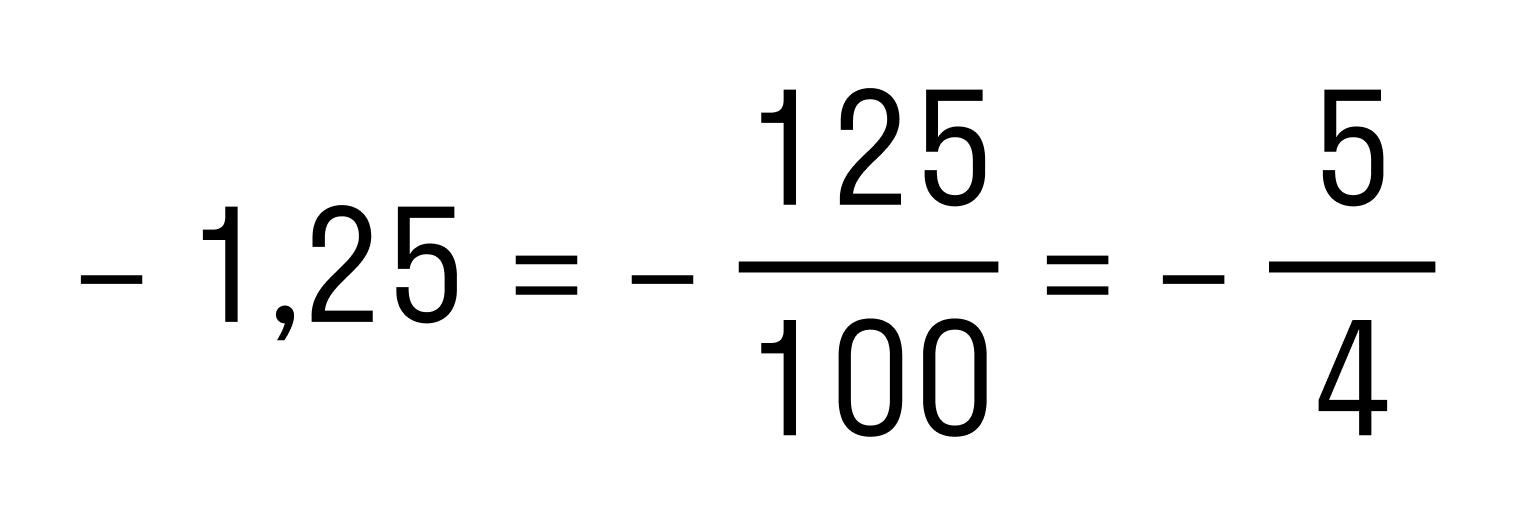
 Е. m × a n = a (m + n)
Е. m × a n = a (m + n)