Построение графиков сложных функций
Пояснительная записка к работе
«Построение графиков сложных функций»
Выполнил: Черемисин Дмитрий ученик 11Б класса
Преподаватель: Черемисина Галина Артуровна
Образовательное учреждение: МОУ-гимназия №13 п. Краснообска Новосибирского района Новосибирской области
Предмет: алгебра, алгебра и начала анализа
Тема: график сложной функции
Класс: 9 — 10 — 11 классы
Цель руководителя:
привить навыки эффективного использования ИКТ в школе и в жизни;
продолжать формировать интерес к математике посредством рассмотрения внепрограммного материала;
воспитывать осознанное отношение к процессу работы, прививать чувство ответственности за качество выполняемого проекта;
содействовать развитию у учащихся умения систематизировать материал;
осуществлять самоконтроль за процессом выполнения и оформления работы
Самостоятельная работа старшеклассника-гимназиста – это особым образом организованная деятельность, включающая в свою структуру такие компоненты, как:
уяснение цели поставленной учебной задачи;
четкое и системное планирование самостоятельной работы;
поиск необходимой учебной и научной информации;
освоение информации и её логическая переработка;
выработка собственной позиции;
представление, обоснование и защита полученного результата;
проведение самоанализа и самоконтроля.
Этот проект позволит учителю эффективно использовать ИТ в процессе преподавания, делая с их помощью уроки более увлекательными и насыщенными.
Цель работы:
Овладеть умением представлять сложную функцию в виде композиции двух функций
Освоить приём построения эскиза графика функции без применения производной
Показать возможность использования схемы построения графиков сложных функций вида y = f(φ(x))
В работе рассматриваются функции вида y = f(φ(x)), где φ(x) – любая из основных элементарных функций, а f – любая из следующих операций над ними: прибавление к функции какого-либо числа, умножение функции на число, деление единицы на функцию, возведение функции в положительную степень, извлечение корня из функции, нахождение показательной функции от функции, логарифмирование функции, нахождение модуля функции, нахождение тригонометрических функций от функции.
Эта работа может быть предложена в качестве развивающего компонента на уроках алгебры (демонстрация презентации при изучении темы «Исследование функции» и в рамках предметной недели).
Разрешение на публикацию работы моего сына есть!
График сложных функции
Цель урока:
Систематизировать и расширить знания учащихся по теме: “Графики функций”
Задачи урока:
- Использовать графики функций в задачах с параметром.
- Расширить знания при построении графиков функций, связанных с модулем.
- Исследовать и строить графики суперпозиции функций.
- Получить новые знания при построении графиков суммы, разности, произведения, частного функций.
План урока:
- Формулировка темы, цели, задач урока.
- Обсуждение домашнего задания с приобщением задач с параметром.
- Исследование и построение графиков функций, связанных с модулем (работа у доски, в парах, в группах).
- Исследование и построение графиков суммы и произведения функций.
- Исследование и построение графиков суперпозиции функций.
- Домашнее задание в виде творческой работы.
- Итоги урока. Рефлексия.
1. Обсуждение домашнего задания:
Построить график функций и описать свойства:
а)
б)
Правильность построения графиков проверяется с помощью мультимедийного проектора. Свойства функций проговариваются учащимися устно.
Дополнительный вопрос учителя по домашнему заданию:
Найдите все значения параметра a , при каждом из которых уравнение
а)
б)
имеет ровно один, ровно два и ровно один корень.
Вопрос к классу: Сформулируйте определение функции.
2. Построение графиков функций, связанных с модулем (работа в тетрадях).
Построить графики следующих функций:
а)
б)
в)
г)
д)
е)
С помощью ранее построенных графиков, постройте графики следующих функций:
а)
б)
в)
г)
д)
е)
Укажите особенности графиков функций.
Правильность построения графиков проверяется с помощью мультимедийного проектора. Работа в парах, с последующей проверкой и оценкой.
Вывод:
Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОХ или выше, и симметрично отразить относительно оси ОХ ту часть графика функции, которая расположена ниже оси ОХ.
Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОУ или справа от нее, и симметрично отразить эту часть относительно оси ОУ.
Вопрос классу: Сформулируйте определение графика функции?
Работа в группах.
Построить график и описать свойства следующих функций:
а)
б)
в)
г)
д)
е)
ж)
з)
Работают 6 групп, два — три человека работают у доски. Заранее желательно обсудить какая функция является исходной.
Правильность построения графиков проверяется с помощью мультимедийного проектора.
Учащиеся, работавшие у доски, должны назвать особенности построенных графиков функций. Уполномоченные в группах должны назвать вертикальные и горизонтальные асимптоты для графиков своих функций.
Вопрос классу: Сформулируйте определение сложной функции?
3. Два учащихся выполняют задание у доски:
Построить графики и описать свойства следующих функций:
а)
б)
В это время идет исследование:
Как построить график суммы функций ?
- Найти область определения функции.
- Произвести сложение ординат точек графиков.
Например: Постройте график функции
Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.
Проверка с помощью мультимедийного проектора.
Здесь же, с помощью проектора, рассмотреть другой пример графика суммы функций
По аналогии обсудить: как построить график разности функций.
Как построить график произведения функций ?
- Найти область определения функции.
- Произвести умножение ординат точек графиков.
Например: Постройте график функции
Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.
Проверка с помощью мультимедийного проектора. С помощью проектора рассмотреть другой пример графика произведения функций
По аналогии обсудить: как построить график частного функций.
Рассмотреть с помощью проектора график функции
4. С помощью проектора, проверить правильность построения графиков суперпозиции функций (проанализировать работу двух учащихся, которые ранее работали у доски, показать особенности графиков).
Творческое домашнее задание:
Построить графики суммы, разности произведения функций, график сложной функции (подсказка в учебнике после п.2).
Итог урока:
Построение графиков функций один из самых интересных вопросов в курсе алгебры. Графики сложных функций чаще всего получаются очень красивыми и необычными. Поэтому изучение этого материала приносит не только практическую пользу
(например: в физике при изучении волновых явлений), но и эстетическое наслаждение.
Рефлексия:
- Что вам понравилось (или не понравилось) на уроке?
- Что нового вы узнали?
- Ваши пожелания?
Приложение.
Построение графиков сложных функций
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Время реализации практикума 4 часа.
Цели урока:
- образовательная: закрепить знания по формированию массивов данных в табличной форме, отработать навык построения графиков сложных функций;
- развивающая: развивать алгоритмическое мышление; умение применять полученные знания при решении задач; умение рассуждать; развивать познавательный интерес;
- воспитательная: прививать учащимся навык самостоятельности в работе, воспитывать трудолюбие, чувство уважения к науке.
Тип урока: Урок обобщения и изучение нового материала.
Форма урока: Комбинированная.
Учебно-методическое оснащение урока:
- ПК, проектор;
- ПО: MS Windows, MS Excel;
- Технологические карты.
План урока.
1. Организационный этап.
2. Объявление темы и целей урока.
3. Повторение изученного материала.
4. Основная часть.
4.1. Построение трехмерных поверхностей (гиперболического параболоида, эллиптического параболоида).
4.2. Построение графиков сложных тригонометрических функций, заданными параметрическими уравнениями. (построение графика фигуры Лиссажу).
5. Закрепление полученных знаний. Компьютерный практикум.
5.1. Построение трехлепестковой розы.
5.2. Построение графика четырехлепестковой розы.
6. Проверка работы учащихся.
7. Подведение итогов урока.
8. Домашнее задание.
Ход урока
| № | Этапы урока | Действие учителя | Действия учащихся |
| 1 | Организационный этап. | Проверка наличия учащихся, готовность к
уроку. Постановка целей и задач урока |
|
| 2 | Объявление темы и целей урока | Сегодня мы познакомимся с разными сложными графиками и научимся строить графики трехмерных поверхностей и сложные тригонометрические функции. | Слайд № 1, Слайд № 2. |
| 3 | Повторение изученного материала. | Вопросы учащимся Слайд № 3. |
Отвечают на вопросы Слайд № 3. |
| 4 | 4. Основная часть. | Знакомит с поверхностью
эллипти?ческого параболоида. Параболоиды в мире техники и литературы. Материал из Википедии Слайд № 4, 5,6. |
Слайд № 4, 5,6. |
| 5 | 4.1. Построение трехмерных поверхностей (гиперболического параболоида, эллиптического параболоида). | Пример с подробным объяснением учителя. Построение графика гиперболического параболоида. Выдает Технологическая карта № 1 (приложение 1) С подробным объяснением учителя. Построение графика эллиптического параболоида. Выдает Технологическая карта № 2. (приложение 3) |
Получают Технологическая карта № 1. (приложение 1) Строят график. гиперболического параболоида. (приложение 2)
Строят график эллиптического параболоида. (приложение 4) |
| 6 | 4.2. Построение графиков сложных тригонометрических функций, заданными параметрическими уравнениями. (построение графика фигуры Лиссажу ). | Ознакомление с полярной системой
координат. Посмотреть связь между декартовыми и
полярными координатами. Использование
параболоидов в мире технике и
литературе.Знакомятся с графиками сложных
функций. (Материал из Википедии – свободной энциклопедии). Показывает Слайд № 7 — 14 С подробным объяснением учителя. Построение графика фигуры Лиссажу Выдает Технологическая карта № 3. (приложение 5) |
Получают Технологическая карта № 3. (приложение 5)
Слайд № 7 — 14
Строят график фигуры Лиссажу (приложение 6) |
| 7 | Закрепление полученных знаний.
Компьютерный практикум. 5.1. Построение трехлепестковой розы. (1 вариант) |
Самостоятельно строят график
трехлепестковой розы. Выдает Технологическая карта № 4. (приложение 7) |
Получают Технологическая карта № 4. (приложение 7) Строят график (приложение 8) |
| 8 | 5.2. Построение графика четырехлепестковой розы. (2 вариант) | Самостоятельно строят график четырехлепестковой розы. | Строят график (приложение 9) |
| 9 | Проверка работы учащихся. | Проверяет работу. | Сдают по желаниюКонтрольные точки 1,2,3,4,5. (все графики) |
| 10 | Подведение итогов урока. | Подводятся итоги урока, выставляются оценки с аргументацией (используются контрольные точки). Постановка задач для следующего урока. | |
| Домашнее задание. | Повторить материал по теме “Построение графиков в электронных таблицах” |
Ход урока
1. Организационный этап.
Проверка наличия учащихся, готовность к уроку.
Постановка целей и задач урока
2. Объявление темы и целей урока. Слайд № 1,2.
Учитель: Сегодня мы будем строить необычные графики, графики трехмерных поверхностей: гиперболического параболоида, эллиптического параболоида. Построение графиков является частным случаем построения диаграмм. Графики позволяют анализировать закономерности изменения величин. Мы будем работать с электронными таблицами, которые позволяют обрабатывать большие массивы числовых данных. В результате вы получите интересные, красивые графики, сложные графики. Построив их, вы сможете рассмотреть проекции фигуры на плоскость.
3. Повторение изученного материала. Слайд № 3.
Вопросы:.
- Назначение электронных таблиц, применение в каких отраслях жизни?
- Перечислите основные функции электронных таблиц.
- Какими способами можно включить Мастер диаграмм?
- Назовите основные типы диаграмм?
- Как связана таблица и построенная диаграмма?
- Что такое диаграмма и какие действия возможны с ней?
- В формулах вы будите использовать ссылки.
Вопросы:
- Какие основные типы ссылок вы знаете?
- Назовите различия между относительными и абсолютными ссылками проявляются при копировании формулы из активной ячейки в другую ячейку?
4. Основная часть. Использование этих графиков в мире техники и в литературе. Слайды № 4,5,6.
4.1. Построение трехмерных поверхностей (гиперболического параболоида, эллиптического параболоида).
Пример с подробным объяснением учителя.
Задание 1. График гиперболического параболоида описывается уравнением z = (х/а)2 — (у/в)2, а эллиптического параболоида z = (х/а)2 + (у/в)2. Диапазон изменения переменных х и у – квадрат (-5;5)C (-5;5) с шагом 0,5. Переименуйте Лист 2, в “График 2” для гиперболического параболоида
Технология работы. Выдается технологическая карта с подробным построением графика.
Технологическая карта № 1. Приложение 1.
Контрольная точка 1. Представьте преподавателю результаты работы.
Приложение 2
Задание 2. Построение графика эллиптического параболоида z = (х/а)2 + (у/в)2. Диапазон изменения переменных х и у – квадрат (-5;5)C (-5;5) с шагом 0,5.
Построить график согласно таблице на Листе 3.
Технология работы. Выдается технологическая карта с подробным построением графика.
Технологическая карта № 2. Приложение 3.
Контрольная точка 2. Представьте преподавателю результаты работы.
Приложение 4.
4.2. Построение графиков сложных тригонометрических функций, заданными параметрическими уравнениями (графика фигуры Лиссажу).
Ознакомление с полярной системой координат. Посмотреть связь между декартовыми и полярными координатами. Использование параболоидов в мире технике и литературе.
(Материал из Википедии – свободной энциклопедии). Слайды № 4-17.
Задание № 3. Построить график фигуры Лиссажу. Пример с подробным объяснением учителя.
Технология работы. Выдается технологическая карта с подробным построением графика.
Технологическая карта № 3. Приложение 5.
Контрольная точка 3. Представьте преподавателю результаты работы.
Приложение 6.
5. Закрепление полученных знаний. Компьютерный практикум.
При решении этих задач закрепляются умения учащихся заполнять таблицы и строить график.
5.1. Построение трехлепестковой розы.
Задание 4. Построить график трехлепестковой розы r=sin 3a, для этого необходимо заполнить столбец х=r*cos a, у=r*sin a. Осуществить переход от градусной меры в радианную по формуле =ПИ()/180*ячейку с градусной мерой. Перейти на Лист 5 и переменуйте в “График 5”.
Технология работы.
Выдается технологическая карта с подробным построением графика.
Технологическая карта № 4. Приложение 7.
Контрольная точка 5. Представьте преподавателю результаты работы.
Приложение 8.
5.2. Построение четырехлепестковой розы
Задание 5. Построить график четырехлепестковой розы r=sin 2a, для этого необходимо заполнить столбец х=r*cos a, у=r*sin a. Осуществить переход от градусной меры в радианную по формуле =ПИ()/180*ячейку с градусной мерой. Перейти на Лист 6 и переменуйте в “График 6”.
Контрольная точка 6. Представьте преподавателю результаты работы
Приложение 9.
6. Проверка работы учащихся.
Учащиеся демонстрируют подготовленные файлы выполненной работы.
7. Подведение итогов урока.
Научились строить графики сложных функций, получили практические навыки работы с большими таблицами.
Подводятся итоги урока, выставляются оценки с аргументацией (используются контрольные точки). Постановка задач для следующего урока.
8. Домашнее задание.
Повторить материал по теме “Построение графиков в электронных таблицах”.
Индивидуальный проект на тему «Построение сложных тригонометрических графиков»
Министерство образования и молодежной политики Ставропольского края
Государственное бюджетное профессиональное образовательное учреждение
Георгиевский региональный колледж «Интеграл»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
По дисциплине « Математика: алгебра, начала математического анализа, геометрия»
На тему: «Построение сложных тригонометрических графиков»
Выполнила студентка группы ДУ-61, обучающаяся по специальности
«Документационное обеспечение управления и архивоведение »
Куренкова Надежда Алексеевна
Руководитель: преподаватель Серкова Н.А.
Дата сдачи: « » 2017г.
Дата защиты: « » 2017г.
Георгиевск 2017г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ЦЕЛЬ ПРОЕКТА:
Цель: выявление методов построения графиков сложных тригонометрических функций.
Задачи:
проанализировать литературу по проблеме исследования;
раскрыть сущность методов построения графиков сложных тригонометрических функций;
подобрать и разработать творческие задания, способствующие развитию навыков построения графиков сложных тригонометрических функций
Актуальность исследования: Анализ материала, посвящённого построению графиков сложных тригонометрических функций в учебных пособиях «Алгебра и начала математического анализа» разных авторов, учёт целей изучения данной темы. Атак же обязательных результатов обучения, связанных с рассматриваемой темой.
Основной целью написания данного проекта является представление общих методов построения графиков сложных тригонометрических функций.
Содержание
Введение
Определение синуса, косинуса, тангенса и котангенса.
Графики функций: у=sinx, y=cosx, y=tgx и y=ctgx.
3. Построение графиков с помощью упрощения формулы. Примеры.
4.Заключение
5.Список источников
Введение
Функция выражает зависимость между переменными величинами. Каждая область знаний химия, физика, биология, социология и др. имеет свои объекты изучения, устанавливает свойства и взаимосвязи между этими объектами в реальном мире. Впервые функция вошла в математику под именем “переменная величина”, в труде французского математика и философа Рене Декарта в 1637 году. Сам термин “функция” впервые встречается в рукописи немецкого математика и философа Г.Лейбница. Леонард Эйлер ввёл принятые сейчас обозначения для функций. Сложный, очень длительный путь развития понятия функции. С ним связаны имена Н.И.Лобачевского, Л.Дирихле, Г. Кантора. Сейчас многие науки берут на вооружение математический аппарат. Такие функциональные зависимости, например, возраст деревьев, развитие папоротника изучает наука биология. Функции помогают описывать процессы механического движения тел небесных и земных. С помощью них учёные рассчитывают траектории движения космических кораблей и решают множество технических проблем. Наряду с другими функциями тригонометрические занимают важное место. Тригонометрия возникла из практических нужд человека. Современный вид тригонометрии придал крупнейший математик 18 столетия Леонард Эйлер. Почему летом жарко? Многие считают, что летом жарче, так как Земля находится ближе всего к солнцу, но это не так. Орбита Земля – это почти круг, в центре которого находится солнце, и расстояние от Земли меняется незначительно из месяца в месяц. Всё дело в наклоне земной оси по отношению к плоскости земной орбиты. Зимой солнце невысоко поднимается над горизонтом, его лучи лишь скользят по земле. Летом солнце приближается к зениту, лучи его падают почти отвесно. Поток солнечной энергии одинаков во все времена. Он зависит от угла падения лучей. Меняется угол падения и меняется доля солнечной энергии. Зависимость солнечной энергии от угла падения лучей и выражает график y = sinx.
В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в школьном курсе алгебры за 10 класс. Тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций (до применения производной), а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание. Все выше сказанное и обуславливает актуальность выбора темы для данной работы.
1. Определение синуса и косинуса
Синус, одна из тригонометрических функций, обозначение sin. Синус острого угла в прямоугольном треугольнике называется отношение катета, лежащего против этого угла, к гипотенузе. Инд. математики синус обозначали словом «джива» (букв. — тетива лука). Арабы переделали этот термин в «джиба», который в дальнейшем превратился в «джайо» — обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus.
Косинус (новолат. cosinus, сокращение от complementi sinus — синус дополнения), одна из тригонометрических функций; обозначение cos. К. острого угла в прямоугольном треугольнике называется отношение катета, прилежащего к этому углу, к гипотенузе.
Тангенс (от лат. tangens — касающийся), одна из тригонометрических функций; обозначение tg. Т. острого угла в прямоугольном треугольнике называется отношение противолежащего катета к катету, прилежащему к этому углу.
Котангенс (новолат. cotangens, сокращение от complementi tangens — тангенс дополнения), одна из тригонометрических функций, обозначение ctg. К. острого угла в прямоугольном треугольнике называется отношение катета, прилежащего к этому углу, к противолежащему катету.
Синусом α называется отношение AB/OB (отношение противолежащего катета к гипотенузе)
Косинусом α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе)
Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
Секансом α называется отношение ОB/OA (отношение гипотенузы к прилежащему катету)
Косекансом α называется отношение ОB/AB (отношение гипотенузы к противолежащему катету)
2. Графики функций: у=sinx, y=cosx, y=tgx и y=ctgx


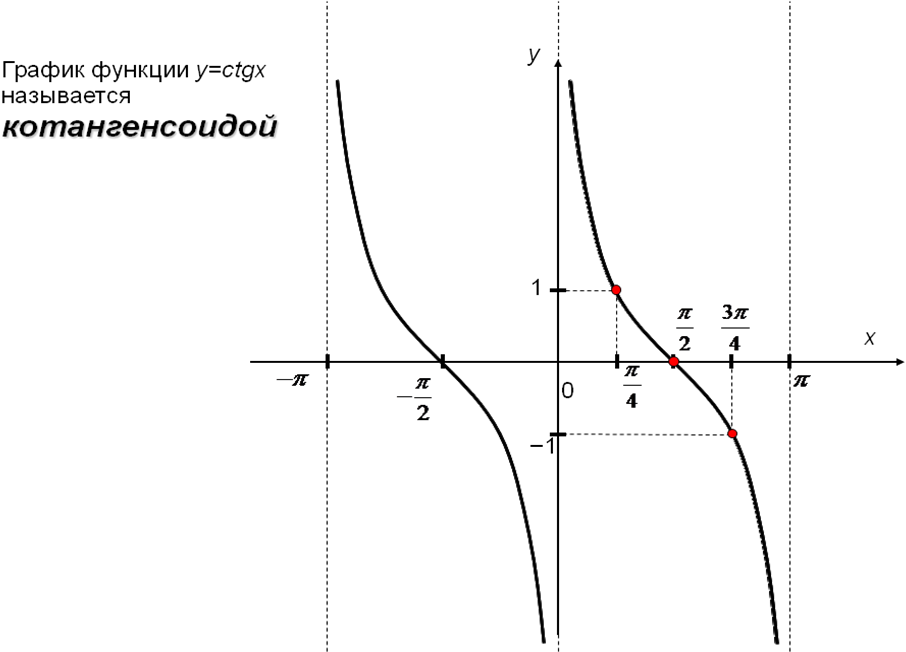
3. Построение графиков с помощью упрощения уравнения функции. При построении графиков функций сложного вида можно примерно придерживаться следующего плана.
Найти область определения и область значений функции.
Выяснить, является ли функция четной (нечетной).
Выяснить, является ли функция периодической.
Найти точку пересечения графика функции с осью ординат.
Найти нули функции и промежутки знакопостоянства.
Вычислить производную функции f(x) и определить точки, в которых могут существовать экстремумы.
Найти промежутки монотонности функции.
Определить экстремумы функции.
Вычислить вторую производную f(x)
Определить точки перегиба.
Найти промежутки выпуклости функции.
Найти асимптоты графика.
Найти значения функции в нескольких контрольных точках.
Построить эскиз графика функции.
Примеры
1. y=
ОДЗ: sin x ≠ 0
x ≠ πk;
y===
y=2 cos x │sin x│
a) Если sin x˃0, то y=2 cos x │sin x│
( 2πk < x < π+2πk ) y = sin 2x
T==π

b) Если sin x˂0, то y=-2cos x * sin x
( π+2πk ˂ x ˂ 2π+2πk ) y=-sin 2x
2. y=
ОДЗ: cos x ≠0
x≠;
y= =˃ y=;
a) Если cos x˃0, то y=;
( — y= cos x

b) Если cos x˂0, то y=-cos x
(
3. y= на [0;π]
ОДЗ: 2x ≠

x≠ k=0,1,2,3,4
y= ;

а) Если sin 2x˂0, то y= -=-sin2x
2πk ˂2x˂ π+2πk
б) Если sin 2x˂0, то y= sin2x
π+2πk ˂2x˂ 2π+2πk
4. y= на []
y=
ОДЗ: ctg 2x≠1
2x ≠ πk

x≠ k=0,1
2x ≠
x ≠ k=0,1,2,-1,-2
5. y=
=│cos 2x│*tg 2x=

a) Если cos 2x˂0, то y=-sin 2x
—
b) Если cos 2x˂0, то y=-sin 2x
Заключение
Таким образом, цель нашей работы –представить способы построения графиков сложных тригонометрических функций — выполнена.
В данном проекте дано определение синуса, косинуса, тангенса и котангенса, представлены способы построения графиков сложных тригонометрических функций и примеры функций, в которых используются данные методы. Анализ научной литературы, учебников математики позволил структурировать отобранный материал в соответствии с целями исследования, подобрать и разработать эффективные методы построения графиков сложных тригонометрических функций. В работе представлены методы построения графиков сложных тригонометрических функций и примеры функций, в которых используются данные методы.
Алгебра и начала математического анализа. 10-11 классы. Задачник для учащихся общеобразовательных учреждений (базовый уровень)/ [А.Г. Мордкович и др.] – 10-е издание- Москва: Мнемозина, 2009.
www. wikipedia.org
Выступление на НПК по теме «Построение графиков сложных функций»
Исследовательская работа по теме:
«Построение графиков сложных функций»
Выполнила:
Ганиева Айгуль Азатовна
9 б класс
МБОУ СОШ №3
Руководитель: Гайнутдинова
Ольга Николаевна
Проблемный вопрос:
Как можно построить графики сложных функций?
Цели и задачи
Овладеть умением представлять сложную функцию в виде композиции двух функций
Освоить приём построения эскиза графика функции без применения производной
Показать возможность использования схемы построения графиков сложных функций вида y=f(φ(x))
изучить области, в которых применяется функция и её свойства
Введение
Во многих задачах график является лишь вспомогательным элементом решения.
Построение графика сложной функции вида y = f(φ(x)) без использования производной можно осуществлять элементарными способами по некоторой схеме.
Все указанные операции можно проводить непосредственно над графиками основных элементарных функций (понимая под этим выполнение операций над соответствующими координатами), поскольку эти графики известны. Как правило, график функции y = f(φ(x)) трудно, а порой и просто невозможно построить, используя общую схему исследования функции.
Формула для задания сложной функции
y=f(g(x)) –
– сложная функция
g(x) – внутренняя функция
Пример.

g(x) = х2 — 4 – внутренняя функция
f(t) = – внешняя функция
f(t) – внешняя функция
Мы предположили, что функциональные зависимости существуют во всех сферах жизни человека. Сейчас мы попытаемся это доказать.
Основная часть
С хема построения графика сложной функции
хема построения графика сложной функции
Построение графиков функций вида

Построение графиков функций вида
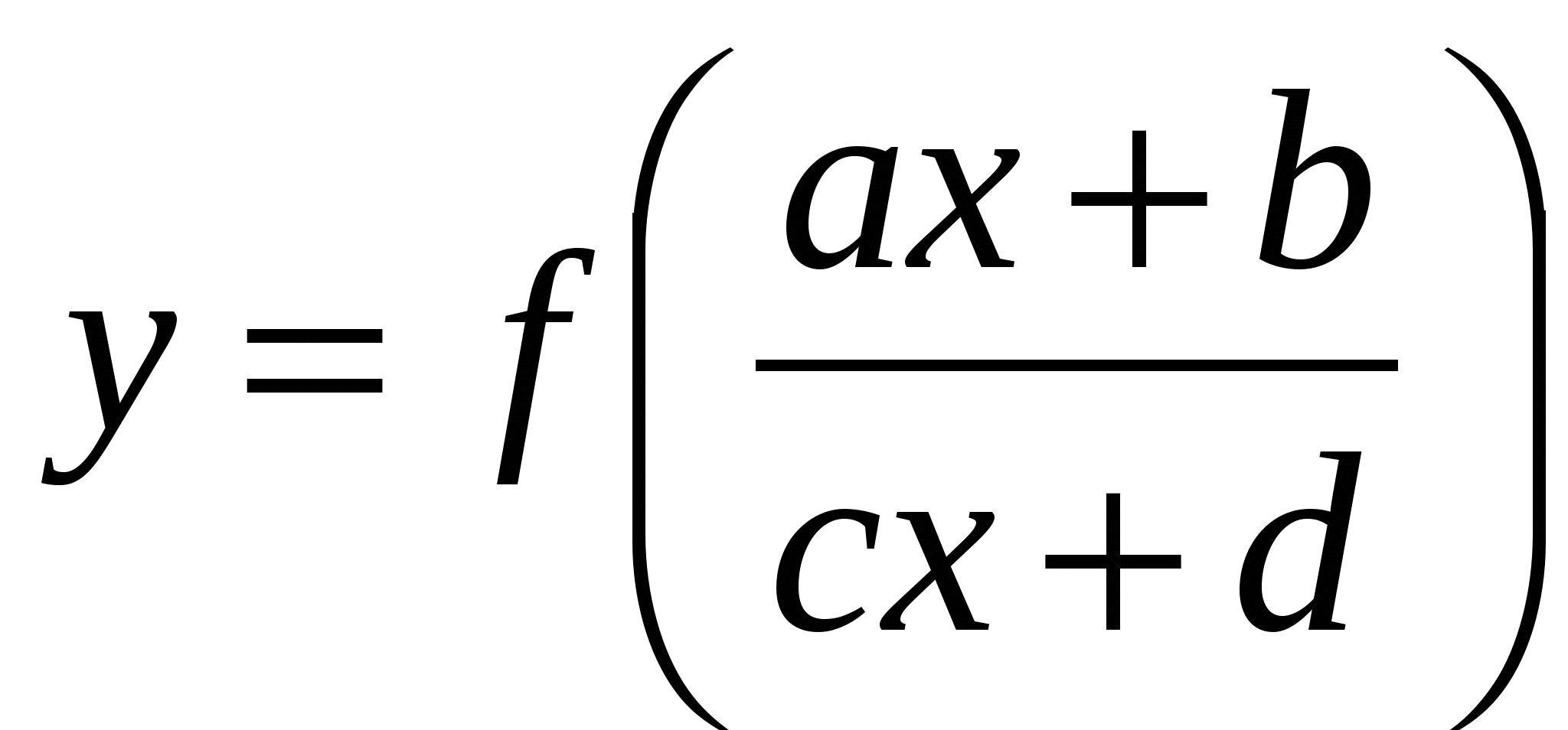
Построение графиков функций вида
Схема построения графика сложной функции у = f(φ(x))
Найти область определения исследуемой сложной функции, а также граничные значения функции.
Построить график внешней и внутренней функции.
Построить график функции у1 = φ(х). Отметить на этом графике характерные точки, т. е. нули и точки разрыва, найти граничные точки, одну — две промежуточные точки;
Произвести заданные операции над ординатами выбранных точек.
Нанести полученные точки и предельные значения на рисунок, помещённый под графиком функции у1 = φ(х) так, чтобы у1 была продолжением оси у.
Соединить полученные точки сплошной линией в тех промежутках, в которых функция непрерывна, и учесть (если она имеется) симметрию графика относительно точки или прямой.

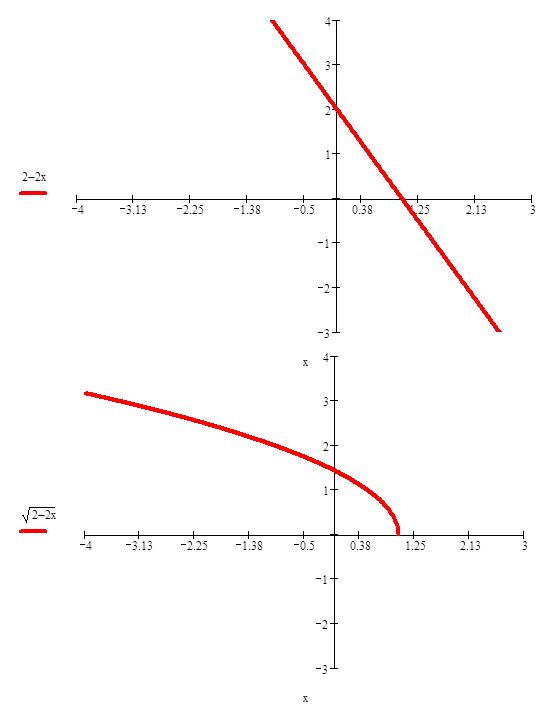
Построение графиков функций вида


Сначала надо построить график линейной функции (внутренней функции)
Найти точки пересечения графика с осью x и y.
Затем в той системе координат надо построить график внешней функции, используя точки пересечения первого графика.
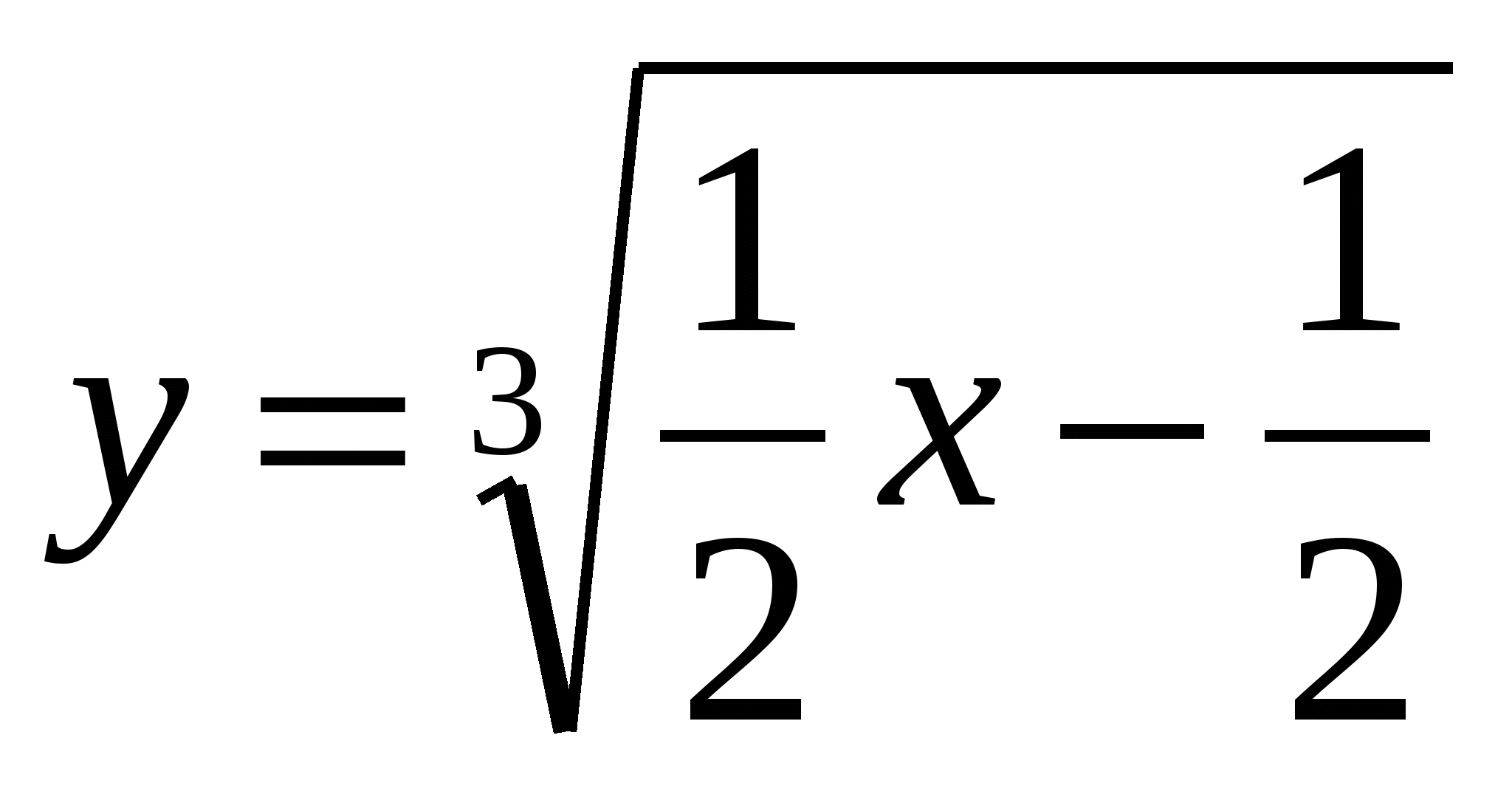
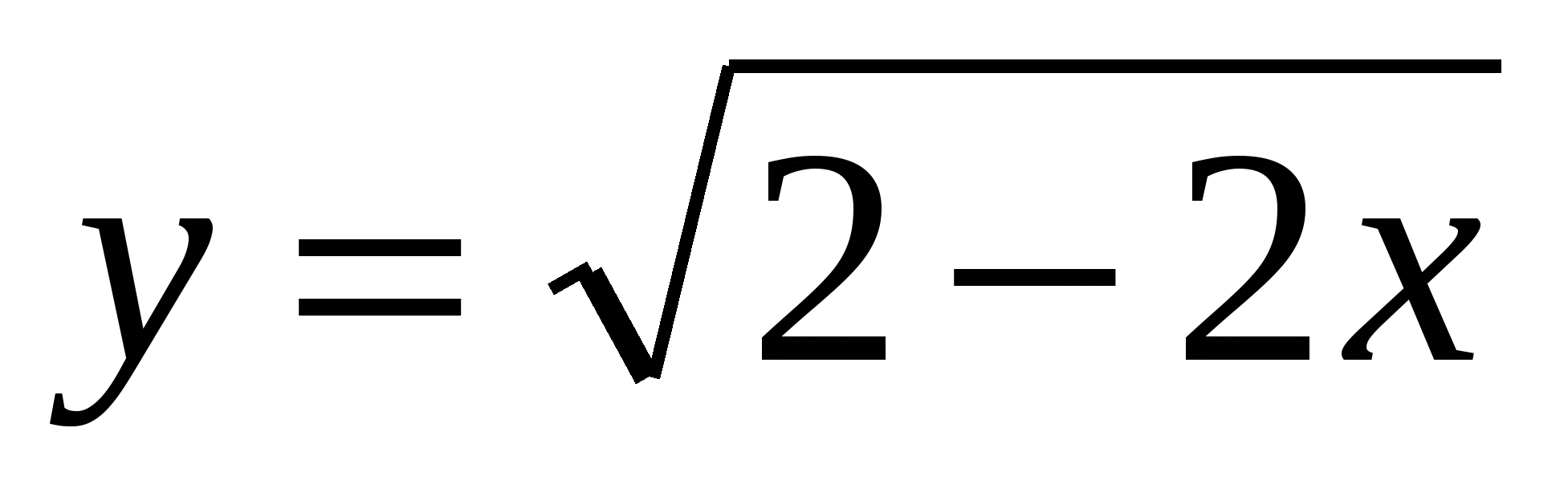
П остроение графиков функций вида
остроение графиков функций вида
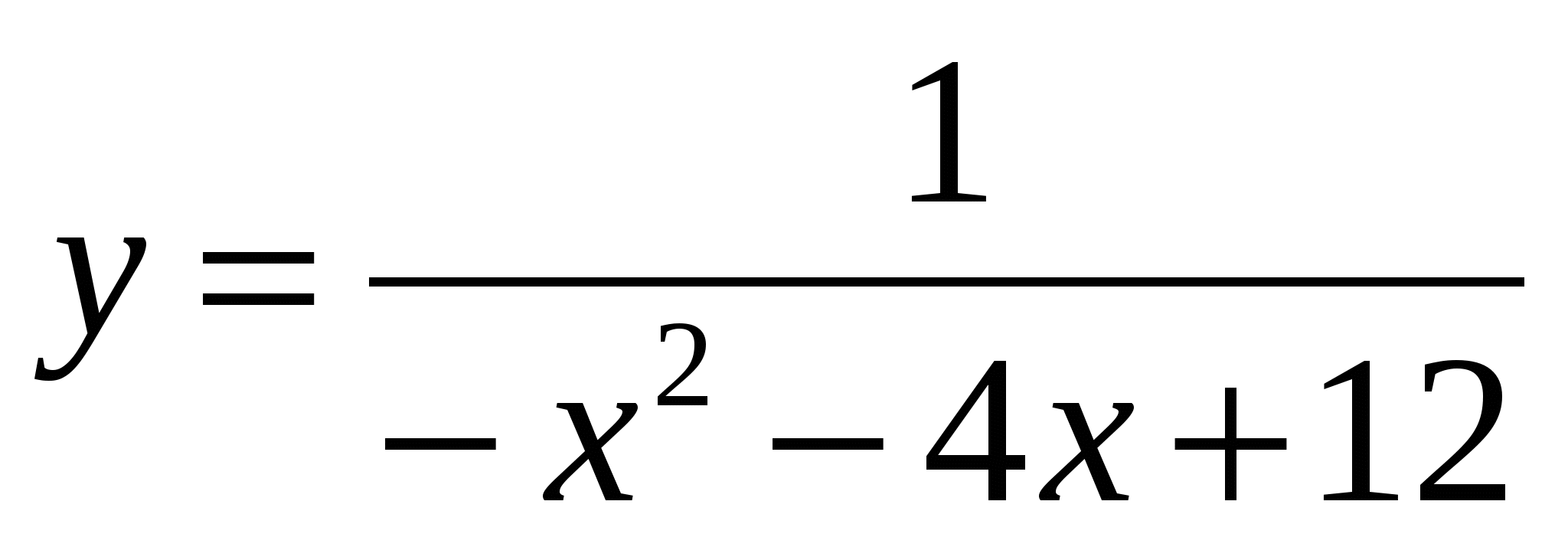

Применение функций в точных науках
Графики зависимости физических величин,
параболоиды,
отображение звуковых волн с помощью периодической функции
Периодическая функция
F(x)=F(x±nT)
Звук, колебания за просторами Земли.
Фазы звуковой волны
Для описания относительных временных свойств двух звуковых волн (или разных частей одной волны) вводится понятие фазы звуковой волны.
Графики пословиц
«Посев хуже недосева», «Каши маслом не испортишь»,
«Чем дальше в лес, тем больше дров», «Горяч на почине, да скоро остыл»
Дни солнцестояния
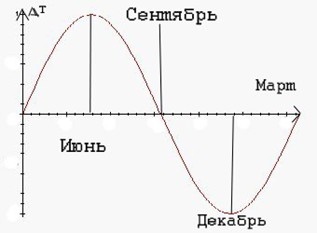
С помощью графика мы можем увидеть, что точки, где график, похожий на график синуса, пересекает ось времени соответствуют 23 сентября и 21 марта
Основные результаты
Для построения графика функции любой сложности необходимо знать и применять свойства элементарных функций (область определения, нули функции, четность и нечетность, периодичность и т. д.).
График сложной функции y = f(φ(x)) можно построить с помощью упрощенной схемы, если использовать операции над графиками (понимая под этим выполнение операций над соответствующими координатами).
Я надеюсь, что мои исследования убедили Вас в том, что функция является неотъемлемой частью нашей жизни и наук в целом.
Эта работа может быть предложена в качестве развивающего компонента на уроках алгебры (демонстрация презентации при изучении темы «Исследование функции» и в рамках предметной недели).
Рене Декарта сказал:
“Прямая – есть кратчайшее расстояние между двумя точками”.
И следуя этому правилу, я призываю вас в своем развитии по восходящей линии, не страшась усталости, не обходя трудностей, идти по прямой от точки не знания к точке знания.
Список ресурсов:
Гусев В.А., Мордкович А.Г. Математика: Справочные материалы. – М.: Просвещение, 1988
Гурский И. П. Графики сложных функций
Дворянинов С. В. О построении графиков сложных функций на основе свойства монотонности. Журнал «Математика в школе»
Дорофеев Г.В. Пособие по математике для поступающих в вузы. – М.: Наука, 1972
Костюкова Н.К. Научно-исследовательская работа учащихся. – М.: Математика в школе №5, 1999
Райхмист Р.Б. Графики функций: задачи и упражнения. – М.: Школа — Пресс, 1997
Рывкин А.А. Справочник по математике – М.: Высшая школа, 1987
Факультативный курс по математике — М.: Просвещение, 1991
http://mathem.by.ru/index.html