Смешанные числа | Формулы с примерами

Смешанное число — это сумма натурального числа и правильной дробия, записанная без знака «+».

Пример

213 = 2 +13;

325 = 3 +25;

577 = 5 +1313;

Приведение смешанного числа в виде неправильной дроби

Чтобы смешанную дробь привести к неправильной, надо умножить целую часть на знаменатель и добавить к полученному результату числитель.

Пример

Наглядный пример

Приведение неправильной дроби в виде смешанного числа

Чтобы неправильную дробь привести к смешанной, нужно числитель поделить на знаменатель.

Пример

Наглядный пример

formula-xyz.ru

Математика для блондинок: Смешанные дроби

Вот такой вот крик души:

Весь день вожусь с примером со смешанными дробями и десятичными дробями! Никак не могу понять, как такой решить?!?

Пример на смешанные дроби

Да, этот пример на смешанные дроби действительно выглядит как тираннозавр Рекс (он же Тирекс) в глазах млекопитающих. Ничего, наши предки пережили динозавров, и мы, как-нибудь, математиков переживем. Для этого достаточно уметь пользоваться своими знаниями.

Начнем с третьего слагаемого. Что такое дробная черта? Это один из вариантов записи математической операции деления. Значит, дробную черту на двоеточие (или наоборот) мы можем менять так, как нам захочется. Что ещё полезного мы знаем о дробях? Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй дроби. Если говорить по-человечески, то вторую дробь необходимо перевернуть вверх ногами и можно выполнять умножение. А ещё мы знаем, что любую десятичную дробь можно записать в виде дроби обычной. Что ещё полезного можно делать с дробями? Дроби можно сокращать, уменьшая числитель и знаменатель в одинаковое количество раз. Ну, и основное правило дробных выражений — сперва выполняются действия в числителе и знаменателе, только после этого числитель делится на знаменатель. А теперь смотрите, как мы воспользуемся этими знаниями.

Большая дробь

Вот так просто (или сложно — кому как) наша большая дробь с дробями превратилась в одно число. Весь смысл этих плясок шаманов с бубнами под названием «действия с дробями» — получить максимально простое число, дробь или алгебраическое выражение.

Вот теперь настало время сложить смешанные дроби. Для этого смешанные дроби нужно превратить в неправильные дроби и выполнить сложение дробей. Как мы знаем, дроби можно складывать только тогда, когда знаменатели дробей равны. А значит, дроби нужно привести к общему знаменателю. Вот этим мы и займемся.

Смешанные дроби

Вот. Пример на смешанные дроби мы решили. Могу вам предложить и другой вариант решения. Достаточно вспомнить, что любую смешанную дробь можно представить как сумму целого числа и дроби. Математические действия можно выполнять отдельно для целых чисел и отдельно для дробных чисел. Сейчас мы под микроскопом рассмотрим этот вариант решения.

Смешанные дроби как сумма

Честно признаюсь, я понятия не имею, какой из способов вычисления смешанных дробей математики считают правильным. Но с точки зрения математики, не имеет никакого значения, как вы будете складывать и вычитать эти дроби — результат всегда будет одним и тем же.

www.webstaratel.ru

Дроби Википедия

У этого термина существуют и другие значения, см. Дробь.

8 / 13{\displaystyle 8~/~13}		813{\displaystyle {\frac {8}{13}}}	числитель
числитель	знаменатель		знаменатель
Две записи одной дроби

Дробь в математике — число, состоящее из одной или нескольких равных частей (долей) единицы^[1]. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на два формата: обыкновенные вида ±mn{\displaystyle \pm {\frac {m}{n}}} и десятичные вида 0,1234{\displaystyle 0{,}1234}.

В записи дроби вида X/Y{\displaystyle X/Y} или XY{\displaystyle {\frac {X}{Y}}} число перед (над) чертой называется числителем, а число после черты (под чертой) — знаменателем. Первый играет роль делимого, второй — делителя.

Содержание

• 1 Виды дробей
  • 1.1 Обыкновенные дроби
    • 1.1.1 Обозначения обыкновенных дробей
    • 1.1.2 Правильные и неправильные дроби
    • 1.1.3 Смешанные дроби
    • 1.1.4 Составные дроби
  • 1.2 Десятичные дроби
• 2 Значение дроби и основное свойство дроби
• 3 Действия с дробями
  • 3.1 Приведение к общему знаменателю
  • 3.2 Сравнение
  • 3.3 Сложение и вычитание
  • 3.4 Умножение и деление
  • 3.5 Преобразование между разными форматами записи
• 4 История и этимология термина
• 5 Обобщения
• 6 См. также
• 7 Литература
• 8 Примечания

Виды дробей[ | ]

Обыкновенные дроби[ | ]

Наглядное представление дроби 3/4

О

ru-wiki.ru

Правильные и неправильные дроби

Обыкновенные дроби делятся на \textit{правильные} и \textit{неправильные} дроби. Такое разделение основано на сравнении числителя и знаменателя.

Правильные дроби

Правильной дробью называется обыкновенная дробь $\frac{m}{n}$, у которой числитель меньше знаменателя, т.е. $m

Пример 1

Например, дроби $\frac{1}{3}$, $\frac{9}{123}$, $\frac{77}{78}$, $\frac{378567}{456298}$ являются правильными, так как в каждой из них числитель меньше знаменателя, что отвечает определению правильной дроби.

Существует определение правильной дроби, которое базируется на сравнении дроби с единицей.

Обыкновенная дробь $\frac{m}{n}$ является правильной, если она меньше единицы:

Пример 2

Например, обыкновенная дробь $\frac{6}{13}$ является правильной, т.к. выполняется условие $\frac{6}{13}

Неправильные дроби

Неправильной дробью называется обыкновенная дробь $\frac{m}{n}$, у которой числитель больше или равен знаменателю, т.е. $m\ge n$.

Пример 3

Например, дроби $\frac{5}{5}$, $\frac{24}{3}$, $\frac{567}{113}$, $\frac{100001}{100000}$ являются неправильными, так как в каждой из них числитель больше или равен знаменателю, что соответствует определению неправильной дроби.

Дадим определение неправильной дроби, которое базируется на ее сравнении с единицей.

Обыкновенная дробь $\frac{m}{n}$ является неправильной, если она равна или больше единицы:

\[\frac{m}{n}\ge 1\]

Пример 4

Например, обыкновенная дробь $\frac{21}{4}$ является неправильной, т.к. выполняется условие $\frac{21}{4} >1$;

обыкновенная дробь $\frac{8}{8}$ является неправильной, т.к. выполняется условие $\frac{8}{8}=1$.

Рассмотрим более подробно понятие неправильной дроби.

Возьмем для примера неправильную дробь $\frac{7}{7}$. Значение этой дроби — взяли семь долей предмета, который поделен на семь одинаковых долей. Таким образом, из семи долей, которые есть в наличии, можно составить весь предмет. Т.е. неправильная дробь $\frac{7}{7}$ описывает целый предмет и $\frac{7}{7}=1$. Итак, неправильные дроби, у которых числитель равен знаменателю, описывают один целый предмет и такая дробь может быть заменена на натуральное число $1$.

Рассмотрим далее неправильные дроби:

• $\frac{5}{2}$ — достаточно очевидно, что из этих пяти вторых долей можно составить $2$ целых предмета (один целый предмет будут составлять $2$ доли, а для составления двух целых предметов нужны $2+2=4$ доли) и остается одна вторая доля. Т.е., неправильная дробь $\frac{5}{2}$ описывает $2$ предмета и $\frac{1}{2}$ долю этого предмета.

• $\frac{21}{7}$ — из двадцати одной седьмых долей можно составить $3$ целых предмета ($3$ предмета по $7$ долей в каждом). Т.е. дробь $\frac{21}{7}$ описывает $3$ целых предмета.

Из рассмотренных примеров можно сделать следующий вывод: неправильную дробь можно заменить натуральным числом, если числитель нацело делится на знаменатель (например, $\frac{7}{7}=1$ и $\frac{21}{7}=3$), или суммой натурального числа и правильной дроби, если числитель нацело не делится на знаменатель (например,$\ \frac{5}{2}=2+\frac{1}{2}$). Поэтому такие дроби и называются неправильными.

Определение 1

Процесс представления неправильной дроби в виде суммы натурального числа и правильной дроби (например, $\frac{5}{2}=2+\frac{1}{2}$) называется выделением целой части из неправильной дроби.

При работе с неправильными дробями прослеживается тесная связь между ними и смешанными числами.

Неправильная дробь часто записывается в виде смешанного числа — числа, которое состоит из целой и дробной части.

Чтобы записать неправильную дробь в виде смешанного числа, необходимо разделить числитель на знаменатель с остатком. Частное будет составлять целую часть смешанного числа, остаток — числитель дробной части, а делитель — знаменатель дробной части.

Пример 5

Записать неправильную дробь $\frac{37}{12}$ в виде смешанного числа.

Решение.

Разделим числитель на знаменатель с остатком:

\[\frac{37}{12}=37:12=3\ (остаток\ 1)\] \[\frac{37}{12}=3\frac{1}{12}\]

Ответ. $\frac{37}{12}=3\frac{1}{12}$.

Чтобы записать смешанное число в виде неправильной дроби, необходимо знаменатель умножить на целую часть числа, к произведению, которое получилось, прибавить числитель дробной части и записать полученную сумму в числитель дроби. Знаменатель неправильной дроби будет равен знаменателю дробной части смешанного числа.

Пример 6

Записать смешанное число $5\frac{3}{7}$ в виде неправильной дроби.

Решение.

\[5\frac{3}{7}=\frac{5\cdot 7+3}{7}=\frac{38}{7}\]

Ответ. $5\frac{3}{7}=\frac{38}{7}$.

Сложение смешанного числа и правильной дроби

Сложение смешанного числа $a\frac{b}{c}$ и правильной дроби $\frac{d}{e}$ выполняет прибавлением к данной дроби дробной части данного смешанного числа:

\[a\frac{b}{c}+\frac{d}{e}=a+\left(\frac{b}{c}+\frac{d}{e}\right)\]

Пример 7

Выполнить сложение правильной дроби $\frac{4}{15}$ и смешанного числа $3\frac{2}{5}$.

Решение.

Воспользуемся формулой сложения смешанного числа и правильной дроби:

\[\frac{4}{15}+3\frac{2}{5}=3+\left(\frac{2}{5}+\frac{4}{15}\right)=3+\left(\frac{2\cdot 3}{5\cdot 3}+\frac{4}{15}\right)=3+\frac{6+4}{15}=3+\frac{10}{15}\]

По признаку деления на число \textit{5 }можно определить, что дробь $\frac{10}{15}$ — сократима. Выполним сокращение и найдем результат сложения:

\[3+\frac{10}{15}=3+\frac{10:5}{15:5}=3+\frac{2}{3}=3\frac{2}{3}\]

Итак, результатом сложения правильной дроби $\frac{4}{15}$ и смешанного числа $3\frac{2}{5}$ будет $3\frac{2}{3}$.

Ответ: $3\frac{2}{3}$

Сложение смешанного числа и неправильной дроби

Сложение неправильной дроби и смешанного числа сводят к сложению двух смешанных чисел, для чего достаточно выделить целую часть из неправильной дроби.

Пример 8

Вычислить сумму смешанного числа $6\frac{2}{15}$ и неправильной дроби $\frac{13}{5}$.

Решение.

Сначала выделим целую часть из неправильной дроби $\frac{13}{5}$:

\[\frac{13}{5}=2\frac{3}{5}\]

Далее сложение смешанного числа и неправильной дроби сводится к сложению двух смешанных чисел:

\[6\frac{2}{15}+2\frac{3}{5}=6\frac{2}{15}+2\frac{3\cdot 3}{5\cdot 3}=6+2+\frac{2}{15}+\frac{9}{15}=8+\frac{11}{15}=8\frac{11}{15}\]

Ответ: $8\frac{11}{15}$.

spravochnick.ru

Смешанные дроби | Математика

Смешанные дроби (смешанные числа) — это числа, запись которых содержит целую и дробную часть

(где дробная часть — правильная дробь).

Например,

   

— смешанные дроби (или смешанные числа).

Смешанные дроби можно представить в виде суммы его целой и дробной частей.

Например, 

   

   

   

   

И обратно, сумму целого числа и дроби можно представить в виде смешанной дроби (смешанного числа).

Например,

   

   

   

Смешанные дроби можно переводить в обыкновенные неправильные дроби.

Выделив из неправильной дроби целую часть, получаем смешанное число.

Смешанные дроби можно складывать, вычитать, умножать, делить, возводить в степень. Как выполнять различные  действия над смешанными числами, мы рассмотрим позже.

Светлана МихайловнаДроби с одинаковыми знаменателями

www.for6cl.uznateshe.ru

как научиться решать с ними примеры? :: SYL.ru

При слове «дроби» у многих бегут мурашки. Потому что вспоминается школа и задания, которые решались на математике. Это являлось обязанностью, которую необходимо было выполнить. А что если относиться к заданиям, содержащим правильные и неправильные дроби, как к головоломке? Ведь многие взрослые решают цифровые и японские кроссворды. Разобрались в правилах, и все. Так же и здесь. Стоит только вникнуть в теорию — и все встанет на свои места. А примеры превратятся в способ потренировать мозг.

Какие виды дробей существуют?

Для начала о том, что это такое. Дробь — число, которое имеет некоторую часть от единицы. Ее можно записать в двух видах. Первый носит название обыкновенной. То есть такая, у которой есть горизонтальная или наклонная черта. Она приравнивается к знаку деления.

В такой записи число, стоящее над черточкой, называется числителем, а под ней — знаменателем.

Среди обыкновенных выделяют правильные и неправильные дроби. У первых числитель по модулю всегда меньше знаменателя. Неправильные потому так и называются, что у них все наоборот. Значение правильной дроби всегда меньше единицы. В то время как неправильная всегда больше этого числа.

Есть еще смешанные числа, то есть такие у которых имеются целая и дробная части.

Второй вид записи — десятичная дробь. О ней отдельный разговор.

Чем отличаются неправильные дроби от смешанных чисел?

По своей сути, ничем. Это просто разная запись одного и того же числа. Неправильные дроби после несложных действий легко становятся смешанными числами. И наоборот.

Все зависит от конкретной ситуации. Иногда в заданиях удобнее использовать неправильную дробь. А порой необходимо перевести ее в смешанное число и тогда пример решится очень легко. Поэтому, что использовать: неправильные дроби, смешанные числа, — зависит от наблюдательности решающего задачу.

Смешанное число еще сравнивают с суммой целой части и дробной. Причем вторая всегда меньше единицы.

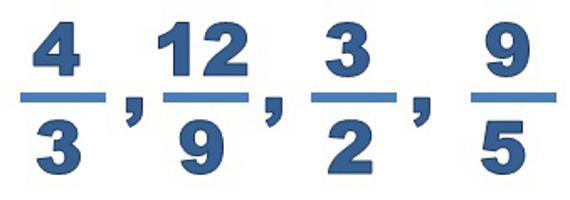
Как представить смешанное число в виде неправильной дроби?

Если требуется выполнить какое-либо действие с несколькими числами, которые записаны в разных видах, то нужно сделать их одинаковыми. Один из методов — представить числа в виде неправильных дробей.

Для этой цели потребуется выполнить действия по такому алгоритму:

• умножить знаменатель на целую часть;
• прибавить к результату значение числителя;
• записать ответ над чертой;
• знаменатель оставить тем же.

Вот примеры того, как записать неправильные дроби из смешанных чисел:

• 17 ¼ = (17 х 4 + 1) : 4 = 69/4;
• 39 ½ = (39 х 2 + 1) : 2 = 79/2.

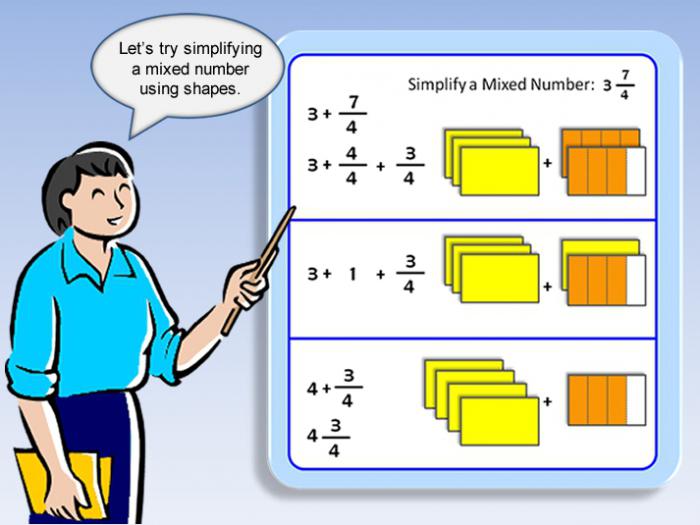
Как записать неправильную дробь в виде смешанного числа?

Следующий прием противоположен рассмотренному выше. То есть когда все смешанные числа заменяются на неправильные дроби. Алгоритм действий будет таким:

• разделить числитель на знаменатель до получения остатка;
• записать частное на месте целой части смешанного;
• остаток следует разместить над чертой;
• делитель будет знаменателем.

Примеры такого преобразования:

76/14; 76:14 = 5 с остатком 6; ответом будет 5 целых и 6/14; дробную часть в этом примере нужно сократить на 2, получится 3/7; итоговый ответ — 5 целых 3/7.

108/54; после деления получается частное 2 без остатка; это значит, что не все неправильные дроби удается представить в виде смешанного числа; ответом будет целое — 2.

Как целое число превратить в неправильную дробь?

Бывают ситуации, когда необходимо и такое действие. Чтобы получить неправильные дроби с заранее известным знаменателем, потребуется выполнить такой алгоритм:

• умножить целое число на нужный знаменатель;
• записать это значение над чертой;
• разместить под ней знаменатель.

Самый простой вариант, когда знаменатель равен единице. Тогда ничего умножать не нужно. Достаточно просто написать целое число, которое дано в примере, а под чертой расположить единицу.

Пример: 5 сделать неправильной дробью со знаменателем 3. После умножения 5 на 3 получается 15. Это число будет знаменателем. Ответ задания дробь: 15/3.

Два подхода к решению заданий с разными числами

В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.

В первом подходе смешанное число будет представлено в виде неправильной дроби.

После выполнения действий, описанных выше, получится такое значение: 13/5.

Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.

При нахождении разности эти же числа вычитаются: 143 — 70 = 73. Ответом будет дробь: 73/55.

При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.

Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5 : 14/11 = 13/5 х 11/14 = 143/70.

Во втором подходе неправильная дробь обращается в смешанное число.

После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.

Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.

При вычитании знак «+» заменяется на «-». 2 — 1 = 1, 33/55 — 15/55 = 18/55. Для проверки ответ из предыдущего подхода нужно перевести в смешанное число: 73 делится на 55 и получается частное 1 и остаток 18.

Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.

www.syl.ru

Дробь (математика) — это… Что такое Дробь (математика)?

У этого термина существуют и другие значения, см. Дробь.

8	/ 13		числитель
числитель	знаменатель		знаменатель
Две записи одной дроби

Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы^[1]. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.

Виды дробей

Обыкновенные дроби

Наглядное представление дроби

Обыкновенная (или простая) дробь — запись рационального числа в виде или где Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем.

Обозначения обыкновенных дробей

Есть несколько видов записи обыкновенных дробей в печатном виде:

• ½
• 1/2 или (наклонная черта называется «солидус»^[2])
• выключная формула: (горизонтальная черта называется Винкулиум (англ.))
• строчная формула:

Правильные и неправильные дроби

Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, и представляет рациональное число, по модулю большее или равное единице.

Например, дроби , и  — правильные дроби, в то время как , , и  — неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.

Смешанные дроби

Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.

Например, . В строгой математической литературе такую запись предпочитают не использовать из-за схожести обозначения смешанной дроби с обозначением произведения целого числа на дробь, а также из-за более громоздкой записи и менее удобных вычислений.

Высота дроби

Высота обыкновенной дроби — модуль суммы числителя и знаменателя этой дроби. Высота рационального числа — модуль суммы числителя и знаменателя несократимой обыкновенной дроби, соответствующей этому числу.

Например, высота дроби равна . Высота же соответствующего рационального числа равна , так как дробь сокращается на .

Составные дроби

Многоэтажной, или составной, дробью называется выражение, содержащее несколько горизонтальных (или реже — наклонных) черт:

или или

Десятичные дроби

Десятичной дробью называют позиционную запись дроби. Она выглядит следующим образом:

Пример: .

Часть записи, которая стоит до позиционной запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая в этом случае либо имеет конечное число знаков после запятой, либо является периодической дробью.

Вообще говоря, для позиционной записи числа́ можно использовать не только десятичную систему счисления, но и другие (в том числе и специфические, такие, как фибоначчиева).

Значение дроби и основное свойство дроби

Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать разные дроби, как обыкновенные, так и десятичные.

Если умножить числитель и знаменатель дроби на одинаковую величину:

то значение дроби останется прежним, хотя дроби — разные. Например:

И обратно, если числитель и знаменатель заданной дроби имеют общий делитель, то обе части можно разделить на него; такая операция называется сокращением дроби. Пример:

 — здесь числитель и знаменатель дроби сократили на общий делитель 4.

Несократимой называется дробь, числитель и знаменатель которой взаимно просты, т. е. не имеют общих делителей, кроме

Для десятичной дроби запись почти всегда однозначна, однако имеются исключения. Пример:

 — две разные дроби соответствуют одному числу.

Действия над дробями

В этом разделе рассматриваются действия над обыкновенными дробями. О действиях над десятичными дробями см. Десятичная дробь.

Приведение к общему знаменателю

Для сравнения, сложения и вычитания дробей их следует преобразовать (привести) к виду с одним и тем же знаменателем. Пусть даны две дроби: и . Порядок действий:

• Находим наименьшее общее кратное знаменателей: .
• Умножаем числитель и знаменатель первой дроби на .
• Умножаем числитель и знаменатель второй дроби на .

После этого знаменатели обеих дробей совпадают (равны M). Вместо наименьшего общего кратного можно в простых случаях взять в качестве M любое другое общее кратное, например, произведение знаменателей. Пример см. ниже в разделе Сравнение.

Сравнение

Чтобы сравнить две обыкновенные дроби, следует привести их к общему знаменателю и сравнить числители получившихся дробей. Дробь с бо́льшим числителем будет больше.

Пример. Сравниваем и . НОК(4, 5) = 20. Приводим дроби к знаменателю 20.

Следовательно,

Сложение и вычитание

Чтобы сложить две обыкновенные дроби, следует привести их к общему знаменателю. Затем сложить числители, а знаменатель оставить без изменений:

+ = + =

НОК знаменателей (здесь 2 и 3) равно 6. Приводим дробь к знаменателю 6, для этого числитель и знаменатель надо умножить на 3.
Получилось . Приводим дробь к тому же знаменателю, для этого числитель и знаменатель надо умножить на 2. Получилось .
Чтобы получить разность дробей, их также надо привести к общему знаменателю, а затем вычесть числители, знаменатель при этом оставить без изменений:

 — =  — =

НОК знаменателей (здесь 2 и 4) равно 4. Приводим дробь к знаменателю 4, для этого надо числитель и знаменатель умножить на 2. Получаем .

Умножение и деление

Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:

В частности, чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:

В общем случае, числитель и знаменатель результирующей дроби могут не быть взаимно простыми, и может потребоваться сокращение дроби, например:

Чтобы поделить одну обыкновенную дробь на другую, нужно умножить первую на дробь, обратную второй:

Например,

Преобразование между разными форматами записи

Чтобы преобразовать обыкновенную дробь в дробь десятичную, следует разделить числитель на знаменатель. Результат может иметь конечное число десятичных знаков, но может быть и бесконечной периодической дробью. Примеры:

 — бесконечно повторяющийся период принято записывать в круглых скобках.

Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на соответствующую степень 10. Затем к результату приписывается целая часть со знаком, формируя смешанную дробь. Пример:

История и этимология

Русский термин дробь, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. Фундамент теории обыкновенных дробей заложили греческие и индийские математики.

Впервые в Европе данный термин употребил Леонардо Пизанский (1202). Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. Полноценная теория обыкновенных дробей и действий с ними сложилась в XVI веке (Тарталья, Клавиус).

В древней Руси дроби называли долями или ломаными числами. Термин дробь, как аналог латинского fractura, используется в «Арифметике» Магницкого (1703) как для обыкновенных, так и для десятичных дробей.

Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную^[3]. Персидский математик и астроном Джамшид Гияс-ад-дин ал-Каши (1380—1429) в трактате «Ключ арифметики» объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на 5 веков раньше^[4].

В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).

Обобщения

См. также

Литература

Примечания

partners.academic.ru