Виды интегралов
Неопределенный и определенный интегралы
ОПРЕДЕЛЕНИЕ Неопределенный интеграл – это множество всех первообразных некоторой функции :
Например.
Подробнее про неопределенные интегралы читайте по ссылке.
ОПРЕДЕЛЕНИЕ Определённый интеграл от функции на отрезке – предел интегральных сумм при стремлении диаметра разбиения к нулю, если он существует независимо от разбиения и выбора точек внутри элементарных отрезков:
Например.
Подробнее про определенные интегралы читайте по ссылке.
Собственный и несобственный интегралы
ОПРЕДЕЛЕНИЕ Собственный интеграл – это определенный интеграл, для которого ограниченной является как подынтегральная функция, так и область интегрирования.Например.
ОПРЕДЕЛЕНИЕ Несобственный интеграл – определенный интеграл, для которого неограниченна либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе.Пусть функция определена на полуоси и интегрируема на любом отрезке . Предел интеграла при называется несобственным интегралом первого рода функции от a до и обозначается :
Например.
Подробнее про несобственные интегралы читайте по ссылке.
Сходящийся и расходящийся интегралы
ОПРЕДЕЛЕНИЕ Если предел существует и конечен, то несобственный интеграл первого рода называется сходящимся.Например.
В противном случае несобственный интеграл первого рода называется расходящимся.
Например.
ОПРЕДЕЛЕНИЕ Если предел конечен, то несобственный интеграл первого рода называется сходящимся.Например.
ОПРЕДЕЛЕНИЕЕсли предел не существует или бесконечен, то несобственный интеграл второго рода называется расходящимся.
Например.
ОПРЕДЕЛЕНИЕ Кратным или многократным интегралом называется множество интегралов, взятых от переменных:
Например.
Криволинейные и поверхностные интегралы
Например. , где
ОПРЕДЕЛЕНИЕ Если на кривой определены функции и , то криволинейным интегралом второго рода называется интеграл вида .Например. , где
Подробнее про криволинейные интегралы читайте по ссылке.
ОПРЕДЕЛЕНИЕ Поверхностным интегралом первого рода от функции по некоторой поверхности называется интеграл .Например. , где − часть плоскости , лежащая в первом октанте.
ОПРЕДЕЛЕНИЕ Поверхностным интегралом второго рода по фиксированной стороне двусторонней поверхности называется интеграл вида .Например. , где − часть внутренней поверхности эллипсоида
Например.
ОПРЕДЕЛЕНИЕ Интеграл называется интегралом, зависящим от параметра .Например.
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
собственный интеграл — ПриМат
$\Box$ Рассмотрим производную заданной функции по определению
$${ J }^{ \prime }\left( y \right) =\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }.$$
Тогда для доказательства теоремы нам необходимо убедиться в равенстве
$$\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \Rightarrow$$ $$\Rightarrow \lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\quad \left( 1 \right).$$
Для дальнейшей работы проанализируем отношение
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }.$$
Так как функция $f$ и ее производная – дифференцируемые на заданном прямоугольнике функции, то мы имеем право воспользоваться теоремой Лагранжа о среднем значении*
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }=$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx },\quad { \theta }_{ x }\in \left( 0,1 \right).$$
Вернемся к отношению находящемуся под знаком предела формулы $(1)$:
$$\frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } =$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx }-\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx }=$$ $$ =\intop_{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx }.$$
Аналогично доказательству предыдущего свойства, так как $\frac { \partial }{ \partial y } f\left( x,y \right)$ непрерывна на заданном прямоугольнике, то по теореме Кантора она равномерно непрерывна на нем же. Тогда запишем условие равномерной непрерывности, что поможет оценить нам выражение под знаком предела формулы $(1)$:
$$\forall \varepsilon > 0 \quad \exists { \delta }_{ \varepsilon }>0:\forall x\in \left[ a,b \right] ; \forall y,y+\Delta y\in \left[ c,d \right]:\left| y+\Delta y-y \right|=$$ $$=\left| \Delta y \right| <{ \delta }_{ \varepsilon }\Rightarrow \left| \frac { \partial }{ \partial y } f\left( x,y+\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| <\frac { \varepsilon }{ b-a }.$$
Принимая во внимание тот факт, что ${ \theta }_{ x } \in \left( 0,1 \right)$, автоматически при тех же условиях будет выполняться неравенство
$$\left| \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| <\frac { \varepsilon }{ b-a }.$$
Тогда можем записать
$$\left| \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right| =$$ $$=\left| \intop _{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx } \right| \le$$ $$\le \intop _{ a }^{ b }{ \left| \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| dx } \le \left( b-a \right) \frac { \varepsilon }{ b-a } =\varepsilon.$$
Отсюда следуя определению предела функции по Коши
$$\lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\Rightarrow$$ $$\Rightarrow\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } ={ J }^{ \prime }\left( y \right). \blacksquare$$
[свернуть]
ib.mazurok.com
Собственные интегралы, зависящие от параметра, и их свойства — ПриМат
$\Box$ Рассмотрим производную заданной функции по определению
$${ J }^{ \prime }\left( y \right) =\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }.$$
Тогда для доказательства теоремы нам необходимо убедиться в равенстве
$$\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \Rightarrow$$ $$\Rightarrow \lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\quad \left( 1 \right).$$
Для дальнейшей работы проанализируем отношение
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }.$$
Так как функция $f$ и ее производная – дифференцируемые на заданном прямоугольнике функции, то мы имеем право воспользоваться теоремой Лагранжа о среднем значении*
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }=$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx },\quad { \theta }_{ x }\in \left( 0,1 \right).$$
Вернемся к отношению находящемуся под знаком предела формулы $(1)$:
$$\frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } =$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx }-\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx }=$$ $$ =\intop_{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx }.$$
Аналогично доказательству предыдущего свойства, так как $\frac { \partial }{ \partial y } f\left( x,y \right)$ непрерывна на заданном прямоугольнике, то по теореме Кантора она равномерно непрерывна на нем же. Тогда запишем условие равномерной непрерывности, что поможет оценить нам выражение под знаком предела формулы $(1)$:
$$\forall \varepsilon > 0 \quad \exists { \delta }_{ \varepsilon }>0:\forall x\in \left[ a,b \right] ; \forall y,y+\Delta y\in \left[ c,d \right]:\left| y+\Delta y-y \right|=$$ $$=\left| \Delta y \right| <{ \delta }_{ \varepsilon }\Rightarrow \left| \frac { \partial }{ \partial y } f\left( x,y+\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| <\frac { \varepsilon }{ b-a }.$$
Принимая во внимание тот факт, что ${ \theta }_{ x } \in \left( 0,1 \right)$, автоматически при тех же условиях будет выполняться неравенство
$$\left| \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| <\frac { \varepsilon }{ b-a }.$$
Тогда можем записать
$$\left| \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right| =$$ $$=\left| \intop _{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx } \right| \le$$ $$\le \intop _{ a }^{ b }{ \left| \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| dx } \le \left( b-a \right) \frac { \varepsilon }{ b-a } =\varepsilon.$$
Отсюда следуя определению предела функции по Коши
$$\lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\Rightarrow$$ $$\Rightarrow\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } ={ J }^{ \prime }\left( y \right). \blacksquare$$
[свернуть]
ib.mazurok.com
Собственные интегралы. Признаки сходимости. Свойства равномерно сходящихся несобственных интегралов
1. Собственные интегралы, зависящие от параметра [2,5]
Пусть в прямоугольнике 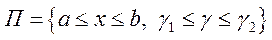 определена
функция
определена
функция 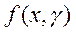 , интегрируемая по
, интегрируемая по 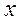 на
сегменте
на
сегменте 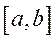 при любом фиксированном
при любом фиксированном 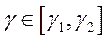 . В этом случае на
. В этом случае на  определена
функция
определена
функция 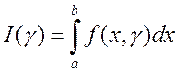 , называемая интегралом, зависящим от
параметра
, называемая интегралом, зависящим от
параметра 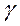 .
.
Теорема 1. Если 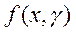 непрерывна
в прямоугольнике
непрерывна
в прямоугольнике 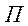 , то функция
, то функция 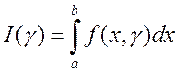 :
:
1) непрерывна на сегменте  ;
;
2) интегрируема на сегменте  и
справедливо равенство
и
справедливо равенство
 .
.
41) Рассмотрим приращение 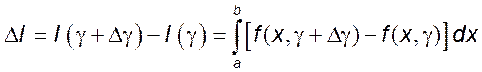 . Для доказательства
непрерывности функции
. Для доказательства
непрерывности функции 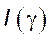 необходимо доказать, что
необходимо доказать, что 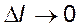 при
при 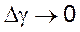 . Так
как функция
. Так
как функция 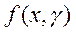 непрерывна на замкнутом множестве, то по
теореме Кантора она равномерно непрерывна на нем. Следовательно,
непрерывна на замкнутом множестве, то по
теореме Кантора она равномерно непрерывна на нем. Следовательно,
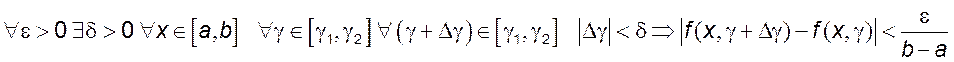 .
.
Откуда по теореме о среднем получаем, что 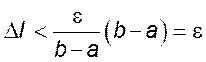 .
.
2) Так как функция 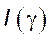 непрерывна
на сегменте
непрерывна
на сегменте  , то она интегрируема на этом сегменте,
т.е. существует двойной интеграл
, то она интегрируема на этом сегменте,
т.е. существует двойной интеграл 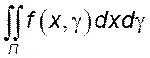 . Следовательно,
повторные интегралы (фигурирующих в соотношении ) равны, что доказывает справедливость формулы 3
. Следовательно,
повторные интегралы (фигурирующих в соотношении ) равны, что доказывает справедливость формулы 3
Теорема 2. Если функция 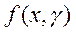 и ее
частная производная
и ее
частная производная 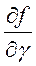 непрерывны в прямоугольнике
непрерывны в прямоугольнике 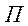 , то функция
, то функция 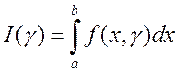 непрерывно
дифференцируема на сегменте
непрерывно
дифференцируема на сегменте  и ее производная
и ее производная 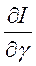
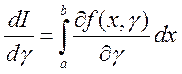 .
.4Рассмотрим
вспомогательную функцию 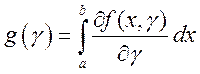 . Так как
. Так как 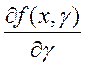 непрерывна в прямоугольнике
непрерывна в прямоугольнике  , то по предыдущей теореме
, то по предыдущей теореме 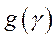 непрерывна на
непрерывна на  и
интеграл от функции
и
интеграл от функции 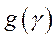 может быть найден по формуле .
может быть найден по формуле .
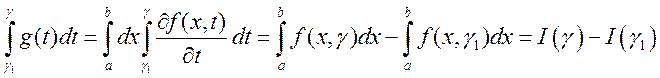
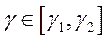 .
.Следовательно, 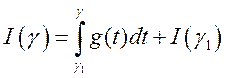 . Производная от
интеграла с переменным верхним пределом от непрерывной функции существует и
равна значению этой функции в точке
. Производная от
интеграла с переменным верхним пределом от непрерывной функции существует и
равна значению этой функции в точке 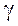 , поэтому
, поэтому
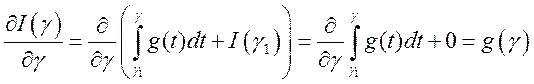 .3
.3
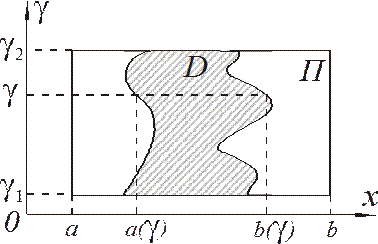 Общий случай. Если при любом фиксированном
Общий случай. Если при любом фиксированном 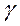 из сегмента
из сегмента  функция
функция 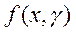
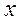 на
сегменте
на
сегменте 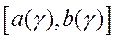 , то на сегменте
, то на сегменте  определена
функция
определена
функция 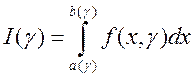 ,
,
представляющая собой интеграл, зависящий от параметра, у которого пределы интегрирования также зависят от параметра.
Теорема 3. Пусть функция 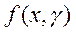 непрерывна
на прямоугольнике
непрерывна
на прямоугольнике 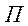 , а функции
, а функции 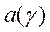 и
и 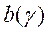
 . Тогда функция
. Тогда функция 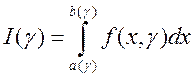 непрерывна
на сегменте
непрерывна
на сегменте  .
.4Пусть 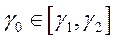 – фиксировано. Представим
– фиксировано. Представим 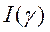 в следующей форме
в следующей форме
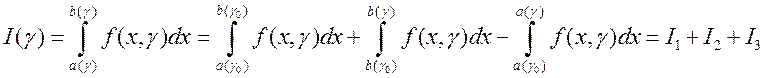 .
.
Так как 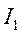 – интеграл, зависящий
от параметра
– интеграл, зависящий
от параметра 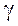 , с постоянными пределами интегрирования и
с непрерывной подынтегральной функцией, то в силу теоремы 1 этот интеграл
является непрерывной функцией от
, с постоянными пределами интегрирования и
с непрерывной подынтегральной функцией, то в силу теоремы 1 этот интеграл
является непрерывной функцией от 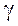
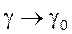 стремится к
стремится к 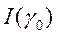 .
.Для интегралов 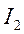 и
и 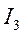 справедливы следующие оценки (теорема о
среднем):
справедливы следующие оценки (теорема о
среднем):
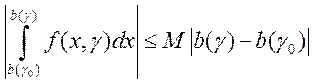 ,
, 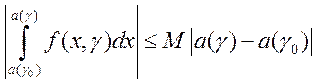 ,
,
где 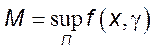 . Так
как функции
. Так
как функции 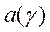
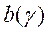 непрерывны
на сегменте
непрерывны
на сегменте  , то при
, то при 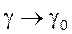
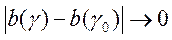 и
и 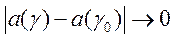 , а
значит и интегралы
, а
значит и интегралы 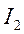 ,
, 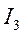 также
стремятся к 0. Таким образом, предел правой части при
также
стремятся к 0. Таким образом, предел правой части при 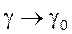 существует и равен
существует и равен 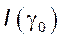 .
Следовательно, функция
.
Следовательно, функция 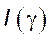 непрерывна в любой точке
непрерывна в любой точке 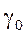 сегмента
сегмента  .3
.3Следствие. Если 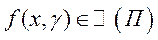 ,
, 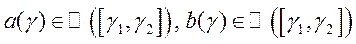 , то
, то 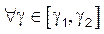
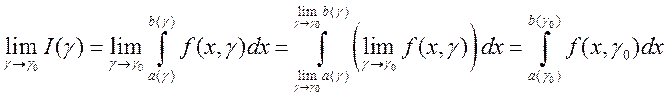 .
.
Теорема 4. Пусть функция 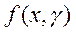 и ее
производная
и ее
производная 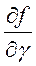 непрерывны в прямоугольнике
непрерывны в прямоугольнике 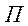
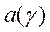 и
и 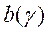 дифференцируемы
на сегменте
дифференцируемы
на сегменте  . Тогда функция
. Тогда функция 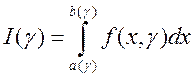 дифференцируема
на сегменте
дифференцируема
на сегменте  , причем
, причем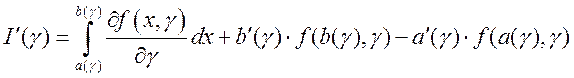 .
.
4Пусть 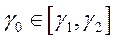 – фиксировано. Представим
– фиксировано. Представим 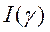 в виде .
в виде .
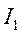 – интеграл, зависящий от
параметра
– интеграл, зависящий от
параметра 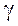 , с постоянными пределами интегрирования и
с непрерывной подынтегральной функцией, поэтому, в силу теоремы 2, функция
, с постоянными пределами интегрирования и
с непрерывной подынтегральной функцией, поэтому, в силу теоремы 2, функция 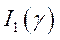 дифференцируема на сегменте
дифференцируема на сегменте  и
и 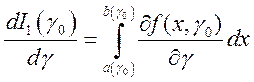 .
.
По определению производной для функции 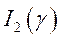 получим
получим 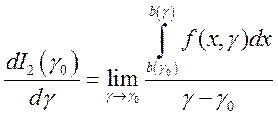 .
.
По формуле среднего значения 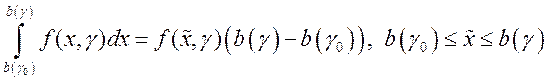 . Из непрерывности
функции
. Из непрерывности
функции 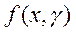 следует, что
следует, что 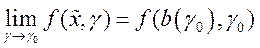 ; а из
и дифференцируемости функции
; а из
и дифференцируемости функции 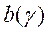 следует, что
следует, что 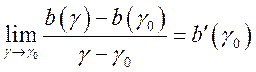 . Поэтому
. Поэтому
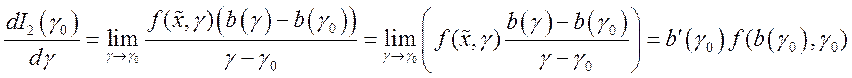 .
.
Аналогично доказывается, что 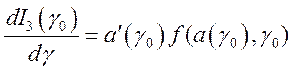 . Так
как
. Так
как 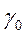 произвольная точка сегмента
произвольная точка сегмента  , то можно утверждать, что функция
, то можно утверждать, что функция 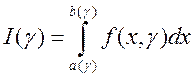 дифференцируема на сегменте
дифференцируема на сегменте  и ее производная может быть вычислена по
формуле .3
и ее производная может быть вычислена по
формуле .3
\\\\\\\\\\\\\\\\\\\\\\\\\
2. Несобственные
интегралы от ограниченных функций,
зависящие от параметра
Пусть в полуполосе 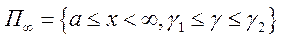 задана
функция
задана
функция 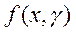 , интегрируемая по
, интегрируемая по 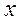 в
несобственном смысле на полупрямой
в
несобственном смысле на полупрямой 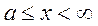 при любом фиксированном
при любом фиксированном 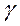 из сегмента
из сегмента  . При
этих условиях на сегменте
. При
этих условиях на сегменте  определена функция
определена функция 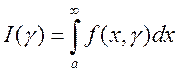 , называемая несобственным интегралом
первого рода, зависящим от параметра
, называемая несобственным интегралом
первого рода, зависящим от параметра 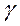 . При
этом говорят, что интеграл сходится на сегменте
. При
этом говорят, что интеграл сходится на сегменте  .
.
Несобственный интеграл называется равномерно
сходящимся по параметру 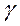 на сегменте
на сегменте  , если он сходится на сегменте
, если он сходится на сегменте  и если
и если 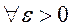 можно
указать такое
можно
указать такое 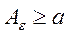 , зависящее только от
, зависящее только от 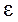 , что
, что 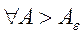 и
и 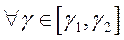 выполняется неравенство
выполняется неравенство 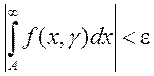 .
.
2.1. Признаки сходимости
Теорема 5 (критерий Коши). Для того, чтобы
несобственный интеграл равномерно сходился по параметру 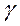 на
сегменте
на
сегменте  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 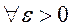 можно было указать число
можно было указать число 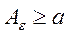 , зависящее только от
, зависящее только от 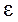 и такое, что
и такое, что 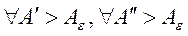 и
и 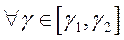 :
:
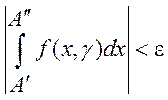 .
.
Следствие. Несобственный интеграл 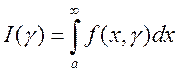 ,
, 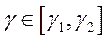 сходится
равномерно на сегменте
сходится
равномерно на сегменте  , если
, если 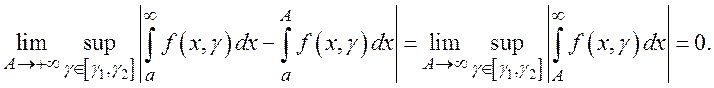
Теорема 6 (признак Вейерштрасса). Пусть функция 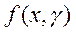 определена в полуполосе
определена в полуполосе 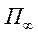 и для каждого
и для каждого 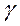 из
сегмента
из
сегмента  интегрируема по
интегрируема по 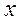 на
любом сегменте
на
любом сегменте  . Пусть далее для всех точек
полуполосы
. Пусть далее для всех точек
полуполосы 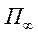 выполняется неравенство
выполняется неравенство 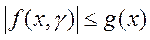 , т.е.
, т.е. 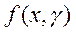 равномерно
ограничена на
равномерно
ограничена на 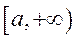 . Тогда из сходимости интеграла
. Тогда из сходимости интеграла 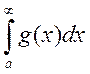 вытекает равномерная сходимость по
вытекает равномерная сходимость по 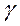 на сегменте
на сегменте  интеграла
интеграла 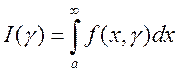 .
.
4Так как 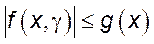 , то
, то 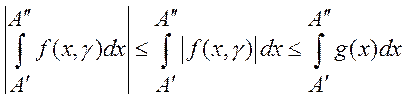 . Из
сходимости
. Из
сходимости 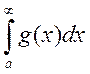 следует (по критерию Коши) равномерная
сходимость интеграла
следует (по критерию Коши) равномерная
сходимость интеграла 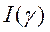 .3
.3
Следствие. Пусть функция 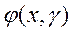 ,
определенная в полуполосе
,
определенная в полуполосе 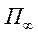 , ограничена в этой полуполосе
и при каждом
, ограничена в этой полуполосе
и при каждом 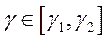 интегрируема по
интегрируема по 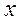 на любом сегменте
на любом сегменте  .
Тогда, если сходится интеграл
.
Тогда, если сходится интеграл 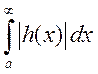 , то сходится равномерно
по
, то сходится равномерно
по 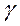 на сегменте
на сегменте  интеграл
интеграл 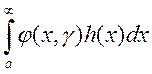 .
.
Теорема 7. (Признаки Дирихле и Абеля).
Теорема 8 (Признак Дини). Пусть функция 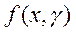 непрерывна и неотрицательна в полуполосе
непрерывна и неотрицательна в полуполосе 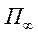 , и пусть для каждого
, и пусть для каждого 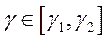 сходится несобственный интеграл
сходится несобственный интеграл 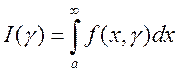 . Пусть далее функция
. Пусть далее функция 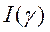 непрерывна на сегменте
непрерывна на сегменте  . Тогда интеграл
. Тогда интеграл 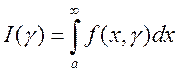 сходится
равномерно по
сходится
равномерно по 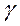 на этом сегменте.
на этом сегменте.
Замечания.
1. Признаки Вейерштрасса, Дирихле и Абеля являются достаточными.
2. Для доказательства неравномерной сходимости обычно используют критерий Коши и его следствие.
3. Признак Вейерштрасса дает абсолютную сходимость. А признаки Дирихле и Абеля обычно используют при доказательстве условной сходимости.
vunivere.ru