Презентация к уроку по алгебре (6 класс) на тему: Сравнение чисел
Слайд 2
Назовите координаты точек, изображенных на координатной прямой Назовите точки, которые лежат левее нуля Назовите точки, которые лежат правее нуля.
Слайд 3
Между какими целыми числами на координатной прямой расположено число: -3 0 2,6
Слайд 4
Найди соответствие 7 0,1 5 -0,5 -0,1 -5 0,5 -7
Слайд 5
«Восстанови равенство» │12│= │0│= │- 6│= 12 6 0
Слайд 6
Числа отрицательные новые для вас Лишь совсем недавно изучил ваш класс Сразу же прибавилось вам теперь мороки: Изучить все правила сравнения на уроке.
Слайд 7
СРАВНЕНИЕ ЧИСЕЛ
Слайд 8
Девиз: Вместе возьмемся, всего добьемся
Слайд 9
15 28 13,7 8,6 12,3 о -8 6 — 25 -32.
Слайд 11
1 Вывести правило сравнения положительных чисел и нуля. 1. Отметьте точки на координатной прямой : А(3), В( 5), D(1), O(0). 2 . Левее или правее находятся точки относительно нуля? 3 . Сравните с помощью координатной прямой числа: 3 * 0 5 * 0 1 * 0 4 . Сформулируйте правило сравнения любого положительного числа и нуля. Приведите свои примеры. Положительное число всегда ……… нуля больше
Слайд 12
Вывести правило сравнения отрицательных чисел и нуля . 1. Отметьте на координатной прямой точки: А(-3), В( -5), D (-1), O (0). 2. Левее или правее расположены точки относительно нуля? 3. Сравните с помощью координатной прямой числа: -3 * 0 -5 * 0 0 * -1 4. Сделайте вывод о сравнении любых отрицательных чисел с нулем. Приведите свои примеры. Отрицательное число всегда ………..… нуля. меньше
Слайд 13
3. Вывести правило сравнения положительных и отрицательных чисел 1.Отметьте на координатной прямой точки: А(-5), В( 2), O(0), С(-2) 2. Точки с какой координатой лежит левее точки О(0), какая правее токи О(0)? 3.Выполните сравнение: -5 * 2 -2 * 2 4 . Какое больше из чисел положительное или отрицательное? 5 . Сформулируйте правило сравнения отрицательных и положительных чисел . 6. приведите свои примеры Положительное число всегда ……….. отрицательного. больше
Слайд 14
1. Отметьте на координатной прямой точки: А(-3), В( -2). 2. Точка с какой координатой лежит левее ? 3. Найдите модули этих чисел. |- 3| = |-2|= 4. Сравните модули. Какой из двух модулей больше? |- 3| * |-2| 5. Сравните числа -3 и -2. Какое число будет меньше? -3 * -2 6. Какое из двух отрицательных чисел будет меньше? 7. Сформулируйте правило сравнения двух отрицательных чисел. Приведите свои примеры. IV. Вывести правило сравнения двух отрицательных чисел. Из двух отрицательных чисел меньше то, модуль которого ………. больше
Слайд 15
1.Положительное число всегда больше отрицательного . 2. Из двух отрицательных чисел меньше то, модуль которого больше . 3.Отрицательное число всегда меньше нуля . 4. Положительное число всегда больше нуля.
Слайд 16
*** Точка с меньшей координатой лежит на координатном луче левее точки с большей координатой
Слайд 17
-5>2
Слайд 18
-48
Слайд 19
0
Слайд 20
4>0
Слайд 21
7>-12
Слайд 22
-20
Слайд 23
0>-9
Слайд 24
Положительное число всегда ……….. отрицательного. больше Из двух отрицательных чисел меньше то, модуль которого ………. больше Отрицательное число всегда ………..… нуля. меньше Положительное число всегда ……… нуля. больше
Слайд 25
Я хорошо понял, как сравнивают числа и могу научить другого -Я не все понял, у меня были затруднения
Слайд 26
Спасибо Вам за урок! Вы- большие молодцы!
nsportal.ru
Сравнение чисел
Вы знаете, что числа можно сравнивать. Давайте вспомним, какие числа вы уже умеете сравнивать:

Следовательно, вы умеете сравнивать любые положительные числа друг с другом и с нулём. А как вы думаете, отрицательные числа можно сравнивать? Конечно! И отрицательные друг с другом, и отрицательные с положительными, и отрицательные с нулём. Сегодня на уроке мы об этом и поговорим.
Давайте начертим координатную прямую, отметим на ней начало отсчёта, выберем единичный отрезок и укажем направление.

Напомним, на горизонтальной координатной прямой положительные числа изображаются правее нуля, а отрицательные
 .
Вы знаете, что
.
Вы знаете, что  . Отметим на координатной прямой точки А(1) и В(
. Отметим на координатной прямой точки А(1) и В( ).
).
Понятно, что точка А на координатной прямой расположена левее точки В.
Напомним, правило: на горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой. Соответственно, на горизонтальной координатной прямой точка с меньшей координатой лежит левее точки с большей координатой .
А теперь давайте возьмём два отрицательных числа, например,
– 2 и –  .
Как сравнить такие числа? Отметим на координатной прямой точки С(– 2) и D(–
.
Как сравнить такие числа? Отметим на координатной прямой точки С(– 2) и D(–  ).
).

Запишем правило сравнения любых чисел:
Из двух чисел больше то, которое изображается на горизонтальной координатной прямой правее. И, соответственно, из двух чисел меньше то, которое изображается на горизонтальной координатной прямой левее.
Пример

Если рассматривать вертикальную координатную прямую, то в сформулированном правиле сравнения нужно заменить слово «правее» на «выше», а слово «левее» – на «ниже».
Сформулируем правило сравнения чисел на вертикальной координатной прямой.
Из двух чисел больше то, которое изображается на вертикальной координатной прямой выше. И, соответственно, из двух чисел меньше то, которое изображается на вертикальной координатной прямой ниже.
Хотелось бы сразу уточнить, что все положительные числа больше нуля, а все отрицательные – меньше нуля.

Любое отрицательное число меньше положительного.
Вообще очень удобно сравнивать числа при помощи понятия « модуль числа». Так как большее из двух положительных чисел на координатной прямой изображается правее, т.е. дальше от начала отсчёта, то это число имеет больший модуль.

Запомните, из двух положительных чисел больше то, чей модуль больше.
Так как большее из двух отрицательных чисел на координатной прямой изображается правее, т.е. ближе к началу отсчёта, то это число имеет меньший модуль.
Запомните, из двух отрицательных чисел больше то, чей модуль меньше.
Чтобы научиться легко сравнивать отрицательные числа, не пользуясь координатной прямой, давайте порассуждаем. Когда теплее – при – 25° или при – 5°?

Конечно, каждому понятно, что теплее при -5.
А сейчас забудем о температуре и зададим такой вопрос: какое из чисел -25 и -5 больше? Ясно, что

В чём можно убедиться, используя координатную прямую:

Задание
Расположите числа в порядке возрастания:
 .
.
Решение:

Задание
Расположите числа в порядке убывания:

Решение:

Итоги
Из двух чисел больше то, которое изображается на горизонтальной координатной прямой правее. И, соответственно, из двух чисел меньше то, которое изображается на горизонтальной координатной прямой левее.
Все положительные числа больше нуля.
Все отрицательные – меньше нуля.
Любое отрицательное число меньше положительного.
Из двух положительных чисел больше то, чей модуль больше.
Из двух отрицательных чисел больше то, чей модуль меньше.
videouroki.net
Сравнение чисел | Формулы с примерами
Сравнение рациональных чисел в математике
Определение
При сравнении
которое на координатной прямой находится правее.
Соответственно меньшее то, которое левее.
Сравнение целых чисел в пределах 10
Пример
| — 5 | 1 > — 4; | 6 > — 5; | — 4 | — 1 > — 5. |
Сравнение двузначных чисел на координатной прямой
Пример
| — 15 | 12 > — 14; | 16 > — 15; | — 14 | — 11 > — 15. |
Правила сравнения чисел
Правило ! Любое положительно число больше нуля.| 1 > 0; | 11 > 0; | 0, 002 > 0; | 10, 3231 > 0 | 235, 0902 > 0. |
! Любое отрицательное число меньше нуля.
| — 1 | — 13 | — 0, 0321 | — 310, 3231 | — 1235, 1235 |
! Любое отрицательное число меньше положительного.
Правило
! Из двух отрицательных чисел больше то, модуль которого, меньше.
| — 700 | — 4 > — 20,5; | — 66 > — 22; | — 1,43 |
! Направления возрастания чисел при движении по координатной
прямой — слева направо.

formula-xyz.ru
План-конспект урока по математике (6 класс): сравнение чисел с помощью координатной прямой
Государственное бюджетное общеобразовательное учреждение школа-интернат №9 Калининского района Санкт-Петербурга.
Конспект урока математики в 6 классе на тему:
«Сравнение чисел с помощью координатной прямой»
Выполнила: учитель математики
ГБОУ школы-интерната №9
Лосева Л.В.
Санкт-Петербург
2019 год
Аннотация урока.
Класс – 6 «а»
Учебник — «Математика» 6, авторы – Н.Я. Виленкин и др.
Тип урока – урок комплексного применения учебных умений
Тема урока: «Сравнение чисел с помощью координатной прямой»
Цель урока: продолжить формирование навыка сравнения чисел; проверить знания, умения по изученной теме; развивать умение самостоятельно работать; воспитывать уверенность в себе, своих знаниях.
Задачи урока:
• отработать умение сравнивать числа
• развивать зрительное восприятие, память, интерес к предмету, математическую речь;
• воспитывать сознательное отношение к учебному труду, самостоятельность.
Планируемые результаты
предметные
- Изображать точками координатной прямой положительные и отрицательные рациональные числа.
- Записывать модуль числа.
- Сравнивать и упорядочивать рациональные числа. Называть числа, противоположные данным.
метапредметные
Регулятивные:
отбирать инструменты для оценивания своей деятельности, осуществлять самоконтроль своей деятельности в рамках предложенных условий и требований;
оценивать свою деятельность, аргументируя причины достижения или отсутствия планируемого результата;
Познавательные:
определять необходимые ключевые поисковые слова и запросы;
Коммуникативные:
учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.
личностные
Формирование устойчивой мотивации к обучению на основе алгоритма выполнения задачи
Методы обучения: словесные, практические, наглядные, самостоятельная работа.
Формы организации работы учащихся:
- фронтальная;
- индивидуальная.
Технические условия: урок проводится в кабинете с компьютерным оборудованием:
- мультимедийный проектор;
- компьютер;
Структура урока:
- Организационный этап (1 мин.)
- Устная работа, определение темы урока, цели (5 мин.)
- Проверка изученного материала(10 мин.)
- Физкультминутка(3 мин)
- Проверка изученного материала (17 мин.)
- Подведение итогов урока (3 мин.)
- Домашнее задание (1 мин)
Ход урока
1. Организационный момент
Французский писатель Анатоль Франс однажды заметил: « Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом.». Последуем этому совету писателя, постараемся быть внимательными, будем «поглощать знания» с большим желанием, ведь они пригодятся вам в дальнейшем.
2. Устная работа
Разделите числа на две группы.
Как вы назовете эти группы?
Какое число не вошло ни в одну из групп?
11 -25,3 18,7 5 -58,81 0 -1,21.
С какими числами мы сегодня будем работать?
Тема нашего урока? « Сравнение чисел с помощью координатной прямой».
Как вы думаете, какова цель нашего урока? (Ответы учащихся).
Итак, задача сегодняшнего урока — доказать, что отрицательные числа не смогут поставить вас в трудное положение. Буду рада вашим хорошим ответам.
Где в науке и в жизни используют отрицательные числа?
3. Проверка изученного материала.
Задания для самостоятельной работы с самопроверкой. На полях тетради учащиеся выставляют заработанные баллы за задания
№1. Ответьте «да» или «нет» (максимально 7 баллов)
- Числа со знаком «-» называются отрицательными.
- l-7,5l=-7,5.
- Два числа, отличающихся только знаком, называются противоположными.
- Число 0 — положительное число.
- Целые числа – это натуральные, им противоположные и 0.
- -(-7)=7.
- 0 всегда меньше отрицательного числа.
№2 (максимально 3 балла)
-7 4 2,5 5 -4 -5 0 1
Из перечисленных чисел выберите:
1) Пары противоположных чисел
2) Числа, модуль которых равен 4
3) Числа, которые меньше 1
№3 Впишите нужное слово (максимально 4 балла)
- Положительное число всегда _________ отрицательного.
- Положительное число всегда _________ нуля.
- отрицательное число всегда _________ нуля.
- Из двух отрицательных чисел меньше то, _________
3. Физкультминутка.
Поднимает руки класс — это «раз»,
Повернулась голова — это «два».
Руки вниз, вперед смотри — это «три».
Руки в стороны пошире развернули на «четыре».
С силой их к плечам прижать — это «пять».
Всем ребятам тихо сесть — это «шесть».
5. Проверка изученного материала. (продолжение)
№4 Отметьте на координатной прямой (максимально 3 балла):
- Числа, модуль которых равен 3
- Число, противоположное числу 4
- Число, расположенное на 5 единичных отрезков правее 0
№5 Сравните (максимально 6 баллов)
- -5 и 2
- -20 и -40
- 0 и -15
- 4 и 0
- 7 и -20
- -5 и -4
№6 Вычислите (максимально 3 балла)
- l-9,5l-l4,2l
- l4,3l+l-3,3l
- l-3l∙l-5l
№7 Решите уравнение (максимально 2 балла)
- -х=7,75
- -х=-2,4
№8 Между какими последовательными целыми числами расположено число -4,2 (2 балла)
6. Подведение итогов урока
Подведем итоги. Согласно таблице поставьте себе оценку за урок.
15 – 22 б «3»
23 – 28 б «4»
29 – 30 б «5»
Урок подходит к концу.
— Какую цель мы ставили на уроке?
— Выполнили мы ее?
Рефлексия
Продолжите одно из предложений :
Я умею…
Было интересно….
Было трудно….
Мне нужно потренироваться …
7. Домашнее задание (карточки)
Спасибо за урок. Урок окончен
nsportal.ru
Конспект урока в 6 классе по теме «Сравнение чисел»
Урок в 6 классе
Сравнение чисел
Тип урока обобщения и систематизации знаний
Формируемые результаты
Предметные: формировать умение применять правила сравнения отрицательных чисел, положительных и отрицательных чисел при решении задач.
Личностные: формировать умение представлять результат своей деятельности
Метапредметные: формировать умения осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией.
Планируемые результаты: учащийся научится сравнивать отрицательные числа, положительные и отрицательные числа
Оборудование: компьютер, проектор, презентация
Ход урока
Организационный момент. Стихотворение (читает учитель) Слайд-заставка
В жизни по-разному можно жить:
В горе можно и в радости.
Вовремя есть, вовремя пить,
Вовремя делать гадости…
А можно и так: на рассвете встать
И, помышляя о чуде.
Рукой раскалённое солнце достать
И подарить его людям!
О чем это стихотворение?
Из всех наук, которые человек должен знать, главная наука есть наука о том, как жить, делая как можно меньше зла и как можно больше добра. В жизни всегда много противоположностей. Добро и зло идут рядом, но чем больше хороших поступков мы совершим, чем больше хороших людей будет на земле, тем лучше будет жизнь на нашей планете.
-Что в вашем понимании хороший человек?
-А какие качества присущи плохим людям?
Постановка цели урока, мотивация
Чтобы связать эти качества с темой нашего урока, определить цели урока, выполните задание. (самостоятельно, самопроверка)
Поставь точки в таком порядке, как стоят их координаты
(на слайде –точки на прямой, координаты)
Слово – СРАВНЕНИЕ
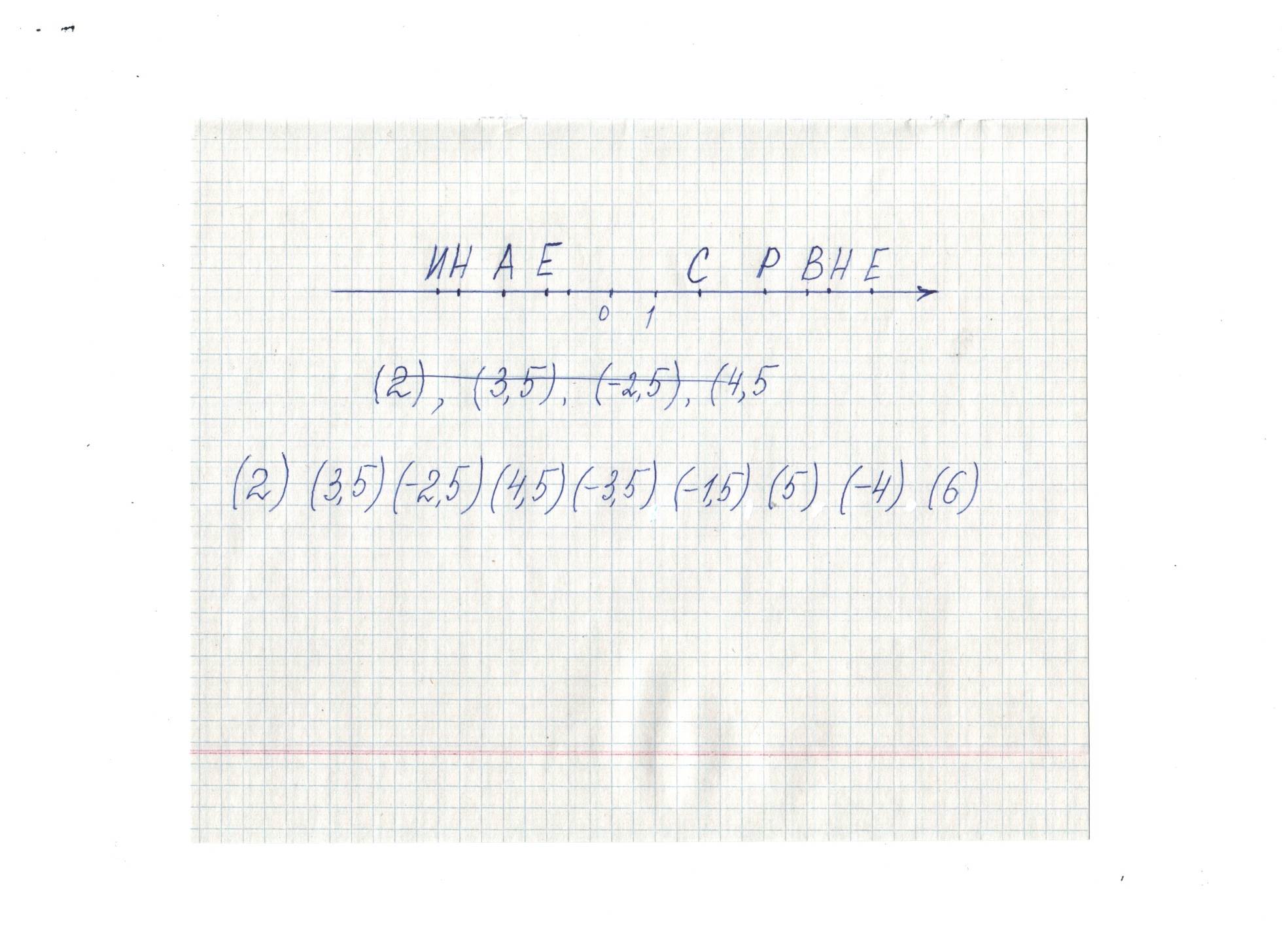
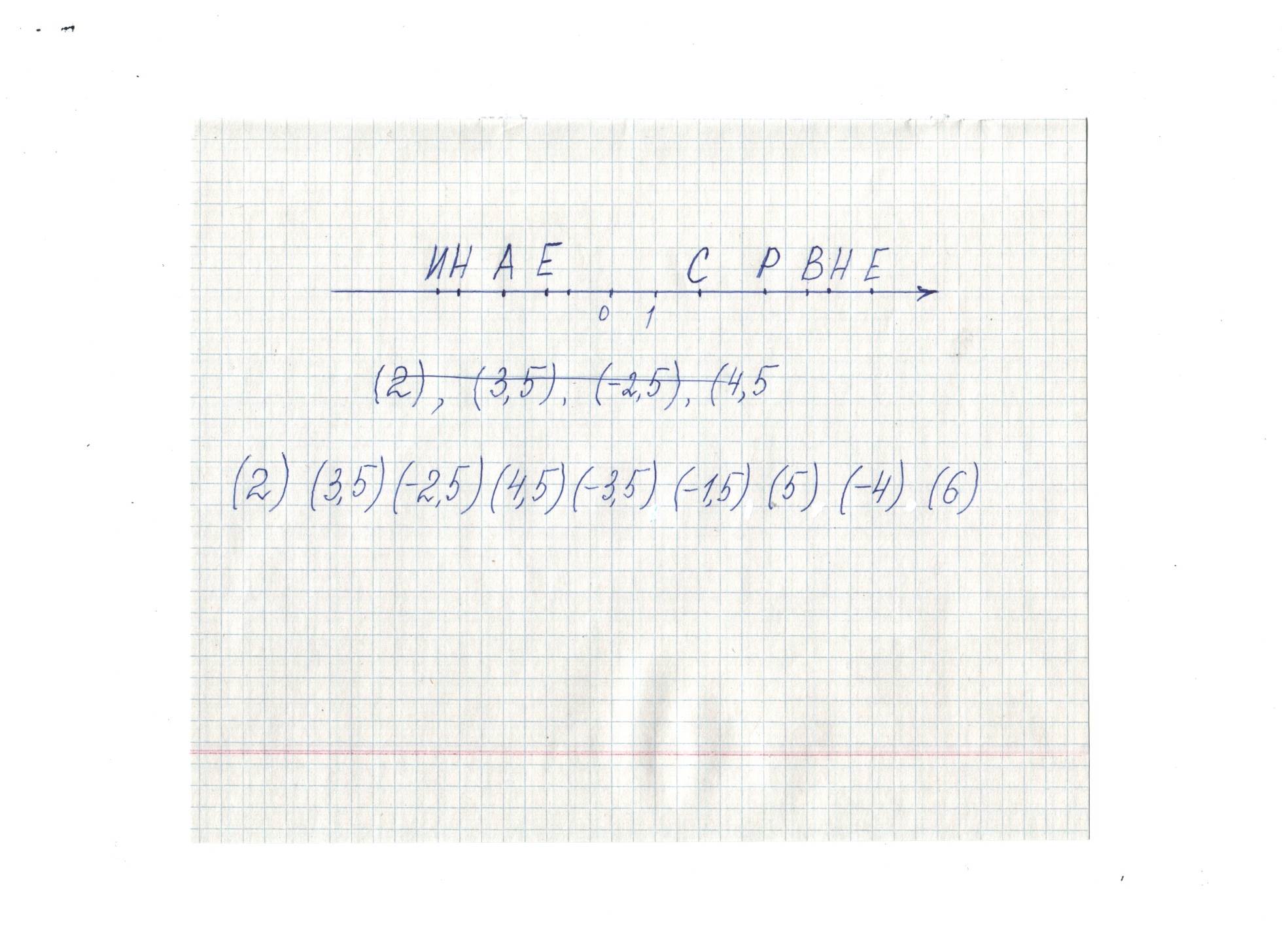
Домашнее задание (на слайде)
На «3» -сообщение по теме «Положительные и отрицательные числа»
На «4» — составить кроссворд по теме «Положительные и отрицательные числа»
На «5» — составить карточку из 5 заданий (приложить ответы) по теме «Положительные и отрицательные числа»
Актуализация знаний
а) «Установи соответствие» (Работа в парах, у каждой пары –вопросы и ответы)
проверка по слайду
Положительные и отрицательные числа; положительные числа, отрицательные числа
Нуль
Прямая, на которой выбрано начало отсчета, единичный отрезок и направление
Числа, отличающиеся только знаками
Нуль
Расстояние на координатной прямой от начала отсчета до точки, изображающей это число
Равен самому числу
Равен нулю
Равен числу, противоположному данному
Модули противоположных чисел равны
Из двух чисел на координатной прямой больше то, которое расположено правее, меньше то, которое расположено левее
Из двух отрицательных чисел больше то, модуль которого меньше
Любое положительное больше любого отрицательного
Любое положительное число больше нуля
Любое отрицательное число меньше нуля
б) устный счет (на слайде)
Найдите значение выражения
I-7,2I-I3,4I
I-12I *I-8I
I-48I:I-0,6I
I0,7I*I-0,8I
Физминутка (слайд)
«Потрудились — отдохнем,
встанем, глубоко вздохнем.
Руки в стороны, вперед, влево, вправо, поворот.
Три наклона, прямо встать
Руки вниз и вверх поднять
Руки плавно опустили, всем улыбки подарили».
Обобщение и систематизация знаний
Фронтальная работа
Сравните числа (на слайде)
1) – 6 и 7
2) 56 и – 56,1
3) 67 и 6,7
4) – 5,67 и – 5,6
5) 76 и 0
6) 0 и – 34
7) 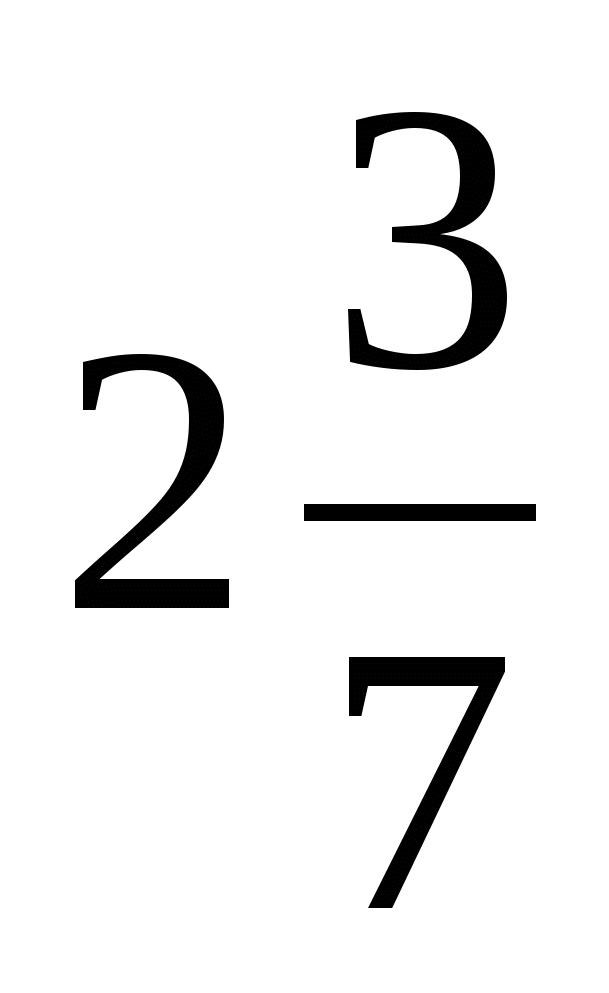 и
и 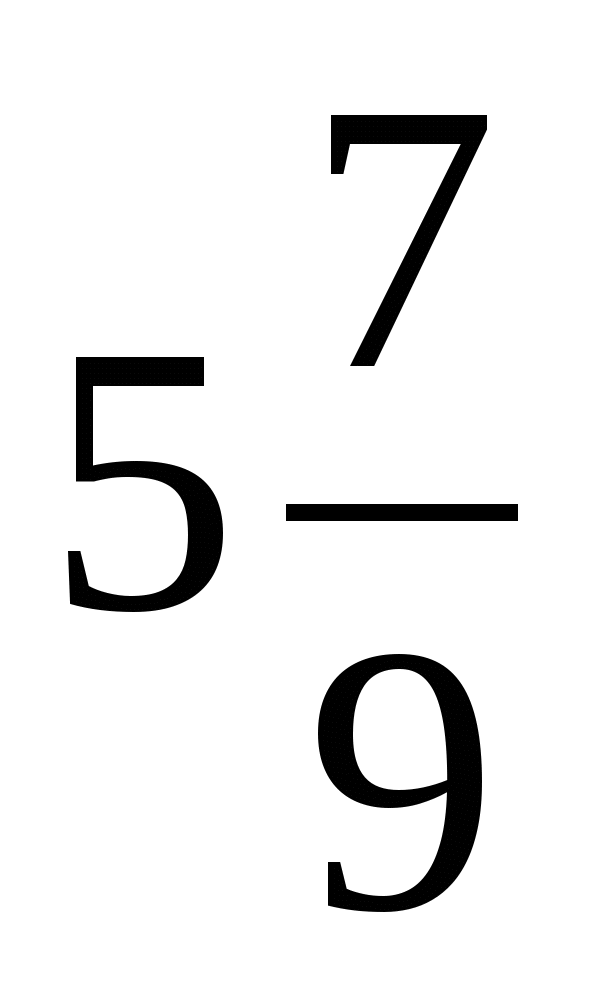
8) 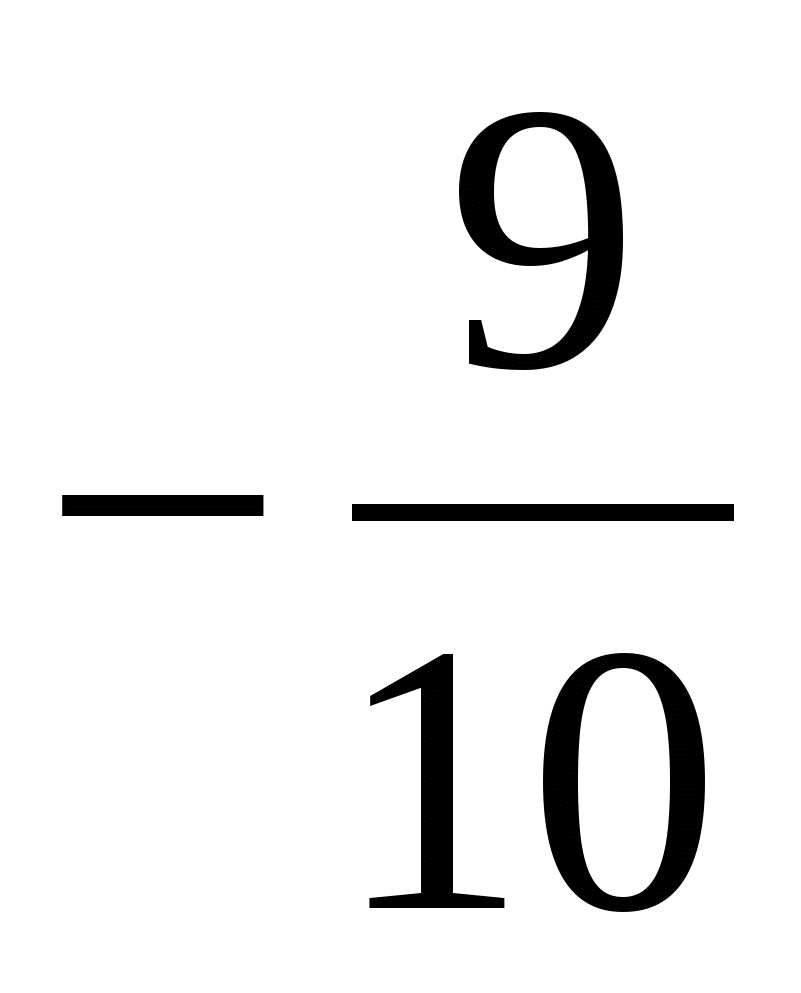 и
и 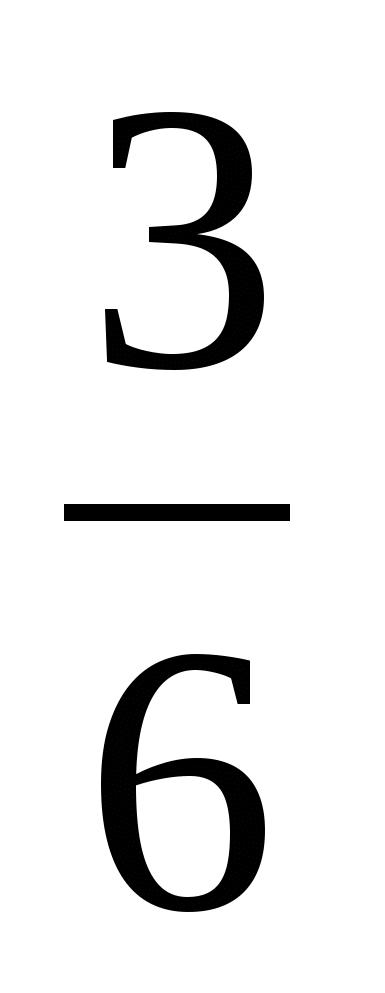
9)  и
и 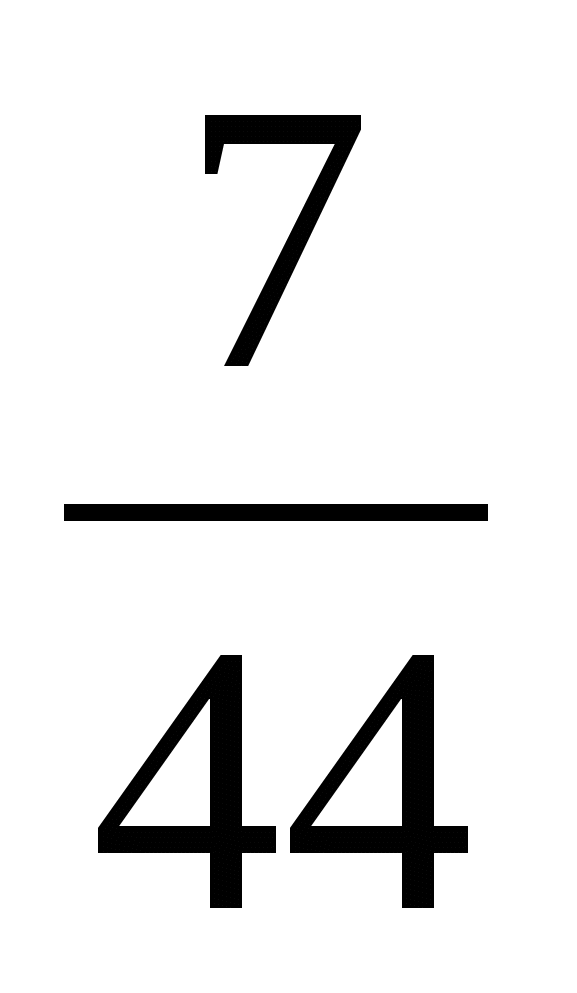
2. Используя чертеж (экран,плакат), отметьте на координатной прямой число 0, если известно, что
1) а и в – положительные числа
2) а и в – отрицательные числа
3) а и в – противоположные числа
4) а и в – числа разных знаков
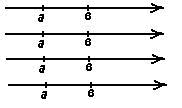
3.Используя рисунок (на слайде), заполните пропуски знаками <, > или =
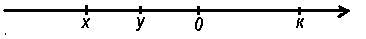
1) У,,,,,,,0 2) Х,,,,,0 3)У,,,,,0 4) К,,,,,0 5) К,,,,,Х 6) У ,,,,,Х 7) 
4. (на слайде) Найдите соседние целые числа, между которыми заключены числа:
,,,,,,,,,< 3 <,,,,,,,,,,
,,,,,,,,,< 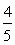 <,,,,,,,,,,
<,,,,,,,,,,
,,,,,,,,,< -2 <,,,,,,,,
,,,,,,,< 0,31<,,,,,,,,,
,,,,,,,< 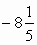 <,,,,,,,
<,,,,,,,
Работа в группах (задание на карточках и на слайде)
а) Расположите числа
1 группа: в порядке возрастания, выписав буквы, соответствующие этим числам.
0
-1,5
-39
-51,5
-0,1
-51,456
-1,99
-0,3
-51,1
-0,01
Е
А
И
В
М
Ы
Т
Е
Ч
О
Ответ: Вычитаемое
2 группа в порядке убывания, выписав буквы, соответствующие этим числам.
-1
0,19
0,5
-11,06
0
-0,1
3
-11,58
-1,8
-0,05
11,9
-2
Я
Б
И
Е
А
Л
Р
О
Е
В
П
М
Ответ: Прибавляемое
Так назывались когда-то отрицательные и положительные числа
б) Найдите пары противоположных чисел и вычеркните буквы, им соответствующие. Из оставшихся букв вы получите другое название отрицательных и положительных чисел.
3 группа
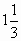
5
5,4
3
-5
2,5
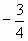
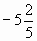
8
0,75
Д
С
М
О
К
Л
У
Е
Г
Ж
Ответ: Долг
4 группа
-0,2
5
8
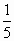
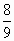
64
-32
-65
6
32
1
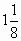
0,6
Р
И
М
Ф
У
Щ
Ю
Е
С
Б
Т
В
О
Ответ:Имущество
II. Группа 1
1. Отметьте точки на координатной прямой: А(-2) ,У(2),С(-4,5),Е(4,5), В(3) ,Х(7), Н(-6)
2.Вычислите:
|-9,55|-|-4,22|
|-5,86| |-2|
|4,3|+ |-3,7|
Группа 2
1.Вычислите:
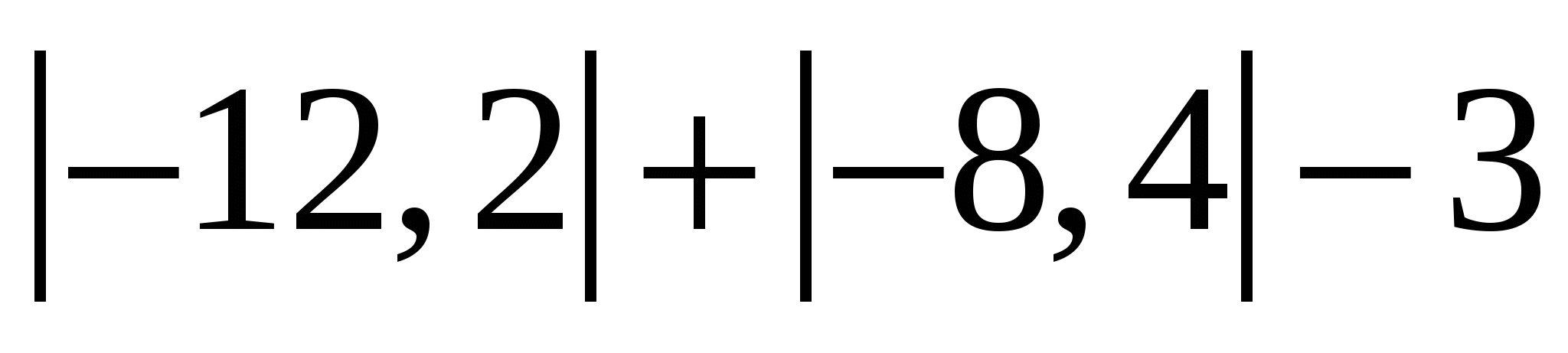
|1|:|-0,5|
|3|- |-3|
2. Отметьте точки на координатной прямой: О(0), А(-0,5), В(2), С(-3,5), Д(2,5), D(-2,5), Е(-1,2).
Группа3
1.Расположите числа в порядке убывания
7,6; -12; 2,78; 0; 0,6; -52,36; -48,66; 12,3; 8,55;
2.Сравните числа: Какими правилами вы пользовались для сравнения чисел?
а) I58I I-145I; б) I -63,2I I 62,3I;
в)8,5 -7,5; г) -1\3 -0,5
Группа 4.
1.Расположите числа в порядке возрастания
7,6; -12; 2,78; 0; 0,6; -52,36; -48,66; 12,3; 8,55;
2.Сравните числа: Какими правилами вы пользовались для сравнения чисел?
а) I-58I I145I; б) I 63,2I I -62,3I;
в) -8,5 -7,5; г) -1\2 -0,5
Плакаты вывешивают на доске. Проверка по слайду
Контроль и коррекция знаний
Индивидуальная работа с проверкой в парах
Вариант 1
1. Укажите верное неравенство.
а) -5>2; б)-20<-40;
в)-48<-36; г)0<-15
2. Укажите неверное неравенство.
а) 4>0; б)-5>-4;
в)7>-12; г)0>-9
3. Расположите числа -100, -200 и 50 в порядке возрастания.
а) -100,-200,50; б) 50,-100,-200;
в) -200,-100,50; г) 50,-200,-100
4. Сравните числа |-5,17| и |5,17|.
а) |-5,17| < |5,17|;
б) |-5,17| > |5,17|;
в) |-5,17| = |5,17|;
г) сравнить нельзя.
5. Решите уравнение -X=5,75.
Вариант 2
1. Укажите верное неравенство.
а) -4>2; б)-55<-45;
в)-10<-36; г)0=15
2. Укажите неверное неравенство.
а) 4>3; б)-1>-4;
в)7>-12; г)-10>9
3. Расположите числа -500, -300 и 60 в порядке убывания.
а) -300,-500,60; б) 60,-500,-300;
в) -500,-300,60; г) 60,-300,-500
4. Сравните числа |-3,27| и |3,27|.
а) |-3,27| < |3,27|;
б) |-3,27| > |3,27|;
в) |-3,27| = |3,27|;
г) сравнить нельзя.
5. Решите уравнение — X= -8,35.
Итог урока
а)оценивание по оценочным листам
б)рефлексия
Ребята у вас на столе лежат вагончики и смайлики трех видов:
 -Я хорошо понял, как сравнивают числа
-Я хорошо понял, как сравнивают числа
 —Я не все понял, у меня были ошибки
—Я не все понял, у меня были ошибки
 -Я не понял, как сравнивают числа
-Я не понял, как сравнивают числа
Ваша задача — выберите смайлик своего успеха на уроке и положите в карманчик вагончика. И мы с вами соберем состав «Поезда успеха» во главе с паровозиком.
В добрый путь! (Музыка из мультфильма «Паровозик из Ромашково»)
infourok.ru
Алгебра. Урок 2. Числовые неравенства. Координатная прямая
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Координатной прямой называют прямую линию с выбранными на ней началом отсчета (ноль), единичным отрезком и направлением. Каждому натуральному числу можно поставить в соответствие единственную точку на координатной прямой.
Для того, чтобы сравнить два числа, расположенных на координатной прямой, необходимо обратить внимание на то, как они расположены друг относительно друга.
Если число a расположено левее числа b, то a<b
Если число a расположено правее числа b, то a>b
В ОГЭ существует несколько типов заданий, связанных с расположением чисел на координатной прямой. Для того, чтобы начать решать примеры, вспомним еще некоторые понятия.
|a|={ a, a>0 0, a=0−a, a<0
Модуль отбирает у чисел знаки.
Если число положительное, то при взятии модуля этого числа результат – положительное число.
Если число равно нулю, то при взятии модуля нуля результат – ноль.
Если число отрицательное, то при взятии модуля этого числа результат – положительное число.
Примеры:
|−1|=1; |−5|=5; |7|=7; |0|=0.
Наверняка у вас возникает вопрос, почему в формуле раскрытия модуля |a|=−a, если a<0? Ведь после взятия модуля отрицательные числа становятся положительными.
Для ответа на этот вопрос, давайте подумаем, как у отрицательного числа отобрать знак минус? Если отрицательное число домножить на −1, то оно станет положительным.
Примеры:
|−1|=−(−1)=1
|−5|=−(−5)=5
a – арифметический квадратный корень из неотрицательного числа – такое неотрицательное число, квадрат которого равен a.
Примеры:
22=4⇒4=232=9⇒9=342=16⇒16=4
Но не из каждого числа можно извлечь квадратный корень. Например, придумать такое конечное положительное число, которое в квадрате будет давать 3, невозможно.
Иррациональное число – это число, которое не является рациональным, то есть не может быть представлено в виде дроби.
3 – есть число иррациональное.
В ОГЭ встречаются задания, в которых нужно оценить, где расположен корень из числа, между какими величинами.
Для того, чтобы оценивать расположение иррациональных чисел на координатной оси, будем использовать операцию возведения в квадрат.
Скачать домашнее задание к уроку 2.
epmat.ru
| 1. |
Целое число и 0
Сложность: среднее |
1 |
| 2. |
Положительное и отрицательное число (десятичные дроби)
Сложность: среднее |
1 |
| 3. |
Смешанное число между двумя целыми числами
Сложность: лёгкое |
1 |
| 4. |
Сравнение
Сложность: среднее |
2 |
| 5. |
Сравнение отрицательных десятичных дробей
Сложность: среднее |
2 |
| 6. |
Наибольшее/наименьшее число
Сложность: среднее |
2 |
| 7. |
Предложение в виде неравенства
Сложность: среднее |
2 |
| 8. |
Числа в порядке возрастания
Сложность: среднее |
4 |
| 9. |
Сравнение буквенных выражений
Сложность: сложное |
3 |
| 10. |
Сравнение отрицательных обыкновенных дробей (звёздочка)
Сложность: сложное |
3 |
| 11. |
Сравнение отрицательных десятичных дробей (звёздочка)
Сложность: сложное |
3 |
www.yaklass.ru