Что такое степень с натуральным показателем (В.А. Тарасов)
Тема: Степень с натуральным показателем и ее свойства
Урок: Что такое степень с натуральным показателем
Откуда появилась степень.
Выражение а+а+а в математике можно заменить на а+а+а=3а.
Выражение а+а+а+а+а можно представить в виде а+а+а+а+а=5а.
То есть, если в выражении n одинаковых слагаемых, каждое из которых а, то его можно кратко записать na.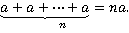 
А умножение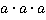 
, можно кратко записать так: а3, читается: а в кубе или третья степень числа а.
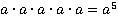
А если в выражение n одинаковых сомножителей, каждый из которых а, то мы будем писать:
= an – n-ная степень числа а.
Определение. Степенью an называется произведение n одинаковых сомножителей,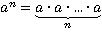 
, где n— натуральное число n={2,3,…..}; а – любое число.
Терминология: an
а – основание степени,
n – показатель степени,
an– степень, или а в n-ой степени, или n-ая степень числа а.Пример 1: Записать произведение в виде степени, назвать основание и показатель степени, вычислить, если возможно.
1. 
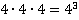– это по определению 4 в кубе или третья степень числа 4, 4— основание степени, 3— показатель степени. Результат:
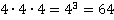
Ответ: 64
2. 
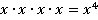– по определению, это x в четвертой степени, x – основание степени, 4 – показатель степени. Дальше вычислять нельзя, потому что
Ответ: 
3. 
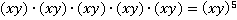
Это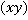
в пятой степени, 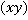– это основание степени, 5 – показатель степени, он показывает сколько раз основание умножается на себя. Замечание: от переменных мест сомножителей произведение не меняется, запишем это выражение по-другому:
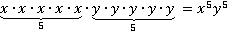
Значит, выражение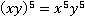 
.
Ответ: .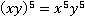
4. 
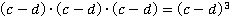– это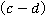
в кубе, 3 – это показатель степени, 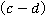– основание степени.
Ответ: 
5. 
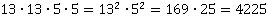
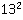– вторая степень числа 13 , 
– вторая степень числа 5.
Ответ: 4225
6. 
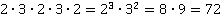
– третья степень числа 2,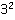 
– вторая степень числа 3.
Ответ: 72
В степени an может отдельно меняться показатель степени или основание степени.
Пример 2: Вычислить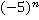 
, если
a) n=2
b) n=3
c) n=4
Решение:
a)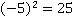 
так как стоит четная степень, минус пропадает.
b)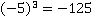 
c) 
– так как стоит четная степень, минус пропадает.
Ответ: a) 25; b)-125; c)625;
В этом примере менялся показатель степени, а основание не менялось. Рассмотрим пример, когда меняется основание.
Пример 3: Вычислить: b4, где
a) b=1
b) b=-3
c) b=
d) b=
Ответ:
a)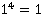 
b)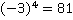 
c) 
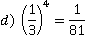
Вспомним, что натуральные числа — это 1,2,3 и так далее.
n={1,2,3,…..}
По нашему определению:
an = , (1)
n={2,3,…..}
Нужно еще одно определение для случая n=1. Что же такое а1?
a1=a (2)
Пример.
()1=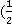
(-2)1=-2
31=3.
Итак, теперь мы знаем, что такое an, ,где n={1,2,3,…..} – любое натуральное число.
Рассмотрим геометрические задачи, в которых участвуют степени.
Задача: вычислить площадь квадрата, сторона которого равна а, где
a) а=3 см
b) а=7 см
c) а=1,5 см
Замечание. Если у нас есть квадрат со стороной а, то его площадь равна а2 или вторая степень числа а.
S=a2
Ответ:
S=32=9 см2
S=72=49 см2
S=1,52=2,25 см2
Итак, геометрическая задача потребовала от нас знание степени.
И в заключение, несколько примеров на вычисление. Задач много, но ключ к решению – первое и второе определение.
Вычислить:
a)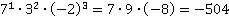 
Как видим, вычисления могут быть разные, но ключ к решению одинаковый.
b) Вычислить при а=1 следующее выражение:
а2=12=1
а3=13=1
При а=-1 будет чуть посложнее:
а2=(-1)2=1
а3=(-13)=-1
а4=(-1)4=1
и т.д. -1 будет мерцать то 1, то -1 в зависимости от того четный или нечетный показатель.
Итак, наша задача была рассмотреть, что такое степень с натуральным показателем. Мы рассмотрели 2 основных определения (1) и (2), выучили терминологию аn, где n – это показатель степени,
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Школьная математика (Источник).
2. Школьный помощник (Источник).
Рекомендованное домашнее задание
1. Записать произведение в виде степени, назвать основание и показатель степени, вычислить, если возможно.
а)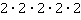 
б)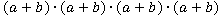
в)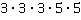 
2. Вычислить (-2)n, если
а) n=2 б) n=3 в) n=4
3. Вычислить: а5, где
а) а=1
б) а=-2
в) а=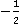
4. Вычислить площадь квадрата, сторона которого равна а/2, где
а) а=6 см
б) а=8 дм
в) а=3 м
interneturok.ru
1.1.2 Степень с натуральным показателем
Видеоурок 1: Свойства степени с натуральным показателем
Видеоурок 2: Степень с натуральным показателем и ее свойства
Лекция: Степень с натуральным показателем
Степень с натуральным показателем
Под степенью некоторого числа «а» с некоторым показателем «n» понимают произведение числа «а» само на себя «n» раз.
Когда говорят о степени с натуральным показателем, это означает, что число «n» должно быть целым и не отрицательным.
а — основание степени, которое показывает, какое число следует умножать само на себя,
n — показатель степени — он говорит, сколько раз основание нужно умножить само на себя.
Например:
84 = 8 * 8 * 8 * 8 = 4096.
В данном случае под основанием степени понимают число «8», показателем степени считается число «4», под значением степени понимается число «4096».
Самой большой и распространенной ошибкой при подсчете степени является умножение показателя на основание — ЭТО НЕ ВЕРНО!
Когда речь идет о степени с натуральным показателем, имеется в виду, что только показатель степени (n) должен быть натуральным числом.
В качестве основания можно брать любые числа с числовой прямой.
Например,
(-0,1)3 = (-0,1) * (-0,1) * (-0,1) = (-0,001).
Математическое действие, которое совершается над основанием и показателем степени, называется возведение в степень.
Сложение \ вычитание — математические действия первой ступени, умножение \ деление — действие второй ступени, возведение степени — это математическое действие третьей ступени, то есть одной из высших.
Данная иерархия математических действий определяет порядок при расчете. Если данное действие встречается в задачах среди двух предыдущих, то оно делается в первую очередь.
Например:
15 + 6 *22 = 39
В данном примере необходимо сначала возвести 2 в степень, то есть
22 = 4,
затем полученный результат умножить на 6, то есть
4 * 6 = 24,
затем
24 + 15 = 39.
Степень с натуральным показателем используется не только для конкретных вычислений, но и для удобства записи больших чисел. В данном случае еще используется понятие «стандартный вид числа». Данная запись подразумевает умножение некоторого числа от 1 до 9 на основание степени равное 10 с некоторым показателем степени.
Например, для записи радиуса Земли в стандартном виде используют следующую запись:
6400000 м = 6,4 * 106 м,
а масса Земли, например, записывается следующим образом:
6 * 1024 кг.
Свойства степени
Для удобства решений примеров со степенями необходимо знать основные их свойства:
1. Если Вам необходимо умножить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.
an * am = an+m
Например:
52 * 54 = 56.
2. Если необходимо разделить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть. Обратите внимани, для действий со степенями с натуральным показателем показатель степени делимого должен быть больше показателя степени делителя. В противном случае, частным данного действия будет число с отрицательным показателем степени.
an / am = an-m
Например,
54 * 52 = 52.
3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.
(an )m = an*m
Например,
(54 )2 = 58.
4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.
(a * b)m = am * bm
Например,
(5 * 8 )2 = 52 * 82.
5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.
(a / b)m = am / bm
6. Любое число, которое возводится в показатель степени, равный единице, равно первоначальному числу.
а1 = а
Например,
51 = 5.
7. При возведении любого числа в степень с показателем ноль, результатом данного вычисления всегда будет единица.
а0 = 1
Например,
70 = 1.
cknow.ru
1.1.2 Степень с натуральным показателем
Видеоурок 1: Свойства степени с натуральным показателем
Видеоурок 2: Степень с натуральным показателем и ее свойства
Лекция: Степень с натуральным показателем
Степень с натуральным показателем
Под степенью некоторого числа «а» с некоторым показателем «n» понимают произведение числа «а» само на себя «n» раз.
Когда говорят о степени с натуральным показателем, это означает, что число «n» должно быть целым и не отрицательным.
а — основание степени, которое показывает, какое число следует умножать само на себя,
n — показатель степени — он говорит, сколько раз основание нужно умножить само на себя.
Например:
84 = 8 * 8 * 8 * 8 = 4096.
В данном случае под основанием степени понимают число «8», показателем степени считается число «4», под значением степени понимается число «4096».
Самой большой и распространенной ошибкой при подсчете степени является умножение показателя на основание — ЭТО НЕ ВЕРНО!
Когда речь идет о степени с натуральным показателем, имеется в виду, что только показатель степени (n) должен быть натуральным числом.
В качестве основания можно брать любые числа с числовой прямой.
Например,
(-0,1)3 = (-0,1) * (-0,1) * (-0,1) = (-0,001).
Математическое действие, которое совершается над основанием и показателем степени, называется возведение в степень.
Сложение \ вычитание — математические действия первой ступени, умножение \ деление — действие второй ступени, возведение степени — это математическое действие третьей ступени, то есть одной из высших.
Данная иерархия математических действий определяет порядок при расчете. Если данное действие встречается в задачах среди двух предыдущих, то оно делается в первую очередь.
Например:
15 + 6 *22 = 39
В данном примере необходимо сначала возвести 2 в степень, то есть
22 = 4,
затем полученный результат умножить на 6, то есть
4 * 6 = 24,
затем
24 + 15 = 39.
Степень с натуральным показателем используется не только для конкретных вычислений, но и для удобства записи больших чисел. В данном случае еще используется понятие «стандартный вид числа». Данная запись подразумевает умножение некоторого числа от 1 до 9 на основание степени равное 10 с некоторым показателем степени.
Например, для записи радиуса Земли в стандартном виде используют следующую запись:
6400000 м = 6,4 * 106 м,
а масса Земли, например, записывается следующим образом:
6 * 1024 кг.
Свойства степени
Для удобства решений примеров со степенями необходимо знать основные их свойства:
1. Если Вам необходимо умножить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.
an * am = an+m
Например:
52 * 54 = 56.
2. Если необходимо разделить две степени, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть. Обратите внимани, для действий со степенями с натуральным показателем показатель степени делимого должен быть больше показателя степени делителя. В противном случае, частным данного действия будет число с отрицательным показателем степени.
an / am = an-m
Например,
54 * 52 = 52.
3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.
(an )m = an*m
Например,
(54 )2 = 58.
4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.
(a * b)m = am * bm
Например,
(5 * 8 )2 = 52 * 82.
5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.
(a / b)m = am / bm
6. Любое число, которое возводится в показатель степени, равный единице, равно первоначальному числу.
а1 = а
Например,
51 = 5.
7. При возведении любого числа в степень с показателем ноль, результатом данного вычисления всегда будет единица.
а0 = 1
Например,
70 = 1.
cknow.ru
| 1. |
Умножение степеней
Сложность: лёгкое |
1 |
| 2. |
Степень в степени
Сложность: лёгкое |
1 |
| 3. |
Возведение степени в степень (буквы)
Сложность: лёгкое |
2 |
| 4. |
Степень в степени (основание)
Сложность: лёгкое |
2 |
| 5. |
Степень в степени (показатель степени)
Сложность: лёгкое |
2 |
| 6. |
Произведение трёх степеней
Сложность: лёгкое |
2 |
| 7. |
Произведение степеней (основание — бином)
Сложность: лёгкое |
1 |
| 8. |
Частное трёх степеней
Сложность: лёгкое |
2 |
| 9. |
Произведение степеней с одинаковыми основаниями (буквы)
Сложность: лёгкое |
3 |
| 10. |
Произведение двух степеней (числа)
Сложность: лёгкое |
2 |
| 11. |
Частное двух степеней (отрицательное основание)
Сложность: лёгкое |
2 |
| 12. |
Возведение степени в степень (числа)
Сложность: лёгкое |
2 |
| 13. |
Частное двух степеней (дробь)
Сложность: лёгкое |
3 |
| 14. |
Частное двух степеней (отрицательные смешанные числа)
Сложность: лёгкое |
1 |
| 15. |
Произведение степеней с одним основанием (числа)
Сложность: среднее |
3 |
| 16. |
Произведение отрицательных и противоположных степеней
Сложность: среднее |
5 |
| 17. |
Уравнение (частное степеней, целые числа)
Сложность: среднее |
3 |
| 18. |
Дробь (буквы)
Сложность: среднее |
2 |
| 19. |
Произведение степени и степени в степени
Сложность: среднее |
2 |
| 20. |
Деление и умножение степеней
Сложность: среднее |
3 |
| 21. |
Произведение двух дробей
Сложность: среднее |
2 |
| 22. |
Произведение степеней в степени
Сложность: среднее |
3 |
| 23. |
Частное степени в степени и степени
Сложность: среднее |
2 |
| 24. |
Умножение и деление степеней
Сложность: среднее |
1 |
| 25. |
Вычисление выражения со степенями
Сложность: среднее |
1 |
www.yaklass.ru
| 1. | Произведение в виде степени (положительные числа) | 1 вид — рецептивный | лёгкое | 3,5 Б. | Запись произведения в виде степени по определению. |
| 2. | Основание и показатель степени (числа) | 1 вид — рецептивный | лёгкое | 3 Б. | Определение основания и показателя степени. |
| 3. | Степень бинома | 1 вид — рецептивный | лёгкое | 1,5 Б. | Запись произведения биномов в виде степени. |
| 4. | Основание и показатель степени (бином) | 1 вид — рецептивный | лёгкое | 2 Б. | Определение основания и показателя степени. |
| 5. | Произведение одинаковых множителей (одночлен) | 1 вид — рецептивный | лёгкое | 1 Б. | Представление степени в виде произведения одинаковых множителей. |
| 6. | Произведение одинаковых множителей (бином) | 1 вид — рецептивный | лёгкое | 1 Б. | Представление степени в виде произведения одинаковых множителей. |
| 7. | Степень числа (показатель степени — n) | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление степени. |
| 8. | Степень числа (основание) | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление степени. |
| 9. | Значение степени (обыкновенная дробь) | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление степени по известному основанию и показателю. |
| 10. | Площадь квадрата | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление площади квадрата. |
| 11. | Квадрат числа (минус перед числом) | 1 вид — рецептивный | лёгкое | 2 Б. | Вычисление значения выражения. |
| 12. | Числовые неравенства, сравнение | 2 вид — интерпретация | лёгкое | 1 Б. | Сравнение, поставить правильный знак неравенства, строгие неравенства. |
| 13. | Возведение в степень десятичных дробей | 2 вид — интерпретация | лёгкое | 1 Б. | Возведение в степень. |
| 14. | Возведение в степень целых чисел | 2 вид — интерпретация | лёгкое | 1 Б. | Возведение в квадрат и куб целых чисел, минус в степень не возводится. |
| 15. | Возведение в степень дробей (смешанных чисел) | 2 вид — интерпретация | среднее | 2 Б. | Возведение в степень дробей (смешанных чисел). |
| 16. | Произведение степеней и простых чисел | 2 вид — интерпретация | среднее | 3 Б. | Представление числа в виде произведения степеней и простых чисел. |
| 17. | Произведение (целые числа) | 2 вид — интерпретация | среднее | 3 Б. | Вычисление значения выражения. |
| 18. | Частное (чётная степень) | 2 вид — интерпретация | среднее | 3 Б. | Вычисление значения числового выражения. |
| 19. | Дробь | 2 вид — интерпретация | среднее | 3 Б. | Вычисление значения выражения. |
| 20. | Разность произведений | 2 вид — интерпретация | среднее | 4 Б. | Вычисление числового значения выражения. |
| 21. | Сумма произведений | 2 вид — интерпретация | среднее | 5 Б. | Вычисление значения выражения. |
| 22. | Уравнение | 3 вид — анализ | среднее | 5 Б. | Решение уравнения. |
| 23. | Убывание (возрастание) степеней | 3 вид — анализ | среднее | 4 Б. | Расположение чисел в порядке убывания (возрастания). |
www.yaklass.ru
Степень числа. Степень с натуральным показателем
Правило чтения и записи степеней с натуральным показателем
Краткую запись произведения одинаковых сомножителей очень удобно использовать, — длинная строка описания математических действий сокращается до записи нескольких шагов:
17^5=17 \cdot 17 \cdot 17 \cdot 17 \cdot 17=1\,419\,857
17 — основание степени,
5 — показатель степени,
1419857 — значение степени.
Степень с нулевым показателем равна 1, при условии, что a \neq 0:
a^0=1.
Например: 2^0=1
Когда нужно записать большое число обычно используют степень числа 10.
Например, один из самых древних динозавров на Земле жил около 280 млн. лет назад. Его возраст записывается следующим образом: 2,8 \cdot 10^8.
Каждое число большее 10 можно записать в виде a \cdot 10^n, при условии, что 1 < a < 10 и n является положительным целым числом. Такую запись называют стандартным видом числа.
Примеры таких чисел: 6978=6,978 \cdot 10^3, 569000=5,69 \cdot 10^5.
Можно говорить как и «a в n-ой степени», так и «n-ая степень числа a» и «a в степени n».
4^5 — «четыре в степени 5 » или «4 в пятой степени» или также можно сказать «пятая степень числа 4»
В данном примере 4 — основание степени, 5 — показатель степени.
Приведем теперь пример с дробями и отрицательными числами. Для избежания путаницы принято записывать основания, отличные от натуральных чисел, в скобках:
(7,38)^2, \left(\frac 12 \right)^7, (-1)^4 и др.
Заметьте также разницу:
(-5)^6 — означает степень отрицательного числа −5 с натуральным показателем 6.
-5^6 — соответствует числу противоположному 5^6.
Свойства степеней с натуральным показателем
Основное свойство степени
a^n \cdot a^k = a^{n+k}
Основание остается прежним, а складываются показатели степеней.
Например: 2^3 \cdot 2^2 = 2^{3+2}=2^5
Свойство частного степеней с одинаковыми основаниями
a^n : a^k=a^{n-k}, если n > k.
Показатели степени вычитаются, а основание остается прежним.
Данное ограничение n > k вводится для того, чтобы не выходить за рамки натуральных показателей степени. Действительно, при n > k показатель степени a^{n-k} будет являться натуральным числом, иначе он будет либо отрицательным числом (k < n), либо нулем (k-n).
Например: 2^3 : 2^2 = 2^{3-2}=2^1
Свойство возведения степени в степень
(a^n)^k=a^{nk}
Основание остается прежним, перемножаются лишь показатели степеней.
Например: (2^3)^6 = 2^{3 \cdot 6}=2^{18}
Свойство возведения в степень произведения
В степень n возводится каждый множитель.
a^n \cdot b^n = (ab)^n
Например: 2^3 \cdot 3^3 = (2 \cdot 3)^3=6^3
Свойство возведения в степень дроби
\frac{a^n}{b^n}=\left(\frac{a}{b} \right) ^n, b \neq 0
В степень возводится и числитель и знаменатель дроби. \left(\frac{2}{5} \right)^3=\frac{2^3}{5^3}=\frac{8}{125}
academyege.ru
| 1. |
Произведение в виде степени (положительные числа)
Сложность: лёгкое |
3,5 |
| 2. |
Основание и показатель степени (числа)
Сложность: лёгкое |
3 |
| 3. |
Степень бинома
Сложность: лёгкое |
1,5 |
| 4. |
Основание и показатель степени (бином)
Сложность: лёгкое |
2 |
| 5. |
Произведение одинаковых множителей (одночлен)
Сложность: лёгкое |
1 |
| 6. |
Произведение одинаковых множителей (бином)
Сложность: лёгкое |
1 |
| 7. |
Степень числа (показатель степени — n)
Сложность: лёгкое |
2 |
| 8. |
Степень числа (основание)
Сложность: лёгкое |
2 |
| 9. |
Значение степени (обыкновенная дробь)
Сложность: лёгкое |
2 |
| 10. |
Площадь квадрата
Сложность: лёгкое |
2 |
| 11. |
Квадрат числа (минус перед числом)
Сложность: лёгкое |
2 |
| 12. |
Числовые неравенства, сравнение
Сложность: лёгкое |
1 |
| 13. |
Возведение в степень десятичных дробей
Сложность: лёгкое |
1 |
| 14. |
Возведение в степень целых чисел
Сложность: лёгкое |
1 |
| 15. |
Возведение в степень дробей (смешанных чисел)
Сложность: среднее |
2 |
| 16. |
Произведение степеней и простых чисел
Сложность: среднее |
3 |
| 17. |
Произведение (целые числа)
Сложность: среднее |
3 |
| 18. |
Частное (чётная степень)
Сложность: среднее |
3 |
| 19. |
Дробь
Сложность: среднее |
3 |
| 20. |
Разность произведений
Сложность: среднее |
4 |
| 21. |
Сумма произведений
Сложность: среднее |
5 |
| 22. |
Уравнение
Сложность: среднее |
5 |
| 23. |
Убывание (возрастание) степеней
Сложность: среднее |
4 |
www.yaklass.ru