Степени с натуральным показателем таблица – Таблица степеней

Posted on by alexxlab

Таблица степеней

Таблица степеней от 1 до 10

11=1

12=1

13=1

14=1

15=1

16=1

17=1

18=1

19=1

1

10=1

21=2

22=4

23=8

24=16

25=32

26=64

27=128

28=256

29=512

210=1024

31=3

32=9

33=27

34=81

35=243

36=729

37=2187

38=6561

39=19683

310=59049

41=4

42=16

43=64

44=256

45=1024

46=4096

47=16384

48=65536

49=262144

410=1048576

51=5

52=25

53=125

54=625

55=3125

56=15625

57=78125

58=390625

59=1953125

510=9765625

61=6

62=36

63=216

64=1296

65=7776

66=46656

67=279936

68=1679616

69=10077696

610=60466176

71=7

72=49

73=343

74=2401

75=16807

76=117649

77=823543

78=5764801

79=40353607

710=282475249

81=8

82=64

83=512

84=4096

85=32768

86=262144

87=2097152

88=16777216

89=134217728

810=1073741824

91=9

92=81

93=729

94=6561

95=59049

96=531441

97=4782969

98=43046721

99=387420489

910=3486784401

10

1=10

102=100

103=1000

104=10000

105=100000

106=1000000

107=10000000

108=100000000

109=1000000000

1010=10000000000
n 1 2 3 4 5 6 7 8 9 10
1n 1 1 1 1 1
1		 1 1 1 1
2n 2 4 8 16 32 64 128 256 512 1024
3n 3 9 27 81 243 729 2187 6561 19683 59049
4n 4 16 64 256 1024 4096 16384 65536 262144 1048576
5n 5 25 125 625 3125 15625 78125 390625 1953125 9765625
6n 6 36 216 1296 7776 46656 279936 1679616 10077696 60466176
7n 7 49 343 2401 16807 117649 823543 5764801 40353607 282475249
8n 8 64 512 4096 32768 262144 2097152 16777216 134217728 1073741824
9n 9 81 729 6561 59049 531441 4782969 43046721 387420489 3486784401
10n 10 100 1000 10000 100000 1000000 10000000 100000000 1000000000 10000000000
Таблица степеней

возвести число в степень

В таблице степеней содержатся значения натуральных положительных чисел от 1 до 10.

Запись 35 читают «три в пятой степени». В этой записи число 3 называют основанием степени, число 5 показателем степени, выражение 35 называют степенью.

Показатель степени указывает сколько множителей в произведение, 35=3×3×3×3×3=243

Чтобы скачать таблицу степеней нажмите на уменьшенное изображение.

calcs.su

Таблица степеней по алгебре

На этой странице размещена таблица степеней от 2 до 10 для натуральных чисел от 1 до 20. Пример использования: находим в таблице число 9 (слева), затем во втором столбике видим квадрат числа, который равен 81. В третьем столбце таблицы значения кубов. Смотрите также: таблица квадратов, таблица корней.

https://uchim.org/matematika/tablica-stepenej — uchim.org

Таблица степеней

Пример: 23=8
Степень:
Число2345678910
2481632641282565121 024
3927812437292 1876 56119 68359 049
416642561 0244 09616 38465 536262 1441 048 576
5251256253 12515 62578 125390 6251 953 1259 765 625
6362161 2967 77646 656279 9361 679 61610 077 69660 466 176
7493432 40116 807117 649823 5435 764 80140 353 607282 475 249
8645124 09632 768262 1442 097 15216 777 216134 217 7281 073 741 824
9817296 56159 049531 4414 782 96943 046 721387 420 4893 486 784 401
101001 00010 000100 0001 000 00010 000 000100 000 0001 000 000 00010 000 000 000
111211 33114 641161 0511 771 56119 487 171214 358 8812 357 947 69125 937 424 601
121441 72820 736248 8322 985 98435 831 808429 981 6965 159 780 35261 917 364 224
131692 19728 561371 2934 826 80962 748 517815 730 72110 604 499 373137 858 491 849
141962 74438 416537 8247 529 536105 413 5041 475 789 05620 661 046 784289 254 654 976
152253 37550 625759 37511 390 625170 859 3752 562 890 62538 443 359 375576 650 390 625
162564 09665 5361 048 57616 777 216268 435 4564 294 967 29668 719 476 7361 099 511 627 776
172894 91383 5211 419 85724 137 569410 338 6736 975 757 441118 587 876 4972 015 993 900 449
183245 832104 9761 889 56834 012 224612 220 03211 019 960 576198 359 290 3683 570 467 226 624
193616 859130 3212 476 09947 045 881893 871 73916 983 563 041322 687 697 7796 131 066 257 801
204008 000160 0003 200 00064 000 0001 280 000 00025 600 000 000512 000 000 00010 240 000 000 000
214419 261194 4814 084 10185 766 1211 801 088 54137 822 859 361794 280 046 58116 679 880 978 201
2248410 648234 2565 153 632113 379 9042 494 357 88854 875 873 5361 207 269 217 79226 559 922 791 424
2352912 167279 8416 436 343148 035 8893 404 825 44778 310 985 2811 801 152 661 46341 426 511 213 649
2457613 824331 7767 962 624191 102 9764 586 471 424110 075 314 1762 641 807 540 22463 403 380 965 376
2562515 625390 6259 765 625244 140 6256 103 515 625152 587 890 6253 814 697 265 62595 367 431 640 625

Свойства степени — 2 части

Таблица основных степеней по алгебре в компактном виде (картинка, удобно, чтобы распечатать), сверху числа, сбоку степени:

таблица степеней
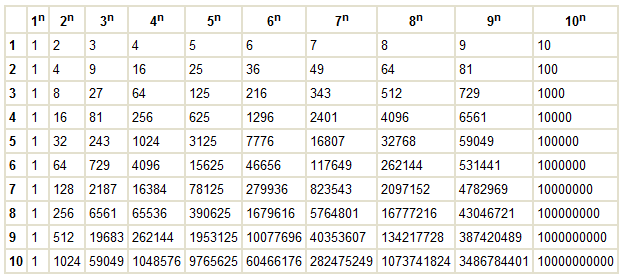
(можно открыть в новом окне, нажав на картинку)

Полную математическую таблицу можно бесплатно скачать, просто сохранив картинку выше с помощью правой кнопки мыши.

Всё для учебы » Математика в школе » Таблица степеней по алгебре

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:


Ссылка: https://uchim.org/matematika/tablica-stepenej

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

uchim.org

Таблица степеней

Что такое степень числа?

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

\[ \underbrace{a \cdot a \cdot a \cdot a \cdot \cdots \cdot a = a ^{n} }_{n — \text множителей} \]

Запись «an» читается так: «а в степени n» или «n-ая степень числа a».

где:
a — основание степени;
n — показатель степени.

Таблица степеней от 1 до 10

n 1 2 3 4 5 6 7 8 9 10
1n 1 1 1 1 1 1 1 1 1 1
2n 2 4 8 16 32 64 128 256 512 1 024
3n 3 9 27 81 243 729 2 187 6 561 19 683 59 049
4n 4 16 64 256 1 024 4 096 16 384 65 536 262 144 1 048 576
5n 5 25 125 625 3 125 15 625 78 125 390 625 1 953 125 9 765 625
6n 6 36 216 1 296 7 776 46 656 279 936 1 679 616 10 077 696 60 466 176
7n 7 49 343 2 401 16 807 117 649 823 543 5 764 801 40 353 607 282 475 249
8n 8 64 512 4 096 32 768 262 144 2 097 152 16 777 216 134 217 728 1 073 741 824
9n 9 81 729 6 561 59 049 531 441 4 782 969 43 046 721 387 420 489 3 486 784 401
10n 10 100 1 000 10 000 100 000 1 000 000 10 000 000 100 000 000 1 000 000 000 10 000 000 000

Таблица степеней от 1 до 10

1 1 = 1

1 2 = 1

1 3 = 1

1 4 = 1

1 5 = 1

1 6 = 1

1 7 = 1

1 8 = 1

1 9 = 1

1 10 = 1

2 1 = 2

2 2 = 4

2 3 = 8

2 4 = 16

2 5 = 32

2 6 = 64

2 7 = 128

2 8 = 256

2 9 = 512

2 10 = 1024

3 1 = 3

3 2 = 9

3 3 = 27

3 4 = 81

3 5 = 243

3 6 = 729

3 7 = 2187

3 8 = 6561

3 9 = 19683

3 10 = 59049

4 1 = 4

4 2 = 16

4 3 = 64

4 4 = 256

4 5 = 1024

4 6 = 4096

4 7 = 16384

4 8 = 65536

4 9 = 262144

4 10 = 1048576

5 1 = 5

5 2 = 25

5 3 = 125

5 4 = 625

5 5 = 3125

5 6 = 15625

5 7 = 78125

5 8 = 390625

5 9 = 1953125

5 10 = 9765625

6 1 = 6

6 2 = 36

6 3 = 216

6 4 = 1296

6 5 = 7776

6 6 = 46656

6 7 = 279936

6 8 = 1679616

6 9 = 10077696

6 10 = 60466176

7 1 = 7

7 2 = 49

7 3 = 343

7 4 = 2401

7 5 = 16807

7 6 = 117649

7 7 = 823543

7 8 = 5764801

7 9 = 40353607

7 10 = 282475249

8 1 = 8

8 2 = 64

8 3 = 512

8 4 = 4096

8 5 = 32768

8 6 = 262144

8 7 = 2097152

8 8 = 16777216

8 9 = 134217728

8 10 = 1073741824

9 1 = 9

9 2 = 81

9 3 = 729

9 4 = 6561

9 5 = 59049

9 6 = 531441

9 7 = 4782969

9 8 = 43046721

9 9 = 387420489

9 10 = 3486784401

10 1 = 10

10 2 = 100

10 3 = 1000

10 4 = 10000

10 5 = 100000

10 6 = 1000000

10 7 = 10000000

10 8 = 100000000

10 9 = 1000000000

10 10 = 10000000000

Калькулятор степеней онлайн

Онлайн калькулятор расчета степеней

 

Входные данные

Число*

Степень*

Точность

1234567

* Обязательные поля для заполнения

Результат

В таблице степеней содержатся значения натуральных положительных чисел от 1 до 10.

Запись 35 читают «три в пятой степени». В этой записи число 3 называют основанием степени, число 5 показателем степени, выражение 35 называют степенью.

Показатель степени указывает сколько множителей в произведение, 35=3×3×3×3×3=243

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

calcsbox.com

Таблица степеней натуральных чисел | Формулы с примерами

Калькулятор степени натурального числа


Таблица степеней натуральных чисел от 2 до 25

! Наведите на ячейку, для того, чтобы увеличить значение в таблице.

x В степени:
Число 2 3 4 5 6 7 8 9 10
2 4 8 16 32 64 128 256 512 1 024
3 9 27 81 243 729 2 187 6 561 19 683 59 049
4 16 64 256 1 024 4 096 16 384 65 536 262 144 1 048 576
5 25 125 625 3 125 15 625 78 125 390 625 1 953 125 9 765 625
6 36 216 1 296 7 776 46 656 279 936 1 679 616 10 077 696 60 466 176
7 49 343 2 401 16 807 117 649 823 543 5 764 801 40 353 607 282 475 249
8 64 512 4 096 32 768 262 144 2 097 152 16 777 216 134 217 728 1 073 741 824
9 81 729 6 561 59 049 531 441 4 782 969 43 046 721 387 420 489 3 486 784 401
10 100 1 000 10 000 100 000 1 000 000 10 000 000 100 000 000 1 000 000 000 10 000 000 000
11 121 1 331 14 641 161 051 1 771 561 19 487 171 214 358 881 2 357 947 691 25 937 424 601
12 144 1 728 20 736 248 832 2 985 984 35 831 808 429 981 696 5 159 780 352 61 917 364 224
13 169 2 197 28 561 371 293 4 826 809 62 748 517 815 730 721 10 604 499 373 137 858 491 849
14 196 2 744 38 416 537 824 7 529 536 105 413 504 1 475 789 056 20 661 046 784 289 254 654 976
15 225 3 375 50 625 759 375 11 390 625 170 859 375 2 562 890 625 38 443 359 375 576 650 390 625
16 256 4 096 65 536 1 048 576 16 777 216 268 435 456 4 294 967 296 68 719 476 736 1 099 511 627 776
17 289 4 913 83 521 1 419 857 24 137 569 410 338 673 6 975 757 441 118 587 876 497 2 015 993 900 449
18 324 5 832 104 976 1 889 568 34 012 224 612 220 032 11 019 960 576 198 359 290 368 3 570 467 226 624
19 361 6 859 130 321 2 476 099 47 045 881 893 871 739 16 983 563 041 322 687 697 779 6 131 066 257 801
20 400 8 000 160 000 3 200 000 64 000 000 1 280 000 000 25 600 000 000 512 000 000 000 10 240 000 000 000
21 441 9 261 194 481 4 084 101 85 766 121 1 801 088 541 37 822 859 361 794 280 046 581 16 679 880 978 201
22 484 10 648 234 256 5 153 632 113 379 904 2 494 357 888 54 875 873 536 1 207 269 217 792 26 559 922 791 424
23 529 12 167 279 841 6 436 343 148 035 889 3 404 825 447 78 310 985 281 1 801 152 661 463 41 426 511 213 649
24 576 13 824 331 776 7 962 624 191 102 976 4 586 471 424 110 075 314 176 2 641 807 540 224 63 403 380 965 376
25 625 15 625 390 625 9 765 625 244 140 625 6 103 515 625 152 587 890 625 3 814 697 265 625 95 367 431 640 625

formula-xyz.ru

Таблица степеней

Существует множество таблиц значений степеней натуральных чисел. Привести их все не представляется возможным. Здесь мы приведем примеры некоторых таких таблиц и задачи на нахождение значений по таким таблицам.

Таблица степеней первых натуральных чисел

Приведем для начала таблицу для нахождения степеней натуральных чисел от $2$ до $12$ по степеням от $1$ до $10$ (таблица 1). Отметим, что мы не приводим степени числа $1$, потому что единица в любой степени будет равняться самой себе.

Находить по этой таблице значения надо следующим образом: В первом столбце находим число, степень которого нас интересует. Запоминаем номер этой строчки. Затем в первой сроке находим показатель степени и запоминаем найденный столбец. Пересечение найденной строки и столбца и даст нам ответ.

Пример 1

Найти $8^7$

Решение.

Находим в первом столбце число $8$: получаем 8-ю строчку.

Находим в первой строке число $7$: получаем 8-й столбец.

Видим, что на их пересечении находится число $2097152$. Следовательно

$8^7=2097152$

Таблицы степеней натуральных чисел от $1$ до $100$

Также довольно популярны таблицы степеней от $1$ до $100$. Все их привести невозможно, поэтому мы здесь приведем для примера такие таблицы для квадратов и кубов таких натуральных чисел (таблица 2 и таблица 3).

Эти таблицы напоминают всем известные таблицы умножения, поэтому, мы думаем, читателю не составит труда использование данных таблиц.

Пример 2

Найти

а) $76^2$.

б) $28^3$

Решение.

а) Данное значение находим в таблице $2$ в $8$ табличке:

$76^2=5776$

б) Данное значение находим в таблице $3$ в $3$ табличке:

$28^3=21952$

Таблица квадратов натуральных чисел от $10$ до $99$

Еще одной пользующейся популярностью таблицей является таблица квадратов чисел от $10$ до $99$ (таблица 4), то есть всех десятичных чисел.

Находить по этой таблице значения надо следующим образом: В первом столбце находим число десятков интересующего нас числа. Запоминаем номер этой строчки. Затем в первой сроке находим число единиц интересующего числа и запоминаем найденный столбец. Пересечение найденной строки и столбца и даст нам ответ.

Пример 3

Найти $37^2$

Решение.

Находим в первом столбце число $3$: получаем 4-ю строчку.

Находим в первой строке число $7$: получаем 8-й столбец.

Видим, что на их пересечении находится число $1369$. Следовательно

$37^2=1369$

spravochnick.ru

Таблица степеней

Возведение в степень — бинарная операция, происходящая из сокращения для множественного умножения числа на самого себя. Обозначение: ab называется степенью с основанием a и показателем b. Логарифм — обратная к возведению в степень функция.

Ниже представлена таблица степеней от 1 до 10.

1n2n3n4n5n6n7n8n9n10n
112345678910
2149162536496481100
31827641252163435127291000
411681256625129624014096656110000
5132243102431257776168073276859049100000
6164729409615625466561176492621445314411000000
71128218716384781252799368235432097152478296910000000
81256656165536390625167961657648011677721643046721100000000
9151219683262144195312510077696403536071342177283874204891000000000
10110245904910485769765625604661762824752491073741824348678440110000000000

Другие заметки по алгебре и геометрии

edu.glavsprav.ru

Таблица основных степеней — методическая рекомендация. Алгебра, 7 класс.

1. Квадрат числа (целое число или десятичная дробь) 1 вид — рецептивный лёгкое 2 Б. Представление числа в виде квадрата.
2. Куб числа (отрицательное число) 1 вид — рецептивный лёгкое 1 Б. Представление числа в виде куба.
3. Степень обыкновенной дроби 1 вид — рецептивный лёгкое 1 Б. Представление числа в виде степени.
4. Степень числа 10 1 вид — рецептивный лёгкое 1 Б. Запись числа в виде степени с основанием 10.
5. Степень единицы и десяти 1 вид — рецептивный лёгкое 3 Б. Вычисление степени единицы и десяти.
6. Произведение степеней 2 вид — интерпретация лёгкое 2 Б. Вычисление произведения степеней.
7. Сумма степеней (единица, нуль) 2 вид — интерпретация лёгкое 4 Б. Вычисление суммы степеней.
8. Сумма степеней (десятичные дроби) 2 вид — интерпретация среднее 3 Б. Вычисление суммы степеней.
9. Сумма степеней (обыкновенные дроби) 2 вид — интерпретация среднее 3 Б. Вычисление суммы степеней.
10. Сравнение степени с нулём (целые числа) 2 вид — интерпретация среднее 2 Б. Сравнение степени с нулём.
11. Сравнение степеней (обыкновенные дроби) 2 вид — интерпретация среднее 2 Б. Сравнение степеней.
12. Сравнение выражения с нулём 2 вид — интерпретация среднее 2 Б. Сравнение выражения с нулём.
13. Неизвестный показатель степени 2 вид — интерпретация среднее 2 Б. Нахождение неизвестного показателя степени.
14. Сумма разрядных слагаемых 2 вид — интерпретация среднее 3 Б. Запись числа, представленного суммой разрядных слагаемых.
15. Квадрат единицы, нуля и десяти 2 вид — интерпретация среднее 3 Б. Вычисление значения выражения.
16. Расположение чисел по возрастанию (убыванию) 2 вид — интерпретация среднее 5 Б. Расположение чисел по возрастанию (убыванию).
17. Сумма показателей степеней 2 вид — интерпретация среднее 3 Б. Вычисление суммы показателей степеней.
18. Неизвестный показатель степени, уравнение (произведение) 2 вид — интерпретация сложное 4 Б. Нахождение неизвестного показателя степени.
19. Неизвестный показатель степени, уравнение (частное) 2 вид — интерпретация сложное 4 Б. Нахождение неизвестного показателя степени.
20. Уравнение, сводимое к линейному 2 вид — интерпретация сложное 5 Б. Нахождение неизвестного показателя степени.

www.yaklass.ru

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *