Самостоятельная работа «Степень числа», 5 класс
Просмотр
содержимого документа
|
Самостоятельная работа по теме: «Степень числа» Вариант I
а) три в четвертой степени; б) восемь в квадрате.
|
Вариант II
а) два в пятой степени; б) пять в кубе.
|
|
Самостоятельная работа по теме: «Степень числа» Вариант I
а) три в четвертой степени; б) восемь в квадрате.
|
Самостоятельная работа по теме: «Степень числа» Вариант II
а) два в пятой степени; б) пять в кубе.
|
mega-talant.com
| Решение | Преобразуем, степени в числителе по свойству , а степени из знаменателя поднимем в числитель, при этом они изменят знак:
Далее воспользуемся тем фактом, что при умножении степеней с одинаковыми основаниями показатели степеней складываются
Используя свойства степеней: и , получим:
|
ru.solverbook.com
Самостоятельная работа « Степень числа» Вариант 1 1.Найдизначение:
2.Найди значение выражений: а) б) в) г)(13 – 11)⁵. | Самостоятельная работа « Степень числа» Вариант 2 1.Найдизначение:
2.Найди значение выражений: а) б) в) г)(14 – 12)⁶. | Самостоятельная работа « Степень числа» Вариант 1 1.Найдизначение:
2.Найди значение выражений: а) б) в) г)(13 – 11)⁵. | Самостоятельная работа « Степень числа» Вариант 2 1.Найдизначение:
2.Найди значение выражений: а) б) в) г)(14 – 12)⁶. | Самостоятельная работа « Степень числа» Вариант 1 1.Найдизначение:
2.Найди значение выражений: а) б) в) г)(13 – 11)⁵. | Самостоятельная работа « Степень числа» Вариант 2 1.Найдизначение:
2.Найди значение выражений: а) б) в) г)(14 – 12)⁶. |
multiurok.ru
Задание №2 ЕГЭ по математике базовый уровень
Операции со степенями
Описание задания
Во задании №2 ЕГЭ по математике необходимо продемонстрировать знания работы со степенными выражениями.
Тематика заданий: операции со степенями
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
Теория к заданию №2
Правила обращения со степенями можно представить следующим образом:

Кроме этого, следует напомнить об операциях с дробями:

Теперь можно перейти к разбору типовых вариантов! 🙂
Разбор типовых вариантов заданий №2 ЕГЭ по математике базового уровня
Во всех заданиях, аналогично первому заданию, нам необходимо найти значение выражения.
Вариант 2МБ1
 Алгоритм выполнения:
Алгоритм выполнения:
- Представить число с отрицательным показателем в виде правильной дроби.
- Выполнить первое умножение.
- Представить степени чисел в виде простых чисел, заменив степени их умножением.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть: 10-1 = 1/101 = 1/10
Выполним первое умножение, то есть умножение целого числа на правильную дробь. Для этого числитель дроби умножим на целое число, а знаменатель оставим без изменения.
9 · 1/10 = (9 · 1)/10 = 9/10
Первая степень числа всегда есть само число.
101 = 10
Вторая степень числа – это число умноженное само на себя.
102 = 10 · 10 = 100
Вычислим значение выражения, учитывая, что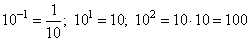
получим:
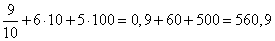
Ответ: 560,9
Вариант 2МБ2
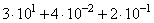
Алгоритм выполнения:
- Представить первую степень числа в виде целого числа.
- Представить отрицательные степени чисел в виде правильных дробей.
- Выполнить умножение целых чисел.
- Выполнить умножение целых чисел на правильные дроби.
- Выполнить сложение.
Решение:
Первая степень числа всегда есть само число. (101 = 10)
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть:
10-1 = 1/101 = 1/10
10-2 = 1/102 = 1/(10 · 10) = 1/100
Выполним умножение целых чисел.
3 · 101 = 3 · 10 = 30
Выполним умножение целых чисел на правильные дроби.
4 · 10-2 = 4 · 1/100 = (4 ·1)/100 = 4/100
2 · 10-1 = 2 · 1/10 = (2 · 1)/10 = 2/10
Вычислим значение выражения, учитывая, что
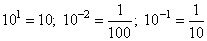
получим:
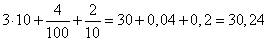
Ответ: 30,24
Вариант 2МБ3
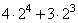
Алгоритм выполнения:
- Представить степени чисел в виде умножения и вычислить значение степеней чисел.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Представим степени чисел в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
24 = 2 · 2 · 2 · 2 = 16
23 = 2 · 2 · 2 = 8
Выполним умножение:
4 · 24 = 4 · 16 = 64
3 · 23 = 3 · 8 = 24
Вычислим значение выражения:
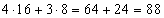
Ответ: 88
Вариант 2МБ4
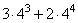
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
44 = 4 · 43
Вынесем общий множитель за скобку
3 · 43 + 2 · 44 = 43 · (3 + 2 · 4)
Выполним действие в скобках.
(3 + 2 · 4) = (3 + 8) = 11
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
43 = 4 · 4 · 4 = 64
Вычислим значение выражения, учитывая, что
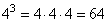
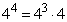
получим:
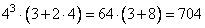
Ответ: 704
Вариант 2МБ5
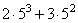
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
53 = 5 · 52
Вынесем общий множитель за скобку
2 · 53 + 3 · 52 = 52 · (2 · 5 + 3)
Выполним действие в скобках.
(2 · 5 + 3) = (10 + 3) = 13
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
52 = 5 · 5 = 25
Вычислим значение выражения, учитывая, что
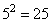 , а
, а 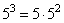
получим:
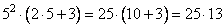
Выполняем умножение в столбик, имеем:
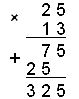
Ответ: 325
Вариант 2МБ6
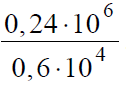
Решение:
В данном задании удобней привести значения к более привычному виду, а именно записать числа в числителе и знаменателе в стандартном виде:
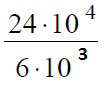
После этого можно выполнить деление 24 на 6, в результате получим 4.
Десять в четвертой степени при делении на десять в третьей степени даст десять в первой, или просто десять, поэтому мы получим:
4 • 10 = 40
Ответ: 40
Вариант 2МБ6
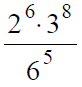
Решение:
В данном случае мы должны заметить, что число 6 в знаменателе раскладывается на множители 2 и 3 в степени 5:
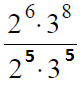
После этого можно выполнить сокращения степеней у двойки: 6-5=1, у тройки: 8-5=3.
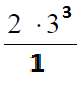
Теперь возводим 3 в куб и умножаем на 2, получая 54.
Ответ: 54
Вариант 2МБ6

Алгоритм выполнения
- Применяем к числителю св-во степеней (ах)у=аху. Получаем 3–6.
- Применяем к дроби св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
(3–3)2 /3–8 = 3–6 /3–8= 3–6–(–8)) = 3–6+8 = 32 = 9
Ответ: 9
Вариант 2МБ7

Алгоритм выполнения
- Используем для степени в числителе (149) св-во (аb)х=ax·bx. 14 разложим на произведение 2 и 7. Получим произведение степеней с основаниями 2 и 7.
- Преобразуем выражение в 2 дроби, каждая из которых будет содержать степени с одинаковыми основаниями.
- Применяем к дробям св-во степеней ax/ay=ax–y.
- Находим полученное произведение.
Решение:
149 / 27·78 = (2·7)9 / 27·78 = 29·79 / 27 78 = 29–7·79–8 = 22·71 = 4·7 = 28
Ответ: 28
Вариант 2МБ8
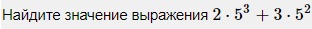
Алгоритм выполнения
- Выносим за скобки общий множитель 52=25.
- Выполняем в скобках умножение чисел 2 и 5. Получаем 10.
- Выполняем в скобках сложение 10 и 3. Получаем 13.
- Выполняем умножение общего множителя 25 и 13.
Решение:
2·53+3·52 = 52·(2·5+3) = 25·(10+3) = 25·13 = 325
Ответ: 325
Вариант 2МБ9

Алгоритм выполнения
- Возводим в квадрат (–1). Получим 1, поскольку происходит возведение в четную степень.
- Возводим (–1) в 5-ю степень. Получим –1, т.к. происходит возведение в нечетную степень.
- Выполняем действия умножения.
- Получаем разность двух чисел. Находим ее.
Решение:
6·(–1)2+4·(–1)5 = 6·1+4·(–1) = 6+(–4) = 6–4 = 2
Ответ: 2
Вариант 2МБ10

Алгоритм выполнения
- Преобразуем множители 103 и 102 в целые числа.
- Находим произведения путем переноса десят.запятой вправо на соответствующее число знаков.
- Находим результирующую сумму.
Решение:
9,4·103+2,2·102 = 9,4·1000+2,2·100 = 9400+220 = 9620
Ответ: 9620
Вариант 2МБ11

Алгоритм выполнения
- Преобразуем 102 в целое число и выполняем умножение в числителе путем переноса деся.запятой.
- Преобразуем 10–2 в десят.дробь и выполняем умножение в знаменателе путем переноса десят.запятой влево.
- Домножаем числитель и знаменатель на 100, чтобы избавиться от десят.запятой в знаменателе.
- Находим результат путем деления числителя дроби на ее знаменатель.
Решение:
1,6·102 / 4·10–2 = 1,6·100 / 4·0,01 = 160/ 0,04 = 160·100 / 0,04·100 = 16000 / 4 = 4000
Ответ: 40000
Вариант 2МБ12

Алгоритм выполнения
- Применяем к дроби св-ва степеней ax·ay=ax+y и ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
3–10·35 / 3–7 = 3–10+5 /3–7 = 3–5 / 3–7 = 3–5–(–7)) = 3–5+7 = 32 = 9
Ответ: 9
Вариант 2МБ13

Алгоритм выполнения
- Представляем выражение в знаменателе как степень с основанием 8. Далее применяем св-во степеней (ах)у=аху, получаем 812.
- Применяем к дроби св-во степеней ax/ay=ax–y.
Решение:
813 /646 =813 / (82)6 =813 /812 = 813–12 = 81 = 8
Ответ: 8
Вариант 2МБ14

Алгоритм выполнения
- Преобразуем степени в числителе дроби и в делителе (число 92) так, чтобы получились степени с основанием 3.
- Используем св-во степеней (ах)у=аху для преобразованных степеней.
- Используем св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
274 /36 : 92 =(33)4 / 36 : (32)2 = 312/36 : 34 = 312–6–4 = 32 = 9
Ответ: 9
Вариант 2МБ15
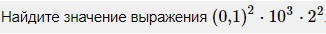
Алгоритм выполнения
- Возводим каждый из множителей в соответствующую степень. Получим соответственно: 0,01, 1000, 4.
- Перемножаем 0,01 и 1000 путем переноса десят.запятой вправо на 3 знака. Получим 10.
- Умножаем 10 на 4.
Решение:
(0,1)2·103·22 = 0,01·1000·4 = 10·4 = 40
Ответ: 40
 Скачать PDF
Скачать PDF Распечатать
Распечататьspadilo.ru
Тест по математике на тему «Действия со степениями»
Данную карточку можно использовать при отработке темы «Действия со степенями». Выполняя задания, учащиеся проговаривают правила и одновременно выполняют задания
— возведение степени в степень;
— умножение степеней;
— деление степеней.
Можно организовать групповую форму работы (сильный учащийся- слабый), индивидуальное выполнение учащимся с элементами самопроверки или проверяет учитель.
Также можно использовать при подготовке к Г(И)А выпускников 9 класса или со слабоуспевающими учащимися.
КАРТОЧКА ЗАДАНИЕ по теме «Действия со степенями»
Найдите значение выражения: 
Образец решения:
Числитель – это выражение, записанное над чертой. В числителе степень c-4 возводят в степень (–6). При возведении степени в степень основание оставляют тем же, а показатели перемножают, При умножении двух отрицательных чисел надо: 1. Поставить знак «+» 2. Перемножить модули этих чисел.
При умножении степеней с одинаковым основанием основание остается без изменения, а показатели степеней складывают:

При делении степеней с одинаковым основанием основание остается без изменения, а из показателя степени делимого вычитают показатель степени делителя:

т.е. 


ИСПОЛЬЗОВАНИЕ КАЛЬКУЛЯТОРА ИЛИ ДРУГОЙ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКОЙ ЗАПРЕЩЕНО !!!
№ 156933 
№ 156943 
№ 156953 
№ 156963 
№ 156973 
№ 156983 
№ 156993 
№ 157003 
№ 157013 
№ 157023 
№ 157033 
№ 157043 
№ 157053 
№ 157063 
№ 157073 
№ 156935 
№ 156945 
№ 156955 
№ 156965 
№ 156975 
№ 156985 
№ 156995 
№ 157005 
№ 157015 
№ 157025 
№ 157035 
№ 157045 
№ 157055 
№ 157065 
№ 157075 
№ 156937 
№ 156947 
№ 156957 
№ 156967 
№ 156977 
№ 156987 
№ 156997 
№ 157007 
№ 157017 
№ 157027 
№ 157037 
№ 157047 
№ 157057 
№ 157067 
№ 157077 
№ 156939 
№ 156949 
№ 156959 
№ 156969 
№ 156979 
№ 156989 
№ 156999 
№ 157009 
№ 157019 
№ 157029 
№ 157039 
№ 157049 
№ 157059 
№ 157069 
№ 157079 
№ 156941 
№ 156951 
№ 156961 
№ 156971 
№ 156981 
№ 156991 
№ 157001 
№ 157011 
№ 157021 
№ 157031 
№ 157041 
№ 157051 
№ 157061 
№ 157071 
№ 157081 
infourok.ru
Задания по профильной математике ЕГЭ с разбором решений
Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).
Минимальный порог — 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).
 Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:
Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:
Задание № 1 — проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1. В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.
Решение:
1) Найдем количество потраченной воды за месяц:
177 — 172 = 5 (куб м)
2) Найдем сколько денег заплатят за потраченную воду:
34,17 · 5 = 170,85 (руб)
Ответ: 170,85.
Задание № 2 —является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.
#ADVERTISING_INSERT#Задание № 2 проверяет умение читать диаграммы.
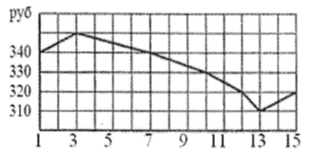
Пример 2. На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?
Решение:
1) 340 · 1000 = 340000 (руб) — бизнесмен потратил 7 апреля при покупке 1000 акций.
2) 1000 · 3/4 = 750 (акций) — составляют 3/4 от всех купленных акций.
3) 330 · 750 = 247500 (руб) — бизнесмен получил 10 апреля после продажи 750 акций.
4) 1000 – 750 = 250 (акций) — остались после продажи 750 акций 10 апреля.
5) 310 · 250 = 77500 (руб) — бизнесмен получил 13 апреля после продажи 250 акций.
6) 247500 + 77500 = 325000 (руб) — бизнесмен получил после продажи 1000 акций.
7) 340000 – 325000 = 15000 (руб) — потерял бизнесмен в результате всех операций.
Ответ: 15000.
Чтобы продолжить чтение, авторизуйтесь на сайте.
rosuchebnik.ru
ТОГИС задача «Степень числа»
Приведенные рассуждения вполне можно осуществить устно – 122, конечно, нужно помнить, удвоенные произведения квадратов двучленов слева и справа от 122 взаимно уничтожаются и их можно не считать, а 5·144 = 500 + 200 + 20, – не сложно.Воспользуемся этим приемом и устно найдем сумму:
482 + 492 + 502 + 512 + 522 = 5·502 + 10 = 5·2500 + 10 = 12510.
Усложним:
842 + 872 + 902 + 932 + 962 = 5·8100 + 2·9 + 2·36 = 40500 + 18 + 72 = 40590.
Ряд Рачинского
Алгебра дает нам средство поставить вопрос об этой интересной особенности ряда чисел
10, 11, 12, 13, 14
более широко: единственный ли это ряд из пяти последовательных чисел, сумма квадратов первых трех из которых равна сумме квадратов двух последних?
Обозначив первое из искомых чисел через x, имеем уравнение
x2 + (х + 1)2 + (x + 2)2 = (x + 3)2 + (x + 4)2.
Удобнее, однако, обозначить через х не первое, а второе из искомых чисел. Тогда уравнение будет иметь более простой вид
(x – 1)2 + x2 + (x + 1)2 = (x + 2)2 + (x + 3)2.
Раскрыв скобки и сделав упрощения, получаем:
x2 – 10x – 11 = 0,
откуда
х1 = 11, x2 = –1.
Существуют, следовательно, два ряда чисел, обладающих требуемым свойством: ряд Рачинского
10, 11, 12, 13, 14
и ряд
–2, –1, 0, 1, 2.
В самом деле,
(–2)2 +(–1)2 + 02 = 12 + 22.
Закончить я хотела бы светлыми и трогательными воспоминаниями автора авторского блога В. Искры в статье « О квадратах двузначных чисел и не только о них…»
Когда-то, в году примерно 1962-м, наша «математичка», Любовь Иосифовна Драбкина, дала эту задачу и нам, 7-классникам.
Я тогда очень увлекался только что появившимся КВН-ом. Болел за команду подмосковного города Фрязино. «Фрязинцы» отличались особым умением применять логический «экспресс-анализ» для решения любой задачи, «вытягивания» самого каверзного вопроса.
Быстро посчитать в уме я не мог. Однако, применив «фрязинский» метод, я прикинул, ответ должен выражаться целым числом. Иначе — это уже не «устный счет»! Этим числом не могла быть единица – даже если бы в числителе стояли одинаковые 5 сотен, ответ получался явно больше. С другой стороны, и до числа «3» он явно де дотягивал.
– Два!!! – выпалил я, на секунду опередив моего друга, Леню Струкова, лучшего математика нашей школы.
– Да, действительно два, – подтвердил Леня.
– Как Вы считали? – спросила Любовь Иосифовна.
– Я никак не считал. Интуиция – ответил я под хохот всего класса.
– Если не считал – ответ не считается – «скаламбурила» Любовь Иосифовна. Леня, а ты тоже не считал?
– Нет, почему же, степенно ответил Леня. Надо было сложить 121, 144, 169 и 196. Я попарно сложил числа первое и третье, второе и четвертое. Так удобнее. Получилось 290+340. Общая сумма, включая первую сотню – 730. Делим на 365 – получаем 2.
– Молодец! Но на будущее запомните – в ряду двузначных чисел – у первых пяти его представителей – есть удивительное свойство. Сумма квадратов первых трех чисел ряда (10, 11 и 12) равна сумме квадратов следующих двух (13 и 14). И равняется эта сумма 365. Легко запомнить! Столько дней в году. Если год не високосный. Зная это свойство, ответ можно получить за секунду. Без всякой интуиции…
Методический комментарий
Данная задача межпредметная и может применяться на уроках алгебры, истории, рисования. Поставленные в задаче вопросы позволят значительно расширить и углубить знания учащихся о нахождении степени числа, развить быстроту устного счета, используя ряды Рачинского.
Навыки устного счёта помогают стать учащимся внимательными, рефлексивными, закалять характер и волю к отличным результатам. Путь, к решению жизненных проблем, начинается в школе – в работе над собой. А математика, как известно, приводит ум в порядок.
Данная задача может быть использована при изучении материала 7 класса, а также на этапе итогового повторения курса математики в 8-9 классах общеобразовательной школы.
Список литературы
1. Персональный сайт Гузеева В.В. [Электронный ресурс]. – 2014. – Режим доступа: http://www.gouzeev.ru/.
2. Сайт «ТОГИС-клуб» [Электронный ресурс]. – 2014. – Режим доступа: http://www.togisklub.ru/.
3. Сухарева, И. А. Опыт ТОГИС-шагов в начальной школе «Дарина» [Текст] / И. А. Сухарева, Е. В. Тимофеева // Педагогические технологии. — 2011. — № 3. — С. 101-103.
infourok.ru





















 ;
;  ;
;  ;
; .
. – 25;
– 25; :
:  ;
; ∙
∙  ;
; ;
;  ;
;  ;
; :
:  ∙
∙  ;
;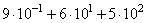 Алгоритм выполнения:
Алгоритм выполнения:


