Функции y=tgx, ctg x. Их свойства и графики
Вопросы занятия:
· рассмотреть тангенс и котангенс как функции аргумента x;
· познакомиться с основным свойствам функций y=tg x, ctg x;
· построить графики функций y=tg x, ctg x.
Материал урока.
Для того, чтобы найти область определения функции y = tg x давайте ещё раз вспомним определение тангенса x.

Найдём область значений функции y = tg x.

Найдём период функции y = tg x. И исследуем её на чётность.


Поскольку функция y = tg x – периодичная функция с периодом π, то можно построить график функции на промежутке [-π/2; π/2], а затем сдвинуть построенную ветвь влево и вправо на π, 2π, 3π и так далее.
Поскольку функция нечётная, то можно построить на промежутке [0; π/2] и отобразить относительно начала координат.
Для построения графика на промежутке [0; π/2], составим таблицу значений тангенса для основных точек из этого промежутка. Отметим эти точки на координатной плоскости.

Отобразим полученную часть графика относительно начала координат.

Сдвинем построенную ветвь влево и вправо на π.

По построенному графику легко определить основные свойства функции y = tg x.
Исследование на монотонность.

Исследование на ограниченность.

Наибольшее и наименьшее значение функции.

Исследование на непрерывность.

Давайте, ещё раз перечислим все свойства функции y = tg x.

Проведя аналогичные рассуждения, можно построить график функции y = ctg x на промежутке [0; π], затем отразить симметрично относительно начала координат и сдвинуть получившуюся ветвь влево и вправо.

Давайте, перечислим все свойства функции y = ctg x.

videouroki.net
Функция y=ctgx. Свойства функции y=ctgx
| | | | | | | | | | | | | Функция y=ctgx | | | | | |Функция
· Область определения: множество всех действительных чисел кроме ,
· Множество значений:
· Функция периодическая. Основной период равен
· Функция нечетная
· Точки пересечения графика с осями: с осью Ох , ; с осью Oy: нет точек пересечения.
· Интервалы знакопостоянства: при , ; y<0 при , .
· Наибольшего и наименьшего значения нет
· Прямые ,- вертикальные асимптоты графика функции
primer.by
Функции y = tgx, y = ctgx, их свойства и график. Алгебра, 10 класс: уроки, тесты, задания.
| 1. |
Определение значения функции y = tgx и y = ctgx
Сложность: лёгкое |
1 |
| 2. |
Определение значения тригонометрической функции
Сложность: лёгкое |
1 |
| 3. |
Определение знака выражения
Сложность: лёгкое |
1 |
| 4. | Свойства функции y = tgx Сложность: среднее | 1 |
| 5. |
Область определения и множество значений тригонометрических функций
Сложность: среднее |
2 |
| 6. |
Сравнение свойств тригонометрических функций
Сложность: среднее |
1 |
| 7. |
Работа с графиком функции y = tgx
Сложность: сложное |
6 |
| 8. |
Нахождение корней уравнения tgx = а с использованием графика
Сложность: сложное |
10 |
| 9. |
Доказать равенство с применением свойств функции y = tgx
Сложность: сложное |
1 |
www.yaklass.ru
Тригонометрические функции, их свойства и графики.
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим
функциям присуще понятие периодичности (повторяемости
значений функции при различных значениях
аргумента, отличных друг от друга на
величину периода 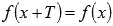 ,
где Т —
период), поэтому, в список свойств
тригонометрических функций добавлен
пункт «наименьший
положительный период».
Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.
,
где Т —
период), поэтому, в список свойств
тригонометрических функций добавлен
пункт «наименьший
положительный период».
Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Функция синус y = sin(x).
Изобразим график функции синус, его называют «синусоида».

Свойства функции синус y = sinx.
Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при
 .
.Наименьший положительный период функции синуса равен двум пи:
 .
.Функция обращается в ноль при
 ,
где
,
где  , Z –
множество целых чисел.
, Z –
множество целых чисел.Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть
 .
.Функция синус — нечетная, так как
 .
.Функция убывает при
 , возрастает
при
, возрастает
при  .
.Функция синус имеет локальные максимумы в точках
 ,
локальные
минимумы в точках
,
локальные
минимумы в точках  .
.Функция y = sinx вогнутая при
 ,
выпуклая
при
,
выпуклая
при  .
.Координаты точек перегиба
 .
.Асимптот нет.
Функция косинус y = cos(x).
График функции косинус (его называют «косинусоида») имеет вид:
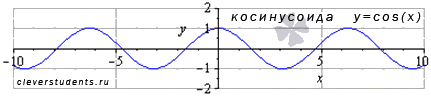
Свойства функции косинус y = cosx.
Функция тангенс y = tg(x).
График функции тангенс (его называют «тангенсоида») имеет вид:

Свойства функции тангенс y = tgx.
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют «котангенсоида»):
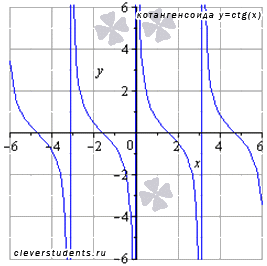
Свойства функции котангенс y = ctgx.
studfile.net
Внеклассный урок — Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x
Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
Свойства функции y = sin x:
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это нечетная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: 6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках [2πn; π + 2πn] функция принимает положительные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
Для построения графика функции y = sin x удобно применять следующие масштабы:
— на листе в клетку за единицу отрезка примем длину в две клетки.
— на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x.
— на оси y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x:
|
0 | π | π | π | 2π | 5π | |
| | 1 | √3 | | √3 | 1 | |
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке [0; π]. Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
Функция y = cos x.
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x:
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: 6) На отрезке [0; π] функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. 9) Точки минимума функции: π + 2πn. наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
Функция y = mf(x).
Возьмем предыдущую функцию y = cos x. Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f(kx).
Если функция y = mf(x) приводит к растяжению синусоиды от оси x либо сжатию к оси x, то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y.
Причем k – любое действительное число.
При 0 < k < 1 синусоида растягивается от оси y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x.
Графиком функции y = tg x является тангенсоида.
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.
Свойства функции y = tg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида Это означает, что на графике функции нет точки, принадлежащей прямой x = π/2, 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция на интервале (–π/2; π/2). 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция возрастает на интервале (–π/2; π/2). 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
Свойства функции y = ctg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция. 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число. 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
raal100.narod.ru
Функция y=tgx, ее свойства и график . Видеоурок. Алгебра 10 Класс
Тема: Тригонометрические функции
Урок: Функция y=tgt, её свойства и график
Напоминание:
Определение: Функцией  называется закон, по которому каждому допустимому значению
называется закон, по которому каждому допустимому значению 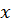 ставится в соответствие единственное значение y.
ставится в соответствие единственное значение y.
Множество всех точек координатной плоскости 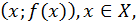 называется графиком функции
называется графиком функции 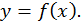
На отрезке  задана функция
задана функция  (рис. 1).
(рис. 1).
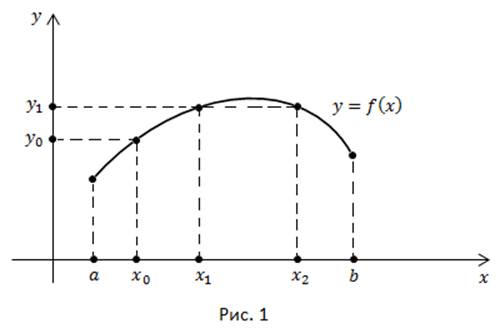
По определению, каждому значению  ставится в соответствие только одно значение
ставится в соответствие только одно значение  И обратно: значение функции
И обратно: значение функции 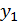 может достигаться при нескольких значениях аргумента:
может достигаться при нескольких значениях аргумента: 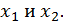
Дадим определение функции 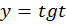 или
или  .
.
Нам важен закон, по которому каждому значению 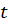 ставится в соответствие
ставится в соответствие 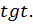
Зададим произвольное 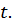 Значение
Значение 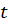 откладывается на числовой окружности по часовой стрелке либо против часовой стрелки, в зависимости от знака
откладывается на числовой окружности по часовой стрелке либо против часовой стрелки, в зависимости от знака 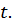 Получаем единственную точку M с единственной парой координат (рис. 2).
Получаем единственную точку M с единственной парой координат (рис. 2).
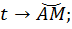

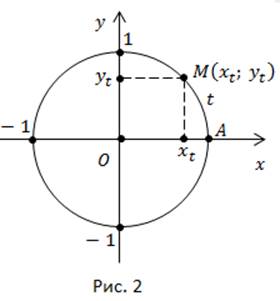
Координату  называют косинусом числа
называют косинусом числа 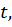 координату
координату  синусом числа
синусом числа 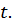
Тангенсом числа 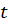 называется отношение синуса
называется отношение синуса 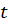 к косинусу
к косинусу 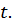
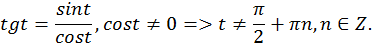
Нам известно, что каждому значению аргумента 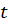 ставится в соответствие единственное значение функции
ставится в соответствие единственное значение функции 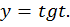 Покажем это графически.
Покажем это графически.
Проведем касательную к числовой окружности в точке A. Заданному значению 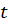 соответствует единственная точка M, единственная прямая OM и единственная точка T пересечения прямой OM и касательной (рис. 3).
соответствует единственная точка M, единственная прямая OM и единственная точка T пересечения прямой OM и касательной (рис. 3).
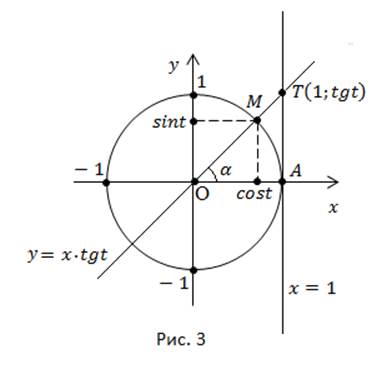
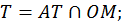
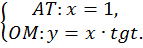
Наша цель – найти координаты точки T, для этого решим систему уравнений.
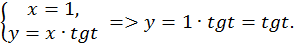
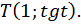
Ордината точки 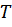 равна
равна 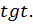
Прямую 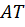 называют линией тангенсов.
называют линией тангенсов.
Докажем, что область значений тангенса – это все действительные числа, 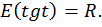
Доказательство:
Зададим любое действительное значение  и докажем, что оно достигается хотя бы при одном значении аргумента.
и докажем, что оно достигается хотя бы при одном значении аргумента.
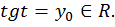
Отложим  на линии тангенсов, получим точку
на линии тангенсов, получим точку 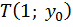 (рис. 4).
(рис. 4).

Соединим её с точкой O, получим прямую 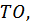 которая пересекает числовую окружность хотя бы в одной точке M, а, значит, существует единственная дуга
которая пересекает числовую окружность хотя бы в одной точке M, а, значит, существует единственная дуга 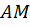 и хотя бы одно значение
и хотя бы одно значение 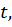 которое равно длине дуги.
которое равно длине дуги.
Любому действительному значению аргумента соответствует единственное значение функции. Но любому значению функции соответствует хотя бы одно значение аргумента.
Таким образом, мы задали любое значение функции и доказали, что оно достигается хотя бы при одном значении аргумента.
Отметим два важных свойства функции 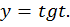
1. Нечетность функции.
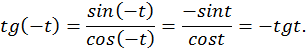
Т.е. 
2. Докажем, что период функции равен 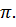
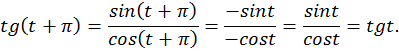
Таким образом, для любого значения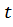 выполняется
выполняется 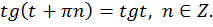
Эти свойства функции 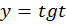 позволяют нам легко построить её график. Период функции равен
позволяют нам легко построить её график. Период функции равен 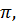 значит, мы можем изучить её свойства и построить график на любом участке длиной
значит, мы можем изучить её свойства и построить график на любом участке длиной 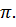
Нечетность функции позволяет симметрично отобразить участок графика относительно начала координат.
С учетом этого построим график функции 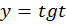 на промежутке
на промежутке 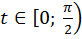 (рис. 5).
(рис. 5).
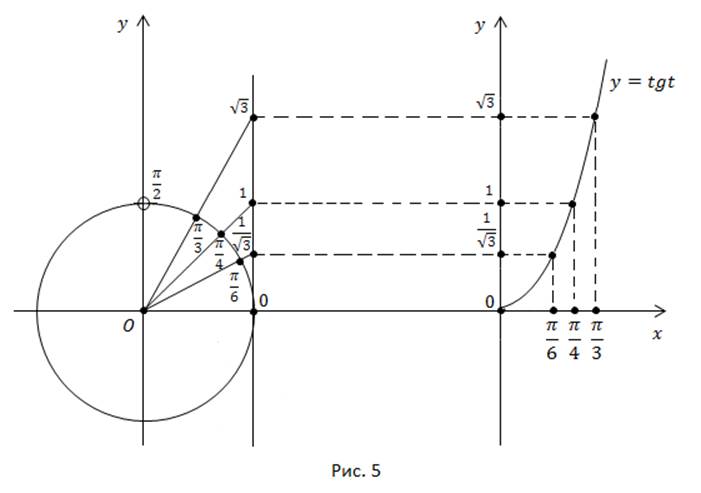
Мы получили график функции на заданном промежутке. Можно было построить график и по известным табличным значениям. Например:
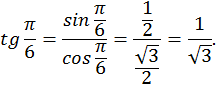
Из построенного графика функции на промежутке 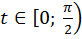 видно, что функция возрастает. Докажем это.
видно, что функция возрастает. Докажем это.
Рассмотрим график 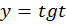 на промежутке
на промежутке 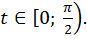 Точки
Точки 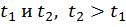 (рис. 6).
(рис. 6).
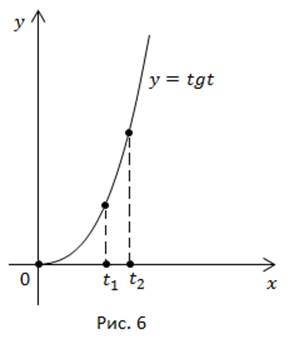
Докажем, что 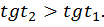
Доказательство:
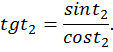
На промежутке 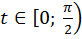 функция
функция 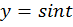 возрастает, значит
возрастает, значит 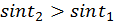 (рис. 7).
(рис. 7).
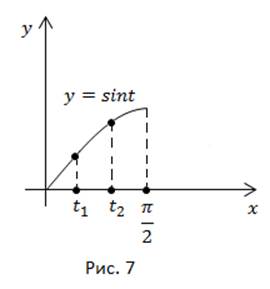
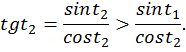
На промежутке 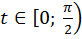 функция
функция 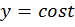 убывает, значит
убывает, значит 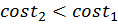 (рис. 8).
(рис. 8).
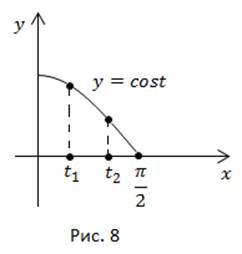

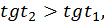 значит, функция
значит, функция 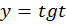 возрастает на промежутке
возрастает на промежутке 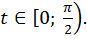
Зная свойства функции, мы можем построить её график на всей области определения.

В точках 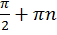 проходят вертикальные асимптоты (рис. 9).
проходят вертикальные асимптоты (рис. 9).
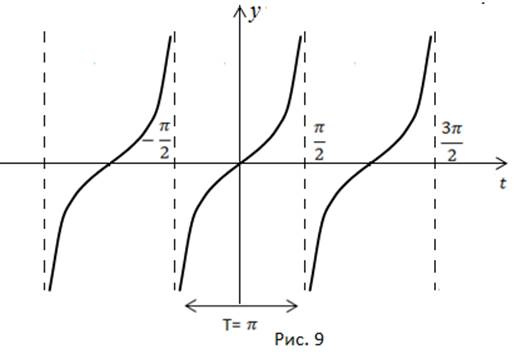
Рассмотрим основные свойства функции 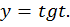
1) Область определения: 
2) Функция периодическая с периодом 
3) Функция нечетная.
4) Функция возрастает и непрерывна на любом интервале
interneturok.ru
Урок 5. свойства и график функции y=tgx и y=ctg x — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №5. Свойства и график функции y=tgx и y=ctg x
Перечень вопросов, рассматриваемых в теме
- Изучение и объяснение свойств функций y=tgx и y=ctgx с помощью графика;
- Определение свойств и положения графика тригонометрических функций вида y=|tg(k|x|+b)| y=|ctg(k|x|+b|;
- Объяснение зависимости свойств и положения графика функции вида y=|tg(k|x|+b)| и y=|ctg(k|x|+b| от значения коэффициентов k,b.
Глоссарий по теме
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Тангенсоида –график функции у = tgx; плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла).
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].–Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Вычислите:
1.  ;
;
2. 
Ответ: 

Объяснение нового материала
Изучение свойств функции y=tgx начнем с построения графика. Обратимся к единичной окружности:

рис.1 Тригонометрический круг
Переносим основные значения углов на координатную плоскость. По оси абсцисс откладываем угол в радианах, по оси ординат – значения тангенса угла.

рис.2 График y=tgx на промежутке 
Как любая тригонометрическая функции, функция тангенса периодическая, делая параллельный перенос получаем:

рис.3 График y=tgx
Заметим, что график симметричен относительно начала координат, следовательно функция тангенса нечётная. Используя построенный нами график, выведем основные свойства y=tgx:
1. Область определения функции y = tgx все действительные числа, кроме чисел вида 
2. Функция периодическая с периодом , т.к. 
3. Функция нечётная, т.к.  . График нечётной функции симметричен относительно начала координат;
. График нечётной функции симметричен относительно начала координат;
4. Функция возрастает на всём интервале;
5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;
6. 
7. Функция  принимает:
принимает:
- значение, равное 0, при
 ;
; - положительные значения на интервале

- отрицательные значения на интервале

Для построения графика  можно придерживаться алгоритму рассмотренному при построении графика
можно придерживаться алгоритму рассмотренному при построении графика  , однако
, однако  (формула приведения). Т.е. смещая тангенсоиду на
(формула приведения). Т.е. смещая тангенсоиду на  единиц влево и делаем симметрию относительно оси Ох за счёт коэффициента –1, получаем:
единиц влево и делаем симметрию относительно оси Ох за счёт коэффициента –1, получаем:

рис.3 График y=сtgx
Основные свойства y=сtgx:
1. Область определения функции y = сtgx все действительные числа, кроме чисел вида 
2. Функция периодическая с периодом  ;
;
3. Функция нечётная. График нечётной функции симметричен относительно начала координат;
4. Функция убывает на всём интервале;
5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;
6.  .
.
Примеры и разборы решения заданий тренировочного модуля:
Пример 1.
Найдем все корни уравнения  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Построим графики функций  и
и  (рис. 6)
(рис. 6)

Рис. 4 – графики функций  и
и  .
.
Графики пересекаются в трёх точках, абсциссы которых  являются корнями уравнения
являются корнями уравнения  .
. 
Ответ: 
Пример 2. Найти все решения неравенства  , принадлежащие отрезку
, принадлежащие отрезку  .
.

рис.5 графики функций  и
и 
Графики пересекаются в трёх точках, абсциссы которых  являются корнями уравнения
являются корнями уравнения  .
. 
Ответ: 
resh.edu.ru
 .
.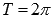 .
.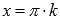 ,
где
,
где 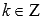 , Z –
множество целых чисел.
, Z –
множество целых чисел.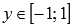 .
. .
.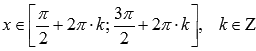 , возрастает
при
, возрастает
при 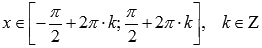 .
. ,
локальные
минимумы в точках
,
локальные
минимумы в точках 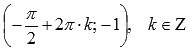 .
. ,
выпуклая
при
,
выпуклая
при 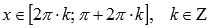 .
. .
. ;
;
