Функция обратной пропорциональности и её график

Сегодня мы рассмотрим, какие величины называются обратно пропорциональными, как выглядит график обратной пропорциональности и как все это может вам пригодится не только на уроках математики, но и вне школьных стен.

Такие разные пропорциональности

Пропорциональностью называют две величины, которые взаимно зависимы друг от друга.

Зависимость может быть прямой и обратной. Следовательно, отношения между величинами описывают прямая и обратная пропорциональность.

Прямая пропорциональность – это такая зависимость двух величин, при которой увеличение либо уменьшение одной из них ведет к увеличению либо уменьшению другой. Т.е. их отношение не изменяется.

Например, чем больше усилий вы прилагаете для подготовки к экзаменам, тем выше ваши оценки. Или чем больше вещей вы берете с собой в поход, тем тяжелее нести ваш рюкзак. Т.е. количество затраченных на подготовку к экзаменам усилий прямо пропорционально полученным оценкам. И количество запакованных в рюкзак вещей прямо пропорционально его весу.

Обратная пропорциональность – это функциональная зависимость, при которой уменьшение либо увеличение в несколько раз независимой величины (ее называют аргументом) вызывает пропорциональное (т.е. во столько же раз) увеличение либо уменьшение зависимой величины (ее называют функцией).

Проиллюстрируем простым примером. Вы хотите купить на рынке яблок. Яблоки на прилавке и количество денег в вашем кошельке находятся в обратной пропорциональности. Т.е. чем больше вы купите яблок, тем меньше денег у вас останется.

Функция и ее график

Функцию обратной пропорциональности можно описать как y = k/x . В котором x ≠ 0 и k ≠ 0.

Эта функция обладает следующими свойствами:

1. Областью ее определения является множество всех действительных чисел, кроме x = 0. D (y ): (-∞; 0) U (0; +∞) .
2. Областью значений являются все действительные числа, кроме
   y = 0. Е(у): (-∞; 0) U (0; +∞) .
3. Не имеет наибольших и наименьших значений.
4. Является нечетной и ее график симметричен относительно начала координат.
5. Непериодическая.
6. Ее график не пересекает оси координат.
7. Не имеет нулей.
8. Если k > 0 (т.е. аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k
9. При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные – (0; +∞). При убывании аргумента (k

График функции обратной пропорциональности называется гиперболой. Изображается следующим образом:

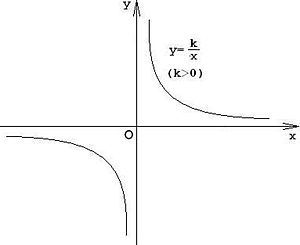
Задачи на обратную пропорциональность

Чтобы стало понятнее, давайте разберем несколько задач. Они не слишком сложные, а их решение поможет вам наглядно представить, что такое обратная пропорциональность и как эти знания могут пригодиться в вашей обычной жизни.

Задача №1. Автомобиль движется со скоростью 60 км/ч. Чтобы доехать до места назначения, ему потребовалось 6 часов. Сколько времени ему потребуется, чтобы преодолеть такое же расстояние, если он будет двигаться со скоростью в 2 раза выше?

Можем начать с того, что запишем формулу, которая описывает отношения времени, расстояния и скорости: t = S/V. Согласитесь, она очень напоминает нам функцию обратной пропорциональности. И свидетельствует о том, что время, которое автомобиль проводит в пути, и скорость, с которой он движется, находятся в обратной пропорциональности.

Чтобы убедиться в этом, давайте найдем V 2 , которая по условию выше в 2 раза: V 2 = 60 * 2 = 120 км/ч. Затем рассчитаем расстояние по формуле S = V * t = 60 * 6 = 360 км. Теперь совсем несложно узнать время t 2 , которое требуется от нас по условию задачи: t 2 = 360/120 = 3 ч.

Как видите время в пути и скорость движения действительно обратно пропорциона

Прямая и обратная пропорциональность ℹ️ определение, основные свойства, формулы, правила построения графиков функций, значение коэффициента пропорциональности

Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.

Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.

Прямая пропорциональность

Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.

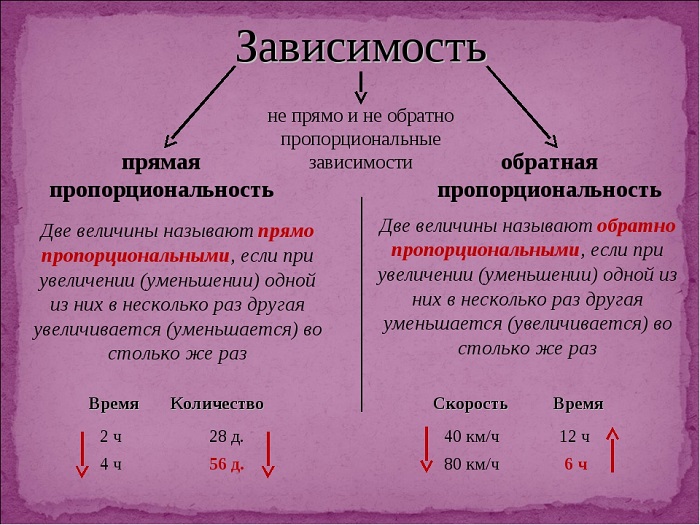
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.

Функция прямой пропорциональности и ее график

Эта зависимость описывается следующей формулой:

y = k * x.

Здесь k и называется коэффициентом пропорциональности.

Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.

Пример построения

Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).

Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k < 0 (справа).

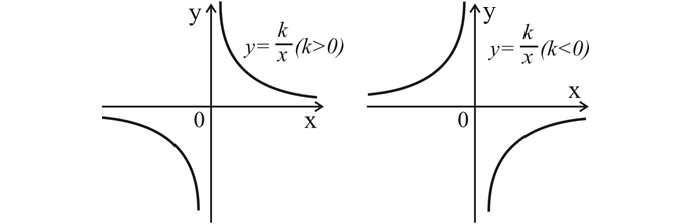
Свойства функции прямой пропорциональности

Основные свойства следующие:

• область определения, значений составляют все действительные числа;

• является нечетной;

• возрастает при всех значениях x, если k > 0;

• если коэффициент со знаком «-», т. е. если k < 0, то убывает;

• если k > 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k < 0, то прямая находится во 2 — 4 четвертях и образует тупой угол с осью Х.

Обратная пропорциональность

Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.

Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).

Функция обратной пропорциональности и ее график

Функция задается формулой:

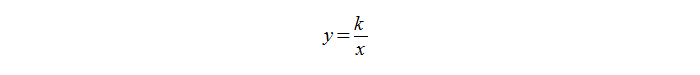
где k – любое действительное число, кроме 0.

График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).

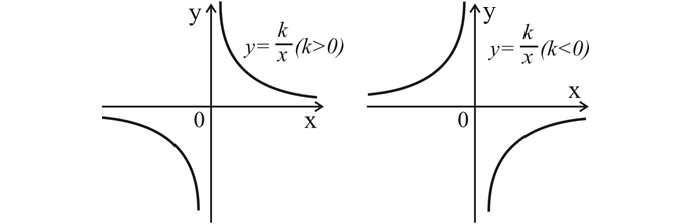
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.

Пример построения

Нужно построить график функции y = 8/x. 

Вот так выглядит таблица для данной функции:

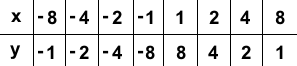
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:

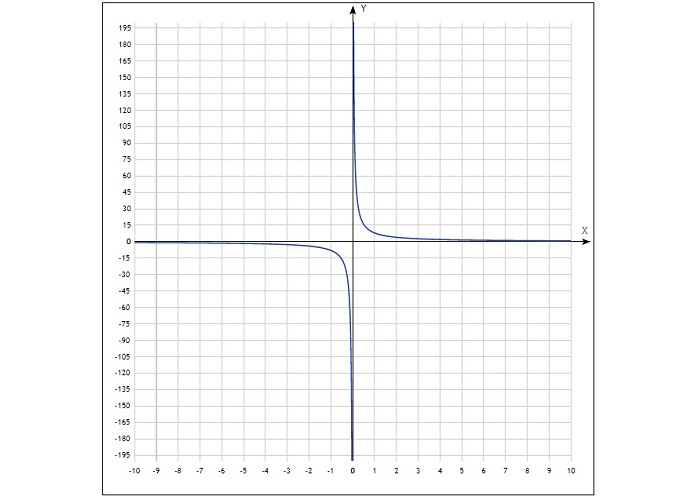
Свойства функции обратной пропорциональности

Основные следующие:

• области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;

• если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;

• оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.

К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше. 

Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.

Обратная пропорциональность Википедия

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным^[1].

Равенство между отношениями двух или нескольких пар чисел или величин в математике называется пропорцией.

Пример[ | ]

Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму при одинаковых условиях всегда будет равно плотности:

1,6:2=4:5=5,6:7=0,8.{\displaystyle 1{,}6:2=4:5=5{,}6:7=0{,}8.}

Коэффициент пропорциональности[ | ]

Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой^[1].

Символ[ | ]

Математический символ ∝{\displaystyle \propto } используется для указания пропорциональности двух величин. Например, A∝B{\displaystyle A\propto B}.

В Юние для отображения используется символ U+221D.

Прямо пропорциональные величины[ | ]

Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) во столько же раз. Пример: такие величины, как скорость объекта и пройденное им расстояние являются прямо пропорциональными.

Обратная пропорциональность[ | ]

Разработка урока по алгебре «Функция обратно пропорциональной зависимости и её свойства(урок 1), (9 класс)

муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа №45

Разработка урока по теме

«Функция и её свойства»,

урок 1,

алгебра, 9 класс.

Автор учитель математики

высшей категории

МАОУ СОШ №45 г. Калининграда

Гавинская Елена Вячеславовна.

г. Калининград

2016 – 2017 учебный год

Автор – Гавинская Елена Вячеславовна

Образовательное учреждение – муниципальное автономное общеобразовательное учреждение города Калининграда средняя общеобразовательная школа № 45

Предмет – математика (модуль «Алгебра»)

Класс – 9

Тема – «Функция и её свойства» (урок 1)

Учебно-методическое обеспечение:

Алгебра. 9 класс: учебник для общеобразовательных учреждений /Ю.М.Колягин и др., — М.: Просвещение, 2014 г.

Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010

Цель:

ознакомить учащихся с функцией при различных значениях коэффициента к; обучение построению графика функции и чтению этого графика.

Задачи обучающие:

• формирование функциональных представлений на наглядном материале;

• формирование умений построения графиков функции ;

• формирование навыков чтения графиков, умения отражать свойства функции на графике;

развивающие:

• формирование способности анализировать, обобщать полученные знания;

• развитие навыков применения компьютерных технологий;

• формирование логического мышления;

воспитательные:

• активизировать интерес к получению новых знаний,

• воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.

Обоснование выбора методов, средств и форм обучения:

оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.

Оборудование и материалы для урока: проектор, экран (интерактивная доска, далее ИД), компьютеры или ноутбуки индивидуально для каждого учащегося, презентация для сопровождения урока, раздаточный материал.

Тип урока: комбинированный.

Структура урока:

Целесообразность использования медиа продукта на занятии продиктована следующими факторами:

1. интенсификацией учебно-воспитательного процесса:

• автоматизацией процесса контроля,

• улучшением наглядности изучаемого материала,

• увеличением количества предлагаемой информации,

• уменьшением времени подачи материала;

2. повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.

Обоснование выбора форм и методов работы на обобщающем уроке по теме «Функция и её свойства» (урок 1) и методические рекомендации по применению презентации на уроке.

Тема «Функция и её свойства» (первый урок по теме) входит в тему «Степенная функция» по авторскому планированию Ш.А.Алимова или Ю.М.Колягина. В заданиях ОГЭ прошлых лет указанная тема встречается как основной компонент при решении заданий. Поэтому предлагаемые формы и методы работы по данной теме способствуют отработке навыков применения понятия функции к решению различных заданий. Задания, предложенные на уроке, подбирались с учетом возрастных особенностей учащихся и способствуют развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях с учетом меж предметных связей при решении задач практического содержания. Предложенные формы и методы применяются для групповой, самостоятельной и фронтальной работ. Однако их можно использовать и как тренажёр для отдельного учащегося, работающего за компьютером.

И последнее примечание: все учащиеся класса с начала учебного года разделены на три типологические группы: группа А – самые «слабые» учащиеся, группа В – «средние» учащиеся, группа С – учащиеся с высоким уровнем обученности по предмету.

Ход урока.

1.Организационный момент.

1. Объявляется цель и план урока.

2. Записывается домашнее задание: №186 (2, 4), 187 (1, 2).

2.Актуализация опорных знаний.

Учащимся в парах предлагается разгадать кроссворд.

По горизонтали:

1.Свойство функции, при котором большему значению аргумента соответствует меньшее значение функции.

2.Координата точки, показания которой снимаются по оси Ох.

3.Множество точек плоскости с координатами (х; f(х)).

4.Свойство функции, при котором большему значению аргумента соответствует большее значение функции.

5.Координата точки, показания которой снимаются по оси Оу.

По вертикали:

1.Название графика функции, заданной уравнением у = кх + в.

2.Зависимость между двумя величинами.

3.Название графика функции, заданной уравнением у = ах² +вх +с.

4.Свойство функции, при котором её график симметричен относительно оси Оу.

5.Свойство функции, при котором её график симметричен относительно начала координат.

Проверка ответов с помощью слайда №3.

3.Изложение нового материала.

1)Сначала учитель вводит понятие функции обратно пропорциональной зависимости вида у = . Учащиеся выполняют необходимые записи в тетрадь. Слайд №5.

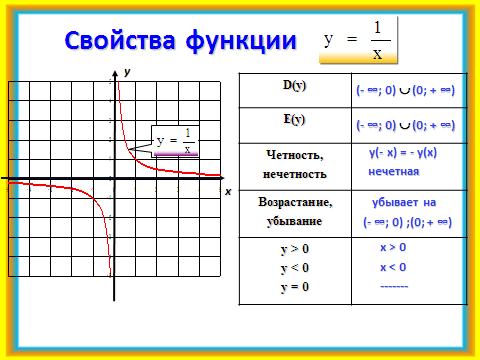
2)Учащимся предлагается в парах построить по точкам график функции у =

Проверка с помощью слайда №6.

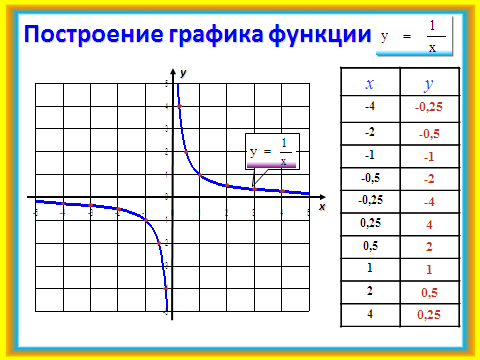
По графику в процессе беседы с учащимися формулируются свойства функции у = . Слайд №7.

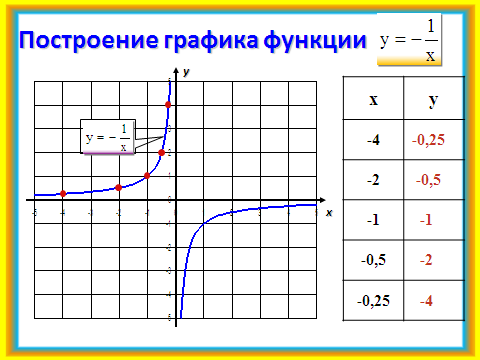
3)Учащимся предлагается в парах построить по точкам график функции у = . Проверка с помощью слайда №8.

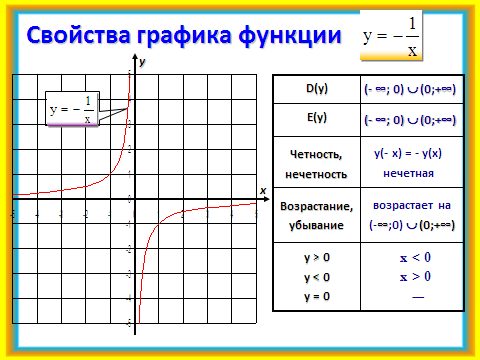
По графику в процессе беседы с учащимися формулируются свойства функции у = . Слайд №9.

4. Гимнастика для глаз.

5. Закрепление первичных знаний.

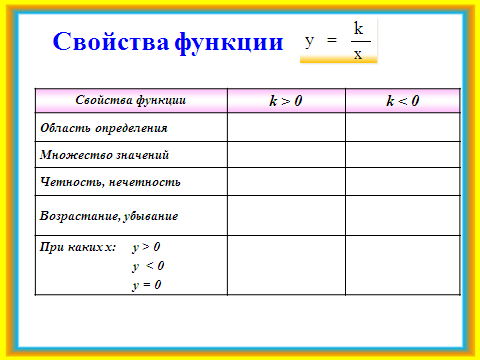
Работая в парах, выполняется задание: построить в одной системе координат графики функций у = и у = . Решение проверяют с помощью учебника (задача 2 из соответствующего параграфа), обобщают свойства функции, заполняя в тетради таблицу. Слайд №10.

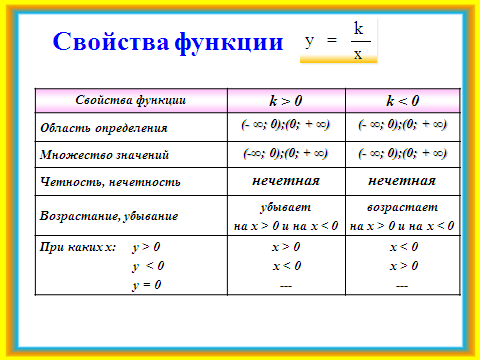
В ходе фронтальной беседы с учащимися обсуждаются задачи физического содержания на применение обратной пропорциональности. Слайд №11.

6.Самостоятельная работа обучающего характера.

С комментированием у доски выполняются №185 (1), 186 (1, 3).

7.Подведение итогов урока, выставление отметок.

Учащимся предлагается ответить на вопрос: что вызвало наибольшие затруднения на уроке? Какова ценность сегодняшнего урока? Чему же мы сегодня с вами научились?

Анкетирование можно провести с помощью системы Verdict:

Выставить отметки за работу на уроке.

Разработка урока по алгебре «Функция обратно пропорциональной зависимости и её свойства(урок 2), (9 класс)

муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа №45

Разработка урока по теме

«Функция и её свойства»,

урок 2,

алгебра, 9 класс.

Автор учитель математики

высшей категории

МАОУ СОШ №45 г. Калининграда

Гавинская Елена Вячеславовна.

г. Калининград

2016 – 2017 учебный год

Автор – Гавинская Елена Вячеславовна

Образовательное учреждение – муниципальное автономное общеобразовательное учреждение города Калининграда средняя общеобразовательная школа № 45

Предмет – математика (модуль «Алгебра»)

Класс – 9

Тема – «Функция и её свойства» (урок 2)

Учебно-методическое обеспечение:

Алгебра. 9 класс: учебник для общеобразовательных учреждений /Ю.М.Колягин и др., — М.: Просвещение, 2014 г.

Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010

Цель:

повторить построение графика функции при различных значениях коэффициента к; научиться применять приемы преобразования графиков, строить вертикальные и горизонтальные асимптоты графика.

Задачи обучающие:

образовательные:

• формирование умений построения графиков функций путем сдвига и деформации графика известной функции ;

• формирование навыков чтения графиков, умения отражать свойства функции на графике;

развивающие:

• формирование способности анализировать, обобщать полученные знания;

• развитие навыков применения компьютерных технологий;

• формирование логического мышления;

воспитательные:

• активизировать интерес к получению новых знаний,

• воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.

Обоснование выбора методов, средств и форм обучения:

оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.

Оборудование и материалы для урока: проектор, экран (интерактивная доска, далее ИД), компьютеры или ноутбуки индивидуально для каждого учащегося, презентация для сопровождения урока, раздаточный материал.

Тип урока: комбинированный.

Структура урока:

Целесообразность использования медиа продукта на занятии продиктована следующими факторами:

1. интенсификацией учебно-воспитательного процесса:

• автоматизацией процесса контроля,

• улучшением наглядности изучаемого материала,

• увеличением количества предлагаемой информации,

• уменьшением времени подачи материала;

2. повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.

Обоснование выбора форм и методов работы на обобщающем уроке по теме «Функция и её свойства» (урок 2) и методические рекомендации по применению презентации на уроке.

Тема «Функция и её свойства» (второй урок по теме) входит в тему «Степенная функция» по авторскому планированию Ш.А.Алимова или Ю.М.Колягина. В заданиях ОГЭ прошлых лет указанная тема встречается как основной компонент при решении заданий. Поэтому предлагаемые формы и методы работы по данной теме способствуют отработке навыков применения понятия функции к решению различных заданий. Задания, предложенные на уроке, подбирались с учетом возрастных особенностей учащихся и способствуют развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях с учетом меж предметных связей при решении задач практического содержания. Предложенные формы и методы применяются для групповой, самостоятельной и фронтальной работ. Однако их можно использовать и как тренажёр для отдельного учащегося, работающего за компьютером.

И последнее примечание: все учащиеся класса с начала учебного года разделены на три типологические группы: группа А – самые «слабые» учащиеся, группа В – «средние» учащиеся, группа С – учащиеся с высоким уровнем обученности по предмету.

Ход урока.

1.Организационный момент.

1. Объявляется цель и план урока.

2. Записывается домашнее задание: №191 (2, 3), описать в тетрадке свойства заданных функций.

2.Актуализация опорных знаний.

1)Учащимся в парах предлагается устно ответить на вопросы:

— Какая функция называется обратной пропорциональностью?

— В каких координатных четвертях расположен график функции при к0, к0?

— Как называется график функции ? Из скольких ветвей он состоит?
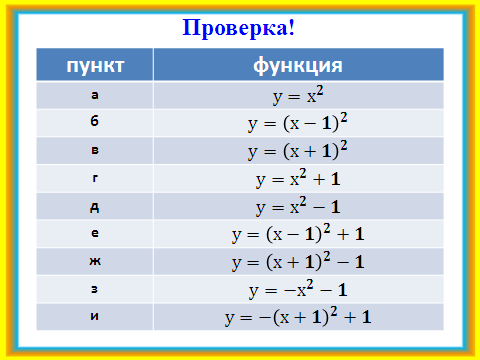
2)Работая в парах, учащиеся записывают уравнения парабол, изображенных на рисунках из Раздаточного материала, если все они получены сдвигом графика функции у = х².

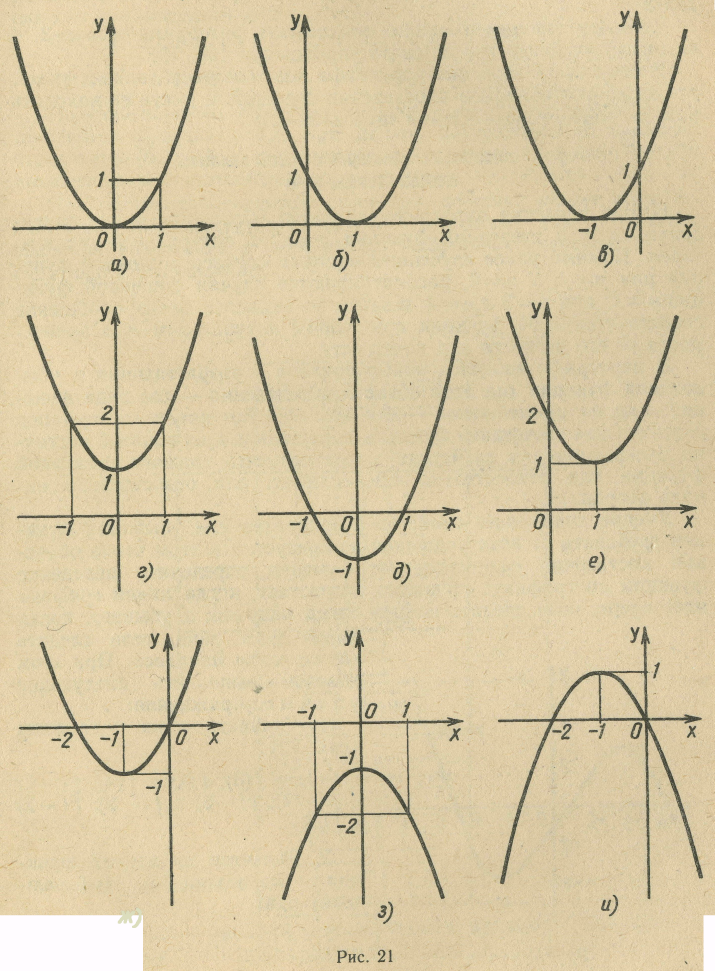
Окончательна проверка с помощью слайда №3.

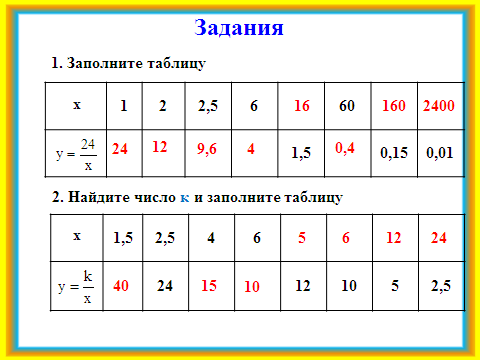
3)Далее ребята заполняют таблицу значений для обратной пропорциональности. Проверка ответов с помощью слайда №4.

3.Изложение нового материала.

1)Сначала учитель вводит понятия сжатия и растяжения для гиперболы с помощью слайдов №6, 7. В ходе фронтальной беседы обсуждаются свойства этих функций.

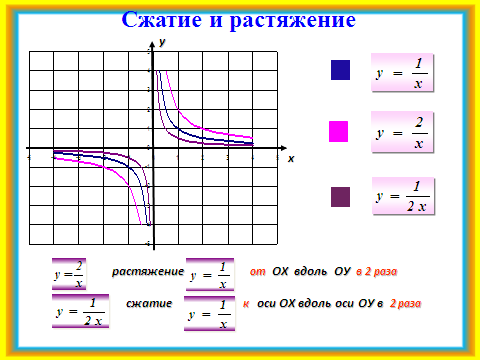
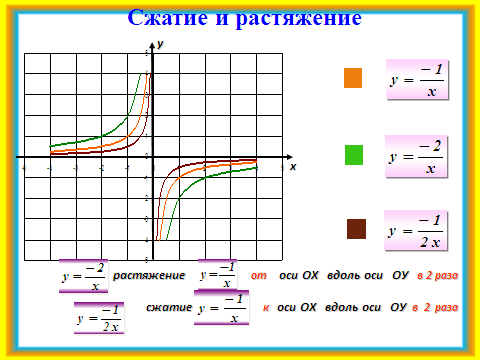
2)Объяснение построения графика функции со сдвигом сопровождается

слайдами №8, 9. В ходе фронтальной беседы обсуждаются свойства этих функций.

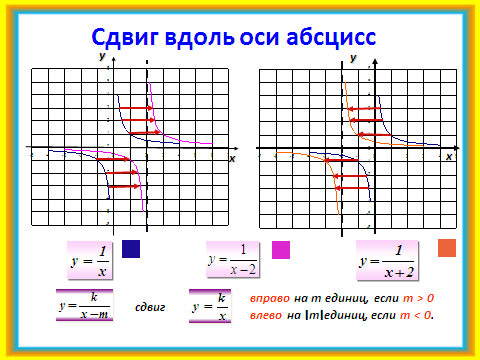
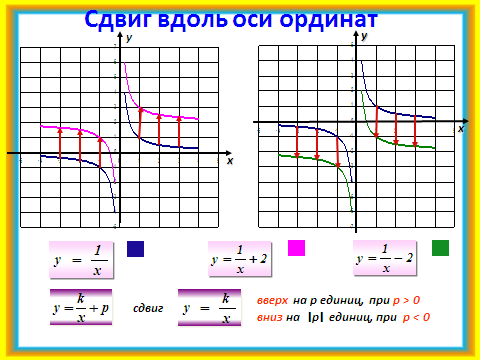
4. Гимнастика для глаз.

5. Закрепление первичных знаний.

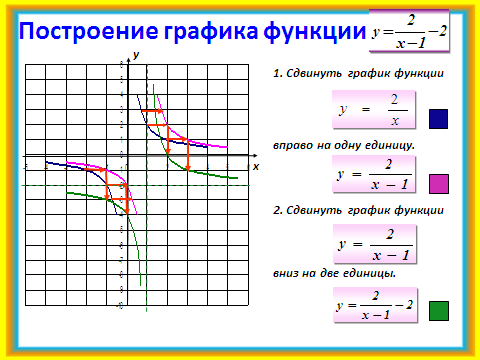
Работая в парах, выполняется задание: построить график функций у = по плану, записанному на доске:

1)построить график функции у = ,

2) построить график функции у = сдвигом графика у = вправо вдоль оси Ох на одну единицу,

3) построить график функции у = сдвигом графика у = вдоль оси Оу на две единицы вниз.

Проверка с помощью слайда №16.

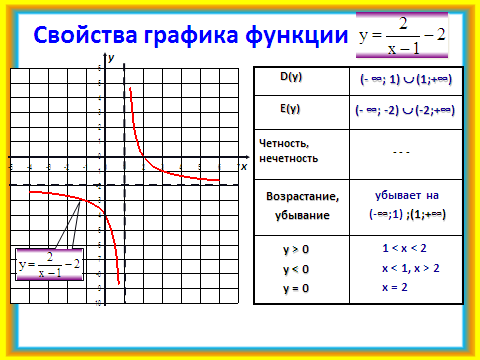
После проверки построения графика учащиеся описывают свойства этой функции. Проверка с помощью слайда №17.

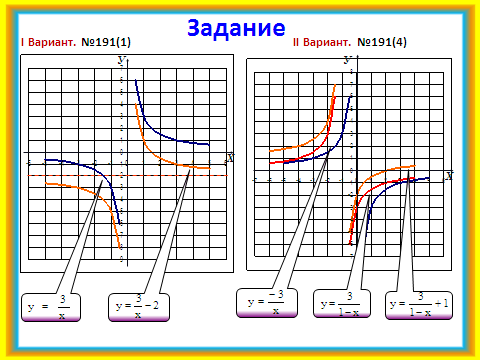
6.Самостоятельная работа обучающего характера.

По вариантам №191 (1, 4). После построения – описать свойства. Проверка устно фронтальным обсуждением и с помощью слайда №19.

7.Подведение итогов урока, выставление отметок.

Учащимся предлагается ответить на вопрос: что вызвало наибольшие затруднения на уроке? Какова ценность сегодняшнего урока? Чему же мы сегодня с вами научились?

Анкетирование можно провести с помощью системы Verdict:

Выставить отметки за работу на уроке.

Пропорциональность — Википедия

Материал из Википедии — свободной энциклопедии

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным^[1].

Равенство между отношениями двух или нескольких пар чисел или величин в математике называется пропорцией.

Пример

Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:

1,6 : 2 = 4 : 5 = 5,6 : 7 = 0,8

Коэффициент пропорциональности

Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой^[1].

Символ

Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.

В Юникоде для отображения используется символ U+221D.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) во столько же раз. Пример: такие величины, как скорость объекта и пройденное им расстояние являются прямо пропорциональными.

Обратная пропорциональность

Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины (аргумента) вызывает пропорциональное уменьшение зависимой величины (функции).

y=kx,x≠0,k≠0{\displaystyle y={\frac {k}{x}},x\neq 0,k\neq 0}

Свойства функции:

См. также

Источники

1. ↑ ^{1 2} М. Я. Выгодский. «Справочник по элементарной математике», М., 1974