Онлайн урок обратная пропорциональность.

Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

 

 

 

 

 

Точки A и B симметричны относительно точки E, если AE = BE.

 

 

 

 

 

 

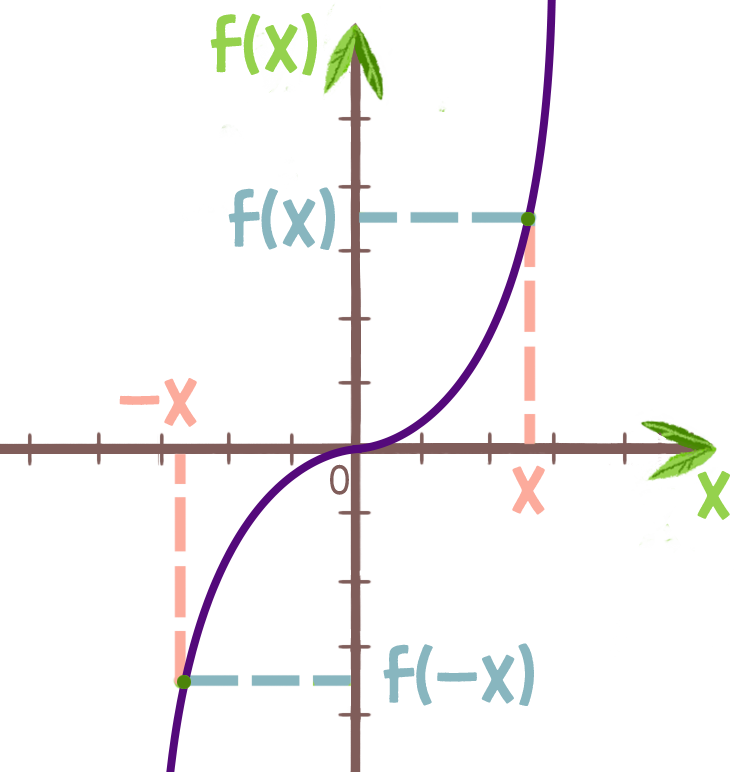
Функция называется нечетной, если для любого х из области определения функции выполняется равенство f(-x) = — f(x). Ее график симметричен относительно начала координат.

 

 

 

 

 

 

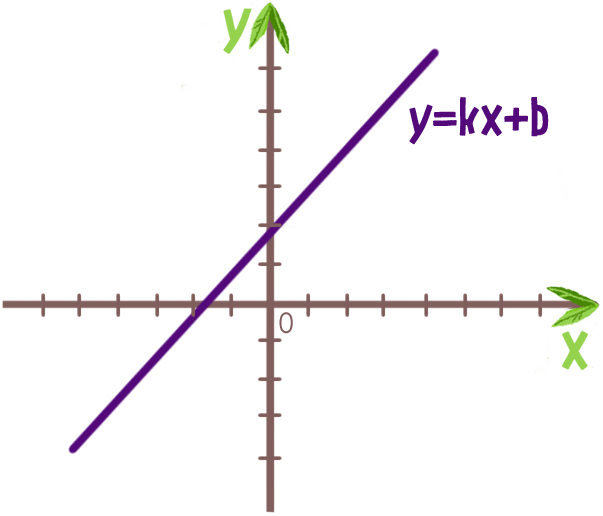
Линейная функция — это функция вида y = kx + b, где k,b — некоторые числа. График линейной функции — прямая.

 

 

 

 

 

 

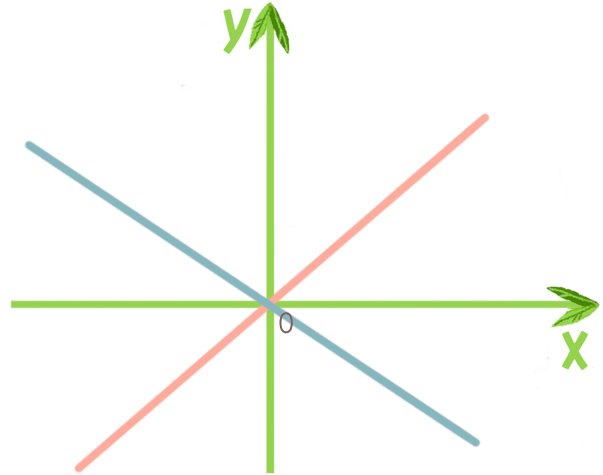
Прямая пропорциональность — это линейная функция, которая проходит через начало координат: y = kx.

 

 

 

 

 

Теперь установи соответствие между картинками и определениями, которые мы только что повторили.

 

 

 

 

 

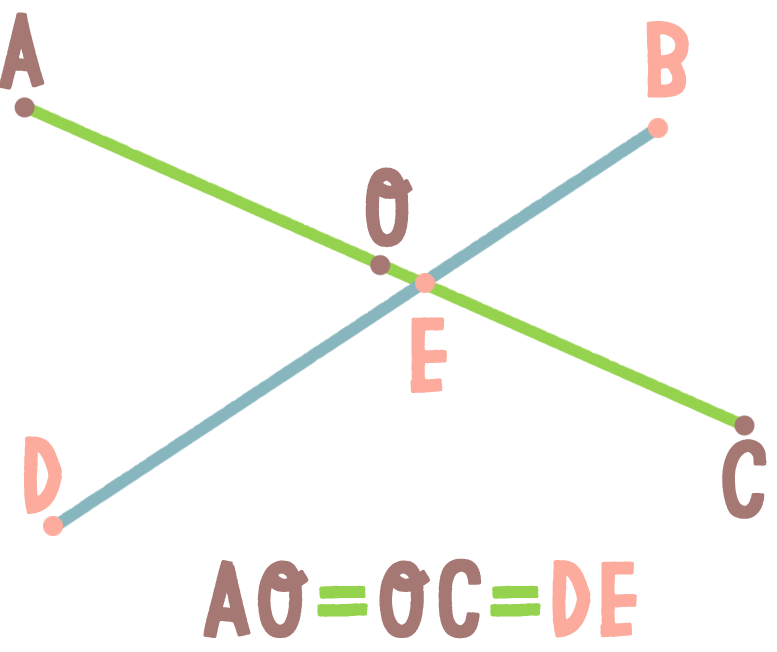
A и B симметричны относительно точки СA и С симметричны относительно точки BD и B симметричны относительно точки EA и C симметричны относительно точки O

 

 

 

 

 

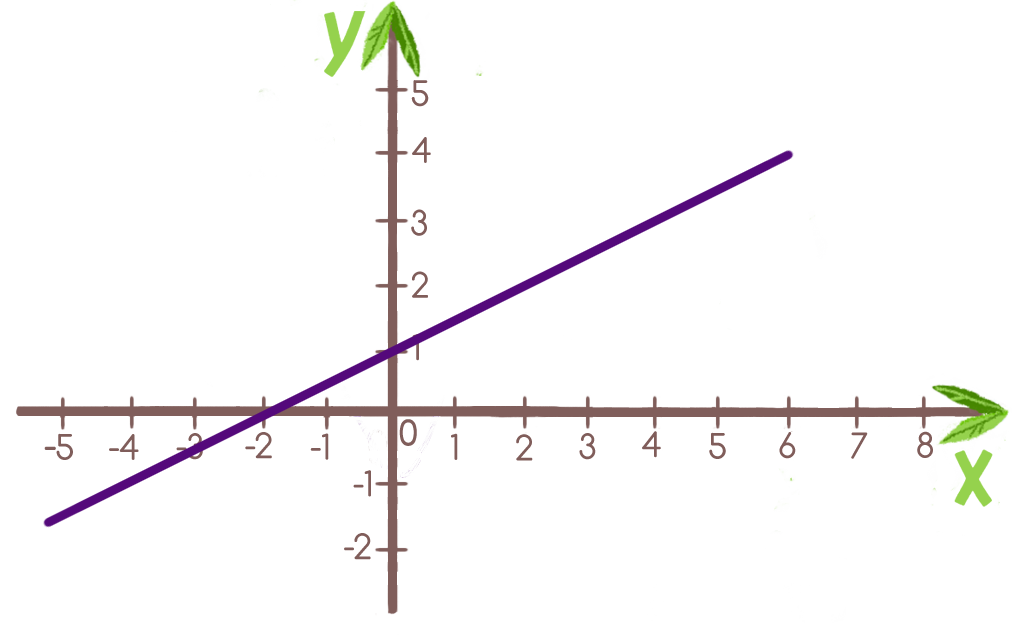
нечетная функциялинейная функцияпрямая пропорциональностьне функция

 

 

 

 

 

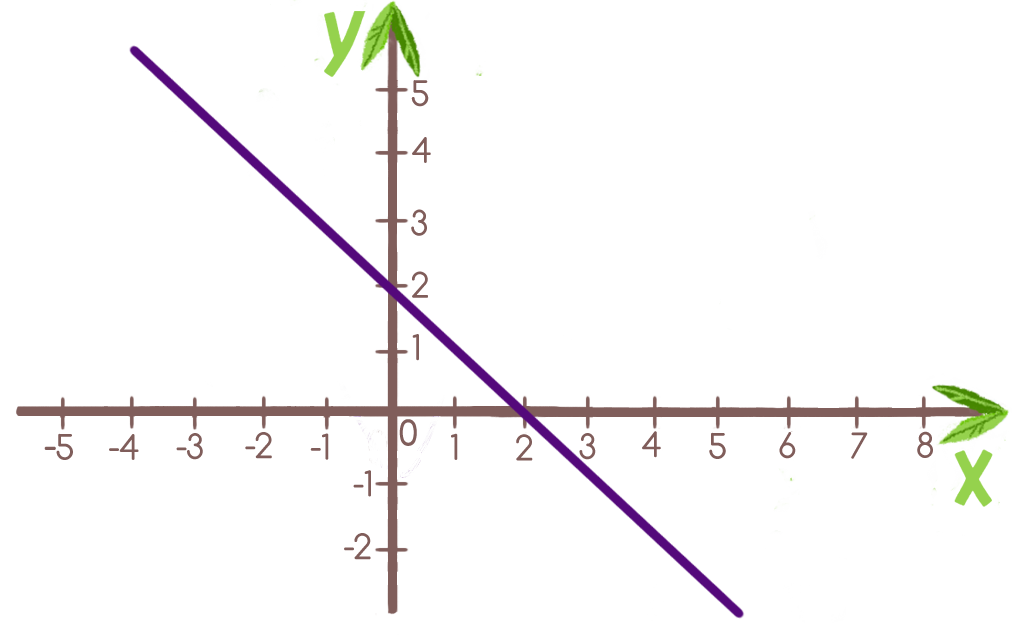
k = 1, b = 2k = -1, b = -2k = -1, b = 2k = -1, b = -2

 

 

 

 

Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:

 

 

1. Обратная пропорциональность и ее график.

2. Асимптоты обратной пропорциональности.

3. Гипербола.

4. Cимметричность графика обратной пропорциональности.

Функция у =k/x (обратная пропорциональность) и ее график

Функция вида у = k/x (k≠0) называется обратной пропорциональностью; k называется коэффициентом обратной пропорциональности. Областью определения функции является множество D(f) = (-∞;0) и (0;+∞) = R\{0}.
Графиком функции у = k/x является гипербола.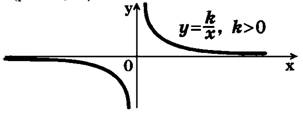

Рис. 1

Если k>0, то ветви гиперболы расположены в I и III координатных угла если k<0, то ветви гиперболы расположены в II и IV координатных углах (рис. 1, 2).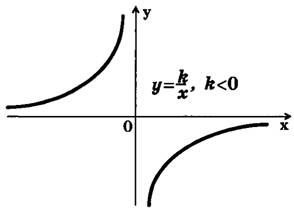

Рис. 2

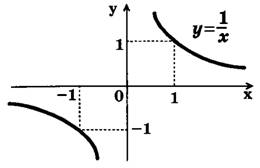
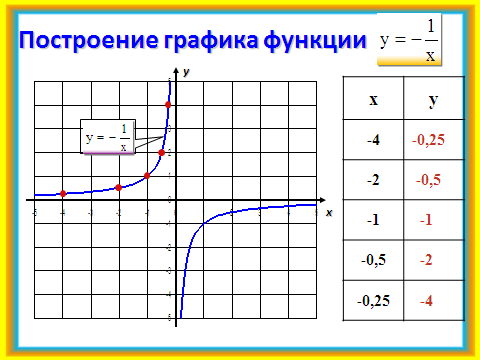
Рассмотрим более подробно функцию у = k/x при k = 1 (у = 1/х).

Функция у = 1/x

Составляем таблицу, учитывая, что при х = 0 функция не определена (табл. 1).
Таблица 1

Строим график функции у = 1/x. Это гипербола (рис. 3).

Прямая и обратная пропорциональность. Коэффициент и формулы

Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.

Пропорциональность величин может быть прямой и обратной.

Прямая пропорциональность

Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто

пропорциональными.

Рассмотрим пример прямой пропорциональности на формуле пути:

s = vt,

где  s  — это путь,  v  — скорость, а  t  — время.

При равномерном движении путь пропорционален времени движения. Если взять скорость  v  равной  5 км/ч,  то пройденный путь  s  будет зависеть только от времени движения  t:

Скорость v = 5 км/ч
Время t (ч)	1	2	4	8	16
Путь s (км)	5	10	20	40	80

Из примера видно, что во сколько раз увеличивается время движения  t,  во столько же раз увеличивается пройденное расстояние  s.  В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.

В данном случае скорость  (v = 5 км/ч)  является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:

следовательно,

5	=	10	=	20	=	40	=	80	= 5.
1		2		4		8		16

Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:

Время  t = 2 ч
Скорость  v (км/ч)	5	15	45	90
Расстояние  s (км)	10	30	90	180

В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время  (

t = 2 ч):

следовательно,

10	=	30	=	90	=	180	= 2.
5		15		45		90

Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.

Формула прямой пропорциональности

Формула прямой пропорциональности:

y = kx,

где  y  и  x  — это переменные величины, а  k  — это постоянная величина, называемая коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных 

y  и  x  равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Обратная пропорциональность

Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.

Рассмотрим пример обратной пропорциональности на формуле пути:

s = vt,

где  s  — это путь,  v  — скорость, а  t  — время.

При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь  s  равным  120 км,  то потраченное на преодоление этого пути время  t  будет зависеть только от скорости движения  v:

Путь  s = 120 км
Скорость  v (км/ч)	10	20	40	80
Время  t (ч)	12	6	3	1,5

Из примера видно, что во сколько раз увеличивается скорость движения  v,  во столько же раз уменьшается время  t.  В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.

В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:

s = vt,

следовательно,

10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.

Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз

.

Формула обратной пропорциональности

Формула обратной пропорциональности:

где  y  и  x  — это переменные величины, а  k  — это постоянная величина, называемая коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных  y  и  x,  равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

xy = k.

«Функция обратной пропорциональности, её свойства и график»

Функция обратной пропорциональности , её график и свойства.

Вариант -1

1. Функция задана формулой у = — а) Найдите область определения; б) Заполни таблицу:

в) Постройте график;

г) Подпишите график.

2. Полученная кривая называется гиперболой , она состоит из двух ветвей.

Этот термин ввёл Аполлоний из г. Пергам (Малая Азия), живший в ІІІ – ІІ вв.до н.э. Гипербола устремляется ввысь настолько быстро и настолько быстро падает, что становиться понятным почему таким термином называется в литературе преувеличение или преуменьшение:

« наметал стог выше тучи», « стал Иванушка ниже былинки в поле». Пословица «Дальше от кумы – меньше греха» — тоже пример гиперболы.

3. Выводы: ( работа в парах) 1.Функция обратной пропорциональности задаётся формулой______________

2.График — ____________________________________________________________

3.Если к >0, графики находятся в ___________ четверти;

Если к<0, графики находятся в ____________ четверти;

4. Используя графики, опишите свойства функции обратной пропорциональности.

Функция обратной пропорциональности , её график и свойства.

Вариант -2

1. Функция задана формулой у =

а) Найдите область определения; б) Заполни таблицу:

в) Постройте график;

г) Подпишите график.

2. Полученная кривая называется гиперболой , она состоит из двух ветвей.

Этот термин ввёл Аполлоний из г. Пергам (Малая Азия), живший в ІІІ – ІІ вв.до н.э. Гипербола устремляется ввысь настолько быстро и настолько быстро падает, что становиться понятным почему таким термином называется в литературе преувеличение или преуменьшение:

« наметал стог выше тучи», « стал Иванушка ниже былинки в поле». Пословица «Дальше от кумы – меньше греха» — тоже пример гиперболы.

3. Выводы: ( работа в парах) 1.Функция обратной пропорциональности задаётся формулой______________

2.График — ____________________________________________________________

3.Если к >0, графики находятся в ___________ четверти;

Если к<0, графики находятся в ____________ четверти;

4. Используя графики, опишите свойства функции обратной пропорциональности.

Разработка урока по алгебре «Функция обратно пропорциональной зависимости и её свойства(урок 3), (9 класс)

муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа №45

Разработка урока по теме

«Функция и её свойства»,

урок 3,

алгебра, 9 класс.

Автор учитель математики

высшей категории

МАОУ СОШ №45 г. Калининграда

Гавинская Елена Вячеславовна.

г. Калининград

2016 – 2017 учебный год

Автор – Гавинская Елена Вячеславовна

Образовательное учреждение – муниципальное автономное общеобразовательное учреждение города Калининграда средняя общеобразовательная школа № 45

Предмет – математика (модуль «Алгебра»)

Класс – 9

Тема – «Функция и её свойства» (урок 3)

Учебно-методическое обеспечение:

Алгебра. 9 класс: учебник для общеобразовательных учреждений /Ю.М.Колягин и др., — М.: Просвещение, 2014 г.

Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010

Цель:

Обобщить и систематизировать знания, полученные при изучении темы «Функция »; подготовка учащихся к выполнению заданий, соответствующих требованиям ОГЭ.

Задачи обучающие:

образовательные:

• закрепление умений построения графиков функций путем сдвига и деформации графика известной функции ;

• закрепление навыков чтения графиков, умения отражать свойства функции на графике;

развивающие:

• формирование способности анализировать, обобщать полученные знания;

• развитие навыков применения компьютерных технологий;

• формирование логического мышления;

воспитательные:

• активизировать интерес к получению новых знаний,

• воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.

Обоснование выбора методов, средств и форм обучения:

оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.

Оборудование и материалы для урока: проектор, экран (интерактивная доска, далее ИД), компьютеры или ноутбуки индивидуально для каждого учащегося, презентация для сопровождения урока, раздаточный материал.

Тип урока: комбинированный.

Структура урока:

Целесообразность использования медиа продукта на занятии продиктована следующими факторами:

1. интенсификацией учебно-воспитательного процесса:

• автоматизацией процесса контроля,

• улучшением наглядности изучаемого материала,

• увеличением количества предлагаемой информации,

• уменьшением времени подачи материала;

2. повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.

Обоснование выбора форм и методов работы на обобщающем уроке по теме «Функция и её свойства» (урок 3) и методические рекомендации по применению презентации на уроке.

Тема «Функция и её свойства» (третий урок по теме) входит в тему «Степенная функция» по авторскому планированию Ш.А.Алимова или Ю.М.Колягина. В заданиях ОГЭ прошлых лет указанная тема встречается как основной компонент при решении заданий. Поэтому предлагаемые формы и методы работы по данной теме способствуют отработке навыков применения понятия функции к решению различных заданий. Задания, предложенные на уроке, подбирались с учетом возрастных особенностей учащихся и способствуют развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях с учетом меж предметных связей при решении задач практического содержания. Предложенные формы и методы применяются для групповой, самостоятельной и фронтальной работ. Однако их можно использовать и как тренажёр для отдельного учащегося, работающего за компьютером.

И последнее примечание: все учащиеся класса с начала учебного года разделены на три типологические группы: группа А – самые «слабые» учащиеся, группа В – «средние» учащиеся, группа С – учащиеся с высоким уровнем обученности по предмету.

Ход урока.

1.Организационный момент.

1. Объявляется цель и план урока.

2. Записывается домашнее задание: построить и исследовать график функции у = — .

2.Проверка домашнего задания.

Выполняется с помощью демонстрации слайдов №3, 4.

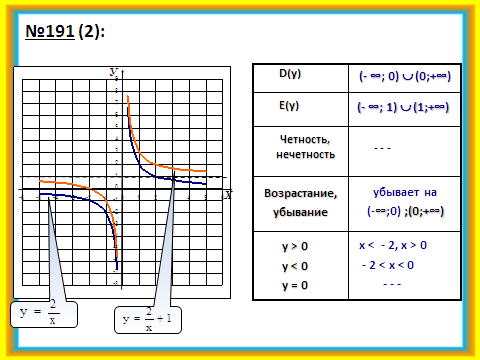
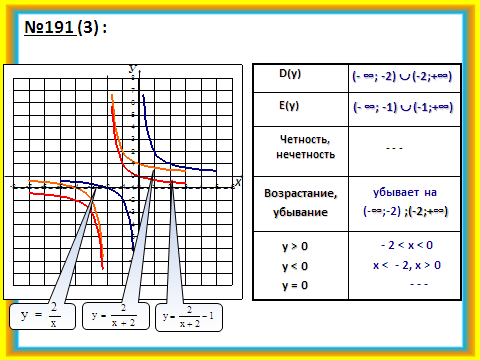
3.Актуализация опорных знаний.

1)Учащимся в парах предлагается устно ответить на вопросы:

— Какая функция называется обратной пропорциональностью?

— В каких координатных четвертях расположен график функции при к0, к0?

— Как называется график функции ? Из скольких ветвей он состоит?

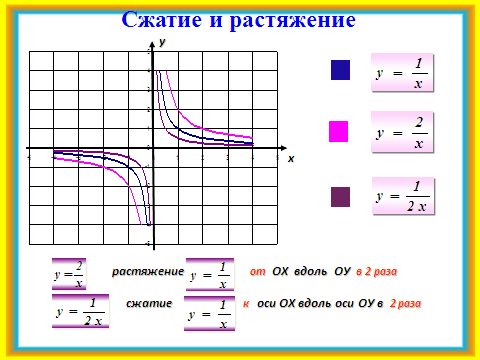
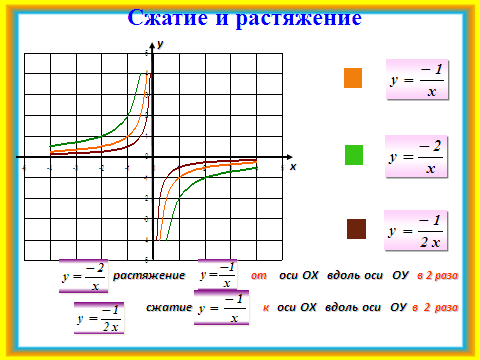
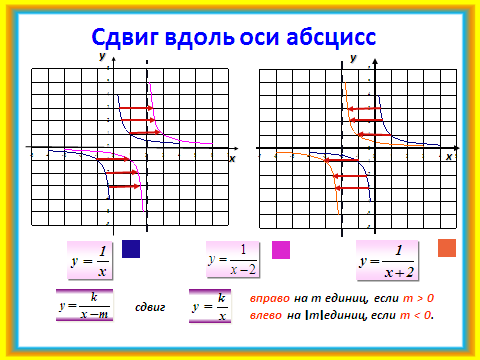
2)Работая устно, фронтально повторяются основные моменты, необходимые для построения графиков сложных функций. По некоторым слайдам можно предложить учащимся сначала повторение в парах. Слайды №6 — 11.

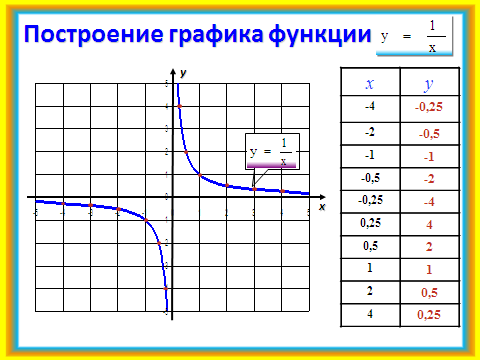
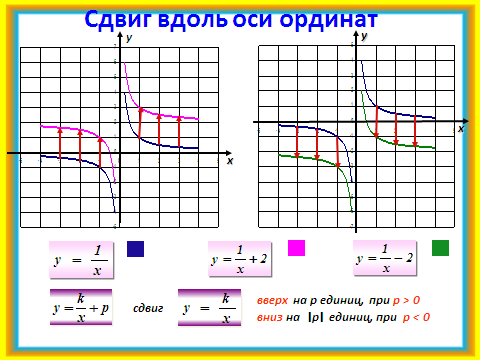
4.Самостоятельная работа.

Половина учащихся выполняет тесты, выполненные в Word, вторая половина учащихся выполняет тесты, выполненные в Excel. Затем учащиеся меняются местами. В результате выполнения тестов учащиеся ответят на 10 вопросов о построении и свойствах графика функции у = (при выполнении теста в Excel ребята сразу получают отметку).

5. Гимнастика для глаз.

6. Решение упражнений.

Работая в парах, выполняются задания (для учащихся группы А – первый уровень, для всех остальных – второй) построить эскизы графиков функций:

I уровень.

1) у = , 2) у =

II уровень.

1) у = , 2) у =

7.Самостоятельная работа (с дифференцированным подходом).

I уровень: выполнить пункт 1, описать свойства функции.

II уровень: выполнить самостоятельную работу полностью.

8.Подведение итогов урока, выставление отметок.

Учащимся предлагается ответить на вопрос: что вызвало наибольшие затруднения на уроке? Какова ценность сегодняшнего урока? Чему же мы сегодня с вами научились?

Анкетирование можно провести с помощью системы Verdict:

Выставить отметки за работу на уроке.

Пропорциональность — Википедия с видео // WIKI 2

Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным^[1].

Равенство между отношениями двух или нескольких пар чисел или величин в математике называется пропорцией.

Энциклопедичный YouTube

• 1/3

  Просмотров:

  11 010

  141 486

  2 277

• ✪ 05. Пропорциональность наказания за грех — Александр Шевченко

• ✪ Математика 6 класс. ОТНОШЕНИЯ. ПРОПОРЦИИ. ПРЯМАЯ И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНЫЕ ЗАВИСИМОСТИ.

• ✪ Прямая пропорциональность и её график, y=kx.

Содержание

Пример

Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму при одинаковых условиях всегда будет равно плотности:

1 , 6 : 2 = 4 : 5 = 5 , 6 : 7 = 0 , 8. {\displaystyle 1{,}6:2=4:5=5{,}6:7=0{,}8.}

Коэффициент пропорциональности

Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой^[1].

Символ

Математический символ ∝ {\displaystyle \propto } используется для указания пропорциональности двух величин. Например, A ∝ B {\displaystyle A\propto B} .

В Юникоде для отображения используется символ U+221D.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) во столько же раз. Пример: такие величины, как скорость объекта и пройденное им расстояние являются прямо пропорциональными.

Обратная пропорциональность

Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины (аргумента) вызывает пропорциональное уменьшение зависимой величины (функции).

y = k x , x ≠ 0 , k ≠ 0 {\displaystyle y={\frac {k}{x}},\;x\neq 0,\;k\neq 0}

Свойства функции:

См. также

Источники

1. ↑ ^{1 2} М. Я. Выгодский. «Справочник по элементарной математике», М., 1974

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Эта страница в последний раз была отредактирована 3 декабря 2019 в 17:52.

Пропорции и отношения, прямая и обратная пропорциональность

Определение: Пропорция — это равенство двух отношений.

или .

Главное свойство пропорций

Произведение крайних членов членов пропорции равно произведению ее средних членов: если

, затем

Свойства пропорций

1. Произведение крайних членов части пропорции равно произведению ее средних членов .
2. Один крайний член пропорции равен произведению его средних членов, деленному на другой крайний член.
3. В каждом соотношении сторон можно поменять местами либо просто средние, либо крайние элементы, либо те и другие одновременно.

Пример нахождения соотношения в математике

Если ,

В пропорции поменять местами средние или конечные элементы, затем снова получить правильное равенство:

и

Производные пропорции

Если указана пропорция , , эта пропорция называется производной.

Наиболее часто используемые производные пропорции

Масштаб

Определение: Масштаб — отношение расстояния на карте к соответствующему расстоянию на реальной местности.

Прямо пропорционально величине

Определение: Две величины называются прямо пропорциональными , если при увеличении значений одной из них в несколько раз значение другой увеличивается на такой же коэффициент.

Задачи прямо пропорциональны величине

Сторона квадрата равна 3. Как изменить периметр квадрата, если его сторону увеличить в 3 раза, 4 раза, 5 раз?

Квадрат стороны 3 DM, периметра 12 DM

Сторона площади, ДМ 9, ДМ 36 периметр

Квадрат бортовой 12 дм, периметр 48 дм

Квадрат боковой 15 дм, периметр 60 дм

Если вы увеличите стороны квадрата в 3 раза (было 3 DM, 9 DM), периметр также увеличится в 3 раза (было 9 DM, 36 DM).

Точно так же, если вы увеличите стороны квадрата в 4 раза (было 3 DM, 12 DM), периметр также увеличится в 4 раза (было 12 DM, 48 DM).

Вывод: если увеличить стороны квадрата в несколько раз, то и периметр увеличится во столько же раз.

Сторона квадрата прямо пропорциональна его периметру.

обратно пропорциональна величине

Определение: Две величины называются пропорциональным обэнто , если при увеличении значения одной из них в несколько раз значение другой уменьшается на тот же коэффициент.

Задачи обратно пропорциональны величине

Расстояние между двумя городами — 160 км. сколько времени нужно, чтобы добраться из одного поселка в другой, если скорость 10 км / ч увеличится в 2 раза, 4 раза, 8 раз?

Скорость движения км / ч 10 раз, ч 16

Скорость движения км / ч 20 раз, ч 8

Скорость движения км / ч 40 раз, ч 4

Скорость км / ч 80 раз, ч 2

При увеличении скорости в 2 раза (было 10 км / ч, 20 км / ч) время уменьшилось (уменьшилось) до 2 раз (16 ч, 8 ч).

Аналогично, при увеличении скорости в 4 раза (было 10 км / ч, 40 км / ч) время сокращалось (уменьшалось) в 4 раза (16 ч, 4 ч).

Вывод: при увеличении скорости в несколько раз время уменьшается во столько же раз.

Скорость обратно пропорциональна времени.

Числа пропорциональны числам , если — коэффициент пропорциональности .

.Пропорция

, прямая вариация, обратная вариация, совместная вариация

Пропорция, прямая вариация, обратная вариация, совместная вариация

В этом разделе определяется, что такое пропорция, прямая вариация, обратная вариация и совместная вариация, и объясняется, как решать такие уравнения.

доля

Пропорция — это уравнение, устанавливающее равенство двух рациональных выражений.Простые пропорции можно решить, применив правило перекрестных произведений.

Если , то ab = bc .

Более сложные пропорции решаются как рациональные уравнения.

Пример 1

Решить .

Примените правило перекрестных произведений.

Чек предоставляется вам.

Пример 2

Решить .

Примените правило перекрестных произведений.

Чек предоставляется вам.

Пример 3

Решить .

Однако x = 4 является посторонним решением, потому что оно делает знаменатели исходного уравнения равными нулю. Проверка, является ли решением, оставлена ​​вам.

Прямое изменение

Фраза « y прямо пропорциональна как x » или « y прямо пропорциональна x » означает, что по мере увеличения x увеличивается и y , а поскольку x увеличивается. меньше, y .Эту концепцию можно перевести двояко.

• для некоторой постоянной k .

  k называется константой пропорциональности . Этот перевод используется, когда желаемым результатом является константа.

• 

  Этот перевод используется, когда желаемый результат представляет собой исходное или новое значение x или y .

Пример 4

Если y изменяется прямо как x , и y = 10, когда x = 7, найдите константу пропорциональности.



Константа пропорциональности — .

Пример 5

Если y изменяется прямо как x , и y = 10, когда x = 7, найдите y , когда x = 12.



Примените правило перекрестных произведений.



Обратное изменение

Фраза « y изменяется обратно пропорционально как x » или « y обратно пропорционально x » означает, что по мере увеличения x , y уменьшается, или наоборот.Это понятие переводится двояко.

• yx = k для некоторой константы k , называемой константой пропорциональности. Используйте этот перевод, если требуется константа.

• y ₁ x ₁ = y ₂ x ₂ .

  Используйте это преобразование, если требуется значение x или y .

Пример 6

Если y изменяется обратно пропорционально x , и y = 4, когда x = 3, найдите константу пропорциональности.



Константа 12.

Пример 7

Если y изменяется обратно пропорционально x и y = 9, когда x = 2, найдите y , когда x = 3.



Совместная вариация

Если одна переменная изменяется как произведение других переменных, это называется совместным изменением . Фраза « y изменяется вместе как x и z » переводится двумя способами.

Пример 8

Если y изменяется вместе как x и z , и y = 10, когда x = 4 и z = 5, найдите константу пропорциональности.



Пример 9

Если y изменяется вместе как x и z , и y = 12, когда x = 2 и z = 3, найдите y , когда x = 7 и z = 4.



Иногда проблема включает как прямые, так и обратные вариации. Предположим, что y изменяется прямо как x и обратно как z . Это включает в себя три переменные и может быть переведено двумя способами:

Пример 10

Если y изменяется прямо как x и обратно как z , и y = 5, когда x = 2 и z = 4, найдите y , когда x = 3 и z = 6.

.

Обратные функции

Обратная функция — наоборот!

Начнем с примера:

Здесь у нас есть функция f (x) = 2x + 3 , записанная в виде блок-схемы:

Обратная функция идет другим путем:

Таким образом, обратное: 2x + 3: (y-3) / 2

Обратное значение обычно отображается путем добавления небольшого «-1» после имени функции, например:

ф ^-1 (у)

Мы говорим « f инверсия y»

Итак, обратное к f (x) = 2x + 3 записывается:

f ^-1 (y) = (y-3) / 2

(я также использовал y вместо x , чтобы показать, что мы используем другое значение.)

Вернуться туда, где мы начали

Самое замечательное в обратном преобразовании состоит в том, что он должен вернуть нам исходное значение:

.

Когда функция f превращает яблоко в банан,
Затем обратная функция f ^-1 превращает банан обратно в яблоко

Пример:

Используя приведенные выше формулы, мы можем начать с x = 4:

f (4) = 2 × 4 + 3 = 11

Затем мы можем использовать обратное для 11:

f ^-1 (11) = (11-3) / 2 = 4

И мы волшебным образом снова получаем 4 !

Мы можем написать это одной строкой:

f ^-1 (f (4)) = 4

«f, обратное f 4, равно 4»

Таким образом, применение функции f, а затем ее обратной f ^-1 возвращает нам исходное значение снова:

f ^-1 (f (x)) = x

Мы также могли бы расположить функции в другом порядке, и он все еще работает:

f (f ^-1 (x)) = x

Пример:

Начать с:

f ^-1 (11) = (11-3) / 2 = 4

А потом:

f (4) = 2 × 4 + 3 = 11

Итак, мы можем сказать:

f (f ^-1 (11)) = 11

«f f, обратное 11, равно 11»

Решить с помощью алгебры

Мы можем вычислить обратное, используя алгебру. Положите y вместо f (x) и решите относительно x:

Функция:		f (x)	=	2x + 3
Вместо f (x) подставьте «y»:		y	=	2x + 3
Вычтем 3 с обеих сторон:		г-3	=	2x
Разделите обе стороны на 2:		(у-3) / 2	=	x
Поменять местами:		х	=	(у-3) / 2
Решение (вместо «x» подставьте «f -1 (y)»):		ж -1 (г)	=	(у-3) / 2

Этот метод хорошо подходит для более сложных инверсий.

Фаренгейта в Цельсия

Полезный пример — преобразование между градусами Фаренгейта и Цельсия:

Для преобразования Фаренгейта в Цельсия: f (F) = (F — 32) × 5 9

Обратная функция (Цельсия обратно к Фаренгейту): f ^-1 (C) = (C × 9 5 ) + 32

Для вас: посмотрите, сможете ли вы сделать шаги, чтобы создать инверсию!

Инверсия общих функций

До сих пор это было легко, потому что мы знаем, что обратное к умножению — это деление, а обратное к сложению — вычитание, но как насчет других функций?

Вот список, который вам поможет:

(Примечание: вы можете узнать больше об обратном синусе, косинусе и касательной.)

Осторожно!

Вы видели «Осторожно!» столбец выше? Это потому, что некоторые инверсии работают только с определенными значениями .

Пример: квадрат и квадратный корень

Когда мы возводим в квадрат отрицательное число , а затем делаем обратное, происходит следующее:

Квадрат: (- 2) ² = 4

Обратная величина (квадратный корень): √ (4) = 2

Но мы не вернули исходное значение! Мы получили 2 вместо −2 .Наша вина в том, что мы не были осторожны!

Таким образом, квадратная функция (как она есть) не имеет обратной

Но мы можем это исправить!

Ограничить домен (значения, которые могут входить в функцию).

Пример: (продолжение)

Только убедитесь, что мы не используем отрицательные числа.

Другими словами, ограничьте его до x ≥ 0 , и тогда мы сможем получить обратное.

Итак, мы имеем такую ​​ситуацию:

• x ² имеет ли инверсию, а не ?
• но {x ² | x ≥ 0} (в котором говорится, что «x возведен в квадрат, такой, что x больше или равен нулю» с использованием нотации создателя множеств) имеет обратное значение.

Нет обратного?

Давайте посмотрим наглядно, что здесь происходит:

Чтобы иметь возможность иметь инверсию, нам нужно уникальных значений .

Просто подумайте … если есть два или более значений x для одного значения y , как мы узнаем, какое из них выбрать, когда вернемся?

Общие функции

Нет обратного

Представьте, что мы перешли от x _{до 1} к определенному значению y, куда мы вернемся? x ₁ или x ₂ ?

В этом случае у нас не может быть обратного.

Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.

Это называется «однозначным соответствием» или биективным, например

Биективная функция

имеет инверсию

Функция должна быть «биективной», чтобы иметь инверсию.

Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.

Домен

и диапазон

Так что же все эти разговоры о «, ограничивающем домен »?

В простейшей форме область — это все значения, которые входят в функцию (а диапазон — это все значения, которые выходят).

В его нынешнем виде функция не имеет обратного значения для функции , потому что некоторые значения y будут иметь более одного значения x.

Но мы могли бы ограничить домен так, чтобы было уникальных x для каждого y …

… и теперь у нас может быть обратное:

Также примечание:

• Функция f (x) переходит из домена в диапазон,
• Обратная функция f ^-1 (y) переходит из диапазона обратно в домен.

Давайте изобразим их оба в терминах x … так что теперь это f ^-1 (x) , а не f ^-1 (y) :

f (x) и f ^-1 (x) похожи на зеркальные изображения
(перевернут по диагонали).

Другими словами:

График f (x) и f ^-1 (x) симметричен по линии y = x

Пример: квадрат и квадратный корень (продолжение)

Первый , мы ограничиваем Домен до x ≥ 0 :

• {x ² | x ≥ 0} «x в квадрате, так что x больше или равно нулю»
• {√x | x ≥ 0} «квадратный корень из x такой, что x больше или равен нулю»

И вы можете видеть, что это «зеркальные отражения»
друг друга по диагонали y = x.

Примечание: когда мы ограничиваем область до x ≤ 0 (меньше или равно 0), обратное значение будет f ^-1 (x) = −√x :

• {x ² | х ≤ 0}
• {−√x | x ≥ 0}

Которые тоже обратные.

.

Ссылка на экспоненциальную функцию

Это общая экспоненциальная функция (см. Ниже e ^x ):

f (x) = a ^x

a — любое значение больше 0

Свойства зависят от значения «а»

• Когда a = 1 , график представляет собой горизонтальную линию при y = 1
• Кроме того, есть два случая, на которые стоит обратить внимание:

a от 0 до 1

Пример: f (x) = (0.5) ^х

Для a от 0 до 1

a выше 1

Пример: f (x) = (2) ^x

Для и и выше 1:

Постройте график здесь (используйте ползунок «a»)

В целом:

• Это всегда больше 0 и никогда не пересекает ось x
• Он всегда пересекает ось y при y = 1 … другими словами, он проходит через (0,1)
• При x = 1 , f (x) = a … другими словами он проходит через (1, а)
• Это инъективная (однозначная) функция

Его домен — вещественные числа:

Его диапазон — положительные действительные числа: (0, + ∞)

Обратный

Таким образом, экспоненциальная функция может быть «обращена» логарифмической функцией.

Естественная экспоненциальная функция

Это экспоненциальная функция «Natural «:

f (x) = e ^x

Где e — «Число Эйлера» = 2.718281828459 … и т. Д.

График f (x) = e ^x

Значение e важно, поскольку оно создает следующие полезные свойства:

В любой момент наклон e ^x равен значению e ^x :

при x = 0 значение e ^x = 1 и наклон = 1
при x = 1 значение e ^x = e и наклон = e
и т. Д…

Область от до , любое значение x также равно e ^x :

.