Смежные и вертикальные углы. Их свойства

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°

Теорема 1. Сумма смежных углов равна 180°.

Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .

Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны

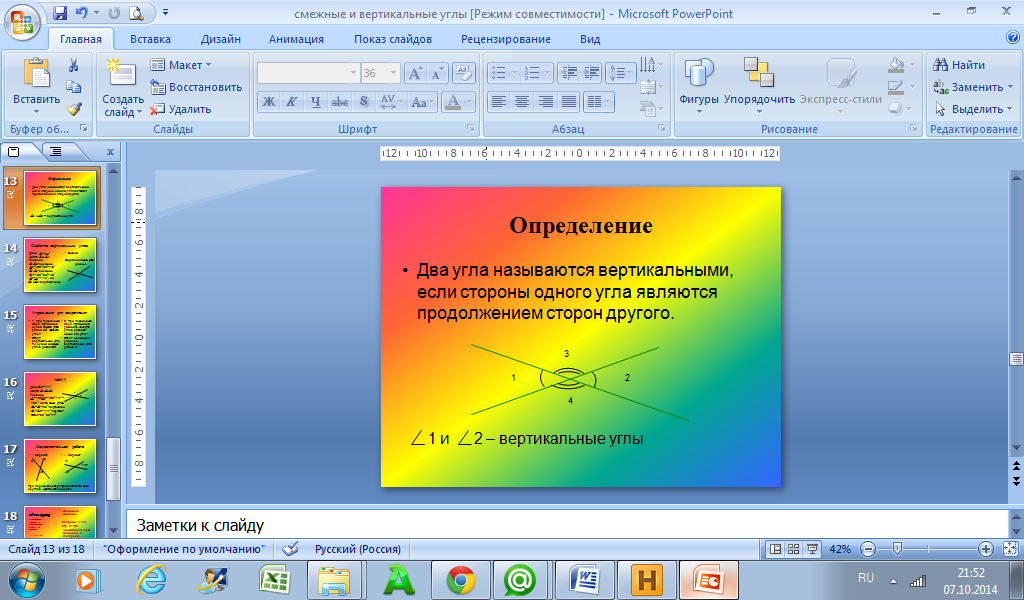
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).

Теорема 2. Вертикальные углы равны.

Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.

Отсюда заключаем, что ∠ АОВ = ∠ COD.

Следствие 1. Угол, смежный с прямым углом, есть прямой угол.

Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

АН — перпендикуляр к прямой

Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Чертежный угольник

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?

Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.

Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.

Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.

Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.

Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1

∠ BOD = ∠ АОС = 180° — 50° = 130°.

Равна двум прямым углам.

Даны два смежных угла : АОВ и ВОС . Требуется доказать, что:

∠АОВ+∠ВОС= d+ d = 2d

Восставим из точки О к прямой АС перпендикуляр OD . Мы разделили угол АОВ на две части AOD и DOB так, что можно написать:

∠AO B = ∠ AO D+∠ D OB

Прибавим к обеим частям этого равенства по одному и тому же углу BOС , отчего равенство не нарушится:

∠ AO B + ∠ BO С = ∠ AOD + ∠ D OB + ∠ BO С

Так как сумма D OB + BOС составляет прямой угол

DO С , то

∠ AO B+ ∠ BO С = ∠ AO D + ∠ DO С = d + d = 2 d,

что и требовалось доказать.

Следствия .

1. Сумма углов (AO B, BOС , СOD , DOE ), расположенных вокруг общей вершины (O ) по одну сторону прямой (AE ) равна 2 d = 180 0 , потому что эта сумма составляет сумму дву

dudley.ru

Вертикальные углы / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Начальные геометрические сведения
5. Вертикальные углы

Вертикальные углы

— это пары углов, имеющие общую вершину и образованные при пересечении двух прямых так, что стороны одного угла являются продолжениями другого.

При пересечении двух прямых получается четыре угла с общей вершиной О (Рис.1), из которых вертикальными будут пары углов 1 и 3, 2 и 4.

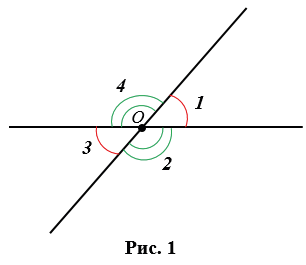
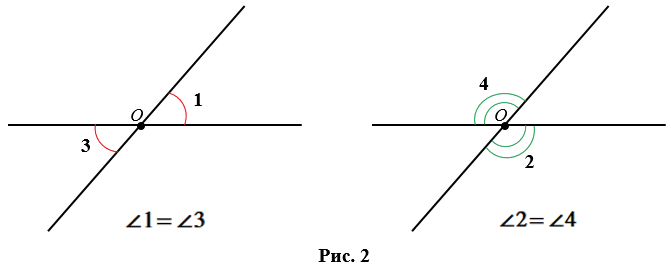
Свойство вертикальных углов: вертикальные углы равны (Рис.2).

 

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 56, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 65, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 174, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 176, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 342, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 345, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 853, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1059, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1147, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

budu5.com

Конспект урока геометрии по теме «Смежные и вертикальные углы и их свойства» для 7 класса

Предмет Геометрия	7 класс	Дата		Урок № 11
Учитель	Гардер Светлана Владимировна
Тема	Смежные и вертикальные углы и их свойства
Цели:	Учащиеся знают определения смежных и вертикальных углов, теоремы о смежных и вертикальных углах; определяют смежные и вертикальные углы; применяют при решении заданий
Задачи:	Математический диктант Выявить остаточный уровень знаний учащихся по теме «Основные понятия геометрии» Откорректировать знания Прослушать слово учителя Познакомиться с материалом презентации Отработать навык на примере задач, выполнить индивидуальное задание по карточкам Откорректировать знания Разобрать домашнее задание Провести рефлексию
Ожидаемые результаты	Результаты обучения для учеников (А)	Результаты обучения для учеников (B)		Результаты обучения для учеников (C)
	Учащиеся знают определения смежных и вертикальных углов, теоремы о смежных и вертикальных углах; определяют смежные и вертикальные углы; применяют при решении заданий, аргументируют, обобщают и систематизируют изученный ранее материал, способны к решению проблемных вопросов	Учащиеся знают определения смежных и вертикальных углов, теоремы о смежных и вертикальных углах; определяют смежные и вертикальные углы; применяют при решении заданий, аргументируют, анализируют, обобщают и систематизируют изученный ранее материал		Учащиеся знают определения смежных и вертикальных углов, теоремы о смежных и вертикальных углах; определяют смежные и вертикальные углы; применяют при решении заданий, аргументируют, сверяют правильность выполнения заданий по образцу
Ресурсы:	Учебник, доска, мел, вопросы по теме «Аксиомы геометрии. Теорема и доказательство теоремы», «Угол. Биссектриса угла», динамическая пауза, презентация по теме «Смежные и вертикальные углы», интерактивное оборудование (ИКТ)
Ход урока
1. Психологический настрой Метод «Ассоциации»: — Какие ассоциации возникают у вас, когда слышите слово «угол»? У					Г	О	Л

Вызов

Деятельность учителя

Деятельность обучающихся

Учитель выявляет уровень усвоения изученного ранее материала, корректирует знания, исправляет ошибки и недочеты. Ориентирует учащихся на выполнение математического диктанта, самопроверки работы учащимися; использует активные методы и формы работы (стратегии), актуализирует знания учащихся, ориентирует учащихся при формулировании цели и проблемного вопроса урока, корректирует знания учащихся

Учащиеся проверяют домашнее задание, задают вопросы учителю, корректируют знания, исправляют ошибки и недочеты. Выполняют математический диктант, самопроверку работы; актуализируют знания, обобщают пройденный ранее материал, формулируют проблемные вопросы и цели урока; учащиеся строят концептуальное кольцо

2. Проверка домашнего задания.

3. Математический диктант

Продолжи предложение: Аксиома — … Теорема- … Доказать теорему значит…

4. Актуализация знаний Стратегия «Дерево знаний»

1. Обобщение и систематизация по теме «Угол. Биссектриса угла»

2. Коррекция ответов учащимися и учителем

Листочки зелёные – Тему предыдущего урока освоил(-а)

Дерево без листочков – Испытывал затруднения при работе над новой темой

5. Целеполагание

Осмысление

Деятельность учителя

Деятельность обучающихся

Учитель определяет основные направления работы, знакомит с содержанием темы (презентация), предлагает исследовать предложенные задания, ориентирует и корректирует выполнение тренировочных заданий, инструктирует в выполнении домашнего задания, оценивает уровень усвоения учащимися новых знаний, наблюдает за тем, как работают учащиеся категории А, В и С

Учащиеся знакомятся с содержанием презентации, исследуют предложенные задания, решают проблемные вопросы, выполняют тренировочные задания, выполняют самопроверку, записывают домашнее задание, знакомятся с инструкцией по выполнению домашнего задания, задают вопросы учителю для коррекции

6. Изучение нового материала

1. Слово учителя

2. Презентация. «Смежные и вертикальные углы»

3. Поэтапная коррекция ответов учащимися и учителем

7. Динамическая пауза

8. Закрепление

1. Поэтапное решение с комментированием, стр. 32 № 68 (1), 71, стр. 33 № 78

2. Работа в парах, стратегия ДЖИГСО

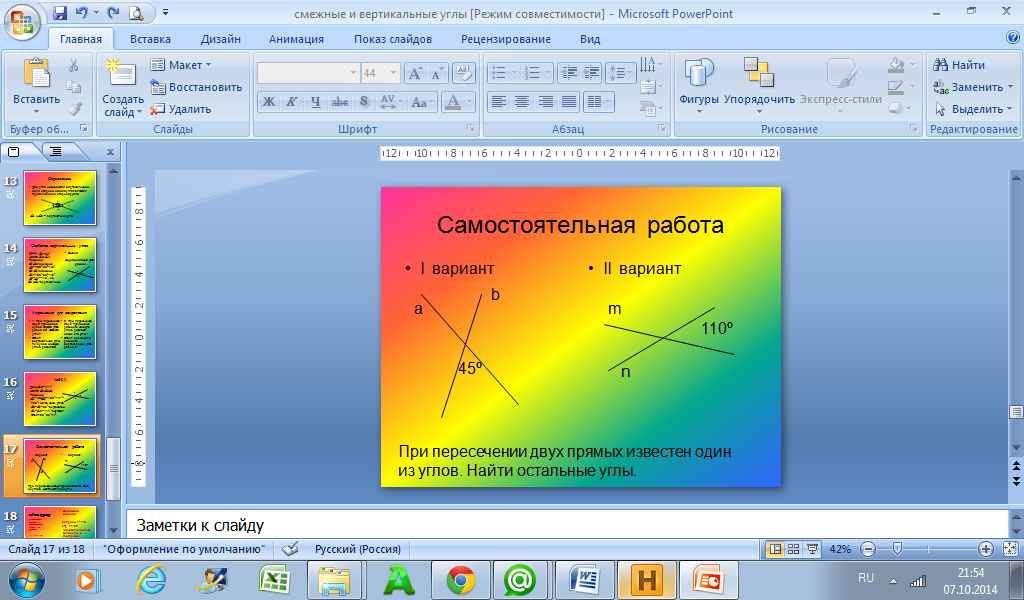
3. Поэтапная коррекция ответов учащихся и учителем

9. Домашнее задание Параграф 4.1, стр. 32 № 68 (3), стр. 33 № 79

Рефлексия

Деятельность учителя

Деятельность обучающихся

Учитель проводит рефлексию, оценивает уровень усвоения учащимися новых знаний (повторения ранее изученного), исследует проблемы

Учащиеся проводят рефлексию, оценивают качество работы, уровень усвоения (повторения), психологического комфорта, определяют совместные результаты работы

10. Рефлексия учащихся Стратегия «Светофор»

Оцените свою деятельность на уроке с помощью «Светофора»

зелёный – все понятно, желтый – есть затруднения, красный – много непонятного –

карточки данных цветов даны учащимся еще до урока.

11. Рефлексия учителя (оценивание)

infourok.ru