Неопределённые и определённые интегралы. Методы интегрирования
| 1. | Табличные интегралы | 1 вид — рецептивный | лёгкое | 1 Б. | Задание на знание табличных интегралов (предлагается выбор ответа). |
| 2. | Определённый интеграл степенной функции | лёгкое |
2 Б.
|
Вычисление определённого интеграла степенной функции с использованием формулы Ньютона-Лейбница. | |
| 3. | Основной интеграл тригонометрической функции | 1 вид — рецептивный | лёгкое | 3 Б. | В вычислении определённого интеграла тригонометрической функции используется формула Ньютона-Лейбница. |
4.
|
Неопределённый интеграл от дробной функции | 2 вид — интерпретация | среднее | 4 Б. | Вычисление неопределённого интеграла, непосредственное интегрирование. |
| 5. | Неопределённый интеграл от дробной тригонометрической функции | 2 вид — интерпретация | среднее |
3 Б.
|
Вычисление неопределённого интеграла от дробной тригонометрической функции, непосредственное интегрирование. |
| 6. | Неопределённый интеграл от показательной функции | 2 вид — интерпретация | среднее | 4 Б. | Вычисление неопределённого интеграла от показательной функции, непосредственное интегрирование. |
7. |
Неопределённый интеграл, метод замены переменной, натуральный логарифм | 2 вид — интерпретация | среднее | 4 Б. | Вычисление неопределённого интеграла с использованием метода замены переменного. |
| 8. | Неопределённый интеграл, метод замены переменной, тригонометрические функции | 2 вид — интерпретация | среднее |
4 Б.
|
Вычисление неопределённого интеграла с использованием метода замены переменного. |
| 9. | Определённый интеграл, функция, содержащая квадратный корень | 2 вид — интерпретация | среднее | 4 Б. | Вычисление определённого интеграла с использованием формулы Ньютона-Лейбница. |
10.
|
Определённый интеграл, тригонометрическая функция | 2 вид — интерпретация | среднее | 4 Б. | Вычисление определённого интеграла с использованием формулы Ньютона-Лейбница. |
| 11. | Определённый интеграл, геометрический смысл | 2 вид — интерпретация | сложное |
4 Б.
|
Вычисление определённого интеграла с использованием его геометрического смысла. |
| 12. | Вычисление силы сжатия пружины | 3 вид — анализ | сложное | 4 Б. | В вычислениях используются определённый интеграл, закон Гука, работа переменной силы. |
13.
|
Физический смысл определённого интеграла | 3 вид — анализ | сложное | 5 Б. | Сила давления воды на пластину. |
Таблица интегралов
| 1. |
| ||||
| 2. |
| ||||
| 3. |
| ||||
4. |
| ||||
| 5. |
| ||||
| 6. |
| ||||
| 7. |
| ||||
| 8. |
| ||||
| 9. |
| ||||
| 10. |
| ||||
11. |
| ||||
| 12. |
| ||||
| 13. |
| ||||
| 14. |
| ||||
| 15. |
| ||||
| 16. |
| ||||
| 17. |
| ||||
| 18. |
| ||||
19. |
| ||||
| 20. |
| ||||
| 21. |
| ||||
| 22. |
| ||||
| 23. |
| ||||
| 24. |
| ||||
| 25. |
| ||||
26. |
| ||||
| 27. |
| ||||
| 28. |
| ||||
| 29. |
| ||||
| 30. |
| ||||
| 31. |
|
Справочник репетитора по математике.
 Список табличных интегралов
Список табличных интеграловТабличные интегралы для занятий по математическому анализу. В помощь студентам первых курсов технических, экономических и математических ВУЗов, преподавателям и репетиторам по математике.
Неопределенных интегралы от основных функций.
1. Интеграл от степенной функции
2. Интеграл от константы
3. Интеграл от синуса
4. Интеграл от косинуса
5. Интеграл от экспоненты
6. Интеграл от показательной функции
7. Интеграл от обратной пропорциональности
8.Интеграл, равный тангенсу
9. Интеграл, равный котангенсу
10. Интеграл от тангенса
11. Интеграл от котангенса
12. Интеграл, равный арксинусу
13. Интеграл, равный минус арккосинусу
Интеграл, равный минус арккосинусу
14. Интеграл от секонса
15. Интеграл от косеконса
16. Интеграл, от обратной величины к разности квадратов
17. Полезный интеграл, сводящийся к арксинусу
18. Полезный интеграл, сводящийся к арктангенсу
19. Интеграл, сводящийся к натуральному логарифму
Комментарий репетитора по математике: к табличным обычно относят простейшие интегралы, в записи которых участвуют элементарные (основные) функции математического анализа. Табличные интегралы можно использовать для вычисления любых других интегралов (типовых или сложных) на любом этапе реализации алгоритма их нахождения. Техника интегрирования допускает следующий план: как только вам встетился табличный интеграл — применяйте его без каких-либо доказательств или вывода.
Интегралы расположены в порядке роста уровня сложности их вывода и частоте использования в решении задач. Удачи в совершенствовании умения вычислять интегралы.
Удачи в совершенствовании умения вычислять интегралы.
Колпаков А.Н., профессиональный репетитор по математике в Москве.Строгино, м. Щукинская.
Математика для блондинок: Таблица интегралов
Не научный бред с элементами реализма на тему неопределенного интеграла.Не просите маня в комментариях найти какой-нибудь интеграл. Я не умею находить интегралы, я могу только над ними по прикалываться. Прежде, чем здесь появится таблица неопределенных интегралов, нужно представить определение неопределенного интеграла. Прямо каламбур получился. Неопределенным интеграл называется так не потому, что определение для него никто не придумал, а потому, что с ним нельзя точно определиться. Математики меня заклюют за такое разъяснение.
| Неопределенный интеграл и его свойства |
 Дальше идет таблица основных неопределенных интегралов.
Дальше идет таблица основных неопределенных интегралов.| Таблица основных неопределенных интегралов |
Если вы любите по вечерам вместо семечек щелкать неопределенные интегралы, тогда большая таблица интегралов для вас. Если вы где-то учитесь, настоятельно рекомендую пользоваться большой таблицей интегралов в качестве ответов, которые обычно размещают в конце учебника. Помните, что вы не в детском садике и задачку без действий вам никто не задаст. Даже в задаче на одно действие между условием и ответом записывают это действие.
Вот большая таблица неопределенных интегралов (картинка 510 на 8 710 пикселей, формат JPG, объем файла 783 килобайта). Эта таблица интегралов содержит 147 представителей этой математической фауны. Я подозреваю, что коллекция эта далеко не полная, но некоторые самые популярные виды интегралов в ней присутствуют. Нажимаете на ссылку — откроется картинка, по виду очень похожая на размотанный рулон туалетной бумаги. Наводите курсор на эту ленту, курсор превращается в лупу со знаком «плюс», жмете. Теперь вы в царстве интегралов. Сохранить память о столь увлекательном путешествии можно при помощи правой кнопки мыши и строчки меню «Сохранить изображение как…». Всё, Третьяковская галерея интегралов переселилась в ваш компьютер.
Наводите курсор на эту ленту, курсор превращается в лупу со знаком «плюс», жмете. Теперь вы в царстве интегралов. Сохранить память о столь увлекательном путешествии можно при помощи правой кнопки мыши и строчки меню «Сохранить изображение как…». Всё, Третьяковская галерея интегралов переселилась в ваш компьютер.
Это для тех, кто не любит читать всё то, что я пишу. Столь солидную таблицу интегралов я самым бесстыдным образом позаимствовал с сайта Интегралы.ру (здесь же есть решение интегралов онлайн). Таблица интегралов разбита на 12 групп, все их мы рассмотрим более подробно на отдельных страницах.
Все эти формулы можно увидеть на отдельных страницах этого сайта.
Таблица интегралов 1 — приведены формулы с переменной в первой и второй степени из 1 и 2 разделов.
Таблица интегралов 2 — приведены формулы с квадратными корнями из разделов 3, 4, 5, 6 и 7.
Таблица интегралов 3 — приведены формулы интегрирования из разделов 8, 9 и 10.
Таблица интегралов
4 — приведены формулы интегрирования показательных, тригонометрических и логарифмических функций из разделов 11 и 12.
Как найти неопределенный интеграл? Очень просто. Тупо берете формулу, тупо подставляете в пример. Лично я так делал. Иногда можно чего-то там перегруппировать, упростить, вынести за знак интеграла… На звание самого лучшего в мире искателя интегралов я не претендовал, о чем нисколько не жалею. Вообще, живых интегралов я за свою жизнь так и не встретил. Все они для меня вымерли, как динозавры, сразу же после окончания учебы. Да, я ещё кое-что о них помню. Только и всего.
Теперь немного бла-бла-бла на тему неопределенных интегралов. Чистый бред. Прошу не путать с заявлением о приеме меня в математики.
Очень интересен каламбур, написанный буковками под таблицей основных
неопределенных интегралов. На первый взгляд получается, что
первообразная на первообразной сидит и первообразной погоняет. Ясно, что
записанное выражение и дураку понятно. Но бывают ещё и особо одаренные
представители рода человеческого, типа меня. У меня просто мозги отключаются, когда я вижу или читаю подобные фразы. Наверное, инстинкт самосохранения срабатывает — мозг боится собственного вывиха. Долго вспоминал, где у меня лево, где право.
Наверное, инстинкт самосохранения срабатывает — мозг боится собственного вывиха. Долго вспоминал, где у меня лево, где право.
Через пару дней напряженной умственной работы, я пришел к выводу, что в левой части описывается ситуация, когда мы точно знаем, от какой первообразной функции мы получили производную. В правой части мы пытаемся угадать, какой первообразной функции принадлежит производная. На динозаврах это гораздо понятнее. Если у нас есть живой динозавр, то мы точно знаем, как он выглядит, и точно можем сказать, как через десятки миллионов лет будут выглядеть его останки. Но вот когда мы сегодня находим останки динозавров, мы не можем точно сказать, как они выглядели — окраску, голос, запах по останкам определить не возможно. Знак равенства стоит на том основании, что из всех возможных вариантов один точно правильный. В отличии от динозавров, математические функции математики представляют в абстрактном виде, вне времени — одновременно и настоящее, и будущее, и прошлое.
Теперь эта же мысль, но языком математических формул. Используем определение и свойства
неопределенных интегралов. Возьмем первообразную функцию с константой и посмотрим, что происходит.
Используем определение и свойства
неопределенных интегралов. Возьмем первообразную функцию с константой и посмотрим, что происходит.
| Первообразная функция |
Здесь получается фокус с тузом в рукаве. В определении неопределенного интеграла константа является частью первообразной функции F(x) и отдельно не выделяется — туз спрятан в рукаве. После интегрирования мы добавляем константу, потерявшуюся при дифференцировании — туз достаем из рукава на всеобщее обозрение. В этом случае главным является не сам фокус, а факт присутствия туза у фокусника как до, так и после демонстрации трюка.
Что такое константа? Это число. Геометрически при помощи изменения константы можно сместить график функции F(x) вдоль оси игреков вниз или вверх. В определении неопределенного интеграла указано, что совокупность всех этих первообразных и представляет из себя этот злополучный интеграл. Но это только одна сторона медали.
В определении не указывается, что вся совокупность первообразных рассматривается в одной, кем-то когда-то выбранной, системе координат. А если мы выберем одну первообразную, тогда изменение константы будет смещать систему координат. С точки зрения выбранной первообразной, неопределенный интеграл — это совокупность всех систем координат, в которых может рассматриваться данная первообразная функция.
Чудеса относительности. Если мы сидим попой на поверхности Земли, то мы видим, как Солнце бегает по небу. Если мы сидим попой на Солнце (не бойтесь поджариться, ведь математика — абстрактная наука и позволяет сидеть на чем угодно), то мы видим, как Земля вращается вокруг собственной оси. Всё зависит от выбранной нами точки зрения, что в математике соответствует выбору системы координат.
Всё зависит от выбранной нами точки зрения, что в математике соответствует выбору системы координат.
С учетом относительности влияния константы на сладкую парочку «функция — система координат», первое предложение в определении неопределенного интеграла можно записать так:
Неопределенный интеграл для функции f(x) — это совокупность всех первообразных данной функции или совокупность всех систем координат данной первообразной функции.
Не знаю, как посмотрят на такое развитие сюжета математики, но получилось слишком заумно. Всё это дело можно упростить, если отказаться от пыток восстановить константу в первообразной функции. Ещё раз проконтролируем свои действия. Если у нас есть первообразная функция с константой или без, мы можем точно сказать, как выглядит её производная. Если у нас есть производная, мы не можем точно сказать, от какой именно первообразной она получена.
Всё дело заключается в том, что при взятии производной происходит изменение системы координат. Если мы рассматриваем производную f(x) в измененной системе координат, то восстановить первоначальную систему координат первообразной функции F(x) невозможно. Нельзя воскресить мертвое. Вместо математической точности у нас
получается гадание на кофейной гуще. И это гадание выражается в
прибавлении константы к скелету первообразной функции.
Если мы рассматриваем производную f(x) в измененной системе координат, то восстановить первоначальную систему координат первообразной функции F(x) невозможно. Нельзя воскресить мертвое. Вместо математической точности у нас
получается гадание на кофейной гуще. И это гадание выражается в
прибавлении константы к скелету первообразной функции.
Задачу эту можно решить на уровне задних парт третьего класса. Почему задних парт? Они находятся дальше всех от испепеляющего светоча знаний, льющегося с классной доски. Почему третьего класса? У них ещё не выработан благоговейный трепет перед учебниками. Просто начинаем фантазировать. Придумываем какое-нибудь новое определение и при помощи него разруливаем ситуацию.
Функция в собственной системе координат Fo(x) — это функция, у которой константа приравнивается к нулю. Так сказать, функция в собственном соку. Классическим примером функций в собственной системе координат можно считать тригонометрические функции. При изучении они рассматриваются без константы.
Поскольку определение неопределенного интеграла уже написано и правила хорошего тона настоятельно не рекомендуют его рихтовать, придумаем еще одно определение какой-нибудь промежуточной фигни. Пусть эта фигня будет называться «определенная первообразная«. Теперь берем определение неопределенного интеграла и на его основе пишем свое определение определенной первообразной.
Определенная первообразная для функции f(x) — это первообразная данной функции в собственной системе координат Fo(x). Если функция f(x) определена и непрерывна на промежутке (a, b) и F(x) — её первообразная, то есть F'(x)=f(x) при a меньше x меньше b
| Определенная первообразная |

| Свойства определенной первообразной |
Дальше ещё несколько слов о константе в неопределенном интеграле. При дифференцировании функции константа превращается в ноль. В математике существует первая, вторая, третья и так далее, производные. Можно предположить, что столько же существует и неопределенных интегралов. Берем результат интегрирования и снова интегрируем. Вот что может получиться…
Ветхий Завет от Матана.
Вначале ничего не было. Потом было слово. Точнее, два слова — Неопределенный Интеграл. И создал Неопределенный Интеграл константу. А потом Он создал переменную. И стала переменная плюс константа. А потом Неопределенный Интеграл создал…
И стала переменная плюс константа. А потом Неопределенный Интеграл создал…
| Первообразная константы |
Если вас не устраивает такая история сотворения мира, эти же формулы можно трактовать как историю Большого Взрыва. Ведь ученые уверяют, что началось всё с точки, то есть с нуля.
Сергей Манулов, давний друг этого сайта, предлагал мне опубликовать в одной таблице интегралы рядом с производными. Так действительно будет нагляднее и понятней. Но здесь есть два момента. Во-первых, таблица получится такой широкой, что в этот сайт явно не влезет. Во-вторых, насколько я помню, таблица производных несколько меньше, чем таблица интегралов. Ну не любят математики играть в производные. Кого интересует исследование всяких каракуль, пусть даже и обличенных в математические формулы? А вот игры в интегралы среди математиков очень даже популярны. По своей популярности они могут уступать разве что играм в комплексные числа. Наверное, так получается потому, что при помощи определенных интегралов можно находить площади криволинейных трапеций или что-то там ещё. Математики играют в свои любимые игрушки и вроде как полезным делом заняты.
По своей популярности они могут уступать разве что играм в комплексные числа. Наверное, так получается потому, что при помощи определенных интегралов можно находить площади криволинейных трапеций или что-то там ещё. Математики играют в свои любимые игрушки и вроде как полезным делом заняты.
Что нужно помнить о неопределенных интегралах? Как молитва заканчивается словом «Аминь», так любой неопределенный интеграл заканчивается словами «плюс константа».
Примеры на интегрирование
Примеры на интегрирование функций подобного состава заданий задают студентам 1, 2 курсов. Это в основном задания для математиков, экономистов, статистов, программистов. Данные интегралы задавали на контрольной работе в ЛНУ им. И. Франка, другие ВУЗы Украины также практикует подобные здания на контрольных по интегрированию. Чтобы формулы в задачах и ответах не повторялись условия заданий выписывать не будем. Всем и так известно что в задачах нужно или «Найти интеграл», или «Вычислить интеграл».
Пример 18. Для раскрытия иррациональности в знаменателе дроби необходимо в подобных примерах выполнять такую замену переменных — «икс» в наименьшей степени. В результате придем к интегралу от дробной функции
дальше выполняем деления числителя на знаменатель и упрощение
Таким образом без громоздких расписаний дробей придем к интегралу
Пример 19. Корневую функцию обозначаем за новую переменную в квадрате (для удобства вычислений). Далее находим дифференциал переменной, подставляем в неопределенный интеграл и выполняем упрощение.
В результате замены получим дробь которая разделяется на два интеграла. Второй интеграл равен разнице логарифмов
Пример 20. Следующие интегралы касаются исключительно тригонометрических функций, а именно их произведения, квадратов, кубов, рациональных функций. Первый из приведенных интегралов нужно свести к синусу. Для этого косинус в 5 степени расписываем на произведение косинуса в 4 степени на косинус, который вносим под дифференциал
Для упрощения вводим замену переменных и приходим к интегрированию полинома
После интегрирования возвращаемся к замене и вместо t везде записываем sin(x).
Пример 21. Для вычисления интеграла нужно снизить степень синуса. Таким образом используем тригонометрические формулы, понижаем степень первой, а дальше находим интеграл по табличным формулам.
Пример 22. Нужно найти интеграл от произведения двойного синуса на тройной косинус. Под дифференциал ничего внести не удастся, поскольку имеем различные переменные. Для упрощения распишем произведение тригонометрических функций через разницу синусов
Пример 23. Данный интеграл без универсальной тригонометрической замены переменных найти не удастся. Поэтому пусть тангенс половины угла равный t, тогда синус превратится по формуле
После раскрытия скобок в знаменателе получим квадратный трехчлен
Для сведения такой дроби к табличному арктангенсу в знаменателе сначала выделяем квадратный трехчлен
Не забываем в конце вернуться к выполненной в начале замены. Это важно при тестах и контрольных.
Пример 24. Здесь можем использовать универсальную тригонометрическую замену, а может пойти другим путем. Вынесем в знаменателе синус в квадрате за скобки и перегруппируем слагаемые в скобках, чтобы по тригонометрическим формулам получить котангенс. Его и обозначим за новую переменную u, вычисляем также дифференциал du и подставляем все в интеграл
Вынесем в знаменателе синус в квадрате за скобки и перегруппируем слагаемые в скобках, чтобы по тригонометрическим формулам получить котангенс. Его и обозначим за новую переменную u, вычисляем также дифференциал du и подставляем все в интеграл
В результате интегрирования получим табличную формулу арктангенса
Пример 25. Необходимо вычислить интеграл от тангенса в квадрате от тройного аргумента. Сначала расписываем тангенс как часть синуса к косинусу. Далее синус в квадрате расписываем через косинус. После деления числителя на знаменатель получим два интеграла которые без труда находим по формулам интегрирования
Как только Вы изучите приведенные схемы и методики сведения интегралов под то или иное правило, научитесь видеть в примерах табличные интегралы и преобразования, которые в несколько шагов позволят Вам найти интеграл — тогда контрольная работа, или «срезы» для Вас не будут препятствием в обучении. Для этого нужно решить с десяток различных интегралов к каждому из приведенных типов. Все остальные после этого будут для Вас подобными, а схема их вычислений очевидной и понятной. Если в обучении встречаются сложные интегралы или сомневаетесь в собственных силах помните — мы всегда готовы оказать помощь. Это предложение актуально не только для студентов стационарной формы обучения, но и для заочников и школьников. В 11 классе в обучении с недавних времен школьникам также приходится иметь дело с интегралами.
Все остальные после этого будут для Вас подобными, а схема их вычислений очевидной и понятной. Если в обучении встречаются сложные интегралы или сомневаетесь в собственных силах помните — мы всегда готовы оказать помощь. Это предложение актуально не только для студентов стационарной формы обучения, но и для заочников и школьников. В 11 классе в обучении с недавних времен школьникам также приходится иметь дело с интегралами.
Готовые решения контрольной по интеграции
Первообразная функция и неопределенный интеграл, страница 2
Отметим, что неопределенный интеграл даже от элементарной функции может не быть элементарной функцией, тогда как операция дифференцирования не выводит нас из класса элементарных функций, т.е. производная любой элементарной функции представляет собой тоже элементарную функцию. Можно доказать, что интегралы от некоторых элементарных функций уже не являются элементарными функциями. Примерами таких интегралов могут служить следующие интегралы:
1. | 2. , | 3. , |
4. , | 5. , | 6. . |
Такие интегралы обычно называют «неберущимися». Однако это не означает, что такие интегралы (первообразные) не существуют. Каждый из указанных интегралов представляет собой функцию, которую нельзя выразить при помощи элементарных функций. Более того, указанные функции не только реально существуют, но и играют большую роль в различных приложениях. Так, например, интеграл 1, называемый интегралом Пуассона или интегралом ошибок, широко используется в теории вероятностей и математической статистике.
В дальнейшем мы будем иметь дело только с такими функциями, которые интегрируются в элементарных функциях, т.е. их первообразные есть элементарные функции.
1.4. Табличные интегралы
Суть
различных методов интегрирования состоит в том, чтобы при помощи различных
преобразований подынтегрального выражения, используя свойства интегралов,
свести исходные интегралы к уже известным интегралам. Набор таких известных
интегралов можно получить, если переписать наоборот таблицу производных
основных элементарных функций. В результате, можно получить следующую таблицу
неопределенных интегралов:
Набор таких известных
интегралов можно получить, если переписать наоборот таблицу производных
основных элементарных функций. В результате, можно получить следующую таблицу
неопределенных интегралов:
1. , | 6. , |
2. , , | 7. , |
2а. , | 8. , |
2б. , | 9. , |
2в. , | 10. , |
3. , | 11. , |
4. , | 12. , |
4а. , | 13. , |
5. , | 14. |
Сделаем замечания в отношении формул 3, 13 и 14. Формула 3 справедлива для любых значений . В самом деле, если u>0, то , если u<0, то . Формулы 13 и 14 занимают исключительное положение в таблице, ибо эти формулы не имеют аналогов в таблице производных. Однако в справедливости этих равенств можно убедиться, продифференцировав их правые части.
Приведенные здесь интегралы называются табличными. В справедливости приведенных равенств можно убедиться при помощи дифференцирования этих равенств. В дальнейшем, мы будем пытаться свести любой интеграл к табличному. Однако для этого нужно знать свойства неопределенных интегралов, вытекающие непосредственно из определения первообразной.
1.4. Свойства неопределенных интегралов
Свойство 1. .
Свойство 2. .
Свойство 3. .
Эти свойства непосредственно вытекают из определения производной. Действительно
Из данных свойств следует, что интегрирование и дифференцирование – взаимно обратные
операции.
Следующие два свойства обычно называют линейными свойствами интеграла:
Свойство 4. .
Свойство 5. , где C = const.
Чтобы доказать эти свойства, нужно взять производную от обеих частей данных равенств и сравнить их. Подчеркнем, что рассматриваемые равенства имеют условный характер: их следует понимать как равенства двух множеств. Это означает, что данные равенства справедливы с точностью до произвольной постоянной.
Зная свойства интегралов и проводя элементарные преобразования подынтегрального выражения, можно легко свести некоторые интегралы к табличным. Вычисление интегралов, которые легко сводятся к табличным, называют иногда табличным интегрированием. При этом полезно иметь в виду следующее свойство:
Свойство 6. .
Чтобы доказать это свойство, нужно продифференцировать обе части данного равенства. Действительно, получаем
.
1.
 5. Примеры
табличного интегрирования
5. Примеры
табличного интегрированияПримеры 1.1. Вычислить интегралы
а) , б) , в) .
Решение. а) Используя свойства 4 и 5, получим
.
б) Воспользуемся свойством 6, где a=2, и табличным интегралом 3. Тогда получим
.
в) Предварительно произведем тригонометрические преобразования подынтегрального выражения, воспользовавшись тождеством: cos2x + sin2x = 1. В результате получим
.
Рассмотрим теперь интегралы, которые сводятся к табличным интегралам вида:
, или .
Обычно к таким интегралам сводятся выражения, которые содержат квадратный трехчлен:
ax2+bx+c.
Подобные интегралы обычно решают методом выделения полного квадрата. Записывая квадратный трехчлен в виде:
a(t2 ± k2),
где
, ,
можно прийти к табличным интегралам, рассматриваемого типа.
Примеры 1.2. Вычислить интегралы
а) , б) .
Решение. а) Выделим из квадратного трехчлена полный квадрат:
x2–2x+2 = (x2–2x+1)+1 = (x–1)2+1.
Тогда
.
б) Выделим полный квадрат из квадратного трехчлена
.
Тогда
.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Дайте определение первообразной.
2. Сколько существует первообразных для одной и той же функции? Как они отличаются дуг от друга
3. Что такое неопределенный интеграл?
4. Как составляется таблица интегралов? Запишите по памяти таблицу интегралов.
5. Какие интегралы называются неберущимися?
6. Для всех ли функций существуют первообразные? Как такие функции называются?
7.
Перечислите свойства интегралов.
УПРАЖНЕНИЯ И ЗАДАЧИ
1. Вычислить интегралы
а) , | б) , | в) , | г) , | д) . |
2. Вычислить интегралы
3. Вычислить интегралы
4. Вычислить интегралы
5. Вычислить интегралы
Символика, определение и свойства неопределённого интеграла. Табличные интегралы
1. Математику уже затем следует учить, что она ум в порядок приводит.
Модуль. Математика. (40 час.)Общая компетентность.Решать примеры, задачи согласно
заданиям, используя определения, теоремы, свойства, формулы.
Результаты деятельности:
1.Решать не сложные задачи с использованием формулы
скалярного произведения векторов, расстояние от точки до
плоскости, уравнения прямых в каноническом виде.
2.
 Решать не сложные примеры вычисления пределов функции,
Решать не сложные примеры вычисления пределов функции,используя теоремы о пределах, 1-й, 2-й замечательные пределы,
правило Лопиталя.
3.Находить производные функций, используя таблицу
производных, правила вычисления производных, производные
сложных функций.
4.Вычислять интегралы, используя свойства, таблицу интегралов,
метод интегрирования по частям.
5.Решать не сложные задачи по теории вероятностей, используя
формулы случайных событий и вероятности событий, функции
распределения случайной величины и функции выборки,
некоторых важнейших распределений.
3. Без математики не постичь глубин философии, без философии не постичь глубин математики; без них обеих не постичь ничего.
Бордас-Демулен4. Что означает в переводе с греческого слово «матема»?
5. Возникла математика на первых этапах создания человеческой культуры в связи с практической деятельностью людей.С самых древних
времён людипроизводя различные работы, встречались с
необходимостью выделения и обозрения тех или иных
совокупностей объектов, участков Земли Жилищных
помещений и т.
 п.Во всех этих случаях нужно было
п.Во всех этих случаях нужно былоустанавливать количественные оценки
рассматриваемых множеств, определять формы
плоских и пространственных фигур, измерять их
площади и объёмы , сравнивать. Вычислять,
преобразовывать.
6. Как называется раздел математики, в котором изучаются производные и их применение к исследованию функции?
7. Сформулируйте основную задачу дифференциального исчисления?
Приходится часто решать и обратнуюзадачу…
По данной функции f (х) требуется найти
функцию F (х) такую ,что F’ (х)=f (х)
Пример из механики. Если в начальный
момент времени t=0, v(t)=0 то при
свободном падении S(t)=gt²⁄2 — эта
формула была получена Галилеем
эксперементально.
Найдите первую и вторую производную
координаты по времени?
S'(t)=
S»(t)=
Более типично для механики
иное положение:
известно ускорение, требуется
найти закон изменения скорости
v(t) , а также координату S(t).

Иными словами по заданной
производной нужно найти
функцию
Какая операция служит для
решения задачи обратной
операции дифференцирования?
12. Операция интегрирования.
С помощью операции интегрированияили интегрального исчисления или
интеграла можно находить функцию по
её производной, вычислять площади и
объёмы пространственных и плоских
фигур, также решать дифференциальные
уравнения и т.п.
Тема урока: Символика,
определение и свойства
неопределённого
интеграла. Табличные
интегралы.
Весь
смысл жизни заключается в
бесконечном завоевании
неизвестного, в вечном усилии
познать больше.
З. Золя.
15. Символика, определение и свойства неопределённого интеграла.
∫— знак интеграла
f(х)
-подынтегральная функция
∫f(х) dх -подынтегральное выражение
16. Определение неопределённого интеграла
Совокупность всех первообразных дляфункции f(х) , определённых на
некотором промежутке Х, называется
неопределённым интегралом от функции
f(х) на этом промежутке и обозначается
символом
∫f (х)dx=F(х)+С
Задание№1
1.
 3 Какое выражение называется
3 Какое выражение называетсянеопределённым интегралом?
А) F'(x)=f(x)
В)∫f(x)dx=F(x)+C
Б)∫F(x)dx=f(x)+C
Г) (f(x)dx)=f(x)dx
1.4 Какое выражение называется
подынтегральным ?
А) ∫
В)f(x)dx
Б)f(x)
Г)F(x)+C
19. А) dx Б) f'(x) В)∫ Г) S
1.5 Знак интеграла?А) dx
Б) f'(x)
В)∫
Г) S
20. Задание№2 2.1 Запишите в тетрадь свойства неопределённого интеграла
2.2 Примените свойстванеопределённого интеграла к данному
интегралу.
А)∫5·(2x+3) dx=
Б)∫(x³+sinx) dx=
В)∫(cosx–sinx) dx=
22. Задание№3 3.1 Вычислите интегралы, используя таблицу интегралов.
1. ∫x dх=2. ∫x dx=
3. ∫3 dx=
4. ∫7 dх=
5. ∫sinx dx=
6.∫cosx dx=
23. 3.2 Вычислите интегралы, используя таблицу основных интегралов и свойства неопределённого интеграла.
24. Я.Каменский
Считайнесчастным тот день или
тот час, в который ты не усвоил
ничего нового и ничего не
прибавил к своему образованию.

Будь мужчиной в учении, юноша!
Твоё достоинство-учиться в полную
меру своих сил. Достоинство
мужчины не быть паразитом,
нахлебником.Презирай лень мысли!
В.А. Сухомлинский.
{n−2}и\,ду\)
34. \(\quad \displaystyle ∫\sin au\sin bu\,du=\frac{\sin (a−b)u}{2(a−b)}−\frac{\sin (a+b) )u}{2(a+b)}+C\)
35. \(\quad \displaystyle ∫\cos au\cos bu\,du=\frac{\sin (a−b)u}{2(a−b)}+\frac{\sin (a+b) )u}{2(a+b)}+C\)
36. \(\quad \displaystyle ∫\sin au\cos bu\,du=-\frac{\cos (a-b)u}{2(a-b)}-\frac{\cos (a+ б)и}{2(а+б)}+С\)
37. \(\quad \displaystyle ∫u\sin u\,du=\sin u−u\cos u+C\)
38. \(\quad \displaystyle ∫u\cos u\,du=\cos u+u\sin u+C\)
39.m u\,du=\) Используйте методы для степеней синуса и косинуса
Таблица интегралов — Исчисление Том 2
Основные интегралы
1. ∫undu=un+1n+1+C,n≠−1∫undu=un+1n+1+C,n≠−1
2. ∫duu=ln|u|+C∫duu=ln|u|+C
3. ∫eudu=eu+C∫eudu=eu+C
4. ∫audu=аулна+C∫audu=аулна+C
∫audu=аулна+C∫audu=аулна+C
5. ∫sinudu=-cosu+C∫sinudu=-cosu+C
6. ∫cosudu=сину+C∫cosudu=сину+C
7. ∫sec2udu=тану+C∫sec2udu=тану+C
8. ∫csc2udu=-cotu+C∫csc2udu=-cotu+C
9.∫secutanudu=secu+C∫secutanudu=secu+C
10. ∫cscucotudu=-cscu+C∫cscucotudu=-cscu+C
11. ∫tanudu=ln|secu|+C∫tanudu=ln|secu|+C
12. ∫котуду=ln|сину|+C∫котуду=ln|сину|+C
13. ∫secudu=ln|secu+tanu|+C∫secudu=ln|secu+tanu|+C
14. ∫cscudu=ln|cscu-cotu|+C∫cscudu=ln|cscu-cotu|+C
15. ∫dua2−u2=sin−1ua+C∫dua2−u2=sin−1ua+C
16. ∫dua2+u2=1atan−1ua+C∫dua2+u2=1atan−1ua+C
17. ∫duuu2−a2=1asec−1ua+C∫duuu2−a2=1asec−1ua+C
Тригонометрические интегралы
18.∫sin2udu=12u−14sin2u+C∫sin2udu=12u−14sin2u+C
19. ∫cos2udu=12u+14sin2u+C∫cos2udu=12u+14sin2u+C
20. ∫tan2udu=tanu-u+C∫tan2udu=tanu-u+C
21. ∫cot2udu=-cotu-u+C∫cot2udu=-cotu-u+C
22. ∫sin3udu=−13(2+sin2u)cosu+C∫sin3udu=−13(2+sin2u)cosu+C
23. ∫cos3udu=13(2+cos2u)sinu+C∫cos3udu=13(2+cos2u)sinu+C
∫cos3udu=13(2+cos2u)sinu+C∫cos3udu=13(2+cos2u)sinu+C
24. ∫tan3udu=12tan2u+ln|cosu|+C∫tan3udu=12tan2u+ln|cosu|+C
25. ∫cot3udu=-12cot2u-ln|sinu|+C∫cot3udu=-12cot2u-ln|sinu|+C
26.∫sec3udu=12секутану+12ln|секу+тану|+C∫sec3udu=12секутану+12ln|секу+тану|+C
27. ∫csc3udu=-12cscucotu+12ln|cscu-cotu|+C∫csc3udu=-12cscucotu+12ln|cscu-cotu|+C
28. ∫sinnudu=−1nsinn−1ucosu+n−1n∫sinn−2udu∫sinnudu=−1nsinn−1ucosu+n−1n∫sinn−2udu
29. ∫cosnudu=1ncosn−1usinu+n−1n∫cosn−2udu∫cosnudu=1ncosn−1usinu+n−1n∫cosn−2udu
30. ∫tannudu=1n−1tann−1u−∫tann−2udu∫tannudu=1n−1tann−1u−∫tann−2udu
31. ∫cotnudu=-1n-1cotn-1u-∫cotn-2udu∫cotnudu=-1n-1cotn-1u-∫cotn-2udu
32.∫secnudu=1n−1tanusecn−2u+n−2n−1∫secn−2udu∫secnudu=1n−1tanusecn−2u+n−2n−1∫secn−2udu
33. ∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu∫cscnudu=−1n−1cotucscn−2u+n−2n−1∫cscn−2udu
34. ∫sinausinbudu=sin(a−b)u2(a−b)−sin(a+b)u2(a+b)+C∫sinausinbudu=sin(a−b)u2(a−b)−sin (а+б)и2(а+б)+С
35. ∫cosaucosbudu=sin(a−b)u2(a−b)+sin(a+b)u2(a+b)+C∫cosaucosbudu=sin(a−b)u2(a−b)+sin (а+б)и2(а+б)+С
∫cosaucosbudu=sin(a−b)u2(a−b)+sin(a+b)u2(a+b)+C∫cosaucosbudu=sin(a−b)u2(a−b)+sin (а+б)и2(а+б)+С
36. ∫sinaucosbudu=−cos(a−b)u2(a−b)−cos(a+b)u2(a+b)+C∫sinaucosbudu=−cos(a−b)u2(a−b) −cos(a+b)u2(a+b)+C
37.∫usinudu=сину-укосу+C∫usinudu=сину-укосу+C
38. ∫ucosudu=cosu+usinu+C∫ucosudu=cosu+usinu+C
39. ∫unsinudu=-uncosu+n∫un-1cosudu∫unsinudu=-uncosu+n∫un-1cosudu
40. ∫ункосуду=унсину-н∫ун-1синуду∫ункосуду=унсину-н∫ун-1синуду
41. 1un+m+n−1n+m∫sinn−2ucosmudu=sinn+1ucosm−1un+m+m−1n+m∫sinnucosm−2udu
Экспоненциальные и логарифмические интегралы
42.∫ueaudu=1a2(au-1)eau+C∫ueaudu=1a2(au-1)eau+C
43. ∫uneaudu=1auneau-na∫un-1eaudu∫uneaudu=1auneau-na∫un-1eaudu
44. ∫eausinbudu=eaua2+b2(asinbu−bcosbu)+C∫eausinbudu=eaua2+b2(asinbu−bcosbu)+C
45. ∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C∫eaucosbudu=eaua2+b2(acosbu+bsinbu)+C
46. ∫lnudu=ulnu-u+C∫lnudu=ulnu-u+C
47. ∫unlnudu=un+1(n+1)2[(n+1)lnu−1]+C∫unlnudu=un+1(n+1)2[(n+1)lnu−1]+ С
48. ∫1ulnudu=ln|lnu|+C∫1ulnudu=ln|lnu|+C
∫1ulnudu=ln|lnu|+C∫1ulnudu=ln|lnu|+C
Гиперболические интегралы
49.∫sinhudu=coshu+C∫sinhudu=coshu+C
50. ∫coshudu=sinhu+C∫coshudu=sinhu+C
51. ∫tanhudu=lncoshu+C∫tanhudu=lncoshu+C
52. ∫cothudu=ln|sinhu|+C∫cothudu=ln|sinhu|+C
53. ∫sechudu=tan−1|sinhu|+C∫sechudu=tan−1|sinhu|+C
54. ∫cschudu=ln|tanh22u|+C∫cschudu=ln|tanh22u|+C
55. ∫sech3udu=tanhu+C∫sech3udu=tanhu+C
56. ∫csch3udu=−cothu+C∫csch3udu=−cothu+C
57. ∫sechutanhudu=−sechu+C∫sechutanhudu=−sechu+C
58.∫cschucothudu=-cschu+C∫cschucothudu=-cschu+C
Обратные тригонометрические интегралы
59. ∫sin-1udu=usin-1u+1-u2+C∫sin-1udu=usin-1u+1-u2+C
60. ∫cos-1udu=ucos-1u-1-u2+C∫cos-1udu=ucos-1u-1-u2+C
61. ∫tan−1udu=utan−1u−12ln(1+u2)+C∫tan−1udu=utan−1u−12ln(1+u2)+C
62. ∫usin-1udu=2u2-14sin-1u+u1-u24+C∫usin-1udu=2u2-14sin-1u+u1-u24+C
63. ∫ucos-1udu=2u2-14cos-1u-u1-u24+C∫ucos-1udu=2u2-14cos-1u-u1-u24+C
64. ∫utan−1udu=u2+12tan−1u−u2+C∫utan−1udu=u2+12tan−1u−u2+C
∫utan−1udu=u2+12tan−1u−u2+C∫utan−1udu=u2+12tan−1u−u2+C
65.∫unsin−1udu=1n+1[un+1sin−1u−∫un+1du1−u2],n≠−1∫unsin−1udu=1n+1[un+1sin−1u−∫un+1du1−u2], n≠−1
66. ∫uncos−1udu=1n+1[un+1cos−1u+∫un+1du1−u2],n≠−1∫uncos−1udu=1n+1[un+1cos−1u+∫un+1du1−u2] ,n≠−1
67. ∫untan−1udu=1n+1[un+1tan−1u−∫un+1du1+u2],n≠−1∫untan−1udu=1n+1[un+1tan−1u−∫un+1du1+ u2],n≠−1
Интегралы с участием
a 2 + u 2 , a > 068. ∫a2+u2du=u2a2+u2+a22ln(u+a2+u2)+C∫a2+u2du=u2a2+u2+a22ln(u+a2+u2)+C
69.∫u2a2+u2du=u8(a2+2u2)a2+u2−a48ln(u+a2+u2)+C∫u2a2+u2du=u8(a2+2u2)a2+u2−a48ln(u+a2+u2)+C
70. ∫a2+u2udu=a2+u2−aln|a+a2+u2u|+C∫a2+u2udu=a2+u2−aln|a+a2+u2u|+C
71. ∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C∫a2+u2u2du=−a2+u2u+ln(u+a2+u2)+C
72. ∫dua2+u2=ln(u+a2+u2)+C∫dua2+u2=ln(u+a2+u2)+C
73. ∫u2dua2+u2=u2(a2+u2)−a22ln(u+a2+u2)+C∫u2dua2+u2=u2(a2+u2)−a22ln(u+a2+u2)+C
74. ∫duua2+u2=−1aln|a2+u2+au|+C∫duua2+u2=−1aln|a2+u2+au|+C
∫duua2+u2=−1aln|a2+u2+au|+C∫duua2+u2=−1aln|a2+u2+au|+C
75. ∫duu2a2+u2=−a2+u2a2u+C∫duu2a2+u2=−a2+u2a2u+C
76.∫du(a2+u2)3/2=ua2a2+u2+C∫du(a2+u2)3/2=ua2a2+u2+C
Интегралы с участием
u 2 − a 2 , a > 077. ∫u2−a2du=u2u2−a2−a22ln|u+u2−a2|+C∫u2−a2du=u2u2−a2−a22ln|u+u2−a2|+C
78. ∫u2u2−a2du=u8(2u2−a2)u2−a2−a48ln|u+u2−a2|+C∫u2u2−a2du=u8(2u2−a2)u2−a2−a48ln|u+u2−a2 |+С
79. ∫u2-a2udu=u2-a2-acos-1a|u|+C∫u2-a2udu=u2-a2-acos-1a|u|+C
80. ∫u2−a2u2du=−u2−a2u+ln|u+u2−a2|+C∫u2−a2u2du=−u2−a2u+ln|u+u2−a2|+C
81.∫duu2−a2=ln|u+u2−a2|+C∫duu2−a2=ln|u+u2−a2|+C
82. ∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C∫u2duu2−a2=u2u2−a2+a22ln|u+u2−a2|+C
83. ∫duu2u2−a2=u2−a2a2u+C∫duu2u2−a2=u2−a2a2u+C
84. ∫du(u2−a2)3/2=−ua2u2−a2+C∫du(u2−a2)3/2=−ua2u2−a2+C
Интегралы с участием
a 2 − u 2 , a > 0 85. ∫a2−u2du=u2a2−u2+a22sin−1ua+C∫a2−u2du=u2a2−u2+a22sin−1ua+C
∫a2−u2du=u2a2−u2+a22sin−1ua+C∫a2−u2du=u2a2−u2+a22sin−1ua+C
86. ∫u2a2−u2du=u8(2u2−a2)a2−u2+a48sin−1ua+C∫u2a2−u2du=u8(2u2−a2)a2−u2+a48sin−1ua+C
87.∫a2−u2udu=a2−u2−aln|a+a2−u2u|+C∫a2−u2udu=a2−u2−aln|a+a2−u2u|+C
88. ∫a2−u2u2du=−1ua2−u2−sin−1ua+C∫a2−u2u2du=−1ua2−u2−sin−1ua+C
89. ∫u2dua2−u2=−u2a2−u2+a22sin−1ua+C∫u2dua2−u2=−u2a2−u2+a22sin−1ua+C
90. ∫duua2−u2=−1aln|a+a2−u2u|+C∫duua2−u2=−1aln|a+a2−u2u|+C
91. ∫duu2a2−u2=−1a2ua2−u2+C∫duu2a2−u2=−1a2ua2−u2+C
92. ∫(a2−u2)3/2du=−u8(2u2−5a2)a2−u2+3a48sin−1ua+C∫(a2−u2)3/2du=−u8(2u2−5a2)a2−u2+ 3a48sin−1ua+C
93. ∫du(a2−u2)3/2=ua2a2−u2+C∫du(a2−u2)3/2=ua2a2−u2+C
Интегралы с участием 2
au − u 2 , a > 094.∫2au-u2du=u-a22au-u2+a22cos-1(a-ua)+C∫2au-u2du=u-a22au-u2+a22cos-1(a-ua)+C
95. ∫du2au-u2=cos-1(a-ua)+C∫du2au-u2=cos-1(a-ua)+C
96. ∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C
∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C∫u2au-u2du=2u2-au-3a262au-u2+a32cos-1(a-ua)+C
97. ∫duu2au-u2=-2au-u2au+C∫duu2au-u2=-2au-u2au+C
Интегралы с участием
a + bu , a ≠ 098. ∫udua+bu=1b2(a+bu-aln|a+bu|)+C∫udua+bu=1b2(a+bu-aln|a+bu|)+C
99. ∫u2dua+bu=12b3[(a+bu)2−4a(a+bu)+2a2ln|a+bu|]+C∫u2dua+bu=12b3[(a+bu)2−4a(a +bu)+2a2ln|a+bu|]+C
100.∫duu(a+bu)=1aln|ua+bu|+C∫duu(a+bu)=1aln|ua+bu|+C
101. ∫duu2(a+bu)=−1au+ba2ln|a+buu|+C∫duu2(a+bu)=−1au+ba2ln|a+buu|+C
102. ∫udu(a+bu)2=ab2(a+bu)+1b2ln|a+bu|+C∫udu(a+bu)2=ab2(a+bu)+1b2ln|a+bu|+ С
103. ∫uduu(a+bu)2=1a(a+bu)−1a2ln|a+buu|+C∫uduu(a+bu)2=1a(a+bu)−1a2ln|a+buu|+ С
104. ∫u2du(a+bu)2=1b3(a+bu−a2a+bu−2aln|a+bu|)+C∫u2du(a+bu)2=1b3(a+bu−a2a+bu− 2aln|a+bu|)+C
105. ∫ua+budu=215b2(3bu−2a)(a+bu)3/2+C∫ua+budu=215b2(3bu−2a)(a+bu)3/2+C
106. ∫udua+bu=23b2(bu−2a)a+bu+C∫udua+bu=23b2(bu−2a)a+bu+C
∫udua+bu=23b2(bu−2a)a+bu+C∫udua+bu=23b2(bu−2a)a+bu+C
107. ∫u2dua+bu=215b3(8a2+3b2u2−4abu)a+bu+C∫u2dua+bu=215b3(8a2+3b2u2−4abu)a+bu+C
108. ∫duua+bu=1aln|a+bu−aa+bu+a|+C,ifa>0=2−atan−1a+bu−a+C,ifa<0∫duua+bu=1aln|a +bu-aa+bu+a|+C,ifa>0=2-atan-1a+bu-a+C,ifa<0
109. ∫a+buudu=2a+bu+a∫duua+bu∫a+buudu=2a+bu+a∫duua+bu
110. ∫a+buu2du=−a+buu+b2∫duua+bu∫a+buu2du=−a+buu+b2∫duua+bu
111. ∫una+budu=2b(2n+3)[un(a+bu)3/2−na∫un−1a+budu]∫una+budu=2b(2n+3)[un(a+bu) )3/2-на∫ун-1а+буду]
112.∫undua+bu=2una+bub(2n+1)−2nab(2n+1)∫un−1dua+bu∫undua+bu=2una+bub(2n+1)−2nab(2n+1)∫un−1dua +бу
113. ∫duuna+bu=−a+bua(n−1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu∫duuna+bu=−a+bua(n −1)un−1−b(2n−3)2a(n−1)∫duun−1a+bu
Интегралы тригонометрических функций — веб-формулы
| Функция | Интеграл | ||
| sin x | — cos x + c | ||
| cos x | sin x + c | ||
| sin 2 x | x /2 — x ∙ x x x x x x x x x ∙ x 2 х | x /2 + x x X x х = сек 2 х | — пр.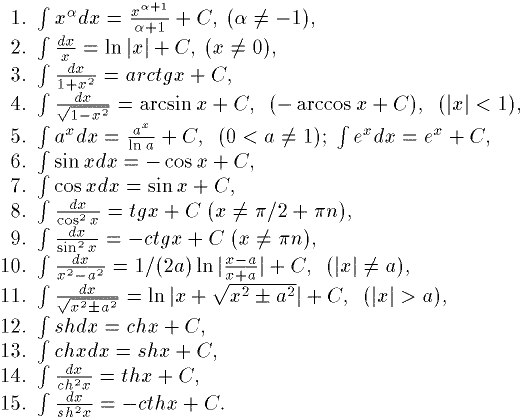 | потому что х | + c | потому что х | + c |
| кроватка x = — csc 2 x | п | грех x | + c | ||
| сек x | п | сек x + загар x | + c | ||
| csc x | -лн | csc x + детская кроватка x | + с | ||
| сек 2 x | желтовато-коричневый x + c | ||
| csc 2 x | — COT x + C |
Пример 1: Рассчитайте следующий интеграл ∫x 2 SIN x 3 DX .
Решение :
∫x 2 sin x 3 dx = ∫ sin x 3 x 2 dx
Положим u = x 3 и du = 3x 2 dx или du/3 = x 2 dx , тогда имеем:
∫x 2 sin x 3 dx
= ∫ sin u du/3
= 1/3 * ∫ sin u du
= 1/3 *(- cos и) + С
= 1/3 *(- cos x 3 ) + C
Пример 2: Вычислить
Решение :
Пусть u = ln t . Итак, du = (1/ t ) dt .
Итак, du = (1/ t ) dt .
Тогда мы имеем:
Пример 3: Вычислить ∫(3 sin x 4 сек 2 x) dx
Решение :
∫(3 sin x 4 сек 2 x) dx
= 3∫ sin xdx — 4∫ сек 2 x dx
= -3 cos x – 4 тангенс x + C
Пример 4: Интегрировать ∫(2+ tan x) 2 dx
Решение :
Таблица интегралов
| 1. |
| ||||
| 2. |
| ||||
3. |
| ||||
| 4. |
| ||||
| 5. |
| ||||
| 6. |
| ||||
| 7. |
| ||||
| 8. |
| ||||
| 9. |
| ||||
10. |
| ||||
| 11. |
| ||||
| 12. |
| ||||
| 13. |
| ||||
| 14. |
| ||||
| 15. |
| ||||
| 16. |
| ||||
17. |
| ||||
| 18. |
| ||||
| 19. |
| ||||
| 20. |
| ||||
| 21. |
| ||||
| 22. |
| ||||
| 23. |
| ||||
24. |
| ||||
| 25. |
| ||||
| 26. |
| ||||
| 27. |
| ||||
| 28. |
| ||||
| 29. |
| ||||
30. |
| ||||
| 31. |
|
Формула интегрирования — Примеры | Список формул интегрирования
Формулы интегрирования могут применяться для интегрирования алгебраических выражений, тригонометрических соотношений, обратных тригонометрических функций, логарифмических и экспоненциальных функций.Интегрирование функций приводит к исходным функциям, для которых были получены производные. Эти формулы интегрирования используются для нахождения первообразной функции. Если продифференцировать функцию f на интервале I, то мы получим семейство функций из I. Если известны значения функций в I, то можно определить функцию f. Этот обратный процесс дифференциации называется интеграцией. Давайте двигаться дальше и узнать о формулах интегрирования, используемых в методах интегрирования.
Давайте двигаться дальше и узнать о формулах интегрирования, используемых в методах интегрирования.
Что такое формулы интегрирования?
Формулы интегрирования в общих чертах представлены в виде следующих шести наборов формул. По сути, интеграция — это способ объединения частей для получения целого. Формулы включают базовые формулы интегрирования, интегрирование тригонометрических отношений, обратные тригонометрические функции, произведение функций и некоторые расширенные наборы формул интегрирования. Интегрирование есть операция, обратная дифференцированию. Таким образом, основной формулой интегрирования является \(\int\) f'(x).дх = f(х) + С
Основные формулы интегрирования
Используя основные теоремы об интегралах, получены обобщенные результаты, которые запоминаются как формулы интегрирования при неопределенном интегрировании.
- ∫ x n .dx = x (n + 1) / (n + 1)+ C
- ∫ 1.dx = х + С
- ∫ e x .
 dx = e x + C
dx = e x + C - ∫1/x.dx = log|x| + С
- ∫ a x .dx = a x /loga+ C
- ∫ e x [f(x) + f'(x)].dx = e x .f(x) + C
Формулы интегрирования тригонометрических функций
Процесс нахождения интеграла — интегрирование. Вот несколько важных формул интегрирования, которые запомнятся для мгновенных и быстрых вычислений. Когда дело доходит до тригонометрических функций, мы упрощаем их и переписываем как интегрируемые функции. Вот список тригонометрических и обратных тригонометрических функций.
- ∫ cosx.dx = sinx + C
- ∫ синх.дх = -cosx + C
- ∫ сек 2 x.dx = tanx + C
- ∫ cosec 2 x.dx = -cotx + C
- ∫ secx.tanx.dx = secx + C
- ∫ cosecx.cotx.dx = -cosecx + C
- ∫ tanx.dx =log|secx| + С
- ∫ cotx.dx = log|sinx| + С
- ∫ secx.dx = log|secx + tanx| + С
- ∫ cosecx.
 dx = log|cosecx — cotx| + С
dx = log|cosecx — cotx| + С
Формулы интегрирования обратных тригонометрических функций:
- ∫1/√(1 — х 2 ).дх = грех -1 х + С
- ∫ /1(1 — x 2 ).dx = -cos -1 x + C
- ∫1/(1 + x 2 ).dx = тангенс -1 x + C
- ∫ 1/(1 +x 2 ).dx = -cot -1 x + C
- ∫ 1/x√(x 2 — 1).dx = сек -1 x + C
- ∫ 1/x√(x 2 — 1).dx = -cosec -1 x + C
Формулы расширенного интегрирования
- ∫1/(х 2 — а 2 ).dx = 1/2a.log|(x — a)(x + a| + C
- ∫ 1/(a 2 — x 2 ).dx = 1/2a.log|(a + x)(a — x)| + С
- ∫1/(x 2 + a 2 ).dx = 1/a.tan -1 x/a + C
- ∫1/√(x 2 — a 2 )dx = log|x + √(x 2 — a 2 )| + С
- ∫ √(x 2 — a 2 ).
 dx =1/2.x.√(x 2 — a 2 )-a 2 /2 log|x + √(1x 9020 2 — а 2 )| + С
dx =1/2.x.√(x 2 — a 2 )-a 2 /2 log|x + √(1x 9020 2 — а 2 )| + С - ∫1/√(a 2 — x 2 ).dx = sin -1 x/a + C
- ∫√(a 2 — x 2 ).dx = 1/2.x.√(a 2 — x 2 ).dx + a 2 /2.sin-1 x/ а + С
- ∫1/√(x 2 + a 2 ).dx = log|x + √(x 2 + a 2 )| + С
- ∫ √(x 2 + a 2 ).dx =1/2.x.√(x 2 + a 2 )+ a 2 /2 . log|x + √(x 2 + a 2 )| + С
Различные формулы интегрирования
Существует 3 типа методов интегрирования, и каждый метод применяется со своими собственными уникальными методами, связанными с нахождением интегралов.Это стандартизированные результаты. Их можно запомнить как формулы интегрирования.
Формула интегрирования по частям:
Когда данная функция является произведением двух функций, мы применяем это интегрирование по формуле частей или частичное интегрирование и вычисляем интеграл. Формула интегрирования при использовании частичного интегрирования задается как:
Формула интегрирования при использовании частичного интегрирования задается как:
∫ f(x).g(x) = f(x).∫g(x).dx -∫(∫g(x).dx.f'(x)).dx + c
Например: ∫ xe x dx имеет вид ∫ f(x).г(х). Таким образом, мы применяем соответствующую формулу интегрирования и вычисляем интеграл.
f(x) = x и g(x) = e x
Таким образом, ∫ xe x dx = x∫e x .dx — ∫( ∫e x .dx. x). дх+ с
= xe x — e x + c
Интегрирование по формуле подстановки:
Когда функция является функцией другой функции, мы применяем формулу интегрирования для подстановки.Если I = ∫ f(x) dx, где x = g(t), так что dx/dt = g'(t), то мы пишем dx = g'(t)
Мы можем написать I = ∫ f(x) dx = ∫ f(g(t)) g'(t) dt
Например: Рассмотрим ∫ (3x +2) 4 dx
Здесь мы можем использовать формулу интегрирования подстановки. Пусть и = (3х+2). ⇒ du = 3. dx
⇒ du = 3. dx
Таким образом, ∫ (3x +2) 4 dx = 1/3. ∫(и) 4 . дю
= 1/3. и 5 / 5 = и 5 /15
= (3x+2) 5 /15
Интегрирование по формуле неполных дробей:
Если нам нужно найти интеграл от P(x)/Q(x), являющийся неправильной дробью, где степень P(x) < степени Q(x), то мы используем интегрирование неполными дробями.Мы разделяем дробь, используя разложение частичной дроби, как P (x) / Q (x) = T (x) + P \ (_1 \) (x) / Q (x), где T (x) - полином от x и P\(_1\) (x)/ Q(x) — правильная рациональная функция. Если A B и C — действительные числа, то у нас есть следующие типы более простых дробей, которые связаны с различными типами рациональных функций.
| Форма рациональных дробей | Форма дробей |
|---|---|
| (px + q)/(x-a)(x — b) | А/(х — а) + В/ (х-б) |
| (px + q)/(x-a) n | А 1 /(х-а) + А 2 /(х-а) 2 + . ……… А н /(х-а) н ……… А н /(х-а) н |
| (px 2 + qx + r)/(ax 2 + bx + c) | (Ax + B)/(ax 2 + bx + c) |
| (px 2 + qx + r)/(ax 2 + bx + c) n | (А 1 х + В 1 )/(ах 2 + Ьх + с) + (А 2 х + В 2 )/(ах 2 + Ьх0 + с) 2 2 + …(A n x + B n )/(ax 2 + bx + c) n |
| (px 2 + qx + r)/(x-a)(x-b)(x-c) | А/(х — а) + В/ (х-б) + С/ (х-с) |
| (px 2 + qx + r)/(x 2 +bx +c) | А/(х-а) +(Вх+С)/(х 2 +bх +с) |
Например: ∫ 3x+7/ x 2 -3x + 2
Разложив его на неполные дроби, получим
3x+7/x 2 -3x + 2 = A/(x-2) + B/(x-1)
= А(х-1) + В(х-2)/(х-2)(х-1)
Приравнивая числители, получаем 3x +7 = A(x-1)+B(x-2)
Найдите B, задав x = 1⇒ 10 = B
Найдите A, дав x = 2⇒ 13 = A
Таким образом, 3x+7/x 2 -3x + 2 = 13/(x-2) + 10(x-1)
Применяя формулы интегрирования, получаем
∫ (3x+7/x 2 -3x + 2) = ∫ 13/(x-2) + ∫ 10(x-1)
∫ (3x+7/x 2 -3x + 2) = 13 log |x-2| — 10 log |x-1| + С
Применение формул интегрирования
Вообще есть два типа интегралов. b g(x) dx\) = G(b) — G(a)
b g(x) dx\) = G(b) — G(a)
Неопределенная формула интегрирования
Это интеграции, которые не имеют ранее существовавшего значения лимитов; тем самым делая окончательное значение интеграла неопределенным. Здесь C — постоянная интегрирования. ∫ г'(х) = г(х) + С
Мы применяем формулы интегрирования, обсуждавшиеся до сих пор, для аппроксимации площади, ограниченной кривыми, для оценки среднего расстояния, задач, ориентированных на скорость и ускорение, для нахождения среднего значения функции, для аппроксимации объема и площади поверхности твердых тел, в нахождении центра масс и работы, в оценке длины дуги, в нахождении кинетической энергии движущегося тела с помощью несобственных интегралов.3\) 5т
= -t 3 /3 + 5t 2 /2
= [(-27/3-1/3)+(45/2 — 5/2)]
= -28/3 +40/3 =12/3
Водоизмещение =4
Расстояние между двумя точками равно абсолютному значению их смещения. Общее расстояние, пройденное между позициями 1 и 3 и в обратном направлении, равно 4 + 4 = 8
.
Таким образом, перемещение объекта равно 4, а расстояние, пройденное объектом, равно 4 + 4 = 8
Давайте посмотрим, как использовать формулы неопределенного интегрирования в следующих решенных примерах.
Часто задаваемые вопросы о формулах интегрирования
Для чего используются формулы интегрирования или интегральный УФ?
Интегральный UV используется для интегрирования произведения двух функций. Формула интегрирования по этому правилу: ∫u v dx = u∫v dx −∫u’ (∫v dx) dx. u — функция u(x) v — функция v(x)
Как интегрировать с помощью формул интегрирования?
Мы можем использовать следующие шаги для интеграции:
- Сначала определите небольшую часть объекта в определенных размерах, которые при многократном добавлении составляют весь объект.
- Используйте формулы интегрирования для этой небольшой детали по различным измерениям.
Для чего нужны формулы интегрирования?
Интеграция используется для нахождения площади любых объектов. Примеры из реальной жизни — найти центр масс объекта, центр тяжести и момент инерции массы для внедорожника. Он также используется для расчета скорости и траектории объекта, прогнозирования выравнивания планет и в электромагнетизме.Используйте формулы интегрирования во всех этих случаях.
Примеры из реальной жизни — найти центр масс объекта, центр тяжести и момент инерции массы для внедорожника. Он также используется для расчета скорости и траектории объекта, прогнозирования выравнивания планет и в электромагнетизме.Используйте формулы интегрирования во всех этих случаях.
Какие методы интеграции включают формулы интеграции?
Замена, интегрирование по частям, правило обратной цепочки и разложение частичной дроби — вот несколько методов интегрирования.
Что такое формула интегрирования интегрального УФ?
Формула интегрального UV используется для интегрирования произведения двух функций. Формула интегрирования УФ-формы имеет вид \(\int\) u.v.du = u.dv-\(\int\) v.du.
Какие формулы интегрирования для тригонометрических функций?
Тригонометрические функции упрощаются до интегрируемых функций, а затем вычисляются их интегралы. Основные формулы интегрирования тригонометрических функций следующие.
- ∫ cosx.
 dx = sinx + C
dx = sinx + C - ∫ sinx.dx = -cosx + C
- ∫ сек 2 x.dx = tanx + C
- ∫ cosec 2 x.dx = -cotx + C
- ∫ сек.tanx.dx = secx + C
- ∫ cosecx.cotx.dx = -cosecx + C
- ∫ tanx.dx =log|secx| + С
- ∫ cotx.dx = log|sinx| + С
- ∫ secx.dx = log|secx + tanx| + С
- ∫ cosecx.dx = log|cosecx — cotx| + С
Как применить формулы интегрирования для поиска интегрируемого LN?
∫ ln(x) dx имеет UV-форму. Примените формулу интегрирования по правилу частей, используя следующие шаги, чтобы интегрировать LN.
1) Определить uv: Возьмем u= ln(x) и dv = 1.dx ⇒ du = 1/x и v = x
2) Применить формулу: ∫ uv dx = uv -∫ vdu
= х. ln(x) — ∫ x. 1/х
= х пер(х) — х + С
3) Упростите и оцените интеграл.
Как использовать формулы интегрирования?
Мы можем использовать следующие шаги для интеграции:
1) Сначала определите небольшую часть объекта в определенных размерах, которые при многократном добавлении составляют весь объект. {{{n}+{1}}}}}{{{n}+{1}}}+{C}{\quad\text{if}\quad}{n}\ne- {1}\\{\ln}{\left|{x}\right|}+{C}{\quad\text{if}\quad}{n}=-{1}\\ \end{массив} \правильно.{{2}}{\left({x}\right)}{d}{x}=-{\cot {{\left({x}\right)}}}+{C}$$$ $$$\int{\sec{{\left({x}\right)}}}{\tan{{\left({x}\right)}}}{d}{x}={\ sec{{\left({x}\right)}}}+{C}$$$ $$$\int{\csc{{\left({x}\right)}}}{\ детская кроватка {{\ влево ({x} \ вправо)}}} {d} {x} = — {\ csc {{\ влево ({x} \ вправо)}}} + {C} $ $ $ $$$\int{\tan{{\left({x}\right)}}}{d}{x}=-{\ln}{\left|{\cos{{\left({x}} \right)}}}\right|}+{C}={\ln}{\left|{\sec{{\left({x}\right)}}}\right|}+{C}$$ $ $$$\int{\cot{{\left({x}\right)}}}{d}{x}={\ln}{\left|{\sin{{\left( {x}\right)}}}\right|}+{C}$$$ $$$\int{\sec{{\left({x}\right)}}}{d}{ х} = {\ пер} {\ влево | {\ сек {{\ влево ({х} \ вправо)}}} + {\ загар {{\ влево ({х} \ вправо)}}} \ вправо |} +{C}$$$ $$$\int{\csc{{\left({x}\right)}}}{d}{x}={\ln}{\left|{\ csc {{\ влево ({x} \ вправо)}}} — {\ кроватка {{\ влево ({x} \ вправо)}}} \ вправо |} + {C} $ $ $ $ $ $\int\frac{{{d}{x}}}{\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}} ={\operatorname{arcsin}{{\left(\frac{{x}}{{a}}\right)}}}+{C}$$$ $$$\int\frac{{ {d}{x}}}{{{{a}}^{{2}}+{{x}}^{{2}}}}=\frac{{1}}{{a}}{\ operatorname {arctan} {{\ left (\ frac {{x}} {{a}} \ right)}}} + {C} $ $ $ $ $ $ \ int \ frac {{{d} {x}}}{{{x}\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}}}=\frac{{1}}{ {a}}\text{arcsec}{\left(\frac{{x}}{{a}}\right)}+{C}$$$ $$$\int\frac{{{ d}{x}}}{{{{a}}^{{2}}-{{x}}^{{2}}}}=\frac{{1}}{{{2}{a} }}{\ln}{\left|\frac{{{x}+{a}}}{{{x}-{a}}}\right|}+{C}$$$ $ $$\int\frac{{{d}{x}}}{{{{x}}^{{2}}-{{a}}^{{2}}}}=\frac{{1} }{{{2}{a}}}{\ln}{\left|\frac{{{x}-{a}}}{{{x}+{a}}}\right|}+{C }$$$ Экспоненциальные и логарифмические формы $$$\int{x}{{e}}^{{{a}{x}}}{d}{x}=\ frac{{1}}{{{{a}}^{{2}}}}{\left({a}{x}-{1}\right)}{{e}}^{{{a} {x}}}+{C}$$$ $$$\int{{x}}^{{n}}{{e}}^{{{a}{x}}}{d }{x}=\frac{{1}}{{a}}{{x}}^{{n}}{{e}}^{{{a}{ x}}}-\frac{{n}}{{a}}\int{{x}}^{{{n}-{1}}}{{e}}^{{{a}{x} }}{d}{x}$$$ $$$\int{{e}}^{{{a}{x}}}{\sin{{\left({b}{x} \right)}}}{d}{x}=\frac{{{{e}}^{{{a}{x}}}}}{{{{a}}^{{2}}+{ {b}}^{{2}}}}{\left({\operatorname{asin}{{\left({b}{x}\right)}}}-{b}{\cos{{\left ({b}{x}\right)}}}\right)}+{C}$$$ $$$\int{{e}}^{{{a}{x}}}{ \cos{{\left({b}{x}\right)}}}{d}{x}=\frac{{{{e}}^{{{a}{x}}}}}{{ {{a}}^{{2}}+{{b}}^{{2}}}}{\left({\operatorname{acos}{{\left({b}{x}\right)} }}+{b}{\sin{{\left({b}{x}\right)}}}\right)}+{C}$$$ $$$\int{\ln{ {\ влево ({х} \ вправо)}}} {д} {х} = {х} {\ влево ({\ пер {{\ влево ({х} \ вправо)}}} — {1} \ вправо )}+{C}$$$ $$$\int{{x}}^{{n}}{\ln{{\left({x}\right)}}}{d}{ x}=\frac{{{{x}}^{{{n}+{1}}}}}{{{{\left({n}+{1}\right)}}^{{2} }}}{\left({\left({n}+{1}\right)}{\ln{{\left({x}\right)}}}-{1}\right)}+{C }$$$ $$$\int\frac{{1}}{{{x}{\ln{{\left({x}\right)}}}}}{d}{x} = {\ пер {\ влево | {\ пер { {\ влево ({и} \ вправо)}}} \right|}+{C}$$$ Тригонометрические формы $$$\int{{\sin}}^{{2}}{\left({x}\right) }{d}{x}=\frac{{1}}{{2}}{x}-\frac{{1}}{{4}}{\sin{{\left({2}{x} \right)}}}+{C}$$$ $$$\int{{\cos}}^{{2}}{\left({x}\right)}{d}{x }=\frac{{1}}{{2}}{x}+\frac{{1}}{{4}}{\sin{{\left({2}{x}\right)}}} +{C}$$$ $$$\int{{\tan}}^{{2}}{\left({x}\right)}{d}{x}={\tan{ {\left({x}\right)}}}-{x}+{C}$$$ $$$\int{{\cot}}^{{2}}{\left({ x}\right)}{d}{x}=-{\cot {{\left({x}\right)}}}-{x}+{C}$$$ $$$\ int{{\sin}}^{{3}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{3}}{\left({2 }+{{\sin}}^{{2}}{\left({x}\right)}\right)}{\cos{{\left({x}\right)}}}+{C} $$$ $$$\int{{\cos}}^{{3}}{\left({x}\right)}{d}{x}=\frac{{1}}{ {3}}{\left({2}+{{\cos}}^{{2}}{\left({x}\right)}\right)}{\sin{{\left({x}) \right)}}}+{C}$$$ $$$\int{{\tan}}^{{3}}{\left({ x}\right)}{d}{x}=\frac{{1}}{{2}}{{\tan}}^{{2}}{\left({x}\right)}+{ \ln}{\left|{\cos{{\left({x}\right)}}}\right|}+{C}$$$ $$$\int{{\cot}} ^{{3}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{2}}{{\cot}}^{{2}}{ \left({x}\right)} — {\ln}{\left|{\sin{{\left({x}\right)}}}\right|}+{C}$$$ $$$\int{{\sec}}^{{3}}{\left({x}\right)}{d}{x}=\frac{{1}}{{2}}{\ сек {{\ влево ({х} \ вправо)}}} {\ загар {{\ влево ({х} \ вправо)}}} + \ гидроразрыва {{1}} {{2}} {\ ln} { \left|{\sec{{\left({x}\right)}}}+{\tan{{\left({x}\right)}}}\right|}+{C}$$$ $$$\int{{\csc}}^{{3}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{2} }{\csc{{\left({x}\right)}}}{\cot{{\left({x}\right)}}}+\frac{{1}}{{2}}{\ ln}{\left|{\csc{{\left({x}\right)}}} — {\cot{{\left({x}\right)}}}\right|}+{C}$ $$ $$$\int{{\sin}}^{{n}}{\left({x}\right)}{d}{x}=-\frac{{1}}{ {n}}{{\sin}}^{{{n}-{1}}}{\left({x}\right)}{\cos{{\left({x}\right)}}} +\frac{{{n}-{1}}}{{n}}\int{{\sin}}^{{{n}-{2}}}{\left({x}\right)} {д}{х}$$$ $$$\int{{\cos}}^{{n}}{\left({x}\right)}{d}{x}=\frac{{1}}{{n} }{{\cos}}^{{{n}-{1}}}{\left({x}\right)}{\sin{{\left({x}\right)}}}+\frac {{{n}-{1}}}{{n}}\int{{\cos}}^{{{n}-{2}}}{\left({x}\right)}{d} {x}$$$ $$$\int {{\tan}}^{{n}}{\left({x}\right)}{d}{x}=\frac{{1 }}{{{n}-{1}}}{{\tan}}^{{{n}-{1}}}{\left({x}\right)}-\int{{\tan} }^{{{n}-{2}}}{\left({x}\right)}{d}{x}$$$ $$$\int{{\cot}}^{ {n}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{{n}-{1}}}{{\cot}}^{{ {n}-{1}}}{\left({x}\right)}-\int{{\cot}}^{{{n}-{2}}}{\left({x}\right )}{d}{x}$$$ $$$\int{{\sec}}^{{n}}{\left({x}\right)}{d}{x}= \frac{{1}}{{{n}-{1}}}{\tan{{\left({x}\right)}}}{{\sec}}^{{{n}-{2 }}}{\left({x}\right)}+\frac{{{n}-{2}}}{{{n}-{1}}}\int{{\sec}}^{{ {n}-{2}}}{\left({x}\right)}{d}{x}$$$ $$$\int{{\csc}}^{{n}} {\ left ({x} \ right)} {d} {x} = — \ frac {{1}} {{{n} — {1}}} {\ cot {{\ left ({x} \ right) )}}}{{\csc}}^{{{n}-{2}}}{\left({x}\right)} +\frac{{{n}-{2}}}{{{n}-{1}}}\int{{\csc}}^{{{n}-{2}}}{\left({ x}\right)}{d}{x}$$$ $$$\int{\sin{{\left({a}{x}\right)}}}{\sin{{\ влево ({b} {x} \ right)}}} {d} {x} = \ frac {{{\ sin {{\ left ({\ left ({a} — {b} \ right)} {x }\right)}}}}}{{{2}{\left({a}-{b}\right)}}}-\frac{{{\sin{{\left({\left({a }+{b}\right)}{x}\right)}}}}}{{{2}{\left({a}+{b}\right)}}}+{C}$$$ $$$\int{\cos{{\left({a}{x}\right)}}}{\cos{{\left({b}{x}\right)}}}{d }{x}=\frac{{{\sin{{\left({\left({a}-{b}\right)}{x}\right)}}}}}{{{2}{\ влево ({а} — {b} \ вправо)}}} + \ гидроразрыва {{{\ грех {{\ влево ({\ влево ({а} + {b} \ вправо)} {х} \ вправо)} }}}}{{{2}{\left({a}+{b}\right)}}}+{C}$$$ $$$\int{\sin{{\left( {a}{x}\right)}}}{\cos{{\left({b}{x}\right)}}}{d}{x}=-\frac{{{\cos{{\ влево ({\ влево ({a} — {b} \ вправо)} {x} \ вправо)}}}}} {{{2} {\ влево ({a} — {b} \ вправо)}}} -\frac{{{\cos{{\left({\left({a}+{b}\right)}{x}\right)}}}}}{{{2}{\left({a }+{b}\right)}}}+{C}$$$ $$$\int{x}{\sin{{\left({x}\right)}}}{d} {х} = {\ грех {{\left({x}\right)}}}-{x}{\cos{{\left({x}\right)}}}+{C}$$$ $$$\ int{x}{\cos{{\left({x}\right)}}}{d}{x}={\cos{{\left({x}\right)}}}+{x}{ \sin{{\left({x}\right)}}}+{C}$$$ $$$\int{{x}}^{{n}}{\sin{{\left ({x}\right)}}}{d}{x}=-{{x}}^{{n}}{\cos{{\left({x}\right)}}}+{n} \int{{x}}^{{{n}-{1}}}{\cos{{\left({x}\right)}}}{d}{x}$$$ $ $$\int{{x}}^{{n}}{\cos{{\left({x}\right)}}}{d}{x}={{x}}^{{n}} {\sin{{\left({x}\right)}}}-{n}\int{{x}}^{{{n}-{1}}}{\sin{{\left({x} }\right)}}}{d}{x}$$$
{{{n}+{1}}}}}{{{n}+{1}}}+{C}{\quad\text{if}\quad}{n}\ne- {1}\\{\ln}{\left|{x}\right|}+{C}{\quad\text{if}\quad}{n}=-{1}\\ \end{массив} \правильно.{{2}}{\left({x}\right)}{d}{x}=-{\cot {{\left({x}\right)}}}+{C}$$$ $$$\int{\sec{{\left({x}\right)}}}{\tan{{\left({x}\right)}}}{d}{x}={\ sec{{\left({x}\right)}}}+{C}$$$ $$$\int{\csc{{\left({x}\right)}}}{\ детская кроватка {{\ влево ({x} \ вправо)}}} {d} {x} = — {\ csc {{\ влево ({x} \ вправо)}}} + {C} $ $ $ $$$\int{\tan{{\left({x}\right)}}}{d}{x}=-{\ln}{\left|{\cos{{\left({x}} \right)}}}\right|}+{C}={\ln}{\left|{\sec{{\left({x}\right)}}}\right|}+{C}$$ $ $$$\int{\cot{{\left({x}\right)}}}{d}{x}={\ln}{\left|{\sin{{\left( {x}\right)}}}\right|}+{C}$$$ $$$\int{\sec{{\left({x}\right)}}}{d}{ х} = {\ пер} {\ влево | {\ сек {{\ влево ({х} \ вправо)}}} + {\ загар {{\ влево ({х} \ вправо)}}} \ вправо |} +{C}$$$ $$$\int{\csc{{\left({x}\right)}}}{d}{x}={\ln}{\left|{\ csc {{\ влево ({x} \ вправо)}}} — {\ кроватка {{\ влево ({x} \ вправо)}}} \ вправо |} + {C} $ $ $ $ $ $\int\frac{{{d}{x}}}{\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}} ={\operatorname{arcsin}{{\left(\frac{{x}}{{a}}\right)}}}+{C}$$$ $$$\int\frac{{ {d}{x}}}{{{{a}}^{{2}}+{{x}}^{{2}}}}=\frac{{1}}{{a}}{\ operatorname {arctan} {{\ left (\ frac {{x}} {{a}} \ right)}}} + {C} $ $ $ $ $ $ \ int \ frac {{{d} {x}}}{{{x}\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}}}=\frac{{1}}{ {a}}\text{arcsec}{\left(\frac{{x}}{{a}}\right)}+{C}$$$ $$$\int\frac{{{ d}{x}}}{{{{a}}^{{2}}-{{x}}^{{2}}}}=\frac{{1}}{{{2}{a} }}{\ln}{\left|\frac{{{x}+{a}}}{{{x}-{a}}}\right|}+{C}$$$ $ $$\int\frac{{{d}{x}}}{{{{x}}^{{2}}-{{a}}^{{2}}}}=\frac{{1} }{{{2}{a}}}{\ln}{\left|\frac{{{x}-{a}}}{{{x}+{a}}}\right|}+{C }$$$ Экспоненциальные и логарифмические формы $$$\int{x}{{e}}^{{{a}{x}}}{d}{x}=\ frac{{1}}{{{{a}}^{{2}}}}{\left({a}{x}-{1}\right)}{{e}}^{{{a} {x}}}+{C}$$$ $$$\int{{x}}^{{n}}{{e}}^{{{a}{x}}}{d }{x}=\frac{{1}}{{a}}{{x}}^{{n}}{{e}}^{{{a}{ x}}}-\frac{{n}}{{a}}\int{{x}}^{{{n}-{1}}}{{e}}^{{{a}{x} }}{d}{x}$$$ $$$\int{{e}}^{{{a}{x}}}{\sin{{\left({b}{x} \right)}}}{d}{x}=\frac{{{{e}}^{{{a}{x}}}}}{{{{a}}^{{2}}+{ {b}}^{{2}}}}{\left({\operatorname{asin}{{\left({b}{x}\right)}}}-{b}{\cos{{\left ({b}{x}\right)}}}\right)}+{C}$$$ $$$\int{{e}}^{{{a}{x}}}{ \cos{{\left({b}{x}\right)}}}{d}{x}=\frac{{{{e}}^{{{a}{x}}}}}{{ {{a}}^{{2}}+{{b}}^{{2}}}}{\left({\operatorname{acos}{{\left({b}{x}\right)} }}+{b}{\sin{{\left({b}{x}\right)}}}\right)}+{C}$$$ $$$\int{\ln{ {\ влево ({х} \ вправо)}}} {д} {х} = {х} {\ влево ({\ пер {{\ влево ({х} \ вправо)}}} — {1} \ вправо )}+{C}$$$ $$$\int{{x}}^{{n}}{\ln{{\left({x}\right)}}}{d}{ x}=\frac{{{{x}}^{{{n}+{1}}}}}{{{{\left({n}+{1}\right)}}^{{2} }}}{\left({\left({n}+{1}\right)}{\ln{{\left({x}\right)}}}-{1}\right)}+{C }$$$ $$$\int\frac{{1}}{{{x}{\ln{{\left({x}\right)}}}}}{d}{x} = {\ пер {\ влево | {\ пер { {\ влево ({и} \ вправо)}}} \right|}+{C}$$$ Тригонометрические формы $$$\int{{\sin}}^{{2}}{\left({x}\right) }{d}{x}=\frac{{1}}{{2}}{x}-\frac{{1}}{{4}}{\sin{{\left({2}{x} \right)}}}+{C}$$$ $$$\int{{\cos}}^{{2}}{\left({x}\right)}{d}{x }=\frac{{1}}{{2}}{x}+\frac{{1}}{{4}}{\sin{{\left({2}{x}\right)}}} +{C}$$$ $$$\int{{\tan}}^{{2}}{\left({x}\right)}{d}{x}={\tan{ {\left({x}\right)}}}-{x}+{C}$$$ $$$\int{{\cot}}^{{2}}{\left({ x}\right)}{d}{x}=-{\cot {{\left({x}\right)}}}-{x}+{C}$$$ $$$\ int{{\sin}}^{{3}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{3}}{\left({2 }+{{\sin}}^{{2}}{\left({x}\right)}\right)}{\cos{{\left({x}\right)}}}+{C} $$$ $$$\int{{\cos}}^{{3}}{\left({x}\right)}{d}{x}=\frac{{1}}{ {3}}{\left({2}+{{\cos}}^{{2}}{\left({x}\right)}\right)}{\sin{{\left({x}) \right)}}}+{C}$$$ $$$\int{{\tan}}^{{3}}{\left({ x}\right)}{d}{x}=\frac{{1}}{{2}}{{\tan}}^{{2}}{\left({x}\right)}+{ \ln}{\left|{\cos{{\left({x}\right)}}}\right|}+{C}$$$ $$$\int{{\cot}} ^{{3}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{2}}{{\cot}}^{{2}}{ \left({x}\right)} — {\ln}{\left|{\sin{{\left({x}\right)}}}\right|}+{C}$$$ $$$\int{{\sec}}^{{3}}{\left({x}\right)}{d}{x}=\frac{{1}}{{2}}{\ сек {{\ влево ({х} \ вправо)}}} {\ загар {{\ влево ({х} \ вправо)}}} + \ гидроразрыва {{1}} {{2}} {\ ln} { \left|{\sec{{\left({x}\right)}}}+{\tan{{\left({x}\right)}}}\right|}+{C}$$$ $$$\int{{\csc}}^{{3}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{2} }{\csc{{\left({x}\right)}}}{\cot{{\left({x}\right)}}}+\frac{{1}}{{2}}{\ ln}{\left|{\csc{{\left({x}\right)}}} — {\cot{{\left({x}\right)}}}\right|}+{C}$ $$ $$$\int{{\sin}}^{{n}}{\left({x}\right)}{d}{x}=-\frac{{1}}{ {n}}{{\sin}}^{{{n}-{1}}}{\left({x}\right)}{\cos{{\left({x}\right)}}} +\frac{{{n}-{1}}}{{n}}\int{{\sin}}^{{{n}-{2}}}{\left({x}\right)} {д}{х}$$$ $$$\int{{\cos}}^{{n}}{\left({x}\right)}{d}{x}=\frac{{1}}{{n} }{{\cos}}^{{{n}-{1}}}{\left({x}\right)}{\sin{{\left({x}\right)}}}+\frac {{{n}-{1}}}{{n}}\int{{\cos}}^{{{n}-{2}}}{\left({x}\right)}{d} {x}$$$ $$$\int {{\tan}}^{{n}}{\left({x}\right)}{d}{x}=\frac{{1 }}{{{n}-{1}}}{{\tan}}^{{{n}-{1}}}{\left({x}\right)}-\int{{\tan} }^{{{n}-{2}}}{\left({x}\right)}{d}{x}$$$ $$$\int{{\cot}}^{ {n}}{\left({x}\right)}{d}{x}=-\frac{{1}}{{{n}-{1}}}{{\cot}}^{{ {n}-{1}}}{\left({x}\right)}-\int{{\cot}}^{{{n}-{2}}}{\left({x}\right )}{d}{x}$$$ $$$\int{{\sec}}^{{n}}{\left({x}\right)}{d}{x}= \frac{{1}}{{{n}-{1}}}{\tan{{\left({x}\right)}}}{{\sec}}^{{{n}-{2 }}}{\left({x}\right)}+\frac{{{n}-{2}}}{{{n}-{1}}}\int{{\sec}}^{{ {n}-{2}}}{\left({x}\right)}{d}{x}$$$ $$$\int{{\csc}}^{{n}} {\ left ({x} \ right)} {d} {x} = — \ frac {{1}} {{{n} — {1}}} {\ cot {{\ left ({x} \ right) )}}}{{\csc}}^{{{n}-{2}}}{\left({x}\right)} +\frac{{{n}-{2}}}{{{n}-{1}}}\int{{\csc}}^{{{n}-{2}}}{\left({ x}\right)}{d}{x}$$$ $$$\int{\sin{{\left({a}{x}\right)}}}{\sin{{\ влево ({b} {x} \ right)}}} {d} {x} = \ frac {{{\ sin {{\ left ({\ left ({a} — {b} \ right)} {x }\right)}}}}}{{{2}{\left({a}-{b}\right)}}}-\frac{{{\sin{{\left({\left({a }+{b}\right)}{x}\right)}}}}}{{{2}{\left({a}+{b}\right)}}}+{C}$$$ $$$\int{\cos{{\left({a}{x}\right)}}}{\cos{{\left({b}{x}\right)}}}{d }{x}=\frac{{{\sin{{\left({\left({a}-{b}\right)}{x}\right)}}}}}{{{2}{\ влево ({а} — {b} \ вправо)}}} + \ гидроразрыва {{{\ грех {{\ влево ({\ влево ({а} + {b} \ вправо)} {х} \ вправо)} }}}}{{{2}{\left({a}+{b}\right)}}}+{C}$$$ $$$\int{\sin{{\left( {a}{x}\right)}}}{\cos{{\left({b}{x}\right)}}}{d}{x}=-\frac{{{\cos{{\ влево ({\ влево ({a} — {b} \ вправо)} {x} \ вправо)}}}}} {{{2} {\ влево ({a} — {b} \ вправо)}}} -\frac{{{\cos{{\left({\left({a}+{b}\right)}{x}\right)}}}}}{{{2}{\left({a }+{b}\right)}}}+{C}$$$ $$$\int{x}{\sin{{\left({x}\right)}}}{d} {х} = {\ грех {{\left({x}\right)}}}-{x}{\cos{{\left({x}\right)}}}+{C}$$$ $$$\ int{x}{\cos{{\left({x}\right)}}}{d}{x}={\cos{{\left({x}\right)}}}+{x}{ \sin{{\left({x}\right)}}}+{C}$$$ $$$\int{{x}}^{{n}}{\sin{{\left ({x}\right)}}}{d}{x}=-{{x}}^{{n}}{\cos{{\left({x}\right)}}}+{n} \int{{x}}^{{{n}-{1}}}{\cos{{\left({x}\right)}}}{d}{x}$$$ $ $$\int{{x}}^{{n}}{\cos{{\left({x}\right)}}}{d}{x}={{x}}^{{n}} {\sin{{\left({x}\right)}}}-{n}\int{{x}}^{{{n}-{1}}}{\sin{{\left({x} }\right)}}}{d}{x}$$$
$$$\int{{\sin}}^{{n}}{\left({x}\right)}{ {\cos}}^{{m}}{\left({x}\right)}{d}{x}=-\frac{{{{\sin}}^{{{n}-{1} }}{\left({x}\right)}{{\cos}}^{{{m}+{1}}}{\left({x}\right)}}}{{{n}+ {m}}}+\frac{{{n}-{1}}}{{{n}+{m}}}\int{{\sin}}^{{{n}-{2}}} {\left({x}\right)}{{\cos}}^{{m}}{\left({x}\right)}{d}{x}=$$$
$$$= \frac{{{{\sin}}^{{{n}+{1}}}{\left({x}\right)}{{\cos}}^{{{m}-{1}} }{\left({x}\right)}}}{{{n}+{m}}}+\frac{{{m}-{ 1}}}{{{n}+{m}}}\int{{\sin}}^{{n}}{\left({x}\right)}{{\cos}}^{{{ m}-{2}}}{\left({x}\right)}{d}{x}$$$
Обратные тригонометрические формы $$$\int{\operatorname {arcsin}{{\left({x}\right)}}}{d}{x}={x}{\operatorname{arcsin}{{\left({x}\right)}}}+\sqrt {{{1}-{{x}}^{{2}}}}+{C}$$$ $$$\int{\operatorname{arccos}{{\left({x}\ right)}}}{d}{x}={x}{\operatorname{arccos}{{\left({x}\right)}}}-\sqrt{{{1}-{{x}}^ {{2}}}}+{C}$$$ $$$\int{\operatorname{arctan}{{\left({x}\right)}}}{d}{x}= {x}{\operatorname{arctan}{{\left({x}\right)}}}-\frac{{1}}{{2}}{\ln{{\left({1}+{{ x}}^{{2}}\right)}}}+{C}$$$ $$$\int{x}{\operatorname{arcsin}{{\left({x}\right )}}}{d}{x}=\frac{{{2}{{x}}^{{2}}-{1}}}{{4}}{\operatorname{arcsin}{{\left ({x}\right)}}}+\frac{{{x}\sqrt{{{1}-{{x}}^{{2}}}}}}{{4}}+{C} $$$ $$$\int{x}{\operatorname{arccos}{{\left({x}\right)}}}{d}{x}=\f rac{{{2}{{x}}^{{2}}-{1}}}{{4}}{\operatorname{arccos}{{\left({x}\right)}}}-\ frac{{{x}\sqrt{{{1}-{{x}}^{{2}}}}}}{{4}}+{C}$$$ $$$\int {x}{\operatorname{arctan}{{\left({x}\right)}}}{d}{x}=\frac{{{{x}}^{{2}}+{1}} }{{2}}{\operatorname{arctan}{{\left({x}\right)}}}-\frac{{x}}{{2}}+{C}$$$ $$$\int{{x}}^{{n}}{\operatorname{arcsin}{{\left({x}\right)}}}{d}{x}=\frac{{1}} {{{n}+{1}}}{\left({{x}}^{{{n}+{1}}}{\operatorname{arcsin}{{\left({x}\right)} }}-\int\frac{{{{x}}^{{{n}+{1}}}}}{{\sqrt{{{1}-{{x}}^{{2}}} }}}{d}{x}\right)}$$$, $$${n}\ne-{1}$$$ $$$\int{{x}}^{{n }}{\operatorname{arccos}{{\left({x}\right)}}}{d}{x}=\frac{{1}}{{{n}+{1}}}{\left ({{x}}^{{{n}+{1}}}{\operatorname{arccos}{{\left({x}\right)}}}+\int\frac{{{{x}} ^{{{n}+{1}}}}}{{\sqrt{{{1}-{{x}}^{{2}}}}}}}{d}{x}\right)}$ $$, $$${n}\ne-{1}$$$ $$$\int{{x}}^{{n}}{\operatorname{arctan}{{\left({ x}\right)}}}{d}{x}=\frac{{1}}{{{n}+{1}}}{\left({{x}}^{{{n} +{1}}}{\operatorname{arctan}{{\left({x}\right)}}}-\int\frac{{{{x}}^{{{n}+{1}}} }}{{{1}+{{x}}^{{2}}}}{d}{x}\right)}$$$, $$${n}\ne-{1}$$$ Гиперболические формы $$$\int{\sinh{{\left({x}\right)}}}{d}{x}={\cosh{{\left({ x}\right)}}}+{C}$$$ $$$\int{\cosh{{\left({x}\right)}}}{d}{x}={\ sinh{{\left({x}\right)}}}+{C}$$$ $$$\int{\tanh{{\left({x}\right)}}}{d }{x}={\ln{{\left({\cosh{{\left({x}\right)}}}\right)}}}+{C}$$$ $$$ \ int {\ coth {{\ left ({x} \ right)}}} {d} {x} = {\ ln} {\ left | {\ sinh {{\ left ({x} \ right)}} }\right|}+{C}$$$ $$$\int{\operatorname{sech}{{\left({x}\right)}}}{d}{x}={\ имя_оператора {arctan}} {\ left | {\ sinh {{\ left ({x} \ right)}}} \ right |} + {C} $$$ $$$\int{\csch{ {\ left ({x} \ right)}}} {d} {x} = {\ ln} {\ left | {\ tanh {{\ left (\ frac {{1}} {{2}} {x }\right)}}}\right|}+{C}$$$ $$$\int{{\operatorname{s ech}}}^{{2}}{\left({x}\right)}{d}{x}={\tanh{{\left({x}\right)}}}+{C}$ $$ $$$\int{{\csch}}^{{2}}{\left({x}\right)}{d}{x}=-{\coth{{\left( {x}\right)}}}+{C}$$$ $$$\int{\operatorname{sech}{{\left({x}\right)}}}{\tanh{{ \left({x}\right)}}}{d}{x}=-{s}{e}{c}{h}{\left({x}\right)}+{C}$$$ $$$\int{\csch{{\left({x}\right)}}}{\coth{{\left({x}\right)}}}{d}{x}= -{c}{s}{c}{h}{\left({x}\right)}+{C}$$$ Формы, включающие $$$\sqrt{{{{a}} ^{{2}}+{{x}}^{{2}}}}$$$, $$${a}>{0}$$$ $$$\int\sqrt{ {{{a}}^{{2}}+{{x}}^{{2}}}}{d}{x}=\frac{{x}}{{2}}\sqrt{{{ {a}}^{{2}}+{{x}}^{{2}}}}+\frac{{{{a}}^{{2}}}}{{2}}{\ln {{\left({x}+\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}\right)}}}+{C}$$ $ $$$\int{{x}}^{{2}}\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}} {d}{x}=\frac{{x}}{{8}}{\left({{a}}^{{2}}+{2}{{x}}^{{2}}\ справа)}\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}-\frac{{{{a}}^{{4}}}} {{8}}{\ пер {{\ л eft({x}+\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}\right)}}}+{C}$$$ $$$\int\frac{{\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}}}{{x}}{d} {x}=\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}-{a}{\ln}{\left|\frac{{{ a}+\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}}}{{x}}\right|}+{C}$$$ $$$\int\frac{{\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}}}{{{{x} }^{{2}}}}{d}{x}=-\frac{{\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}} }}{{x}}+{\ln{{\left({x}+\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}\ справа)}}}+{C}$$$ $$$\int\frac{{{d}{x}}}{{\sqrt{{{{a}}^{{2}} +{{x}}^{{2}}}}}}={\ln{{\left({x}+\sqrt{{{{a}}^{{2}}+{{x}} ^{{2}}}}\right)}}}+{C}$$$ $$$\int\frac{{{{x}}^{{2}}{d}{x }}}{{\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}}}=\frac{{x}}{{2}}\ sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}-\frac{{{{a}}^{{2}}}}{{2} }{\ln{{\left({x}+\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}\right)}}}+{ C}$$$ $$$\int\frac{{{d}{x}}}{{{x}\sqrt{{{{a}}^{{2}}+{{x }}^{{2}}}}}}=-\frac{{1}}{{a}}{\ln}{\left|\frac{{\sqrt{{{{a}}^ {{2}}+{{x}}^{{2}}}}+{a}}}{{x}}\right|}+{C}$$$ $$$\int \frac{{{d}{x}}}{{{{x}}^{{2}}\sqrt{{{{a}}^{{2}}+{{x}}^{{2 }}}}}}=-\frac{{\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}}}{{{{a}} ^{{2}}{x}}}+{C}$$$ $$$\int\frac{{{d}{x}}}{{{{\left({{a} }^{{2}}+{{x}}^{{2}}\right)}}^{{\frac{{3}}{{2}}}}}}=\frac{{x} }{{{{a}}^{{2}}\sqrt{{{{a}}^{{2}}+{{x}}^{{2}}}}}}+{C}$ $$ Формы с участием $$$\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}$$$, $$${a }>{0}$$$ $$$\int\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}{d} {x}=\frac{{x}}{{2}}\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}+\frac{{ {{a}}^{{2}}}}{{2}}{\operatorname{arcsin}{{\left(\frac{{x}}{{a}}\right)}}}+{C }$$$ $$$\int{{x}}^{{2}}\sqrt{{{{a}}^{{2}}-{{x}}^{{2} }}}{d}{x}=\frac{{x}}{{8}}{\left({2}{{x}}^{{2}}-{{a}}^{{2 }}\right)}\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}+\frac{{{{a}}^{{4} }}}{{8}}{\operatorname{arcsin}{{\left(\frac{{x}}{{a}}\right)}}}+{C}$$$ 9 0349 $$$\int\frac{{\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}}}{{x}}=\sqrt{ {{{a}}^{{2}}-{{x}}^{{2}}}}-{a}{\ln}{\left|\frac{{{a}+\sqrt{{ {{a}}^{{2}}-{{x}}^{{2}}}}}}{{x}}\right|}+{C}$$$ $$$ \int\frac{{\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}}}{{{{x}}^{{2}} }}{d}{x}=-\frac{{1}}{{x}}\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}} }-{\operatorname{arcsin}{{\left(\frac{{x}}{{a}}\right)}}}+{C}$$$ $$$\int\frac{ {{{x}}^{{2}}}}{\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}}{d}{x }=-\frac{{x}}{{2}}\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}+\frac{{{ {a}}^{{2}}}}{{2}}{\operatorname{arcsin}{{\left(\frac{{x}}{{a}}\right)}}}+{C} $$$ $$$\int\frac{{{d}{x}}}{{{x}\sqrt{{{{a}}^{{2}}-{{x}} ^{{2}}}}}}=-\frac{{1}}{{a}}{\ln}{\left|\frac{{{a}}+\sqrt{{{{a}}^ {{2}}-{{x}}^{{2}}}}}}{{x}}\right|}+{C}$$$ $$$\int\frac{{ {d}{x}}}{{{{x}}^{{2}}\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}} }}=-\frac{{1}}{{{{a}}^{{2}}{x}}}\sqrt{{{{a}}^{{2}}-{{x}} ^{{2}}}}+{C}$$$ $$$\i nt {{\ left ({{a}} ^ {{2}} — {{x}} ^ {{2}} \ right)}} ^ {{\ frac {{3}} {{2}}} }{d}{x}=-\frac{{x}}{{8}}{\left({2}{{x}}^{{2}}-{5}{{a}}^{ {2}}\right)}\sqrt{{{{a}}^{{2}}-{{x}}^{{2}}}}+\frac{{{3}{{a}} ^{{4}}}}{{8}}{\operatorname{arcsin}{{\left(\frac{{x}}{{a}}\right)}}}+{C}$$$ $$$\int\frac{{{d}{x}}}{{{{\left({{a}}^{{2}}-{{x}}^{{2}} \right)}}^{{\frac{{3}}{{2}}}}}}=\frac{{x}}{{{{a}}^{{2}}\sqrt{{{ {a}}^{{2}}-{{x}}^{{2}}}}}}+{C}$$$ Форма с участием $$$\sqrt{{{{x }}^{{2}}-{{a}}^{{2}}}}$$$, $$${a}>{0}$$$ $$$\int\ sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}{d}{x}=\frac{{x}}{{2}}\sqrt{ {{{x}}^{{2}}-{{a}}^{{2}}}}-\frac{{{{a}}^{{2}}}}{{2}}{ \ln}{\left|{x}+\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}\right|}+{C}$$ $ $$$\int{{x}}^{{2}}\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}} {d}{x}=\frac{{x}}{{8}}{\left({2}{{x}}^{{2}}-{{a}}^{{2}}\ справа)}\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}-\frac{{{{a}}^{{4}}}} {{8}}{\ln}{\left|{x}+\sqrt{{{{x}}^{{2}}-{{a}}^{{2} }}}\right|}+{C}$$$ $$$\int\frac{{\sqrt{{{{x}}^{{2}}-{{a}}^{ {2}}}}}}{{x}}{d}{x}=\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}- {a}\cdot{\operatorname{arccos}{{\left(\frac{{a}}{{{\left|{u}\right|}}}\right)}}}+{C}$$ $ $$$\int\frac{{\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}}}{{{{x }}^{{2}}}}{d}{x}=-\frac{{\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}} }}}{{x}}+{\ln}{\left|{x}+\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}} \right|}+{C}$$$ $$$\int\frac{{{d}{x}}}{\sqrt{{{{x}}^{{2}}-{ {a}}^{{2}}}}}={\ln}{\left|{x}+\sqrt{{{{x}}^{{2}}-{{a}}^{{ 2}}}}\right|}+{C}$$$ $$$\int\frac{{{{x}}^{{2}}}}{{\sqrt{{{{ x}}^{{2}}-{{a}}^{{2}}}}}}{d}{x}=\frac{{x}}{{2}}\sqrt{{{{ x}}^{{2}}-{{a}}^{{2}}}}+\frac{{{{a}}^{{2}}}}{{2}}{\ln} {\left|{x}+\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}\right|}+{C}$$$ $$$\int\frac{{{d}{x}}}{{{{x}}^{{2}}\sqrt{{{{x}}^{{2}}-{{ a}}^{{2}}}}}}=\frac{{\sqrt{{{{x}}^{{2}}-{{a}}^{{2}}}}}}}{ {{{a}}^{{2}}{x}}}+{C}$$$ $$$\int\frac{{{d}{x}}}{{{{\left({{x}}^{{2}}-{{a}}^{{2}}\ справа)}}^{{\frac{{3}}{{2}}}}}}=-\frac{{x}}{{{{a}}^{{2}}\sqrt{{{ {x}}^{{2}}-{{a}}^{{2}}}}}}+{C}$$$ Формы с участием $$${a}+{b} {x}$$$ $$$\int\frac{{x}}{{{a}+{b}{x}}}{d}{x}=\frac{{1} }{{{{b}}^{{2}}}}{\left({a}+{b}{x}-{a}{\ln}{\left|{a}+{b}{ x}\right|}\right)}+{C}$$$ $$$\int\frac{{{{x}}^{{2}}}}{{{a}+{ b}{x}}}{d}{x}=\frac{{1}}{{{2}{{b}}^{{3}}}}{\left({{\left({a }+{b}{x}\right)}}^{{2}}-{4}{a}{\left({a}+{b}{x}\right)}+{2}{{ a}}^{{2}}{\ln}{\left|{a}+{b}{x}\right|}\right)}+{C}$$$ $$$\ int\frac{{{d}{x}}}{{{x}{\left({a}+{b}{x}\right)}}}=\frac{{1}}{{a} }{\ln}{\left|\frac{{x}}{{{a}+{b}{x}}}\right|}+{C}$$$ $$$\int \frac{{{d}{x}}}{{{{x}}^{{2}}{\left({a}+{b}{x}\right)}}}=-\frac{ {1}}{{{a}{x}}}+\frac{{b}}{{{{a}}^{{2}}}}{\ln}{\left|\frac{{{ a}+{b}{x}}}{{x}}\right|}+{C}$$$ $$$\int\frac{{x}}{{{{\left({a}+{b}{x}\right)}}^{{2}}}}{d}{x}= \frac{{a}}{{{{b}}^{{2}}{\left({a}+{b}{x}\right)}}}+\frac{{1}}{{ {{b}}^{{2}}}}{\ln}{\left|{a}+{b}{x}\right|}+{C}$$$ $$$\ int\frac{{{d}{x}}}{{{x}{{\left({a}+{b}{x}\right)}}^{{2}}}}=\frac{ {1}}{{{a}{\left({a}+{b}{x}\right)}}}-\frac{{1}}{{{{a}}^{{2}} }}{\ln}{\left|\frac{{{a}+{b}{x}}}{{x}}\right|}+{C}$$$ $$$\ int\frac{{{{x}}^{{2}}}}{{{{\left({a}+{b}{x}\right)}}^{{2}}}}{d }{x}=\frac{{1}}{{{{b}}^{{3}}}}{\left({a}+{b}{x}-\frac{{{{a}) }^{{2}}}}{{{a}+{b}{x}}}-{2}{a}{\ln}{\left|{a}+{b}{x}\right |}\right)}+{C}$$$ $$$\int{x}\sqrt{{{a}+{b}{x}}}{d}{x}=\frac {{2}}{{{15}{{b}}^{{2}}}}{\left({3}{b}{x}-{2}{a}\right)}{{\ left({a}+{b}{x}\right)}}^{{\frac{{3}}{{2}}}}+{C}$$$ $$$\int \ frac {{x}} {\ sqrt {{{a} + {b} {x}}}}} {d} {x} = \ frac {{2}} {{{3} {{b} }^{{2}}}}{\left({b}{x}-{2}{a}\right)}\sqrt{{{a}+{b}{x}}}+{C} $$$ $$$\int\frac{ {{{x}}^{{2}}}}{{\sqrt{{{a}+{b}{x}}}}}{d}{x}=\frac{{2}}{{ {15}{{b}}^{{3}}}}{\left({8}{{a}}^{{2}}+{3}{{b}}^{{2}}{ {x}}^{{2}}-{4}{a}{b}{x}\right)}\sqrt{{{a}+{b}{x}}}+{C}$$$ $$$\int\frac{{{d}{x}}}{{{x}\sqrt{{{a}+{b}{x}}}}}={\left\{ \begin{array}{c}\frac{{1}}{{\sqrt{{{a}}}}}{\ln}{\left|\frac{{\sqrt{{{a}}+{b }{x}}}-\sqrt{{{a}}}}}{{\sqrt{{{a}+{b}{x}}}+\sqrt{{{a}}}}}\right |}+{C}{\quad\text{if}\quad}{a}>{0}\\\frac{{2}}{{\sqrt{{-{a}}}}}{\operatorname {arctan}{{\left(\ sqrt{{\frac{{{a}+{b}{x}}}{{-{a}}}}}\right)}}}+{C}{\ quad\text{if}\quad}{a}<{0}\\ \end{массив}\right. {{2}}}}}}{{{a}{x}}}+{C}$$$
{{2}}}}}}{{{a}{x}}}+{C}$$$Справочник по математическим формулам и интегралам
Выбрать все основные сведения
Доступ к полному тексту
книга CheckabStract только
1 — числовые, алгебраические и аналитические результаты для серии и исчисления
стр. 25-99
Выбор 2 — Функции и идентичности
Книга Checkabstract только
2 — Функции и идентичности
Страницы 101-137
Выбрать 3 — Производные элементарных функций
Глава книгиТолько реферат
3 — Производные элементарных функций
Страниц 13 9-143
Выберите 4 — неопределенные интегралы алгебраических функций
Книга CheckabStact только
4 — неопределенные интегралы алгебраических функций
стр. 145-165
Выбор 5 — неопределенные интегралы экспоненциальных функций
CheckabStact только
5 — неопределенные интегралы экспоненциальных функций
стр. 167-171
167-171
Выбрать 6 — неопределенные интегралы логарифмических функций
Книга CheckabStract только
6 — неопределенные интегралы логарифмических функций
страницы 173-178
Выбрать 7 — неопределенные интегралы гиперболических функций
Книга CheckabStract только
7 — неопределенные интегралы гиперболических функций
стр. 179-189
страницы 179-189
Выбор 8 — неопределенные интегралы с участием обратных гиперболических функций
9239 2 8 — неопределенные интегралы с участием обратных гиперболических функций
стр. 191-195
Выбор 9 — неопределенные интегралы тригонометрических функций
Книга Checkabstract только
9 — неопределенные интегралы тригонометрических функций
стр. 197-213
Выбор 10 — неопределенные интегралы обратных тригонометрических функций
Книга CheckabStact Только
10 — неопределенные интегралы обратных тригонометрических функций
стр. 215-219
215-219
Выбор 11 — Гамма, бета, PI и PI и PSI функции
Книга CheckabStact только
11 — Гамма, бета, PI, PI и PI и PSI функции
стр. 221-228
Выбор 12 — эллиптические интегралы и функции
Книга Checkabstract только
12 — эллиптические интегралы и функции
страницы 229-238
Выберите 13 — Интегралы вероятности и Функция ошибки
книга CheckabStact только
13 — Функция вероятностей и ошибка
стр. 239-244
стр. 239-244
Выбор 14 — Френенельные интегралы, синусоиментные и косинусные интегралы
Книга CheckabStact только
14 — Френеляционные интегралы, Синус и косинусные интегралы
стр. 245-248
Выбрать 15 — Определенные интегралы
Книги Checkabstract только
15 — Определенные интегралы
стр. 249-256
стр. 249-256
Выбор 16 — Различные формы серии Фурье
Книга CheckabStact только
16 — разные формы серии Фурье
стр. 257-268
257-268
Выбрать 17 — Бессельские функции
книга CheckabStact только
17 — Бессельские функции
стр. 269-284
Выбор 18 — Ортогональные многочлены
Глава книгиТолько реферат
18 — Ортогональные Polynomials
стр. 282393
стр. 285-297
Выбор 19 — преобразование Лапласа
книга CheckabStact только
19 — преобразование Лапласа
стр. 299-305
Выбор 20 — Фурье преобразования
книга CheckabStract только
20 — Фурье трансформирует
стр. 307-314
Выбрать 21 — Численная интеграция
Книга Checkabstract только
21 — Численная интеграция
стр. 315-320
Выбор 22 — Решения стандартных обыкновенных дифференциальных уравнений
Книга ChemabStact только
22 — Решения стандартных обыкновенных дифференциальных уравнений
стр. 321-352
321-352
Выбрать 23 — Векторный анализ
Книга CheckabStract только
23 — Векторный анализ
стр. 353-368
Выбор 24 — Системы ортогональных координат
Книга Checkabstract только
24 — Системы ортогональных координат
стр. 369-379
Выбор 25 — Частичные дифференциальные уравнения и специальные функции
Книга CheckabStact Только
25 — Частичные дифференциальные уравнения и специальные функции
Страницы 381 -402
Выбрать 26 — Z-Transform
книга CheckabStract только
26 —
Z -Transformстр. 403-408
стр. 403-408
Выбор 27 — Численное приближение
Книга Checkabstract Только
27 — Численное приближение
стр. 409-417
Выбор 28 — Решения эллиптических, параболических и гиперболических уравнений
Книга CheckabStract Только
28 — Решения эллиптических, параболических и гиперболических уравнений
стр.
 ,
, .
. dx = e x + C
dx = e x + C dx = log|cosecx — cotx| + С
dx = log|cosecx — cotx| + С dx =1/2.x.√(x 2 — a 2 )-a 2 /2 log|x + √(1x 9020 2 — а 2 )| + С
dx =1/2.x.√(x 2 — a 2 )-a 2 /2 log|x + √(1x 9020 2 — а 2 )| + С dx = sinx + C
dx = sinx + C