мера средней кинетической энергии молекул. Видеоурок. Физика 10 Класс

На этом уроке мы будем разбирать физическую величину, уже знакомую нам из курса восьмого класса – температуру. Мы дополним её определение как меру теплового равновесия и меру средней кинетической энергии. Опишем недостатки одних и преимущества других методов измерения температур, введём понятие шкалы абсолютных температур и, наконец, выведем зависимость кинетической энергии молекул газа и давления газа от температуры.

Как уже было сказано выше, понятие температура не является новым для нас. В восьмом классе мы определяли её как меру нагретости тела. Теперь же мы расширим это понятие. Ведь температура является очень важным макропараметром, который определяет величину теплового хаотического движения молекул и атомов.

Для начала вспомним, как нужно измерять температуру какого-либо тела. Мы приводим прибор для измерения температуры – термометр –  в контакт с телом, температуру которого хотим замерить, и ждём некоторое время. Зачем мы это делаем? Чтобы температура тела и температура термометра стали одинаковыми (термометр способен показывать лишь свою температуру). Или же говорят, что термометр и тело находятся в состоянии теплового равновесия.

Определение. Тепловое равновесие – такое состояние тела, при котором его макроскопические параметры не меняются длительное время.

Так вот температура – мера теплового равновесия тела или системы тел. И сведения о температурах двух тел дают нам представление о направлении перехода тепла – от более нагретого тела к менее нагретому.

Следует отметить, что наиболее распространённые в быту термометры – ртутные, спиртовые и т.д. (рис. 1) – не отвечают физическим стандартам измерения температур.

Рис. 1. Спиртовой и ртутный термометры соответственно (Источник), (Источник)

Причины этому две:

1. Различные термометры используют различные вещества в качестве индикатора, поэтому на одно и то же изменение температуры в зависимости от свойств конкретного вещества термометры реагируют по-разному;
2. Произвольность выбора начала отсчёта шкалы температур.

Поэтому для любых точных замеров температур такие термометры не годятся. И начиная с восемнадцатого века, используются более точные термометры, коими является газовые термометры (см. рис. 2)

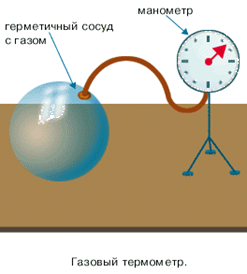
Рис. 2. Газовый термометр (Источник)

Причиной этого является тот факт, что газы расширяются одинаково при изменении температуры на одинаковые значения. Для газовых термометров справедливо следующее:

При  

При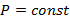  

То есть для измерения температуры либо фиксируется изменение давления при постоянном объёме, либо объём при постоянном давлении.

В газовых термометрах часто используют разреженный водород, который, как мы помним, очень хорошо подходит под модель идеального газа.

         

Кроме неидеальности бытовых термометров имеет место быть неидеальность многих шкал, которые используются в быту. В частности, шкала Цельсия, как наиболее нам знакомая. Как и в случае с термометрами эти шкалы выбирают случайным образом начальный уровень (для шкалы Цельсия это температура плавления льда). Поэтому для работы с физическими величинами необходима другая, абсолютная шкала.

Эту шкалу ввёл в 1848 г английский физик Уильям Томпсон (лорд Кельвин) (рис. 3). Зная, что при росте температур тепловая скорость движения молекул и атомов тоже растёт, нетрудно установить, что при уменьшении температур скорость будет падать и при определённой температуре рано или поздно станет нулём, как и давление (исходя и основного уравнения МКТ). Эту температуру и выбрали за начало отсчёта. Совершенно очевидно, что температура не может достигнуть значения меньше этого значения, поэтому оно получило название «абсолютный ноль температур». Для удобства же 1 градус по шкале Кельвина был приведён в соответствии с 1 градусом по шкале Цельсия.

Итак, получаем следующее:

Обозначение температуры – ;

Единица измерения – К, «кельвин»

Перевод к шкале Кельвина: 

Следовательно, абсолютный ноль температур – это температура

Рис. 3. Уильям Томпсон (Источник)   

Теперь для определения температуры как меры средней кинетической энергии молекул имеет смысл обобщить те рассуждения, которые мы приводили в определении абсолютной шкалы температур:

Итак, как видим, температура и правда является мерой средней кинетической энергией поступательного движения. Конкретное же формульное соотношение вывел австрийский физик Людвиг Больцман (рис. 4):

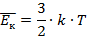
Здесь  – так называемый коэффициент Больцмана. Это константа, численно равная:

Как мы видим, размерность этого коэффициента – 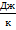, то есть это своего рода коэффициент пересчёта из шкалы температур в шкалу энергий, ведь мы понимаем теперь, что, по сути, должны были измерять температуру в единицах энергии.

Теперь рассмотрим, как будет зависеть давление идеального газа от температуры. Для этого запишем основное уравнение МКТ в следующем виде:

и подставим в эту формулу выражение для связи средней кинетической энергии с температурой. Получим:

Рис. 4. Людвиг Больцман (Источник)

На следующем занятии мы сформулируем уравнение состояния идеального газа.

 

Список литературы

1. Мякишев Г.Я., Синяков А.З. Молекулярная физика. Термодинамика. – М.: Дрофа, 2010.
2. Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Илекса, 2005.
3. Касьянов В.А. Физика 10 класс. – М.: Дрофа, 2010.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Большая Энциклопедия Нефти Газа (Источник).
2. youtube.com (Источник).
3. E-science.ru (Источник).

 

Домашнее задание

1. Стр. 66: №  478–481. Физика. Задачник. 10-11 классы.  Рымкевич А.П. – М.: Дрофа, 2013. (Источник)
2. Как определяют шкалу температур по Цельсию?
3. Укажите температурный диапазон по шкале Кельвина для вашего города летом и зимой.
4. Воздух состоит в основном из азота и кислорода. Кинетическая энергия молекул какого газа больше?
5. *Чем отличается расширение газов от расширения жидкостей и твёрдых тел?

Температура. Средняя кинетическая энергия | LAMPA

Все, кто читает этот курс физики, наверняка имеют представление о том, что такое температура. Чисто бытовое представление, интуитивное понимание. На вопрос «Что такое температура?» многие бы ответили: «Ну, температура – это такая штукенция, что если температура большая – то тело горячее, а если температура низкая – то тело холодное».

В принципе – верно. Температура характеризует степень нагретости тела. Высокая температура – сильно нагретое тело. Низкая температура – слабо нагретое тело.

Но такое «интуитивное» описание не годится для такой достаточно строгой науки, как физика. Нужно понять детальнее – а что же такое температура?

Надо сказать, что долгое время сами учёные тоже этого не понимали. Понимание пришло позже – вместе с опытом. Попробуем мысленно повторить опыт, который помог разобраться в том, что такое температура.

Возьмём три различных газа. Ну, например, это могли бы быть – кислород О2\text{О}_2О2​, углекислый газ СО2\text{СО}_2СО2​ и метан СН4\text{СН}_4СН4​. Молекулы разные, газы разные. Но сделаем так, чтобы у них были одинаковые температуры, одинаковая степень нагретости – то есть, например, чтобы нами ощущалось, что каждый из сосудов нагрет одинаково до некоторой температуры.

У каждого из газов в этих сосудах может быть своё давление ppp, свой объём сосуда VVV, своё количество молекул NNN.

Опытным путём была установлена интересная вещь! Оказалось, что величина pVN\frac{pV}{N}NpV​ для каждого из газов одной и той же температуры – одинакова! Кому-то повезло. Он решил перемножить объём и давление и разделить на количество молекул. И получил, что эта величина одинаковая для разных газов одинаковой температуры.

p1V1N1=p2V2N2=p3V3N3\frac{p_1 V_1}{N_1} = \frac{p_2 V_2}{N_2} = \frac{p_3 V_3}{N_3}N1​p1​V1​​=N2​p2​V2​​=N3​p3​V3​​

Стоп. А ведь по условию мы выстроили опыт так, что у газов одинакова температура.

Хм… Если у газов одинакова температура и одинакова вот такая странная величина pVN\frac{pV}{N}NpV​, тогда… может быть, величина pVN\frac{pV}{N}NpV​ и есть температура? Обозначим такую температуру пока непонятной буквой θ\thetaθ:

θ=pVN\theta = \frac{pV}{N}θ=NpV​.

θ\thetaθ – это такая греческая буква; произносится как «тета».

Попробуем прикинуть, чему равна θ\thetaθ для газов в обычном состоянии, например, воздуха, который нас окружает. Давление возьмём атмосферное p≈105p \approx 10^5p≈105 Па, количество молекул N≈6⋅1023N \approx 6 \cdot 10^{23}N≈6⋅1023 (один моль вещества). Забегая вперёд, можно сказать: известно, что один моль любых газов (при условиях, когда газ можно считать идеальным) при нормальных условиях занимает объём V≈22,4⋅10−3 м3V \approx 22,4 \cdot 10^{-3}\text{ }м^3V≈22,4⋅10−3 м3. Тогда температура θ=pVN=105Па⋅22,4⋅10−3м36⋅1023≈3,7⋅10−21\theta = \frac{pV}{N} = \frac{10^5 Па \cdot 22,4 \cdot 10^{-3} м^3}{6 \cdot 10^{23}} \approx 3,7 \cdot 10^{-21}θ=NpV​=6⋅1023105Па⋅22,4⋅10−3м3​≈3,7⋅10−21. Кстати, температура получается…

Определение температуры. Энергия теплового движения молекул

Определение температуры. Энергия теплового движения молекул

«Физика — 10 класс»

Какие макропараметры используют для описания состояния газа?

Справедливо ли утверждение: «Чем быстрее движутся молекулы газа, тем выше его температура»?

Средняя кинетическая энергия молекул газа при тепловом равновесии.

Возьмём сосуд, разделённый пополам перегородкой, проводящей тепло. В одну половину сосуда поместим кислород, а в другую — водород, имеющие разную температуру. Спустя некоторое время газы будут иметь одинаковую температуру, не зависящую от рода газа, т. е. будут находиться в состоянии теплового равновесия. Для определения температуры выясним, какая физическая величина в молекулярно-кинетической теории обладает таким же свойством.

Из курса физики основной школы известно, что, чем быстрее движутся молекулы, тем выше температура тела. При нагревании газа в замкнутом сосуде давление газа возрастает. Согласно же основному уравнению молекулярно-кинетической теории (9.7) давление газа р прямо пропорционально средней кинетической энергии поступательного движения молекул:

Так как концентрация молекул газа то из уравнения (9.7) получаем или или, согласно формуле (8.8),

При тепловом равновесии, если давление и объём газа массой m постоянны и известны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.

Можно предположить, что при тепловом равновесии именно средние кинетические энергии молекул всех газов одинаковы.

Конечно, это пока только предположение. Его нужно экспериментально проверить. Практически такую проверку произвести непосредственно невозможно, так как измерить среднюю кинетическую энергию молекул очень трудно. Но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:

Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при

Газы в состоянии теплового равновесия.

Рассмотрим следующий опыт. Возьмём несколько сосудов, заполненных различными газами, например водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами. Это позволяет измерить давление в каждом сосуде. Массы газов известны, тем самым известно число молекул в каждом сосуде.

Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться (рис. 9.4). После этого можно утверждать, что все газы имеют одинаковую температуру 0 °С. Давления газов р, их объёмы V и число молекул N различны. Найдём отношение для водорода. Если, к примеру, водород, количество вещества которого равно 1 моль, занимает объём V_H2 = 0,1 м³ , то при температуре 0 °С давление оказывается равным р_Н2 = 2,265 • 10⁴ Па. Отсюда

Если взять водород в объёме, равном kV_H2, то и число молекул будет равно kN_A и отношение останется равным 3,76 • 10^-21 Дж.

Такое же значение отношения произведения давления газа на его объём к числу молекул получается и для всех других газов при температуре тающего льда. Обозначим это отношение через Θ₀. Тогда

Таким образом, наше предположение оказалось верным.

Средняя кинетическая энергия , а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение

Соотношение (9.10) не является абсолютно точным. При давлениях в сотни атмосфер, когда газы становятся весьма плотными, отношение перестаёт быть строго определённым, не зависящим от занимаемых газами объёмов. Оно выполняется для газов, когда их можно считать идеальными.

Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту отношение по-прежнему будет одним и тем же для всех газов, но больше, чем предыдущее:

Определение температуры.

Можно, следовательно, утверждать, что величина Θ растёт с повышением температуры. Более того, Θ ни от чего, кроме температуры, не зависит. Ведь для идеальных газов Θ не зависит ни от рода газа, ни от его объёма или давления, а также от числа частиц в сосуде.

Этот опытный факт позволяет рассматривать величину Θ как естественную меру температуры, как параметр газа, определяемый через другие макроскопические параметры газа.
В принципе можно было бы считать температурой и саму величину Θ и измерять температуру в энергетических единицах — джоулях.
Однако, во-первых, это неудобно для практического использования (температуре 100 °С соответствовало бы очень малое значение — порядка 10^-21 Дж), а во-вторых, и это главное, уже давно температуру принято выражать в градусах.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика

Почему тепловые явления изучаются в молекулярной физике — Основные положения молекулярно-кинетической теории. Размеры молекул — Примеры решения задач по теме «Основные положения МКТ» — Броуновское движение — Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел — Идеальный газ в МКТ. Среднее значение квадрата скорости молекул — Основное уравнение молекулярно-кинетической теории газов — Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» — Температура и тепловое равновесие — Определение температуры. Энергия теплового движения молекул — Абсолютная температура. Температура — мера средней кинетической энергии молекул — Измерение скоростей молекул газа — Примеры решения задач по теме «Энергия теплового движения молекул» — Уравнение состояния идеального газа — Примеры решения задач по теме «Уравнение состояния идеального газа» — Газовые законы — Примеры решения задач по теме «Газовые законы» — Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»

Абсолютная температура. Температура — мера средней кинетической энергии молекул

Абсолютная температура. Температура — мера средней кинетической энергии молекул

«Физика — 10 класс»

Абсолютная температура.

Вместо температуры Θ, выражаемой в энергетических единицах, введём температуру, выражаемую в привычных для нас градусах.

Будем считать величину Θ прямо пропорциональной температуре Т, измеряемой в градусах:

Θ = kТ,           (9.12)

где k — коэффициент пропорциональности.

>Определяемая равенством (9.12) температура называется абсолютной.

Такое название, как мы сейчас увидим, имеет достаточные основания. Учитывая определение (9.12), получим

По этой формуле вводится температурная шкала (в градусах), не зависящая от вещества, используемого для измерения температуры.

Температура, определяемая формулой (9.13), очевидно, не может быть отрицательной, так как все величины, стоящие в левой части этой формулы, заведомо положительны. Следовательно, наименьшим возможным значением температуры Т является значение Т = 0, если давление р или объём V равны нулю.

Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.

Это самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказывал Ломоносов.

Английский учёный У. Томсон (лорд Кельвин) (1824—1907) ввёл абсолютную шкалу температур. Нулевая температура по абсолютной шкале (её называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.

Единица абсолютной температуры в СИ называется кельвином (обозначается буквой К).

Постоянная Больцмана.

Определим коэффициент k в формуле (9.13) так, чтобы изменение температуры на один кельвин (1 К) было равно изменению температуры на один градус по шкале Цельсия (1 °С).

Мы знаем значения величины Θ при 0 °С и 100 °С (см. формулы (9.9) и (9.11)). Обозначим абсолютную температуру при 0 °С через Т₁, а при 100 °С через Т₂. Тогда согласно формуле (9.12)

Θ₁₀₀ — Θ₀ = k(T₂ -T₁),

Θ₁₀₀ — Θ₀ = k • 100 K = (5,14 — 3,76) • 10^-21 Дж.

Отсюда

Коэффициент

k = 1,38 • 10^-23 Дж/К         (9.14)

называется постоянной Больцмана в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории газов.

Постоянная Больцмана связывает температуру Θ в энергетических единицах с температурой Т в кельвинах.

Это одна из наиболее важных постоянных в молекулярно-кинетической теории.

Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0 °С. Так как при 0 °С kT₁ = 3,76 • 10^-21 Дж, то

Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:

Т (К) = (f + 273) (°С).         (9.15)

Изменение абсолютной температуры ΔТ равно изменению температуры по шкале Цельсия Δt: ΔТ(К) = Δt (°С).

На рисунке 9.5 для сравнения изображены абсолютная шкала и шкала Цельсия. Абсолютному нулю соответствует температура t = -273 °С.

В США используется шкала Фаренгейта. Точка замерзания воды по этой шкале 32 °F, а точка кипения 212 °Е Пересчёт температуры из шкалы Фаренгейта в шкалу Цельсия производится по формуле t(°C) = 5/9 (t(°F) — 32).

Отметим важнейший факт: абсолютный нуль температуры недостижим!

Температура — мера средней кинетической энергии молекул.

Из основного уравнения молекулярно-кинетической теории (9.8) и определения температуры (9.13) вытекает важнейшее следствие:
абсолютная температура есть мера средней кинетической энергии движения молекул.

Докажем это.

Из уравнений (9.7) и (9.13) следует, что Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:

Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.

Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надёжное обоснование. Соотношение (9.16) между температурой и средней кинетической энергией поступательного движения молекул установлено для идеальных газов.

Однако оно оказывается справедливым для любых веществ, у которых движение атомов или молекул подчиняется законам механики Ньютона. Оно верно для жидкостей, а также и для твёрдых тел, где атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решётки.

При приближении температуры к абсолютному нулю энергия теплового движения молекул приближается к нулю, т. е. прекращается поступательное тепловое движение молекул.

Зависимость давления газа от концентрации его молекул и температуры. Учитывая, что из формулы (9.13) получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:

Из формулы (9.17) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.

Отсюда следует закон Авогадро, известный вам из курса химии.

Закон Авогадро:

В равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика

Почему тепловые явления изучаются в молекулярной физике — Основные положения молекулярно-кинетической теории. Размеры молекул — Примеры решения задач по теме «Основные положения МКТ» — Броуновское движение — Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел — Идеальный газ в МКТ. Среднее значение квадрата скорости молекул — Основное уравнение молекулярно-кинетической теории газов — Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» — Температура и тепловое равновесие — Определение температуры. Энергия теплового движения молекул — Абсолютная температура. Температура — мера средней кинетической энергии молекул — Измерение скоростей молекул газа — Примеры решения задач по теме «Энергия теплового движения молекул» — Уравнение состояния идеального газа — Примеры решения задач по теме «Уравнение состояния идеального газа» — Газовые законы — Примеры решения задач по теме «Газовые законы» — Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»