Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Теорема Пифагора

      Теорема Пифагора. В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.

      Доказательство. Докажем, что длины сторон произвольного прямоугольного треугольника ABC (рис.1)

Рис.1

удовлетворяют равенству

c² = a² + b²

      С этой целью рассмотрим квадратквадрат со стороной, равной c, изображённый на рисунке 2.

Рис.2

      Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC (рис.3, рис.4), и площади квадрата со стороной, равной a – b (рис.5).

Рис.3

Рис.4

Рис.5

      Поэтому справедливо равенство

что и требовалось доказать.

Теорема косинусов

      Теорема косинусов. Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

      Доказательство. Рассмотрим сначала треугольник ABC, у которого углы A и С – острые (рис.6).

Рис.6

      Докажем, что длины сторон этого треугольника удовлетворяют равенству

a2 = b 2 + c 2 – – 2bc cos A

(1)

      С этой целью проведём высоту BD из вершины B (рис.7).

Рис.7

      В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства

BD = c sin A,   AD = c cos A,   DC = b – AD = b – c cos A.

      Из теоремы Пифагора, применённой к прямоугольному треугольнику BDC, получим

a ² = BD ² + DC ² =
= c ² sin² A + (b – c cos A)² =
= c ² sin² A + b² –
– 2 bc cos A + c ² cos² A =
= b² + c ² – 2 bc cos A.

      Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана.

      Замечание 1. Для того, чтобы получить полное доказательство теоремы косинусов, необходимо рассмотреть также и следующие случаи:

1. Угол A – острый, угол C – тупой (рис.8)

   

   Рис.8

2. Угол A – прямой (рис. 9).

   

   Рис.6

3. Угол A – тупой (рис.10).

   

   Рис.10

      Во всех перечисленных случаях доказательства теоремы косинусов проводятся совершенно аналогично тому, как это было сделано для случая острых углов A  и C, и мы рекомендуем читателю провести эти доказательства в качестве полезного и несложного упражнения.

      Замечание 2. В случае, когда угол A является прямым углом, формула (1) принимает вид

a² = b² + c²,

откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов.

      Замечание 3. Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например,

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Теорема косинусов | Треугольники

Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

 

Дано:

∆ ABC.

Доказать:

 

   

Доказательство:

 

I. Если треугольник ABC — остроугольный.

1) Опустим перпендикуляр CD на сторону AB.

2) Рассмотрим прямоугольный треугольник ADC.

По теореме Пифагора,

   

По определению косинуса острого угла в прямоугольном треугольнике,

   

следовательно,

   

3) Рассмотрим прямоугольный треугольник BDC.

   

По теореме Пифагора

   

   

   

Упрощаем

   

   

Откуда

   

 

 II. Если треугольник ABC — тупоугольный.

1) Опускаем перпендикуляр CD на прямую, содержащую сторону AB.

2) Рассмотрим прямоугольный треугольник ADC.

По теореме Пифагора,

   

По определению косинуса,

   

Так как углы A и CAD — смежные, то ∠CAD=180º-∠A. По формуле приведения

   

   

   

3) Рассмотрим прямоугольный треугольник BDC.

   

   

Дальнейшая часть доказательства полностью повторяет рассуждения пункта I.

III. Если треугольник ABC — прямоугольный, где ∠A=90º, получаем теорему Пифагора (cos90º=0).

Скалярное произведение векторов: теория и решения задач

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Почему скалярное произведение векторов называется именно скалярным и что представляет собой? Чем оно отличается от результатов других операций над векторами? Что такое скаляр? Скаляр — это число. И скалярное произведение векторов — это тоже число. Этим оно и отличается от уже рассмотренной

суммы векторов, и от векторного произведения векторов, которое ещё предстоит рассмотреть. В отличие от скалярного произведения, сумма векторов — это вектор, и векторное произведение — тоже вектор.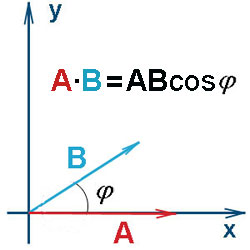

Определение 1. Скалярным произведением векторов называется число (скаляр), равное произведению длин (модулей) этих векторов на косинус угла между ними. Формула скалярного произведения векторов согласно определению 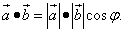1:    (1)

Можно встретить и другое название этой операции: внутреннее произведение.

Скалярное произведение вектора на себя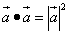

называется скалярным квадратом.

На этом уроке будем решать распространённые задачи не только на непосредственное вычисление скалярного произведения, но и на выяснение ортогональности (перпендикулярности) векторов, вида угла (тупой, острый, прямой) между векторами, вычисление скалярного произведения векторов, которые даны в координатах, вычисление длин диагоналей параллелограма, построенного на вектора. Но все по порядку. Перед каждым видом задач будем обращать внимание на то, что на этот счёт гласит теория. По ходу урока вам пригодится онлайн-калькулятор для проверки решения задач на скалярное произведение векторов.

Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:

Пример 1. Даны векторы . Найти скалярное произведение векторов 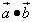, если их длины и угол между ними представлены следующими значениями:

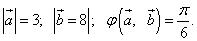
Решение:

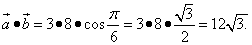
Справедливо и другое определение, полностью равносильное определению 1.

Определение 2. Скалярным произведением векторов называется число (скаляр), равное произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:

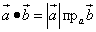   (2)

или

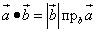   (3)

Задачу с применением этой формулы решим после следующего важного теоретического пункта.

То же самое число можно получить, если перемножаемые векторы заданы своими координатами.

Определение 3.

Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.

На плоскости

Если два вектора 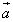и 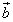на плоскости определены своими двумя декартовыми прямоугольными координатами

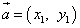
и

,

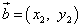то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:

.

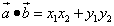Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

В пространстве

Если два вектора 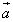и 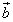в пространстве определены своими тремя декартовыми прямоугольными координатами

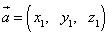
и

,

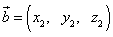то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:

.

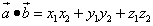Задача на нахождение скалярного произведения рассмотренным способом — после разбора свойств скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые векторы.

Геометрические свойства

В определениях изучаемой операции мы уже касались понятия угла между двумя векторами. Пора уточнить это понятие.

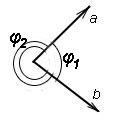
На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно обратить внимание: между этими векторами существуют два угла — φ1 и φ2. Какой из этих углов фигурирует в определениях и свойствах скалярного произведения векторов? Сумма рассмотренных углов равна 2π и поэтому косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения. Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π, то есть 180 градусов. На рисунке этот угол обозначен как φ1.

1. Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или π/2), если скалярное произведение этих векторов равно нулю

:

.

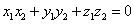Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.

2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше π/2) тогда и только тогда, когда их скалярное произведение положительно.

3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше π/2) тогда и только тогда, когда их скалярное произведение отрицательно.

Пример 3. В координатах даны векторы:

.

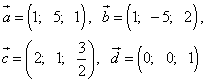
Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?

Решение. Вычислять будем путём сложения произведений соответствующих координат.

.

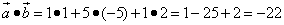Получили отрицательное число, поэтому векторы образуют тупой угол.

.

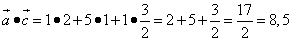Получили положительное число, поэтому векторы образуют острый угол.

.

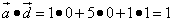Получили положительное число, поэтому векторы образуют острый угол.

.

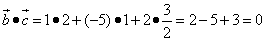Получили нуль, поэтому векторы образуют прямой угол.

.

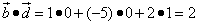Получили положительное число, поэтому векторы образуют острый угол.

.

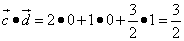Получили положительное число, поэтому векторы образуют острый угол.

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

---

Пример 4. Даны длины двух векторов и угол между ними:

.

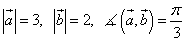Определить, при каком значении числа 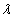векторы 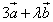и 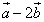ортогональны (перпендикулярны).

Решение. Перемножим векторы по правилу умножения многочленов:

.

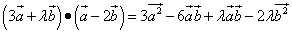Теперь вычислим каждое слагаемое:

.

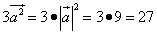
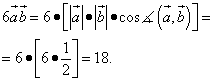
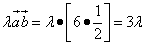
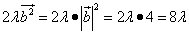Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:

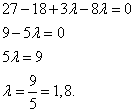
Ответ: мы получили значение λ = 1,8, при котором векторы ортогональны.

---

Решить задачу самостоятельно, а затем посмотреть решение

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

Иногда выигрышным для наглядности является представление двух перемножаемых векторов в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:

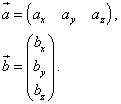
Тогда скалярное произведение векторов будет произведением этих матриц:

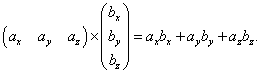
Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным числом.

В матричной форме удобно представлять произведение абстрактных n-мерных векторов. Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.

Пример 7. Найти скалярные произведения пар векторов

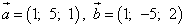
и

,

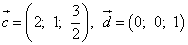используя матричное представление.

Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй — в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на матрицу-столбец:

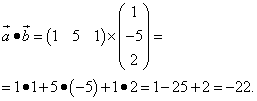
Аналогично представляем вторую пару и находим:

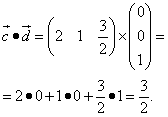
Как видим, результаты получились те же, что и у тех же пар из примера 2.

---

Вывод формулы косинуса угла между двумя векторами очень красив и краток.

Чтобы выразить скалярное произведение векторов

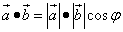                              (1)

в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:

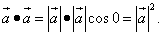
То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины. Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:

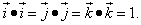
Так как векторы

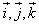
попарно перпендикулярны, то попарные произведения ортов будут равны нулю:

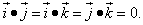
Теперь выполним умножение векторных многочленов:

 

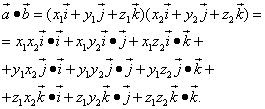
Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:

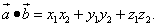
Получаем формулу косинуса угла между двумя векторами:

---

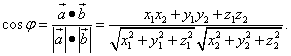
Пример 8. Даны три точки A(1;1;1), B(2;2;1), C(2;1;2).

Найти угол .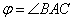

Решение. Находим координаты векторов:

,

.

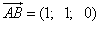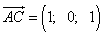По формуле косинуса угла получаем:

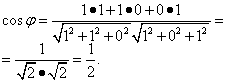
Следовательно, .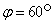

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

---

Пример 9. Даны два вектора

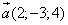
и

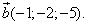
Найти сумму, разность, длину, скалярное произведение и угол между ними.

Решение.

1.Сумма

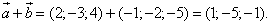
2.Разность

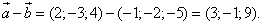
3.Длина

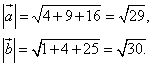
4.Скалярное произведение

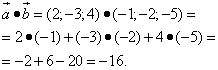
5.Угол между и :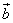

Решить задачи самостоятельно, а затем посмотреть решения

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

---

Пример 13. Среди векторов

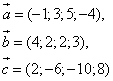
Найти а) коллинеарные; б) ортогональные.

Решение.

а) проверим пропорциональность соответствующих координат векторов — условие коллинеарности (повторение материала предыдущей части темы «Векторы»).

Для векторов 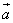и :

 

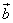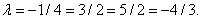
Равенство не выполняется.

Для векторов 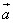и :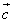

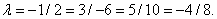
Равенство выполняется.

Для векторов 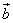и :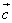

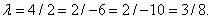
Равенство не выполняется.

Наше исследование показало, что коллинеарны векторы 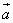и .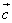

б) найдём скалярные произведения векторов.

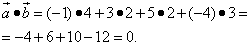
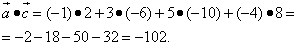
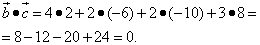
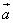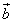Наше исследование показало, что ортогональны векторы и 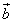и и .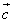

Расчёт работы постоянной силы

Посмотрите ещё раз на рисунок в начале статьи. Пусть материальная точка перемещается прямолинейно из начала координат в конец вектора B под действием постоянной силы F = A, образующей угол 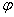с перемещением S = A. Из физики известно, что работа силы F при перемещении S равна 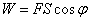. Таким образом, работа постоянной силы при прямолинейном перемещении её точки приложения равна скалярному произведению вектора силы F = B на вектор перемещения S = A.

Скалярное произведение векторов позволяет находить угол между двумя векторами. Поэтому оно часто встречается в последующих разделах математики, особенно, аналитической геометрии. Стоит ли говорить о том, что нахождение скалярного произведения векторов — фундаментальный навык для любого будущего инженера, проектирующего всё что угодно, от гладильных досок и лестниц-стремянок до зданий, или для программиста, собирающегося разрабатывать игры?

Экономический смысл скалярного произведения векторов

В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение

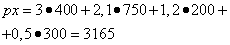
выражает суммарную стоимость всех товаров x.

Поделиться с друзьями

Начало темы «Векторы»

Продолжение темы «Векторы»

Теорема косинусів — Вікіпедія

Теорема косинусів — це твердження про властивість довільних трикутників, що є узагальненням теореми Піфагора. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших його сторін без подвоєного добутку цих сторін на косинус кута між ними.

У тригонометрії закон косинусів (також відомий як формула косинуса, правило косинусу або теорема Аль-Каші) пов’язує довжини сторін трикутника з косинусом одного з його кутів. Нехай a,b,c{\displaystyle a,b,c} сторони трикутника ABC{\displaystyle ABC}, а α,β,γ{\displaystyle \alpha ,\beta ,\gamma } це його кути, протилежні вказаним сторонам. Тоді,

c2=a2+b2−2abcos⁡γ{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \gamma \;};

a2=b2+c2−2bccos⁡α{\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha };

b2=a2+c2−2accos⁡β{\displaystyle b^{2}=a^{2}+c^{2}-2ac\cos \beta }.

Позначення кутів і сторін трикутника

Ця формула корисна для знаходження третьої сторони трикутника якщо відомі інші дві сторони та кут між ними, та для знаходження його кутів, якщо відомі довжини його сторін.^[1]

Із теореми косинусів: Косинус деякого кута трикутника дорівнює відношенню суми квадратів сторін, прилеглих до цього кута без квадрата протилежної йому сторони до подвоєного добутку прилеглих до кута сторін.

cos⁡α=b2+c2−a22bc{\displaystyle \cos \alpha ={\frac {b^{2}+c^{2}-a^{2}}{2bc}}};

cos⁡β=a2+c2−b22ac{\displaystyle \cos \beta ={\frac {a^{2}+c^{2}-b^{2}}{2ac}}};

cos⁡γ=a2+b2−c22ab{\displaystyle \cos \gamma ={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}.

Якщо c2=a2+b2{\displaystyle c^{2}=a^{2}+b^{2}\;} ⇔ cos⁡γ=0.{\displaystyle \cos \gamma =0.\;}

Твердження cos⁡γ=0{\displaystyle \cos \gamma =0} означає, що γ=90∘{\displaystyle \gamma =90^{\circ }} є прямим кутом, оскільки a,b{\displaystyle a,b} додатні. Іншими словами, це теорема Піфагора. Хоча теорема косинусів є загальнішою ніж теорема Піфагора, вона не може використовуватись для її доказу, оскільки теорема Піфагора сама використовується для доведення теореми косинусів.

Наслідки з теореми косинусів[ред. | ред. код]

За теоремою Піфагора у прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Якщо для довільного трикутника порівнювати квадрат сторони з сумою квадратів двох інших сторін, то, як зрозуміло з теореми косинусів, що буде більше залежить від того чи буде кут між цими сторонами гострим чи тупим. А саме, якщо квадрат сторони трикутника менший за суму квадратів двох інших сторін, то протилежний йому кут є гострим:

a2<b2+c2{\displaystyle a^{2}<b^{2}+c^{2}} або b2+c2−a2>0{\displaystyle b^{2}+c^{2}-a^{2}>0}, то α{\displaystyle \alpha } — гострий. Якщо квадрат деякої сторони трикутника більший від суми квадратів двох інших сторін, то протилежний йому кут є тупим:

Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін

a2>b2+c2{\displaystyle a^{2}>b^{2}+c^{2}} або b2+c2−a2<0{\displaystyle b^{2}+c^{2}-a^{2}<0}, то α{\displaystyle \alpha } — тупий. Якщо квадрат деякої сторони трикутника дорівнює сумі квадратів двох інших сторін, то протилежний йому кут є прямим:

a2=b2+c2{\displaystyle a^{2}=b^{2}+c^{2}} або b2+c2−a2=0{\displaystyle b^{2}+c^{2}-a^{2}=0}, то α{\displaystyle \alpha } — прямий.

Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін. Для паралелограма ABCD{\displaystyle ABCD} можна записати рівність:

AC2+BD2=AB2+BC2+CD2+AD2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+AD^{2}}^[2].

Доведення (для гострого кута)[ред. | ред. код]

Нехай a,b,c{\displaystyle a,b,c} це сторони трикутника ABC{\displaystyle ABC}, а A, B і C — це кути протилежні цим сторонам. Проведемо відрізок з вершини кута B, що утворює прямий кут із протилежною стороною b. Якщо довжина цього відрізка x, тоді sin⁡C=xa,{\displaystyle \sin C={\frac {x}{a}},\;} звідки x=a⋅sin⁡C.{\displaystyle x=a\cdot \sin C.\;}

Це означає, що довжина цього відрізку a⋅sin⁡C.{\displaystyle a\cdot \sin C.} Схожим чином, довжина частини b що з’єднує точку перетину відрізку із стороною b та кут C рівна a⋅cos⁡C.{\displaystyle a\cdot \cos C.} Решта довжини b рівна b−a⋅cos⁡C.{\displaystyle b-a\cdot \cos C.} Ми маємо два прямокутних трикутники, один з катетами a⋅sin⁡C,{\displaystyle a\cdot \sin C,\;} b−a⋅cos⁡C,{\displaystyle b-a\cdot \cos C,\;} і гіпотенузою c. Звідси, відповідно до теореми Піфагора:

Доведення теореми косинусів з використанням векторів[ред. | ред. код]

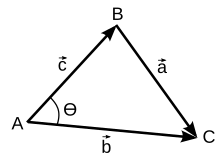Векторний трикутник

Використовуючи вектори, ми можемо легко довести теорему косинусів. Нехай ми маємо довільний трикутник із вершинами A, B, і C що утворений векторами a, b, і c, нам відомо, що:

• a=b−c{\displaystyle \mathbf {a=b-c} } звідси
• (b−c)⋅(b−c)=b⋅b−2b⋅c+c⋅c.{\displaystyle \mathbf {(b-c)\cdot (b-c)=b\cdot b-2b\cdot c+c\cdot c} .\;}

Згадавши чому дорівнює добуток двох векторів, отримаємо

• |a|2=|b|2+|c|2−2|b||c|cos⁡θ.{\displaystyle \mathbf {|a|^{2}=|b|^{2}+|c|^{2}-2|b||c|} \cos \theta .}

Теорема косинусів була доведена геометрично в «Началах» Евкліда. «Начала» відіграли важливу роль у розвитку математичної науки. Історичне значення цієї праці полягає в тому, що в ній уперше здійснено спробу логічної побудови геометрії на основі аксіоматики. Стихії Евкліда проклали шлях до відкриття закону косинусів. У XV столітті перський математик і астроном Джамшид аль-Каші подав перше явне твердження закону косинусів у формі, придатній для тріангуляції. Він надав точні тригонометричні таблиці та висловив теорему у формі, придатній для сучасного використання. Теорема косинусів була вперше сформульована і набула популярності у західному світі французьким математиком Франсуа Вієтом в XVI столітті. На початку XIX століття її стали записувати як теорему косинусів у її нинішній символічній формі.

↑ Геометрія (Мерзляк) 9 клас 2017. Шкільні підручники онлайн (uk). Процитовано 2019-12-29. 

↑ Гусев В. А., Мордкович А. Г. Математика: Справочные материалы: Книга для учащихся ОНЛАЙН. edu-lib.com (ru). Процитовано 2019-12-29. 

Теорема синусов — Википедия

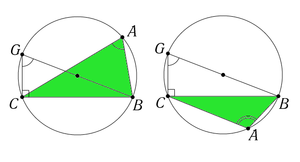
Достаточно доказать, что

asin⁡α=2R.{\displaystyle {\frac {a}{\sin \alpha }}=2R.}

Проведем диаметр |BG|{\displaystyle |BG|} для описанной окружности. По свойству углов, вписанных в окружность, угол GCB{\displaystyle GCB} прямой, а угол CGB{\displaystyle CGB} равен либо α{\displaystyle \alpha }, если точки A{\displaystyle A} и G{\displaystyle G} лежат по одну сторону от прямой BC{\displaystyle BC}, либо π−α{\displaystyle \pi -\alpha } в противном случае. Поскольку sin⁡(π−α)=sin⁡α{\displaystyle \sin(\pi -\alpha )=\sin \alpha }, в обоих случаях получаем

a=2Rsin⁡α{\displaystyle a=2R\sin \alpha }.

Повторив то же рассуждение для двух других сторон треугольника, получаем:

asin⁡α=bsin⁡β=csin⁡γ=2R.{\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R.}

Сферическая теорема синусов — Википедия

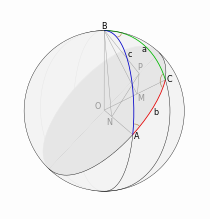Рисунок к доказательству теоремы синусов с помощью проекций.

Доказательство с помощью проекций^[1]. На рисунке показан сферический треугольник ABC на сфере радиуса R с центром в точке O. BP — перпендикуляр к плоскости большого круга, проходящего через сторону b, BM — перпендикуляр к OC, BN — перпендикуляр к OA. По утверждению, обратному теореме о трёх перпендикулярах, PM — перпендикуляр к OC, PN — перпендикуляр к OA. Заметим, что угол PMB равен π — C, кроме того, BN = R sin c и BM = R sin a. Далее, проецируем BN и BM на BP, получаем:

BP=BNsin⁡∠BNP=Rsin⁡csin⁡A,{\displaystyle BP=BN\sin \angle BNP=R\sin c\sin A,}

BP=BMsin⁡∠PMB=Rsin⁡asin⁡(π−C)=Rsin⁡asin⁡C,{\displaystyle BP=BM\sin \angle PMB=R\sin a\sin(\pi -C)=R\sin a\sin C,}

sin⁡asin⁡A=sin⁡csin⁡C{\displaystyle {\frac {\sin a}{\sin A}}={\frac {\sin c}{\sin C}}}

Аналогично получаем второе равенство.

Доказательство, опирающееся на уже доказанные соотношения между сторонами и углами сферического прямоугольного треугольника. Опустим из вершины C перпендикуляр CD = h на сторону с или её продолжение. Выразим h двояким образом из возникших при этом прямоугольных треугольников ACD и BCD:

sin⁡h=sin⁡bsin⁡A=sin⁡asin⁡B.{\displaystyle \sin h=\sin b\sin A=\sin a\sin B.}

Отсюда получаем пропорцию

sin⁡asin⁡A=sin⁡bsin⁡B,{\displaystyle {\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}},}

к которой аналогичным образом добавляем отношение третьей пары «сторона-угол».