Формулы Виета — Википедия

У этого термина существуют и другие значения, см. Виет.

Формулы Виета — формулы, связывающие коэффициенты многочлена и его корни.

Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

Эти тождества неявно присутствуют в работах Франсуа Виета. Однако Виет рассматривал только положительные вещественные корни, поэтому у него не было возможности записать эти формулы в общем виде.^{[1]:138—139}

Если c1,c2,…,cn{\displaystyle c_{1},c_{2},\ldots ,c_{n}} — корни многочлена

xn+a1xn−1+a2xn−2+…+an,{\displaystyle x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots +a_{n},}

(каждый корень взят соответствующее его кратности число раз), то коэффициенты a1,…,an{\displaystyle a_{1},\ldots ,a_{n}} выражаются в виде симметрических многочленов от корней^[2], а именно:

a1=−(c1+c2+…+cn)a2=c1c2+c1c3+…+c1cn+c2c3+…+cn−1cna3=−(c1c2c3+c1c2c4+…+cn−2cn−1cn)…an−1=(−1)n−1(c1c2…cn−1+c1c2…cn−2cn+…+c2c3…cn)an=(−1)nc1c2…cn{\textstyle {\begin{matrix}a_{1}&=&-(c_{1}+c_{2}+\ldots +c_{n})\\a_{2}&=&c_{1}c_{2}+c_{1}c_{3}+\ldots +c_{1}c_{n}+c_{2}c_{3}+\ldots +c_{n-1}c_{n}\\a_{3}&=&-(c_{1}c_{2}c_{3}+c_{1}c_{2}c_{4}+\ldots +c_{n-2}c_{n-1}c_{n})\\&&\ldots \\a_{n-1}&=&(-1)^{n-1}(c_{1}c_{2}\ldots c_{n-1}+c_{1}c_{2}\ldots c_{n-2}c_{n}+\ldots +c_{2}c_{3}…c_{n})\\a_{n}&=&(-1)^{n}c_{1}c_{2}\ldots c_{n}\end{matrix}}}

Иначе говоря, (−1)kak{\displaystyle (-1)^{k}a_{k}} равно сумме всех возможных произведений из k{\displaystyle k} корней.

Следствие: из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленный.

Если старший коэффициент многочлена не равен единице:

a0xn+a1xn−1+a2xn−2+…+an,{\displaystyle a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots +a_{n},}

то для применения формулы Виета необходимо предварительно разделить все коэффициенты на a0{\displaystyle a_{0}} (это не влияет на значения корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему:

aka0=(−1)k∑1⩽i1<i2<⋯<ik⩽nci1ci2⋯cik, k=1,2…n{\displaystyle {\frac {a_{k}}{a_{0}}}=(-1)^{k}\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}c_{i_{1}}c_{i_{2}}\cdots c_{i_{k}},\ k=1,2\dots n}

Доказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням, учитывая, что a0=1{\displaystyle a_{0}=1}

xn+a1xn−1+a2xn−2+…+an=(x−c1)(x−c2)⋯(x−cn){\displaystyle x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots +a_{n}=(x-c_{1})(x-c_{2})\cdots (x-c_{n})}

Приравнивая коэффициенты при одинаковых степенях x{\displaystyle x} (теорема единственности), получаем формулы Виета.

Квадратное уравнение[править | править код]

Если x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} — корни квадратного уравнения  ax2+bx+c=0{\displaystyle \ ax^{2}+bx+c=0} ,то

{ x1+x2= −ba x1x2= ca{\displaystyle {\begin{cases}~x_{1}+x_{2}=~-{\dfrac {b}{a}}\\~x_{1}x_{2}=~{\dfrac {c}{a}}\end{cases}}}

В частном случае, если a=1{\displaystyle a=1} (приведенная форма x2+px+q=0{\displaystyle x^{2}+px+q=0}), то

{ x1+x2=−p x1x2=q{\displaystyle {\begin{cases}~x_{1}+x_{2}=-p\\~x_{1}x_{2}=q\end{cases}}}

Кубическое уравнение[править | править код]

Если x1,x2,x3{\displaystyle x_{1},x_{2},x_{3}} — корни кубического уравнения p(x)=ax3+bx2+cx+d=0{\displaystyle p(x)=ax^{3}+bx^{2}+cx+d=0}, то

{x1+x2+x3=−bax1x2+x1x3+x2x3=cax1x2x3=−da{\displaystyle {\begin{cases}x_{1}+x_{2}+x_{3}=-{\dfrac {b}{a}}\\x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3}={\dfrac {c}{a}}\\x_{1}x_{2}x_{3}=-{\dfrac {d}{a}}\end{cases}}}

Из приведенного выше доказательства видно, что формулы Виета получаются чисто алгебраически из свойств сложения и умножения. Поэтому они применимы к многочленам с коэффициентами из произвольной области целостности K{\displaystyle \mathbb {K} }, если старший коэффициент многочлена равен единице K,{\displaystyle \mathbb {K} ,} а корни располагаются в алгебраическом замыкании поля частных для K.{\displaystyle \mathbb {K} .}

Если коэффициенты многочлена берутся из произвольного коммутативного кольца, не являющегося областью целостности (то есть имеющего делители нуля), то формулы Виета, вообще говоря, не выполняются. Например, рассмотрим в качестве K{\displaystyle \mathbb {K} } кольцо вычетов по модулю 8 и многочлен P(x)=x2−1.{\displaystyle P(x)=x^{2}-1.} Он имеет в этом кольце не два, а четыре корня: 1,3,5,7.{\displaystyle 1,3,5,7.} Поэтому использованное в доказательстве разложение на линейные множители, число которых равно числу корней, не имеет места, и формулы Виета, как легко проверить, неверны.

• Винберг Э. Б. Алгебра многочленов. Учебное пособие для студентов-заочников III—IV курсов физико-математических факультетов педагогических институтов. — М.: Просвещение, 1980.
• Weisstein, Eric W. Vieta’s Formulas / From MathWorld—A Wolfram Web Resource (англ.)
• Hazewinkel, Michiel, ed. (2001), «Viète theorem» (недоступная ссылка), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 (англ.)
• Funkhouser, H. Gray (1930), «A short account of the history of symmetric functions of roots of equations», American Mathematical Monthly (Mathematical Association of America) 37 (7): 357–365, doi:10.2307/2299273, JSTOR 2299273 (англ.)

Тригонометрическая формула Виета — Википедия

Материал из Википедии — свободной энциклопедии

Тригонометрическая формула Виета — один из способов решения кубического уравнения x3+ax2+bx+c=0{\displaystyle x^{3}+ax^{2}+bx+c=0}

Первым решение этого уравнения нашел Никколо Тарталья, Джероламо Кардано опубликовал его решение в 1545 году под своим именем (см. формула Кардано). Однако формула Виета более удобна для практического применения:

• Вычисляем Q=a2−3b9{\displaystyle Q={\frac {a^{2}-3b}{9}}}
• Вычисляем R=2a3−9ab+27c54{\displaystyle R={\frac {2a^{3}-9ab+27c}{54}}}
• Вычисляем S=Q3−R2{\displaystyle S=Q^{3}-R^{2}}
• Если S>0{\displaystyle S>0}, то вычисляем ϕ=13arccos⁡(RQ3){\displaystyle \phi ={\frac {1}{3}}\arccos \left({\frac {R}{\sqrt {Q^{3}}}}\right)} и имеем три действительных корня:

  x1=−2Qcos⁡(ϕ)−a3{\displaystyle x_{1}=-2{\sqrt {Q}}\cos(\phi )-{\frac {a}{3}}}

  x2,3=−2Qcos⁡(ϕ±23π)−a3{\displaystyle x_{2,3}=-2{\sqrt {Q}}\cos \left(\phi \pm {\frac {2}{3}}\pi \right)-{\frac {a}{3}}}

• Если S<0{\displaystyle S<0}, то заменяем тригонометрические функции гиперболическими. Здесь возможны следующие случаи в зависимости от знака Q{\displaystyle Q}:
  • Q>0{\displaystyle Q>0}:

    ϕ=13Arch⁡(|R|Q3){\displaystyle \phi ={\frac {1}{3}}\,\operatorname {Arch} \left({\frac {|R|}{\sqrt {Q^{3}}}}\right)}

    x1=−2sgn⁡(R)Qch⁡(ϕ)−a3{\displaystyle x_{1}=-2\operatorname {sgn}(R){\sqrt {Q}}\,\operatorname {ch} (\phi )-{\frac {a}{3}}} (действительный корень)

    x2,3=sgn⁡(R)Qch⁡(ϕ)−a3±i3Qsh⁡(ϕ){\displaystyle x_{2,3}=\operatorname {sgn}(R){\sqrt {Q}}\,\operatorname {ch} (\phi )-{\frac {a}{3}}\pm i{\sqrt {3}}{\sqrt {Q}}\,\operatorname {sh} (\phi )} (пара комплексных корней)

  • Q<0{\displaystyle Q<0}:

    ϕ=13Arsh⁡(|R||Q|3){\displaystyle \phi ={\frac {1}{3}}\,\operatorname {Arsh} \left({\frac {|R|}{\sqrt {|Q|^{3}}}}\right)}

    x1=−2sgn⁡(R)|Q|sh⁡(ϕ)−a3{\displaystyle x_{1}=-2\operatorname {sgn}(R){\sqrt {|Q|}}\,\operatorname {sh} (\phi )-{\frac {a}{3}}} (действительный корень)

    x2,3=sgn⁡(R)|Q|sh⁡(ϕ)−a3±i3|Q|ch⁡(ϕ){\displaystyle x_{2,3}=\operatorname {sgn}(R){\sqrt {|Q|}}\,\operatorname {sh} (\phi )-{\frac {a}{3}}\pm i{\sqrt {3}}{\sqrt {|Q|}}\,\operatorname {ch} (\phi )} (пара комплексных корней)

  • Q=0{\displaystyle Q=0}:

  x1=−c−a3273−a3{\displaystyle x_{1}=-{\sqrt[{3}]{c-{\frac {a^{3}}{27}}}}-{\frac {a}{3}}} (действительный корень)

  x2,3=−a+x12±i2|(a−3×1)(a+x1)−4b|{\displaystyle x_{2,3}=-{\frac {a+x_{1}}{2}}\pm {\frac {i}{2}}{\sqrt {|(a-3x_{1})(a+x_{1})-4b|}}} (пара комплексных корней)

• Если S=0{\displaystyle S=0}, то уравнение вырождено и имеет меньше 3 различных решений (второй корень кратности 2):

  x1=−2sgn⁡(R)Q−a3=−2R3−a3{\displaystyle x_{1}=-2\operatorname {sgn}(R){\sqrt {Q}}-{\frac {a}{3}}=-2{\sqrt[{3}]{R}}-{\frac {a}{3}}}

  x2=sgn⁡(R)Q−a3=R3−a3{\displaystyle x_{2}=\operatorname {sgn}(R){\sqrt {Q}}-{\frac {a}{3}}={\sqrt[{3}]{R}}-{\frac {a}{3}}}

• Исходный многочлен имеет вид P(x1)=x13+a⋅x12+b⋅x1+c{\displaystyle P(x_{1})=x_{1}^{3}+a\cdot x_{1}^{2}+b\cdot x_{1}+c}.

• Подстановкой x1=x−a3{\displaystyle x_{1}=x-{\frac {a}{3}}} приводим многочлен к виду Q(x)=x3+p⋅x+q{\displaystyle Q(x)=x^{3}+p\cdot x+q}, где p=b−a23{\displaystyle p=b-{\frac {a^{2}}{3}}} и q=2a327−ab3+c{\displaystyle q={\frac {2a^{3}}{27}}-{\frac {ab}{3}}+c}.

• Ищем решение уравнения Q(x)=x3+p⋅x+q=0{\displaystyle Q(x)=x^{3}+p\cdot x+q=0} в виде x=A⋅cos⁡φ{\displaystyle x=A\cdot \cos \varphi }, получаем уравнение A3⋅cos3⁡φ+Ap⋅cos⁡φ=−q{\displaystyle A^{3}\cdot \cos ^{3}\varphi +Ap\cdot \cos \varphi =-q}.

• Заметим что в случае p<0{\displaystyle p<0} при A=−4p3{\displaystyle A={\sqrt {-{\frac {4p}{3}}}}} это уравнение приобретает вид A34⋅(4cos3⁡φ−3cos⁡φ)=−q{\displaystyle {\frac {A^{3}}{4}}\cdot {\Big (}4\cos ^{3}\varphi -3\cos \varphi {\Big )}=-q}.

• Используя тригонометрическое тождество cos⁡3φ=4cos3⁡φ−3cos⁡φ{\displaystyle \cos 3\varphi =4\cos ^{3}\varphi -3\cos \varphi } приходим к уравнению вида cos⁡3φ=−4qA3{\displaystyle \cos 3\varphi =-{\frac {4q}{A^{3}}}}.

• Решение этого уравнения имеет вид φk=13arccos⁡(−4qA3)+2πk3{\displaystyle \varphi _{k}={\frac {1}{3}}\arccos {\Big (}-{\frac {4q}{A^{3}}}{\Big )}+{\frac {2\pi k}{3}}}, где k{\displaystyle k} пробегает значения 1, 2, 3.

• Подставляя полученные значения φk{\displaystyle \varphi _{k}} в выражение для переменной x{\displaystyle x}, получаем ответ xk=A⋅cos⁡φk{\displaystyle x_{k}=A\cdot \cos \varphi _{k}}

Формула Виета — решение кубических уравнений

Формула Виета

Рассмотрим кубическое уравнение:
(1)   .
Сделаем подстановку:
.
Получаем уравнение приведенного вида:
(2)   ,
где
(3)   ;   .

Тригонометрическая формула Виета, для корней , , приведенного кубического уравнения (2), имеет вид:
(4)   ;
(5)   ;
где
(6)   ;   .

Условие применимости формулы Виета

Поскольку , то формула Виета применима при
.

Действительно, из (6) имеем:
;   .
Возводим в квадрат и выполняем преобразования:
;
;
.

Как показано на странице “Решение кубических уравнений”, при выполнении условия , кубическое уравнение имеет три действительных корня. То есть формула Виета применяется в том случае, когда кубическое уравнение имеет действительные корни.

Вывод формулы Виета

Для вывода формулы Виета, используем формулу Кардано:
(7)   ;
(8)   ;
(9)   ;
(10)   ;
(11)   .

Считаем, что .
Из (11) следует, что в этом случае, . Квадратный корень из имеет два значения. Мы можем взять любое значение. Возьмем со знаком плюс (при выборе другого значения, со знаком минус, и поменяются местами и мы не получим ничего нового):
.
Тогда
,
где – целое. Здесь мы ввели модуль и аргумент числа .
;
;
;   .

Извлекаем кубический корень:
.
При , мы имеем три значения кубического корня.
По формуле (10) находим:
.
По формуле (7) имеем:
.

Полагая , мы получаем три корня приведенного уравнения:
;
;
.

Формула Виета доказана.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

Автор: Олег Одинцов.     Опубликовано: 30-09-2016

Решение кубических уравнений

Здесь мы рассматриваем решение кубических уравнений вида
(1)   .
Далее считаем, что – это действительные числа.

Если исходное уравнение имеет вид:
(2)   ,
то разделив его на , получаем уравнение вида (1) с коэффициентами
.

Уравнение (1) имеет три корня: , и . Один из корней всегда действительный. Действительный корень мы обозначаем как . Корни и могут быть либо действительными, либо комплексно сопряженными. Действительные корни могут быть кратными. Например, если , то и – это двукратные корни (или корни кратности 2), а – простой корень.

Если известен один корень

Пусть нам известен один корень кубического уравнения (1). Обозначим известный корень как . Тогда разделив уравнение (1) на , получим квадратное уравнение. Решая квадратное уравнение, найдем еще два корня и .

Для доказательства воспользуемся тем, что кубический многочлен можно представить в виде:
.
Тогда, разделив (1) на , получаем квадратное уравнение.

Примеры деления многочленов представлены на странице
“Деление и умножение многочлена на многочлен уголком и столбиком”.
Решение квадратных уравнений рассмотрено на странице
“Корни квадратного уравнения”.

Если один из корней – целый

Если исходное уравнение имеет вид:
(2)   ,
и его коэффициенты , , , – целые числа, то можно попытаться найти целый корень. Если это уравнение имеет целый корень, то он является делителем коэффициента . Метод поиска целых корней заключается в том, что мы находим все делители числа и проверяем, выполняется ли для них уравнение (2). Если уравнение (2) выполняется, то мы нашли его корень. Обозначим его как . Далее делим уравнение (2) на . Получаем квадратное уравнение. Решая его, находим еще два корня.

Примеры определения целых корней даны на странице
Примеры разложения многочленов на множители > > >.

Поиск рациональных корней

Если в уравнении (2) , , , – целые числа, причем , и целых корней нет, то можно попытаться найти рациональные корни, то есть корни вида , где и – целые.

Для этого умножим уравнение (2) на и сделаем подстановку :
;
(3)   .
Далее ищем целые корни уравнения (3) среди делителей свободного члена .

Если мы нашли целый корень уравнения (3), то, возвращаясь к переменной , получаем рациональный корень уравнения (2):
.

Формулы Кардано и Виета для решения кубического уравнения

Если нам не известен ни один корень, и целых корней нет, то найти корни кубического уравнения можно по формулам Кардано.

Рассмотрим кубическое уравнение:
(1)   .
Сделаем подстановку:
.
После этого уравнение приводится к неполному или приведенному виду:
(4)   ,
где
(5)   ;   .

Формула Кардано для неполного (приведенного) кубического уравнения имеет вид:
;
;
;
;
.
По формуле Кардано, мы находим три корня величины . Затем, используя формулу   , находим значения величины .

После разделения кубических корней величины , формула Кардано принимает следующий вид:
(6)   ,   ,
где
(7)   ;   ;   ;
(8)   .

При , для и нужно выбирать действительные корни, которые автоматически связаны соотношением   . При этом мы получим одно действительное решение и два комплексно сопряженных и .

При имеем:
;   ;   .
В этом случае мы имеем два кратных действительных корня. Если , то мы имеем три кратных корня.

При мы имеем три действительных корня. При этом и – комплексные. Поэтому решение приводится к тригонометрической форме, которая имеет название формулы Виета:
(9)   ;
(10)   ,
где
(11)   ;   .

Примеры решений по формулам Кардано и Виета

Решить кубические уравнения:
;
.

Решение примеров > > >

Онлайн калькулятор > > >

---

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

Автор: Олег Одинцов.     Опубликовано: 30-04-2016   Изменено: 02-10-2016

Теорема Виета ℹ️ формулировка и формула для квадратного и кубического уравнения, доказательство обратной теоремы, методы, правила и примеры решения задач

Общие сведения

Для применения формул теоремы Виета для квадратного уравнения следует разобрать некоторые термины и математические определения. Квадратным уравнением вида Am² + Bm + C = 0 называется многочлен второй степени, состоящий из коэффициента А при некоторой неизвестной в квадрате и суммы произведения второго коэффициента на неизвестную величину и константы С. Этот многочлен преобразовывается в уравнение только при равенстве нулевому значению. Константу С еще называют свободным членом.

Корнями называются такие значения неизвестных, при подстановке которых тождество считается верным. Следует отметить, что в результате отдельных математических преобразований появляются дополнительные корни. Особенно это касается различных замен в тригонометрических функциях. Однако при подстановке корней равенство не соблюдается. Математики называют их ложными. После решения уравнения специалисты рекомендуют произвести подстановку этих значений в исходное уравнение. Этот прием помогает избавиться от нежелательных решений.

Поиск корней при помощи теоремы Виета принадлежит к быстрым методикам, поскольку избавляет человека от ненужных расчетов по формулам с применением дискриминанта.

Виды квадратных уравнений

Квадратные уравнения бывают нескольких видов, поскольку не во всех случаях коэффициенты получаются отличными от нуля. Математики классифицировали их на 2 типа:

• полные;
• неполные.

Первыми называются выражения со всеми коэффициентами (A, B и C), отличными от нуля. Если число перед неизвестной не указано, то считается, что оно эквивалентно 1. Неполными считаются любые уравнения, в которых отсутствует B или C. Однако бывают случаи, когда оба последних коэффициента соответствуют нулю, тогда тождество имеет следующий вид: Am² = 0. Кроме того, существует еще один критерий распределения на виды, основанный на степени приведенности. По этому признаку выражения делятся на приведенные и неприведенные классы.

К первым следует отнести любые равенства, у которых коэффициент равен 1. Во всех остальных случаях (А > 1) тождества являются неприведенными.

Условие использования закона

Закон Виета применим не ко всем уравнениям. Математики сформулировали важные условия, при соблюдении которых возможно воспользоваться этим правилом: уравнение должно быть приведенным и иметь значение дискриминанта больше 0. Из этого условия можно сделать вывод: когда равенство невозможно преобразовать к приведенному, следует применять другие методики нахождения корней, а не правило Виета.

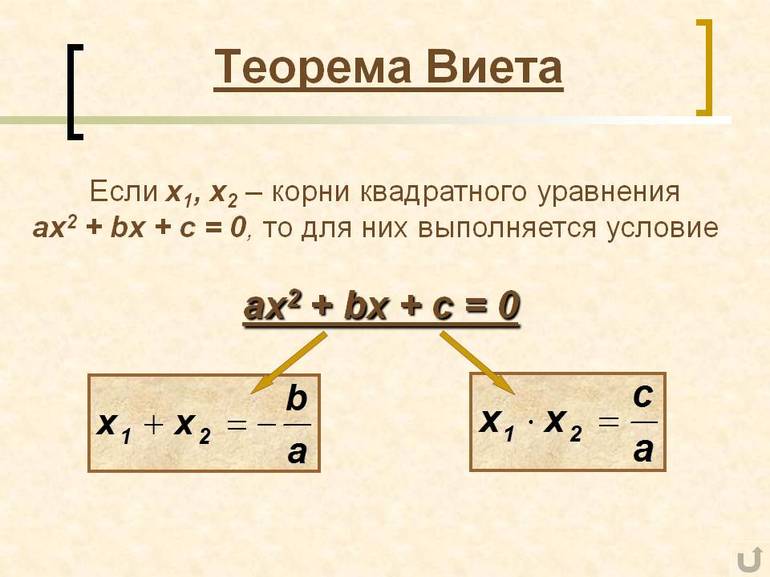
Существует простой алгоритм преобразования уравнения к необходимому виду. Для этого нужно выполнить несложную операцию деления каждого коэффициента на

А. Например, следует преобразовать уравнение 4p² + 8p + 16 = 0 в приведенное. Следуя описанному алгоритму, получается такое соотношение: [(4p²) / 4] + [8p / 4] + [16 / 4] = 4p² + 2p + 4 = 0.

Специалисты рекомендуют избегать ситуаций получения обыкновенных дробей в результате преобразования. Примером является тождество 3p² + 2p — 4 = 0. Его можно свести к приведенному, но применить теорему будет весьма сложно, поскольку равенство будет иметь такой вид: p² + (2p / 3) — (4 / 3) = 0. Рекомендуется решать такие уравнения, используя другие методики (построение графика функции, при помощи программ или по формуле дискриминанта).

Применение теоремы

Формулировка закона Виета для квадратного уравнения A

m² + Bm + C = 0 следующая: сумма корней соответствует коэффициенту А, взятому с противоположным знаком, а результат произведения эквивалентен свободному члену С. Решение осуществляется методом подбора соответствующих числовых значений. Однако каждая теорема должна доказываться.

Чтобы осуществить эту операцию, нужно воспользоваться специальными формулами корней, используя дискриминант. Нужно предположить, что для уравнения Am² + Bm + C = 0 справедливы два равенства: m1 + m2 = -B и m1 * m2 = C. Выражая значения корней через дискриминант в обобщенном виде, можно получить такие тождества:

1. m1 = [-B — D^(½)] / (2 * A).
2. m2 = [-B + D^(½)] / (2 * A).

Далее нужно найти сумму m1 и m2: [-B — D^(½)] / (2 * A) + [-B + D^(½)] / (2 * A). Чтобы упростить полученное выражение, следует воспользоваться таким алгоритмом:

1. Привести дроби к общему знаменателю: [(-B — D^(½)) + (-B + D^(½))]/(2 * А).
2. Упростить выражение (разложение на множители): [-B — D^(½) — B + D^(½)]/(2 * А) = (-2B) / (2 * A) = — B / A = -B / 1 (А = 1).

После этого нужно доказать, что произведение корней эквивалентно С. Для этого необходимо перемножить m1 = [-B — D^(½)] / (2 * A) и m2 = [-B + D^(½)] / (2 * A), воспользовавшись правилом умножения дробей обыкновенного типа по такой методике:

1. Перемножить числители и знаменатели: [-B — D^(½)] / (2 * A) * [-B + D^(½)] / (2 * A) = [(-B + D^(½)) * (-B — D^(½))] / (4 * A²).
2. Упростить: [B² — D] / 4A² = [B ² — (-B² — 4 * A * C)] / 4A² = (B² — B² + 4 * C) / 4 = C (при А = 1).

Вторая формула доказана. Однако перед решением обязательно следует вычислить значение дискриминанта, поскольку при D = 0 уравнение имеет только один корень. Существует обратная теорема Виета. У нее такая формулировка: если сумма чисел m1 и m2 соответствует некоторому значению В, взятому с противоположным знаком, а также их произведение эквивалентно свободному члену многочлена второй степени, значит, они являются корнями Аm ² + Bm + C = 0. Это утверждение имеет доказательство, для которого следует выполнить следующие шаги:

1. Подставить m1 и m2 в исходное уравнение: m² — (m1 + m2) * m + m1 * m2 = 0.
2. Раскрыть скобки и привести подобные слагаемые: m² — (m1 * m — m2 * m + m1 * m2 = (m — m1) * (m — m2) = 0.
3. Найти корни тождества в пункте 2: m = m1 и m = m2.

Следовательно, теорема доказана, поскольку числа m1 и m2 являются корнями уравнения. Далее нужно рассмотреть приведенные кубические уравнения и порядок применения утверждения Виета.

Кубические равенства с неизвестным

Можно также применять теорему Виета для кубического уравнения вида А * m³ + B * m² + C * m + D = 0. Коэффициент А должен быть равен 1. Находятся корни при помощи перебора значений, но сделать это сложно, поскольку необходимо решить систему, состоящую из трех равенств:

1. m1 + m2 + m3 = -B.
2. m1 * m2 + m1 * m3 + m2 * m3 = C.
3. m1 * m2 * m3 = -D.

Числа m1, m2 и m3 являются корнями. Кроме того, следует обратить внимание на образование ложных результатов, поскольку уравнение является кубическим. Ученые пришли к выводу о том, что чем выше степень, тем больше образовывается ложных ответов. Они рекомендуют применять специальное программное обеспечение для поиска решения. Если его нет под рукой, то можно построить график функции, а затем найти точки пересечения с осью абсцисс. Существуют также специализированные веб-сервисы. Они называются онлайн-калькуляторами.

Примеры решения

Несмотря на простоту теоремы, существует несколько типов упражнений на эту тему. Они делятся на следующие классы:

• простые;
• средние;
• продвинутые;
• сложные.

К первым следует отнести задачи на простой подбор корней. Средними считаются задания на преобразование квадратного уравнения к приведенному.

Продвинутыми являются любые тождества, которые необходимо упростить и привести к коэффициенту А = 1. Сложные — особый вид. Для них следует применить все знания в области математики. Кроме того, нужно осуществить объяснение хода решения. В некоторых случаях необходимо построить таблицу зависимостей и начертить график.

Интересный факт заключается в том, что именно этот класс выражений существенно развивает умственные способности человека на уроках. Встречаются также задачи на пересечения параболы и прямой, которая может проходить под определенным углом. Далее нужно разобрать практическое применение теоремы Виета на примерах с решением для различных классов задач.

Простой и средний

Пусть дано тождество m² — 5 * m + 6 = 0. Необходимо найти его корни. Для решения следует применить такой алгоритм:

1. Найти дискриминант: D = (-5)^2 — 4 * 1 * 6 = 1 (два корня, поскольку D > 0).
2. Методом перебора можно получить решения m1 = 2 и m2 = 3.
3. Проверка I корня: 2² — 5 * 2 + 6 = 4 — 10 + 6 = 0 (соответствует).
4. Подстановка для II: 3² — 5 * 3 + 6 = 9 — 15 + 6 = 0 (соответствует).

Следовательно, тождество решено верно. Далее можно рассмотреть средний тип упражнения. Для этого следует решить уравнение 3 * m² + 33 * m + 30 = 0. Найти корни можно по такому алгоритму:

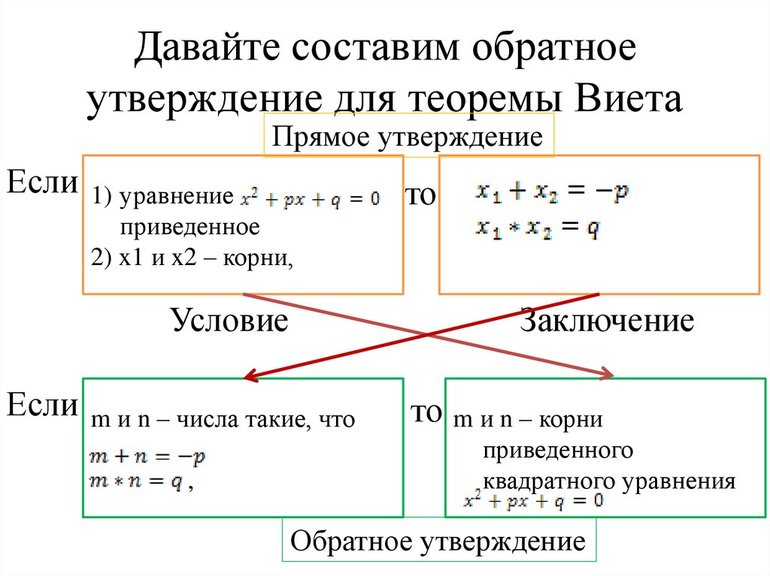
1. Преобразование к приведенному (разделить на А = 3): 3 * m² + 33 * m + 30 = m² + 11 * m + 10 = 0.
2. Найти D: D = 121 — 4 * 10 = 81 > 0 (два).
3. Корни: m1 = -10 и m2 = -1.
4. Проверка: (-10)^2 + 11 * (-10) + 10 = 100 — 110 + 10 = 0 и (-1)^2 + 11 * (-1) + 10 = 1 — 11 + 10 = 0.

​Следовательно, корни m1 и m2 удовлетворяют этому уравнению. Если не получается делить все члены на А, то необходимо рассмотреть решение с помощью дискриминанта или графическим методом.

Продвинутый класс

Для иллюстрации этого вида нужно решить следующее тождество: (m — 4)^2 — 20 = -m (m — 8) + 14. Следует воспользоваться инструкцией такого вида:

1. Раскрыть скобки: m² — 8 * m + 16 — 20 = -m² + 8 * m + 14.
2. Перенести все слагаемые в левую часть и упростить: 2 * m² — 16 * m — 18 = 0.
3. Сократить на 2: m² — 8 * m — 9 = 0.
4. Найти значение D: D = 64 + 36 = 100 > 0 (2).
5. Вычисление корней: m1 = -1 и m2 = 9.
6. Проверка: (-1)^2 — 8 * (-1) — 9 = 1 + 8 — 9 = 0 и 9² — 8 * 9 — 9 = 81 — 72 — 9 = 0.

На основании шестого пункта можно сделать вывод, что корни подобраны правильно. Этот пример показывает, что одной теоремы недостаточно, поскольку следует уметь выполнять математическое преобразование заданного выражения. В этом классе примеров возможен случай, когда величина дискриминанта эквивалентна 0. Следовательно, у тождества с неизвестным всего один корень. К последнему невозможно применить закон Виета.

Сложные упражнения

Примером сложной задачи, которую еще называют «со звездочкой», является следующая: необходимо найти сумму, произведение и сумму квадратов решений уравнения m ² — 7 * m + 12 = 0, не находя корней. По обычной методике нужно доказать, что у выражения с неизвестным существует два корня по формуле дискриминанта: D = 49 — 4 * 12 = 1 > 0. Следовательно, ориентируясь на последнее равенство, условие соблюдается. По теореме Виета получаются ответы на первые два вопроса:

1. m1 + m2 = 7.
2. m1 * m2 = 12.

Затем следует записать сумму квадратов, используя две описанные выше формулы: (m1)^2 + (m2)^2 = (m1)^2 + (m2)^2 — 2 * m1 * m2 — 2 * m1 * m2 = (m1 + m2)^2 — 2 * m1 * m2 = 7 ² — 2 * 12 = 25. Задача решена: 7; 12 и 25.

Следующий пример является довольно распространенным. Существует уравнение 5 * m ² — 15 * m + 30 = 0. Необходимо найти сумму кубов корней и квадрат разности. Многие ученики на протяжении всей истории существования алгебры делают однотипную ошибку. Она заключается в подготовке, то есть записываются соответствующие формулы сокращенного умножения. Если их не знают, то пользуются интернетом или другими источниками. На эту операцию тратится драгоценное время. Чтобы этого избежать, необходимо воспользоваться таким алгоритмом:

1. Сократить на общий множитель, равный 5: m² — 3 * m + 10 = 0.
2. Вычислить величину дискриминанта: D = 9 — 4 * 1 * 10 = -31 < 0.

Следовательно, у равенства с неизвестными корней нет вообще. В результате невозможно найти необходимые значения. Этот прием лишний раз показывает, что можно избежать множества ошибок и не тратить время, пользуясь соответствующим алгоритмом.

Решение квадратных и кубических приведенных уравнений осуществляется при помощи соотношения Виета. Однако важным аспектом при осуществлении этой операции является нахождение величины дискриминанта.

Кубические уравнения, формулы и примеры

Определение и формула кубического уравнения

Решение таких уравнений всегда можно найти с помощью формул Кардано (Джероламо (Джироламо, Иероним) Кардано (1501-1576) — итальянский математик, инженер, философ, медик и астролог).

Формулы Кардано — формулы для нахождения корней приведенного кубического уравнения

   

К такому виду может быть приведено любое кубическое уравнение общего вида (1) заменой . Коэффициенты уравнений (1) и (2) после такой замены связаны соотношениями:

   

Решение приведенного кубического уравнения (2) ищем в виде

   

После подстановки уравнение сводится к виду

   

Функции и выбираются так, чтобы слагаемое

   

Для нахождения функций и нужно решить систему

   

которая после замены , приводится к системе

   

Согласно теореме Виета, значения и являются корнями квадратного уравнения

   

Откуда

   

Выполняя обратную замену, находим три такие пары и , удовлетворяющие условию . А тогда находим три корня уравнения (2) , откуда .

Примеры решения задач

Понравился сайт? Расскажи друзьям!