Все формулы сторон равнобедренной трапеции

---

1. Формула длины основания равнобедренной трапеции через среднюю линию

 

a — нижнее основание

b — верхнее основание

m — средняя линия

 

 

Формулы длины основания:

 

 

2. Формулы длины сторон через высоту и угол при нижнем основании

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α — угол при основании трапеции

h — высота трапеции

 

Формулы всех четырех сторон трапеции:

 

---

 

3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

d — диагонали

α , β — углы между диагоналями

h — высота трапеции

 

Формулы длины сторон трапеции:

справедливо для данной ситуации:

---

 

4. Формулы длины сторон равнобедренной трапеции через площадь

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α , β — углы при основаниях

m — средняя линия

h — средняя линия

 

Формулы длины сторон равнобедренной трапеции через площадь:

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

www-formula.ru

Все формулы высоты равнобедренной трапеции

---

1. Формула высоты равнобедренной трапеции через стороны и углы при основании

 

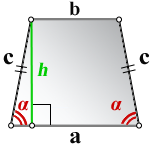
a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α — угол при нижнем основании

h — высота трапеции

 

Формулы длины высоты, (h ):

 

 

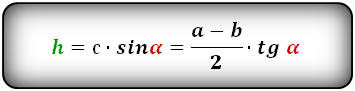
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними

 

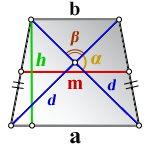
_d — диагонали трапеции

α , β — углы между диагоналями

a , b — основания

h — высота трапеции

m — средняя линия

 

Формулы длины высоты, (h ):

---

 

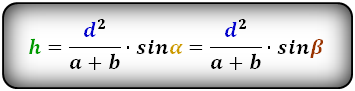
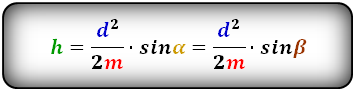
3. Формула высоты равнобедренной трапеции через площадь

 

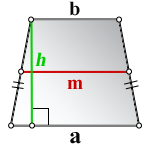
S — площадь трапеции

a , b — основания

h — высота трапеции

m — средняя линия

 

Формулы длины высоты, (h ):

---

---

 

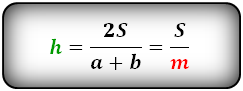
Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

www-formula.ru

Углы при основании равнобедренной трапеции

Утверждение.

(Свойство равнобедренной трапеции)

Углы при основании равнобедренной трапеции равны.

 

   

   

 

 

Дано: ABCD — трапеция,

AD ∥ BC,AB=CD.

Доказать:∠A=∠D, ∠B=∠C.

Доказательство:

 

1) Проведем из вершин тупых углов высоты BF и CK:

   

   

2) Рассмотрим треугольники ABF и DCK.

∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).

AB=CD (по условию),

BF=CK (как высоты трапеции).

Отсюда следует, что треугольники ABF и DCK равны (по катету и гипотенузе).

3) Из равенства треугольников следует равенство соответствующих углов: ∠A=∠D.

4) ∠A+∠ABC=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Отсюда, ∠ABC=180º-∠A.

Аналогично, ∠D+∠DCB — внутренние односторонние при AD ∥ BC и секущей CD, и ∠DCB=180º-∠D.

Так как ∠A=∠D, то и ∠ABC=∠DCB.

Что и требовалось доказать.

www.treugolniki.ru

Все формулы диагонали равнобедренной трапеции

---

1. Формулы длины диагонали равнобедренной трапеции через ее стороны

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

d — диагональ трапеции

 

Формула диагонали трапеции (d ):

 

 

2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

α, β — углы трапеции

d — диагональ трапеции

 

Формулы диагонали трапеции (d ):

 

---

 

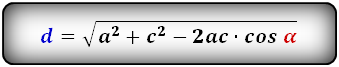
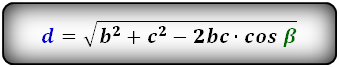
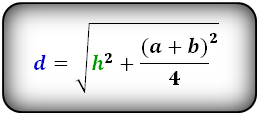
3. Формула длины диагонали равнобедренной трапеции

 

a — нижнее основание

b — верхнее основание

α, β — углы между диагоналями

h — высота трапеции

m — средняя линия трапеции

S — площадь трапеции

d — диагональ трапеции

 

Формулы диагонали трапеции (d ):

Справедливо для данного случая :

---

 

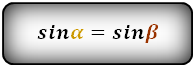
4. Формулы длины диагонали трапеции через высоту и стороны

 

a — нижнее основание

b — верхнее основание

c — равные боковые стороны

h — высота трапеции

α — угол при нижнем основании

d — диагональ трапеции

 

Формулы диагонали трапеции (d ):

---

---

 

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

www-formula.ru

Что такое трапеция, Определение, Виды, Свойства равнобедренной трапеции

Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара противолежащих сторон параллельна. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция. Элементы трапеции Параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции. Виды трапеций Трапеция, у которой боковые стороны равны, называется равнобедренной. Трапеция, у которой один из углов «прямой», называется прямоугольной. Общие свойства Средняя линия трапеции параллельна основаниям и равна их полусумме. Отрезок, соединяющий середины диагоналей, равен полуразности оснований. (Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. Свойства равнобедренной трапеции Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции. Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований. В равнобедренной трапеции углы при любом основании равны. В равнобедренной трапеции длины диагоналей равны. Около равнобедренной трапеции можно описать окружность. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований,

www.terminologija.ru

Определение трапеции. Виды трапеции. Свойства равнобедренной трапеции.

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Трапеция –четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны

Виды трапеции: равнобедренная и прямоугольная

Первое свойство равнобедренной трапеции – у равнобедренной трапеции боковые стороны равны

Второе свойство равнобедренной трапеции – у равнобедренно трапеции углы при основании равны

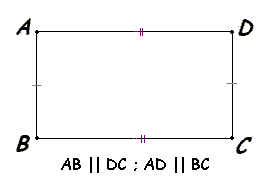
Определение прямоугольника. Свойство прямоугольника. Признак прямоугольника.

Прямоугольник –параллелограмм, у которого все углы прямые

Свойство прямоугольника – диагонали прямоугольника равны

Признак прямоугольника – если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник

Определение ромба. Свойство ромба.

Ромб –параллелограмм, у которого все стороны равны

Свойство ромба – диагонали ромба взаимно перпендикулярны и делят его углы пополам

Определение квадрата. Свойства квадрата.

Квадрат –прямоугольник, у которого все стороны равны

Первое свойство квадрата – все углы квадрата прямые

Второе свойство квадрата – диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам

Понятие площади многоугольника. Единица измерения площадей. Свойства площадей. Площадь квадрата.

 

Площадь многоугольника –это величина той части плоскости, которую занимает многоугольник

Единицы измерения площадей: квадратный сантиметр (см²), квадратный метр (м²), квадратный миллиметр (мм²) и т. д.

Первое свойство площади – равные многоугольники имеют равные площади

Второе свойство площади – если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

Площадь квадрата – площадь квадрата равна квадрату его стороны (S=a²)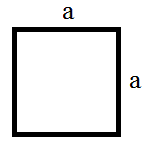

 

Определение высоты параллелограмма. Площадь параллелограмма.

Высота параллелограмма –перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание

Площадь параллелограмма –

произведение основания на высоту

 

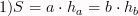
произведение сторон на синус угла между ними

 

 

полупроизведение диагоналей на синус угла между ними

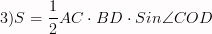
Определение высоты трапеции. Площадь трапеции.

Высота трапеции –перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание. Площадь трапеции –площадь трапеции равна произведению полусуммы её оснований на высоту S= 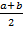h

 

 

произведение средней линии на высоту

полупроизведение диагоналей на синус угла между ними

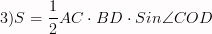
Площадь ромба (через диагонали). Площадь прямоугольника.

Площадь ромба –площадь ромба равна половине произведений его диагоналей

 

Площадь прямоугольника – площадь прямоугольника равна произведению его смежных сторон S=ab

Теорема Пифагора и обратная ей.

Теорема Пифагора –в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

c² = a² + b²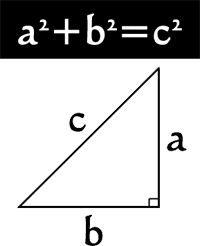

Теорема, обратная теореме Пифагора – если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный

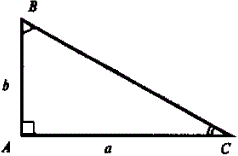
Площадь прямоугольного треугольника. Теорема об отношениях площадей треугольников: с равными высотами; имеющих по равному углу.

Площадь прямоугольного треугольника –площадь прямоугольного треугольника равна половине произведения его катетов

Теорема об отношениях площадей треугольников имеющих по равному углу –если угол одного треугольника равен углу другого, то площади треугольников относятся как произведение сторон, заключающих равные углы

Теорема об отношениях площадей треугольников с равными высотами –если площади двух треугольников равны, то их площади относятся как основания

Определение подобных треугольников. Теоремы об отношениях периметров и площадей подобных треугольников.

Подобные треугольники –два треугольника, углы которых соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого

Теорема об отношении площади подобных треугольников – отношение площадей подобных треугольников равно квадрату коэффициента подобия

 



infopedia.su

Определение трапеции

Трапецией называется четырёхугольник, две стороны которого параллельны, а две другие не параллельны. Параллельные стороны трапеции называются её основаниями, а непараллельные – боковыми сторонами трапеции.

\(ABCD\) – трапеция;

\(AD, \, BC\) – основания, \(AB, \, CD\) – боковые стороны трапеции \(ABCD\)

Свойства трапеции

1. Сумма углов, прилежащих к боковой стороне трапеции, равна \(180^{\circ}\).
2. Каждая диагональ трапеции образует с её основаниями равные углы.
3. При пересечении диагоналей трапеции и продолжений её боковых сторон образуются подобные треугольники, прилежащие к основаниям.
4. Биссектрисы смежных углов трапеции перпендикулярны.

\(ABCD\) – трапеция \(\Rightarrow \, \angle{DAB}+\angle{ABC}=180^{\circ}, \, \angle{ADC}+\angle{DCB}=180^{\circ};\)
\(ABCD\) – трапеция \(\Rightarrow \, \angle{CAD}=\angle{ACB}, \, \angle{BDA}=\angle{DBC};\)
\(ABCD\) – трапеция, \(AC \cap BD=O\) \(\Rightarrow \, \triangle{AOD} \backsim \triangle{COB};\)
\(ABCD\) – трапеция, \(AB \cap CD=E\) \(\Rightarrow \, \triangle{AED} \backsim \triangle{BEC}\)

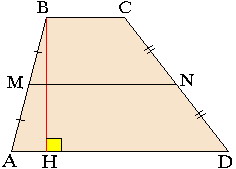
Средняя линия трапеции

Определение. Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.

Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$

Свойства равнобедренной трапеции

1. В равнобедренной трапеции углы при каждом основании равны.
2. Диагонали равнобедренной трапеции равны.
3. Ранобедренную трапецию можно вписать в окружность.

\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, \angle{ABC}=\angle{DCB}, \, \angle{BAD}=\angle{CDA}; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, AC=BD; \)
\(ABCD\) трапеция,\( \, AB=CD \, \Rightarrow \, ABCD\) вписанная

Признаки равнобедренной трапеции

1. Если углы при некотором основании трапеции равны, то эта трапеция равнобедренная.
2. Если диагонали трапеции равны, то эта трапеция равнобедренная.
3. Если трапецию можно вписать в окружность, то эта трапеция равнобедренная.

\( AD||BC, \, M\) – середина \(AB, \, N\) – середина \(CD \, \Rightarrow \) $$ MN||AD, \, MN||BC, \, MN=\frac{1}{2}(AD+BC)$$

Площадь трапеции

1. Площадь трапеции равна половине произведения суммы её оснований на высоту трапеции.
2. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

$$ S=\frac{1}{2}(a+b)h$$		$$ S=\frac{1}{2} d_1d_2\sin{\varphi}$$

tmath.ru