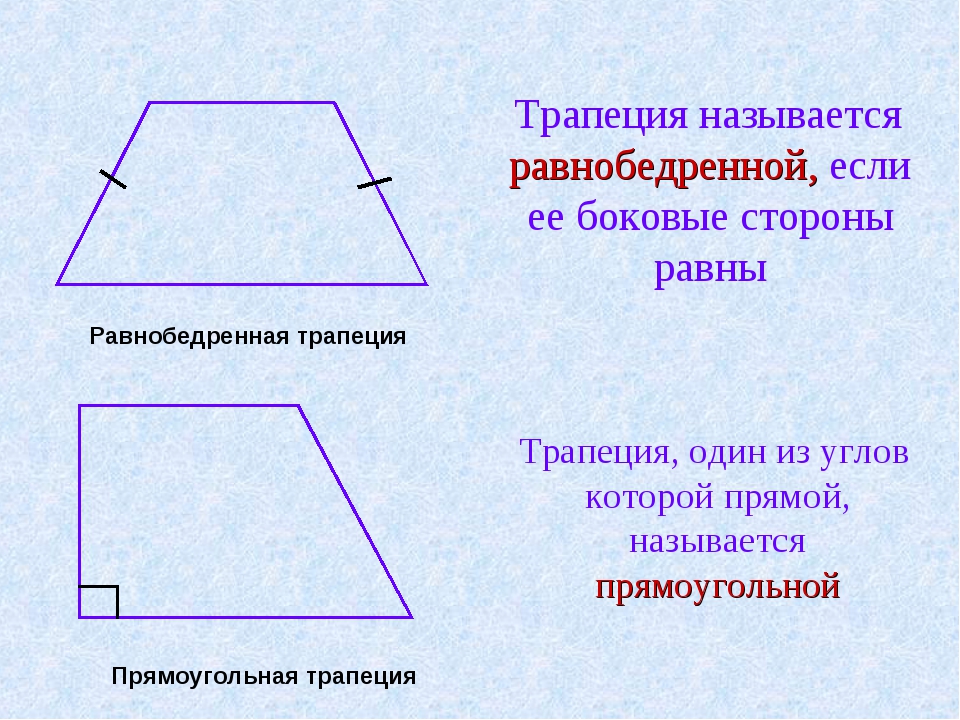
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Определение.
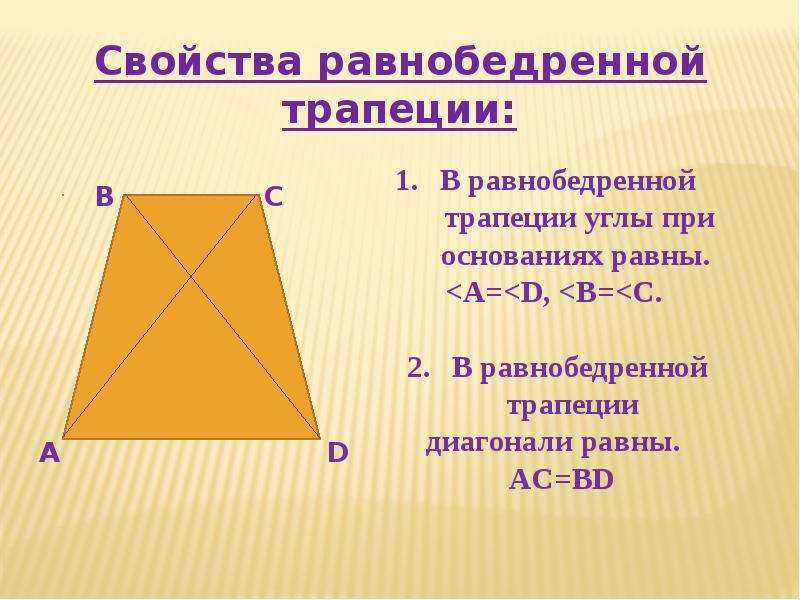
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.| Рис.1 |
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий: 1. В тапеции есть два смежных прямых угла:∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:a = b + d cos α = b + c ctg α = b + √d 2 — c2
b = a — d cos α = a — c ctg α = a — √d 2 — c2
2.
| a = | d1d2 | · sin γ — b = | d1d2 | · sin δ — b |
| c | c |
| b = | d1d2 | · sin γ — a = | d1d2 | · sin δ — a |
| c | c |
| a = | 2S | — b b = | 2S | — a |
| c | c |
c = √d 2 — (a — b)2 = (a — b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
 Формулы боковой стороны через площадь, основы и угол при нижнем основании:
Формулы боковой стороны через площадь, основы и угол при нижнем основании:| d = | S | = | 2S |
| m sin α | (a + b) sin α |
| d = | a — b | = | c | = | h | = √c2 + (a — b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1. Формулы средней линии через основание, высоту (она же равна стороне d ) и угол α при нижнем основании:| m = | a — h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
 Формулы средней линии через основания и боковые стороны сторону:
Формулы средней линии через основания и боковые стороны сторону:| m = | a — | √d 2 — c2 | = | b + | √d 2 — c2 |
| 2 | 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Определение, признаки и свойства произвольной, равнобедренной и прямоугольной трапеции
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет.
Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже.
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу,
- боковые стороны AB и CD — два непараллельных элемента,
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры,
- высота трапеции CH — перпендикулярный основаниям отрезок,
- средняя линия EF — линия, соединяющая середины боковых сторон.

Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
- Средняя линия всегда проходит параллельно обоим основаниям фигуры и численно равна их полусумме: EF = (BC + AD)/2.
- Точка пересечения диагоналей фигуры разделяет их с таким же соотношением длины, с каким относятся основания трапеции: AD : BC = AO : CO = DO : BO.
- Основание можно вычислить, зная длину второго основания и средней линии: BC = 2 · EF — AD, AD = 2 · EF — BC.
- Боковые стороны вычисляются, если известна высота фигуры и синус угла при основании: AB = CH / sinA, CD = CH / sinD.
- Для расчёта высоты необходимо знать, чему равна боковая сторона и прилегающий угол: CH = AB · sinA = CD · sinD.

Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
- При проведении диагоналей образуются 4 треугольника, из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.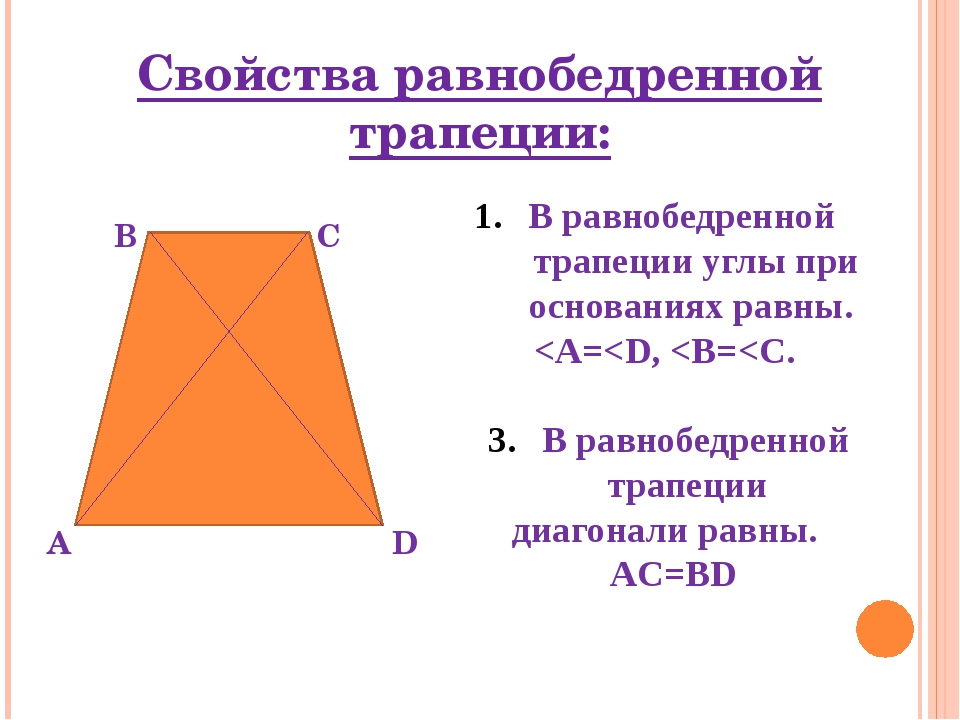
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции.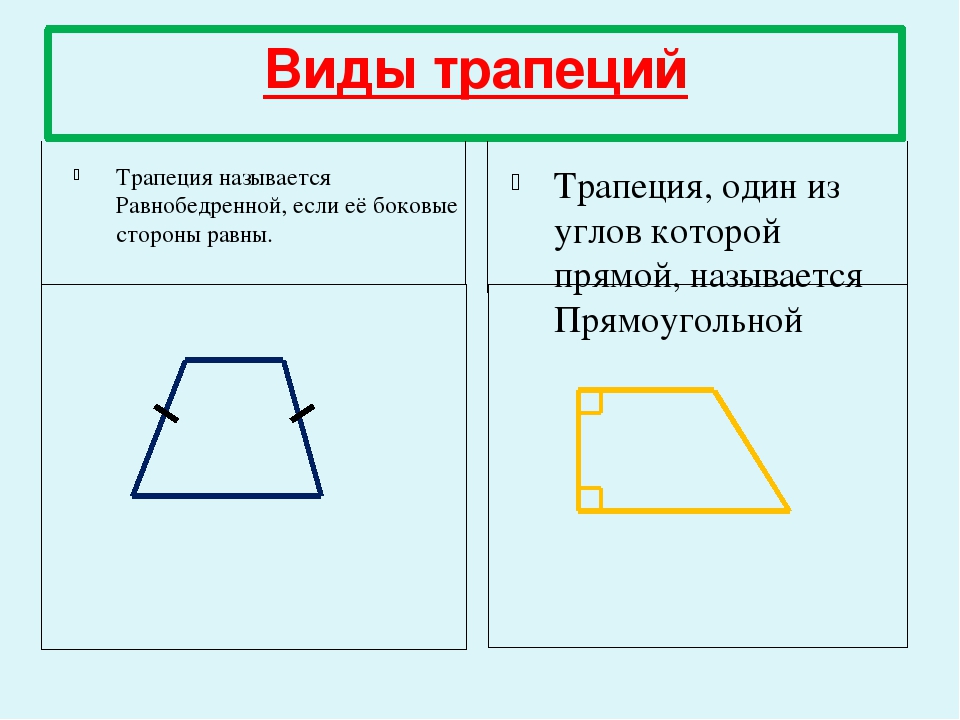 Другие свойства равнобедренной трапеции:
Другие свойства равнобедренной трапеции:
- Прямая, которая проходит через середины оснований фигуры, пересекает их под углом 90 градусов.
- Углы, лежащие при любых основаниях, попарно равны.
- Длины диагоналей совпадают.
- Высота будет равна средней линии, если диагонали проходят перпендикулярно друг к другу.
- Высота, опущенная из вершины к основанию, делит его на 2 отрезка, длина большего вычисляется как половина суммы оснований, а длина меньшего — как половина разности.
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
Что такое трапеция: определение, виды, свойства
В данной публикации мы рассмотрим определение, виды и свойства (касательно диагоналей, углов, средней линии, точки пересечения боковых сторон и т.д.) одной из основных геометрических фигур – трапеции.
Определение трапеции
Трапеция – это четырехугольник, две стороны которого параллельны, а остальные две – нет.
Параллельные стороны называются основаниями трапеции (AD и BC), две другие стороны – боковыми (AB и CD).
Угол при основании трапеции – внутренний угол трапеции, образованный ее основанием и боковой стороной, например, α и β.
Трапеция записывается путем перечисления его вершин, чаще всего, это ABCD. А основаниям обозначаются маленькими латинскими буквами, например, a и b.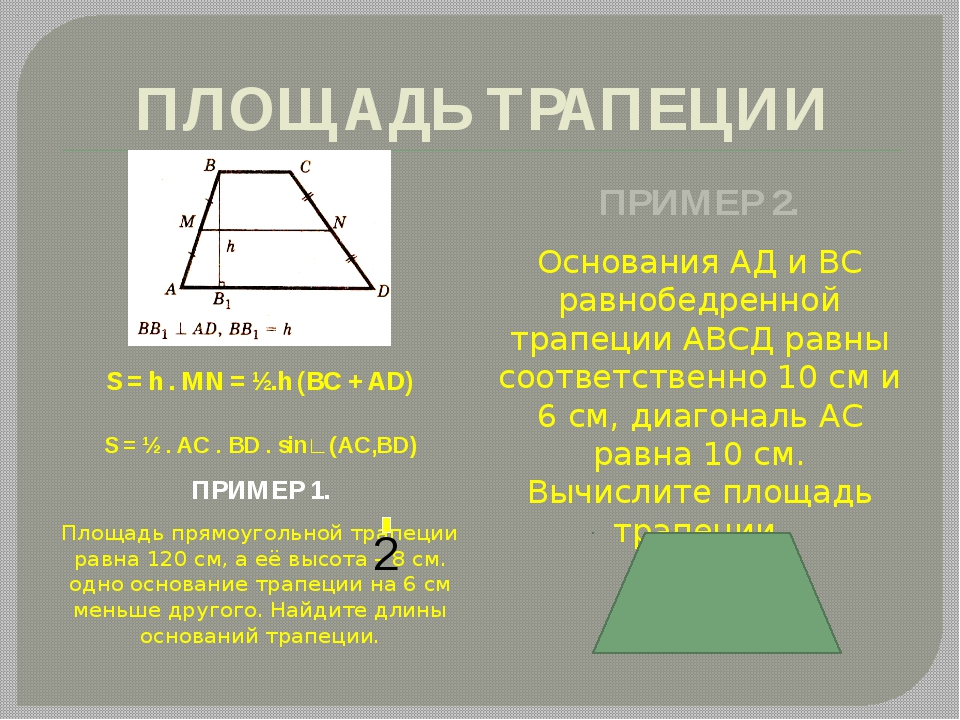
Средняя линия трапеции (MN) – отрезок, соединяющий середины ее боковых сторон.
Виды трапеций
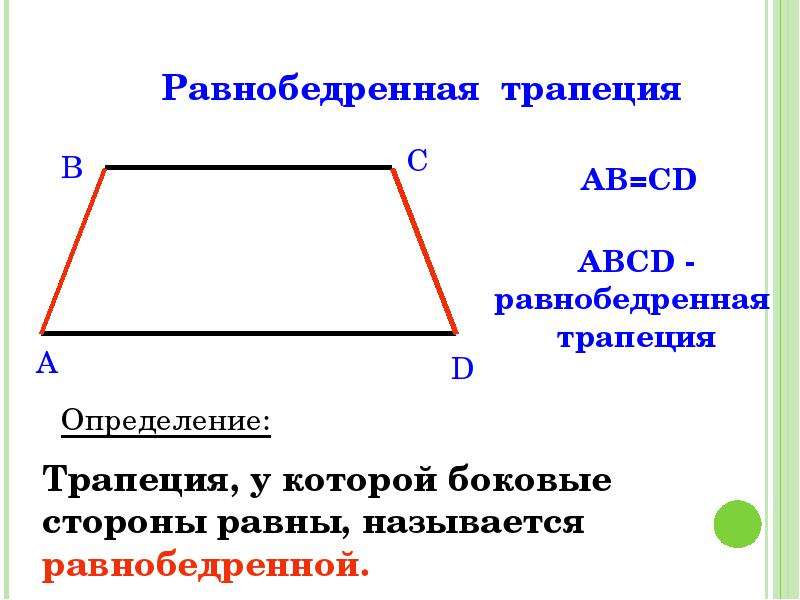
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной (или равнобокой).
AB = CD
Прямоугольная трапеция
Трапеция, у которой оба угла при одной из ее боковых сторон прямые, называется прямоугольной.
∠BAD = ∠ABC = 90°
Разносторонняя трапеция
Трапеция является разносторонней, если ее боковые стороны не равны, и ни один из углов при основании не является прямым.
Свойства трапеции
Перечисленные ниже свойства применимы к любым видам трапеций. Свойства равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Свойство 1
Сумма углов трапеции, прилежащих к одной и той же боковой стороне, равна 180°.
α + β = 180°
Свойство 2
Средняя линия трапеции параллельна ее основаниям и равняется половине их суммы.
Свойство 3
Отрезок, который соединяет середины диагоналей трапеции, лежит на ее средней линии и равняется половине разности оснований.
- KL – отрезок, соединяющий середины диагоналей AC и BD
- KL лежит на средней линии трапеции MN
Свойство 4
Точки пересечения диагоналей трапеции, продолжений ее боковых сторон и середин оснований лежат на одной прямой.
- DK – продолжение боковой стороны CD
- AK – продолжение боковой стороны AB
- E – середина основания BC, т.е. BE = EC
- F – середина основания AD, т.е. AF = FD
Если сумма углов при одном основании равняется 90° (т.е. ∠DAB + ∠ADC = 90°), значит продолжения боковых сторон трапеции пересекаются под прямым углом, а отрезок, который соединяет середины оснований (
Свойство 5
Диагонали трапеции делят ее на 4 треугольника, два из которых (при основаниях) подобны, а два других (при боковых сторонах) равны по площади.
- ΔAED ~ ΔBEC
- SΔABE = SΔCED
Свойство 6
Отрезок, проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, можно выразить через длины оснований:
Свойство 7
Биссектрисы углов трапеции при одинаковой боковой стороне взаимно перпендикулярны.
- AP – биссектриса ∠BAD
- BR – биссектриса ∠ABC
- AP перпендикулярна BR
Свойство 8
В трапецию можно вписать окружность только в том случае, если сумма длин ее оснований равна сумме длин ее боковых сторон.
Т.е. AD + BC = AB + CD
Радиус вписанной в трапецию окружности равен половине ее высоты: R = h/2.
свойства и признаки: площадь, средняя линия прямоугольной, равнобедренной, как найти высоту
С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые параллельны друг другу называются основаниями (отрезки AD и BC).
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет высотой. Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.
[stop]Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований. [/stop]
[/stop]
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная. ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.

- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
- Вокруг любой правильной трапеции можно построить окружность.
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции:
- Если диагонали пересекаются под углом, то половина суммы оснований будет равна длине высоты.
- В случае, когда в правильную трапецию построена, или может быть построена, окружность, то квадрат высоты равен произведению величин оснований.
- Ось симметрии и средняя линия трапеции являются одним и тем же ГМТ.
- Когда диагонали пересекаются под прямым углом, тогда для вычисления площади потребуется формула:
- Окружность вписанная в трапецию, делает величину средней линии равной боковой.

Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
[stop]Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.[/stop]
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения.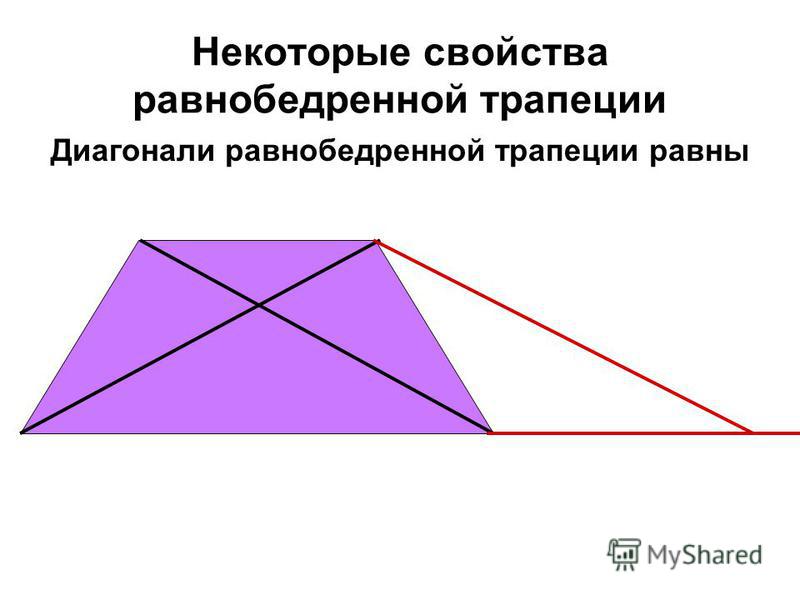 Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Решение:
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда
.Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
[stop]Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.[/stop]
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как:
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
Трапеция. Свойства и элементы трапеции
Виды трапеций
Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная.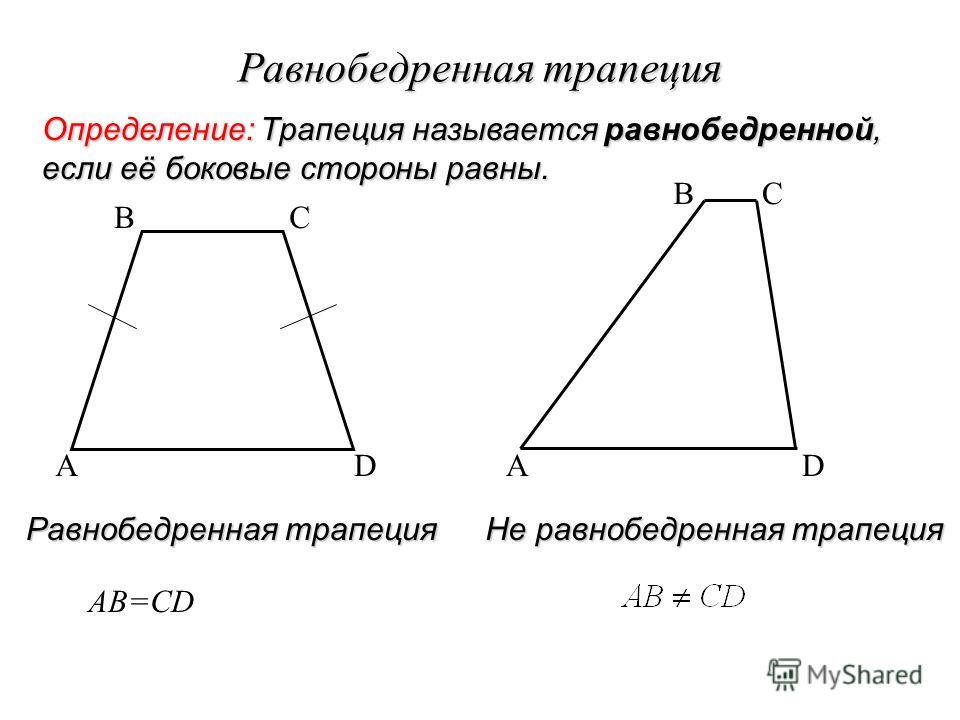
Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b — основания трапеции (a параллельно b),
m, n — боковые стороны трапеции,
d1, d2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b и высоту h: S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h: S = MN\cdot h
- Через диагонали d1, d2 и угол (\sin \varphi) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции, прилежащих к каждой боковой стороне, равна 180^{\circ}:
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC, образованные боковыми сторонами. {2}.
{2}.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
Описанная около трапеции окружность
Каждая равнобокая трапеция может содержать описанную окружность. Только равнобокую трапецию возможно вписать в окружность.
Вписанная в трапецию окружность
Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O.
Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.
«Трапеция. Равнобедренная и прямоугольная трапеция»
План урока.
Урок № 37 по математике в 8 классе.
Трапеция. Равнобедренная и прямоугольная трапеция.
Цель урока
Создать условия для формирования понятия «Трапеция», «Равнобедренная трапеция», «Прямоугольная трапеция», элементов и видов трапеций; для рассмотрения решения задач, в которых раскрываются свойства трапеции.
Планируемые образовательные результаты
1. Предметные умения: умеют объяснять, какой многоугольник называется трапецией (равнобедренной и прямоугольной), знать элементы трапеций, знать свойства и признаки равнобедренной трапеции, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологией.
2. формирование у учащихся понятия “трапеция”; умений называть элементы и виды трапеции; умений называть свойства и признаки трапеции и применять эти свойства при решении простейших задач.
Метапреметные:
Познавательные: проводят информационно-смысловой анализ текста и лекции, осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, умением устанавливать причинно — следственные связи.
Регулятивные: принимают и сохраняют учебную задачу.
Коммуникативные: умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач, работать в группе.
Личностные: умеют контролировать процесс и результат математической деятельности.
Основные понятия.
Трапеция, основания трапеции, боковые стороны трапеции, равнобедренная и прямоугольная трапеция.
Трудовые действия учителя
1.Разработка технологической карты урока. 2. Подготовка презентаций к уроку, наглядных пособий, демонстративного материала, раздаточного материала.
Учебно-методическое обеспечение (средства, оборудование)
Для учителя
1. учебник; 2. индивидуальные задания; 3. презентация; 4. компьютер; 5. интерактивная доска.
Для обучающихся
1. учебник;
2. тестовые задания;
3. цветные карточки;
цветные карточки;
4. листы самооценивания;
Этап (ход) урока, включая демонстрируемые трудовые действия учителя.
Для учителя
Для обучающихся
1. Организационный этап.
Взаимное приветствие. Учитель предлагает определить готовность к уроку. Создает условия для возникновения у обучающихся внутренней потребности включения в учебную деятельность. Знакомит с эпиграфом урока.
Три пути ведут к знанию: путь размышления – это путь благородный, путь подражания – это путь самый легкий; путь опыта – это путь самый горький.(Слайд 1)
Ученики рассаживаются по местам. Проверяются наличие принадлежностей, знакомятся с листами самооценки.
2. Этап актуализация знаний по теме «Четырехугольники»; Подведение учащихся к новой теме.
Предлагает вспомнить ранее изученный материал. 1. Устная работа по готовым чертежам.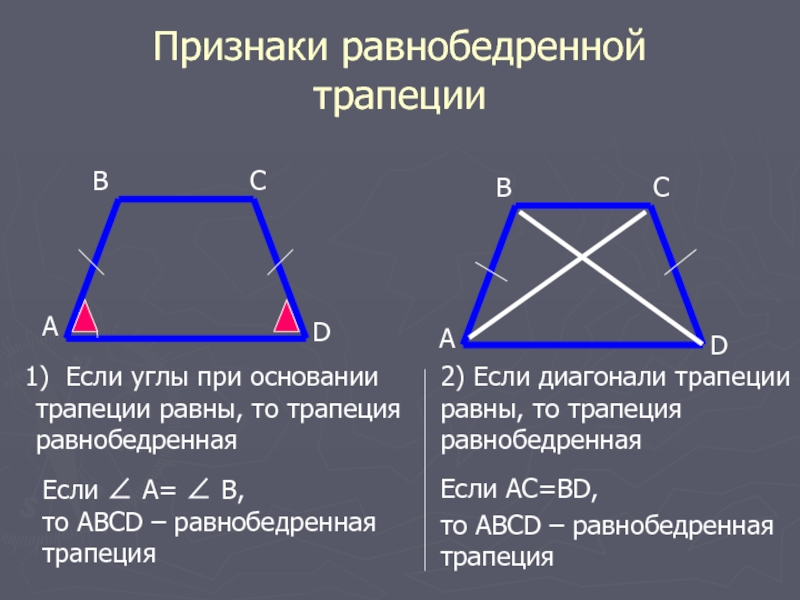 На слайде изображены различные выпуклые четырёхугольники. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и новый четырёхугольник (трапеция) (слайд 2) — Вспомните, с какими четырехугольниками и их свойствами вы хорошо знакомы? 2. Геометрическая разминка. — Выберите верные утверждения: (слайд 3,4) 1.Параллелограмм — это четырехугольник, у которого стороны попарно равны? (да) 2. Сумма углов четырехугольника 1800? (нет) 3. Противоположные углы параллелограмма равны? (да) 4. Диагонали параллелограмма равны? (нет). 5. Диагонали ромба пересекаются и точкой пересечения делятся пополам? (да) 6. Квадрат является ромбом? (да) 7. Диагонали прямоугольника равны? (да) 8. Диагонали ромба являются биссектрисами его углов? (да)
На слайде изображены различные выпуклые четырёхугольники. Среди них известные ребятам параллелограмм, прямоугольник, квадрат, ромб и новый четырёхугольник (трапеция) (слайд 2) — Вспомните, с какими четырехугольниками и их свойствами вы хорошо знакомы? 2. Геометрическая разминка. — Выберите верные утверждения: (слайд 3,4) 1.Параллелограмм — это четырехугольник, у которого стороны попарно равны? (да) 2. Сумма углов четырехугольника 1800? (нет) 3. Противоположные углы параллелограмма равны? (да) 4. Диагонали параллелограмма равны? (нет). 5. Диагонали ромба пересекаются и точкой пересечения делятся пополам? (да) 6. Квадрат является ромбом? (да) 7. Диагонали прямоугольника равны? (да) 8. Диагонали ромба являются биссектрисами его углов? (да)
По ходу работы идет проверка ответов (слайд 5) и выставление баллов в оценочные листы.
Называют четырехугольники.
Выбирают верные утверждения. Работают с сигнальными карточками; зелёные карточки — верно, красные – неверно.
Работают с сигнальными карточками; зелёные карточки — верно, красные – неверно.
3. Этап целеполагания и планирования.
1. Ответы на вопросы по слайду 6:
— Среди представленных фигур, что вы заметили?
— Что общего у этих фигур?
—Чем отличается выделенный четырехугольник от других?
—А кто знает, как называется этот четырехугольник?
-Эта фигура называется трапецией.
-Как вы думаете какова тема сегодняшнего урока?
— Ребята, подумайте, чему бы вы сегодня хотели научиться и что хотели бы узнать нового на уроке о данном четырехугольнике?
— Как вы считаете, какой будет цель нашего урока?
— Какие нужно поставить задачи для достижения нашей цели?
— Записываем в тетрадь дату и тему сегодняшнего урока: «Трапеция».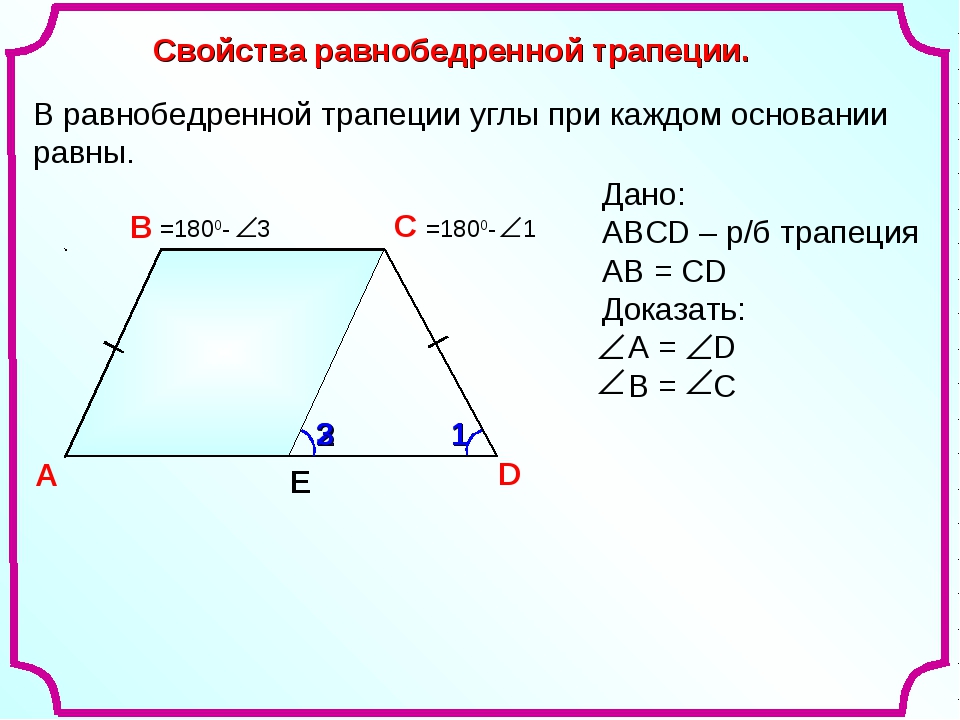
Ответ: «Фигура стоящая справа незакрашена». Ответ: «Все фигуры являются четырехугольниками». Ответ: «Не является параллелограммом. У него две стороны параллельные, а две другие нет».) Ученики либо отвечают, либо нет.
Учащиеся формулируют тему урока.
Ученики ставят перед собой цели урока: — Сформировать понятие трапеции. — Научиться определять виды трапеции, находить её элементы. — Научиться изображать трапецию. — Выяснить свойства и признаки равнобедренной трапеции. — Научиться применять полученные знания в процессе решения задач. Формулируют задачи урока.
Записывают дату и тему урока.
3. Поисковая деятельность по открытию новых знаний.
1. Изображение трапеции. Практическая работа.
Начертите четырехугольник, у которого две стороны параллельны, а две другие – не параллельны (на доске и в тетрадях должен появиться рис.1) — На что похожа эта фигура? —Да, и в правду она похожа на стол и в переводе означает стол.
 Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.
— Как он называется? — Сформулируем точное определение.
3. Элементы трапеции. Учитель предлагает по учебнику (п.44, стр. 103) проверить выдвинутую гипотезу, а также по тексту ознакомиться с элементами трапеции. (слайд 8) 4. Работа по готовым чертежам. Предлагает задание для обсуждения в группах: — Определите, какие из предложенных четырехугольников являются трапециями и почему? (слайд 9) 5.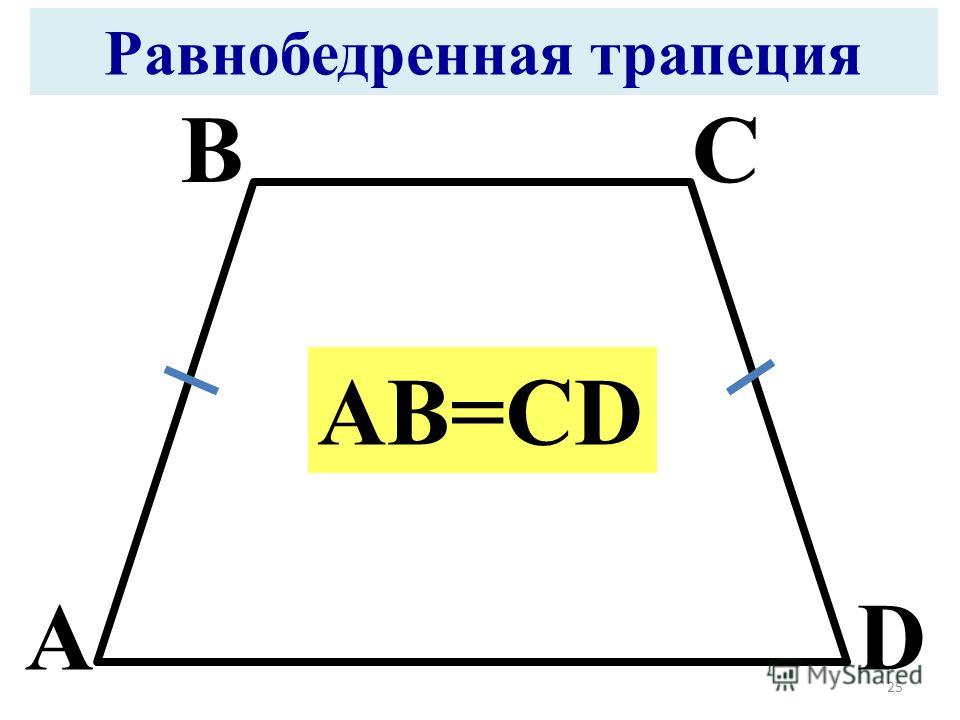 Виды трапеции. — Найдите отличия в представленных трапециях и предложите название каждому виду трапеции (слайд 10.)
Виды трапеции. — Найдите отличия в представленных трапециях и предложите название каждому виду трапеции (слайд 10.)
6. Свойства и признаки равнобедренной трапеции.
Учитель предлагает поделится на группы и провести исследовательскую работу. Задание: исследовать углы и диагонали равнобедренной трапеции, сформулировать свойства и признаки. (слайд 11)
Строят четырехугольник, у которого две стороны параллельны, а две другие – не параллельны.
Ответ: на стол
Идет обсуждение в группах.
Результат работы: учащиеся дают определение трапеции, ключевым моментом в котором должны быть слова «четырехугольник, у которого только одна пара противолежащих сторон параллельна».
Работают по тексту учебника.
Данные слайда учащиеся заносят в конспект.
Каждая группа называет по одной трапеции и объясняет ответ.
Учащиеся обсуждают задание в группах и делают выводы: «что трапеция ABCD содержит прямые углы, а трапеция KLMN имеет равные боковые стороны». Дают предполагаемые названия видов трапеций.
Информация со слайда заносится учащимися в конспект.
Обсуждают в группах и один ученик из группы делает вывод и формулирует свойство равнобедренной трапеции.
Из выясненных свойств ученики составляют признаки равнобедренной трапеции.
4. Физкульминутка.
Используется методика здоровьесберегающей технологий «зрительные метки».
Учитель обращает внимание учащихся на развешанные по периметру класса цветные фигурки четырехугольников и дает задание отыскать среди них трапеции (все фигурки пронумерованы) (слайд 12)
Учащиеся дают в ответ № четырехугольника, который является трапецией.
5. Этап первичного закрепления и применения новых знаний.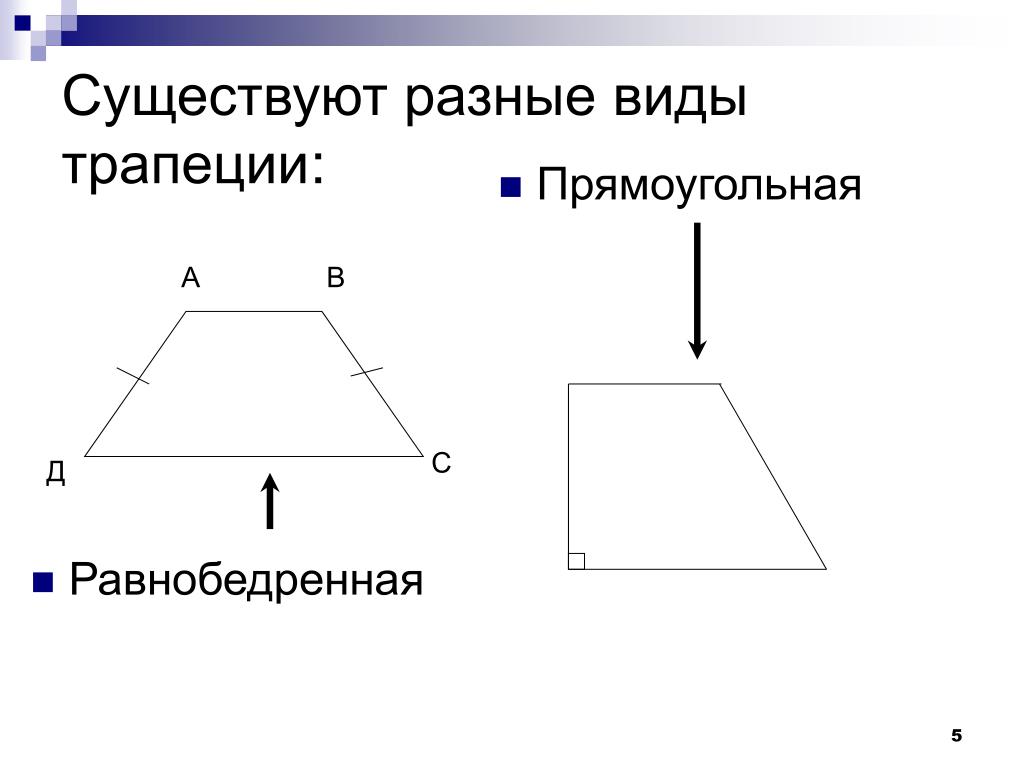
1. Решение задач по готовым чертежам. Учитель предлагает обсудив в парах решить задачи: №1 (устно). Один из углов равнобедренной
трапеции равен 68°. Найдите остальные углы трапеции. №2 (письменно). Дана ABCD – трапеция, ВЕ||CD, АВЕ=75, ВАЕ=40. Найти углы трапеции.
2. Вывод.
—Чему равна сумма двух углов при боковых сторонах трапеции?
— Как найдем второй угол, если первый известен?
Учитель предлагает оценить свою работу и проставить баллы в оценочные листы.
Ученики решают задачи и свои ответы обсуждают в парах. Один ученик решает задачу с комментариями у доски.
Решают задачу в тетрадях , записывают ответы и проверяют свои ответы с ответом ученика, решивший задачу у доски. По ходу решения задач ученики выясняют и делают вывод, что сумма двух углов при боковой стороне трапеции равна 1800 . В оценочных листах проставляют баллы за правильно решенные задачи.
6. Самоконтроль изученного материала.
Самоконтроль изученного материала.
1. Тест.
— А теперь проведем самоконтроль изученного материала. Учитель предлагает ответить на вопросы теста по теме «Трапеция» (приложение № 2).
Выполняют тест, ответы заносят в оценочные листы и проставляют баллы за правильные ответы.
7. Подведение итогов. Оценивание.
1. Подведение итогов урока. Фронтальный опрос (слайд 21):
Какой четырехугольник называется трапецией?
Назовите элементы трапеции и ее виды.
3. Вспомните свойства равнобедренной трапеции.
2. Самооценка.
— Учитель предлагает просуммировать набранные баллы и используя шкалу перевести баллы в оценку за урок.
Отвечают на вопросы, называют основные понятия нового материала.
Заполняют листы самооценки: суммируют полученные баллы за урок и используя шкалу, переводят баллы в оценку.
8. Рефлексия.
Учитель задает вопросы о цели урока, побуждает учащихся к высказыванию мнения, чему они научились на уроке. — Как вы думаете, нам удалось достичь поставленной цели?
Предлагает продолжить предложения. На уроке я узнал…
Мне было интересно, что …
Я разобрался в том, что…
Мне стало понятно ,что…
Мне было увлекательно…
Я познакомился …
Формулируют конечный результат своей работы на уроке. Подводят итог урока.
9. Домашнее задание
Домашнее задание.
п. 44, выучить конспект по рабочей тетради.
Ответить на контрольные вопросы
Решить задачи №386, 387.
Творческое задание. Сделать презентацию на тему «Трапеция в жизни человека»
Записывают домашнее задание в дневники.
Приложение №1
Оценочный лист по теме «Трапеция»
ученика 8 класса _____________________________________________ дата __________
Этап урока
Вид задания
Правильные ответы
Количество баллов
Актуализация.
1.____ 2.____ 3.____ 4.____
5.____ 6.____ 7.____ 8.____
3 б. — за 8-7 правильных ответов
2 б. — за 6-5 правильных ответов
1 б. — за 4-3 правильных ответа
Закрепление и применение новых знаний.
Решение задач.
№1. Ответ:_____________________
№2. Ответ:_____________________
Самоконтроль изученного материала.
Тест
1.___ 2.___ 3.___ 4.___ 5.___
Оценка за урок
Критерии выставления оценок:
«5» – 9 -10 баллов,
«4» – 7-8 баллов,
«3» – 5 -6 баллов.
Приложение №2
Тест по теме «Трапеция»1. Укажите верное утверждение: трапеция – это…
1) параллелограмм;
2) четырехугольник, у которого две стороны равны;
3) четырехугольник, у которого две стороны параллельны;
4) четырехугольник, у которого только две противоположные стороны параллельны.
2. Продолжите определение: трапеция называется равнобедренной, если…
1) две ее боковые стороны равны;
2) две ее соседние стороны равны;
3) любые две стороны трапеции равны;
4) другой ответ.
3. Укажите верное утверждение:
1) Только в прямоугольной трапеции углы при основании равны;
2) Углы при основании равны в любой трапеции;
3) Если трапеция равнобедренная, то противолежащие углы ее равны;
4) У равнобедренной трапеции углы при основании равны.
4. Укажите верное утверждение:
1) Сумма углов, прилежащих к одной стороне трапеции равна 180 градусов;
2) Сумма углов трапеции зависит от ее вида;
3) Сумма углов, прилежащих к боковой стороне и равна 180 градусов;
4) В трапеции сумма углов равна 180 градусов.
5. Укажите верное утверждение:
1) Трапеция может быть только прямоугольной и равнобедренной;
2) Трапеция может быть прямоугольной, равнобедренной;
3) Любой разносторонний четырехугольник можно назвать трапецией;
4) Четырехугольник с параллельными противолежащими сторонами называется трапецией.
Приложение 3
Ключи к тесту «Трапеция»
Правильныйответ
1.
4
2.
1
3.
4
4.
3
5.
4
Запоминаем и применяем свойства трапеции
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.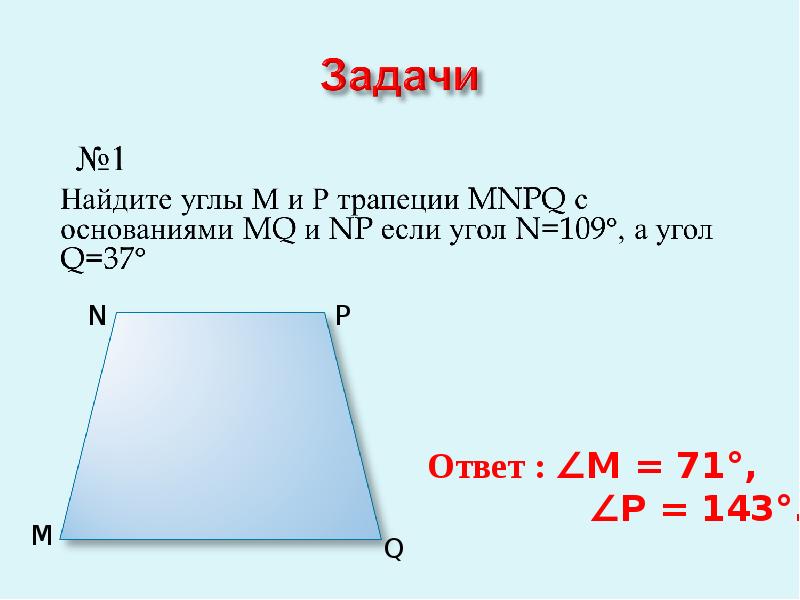
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции.
 Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k2. - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
- Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 1800: α + β = 1800 и γ + δ = 1800.
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 900 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь.
 Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
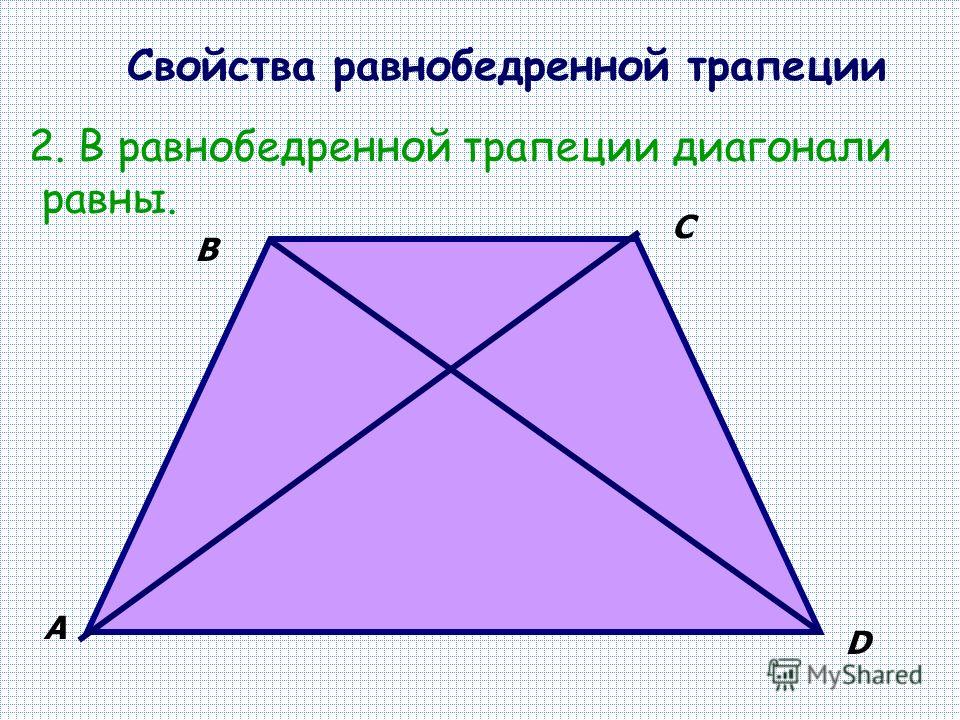
Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны. - Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 1800 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям.
 И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции. - На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2.
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне.
 В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). - Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.

- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*SАМЕ.
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b.
 Радиус окружности можно вычислить по формуле: r = √ab.
Радиус окружности можно вычислить по формуле: r = √ab. - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.

- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 1800 — МЕТ = 1800 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 1500 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 1800. Поэтому КАН = 300 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 300.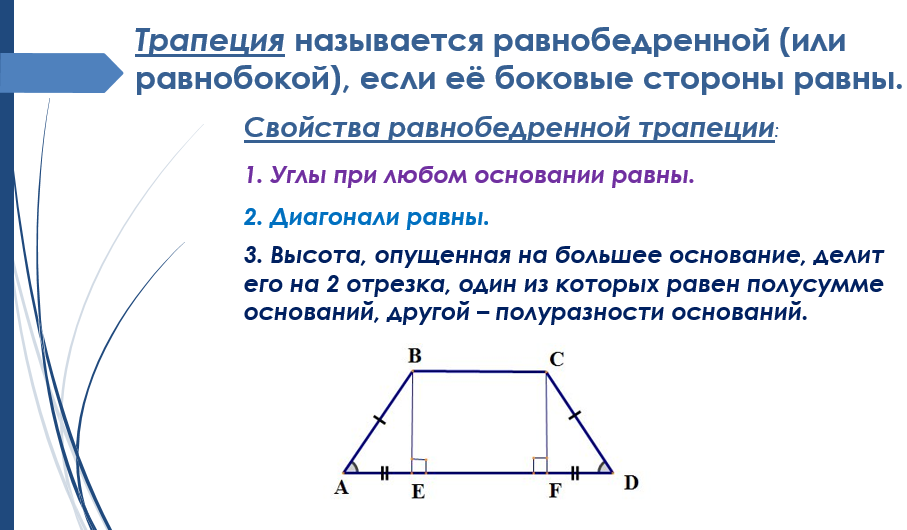 Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: SАКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см2.
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Площадь трапеции — пояснения и примеры
Напомним, трапеция , также называемая трапецией , — это четырехугольник с одной парой параллельных сторон и другой парой непараллельных сторон. Подобно квадрату и прямоугольнику, трапеция также плоская. Следовательно, это 2D.
В трапеции параллельные стороны называются основаниями, а пара непараллельных сторон — ногами. Расстояние по перпендикуляру между двумя параллельными сторонами трапеции называется высотой трапеции.
Проще говоря, основание и высота трапеции перпендикулярны друг другу.
Трапеции могут быть как правыми трапециями (два угла 90 градусов), так и равнобедренными трапециями (две стороны одинаковой длины). Но иметь один прямой угол невозможно, потому что у него есть пара параллельных сторон, которые ограничивают его, образуя два прямых угла одновременно.
Из этой статьи вы узнаете:
- Как найти площадь трапеции,
- Как получить формулу площади трапеции и,
- Как найти площадь трапеции с помощью трапеции формула площади.
Как найти площадь трапеции?
Площадь трапеции — это область, покрытая трапецией в двухмерной плоскости. Это пространство, заключенное в 2D-геометрии.
На рисунке выше трапеция состоит из двух треугольников и одного прямоугольника. Следовательно, мы можем вычислить площадь трапеции, взяв сумму площадей двух треугольников и одного прямоугольника.
Вывести формулу площади трапеции
Площадь трапеции ADEF = (½ x AB x FB ) + ( BC x FB ) + (½ x CD x EC )
= ( ¹ / ₂ × AB × h ) + ( BC × h ) + (¹ / ₂ × CD × h )
= ¹ / ₂ × h × ( AB + 2 BC + CD )
= ¹ / ₂ × h × ( FE + AD )
Но, FE = b 1 и AB = b 2
Следовательно, Площадь a трапеция ADEF ,
= ¹ / ₂ × h × (b 1 + b 2 ) ……………….(Это формула площади трапеции)
Формула площади трапеции
Согласно формуле площади трапеции, площадь трапеции равна половине произведения высоты и суммы двух оснований.
Площадь = ½ x (сумма параллельных сторон) x (расстояние по перпендикуляру между параллельными сторонами).
Площадь = ½ h (b 1 + b 2 )
Где h — высота, а b 1, и b 2 — параллельные стороны трапеции.
Как определить площадь неправильной трапеции?
Неправильная трапеция имеет непараллельные стороны неравной длины. Чтобы найти его площадь, нужно найти сумму оснований и умножить ее на половину высоты.
В вопросе иногда не хватает высоты, что можно найти с помощью теоремы Пифагора.
Как найти периметр трапеции?
Вы знаете, что периметр — это сумма всех длин внешнего края фигуры.Следовательно, периметр трапеции — это сумма длин всех 4 сторон.
Пример 1
Рассчитайте площадь трапеции, высота которой составляет 5 см, а основания — 14 см и 10 см.
Решение
Пусть b 1 = 14 см и b 2 = 10 см
Площадь трапеции = ½ h (b 1 + b 2 ) см 2
= ½ x 5 (14 + 10) см 2
= ½ x 5 x 24 см 2
= 60 см 2
Пример 2
Найдите площадь трапеции с высота 30 мм, а основания 60 мм и 40 мм.
Раствор
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
= ½ x 30 x (60 + 40) мм 2
= ½ x 30 x 100 мм 2
= 1500 мм 2
Пример 3
Площадь трапеции составляет 322 квадратных дюйма. Если длины двух параллельных сторон трапеции составляют 19 дюймов и 27 дюймов, найдите высоту трапеции.
Раствор
Площадь трапеции = ½ часа (b 1 + b 2 ) кв.единицы измерения.
⇒ 322 квадратных дюйма = ½ x в x (19 + 27) кв. дюймов
⇒ 322 квадратных дюйма = ½ x h x 46 кв. дюймы
⇒ 322 = 23h
Разделите обе стороны на 23.
h = 14
Итак, высота трапеции составляет 14 дюймов.
Пример 4
Учитывая, что высота трапеции составляет 16 м, а длина одного основания — 25 м. Рассчитайте размер другого основания трапеции, если его площадь составляет 352 м 2 .
Решение
Пусть b 1 = 25 м
Площадь трапеции = ½ h (b 1 + b 2 ) кв. Единиц
⇒ 352 м 2 = ½ x 16 м x (25 m + b 2 ) кв. Единиц
⇒ 352 = 8 x (25 + b 2 )
⇒ 352 = 200 + 8b 2
Вычтите 200 с обеих сторон.
⇒ 152 = 8b 2
Разделите обе части на 8, чтобы получить;
b 2 = 19
Следовательно, длина другого основания трапеции составляет 19 м.
Пример 5
Рассчитайте площадь трапеции, показанной ниже.
Решение
Поскольку стороны (непараллельные стороны) трапеции равны, высоту трапеции можно рассчитать следующим образом;
Чтобы получить основание двух треугольников, вычтите 15 см из 27 см и разделите на 2.
⇒ (27-15) / 2 см
⇒ 12/2 см = 6 см
12 2 = h 2 + 6 2 По теореме Пифагора высота (h) рассчитывается как;
144 = h 2 + 36.
Вычтем 36 с обеих сторон.
h 2 = 108.
h = 10,39 см.
Следовательно, высота трапеции 10,39 см.
Теперь вычислите площадь трапеции.
Площадь трапеции = ½ ч (b 1 + b 2 ) кв. единицы измерения.
= ½ x 10,39 x (27 + 15) см 2 .
= ½ x 10,39 x 42 см 2 .
= 218,19 см 2 .
Пример 6
Одно основание трапеции на 10 м больше высоты.Если другое основание составляет 18 м, а площадь трапеции равна 480 м 2 , найдите высоту и основание трапеции.
Решение
Пусть высота = x
Другая база равна 10 м, чем высота = x + 10.
Площадь трапеции = ½ h (b 1 + b 2 ) Кв. единицы измерения.
Путем подстановки
480 = ½ * x * (x + 10 + 18)
480 = ½ * x * (x + 28)
Удалите скобки с помощью свойства распределения.
480 = ½x 2 + 14x
Умножьте каждый член на 2.
960 = x 2 + 28x
x 2 + 28x — 960 = 0
Решите квадратное уравнение, чтобы получить;
x = — 48 или x = 20
Подставьте положительное значение x в уравнение высоты и основания.
Высота: x = 20 м.
Другая база = x + 10 = 10 + 20 = 30 м.
Следовательно, другое основание и высота трапеции равны 30 и 20 м соответственно.
Практические задачи- Найдите площадь трапеции, у которой есть параллельные основания длиной 9 единиц и 12 единиц, а высота равна 15 единицам.
- Для трапециевидной фигуры сумма параллельных оснований составляет 25 м, а высота — 10 м. Определите площадь этой фигуры.
- Рассмотрим трапецию площадью 112b квадратных футов, где b — более короткая базовая длина. Какова высота этой трапеции, если длины двух параллельных оснований таковы, что одно основание в два раза больше другого основания?
Форма: трапеция — элементарная математика
Значение
Трапеция — четырехугольник, по крайней мере, с одной парой параллельных сторон.Никакие другие особенности не имеют значения. (В англоязычных странах за пределами Северной Америки эквивалентным термином является трапеция.)
Параллельные стороны могут быть вертикальными, горизонтальными или наклонными. Фактически, по определению, даже это трапеция, потому что у нее есть «по крайней мере одна пара параллельных сторон» (и никакие другие особенности не имеют значения) как есть. На этих фигурах две другие стороны также параллельны, и поэтому они удовлетворяют не только требованиям для того, чтобы быть трапецией (четырехугольник, по крайней мере, с одной парой параллельных сторон), но также и требованиям для того, чтобы быть параллелограммом.
Приведенное выше определение принято в математическом сообществе и, все чаще, в образовательном сообществе. Многие источники, связанные с K-12 образованием, исторически ограничивали определение трапеции, требуя ровно одной пары параллельных сторон. Этот более узкий вид исключает параллелограммы как подмножество трапеций и оставляет только такие фигуры, как, и. Это более узкое определение трактует трапеции, как если бы они были треугольниками с «одной вершиной, отрезанной параллельно противоположной стороне.«Даже с ограниченным определением для учащихся важно видеть нестандартные примеры — асимметричные, как примеры зеленого и коричневого, и в нестандартных ориентациях, как красный пример, — чтобы создаваемое ими изображение фокусировалось на Существенная особенность: пара параллельных сторон.
Классифицирующие трапеции
Параллелограммам с особыми характеристиками, такими как прямые углы или все совпадающие стороны (или и то и другое), даны собственные отличительные имена: прямоугольник, ромб и квадрат.Единственная особенность трапеции , которой присвоено собственное отличительное имя, — это вторая пара параллельных сторон, которая превращает специальную трапецию в параллелограмм. Когда две стороны (кроме оснований) имеют одинаковую длину, трапеция называется равнобедренной («равнобедренная трапеция»), так же как треугольники с двумя сторонами равной длины (кроме основания) называются равнобедренными треугольниками. Никакие другие отличительные названия не используются для трапеций с особыми характеристиками (например, прямые углы или три совпадающие стороны).
Что одним словом?
Суффикс -оид предполагает, что он «похож» на что-то, но не является тем же самым: сфероид похож на сферу, но не обязательно на идеальную сферу; гуманоид похож на человека, но не на человека; и трапеция имеет форму трапеции, но не трапеция. Современное значение трапеции предполагает цирковые качели ( часто имеет трапециевидную форму, сиденье расположено параллельно перекладине, на которой свисает трапеция), но trapeze первоначально означало «стол», из tra ( «четыре», как в tetra- ) pez («нога» или «ступня», которые мы чаще видим как ped как в pedal или pedestrian ).
Как найти длину диагонали трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Трапеция
Трапеция — это четырехугольник с одной парой параллельных сторон. На рисунке ниже показано несколько различных типов трапеций.
Примечание. Некоторые определяют трапецию как четырехугольник, по крайней мере, с одной парой параллельных сторон, подразумевая, что он может содержать две пары параллельных сторон, что сделало бы его параллелограммом.В рамках данной статьи мы определим трапецию как четырехугольник с одной парой параллельных сторон.
Грани трапеции
Параллельные стороны трапеции называются ее основаниями. Непараллельные стороны называются ножками. Высота (или высота) — это отрезок линии, используемый для измерения кратчайшего расстояния между двумя основаниями.
Углы трапеции
В трапеции пара углов, имеющих общее основание, называется базовыми углами.Для трапеций, показанных на диаграмме ниже, A и ∠D — это базовые углы, а ∠B и ∠C — базовые углы. Пара углов рядом с опорой дополнительные: ∠A + ∠B = 180 ° и ∠C + ∠D = 180 °.
Срединный отрезок трапеции
Середина трапеции — это отрезок прямой, соединяющий середину ее ног. Средний сегмент параллелен основаниям и имеет длину, равную половине суммы двух оснований.
На рисунке выше средний сегмент EF делит ветви AB и CD пополам и
Площадь трапеции
Площадь А трапеции равна половине произведения суммы ее оснований и ее высоты.
, где h — высота, а b 1 и b 2 — базовые длины.
Классификация трапеций
Трапеции можно классифицировать как разносторонние или равнобедренные в зависимости от длины ног. Если ноги и углы основания трапеции совпадают, это равнобедренная трапеция. В остальном это разносторонняя трапеция.
| Чешуйчатая трапеция | Равнобедренная трапеция |
|---|---|
| Ноги или углы основания не совпадают | Конгруэнтные ножки и углы основания |
Трапеции также можно классифицировать как прямые трапеции или тупые трапеции в зависимости от их углов.Если одна из ножек перпендикулярна основанию, трапеция представляет собой прямую трапецию. В противном случае трапеция должна содержать два тупых угла и называется тупой трапецией.
| Правая трапеция | Тупая трапеция |
|---|---|
| Одна нога перпендикулярна основаниям. | Два угла тупые. |
Равнобедренные трапеции
Равнобедренная трапеция — это особая трапеция с совпадающими сторонами и углами основания.Он обладает следующими свойствами.
- Две диагонали равнобедренной трапеции совпадают. Они также образуют совпадающие треугольники. На изображенной ниже равнобедренной трапеции диагонали AC и BD совпадают. Поскольку ноги равнобедренной трапеции конгруэнтны, а следующие пары треугольников имеют общее основание, △ ABD ≅ DCA и △ ABC ≅ △ DCB согласно постулату Сторона-Сторона-Сторона.
- Соотношение сегментов, составляющих диагонали трапеции, пропорционально. На диаграмме выше AE = DE, BE = CE и
- Равнобедренная трапеция имеет одну линию симметрии: высоту, разделяющую ее основания пополам.На рисунке выше высота FE делит пополам основания AD и BC. Отражение равнобедренной трапеции ABCE поперек FE сохраняет его, делая FE линией симметрии.
Типы четырехугольников | Бесплатная помощь с домашним заданием
Обзор: что такое четырехугольник?
Четырехугольники — это многоугольники с четырьмя сторонами. Они классифицируются по равным углам и равным сторонам. Есть семь различных типов четырехугольников: параллелограмм, ромб, прямоугольник, квадрат, воздушный змей, трапеция и равнобедренная трапеция.Типы четырехугольников часто пересекаются, поэтому фигура, подходящая к одной категории, может подходить и к другой. У каждого есть свои особенности.
Определения
Четырехугольник называется параллелограммом, если обе пары его противоположных сторон параллельны. Ромб — это четырехугольник со всеми сторонами одинаковой длины. Прямоугольник имеет 4 прямых угла, а квадрат — четыре равные стороны и четыре прямых угла. Эти определения существуют в иерархии отношений. Например, каждый квадрат также является параллелограммом, потому что обе пары его противоположных сторон равны, но каждый параллелограмм не является квадратом.Точно так же каждый квадрат также является ромбом, потому что все четыре стороны имеют одинаковую длину, но каждый ромб не является квадратом. Точно так же каждый квадрат также является прямоугольником, потому что прямоугольник имеет 4 прямых угла, но каждый прямоугольник не является квадратом.
Воздушный змей
Воздушный змей — это особый тип четырехугольника с двумя разными парами последовательных сторон одинаковой длины. Поскольку у ромбов и квадратов также есть стороны одинаковой длины, они тоже воздушные змеи, но обратное неверно. Не каждый воздушный змей — это ромб, потому что все стороны воздушного змея не равны.Точно так же каждый воздушный змей не является параллелограммом, потому что противоположные стороны воздушного змея не обязательно параллельны.
Трапеции
Трапеции — это четырехугольники, у которых одна пара параллельных сторон. Параллельные стороны называются основаниями. Если углы основания равны, трапеция относится к особому типу, называемому равнобедренной трапецией. Прямоугольники — это особый тип равнобедренных трапеций с параллельными противоположными сторонами и равными углами.
Диагонали
Четырехугольники имеют две диагональные линии.В воздушном змее диагональ, соединяющая концы, образует линию симметрии. В ромбе обе диагонали образуют линии симметрии. Линии симметрии обладают мощными свойствами, которые помогают измерять углы, площадь и отношения между геометрическими фигурами.
Заинтересованы в репетиторстве по геометрии? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.
SchoolTutoring Academy — ведущая компания в области образовательных услуг для школьников и школьников. Мы предлагаем репетиторские программы для учащихся K-12, AP и колледжей.Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Ньюарке, Калифорния, посетите: Репетиторство в Ньюарке, Калифорния
Решатель задач геометрии — трапеция
Решатель задач с геометрией
Трапеция
| равнобедренная трапеция | трапеция прямоугольная |
Они дают трекам, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
Трасса 1
Равнобедренная трапеция имеет высоту 20 м, большее основание 80 м, меньшее основание 50 м. Рассчитайте периметр и площадь трапеции.
Колея 2
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание большее 80 см, имеет меньшее основание 50 см. Рассчитайте периметр.
Трасса 3
Прямоугольная трапеция имеет высоту 40 м, основание большее 80 м, меньшее основание 50 м.Рассчитайте периметр и площадь трапеции.
Трасса 4
Равнобедренная трапеция с основанием больше 80 см, имеет меньшее основание 50 см, имеет площадь 1300 см. Рассчитайте высоту трапеции.
Колея 5
Прямоугольник в форме трапеции имеет площадь 1500 см; имеет высоту 30 см. Вычисляет сумму двух оснований.
Колея 6
Равнобедренная трапеция имеет площадь 1500 см; имеет высоту 30 см.Вычисляет сумму двух оснований.
Колея 7
Равнобедренная трапеция имеет периметр 150 см; имеет основание больше 50 см; имеет меньшую базу 30 см. Рассчитайте длину скошенной стороны.
Направляющая 8
Равнобедренная трапеция имеет периметр 150 см, меньшее основание 30 см, наклонную сторону 35 см. Рассчитайте длину более длинного основания.
Колея 9
Равнобедренная трапеция имеет периметр 150 см, основание больше 50 см, наклонную сторону 35 см.Рассчитайте длину более короткого основания.
Колея 10
Прямоугольная трапеция имеет основание больше 50 см, имеет меньшее основание 30 см; имеет наклонную сторону 35 см. Рассчитайте периметр и площадь.
Колея 11
Прямоугольник трапеции имеет периметр 180 см; имеет основание больше 60 см, имеет наклонную сторону 50 см; имеет высоту 40 см. Рассчитайте длину более короткого основания.
Колея 12
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет высоту 40 см.Рассчитайте длину более длинного основания.
Колея 13
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет высоту 40 см; имеет базу больше 60 см. Рассчитайте длину скошенной стороны.
Колея 14
Прямоугольник трапеции имеет периметр 180 см; имеет меньшую базу 30 см; имеет косую сторону 50 см; имеет базу больше 60 см. Рассчитывает длину высоты.
Колея 15
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет высоту 4 см.Рассчитайте меньшую базу.
Колея 16
Равнобедренная трапеция имеет меньшее основание 14 см; имеет скошенную сторону 5 см; имеет высоту 4 см. Вычисляет большую базу.
Колея 17
Равнобедренная трапеция имеет основание больше 20 см, наклонную сторону 5 см; имеет выступ скошенной стороны на большее основание 3 см. Рассчитайте периметр.
Колея 18
Равнобедренный треугольник имеет меньшее основание 14 см; имеет наклонную сторону 5 см. Имеет экранирование наклонной стороны на большем основании 3 см.Рассчитайте периметр.
Трасса 19
Равнобедренная трапеция имеет площадь 2400 см, высоту 40 см, основы составляют треть от другой. Определите периметр.
Дорожка 20
Трапеция образована квадратом и треугольником. Учитывая, что площадь треугольника составляет 6 см, а разница между основаниями трапеции составляет 4 см, вычислите площадь трапеции.
Колея 21
Равнобедренная трапеция имеет наклонную сторону 20 см; имеет основание больше 90 см, имеет меньшее основание, равное 2/3 большего основания.Рассчитайте периметр.
Колея 22
Прямоугольная трапеция эквивалентна 1/4 квадрата с периметром 160 см. Учитывая, что высота трапеции составляет 20 см и 6 см, вычислите площадь прямоугольника, размеры которого совпадают с размерами оснований трапеции.
Направление 23
Прямоугольник в форме трапеции, описанный по кругу, длина скошенной стороны составляет 40 см, а высота равна 3/5 наклонной стороны.Рассчитайте периметр и площадь трапеции.
Дорожка 24
Площадь трапециевидного прямоугольника составляет 2250 см. Зная, что разница размеров проекции наклонной стороны на большее основание и высоты составляет 15 см, а их соотношение составляет 3/4, рассчитайте периметр трапеции.
Трасса 25
Периметр равнобедренной трапеции 250 см, высота 30 см, меньшее основание на 4/7 от большего, равного наклонной стороне.Вычислите площадь трапеции.
Колея 26
Большая база прямоугольной формы трапеции со скошенной стороной под углом 45; зная, что основания 25 см и 15 см, вычисляет площадь трапеции.
Трасса 27
Равнобедренная трапеция ABCD образована тремя равнобедренными равнобедренными треугольниками, периметр каждого из которых равен 170 см, а наклонная сторона составляет 6/5 основания. Рассчитайте периметр трапеции.
Дорожка 28
Равнобедренная трапеция ABCD имеет площадь 900 см. Основание AB является двойным, его высота составляет 20 см. Определите площадь треугольника ACD
Track 29
В равнобедренной трапеции площадь равна 1032 см, а два основания имеют размер 61 см и 25 см соответственно. Вычислите меру высоты и периметра.
Колея 30
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30.Две базы размером 50 см и 30 см соответственно определяют периметр и площадь трапеции.
Дорожка 31
В равнобедренной трапеции сумма и разница размеров двух оснований составляет соответственно 74 см и 14 см. Вычисляет площадь и периметр трапеции, зная, что наклонная сторона равна 25 см.
Колея 32
Периметр равнобедренной трапеции 176 см. Зная, что меньшее основание составляет 4/3 наклонной стороны, а большее основание составляет 19/10 меньшего основания, вычисляется площадь трапеции.
Трасса 33
Каждая из наклонных сторон равнобедренной трапеции составляет треть меньшего основания. Зная, что периметр равен 230 см, а наибольшее основание — 105 см, вычисляется размер меньшего основания и площадь трапеции.
Колея 34
В прямоугольной трапеции нижняя диагональ перпендикулярна наклонной стороне. Зная, что эта диагональная линия и наклонная сторона 24 см и 18 см соответственно, найдите периметр и площадь трапеции.
Колея 35
В прямоугольной трапеции с наклонной стороной образует большое основание под широким углом 30. Рассчитайте периметр трапеции, зная, что высота 11,56 см, а площадь 462,42 см.
Направляющая 36
В трапеции главное основание и вспомогательное основание имеют длину 55 см и 30 см, а периметр — 140 см. Определяет длину наклонных сторон, зная, что одна составляет 6/5 другой.
Колея 37
Разница между основаниями равнобедренной трапеции составляет 30 см, меньшее основание — 5/8 большего основания, периметр — 180 см.Рассчитывает размер наклонных сторон.
Колея 38
Из равнобедренной трапеции вы знаете, что: а) высота составляет 20 см. б) разница между двумя базами 30 см. в) основание больше 80 см. Рассчитайте периметр и площадь трапеции.
Трасса 39
Периметр трапеции, имеющей высоту 34,60 см, составляет 203,49 см. Вычислите площадь трапеции, зная, что наклонные стороны образуют с большим основанием острые углы шириной 45 и 60.
Дорожка 40
Площадь трапециевидного прямоугольника составляет 1080 квадратных сантиметров, а высота — 24 см. Рассчитайте размеры двух оснований, зная, что периметр равен 140 см.
Колея 41
Периметр равнобедренной трапеции составляет 152 см, а длина скошенной стороны — 26 см. Вычислите высоту и площадь трапеции, зная, что меньшее основание имеет длину 40 см.
Направляющая 42
В прямоугольной трапеции основное основание, меньшее основание и высота имеют длину соответственно 60 см, 50 см и 24 см.Вычисляет площадь и периметр трапеции.
Дорожка 43
Вычислите площадь трапеции, у которой большее основание составляет 8/5 меньшего основания, что, в свою очередь, равно высоте, составляющей 50 см.
Трасса 44
Сумма оснований трапеции 80 см, основание 5/3 другого, высота 2/3 вспомогательного основания. Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что одна диагональ равна 25/16 другой.
Дорожка 45
Трапеция образована квадратом со стороной 48 см и двумя треугольниками, катет которых совпадает с одной из двух противоположных сторон квадрата. Гипотенуза двух треугольников составляет 60 см и 50 см соответственно. Рассчитайте периметр и площадь трапеции.
Колея 46
Разносторонняя трапеция имеет периметр 180 см; вычисляет все стороны, зная, что AB = 8/5 DC, DC — AB = 30 см, AD = 2/5 DC.
Дорожка 47
У равнобедренной трапеции ABCD основание CD составляет 15/22 большего основания, наклонные стороны превышают 7 см 3/5 меньшего основания, периметр составляет 124 см. Какой район?
Направляющая 48
Увеличенное основание, высота и наклонная сторона прямоугольника к трапеции, соответственно размером 80 см, 48 см и 50 см. Рассчитайте периметр и площадь трапеции.
Колея 49
Окружность имеет радиус 50 см; две параллельные хорды AB и CD расположены на противоположных частях относительно центра и имеют размер соответственно 96 см и 28 см.Вычисляет площадь и периметр трапеции, в основе которой лежат две хорды.
Трасса 50
Равнобедренная трапеция имеет высоту 20 м, основание больше 80 м, меньшее основание 50 м. Вычислите радиус окружности, описанной трапецией.
Трасса 51
Трапеция имеет основания для диаметра окружности длиной 50 см и параллельную ей веревку длиной 30 см. Рассчитайте периметр и площадь трапеции.
Дорожка 52
В круге с радиусом 50 см сделайте две параллельные хорды, расположенные на противоположных сторонах относительно центра и на расстоянии 14 см и 48 см от него соответственно. Вычисляет площадь и периметр трапеции, у которой есть основания для двух струн.
Колея 53
Прямоугольник и равнобедренная трапеция равны по высоте, периметр прямоугольника 140 см, разница размеров прямоугольника между ними 30 см, наклонная сторона трапеции 25 см.Вычислить:
размер оснований прямоугольника;
протяженность оснований трапеции;
площадь трапеции и прямоугольника;
периметр трапеции.
Направляющая 54
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует наклонной стороне, зная, что площадь трапеции составляет 1320 см.
Дорожка 55
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 28 и 8 см.Вычислите периметр, площадь и две диагонали.
Направляющая 56
Прямоугольная трапеция имеет высоту 24 см и основания соответственно 18 и 10 см. Вычислите периметр, площадь и две диагонали.
Колея 57
Прямоугольная трапеция, сумма оснований 110 см, высота 24 см. Рассчитывает площадь.
Трасса 58
Равнобедренная трапеция, сумма оснований 110 см, высота 24 см.Рассчитывает площадь.
Трасса 59
Равнобедренная трапеция имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Дорожка 60
Прямоугольник трапеции имеет площадь 336 см, сумма оснований 28 см. Рассчитайте высоту.
Колея 61
Равнобедренная трапеция имеет большее основание 50 см, меньшее основание 30 см. Рассчитайте высоту, зная, что наклонная сторона равна 26 см.
Колея 62
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Рассчитайте радиус круга, вписанного в трапецию, зная, что высота 24 см.
Колея 63
Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Колея 64
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см.Рассчитайте радиус круга, вписанного в трапецию, зная, что высота 24 см.
Колея 65
Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Рассчитайте диаметр круга, вписанного в трапецию, зная, что высота 24 см.
Дорожка 66
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Рассчитайте диаметр круга на трапеции, зная, что высота равна 48.75 дюймов.
Колея 67
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см. Вычислите длину круга, окружающего трапецию, зная, что высота составляет 48,75 дюйма.
Колея 68
Равнобедренная трапеция имеет основание большее 80 см, меньшее основание 50 см. Вычислите площадь описанной круговой трапеции, зная, что высота составляет 48,75 дюйма.
Колея 69
Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см.Вычислите:
площадь круга, описанного трапецией, зная, что высота составляет 48,75 дюйма;
расстояние от центра хорды AB;
расстояние каната от центра CD;
длина дуги АВ;
длина дуги CD;
центральный угол АОБ;
центральный угол ХПК;
площадь кругового сектора AOB; площадь кругового сектора наложенным платежом.
Направляющая 70
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1320 см.
Направляющая 71
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 1320 см.
Направляющая 72
Прямоугольная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см.Вычислите радиус окружности, соответствующей трапеции.
Направляющая 73
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Колея 74
Прямоугольник в форме трапеции имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 75
Прямоугольник трапеции имеет периметр 160 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Дорожка 76
Прямоугольник трапеции имеет большое основание 60 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь круга, окружность которого изопериметрическая трапеция.
Направляющая 77
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого.Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1320 см.
Колея 78
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой. Вычислите площадь круга, радиус которого соответствует меньшему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 79
Равнобедренная трапеция имеет высоту 24 см, а основания составляют одну из 5/7 другой.Вычислите площадь круга, радиус которого соответствует большему основанию, зная, что площадь трапеции составляет 1440 см.
Направляющая 80
Прямоугольник в форме трапеции имеет высоту 24 см, а основания составляют 5/6 от другого. Вычислите площадь круга, радиус которого соответствует малой диагонали, зная, что площадь трапеции составляет 1320 см.
Трасса 81
Равнобедренная трапеция имеет высоту 10 см и основания, которые являются одним из 7/17 другого.Вычислите площадь круга, радиус которого соответствует диагонали, зная, что площадь трапеции составляет 240 см.
Направляющая 82
Равнобедренная трапеция имеет высоту 24 см и основание соответственно 60 и 50 см. Вычислите радиус окружности, соответствующей трапеции.
Трасса 83
Равнобедренная трапеция имеет площадь 1320 см и основания соответственно 60 и 50 см. Вычислите площадь круга, радиус которого соответствует высоте трапеции.
Дорожка 84
Прямоугольник в форме трапеции имеет площадь 360 см и основания соответственно 10 см и 20 см. Вычислите площадь круга, диаметр которого меньше диагонали трапеции.
Трасса 85
Равнобедренная трапеция имеет площадь 240 см и основания соответственно 34 см и 14 см. Вычислите площадь круга, диаметр которого соответствует диагонали трапеции.
Направляющая 86
Равнобедренная трапеция имеет периметр 186 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см.Вычислите площадь круга, диаметр которого соответствует основанию трапеции.
Трасса 87
Равнобедренная трапеция имеет большое основание 70 см, меньшее основание 50 см, высоту 24 см. Вычислите площадь круга, окружность которого изопериметрическая трапеция.
Track 88
Рассчитайте площадь и периметр разносторонней трапеции, зная, что большее основание составляет 80 см, а меньшее основание — 50 см, а наклонные стороны имеют длину соответственно 30 см и 20 см.
Направляющая 89
Равнобедренная трапеция имеет меньшее основание 8,4 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 90
Прямоугольная трапеция имеет меньшее основание 19,2 см и выступ скошенной стороны на большем основании 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 91
Прямоугольник в форме трапеции имеет наклонную сторону 18 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 92
Равнобедренная трапеция имеет наклонную сторону 18 см и выступание наклонной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 93
Равнобедренная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 94
Прямоугольная трапеция имеет основание 30 см и выступ скошенной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Направляющая 95
Прямоугольная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что нижняя диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 96
Равнобедренная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что диагональ перпендикулярна наклонной, рассчитайте периметр и площадь трапеции.
Колея 97
Периметр равнобедренной трапеции составляет 204 см, а каждая наклонная сторона — 30 см.Вычислите площадь и протяженность оснований, зная, что большее — это 5/3 второстепенного.
Колея 98
Основание большей формы равнобедренной трапеции с наклонной стороной под углом 45; зная, что основания 35 см и 15 см, вычисляет площадь и периметр трапеции.
***********
Программа для решения задач может давать совершенно неверные ответы.
Что такое трапеция? [Определение, факты и пример]
Что такое трапеция?
Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон.
Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными.
Расстояние по перпендикуляру между параллельными сторонами называется высотой.
Примеры :
Без примеров :
Типы трапеций
Трапеция бывает трех типов, а именно
1. Правая трапеция : Имеет пару прямых углов.
2. Равнобедренная трапеция : имеет равную длину непараллельных сторон. На изображении стороны AD и BC равны.
3. Трапеция из чешуи : у нее нет равных углов и равных сторон.
Свойства трапеции
Трапеция называется параллелограммом, если обе пары ее противоположных сторон параллельны.
Трапеция — это квадрат, если обе пары его противоположных сторон параллельны; все его стороны равной длины и расположены под прямым углом друг к другу.
Трапеция может быть прямоугольником, если обе пары ее противоположных сторон параллельны; его противоположные стороны равны по длине и расположены под прямым углом друг к другу.
Примеры из реальной жизни
Некоторые из многих примеров трапеции — это лицевая сторона коробки для попкорна, сумочки и мостов.
Интересные факты
|
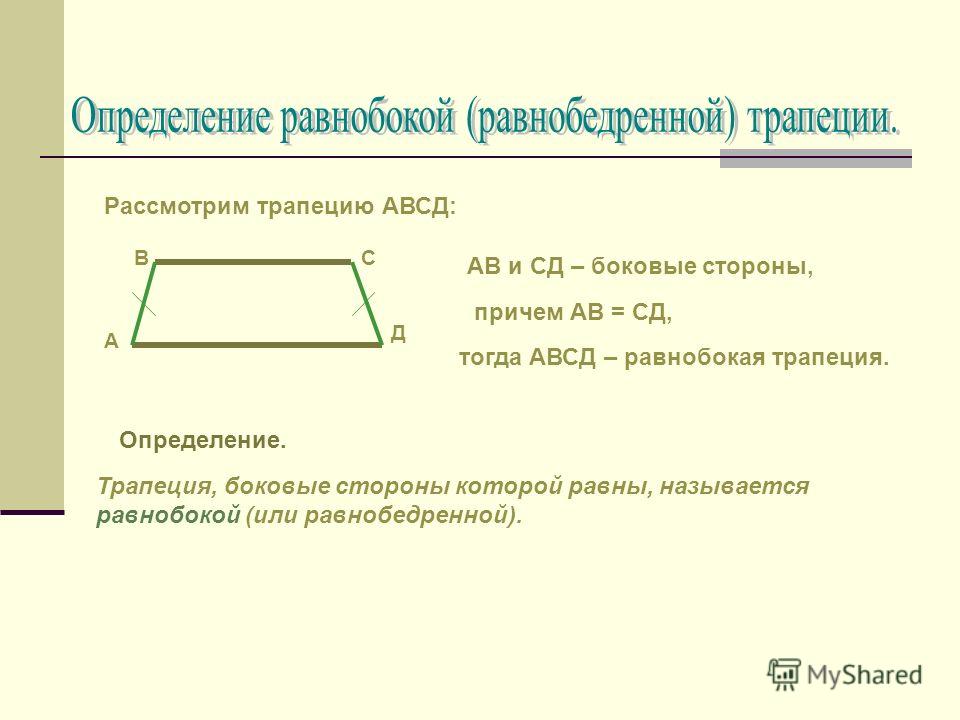 Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.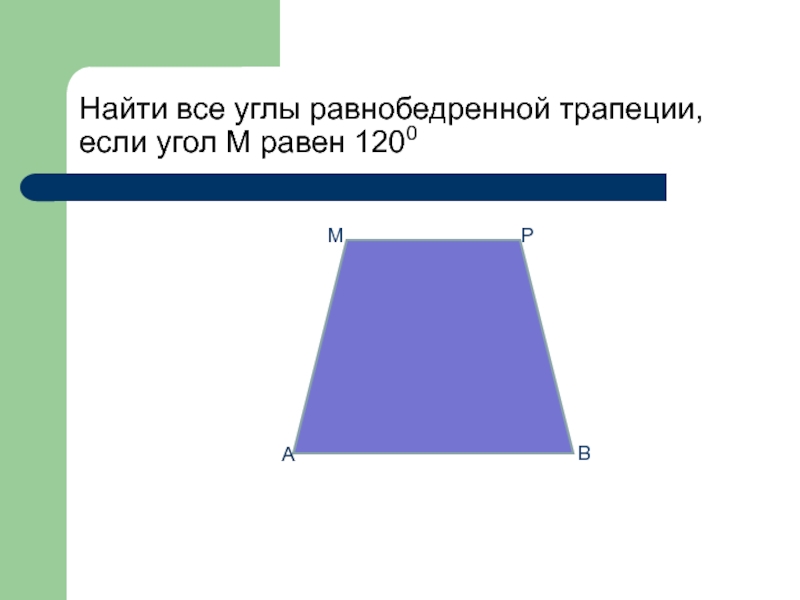

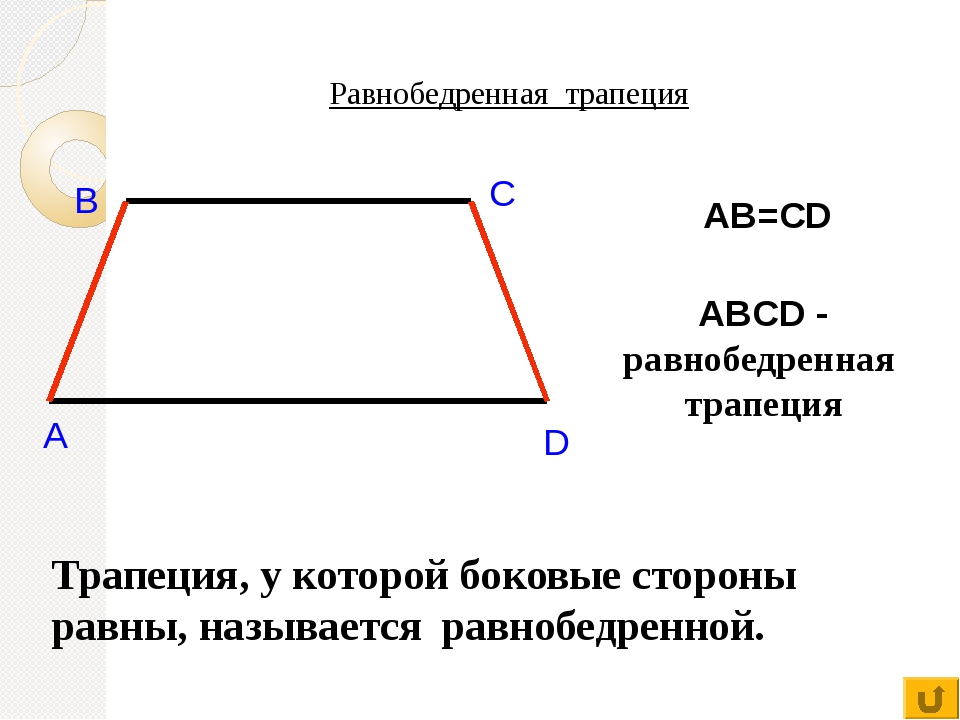

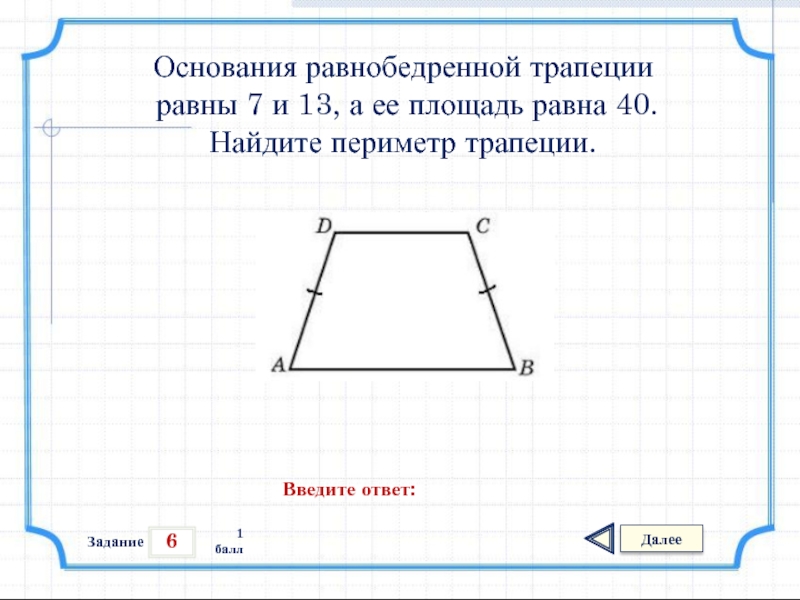 Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только две противолежащие стороны параллельны. 2. Определение трапеции. —Рассмотрим четырехугольник, про который можем сказать, что две противолежащие стороны параллельны, две другие не параллельны. Вниманию учащихся учитель представляет слайд 6 и ставить цель на данный этап урока. – А теперь сравните параллелограмм и трапецию и на основе сравнительного анализа выведите определение трапеции.  Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.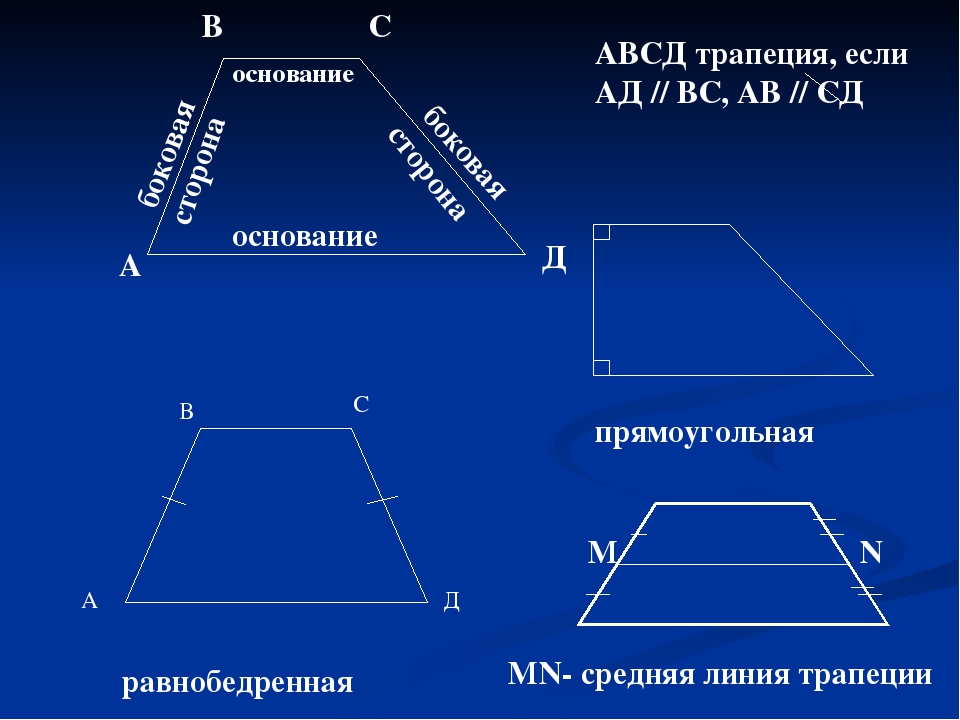
 Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны. И одновременно ТХ – ось симметрии равнобедренной трапеции.
И одновременно ТХ – ось симметрии равнобедренной трапеции. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
 Радиус окружности можно вычислить по формуле: r = √ab.
Радиус окружности можно вычислить по формуле: r = √ab.
