Свойства и признаки равнобедренной трапеции 8 класс
Свойства и признаки
равнобедренной трапеции
Математический диктант
4. Назовите четырехугольник, у которого две стороны параллельны, а две другие нет.
2. Сколько диагоналей можно провести из одной вершины n-угольника, если n = 4, 6.
1. Назовите многоугольник, все виды которого являются выпуклыми многоугольниками.
6. Параллельные стороны в трапеции называются …
3. Чему равна сумма углов выпуклого пятиугольника?
10. В параллелограмме противоположные стороны … и … .
5. Четырехугольник у которого противоположные стороны параллельны ….
8. В четырехугольнике сумма углов равна …
7. В трапеции равные стороны называются …
9.
Проверь себя!!!
1. Треугольник
Оценка «5» — 10 баллов.
Оценка «4» — 8-9 баллов.
Оценка «3» — 6-7 баллов.
Менее 5 баллов – учи определения!!!
2. одна, три.
3. 540.
4. трапеция.
5. параллелограмм
6. основания
7. Боковые стороны
8. 360
9. равны
10. Равны и параллельны
Проверка домашнего задания
Трапеция.
1
2
Прямоугольная трапеция.
1 = 2 (внутренние накрест лежащие при // прямых и секущей)
Равнобедренная трапеция.3
6
Трапеция.
4
5
3 + 4 = 180 (внутренние односторонние при // прямых и секущей)
5 = 6 (соответственные при // прямых и секущей)
Теоремма Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающую вторую прямую, то они пересекут на второй прямой равные между собой отрезки.
Равнобедренная трапеция.
Теоремма средней линии трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.
- Вариант 1. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120 .

- Вариант 2. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона – 10 см, а один из углов равен 60 .
Проверь себя
8 см
6 см
90
90
30
30
30
30
10 см
60
3 см
8 см
3 см
5 см
5 см
6 см
Самостоятельная работа
- Вариант 3. Диагональ АС равнобедренной трапеции АВСД делит пополам угол ВАД. Найдите периметр трапеции, если основание АД равно 12 см, а угол АСД равен 60 .
90
6 см
30
60
30
12 см
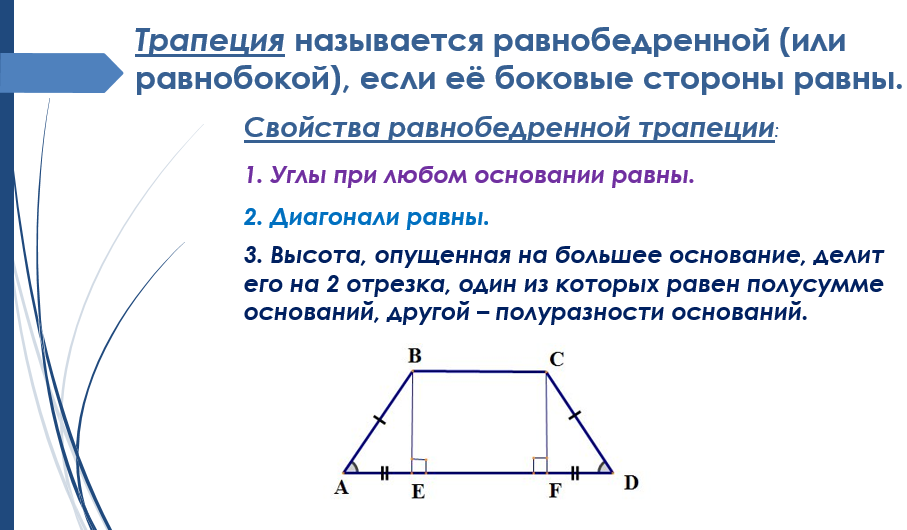
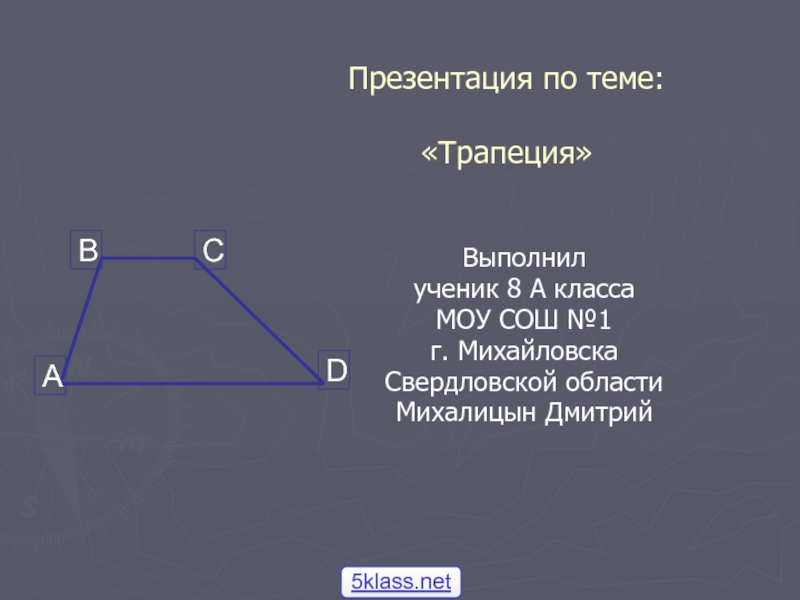
Свойства равнобокой трапеции
1. Углы при основаниях равны.
2. Диагонали равны.
3. Высоты, проведенные из вершин к основанию, делят трапецию на два равных треугольника.
Признаки равнобедренной трапеции.
Запишите самостоятельно.
Решение задач
№ 392(аб), 393(в), 394, 395, 397(а)
Домашнее задание
№ 392(аб), 393(в), 396, 398, 397 (б)
Урок по геометрии «Трапеция»(8 класс)
Дата:
Тема урока: Трапеция.
Цели урока:
Образовательная:
Ввести понятие трапеции и ее элементов, познакомить учащихся видами трапеций;
Рассмотреть некоторые свойства и признаки равнобедренной трапеции;
Научить учащихся применять полученные знания в процессе решения задач.
Развивающая:
Развитие у детей умения обобщать, логически мыслить, применять в своих рассуждениях аналогию, наблюдение, рационально применять свои знания;
Воспитательная:
Воспитание интереса к математике с помощью элементов занимательности, знакомства с историей возникновения понятия «трапеция»
Тип урока: урок изучения нового материала и первичное закрепление знаний.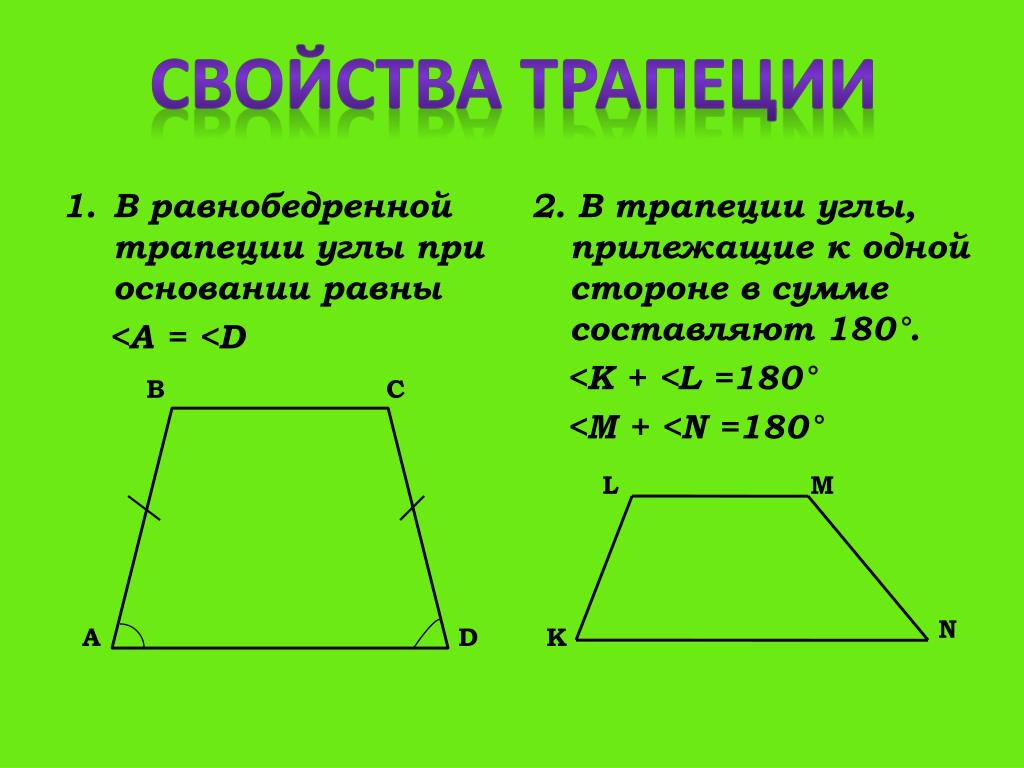
Оборудование: слайды из презентации к уроку, проектор, карточка-тест.
Содержание урока:
Организационный момент (1 мин)
Актуализация опорных знаний (5-7 минут)
Сообщение цели и темы урока. (2-3 минуты)
Изучение нового материала (15 – 20 минут)
Ввести понятие трапеции, ее оснований и боковых сторон.
Ввести понятия равнобедренной трапеции, прямоугольной трапеции.
Изучение свойств равнобедренной трапеции.
Закрепление изученного материала (решение задач на готовых чертежах)
(10-12 минут)Самостоятельная работа в виде теста (3- 4 минуты)
Подведение итогов урока. Рефлексия (2 – 3 минуты)
Домашнее задание (1 минута)
Ход урока:
Организационный момент
Учитель: Здравствуйте, ребята.
Эта тема является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем.
Актуализация опорных знаний
Попробуем систематизировать все, что мы знаем о четырехугольниках.
Слайд 1
Ребята, посмотрите, пожалуйста, на слайд.
На доске представлена схема изучения геометрии 8 класса, но все понятия потеряли свои места. Ваша задача – восстановить порядок изучения материала.
Вспомогательные вопросы:
— Какие бывают четырехугольники? [Выпуклые и невыпуклые]
— Какой четырехугольник называется выпуклым? [четырехугольник – называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины]
— Что вы можете сказать о сумме углов четырехугольника? [Сумма всех углов равна 360°]
— С каким четырехугольником мы уже познакомились?[Параллелограммом]
— Дайте определение параллелограмма? [Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны]
— Какие свойства параллелограмма мы изучили? [В параллелограмме противоположные стороны и углы равны ]; [Диагонали параллелограмма точкой пересечения делятся пополам]
— Какие признаки мы изучили?
[Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм]
[Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм]
[Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм]
— Для чего необходимо использовать признаки, а для чего применять свойства?
[Свойство — это характерная особенность, присущая только этой геометрической фигуре.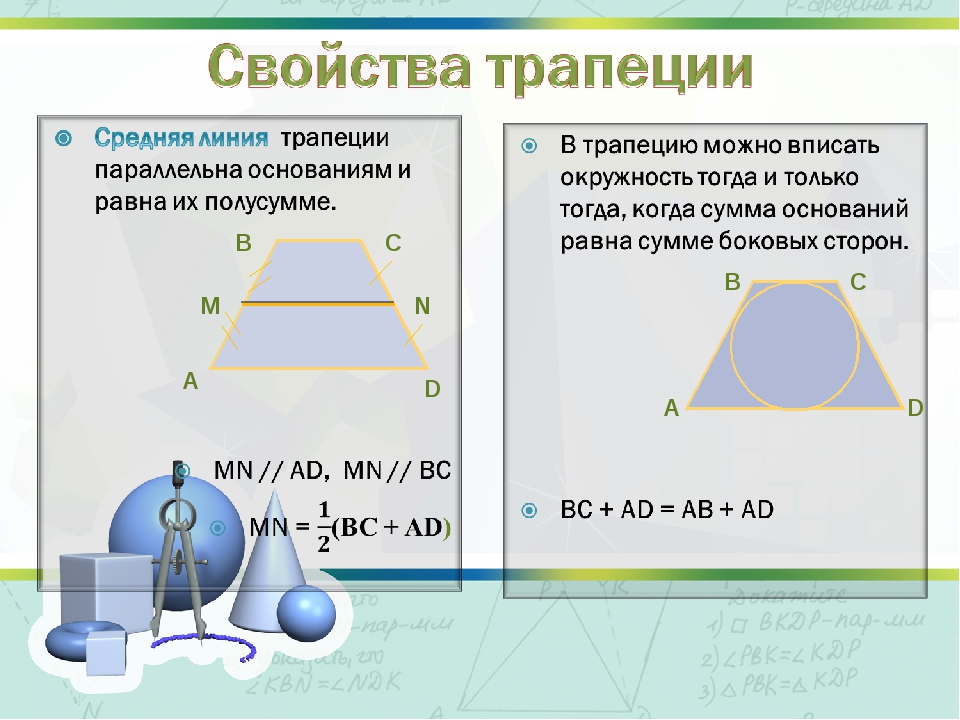
Молодцы! Вы хорошо справились с заданием!
Сообщение цели и темы урока.
Слайд 2
На доске вы видите разные виды четырехугольников.
— Как вы думаете, у всех ли четырехугольников противоположные стороны параллельны? (Выслушиваются ответы учеников).
-А может ли существовать четырехугольник, у которого только одна пара сторон параллельна?
— А как такие четырехугольники называются?
Итак, какова тема нашего урока? [Трапеция]
— Запишем тему урока: Трапеция.
Мы уже изучили параллелограмм, вспомнили с вами структуру изучения темы? По аналогии с параллелограммом, скажите, что мы узнаем о трапеции?
[Сегодня на уроке мы познакомиться с еще одним видом четырехугольников – трапецией, узнаем о её видах, свойствах и признаках; научимся применять эти свойства и признаки при решении задач.
Изучение нового материала
— Правильно, а сейчас послушаем рассказ подготовленный Самуйленковым Степаном и узнаем, почему этот четырехугольник — носит такое название?
Понятие трапеции формировалось в течение длительного периода времени. «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посейдона. Сначала трапецией называли любой четырехугольник, не являющийся параллелограммом . Именно в таком смысле термин «трапеция» использовал Евклид в своих «Началах». Лишь в XVIII в. это слово приобретает современный смысл.
«Трапеция» — слово греческого происхождения, означавшее в древности «столик» (по гречески «трапедзион» означает столик, обеденный стол).
— Спасибо, Степа! [Сообщение оценки]
Ввести понятие трапеции, ее оснований и боковых сторон.
В тетрадях и на доске рисунок и записи
Слайд 3
— Ребята, посмотрите на трапецию и дайте определение трапеции самостоятельно. [Выслушиваются ответы учеников].
[Выслушиваются ответы учеников].
— Проверьте себя, прочитайте определение в учебнике. ( страница 103)
— Как называются параллельные стороны? [Основания]
Как называются две другие стороны? [боковые стороны]
— Параллельные стороны не могут быть равными? [ Нет, так как в противном случае мы имели бы параллелограмм]
— Правильно, поэтому одну из них мы назовем большим, вторую – малым основаниями трапеции.
2. Ввести понятия равнобедренной трапеции, прямоугольной трапеции. В тетрадях и на доске рисунки и записи. Слайд 4.
— Какие стороны у трапеции могут быть равными? [Боковые]
В зависимости от длин боковых сторон и их расположения трапеции могут быть различных видов. Рассмотрим виды трапеции.
В 7 классе мы изучали треугольник, у которого две равные стороны. Как он называется? [равнобедренный]
Как называется трапеция, которой боковые стороны равны? [равнобедренная]
Слайд 5.
— Следующий вид трапеции — прямоугольная трапеция.
Дайте определение прямоугольной трапеции самостоятельно.
Подведем итог: Трапеция – это …[ответ учащихся]
Трапеции бывают …[ответ учащихся]
Какая трапеция называется равнобедренной? прямоугольной …[ответ учащихся]
Изучение свойств равнобедренной трапеции.
— Равнобедренная трапеция обладает основными свойствами. Эти свойства мы выведем, решая задачу.
Рассмотрим задачу с учебника №388(а)
№ 388 (а).
В равнобедренной трапеции углы при основании равны.
1. Дополнительные построения: СЕ||АВ.
2. ABСЕ – параллелограмм (СЕ||АВ, АЕ||ВС) => АВ=СЕ.
3. АВ=СЕ=СD=> СЕD равнобедренный => 1=2.
4. Так как АВ||СЕ, то 3=2 – как соответственные => 3=1.
5. В=180º-3=180º-1=С.
Ч.т.д.
В ходе решения задачи, учитель задает наводящие вопросы:
При решении задач, мы используем свойства и признаки уже изученных фигур.
 Для этого необходимы дополнительные построения. Подумайте, на какие фигуры можно разбить трапецию? Что для этого надо сделать? [Построить отрезок СЕ, такой что СЕ||АВ.]
Для этого необходимы дополнительные построения. Подумайте, на какие фигуры можно разбить трапецию? Что для этого надо сделать? [Построить отрезок СЕ, такой что СЕ||АВ.]Что вы можете сказать о четырехугольнике ABСЕ? [ABСЕ – параллелограмм (СЕ||АВ, АЕ||ВС) => АВ=СЕ.]
Рассмотрим другую фигуру – треугольник СЕD. Какой это треугольник? [Равнобедренный, т.к. АВ=СЕ=СD].
Какими свойствами обладает равнобедренный треугольник? [В равнобедренном треугольнике углы при основании равны, значит 1=2.]Скажите, можно ли утверждать что 3 = 2? Как называются эти углы?
Итак, если 1=2 , а 2=3 значит 3=1Мы доказали равенство углов при большем основании. Как доказать, что В=С?
Что вы можете сказать о А и В? [односторонние]. Что мы знаем про односторонние углы? [сумма односторонних углов равна 180]
Слайд 6. № 388 (б) прочитать задачу.
— Доказательство этого свойства, вы проведете дома самостоятельно.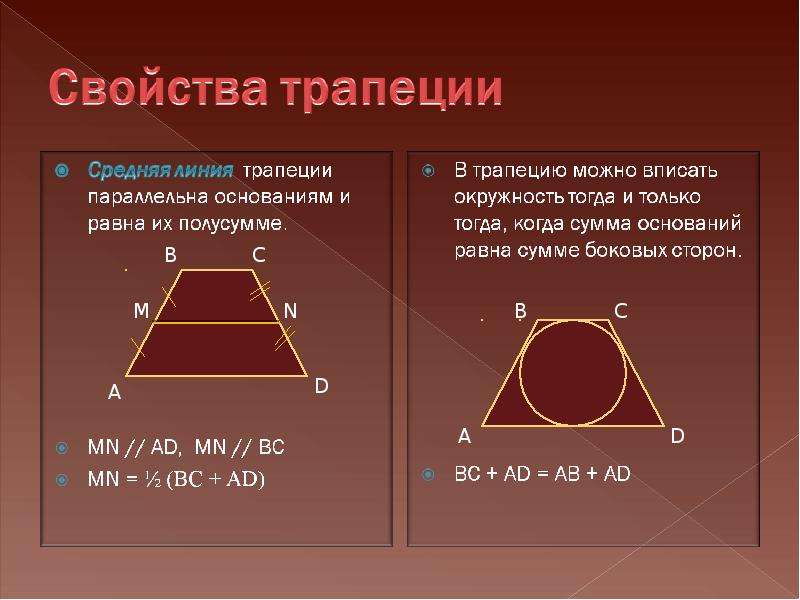
В тетрадях и на доске рисунок и записи:
Слайд 7.
— Сформулируйте утверждения, обратные свойствам равнобедренной трапеции. Как называются эти обратные свойства? [признаки равнобедренной трапеции]
Закрепление изученного материала (решение задач на готовых чертежах)
Сейчас я предлагаю вам узнать имя ученого, спрятанного за сеткой задач. При правильном ответе сектор открывается и появляется часть изображения.
Много интересного рассказывают про этого учёного. Вот, например, один случай. Учёный, наблюдая звёзды, упал в колодец, а стоявшая рядом женщина посмеялась над ним, сказав: «Хочет знать, что делается на небе, а что у него под ногами, не видит»
Этот учёный сформулировал следующие теоремы: а) Вертикальные углы равны; б) В равнобедренном треугольнике углы при основании равны; в)Если на одной стороне угла отложить равные отрезки, и провести через них параллельные прямые, то и на другой стороне угла отложатся равные отрезки.
Слайд 8
Ответы:
( слева – направо, 1 ряд – 2 ряд )
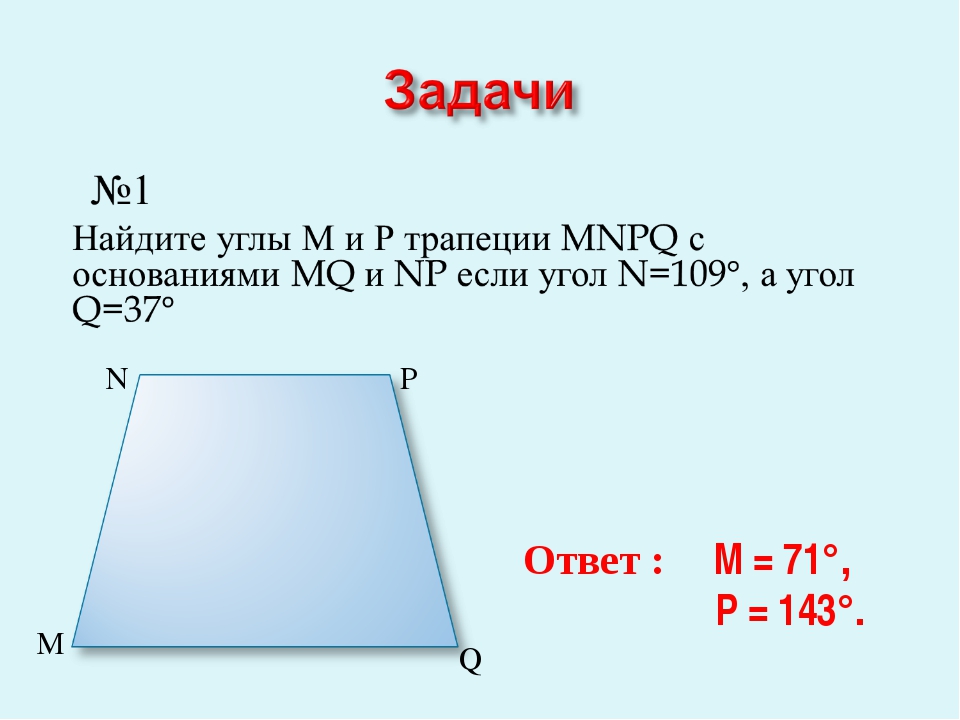
1) Е = N = 80;M = 100.
2) F = 90;M=115
3) К =F = 55;M=R= 125;
4) B = 110;M=130
5) D = 55;C=125;F = 105
6) C = 120;A=60;B = 120
При отсутствии времени количество задач сократить, решив их на следущем уроке.
Самостоятельная работа в виде теста
Слайд 9.
ТЕСТОпределить вид четырехугольника если он имеет:
Трапеция
Паралле-лограмм
Равнобед-ренная
Прямо-угольная
Разносто-ронняя
два прямых угла и все стороны разные
+
два разных острых угла и все разные стороны
+
два одинаковых тупых угла и две одинаковые боковые стороны
+
противоположные стороны равны и углы равны
+
Подведение итогов урока.
 Рефлексия.
Рефлексия.
Ребята, что нового вы узнали на уроке?
Что было особенно интересно?
На что еще необходимо обратить внимание?Домашнее задание
П. 44, записи в тетрадях, № 388(б), № 390.
Придумать и решить задачу на использование свойства или признака трапеции.
Методическая разработка. Конспект урока геометрии по теме «Трапеция». 8-й класс
Цели и задачи урока:
Основные цели:
- Личностные: создание подходящих условий для формирования у учащихся положительной мотивацию к учению
- преодолевать посильные трудности, чувства коллективизма, взаимовыручки и уважения друг к другу, умения вести
- диалог, аккуратности.
- Метапредметные: формирование навыка ставить цели и задачи, изучать поставленную проблему, оценивать результат своей работы
- объекты, создавать, применять и преобразовывать модели, повышать алгоритмическую культуру обучающихся,
- развивать логическое мышление, познавательную активность и навыки научной речи.

- Предметные: повторить виды четырехугольников, сформулировать понятия «трапеция», «равнобедренная трапеция», «прямоугольная трапеция»; рассмотреть признаки и свойства трапеции.
Тип урока: урок изучения нового материала.
Форма работы: фронтальная, индивидуальная, групповая.
Оборудование: компьютер, проектор, плакат с элементами геометрических фигур, карточки с заданиями (распечатки чертежей и заданий из конспекта урок).
План урока:
1. Организационный момент.
2. Актуализация знаний учащихся и подведение учащихся к новой теме.
3.Изучение нового материала.
4. Закрепление умений и получение навыков работы при решении простейших задач на трапецию.
5. Рефлексия. Подведение итогов. Выставление оценок.
6. Домашнее задание.
Ход урока
I. Организационный моментПриветственное слово учителя, проверка домашнего задания.
Эпиграф нашего сегодняшнего урока:
II. Актуализация знаний«Если вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи, то решайте их!»
(Д.Пойа )
Устная работа по готовым чертежам.
На рисунке вы видите пять фигур, назовите и охарактеризуйте те, которые вы уже изучали ранее. Чем различаются данные фигуры и что их объединяет. Теперь давайте рассмотрим последнюю фигуру и так же определим, какими общими признаками с предыдущими она обладает. Чем она отличается от остальных?
Такая фигура, у которой две стороны параллельны, а две другие — не параллельны, называется трапеция.
III. Изучение нового материалаПопробуем сформулировать цели и задачи урока, запишем в тетрадях тему урока и определение.
Трапеция – название происходит от греческого trapezion (столик).
Давайте рассмотрим виды трапеций.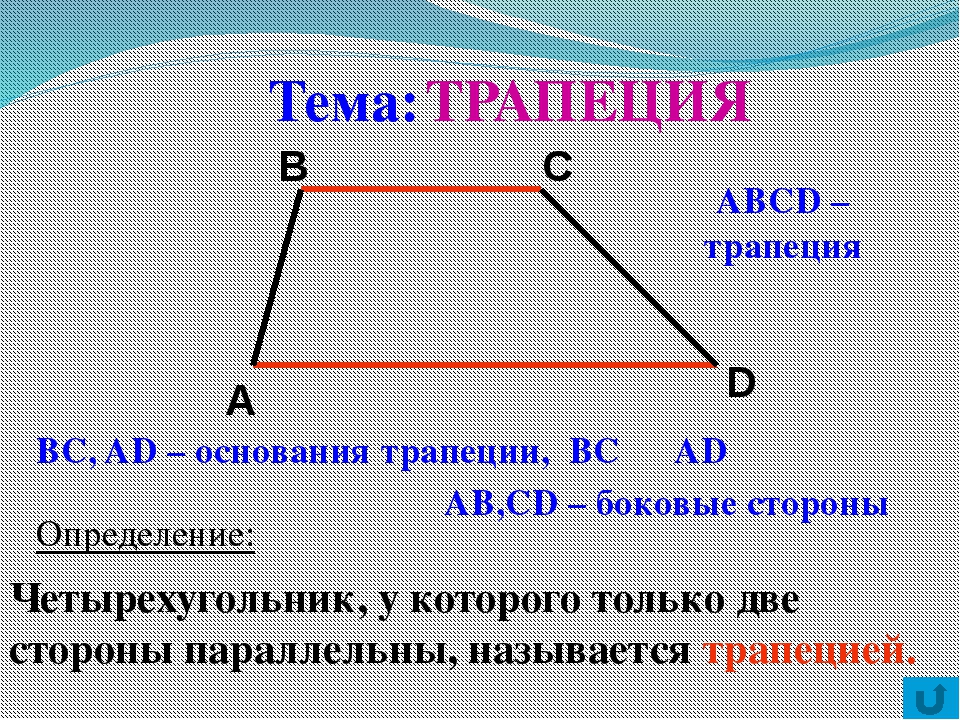 Подумаем, где мы встречались с этой фигурой в повседневной жизни? (учащиеся приводят примеры)
Подумаем, где мы встречались с этой фигурой в повседневной жизни? (учащиеся приводят примеры)
Трапецияя–> – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные.
Виды трапеции.
Равнобедренная – трапеция, у которой боковые стороны равны.
Прямоугольная – трапеция, один из углов которой прямой.
Работа в группах.
Предложить детям разбиться на группы по 4-6 человек. За круглым столом разбейтесь в группах пополам и обсудите свойства равнобедренной трапеции. Одна часть группы исследует диагонали, а другая углы трапеции.
После обсуждения предложить учащимся сформулировать свойства и выписать их, сверить ответы различных групп. Продемонстрировать учащимся верную формулировку и попросить записать в тетрадях.
Свойства равнобедренной трапеции.
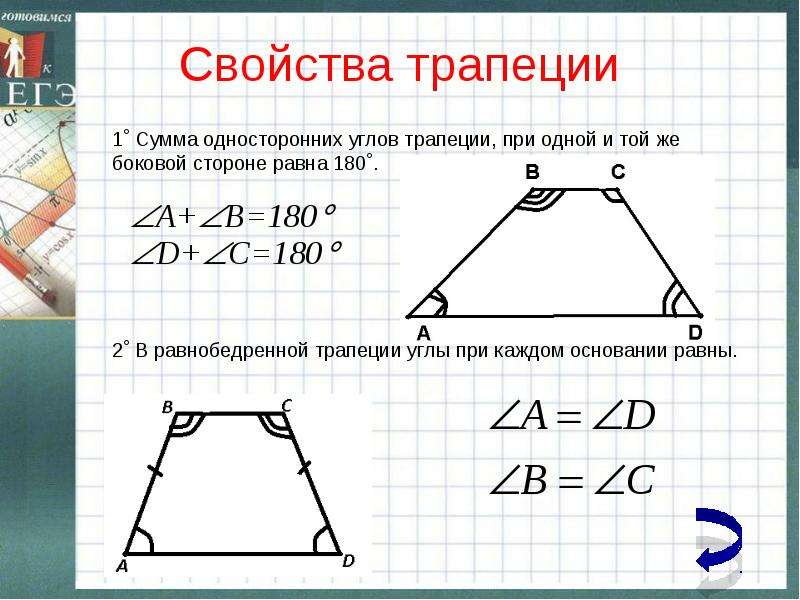
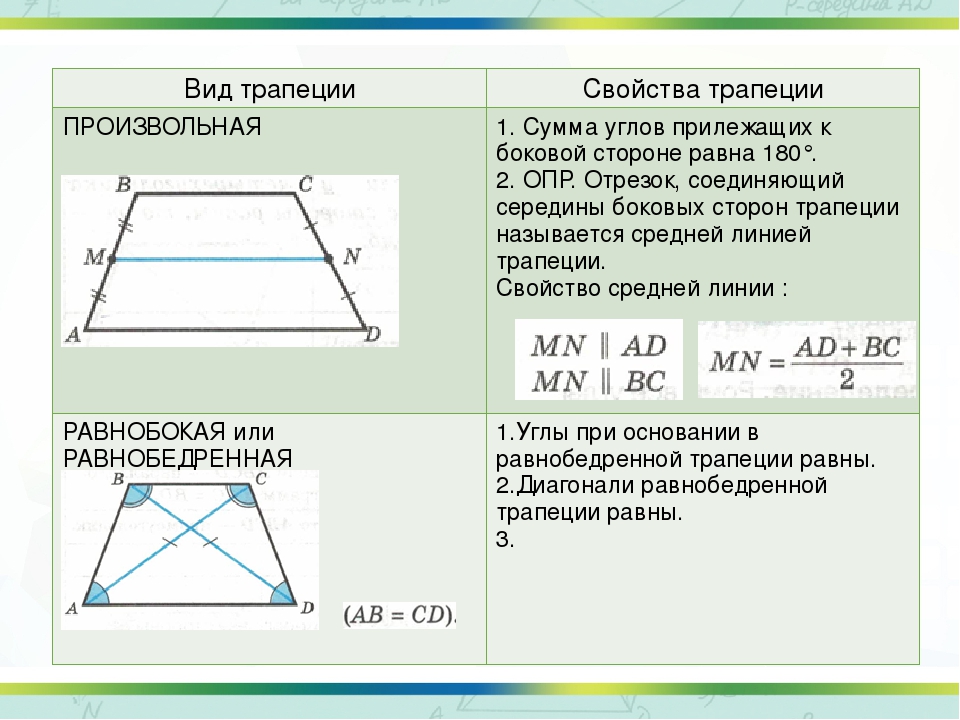
Свойство 1.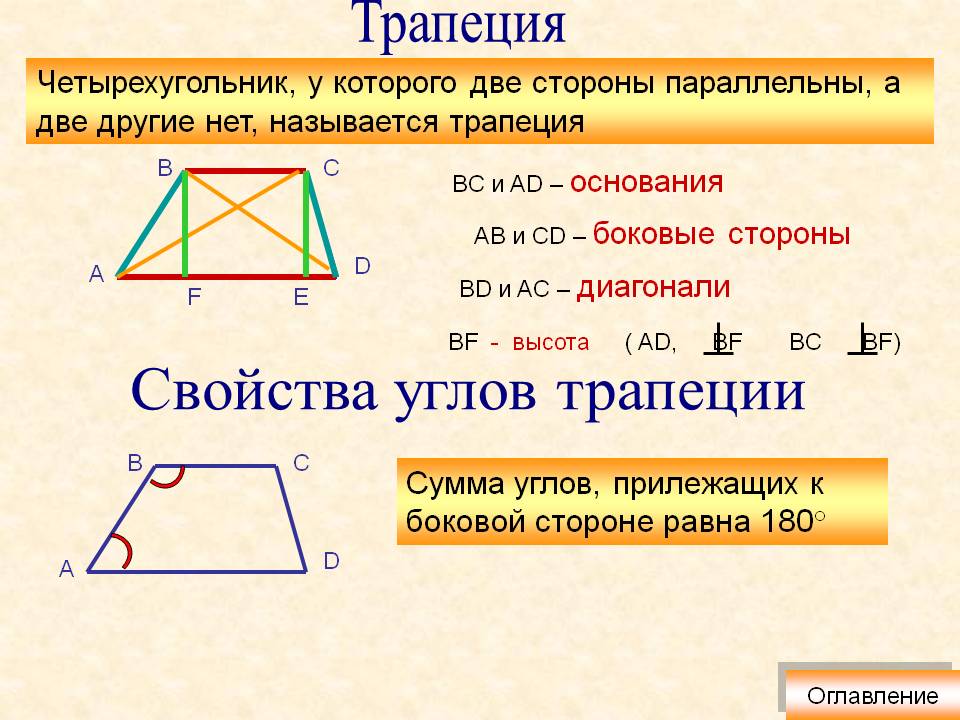 В равнобедренной трапеции углы при каждом основании равны.
В равнобедренной трапеции углы при каждом основании равны.
Свойство 2. В равнобедренной трапеции диагонали равны.
Попробуйте сформулировать утверждения, обратные свойствам, и выясните справедливы они или нет. После этого попробуйте сформулировать Признаки равнобедренной трапеции и выписать их в тетрадь.
Признак 1. Если углы при основании трапеции равны, то она равнобедренная.
Признак 2. Если диагонали трапеции равны, то она равнобедренная.
ФизкультминуткаНа стенах кабинета расположены яркие фигуры четырехугольников. Попросить учащихся зафиксировать голову в одном положении и перемещая только взгляд, определить, сколько среди этих фигур трапеций и сколько из трапеций являются равнобедренными.
IV. Закрепление умений и навыковРешение задач по готовым чертежам.
I уровень
1.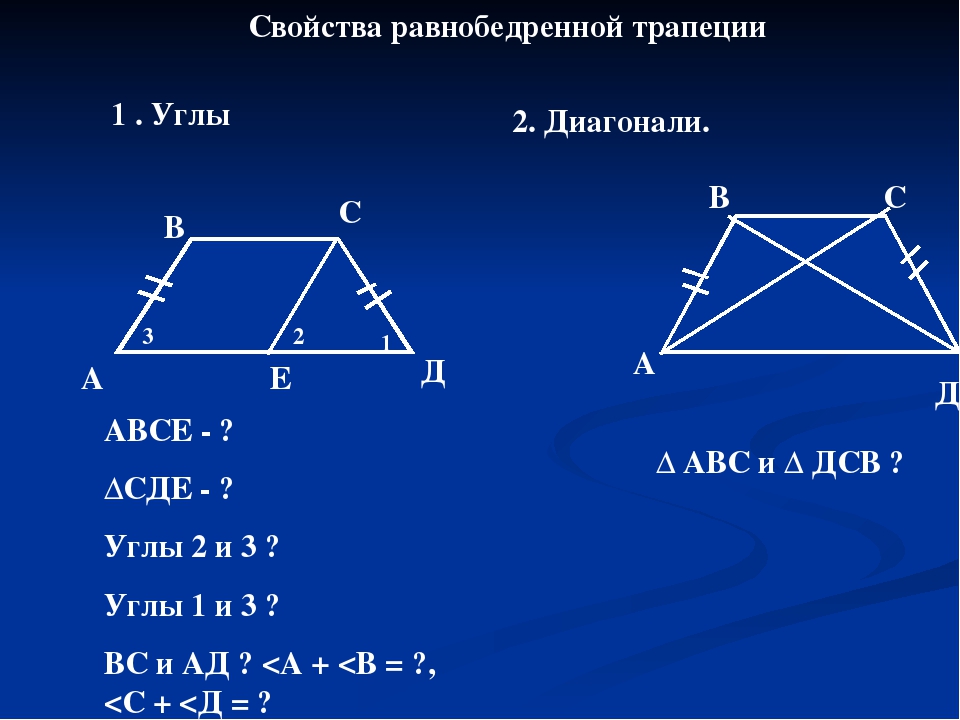 Найдите неизвестные углы трапеции:
Найдите неизвестные углы трапеции:
II уровень
2. Найдите периметр трапеции АВСD:
III уровень
1. Из вершины тупого угла равнобедренной трапеции АВСD проведен перпендикуляр СE к прямой AD, содержащий большее основание. Докажите, что AE=(AD+BC)/2.
2. В прямоугольной трапеции диагонали взаимно перпендикулярны. Большая диагональ составляет с меньшей боковой стороной угол в 600. Докажите, что меньшая диагональ равна полусумме оснований трапеции.
V. РефлексияОтветить на вопросы:
- Какую фигуру мы сегодня изучили?
- Какие виды бывают у трапеции?
- Какими свойствами обладает равнобедренная, прямоугольная трапеция?
Оценить урок и свою работу на уроке.
VI. Домашнее задание1) задачи по готовым чертежам из второго комплекта карточек.
2) п. 59, составить 2 собственные задачи по теме. Повторить определения, свойства и признаки.
Повторить определения, свойства и признаки.
Трапеция 8 класс онлайн-подготовка на Ростелеком Лицей
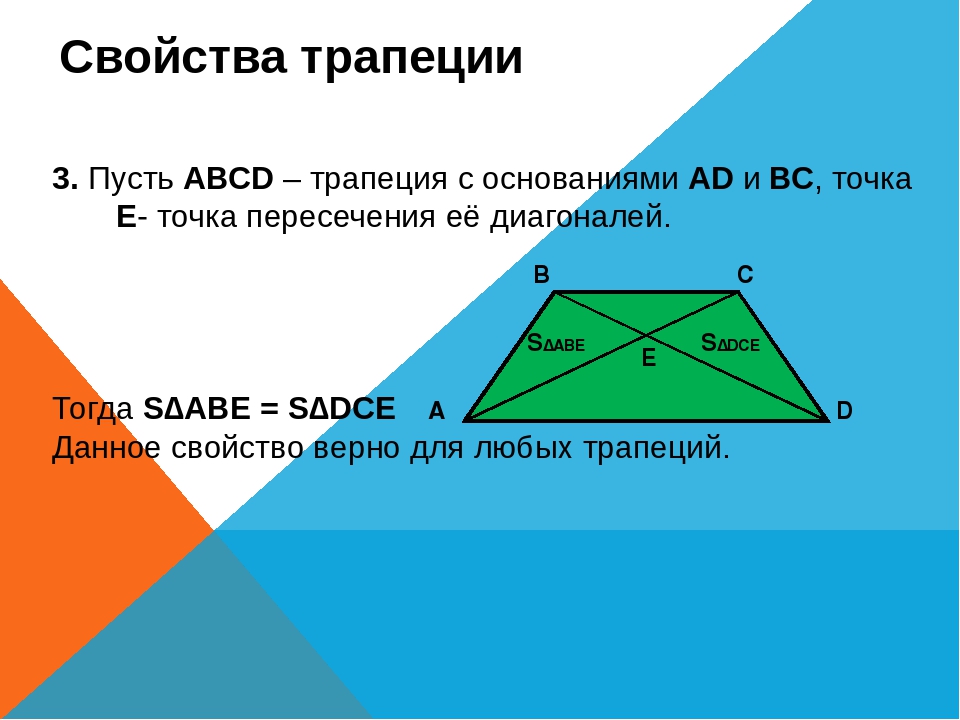
Трапеция.
Как и в параллелограмме, в трапеции две стороны параллельны. Однако существенным отличием является то, что две другие стороны трапеции являются непараллельными. Существует несколько видов трапеции – равнобедренная или равнобокая, прямоугольная трапеция.
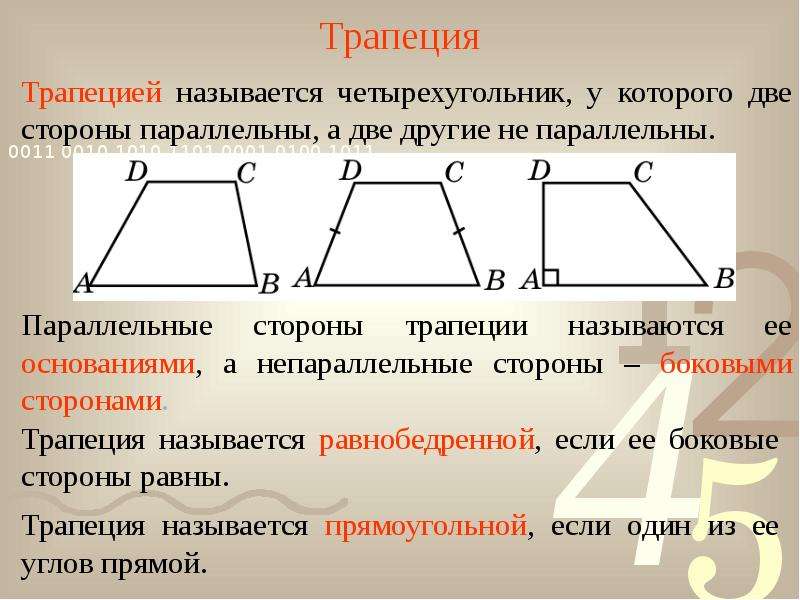
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие – нет.
На рисунке изображена произвольная трапеция. АВ, СD – это боковые стороны (они не параллельны). AD, BC – основания (параллельные стороны).
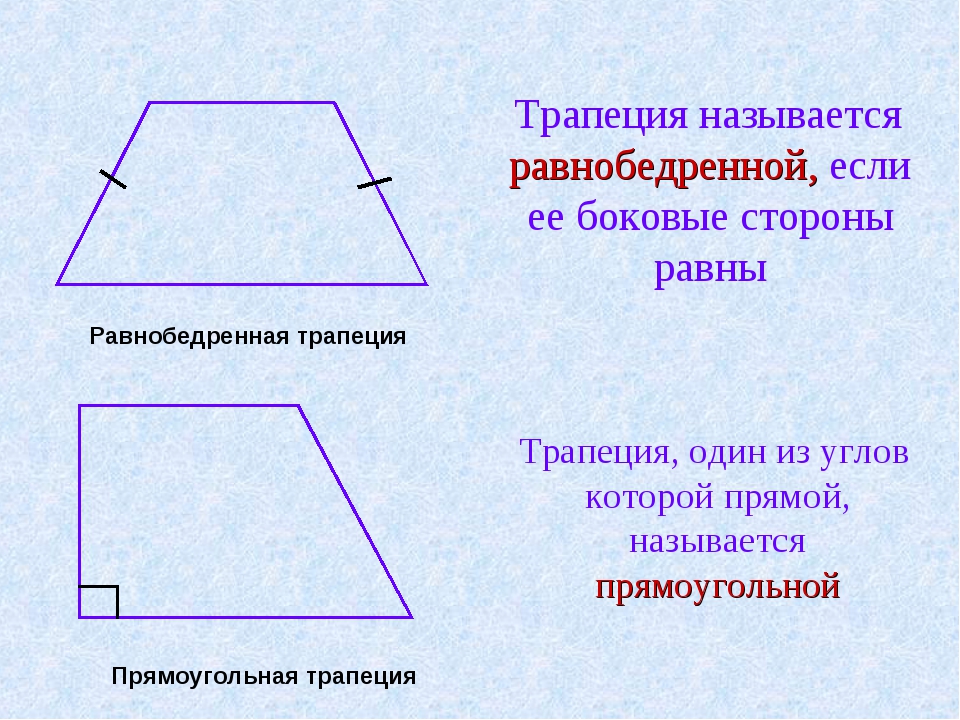
Выделим некоторые виды трапеции (частные случаи).
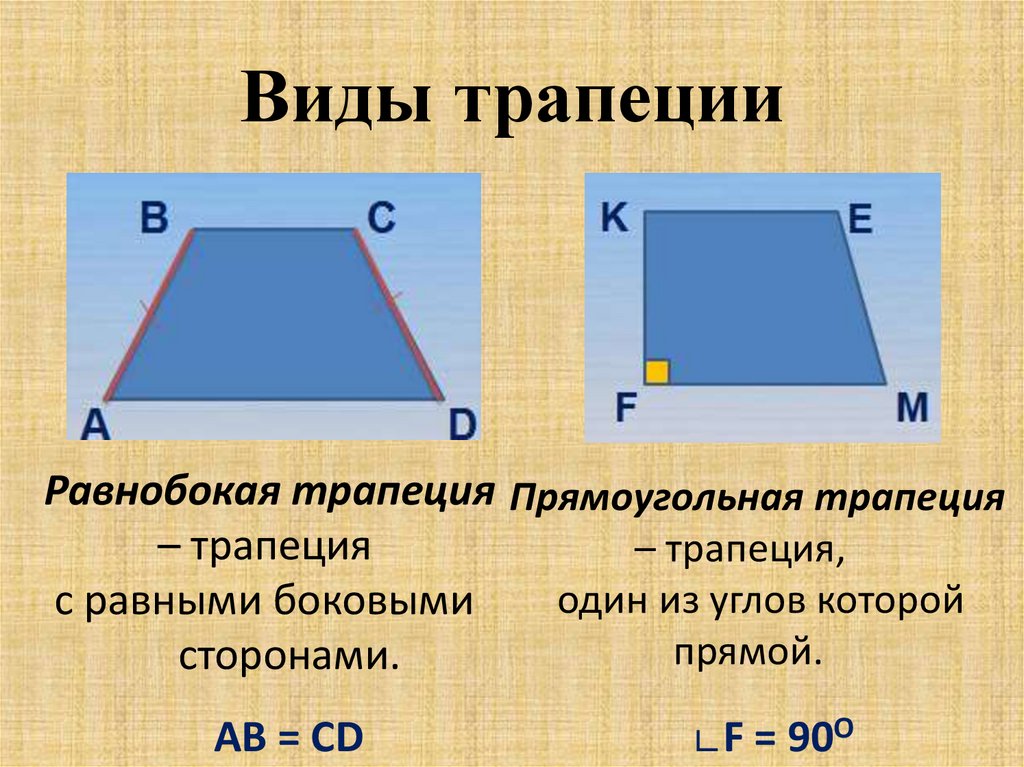
Равнобедренная (равнобокая) трапеция: боковые стороны равны.
Прямоугольная трапеция: один из углов равен 900 (из определения трапеции и свойства параллельных прямых следует, что два угла будут по 900).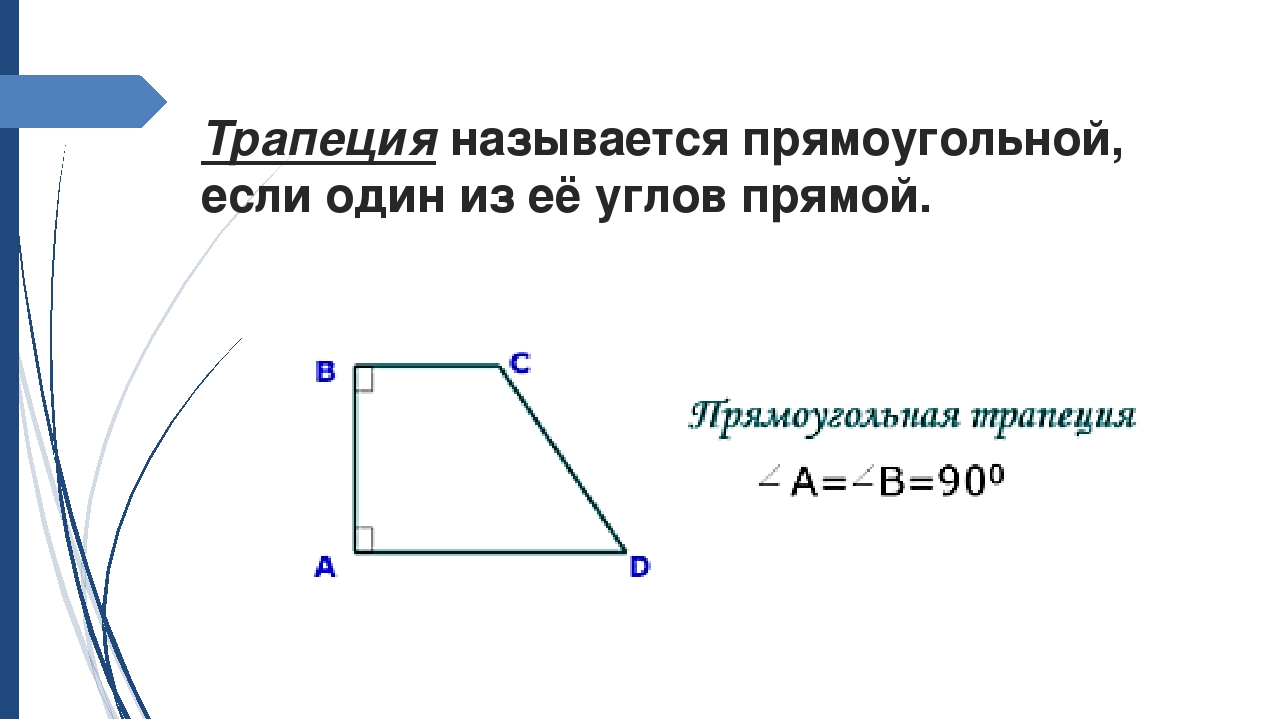
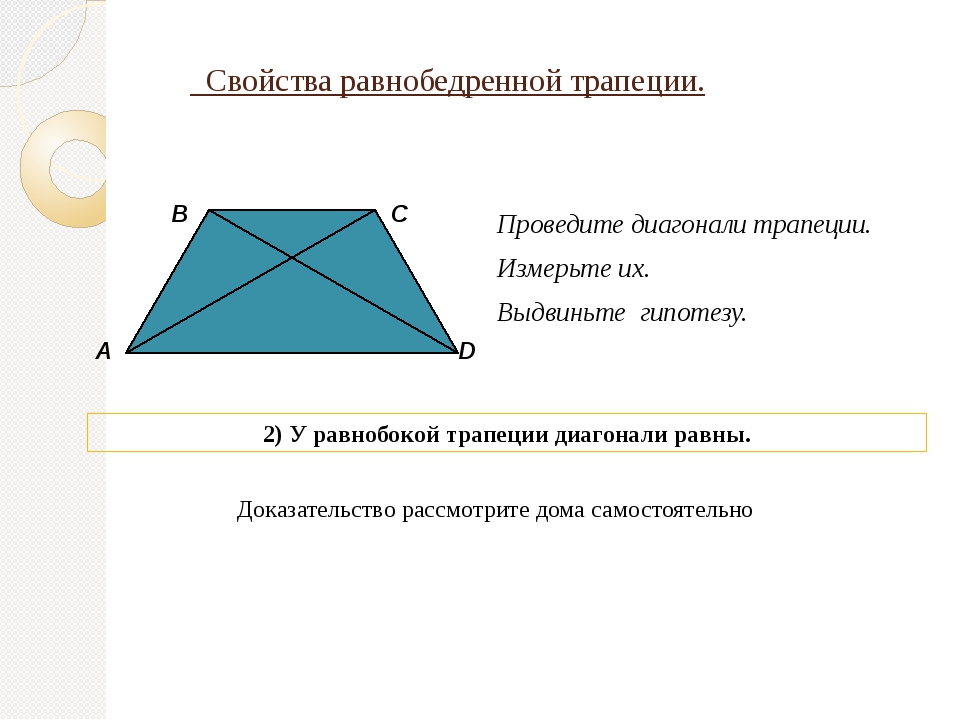
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон.
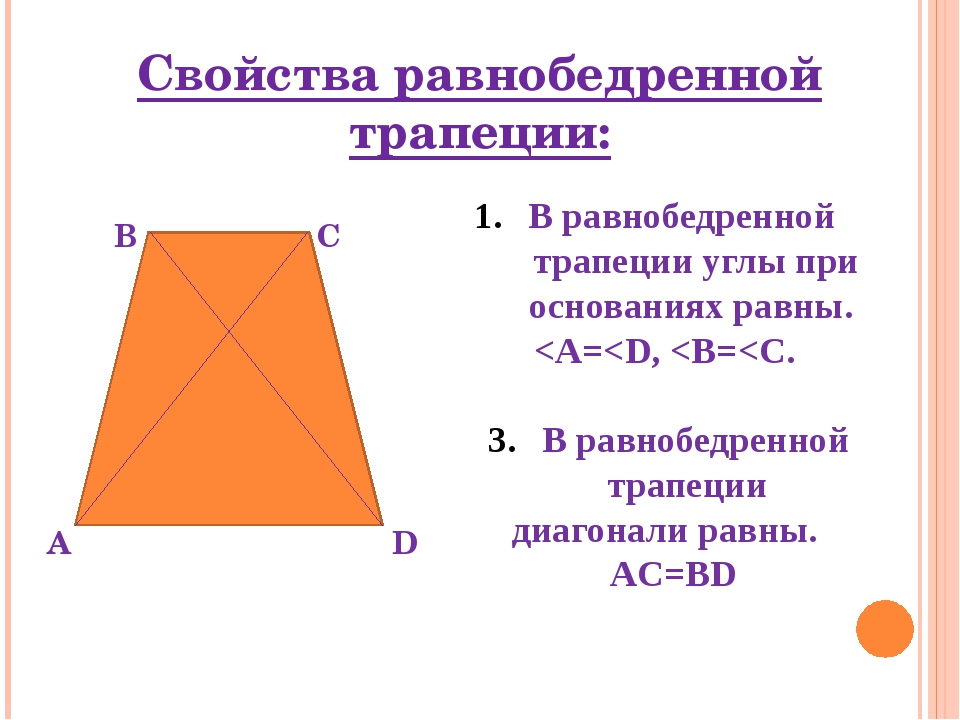
Рассмотрим свойства равнобедренной трапеции.
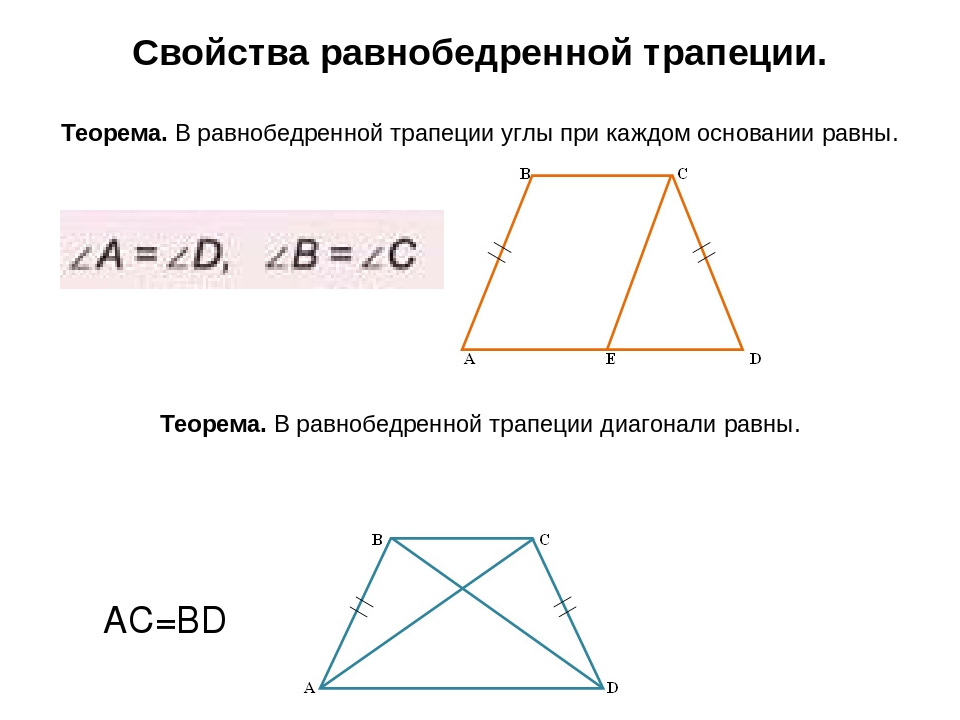
Теорема. В равнобедренной трапеции углы при каждом основании равны.
∠A = ∠D, ∠B = ∠C.
Теорема. В равнобедренной трапеции диагонали равны.
АС = ВD.
Признаки равнобедренной трапеции:
- Если углы при основании трапеции равны, то она равнобедренная.
- Если диагонали трапеции равны, то она равнобедренная.
Разберем задачу.
Дано: АВСD – трапеция; ∠А = 36°, ∠С = 117°.
Найти: ∠В и ∠D.
Решение:
Сумма углов при боковой стороне трапеции равна 1800 – свойство односторонних углов при параллельных прямых. Из этого факта можно получить два равенства:
∠А + ∠В = 180°; ∠С + ∠D = 180°.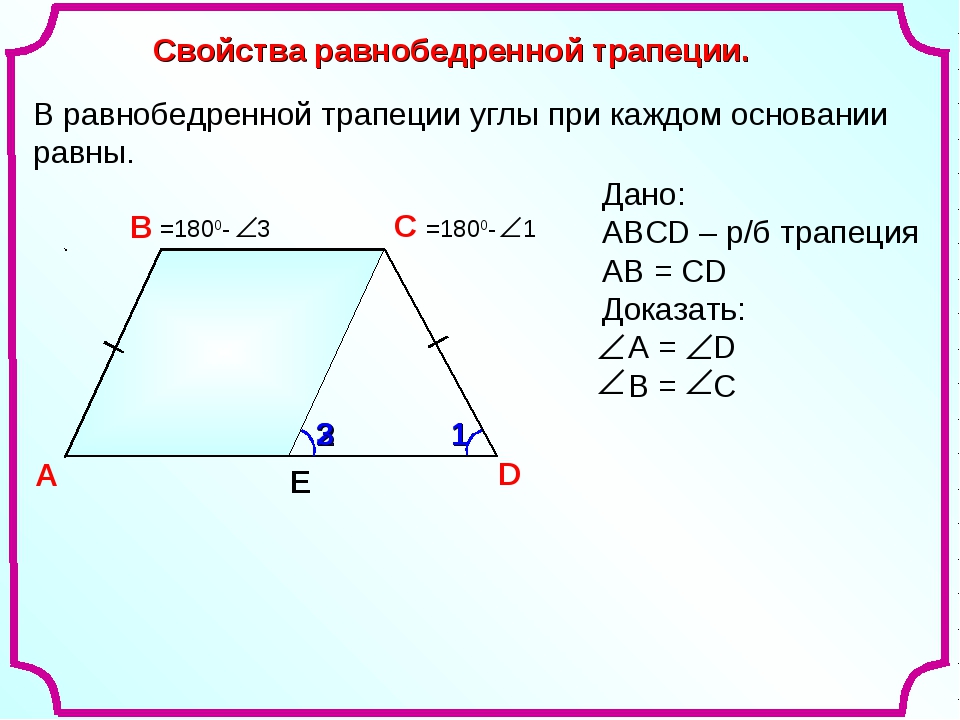 Тогда:
Тогда:
∠В = 180-36 = 144°;
∠D = 180-117 = 63°.
Тема трапеция урок геометрии в 8 классе цели урока
ТЕМА: Трапеция.
Урок геометрии в 8 классе
Цели урока:
Ввести понятие трапеции и ее элементов.
Познакомить учащихся с равнобедренной и прямоугольной трапециями.
Рассмотреть некоторые свойства равнобедренной трапеции.
Научить учащихся применять полученные знания в процессе решения задач.
Развивать внимание, самоконтроль, умение применять теорию при решении задач.
Воспитывать взаимопомощь, самостоятельность.
ЦОР («Открытая математика. Планиметрия», версия 2.6, программа Физикон)
раздаточный материал: карточки с решенными заданиями самостоятельной работы.

Литература:
Учебник «Геометрия, 8, авторы: Л.С.Атанасян, В.Ф.Бутузов, издательство «Просвещение», 2001г.».
Ход урока.
I.Организационный момент.
Сообщить тему урока, сформулировать цели урока.
Показ слайда 1.
II. Актуализация знаний учащихся.
Проверка домашнего задания.
Работа над ошибками самостоятельной работы с использованием готовых ответов и указанием к задачам (объединить учащихся одного варианта по группам для того, чтобы они могли проконсультироваться друг у друга или вместе разобраться в решении задачи).
Решение задач на готовых чертежах с целью подготовки к изучению нового материала.
Показ слайдов 2,3,4,5,6
III.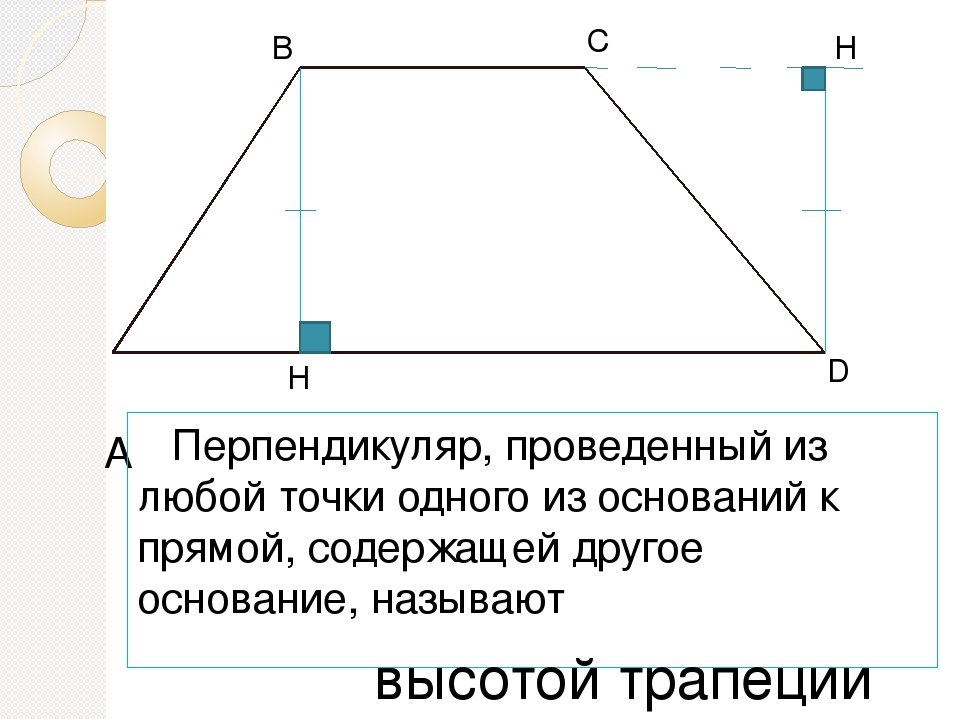 Изучение нового материала
Изучение нового материала
ЦОР – использовать электронный учебник.
Найти: «глава 7» — Модель 7.3 . Трапеция (значок кинопроектор)
Показ фрагмента учебника сопровождать объяснением по плану:
понятие трапеции,
построение трапеции
основания трапеции,
боковые стороны трапеции,
понятие средней линии трапеции.
Сделать соответствующий рисунок в тетради.
Ввести понятия равнобедренной трапеции, прямоугольной трапеции. Показ слайдов 7,8
Задание на построение.
Показ слайда 9.
Чтобы
учащийся мог проверить правильно ли
выполнил построение, продемонстрировать
верный чертеж. — Показ
слайда 10
— Показ
слайда 10
Задача. Показ слайда 11.
Предложить ребятам сделать вывод (об углах при основании равнобедренной трапеции)
Показ слайда 12.
Задача. Показ слайда 13.
Предложить сделать вывод о диагоналях равнобедренной трапеции.
Показ слайда 14.
IV. Закрепление
Решить задачу из учебника №390.
(«Один из углов равнобедренной трапеции равен 68 градусам. Найти остальные углы.»)
Показ слайда 15.
На данном этапе этот слайд сопровождается вопросами к классу:
Какой из углов может иметь градусную меру 68 градусов?
Как найти остальные углы? Какие теоретические утверждения при этом используются?
Решение задачи запишите самостоятельно.

(Ответ: 68, 112 градусов)
Решить задачу из учебника № 392 по вариантам:
вариант1 – а, вариант 2 – б.
(Вариант 1: Основания прямоугольной трапеции равны 4 см и 7 см, один из углов равен 60 градусам. Найдите большую боковую сторону трапеции.
Вариант 2: Основания прямоугольной трапеции равны 10 см и 15 см, один из углов равен 45 градусам. Найдите меньшую боковую сторону трапеции).
3. По желанию ребята рассказывают решение задачи у доски.
V. Итог урока.
Повторить, какой четырехугольник называется трапецией, как называются стороны трапеции, какая трапеция называется равнобедренной, свойства равнобедренной трапеции.
Домашнее задание:
доказать признаки равнобедренной трапеции – выполнить задачу № 389,
рассмотреть и доказать свойство равнобедренной трапеции – выполнить задачу № 386,
решить задачу № 387.

8 класс геометрия Трапеция ØВвести понятие трапеции и
8 класс геометрия Трапеция ØВвести понятие трапеции и ее элементов. ØПознакомить с равнобедренной и прямоугольной трапецией. ØРассмотреть свойства равнобедренной трапеции. 04. 12. 2012 www. konspekturoka. ru 1
А Основание я ва ко ко Бо Бо Основание С Бок овая В D Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. АВСD – трапеция, если ВС∥AD, АВ и СD – боковые стороны, ВС и AD – основания. 04. 12. 2012 www. konspekturoka. ru 2
В С А D Трапеция называется равнобедренной, если ее боковые стороны равны. АВСD – равнобедренная трапеция, если ВС∥ AD, АВ = СD – боковые стороны. 04. 12. 2012 www. konspekturoka. ru 3
В С D А Трапеция называется прямоугольной, если один из углов прямой. АВСD – прямоугольная трапеция, если ВС∥ AD, ∠А = 90° или ∠В= 90°.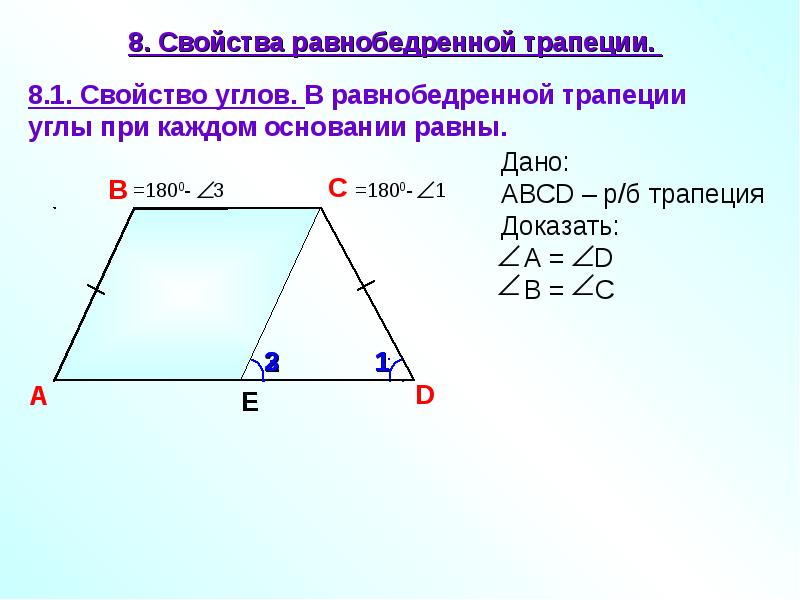 04. 12. 2012 www. konspekturoka. ru 4
04. 12. 2012 www. konspekturoka. ru 4
В С N М D А М – середина АВ N – середина CD MN – средняя линия трапеции 04. 12. 2012 www. konspekturoka. ru 5
Свойства равнобедренной трапеции В С А D 1. В равнобедренной трапеции диагонали равны. 2. В равнобедренной трапеции углы при каждом основании равны. ВD = AC – диагонали трапеции ∠А = ∠D, ∠В = ∠С – углы при основаниях 04. 12. 2012 www. konspekturoka. ru 6
Признаки равнобедренной трапеции В С А D 1. Если диагонали трапеции равны, то она равнобедренная. 2. Если углы при основании трапеции равны, то она равнобедренная. ВD = AC – диагонали трапеции ∠А = ∠D, ∠В = ∠С – углы при основаниях 04. 12. 2012 www. konspekturoka. ru 7
Теорема Фалеса Если на одной из двух прямых отложить последовательно равных несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. б) l₁ ∥ l₂ а) l₁ ∥ l₂ А₁ А₂ А₃ В₃ А₄ В₄ А₅ l₂ В₅ А₁А₂ В₂ В₁ — параллелограмм А₁А₂ = В₁В₂ 04. 12. 2012 А₂ В₂ А₃ l₁ А₁ В₁ В₁ С D А₄ В₂ В₃ В₄ А₅ В₅ l₁ l₁ ∥ l l l₂ А₂ А₃DC — параллелограмм А₂A₃ = CD www. konspekturoka. ru А₂A₃ = В₂B₃ 8
б) l₁ ∥ l₂ а) l₁ ∥ l₂ А₁ А₂ А₃ В₃ А₄ В₄ А₅ l₂ В₅ А₁А₂ В₂ В₁ — параллелограмм А₁А₂ = В₁В₂ 04. 12. 2012 А₂ В₂ А₃ l₁ А₁ В₁ В₁ С D А₄ В₂ В₃ В₄ А₅ В₅ l₁ l₁ ∥ l l l₂ А₂ А₃DC — параллелограмм А₂A₃ = CD www. konspekturoka. ru А₂A₃ = В₂B₃ 8
1 Задача Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции. В E . А С Доказательство Пусть Е – середина АВ. Проведем ЕF ∥ BC ∥ AD. . F Точка F – середина CD (по теореме Фалеса). D Докажем, что ЕF — единственный Через точки Е и F можно провести только одну прямую (аксиома) т. е. отрезок, соединяющий середины боковых сторон трапеции ABCD параллелен основаниям, ч. т. д. 04. 12. 2012 www. konspekturoka. ru 9
А 2 Задача Дано: Найти: В АВСD – трапеция, ∠A = 36°, ∠C = 117° ∠В = ? , ∠D = ? С 117° Решение АВСD – трапеция, то ВС∥ AD. ∠А + ∠В = 180° 36° + ∠В = 180° D 36° ∠В = 180° — 36° ∠В = 144° ∠С + ∠D = 180° ∠ 117° + ∠D = 180° — ∠ 117° ∠D = 63° Ответ: ∠В = 144°, ∠D = 63° 04.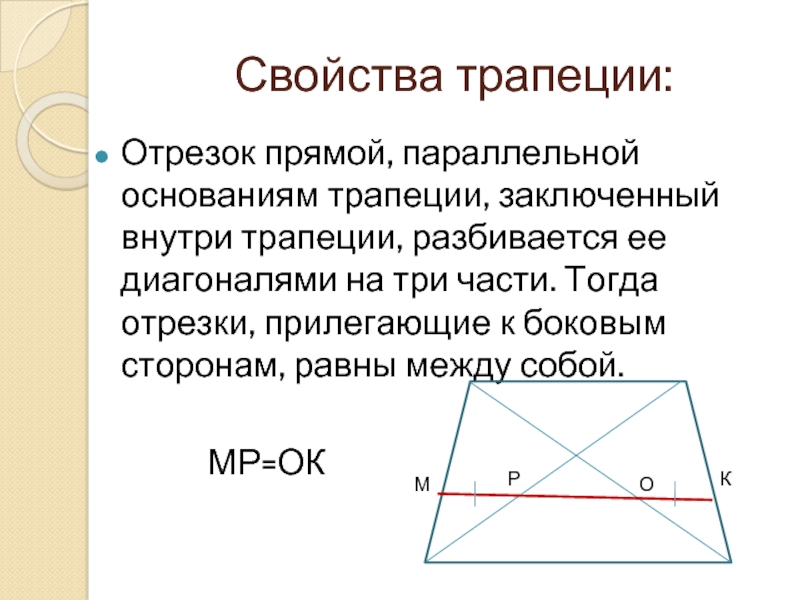 12. 2012 www. konspekturoka. ru 10
12. 2012 www. konspekturoka. ru 10
А 3 Задача Дано: АВСD – равнобокая трапеция, ∠A = 68°, Найти: В ∠В = ? , ∠С -? , ∠D = ? Решение С Если АВСD – равнобокая трапеция, то ∠A = ∠D = 68°, ∠ 68°+ ∠В = 180° 68° D ∠В = 180° — ∠ 68° ∠В = 112° ∠В = ∠С = 112°, Ответ: 04. 12. 2012 ∠D = 68°, ∠В = 112°, ∠С = 112°. www. konspekturoka. ru 11
4 Задача АВСD – прямоугольная трапеция, ∠D = 90°, BC = 4 см, AD = 7 см, ∠A = 60° Дано: Найти: АВ — ? В 4 см Решение С Проведем ВВ₁ ⊥ AD AВ₁ = AD — B₁D AВ₁ = 7 — 4 = 3 (см) 60° ∟ А В₁ 7 см D Рассмотрим ∆ АBВ₁: ∠A = 60° — по условию, ∠В₁ = 90° так как ВВ₁ ⊥ AD, то ∠В = 30° AВ₁ = ½АВ – по свойству прямоугольного треугольника, АВ = 3· 2 = 6 (см). Ответ: 6 (см). 04. 12. 2012 www. konspekturoka. ru 12
Ответить на вопросы: ØКакой четырехугольник называется трапецией? ØКак называются стороны трапеции? ØКакая трапеция называется прямоугольной? Равнобедренной ØСформулируйте свойства равнобедренной трапеции.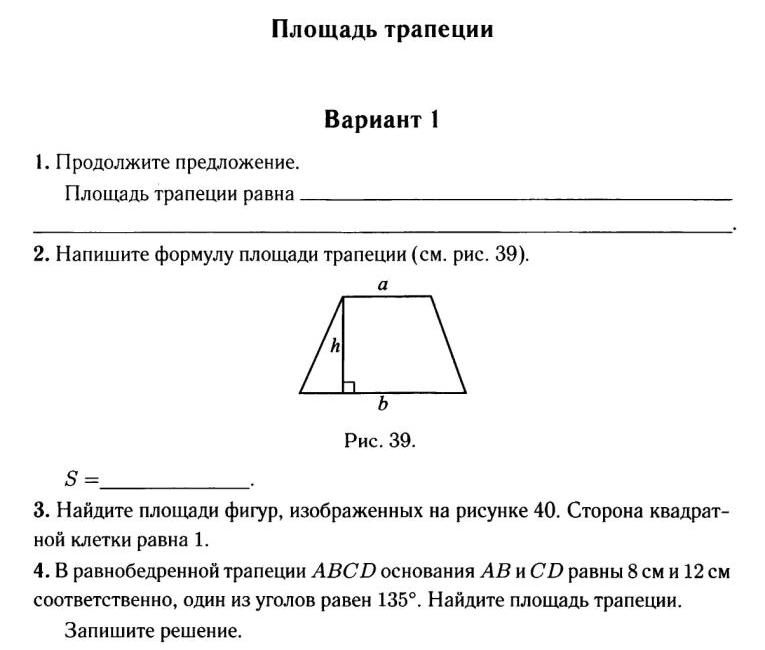 ØСформулируйте признаки равнобедренной трапеции. ØЧто такое средняя линия трапеции? Свойство средней линии трапеции. Спасибо за внимание! 04. 12. 2012 www. konspekturoka. ru 13
ØСформулируйте признаки равнобедренной трапеции. ØЧто такое средняя линия трапеции? Свойство средней линии трапеции. Спасибо за внимание! 04. 12. 2012 www. konspekturoka. ru 13
Презентация «Трапеция» — геометрия, презентации
библиотека
материалов
Содержание слайдов
Номер слайда 1
Номер слайда 2
Какая фигура лишняя? Почему?
Номер слайда 3
Тема урока: ТРАПЕЦИЯ
Номер слайда 4
Номер слайда 5
Четырёхугольник АВСD называется трапецией.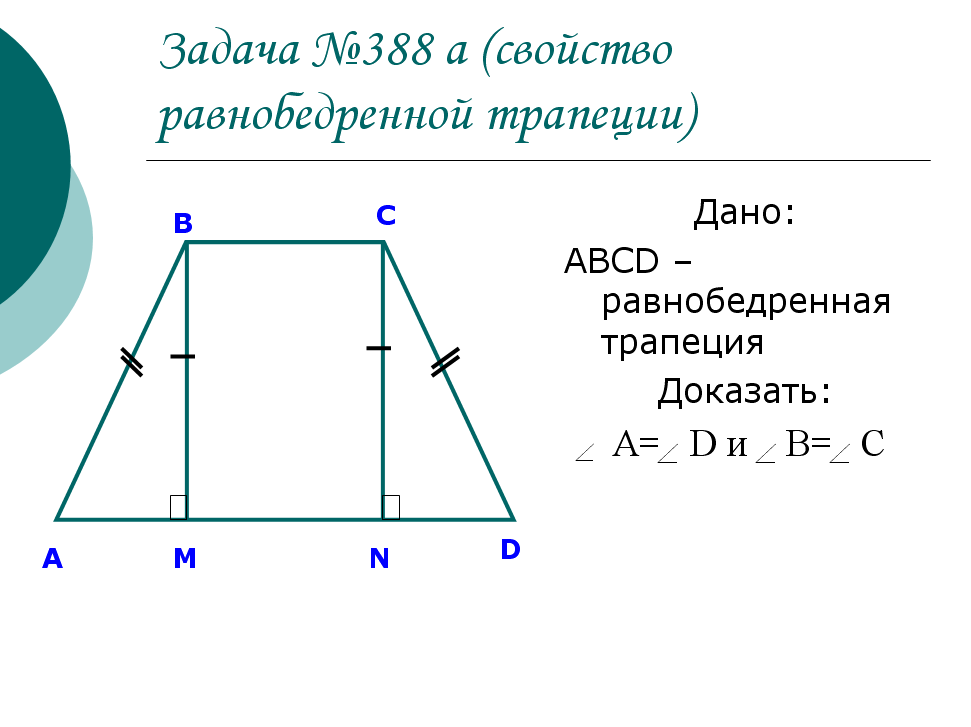 Трапеция – это четырёхугольник, у которого только две противолежащие стороны параллельны.
Трапеция – это четырёхугольник, у которого только две противолежащие стороны параллельны.
Номер слайда 6
Элементы трапеции А В D С Основание Основание Боковая сторона Боковая сторона
Номер слайда 7
Задание Среди фигур укажите трапеции, назовите основания и боковые стороны А В С D N T M K S P T O K S M L А T B N V R T С
Номер слайда 8
Высота трапеции.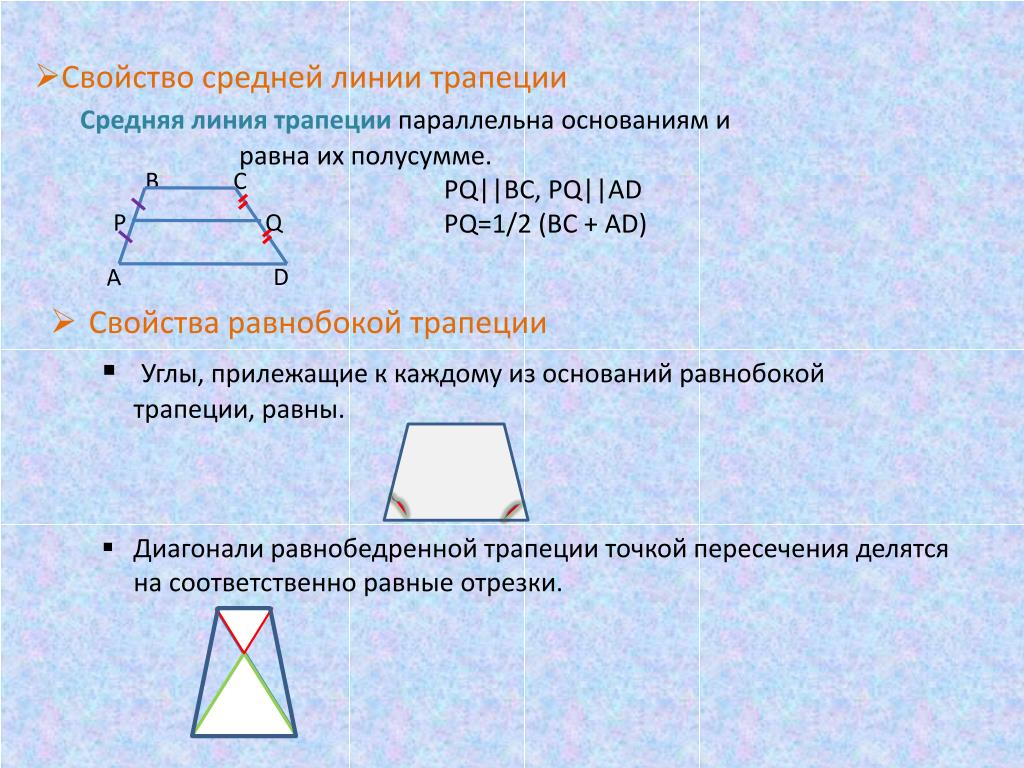 Высота трапеции- перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований на прямую, содержащую другое основание
Высота трапеции- перпендикуляр, опущенный из любой точки прямой, содержащей одно из оснований на прямую, содержащую другое основание
Номер слайда 9
Сложите из данных фигур трапеции.
Номер слайда 10
. 1. 2. 3. 4. Что общего у фигур 1 и 2? Как называется треугольник с прямым углом? Как можно назвать такую трапецию? Что общего у фигур 3 и 4? Как называется треугольник, у которого две стороны равны? Как можно назвать такую трапецию?
1. 2. 3. 4. Что общего у фигур 1 и 2? Как называется треугольник с прямым углом? Как можно назвать такую трапецию? Что общего у фигур 3 и 4? Как называется треугольник, у которого две стороны равны? Как можно назвать такую трапецию?
Номер слайда 11
Игра «Ассоциации»
Номер слайда 12
Исследование
Номер слайда 13
Задание: найди ошибки A В С D 12 10 A A В В С С D D 1) 2) 3) ) ) 500 550 ) ) 600 600 10 8
Номер слайда 14
Решите задачи : 1.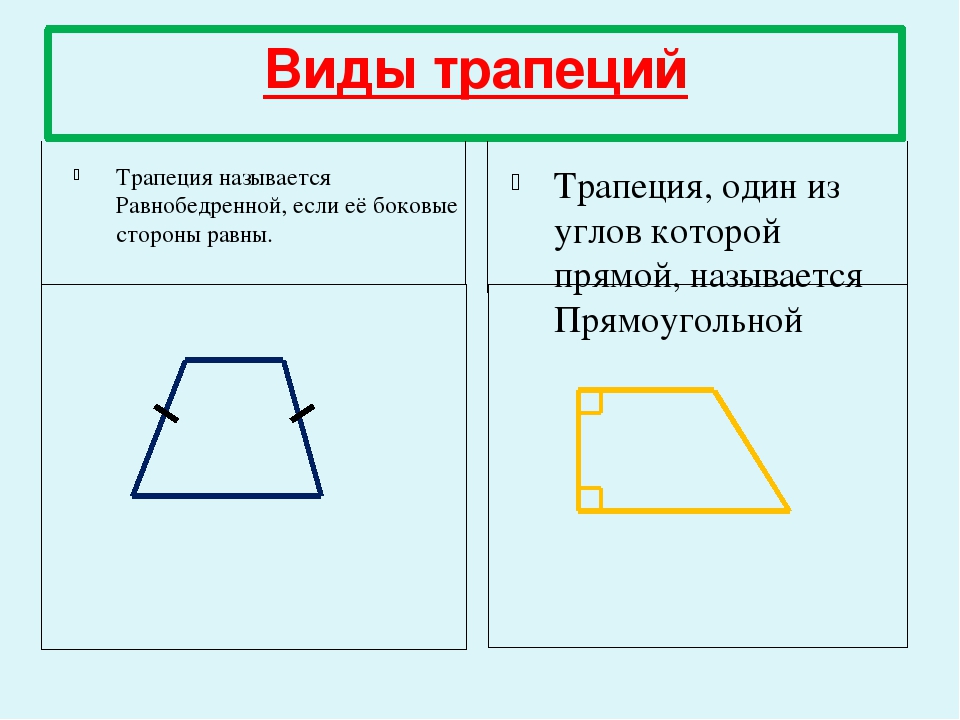 НАЙТИ УГЛЫ ТРАПЕЦИИ
НАЙТИ УГЛЫ ТРАПЕЦИИ
Номер слайда 15
Решите задачу : 2. НАЙТИ УГЛЫ РАВНОБЕДРЕННОЙ ТРАПЕЦИИ
Номер слайда 16
Решение: ˂P=˂D= 350 (углы при основании равнобокой трапеции) ˂E= 1800 -350 = 1450 (соседние углы четырехугольника) ˂M=˂E= 1450 (углы при основании равнобокой трапеции)
Номер слайда 17
Какой четырёхугольник называется трапецией? Какая трапеция называется равнобедренной? Какая трапеция называется прямоугольной? Сформулируйте свойства равнобедренной трапеции.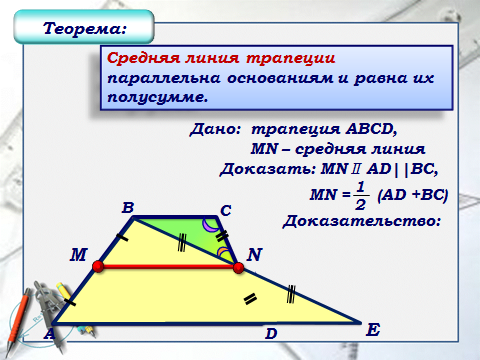 Самое главное сегодня!
Самое главное сегодня!
Номер слайда 18
Домашнее задание
Номер слайда 19
«Сел в калошу» «Работал спустя рукава» «Без сучка, без задоринки»
Номер слайда 20
Желаю успехов!
Форма, свойства, формула, определение, примеры
Трапеция очаровательна, потому что она определяется на основе географии, к которой вы принадлежите.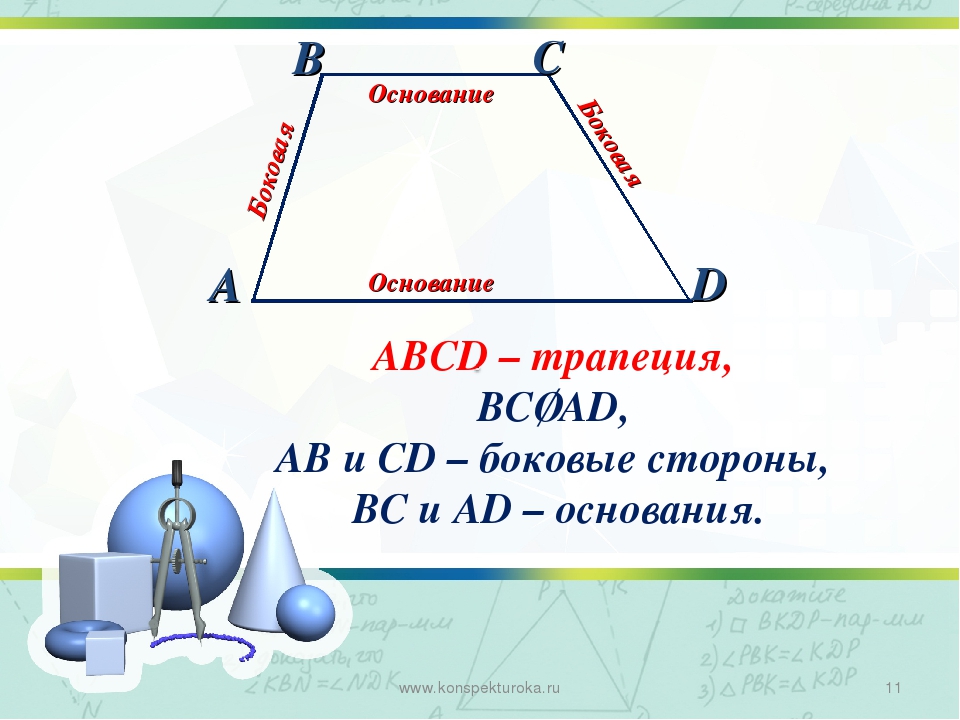 Если вы посещаете Великобританию по обмену и просите студента нарисовать для вас трапецию, то он нарисует ее как трапецию. Трапецию также называют трапецией в некоторых частях мира, и это тип четырехугольника с одной парой противоположных сторон, параллельных друг другу.
Если вы посещаете Великобританию по обмену и просите студента нарисовать для вас трапецию, то он нарисует ее как трапецию. Трапецию также называют трапецией в некоторых частях мира, и это тип четырехугольника с одной парой противоположных сторон, параллельных друг другу.
Что такое трапеция?
Трапеция, также известная как трапеция, представляет собой четырехугольник или четырехугольник.Он имеет один набор противоположных сторон, которые параллельны, и набор непараллельных сторон. Параллельные стороны известны как основания, а непараллельные стороны известны как катеты трапеции.
Определение трапеции
Трапеция — это четырехсторонняя замкнутая двумерная фигура, имеющая площадь и периметр. Две стороны фигуры параллельны друг другу и называются основаниями трапеции. Непараллельные стороны известны как стороны или боковые стороны трапеции.Кратчайшее расстояние между двумя параллельными сторонами называется высотой. Поскольку противоположные стороны параллельны друг другу, вычислить площадь трапеции несложно.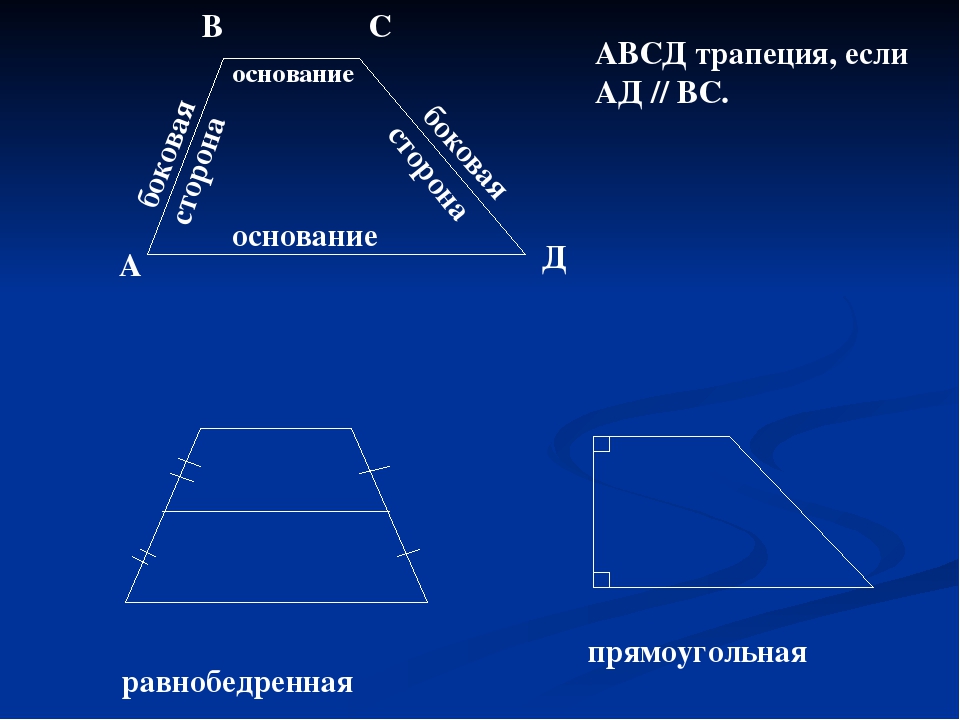
Свойства трапеции
Эти свойства трапеции отличают ее от других четырехугольников:
- Основания (верхнее и нижнее) параллельны друг другу
- Противоположные стороны равнобедренной трапеции имеют одинаковую длину
- Углы рядом друг с другом в сумме дают 180°
- Медиана параллельна обоим основаниям
- Длина медианы равна среднему значению обоих оснований i.е. (а +б)/2
- Если обе пары противоположных сторон трапеции параллельны, она считается параллелограммом
- Если обе пары противоположных сторон параллельны, все стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то трапецию можно рассматривать как квадрат
- Если обе пары противоположных сторон параллельны, ее противоположные стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то трапецию можно рассматривать как прямоугольник
Типы трапеций
Существует три типа трапеций, они приведены ниже:
- Равнобедренная трапеция
- Лестничная трапеция
- Правая трапеция
Равнобедренная трапеция
Если катеты или непараллельные стороны трапеции равны по длине, то она называется равнобедренной трапецией.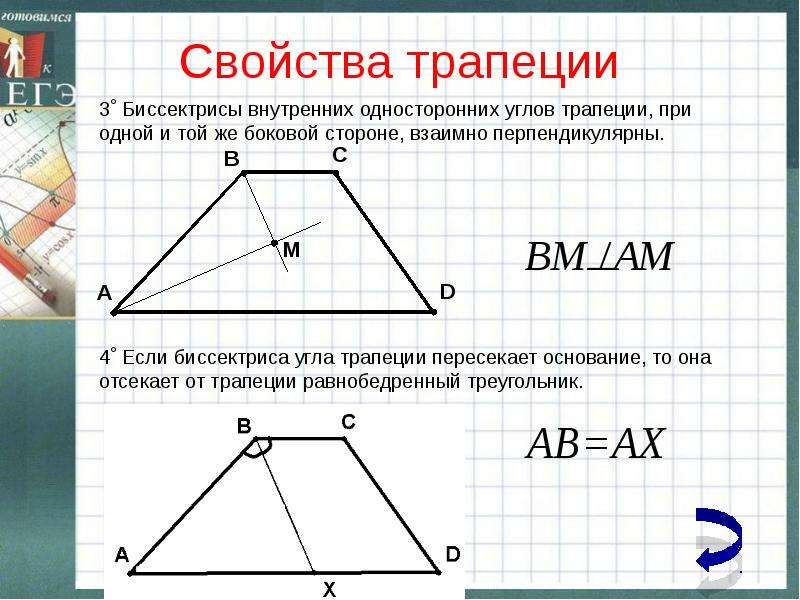 Углы параллельных сторон (основания) в равнобедренной трапеции равны между собой. У равнобедренной трапеции есть линия симметрии и обе диагонали равны по длине.
Углы параллельных сторон (основания) в равнобедренной трапеции равны между собой. У равнобедренной трапеции есть линия симметрии и обе диагонали равны по длине.
В приведенной ниже равнобедренной трапеции XYZW, XY и WZ называются основаниями трапеции. WX и YZ называются катетами трапеции, так как они не параллельны друг другу.
Лестничная трапеция
Если ни стороны, ни углы трапеции не равны, то это разносторонняя трапеция.В приведенной ниже разносторонней трапеции все четыре стороны, то есть AB, BC, CD и DA, имеют разную длину. Основания, то есть DC и AB, параллельны друг другу, но имеют разную длину.
Правая трапеция
Прямоугольная трапеция, также называемая прямоугольной трапецией, имеет пару прямых углов. Эти виды трапеций используются для оценки площадей под кривой. В приведенной ниже прямой трапеции или прямоугольной трапеции есть два прямых угла, один в точке D, а другой в точке A.Одна пара противоположных сторон, то есть DC и AB, параллельны друг другу.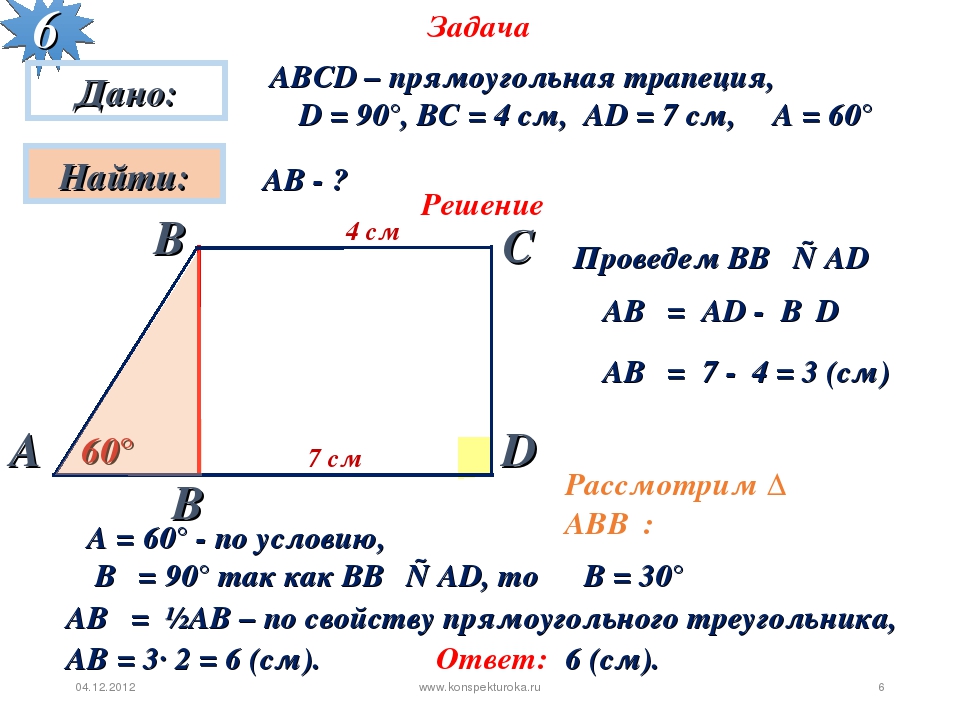
Формула трапеции
Есть две основные формулы трапеции, это:
- Площадь трапеции
- Периметр трапеции
Площадь трапеции
Площадь трапеции вычисляется путем измерения среднего значения параллельных сторон и умножения его на высоту. Чтобы найти площадь трапеции, нужно знать длины двух ее параллельных сторон и расстояние (высоту) между ними.Это количество единичных квадратов, которые могут быть помещены внутри фигуры, и измеряется в квадратных единицах, таких как см 2 , м 2 , 2 дюймов и т. д. Формула площади (A) трапеция рассчитывается на основании, т.е. a и b, и высота которой равна h, которая является перпендикулярным расстоянием между a и b.
Отсюда площадь трапеции вычисляется по следующей формуле:
Площадь = [(AB + CD)/2] × ч
А = [(а + b)/2] × ч
Где,
- AB и CD = параллельные стороны
- а = короткая база
- b = удлиненная база
- h = высота или высота над уровнем моря
Периметр трапеции
Периметр трапеции определяется как общая длина границы формы, т.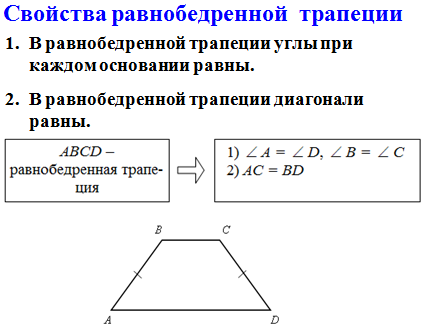 е.е. сумма всех его сторон. Так как трапеция является двумерной фигурой, то и периметр будет лежать только в двумерной плоскости. Рассмотрим трапецию ABCD, как показано ниже, с размерами сторон a, b, c и d. Давайте рассмотрим формулу трапеции. Формула периметра трапеции рассчитывается путем нахождения суммы всех сторон, т. Е. AB + BC + CD + DA
е.е. сумма всех его сторон. Так как трапеция является двумерной фигурой, то и периметр будет лежать только в двумерной плоскости. Рассмотрим трапецию ABCD, как показано ниже, с размерами сторон a, b, c и d. Давайте рассмотрим формулу трапеции. Формула периметра трапеции рассчитывается путем нахождения суммы всех сторон, т. Е. AB + BC + CD + DA
Периметр трапеции = сумма всех сторон = a + b + c + d
где a, b, c и d — стороны трапеции.
☛Похожие темы о трапеции
Ниже перечислены несколько тем, связанных с трапецией.
Часто задаваемые вопросы о трапеции
Что такое трапеция?
Трапеция — это четырехсторонняя замкнутая 2D-форма, имеющая площадь и периметр. Его также называют трапецией. Стороны трапеции параллельны друг другу и называются основаниями трапеции. Непараллельные стороны известны как стороны или боковые стороны трапеции.Кратчайшее расстояние между двумя параллельными сторонами называется высотой.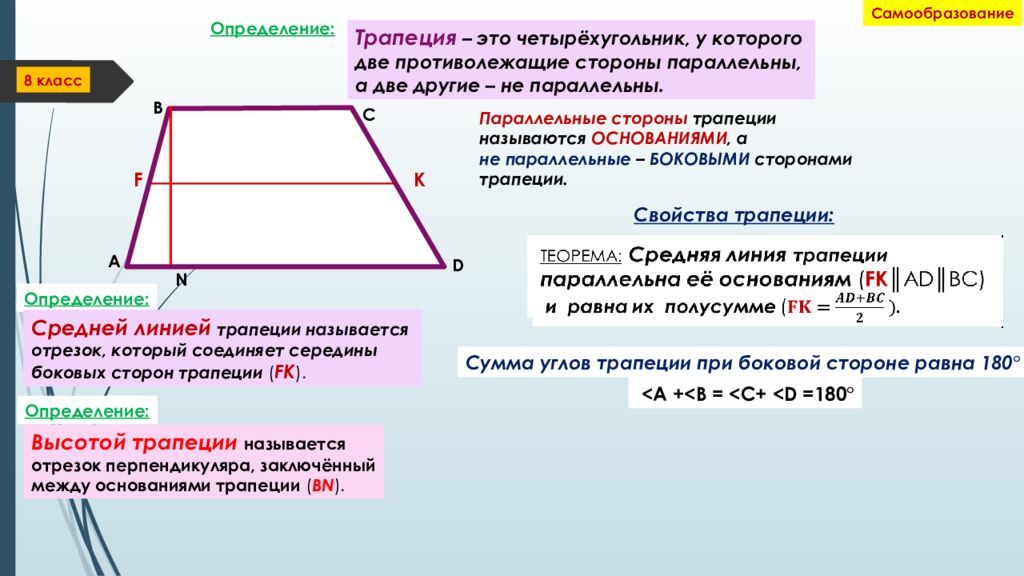
Какие бывают трапеции?
Трапеции классифицируются на основе характера их сторон. Ниже перечислены основные типы трапеций:
- Равнобедренная трапеция
- Лестничная трапеция
- Правая трапеция
Каковы основные свойства трапеции?
Есть много свойств трапеции некоторые из них перечислены ниже:
- Верхнее и нижнее основания трапеции параллельны.
- Равнобедренная трапеция состоит из равных по длине противоположных сторон.
- Углы рядом друг с другом в сумме дают 180°.
Как найти площадь трапеции?
Площадь трапеции вычисляется путем вычисления среднего значения двух параллельных сторон и умножения его на высоту.
Площадь = [(a + b)/2] × h, где a и b — длины оснований, а h — высота.
Какое уравнение трапеции?
Есть два уравнения трапеции.Одно уравнение вычисляет его площадь; другой — его периметр. Периметр трапеции PQRS определяется как Периметр = PQ + QR + RS + PS.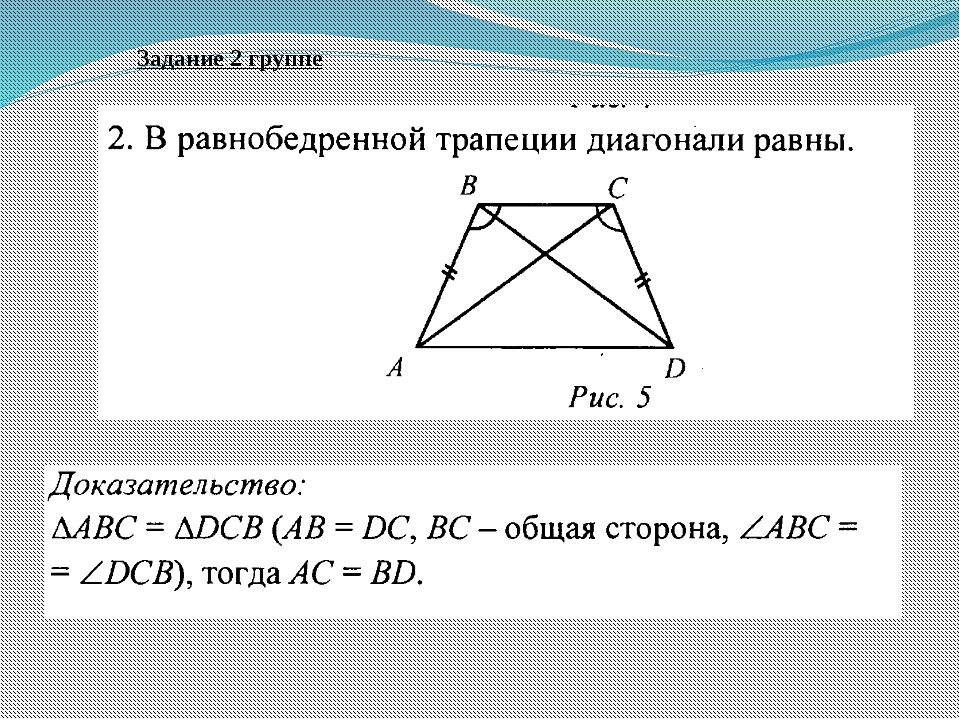 Площадь трапеции = [(a + b)/2] x h, где a и b — длины оснований, а h — высота.
Площадь трапеции = [(a + b)/2] x h, где a и b — длины оснований, а h — высота.
Является ли трапеция четырехугольником?
Поскольку у трапеции четыре стороны, она автоматически становится четырехугольником. У него есть две стороны, которые параллельны, и две стороны, которые не параллельны.
Каковы три атрибута трапеции?
Тремя основными атрибутами трапеции являются следующие
- Углы при основании и диагонали равны, если трапеция равнобедренная
- Точка пересечения диагоналей лежит на одной прямой с серединами двух противоположных сторон
- Противоположные стороны равнобедренной трапеции конгруэнтны
Как найти недостающую сторону трапеции?
Недостающую сторону трапеции можно определить по предоставленной вам информации.Если у вас есть площадь и длина основания, вы можете найти длину высоты. Вы также можете определить длину недостающей стороны, если знаете периметр и длину трех других сторон трапеции.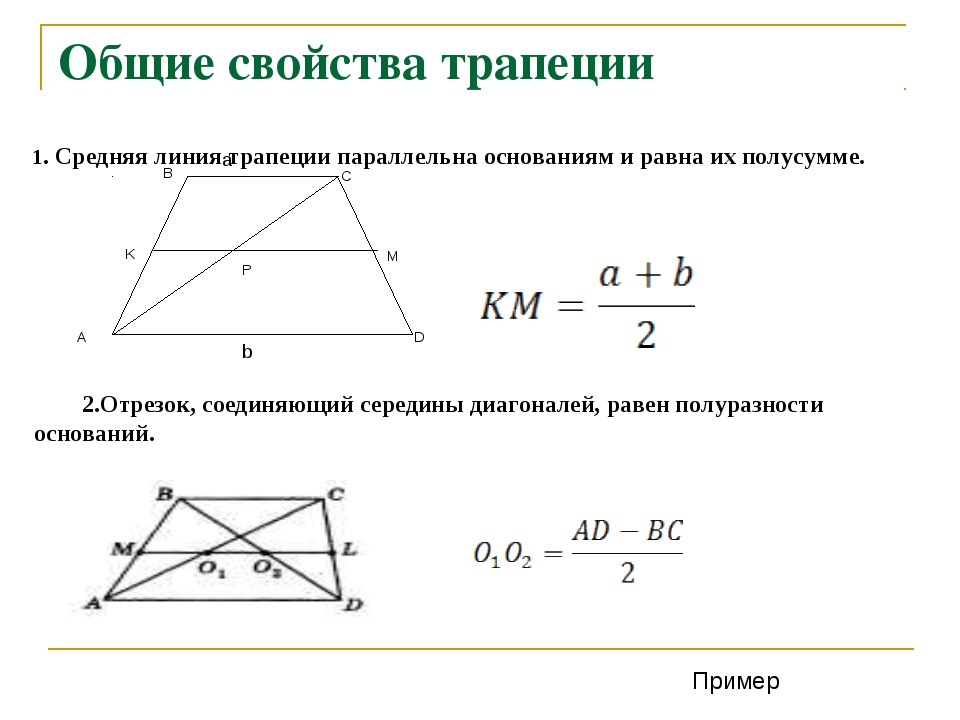
Равны ли диагонали трапеции?
Трапеции бывают трех видов — равнобедренные, разносторонние и прямые. В случае равнобедренной трапеции диагонали равны, так как непараллельные или катеты трапеции равны по длине.В случае разносторонней и прямой трапеции диагонали не равны.
Как рассчитать высоту трапеции, используя формулу трапеции?
Формула площади трапеции, A = [(a + b)/2] × h
Чтобы рассчитать высоту трапеции, мы можем вычислить площадь трапеции по формуле
.
h = 2А/(а+b). Где «a» — более короткое основание, «b» — более длинное основание, «h» — расстояние между двумя основаниями, а A — площадь трапеции.
Каковы две основные формулы трапеций?
Две основные формулы трапеций:
Периметр трапеции равен сумме всех сторон.Выражается как P = a + b + c + d. Где a, b, c и d — стороны трапеции.
Формула площади трапеции, A = [(a + b)/2] × h.
трапеция и ее теоремы
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться!!!
В этом разделе мы обсудим некоторые трапеции и их теоремы.Трапеция – это четырехугольник, у которого хотя бы одна пара параллельна.АБ || КОМПАКТ ДИСК. (если есть две пары параллельных прямых, то это параллелограмм)
Когда непараллельные стороны у трапеции равны, то она называется равнобедренной трапецией.
Теорема 1. Трапеция равнобедренная тогда и только тогда, когда углы при основании равны.
Дано: ABCD — равнобедренная трапеция. AD = ВС и АВ || КОМПАКТ ДИСК.
Докажите: ∠C = ∠d
Пример: В трапеции PQRS, PQ||RS и PS = QR.Если ∠S = 60 0 , то найдите остальные углы. Решение: PQ||RS и PS = QR, поэтому трапеция PQRS является равнобедренной трапецией. В равнобедренной трапеции углы при основании равны (трапеция и ее теоремы). 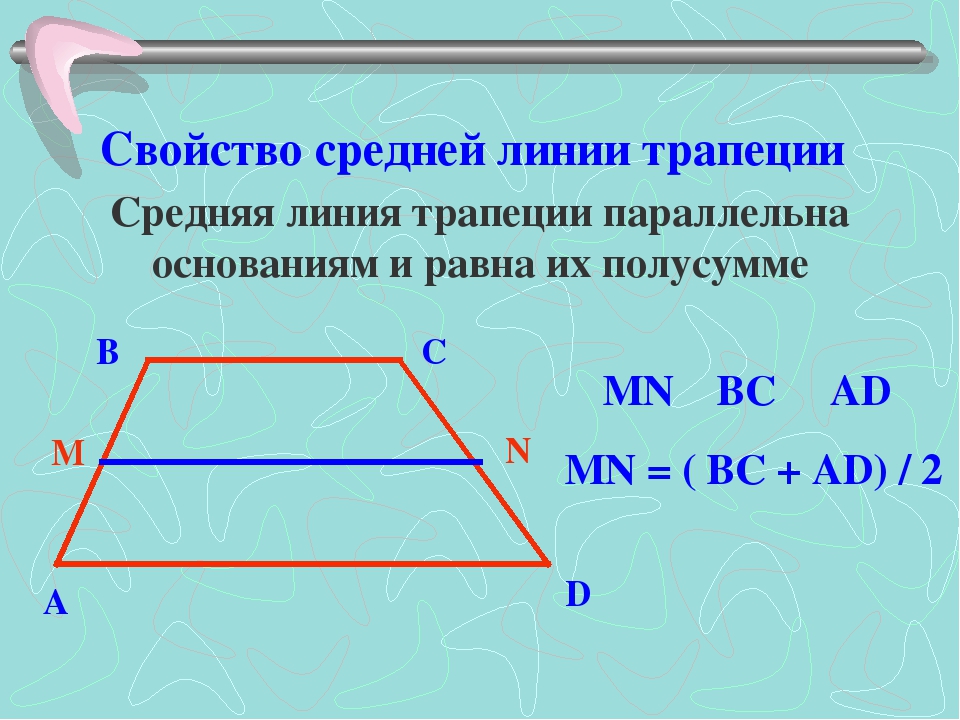 = ∠Q = x = ∠Q = x Сумма всех углов четырехугольника равна 360. ∴ ∠P + ∠Q + ∠S + ∠R = 360 x + x + 60 + 60 = 360 2x +120 = 360 2x = 360 -120 2X = 240 ∴ x = 240/2 x = 120 ∠p = ∠q = 120 0 __________________________________________________________________________________________________ Некоторые важные теоремы трапециевидов приведены ниже:
Практика 1) В трапеции ABCD,AB|| CD и ВС = AD. Если m∠C=65 0 , то найти m∠D. 2) PQRS — трапеция, в которой PQ || РС. Если ∠P = ∠Q = 40, найдите величины двух других углов. 3) В трапеции ABCD ∠B= 120 0 Найти m∠C. 4) В четырехугольнике HELP, если EP = LH, то какой это четырехугольник? 5) В четырехугольнике углы относятся как 4:5:3:6.Найдите меры каждого угла. 6) Если три угла трапеции равны 130 0 ,120 0 ,50 0 и 2x 0 . Найдите х и четвертый угол. 7) Нарисуйте равнобедренную трапецию с именем PQRS, PS||QR и PQ = SR. Четырехугольник • Введение в четырехугольник Домашняя страница Covid-19 повлиял на физическое взаимодействие между людьми. Не позволяйте этому влиять на ваше обучение. Как найти периметр трапецииЕсли вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Чтобы подать уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. Отправьте жалобу нашему назначенному агенту по адресу: Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже:
Свойства среднего сегмента трапеции — Задача 1 Средний сегмент трапеции соединяет середины двух конгруэнтных сторон трапеции и параллелен паре параллельных сторон. Длина среднего сегмента равна сумме двух оснований, деленной на 2. Помните, что основания трапеции — это две параллельные стороны. Чтобы найти углы внутри трапеции, помните, что, поскольку две стороны параллельны, другие стороны можно рассматривать как трансверсали, образующие соответствующие углы и внутренние углы той же стороны. Используя то, что известно о соответствующих и односторонних внутренних углах, можно найти меры недостающих углов трапеции. В этой задаче нас просят найти длину этого отрезка и величину этих двух углов. Итак, давайте начнем с того, что мы знаем об этой проблеме? Я вижу, что эта точка является серединой этой стороны, а эта точка является серединой другой стороны. Так как у меня есть две параллельные стороны, это будет трапеция, а так как это середины, я создал средний сегмент и две ключевые вещи, которые я знаю о средних сегментах, во-первых, что они параллельны два основания, так что я собираюсь вернуться сюда и отметить этот средний отрезок как параллельный, и я также знаю, что длина моего среднего отрезка является средним значением двух оснований, поэтому, если вы сложите два основания и разделить на 2, вы получите длину вашего среднего сегмента. Итак, давайте сначала найдем. «а» — это расстояние до середины нашего отрезка, поэтому я собираюсь сказать, что а равно среднему значению двух оснований, равных 10 и 18. Итак, 10 и 18 равно 28, поэтому а равно 28, делённому на 2, поэтому а равно 14, а единицами здесь являются сантиметры, поэтому я напишу 14 см. Теперь найдем х. Ну, так как эти две линии параллельны, я могу думать об этой стороне прямо здесь как о поперечной, создающей соответствующие углы, которые всегда конгруэнтны. Таким образом, x равен 55 градусам, потому что соответствующие углы должны быть равны.Теперь, чтобы найти y, мне нужно посмотреть на эту сторону как на секущую. Это можно выяснить несколькими способами. Первый способ состоит в том, чтобы сказать, что 120 градусов соответствуют этому углу прямо здесь, поэтому этот угол должен быть 120 градусов. 120 градусов и y находятся на одной стороне поперечной, и она находится между двумя параллельными линиями, так что это одна и та же сторона, что означает, что y плюс 120 градусов должны быть дополнительными, поэтому, если я вычту 120 градусов, то я вижу, что y должен быть 60 градусов. Итак, две ключевые вещи в решении этой задачи: одна из них помнила, что середина и трапеция параллельны двум основаниям, а ее длина равна сумме двух оснований, деленной на 2. 14 примеров трапеций в реальной жизни — StudiousGuyТрапецией называется четырехугольник, у которого по крайней мере две стороны параллельны друг другу. Это двумерная плоская геометрическая фигура. Площадь трапеции равна половине произведения перпендикулярного расстояния между параллельными сторонами и суммы длин параллельных сторон. Периметр трапеции можно вычислить, вычислив сумму длин сторон.Трапецию также называют трапецией. Указатель статей (щелкните, чтобы перейти) Типы ТрапециевиднаяВ геометрии есть в основном три типа трапеций, а именно: правильная трапеция, равнобедренная трапеция и разносторонняя трапеция. 1. Правая трапеция Прямоугольная трапеция обязательно состоит из пары прямых углов. Равнобедренная трапеция — это тип трапеции, у которой непараллельные стороны равны по длине. 3. Трапециевидная трапецияРазносторонняя трапеция или разносторонняя трапеция — это трапеция, не содержащая равных сторон или равных углов. Свойства трапеции1. Сумма всех внутренних углов трапеции равна 360°. 2. У трапеции есть пара параллельных сторон и пара непараллельных сторон. 3. Диагонали трапеции делят друг друга пополам. 4. Длина середины трапеции равна половине суммы параллельных оснований. 5. Сумма углов, образованных между параллельными сторонами и одной из непараллельных сторон, равна 180°. Примеры объектов трапециевидной формы 1. Стекло Ширина стекла уменьшается при движении вниз. Колпак лампы — еще один пример предметов трапециевидной формы, используемых в реальной жизни. Он состоит из пары параллельных сторон и пары непараллельных сторон. 3. Баночка для попкорнаТрапециевидную форму баночки для попкорна легко узнать. Верх и низ ванны составляют параллельные стороны, тогда как другие стороны образуют непараллельные стороны. 4.Цветочный горшокЕсли вы посмотрите на двухмерную проекцию цветочного горшка, вы легко увидите трапециевидную форму. 5. Сумочка Посмотрите на форму сумочки. Вы можете легко заметить, что верхняя и нижняя части мешка параллельны друг другу, а остальные его стороны не параллельны. Таким образом, сумочка является ярким примером предметов трапециевидной формы, используемых в реальной жизни. Структура ведра аналогична структуре трапеции, поскольку состоит из пары параллельных прямых и пары непараллельных прямых. 7. ГитараПримерно в 1970 году трапециевидные кастомные гитары, сделанные Крисом Мартином, стали довольно популярными. Даже сейчас есть определенные места, где можно увидеть такие трапециевидные гитары. 8. КольцоЕсли вы держите кольцо и смотрите на драгоценный камень, закрепленный внутри корпуса на его вершине, вы можете легко увидеть трапециевидную форму.Верхняя часть плоского драгоценного камня и базовая линия корпуса имеют тенденцию образовывать две параллельные линии, в то время как боковые линии корпуса образуют непараллельные линии. 9. Ванна Одной из распространенных форм, выбранных компаниями-производителями скобяных изделий для изготовления ванны, является трапеция. Контейнер, используемый в тачке, обычно имеет трапециевидную форму.Трапециевидная форма контейнера позволяет вмещать сравнительно больше материала, чем другие формы. 11. ЛопатаЛезвие лопаты образует форму четырехугольника, состоящего из пары параллельных прямых и пары непараллельных прямых. Следовательно, это яркий пример трапециевидных объектов в реальной жизни. 12. НавесыНавесы, устанавливаемые на крышах домов и торговых прилавков, в основном имеют трапециевидную форму. 13. ЛодкаТрапециевидную форму в реальной жизни можно легко наблюдать, взглянув на основание бумажного кораблика. Некоторые из лодок, используемых для водного транспорта, также имеют трапециевидную форму. 14. Замок Замки бывают самых разных форм. ЧетырехугольникиЧетырехугольник представляет собой замкнутую плоскую фигуру, ограниченную четырьмя линиями сегменты.Например, показанная здесь цифра ABCD представляет собой четырехугольник. Отрезок, проведенный из одной вершины четырехугольника в противоположную вершина называется диагональю четырехугольника. Например, AC является диагональю четырехугольника ABCD , а также BD . Типы четырехугольников и их свойства Существует шесть основных типов четырехугольников: 1.Прямоугольник
2. Квадрат
3. Параллелограмм
4. Ромб
5.  Трапеция Трапеция
6.Воздушный змей
Теорема 3 Докажите, что сумма углов четырехугольника равна 360. Доказательство: Следовательно, сумма углов четырехугольника равна 360. Применение свойств углов в четырехугольниках Доказанные теоремы можно использовать для доказательства других теорем. Они также может быть использован для нахождения значений прочислительных в задаче. Пример 14Найдите значение прочислительного x на прилагаемой диаграмме. Обоснуйте свой ответ. Решение:Пример 15 Найдите значение каждой процифры в изображенном здесь воздушном змее. Назови причины за ваши ответы. Решение:Пример 16 Найдите значение каждой из прочислительных на прилагаемой диаграмме.Давать
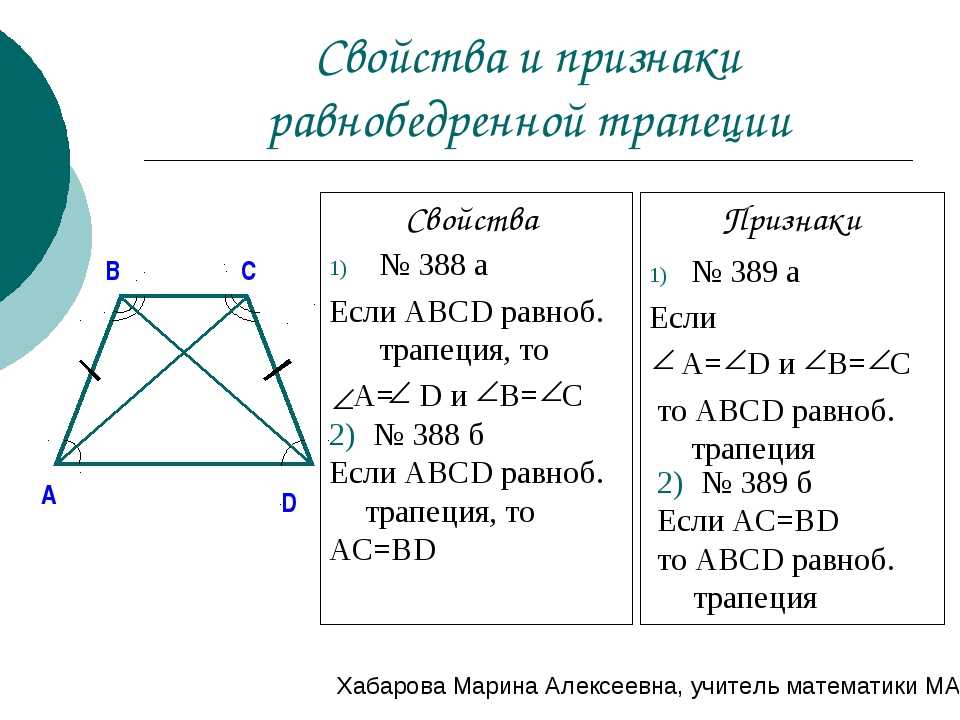
причины ваших ответов. Решение:Пример 17 Найдите значение прочислительного на прилагаемой диаграмме. Давать причины вашего ответа. Решение:Пример 18 Найдите значение каждой из прочислительных на прилагаемой диаграмме.Давать причины ваших ответов. Решение:Пример 19 Найдите значение прочислительного на прилагаемой диаграмме. Давать причины вашего ответа. Решение:Ключевые термины четырехугольник, диагональ четырехугольник, прямоугольник, квадрат, параллелограмм, ромб, трапеция, правильная трапеция, воздушный змей, сумма углов четырехугольника Свойства трапеции. Узнайте о форме, площади и формуле Узнайте о форме, площади и формулеТрапеция представляет собой выпуклый четырехугольник с двумя параллельными сторонами противоположной длины и двумя неравными сторонами. Давайте погрузимся в мир изучения и понимания свойств трапеции . Люди обычно полагаются на разные формы для построения, создания или измерения чего-либо. Одна из самых распространенных форм – трапеция. Это двумерная фигура, представляющая собой стол, нарисованный на бумаге. Узор трапеции можно увидеть в таких предметах, как стакан с водой, настольная лампа, цветочный горшок и лодки. Одним из основных применений трапеции является правило трапеций, где площадь под кривой делится на различное количество трапеций. При рассмотрении нескольких приложений, таких как строительство, дизайн интерьера, анимация, 3D-печать и другие области работы, важно правильно измерить размер, форму, объем и другие аспекты формы. В этой статье мы изучим типы трапеций, такие как неправильные трапеции, и даже проверим решенные примеры, чтобы знать, как решать практические задачи. В этой статье студенты смогут узнать все о трапециях. Читайте дальше, чтобы узнать обо всех различных аспектах Trapezium и о том, как решить связанные с ними проблемы. Что такое Трапеция?Трапеция — выпуклый четырехугольник, у которого хотя бы одна пара параллельна. Параллельные стороны называются основаниями, а две другие стороны называются катетами или боковыми сторонами. Трапеция — это \(4\)-сторонняя плоская фигура с прямыми сторонами, у которой пара противоположных сторон параллельна.
Форма трапеции Трапеция представляет собой замкнутую форму с четырьмя сторонами. На приведенном выше рисунке показан четырехугольник \(ABCD\), в котором противоположные стороны \(AB\) и \(DC\) параллельны друг другу, а противоположные стороны \(AD\) и \(BC\) не параллельны относительно друг друга, поэтому четырехугольник \(ABCD\) является трапецией. Так как мы узнали, что стороны \(AB\) и \(CD\) являются параллельными сторонами трапеции, мы получаем две пары внутренних углов. Одна пара — это \(\угол A\) и \(\угол D\), а другая пара — это \(\угол B\) и \(\угол C.\цирк.\) Изучите концепции 10-го экзамена CBSE Изучите концепции 10-го экзамена CBSE Типы трапеций По сторонам углов трапеции можно разделить на три типа. На приведенном выше рисунке показана трапеция \(ABCD\), у которой непараллельные стороны \(AD\) и \(BC\) имеют одинаковую длину. Практика 10-го экзамена CBSE Вопросы 3. Острая трапеция: Острая трапеция имеет два смежных острых угла на более длинном крае основания, а тупая трапеция имеет по одному острому и одному тупому углу на каждом основании. Свойства трапецииТермин трапеция в переводе с греческого означает «столик». Его свойства следующие:
Площадь и периметр трапецииПлощадь трапеции можно рассчитать по следующей формуле: \({\rm{Площадь}}\,{\rm{из}}\,{\rm{a}}\,{\rm{трапеция}} = \frac{1}{2}\, \times \,\,{\rm{Сумма}}\,{\rm{из}}\,{\rm{параллельно}}\, {\rm{стороны}}\, \times \,{\rm{Расстояние} } \, {\ rm {между}} \, {\ rm {}} \, {\ rm {параллельно}} \, {\ rm {стороны}} \) Пусть \({b_1}\) и \({b_2}\) — длины этих оснований. Попытка 10-го экзамена CBSE Пробные тесты Давайте разберемся, как мы пришли к этой формуле. Для данной трапеции пусть \({b_1}\) и \({b_2}\) — длины оснований, а \(h\) — высота. Теперь нарисуйте сегмент (как показано на рисунке ниже) параллельно основаниям, которые находятся посередине между основаниями.\circ \) \(\угол 2 = \угол 6\) и \(\угол 3 = \угол 8\) Теперь переверните верхнюю часть трапеции и поместите ее рядом с нижней трапецией, как показано на следующем рисунке:
Теперь, если мы присмотримся, полученная форма имеет форму параллелограмма. Длина его основания равна \(\left( {{b_1} + {b_2}} \right),\), а высота \(\frac{1}{2}h.\) Практика 10-го экзамена CBSE Вопросы ПериметрВ геометрии периметр может быть определен как путь или граница, окружающая фигуру. Его также можно определить как длину контура фигуры. Трапеция здесь не исключение. Следовательно, периметр трапеции равен сумме длин ее четырех сторон. Четыре стороны данной трапеции \(ABCD\) равны \(AB,\,BC,\,CD\) и \(AD.\) Периметр трапеции \(=AB + BC + CD + AD\) Трапеция и трапеция Трапеция представляет собой четырехугольник и двумерную фигуру, у которой ровно одна пара параллельных сторон противоположна друг другу. Что такое неправильная трапеция? У трапеции одна пара параллельных сторон, а две другие стороны непараллельны. Площадь трапеции — это количество места, которое она занимает или заключает в себе на плоскости. Площадь обычно измеряется в квадратных единицах, таких как квадратные метры, квадратные футы, квадратные дюймы и т. д. Решенные примеры Вопрос-1: Если сумма параллельных сторон трапеции \(8\,{\rm{см}}\) и расстояния между ними равна \(5\,{\rm{см, }}\) тогда какова площадь трапеции? Вопрос-2: Найдите площадь трапеции, у которой сумма параллельных сторон равна \(80\,{\rm{см,}}\), а высота равна \(20\,{\rm {см}}{\rm{.}}\) Вопрос-4: Найдите периметр трапеции, стороны которой равны \(5\,{\rm{см}},\,6\,{\rm{см}},\,7\,{\rm {см}}\) и \({\rm{8}}\,{\rm{см}}{\rm{.}}\) РезюмеВ этой статье мы исследовали целый новый мир трапеций. Мы узнали, что такое трапеция и как найти площадь трапеции. Мы также познакомились с различными типами трапеций и узнали, что делает их уникальными в своем роде. Мы также узнали, где мы называем трапецию трапецией, ее определение и особенности. Попытка 10-го экзамена CBSE Пробные тесты Часто задаваемые вопросы
|
 Для этого необходимы дополнительные построения. Подумайте, на какие фигуры можно разбить трапецию? Что для этого надо сделать? [Построить отрезок СЕ, такой что СЕ||АВ.]
Для этого необходимы дополнительные построения. Подумайте, на какие фигуры можно разбить трапецию? Что для этого надо сделать? [Построить отрезок СЕ, такой что СЕ||АВ.] Рефлексия.
Рефлексия.

 Таким образом, если вы не уверены, что содержимое находится
на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Таким образом, если вы не уверены, что содержимое находится
на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.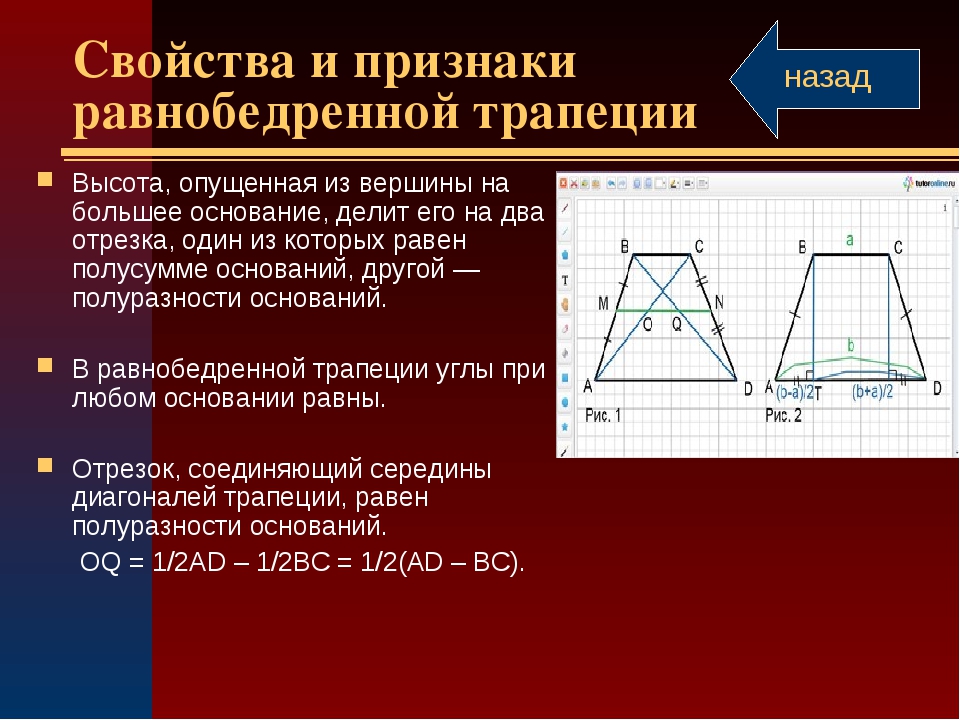 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.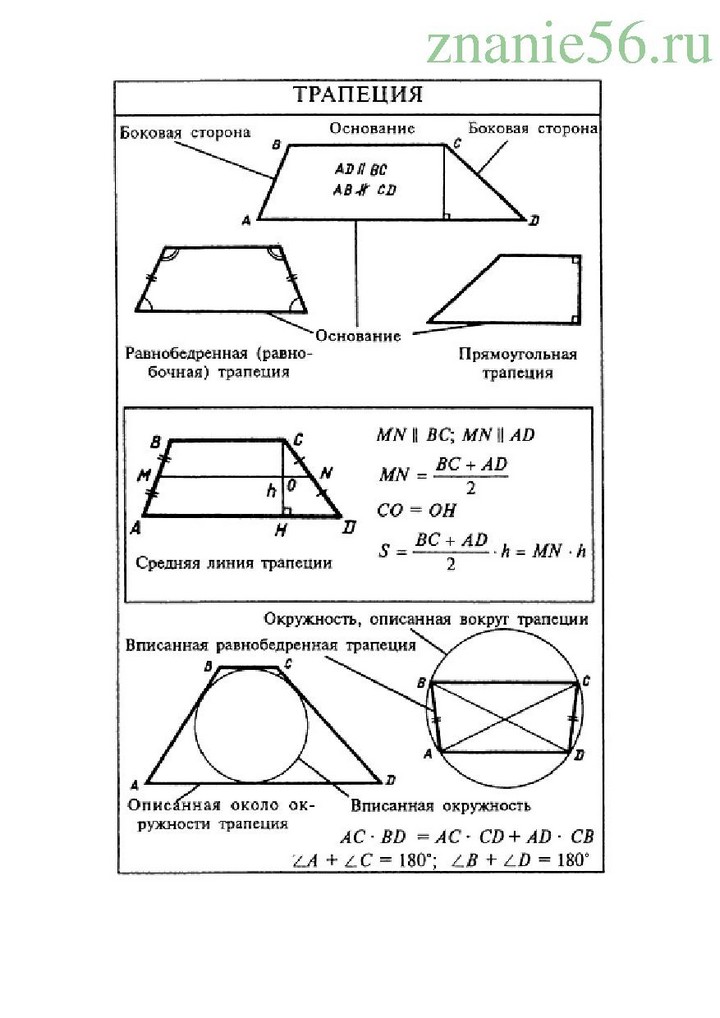
 Следовательно, один из лучших примеров трапеции можно увидеть, наблюдая за формой стакана для питья.
Следовательно, один из лучших примеров трапеции можно увидеть, наблюдая за формой стакана для питья.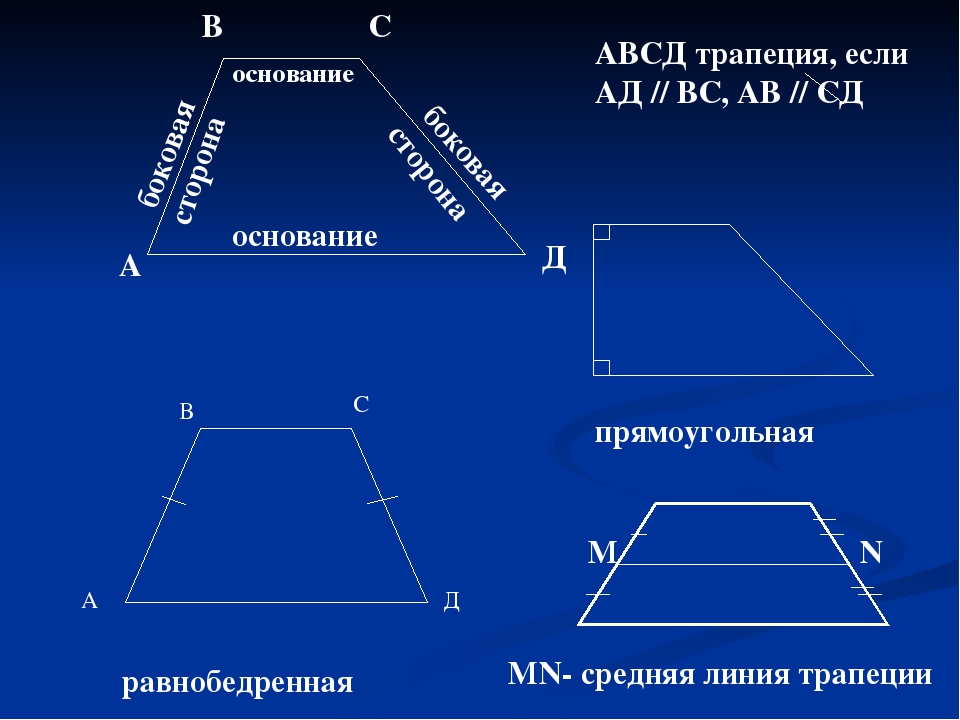
 Другие формы могут включать прямоугольник, круг и т. д.
Другие формы могут включать прямоугольник, круг и т. д.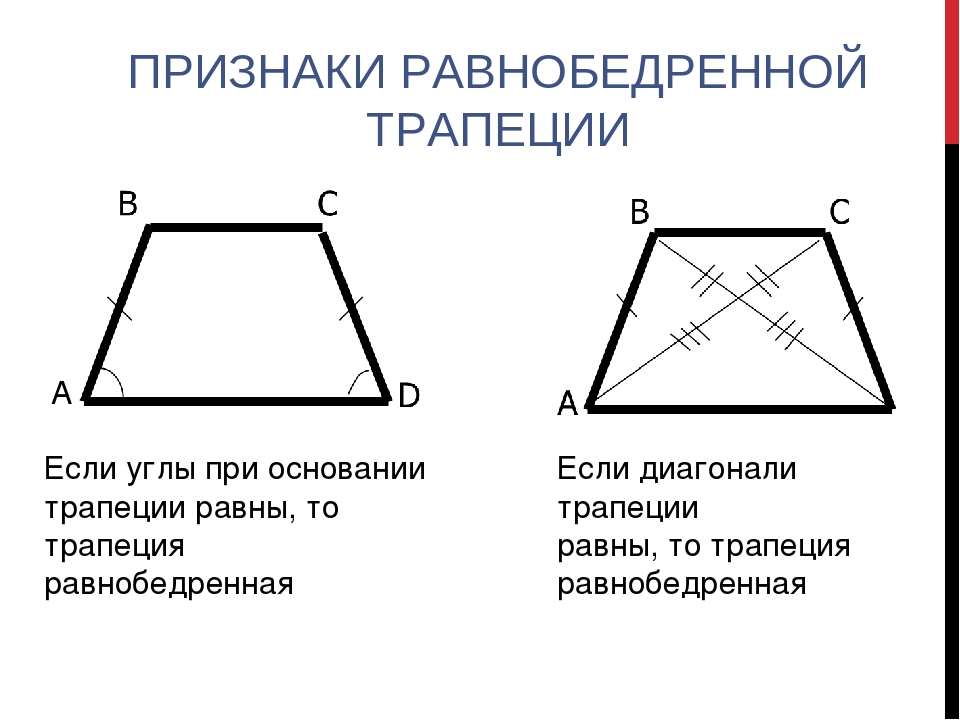 Из них наиболее популярны замки трапециевидной формы.
Из них наиболее популярны замки трапециевидной формы.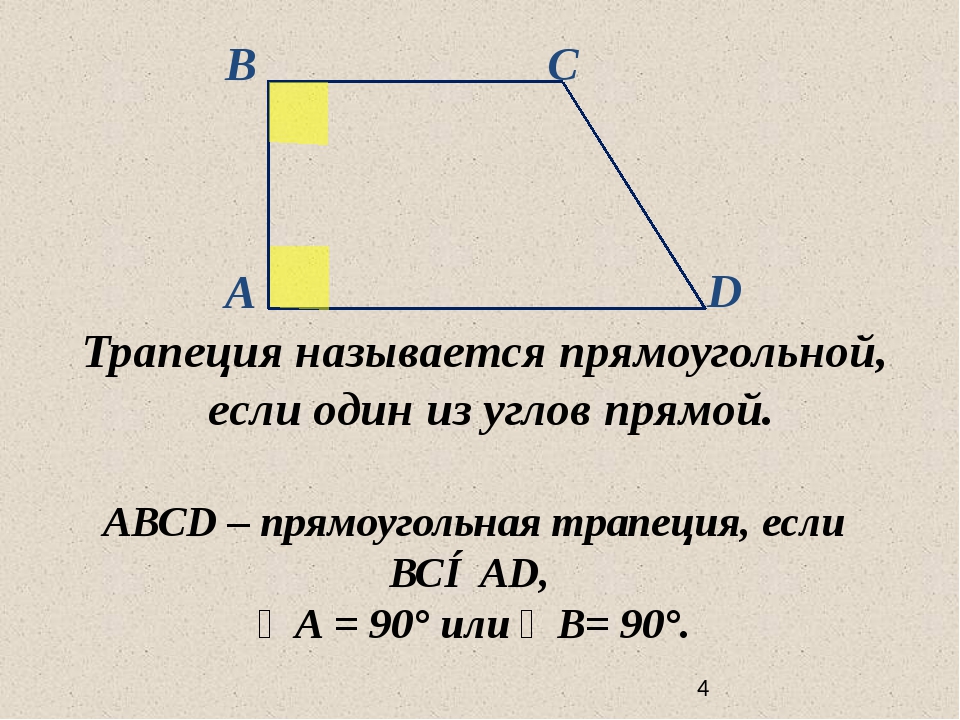


 Одна пара сторон равна, а другая пара нет.
Одна пара сторон равна, а другая пара нет.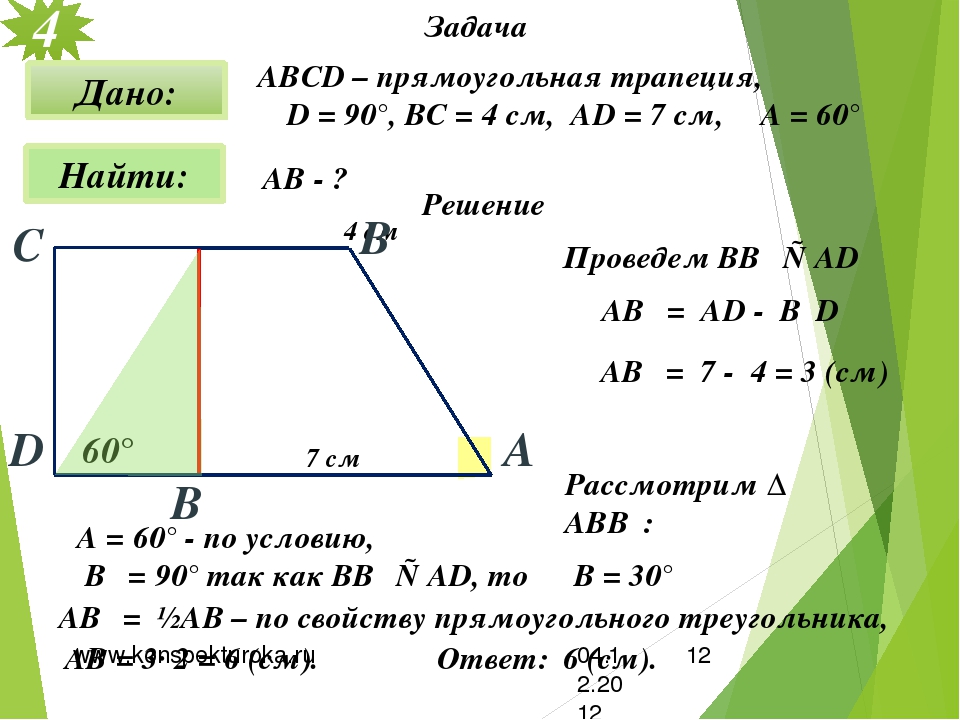 \цирк\)
\цирк\)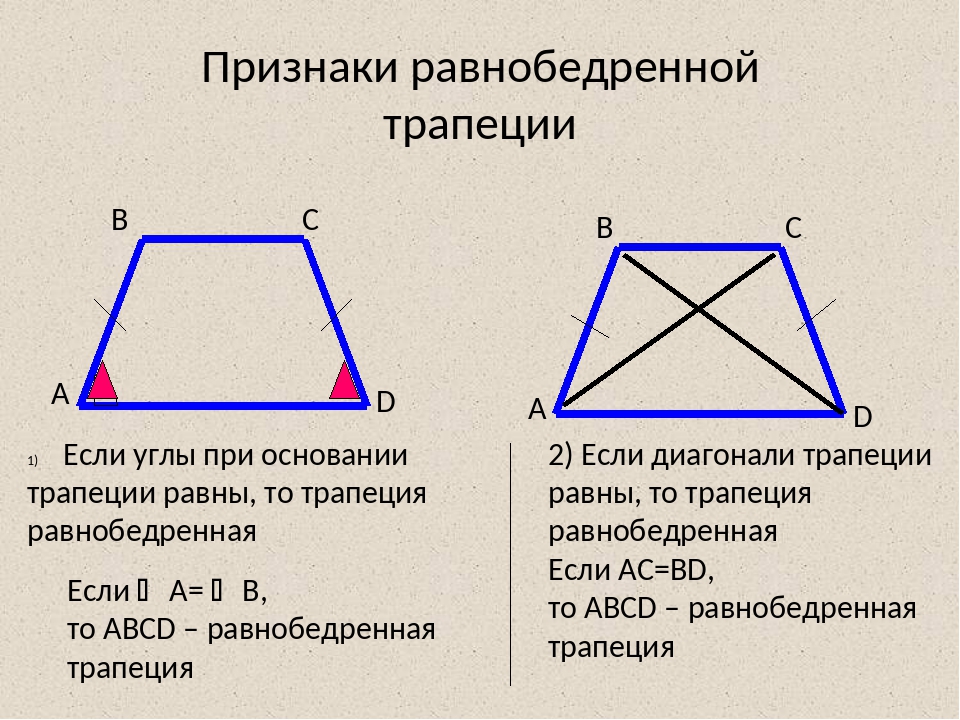 Расстояние между основаниями называется высотой трапеции. Пусть \(h\) будет высотой. Тогда формула принимает вид: \(A = \frac{1}{2}\left( {{b_1} + {b_2}} \right) \times h\)
Расстояние между основаниями называется высотой трапеции. Пусть \(h\) будет высотой. Тогда формула принимает вид: \(A = \frac{1}{2}\left( {{b_1} + {b_2}} \right) \times h\) \)
\) \circ \) даст сумму \(2\) углов на образованной противоположной стороне \(y.\). После того, как сумма определена, можно получить меру четвертого угла, разделив сумму на \( 2.\)
\circ \) даст сумму \(2\) углов на образованной противоположной стороне \(y.\). После того, как сумма определена, можно получить меру четвертого угла, разделив сумму на \( 2.\) {\rm{ 2}}}.{\rm{2}}}\)
{\rm{ 2}}}.{\rm{2}}}\) 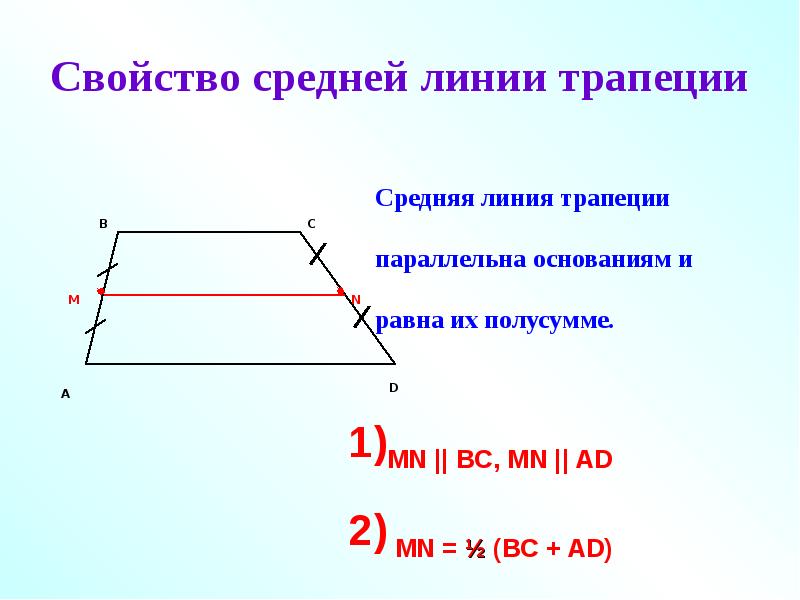 \цирк\)
\цирк\)