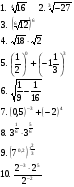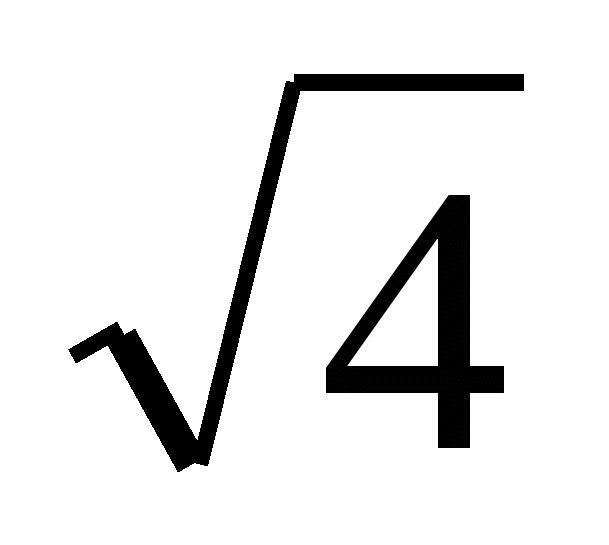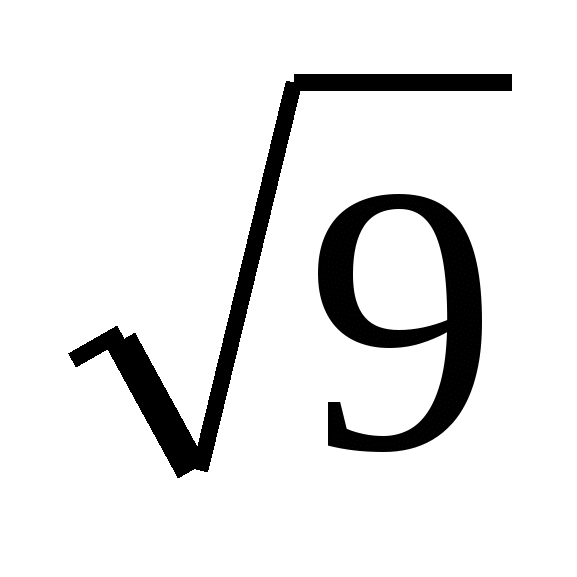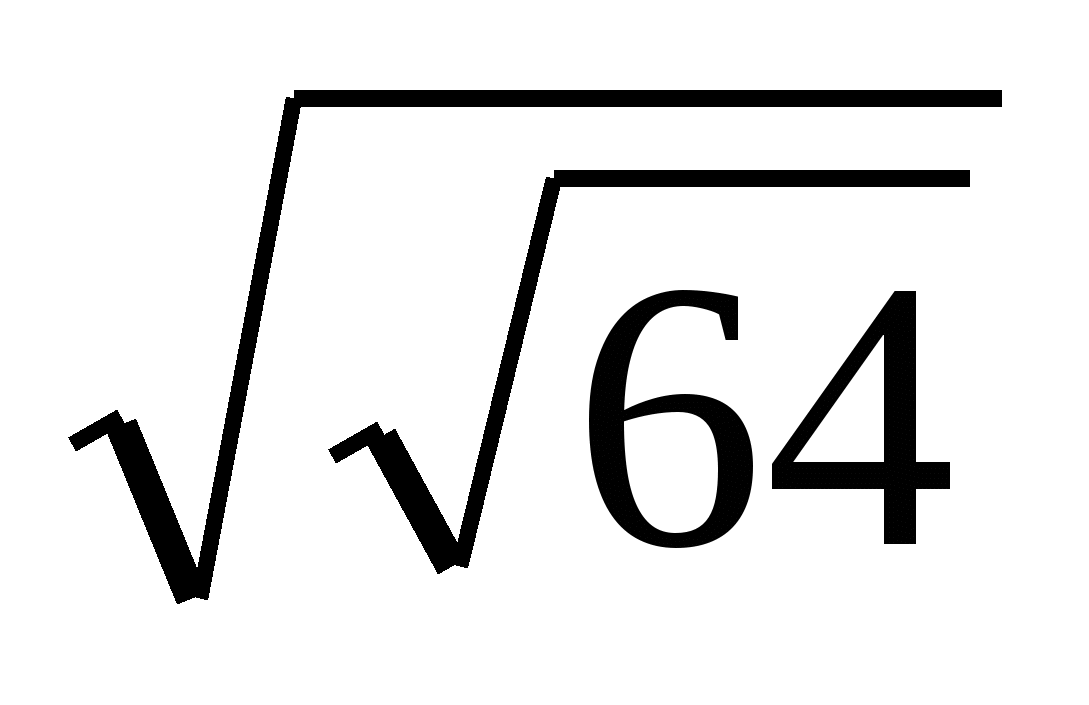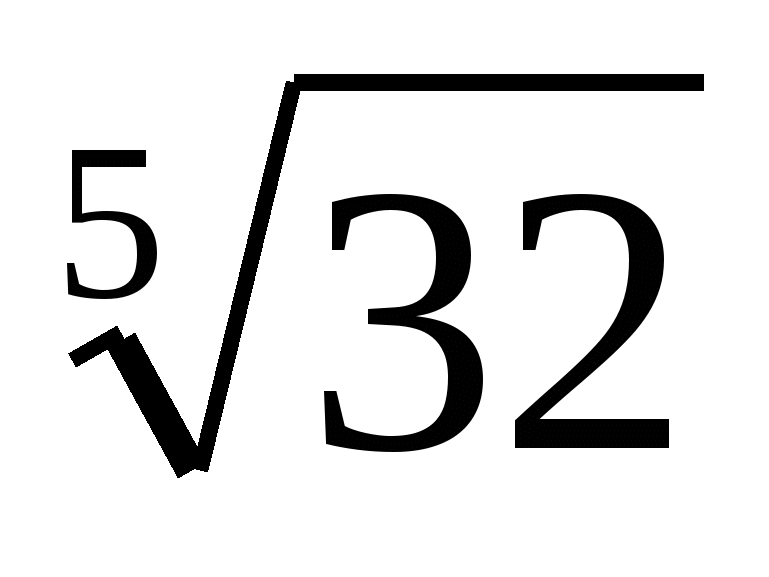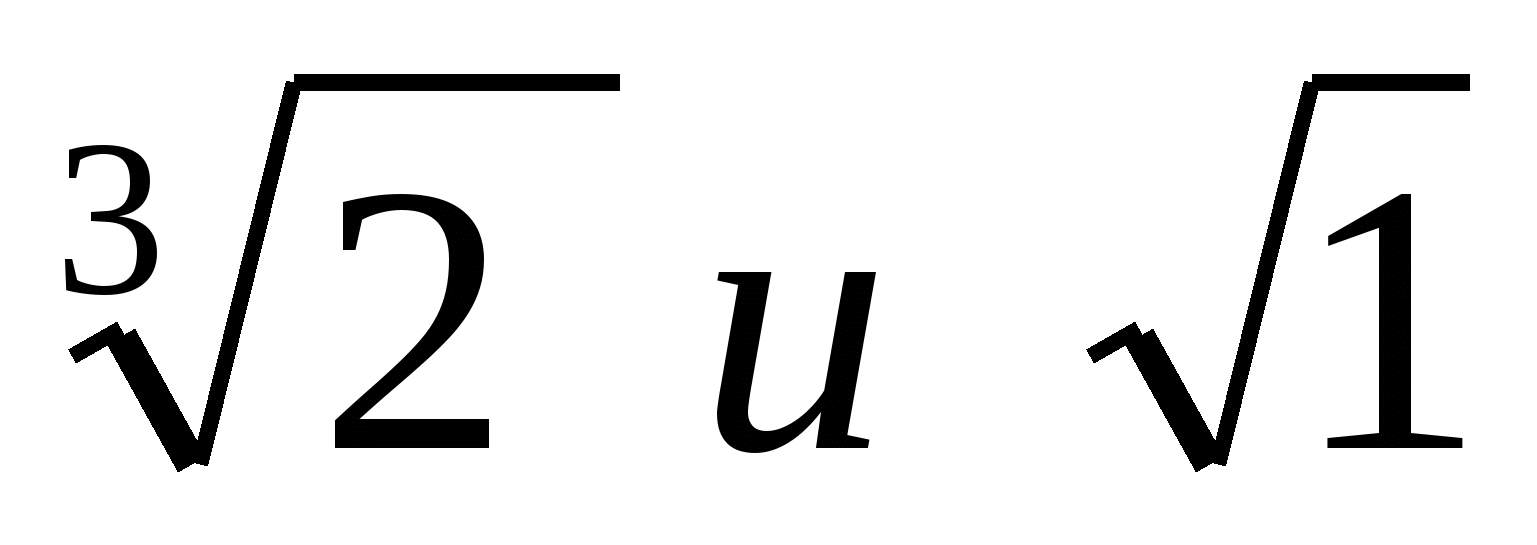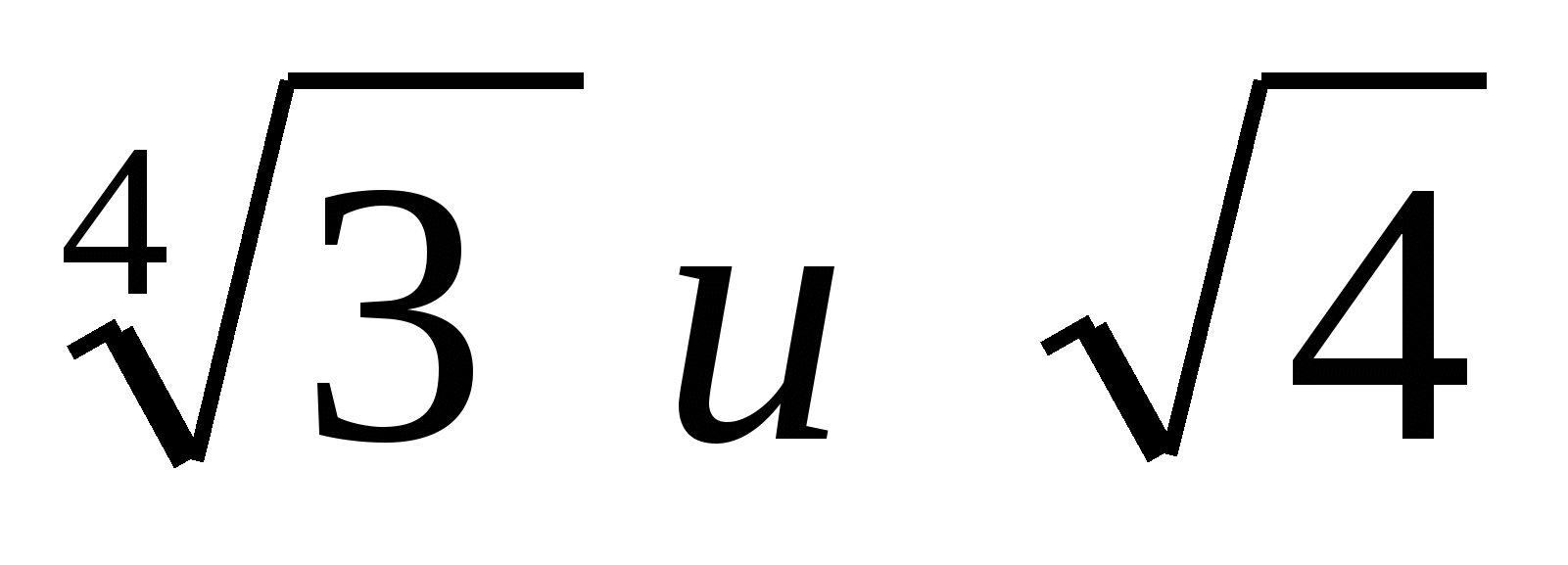степени, корни (подготовка к ЕГЭ)
К учебнику: Алгебра и начала математического анализа. 10 класс. Углубленный уровень. Муравин Г.К., Муравина О.В. М.: 2013. — 320 с.
К уроку: 5. Степенная функция у = хп при натуральном п
К учебнику: Алгебра и начала математического анализа. 10 класс. Углубленный уровень. Муравин Г.К., Муравина О.В. М.: 2013. — 320 с.
К уроку: 6. Понятие корня л-й степени
К учебнику: Алгебра и начала математического анализа. 10 класс. Углубленный уровень. Муравин Г.К., Муравина О.В. М.: 2013. — 320 с.
К уроку: 7. Свойства арифметических корней
К учебнику: Алгебра и начала математического анализа. 10 класс. Углубленный уровень. Муравин Г.К., Муравина О.В. М.: 2013. — 320 с.
К уроку: 8. Степень с рациональным показателем
К учебнику: Алгебра и начала математического анализа (базовый и углубленный уровень), 10 класс, Колягин Ю.М., Ткачёва M.B. и др., Изд. «Просвещение»
К учебнику: Алгебра и начала математического анализа (базовый и углубленный уровень), 10 класс, Никольский С.М., Потапов М.К. и др., Изд. «Просвещение»
К учебнику: Алгебра и начала математического анализа (углубленный уровень), 10 класс, Пратусевич М.Я., Столбов К.М. и др., Изд. «Просвещение»
К учебнику: Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. 18-е изд., стер. — М.: 2014. — 312 с.
К уроку: 2. Обобщение понятия степени
К учебнику: Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. 18-е изд., стер. — М.: 2014. — 312 с.
К уроку: § 4. Степенная функция. Иррациональные выражения, уравнения и неравенстваК учебнику: Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. 18-е изд., стер. — М.: 2014. — 312 с.
К уроку: 4. Алгебраические выражения
К учебнику: Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. 18-е изд., стер. — М.: 2014. — 312 с.
К уроку: 5. Упрощение иррациональных выражений
К учебнику: Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. 18-е изд., стер. — М.: 2014. — 312 с.
К уроку: 6. Уничтожение иррациональности в знаменателе или в числителе
К учебнику: Алгебра и начала математического анализа. 11 класс. Учебник. (базовый и углублённый уровни). Мордкович А.Г., Семенов П.В. 2-е изд. — М.: 2014. — 311с.
К уроку: Глава 2. Степени и корни. Степенные функции
К учебнику: Алгебра и начала математического анализа. 11 класс. Учебник. (базовый и углублённый уровни). Мордкович А.Г., Семенов П.В. 2-е изд. — М.: 2014. — 311с.
К уроку: § 4. Понятие корня n-й степени из действительного числа
К уроку: § 5. Функции у — yjx, их свойства и графики
К учебнику: Алгебра и начала математического анализа. 11 класс. Учебник. (базовый и углублённый уровни). Мордкович А.Г., Семенов П.В. 2-е изд. — М.: 2014. — 311с.
К уроку: § 7. Преобразование иррациональных выражений
К учебнику: Алгебра и начала математического анализа. 11 класс. Учебник. (базовый и углублённый уровни). Мордкович А.Г., Семенов П.В. 2-е изд. — М.: 2014. — 311с.К уроку: § 8. Понятие степени с любым рациональным показателем
К учебнику: Алгебра и начала математического анализа. 11 класс. Учебник. (базовый и углублённый уровни). Мордкович А.Г., Семенов П.В. 2-е изд. — М.: 2014. — 311с.
К уроку: § 9. Степенные функции, их свойства и графики
К учебнику: Алгебра и начала математического анализа. 11 класс. Учебник. (базовый и углублённый уровни). Мордкович А.Г., Семенов П.В. 2-е изд. — М.: 2014. — 311с.
К уроку: § 10. Извлечение корней из комплексных чисел
К учебнику: Алгебра и начала математического анализа, 11 класс, Колягин Ю.М., Ткачёва М.В. и др., Изд. «Просвещение»
К учебнику: Алгебра и начала математического анализа (базовый и углубленный уровень), 11 класс, Никольский С.М., Потапов М.К. и др., Изд. «Просвещение»К учебнику: Алгебра и начала математического анализа (углубленный уровень), 11 класс, Пратусевич М.Я., Столбов К.М. и др., Изд. «Просвещение»
К учебнику: Алгебра и начала математического анализа. 10-11 классы. (базовый и углубленный уровни) Алимов А.Ш., Колягин Ю.М. и др. 3-е изд. — М.: Просвещение, 2016. — 464 с.
К учебнику: Алгебра и начала математического анализа. 10-11 классы. (базовый и углубленный уровни) Алимов А.Ш., Колягин Ю.М. и др. 3-е изд. — М.: Просвещение, 2016. — 464 с.
К уроку: § 5. Степень с рациональным и действительным показателями
К учебнику: Алгебра и начала математического анализа. 10-11 классы. (базовый и углубленный уровни) Алимов А.Ш., Колягин Ю.М. и др. 3-е изд. — М.: Просвещение, 2016. — 464 с.
К уроку: Упражнения к главе I
К учебнику: Алгебра и начала математического анализа. 10-11 классы. (базовый и углубленный уровни) Алимов А.Ш., Колягин Ю.М. и др. 3-е изд. — М.: Просвещение, 2016. — 464 с.
К уроку: Глава II. Степенная функции
К учебнику: Алгебра и начала математического анализа. 10-11 классы. (базовый и углубленный уровни) Алимов А.Ш., Колягин Ю.М. и др. 3-е изд. — М.: Просвещение, 2016. — 464 с.
К уроку: Упражнения для итогового повторения курса алгебры и начал математического анализа
К учебнику: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1. Учебник (базовый уровень) Мордкович А.Г. 14-е изд., стер. — М.: 2013. — 400 с.
К уроку: ГЛАВА 6. Степени и корни, степенные функции
К учебнику: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1. Учебник (базовый уровень) Мордкович А.Г. 14-е изд., стер. — М.: 2013. — 400 с.
К уроку: § 33. Понятие корня п-й степени из действительного числа
К учебнику: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1. Учебник (базовый уровень) Мордкович А.Г. 14-е изд., стер. — М.: 2013. — 400 с.
К уроку: § 34. Функции у = у[х, их свойства и графики
К учебнику: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1. Учебник (базовый уровень) Мордкович А.Г. 14-е изд., стер. — М.: 2013. — 400 с.
К уроку: § 35. Свойства корня п-й степени
К учебнику: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1. Учебник (базовый уровень) Мордкович А.Г. 14-е изд., стер. — М.: 2013. — 400 с.
К уроку: § 36. Преобразование выражений, содержащих радикалы
К учебнику: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1. Учебник (базовый уровень) Мордкович А.Г. 14-е изд., стер. — М.: 2013. — 400 с.
К уроку: § 37. Обобщение понятия о показателе степени
К учебнику: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1. Учебник (базовый уровень) Мордкович А.Г. 14-е изд., стер. — М.: 2013. — 400 с.
К уроку: § 38. Степенные функции, их свойства и графики
infourok.ru
Пособие по теме Корни и степени
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА: алгебра и начало математического анализа; геометрия
Тема: «КОРНИ И СТЕПЕНИ»
Специальность: 34.02.01 Сестринское дело Курс: 1
(базовой подготовки)
Купино
2018
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2018 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено для повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятия: корня натуральной степени, степени с действительным и рациональным показателями, их свойств. Алгоритма нахождение значений степеней с рациональными показателями и подготовится к занятию по теме «Корни и степени».
Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения и свойства корней и степеней по теме Корни и степени, тест для самоконтроля и ключи к тесту.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Корни и степени
Из практики решения-все более сложных алгебраических задач и оперирования со степенями возникла необходимость обобщения понятия степени и расширения его посредством введения в качестве показателя нуля, отрицательных и дробных чисел.
Равенство а0 = 1 (для 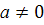 ) применял в своих трудах в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель был введен Н. Шюке в XV в. Последний ввел и отрицательные показатели степени. Идея дробных показателей содержится у французского математика Н. Орема (XIV в.) в его
) применял в своих трудах в начале XV в. самаркандский ученый ал-Каши. Независимо от него нулевой показатель был введен Н. Шюке в XV в. Последний ввел и отрицательные показатели степени. Идея дробных показателей содержится у французского математика Н. Орема (XIV в.) в его
труде «Алгоризм пропорций». Вместо нашего знака 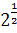 он писал
он писал 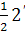 , вместо
, вместо 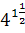 он писал
он писал 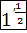 4. Орем словесно формулирует правила действий со степенями, например (в современной записи):
4. Орем словесно формулирует правила действий со степенями, например (в современной записи): 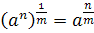 ,
, 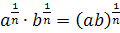 и т.п.
и т.п.
Позже дробные, как и отрицательные, показатели встречаются в «Полной арифметике» (1544) немецкого математика М. Штифеля и у С. Стевина. Последний пишет о том, что корень степени п из числа а можно считать как степень а с дробным показателем 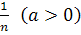 .
.
О целесообразности введения нулевого, отрицательных и дробных показателей и современных символов впервые подробно писал в 1665 г, английский математик Джон Валлис. Его дело завершил И. Ньютон, который стал систематически применять новые символы, после чего они вошли в общий обиход.
Введение степени с рациональным показателем является одним из многих примеров обобщения понятия математического действия. Степень с нулевым, отрицательным и дробным показателями определяется таким образом, чтобы к ней были применимы те же правила действий, которые имеют место для степени с натуральным показателем, т. е. чтобы сохранились основные свойства первоначально определенного понятия степени, а именно:
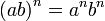
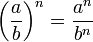
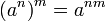
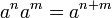
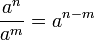
Новое определение степени с рациональным показателем не противоречит старому определению степени с натуральным показателем, т. е. смысл нового определения степени с рациональным показателем сохраняется и для частного случая степени с натуральным показателем. Этот принцип, соблюдаемый при обобщении математических понятий, называется принципом перманентности (сохранения, постоянства). В несовершенной форме его высказал в 1830 г. английский математик Дж. Пикок, полностью и четко его установил немецкий математик Г. Ганкель в 1867 г. Принцип перманентности соблюдается и при обобщении понятии числа и расширении его до понятия действительного числа, а до этого — при введении понятия умножения на дробь и т. п.
Степенная функция и графическое решение уравнений и неравенств
Благодаря открытию метода координат и аналитической геометрии начинай с XVII в. стало возможным общеприменимое графическое исследование функций и графическое решение уравнений.
Степенной функцией называют функцию вида
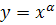 , (1)
, (1)
где α— постоянное вещественное число. Вначале мы ограничимся, однако, лишь рациональными значениями α и вместо равенства (1) запишем:
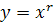 , (2)
, (2)
где 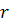 — рациональное число. Для
— рациональное число. Для 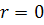 и
и 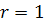 по определению соответственно имеем:
по определению соответственно имеем:
у =1, у =х.
Графиком первой из этих функций на плоскости является прямая, параллельная оси Ох, а второй — биссектриса 1-го и 3-го координатных углов.
При 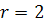 графиком функций является парабола
графиком функций является парабола 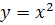 . Декарт, который первое неизвестное обозначал через z, второе — через у, третье — через x:, записывал уравнение параболы так:
. Декарт, который первое неизвестное обозначал через z, второе — через у, третье — через x:, записывал уравнение параболы так: 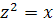 (z— абсцисса). Параболой он часто пользовался для решения уравнений. Чтобы решить, например, уравнение 4-й степени
(z— абсцисса). Параболой он часто пользовался для решения уравнений. Чтобы решить, например, уравнение 4-й степени
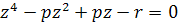 (3)
(3)
Декарт с помощью подстановки
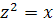 (4)
(4)
получил квадратное уравнение с двумя неизвестными:
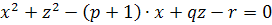 (5)
(5)
изображающее окружность, расположенную в одной плоскости (zх) с параболой (4). Таким образом, Декарт, вводя вторую неизвестную (х), разбивает уравнение (3) на два уравнения (4) и (5), каждое из которых представляет определенное геометрическое место точек. Ординаты точек их пересечения и дают корни уравнения (3).
Притча:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному замку. «Кто первым откроет, тот и будет первым помощником». Никто даже не притронулся к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, а надеешься на собственные силы и не боишься сделать попытку».
И мы сегодня будем пытаться, пробовать, чтобы прийти к правильному решению.
Задание
1. С каким математическим понятием связаны слова:
Основание
Показатель (Ответ в конспект)
2. Какими словами можно объединить слова:
Рациональное число
Целое число
Натуральное число
Иррациональное число (Ответ в конспект)
3. Итак, ар, где р – число действительное.
Приведите примеры (выберете из выражений 5–2, 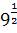 , 43,
, 43, 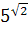 ) степени
) степени
– с натуральным показателем
– с целым показателем
– с рациональным показателем
– с иррациональным показателем (Ответ в конспект)
4. Какие действия (математические операции) можно выполнять со степенями? Установите соответствие:



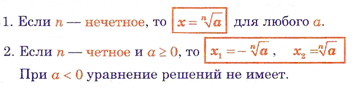


Вариант 1
Вариант 2
Домашняя контрольная работа «Корни и степени».
Вариант №1 [Вариант №2].
1)Вычислить:

2) Упростить выражение при а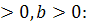
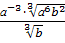
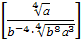 ;
;
3) Сократить дробь 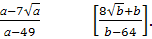
4) Сравнить числа 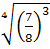 и
и 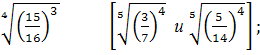
Литература
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2012
Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012
Интернет-ресурсы
http://school-collection.edu.ru – Электронный учебник «Математика в
школе, XXI век».
http://fcior.edu.ru — информационные, тренировочные и контрольные материалы.
www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов
infourok.ru
Тренажёр для подготовки к ЕГЭ на тему «Степени и корни» (11 класс)
Тренажёр по подготовке к ЕГЭ по теме «Степени и корни» Время выполнения: 10 минут На листочке ответов записать значение числового выражения. Вычислить.
Критерии оценивания: Каждое верно выполненное задание оценивается в 1 балл. 5 | 4 | 3 | 2 |
10 | 8-9 | 6-7 | 0-5 |
Тренажёр по подготовке к ЕГЭ по теме «Степени и корни»
Время выполнения: 10 минут
На листочке ответов записать значение числового выражения.
Вычислить.
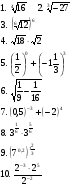
Критерии оценивания:
Каждое верно выполненное задание оценивается в 1 балл.
5
4
3
2
10
8-9
6-7
0-5
Тренажёр по подготовке к ЕГЭ по теме «Степени и корни»
Время выполнения: 10 минут
На листочке ответов записать значение числового выражения.
Вычислить.
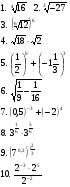
Критерии оценивания:
Каждое верно выполненное задание оценивается в 1 балл.
5
4
3
2
10
8-9
6-7
0-5
Тренажёр по подготовке к ЕГЭ по теме «Степени и корни»
Время выполнения: 10 минут
На листочке ответов записать значение числового выражения.
Вычислить.
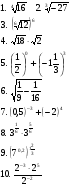
Критерии оценивания:
Каждое верно выполненное задание оценивается в 1 балл.
5
4
3
2
10
8-9
6-7
0-5
Тренажёр по подготовке к ЕГЭ по теме «Степени и корни»
Время выполнения: 10 минут
На листочке ответов записать значение числового выражения.
Вычислить.
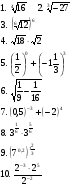
Критерии оценивания:
Каждое верно выполненное задание оценивается в 1 балл.
5
4
3
2
10
8-9
6-7
0-5
Тренажёр по подготовке к ЕГЭ по теме «Степени и корни»
Время выполнения: 10 минут
На листочке ответов записать значение числового выражения.
Вычислить.
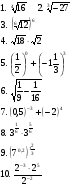
Критерии оценивания:
Каждое верно выполненное задание оценивается в 1 балл.
5
4
3
2
10
8-9
6-7
0-5
infourok.ru
Тематические тренажеры. Степени и корни.
Степени и корни.
Вычислите:
1. 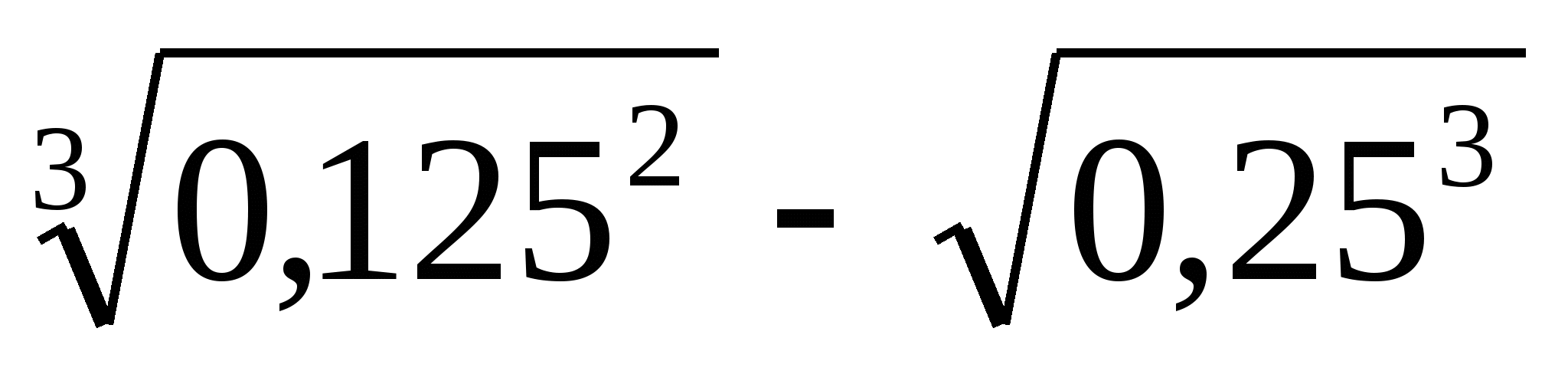
1) 0,375 2) 0,125 3) -0,25 4) 0
2. 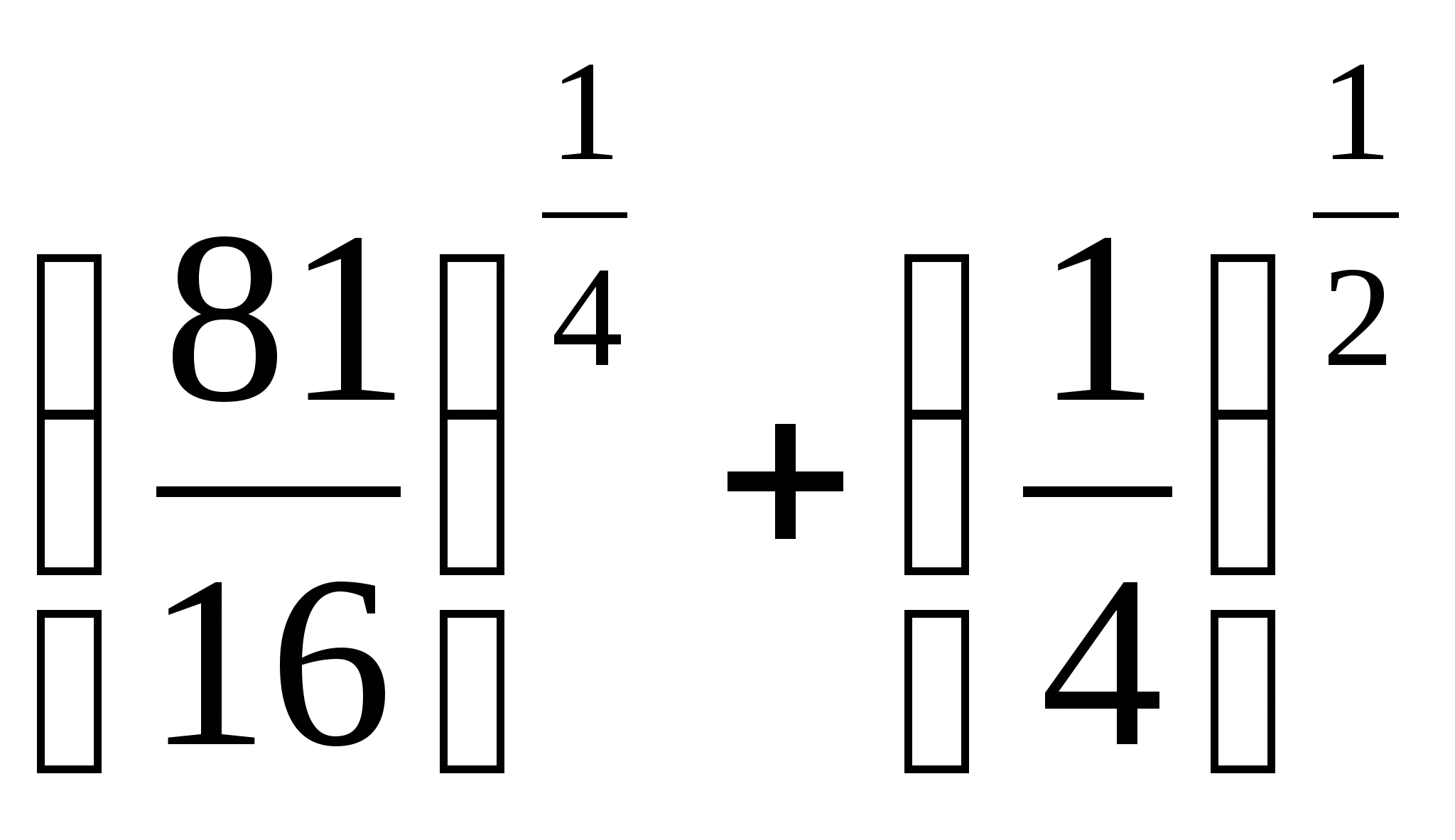
1) 2 2) 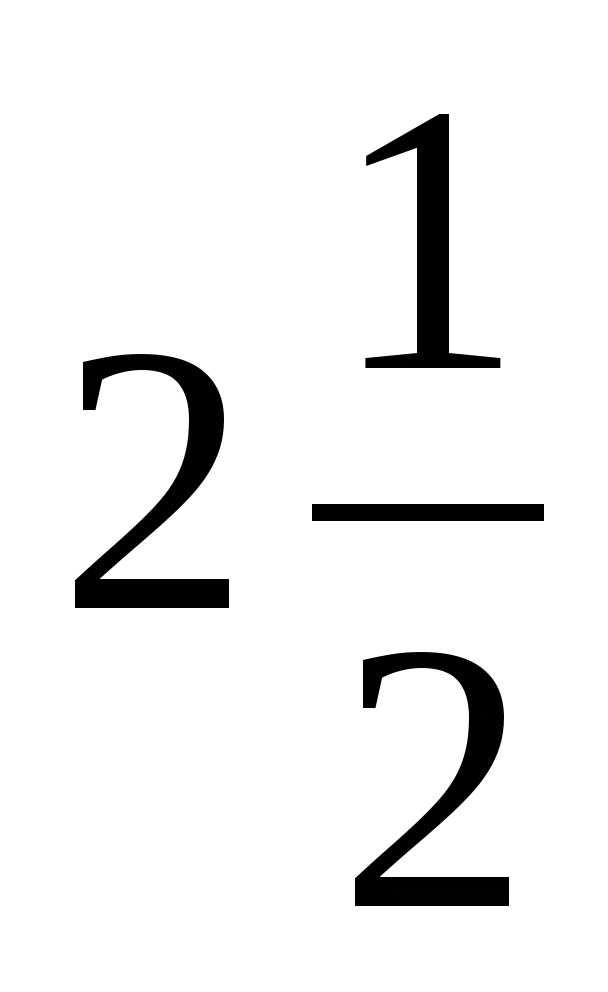 3) 3 4)
3) 3 4) 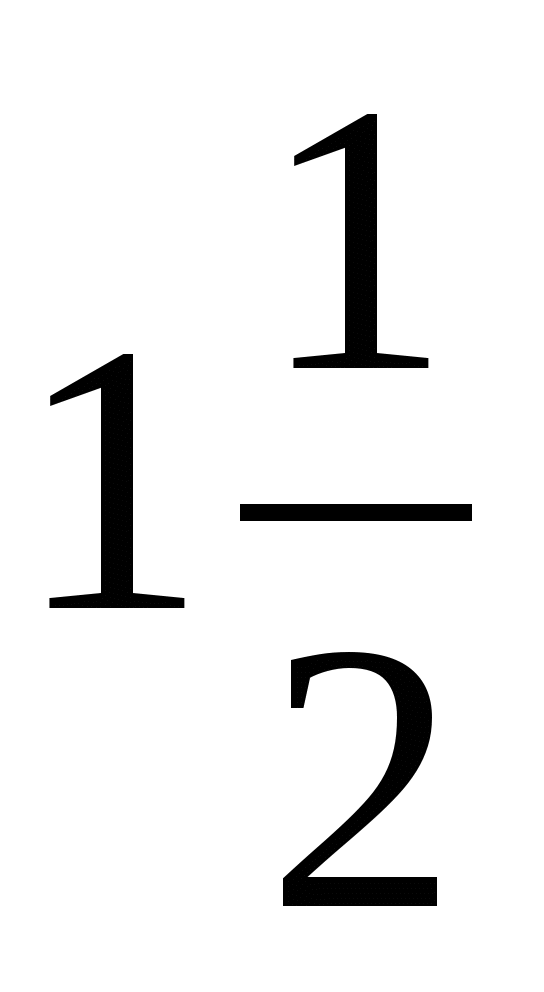
3. 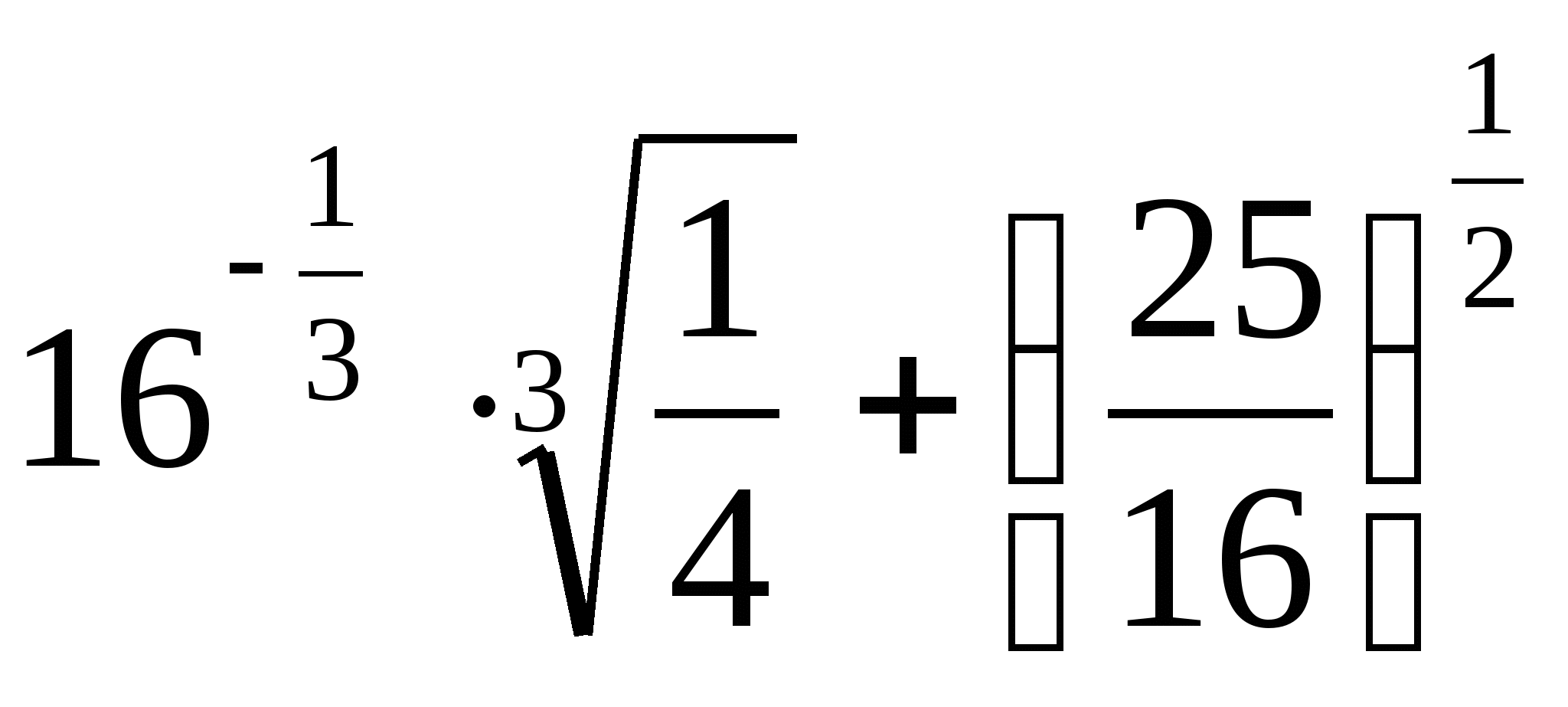
1) 1 2) 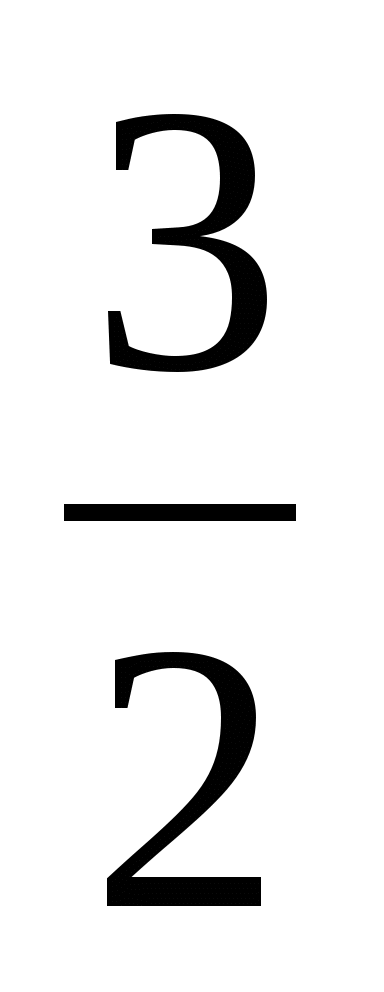 3)
3) 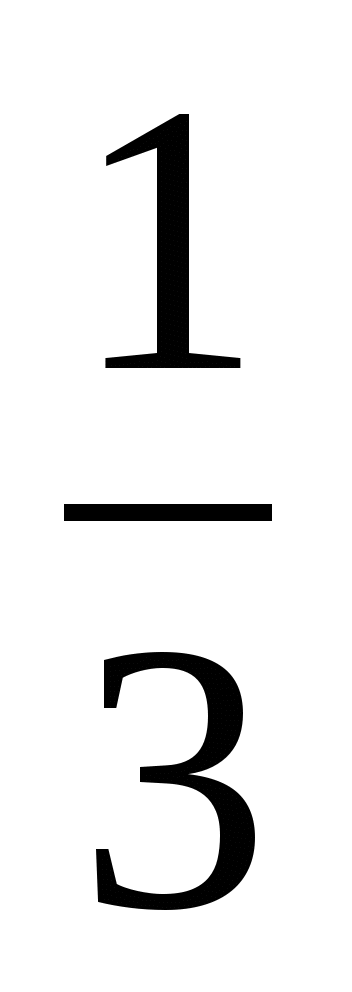 4)
4) 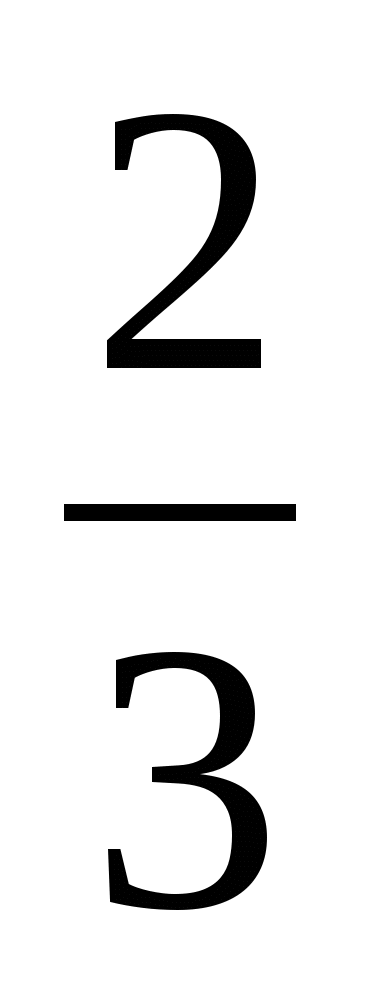
4. 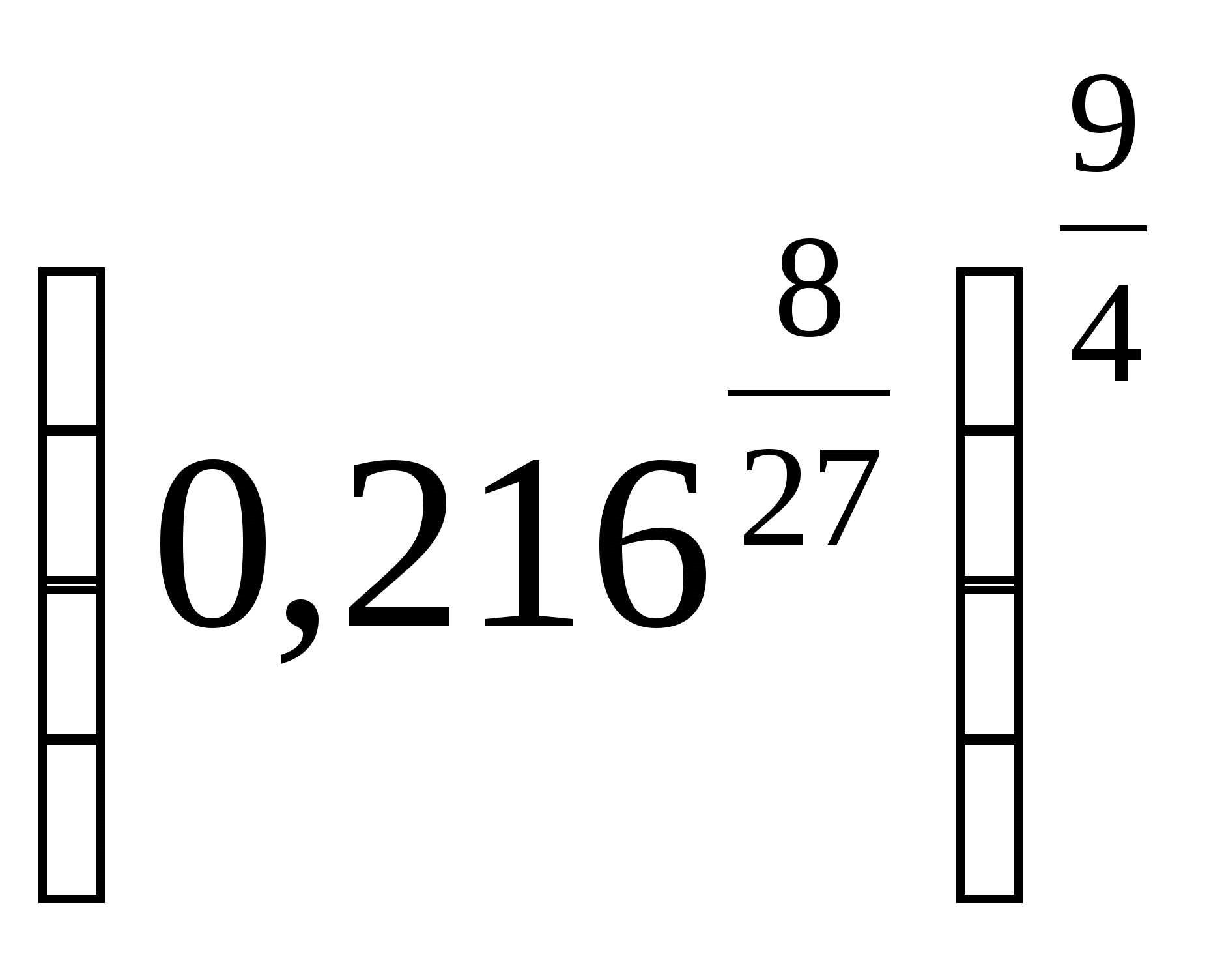
1) 0,36 2) 3,6 3) 0,6 4) 0,18
5. 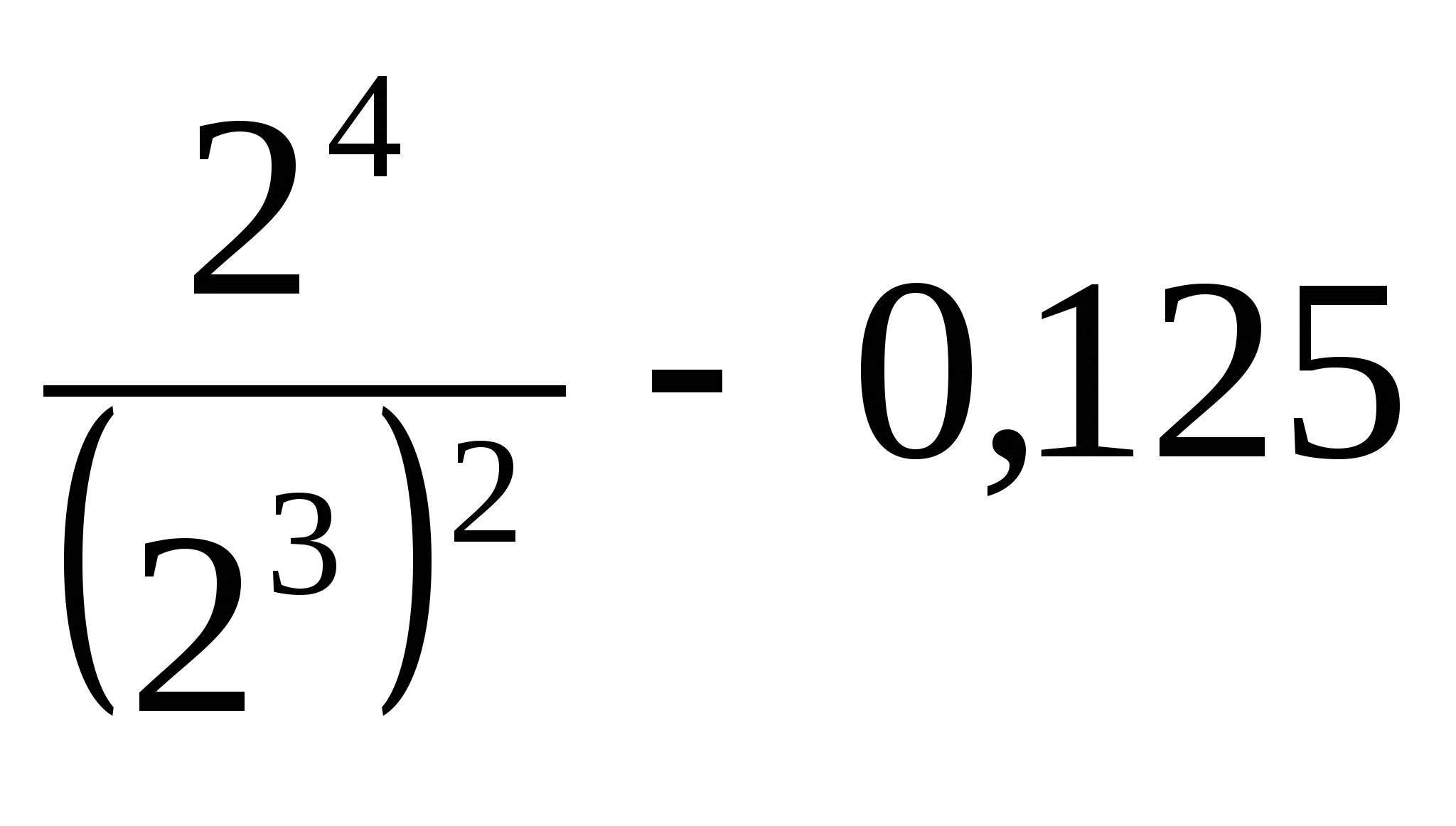
1) 0,125 2) — 0,75 3) — 0,1 4) — 1,5
6. 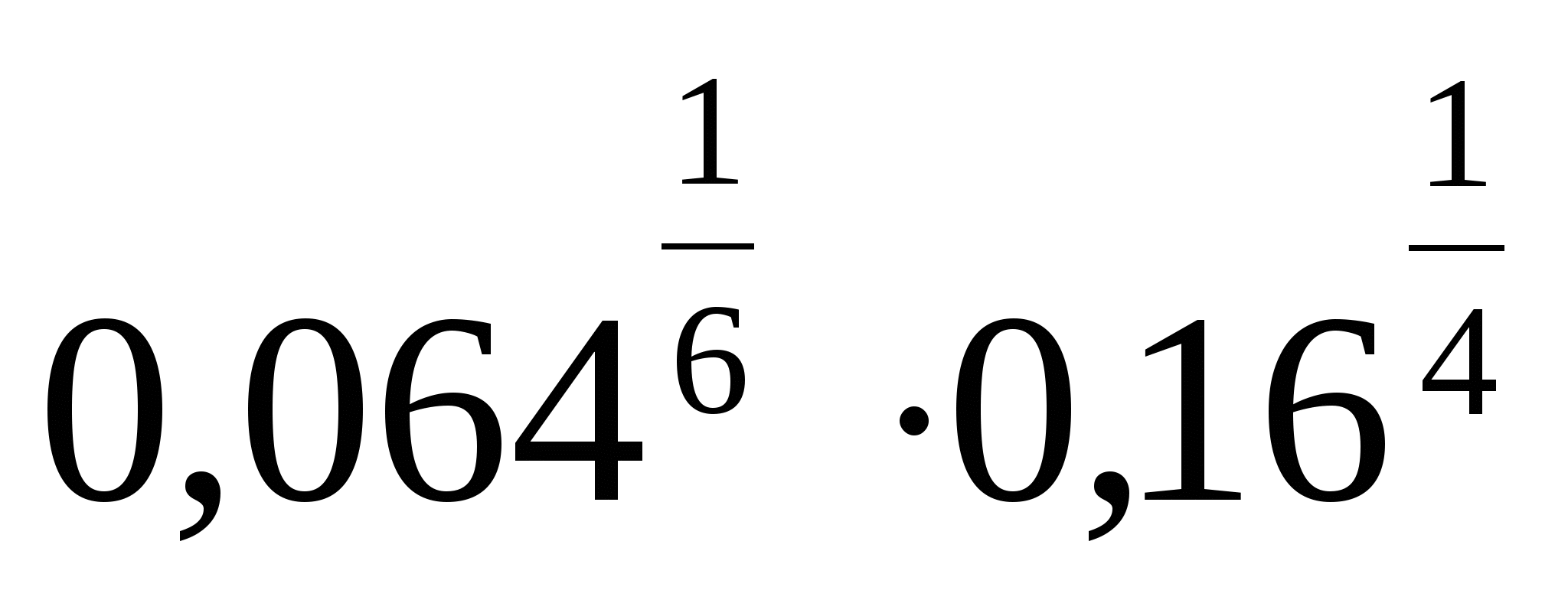
1) 0,04 2) 0,4 3) 0,2 4) 0,8
7. 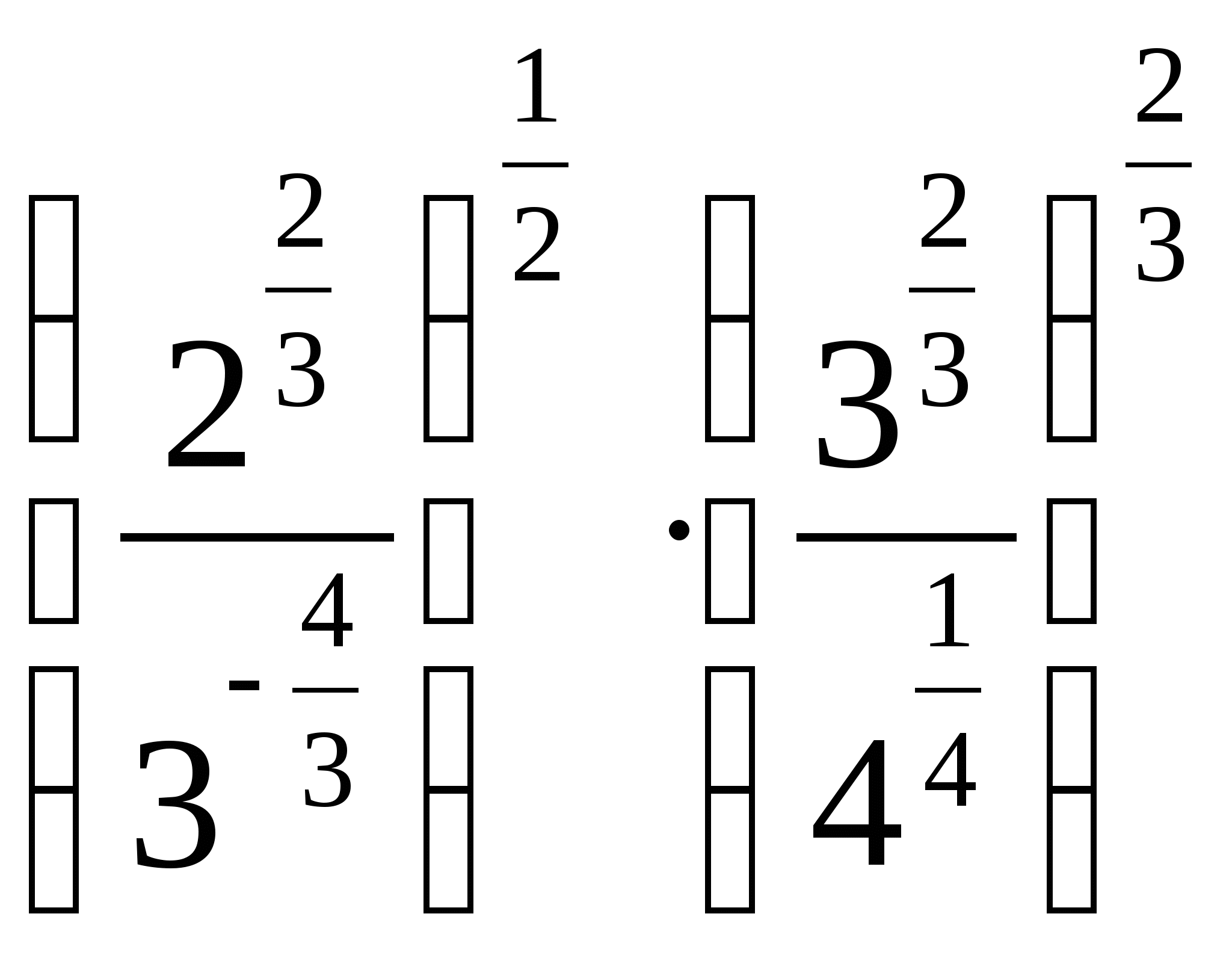
1) 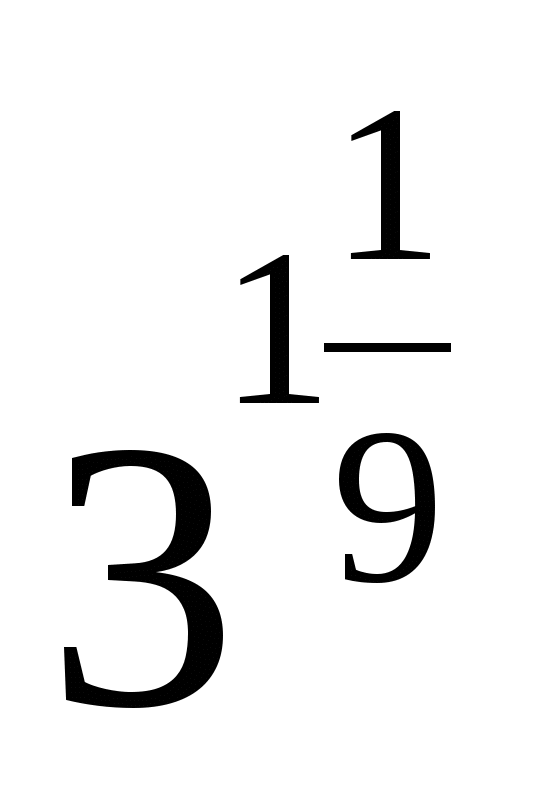 2)
2) 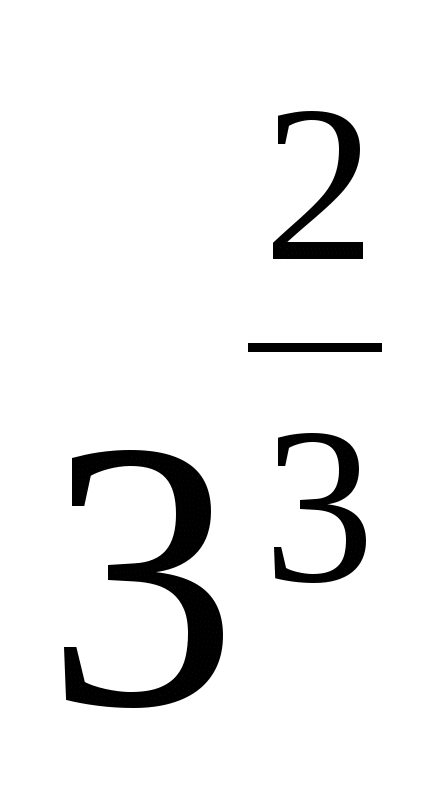 3)
3) 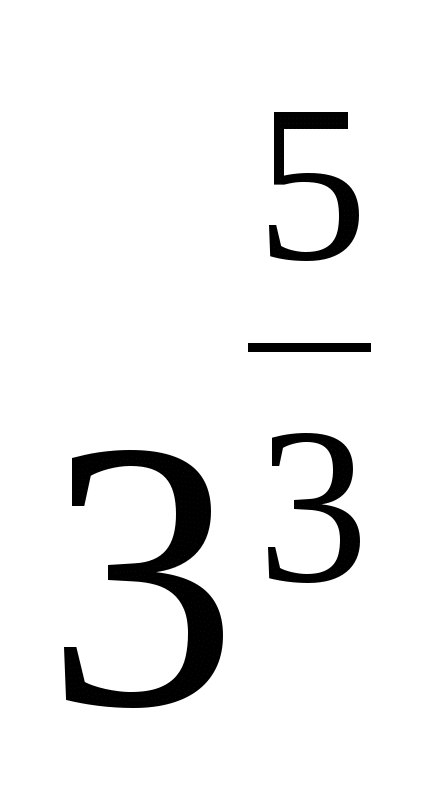 4) 3
4) 3
8. 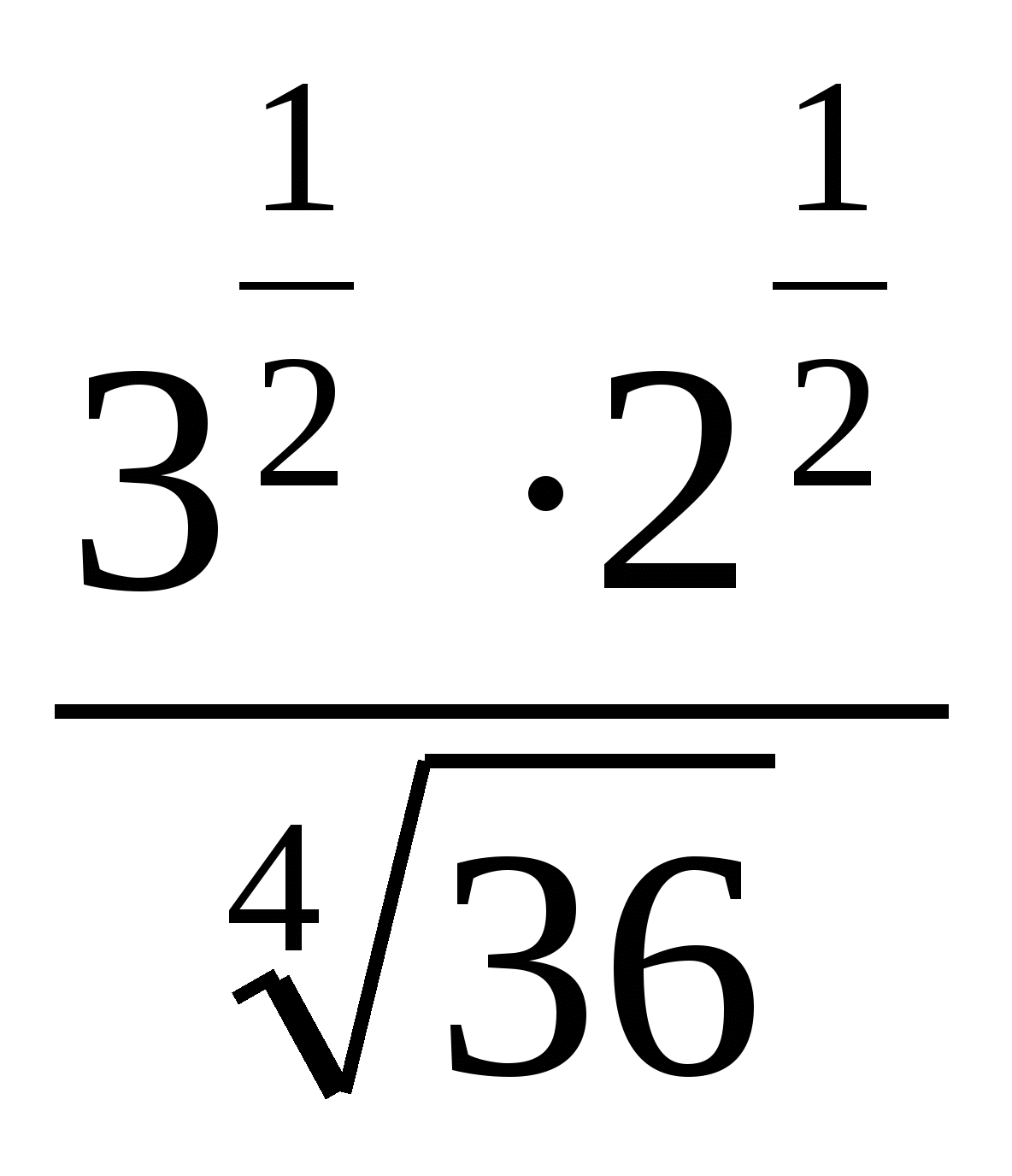
1) 1 2) 2 3) 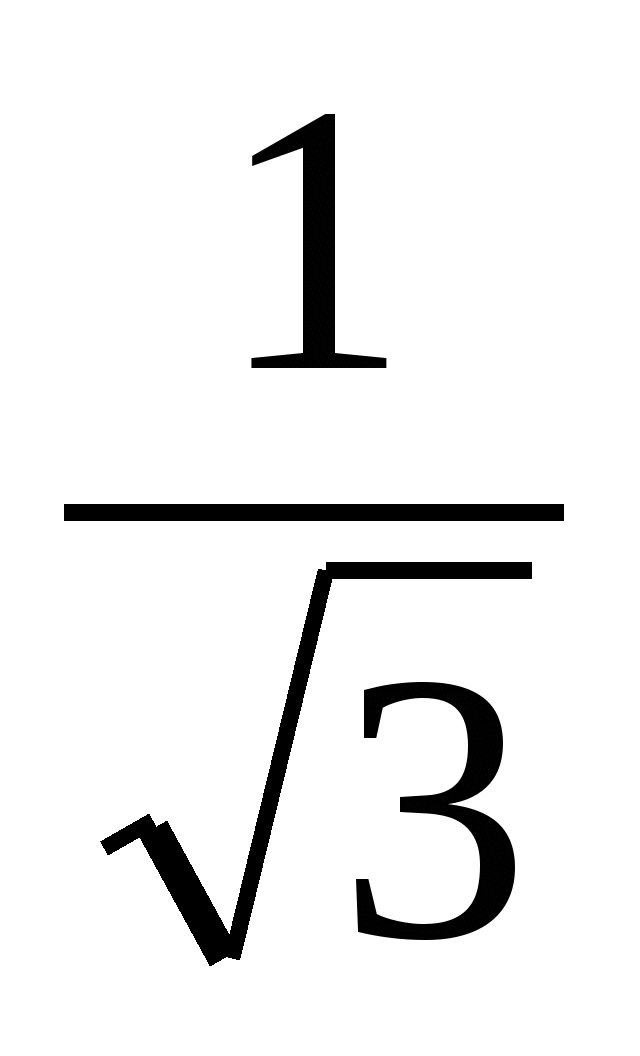 4)
4) 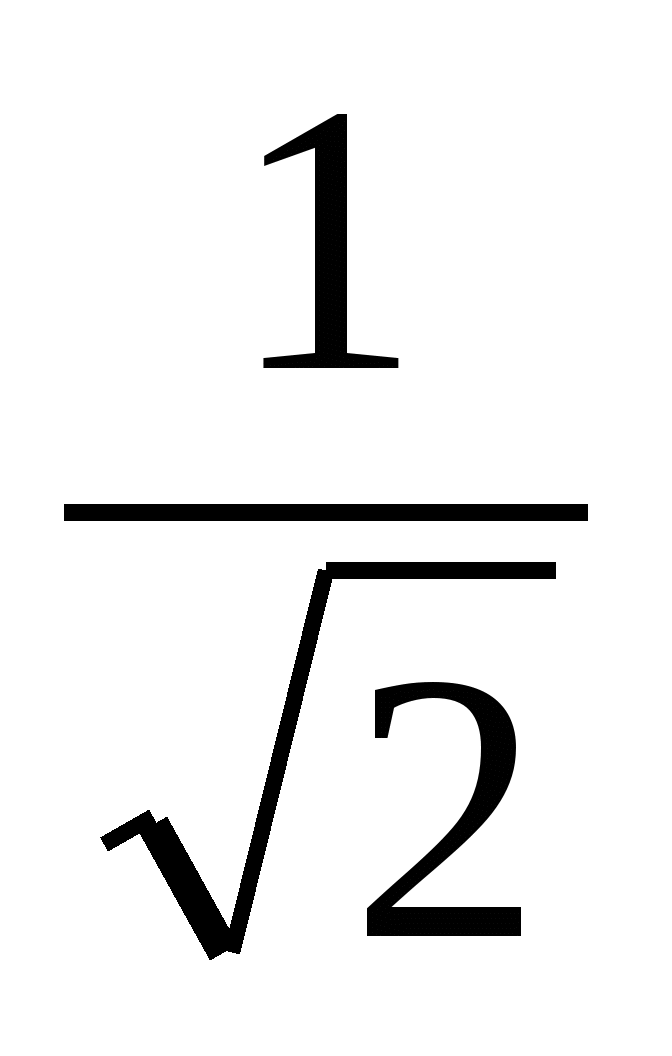
9. 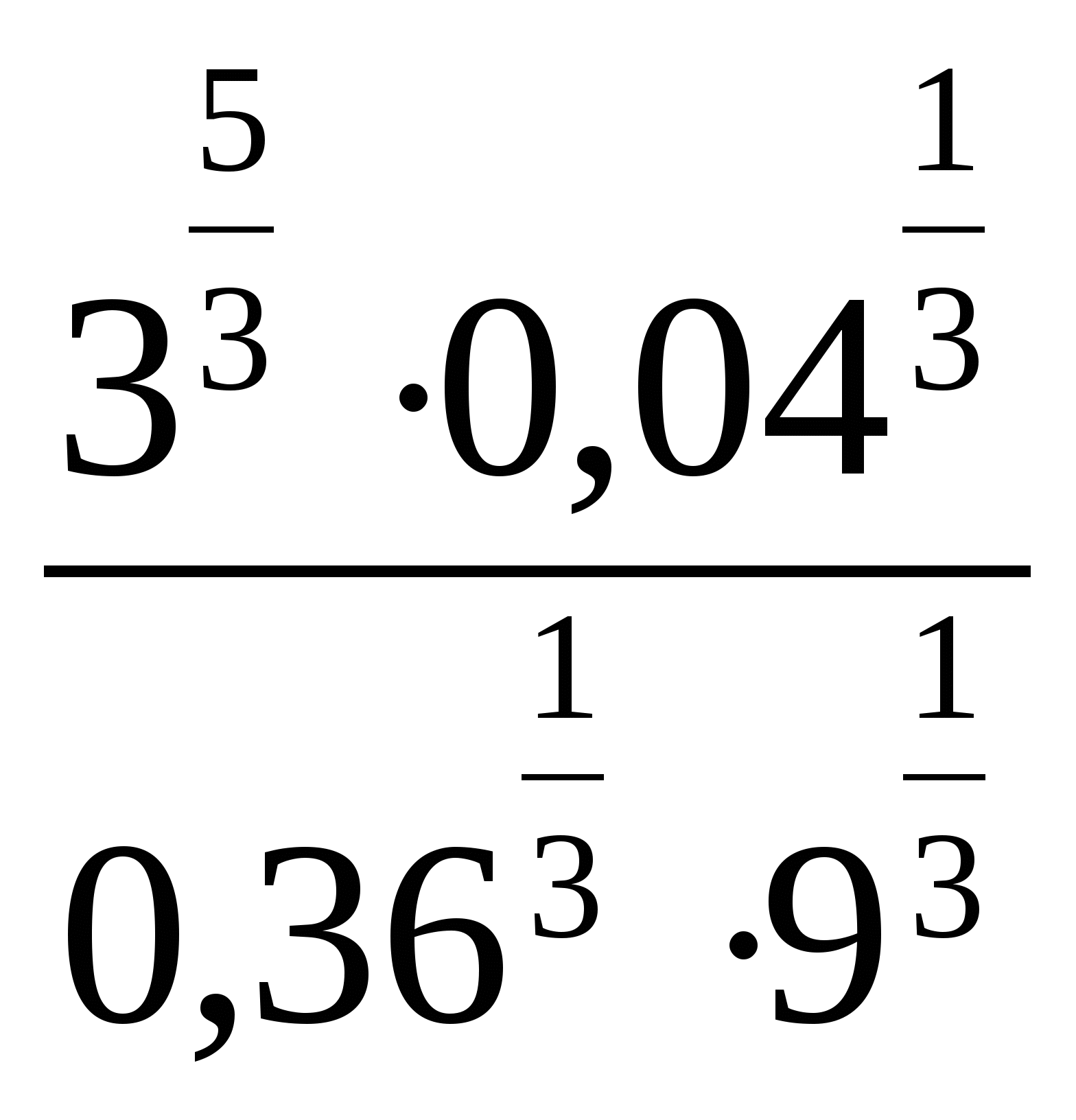
1) 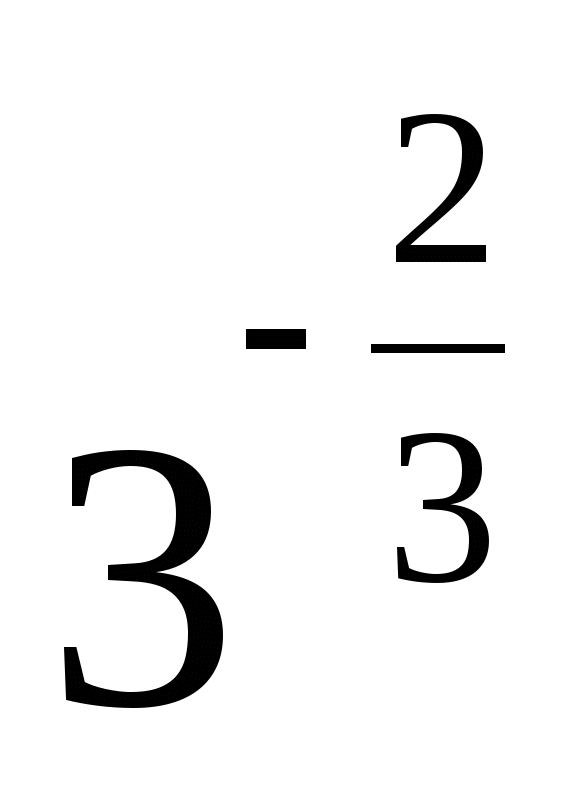 2)
2) 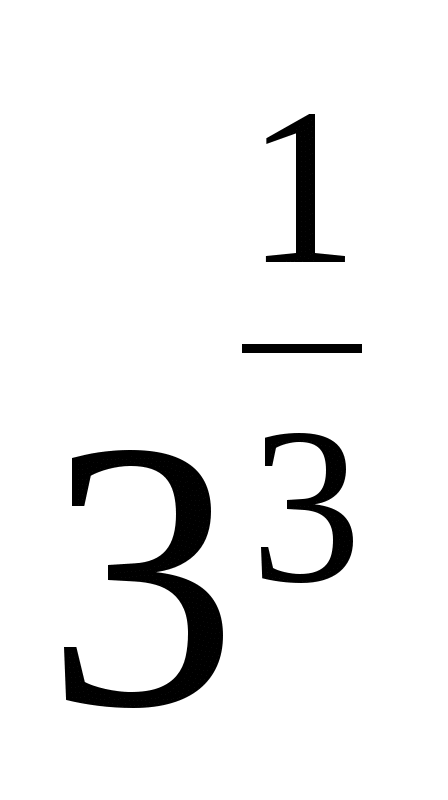 3)
3) 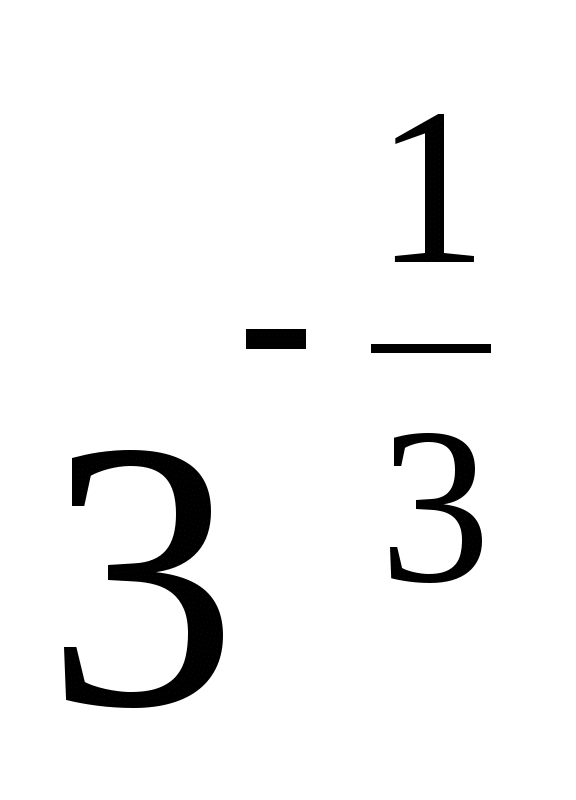 4)
4) 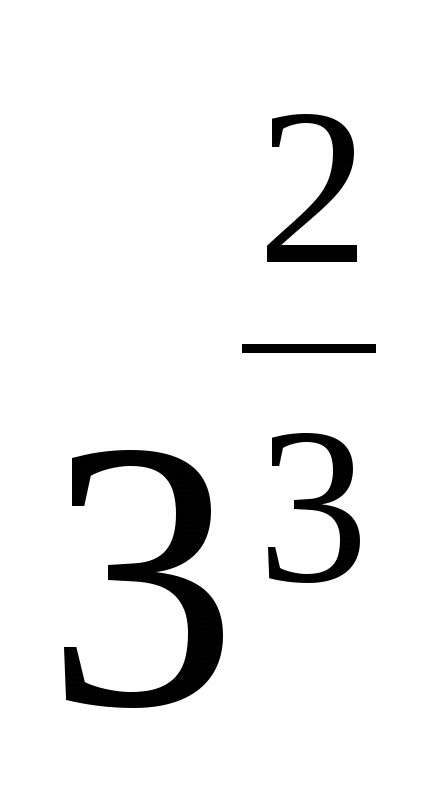
10. 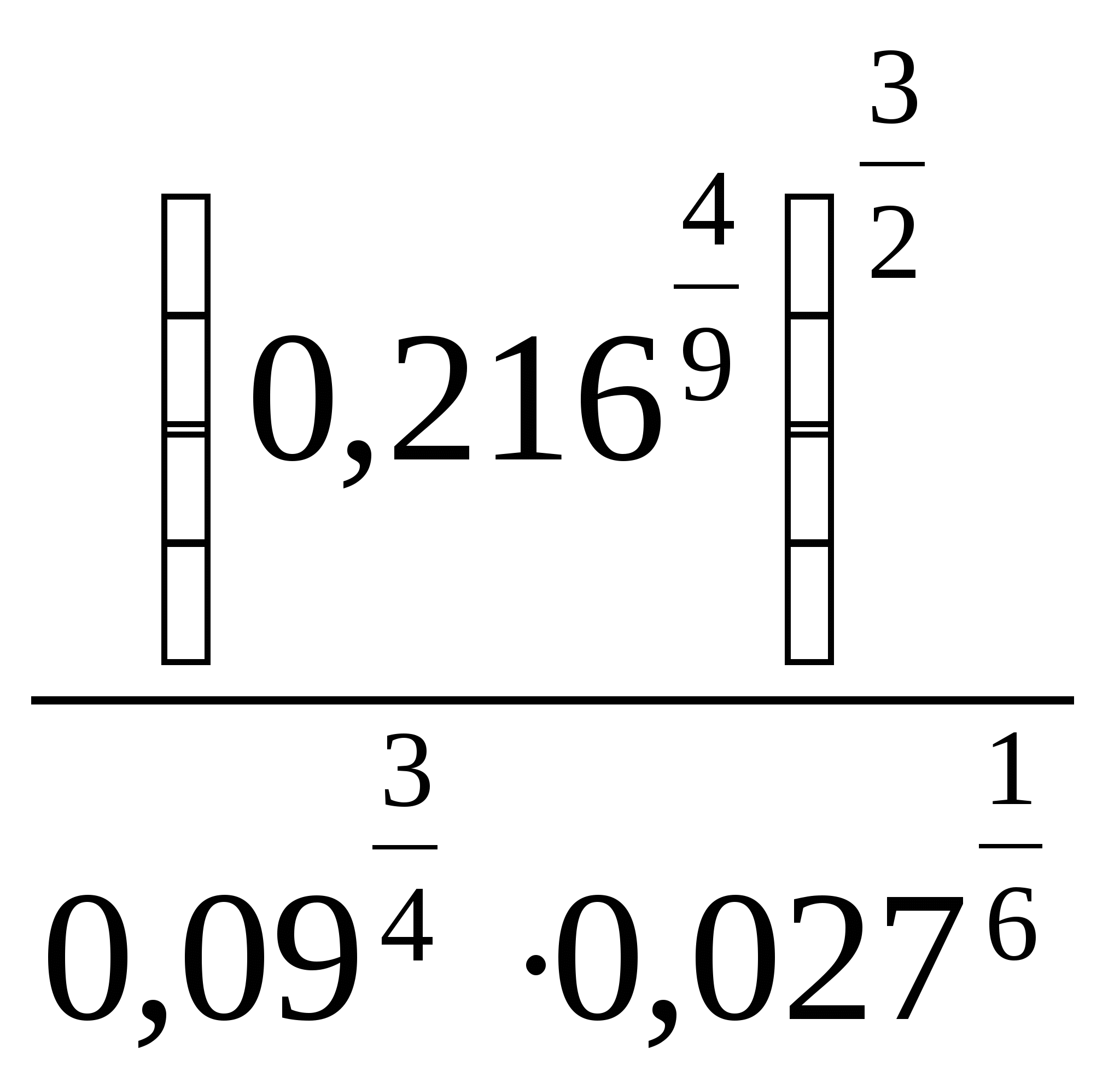
1) 0,04 2) 0,4 3) 4 4) 0,16
11. 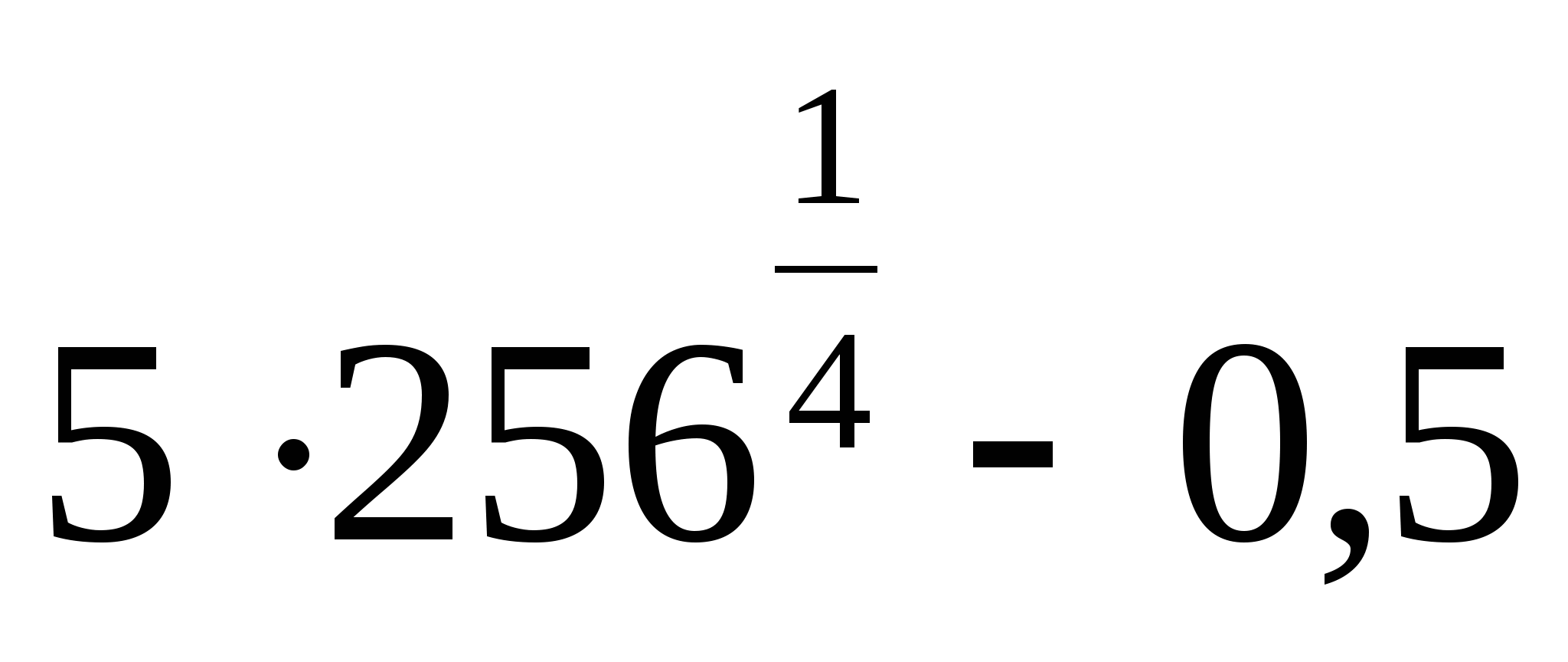
1) 20,5 2) 256,5 3) 19,5 4) 79,5
12. 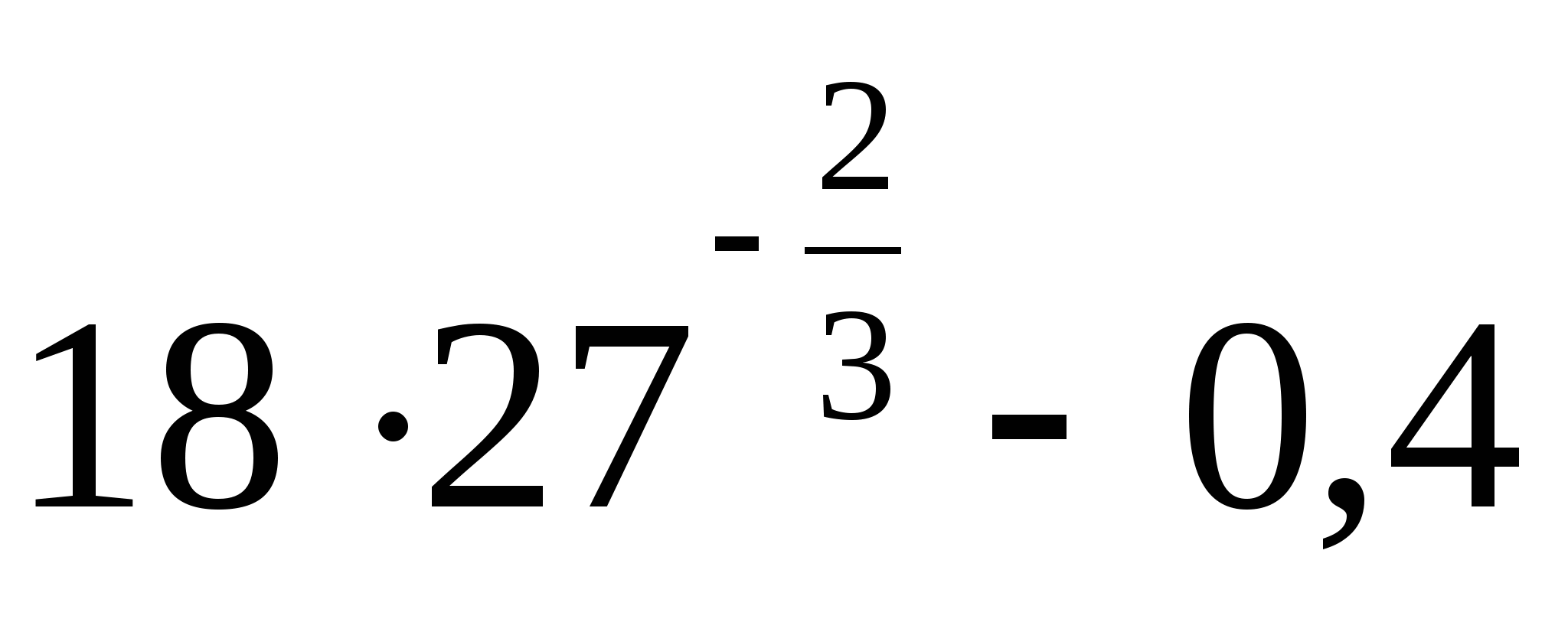
1) 1,6 2) 161,6 3) 2,6 4) 5,6
13. 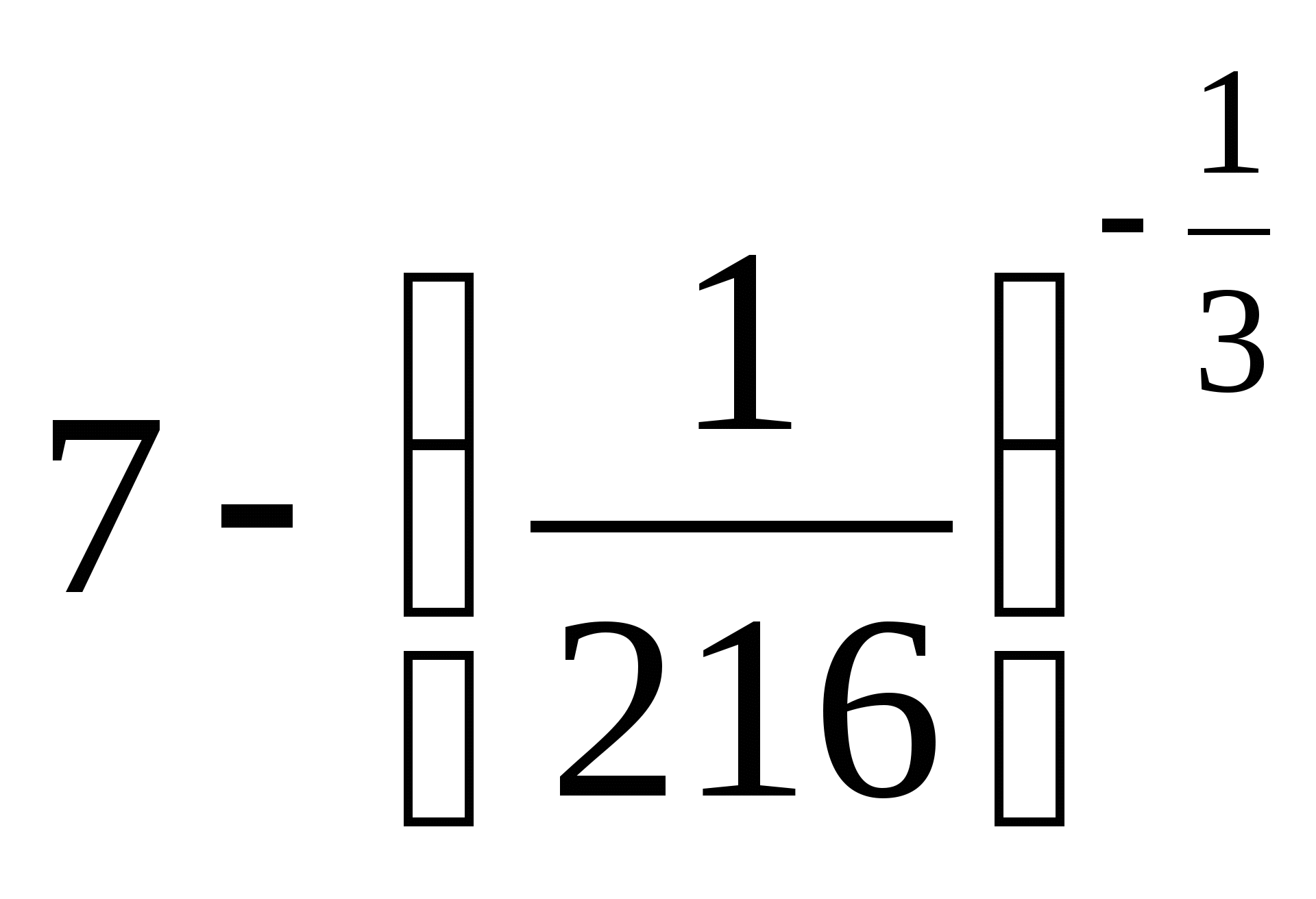

1) 0 2) 1 3) 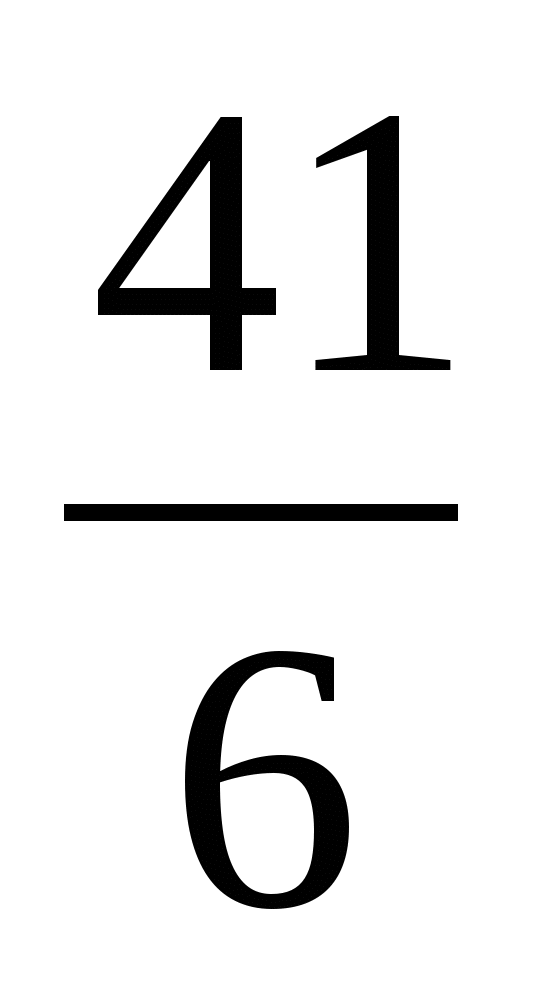 4) 4
4) 4
14. 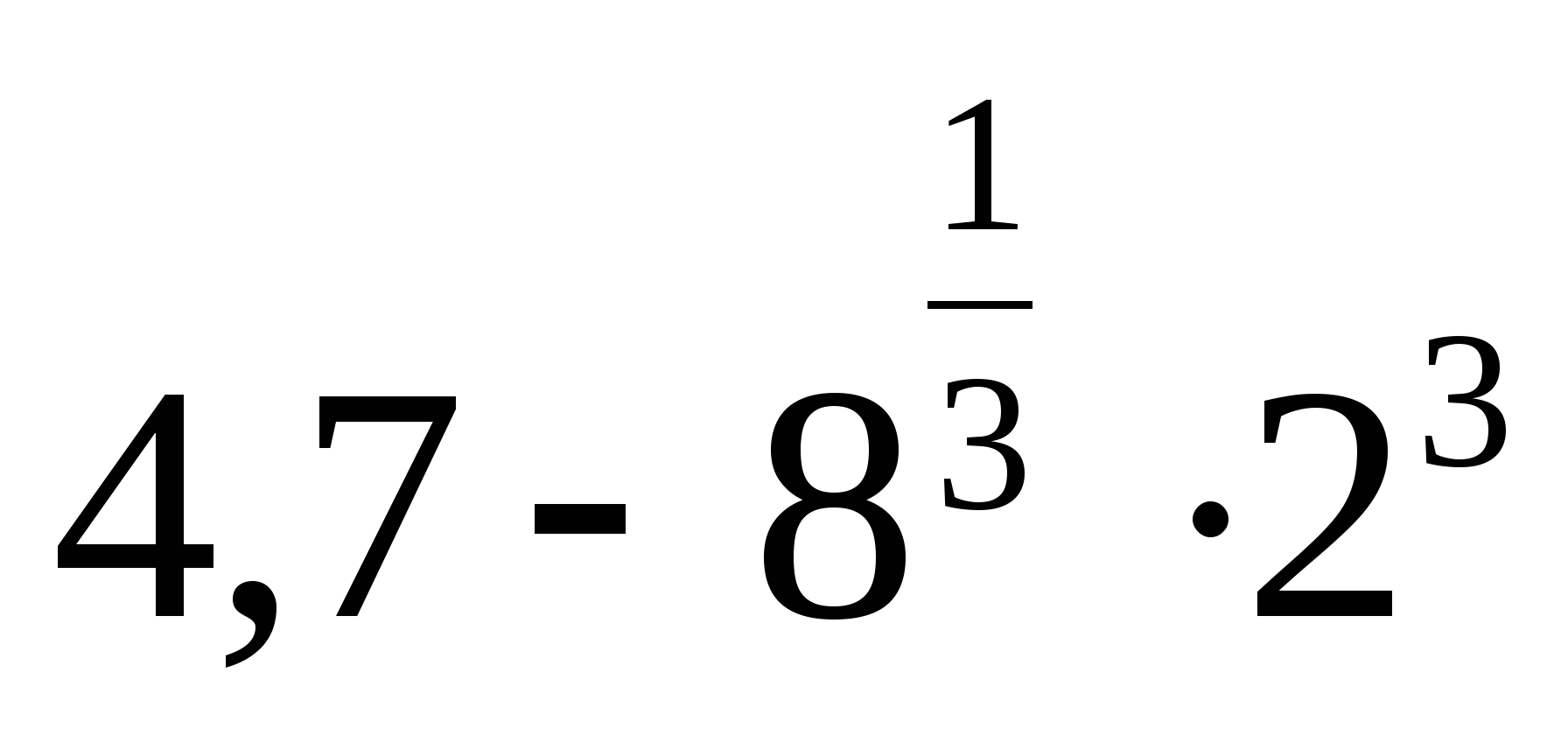
1) -11,3 2) 5,3 3) — 7,3 4) 11,3
15. 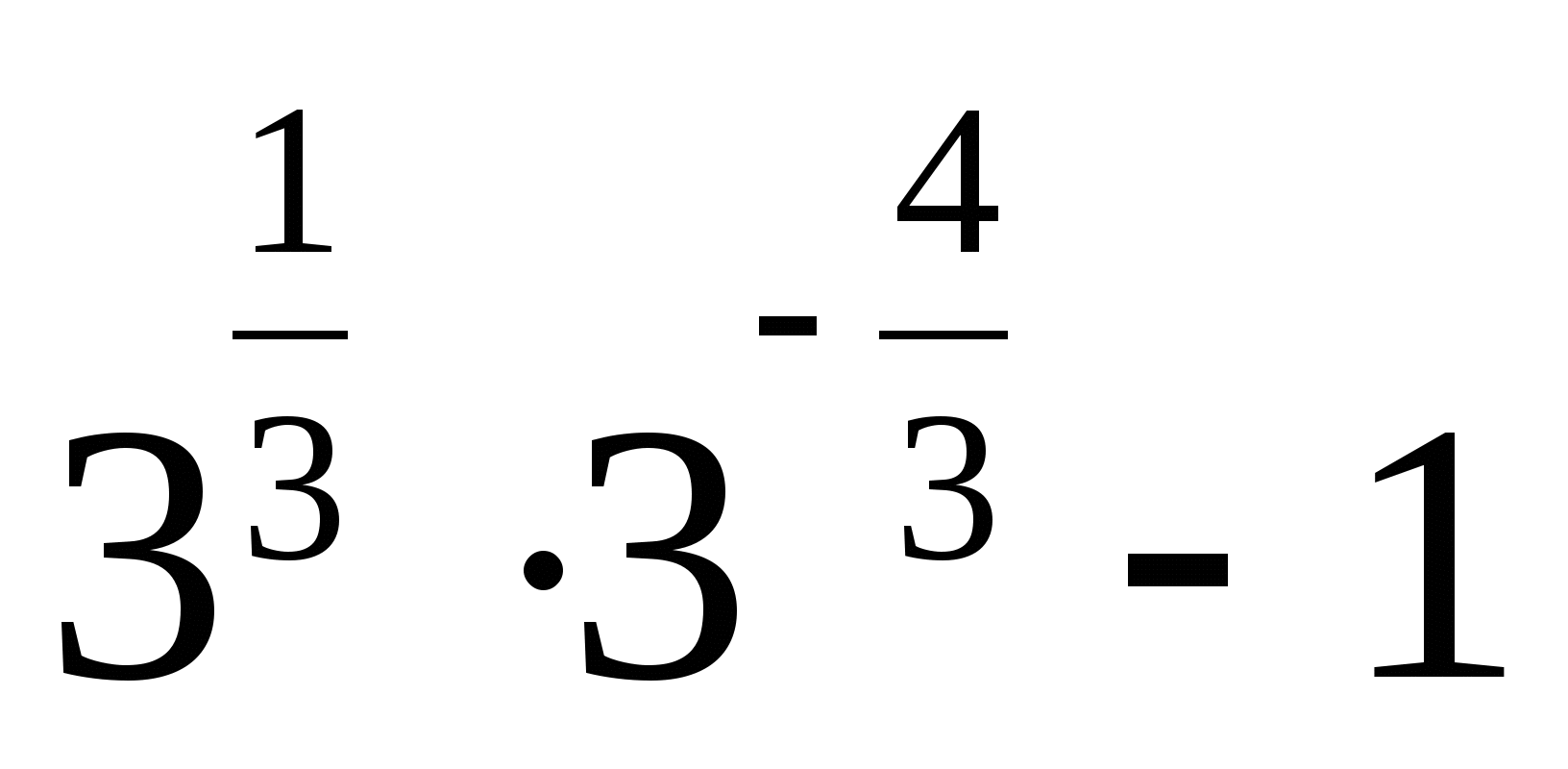
1) 2 2) 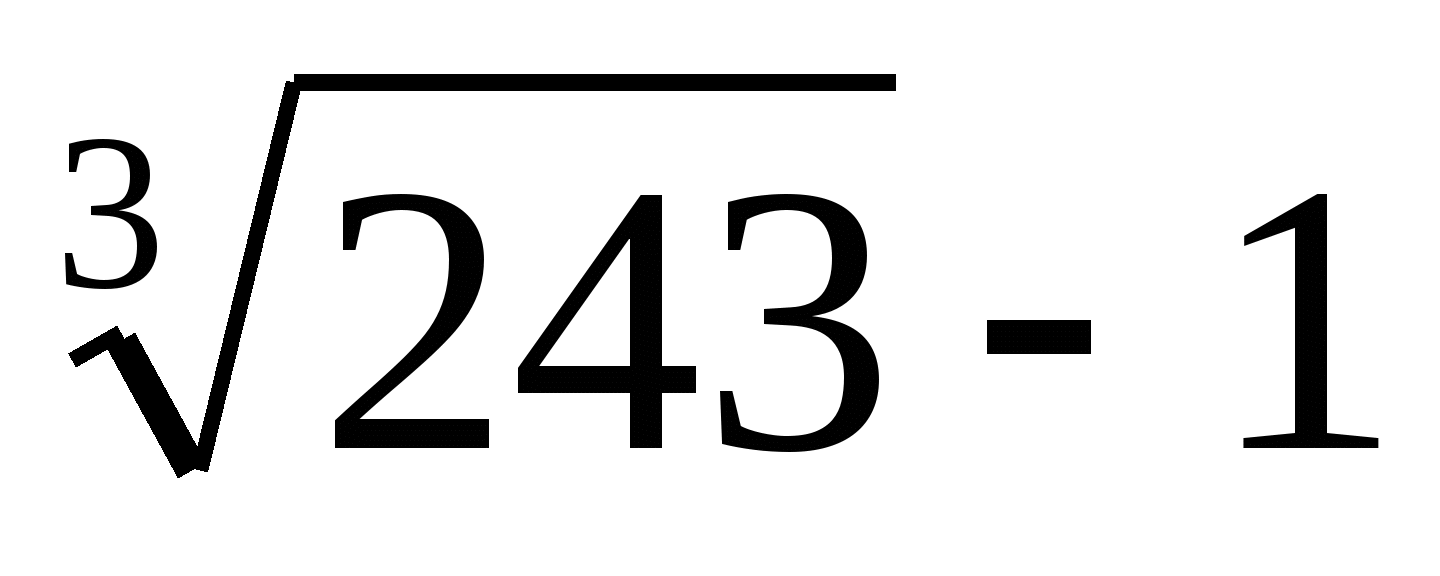 3)
3) 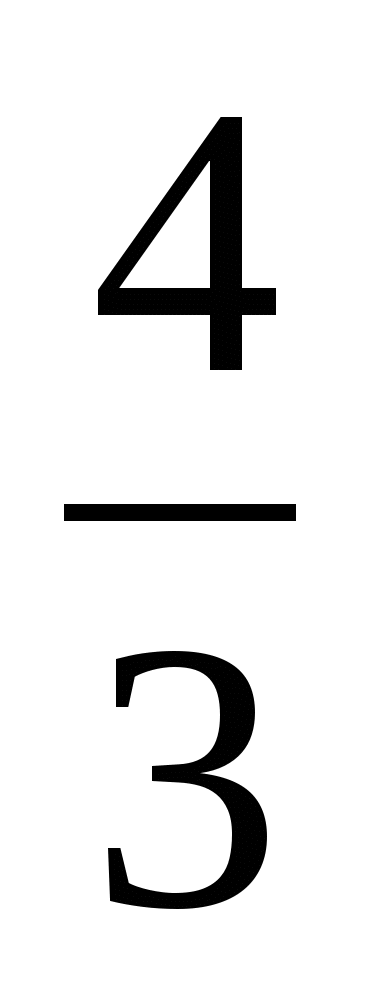 4)
4) 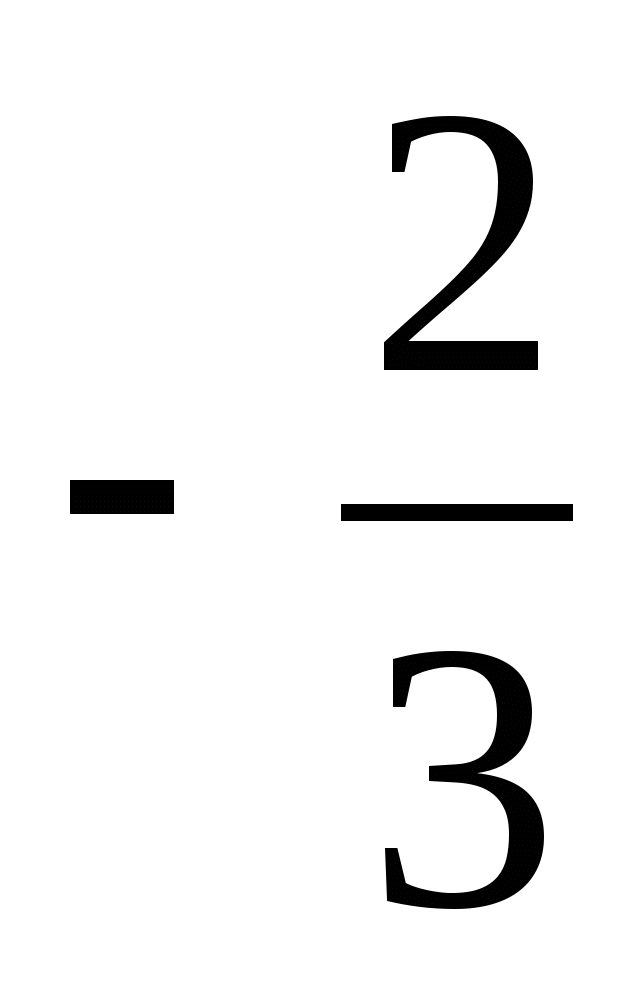
16. 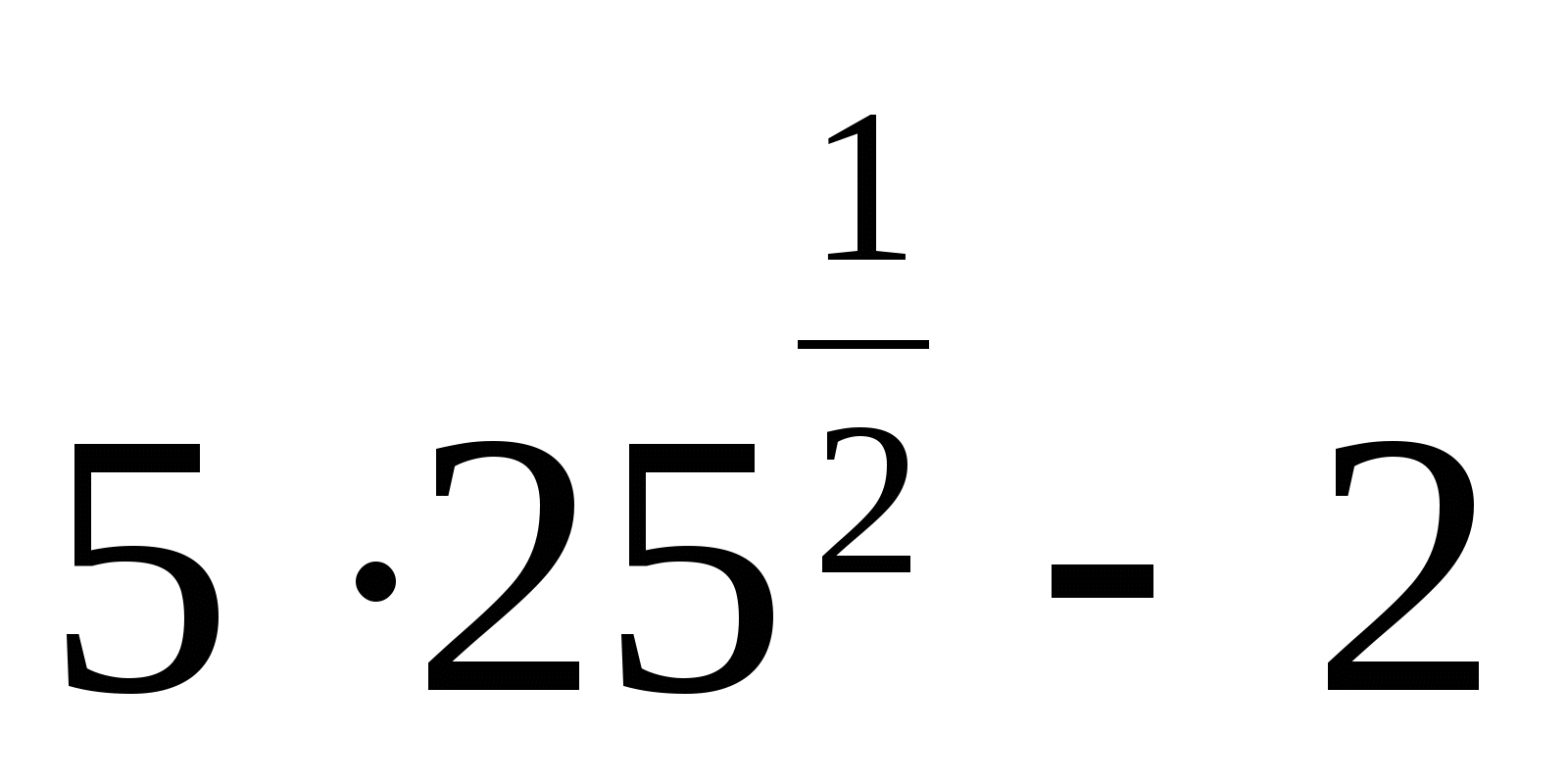
1) 8 2) 23 3) 123 4) 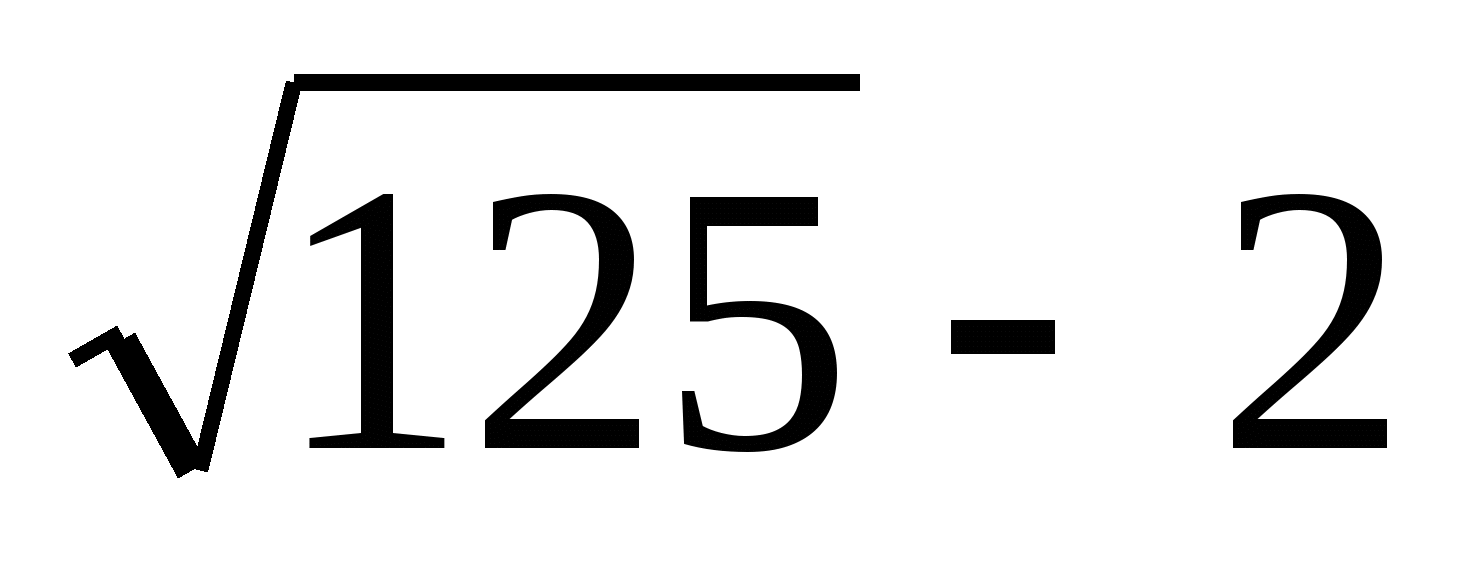
17. 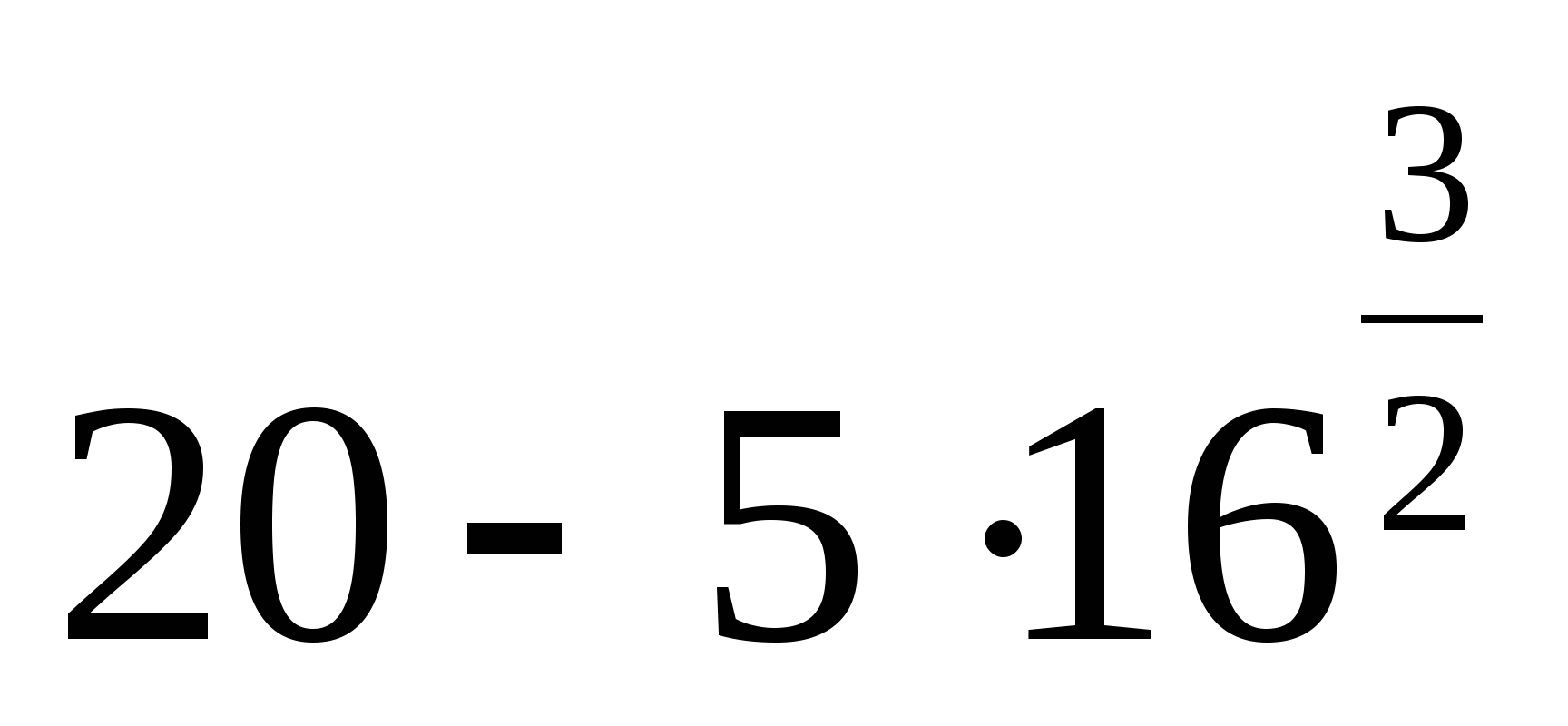
1) 0 2) 10 3) — 20 4) — 300
18. 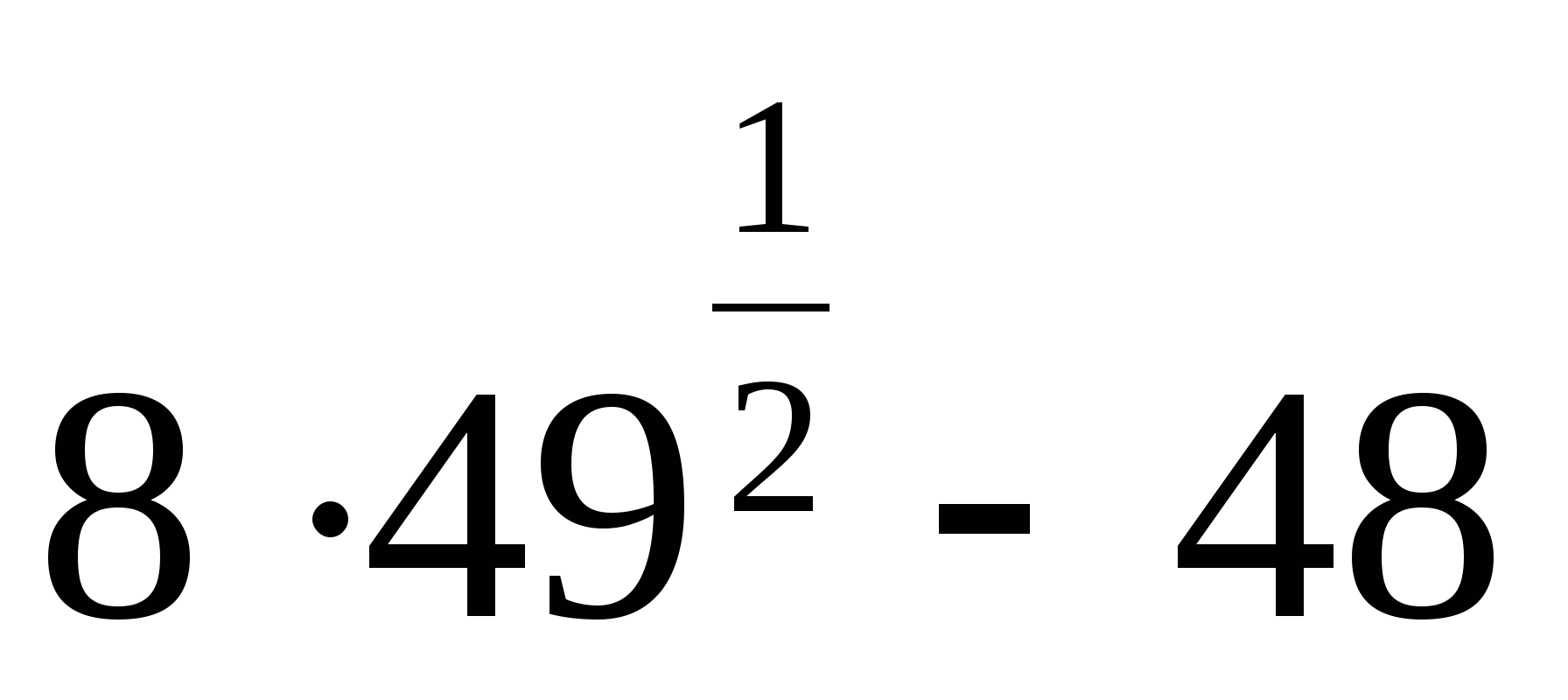
1) 0 2) 1 3) 8 4) 344
19. 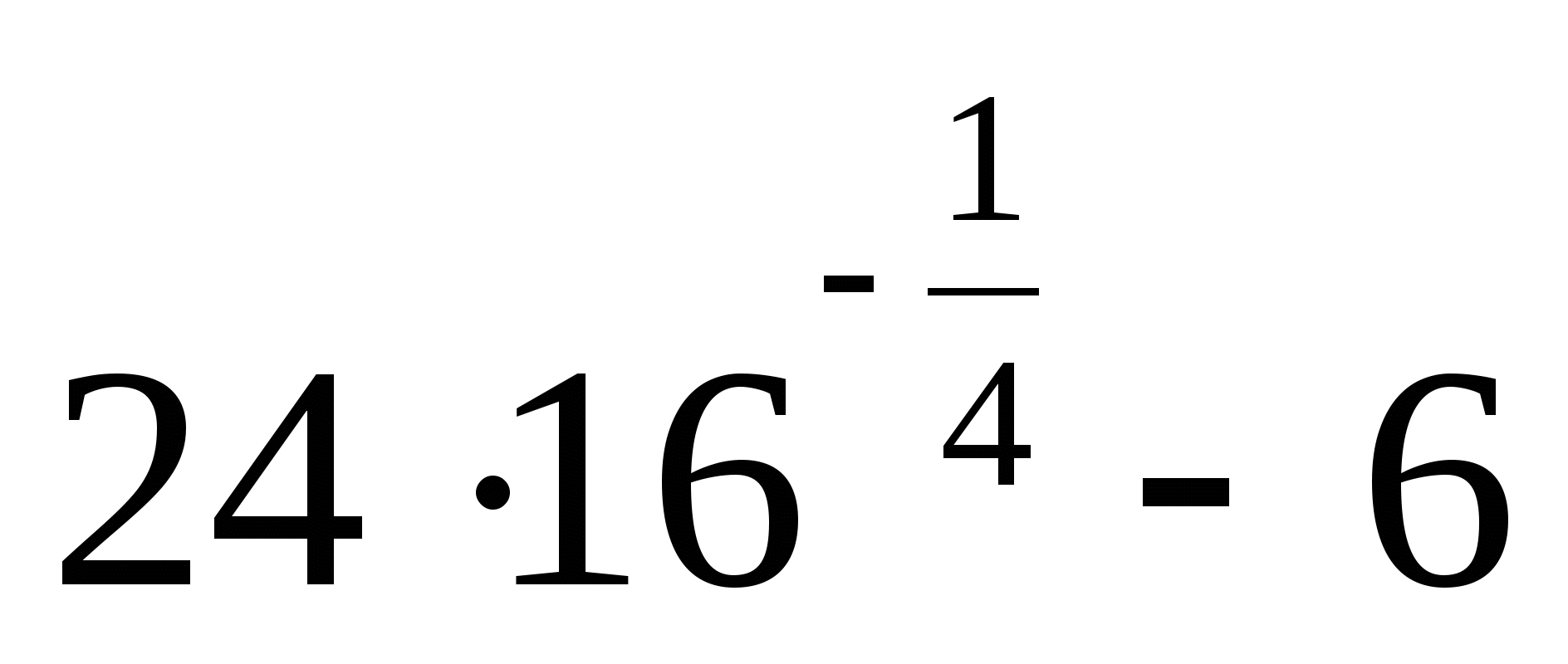
1) 0 2) 6 3) 42 4) 90
20. 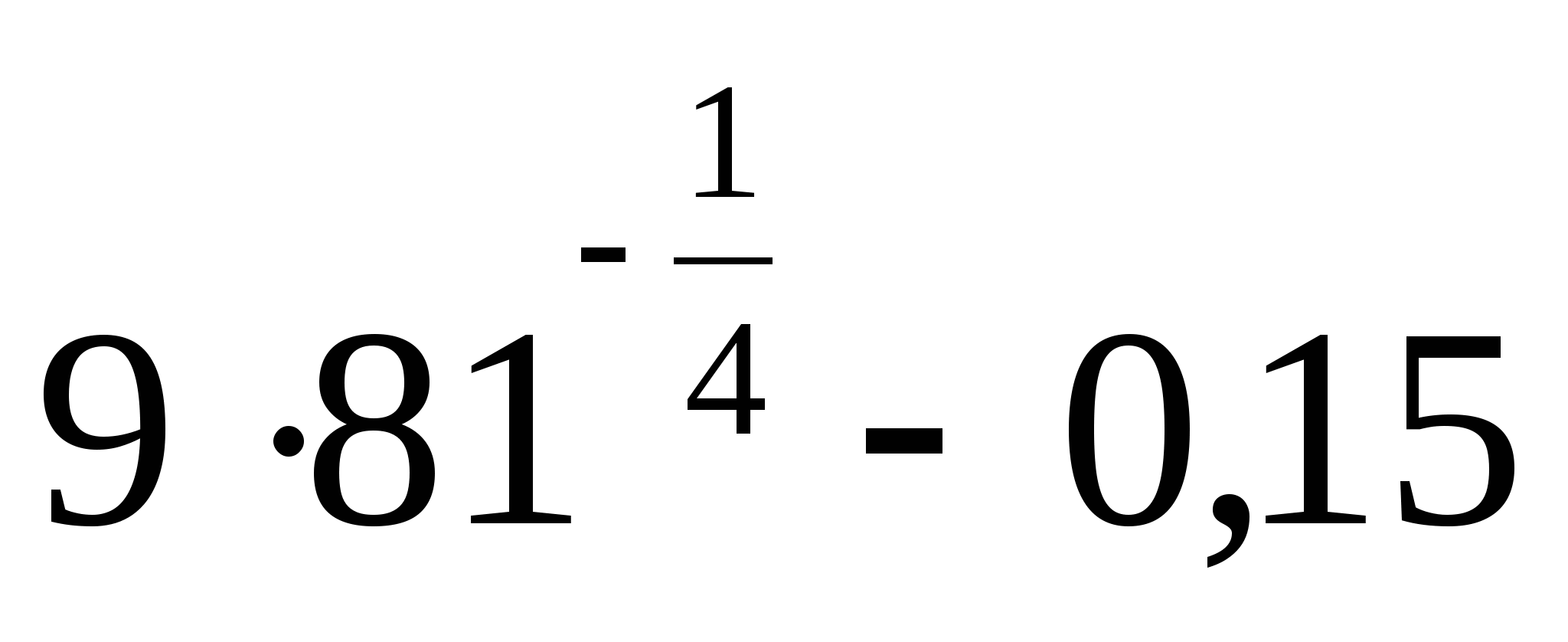
1) -27,15 2) — 81,15 3) 0,85 4) 2,85
21. 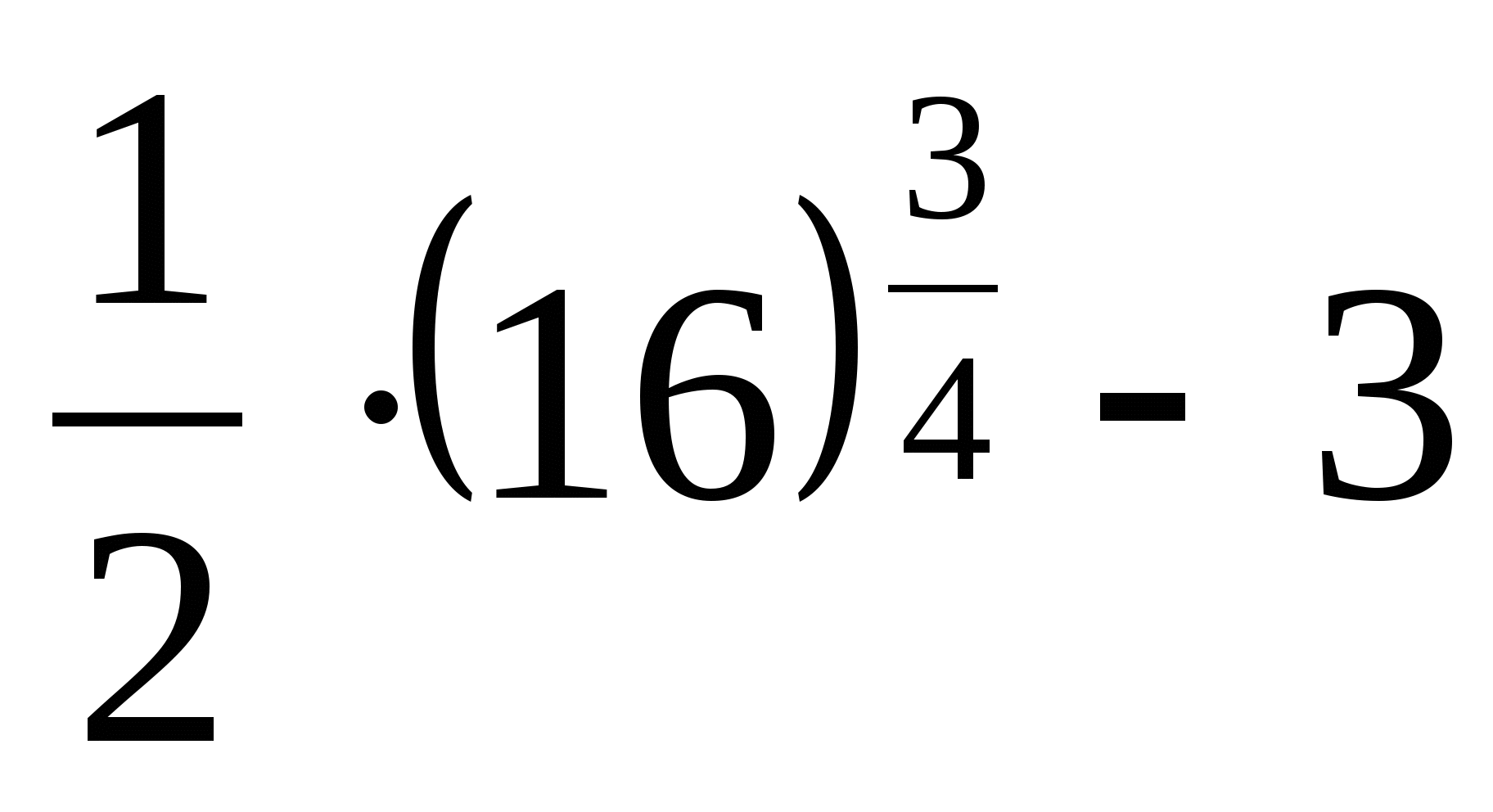
1) — 1 2) 1 3) 5 4) 13
22. 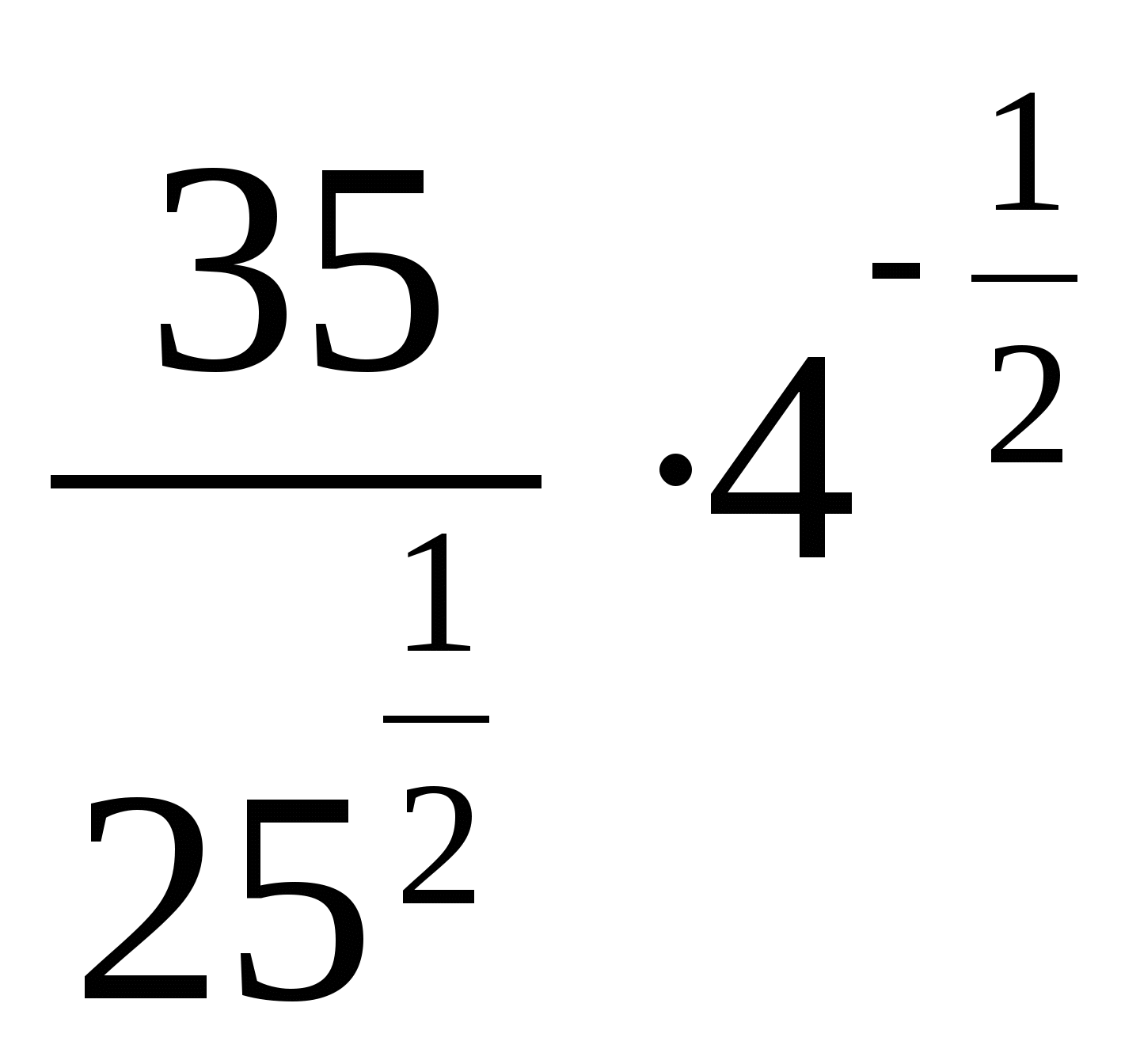
1) 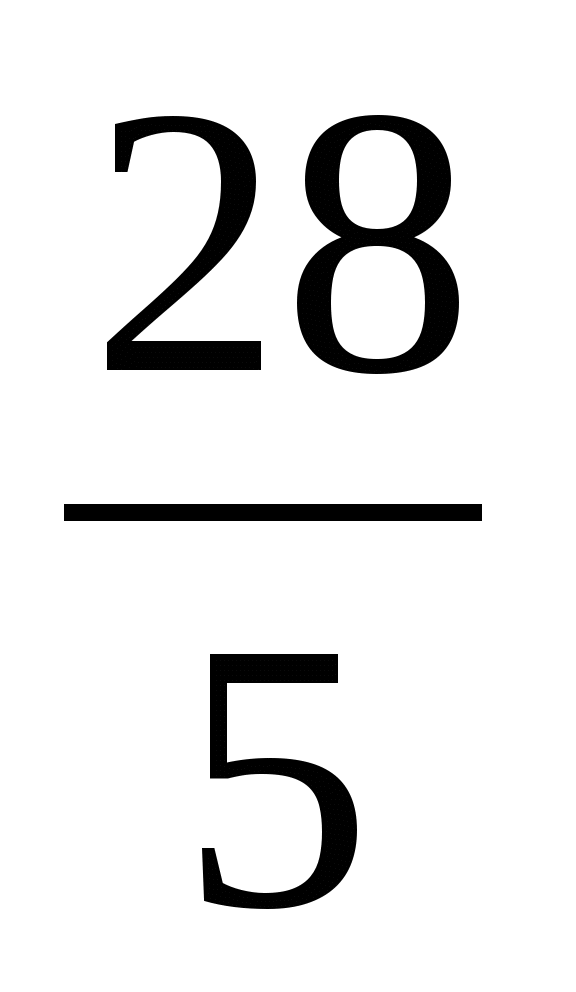 2) 1 3) 3,5 4) 14
2) 1 3) 3,5 4) 14
23. 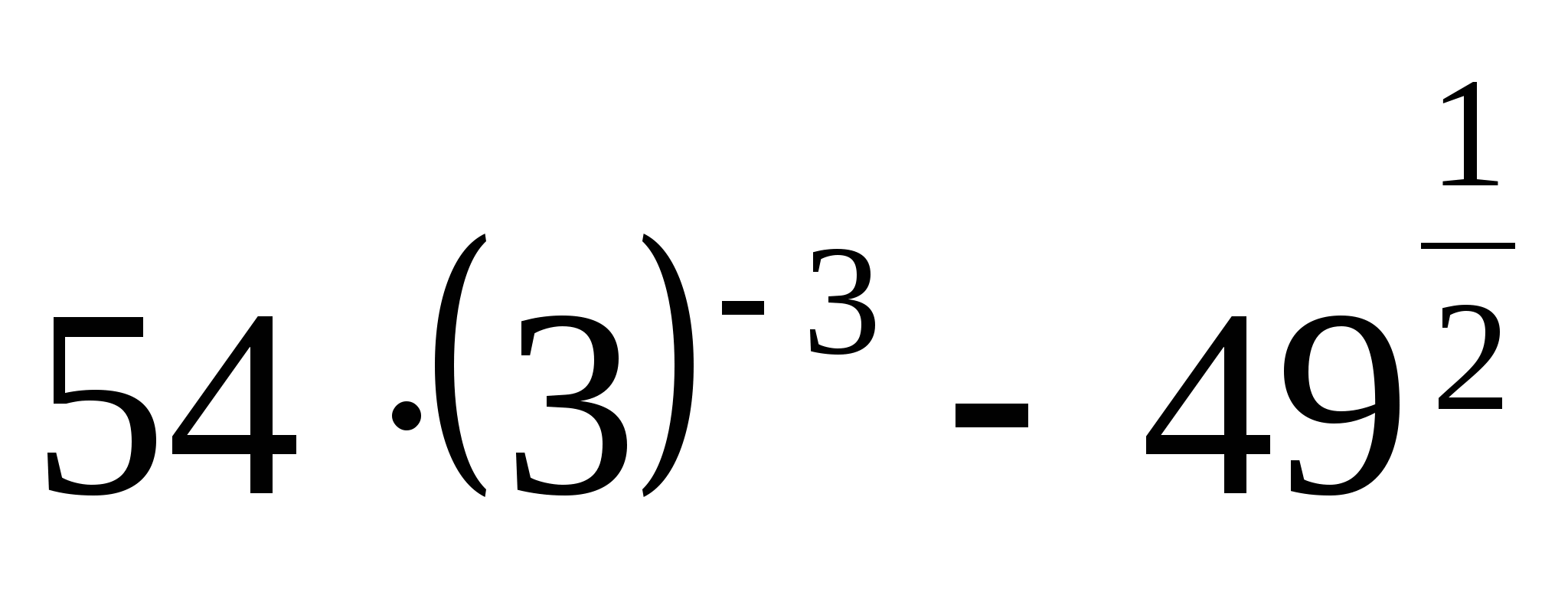
1) — 1 2) — 5 3) 5 4) 113
24. 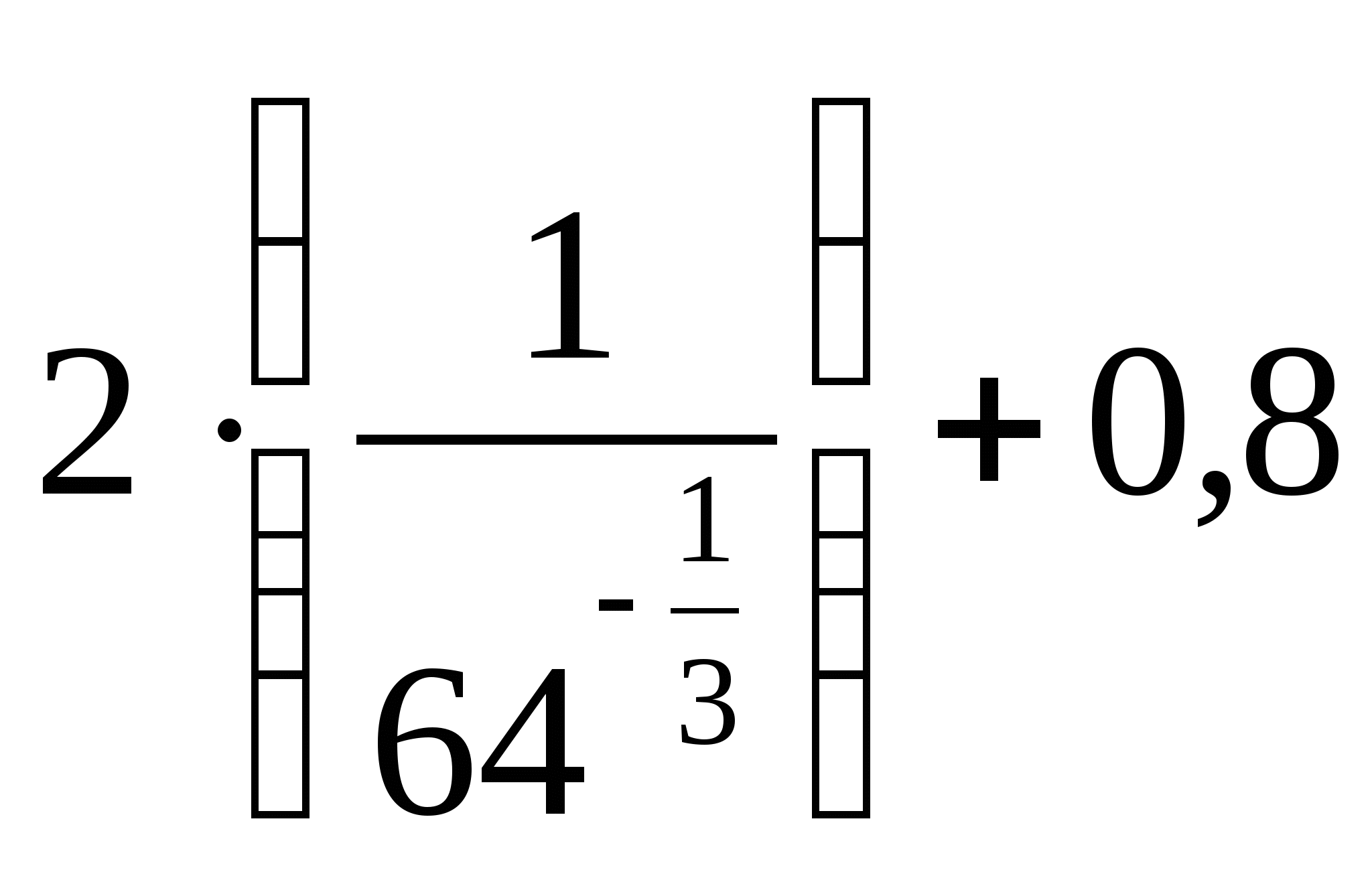
1) 1,3 2) 5,2 3) 8,8 4) 16,8
25. 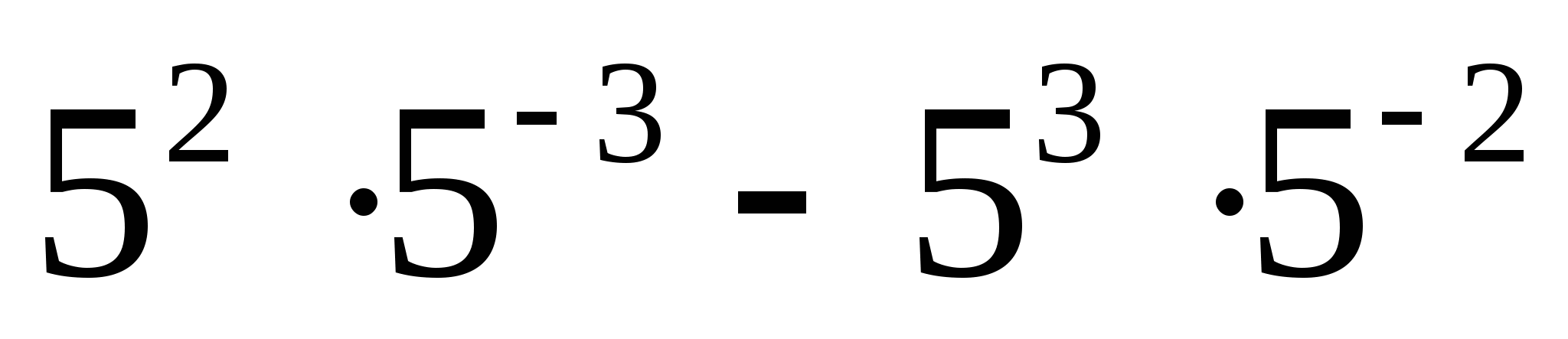
1) — 4,8 2) 0 3) 6200 4) — 10
26. 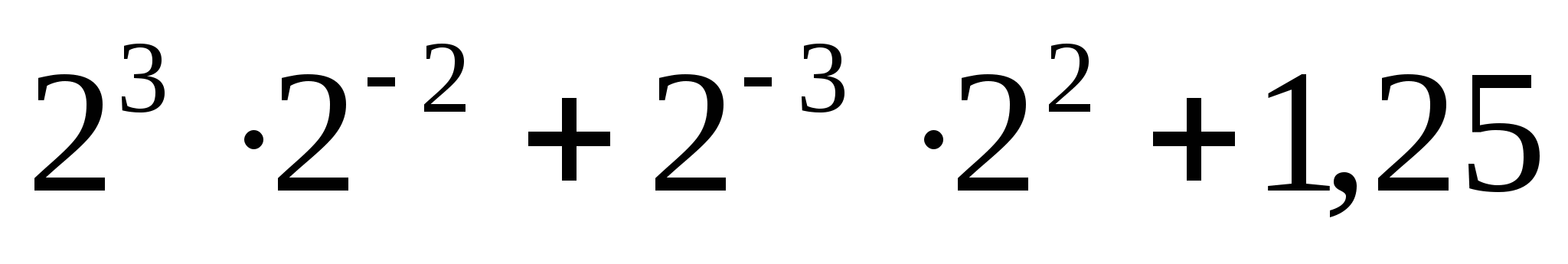
1) 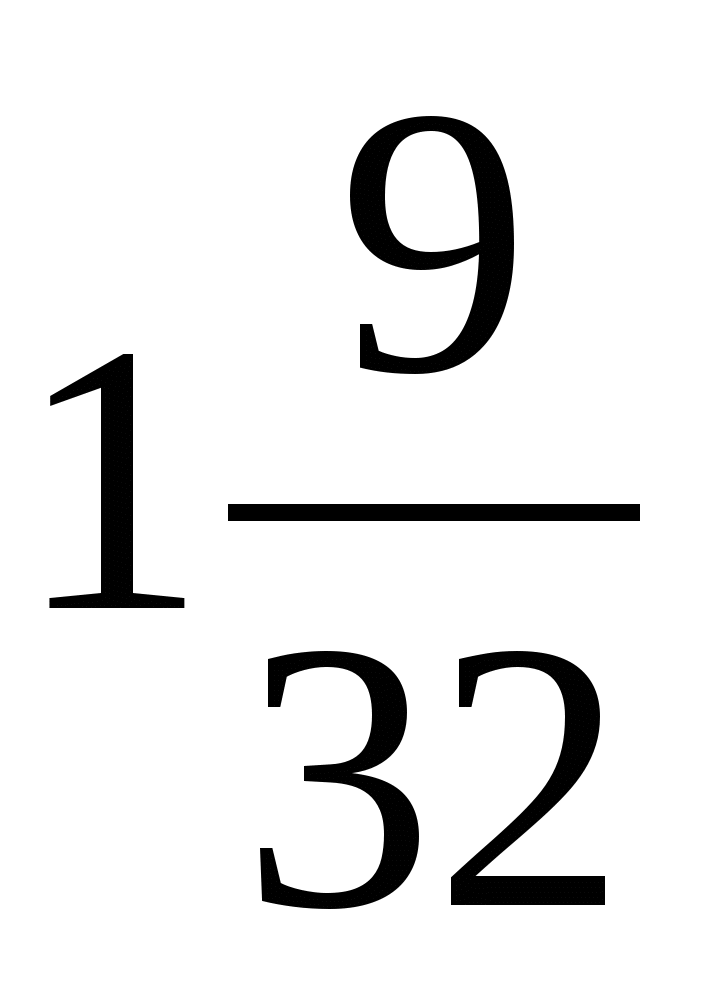 2) 2,5 3) 3,75 4) 1,25
2) 2,5 3) 3,75 4) 1,25
27. 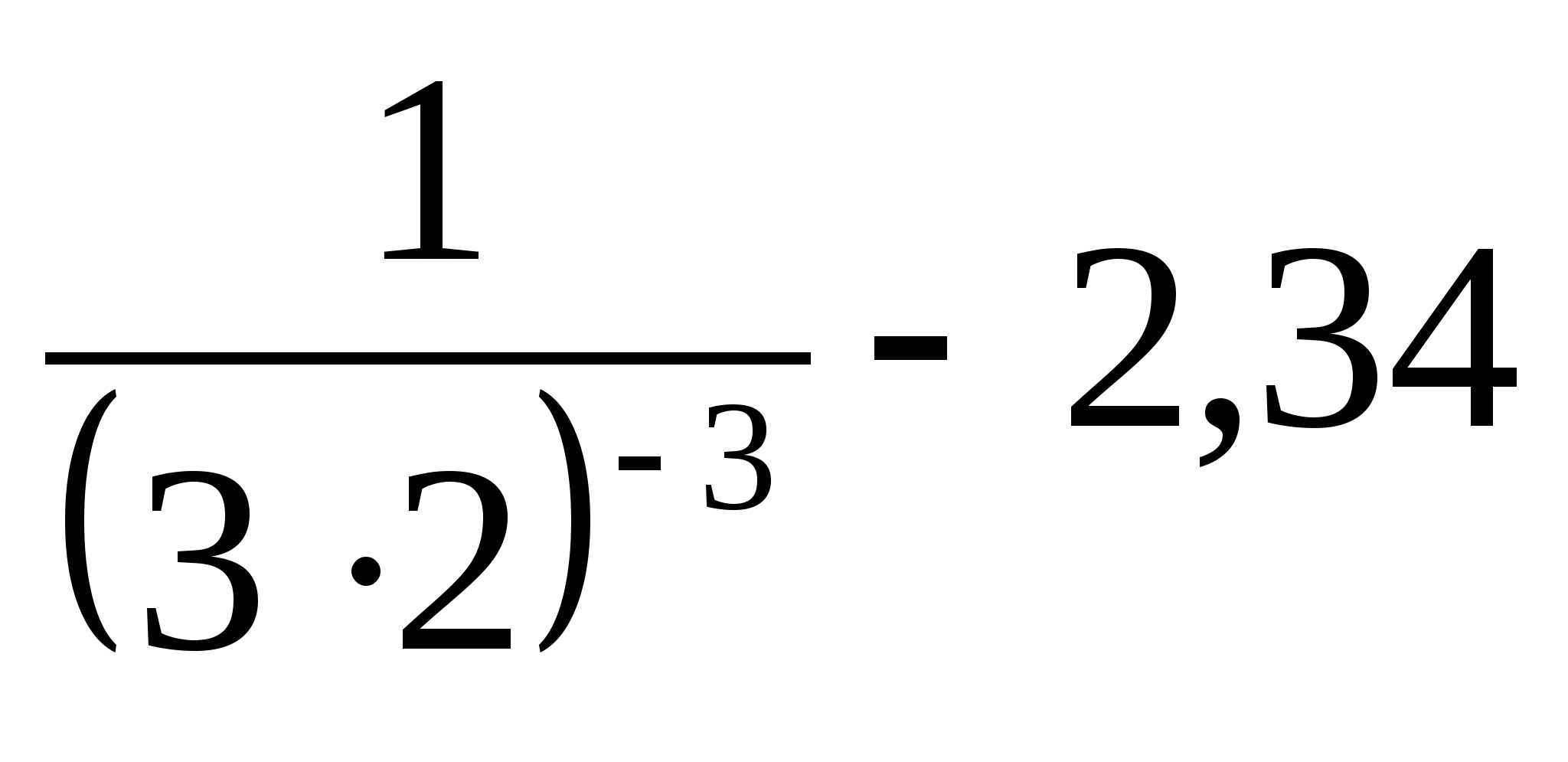
1) 213,66 2) 122,66 3) -2,332 4) 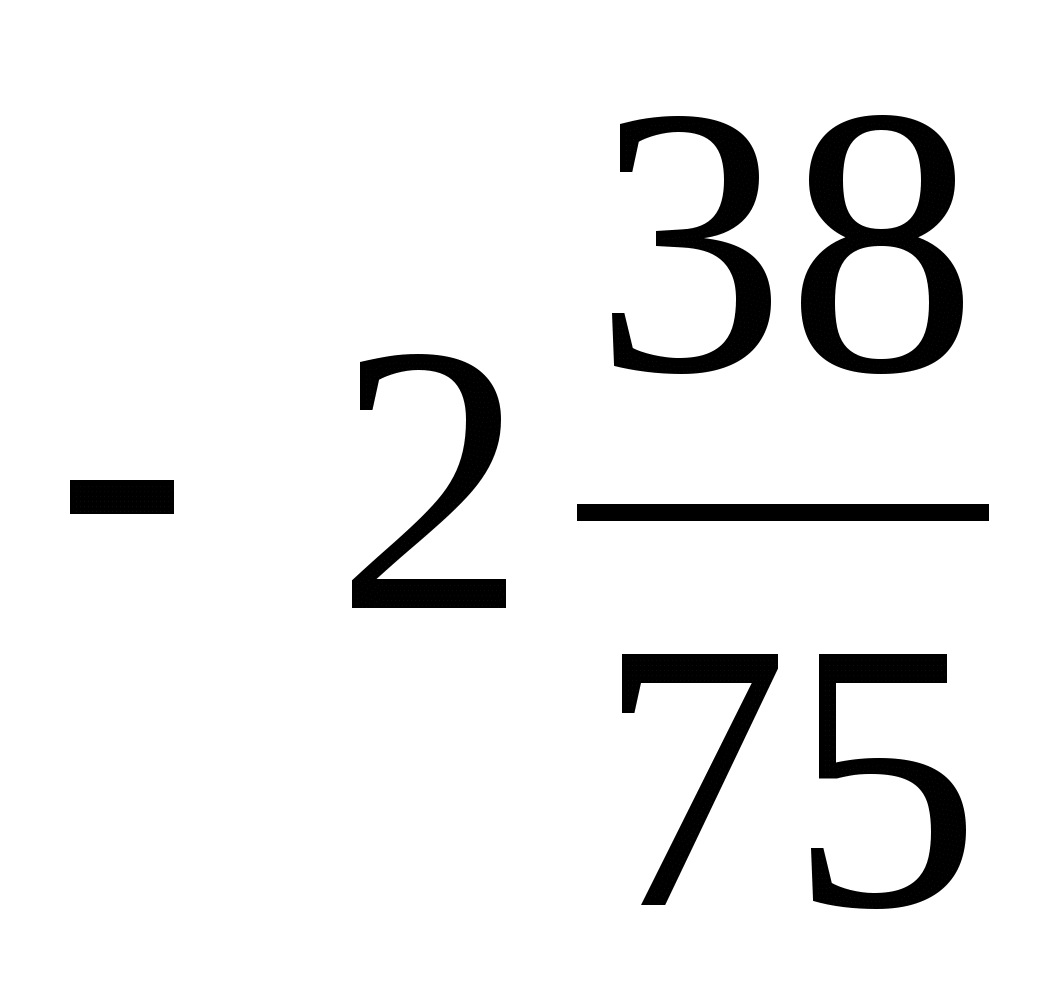
infourok.ru
Корень п-ой степени для студентов 1 курса СПО
ПЛАН-КОНСПЕКТ ЗАНЯТИЯ
ФИО (полностью)
Кривова Галина Валерьевна
Место работы
ГБОУ СПО «Электростальский колледж» г.о. Электросталь, Московской области
Должность
Преподаватель
Предмет
Математика
Курс
1
Тема занятия
Базовые учебник, сборник задач
Мордкович А.Г., Денищева Л.О. и др. Алгебра и начала математического анализа. Учебник для учащихся (профильный уровень). Москва, Мнемозина. 2009 г.
Мордкович А.Г. и др. Алгебра и начала математического анализа. Задачник для учащихся (профильный уровень). Москва, Мнемозина, 2009 г.
Тип занятия: практическое занятие
Цель занятия: обучить решению заданий на нахождение корня п-ой степени.
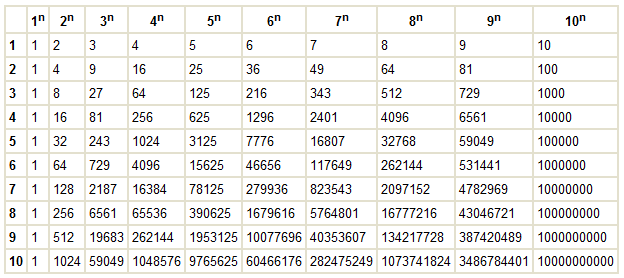
Образовательная задача: сформировать умение применять определение и свойства корней при решении заданий, используя графики функций и таблицу степеней; способствовать индивидуализации и дифференциации обучения с помощью применения разноуровневых задач и информационно-коммуникационных технологий
Развивающая задача: развитие умений анализировать, обобщать изучаемые факты, развитие навыков самоконтроля, взаимоконтроля и самостоятельной работы
Воспитательная задача: воспитание настойчивости в достижении цели и заинтересованности в конечном результате труда.
10. Формируемые УУД:
осуществление информационного поиска,
выявление существенной информации, выдвижение гипотезы, её проверка,
построение логической цепочки рассуждений,
анализ ситуации, моделирование, использование знаково-символических действий.
Технология: групповая
Формы работы учащихся: фронтальная, индивидуальная, групповая
Оборудование: опорный план на доске, презентация к уроку, раздаточный материал: карточки с заданием для индивидуальной работы.
СТРУКТУРА И ХОД ЗАНЯТИЯ
№
Этап
Используемые специальные средства, ЭОР
Деятельность учителя
(с указанием действий со специальными средствами, например, демонстрация)
Деятельность ученика
Формируемые
УУД СУД
1
2
3
5
6
7
1
Орг.момент
Конспекты, сообщения и презентации
Здравствуйте, ребята. Сегодня на уроке мы познакомимся со следующими понятиями: корень n-ой степени, арифметический корень n-ой степени из числа, с решениями уравнений вида хn=a.
Сейчас ребята, познакомят вас с историей возникновения квадратного корня, термина “радикал”, т.е. корень, и напомнят определение квадратного корня.
(Доклад – читает учащийся).
Записывают в тетрадях цели на данное занятие и выступают с сообщениями и презентациями.
Умение ясно, точно, грамотно излагать свои мысли в устной и письменной форме.
2
Исторические справки
(приложение 1)
Выслушивает выступления учащихся
Умение высказывать свои мысли перед сверстниками
Развитие познавательных интересов и инициативы студентов
3
Актуализация знаний проводится в форме фронтального опроса.
презентация
(приложение 2)
Аналогично определим корень n-ой степени. Корнем n-ой степени из числа а называется такое число, n-ая степень которого равна а.
Примеры:
Корень третьей степени из числа 27 равен 3, т.к. 33=27.
Корень шестой степени из числа 64 равен 2 и (-2), т.к. 26=64 и (-2)6=64.
Согласно данному определению, корень n-ой степени из числа а – это решение уравнения хn=а. Число корней данного уравнения зависит от n и а.
Рассмотрим функцию f(x)=xn. Эта функция при любом n возрастает на промежутке от нуля до бесконечности и
принимает все значения из этого промежутка.
Учащиеся отвечают на вопросы, обосновывают ответы.
Умение строить речевое высказывание умение сравнивать и анализировать.
-моделирование
-сравнение, анализ
-обсуждение проблемы
-поиск путей решения проблемы
-сравнение предметов, объектов
-работа с моделями
-сотрудничество с учителем и сверстниками,
-умение точно выражать свои мысли в соответствии с задачами и условиями коммуникации
-соблюдать простейшие нормы речевого элемента
-вести диалог
-участвовать в коллективном обсуждении проблемы
Развитие познавательных интересов и инициативы студентов.
Разминка: Устный счет. Задаваемые вопросы ученикам:
Вычислить:
23
32
33
42




4
Обобщение знаний о корне с использованием презентации
Телевизор, презентация, слайды
Выслушивает ответы учащихся и корректирует их.
Учащиеся зачитывают информацию на слайдах.
Соблюдать простейшие нормы речевого этикета; умение высказывать свои мысли перед сверстниками.
Развитие познавательных интересов и инициативы студентов
5
Решение задач
Контролирует и оценивает выступления учащихся.
Выступление трёх учащихся, приготовивших решение задач с применением корней.
Остальные – участвуют в обсуждении задачи, конспектируют.
Обсуждение проблемы, построение логической цепи рассуждений, умение точно выражать свои мысли в соответствии с задачами и условиями, умение высказывать свои мысли перед сверстниками.
Развитие познавательных интересов и инициативы студентов
6
Практическая работа в группах
(Приложение 3)
Дает консультации по группам, если они необходимы.
По группам решают задачи (приложение)
планирование работы в группе и с учителем
-моделировать ситуацию поведения
корректировать способы действия
умение осуществлять действия по образцу, по алгоритму
— умение сохранять заданную цель
-строить логическое рассуждение, включающее установление причинно-следственных связей
— подведение под понятия,
-умение видеть указанную ошибку и исправлять её
-умение ценить взаимопомощь
-развитие познавательных интересов и инициативы студентов
7
Подведение итогов работы в группах
Контролирует и оценивает выступления учащихся.
Выступление представителей каждой группы с решенными задачами. Все остальные, кратко записывают решения задач.
8
Подведение итогов занятия
Преподаватель подводит итоги занятия вместе со студентами
Заключение.
Хотелось бы сказать, что хорошее математическое образование и развитие математических способностей необходимы не только тому, кто впоследствии займется научными исследованиями в области математики, физики, астрономии или инженерного дела, но и тому, кто станет экономистом, агрономом и просто квалифицированным рабочим. Математический стиль мышления нужен также будущим юристам, историкам, биологам, врачам и лингвистам.
Слушают и комментируют итоги вместе с преподавателем
Развитие познавательных интересов и инициативы студентов
9
Домашнее задание
(приложение 4)
Преподаватель комментирует домашнее задание на карточке
(приложение 2)
Получают карточку с домашней работой по вариантам
Развитие познавательных интересов самостоятельности студентов
ПРИЛОЖЕНИЕ 1
Историческая справка о корнях
Начало формы
Конец формы
Вступление.
Датский физик Нильс Бор говорил, что математика является значительно большим, чем наука, поскольку она является языком науки. Математика превратилась в необходимое орудие познания, без которого многие естествоиспытатели не мыслят себе саму возможность развития их областей знания.
Впервые взглянув на такие выражения:
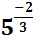 ,
, 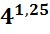 , (
, (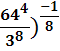 , думаешь:
, думаешь:
« Как же их решать?! С чего начать? И какой же будет здесь ответ – положительный или отрицательный, простое число или десятичная дробь?» но стоит только вникнуть в тему, все становится понятным, нет ничего сложного…
Историческая справка
Название «радикал» происходит от латинских слов radix- «корень», radicalis- «коренной». Начиная с  ΙΙΙ века европейские математики обозначали корень этим словом, или, сокращенно, r. В 1525 г. В книге К. Рудольфа «Быстрый и красивый счет при помощи искусных правил алгебры, обычно называемых Косс» появилось обозначение V для знака квадратного корня, корень кубический обозначался там как VVV. В 1626 году голландский математик А. Жирар ввел обозначение
ΙΙΙ века европейские математики обозначали корень этим словом, или, сокращенно, r. В 1525 г. В книге К. Рудольфа «Быстрый и красивый счет при помощи искусных правил алгебры, обычно называемых Косс» появилось обозначение V для знака квадратного корня, корень кубический обозначался там как VVV. В 1626 году голландский математик А. Жирар ввел обозначение 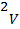 ,
,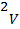 и т. д., которое стало быстро вытеснять знак r; при этом над покоренным выражением ставилась горизонтальная черта. Тогда писали V x + у вместо современного
и т. д., которое стало быстро вытеснять знак r; при этом над покоренным выражением ставилась горизонтальная черта. Тогда писали V x + у вместо современного 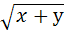 .
.
Современное обозначение корня впервые появилось в книге Р. Декарта «Геометрия», изданной в 1637 г. Приближенное значение квадратных корней из целых чисел умели находить ещё в Древнем Вавилоне около 4 тыс. лет назад. При этом вавилонские учёные пользовались следующим методом: число а представляли в виде суммы в²+с, где с мало по сравнению с в², и полагали 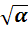 = в + с /2в.
= в + с /2в.
Например: 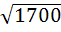 =
= 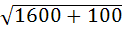 =
=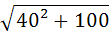 =40+
=40+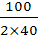 =41
=41 (пример взят из вавилонской клинописной таблички). Для сравнения укажем более точное значение корня
(пример взят из вавилонской клинописной таблички). Для сравнения укажем более точное значение корня 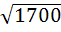 =41,23105. Заметим, что такой способ приближенного извлечения квадратного корня часто называют вавилонским методом извлечения квадратного корня.
=41,23105. Заметим, что такой способ приближенного извлечения квадратного корня часто называют вавилонским методом извлечения квадратного корня.
ПРИЛОЖЕНИЕ 2
Начало формы
Конец формы
Определение корня n-ой степени.
Радикалом (или знаком корня) называют знак 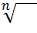 , применяемый для обозначения операции извлечения корня n-ой степени из некоторого числа, корень n-ой степени из числа a обозначается
, применяемый для обозначения операции извлечения корня n-ой степени из некоторого числа, корень n-ой степени из числа a обозначается 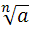 . При n
. При n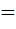 2 показатель корня опускают и пишут
2 показатель корня опускают и пишут 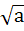 вместо
вместо 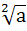 . Корень второй степени обычно называют квадратным корнем, а корень третьей степени – кубическим корнем. При извлечении корня четной степени из неотрицательного числа а запись
. Корень второй степени обычно называют квадратным корнем, а корень третьей степени – кубическим корнем. При извлечении корня четной степени из неотрицательного числа а запись 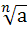 обозначает арифметический корень из числа а (т. е. такое неотрицательное число в, что
обозначает арифметический корень из числа а (т. е. такое неотрицательное число в, что  =а).
=а).
При четном n существует два корня n-ой степени из любого положительного числа а; корень n-ой степени из числа 0 равен нулю; корней четной степени из отрицательных чисел не существует.
При нечетных значениях n функция 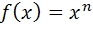 возрастает на всей числовой прямой; её область значений – множество всех действительных чисел.
возрастает на всей числовой прямой; её область значений – множество всех действительных чисел.
Применяя теорему о корне, находим, что уравнение, 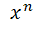 =а имеет один корень при любом а и, в частности, при а
=а имеет один корень при любом а и, в частности, при а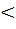 0. Этот корень для любого значения а (в том числе и а отрицательного) обозначают
0. Этот корень для любого значения а (в том числе и а отрицательного) обозначают 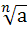 .
.
Итак, при нечетном n существует корень n-ой степени
из любого числа а, и при том только один.
Для корней нечетной степени справедливо равенство: 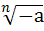 =-
=-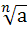 .
.
Степенью числа а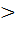 0 с рациональным показателем r=
0 с рациональным показателем r= 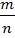 , где — целое число, а n — натуральное (n
, где — целое число, а n — натуральное (n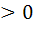 ), называется число
), называется число 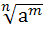 .
.
Свойства корня -ой степени.
Для любого натурального n, целого 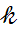 и любых неотрицательных чисел а и в выполнено равенство:
и любых неотрицательных чисел а и в выполнено равенство:
1) 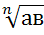 =
= 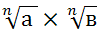
2) 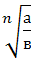 =
= 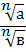 (причем в
(причем в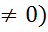
3) 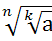 =
= 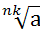 (k
(k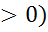
4) 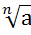 =
= 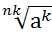 (k
(k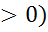
5) 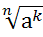 = (
= (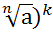 (если k
(если k 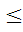 0, то а
0, то а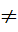 0)
0)
ТАБЛИЦА СТЕПЕНЕЙ ЧИСЕЛ
Примеры
1) Найдите значения выражений:

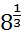 ;
; 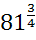 ;
; 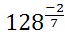 .
.
По определению степени с рациональным показателем и свойствами корней, имеем:

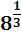 =
= 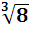 = 2,
= 2, 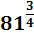 =
= 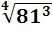 = (
= (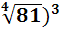 =
= 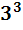 = 27,
= 27,
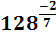 =
= 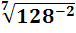 =(
=( 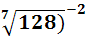 =
= 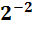 =
= 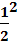 =
=  .
.
2) Сравним числа : 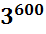 и
и 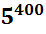 .
.
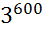 =
= 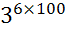 =
= 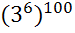 =
= 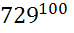 ;
;
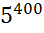 =
= 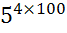 =
= 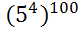 =
= 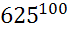 ,
,
Т. к. 625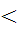 729, то
729, то 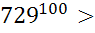
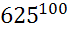 , значит
, значит 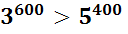 .
.
ПРИЛОЖЕНИЕ 3
Работа по группам
Вариант I
Вариант II
Вариант I I I
Обязательный уровень (с выбором ответа)
А1. Вычислить: 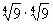
1) 81; 2) 9; 3) 3;
А1. Вычислить: 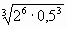
1) 1; 2) 2; 3) 20;
А1. Вычислить: 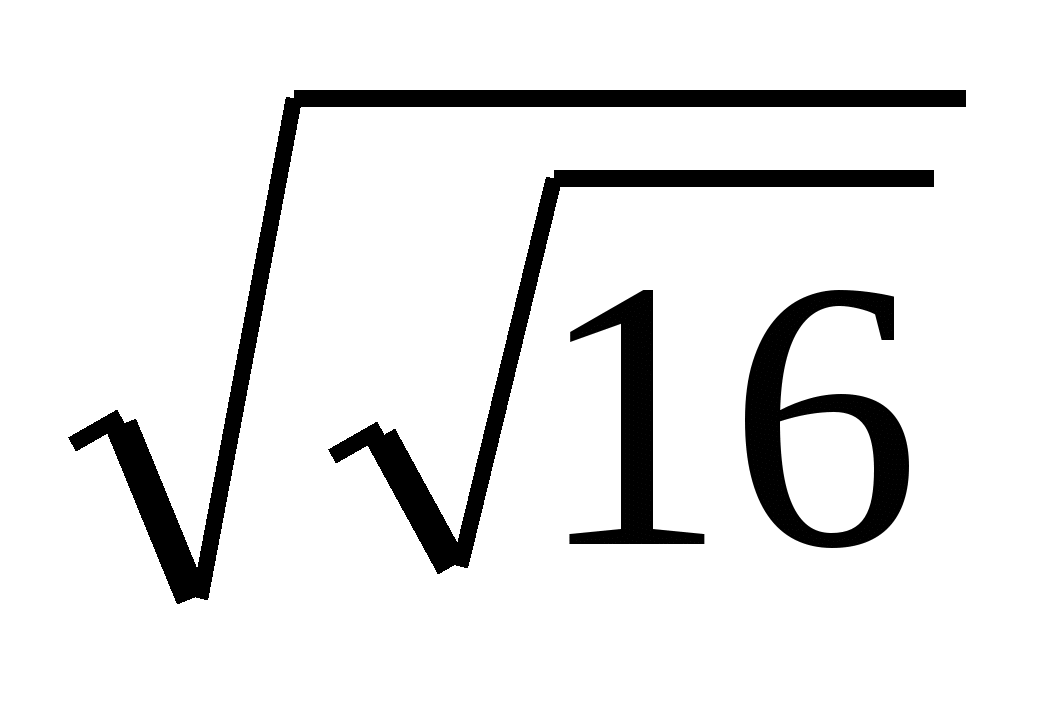
1) 1; 2) 2; 3) 20;
А2. Вычислить: -2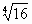
1) -8; 2) 4; 3) -4;
А2. Вычислить 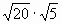
1) 100; 2) 10; 3) 1;
А2. Вычислить 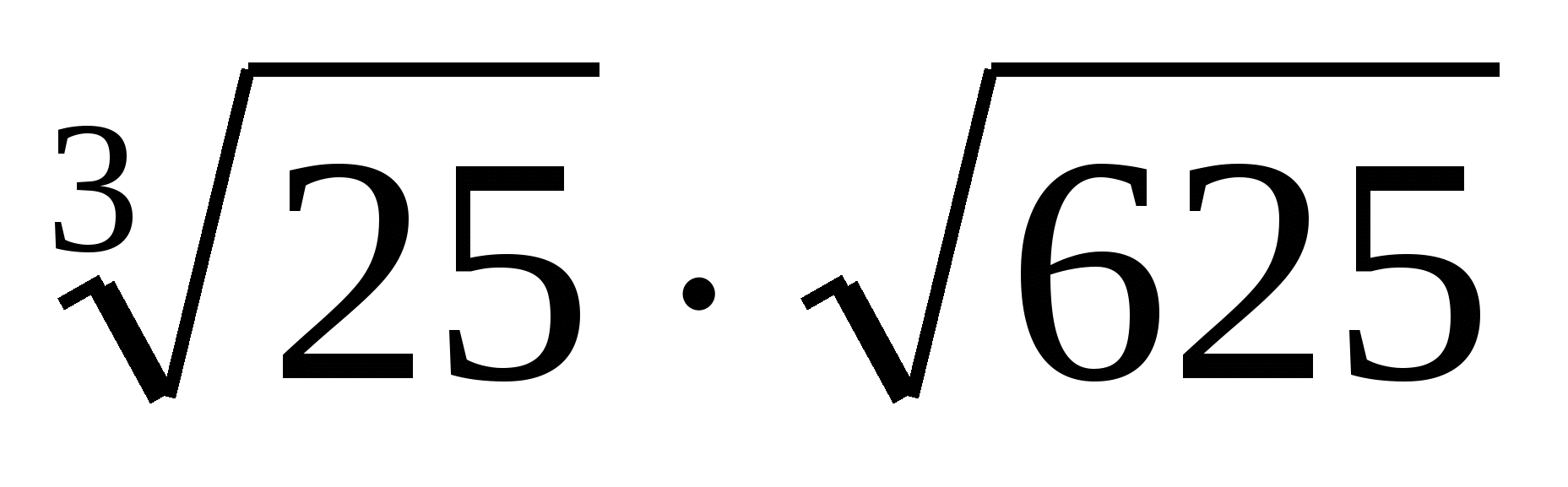
1) 25; 2) 5; 3) 125;
А3. Вычислить: 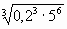
1) 50; 2) 25; 3) 5;
А3. Вычислить: -6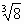
1) — 24; 2) – 12; 3) 12;
А3. Вычислить: -2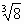
1) — 24; 2) – 4; 3) 12;
А4. Решить уравнение: х6=64
1) 2; 2) -4; 4 3) -2; 2
А4. Решить уравнение: х5=32
1) -2; 2) 2; 3) -2; 2
А4. Решить уравнение: х5=243
1) -2; 2) 3; 3) -2; 2
Обязательный уровень (указать ответ)
А5. Вычислить:
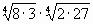 =
=
Ответ:
А5. Вычислить:
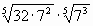
Ответ:
А5. Вычислить:
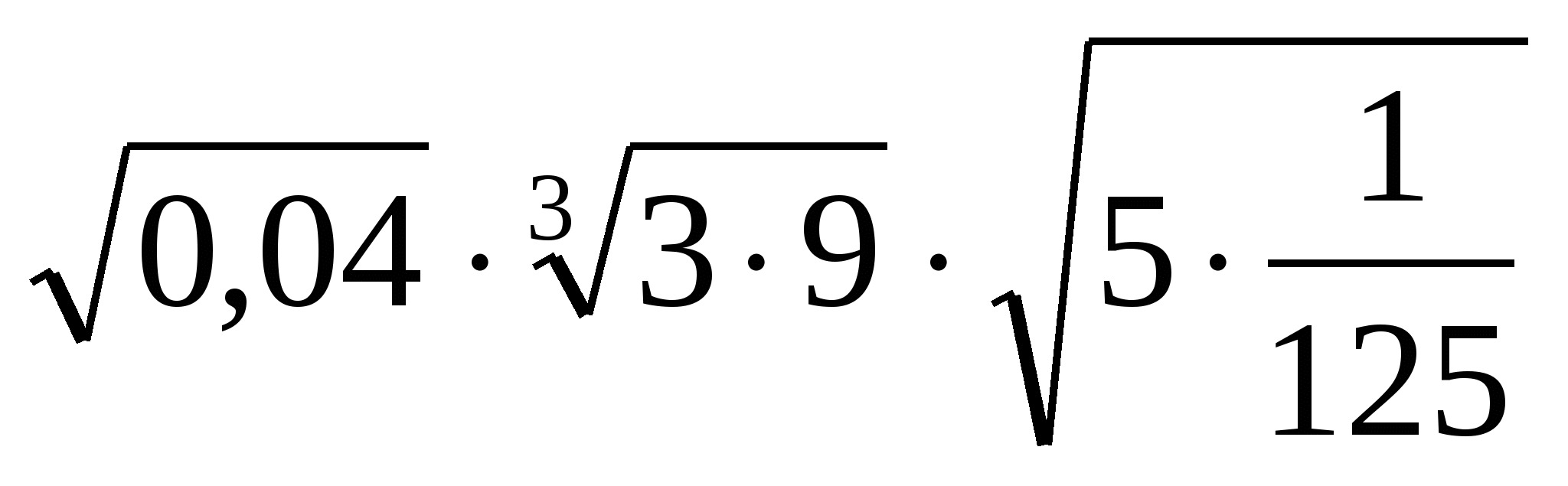
Ответ:
А6. Преобразовать выражение:
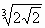 =
=
Ответ:
А6. Преобразовать выражение:
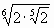
Ответ:
А6. Преобразовать выражение:
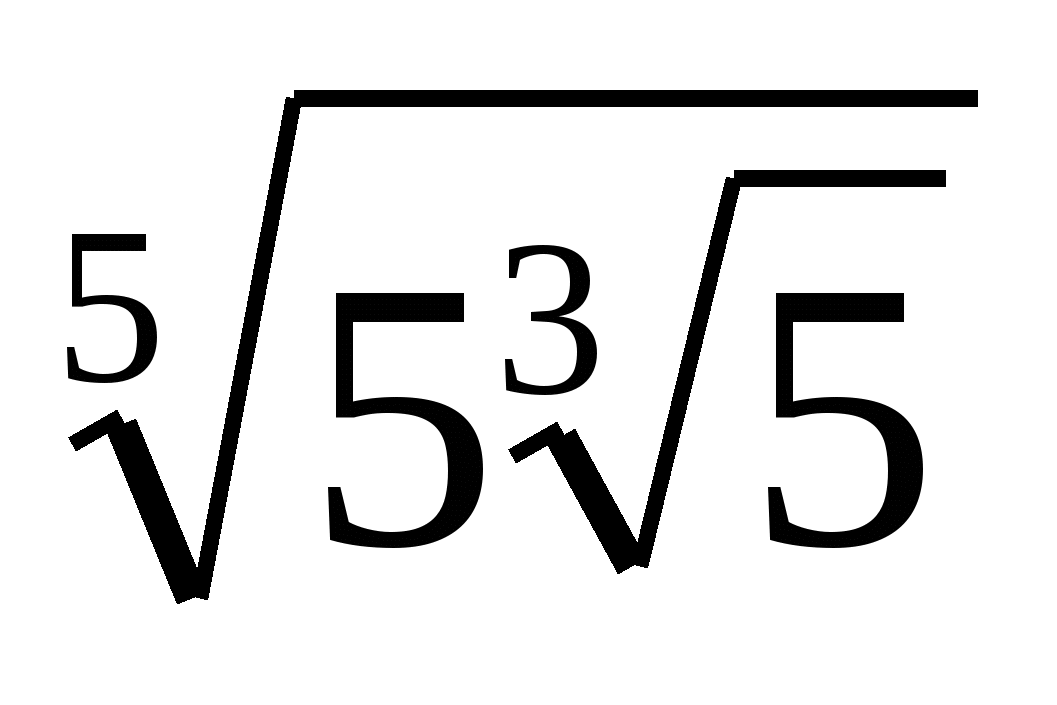
Ответ:
ПРИЛОЖЕНИЕ 4
Домашнее задание
Домашняя работа
Корень n – ой степени. В. 1.
Домашняя работа
Корень n – ой степени. В. 2.
Вычислить:
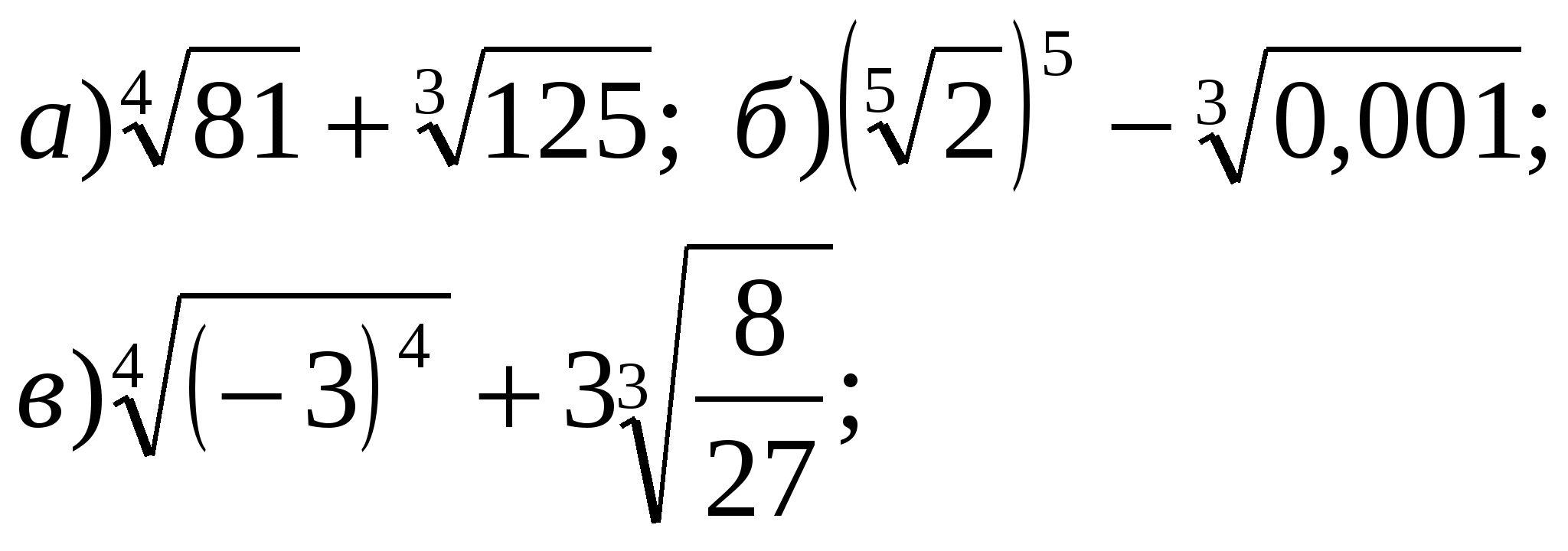
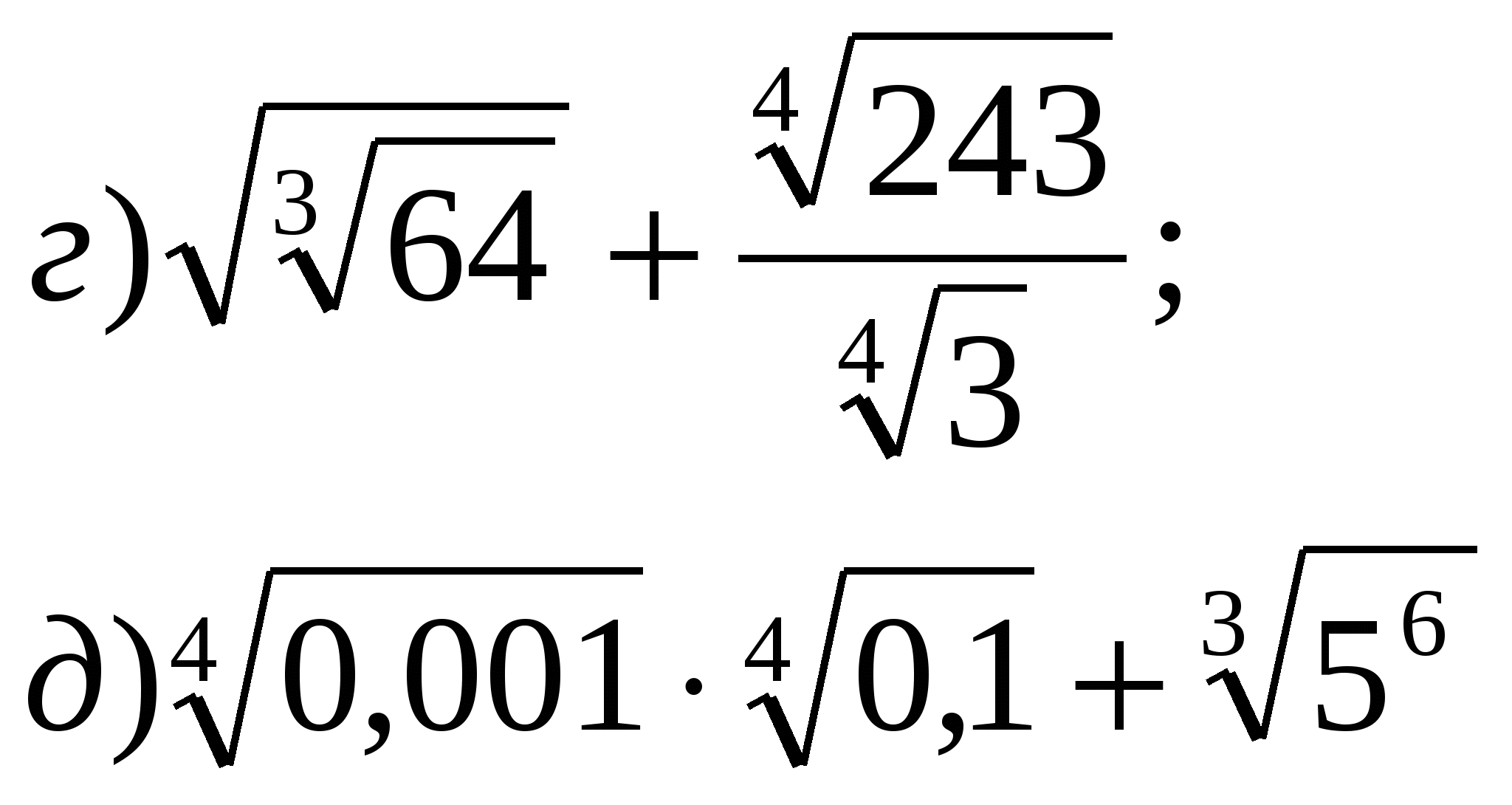
Решите уравнение:
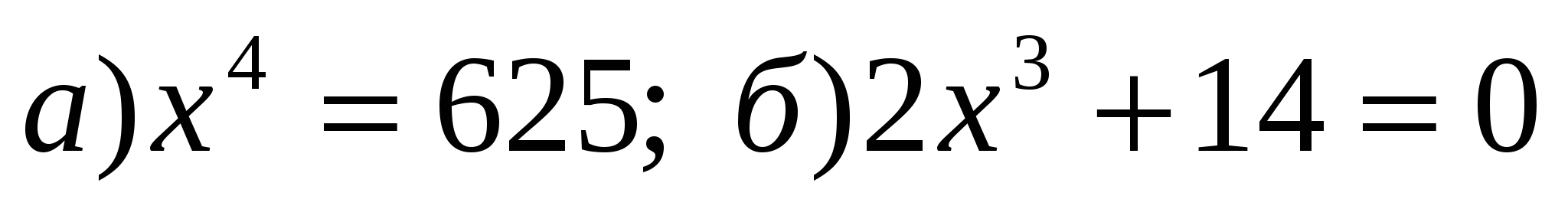
Сравните числа:

4. а) Внесите множитель под знак корня: 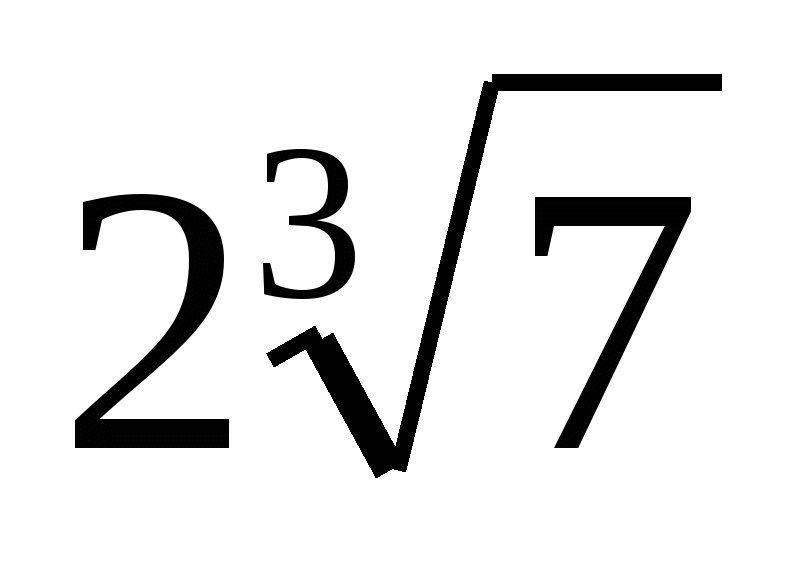
б) Вынесите множитель
из – под знака корня: 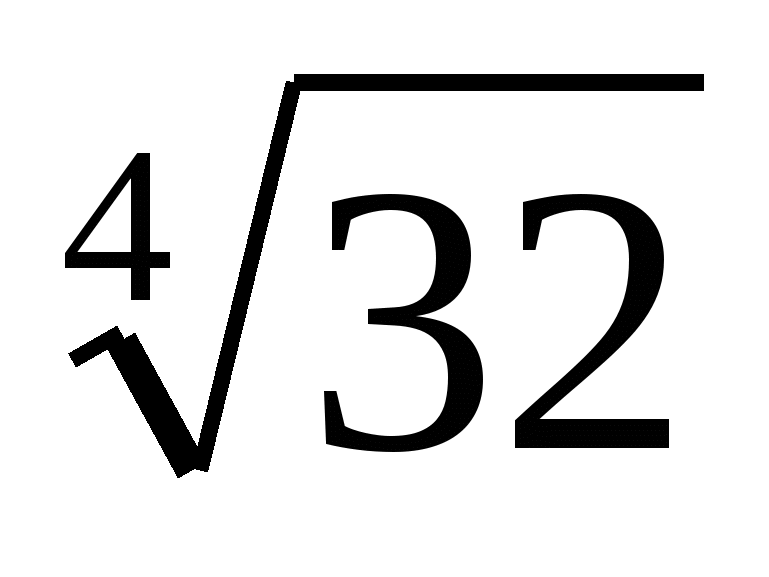
Вычислить:
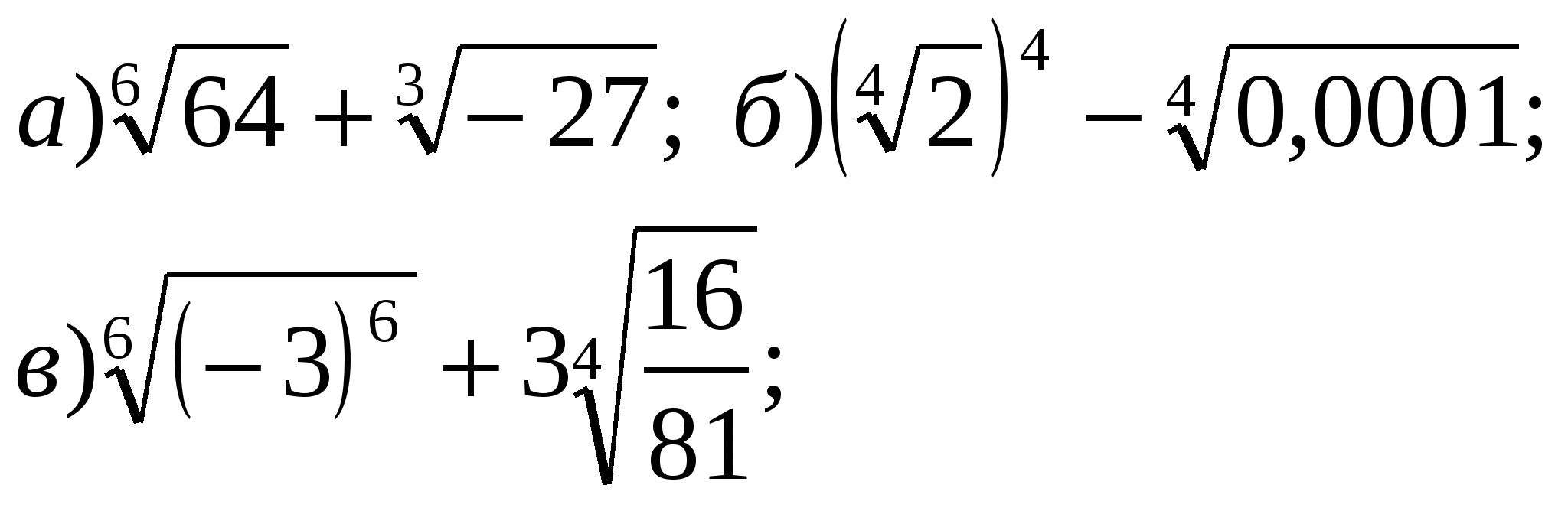
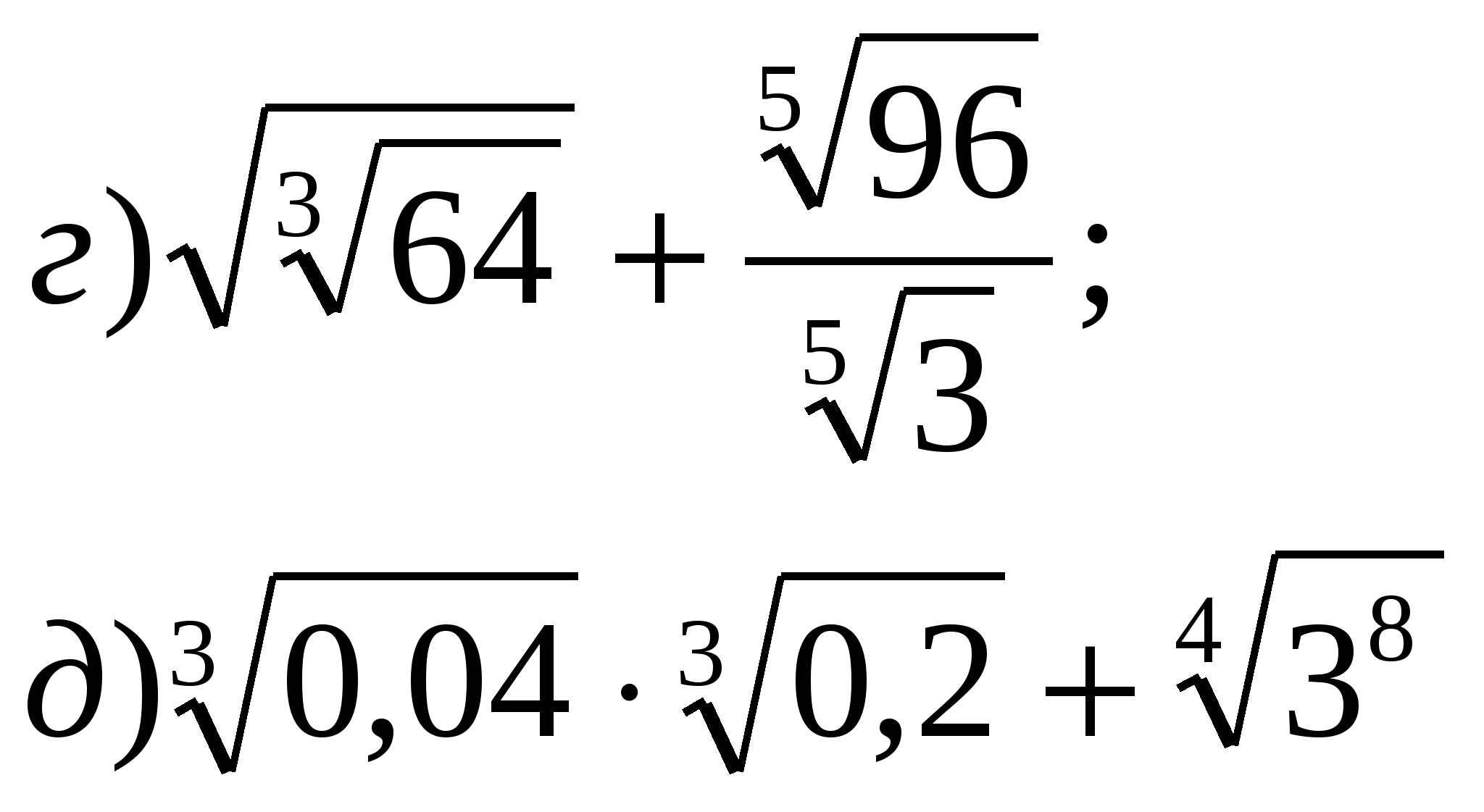
Решите уравнение:
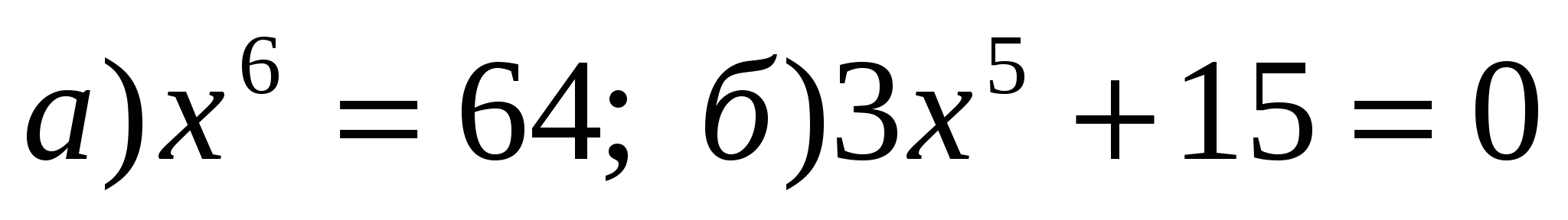
Сравните числа:

4. а) Внесите множитель под знак корня: 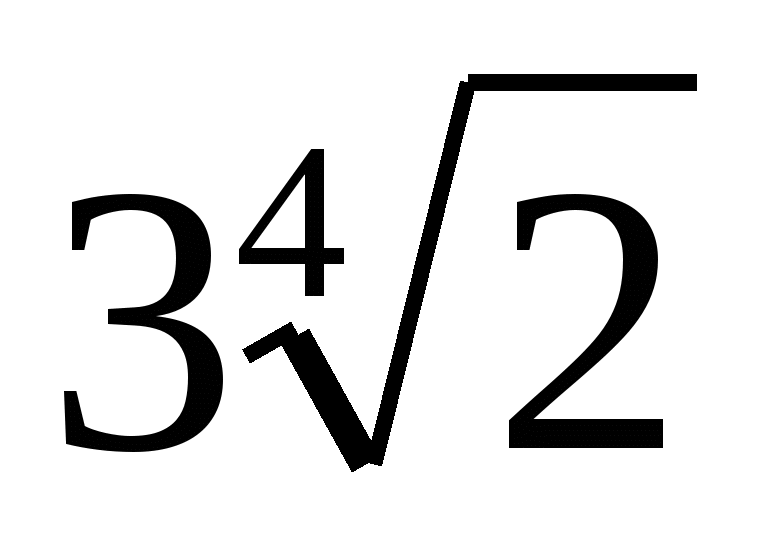
б) Вынесите множитель
из – под знака корня: 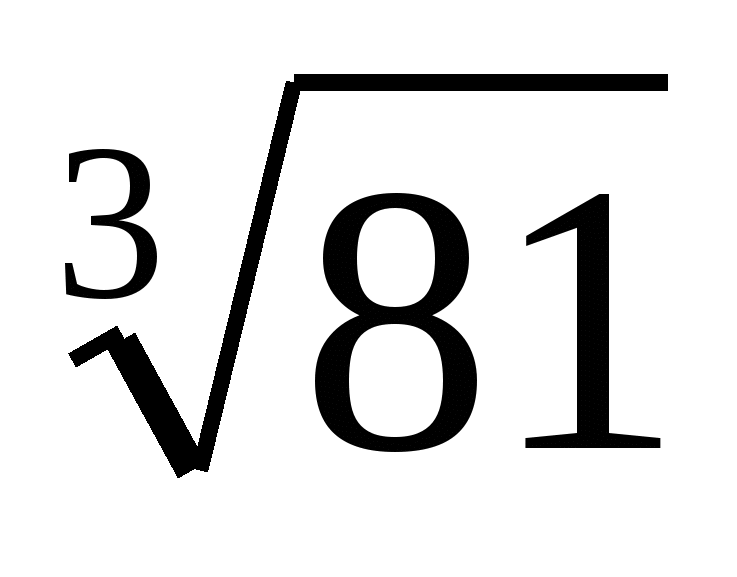
infourok.ru
Зачёт по теме «Степени и корни»
Зачётная работа по алгебре в 10 классе за 1 триместр
Вариант 1.
1. Вычислите: а)  б)
б)  в)
в)  .
.
2. Вычислите 
3. Расположите в порядке возрастания числа: 
4. Решите уравнения: а)  б)
б) 
5. Решите неравенства: а)  б)
б)  .
.
6. Укажите решение системы уравнений 
7. Даны две функции, определённые на всей числовой оси: f(x) – нечетная и g(x) – четная.
Известно, что f(-2) = 1 и g(– 4) = 3. Вычислите f(2) + g(4) + f(-2) –3 f(0).
f(0).
8. Найдите обратную функцию для функции  и изобразите оба графика
и изобразите оба графика
в единой координатной системе.
9. Упростите выражение: 
10. Вычислите  .
.
Зачётная работа по алгебре в 10 классе за 1 триместр
Вариант 2.
1. Вычислите: а)  б)
б)  в)
в)  .
.
2. Вычислите 
3. Расположите в порядке убывания числа: 
4. Решите уравнения: а)  б)
б)  .
.
5. Решите неравенства: а) б)
б)  .
.
6. Укажите решение системы уравнений 
7. Даны две функции, определённые на всей числовой оси: f(x) – четная и g(x) – нечетная.
Известно, что f(2) = 1 и g(–1) = -3. Вычислите f(–2) + g(1) + f(2) –2 g(0).
g(0).
8. Найдите обратную функцию для функции и изобразите оба графика
в единой координатной системе.
9. Упростите выражение:
10. Вычислите .
Зачётная работа по алгебре в 10 классе за 1 триместр
Вариант 3.
1. Вычислите: а) б) в) .
2. Вычислите .
3. Расположите в порядке возрастания числа:
4. Решите уравнения: а) б) .
5. Решите неравенства: а) б) .
6. Укажите решение системы уравнений
7. Даны две функции, определённые на всей числовой оси: f(x) – нечетная и g(x) – четная.
Известно, что f(5) = 2 и g(– 4) = 7. Вычислите f(-5) + g(4) + f(5) –6 f(0).
f(0).
8. Найдите обратную функцию для функции и изобразите оба графика
в единой координатной системе.
9. Упростите выражение:
10. Вычислите .
Зачётная работа по алгебре в 10 классе за 1 триместр
Вариант 4.
1. Вычислите: а) б) в) .
2. Вычислите .
3. Расположите в порядке убывания числа:
4. Решите уравнения: а) б) .
5. Решите неравенства: а) б) .
6. Укажите решение системы уравнений
7. Даны две функции, определённые на всей числовой оси: f(x) – четная и g(x) – нечетная.
Известно, что f(2) = 8 и g(–3) = – 6. Вычислите f(–2) + g(3) + f(2) – 45 g(0).
g(0).
8. Найдите обратную функцию для функции и изобразите оба
графика в единой координатной системе.
9. Упростите выражение:
10. Вычислите .
multiurok.ru
Методическая разработка урока по теме «Корни натуральной степени и их свойства»
«Корни натуральной степени из числа и их свойства».
Цели занятия:
— сформулировать определение корня натуральной степени из числа;— рассмотреть свойства арифметических корней.
Воспитательные:
— воспитывать положительное отношение к приобретению новых знаний;
— вызвать заинтересованность новым для студентов подходом изучения математики.
Развивающие:
— формировать навыки познавательного мышления;
— формировать умения и навыки учебного труда.
Задачи занятия: сформировать умение вычислять арифметические корни натуральной степени, корни нечетной степени; пользоваться свойствами арифметического корня.
Планируемый результат: студент знает определение арифметического корня натуральной степени и корня нечетной степени. Знает свойства арифметического корня натуральной степени. Умеет извлекать кори натуральной степени. Умеет использовать свойства корня натуральной степени при решении задач.
Структура занятия:
1. Организованный момент.
2. Самостоятельная работа по теме «Действительные и комплексные числа».
3. Объяснение темы «Корни натуральной степени из числа и их свойства»
Основные определения.
Свойства корня натуральной степени из числа
Решение ключевых задач.
Вычисление корней натуральной степени
5. Решение упражнений.
6. Подведение итогов урока. Домашнее задание.
Ход занятия:
1. Организованный момент. Приветствие учащихся. Сообщение темы и целей занятия. Проверка готовности студентов к занятию.
2. Самостоятельная работа по теме «Действительные и комплексные числа».
3. Объяснение нового материала.
Определение. Арифметическим корнем натуральной степени из неотрицательного числа  называется неотрицательное число,
называется неотрицательное число, 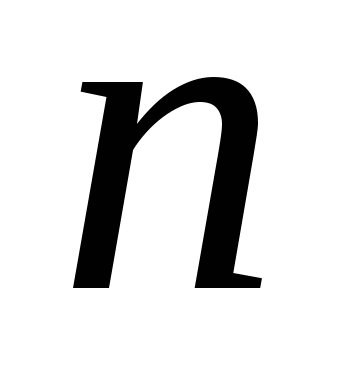 -я степень которого равна
-я степень которого равна  .
.
Обозначение: 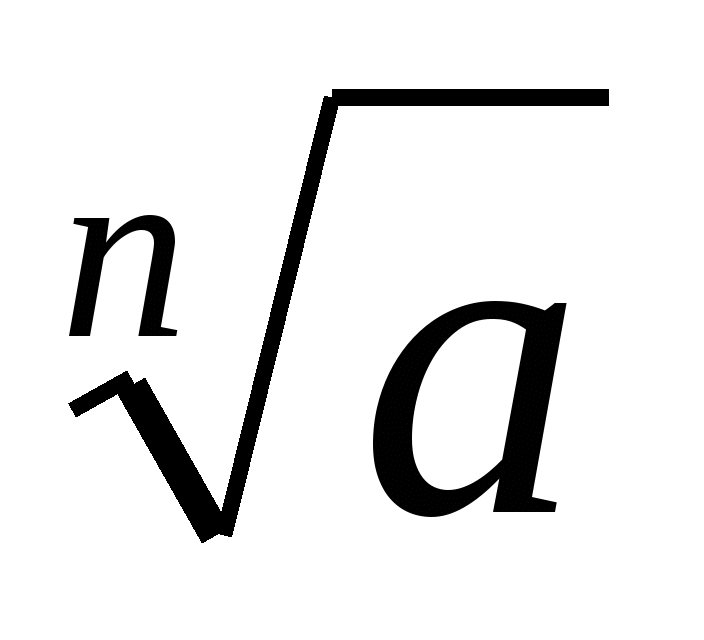 , где
, где  – подкоренное выражение. Если
– подкоренное выражение. Если  , то пишут
, то пишут 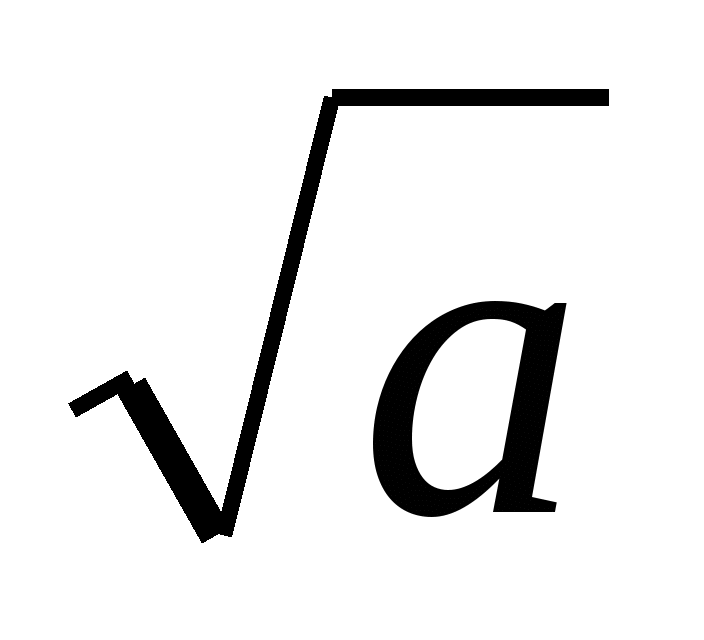 .
.
Чтобы, используя определение, доказать, что корень 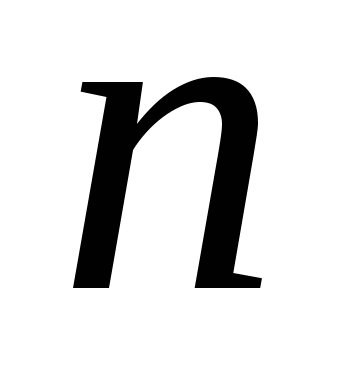 -й степени
-й степени 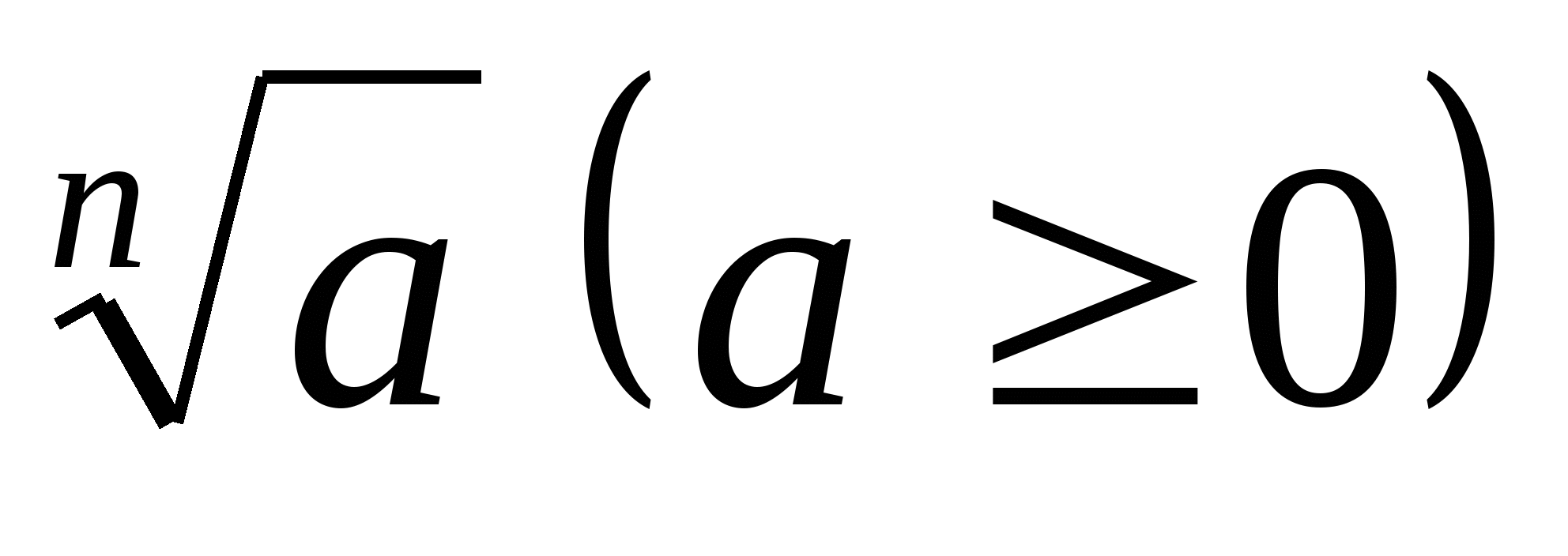 равен
равен 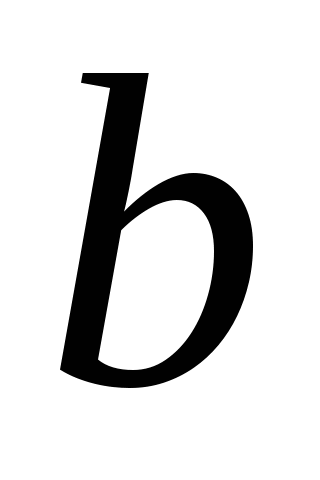 , нужно показать, что:
, нужно показать, что: 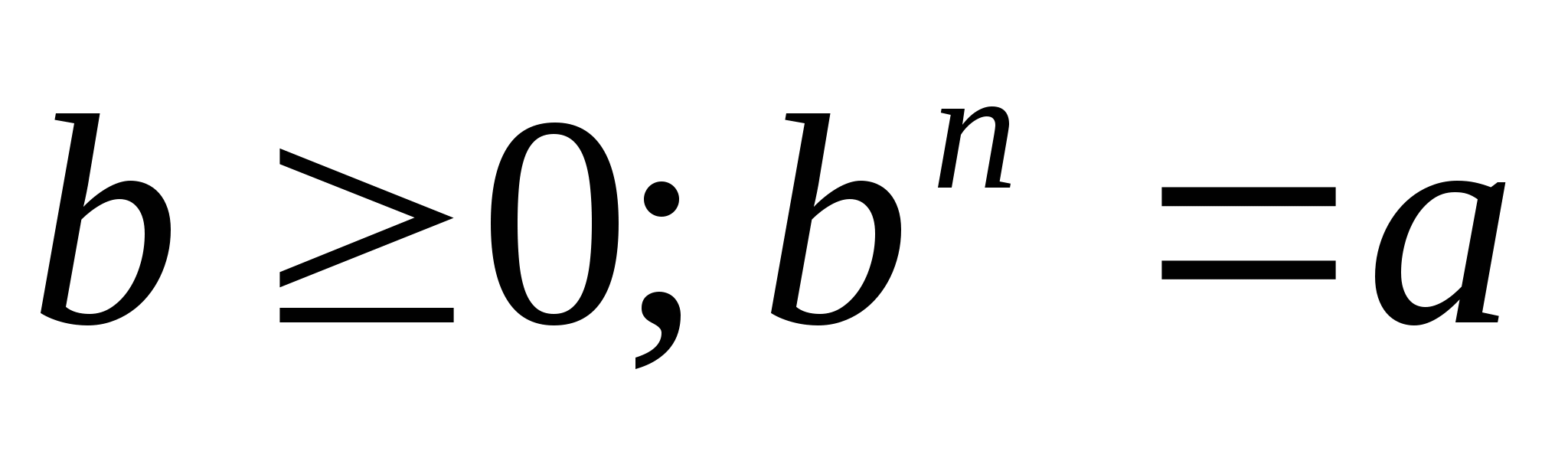 .
.
Определение. Действие, посредством которого отыскивается корень 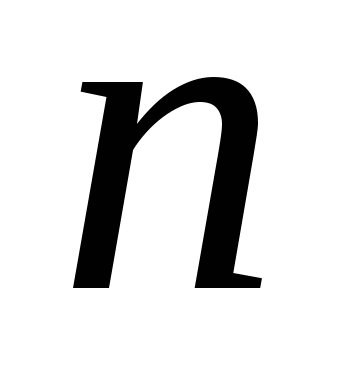 -й степени, называется извлечением корня
-й степени, называется извлечением корня 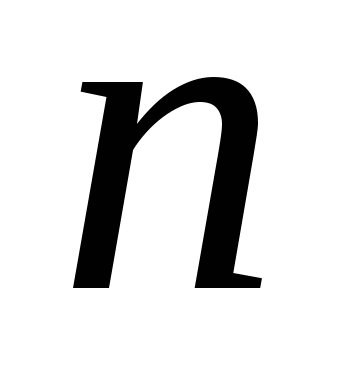 -ой степени.
-ой степени.
Определение. Для любого нечетного натурального числа уравнение 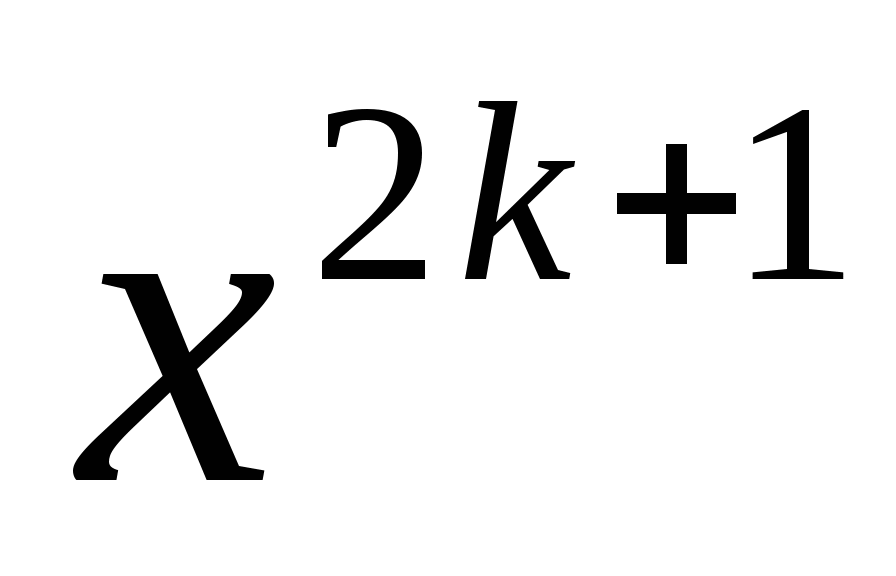 при
при 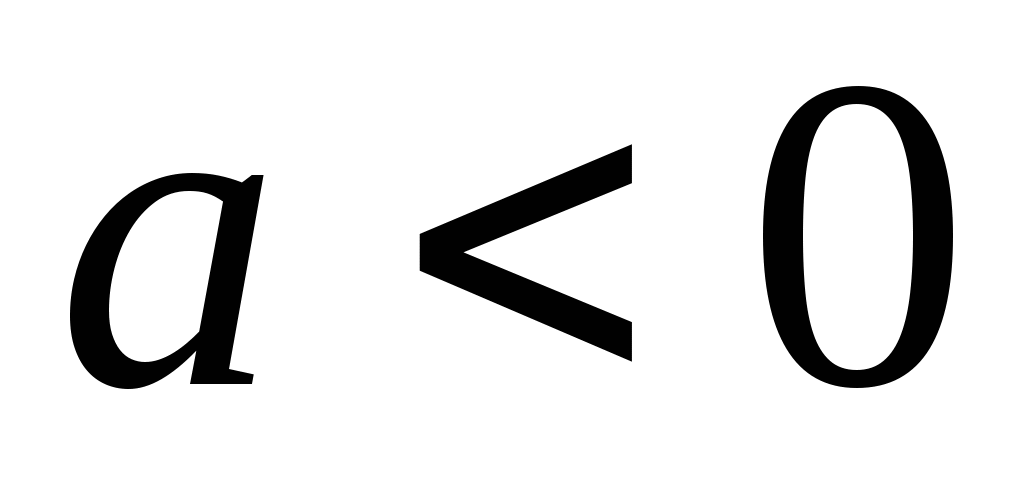 имеет только один корень, причем отрицательный. Этот корень обозначается, как и арифметический корень, символом
имеет только один корень, причем отрицательный. Этот корень обозначается, как и арифметический корень, символом 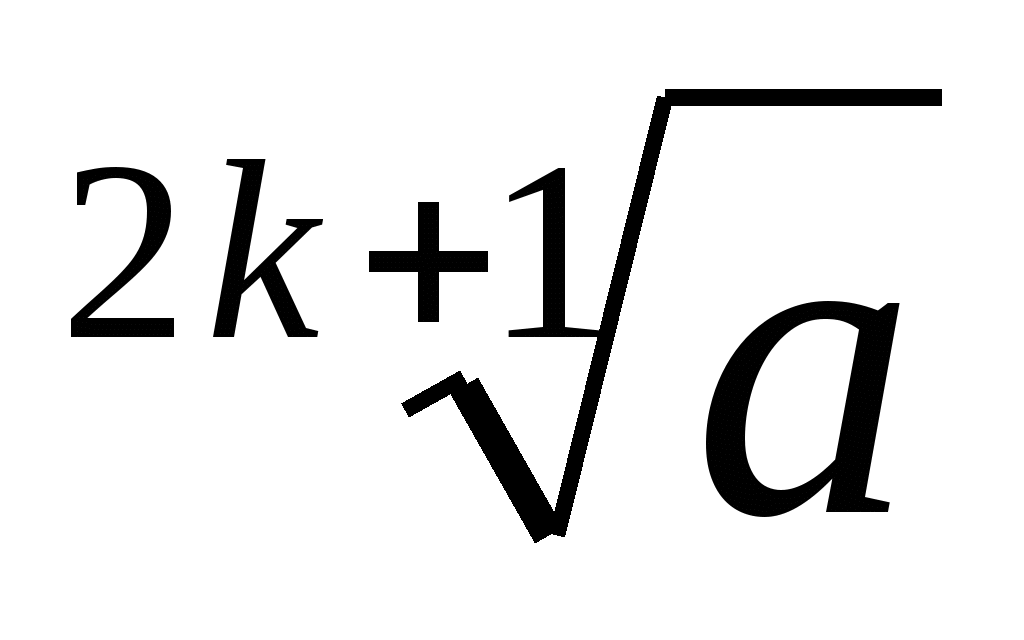 . Его называют корнем нечетной степени из отрицательного числа.
. Его называют корнем нечетной степени из отрицательного числа.
Свойства арифметических корней
Арифметический корень 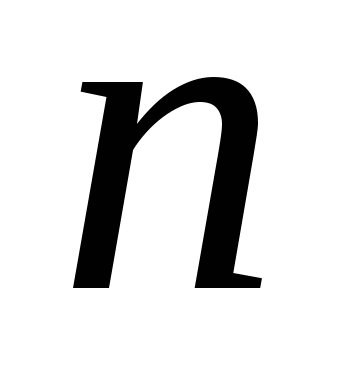 -й степени обладает следующими свойствами: если
-й степени обладает следующими свойствами: если 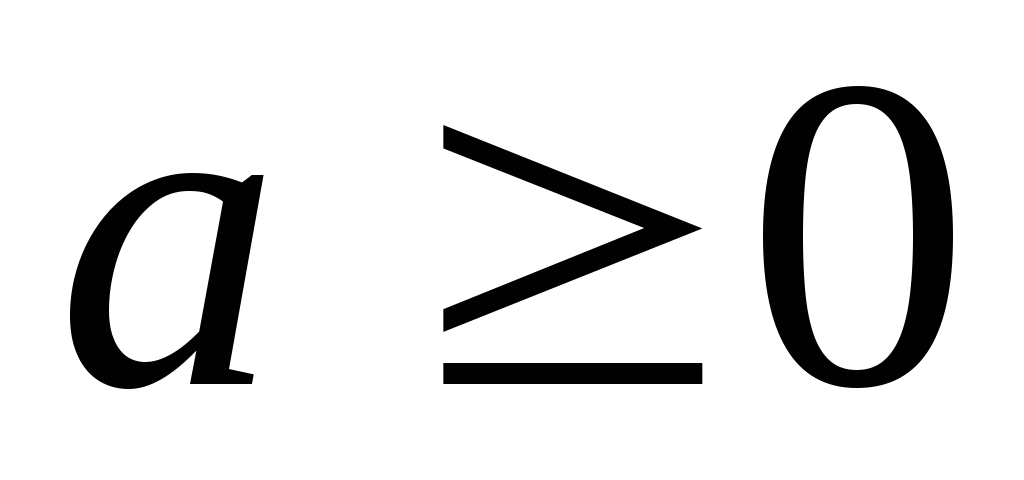 ,
, 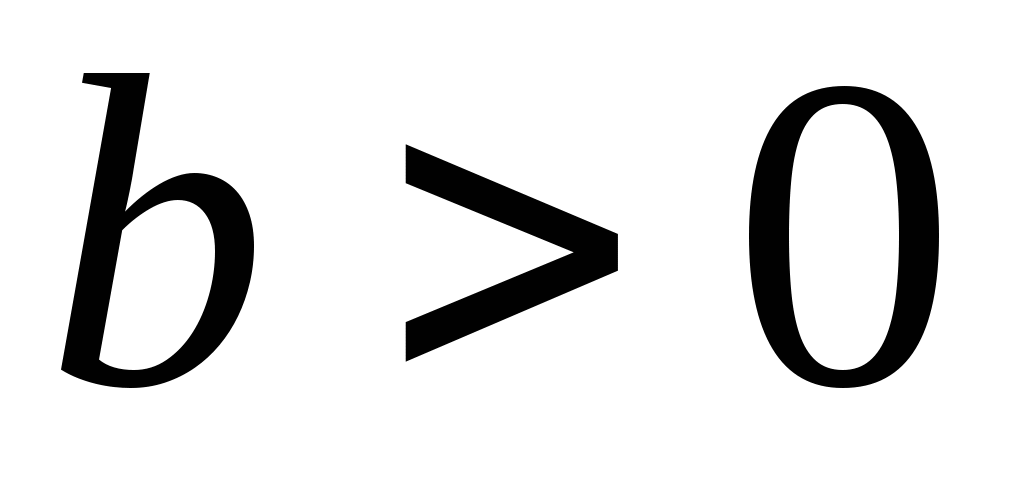 и
и 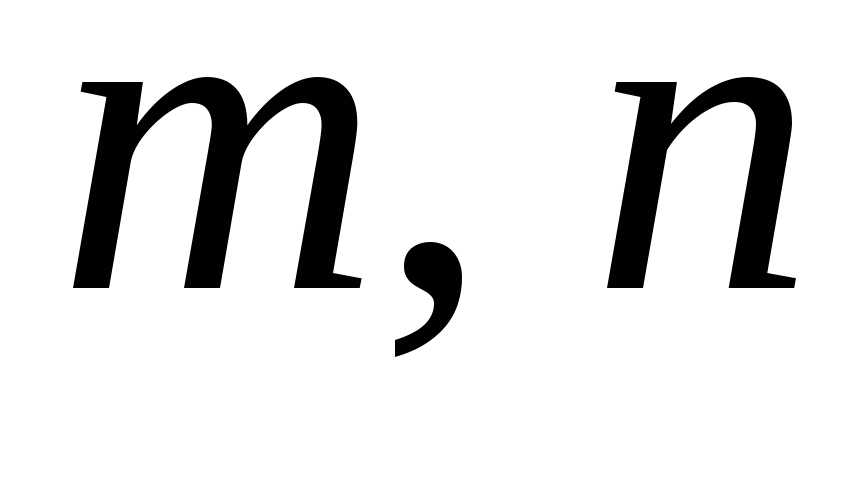 – натуральные числа, причем
– натуральные числа, причем 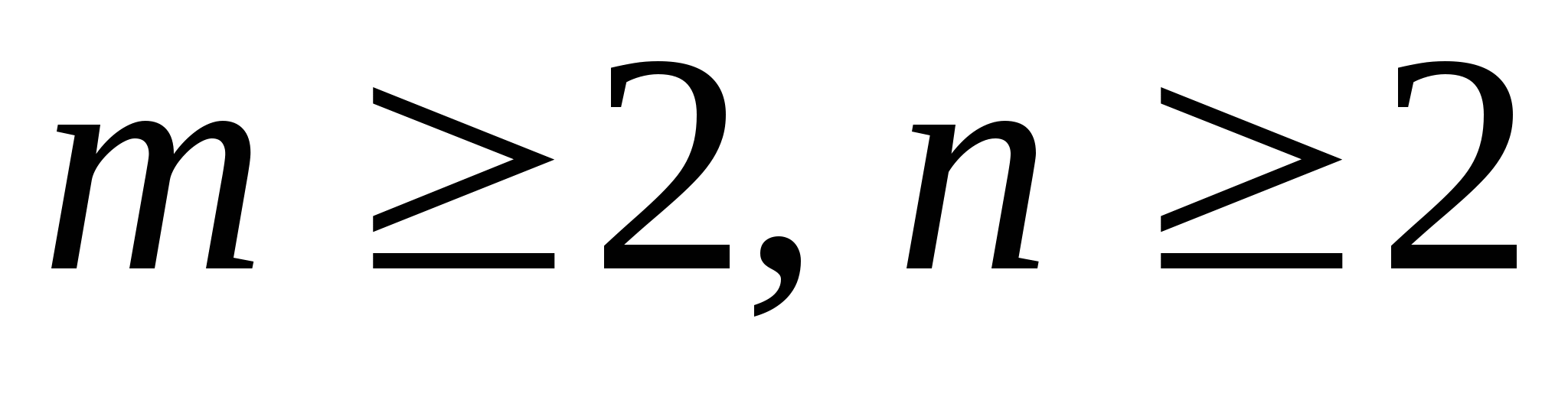 , то
, то
1. 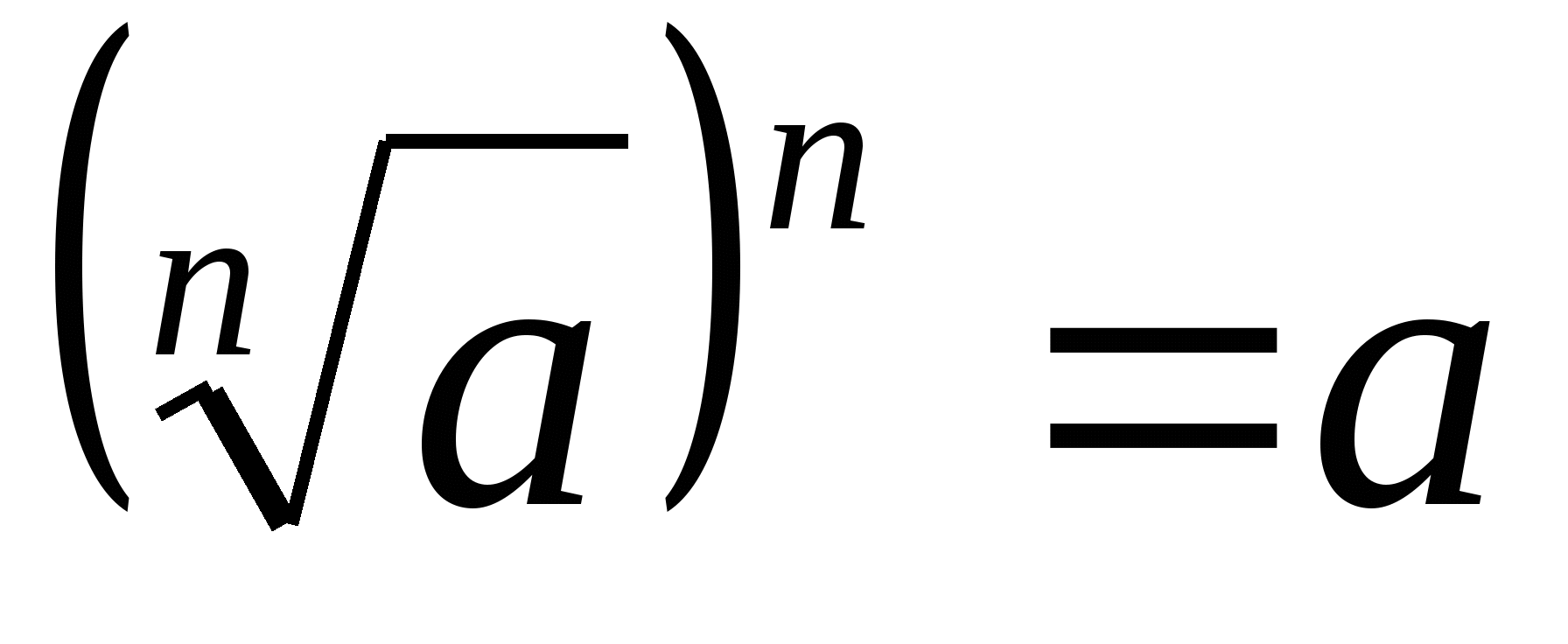
2. 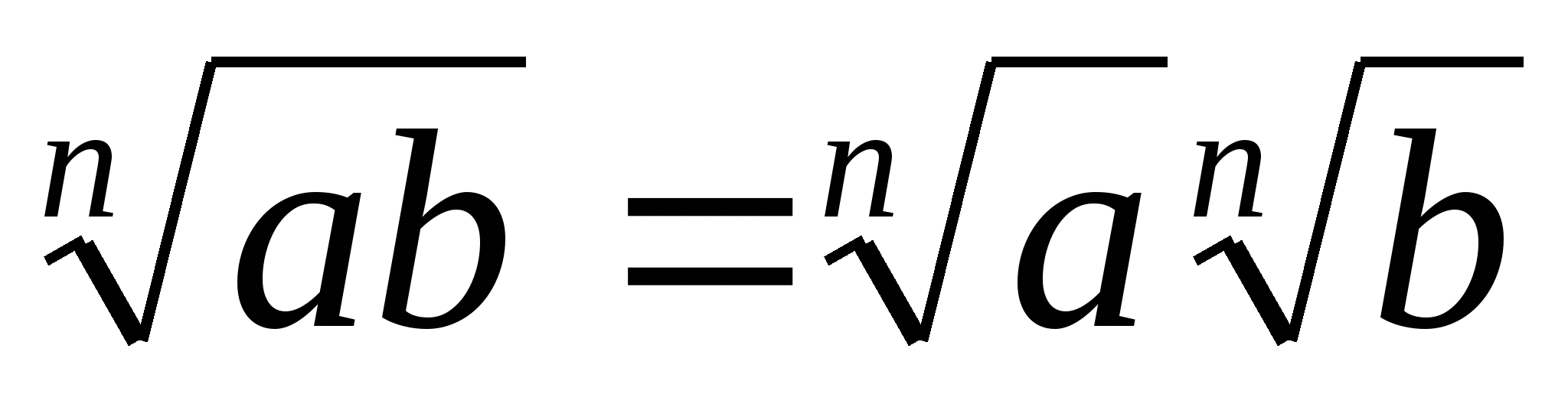
3. 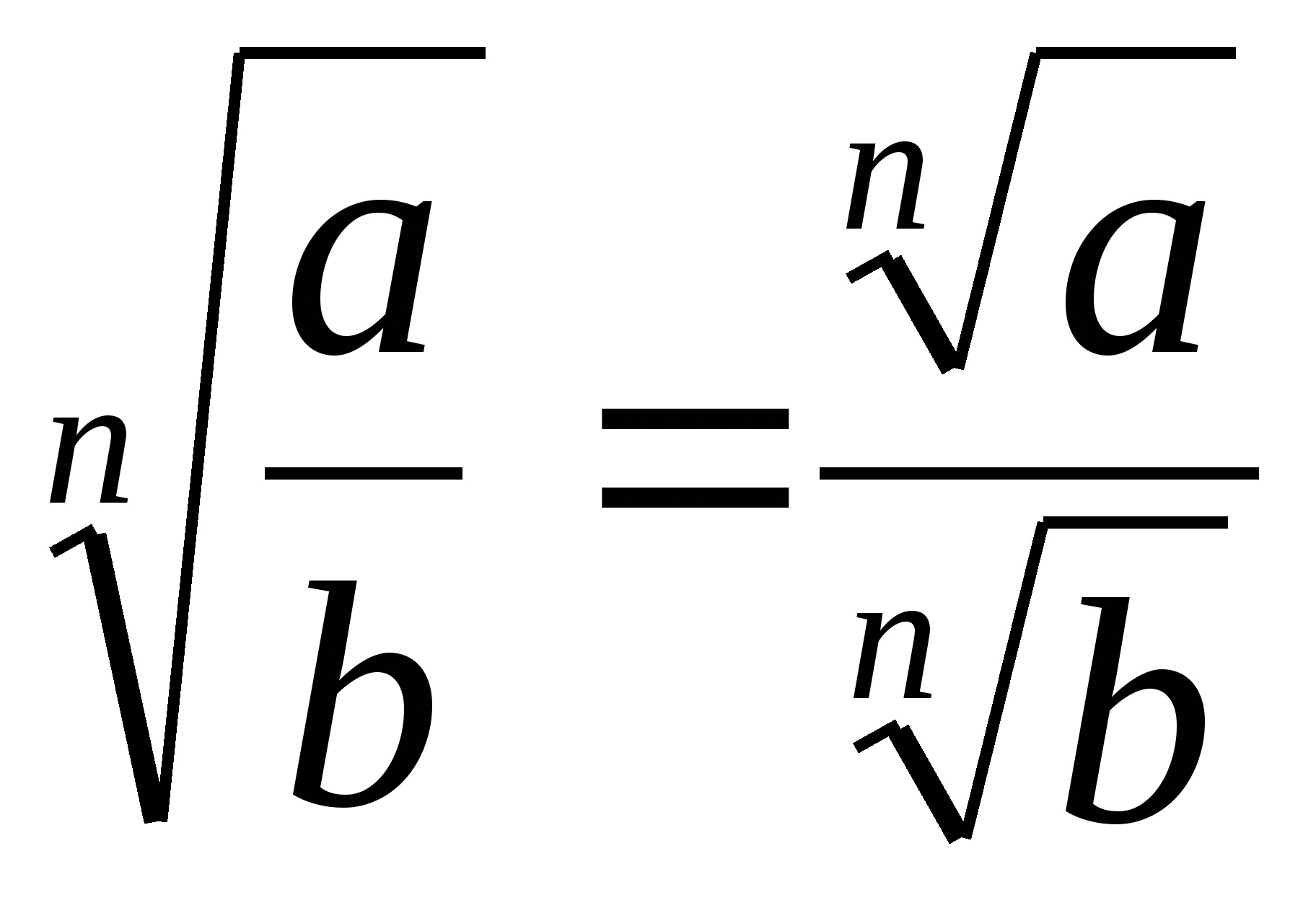 ,
, 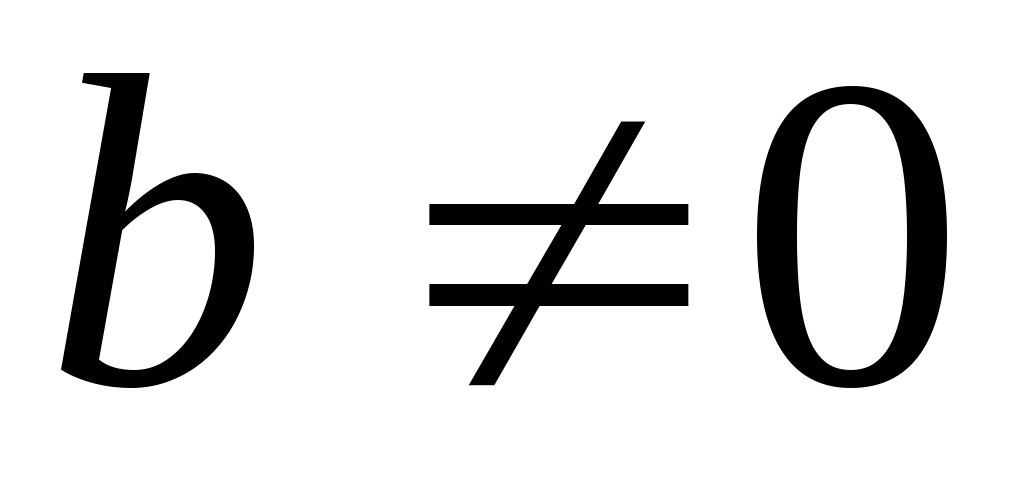
4. 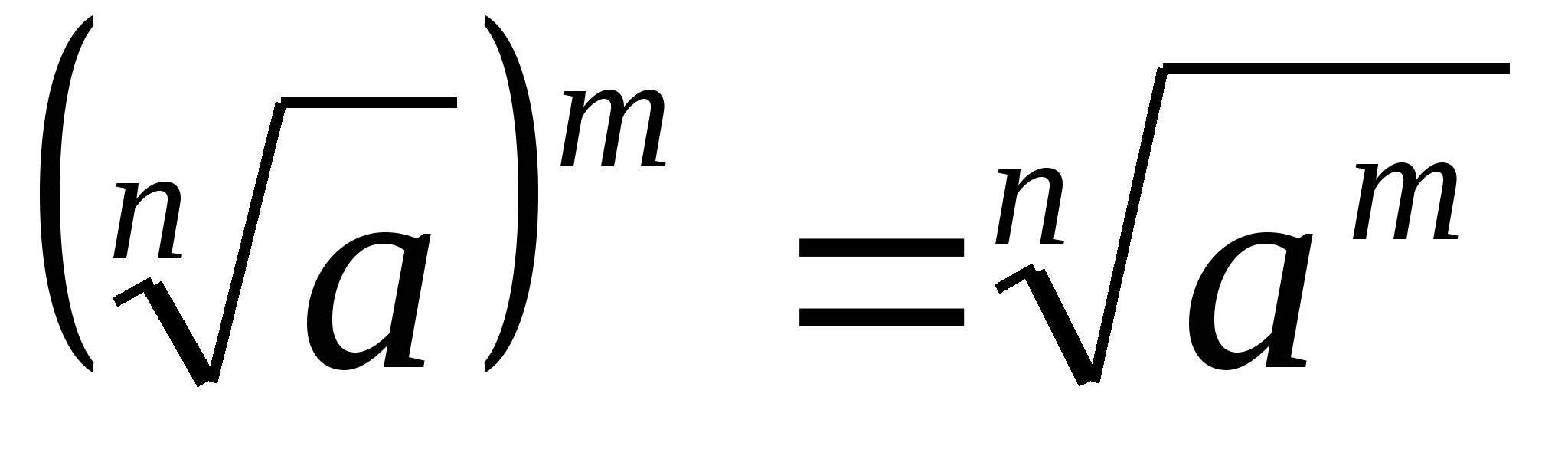
5. 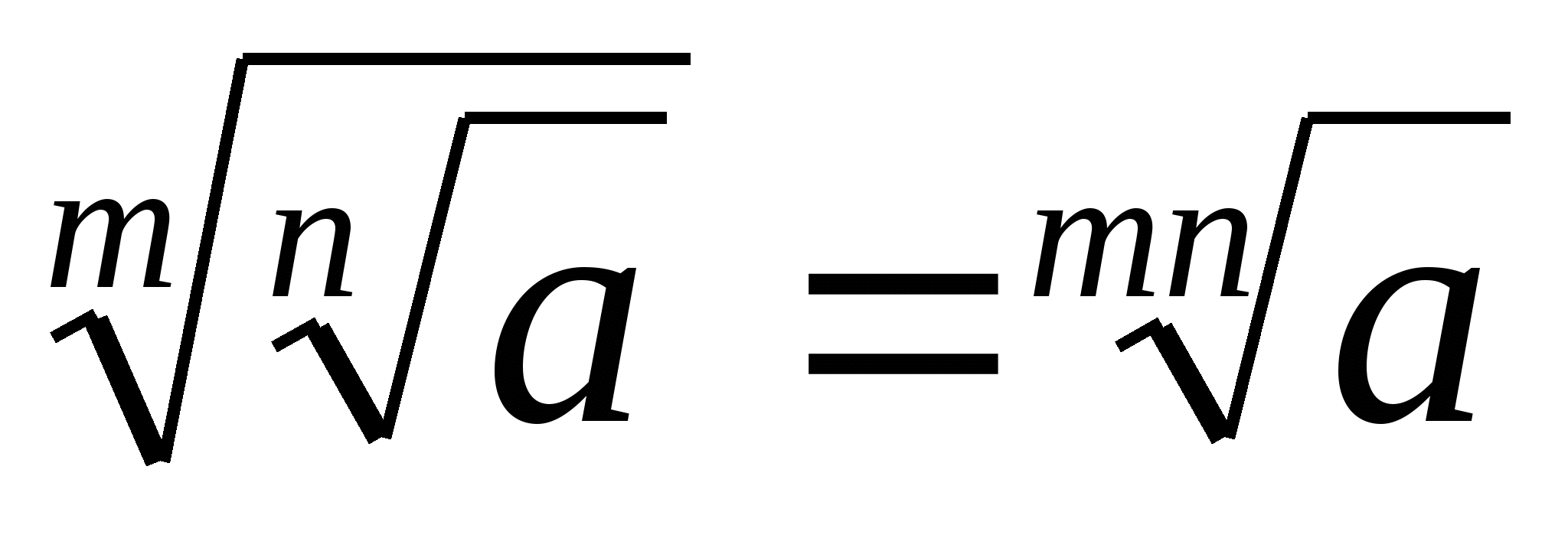
6. 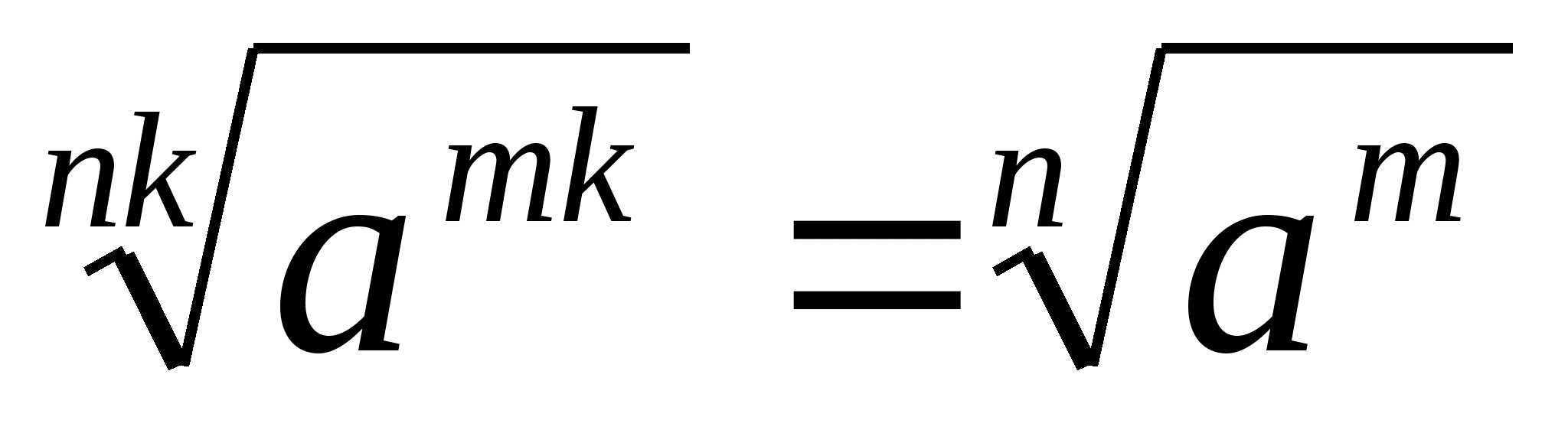 .
.
4. Решение ключевых задач.
Пример 1. 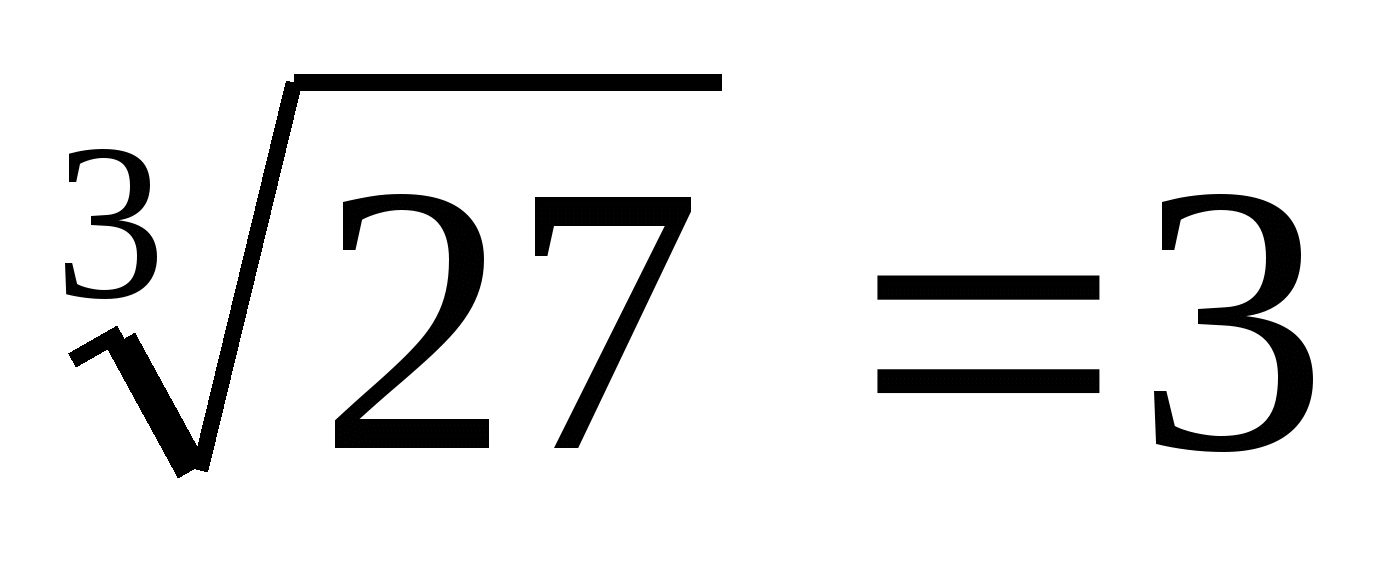 , так как
, так как 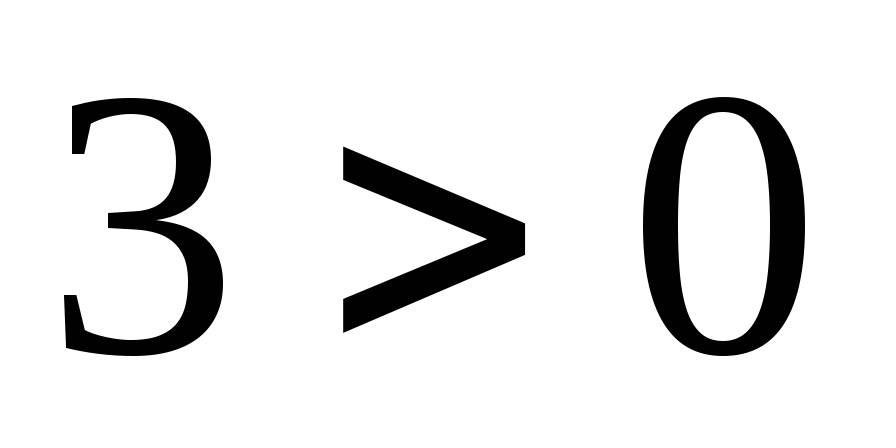 и
и 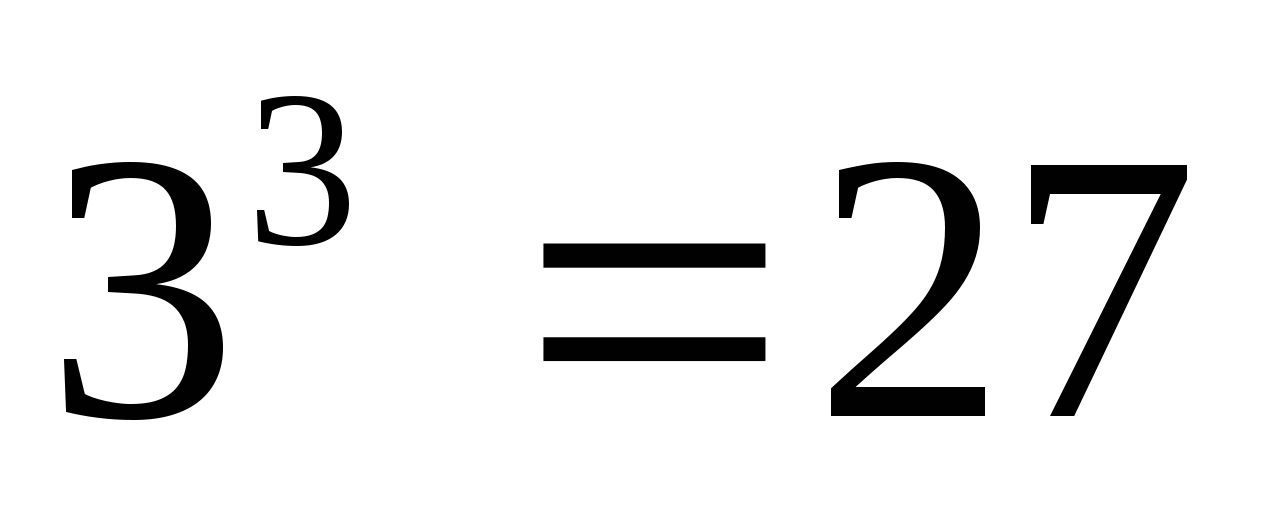 .
.
Пример 2. 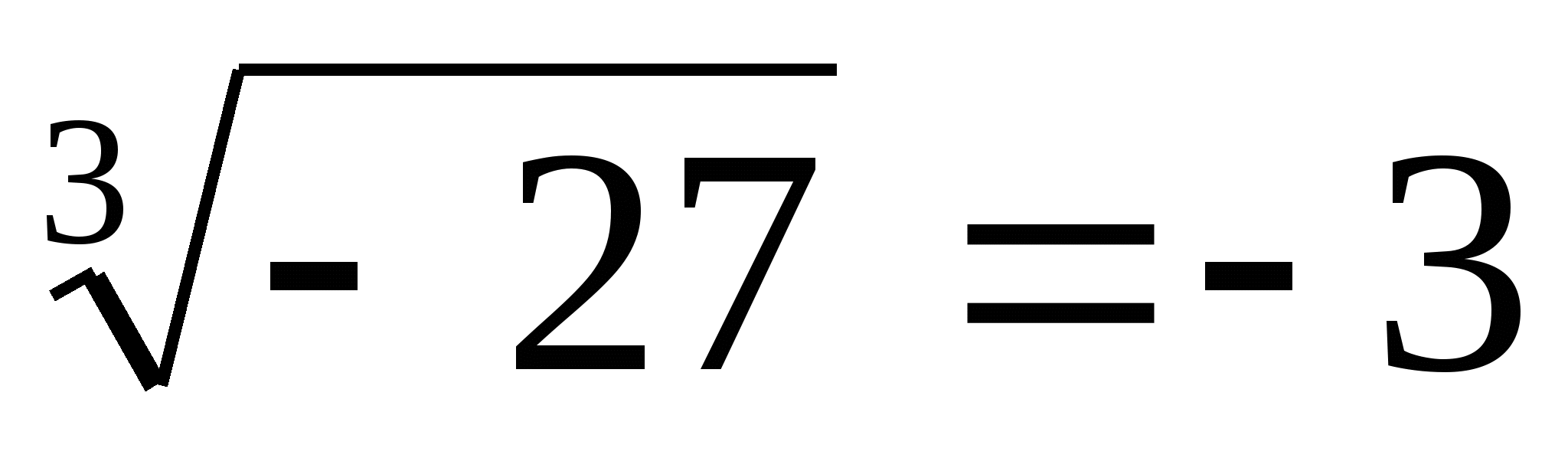 ,
, 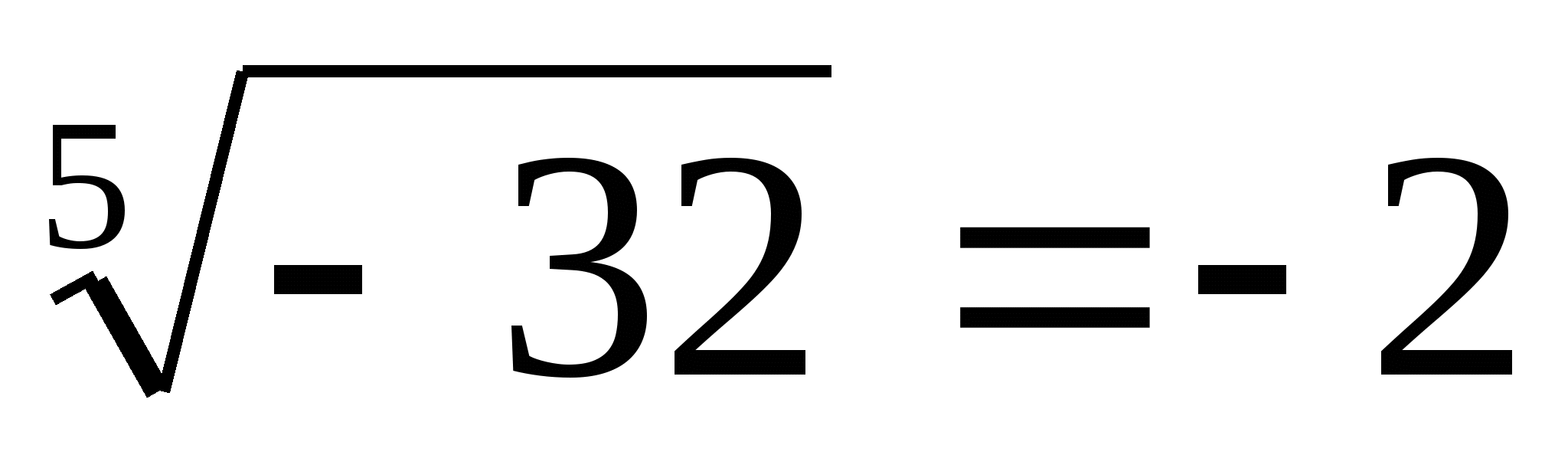
Пример 3. Вычислить 1. 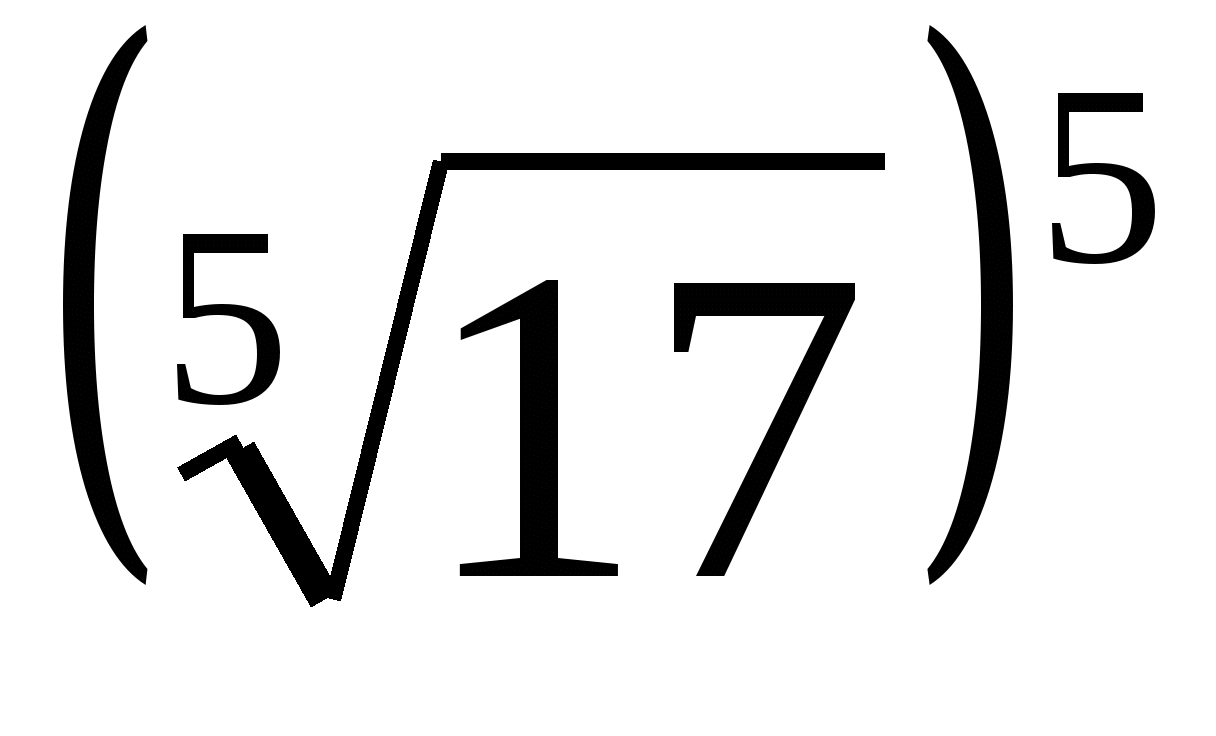 ;
;
Решение. Используя свойства арифметического корня натуральной степени, получаем: 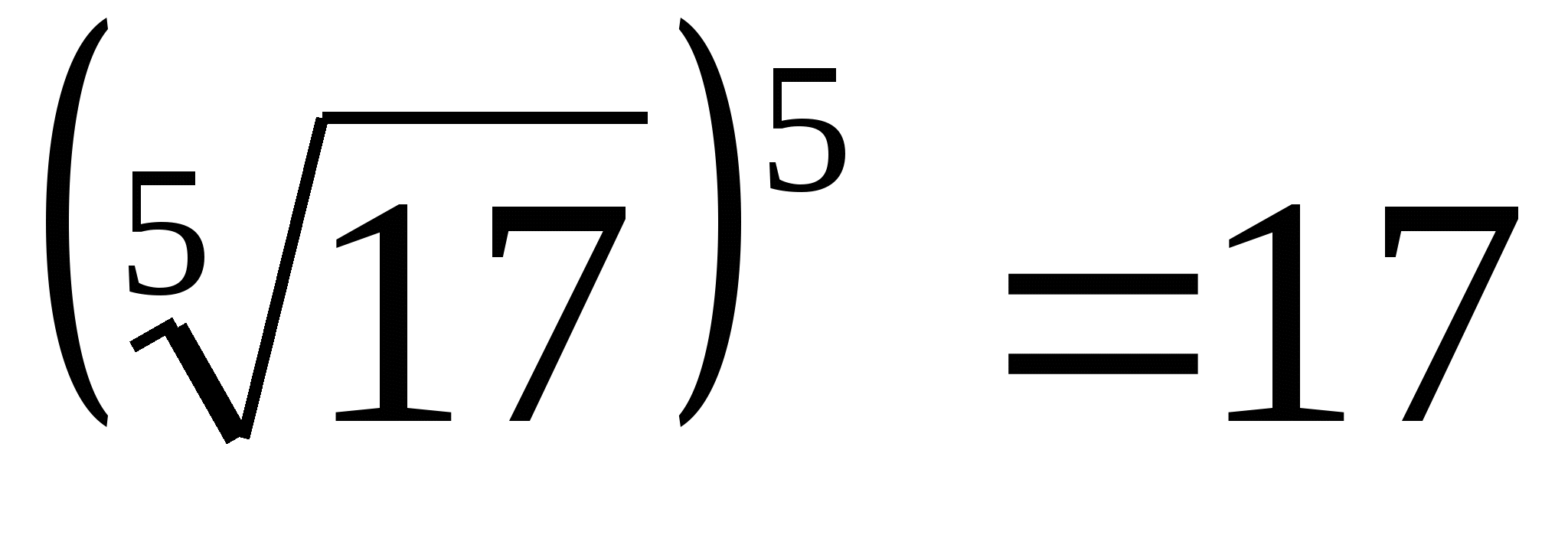 .
.
5. Решение упражнений.
1. Вычислить
1. 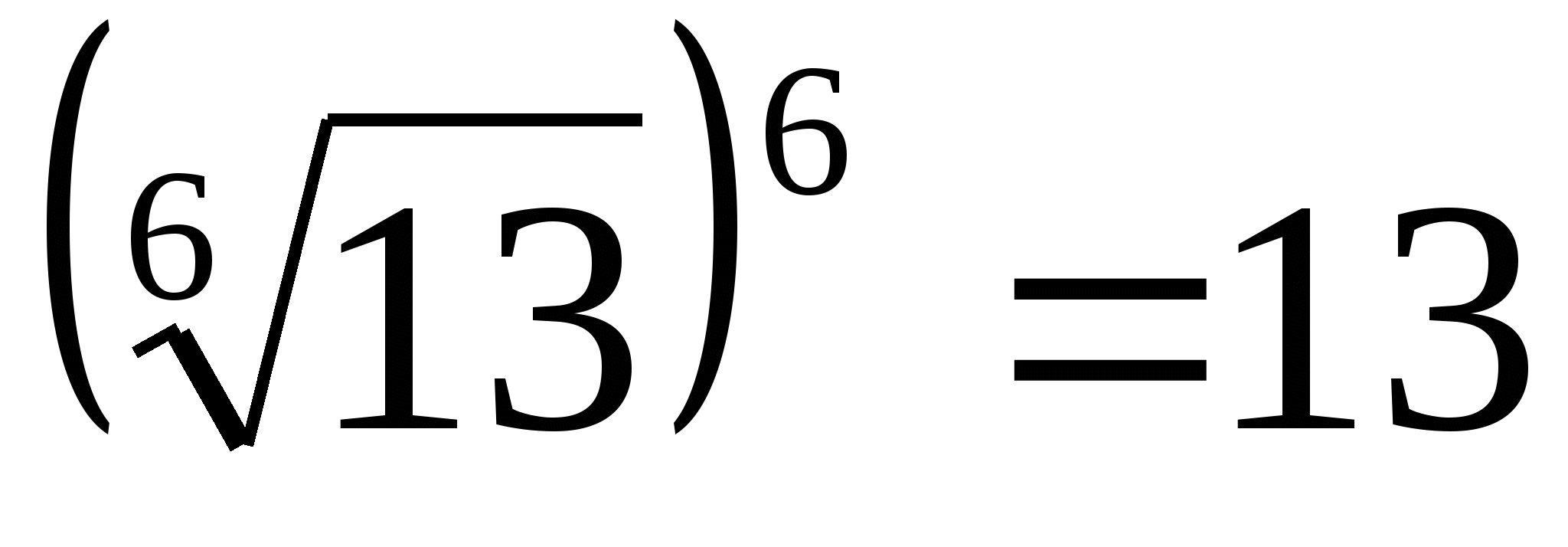 ;
;
2. 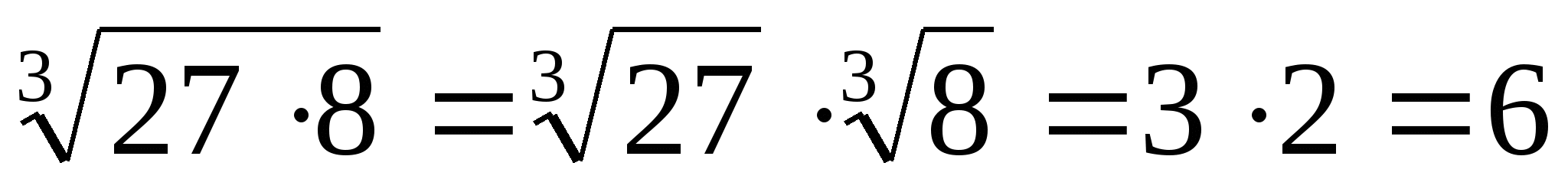 ;
;
3. 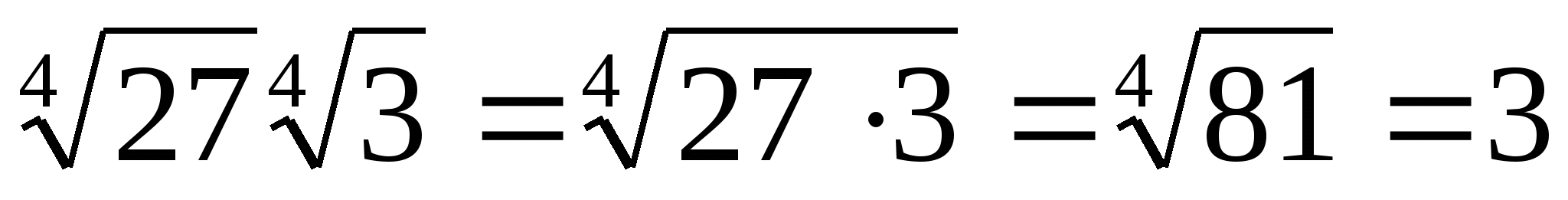
4. 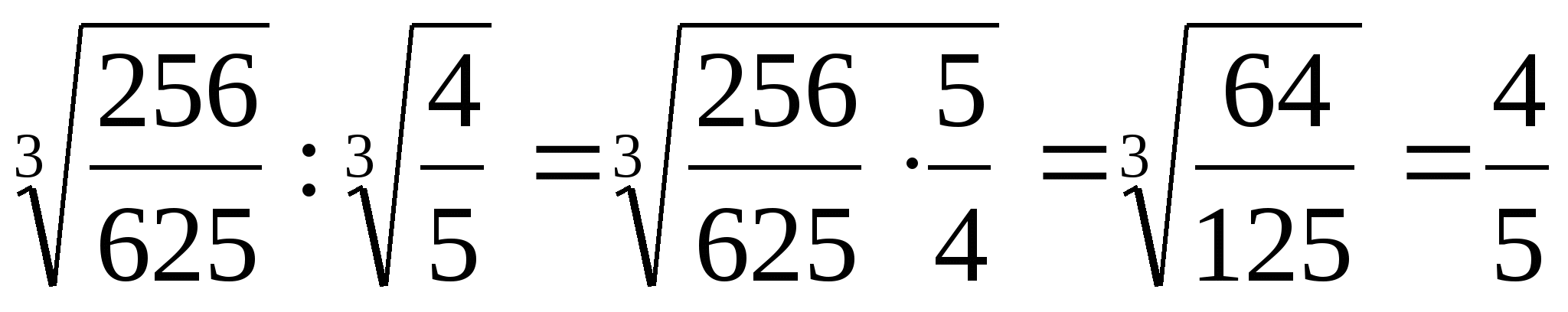 ;
;
5. 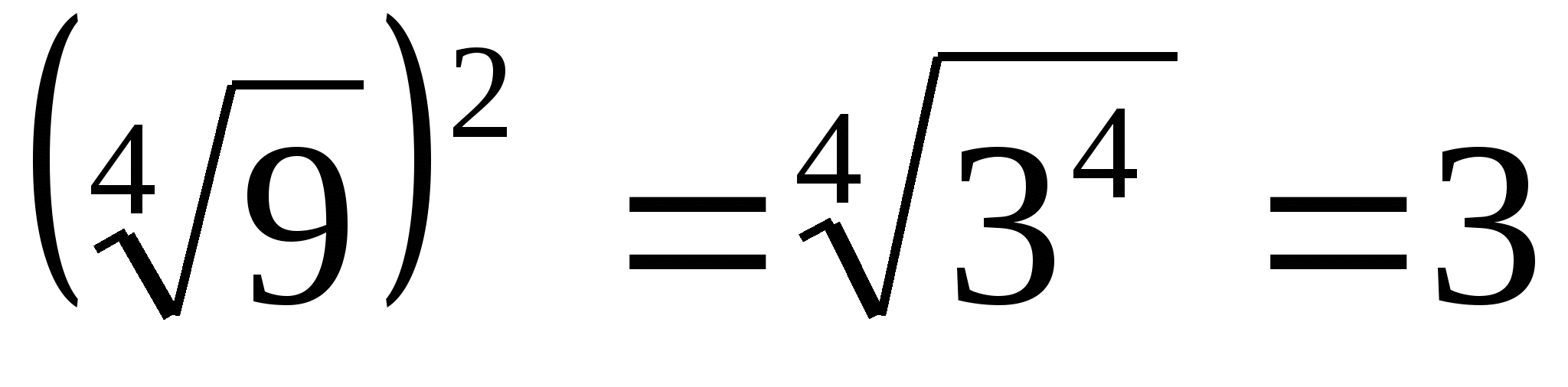 ;
;
6. 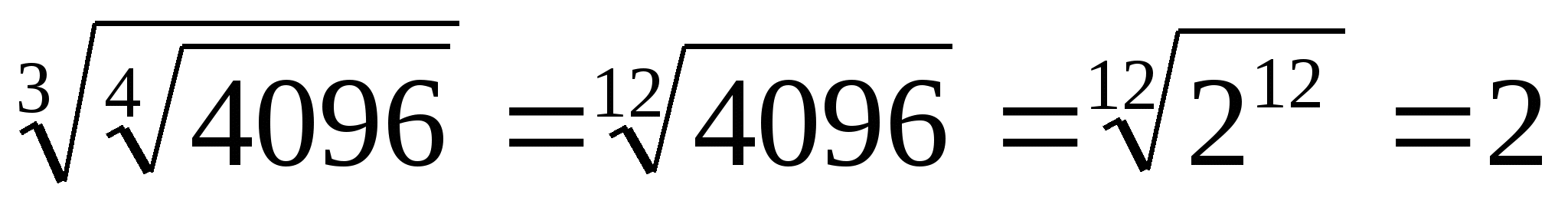 ;
;
7. 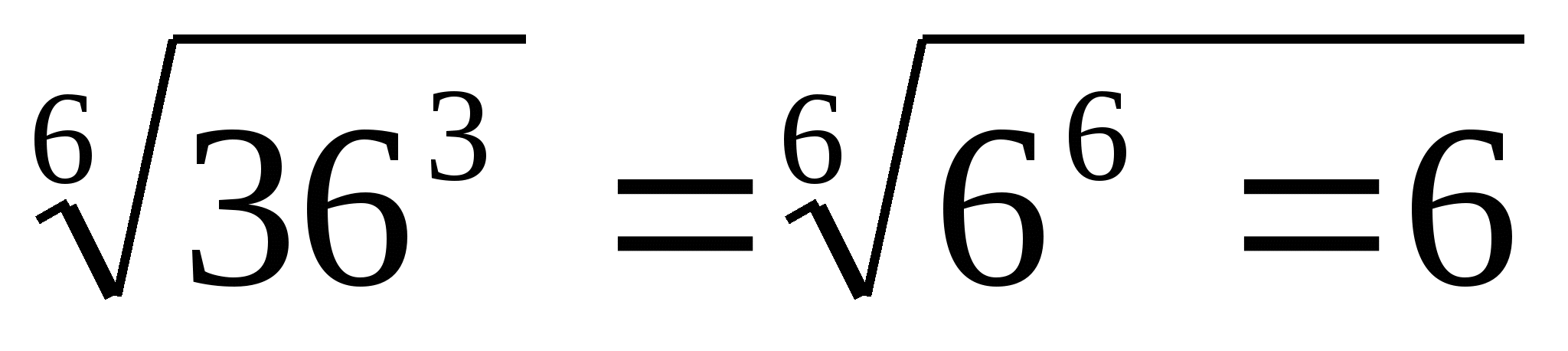 .
.
2. Найти значение выражений:
1) 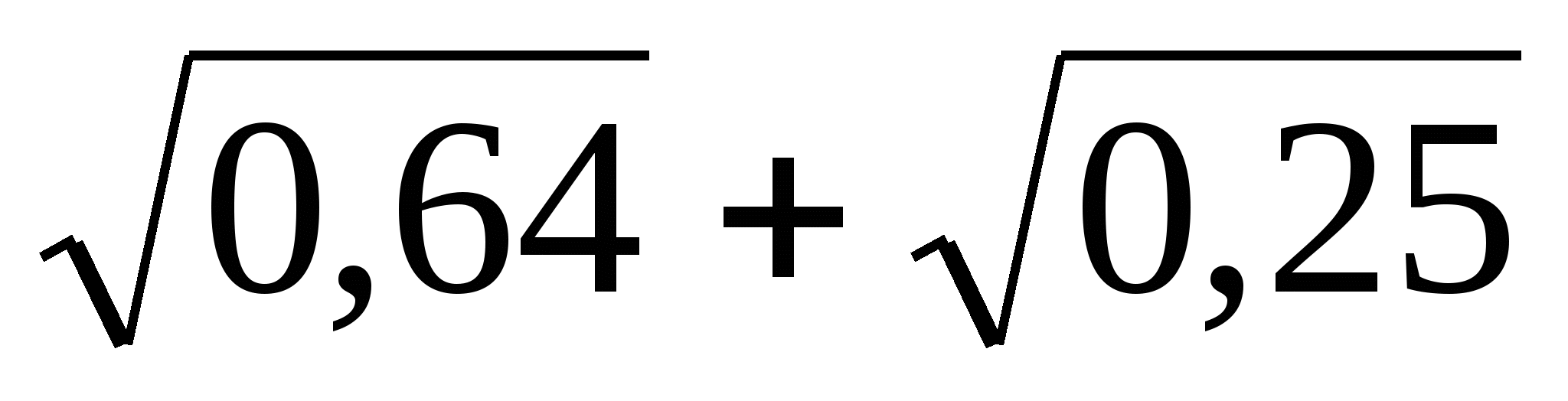 ; 2)
; 2) 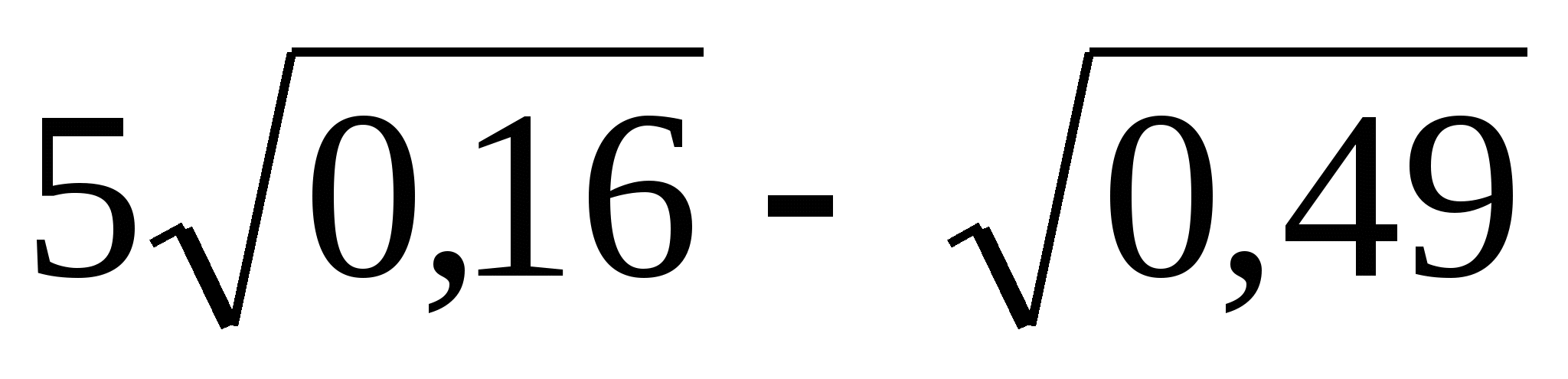 .
.
Решение.
1) В данном выражении первым действием является извлечение квадратного корня из числа. Вторым действием — сложение полученных результатов. При вычислении используем 1-ое свойство корней:
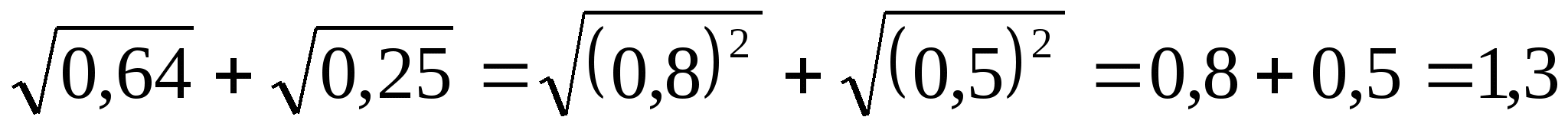 .
.
2) Аналогично предыдущему примеру, первым действием является извлечение квадратного корня из числа. Вторым и третьим действиями — умножение и разность полученных результатов. При вычислении используем 1-ое свойство корней:
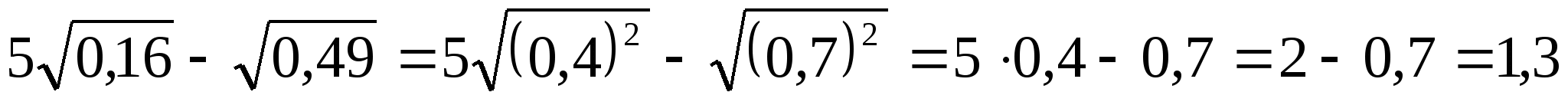 .
.
3. Вычислить. 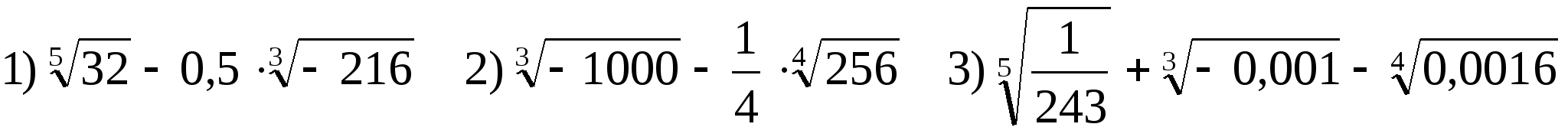
Решение.
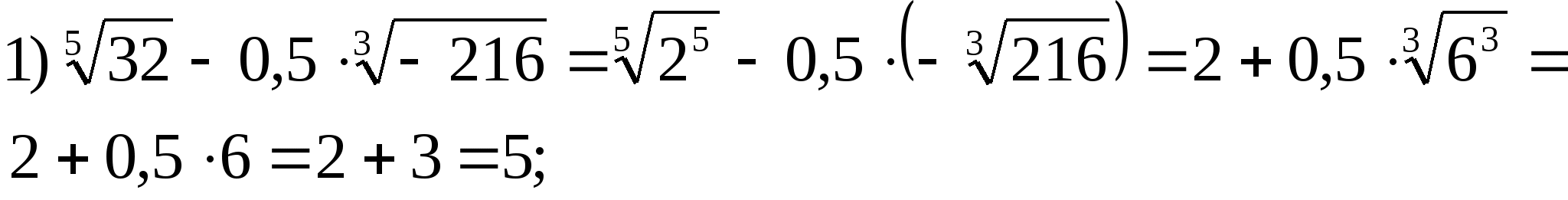
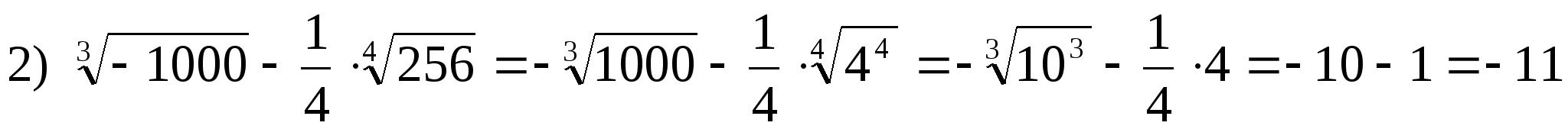 ;
;
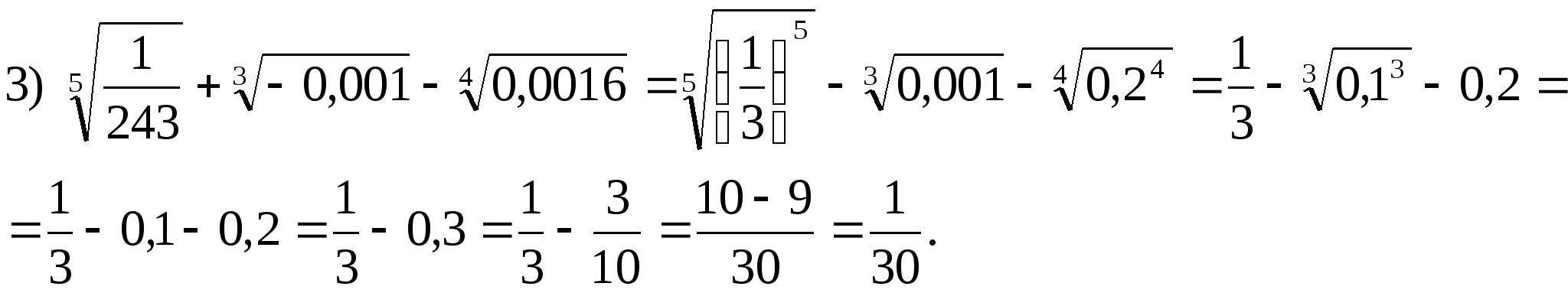
Задание 1. Вычислить (резерв)
1)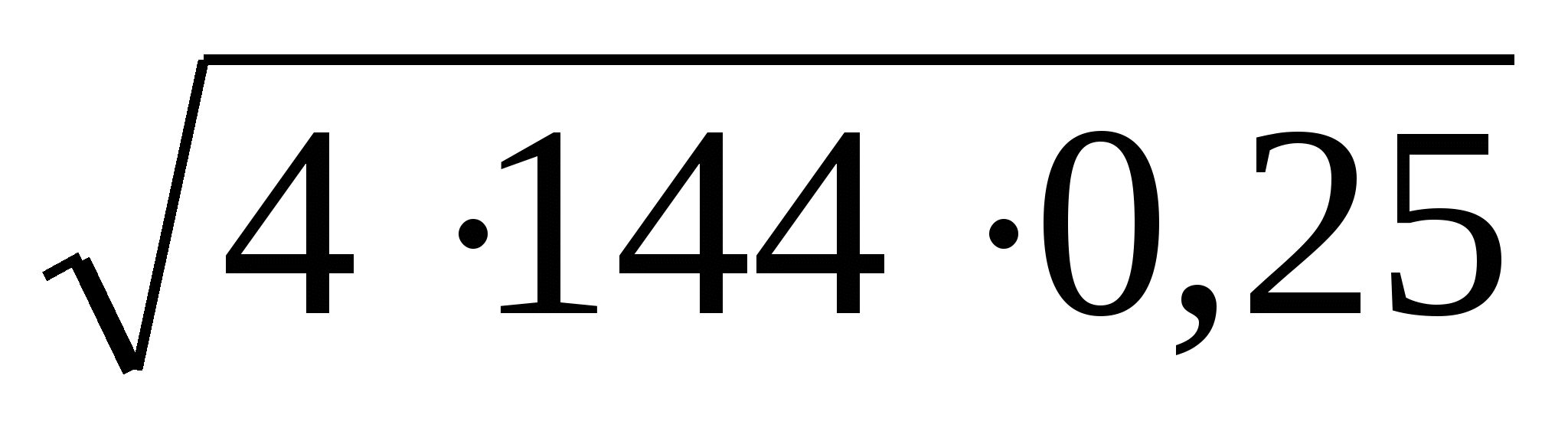 ; 2)
; 2) 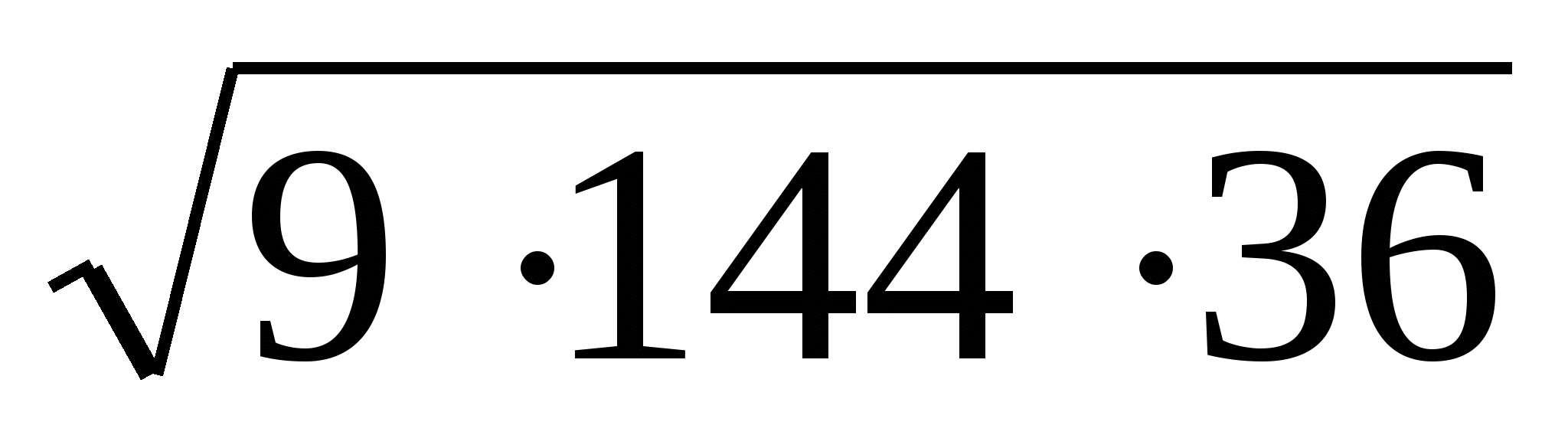 ;
;
3) 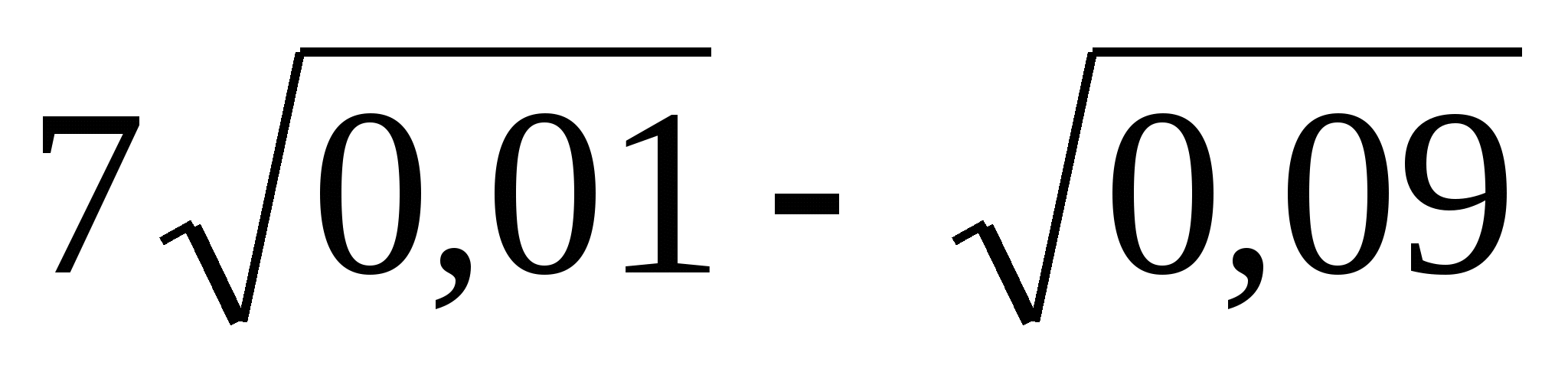 ; 4)
; 4) 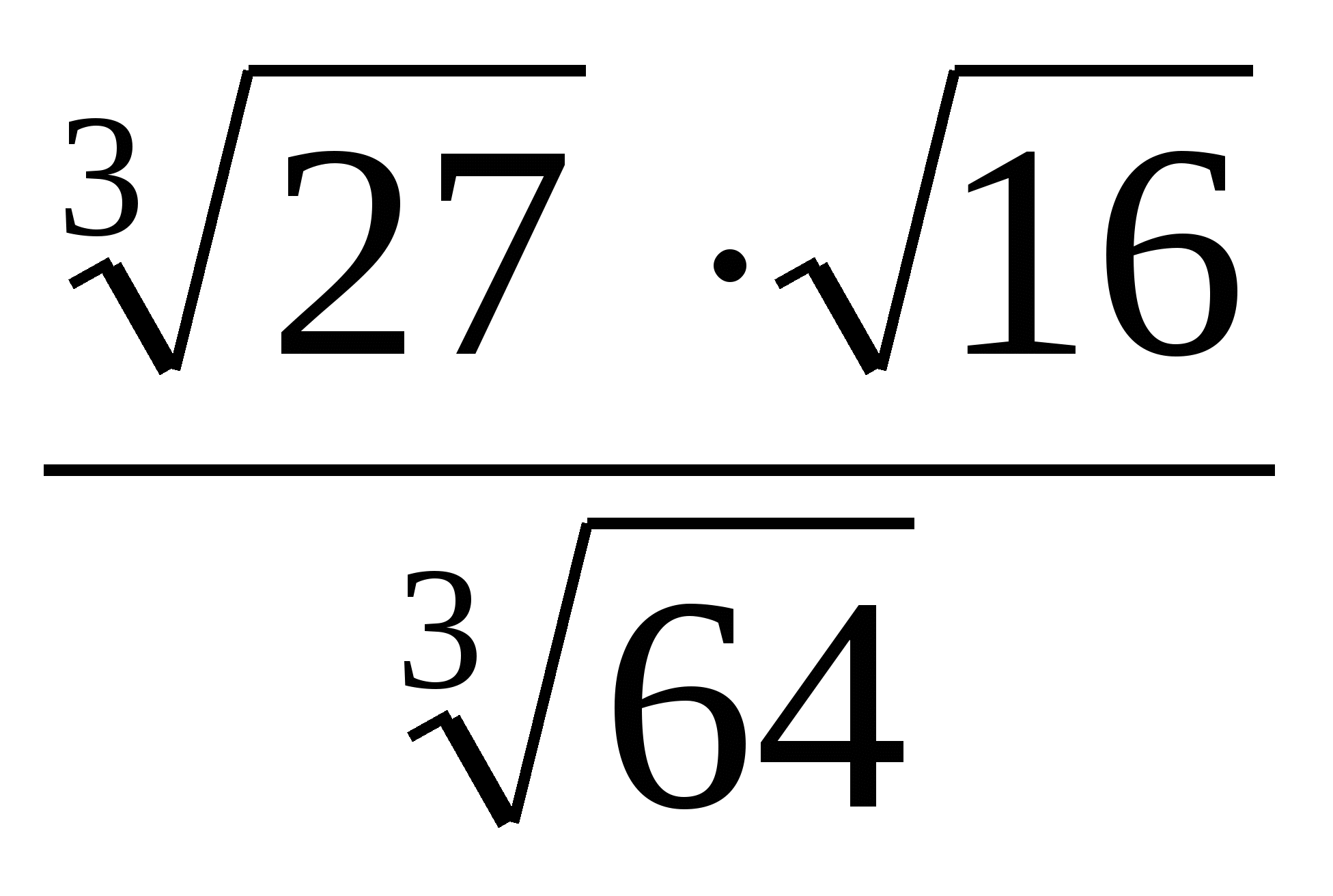 ;
;
5) 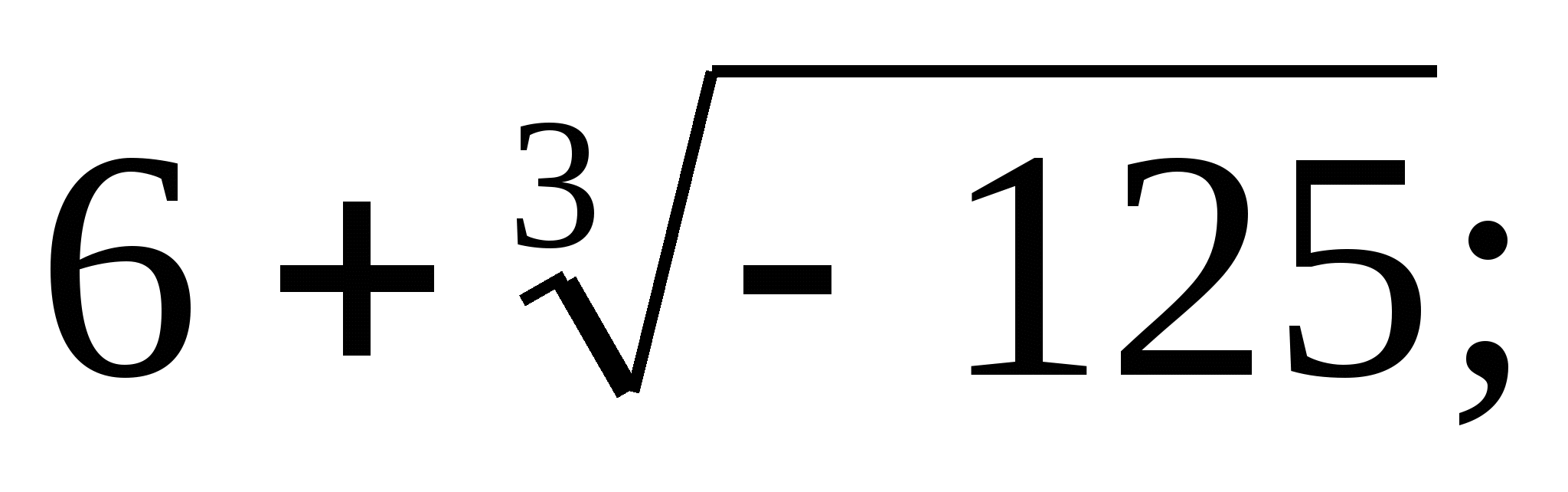 6)
6) 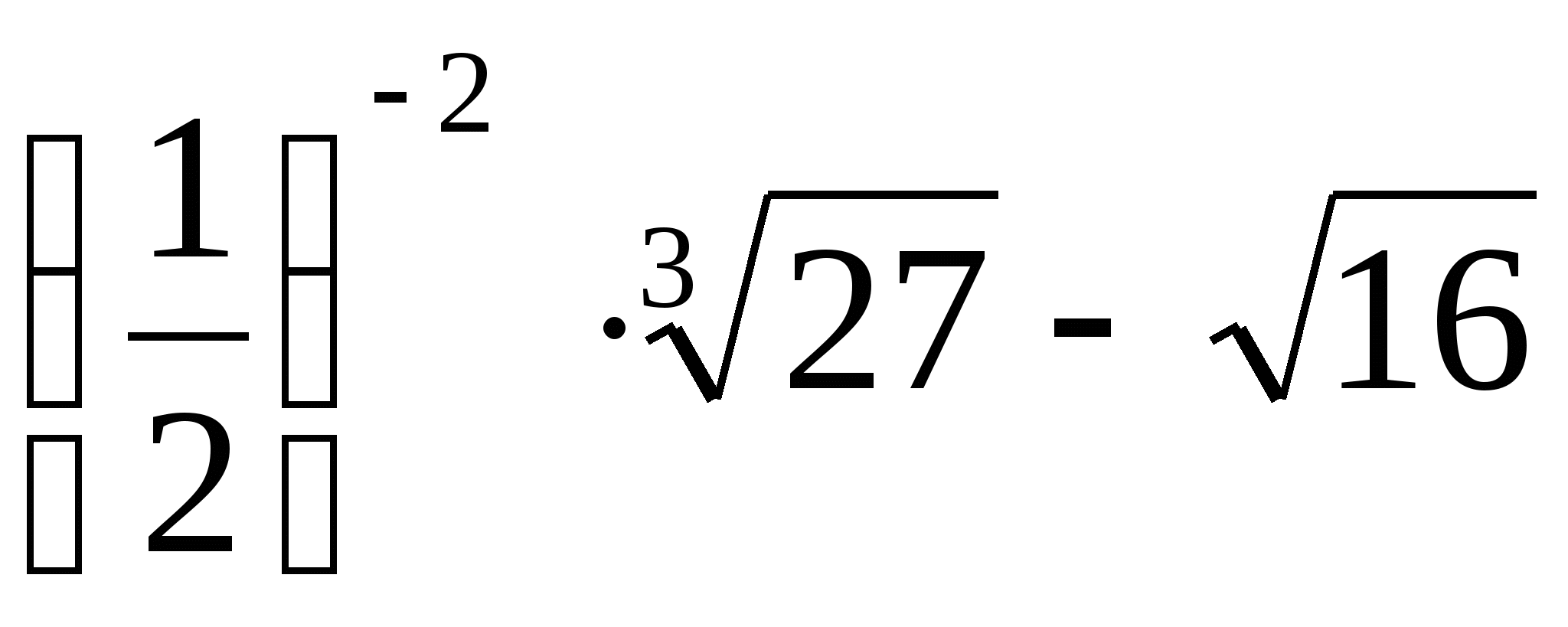 ;
;
7) 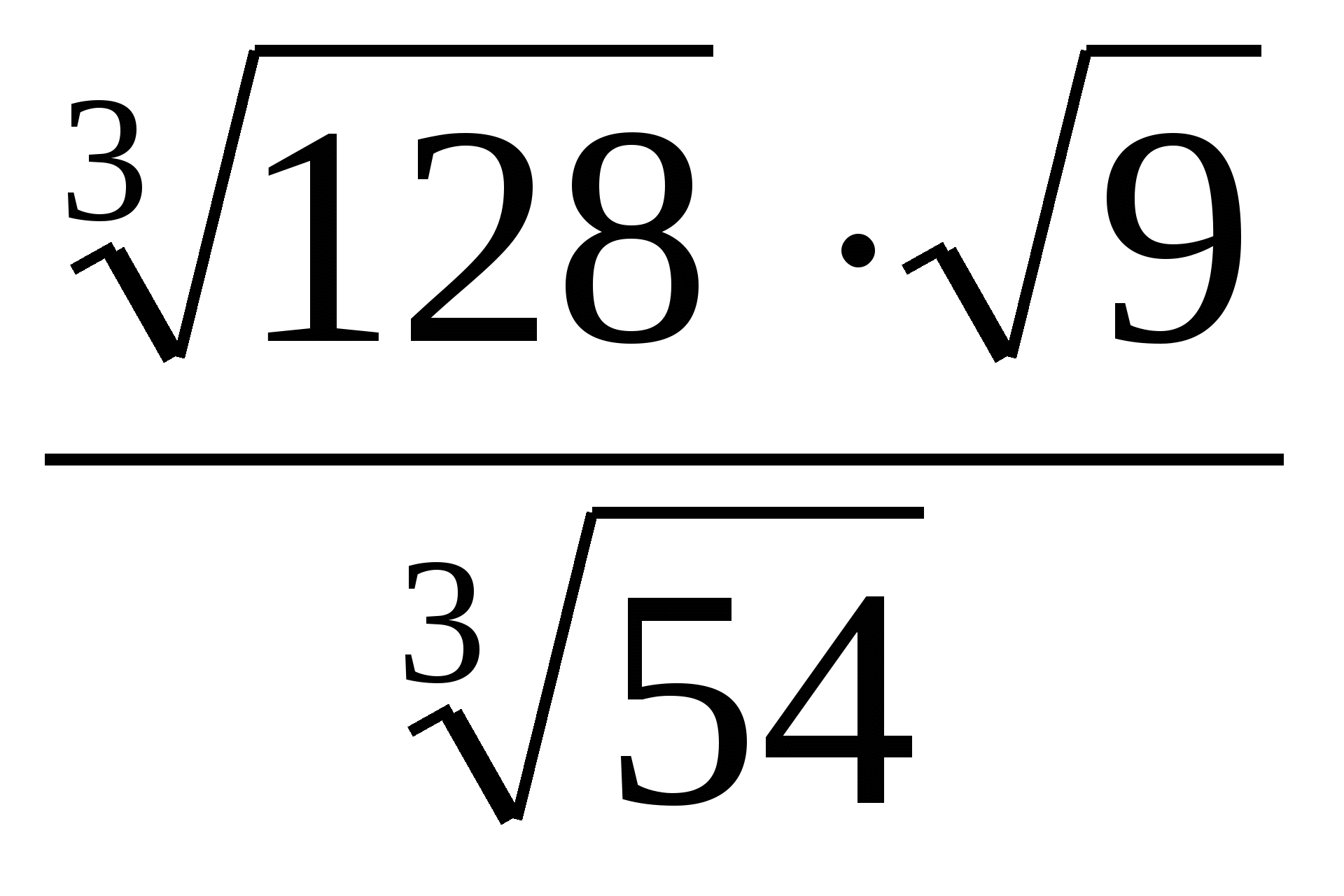 ; 8)
; 8) 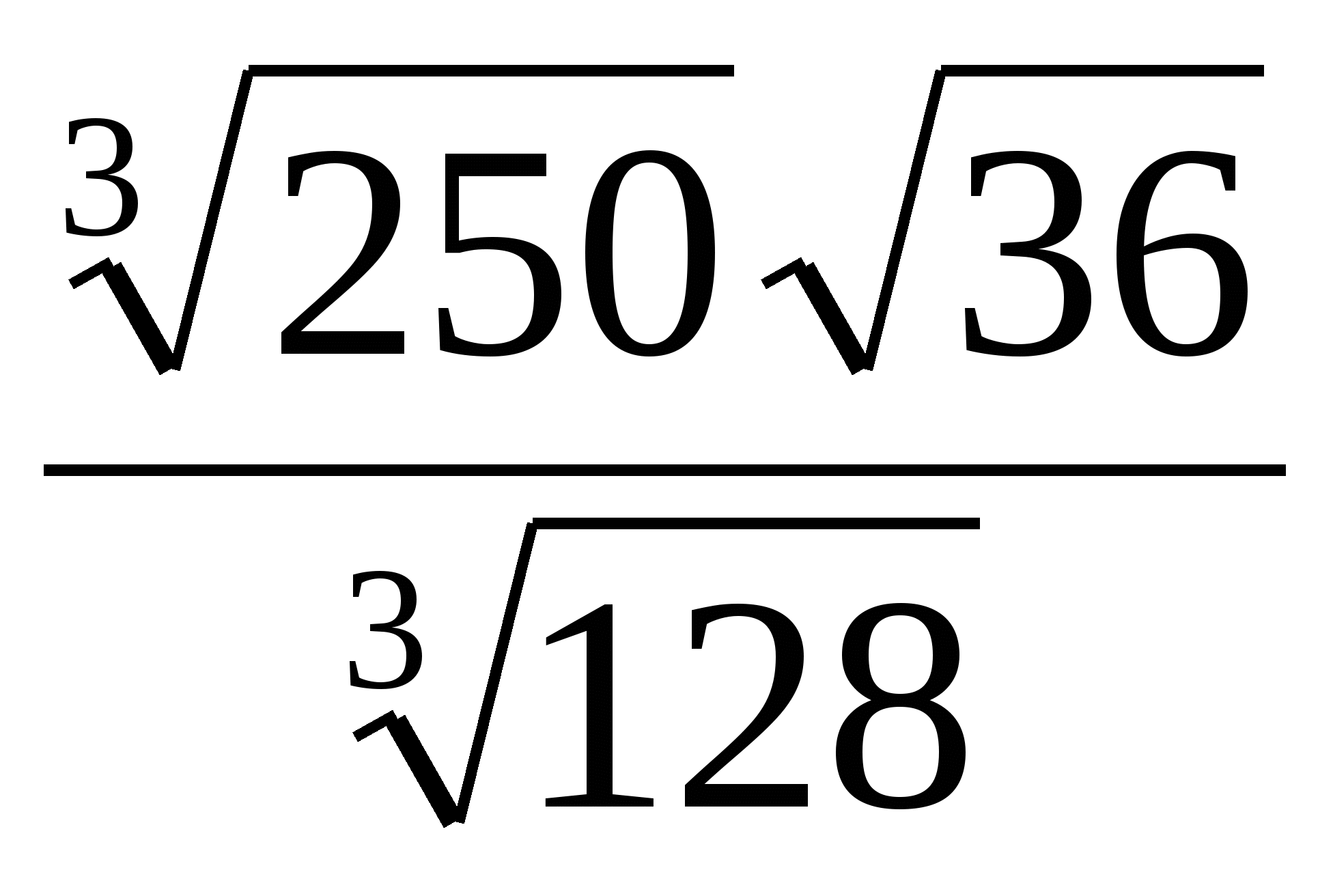 ;
;
9) 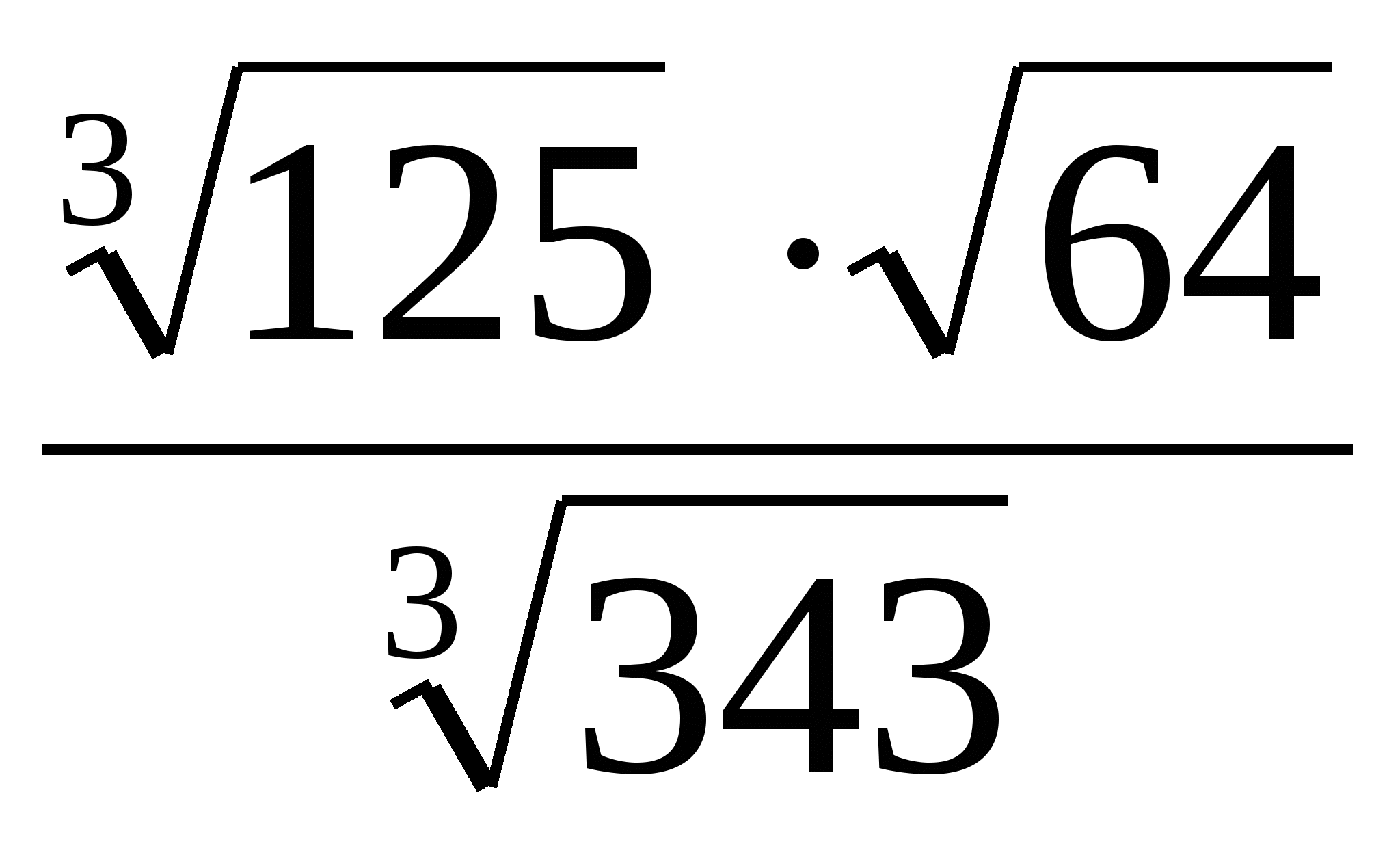 ; 10)
; 10) 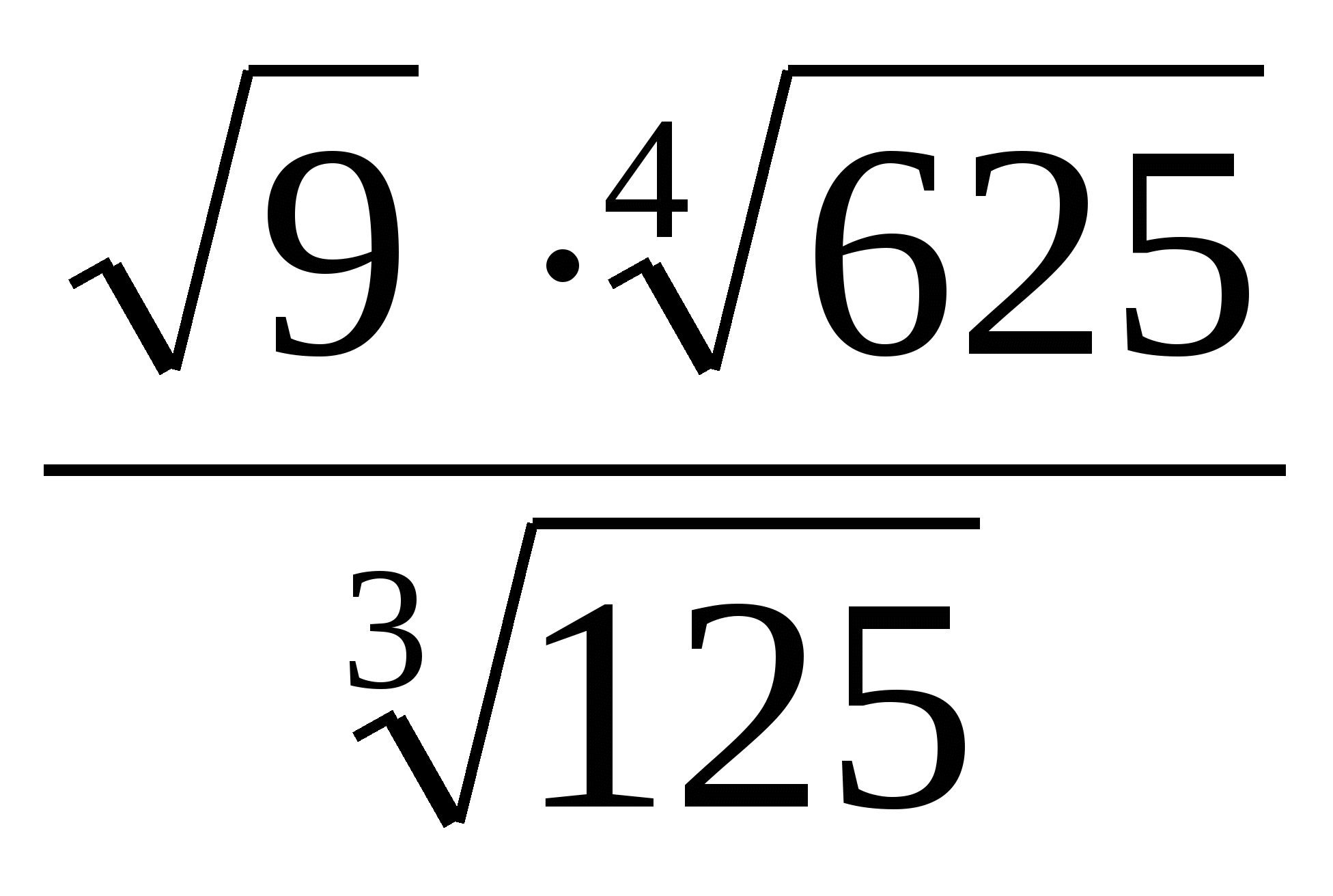 ;
;
11) 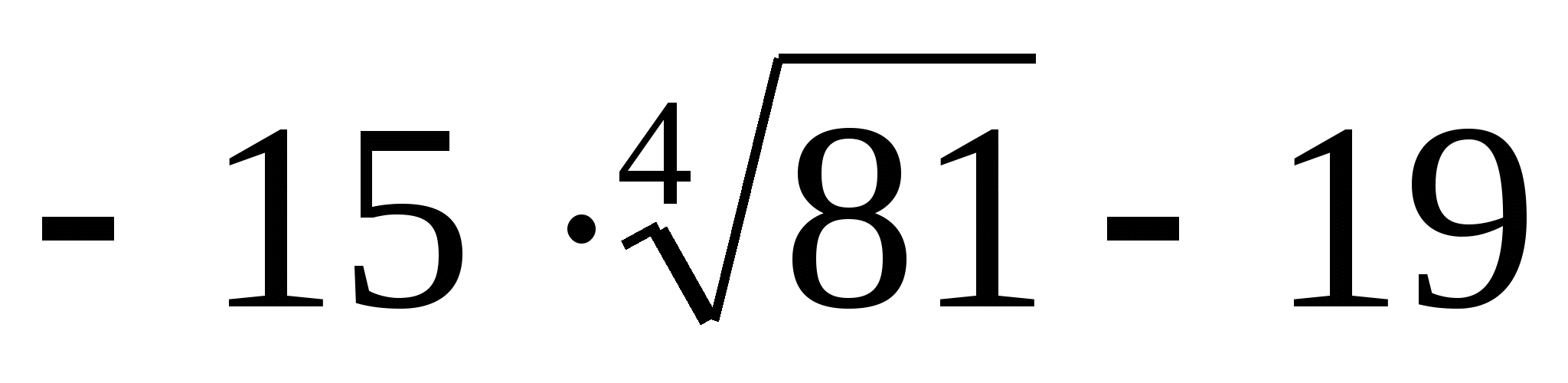 ; 12)
; 12) 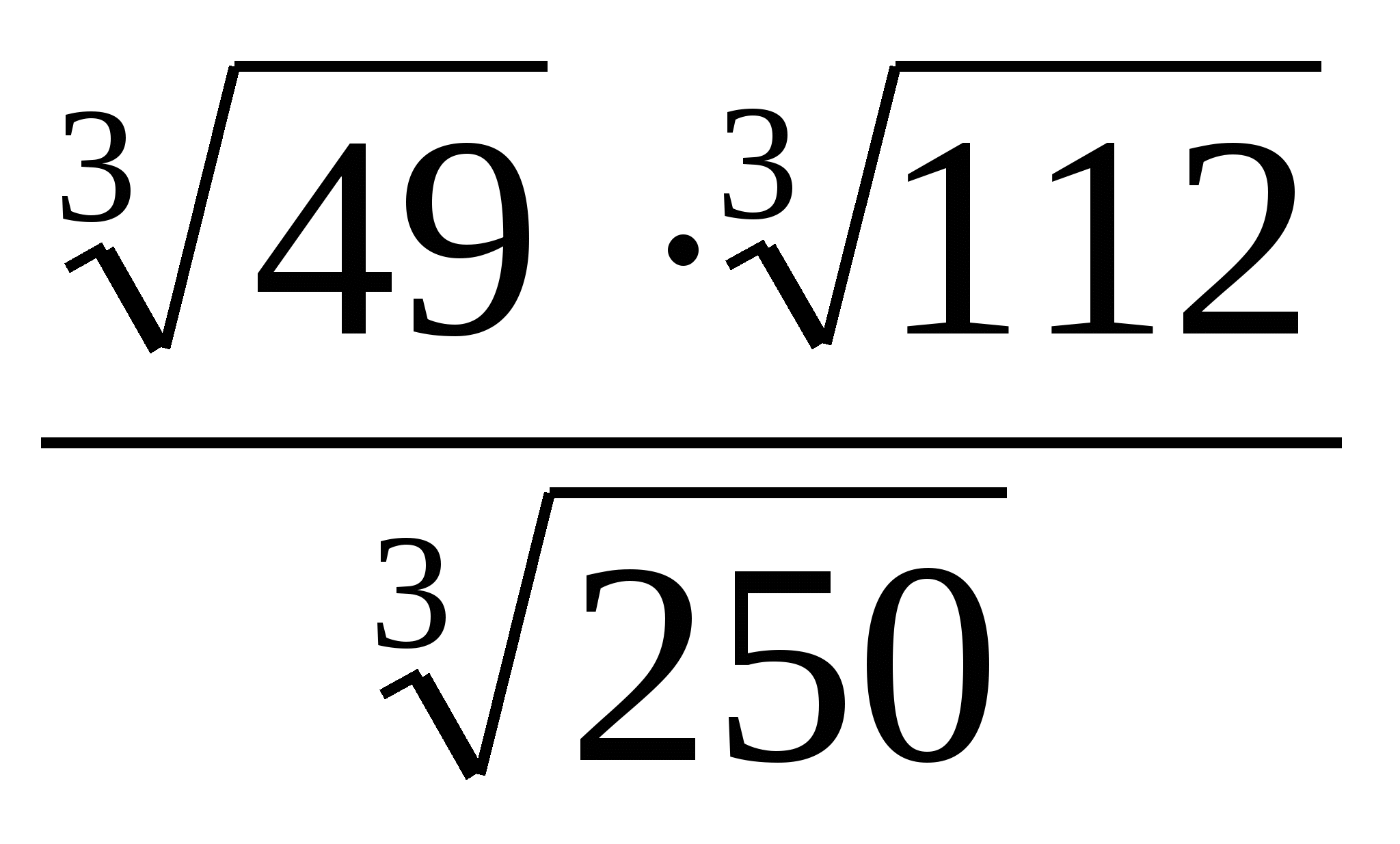
6. Подведение итогов урока. Выставление оценок. Домашнее задание: выучить теоретический материал, задание 1 (нечетные).
infourok.ru