Окружность — Википедия

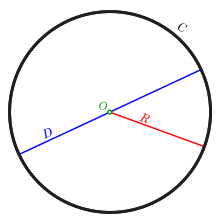Окружность (C), её центр (O), радиус (R) и диаметр (D)

Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки^[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части^[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.

Построение окружности циркулем

Практическое построение окружности возможно с помощью циркуля.

Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.

Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Далее всюду буква R{\displaystyle R} обозначает радиус окружности.

Прямая может иметь с окружностью не более двух общих точек.

Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D=2R,{\displaystyle D=2R,} он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды^[3].

Хорда разбивает круг на две части, называемые

сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)^[3].

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Для заданной окружности имеют место следующие свойства^[3].

• Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
• Равным хордам соответствуют равные дуги, и наоборот.

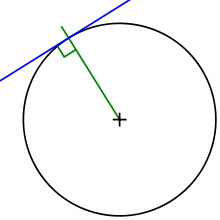
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности

[4].

Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности^[5].

• 

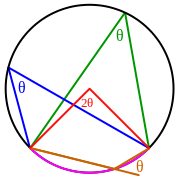
  Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)

• 

  К расчёту длины дуги и хорды

Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.

Из определения радиана следует, что длина L{\displaystyle L} любой дуги окружности связана с центральным углом θ{\displaystyle \theta }, опирающимся на эту дугу, простым соотношением^[6]: L=Rθ.{\displaystyle L=R\theta .} (при этом длина хорды, стягивающей ту же дугу, равна 2Rsin⁡θ2<L{\displaystyle 2R\sin {\theta \over 2}<L}). Поскольку длина окружности равна 2πR{\displaystyle 2\pi R}, с ростом угла значение его радианной меры меняется от 0 до 2π.{\displaystyle 2\pi .}

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол

θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.

Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.

Свойства вписанных углов:

• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
• Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

Другие свойства:

• Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
• Угол между пересекающимися хордами равен
  полусумме мер дуги, лежащей в угле, и дуги напротив неё.
• Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.

• Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
• Говорят, что две окружности касаются, если они имеют единственную общую точку. Точка касания двух окружностей лежит на прямой, проходящей через их центры.
• Теорема о секущих: Если через произвольную точку E{\displaystyle E} проведена секущая, то произведение расстояний от этой точки до точек пересечения секущей с окружностью не зависит от выбора секущей (и равно абсолютной величине степени точки относительно окружности). Если точка E{\displaystyle E} лежит вне окружности, то из нее к окружности можно провести касательную. Квадрат длины отрезка касательной до точки касания будет равен той же величине.

• Как частный случай предыдущего, при пересечении двух хорд в произвольной точке E{\displaystyle E} получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рисунок), т. е. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.

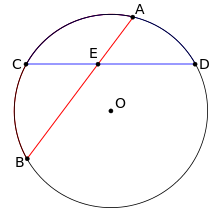AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED} 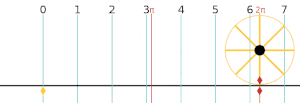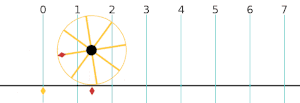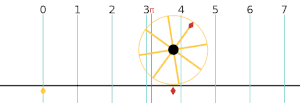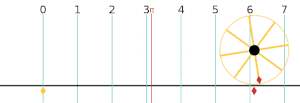Если радиус круга равен 1, то его окружность равна 2π.

Длина окружности:

C=2πR=πD.{\displaystyle C=2\pi R=\pi D.}

Радиус окружности:

R=C2π=D2.{\displaystyle R={\frac {C}{2\pi }}={\frac {D}{2}}.}

Диаметр окружности:

D=Cπ=2R.{\displaystyle D={\frac {C}{\pi }}=2R.}

Площадь круга радиуса R:

S=πR2=πD24.{\displaystyle S=\pi R^{2}={\frac {\pi D^{2}}{4}}.}

Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:

S=πR2α360∘.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.}

Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:

S=πR2α360∘−R2sin⁡α2.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.}

Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.

Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.

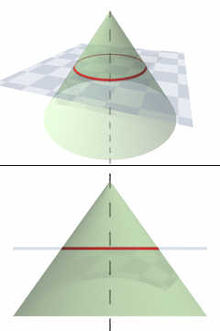Окружность получается как сечение конуса плоскостью, перпендикулярной его оси

Аналитическая геометрия окружностей[править | править код]

С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.

Декартовы координаты[править | править код]

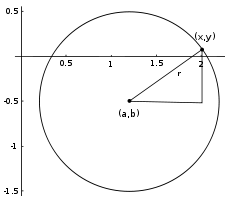Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)

Общее уравнение окружности записывается как:

x2+y2+Ax+By+C=0,{\displaystyle x^{2}+y^{2}+Ax+By+C=0,}

или

(x−x0)2+(y−y0)2=R2,{\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}

где

2×0=−A,2y0=−B,2R=A2+B2−4C.{\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}

Точка (x0,y0){\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R{\displaystyle R} — её радиус.

Уравнение окружности радиуса R{\displaystyle R} с центром в начале координат:

x2+y2=R2.{\displaystyle x^{2}+y^{2}=R^{2}.}

Уравнение окружности, проходящей через точки (x1,y1),(x2,y2),(x3,y3),{\displaystyle \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),} не лежащие на одной прямой (с помощью определителя):

|x2+y2xy1x12+y12x1y11x22+y22x2y21x32+y32x3y31|=0.{\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}

Тогда в явном виде координаты центра окружности определяются по формулам:

x0=−12y1(x22+y22−x32−y32)+y2(x32+y32−x12−y12)+y3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

y0=12×1(x22+y22−x32−y32)+x2(x32+y32−x12−y12)+x3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}

Окружность также можно описать с помощью параметрического уравнения:

{x=x0+Rcos⁡φy=y0+Rsin⁡φ,0⩽φ<2π.{\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .}

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

y=y0±R2−(x−x0)2.{\displaystyle y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.}

Если центр окружности совпадает с началом координат, функции принимают вид:

y=±R2−x2.{\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}

Полярные координаты[править | править код]

Окружность радиуса R{\displaystyle R} с центром в точке (ρ0,ϕ0){\displaystyle \left(\rho _{0},\phi _{0}\right)}:

ρ2−2ρρ0cos⁡(ϕ−ϕ0)+ρ02=R2.{\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}

Если полярные координаты центра окружности ρ0=R,ϕ0=α,{\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:

ρ(φ)=2Rcos(φ−α),α−π2⩽φ⩽α+π2.{\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.}

Если же центр является началом координат, то уравнение будет иметь вид

ρ=R.{\displaystyle \rho =R.}

Комплексная плоскость[править | править код]

На комплексной плоскости окружность задаётся формулой:

|z−z0|=R{\displaystyle \left|z-z_{0}\right|=R}

или в параметрическом виде

z=z0+Reit,t∈R.{\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .}

Окружности в пространстве[править | править код]

В пространстве окружность радиуса R{\displaystyle R} с центром в точке M0(x0,y0,z0){\displaystyle M_{0}(x_{0},y_{0},z_{0})} можно определить как контур диаметрального сечения сферы

(x−x0)2+(y−y0)2+(z−z0)2=R2{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}}

плоскостью

a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0{\displaystyle a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0},

где a,b,c{\displaystyle a,b,c} — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы

{(x−x0)2+(y−y0)2+(z−z0)2=R2,a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0.{\displaystyle {\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}}

Например, при a=c≠0{\displaystyle a=c\neq 0} решения этой системы можно задать параметрически следующим образом:

{x=x0+Ra2+c2⋅(c⋅cos⁡t−a⋅b⋅sin⁡ta2+b2+c2),y=y0+R⋅a2+c2a2+b2+c2⋅sin⁡t,z=z0−Ra2+c2⋅(a⋅cos⁡t+b⋅c⋅sin⁡ta2+b2+c2),t∈[0;2π).{\displaystyle {\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).}

Касательные и нормали[править | править код]

Уравнение касательной к окружности в точке (x1,y1){\displaystyle \left(x_{1},y_{1}\right)} определяется уравнением

(A2+x1)x+(B2+y1)y+(A2x1+B2y1+C)=0.{\displaystyle \left({\frac {A}{2}}+x_{1}\right)x+\left({\frac {B}{2}}+y_{1}\right)y+\left({\frac {A}{2}}x_{1}+{\frac {B}{2}}y_{1}+C\right)=0.}

Уравнение нормали в той же точке можно записать как

x−x12x1+A=y−y12y1+B.{\displaystyle {\frac {x-x_{1}}{2x_{1}+A}}={\frac {y-y_{1}}{2y_{1}+B}}.}

Концентрические и ортогональные окружности[править | править код]

Концентрические окружности

Окружности с общим центром, но разными радиусами, называются концентрическими. Две окружности, заданные уравнениями:

x2+y2+A1x+B1y+C1=0,x2+y2+A2x+B2y+C2=0{\displaystyle x^{2}+y^{2}+A_{1}x+B_{1}y+C_{1}=0,\;\;\;x^{2}+y^{2}+A_{2}x+B_{2}y+C_{2}=0}

являются концентрическими в том и только в том случае, когда A1=A2{\displaystyle A_{1}=A_{2}} и B1=B2.{\displaystyle B_{1}=B_{2}.}

Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие

A1A2+B1B2=2(C1+C2).{\displaystyle A_{1}A_{2}+B_{1}B_{2}=2\left(C_{1}+C_{2}\right).}

ru.wikipedia.org

Дополнительные углы — Википедия

Материал из Википедии — свободной энциклопедии

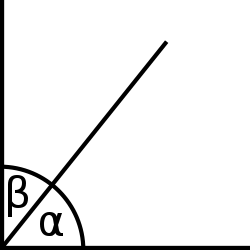Пара дополнительных углов, дополняющих друг друга до 90 градусов

Дополни́тельные углы́ — это пара углов, которые дополняют друг друга до 90 градусов.

Если два дополнительных угла являются соседними (то есть имеют общую вершину и разделяются только одной стороной), их не общие стороны образуют прямой угол.

В евклидовой геометрии два острых угла прямоугольного треугольника являются дополнительными, потому что сумма внутренних углов треугольника составляет 180 градусов, а прямой угол равен 90 градусам.

Синус одного из углов равен косинусу его дополнительного угла. Если углы A и B являются дополнительными, то верны равенства: sin2⁡A+sin2⁡B=1{\displaystyle \sin ^{2}A+\sin ^{2}B=1} и cos2⁡A+cos2⁡B=1.{\displaystyle \cos ^{2}A+\cos ^{2}B=1.}

Тангенс одного из углов равен котангенсу его дополнительного угла. Тангенсы дополнительных углов взаимно обратны.

Секанс одного из углов равен косекансу его дополнительного угла.

Префикс «ко-» в названиях некоторых тригонометрических функций происходит лат. complementum — дополнение.

ru.wikipedia.org

Двугранный угол — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 июня 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 июня 2019; проверки требуют 2 правки.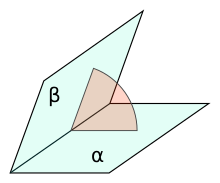 Двугранный угол и линейный угол двугранного угла 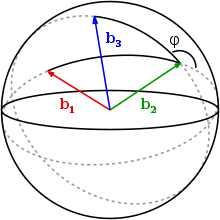Двугранный угол трёх векторов (как внешний сферический угол)

Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой^[1].

Полуплоскости называются гранями двугранного угла, а их общая прямая — ребром.

Прямой угол в двугранном угле, равном 45 градусам (анимация)

Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней. Линейный угол между этими двумя лучами и будет равен по величине двугранному углу. Если один из лучей не перпендикулярен ребру, то величина линейного угла между лучами в общем случае будет отлична от величины двугранного угла. Например, в любой двугранный угол (в том числе больший 90 градусов) можно поместить прямой угол так, чтобы его вершина лежала на ребре двугранного угла, а стороны принадлежали его граням. В этом легко убедиться, размещая угольник в приоткрытой книге.

У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.

Величины двугранных углов правильных многогранников:

где φ = (1 + √5)/2 — золотое сечение.

• Двугранным углом также называется пересечение двух полупространств в n{\displaystyle n}-мерном Евклидовом пространстве.

1. ↑ Д-Коо // «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — : «Советская энциклопедия», 1979. — Т. 2. — С. 50. — 1104 с. — (51[03] М34). — 148 800 экз.

ru.wikipedia.org

Вершина (геометрия) — Википедия

В геометрии вершина — это вид точки, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников^[1].

Вершина угла[править | править код]

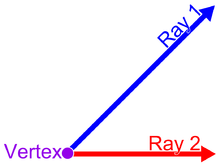Вершина угла — это точка, окуда берут начало два луча.

Вершина угла — это точка, откуда берут начало два луча; где сходятся два отрезка; где две прямые пересекаются; где любая комбинация лучей, отрезков и прямых, образующих две (прямолинейные) «стороны», которые сходятся в одной точке^[2].

Вершина многоугольника многогранника[править | править код]

Вершина — это угловая точка многоугольника или многогранника (любой размерности), иначе говоря его 0-мерная граней.

В многоугольнике вершина называется «выпуклой», если внутренний угол многоугольника меньше π радиан (180° — два прямых угла). В противном случае вершина называется «вогнутой».

Более обще, вершина многогранника является выпуклой, если пересечение многогранника с достаточно малой сферой, имеющей вершину в качестве центра, представляет собой выпуклую фигуру; в противном же случае вершина является вогнутой.

Вершины многогранника связаны с вершинами графа, поскольку многогранника является графом, вершины которого соответствуют вершинам многогранника^[3], а следовательно, граф многогранника можно рассматривать как одномерный симплициальный комплекс, вершинами которого служат вершины графа. Однако, в теории графов вершины могут иметь менее двух инцидентных рёбер, что обычно не разрешается для вершин геометрических. Также имеется связь между геометрическими вершинами и вершинами кривой, точками экстремумов её кривизны — вершины многоугольника в некотором смысле являются точками бесконечной кривизны, и, если многоугольник приблизить гладкой кривой, точки экстремальной кривизны будут лежать вблизи вершин многоугольника^[4]. Однако, приближение многоугольника с помощью гладкой кривой даёт дополнительные вершины в точках минимальной кривизны.

Вершины плоских мозаик[править | править код]

Вершина плоской мозаики (замощения) — это точка, где встречаются три и более плиток мозаики^[5], но не только: плитки замощения также являются многоугольниками, а вершины мозаики являются вершинами этих плиток. Более обще, замощение можно рассматривать как вид топологического CW-комплекса. Вершины других видов комплексов, таких как симплициальные, — это грани нулевой размерности.

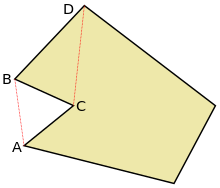Вершина B является «ухом», поскольку открытый отрезок между вершинами C и D лежит полностью внутри многоугольника. Вершина C является «ртом», поскольку открытый отрезок между A и B лежит полностью вне многоугольника.

Вершина xi{\displaystyle x_{i}} простого многоугольника P{\displaystyle P} является основной вершиной, если диагональ [xi−1,xi+1]{\displaystyle [x_{i-1},x_{i+1}]} пересекает границы P{\displaystyle P} только в точках xi−1{\displaystyle x_{i-1}} и xi+1{\displaystyle x_{i+1}}. Существует два типа основных вершин: «уши» и «рты» (см. ниже)^[6].

«Уши»[править | править код]

Основная вершина xi{\displaystyle x_{i}} простого многоугольника P{\displaystyle P} называется «ухом», если диагональ [xi−1,xi+1]{\displaystyle [x_{i-1},x_{i+1}]} лежит полностью в P{\displaystyle P}. (см. также выпуклый многоугольник)

«Рты»[править | править код]

Основная вершина xi{\displaystyle x_{i}} простого многоугольника P{\displaystyle P} называется «ртом», если диагональ [xi−1,xi+1]{\displaystyle [x_{i-1},x_{i+1}]} лежит вне P{\displaystyle P}.

Любая поверхность трёхмерного выпуклого многогранника имеет эйлерову характеристику:

V−E+F=2,{\displaystyle V-E+F=2,}

где V{\displaystyle V} — число вершин, E{\displaystyle E} — число рёбер, а F{\displaystyle F} — число граней. Это равенство известно как уравнение Эйлера. К примеру, куб имеет 12 рёбер и 6 граней, а потому — 8 вершин: 8−12+6=2{\displaystyle 8-12+6=2} .

В компьютерной графике объекты часто представляются как триангулированные многогранники, в которых вершинам объекта сопоставляются не только три пространственные координаты, но и другая необходимая для правильного построения изображения объекта графическая информация, такая как цвет, отражательная способность, текстура, нормали вершин^[7]. Эти свойства используются при построении изображения с помощью вершинного шейдера, части обработчика вершин^[en].

1. ↑ Weisstein, Eric W. Vertex (англ.) на сайте Wolfram MathWorld.
2. ↑ Heath, 1956.
3. ↑ McMullen, Schulte, 2002, с. 29.
4. ↑ Bobenko, Schröder, Sullivan, Ziegler, 2008.
5. ↑ Jaric, 1989, с. 9.
6. ↑ Devadoss, O’Rourke, 2011.
7. ↑ Christen, 2009.

• Thomas L. Heath. The Thirteen Books of Euclid’s Elements. — 2nd ed. — New York: Dover Publications, 1956. — ISBN v1: 0-486-60088-2 , v2: 0-486-60089-0 , v3: 0-486-60090-4. (Аутентичный перевод книги Евклида «Начала» с обширными историческими исследованиями и детальными комментариями по тексту книги.)
• Lanru Jing, Ove Stephansson. Fundamentals of Discrete Element Methods for Rock Engineering: Theory and Applications. — 2007. — ISBN 978-0-444-82937-5.
• Peter McMullen, Egon Schulte. Abstract Regular Polytopes. — Cambridge University Press, 2002. — ISBN 0-521-81496-0.
• Introduction to the Mathematics of Quasicrystals / M.V. Jaric. — Academic Press, 1989. — Т. 2. — (Aperiodicity and Order). — ISBN 0-12-040602-0.
• Alexander I. Bobenko, Peter Schröder, John M. Sullivan, Günter M. Ziegler^[en]. Discrete differential geometry. — Birkhäuser Verlag AG, 2008. — ISBN 978-3-7643-8620-7.
• Satyan Devadoss, Joseph O’Rourke. Discrete and Computational Geometry. — Princeton University Press, 2011. — ISBN 978-0-691-14553-2.
• Martin Christen. Clockworkcoders Tutorials: Vertex Attributes. — Khronos Group, 2009.

ru.wikipedia.org

Телесный угол — Википедия

Материал из Википедии — свободной энциклопедии

Телесный угол

Теле́сный у́гол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью,

стягивающей данный телесный угол). Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность. Обозначается телесный угол обычно буквой Ω.

Телесный угол измеряется отношением площади той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса сферы:

Ω=SR2.{\displaystyle \Omega \,=\,{S \over R^{2}}.}

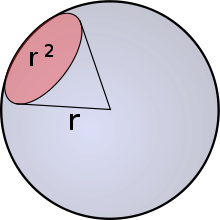
Телесные углы измеряются отвлечёнными (безразмерными) величинами. Единицей измерения телесного угла в системе СИ является стерадиан, равный телесному углу, вырезающему из сферы радиуса r поверхность с площадью r². Полная сфера образует телесный угол, равный 4π стерадиан (полный телесный угол), для вершины, расположенной внутри сферы, в частности, для центра сферы; таким же является телесный угол, под которым видна любая замкнутая поверхность из точки, полностью охватываемой этой поверхностью, но не принадлежащей ей. Кроме стерадианов, телесный угол может измеряться в квадратных градусах, квадратных минутах и квадратных секундах, а также в долях полного телесного угла.

Телесный угол имеет нулевую физическую размерность.

Двойственный телесный угол к данному телесному углу Ω определяется как угол, состоящий из лучей, образующих с любым лучом угла Ω неострый угол.

Коэффициенты пересчёта единиц телесного угла.

Ω{\displaystyle \Omega }	Стерадиан	Кв. градус	Кв. минута	Кв. секунда	Полный угол
1 стерадиан =	1	(180/π)² ≈ ≈ 3282,806 кв. градусов	(180×60/π)² ≈ ≈ 1,1818103⋅107 кв. минут	(180×60×60/π)² ≈ ≈ 4,254517⋅1010 кв. секунд	1/4π ≈ ≈ 0,07957747 полного угла
1 кв. градус =	(π/180)² ≈ ≈ 3,0461742⋅10−4 стерадиан	1	60² = = 3600 кв. минут	(60×60)² = = 12 960 000 кв. секунд	π/(2×180)² ≈ ≈ 2,424068⋅10−5 полного угла
1 кв. минута =	(π/(180×60))² ≈ ≈ 8,461595⋅10−8 стерадиан	1/60² ≈ ≈ 2,7777778⋅10−4 кв. градусов	1	60² = = 3600 кв. секунд	π/(2×180×60)² ≈ ≈ 6,73352335⋅10−9 полного угла
1 кв. секунда =	(π/(180×60×60))² ≈ ≈ 2,35044305⋅10−11 стерадиан	1/(60×60)² ≈ ≈ 7,71604938⋅10−8 кв. градусов	1/60² ≈ ≈ 2,7777778⋅10−4 кв. минут	1	π/(2×180×60×60)² ≈ ≈ 1,87042315⋅10−12 полного угла
Полный угол =	4π ≈ ≈ 12,5663706 стерадиан	(2×180)²/π ≈ ≈ 41252,96125 кв. градусов	(2×180×60)²/π ≈ ≈ 1,48511066⋅108 кв. минут	(2×180×60×60)²/π ≈ ≈ 5,34638378⋅1011 кв. секунд	1

Для произвольной стягивающей поверхности S телесный угол Ω, под которым она видна из начала координат, равен

Ω=∫SdΩ=∬Ssin⁡ϑdφdϑ=∫S(r/r)⋅ndSr2,{\displaystyle \Omega =\int \limits _{S}d\Omega =\iint \limits _{S}\sin \vartheta \,d\varphi \,d\vartheta =\int \limits _{S}{\frac {(\mathbf {r} /r)\cdot \mathbf {n} dS}{r^{2}}},}

где r,ϑ,φ{\displaystyle r,\vartheta ,\varphi } — сферические координаты элемента поверхности dS,{\displaystyle dS,} r{\displaystyle \mathbf {r} } — его радиус-вектор, n{\displaystyle \mathbf {n} } — единичный вектор, нормальный к dS.{\displaystyle dS.}

1. Полный телесный угол (полная сфера) равен 4π стерадиан.
2. Сумма всех телесных углов, двойственных к внутренним телесным углам выпуклого многогранника, равна полному углу.

• Треугольник с координатами вершин r1{\displaystyle \mathbf {r} _{1}}, r2{\displaystyle \mathbf {r} _{2}}, r3{\displaystyle \mathbf {r} _{3}} виден из начала координат под телесным углом

Ω=2arctg(r1r2r3)r1r2r3+(r1⋅r2)r3+(r2⋅r3)r1+(r3⋅r1)r2,{\displaystyle \Omega =2\,\mathrm {arctg} \,{\frac {(\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})}{r_{1}r_{2}r_{3}+(\mathbf {r} _{1}\cdot \mathbf {r} _{2})r_{3}+(\mathbf {r} _{2}\cdot \mathbf {r} _{3})r_{1}+(\mathbf {r} _{3}\cdot \mathbf {r} _{1})r_{2}}},}

где (r1r2r3){\displaystyle (\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})} — смешанное произведение данных векторов, (ri⋅rj){\displaystyle (\mathbf {r} _{i}\cdot \mathbf {r} _{j})} — скалярные произведения соответствующих векторов, полужирным шрифтом обозначены векторы, нормальным шрифтом — их длины. Используя эту формулу, можно вычислять телесные углы, стянутые произвольными многоугольниками с известными координатами вершин (для этого достаточно разбить многоугольник на непересекающиеся треугольники).

• Телесный угол при вершине прямого кругового конуса с углом раствора α равен Ω=2π(1−cos⁡α2).{\displaystyle \Omega =2\pi \left(1-\cos {\frac {\alpha }{2}}\right).} Если известны радиус основания R{\displaystyle R} и высота H{\displaystyle H} конуса, то Ω=2π(1−HR2+h3).{\displaystyle \Omega =2\pi \left(1-{\frac {H}{\sqrt {R^{2}+H^{2}}}}\right).} Когда угол раствора конуса мал, Ω≈πα24{\displaystyle \Omega \approx {\frac {\pi \alpha ^{2}}{4}}} (угол α{\displaystyle \alpha } выражен в радианах), или Ω≈0,000239α2{\displaystyle \Omega \approx 0{,}000239\alpha ^{2}} (угол α{\displaystyle \alpha } выражен в градусах). Так, телесный угол, под которым с Земли видны Луна и Солнце (их угловой диаметр примерно равен 0,5°), составляет около 6⋅10⁻⁵ стерадиан, или ≈0,0005 % площади небесной сферы (то есть полного телесного угла).

• Телесный угол двугранного угла в стерадианах равен удвоенному значению двугранного угла в радианах.

Ω=4arctg⁡tg⁡(θs2)tg⁡(θs−θa2)tg⁡(θs−θb2)tg⁡(θs−θc2),{\displaystyle \Omega =4\,\operatorname {arctg} {\sqrt {\operatorname {tg} \left({\frac {\theta _{s}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}},} где θs=θa+θb+θc2{\displaystyle \theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}} — полупериметр.

Через двугранные углы α,β,γ{\displaystyle \alpha ,\beta ,\gamma } телесный угол выражается как:

Ω=α+β+γ−π.{\displaystyle \Omega =\alpha +\beta +\gamma -\pi .}

• Телесный угол, под которым видна грань правильного N-гранника из его центра, равна 1N{\displaystyle {\frac {1}{N}}} полного телесного угла, или 4πN{\displaystyle {\frac {4\pi }{N}}} стерадиан.

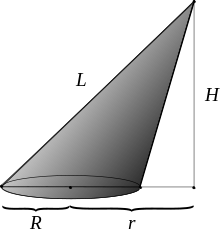
• Телесный угол при вершине наклонного кругового конуса Телесный угол, под которым виден круг радиусом R из произвольной точки пространства (то есть телесный угол при вершине произвольного кругового конуса, не обязательно прямого) вычисляется с использованием полных эллиптических интегралов 1-го и 3-го рода^[1]:

Ω=2π+2HL(r−Rr+RΠ(α2,k)−K(k)){\displaystyle \Omega =2\pi +{\frac {2H}{L}}\left({\frac {r-R}{r+R}}\,\Pi (\alpha ^{2},k)-K(k)\right)} при r≤R,{\displaystyle r\leq R,}

Ω=2HL(r−Rr+RΠ(α2,k)−K(k)){\displaystyle \Omega ={\frac {2H}{L}}\left({\frac {r-R}{r+R}}\,\Pi (\alpha ^{2},k)-K(k)\right)} при r>R,{\displaystyle r>R,}

где K(k){\displaystyle K(k)} и Π(α2,k){\displaystyle \Pi (\alpha ^{2},k)} — полные нормальные эллиптические интегралы Лежандра 1-го и 3-го рода, соответственно;

r{\displaystyle r} — расстояние от центра основания конуса до проекции вершины конуса на плоскость основания;

H{\displaystyle H} — высота конуса;

L=h3+(r+R)2{\displaystyle L={\sqrt {H^{2}+(r+R)^{2}}}} — длина максимальной образующей конуса;

k=4rRL;{\displaystyle k={\frac {\sqrt {4rR}}{L}};}

α=4rRr+R.{\displaystyle \alpha ={\frac {\sqrt {4rR}}{r+R}}.}

ru.wikipedia.org

Двуугольник — Википедия

Материал из Википедии — свободной энциклопедии

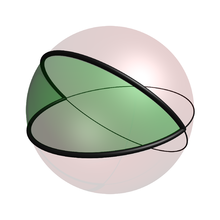Правильный двуугольник на поверхности сферы

Двуугольник  — многоугольник с двумя сторонами и двумя углами. В Евклидовой геометрии двуугольник считается вырожденной фигурой, так как его две стороны совпадают. В сферической геометрии четыре двуугольника образуются при пересечении двух больших окружностей.

• Площадь сферического двуугольника определяется формулой S=2αR2{\displaystyle S=2\alpha R^{2}}, где R{\displaystyle R} — радиус сферы, а α{\displaystyle \alpha } — угол двуугольника в радианах.

Термин двуугольник иногда используется для плоской фигуры, ограниченной двумя дугами окружностей или двумя гладкими кривыми с общими концами. В последнем случае употребляется термин криволинейный двуугольник. Такой двуугольник можно назвать луночкой. Частным случаем дуговых двуугольников являются луночки Гиппократа — фигуры, указанные Гиппократом Хиосским (V в. до н. э.), каждая из которых ограничена дугами двух окружностей и для каждой из которых с помощью циркуля и линейки можно построить равновеликие многоугольники.

• Weisstein, Eric W. Digon (англ.) на сайте Wolfram MathWorld.

1. ↑ Степанов Н. Н. §44. Определение площади двуугольника и сферического треугольника // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 98-100. — 154 с.

Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

ru.wikipedia.org

Трёхгранный угол — Википедия

Материал из Википедии — свободной энциклопедии

Рис. 1. Трёхгранный угол.

Трёхгранный угол — это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трёхгранного угла. Стороны углов называются рёбрами, плоские углы при вершине трёхгранного угла называются его гранями. Каждая из трёх пар граней трёхгранного угла образует двугранный угол (ограниченный третьей гранью, не входящей в пару; при потребности естественным образом снимается это ограничение, в результате чего получаются необходимые полуплоскости, образующие весь двугранный угол без ограничения). Если поместить вершину трёхгранного угла в центр сферы, на её поверхности образуется ограниченный им сферический треугольник, стороны которого равны плоским углам трёхгранного угла, а углы — его двугранным углам.

Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов.

Сумма плоских углов трёхгранного угла[править | править код]

Сумма плоских углов трёхгранного угла меньше 360 градусов.

Доказательство

Рис. 2. Трёхгранный угол.

Пусть дан трёхгранный угол (см. Рис. 2), α, β, γ — его плоские углы, A, B, C — двугранные углы, составленные плоскостями углов β и γ, α и γ, α и β.

Первая теорема косинусов для трёхгранного угла: cos⁡α=cos⁡βcos⁡γ+sin⁡βsin⁡γcos⁡A{\displaystyle \cos {\alpha }=\cos {\beta }\cos {\gamma }+\sin {\beta }\sin {\gamma }\cos {A}}

Вторая теорема косинусов для трёхгранного угла: cos⁡A=−cos⁡Bcos⁡C+sin⁡Bsin⁡Ccos⁡α{\displaystyle \cos {A}=-\cos {B}\cos {C}+\sin {B}\sin {C}\cos {\alpha }}

Доказательство Второй теоремы косинусов для трёхгранного угла

Пусть OABC – данный трёхгранный угол. Опустим перпендикуляры из внутренней точки трёхгранного угла на его грани и получим новый трёхгранный угол полярный (двойственный данному). Плоские углы одного трёхгранного угла дополняют двугранные углы другого и двугранные углы одного угла дополняют плоские другого до 180 градусов. Т. е. плоские углы полярного угла соответственно равны: 180 — А ; 180 — В ; 180 — С, а двугранные — 180 — α; 180 — β ; 180 — γ

Напишем первую теорему косинусов для него

cos⁡(π−A)=cos⁡(π−α)sin⁡(π−B)sin⁡(π−C)+{\displaystyle \cos({\pi -A})=\cos({\pi -\alpha })\sin({\pi -B})\sin({\pi -C})+}

+cos⁡(π−B)cos⁡(π−C){\displaystyle +\cos({\pi -B})\cos({\pi -C)}}

и после упрощений получаем:

cos⁡A=cos⁡αsin⁡Bsin⁡C−cos⁡Bcos⁡C{\displaystyle \cos {A}=\cos {\alpha }\sin {B}\sin {C}-\cos {B}\cos {C}}

sin⁡αsin⁡A=sin⁡βsin⁡B=sin⁡γsin⁡C{\displaystyle {\sin {\alpha } \over \sin A}={\sin \beta \over \sin B}={\sin \gamma \over \sin C}}, где α, β, γ — плоские углы трёхгранного угла; A, B, C — противолежащие им двугранные углы (см. Рис. 2).

ru.wikipedia.org