УГОЛ — это… Что такое УГОЛ?
— геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало — вершиной У. Пусть [ ВА),[ ВС) — стороны угла, В — его вершина,  — плоскость, определяемая сторонами У. Фигура
— плоскость, определяемая сторонами У. Фигура  делит плоскость
делит плоскость  на две фигуры
на две фигуры  Фигура
Фигура 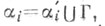 i==l, 2, также наз. У. или плоским углом,
i==l, 2, также наз. У. или плоским углом, 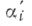 наз. внутренней областью плоского У.
наз. внутренней областью плоского У. 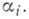
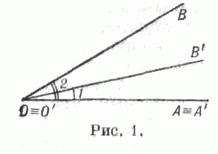
Два угла наз. равными (или конгруэнтными), если они могут быть совмещены так, что совпадут их соответствующие стороны и вершины. От любого луча на плоскости в данную сторону от него можно отложить единственный У., равный данному У. Сравнение У. осуществляется двумя способами. Если У. рассматривается как пара лучей с общим началом, то для выяснения вопроса, какой из двух У. больше, необходимо совместить в одной плоскости вершины У. и одну пару их сторон (см. рис. 1). Если вторая сторона одного У. окажется расположенной внутри другого У., то говорят, что первый У. меньше, чем второй. Второй способ сравнения У. основан на сопоставлении каждому У. нек-рого числа. Равным У. будет соответствовать одинаковое число градусов или радиан (см.
ниже), большему У.- большее число, меньшему -меньшее.
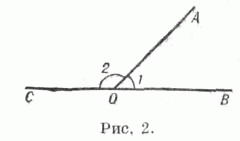
Два У. наз. смежными, если у них общая вершина и одна сторона, а две другие стороны образуют прямую (см. рис. 2). Вообще, У., имеющие общую вершину и одну общую сторону, наз. прилежащими. У. наз. вертикальными, если стороны одного являются продолжениями за вершину сторон другого У. Вертикальные У. равны между собой. У., у к-рого стороны образуют прямую, наз. развернутым. Половина развернутого У. наз. прямым У. Прямой У. можно эквивалентно определить иначе: У., равный своему смежному, наз. прямым. Внутренняя область плоского У., не превосходящего развернутого, является выпуклой областью на плоскости. За единицу измерения У. принимается 90-я доля прямого У., наз. градусом.
Используется и т. мера У. Числовое значение радианной меры У. равно длине дуги, высекаемой сторонами У. из единичной окружности. Один радиан приписывается У., соответствующему дуге, длина к-рой равна ее радиусу. Развернутый У. равен 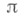
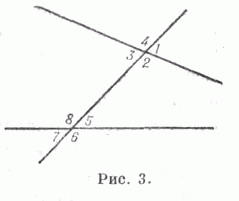
При пересечении двух прямых, лежащих в одной плоскости, третьей прямой образуются У. (см. рис. 3): 1 и 5, 2 и 6, 4 и 8, З и 7 — наз. соответственными; 2 и 5, 3 и 8 — внутренними односторонними; 1 и 6, 4 и 7 — внешними односторонними; 3 и 5, 2 и 8- внутренними накрест лежащими; 1 и 7, 4 и 6 — внешними накрест лежащими.
В практич. задачах целесообразно рассматривать У. как меру поворота фиксированного луча вокруг его начала до заданного положения. В зависимости от направления поворота У. в этом случае можно рассматривать как положительные, так и отрицательные. Тем самым У. в этом смысле может иметь своей величиной любое действительное число. У. как мера поворота луча рассматривается в теории тригонометрич. функций: для любых значений аргумента (У.) можно определить значения тригонометрич. функций. Понятие У. в геометрич. системе, в основу к-рой положена точечно-векторная аксиоматика, в корне отличается от определений У. как фигуры — в этой аксиоматике под У. понимают определенную метрич. величину, связанную с двумя векторами с помощью операции скалярного умножения векторов. Именно, каждая пара векторов аи bопределяет нек-рый угол 
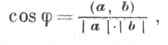
где (a, b) — скалярное произведение векторов.
Понятие У. как плоской фигуры и как нек-рой числовой величины применяется в различных геометрич. задачах, в к-рых У. определяется специальным образом. Так, под У. между пересекающимися кривыми, имеющими определенные касательные в точке пересечения, понимают У., образованный этими касательными.
За угол между прямой и плоскостью принимается У., образованный прямой и ее прямоугольной проекцией на плоскость; он измеряется в пределах от 0
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
dic.academic.ru
Острый угол — это… Что такое Острый угол?

«∠», обозначение угла в математике
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги
s к длине окружности L, в радианах — отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
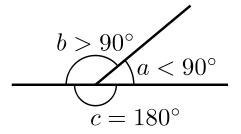
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:
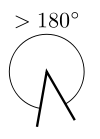
Невыпуклый угол
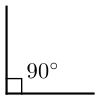
Прямой угол
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: 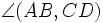
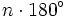 , считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме
, считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме 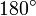 или, что по нашему соглашению то же самое,
или, что по нашему соглашению то же самое, 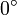 ). Ориентированные углы обладает следующими свойствами: а)
). Ориентированные углы обладает следующими свойствами: а) 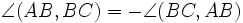 ; б)
; б) 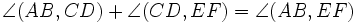 ; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда
; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда 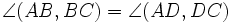 .
.Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation. 2010.
dic.academic.ru
Величина угла — это… Что такое Величина угла?

«∠», обозначение угла в математике
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
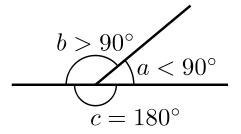
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:

Невыпуклый угол

Прямой угол
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: 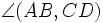 ) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на
) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на 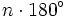 , считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме
, считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме 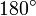 или, что по нашему соглашению то же самое,
или, что по нашему соглашению то же самое, 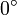 ). Ориентированные углы обладает следующими свойствами: а)
). Ориентированные углы обладает следующими свойствами: а) 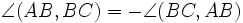 ; б)
; б) 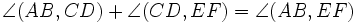 ; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда
; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда 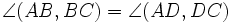 .
.
Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation. 2010.
dic.academic.ru
Полный угол — это… Что такое Полный угол?

«∠», обозначение угла в математике
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
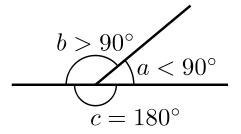
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:

Невыпуклый угол

Прямой угол
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: 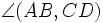 ) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на
) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на 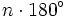 , считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме
, считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме 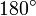 или, что по нашему соглашению то же самое,
или, что по нашему соглашению то же самое, 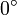 ). Ориентированные углы обладает следующими свойствами: а)
). Ориентированные углы обладает следующими свойствами: а) 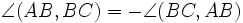 ; б)
; б) 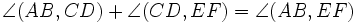 ; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда
; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда 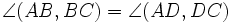 .
.
Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation. 2010.
dic.academic.ru