Умножения и деление отрицательных чисел. Решение примеров.
В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел.
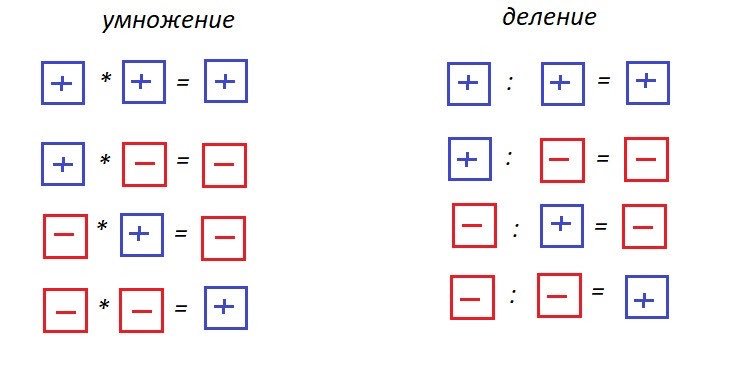
- \(«—«-\) при умножении минус на минус результат становится положительным;
- \(«-+»-\) при умножении минуса на плюс результат становится отрицательным;
- \(«+-«-\) при умножении плюса на минус результат становится отрицательным;
- \(«++»-\) при умножении плюса на плюс результат становится положительным.
Примеры умножения отрицательных чисел.
Задача 1. Вычислить: \((-4)*(-4)\) и \((-6)*(-5).\)
Решение.
Отрицательное число при умножении на отрицательное станет положительным согласно правилу.
- \((-4)*(-4)=16\)
- \((-6)*(-5)=30\)
Ответ: \(16;30.\)
Задача 2. Вычислить: \((-10)*12\) и \((-7)*4.
Решение.
Отрицательное при умножении на положительное число станет отрицательным согласно правилу.
-10 * 12= -120
(-7)*4=-28
Ответ: \(-120; -28\)
Задача 3. Вычислить: \(11*(-11)\) и \(13*(-6).\)
Решение.
Положительное при умножении на отрицательное число станет отрицательным согласно правилу.
- \(11*(-11)=-121\)
- \(13*(-6)=-78\)
Ответ: \(-121;-78.\)
Деление отрицательных чисел
При делении действуют те же правила знаков, что и при умножении. Делить на ноль нельзя.
- \(«—«-\) при делении минус на минус результат становится положительным;
- \(«-+»-\)при делении минуса на плюс результат становится отрицательным;
- \(«+-«-\)при делении плюса на минус результат становится отрицательным;
- \(«++»-\) при делении плюса на плюс результат становится положительным.

Задача 4. Вычислить: \((-16)*(-4)\) и \((-6)*(-2)\).
Решение.
- \(-16:(-4)=4\)
- \((-6):-2=3\)
Ответ: \(4;3.\)
Задача 5. Вычислить: \((-10):5\) и \((-12):6\).
Решение.
- \((-10):5=-2\)
- \((-12):6=-2\)
Ответ: \(-2;-2.\)
Задача 3. Вычислить: \(121:(-11)\) и \(169:(-13)\).
Решение.
- \(121:(-11)=-11\)
- \(169:(-13)=-13\)
Ответ: \(-11;-13.\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Как правильно умножать отрицательные числа?
Основные определения
Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:
Два главных определения:
Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.
Запоминаем!
Положительные числа — это те, что больше нуля, а отрицательные — меньшие.
Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».
Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!
Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).
Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:
Смотрите:
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения
|
Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.
Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:
А вот как умножить два числа с разными знаками:
- перемножить модули этих чисел
- перед полученным числом поставить знак минус
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
- «—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс - «-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус - «+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус - «++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.
Примеры умножения отрицательных чисел
Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)
Как решаем:
Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:
- (-2)∗(-2) = 4
- (-3)∗(-7) = 21
Ответ: 4; 21.
Пример 2. Вычислить: (-11)∗11 и (-20)∗2
Как решаем:
Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус.
- -11 * 11 = -121
- (-20) * 2 = -40
Ответ: -121; -40.
Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)
Как решаем:
Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:
- 5 ∗ (-5)= -25
- 12 ∗ (-8)= -96
Ответ: -25; -96.
Пример 4. Вычислить произведение: (-0,125 ) * (-6)
Как решаем:
- Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6. - Выполним умножение десятичной дроби на натуральное число столбиком:
Ответ: 0,75.
Развивайте математическое мышление детей на наших уроках математики вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой.
Приходите на бесплатный вводный урок вместе с ребенком: познакомимся, порешаем задачки и вдохновим на учебу!
Умножение
здравствуйте тема данного видео рока умножения давайте попробуем умножить число -3 на число 2 мы с вами знаем что умножение на натуральное число мы можем заменить суммой то есть вместо того чтобы умножать минус 3 на 2 мы можем дважды прибавить -3 то есть это все равно что минус 3 плюс минус 3 такие выражением и считать умеем это будет минус 6 аналогично мы можем посчитать 3 умноженное на минус 2 данном случае мы можем трижды взять минус 2 это будет минус 2 плюс минус 2 и плюс минус 2 это снова будет -6 обратить внимание шестерка у нас может получиться если мы 3 просто умножим на 2 просто перед результатом появляется знак минус таким образом у нас получается правило если мы умножаем два числа с разными знаками нужно просто умножить их модули и перед результатом поставить знак минус например давайте умножим минус 5 на 7 вы просто 5 умножаем на 7 это будет 35 и перед результатов обязательно знак минус или например 8 умножим на минус 6 снова мы просто 8 умножаем на 6 это будет 48 и перед результатом ставим знак минус теперь попробуем умножить два отрицательных числа для начала воспользуемся следующем мы знаем что два например умноженное на 3 это 6 только что мы посчитали что два умноженное на минус 3 будет минус 6х минус 2 умноженное на 3 также будет -6 обратите внимание на первое выражение и например на второе второе отличается тем что мы изменили знак одного из множителей если мы изменили знак одного из множителей то и знак произведения изменился аналогично здесь мы изменили знак одного из множителей значит изменилась и изменилась произведение тогда если мы изменим еще раз знак одного из множителей например вот здесь мы вместо 3 сделаем -3 то у нас знак произведений снова изменится было минус 6 станет 6 таким образом минус 2 умноженное на минус 3 дает 6 отсюда мы получаем следующее правило чтобы умножить два отрицательных числа мы просто перемножаем их модули результат будет со знаком плюс таким образом можем обобщить следующее что если мы отрицательное число умножаем на положительное результат у нас отрицательный если положительное умножаем на отрицательное результат снова отрицательный но если мы умножаем два положительных естественный результат положительный и если мы умножаем два отрицательных числа как вас здесь то результат тоже будет плюс таким образом мы можем заметить что если умножается два числа с разными знаками то результат всегда минус есть умножается два числа с одинаковыми знаками то результат будет плюс закрепим пройдена на примерах попробуем умножить данные числа минус 5 умножить на 6 отрицательное число умножаем на положительный результат будет отрицательной и 5 6 это 39 умножаем на -3 и снова мы плюс умножаем на минус значит результат с минусом и 9 на 3 будет 27 -8 умножаем на минус семь минус на минус у нас дает плюс 7 и 8 56 минус 10 на 11 у нас с минус умножается на плюс значит результат с минусом 10 на 11 110 -11 на минус 12 2 минус а значит результат будет с плюсом осталось 11 умножить на 12 это 132 минус 1,44 умножаем на 0 при умножении на 0 у нас всегда получается 0 минус две третьих умножаем на 3 8 результаты нас будет с минусом а здесь мы просто посчитаем мы можем сократить тройки сократить 2 и 8 снизу останется 4 сверху 1 значит минус 1 4 4 15х минус пять восьмых снова смотрим результат у нас будет с минусом а теперь это сокращает 4 и 8 сокращаем будет 2 5 15 на 5 здесь останется 3 значит сверху нас один снизу дважды 36 минус 1 6 минус 5 9 на минус 12 25 2 минус а значит результат будет с плюсом теперь считаем 5 25 сокращаем здесь останется 512 и 9 сокращаем на 3 здесь будет 3 здесь будет 4 значит результат будет 4 а снизу трижды 515 415 1 целый 1 8 умножаем на минус 5 целых 1 3 сначала определим результат знак результата он очевидно минус потому что мы плюс умножаем на минус это / и переводим в неправильные одна целое 1 8 это девять восьмых 5 целых 1 3 5 на 3 15 плюс 1 16 16 тыс и останется просто сократить 16 и 8 сокращается здесь будет 239 сокращается здесь останется 3 и того будет -6 аналогично здесь результат у нас будет со знаком минус а это переводим неправильный 23 на 5-15 плюс 3 1818 5 умножаем на 6 на 4 24 плюс 125 на двадцать пять четвертых сокращаем двадцать пять на пять останется 5 18 4 сокращаем на 2 здесь 9 здесь два итого получаем минус сверху 9 и 545 вторых и последний пример минус 3 целых 1 5 на 1 целый две десятых снова определяем знака результата минус на плюс будет минус и просто переводим неправильно дробь 3 целых 1 5 это 16 5 1 целых две десятых мы можем записать как 12 десятых и останется просто посчитать данном случае мы можем сократить например 16 и 10 на 2 здесь останется 5 здесь останется 8 больше ничего не сокращается просто перемножаем 8 умножаем на 12 это будет 96 снизу 5 5 25 таким образом подводя итоги для того чтобы умножить отрицательное число на положительное или положительное на отрицательное мы просто перемножаем эти числа перед результатом ставим знак минус если у нас умножается два отрицательных числа то мы просто перемножаем модули результат будет со знаком плюс она этом данный видео урок окончен [музыка]
Узнаем как понять, почему «плюс» на «минус» дает «минус» ?
Слушая учителя математики, большинство учеников воспринимают материал как аксиому. При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
При этом мало кто пытается добраться до сути и разобраться, почему «минус» на «плюс» дает знак «минус», а при умножении двух отрицательных чисел выходит положительное.
Законы математики
Большинство взрослых не в силах объяснить ни себе, ни своим детям, почему так получается. Они твердо усвоили этот материал в школе, но при этом даже не попытались выяснить, откуда взялись такие правила. А зря. Зачастую современные дети не столь доверчивы, им необходимо докопаться до самой сути и понять, скажем, почему «плюс» на «минус» дает «минус». А иногда сорванцы специально задают каверзные вопросы, дабы насладиться моментом, когда взрослые не могут дать вразумительного ответа. И совсем уж беда, если впросак попадает молодой учитель…
Кстати, следует отметить, что упомянутое выше правило действенно как для умножения, так и для деления. Произведение отрицательного и положительного числа даст лишь «минус. Если речь идет о двух цифрах со знаком «-», то в результате получится положительное число. То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
То же касается и деления. Если одно из чисел будет отрицательным, то частное тоже будет со знаком «-».
Для объяснения правильности этого закона математики, необходимо сформулировать аксиомы кольца. Но для начала следует понять, что это такое. В математике кольцом принято называть множество, в котором задействованы две операции с двумя элементами. Но разбираться с этим лучше на примере.
Аксиома кольца
Существует несколько математических законов.
- Первый из них переместительный, согласно ему, C + V = V + C.
- Второй называется сочетательным (V + C) + D = V + (C + D).
Им же подчиняется и умножение (V х C) х D = V х (C х D).
Никто не отменял и правил, по которым открываются скобки (V + C) х D = V х D + C х D, также верно, что C х (V + D) = C х V + C х D.
Кроме того, установлено, что в кольцо можно ввести специальный, нейтральный по сложению элемент, при использовании которого будет верно следующее: C + 0 = C. Кроме того, для каждого C есть противоположный элемент, который можно обозначить, как (-C). При этом C + (-C) = 0.
При этом C + (-C) = 0.
Выведение аксиом для отрицательных чисел
Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.
Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.
Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.
Исходя из этого, становится ясно, что V = D.
Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.
Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).
Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.
Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.
Умножение и деление двух чисел со знаком «-»
Если не углубляться в математические нюансы, то можно попробовать более простым способом объяснить правила действий с отрицательными числами.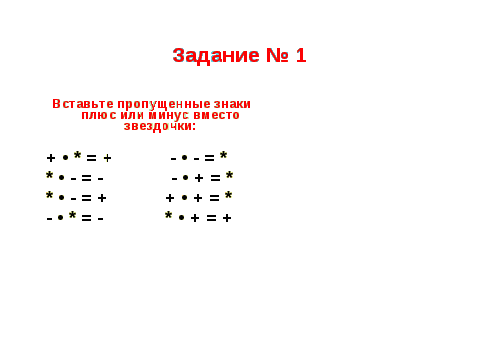
Допустим, что C — (-V) = D, исходя из этого, C = D + (-V), то есть C = D — V. Переносим V и получаем, что C + V = D. То есть C + V = C — (-V). Этот пример объясняет, почему в выражении, где идут два «минуса» подряд, упомянутые знаки следует поменять на «плюс». Теперь разберемся с умножением.
(-C) х (-V) = D, в выражение можно добавить и вычесть два одинаковых произведения, которые не поменяют его значения: (-C) х (-V) + (C х V) — (C х V) = D.
Вспомная о правилах работы со скобками, получаем:
1) (-C) х (-V) + (C х V) + (-C) х V = D;
2) (-C) х ((-V) + V) + C х V = D;
3) (-C) х 0 + C х V = D;
4) C х V = D.
Из этого следует, что C х V = (-C) х (-V).
Аналогично можно доказать, что и в результате деления двух отрицательных чисел выйдет положительное.
Общие математические правила
Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.
Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.
правило, примеры, умножение отрицательных чисел на положительные
В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение.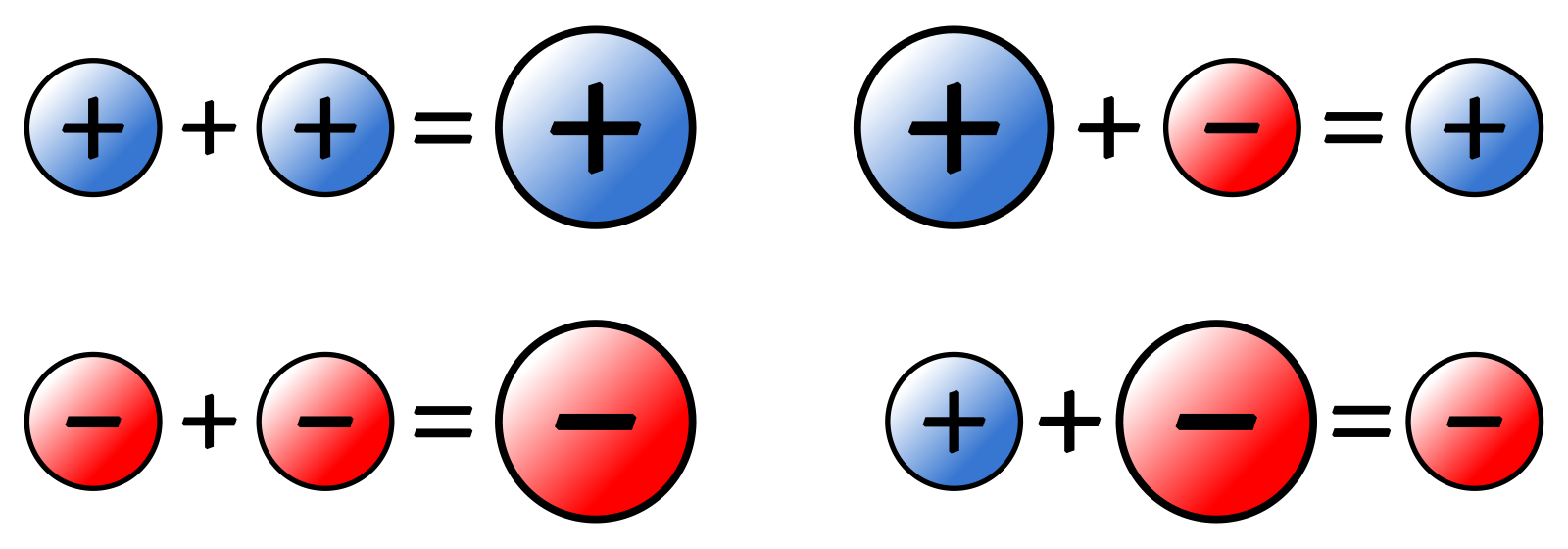 Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Умножение отрицательных чисел
Определение 1Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, -b данное равенство считается верным.
(-а)·(-b)=a·b.
Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (-а)·(-b)=a·b. Статья умножение чисел с разными знаками рассказывает о том, что равенств а·(-b)=-a·b справедливое, как и (-а)·b=-a·b. Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
(-a)·(-b)=(-a·(-b))=-(-(a·b))= a·b.
Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.
Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.
Примеры умножения отрицательных чисел
Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.
Пример 1Произвести умножение чисел -3 и -5.
Решение.
По модулю умножаемые данные два числа равны положительным числам 3 и 5. Их произведение дает в результате 15. Отсюда следует, что произведение заданных чисел равно 15
Запишем кратко само умножение отрицательных чисел:
(-3)·(-5)=3·5=15
Ответ: (-3)·(-5)=15.
При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 2Вычислить произведение (-0,125)·(-6).
Решение.
Используя правило умножения отрицательных чисел, получим, что (−0,125)·(−6)=0,125·6. Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:
Получили, что выражение примет вид (−0,125)·(−6)=0,125·6=0,75.
Ответ: (−0,125)·(−6)=0,75.
В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.
Пример 3Необходимо произвести умножение отрицательного -2 на неотрицательное log5 13.
Решение
Находим модули заданных чисел:
-2=2 и log513=-log5 3=log5 3.
Следуя из правил умножения отрицательных чисел, получим результат -2·log5 13=-2·log5 3=2·log5 3. Это выражение и является ответом.
Ответ: -2·log5 13=-2·log5 3=2·log5 3.
Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.
Возведение в степень разных чисел (отрицательных, дробей, нуля,…)
Если возводим в степень отрицательное число, то действует обычное правило умножения (минус на минус дает плюс):
(-3)2 = 9
Т.к. (-3)*(-3) — минусы дали плюс.
Также и
(-3)4 = 81
И при таком варианте:
(-3)3 = -27
или то же самое:
(-3)*(-3)*(-3) = 9*(-3)
У нас остается лишний минус, которому нет пары.
Можно сразу понять будет ли число все ещё отрицательным, после возведения в степень:
если показатель степени нечетный (1, 3, 5, 7, 9,…), то результат обязательно будет отрицательным,
если показатель степени четный (2, 4, 6, 8,..), то получившееся число всегда будет положительным.
Если мы возводим в степень дробь, то перемножаем верхнюю часть саму на себя и нижнюю.
Еще одно интересное свойство степеней: если мы перемножаем степени с одинаковыми основаниями, то мы можем просто сложить показатели этих степеней.
Смотрите, как это выглядит в буквах:
bx * by = bx+y
Вместо букв мы можем подставить любые числа, например,
23 * 24 = 23+4 = 27 = 128
Проверяем:
23 = 8
24 = 16
8*16 = 128
или
27 = 2 * 2 * 2 * 2 * 2 * 2 * 2 = 128
Такие фокусы можно проделывать и с большим количеством перемножаемых степеней, а не только с двумя.
Соответственно, если мы делим степени с одинаковыми основаниями, то можем просто отнимать показатели степени.
bx : by = bx-y
Снова подставляем числа:
Считаем:
35 : 33 = 35-3 = 32 = 9
Проверяем:
35 = 243
33 = 27
243:27 = 9 = 3*3
Всё получилось верно.
А вот если мы имеем разные основания и одинаковый показатель степени для каждого из них, то мы можем сначала перемножить основания, а затем возвести их в степень:
mx * nx = (mn)x
Числовая проверка:
23 * 53 = (2*5)3
2*2*2 = 8
5*5*5 = 125
8*125 = 1000
Или
2*5 = 10
10*10*10 = 1000
Магия цифр снова подтвердилась.
При делении, мы сначала разделим основания:
mx : nx = (m : n)x
Так можно сделать, только если n ≠ 0 (n не равно нулю), поскольку на 0 делить нельзя.
Посмотрим формулу в числах.
82 : 42 = (8 : 4)2
82 = 64
42 = 16
64 : 16 = 4
Или
8 : 4 = 2
22 = 4
Всё верно.
И еще пара моментов:
Если возводим в любую степень ноль, то всегда получаем ноль
0n = 0
0*0*0*0*0*0*0,… всегда ноль.
Если возводим в любую степень единицу, то всегда получаем единицу
1n = 1 (n, как во всех выражениях с буквами, это любое число)
1*1*1*1*1,… всегда единица.
Добавить интересную новость
Отрицательные дроби. Действия с отрицательными дробями
Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
-2 : 7 и 2 : (-7),
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус
можно ставить перед дробью, перед числителем или перед знаменателем:
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
Пример.
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | . |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
Таким образом:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Пример.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | — | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
Пример.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
Пример.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Пример.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Умножение отрицательного числа дает положительный результат
Когда мы умножаем:
Да, действительно, два отрицания дают положительный результат, и мы объясним , почему , на примерах!
Знаки
Давайте поговорим о знаков .
«+» — положительный знак, «-» — отрицательный.
Когда число имеет без знака , это обычно означает, что положительное .
И мы можем поставить () вокруг чисел, чтобы избежать путаницы.
Пример: 3 × −2 можно записать как 3 × (−2)
Два знака: правила
«Два одинаковых знака образуют положительный знак,
два разных знака образуют отрицательный знак»
Пример: (−2) × (+5)
Знаки — и + (отрицательный знак и положительный знак), поэтому они в отличие от знаков (они отличаются друг от друга)
Таким образом, результат должен быть отрицательным :
(−2) × (+5) = −10
Пример: (−4) × (−3)
Знаки — и — (оба являются отрицательными знаками), поэтому они как знаки (как друг друга)
Таким образом, результат должен быть положительным :
(−4) × (−3) = +12
Почему умножение двух отрицательных чисел дает положительное?
Ну, сначала объяснение «здравого смысла»:
Когда я говорю «Ешь!» Я призываю вас поесть (положительный результат)
Но когда я говорю «Не ешь!» Я говорю об обратном (отрицательном).
Теперь, если я говорю: «Не ешьте , а НЕ !», Я говорю, что не хочу, чтобы вы умирали с голоду, поэтому я снова говорю: «Ешьте!» (положительный).
Итак, два негатива дают положительный результат, и если это вас устраивает, то вам больше не нужно читать.
Направление
Все дело в направлении. Помните числовую черту?
Итак, малыш Стивен делает свои первые шаги. Он делает 2 шага за раз и делает это три раза, поэтому он делает 2 шага x 3 = 6 шагов вперед:
Теперь Малыш Стивен тоже может отступить (он умный маленький парень).Его отец ставит его в исходное положение, а затем Стивен делает два шага назад и делает это три раза:
И снова папа Стивена ставит его на старт, но лицом в другую сторону. Стивен делает 2 шага вперед (для него!), Но движется в отрицательном направлении. Он делает это 3 раза:
Снова вернувшись на старт (спасибо, папа!), Все еще глядя в отрицательном направлении, он пытается ходить задом, снова делая два шага за раз, и он делает это три раза:
Итак, идя назад, смотря в отрицательную сторону, он движется в положительном направлении.
Попробуйте сами! Попробуйте идти вперед и назад, затем снова, но лицом в другую сторону.
Другие примеры
Пример: деньги
| Сэм дает вам три купюры по 10 долларов: | +3 × +10 = вы получаете 30 долларов | |
| Сэм дает вам три долга по 10 долларов: | +3 × −10 = вы теряете 30 долларов | |
| Сэм берет у вас три купюры по 10 долларов: | −3 × +10 = вы теряете 30 долларов | |
| Сэм берет у вас три долга по 10 долларов: | −3 × −10 = вы получаете 30 долларов |
Пример: видео бегущих людей
человек бегут вперед, видео нормальное:
Все нормально, люди бегут вперед: +1 × +1 = +1
Люди бегут вперед, а видео назад :
Похоже, люди бегут задом наперед: +1 × −1 = −1
Люди бегут назад , видео нормальное:
Вы видите людей, бегущих назад: -1 × +1 = -1
Люди бегут назад , но видео в назад :
Похоже, люди бегут вперед: -1 × -1 = +1
Пример: повышение / понижение уровня в резервуаре
В баке 30 000 литров, каждый день вывозится 1000 литров. Сколько было воды в баке 3 дня назад ?
Сколько было воды в баке 3 дня назад ?
Мы знаем, что количество воды в резервуаре меняется на -1000 каждый день, и нам нужно вычесть это 3 раза (чтобы вернуться на назад на 3 дня ), поэтому изменение составит:
−3 × −1,000 = +3,000
Полный расчет:
30 000 + (-3 × -1 000) = 30 000 + 3 000 = 33 000
Итак, 3 дня назад в баке было 33 000 литров воды.
Таблица умножения
Вот с другой стороны, посмотреть на это.
Начните с таблицы умножения (достаточно 4 × 4):
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
| 4 | 4 | 8 | 12 | 16 |
Теперь посмотрим, что произойдет, когда мы перейдем к негативов !
Поехали назад через ноль:
| × | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| -4 | -4 | -8 | -12 | -16 |
| -3 | -3 | -6 | -9 | -12 |
| -2 | -2 | -4 | -6 | -8 |
| -1 | –1 | -2 | -3 | -4 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 6 | 8 |
| 3 | 3 | 6 | 9 | 12 |
| 4 | 4 | 8 | 12 | 16 |
Посмотрите на столбец «4»: это -16, -12, -8, -4, 0, 4, 8, 12, 16 . Каждый раз становясь на 4 больше.
Каждый раз становясь на 4 больше.
Посмотрите еще раз на эту таблицу, убедитесь, что вам удобно, как она работает, потому что …
… теперь идем левее , через ноль:
| × | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| -4 | 16 | 12 | 8 | 4 | 0 | -4 | -8 | -12 | -16 |
| -3 | 12 | 9 | 6 | 3 | 0 | -3 | -6 | -9 | -12 |
| -2 | 8 | 6 | 4 | 2 | 0 | -2 | -4 | -6 | -8 |
| -1 | 4 | 3 | 2 | 1 | 0 | –1 | -2 | -3 | -4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | -4 | -3 | -2 | –1 | 0 | 1 | 2 | 3 | 4 |
| 2 | -8 | -6 | -4 | -2 | 0 | 2 | 4 | 6 | 8 |
| 3 | -12 | -9 | -6 | -3 | 0 | 3 | 6 | 9 | 12 |
| 4 | -16 | -12 | -8 | -4 | 0 | 4 | 8 | 12 | 16 |
Тот же образец: мы можем следовать по строке (или столбцу), и значения меняются последовательно:
- Следуйте ряду «4»: это идет -16, -12, -8, -4, 0, 4, 8, 12, 16 .
 Каждый раз становясь на 4 больше.
Каждый раз становясь на 4 больше. - Следуйте за строкой «-4»: это идет 16, 12, 8, 4, 0, -4, -8, -12, -16 . Каждый раз становится на 4 меньше.
- и т.д …
Так что все идет по аккуратной схеме!
Как насчет умножения 3 или более чисел вместе?
Умножьте два за раз и следуйте правилам.
Пример: Что такое (−2) × (−3) × (−4)?
Сначала умножаем (−2) × (−3). Два подобных знака означают положительный знак, поэтому:
(−2) × (−3) = +6
Далее умножаем +6 × (−4).Два непохожих знака образуют отрицательный знак, поэтому:
+6 × (−4) = −24
Результат: (−2) × (−3) × (−4) = −24
Умножение и деление отрицательных чисел
Purplemath
Если перейти от сложения и вычитания, как вы производите умножение и деление с отрицательными числами? Собственно, сложную часть мы уже рассмотрели: вы уже знаете правила «знака»:
плюс раз плюс плюс
(добавление большого количества горячих кубиков повышает температуру)
минус раз плюс минус
(удаление большого количества горячих кубиков снижает температуру)
плюс умножить на минус — это минус
(добавление большого количества холодных кубиков снижает температуру)
минус умножить на минус равно плюс
(удаление большого количества холодных кубиков повышает температуру)
MathHelp.
 com
comПравила знаков действуют одинаково для деления; просто замените «раз» на «деленное на». Вот пример правил в разделе:
(Помните, что дроби — это просто еще одна форма деления! «Дроби — это деление»!)
Некоторым людям нравится думать об отрицательных числах в терминах долгов.Так, например, если вы должны 10 долларов шести людям, ваш общий долг составит 6 × 10 долларов = 60 долларов. В этом контексте имеет смысл получить отрицательный ответ. Но в каком контексте может иметь смысл деление отрицательного на отрицательное (и получение положительного)?
Подумайте о том, чтобы перекусить в кафе. Когда вы идете платить, у ребенка возникают проблемы с использованием вашей дебетовой карты. Он проводит по ней шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет в Интернете. По сумме можно сказать, что да, он действительно взимал с вас или более одного раза.Некоторая часть этого общего дебета (отрицательная на вашем счете) неверна.
Он проводит по ней шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет в Интернете. По сумме можно сказать, что да, он действительно взимал с вас или более одного раза.Некоторая часть этого общего дебета (отрицательная на вашем счете) неверна.
Прежде чем звонить в банк для исправления ситуации, вы хотите подтвердить количество превышенных комиссий. Как в этом разобраться? Вы можете разделить всю сумму (скажем, 76,02 доллара США) на сумму, указанную в квитанции (скажем, 12,67 доллара США), которая является суммой одного платежа. Каждое списание является минусом на вашем счету, поэтому математика составляет:
.(- 76,02 доллара) ÷ (- 12 долларов.67) = 6
Итак, всего действительно было шесть зарядов. Количество зарядов, 6, при подсчете количества событий, должно быть положительным. В этом реальном контексте деление минуса на минус и получение плюса имеет смысл. И теперь вы знаете, что нужно указать службе поддержки клиентов отменить ровно пять начислений.
И теперь вы знаете, что нужно указать службе поддержки клиентов отменить ровно пять начислений.
Вы можете заметить, что люди отменяют знак минус.Они пользуются тем, что «минус, умноженный на минус, равен плюсу». Например, предположим, что у вас есть (–2) (- 3) (- 4). Любые два отрицательных результата при умножении становятся одним положительным. Так что выберите любые два из перемноженных (или разделенных) отрицаний и «отмените» их знаки:
Упростить (–2) (- 3) (- 4).
Начну с того, что уберу одну пару знаков «минус».Потом размножу как обычно.
(–2) (- 3) (- 4)
= (–2) (- 3) (–4)
= (+6) (–4)
= –24
Если вам дано длинное умножение с отрицательными числами, просто уберите знаки «минус» в парах:
Упростить (–1) (- 2) (- 1) (- 3) (- 4) (- 2) (- 1).

Первое, что я сделаю, это сосчитаю знаки «минус». Один два три четыре пять шесть семь. Итак, есть три пары, которые я могу отменить, оставив одну. В результате мой окончательный ответ должен быть отрицательным. Если я получу положительный результат, я буду знать, что сделал что-то не так.
(–1) (- 2) (- 1) (- 3) (- 4) (- 2) (- 1)
= (–1) (- 2) (–1) (- 3) (- 4) (- 2) (- 1)
= (+1) (+ 2) (–1) (- 3) (- 4) (- 2) (- 1)
= (1) (2) (–1) (- 3) (–4) (- 2) (- 1)
= (1) (2) (+1) (+ 3) (–4) (- 2) (- 1)
= (1) (2) (1) (3) (–4) (- 2) (–1)
= (1) (2) (1) (3) (+4) (+ 2) (–1)
= (1) (2) (1) (3) (4) (2) (- 1)
= (2) (3) (4) (2) (- 1)
= 48 (–1)
= –48
Я получил отрицательный ответ и знаю, что мой знак правильный.
Вот еще один пример, показывающий тот же процесс отмены в контексте разделения:
Отрицательные скобки
Основная трудность, с которой люди сталкиваются с негативом, заключается в том, чтобы иметь дело со скобками; в частности, в переносе отрицания через круглые скобки. Обычная ситуация выглядит примерно так:
Если бы у вас было «3 ( x + 4)», вы бы знали, что нужно «распределить» 3 «над» круглыми скобками:
3 ( x + 4) = 3 ( x ) + 3 (4) = 3 x + 12
Те же правила применяются, когда вы имеете дело с негативом.Если у вас проблемы с отслеживанием, используйте маленькие стрелки:
← проведите по экрану , чтобы просмотреть изображение полностью →
Мне нужно взять 3 в скобки:
3 ( x — 5) = 3 ( x ) + 3 (–5) = 3 x — 15
Здесь я возьму «минус» в скобках; Я буду распределять –2 на x и минус 3.
–2 ( x — 3) = –2 ( x ) — 2 (–3) = –2 x + 2 (+3) = –2 x + 6
Обратите внимание, как я внимательно следил за знаками в круглых скобках. «Минус» был сохранен рядом с цифрой 3 за счет использования еще одного набора круглых скобок. Не стесняйтесь использовать символы группировки, чтобы обозначить предполагаемый смысл как для оценщика, так и для вас самих.
Другая проблема, связанная с предыдущей, связана с вычитанием скобок. Вы можете отслеживать знак вычитания, преобразовывая вычитание в умножение на минус:
Начну с маленькой цифры «1» перед круглыми скобками. Затем я нарисую стрелки от этой единицы к терминам в круглых скобках, чтобы напомнить себе о том, что мне нужно сделать.
← проведите по экрану , чтобы просмотреть изображение полностью →
Не бойтесь написать эту маленькую цифру «1» и нарисовать эти маленькие стрелки. Вы должны делать все, что вам нужно, чтобы ваша работа была прямой и постоянно получала правильный ответ.
Вы должны делать все, что вам нужно, чтобы ваша работа была прямой и постоянно получала правильный ответ.
Упростить 6 — (3
x — 4 [1 — x ]).
Я буду работать изнутри, упрощая сначала символы внутренней группировки в соответствии с Порядком операций. Итак, первое, что я сделаю, это возьму –4 через скобки.Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками и, чтобы помочь мне отслеживать тот -1, который я буду распространять, я нарисую маленькие стрелки.
← проведите по экрану , чтобы просмотреть изображение полностью →
Филиал
Упростить
1 / 3 — ( x -2) / 3 .
Это непросто. Они заставляют меня вычесть дробь. Мне нужно объединить дроби, что означает объединение числителей. Чтобы не упустить из виду, что именно означает этот «минус» (а именно, что я вычитаю весь числитель второй дроби, а не только x ), я конвертирую минус с плюсом –1:
← проведите по экрану , чтобы просмотреть изображение полностью →
Обратите внимание, что я преобразовал вычитание дроби в добавление отрицательного числа, умноженного на единицу дроби.Очень легко «потерять» минус, когда вы добавляете такие беспорядочные полиномиальные дроби. Самая частая ошибка — ставить минус на x и забывать отнести его к –2. Будьте особенно осторожны с дробями!
Для дополнительной практики со скобками попробуйте здесь.
URL: https://www. purplemath.com/modules/negative3.htm
purplemath.com/modules/negative3.htm
1.5 Почему ОТРИЦАТЕЛЬНОЕ ВРЕМЯ ОТРИЦАТЕЛЬНО ПОЛОЖИТЕЛЬНО?
Когда мы открываем отрицательные числа, мы, естественно, даже без сомнения, предполагаем, что они подчиняются тем же законам арифметики, что и обычные положительные счетные числа. То есть нам нравится верить, что основные законы, такие как \ (a \ times b = b \ times a \) и \ (a \ times 1 = a \) и \ (a \ times 0 = 0 \), выполняются для всех числа, как положительные, так и отрицательные, и что мы можем раскрывать скобки даже с отрицательными записями и т. д. Конечно, эти правила предполагают, что мы знаем, что априори умеют умножать на отрицательные числа.
УМНОЖЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ НОМЕРОВ
В начальной учебной программе умножение вводится в контексте целых счетных чисел и соответственно определяется как повторное сложение. Например, \ (4 \ times 5 \) читается как «четыре группы по пять» и вычисляется следующим образом: \ (4 \ times 5 = 5 + 5 + 5 + 5 = 20 \).
Например, \ (4 \ times 5 \) читается как «четыре группы по пять» и вычисляется следующим образом: \ (4 \ times 5 = 5 + 5 + 5 + 5 = 20 \).
На самом деле довольно удивительно, что \ (5 \ умножить на 4 \), «пять групп по четыре», дает тот же числовой ответ, что и четыре группы по пять.Вычисление совершенно иное, когда числа 5 и 4 служат для смены ролей.
Вопрос: Как бы вы убедили молодого студента в том, что 193 группы из 307 человек обязательно будут иметь такую же ценность, как 307 групп из 193 человек? Почему мы хотим, чтобы верили, что \ (a \ times b = b \ times a \) для подсчета чисел? (ПОДСКАЗКА: расставьте точки в прямоугольные массивы.)
Повторное сложение позволяет нам умножить положительное число и отрицательное число.Например, \ (2 \ times \ left (-3 \ right) \) можно читать как «две группы отрицательных трех» и поэтому вычисляется как \ (2 \ times \ left (-3 \ right) = — 3 + \; — 3 = -6 \). По сваям и ямам это выглядит так:
По сваям и ямам это выглядит так:
Однако интерпретировать отрицательное умножение на положительное и отрицательное, умноженное на отрицательное, путем повторного сложения проблематично.
Что может означать \ (\ left (-2 \ right) \ times 3 \)? «Отрицательные две группы по три» не имеет смысла.
И \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) одинаково странно: «две отрицательные группы из трех отрицательных».”
На самом деле умножение здесь не имеет значения в контексте повторяющегося сложения. Мы вступили на новую территорию, и если мы хотим открыть наш мир для новых типов чисел, неудивительно, что ранее конкретные, буквальные определения начинают ошибаться. Итак, мы должны провести изощренный сдвиг мышления, отказавшись от вопроса Что такое умножение? вместо этого спросить:
Как бы мы хотели, чтобы вело себя умножение?
Комментарий: Позвольте мне подчеркнуть этот момент. На вопрос: «Что означает умножение отрицательных чисел?» Это вводящий в заблуждение вопрос, и это не тот вопрос, который следует задавать на данном этапе нашей работы: мы все еще пытаемся решить проблему того, каким может быть умножение в мире отрицательных чисел. Чтобы приблизиться к этому, мы сначала должны четко определить, какие особенности арифметики, по нашему мнению, должны оставаться верными.
На вопрос: «Что означает умножение отрицательных чисел?» Это вводящий в заблуждение вопрос, и это не тот вопрос, который следует задавать на данном этапе нашей работы: мы все еще пытаемся решить проблему того, каким может быть умножение в мире отрицательных чисел. Чтобы приблизиться к этому, мы сначала должны четко определить, какие особенности арифметики, по нашему мнению, должны оставаться верными.
Положительные, умноженные на Отрицательные : Кажется убедительным придерживаться концепции «повторного сложения» для произведения отрицательного и положительного:
\ (2 \ times \ left (-3 \ right) = \) две группы отрицательных трех \ (= — 3 + -3 = -6 \).
Большинство людей согласны с тем, что мы должны придерживаться этой идеи.
Отрицательное время Положительное : Это проблематично: \ (\ left (-2 \ right) \ times 3 =? \)
Но кажется убедительным сказать, что закон коммутативности \ (a \ times b = b \ times a \) должен выполняться для всех типов чисел, включая отрицательные числа. В этом случае мы можем написать:
В этом случае мы можем написать:
\ (\ left (-2 \ right) \ times 3 = 3 \ times \ left (-2 \ right) \) три группы отрицательных двоек \ (= — 2 + -2 + -2 = -6 \).
Отрицательное время Отрицательное : Как нам вычислить \ (\ left (-2 \ right) \ times \ left (-3 \ right) \)?
Применение закона коммутативности и представление об этом как о \ (\ left (-3 \ right) \ times \ left (-2 \ right) \) в этом случае не помогает.Итак, какая математика могла бы направить нас в нашем мышлении?
Мы действительно сказали, что нам нравится верить, что все обычные законы арифметики (\ (a \ times b = b \ times a \), \ (a \ times 1 = a \), \ (a \ times 0 = 0 \), раскрывающиеся скобки и т. д.) должны выполняться для всех типов чисел. Поскольку модель площади — это всего лишь представление, которое мы верим в расширяющиеся скобки, модель площади должна работать и для отрицательных чисел!
КЛЮЧЕВОЙ ПРИМЕР: Вот три способа вычислить \ (17 \ times 18 \), считая \ (17 \) либо \ (10 + 7 \), либо \ (20+ \ left (-3 \ right) \) и \ (18 \) как \ (10 + 8 \) или \ (20 + \ left (-2 \ right) \). Несмотря на то, что геометрически не имеет смысла иметь отрицательную длину стороны геометрической фигуры, мы видим, что математика, которую представляет каждая диаграмма, по-прежнему является правильной математикой.
Несмотря на то, что геометрически не имеет смысла иметь отрицательную длину стороны геометрической фигуры, мы видим, что математика, которую представляет каждая диаграмма, по-прежнему является правильной математикой.
Но есть четвертая возможная картина!
Математика раскрывающихся скобок предполагает, что правильное значение \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) равно \ (+ 6 \). (У продукта должен быть ответ \ (306 \).)
УПРАЖНЕНИЕ: Нарисуйте четыре диаграммы, представляющие \ (26 \ times 35 \), и используйте последнюю, чтобы продемонстрировать, почему мы должны установить \ (\ left (-4 \ right) \ times \ left (-5 \ right) = +20 \).
ТОЧНЫЙ ЛОГИЧЕСКИЙ АРГУМЕНТ, ПОЧЕМУ ОТРИЦАТЕЛЬНЫЙ ВРЕМЯ ОТРИЦАТЕЛЬНЫЙ ДОЛЖЕН БЫТЬ ПОЛОЖИТЕЛЬНЫМ Как только мы договоримся, что \ (2 \ times \ left (-3 \ right) = — 6 \) (посредством повторного сложения) и \ (\ left (-3 \ right) \ times 2 = -6 \) (через a убежденность в коммутативности), что отрицательное умножение на отрицательное является положительным, является вынужденным логическим следствием следующих двух основных убеждений арифметики: \ (a \ times 0 = 0 \) и \ (a \ left (b + c \ right) = ab + ас \). Вот почему:
Вот почему:
Докажем \ (\ left (-2 \ right) \ times \ left (-3 \ right) = + 6 \).
По первому правилу мы должны сказать: \ (\ left (-2 \ right) \ times 0 = 0 \).
Переписывая первый ноль, мы должны согласиться с тем, что: \ (\ left (-2 \ right) \ times \ left (3+ \ left (-3 \ right) \ right) = 0 \).
При распределении мы также должны согласиться с тем, что: \ (\ left (-2 \ right) \ times 3 + \ left (-2 \ right) \ times \ left (-3 \ right) = 0 \).
Это читается так: \ (- 6 + \ left (-2 \ right) \ times \ left (-3 \ right) = 0 \).
Отсюда следует, что \ (\ left (-2 \ right) \ times \ left (-3 \ right) \) должно быть \ (+ 6 \).
УПРАЖНЕНИЕ: Создайте аналогичный аргумент, чтобы установить, что \ (\ left (-4 \ right) \ times \ left (-5 \ right) = + 20 \).
ТАК… ЧТО ТАКОЕ УМНОЖЕНИЕ? В контексте положительных целых чисел это повторное сложение.
В контексте положительных и отрицательных целых чисел я лично не знаю, что это такое, кроме математически согласованной операции, установленной так, что если \ (a \) и \ (b \) — положительные целые числа, то \ ( a \ times \ left (-b \ right) = — ab \), и с логическими следствиями \ (\ left (-a \ right) \ times b = b \ times \ left (-a \ right) = — ab \) и \ (\ left (-a \ right) \ times \ left (-b \ right) = ab \).
Люди пытаются придать всему этому конкретный смысл с помощью моделей солдат, идущих по числовым линиям, меняющих направление, систем прибыли и долга, работы с температурами выше и ниже нуля и т. Д. Каждая модель хороша для иллюстрации НЕКОТОРЫХ аспектов арифметики отрицательных чисел, но не всех. Например, идея «убрать пять градусов холода — это то же самое, что добавить пять градусов тепла» может сработать для некоторых, чтобы объяснить, почему \ (- \ left (-5 \ right) \) должно равняться \ (5 \) , но это не объясняет само по себе, почему отрицательное, умноженное на отрицательное, дублируется положительным.
С педагогической точки зрения нам нужно отойти от начинающих учеников думать об умножении отрицательных чисел с помощью моделей, которые пытаются, но в какой-то момент должны потерпеть неудачу, «объяснить», что такое умножение отрицательных чисел. Вместо этого мы должны начать с обсуждения того, что, по нашему мнению, должно быть правдой в отношении умножения в целом и как оно ведет себя. Расширение скобок с помощью модели площади дает студентам убедительную иллюстрацию того, что математика «хочет», чтобы отрицательные значения, умноженные на отрицательные, были положительными.(А для студентов, готовых к этому, это подтверждает аксиоматический подход.) Что на самом деле означает «отрицательное, умноженное на отрицательное, — положительное» — я понятия не имею. Я просто знаю, что это алгебраически непротиворечиво.
УПРАЖНЕНИЕ: a) Докажите, что \ (- a \) и \ (\ left (-1 \ right) \ times a \) — одно и то же число. (ПОДСКАЗКА: \ (a + \ left (-1 \ right) \ times a = 1 \ times a + \ left (-1 \ right) \ times a = \ ldots \). )
)
b) Если вы считаете, что \ (- \ left (-5 \ right) = 5 \), объясните, почему теперь следует, что \ (\ left (-1 \ right) \ times \ left (-1 \ right) = 1 \).
Присоединяйтесь к обсуждению в Facebook и Twitter и любезно поделитесь этой страницей с помощью кнопок ниже.Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet
Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила:
Когда вы умножаете отрицательное число на положительное, произведение всегда отрицательное.
Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.
Это похоже на правило сложения и вычитания: два знака минус становятся плюсом, а плюс и минус становятся минусом. Однако при умножении и делении вы вычисляете результат, как если бы не было знаков минус, а затем смотрите на знаки, чтобы определить, положительный или отрицательный результат. Два примера быстрого умножения:
Два примера быстрого умножения:
$$ 3 \ cdot (-4) = — 12 $$
3 умножить на 4 равно 12.Поскольку существует одно положительное и одно отрицательное число, произведение отрицательное 12.
$$ (- 3) \ cdot (-4) = 12 $$
Теперь у нас есть два отрицательных числа, поэтому результат положительный.
Переходя к делению, вы можете вспомнить, что вы можете подтвердить полученный ответ, умножив частное на знаменатель. Если вы ответили правильно, то произведение этих двух чисел должно совпадать с числителем. Например,
$$ \ frac {12} {3} = 4 $$
Чтобы проверить, является ли 4 правильным ответом, мы умножаем 3 (знаменатель) на 4 (частное):
$$ 3 \ cdot 4 = 12 $$
Что произойдет, если разделить два отрицательных числа? Например,
$$ \ frac {(- 12)} {(- 3)} = \:? $$
Чтобы знаменатель (-3) стал числителем (-12), вам нужно умножить его на 4, поэтому частное равно 4.
Итак, частное отрицательного и положительного чисел отрицательно, и, соответственно, частное положительного и отрицательного чисел также отрицательно. Можно сделать вывод, что:
Когда вы делите отрицательное число на положительное, то частное отрицательное.
Когда вы делите положительное число на отрицательное, частное также становится отрицательным.
Когда вы делите два отрицательных числа, получается положительное частное.
Те же правила верны и для умножения.
ВидеоурокВычислить следующие выражения
$$ (- 4) \ cdot (-12), \: \: \: \: \ frac {-12} {3} $$
предварительное вычисление алгебры — Почему отрицательное умножение на отрицательное = положительное?
Следует понимать одну вещь: этот закон нельзя доказать так же, как можно доказать законы положительной рациональной и интегральной арифметики. Причина этого в том, что негативы лишены какого-либо «внешнего» (внешнего по отношению к математике, т.е. доаксиоматическое, интуитивное, концептуальное, эмпирическое, физическое, и т. Д. ) определение.
Например. Даже не вдаваясь в аксиомы Пеано, я могу доказать, что, где $ a $ и $ b $ — натуральные числа, $ ab = ba $. В самом деле, $ ab $ — это просто процесс взятия $ a $ наборов из $ b $. Возьмите по одному элементу из каждого из этих наборов, образуя набор из $ a $ элементов. Повторите это $ b $ раз: вы явно израсходуете в точности все элементы и получите $ b $ наборов из $ a $ элементов, другими словами, $ ba $.Подобные неформальные (но вполне убедительные, разумные и, я бы сказал, неопровержимые) рассуждения можно использовать, например, для демонстрации правил манипулирования положительными дробями.
Обратите внимание, что в предыдущем абзаце я использовал тот факт, что как положительные целые числа, так и положительное целочисленное умножение имеют преаксиоматические, «физические» определения.
Спросите кого-нибудь, почему произведение двух отрицаний положительно, и лучшее, что они могут сделать, это объяснить , а не доказать . «Ну, отрицательный вид означает« противоположность », поэтому двойное выполнение противоположного означает выполнение обычного, т.е. положительного» не является доказательством, а просто объяснением, служащим для того, чтобы сделать принятую математическую аксиому менее удивительной.Другой распространенный вариант начинается со слов «мы хотели бы, чтобы обычные свойства арифметики выполнялись, поэтому предположим, что они имеют …», но затем остается объяснить, почему так важно, чтобы выполнялись обычные законы арифметики. Сам Эйлер в одной из первых глав своего учебника по алгебре дал следующее в высшей степени сомнительных оправданий. Обосновав $ (- a) b = — (ab) $ по аналогии с долгами, он пишет:
Осталось разрешить случай, когда — умножается на -; или, например, -a на -b.По буквам с первого взгляда очевидно, что это будет ab; но сомнительно, стоит ли ставить перед ним знак + или знак -, все, что мы знаем, это то, что это должен быть один из этих знаков. Теперь я говорю, что это не может быть знак -: for -a by + b дает -ab, а -a by -b не может дать того же результата, что -a by + b …
Без неуважения к Эйлеру (особенно учитывая, что это было задумано как вводный учебник), я думаю, мы можем согласиться с тем, что это довольно сомнительный с философской точки зрения аргумент.
Причина, по которой это невозможно, состоит в том, что не существует преаксиоматического определения того, что на самом деле представляет собой отрицательное число или отрицательное умножение. О, вы, вероятно, могли бы придумать одно, включающее противоположные «направления» и понятия симметрии, но это было бы довольно искусственным и вовсе не явно «лучшим» определением. На мой взгляд, негатив лучше всего понимать как чисто абстрактные объекты. Бывает так — и это довольно загадочно, — что эти совершенно абстрактные законы вычислений приводят к физически значимым результатам.Это было красиво выражено в 1778 году математиком Джоном Плейфэром, когда он обратился к тогдашним спорным вопросам отрицательных и комплексных чисел:
Вот парадокс, который еще предстоит объяснить. Если операции этой воображаемой арифметики непонятны, почему они не совсем бесполезны? Неужели расследование — это искусство настолько механическое, что его можно проводить вручную? Или правда так легко обнаруживается, что для успеха наших исследований не нужен интеллект?
Цитируется в журнале « Negative Math: Как математические правила могут быть положительно искажены» Альберто А.Мартинес.
Одним из способов решения проблемы является идея, что отрицательные числа — это другое название для вычитания . Различия между вычитанием и сложением вынуждают нас, если мы отвергаем отрицания, создавать множество разных правил, охватывающих все различные возможности ($ a — b $, $ b — a $ и $ a + b $, и если конкретная теорема или проблема включает более двух переменных, сложность усугубляется …). Идею негативов можно описать как понимание того, что вместо двух операций и одного типа числа мы можем иметь одну операцию и два типа числа .В самом деле, если вы начнете с некоторых совершенно физически значимых аксиом о вычитании, вы обнаружите, что закон $ (- 1) (- 1) = 1 $, по-видимому, подразумевается внутри них. Подсказка: исходя из очень разумных аксиом $ a (b-c) = ab-ac \, \ a — (b — c) = a — b + c $, рассмотрим произведение $ (a-b) (c-d) $.
Но даже это объяснение меня не совсем удовлетворяет. Я пришел к убеждению, что мое образование обмануло меня, понимая, насколько глубоки отрицательные числа, и я ожидаю, что они будут озадачивать их еще долгие годы.В любом случае, я надеюсь, что кое-что из вышеперечисленного кому-то пригодится.
Почему отрицательное время всегда отрицательно положительно? — Рефлексивный педагог
Существуют разные ответы на этот вопрос, в зависимости от требуемого стандарта доказательства и базовых знаний, которые вы привносите в вопрос.
Математическая последовательность и закономерности
Попробуйте решить каждую из этих проблем, обращая при этом внимание на предыдущий набор проблем.Ищите шаблоны, облегчающие решение проблем.
3 × 3 =?
3 × 2 =?
3 × 1 =?
3 × 0 =?
3 × -1 =?
3 × -2 =?
3 × -3 =?
2 × -3 =?
1 × -3 =?
0 × -3 =?
-1 × -3 =?
-2 × -3 =?
-3 × -3 =?
Ответы на эти проблемы приведены ниже, но я действительно рекомендую сначала найти время, чтобы решить вышеперечисленные задачи самостоятельно, чтобы вы получили представление о том, как учащиеся могут обдумывать этот набор задач.
3 × 3 = 9
3 × 2 = 6
3 × 1 = 3
3 × 0 = 0
На этом этапе многие люди заметят, что ответы каждый раз становятся на 3 меньше, а число, умноженное на 3, каждый раз становится на единицу меньше, поэтому они продолжают этот шаблон, чтобы ответить на следующие вопросы.
3 × -1 = -3
3 × -2 = -6
3 × -3 = -9
Теперь мы уменьшаем первое число в шаблоне на 3, и нужно сделать некоторые выводы о том, каким должен быть ответ.
2 × -3 = -6
1 × -3 = -3
0 × -3 = 0
Теперь можно заметить, что ответы увеличиваются на 3 каждый раз, когда мы увеличиваем первое число, и поэтому разумно продолжить этот шаблон.
-1 × -3 = 3
-2 × -3 = 6
-3 × -3 = 9
Хотя некоторым этот образец может показаться очевидным, когда кто-то все еще находится в середине изучения этой концепции, у него меньше когнитивных способностей, доступных для выполнения поставленной задачи (умножения чисел) и выполнения дополнительной задачи поиска закономерностей в своем ответы, так что именно здесь кто-то другой побуждает их остановиться и поискать закономерности в своей работе до сих пор, будет очень полезно.
Предварительные знания : Необходимо знать, что означают эти символы, что подразумевается под умением одного числа умножить на другое и как работают отрицательные числа с точки зрения обратного отсчета и вычитания.
Математическая непротиворечивость и математические свойства
Давайте посмотрим на проблему, которую мы можем решить более чем одним способом, позаимствованным из Академии Хана.
5 × (3 + -3) =?
Если мы сначала сложим числа внутри скобок, то получится 5 умножить на 0, что равно 0, поскольку 3 + -3 = 0.
5 × (3 + -3) = 0
Но что, если мы сначала распределим 5 через оба термина?
5 × 3 + 5 × -3 =?
Поскольку распределение 5 по сложению не меняет значения выражения, мы знаем, что оно по-прежнему равно 0.
5 × 3 + 5 × -3 = 0
Но это означает, что 5 × 3 и 5 × -3 — противоположные знаки, поэтому, поскольку 5 × 3 = 15, то 5 × -3 равно -15. Давайте посмотрим на другой пример.
-5 × (3 + -3) =?
Мы знаем, что это то же самое, что -5 умножить на 0, поэтому это значение равно 0.
-5 × (3 + -3) = 0
Как и раньше, мы распределяем -5 через оба термина.
-5 × 3 + -5 × -3 =?
Опять же, распределение членов не меняет значения выражения в левой части уравнения, поэтому результат по-прежнему равен 0.
-5 × 3 + -5 × -3 = 0
Мы уже знали, что -5 × 3 равно -15, поэтому мы можем заменить это значение на -5 × 3 в левой части уравнения.
-15 + -5 × -3 = 0
Следовательно, -15 и -5 × -3 являются противоположностями, так как они складываются в 0, поэтому -5 × -3 должно быть положительным.
Ничто в том, что мы сделали для двух приведенных выше примеров, не является специфическим для значения 5 × 3, поэтому мы можем повторить этот аргумент для каждого другого факта умножения, который мы хотим вывести, чтобы эти две идеи можно было обобщить.
Необходимые знания : Необходимо знать, что означают эти символы, что подразумевается под нахождением одного числа, умноженного на другое, как работает свойство распределения и как отрицательные числа могут быть определены как противоположности положительных чисел.
Представительство на числовой строке
Представьте, что мы представляем умножение в виде прыжков на числовой прямой.
3 умножить на 3 на числовой прямойДля 3 × 3 мы рисуем 3 группы по 3, двигаясь вправо. И количество групп, и направление каждой группы справа.
А как насчет 3 × -3? Теперь у нас осталось 3 группы чисел, но число отрицательное.
3 умножить на -3 в числовой строкеЕсли мы найдем -3 × 3, размер и направление умножаемого числа будут такими же, но теперь мы находим -3 группы этого числа. Один из способов подумать об этом — подумать о том, чтобы убрать 3 группы числа.Другой — представить, что -3 умноженное на число является отражением 3-кратного того же числа.
-3 умножить на 3 на числовой прямойТаким образом, -3 × -3 является отражением 3 × -3 поперек числовой прямой.
-3 умножить на -3 в числовой строкеОднако в каком-то смысле этот визуальный аргумент представляет собой просто математическую согласованность, представленную в числовой строке. Если умножение на отрицательное — это отражение через 0 на числовой прямой, и мы думаем, что отрицательные числа являются отражениями через 0 числовой прямой, то умножение отрицательного числа на отрицательное число является двойным отражением.
Контекст
У Карен Лью есть эта аналогия.
Умножение на отрицательное — это повторное вычитание. Когда мы умножаем отрицательное число на отрицательное число, мы получаем меньше отрицательного.
Эта аналогия между умножением и сложением и вычитанием помогает студентам хорошо связать эти два понятия.
Джозеф Рурк поделился этим контекстом.
Игрок теряет 10 долларов в день.Насколько больше у них было денег 5 дней назад?
Здесь убыток за день — одно отрицательное значение, а движение назад во времени — другое.
@M_Teacher_w_T поделился этой аналогией:
«Враг моего врага — мой друг».
Это нацелено не на алгебраические или арифметические свойства чисел, а больше на противоположность отрицательных чисел.
Необходимые знания: Все контексты, которые создают новое понимание, требуют от учащихся достаточно хорошего понимания частей контекста, поэтому особенно важно проверить, как учащиеся понимают идею, когда она представлена в контексте.
Алгебраическое доказательство из первых принципов
От доктора Алекса Юстиса у нас есть алгебраическое доказательство того, что отрицательное умножение на отрицательное является положительным.
Во-первых, он формулирует набор аксиом, применимых к любому кольцу с единицей. Кольцо — это, по сути, система счисления с двумя операциями. Каждая операция закрывается, что означает, что использование этих операций (таких как сложение и умножение действительных чисел) приводит к другому числу в системе счисления.У каждой операции также есть элемент идентичности или элемент, который не изменяет другой элемент в системе при применении к нему. Например, при добавлении 0 — это аддитивный идентификатор. При умножении 1 — это мультипликативное тождество. Полный набор необходимых аксиом приведен ниже.
| Axiom 1 : a + b = b + a | (Аддитивная коммуникативность) | |
| Axiom 2 : () + = a + ( b + c ) | (аддитивная ассоциативность) | |
| Axiom 3 : 0 + a = a | ( | (аддитивная идентичность) |
| (аддитивная инверсия) | ||
| Axiom 5 : 1 × a = a × 1 = a | (Мультипликативная идентичность) | |
| Аксиома 6 : ( a × b ) × c = a × ( b × c ) (Мультипликативная ассоциативность | ) )Axiom 7 : a × ( b + c ) = a × b + a × c | (левое мультипликативное распределение) | 9010om 8106 : ( b + c ) × a = b × a + c × a(Правильное распределение умножения) |
Из этих аксиом мы можем доказать, что отрицательный, умноженный на отрицательный, является положительным.Ниже я воспроизведу доказательство доктора Юстиса и сделаю ссылку на используемые аксиомы. Сначала докажем, что a = — (- a ).
Corrolary 1| a = a + 0 | style = «text-align: right»>(Axiom 3 and Axiom 1) |
| a = a + (- a + — (- a )) | (Аксиома 4 применяется к — a ) |
| a = ( a + (- a )) + (- (- a )) | (Аксиома 2 — ассоциативное свойство) |
| a = 0 + (- (- a )) | (Аксиома 4) |
| a = — (- a ) | (Аксиома 3) |
Итак, теперь мы знаем, что если мы введем отрицательные числа , будет равно — (- 𝑎).
Corrolary 2| 0 = a + (- a ) | (Axiom 4) |
| 0 = (0 + 1) × a + (- a ) | (Аксиома 3 и Аксиома 5) |
| 0 = 0 × a + 1 × a + (- a ) | (Аксиома 8) |
| 0 = 0 × a + ( a + (- a )) | (Axiom 5 и Axiom 2) |
| 0 = 0 × a + 0 | (Axiom 4) |
| 0 = 0 × a | (Аксиома 3 и Аксиома 1) |
Доказательство того, что 0 = 0 × a — это своего рода до боли очевидная идея, которая вряд ли требует доказательства, но устанавливает связь между умножением и аддитивной идентичностью в действительных числах, которая еще не включен в аксиомы выше.
Затем мы докажем, что (−1) × a = — a .
Корролл 3| — a = — a + 0 × a | (Corrolary 2 and Axiom 3) |
| — a = — a + (1 + (−1)) × a | (Axiom 4) |
| — a = — a + 1 × a + (−1) × a | (Axiom 8) | — = (- a + a ) + (−1) × a | (Аксиома 5 и Аксиома 2) |
| — a = 0 + (−1) × a | (Аксиома 4) |
| — a = 0 + (−1) × a | (Аксиома 3) |
Теперь, наконец, мы можем доказать, что (- a ) × ( — b ) = ab .
| (- a ) × (- b ) = ( a × (−1)) × (- b ) | (Corrolary 3) |
| (- a ) × (- b ) = a × ((−1) × (- b )) | (Аксиома 6) |
| (- a ) × (- b ) = a × (- (- b )) | (Corrolary 3) |
| (- a ) × (- b ) = a × b | (Corrolary 1) |
Это последнее «доказательство» вряд ли сможет оправдать то, что отрицательный результат, умноженный на отрицательный, является положительным для любого учащегося.Это то, что является необходимым уровнем обоснования для математика, заинтересованного в строгом доказательстве, который, вероятно, посчитал бы другие обоснования «шаблонными» и недостаточными.
Критическая идея доказательства состоит в том, что предполагаемая аудитория доказательства остается убежденной в истинности идеи, и поэтому я утверждаю, что представленное здесь алгебраическое «доказательство» не является доказательством почти для всех.
Необходимые знания : Пока я проходил и добавлял обоснование для каждого шага доказательства, которое было пропущено, мне нужно было немного свободно владеть исходным набором аксиом.Мне также нужно было не упускать из виду общую цель и уметь распознавать структуру каждой части аргумента и согласовывать эту структуру с аксиомами.
Более простое алгебраическое доказательство
Это алгебраическое доказательство Бенджамина Дикмана намного проще, чем возвращение к доказательству, основанному на аксиомах арифметики.
a + (- a ) = 0
a × b + (- a ) × b = 0 × b
ab + (- ab ) = 0
Отсюда мы можем показать, что ab и — ab имеют противоположные знаки и, следовательно, положительное значение, умноженное на отрицательное, является отрицательным.Используя факт, что умножение коммутативно, отрицательное умножение на положительное также отрицательно.
Точно так же мы можем доказать, что отрицательное, умноженное на отрицательное, является положительным.
a + (- a ) = 0
a × (- b ) + (- a ) × (- b ) = 0 × (- b )
— ab + (- a ) × (- b ) = 0
Поскольку мы знаем, что — ab отрицательно, а сумма этих двух членов равна 0, следовательно (- a ) × (- b ) положительно.
Предварительные знания : Предварительные знания для этого доказательства намного меньше, чем для другого, но оно предполагает изрядную беглость в манипуляциях с алгебраическими структурами.
Заключение:
Учитывая, что цель аргумента о том, что что-то истинно, состоит в том, чтобы убедить другого человека в истинности аргумента, всякий раз, когда кто-либо использует какое-либо оправдание, представление или доказательство, необходимо проверить, что аудитория остается убежденной.
Почему отрицательное число, умноженное на отрицательное, положительное? номер?
Автор: Диана Браун
Это частый вопрос от многие студенты изучают математику в средней и даже старшей школе. это Для большинства неудивительно, что это трудное понятие для понимания учащимися. Отрицательные числа не так легко понять большинству людей. Сложность понимания негатива Иногда отрицательным является то, что мы не делаем этого в повседневной жизни.Ниже несколько методов, которые можно использовать, чтобы помочь учащимся лучше понять значение отрицательного умножить на отрицательное.
Метод первый: денежные представления
Мы можем начать объяснять отрицательное умножение, помогая ученику понять более простые концепции например, положительное умноженное на положительное или положительное умноженное на отрицательное. Например, в случае с деньгами мы можем представляют положительное значение, умноженное на отрицательное, говоря, что каждый раз вычитается 700 долларов месяц для выплаты ипотечного платежа.Через шесть месяцев, сколько денег было вынули из платы по ипотеке? Мы можем выяснить ответ, выполнив умножение.
6 * — 700 долларов = — 4200 долларов. Это иллюстрация положительного времени отрицательный результат отрицательный.
Мы можем использовать тот же метод чтобы представить отрицательное значение, умноженное на отрицательное:
Теперь предположим, что в качестве бонуса работодатель решает выплатить ипотеку сроком на один год.Работодатель снимает ипотечный вычет из ежемесячной зарплаты. Сколько денег получает сотрудник в нашем примере? Мы можем представить «удаляет» отрицательным число и вычислим ответ умножением.
-12 * — 700 долларов = 8 400 долларов
Это иллюстрация отрицательный умноженный на отрицательный, что приводит к положительному результату. Если думать о умножения как группировки, то мы создали положительную группу, убрав отрицательное число двенадцать раз.
Метод Два: математическая иллюстрация
Большинство студентов быстро соглашаются с тем, что отрицательное число может быть представлено как
количество раз -1. Проще понять иллюстрацию отрицательного и положительного. Итак, если мы возьмем число и умножим
количество раз -1 представлено ниже:
(-1) х = -х. Два отрицательных
перемножаемые числа можно представить следующим образом:
(-x) (-y) = (-1) (x) (-1) (y) = (-1) (-1) (x) (y), Итак, что такое (-1) (- 1)?
Первая мы начнем с того, что мы знаем.Например, мы знаем, что -1 (0) = 0.
ср можно переписать (-1) (0) = (-1) (- 1 + 1), затем используя по распределительному свойству в правой части уравнения получаем:
(-1) (-1) + (-1) (1)
Сейчас мы знаем, что (-1) (1) = -1, но мы не уверены, что такое (-1) (- 1), но мы знаем что что бы это ни было, уравнение равно нулю, так как оно не может быть -1 для этого сделало бы уравнение равным -2, тогда оно должно быть +1. Увидеть математика ниже:
0 = (-1) (0) = (-1) (- 1 + 1) = (-1) (-1) + (-1) (1) =? + (-1) поэтому
0 знак равно + (-1), из нашего утверждения выше (-1) (- 1) должно быть +1, чтобы завершить утверждение: 0 =? + (-1).Который может помочь сделать вывод, что отрицательное умножение на отрицательное равняется положительному.
Метод Три: Доказательство
Пусть a и b произвольные два действительных числа. Рассмотрим число x, определенное как
.х = ab + (-a) (b) + (-a) (- b).
Мы можем написать
x = ab + (-a) [(b) + (-b)] (множитель -a)
= ab + (-a) (0)
= ab + 0
= ab.
Также,
x = [a + (-a)] b + (-a) (- b) (вычесть b)
= 0 * b + (-a) (- b)
= 0 + (-a) (-b)
= (-a) (- b).
Итак, у нас
х = ab
и
x = (-a) (- b)
Следовательно, по транзитивности равенства имеем
ab = (-a) (- b).
Метод Четвертый: использование слов для обозначения отрицательного числа
Некоторые люди думают о слове НЕ как о негативном значении. Можно сказать, я НЕ пойду к своим друзьям жилой дом. Это похоже на отрицательную версию о том, чтобы сказать, что я иду в дом своих друзей.Так что, если я сказал это двумя NOTS. Я не собираюсь не ходить в дом к друзьям. Кажется, два НОТА отменяют друг друга и я иду в дом моих друзей выведено. Кажется, что двойное отрицательное утверждение действительно дает положительный утверждение. Еще примеры:
отрицательный * отрицательный | Положительно |
Он не может просто сделать ничего | Он должен что-то сделать |
нередкий посетитель | частый гость |
Я никогда не пойду | Я иду |
Метод Пятерка: Распознавание образов
Давайте посмотрим на последовательность ниже.Обратите внимание, что происходит с правой стороной уравнение при уменьшении первого числа на единицу:
4 х 5 = 20
3 х 5 = 15
2 х 5 = 10
1 х 5 = 5
0 x 5 = 0 Мы замечаем, что числа уменьшаются на 5. Продолжаем:
-1 х 5 = -5
-2 х 5 = -10
-3 х 5 = -15
-4 х 5 = -20. Теперь давайте проделаем ту же последовательность, заменив 5 на -5.
4 х -5 = -20
3 х -5 = -15
2 х -5 = -10
1 х -5 = -5
0 x -5 = 0 Мы замечаем, что числа увеличиваются на 5. Если мы используем ту же логику, что и раньше, мы увидим, что:
-1 х -5 = 5
-2 х -5 = 10
-3 х -5 = 15
-4 x -5 = 20. Следовательно, кажется, что отрицательный результат снова отрицательный положительный.
Метод Шесть: Использование технологии
ср можно использовать систему координат в Geometry Sketchpad для создания линии. Помните, что наклон линии — это подъем за пробегом. Если мы нанесем точку на координатной плоскости и используйте наклон, чтобы построить вторую точку, мы посмотрим на наклон, чтобы определить если линия имеет положительный или отрицательный наклон.
В На следующей диаграмме мы построили точку (2, 2):
Давайте используйте наклон 1/2, чтобы найти следующие три точки.
Сейчас если мы проведем линию через точки, мы увидим, что в результате получится линия с положительным наклоном.
Давайте попробуйте то же самое, начиная с точки (2, 2) и используя наклон -1 / -2. См. Диаграмму ниже для результатов.
Уведомление что линия такая же, как и раньше, наклон положительный. Следовательно, это может быть графический подход. чтобы показать взаимосвязь двух отрицательных чисел.
веб-сайтов используется для помощи в открытии различных методов:
www.mathforum.org
www.ncsu.edu
www.math.toronto.edu
www.mathcentral.com
www.newton.dep.anl.gov
plato.stanford.edu
Вернуться на мою домашнюю страницу 6690
.
 Каждый раз становясь на 4 больше.
Каждый раз становясь на 4 больше.
