Уравнение с х решить: Решение дифференциальных уравнений онлайн. Любые с подробным решением. — Детская игровая комната «Волшебный лес»

Posted on 14.03.197426.01.2022 by alexxlab

Содержание

Уравнение с решением: Решение уравнений бесплатно — Калькулятор Онлайн — ЭкоДом: Дом своими руками

Число «Пи», которое примерно равно ~3. n} \)

6) aⁿ > 0

7) aⁿ > 1, если a > 1, n > 0

8) aⁿm, если a > 1, n

9) aⁿ > a^m, если 0

В практике часто используются функции вида y = a^x, где a — заданное положительное число, x — переменная.
Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является
показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a^x, где а — заданное число, a > 0, $ a \neq 1$

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.

Это свойство следует из того, что степень a

x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.

Чтобы убедиться в этом, нужно показать, что уравнение a^x = b, где а > 0, $ a \neq 1$, не имеет корней,
если $ b \leqslant 0$, и имеет корень при любом b > 0.

3) Показательная функция у = a^x является возрастающей на множестве всех действительных чисел, если a > 1, и
убывающей, если 0
Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = a^x при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = a^x при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.

Если х x при a > 0.

Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a

x при 0
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её).

Таким образом, ось Ох является
горизонтальной асимптотой графика.

Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т. е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения a^x = a^b где а > 0, $ a \neq 1$,
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, $ a \neq 1$ равны
тогда и только тогда, когда равны их показатели.

Решить уравнение 2^3x • 3^x = 576

Так как 2^3x = (2³)^x = 8^x, 576 = 24², то уравнение можно записать в виде

8^x • 3^x = 24², или в виде 24^x = 24², откуда х = 2.

Ответ х = 2

Решить уравнение 3^{х + 1} — 2 • 3^{x — 2} = 25

Вынося в левой части за скобки общий множитель 3^{х — 2}, получаем 3^{х — 2}(3³ — 2) = 25,
3^{х — 2} • 25 = 25,

откуда 3^{х — 2} = 1, x — 2 = 0, x = 2

Ответ х = 2

Решить уравнение 3^х = 7^х

Так как $ 7^x \neq 0 $ , то уравнение можно записать в виде $ \frac{3^x}{7^x} = 1 $, откуда $ \left( \frac{3}{7} \right) ^x = 1 $, х = 0

Ответ х = 0

Решить уравнение 9^х — 4 • 3^х — 45 = 0

Заменой 3^х = t данное уравнение сводится к квадратному уравнению t² — 4t — 45 = 0. {x-2} = 1 \)

x — 2 = 0

Ответ х = 2

Решить уравнение 3^{|х — 1|} = 3^{|х + 3|}

Так как 3 > 0, $ 3 \neq 1$, то исходное уравнение равносильно уравнению |x-1| = |x+3|

Возводя это уравнение в квадрат, получаем его следствие (х — 1)² = (х + 3)², откуда

х² — 2х + 1 = х² + 6х + 9, 8x = -8, х = -1

Проверка показывает, что х = -1 — корень исходного уравнения.

Ответ х = -1

Как решать линейные уравнения — формулы и примеры решения простейших уравнений

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: если а не равно нулю, то у уравнения единственный корень: х = -b : а; если а равно нулю — у уравнения нет корней; если а и b равны нулю, то корень уравнения — любое число.
Квадратное уравнение выглядит так:	ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа.

Что поможет в решении:

если а не равно нулю, то у уравнения единственный корень: х = -b : а;
если а равно нулю — у уравнения нет корней;
если а и b равны нулю, то корень уравнения — любое число.

Квадратное уравнение выглядит так:

ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

кубические
уравнение четвёртой степени
иррациональные и рациональные
системы линейных алгебраических уравнений

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Как решаем:

Перенесем 6x из левой части в правую. Знак меняем на противоположный, то есть минус.
6x −5x = 10
Приведем подобные и завершим решение.
x = 10

Ответ: x = 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Как решаем:

Сократим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | :(−4)
x = −3

Ответ: x = −3.

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Алгоритм решения простого линейного уравнения
Раскрываем скобки, если они есть. Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую. Приводим подобные члены в каждой части уравнения. Решаем уравнение, которое получилось: aх = b. Делим обе части на коэффициент при неизвестном.

Алгоритм решения простого линейного уравнения

Раскрываем скобки, если они есть.
Группируем члены, которые содержат неизвестную переменную в одну часть уравнения, остальные члены — в другую.
Приводим подобные члены в каждой части уравнения.
Решаем уравнение, которое получилось: aх = b.

Делим обе части на коэффициент при неизвестном.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Решаем так:

Перенести 1 из левой части в правую со знаком минус.
6х = 19 — 1
Выполнить вычитание.
6х = 18
Разделить обе части на общий множитель, то есть 6.
х = 2

Ответ: х = 2.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

Решаем так:

Раскрыть скобки
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены.
5х — 3х — 2х = — 12 — 1 + 15 — 2
Приведем подобные члены.
0х = 0

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Решаем так:

Найти неизвестную переменную.
х = 1/8 : 4
х = 1/12

Ответ: 1/12 или 0,83. О десятичных дробях можно почитать здесь.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Решаем так:

4х + 8 = 6 — 7х
4х + 7х = 6 — 8
11х = −2
х = −2 : 11
х = — 0, 18

Ответ: — 0,18.

Пример 5. Решить:

Решаем так:

3(3х — 4) = 4 · 7х + 24
9х — 12 = 28х + 24
9х — 28х = 24 + 12
-19х = 36
х = 36 : (-19)
х = — 36/19

Ответ: 1 17/19.

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

Решаем так:

Раскрыть скобки
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
х — х = 4 — 7
Приведем подобные члены.
0 * х = — 3

Ответ: нет решений.

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Решаем так:

2х + 6 = 5 — 7х
2х + 6х = 5 — 7
8х = −2
х = −2 : 8
х = — 0,25

Ответ: — 0,25.

Урок 26. уравнение. решение уравнений подбором неизвестного числа — Математика — 2 класс

Математика, 2 класс

Урок №26. Уравнение. Решение уравнений подбором неизвестного числа

Перечень вопросов, рассматриваемых в теме:

— Что такое уравнение, корень уравнения?

— Как решить уравнение?

Глоссарий по теме:

Уравнение – равенство, содержащее неизвестное число, которое надо найти.

Корень уравнения – это значение буквы, при котором из уравнения получается верное равенство.

Решить уравнение, значит найти его корни.

Основная и дополнительная литература по теме урока

1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1.– 8-е изд. – М.: Просвещение, 2017. – С. 80-81.

2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1. – 6-е изд., дораб. – М.: Просвещение, 2016. – С. 60.

3. Моро М. И., Волкова С. И. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. 9-е изд. – М.: Просвещение, 2014. – С. 60.

Теоретический материал для самостоятельного изучения

Вы умеете читать буквенные выражения. Например:

Вы уже знаете, что равенства бывают верные и неверные.

Рассмотрим верное равенство с окошком: + 4 = 12

Запишем вместо окошка маленькую латинскую букву , как в буквенное выражение. Какое число надо поместить вместо буквы х, чтобы равенство стало верным?

Это число 8. Получили верное равенство: сумма чисел 8 и 4 равна 12.

х + 4 = 12

х = 8

8 + 4 = 12

Равенство с буквой , которое мы записали – это уравнение.

Неизвестное число обозначается маленькими латинскими буквами, как и в буквенном выражении.

Решить уравнение – значит найти все такие значения х (если они есть), при которых равенство будет верным. Значение буквы, при котором из уравнения получается верное равенство, называется корень уравнения.

Решим уравнение 10 – d = 6 способом подбора.

Возьмём число 5. Сейчас проверим, верно ли подобрали число. Заменим d в уравнении числом 5. Получим равенство: 10 – 5 = 6. Оно неверно. Значит, число подобрали неверно.

Попробуем взять другое число. Например, 4. При подстановке его вместо d получили верное равенство: 10 – 4 = 6. Значит, число четыре – корень уравнения, его решение.

Сейчас мы с вами рассмотрим, как по схеме составить уравнение. Перед нами такая схема. Изучим, что обозначает каждое число в схеме. Число 27 обозначает «целое». Оно состоит из двух частей. Первая «часть» – это число 20, вторая «часть» – это число х.

20 х

Воспользуемся правилом,

ЧАСТЬ + ЧАСТЬ = ЦЕЛОЕ

Запишем равенства:

20 + x = 27

27 – x = 20

Рассмотрим другой пример. Перед вами другая схема. Изучим, где на схеме целое, а где части: х — это «целое», а 30 и 6 – это части.

30 6

Воспользуемся правилом,

Вывод: Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Когда решение уравнения находится легко, пользуются способом подбора. Нужно подобрать такое число, чтобы получилось верное равенство.

Тренировочные задания.

Соедините уравнение с его решением.

Правильные ответы:

2. Выберите и подчеркните среди математических записей уравнения.

15 + 6 = 21

17 – d

b + 3 = 12

3 + 5 > 6

48 – a = 8

9 + e < 39

k – 4 = 10

Правильные ответы:

15 + 6 = 21

17 – d

b + 3 = 12

3 + 5 > 6

48 – a = 8

9 + e < 39

k – 4 = 10

Урок 27. решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30 — Математика — 4 класс

Математика, 4 класс

Урок № 27. Решение уравнений вида: х · 8 = 26 + 70, х : 6 = 18 · 5,80 : х = 46 – 30

Перечень вопросов, рассматриваемых в теме:

— как решать уравнения вида: x∙ 8 = 26 + 70, x : 6 = 18 ∙ 5, 80 : x = 46 – 30

— какой алгоритм решения данных уравнений?

Глоссарий по теме:

Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.

Алгоритм — последовательность действия (шагов)

Решить уравнение – это значит найти такое значение неизвестного числа, при котором равенство будет верным.

Основная и дополнительная литература по теме урока:

1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.1 — М.; Просвещение, 2017. – с.80

2. Моро М.И., Волкова С.И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с.34,35

3. Волкова С.И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.44-45.

4. Волкова С.И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – с.40-41.

5. Кочергина А.В. Учим математику с увлечением (Методическая библиотека). М.: 5 за знания, 2007. – с.159.

Теоретический материал для самостоятельного изучения

Вспомните, как связаны между собой числа при умножении.

Посмотрите, множитель 20, множитель 3, произведение 60.

Если 60 разделить на 20, получится 3.

Если 60 разделить на 3, получится 20.

Значит, если произведение разделить на один из множителей, то получится другой множитель. Это правило потребуется при решении уравнений, в которых неизвестен один из множителей.

20 ∙ 3 = 60

60 : 20 = 3

60 : 3 = 20

Решим уравнение:

произведение неизвестного числа и числа 7 равно числу 91. В нем неизвестен первый множитель. Как его найти? Для нахождения неизвестного первого множителя надо произведение 91 разделить на известный множитель 7. Делим 91 на 7 — получаем 13. Выполним проверку. Подставим в уравнение вместо икс число 13.

13 умножить на 7 получим 91. Получили верное равенство:

91 равно девяносто одному. Значит, решили правильно.

А теперь догадайтесь, как решить уравнение: произведение неизвестного числа и числа 7 равно сумме чисел восьмидесяти и одиннадцати. Найдем значение выражения в правой части уравнения: 80 плюс 11 равно 91. Тем самым мы получили уравнение, которое уже умеем решать. Посмотрите, как записывается решение этого уравнения и его проверка.

Вспомним, как связаны между собой числа при делении.

Посмотрите: делимое 15, делитель 3, частное равно пяти.

Если делитель 3 умножить на частное 5, получим делимое 15.

Если делимое 15 разделить на частное 5, получим делитель 3.

15 : 3 = 5

3 ∙ 5 = 15

15 : 5 = 3

Знание связей между делимым, делителем и частным потребуется для решения уравнений, в которых неизвестен один из компонентов: делимое или делитель. Посмотрите, как решаются такие уравнения. В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.

Во втором уравнении неизвестен делитель. Чтобы его найти, нужно делимое 45 разделить на частное 3.

А как решить такое уравнение? Вычислим произведение в правой части: 18 умножить на 5 получим 90. Получается уравнение, в котором неизвестно делимое. Вы уже знаете, как его решать. Выполним проверку решения уравнения. Подставим число 540 вместо икс, вычислим левую часть и правую часть выражения: 90 равно 90. Значит уравнение решили верно.

Задания тренировочного модуля:

1.К каждой позиции первого столбца подберите соответствующую позицию второго.

91 : х = 13	x = 20
х : 21=4	x = 7
24 ∙x = 96	x = 84
x∙ 3 = 60	x = 4

Правильный ответ:

91 : х = 13	x = 7
х : 21= 4	x = 84
24 ∙x = 96	x = 4
x∙3 = 60	x = 20

2. Выполните вычисления и выделите верный ответ:

7 ∙x = 140 : 2

Варианты ответов: 10, 400, 2

Правильный вариант:

3. {x}}\) (это наименьшая из степеней, входящая в наше уравнение). {2}}-17t+6=0\)

имеет три корня:

$ {{t}_{1}}=3,~{{t}_{2}}=\frac{1}{3},~{{t}_{3}}=-2$.

Последний корень мы, конечно, отбросим, поскольку он меньше нуля. А первые два после обратной замены дадут нам два корня:

$ {{x}_{1}}=1,~{{x}_{2}}=-1$.

Ответ: $ {{x}_{1}}=1,~{{x}_{2}}=-1$.

Этим примером я отнюдь не хотел напугать тебя!

Скорее наоборот, я ставил своей целью показать, что хоть у нас была довольно простая замена, тем не менее она привела к довольно сложному уравнению, решение которого потребовало от нас некоторых особых навыков.

Ну что же, от этого никто не застрахован. Зато замена в данном случае была довольно очевидной.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия

Простейшими тригонометрическими уравнениями называют уравнения вида:

sin x = a , cos x = a ,
tg x = a , ctgx = a .

где a – произвольное число.

Решение уравнения sin

x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	В случае, когда , уравнение решений не имеет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:

В случае, когда , уравнение решений не имеет.

Графическое обоснование решения уравнения sin x = a представлено на рисунке 1

Рис. 1

Частные случаи решения уравнений sin x = a

Уравнение:

sin x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

sin x = 0

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

sin x = 1

Решение:

Решение уравнения cos

x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	В случае, когда , уравнение решений не имеет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a

В случае, когда , уравнение решений не имеет.

Графическое обоснование решения уравнения cos x = a представлено на рисунке 2

Рис. 2

Частные случаи решения уравнений cos x = a

Уравнение:

cos x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

cos x = 0

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

Решение:

Уравнение:

cos x = 1

Решение:

Решение уравнения tg

x = a

Обычная форма записи решения:
Более удобная форма записи решения
Ограничения на число a	Ограничений нет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:

Ограничений нет.

Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.

Рис. 3

Частные случаи решения уравнений tg x = a

Уравнение:

Решение:

Уравнение:

tg x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

tg x = 0

Решение:

Уравнение:

Решение:

Уравнение:

tg x = 1

Решение:

Уравнение:

Решение:

Решение уравнения ctg

x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	Ограничений нет

Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:

Ограничений нет.

Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.

Рис. 4

Частные случаи решения уравнений ctg x = a

Уравнение:

Решение:

Уравнение:

ctg x = – 1

Решение:

Уравнение:

Решение:

Уравнение:

ctg x = 0

Решение:

Уравнение:

ctg x = 1

Решение:

Уравнение:

Решение:

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Решение уравнений

Решение уравнений с одной переменной

An

уравнение

представляет собой математическое выражение, состоящее из знака равенства между двумя числовыми выражениями или выражениями переменных, как в

Икс

знак равно

А

решение

к уравнению это число
который может быть подключен к

Переменная

сделать истинное числовое утверждение.

Пример 1:

Подстановка

для

Икс

знак равно

дает

(

)

знак равно

, в котором говорится

знак равно

; это правда!

Так

это решение.

По факту,

ЕДИНСТВЕННОЕ решение

Икс

знак равно

Некоторые уравнения могут иметь более одного решения, бесконечно много решений или вообще не иметь решений.

Пример 2:

Уравнение

Икс

знак равно

Икс

имеет два решения,

а также

, поскольку

знак равно

а также

знак равно

. Никакой другой номер не работает.

Пример 3:

Уравнение

Икс

знак равно

Икс

верно для

все реальные числа

. Оно имеет

бесконечно много

решения.

Пример 4:

Уравнение

Икс

знак равно

Икс

является

никогда

верно для

любой

настоящий номер. Оно имеет

нет решений

.

набор

содержащее все решения уравнения, называется

набор решений

для этого уравнения.

Уравнение

Набор решений

Икс

знак равно

{

}

Икс

знак равно

Икс

{

}

Икс

знак равно

Икс

(набор всех действительных чисел)

Икс

знак равно

Икс

∅
(пустой набор)

Иногда вас могут попросить решить уравнение над определенным

домен

. Здесь возможности для значений

Икс

ограничены.

Пример 5:

Решите уравнение

Икс

знак равно

Икс

по домену

{

}

Это немного сложное уравнение; это не

линейный

и это не

квадратичный

, поэтому у нас нет хорошего метода ее решения.Однако, поскольку домен содержит только четыре числа, мы можем просто использовать метод проб и ошибок.

знак равно

≠

Итак

набор решений

в данном домене

{

}

Решение уравнений с двумя переменными

Решения для уравнения с одной переменной:

числа

. С другой стороны, решения уравнения с двумя переменными имеют вид

заказанные пары

в виде

(

)

Пример 6:

Уравнение

Икс

знак равно

верно, когда

Икс

знак равно

а также

знак равно

.Итак, заказанная пара

(

)

является решением уравнения.

Есть бесконечно много других решений этого уравнения, например:

(

)

(

)

(

5. 5

4.5

)

и т.п.

Упорядоченные пары, которые являются решениями уравнения с двумя переменными, можно изобразить на

декартова плоскость

. Результатом может быть линия или интересная кривая, в зависимости от уравнения. Смотрите также

построение графиков линейных уравнений

а также

построение графиков квадратных уравнений

Решайте неравенства с помощью программы «Пошаговое решение математических задач»

В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах.Эти методы включают переписывание задач в виде символов. Например, заявленная проблема

«Найдите число, которое при добавлении к 3 дает 7»

можно записать как:

3+? = 7, 3 + n = 7, 3 + x = 1

и так далее, где символы?, N и x представляют число, которое мы хотим найти. Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1.Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.

РЕШЕНИЕ УРАВНЕНИЙ

Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными. Уравнение:

3 + х = 7

будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения.Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.

Пример 1 Определите, является ли значение 3 решением уравнения

4x — 2 = 3x + 1

Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому.

4 (3) — 2 = 3 (3) + 1

12 — 2 = 9 + 1

10 = 10

Отв.3 — это решение.

Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.

Пример 2 Найдите решение каждого уравнения путем осмотра.

а. х + 5 = 12
б. 4 · х = -20

Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИСЛЕНИЯ

В разделе 3.1 мы решили путем проверки несколько простых уравнений первой степени. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.

ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,

3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5

являются эквивалентными уравнениями, потому что 5 — единственное решение каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре.Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.

Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.

Если к обоим элементам прибавляется или вычитается одинаковое количество
уравнения, полученное уравнение эквивалентно исходному
уравнение.

в символах,

a — b, a + c = b + c и a — c = b — c

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

х + 3 = 7

путем вычитания 3 из каждого члена.

Решение Если вычесть 3 из каждого члена, получится

х + 3 — 3 = 7 — 3

или

х = 4

Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одинаково для обоих, а именно 4. В следующем примере показано, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.

Пример 2 Напишите уравнение, эквивалентное

4x- 2-3x = 4 + 6

, объединив одинаковые термины, а затем добавив по 2 к каждому члену.

Объединение одинаковых терминов дает

х — 2 = 10

Добавление 2 к каждому члену дает

х-2 + 2 = 10 + 2

х = 12

Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.

Пример 3 Решить 2x + 1 = x — 2.

Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим

2x + 1-1 = x — 2-1

2х = х — 3

Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим

2х-х = х — 3 — х

х = -3

, где решение -3 очевидно.

Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.

Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.

2 (-3) + 1 = (-3) — 2

-5 = -5

Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано

Если a = b, то b = a

Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,

Если 4 = x + 2, то x + 2 = 4

Если x + 3 = 2x — 5, то 2x — 5 = x + 3

Если d = rt, то rt = d

Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.

Пример 4 Решите 2x = 3x — 9. (1)

Решение Если мы сначала добавим -3x к каждому члену, мы получим

2x — 3x = 3x — 9 — 3x

-x = -9

, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решение равно 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем

2x-2x + 9 = 3x- 9-2x + 9

9 = х

, из которого решение 9 очевидно. При желании последнее уравнение можно записать как x = 9 по симметричному свойству равенства.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ДЕЛЕНИЯ

Рассмотрим уравнение

3x = 12

Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения

, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.

Если оба члена уравнения делятся на одно и то же (ненулевое)
количество, полученное уравнение эквивалентно исходному уравнению.

в символах,

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

-4x = 12

, разделив каждый член на -4.

Решение Разделив оба элемента на -4, получим

При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.

Пример 2 Решите 3y + 2y = 20.

Сначала мы объединяем одинаковые термины, чтобы получить

5лет = 20

Тогда, разделив каждый член на 5, получим

В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.

Пример 3 Решить 4x + 7 = x — 2.

Решение

Сначала мы добавляем -x и -7 к каждому члену, чтобы получить

4x + 7 — x — 7 = x — 2 — x — 1

Далее, объединяя одинаковые термины, получаем

3x = -9

Наконец, мы разделим каждый член на 3, чтобы получить

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ УМНОЖЕНИЯ

Рассмотрим уравнение

Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения

, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.

Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.

в символах,

a = b и a · c = b · c (c ≠ 0)

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

путем умножения каждого члена на 6.

Решение Умножение каждого члена на 6 дает

При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.

Пример 2 Решить

Решение Во-первых, умножьте каждый член на 5, чтобы получить

Теперь разделите каждый член на 3,

Пример 3 Решить.

Решение Во-первых, упростите над дробной чертой, чтобы получить

Затем умножьте каждый член на 3, чтобы получить

Наконец, разделив каждого члена на 5, получим

ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ

Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени. Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.

Шаги для решения уравнений первой степени:

Объедините одинаковые члены в каждом члене уравнения.
Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
Объедините одинаковые термины в каждом элементе.
Используйте свойство умножения для удаления дробей.
Используйте свойство деления, чтобы получить коэффициент 1 для переменной.

Пример 1 Решите 5x — 7 = 2x — 4x + 14.

Решение Во-первых, мы объединяем одинаковые термины, 2x — 4x, чтобы получить

5x — 7 = -2x + 14

Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить

5x — 7 + 2x + 7 = -2x + 14 + 2x + 1

7x = 21

Наконец, мы разделим каждый член на 7, чтобы получить

В следующем примере мы упрощаем над полосой дроби перед применением свойств, которые мы изучали.

Пример 2 Решить

Решение Сначала мы объединяем одинаковые термины, 4x — 2x, чтобы получить

Затем мы добавляем -3 к каждому члену и упрощаем

Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы разделим каждый член на 2, чтобы получить

РЕШЕНИЕ ФОРМУЛ

Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.

Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.

Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть

d = rt

(24) = (3) т

8 = т

Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других. Мы используем те же методы, которые продемонстрированы в предыдущих разделах.

Пример 2 В формуле d = rt найдите t через r и d.

Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить

из которых по закону симметрии

В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.

Пример 3 В уравнении ax + b = c найдите x через a, b и c.

Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить

, затем разделив каждый член на a, мы получим

РЕШЕНИЕ УРАВНЕНИЙ

В этом разделе показан процесс решения уравнений различных форм.Здесь также показано, как проверить свой ответ тремя разными способами:
алгебраически, графически и с использованием концепции эквивалентности.
В следующей таблице приведены частичные списки типичных уравнений.

ЛИНЕЙНЫЕ УРАВНЕНИЯ — Решите относительно x в следующих уравнениях.

x — 4 = 10
Решение
2 x — 4 = 10
Решение
5x — 6 = 3 x — 8
Решение
Решение
Решение
2 (3 x -7) + 4 (3 x + 2) = 6 (5 x + 9) + 3
Решение
Решение

УРАВНЕНИЯ, СОДЕРЖАЩИЕ РАДИКАЛ (S) — Решите для x следующим образом
уравнения.

Решение
Решение
Решение
Решение
Решение
Решение
Решение

УРАВНЕНИЯ, СОДЕРЖАЩИЕ АБСОЛЮТНЫЕ ЗНАЧЕНИЯ — Решите для x в
следующие уравнения.

Решение
Решение
Решение
Решение
Решение

КВАДРАТИЧЕСКИЕ УРАВНЕНИЯ — Решите относительно x следующим образом
уравнения.

x
Решение
Решение
Решение
Решение
Решение

УРАВНЕНИЯ , ВКЛЮЧАЮЩИЕ ДОБИ — Решите для x следующим образом
уравнения.

Решение
Решение
Решение
Решение
Решение

ЭКСПОНЕНЦИАЛЬНЫЕ УРАВНЕНИЯ — Решите для x в следующих
уравнения.

Решение
Решение
Решение
Решение
Решение
Решение
Решение

ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ — Решите для x в следующем
уравнения.

Решение
Решение
Решение
Решение
Решение
Решение
Решение

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ — Решите для x следующим образом
уравнения.

Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение
Решение

[Алгебра]
[Тригонометрия]

[Геометрия]
[Дифференциальные уравнения]

[Исчисление]
[Комплексные переменные]
[Матричная алгебра]

С. Домашняя страница O.S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем

S.O.S. Математика CyberBoard.

Автор: Нэнси Маркус

Свяжитесь с нами

Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США

пользователей онлайн за последний час

Решение уравнения | Энциклопедия.com

Методы решения простых уравнений

Решение более сложных уравнений

Решение уравнений с несколькими переменными

Решение уравнений второй степени и выше

Ресурсы

Решение уравнения — это набор всех значений, которые при замене неизвестных сделать уравнение истинным. Для уравнений с одним неизвестным, возведенным в единственную степень, для определения его решений используются два фундаментальных правила алгебры, включая свойство аддитивности и свойство мультипликативности. Решения для уравнений с несколькими неизвестными переменными находятся с использованием принципов системы уравнений. Уравнения с членами в степени, большей единицы, могут быть решены путем факторизации, а в некоторых конкретных случаях — квадратного уравнения.

Идея решения уравнений существовала еще со времен древних египтян и вавилонян. В то время они использовали простые алгебраические методы для поиска решений практических проблем, связанных с их повседневной жизнью.Методы, используемые древними, были сохранены в трактате, написанном арабским математиком Аль-Коваризми 825 г. н.э.). В эту работу он включает методы решения линейных уравнений, а также уравнений второй степени. Решения некоторых уравнений более высокой степени были разработаны в шестнадцатом веке итальянским математиком Джероламо Кардано (1501–1576).

Уравнение — это алгебраическое выражение, которое обычно связывает неизвестные переменные с другими переменными или константами. Например, уравнение x + 2 = 15 равно y ² = 4. Решение или корень уравнения — это любое значение или набор значений, которые можно подставить в уравнение, чтобы сделать его истинным утверждением. Для первого примера решение для x равно 13. Во втором примере есть два значения, которые делают утверждение истинным, а именно 2 и –2. Эти значения составляют набор решений уравнения.

Используя два основных правила алгебры, можно получить решения многих простых уравнений. Первое правило гласит, что одна и та же величина может быть добавлена к обеим сторонам уравнения без изменения решения уравнения.Например, уравнение x + 4 = 7 имеет решение x = 3. Согласно первому правилу, можно добавить любое число к обеим сторонам уравнения и при этом получить то же решение. При добавлении 4 к обеим частям уравнение становится x + 8 = 11, но решение остается x = 3. Это правило известно как аддитивное свойство равенства. Чтобы использовать это свойство для поиска решения уравнения, все, что требуется, — это выбрать правильное число для добавления. Решение предыдущего примера x + 4 = 7 можно найти, прибавив –4 к обеим сторонам уравнения.Если это сделано, уравнение упрощается до x + 4 — 4 = 7 — 4 или x = 3, и уравнение решается.

Второе фундаментальное правило, известное как мультипликативное свойство равенства, гласит, что каждый член в обеих частях уравнения может быть умножен или разделен на одно и то же число без изменения решения уравнения. Например, решением уравнения y — 2 = 10 является y = 12. Используя правило мультипликативности, можно получить эквивалентное уравнение с тем же набором решений, умножив обе части на любое число, например, 2.Таким образом, уравнение принимает вид 2y– 4 = 20, но решение остается y = 12. Это свойство также можно использовать для решения алгебраических уравнений. В случае уравнения 2x = 14 решение получается делением обеих частей на 2. Когда это делается 2x / 2 = 14/2, уравнение упрощается до x = 7.

Часто оба этих правила должны быть используется для решения одного уравнения, такого как уравнение 4x + 7 = 23. В этом уравнении к обеим сторонам уравнения добавляется –7, и оно упрощается до 4x = 16. Обе части этого уравнения затем делятся на 4 и он упрощается до решения x = 4.

Большинство уравнений даются в более сложной форме, которую можно упростить. Рассмотрим уравнение 4x — x — 5 = 2x + 7. Первый шаг в решении этого уравнения — объединить одинаковые члены с каждой стороны уравнения. В правой части нет одинаковых терминов, но 4x и –x в левой части похожи на термины. Это уравнение в упрощенном виде становится 3x — 5 = 2x + 7. Следующим шагом является удаление неизвестного из одной части уравнения. В этом примере это достигается добавлением –2x к обеим частям уравнения, что дает x — 5 = 7.Используя свойство аддитивности, решение получается добавлением 5 к обеим сторонам уравнения, так что x = 12.

Весь процесс решения алгебраических уравнений с одной переменной можно резюмировать с помощью следующих шагов. Во-первых, удалите скобки, умножив множители. Во-вторых, добавьте одинаковые термины с каждой стороны. В-третьих, удалите неизвестное с одной стороны уравнения, используя мультипликативные или аддитивные свойства. В-четвертых, удалите постоянный член со стороны неизвестного, используя аддитивное свойство. Наконец, исключите любой коэффициент при неизвестном, используя свойство мультипликативности.

Многие алгебраические уравнения содержат более одной переменной, поэтому полный набор решений не может быть найден с помощью методов, описанных до сих пор. Уравнения с двумя неизвестными называются линейными уравнениями и могут быть представлены общей формулой ax + by = c; где a, b и c — константы, а x и y — переменные. Решением этого типа уравнения будет упорядоченная пара x и y, которая делает уравнение истинным.Например, набор решений для уравнения x + y = 7 будет содержать все пары значений x и y, которые удовлетворяют уравнению, такие как (2,5), (3,4), (4,3), и т. д. В общем, чтобы найти решение линейного уравнения с двумя переменными, уравнение переписывается и решается в терминах одной переменной. Решением уравнения x + y = 7 становится любая пара значений, которая делает x = 7 — y истинным.

Часто существует несколько линейных уравнений, связывающих две переменные в одной системе. Все уравнения, связанные с переменными, известны как система уравнений, а их решение — это упорядоченная пара, которая делает каждое уравнение истинным. Эти уравнения решаются методами построения графиков, подстановки и исключения.

Уравнения, содержащие неизвестные в степени единицы, известны как уравнения первой степени. Также существуют уравнения второй степени, которые включают:

КЛЮЧЕВЫЕ УСЛОВИЯ

Аддитивное свойство — Свойство уравнения, в котором указано число, может быть добавлено к обеим сторонам уравнения, не влияя на его решение.

Факторинг —Метод сведения уравнения более высокой степени к продукту уравнений более низкой степени.

Уравнение первой степени —Алгебраическое выражение, содержащее неизвестное в первой степени.

Мультипликативное свойство — Свойство уравнения, которое устанавливает все члены в уравнении, можно умножить на одно и то же число, не влияя на окончательное решение.

Уравнение второй степени —Алгебраическое выражение, содержащее неизвестное во второй степени.

как минимум одна переменная, возведенная в квадрат или в степени двойки. Уравнения также могут быть третьей, четвертой и т. Д. Самым известным уравнением второй степени является квадратное уравнение, которое имеет общий вид ax ² + bx + c = 0; где a, b и c — константы, а a не равно 0. Решение этого типа уравнения часто можно найти с помощью метода, известного как факторинг.

Поскольку квадратное уравнение является произведением двух уравнений первой степени, оно может быть включено в эти уравнения.Например, произведение двух выражений (x + 2) (x — 3) дает одно квадратичное выражение x ² — x — 6. Два выражения (x + 2) и (x — 3) называются коэффициенты квадратного выражения x ² — x — 6. Приняв каждый коэффициент квадратного уравнения равным нулю, можно получить решения. В этом квадратном уравнении решениями являются x = –2 и x = 3.

Нахождение множителей квадратного уравнения не всегда легко. Для решения этой проблемы была изобретена квадратная формула, позволяющая решить любое квадратное уравнение. Квадратное уравнение для общего уравнения формулируется следующим образом: ax ² + bx + c = 0

Чтобы использовать квадратную формулу, числа для a, b и c подставляются в уравнение, и определяются решения для x .

См. Также Системы уравнений.

КНИГИ

Биттингер, Марвин Л. и Давик Элленбоген. Промежуточная алгебра: концепции и приложения . 7-е изд. Ридинг, Массачусетс: Addison-Wesley Publishing, 2006.

Ларсон, Рон. Precalculus . 7-е изд. Бостон, Массачусетс: Houghton Mifflin, 2007.

Лоренц, Фалько. Алгебра. Нью-Йорк: Springer, 2006.

Сетек, Уильям М. Основы математики . Река Аппер Сэдл, Нью-Джерси: Pearson Prentice Hall, 2005.

Perry Romanowski

Решатель уравнений: Wolfram | Alpha

О решении уравнений

Значение называется корнем полинома if.

Наибольший показатель степени появления называется степенью.Если имеет степень, то хорошо известно, что есть корни, если принять во внимание множественность. Чтобы понять, что подразумевается под множественностью, возьмем, например,. Считается, что этот многочлен имеет два корня, оба равны 3.

Человек изучает «теорему о факторах», обычно во втором курсе алгебры, как способ найти все корни, являющиеся рациональными числами. Также можно научиться находить корни всех квадратичных многочленов, используя при необходимости квадратные корни (полученные из дискриминанта).Существуют более сложные формулы для выражения корней многочленов кубической и четвертой степени, а также ряд численных методов аппроксимации корней произвольных многочленов. В них используются методы комплексного анализа, а также сложные численные алгоритмы, и это действительно область постоянных исследований и разработок.

Системы линейных уравнений часто решаются с использованием метода исключения Гаусса или связанных методов. Это также обычно встречается в программах средней школы или колледжа по математике.Для нахождения корней одновременных систем нелинейных уравнений необходимы более совершенные методы. Аналогичные замечания относятся к работе с системами неравенств: линейный случай может быть обработан с использованием методов, описанных в курсах линейной алгебры, тогда как полиномиальные системы более высокой степени обычно требуют более сложных вычислительных инструментов.

Как Wolfram | Alpha решает уравнения

Для решения уравнений Wolfram | Alpha вызывает функции Solve и Reduce языка Wolfram Language, которые содержат широкий спектр методов для всех видов алгебры, от основных линейных и квадратных уравнений до многомерных нелинейных систем.В некоторых случаях используются методы линейной алгебры, такие как исключение Гаусса, с оптимизацией для повышения скорости и надежности. Другие операции полагаются на теоремы и алгоритмы из теории чисел, абстрактной алгебры и других сложных областей для вычисления результатов. Эти методы тщательно спроектированы и выбраны, чтобы позволить Wolfram | Alpha решать самые разнообразные проблемы, а также минимизировать время вычислений.

Хотя такие методы полезны для прямых решений, для системы также важно понимать, как человек решит ту же проблему.В результате в Wolfram | Alpha также есть отдельные алгоритмы для пошагового отображения алгебраических операций с использованием классических методов, которые легко распознаются людьми и которым легко следовать. Это включает в себя исключение, замену, квадратную формулу, правило Крамера и многое другое.

Решение уравнений

Что такое уравнение?

Уравнение говорит, что две вещи равны. Он будет иметь знак равенства «=», например:

Это уравнение говорит: то, что слева (x — 2) равно тому, что справа (4)

Таким образом, уравнение похоже на выражение «, это равно , что »

Что такое решение?

Решение — это значение, которое мы можем ввести вместо переменной (например, x ), которая делает уравнение истинным .

Пример: x — 2 = 4

Когда мы ставим 6 вместо x, получаем:

6–2 = 4

, что соответствует действительности

Итак, x = 6 — решение.

Как насчет других значений x?

Для x = 5 мы получаем «5−2 = 4», что неверно , поэтому x = 5 не является решением .
Для x = 9 мы получаем «9−2 = 4», что неверно , поэтому x = 9 не является решением .
и т. Д.

В этом случае x = 6 — единственное решение.

Вы можете попрактиковаться в решении некоторых анимированных уравнений.

Более одного решения

Может быть более одного решения .

Пример: (x − 3) (x − 2) = 0

Когда x равно 3, получаем:

(3−3) (3−2) = 0 × 1 = 0

, что соответствует действительности

И когда x равно 2, получаем:

(2−3) (2−2) = (−1) × 0 = 0

, что также является истинным

Итак, решения:

x = 3 или x = 2

Когда мы собираем все решения вместе, он называется набором решений

Приведенный выше набор решений: {2, 3}

Решения везде!

Некоторые уравнения верны для всех допустимых значений и называются Identities

Пример:

sin (−θ) = −sin (θ) — одно из тригонометрических тождеств

Попробуем θ = 30 °:

sin (-30 °) = -0. 5 и

−sin (30 °) = −0,5

Значит, истинно для θ = 30 °

Попробуем θ = 90 °:

sin (-90 °) = -1 и

−sin (90 °) = −1

Так же истинно для θ = 90 °

Верно ли для все значения θ ? Попробуйте сами!

Как решить уравнение

Не существует «единого идеального способа» решить все уравнения.

Полезная цель

Но мы часто добиваемся успеха, когда наша цель — получить:

Другими словами, мы хотим переместить все, кроме «x» (или любого другого имени переменной), в правую часть.

Пример: Решить 3x − 6 = 9

Начать с: 3x − 6 = 9

Добавьте 6 к обеим сторонам: 3x = 9 + 6

Разделить на 3: x = (9 + 6) / 3

Теперь у нас x = , что-то ,

и короткий расчет показывает, что x = 5

Как пазл

На самом деле решение уравнения похоже на решение головоломки. И, как и в случае с головоломками, есть вещи, которые мы можем (и не можем) делать.

Вот что мы можем сделать:

Пример: Решить √ (x / 2) = 3

Начать с: √ (x / 2) = 3

Квадрат с обеих сторон: x / 2 ^{= 3 ²}

Вычислить 3 ² = 9: x / 2 = 9

Умножьте обе стороны на 2: x = 18

И чем больше «трюков» и приемов вы изучите, тем лучше вы получите.

Специальные уравнения

Есть специальные способы решения некоторых типов уравнений.Узнайте, как …

Проверьте свои решения

Вы всегда должны проверять, что ваше «решение» действительно — это решение.

Как проверить

Возьмите решения и поместите их в исходное уравнение , чтобы увидеть, действительно ли они работают.

Пример: найти x:

2x x — 3 + 3 = 6 x — 3 (x ≠ 3)

Мы сказали x ≠ 3, чтобы избежать деления на ноль.

Умножим на (x — 3):

2x + 3 (x − 3) = 6

Переместите 6 влево:

2x + 3 (x − 3) — 6 = 0

Разверните и решите:

2x + 3x — 9-6 = 0

5x — 15 = 0

5 (х — 3) = 0

х — 3 = 0

Это можно решить, если x = 3

Проверим:

2 × 3
3–3
+ 3 =
6
3–3

Держись!
Это означает деление на ноль!

И вообще, мы сказали вверху, что x ≠ 3, так что…

x = 3 на самом деле не работает, поэтому:

Есть Нет Решение!

Это было интересно … мы, , думали, что нашли решение, но когда мы оглянулись на вопрос, мы обнаружили, что это запрещено!

Это дает нам моральный урок:

«Решение» дает нам только возможные решения, их нужно проверять!

Подсказки

Запишите, где выражение не определено (из-за деления на ноль, квадратного корня из отрицательного числа или по какой-либо другой причине)
Показать все шаги , чтобы их можно было проверить позже (вами или кем-то еще)

Определение того, является ли целое число решением уравнения

Результаты обучения

Определите, является ли целое число решением уравнения

Определить, является ли число решением уравнения

Решение уравнения похоже на поиск ответа на загадку. Алгебраическое уравнение утверждает, что два алгебраических выражения равны. Решение уравнения — это определение значений переменной, которые делают уравнение истинным. Любое число, которое делает уравнение истинным, называется решением уравнения. Это ответ на загадку!

Решение уравнения

Решение уравнения — это значение переменной, которое делает истинное утверждение при подстановке в уравнение.
Процесс поиска решения уравнения называется решением уравнения.

Найти решение уравнения — это значит найти значение переменной, которая делает уравнение истинным. Можете ли вы распознать решение [латекс] x + 2 = 7? [/ Latex] Если вы сказали [latex] 5 [/ latex], вы правы! Мы говорим, что [latex] 5 [/ latex] является решением уравнения [latex] x + 2 = 7 [/ latex], потому что когда мы заменяем [latex] x [/ latex] [latex] 5 [/ latex], полученное утверждение верно.

[латекс] \ begin {array} {} \\ \ hfill x + 2 = 7 \ hfill \\ \ hfill 5 + 2 \ stackrel {?} {=} 7 \ hfill \\ \\ \ hfill 7 = 7 \ quad \ checkmark \ hfill \ end {array} [/ latex]

Поскольку [latex] 5 + 2 = 7 [/ latex] — верное утверждение, мы знаем, что [latex] 5 [/ latex] действительно является решением уравнения.
Символ [латекс] \ stackrel {?} {=} [/ Latex] спрашивает, равна ли левая часть уравнения правой части. Как только мы узнаем, мы можем изменить знак равенства [latex] \ text {(=)} [/ latex] или знак неравенства [latex] \ text {(\ not =).} [/ Latex]

Определите, является ли число решением уравнения.

Подставьте номер переменной в уравнение.
Упростите выражения в обеих частях уравнения.
Определите, истинно ли полученное уравнение.
- Если это правда, число является решением.
- Если это не так, число не является решением.

пример

Определите, является ли [latex] x = 5 [/ latex] раствором [latex] 6x — 17 = 16 [/ latex].

Решение

infourok.ru/uploads/ex/097c/000ab7db-bae131cd/img11.jpg’ /> The left side becomes 30 minus 17 which is 13. Thirteen is not equal to 16 on the right side of the equation.»> </p> <tbody> <tr> <td/> <td> [латекс] 6x-17 = 16 [/ латекс] </td> </tr> <tr> <td> Замените x [латекс] \ color {red} {5} [/ latex]. </td> <td> [латекс] 6 \ cdot \ color {красный} {5} -17 = 16 [/ латекс] </td> </tr> <tr> <td> Умножить.</td> <td> [латекс] 30-17 = 16 [/ латекс] </td> </tr> <tr> <td> Вычесть. </td> <td> [латекс] 13 = 16 [/ латекс] </td> </tr> </tbody> </table> <p> Итак, [латекс] x = 5 [/ latex] не является решением уравнения [латекс] 6x — 17 = 16 [/ latex]. </p> </p> <h5><span»> пример

Определите, является ли [латекс] y = 2 [/ latex] раствором [латекса] 6y — 4 = 5y — 2 [/ latex].

Показать решение

Решение
Здесь переменная появляется с обеих сторон уравнения. Мы должны заменить [latex] 2 [/ latex] на каждый [latex] y [/ latex].

Решение уравнений по фото онлайн

Один из элементов математики — это уравнения. Они встречаются на всех этапах: от начальной алгебры до высшей математики, а также применяются и в других науках. Уравнения являются основной многих теорий в разнообразных дисциплинах. Поэтому решать их учат уже в школе, и с каждым классом они становятся всё сложнее, и сложнее.

Решать их не всем по зубам. Даже имея понятное объяснение в учебнике и квалифицированного педагога, перед определёнными примерами некоторые ученики оказываются в тупике. Поэтому в данной статье мы рассмотрим решение простых и сложных уравнений по фотографии в режиме онлайн. Расскажем о способах, которые легко и качественно помогут определить неизвестные числа любого примера.

Однако, всё же, рекомендуем использовать описанные приложения не для получения решения задач, а для проверки своей работы, чтобы убедиться, что она решена правильно. Ведь упражнения, которые вам задают выполнить в учебном заведении, понадобится вам в будущем на контрольных работах и экзаменах, и важно научиться решать их самому, ведь доступа к смартфону у вас, возможно, не будет.

Математический онлайн-сканер по фото

Одно из самых качественных приложений подобного рода, заслужило хорошее оценку пользователей и имеет большое количество скачиваний. Подойдёт для устройств под управлением Android.

К функциям и достоинствам этого инструмента можно отнести следующее:

Умеет решать как простые, так и сложные уравнения.
Ему под силу не только уравнения, но и многие другие математические задачи.
Воспринимает задачи по фото — достаточно навести камеру и сфотографировать.
Уравнение можно ввести числами в калькулятор уравнений.
Пошагово расписывает решение уравнения, а не только даёт конечный ответ.
Имеет встроенные простой и тригонометрические калькуляторы.
Есть множество дополнительных утилит для разных задач, не только по математике, но и тригонометрии, химии, физике и другим наукам.
Абсолютно бесплатно и минимум рекламы.

Присутствуют и недостатки — интерфейс только на английском языке. Однако большинство задач можно решить и не зная языка. Поэтому этот минус можно легко нивелировать.

Итак, скачайте приложение для Android можно из Google Play. После установки и запуска нажмите кнопку «Start«.

Перед вами сразу появится камера, готовая к фотографированию уравнения, которое вы не можете решить. Наведите объектив на уравнение, чтобы оно целиком попало в квадрат с синей границей, и нажмите на круглую кнопку снизу, чтобы фотографировать. С помощью перетаскивания вы можете менять границы.

После анализа фото появится версия распознанного уравнения. Здесь желательно проверить, правильно ли приложение распознало все числа и знаки. Если не правильно, то нужно переделать фото, иначе решение получится некорректным. А если правильно, то можно нажать на «Solve«.

Через пару мгновений вы увидите пошаговое решение этого уравнения и итоговый ответ к нему. Желательно проверить решение самому, прежде, чем применять его.

Внизу вы увидите иконки с вкладками с дополнительными функциями, которые тоже могут быть вам полезны. Первая кнопка — это фото-сканер уравнений, который был описан выше. А вторая — калькулятор чисел.

Жестом вверх можно открыть тригонометрический калькулятор.

Третья кнопка — калькулятор уравнений, который поможет их решить.

И четвёртая — дополнительные утилиты.

Вам это может быть интересно: Программа распознавания лиц по фото онлайн.

Замечательное приложение, которое справляется с поставленной задачей не хуже, чем предыдущее. Имеются версии для iOs и Android. Это условно-бесплатная программа, и главный недостаток бесплатной версии — отсутствие шагов решения. То есть приложение выдаст только результат с кратким ходом решения. Но этого может вполне хватить для того, чтобы сверить правильность своего ответа на уравнение.

Вот какие функции и возможности имеются:

В платной версии есть пошаговые решения и отсутствует реклама. В бесплатной — краткое решение и итоговый ответ, есть немного рекламы. А пошаговое присутствует только в некоторых простых задачах.
Умеет решать задачи широкого спектра — от начальной алгебры до высшей математики, включая химические задачи, а также построение графиков и многое другое.
Уравнение для решения можно ввести как онлайн через фото, так и вручную.
Предлагается несколько методов решения уравнений, если это возможно.
Присутствует русский язык.

Скачать Mathway можно из официальных магазинов приложений для Android и iOs. После запуска вы увидите страницу, похожую на чат.

Первым делом здесь следует нажать на три линии вверху слева, чтобы открыть меню задач. В них вы можете познакомиться со всем спектром алгоритмов и выбрать область уравнений, которые сейчас хотите решить по фотографии.

Выберите нужную область задач, а затем загрузите само уравнение в приложение онлайн. Сделать это можно как вручную с помощью клавиатуры, так и через фото. Чтобы сделать решение, в поле ввода нажмите на иконку в виде фотоаппарата.

Откроется камера. Наведите объектив на уравнение так, чтобы оно оказалось в центре экрана и нажмите на белую кнопку, чтобы сфотографировать.

После этого вам нужно будет с помощью границ отметить то уравнение, которое вы хотите решить по фото. Если сфотографировалось несколько задач, то выделить нужно только одну. Двигать границы можно жестом перетаскивания. Когда всё будет готов, нажмите на иконку в виде самолётика внизу.

Если заданное вами уравнение можно решить несколькими методами, то вам будет предложен выбор метода. Если только одним, то вы сразу получите ответ. Также для некоторых простых уравнений может быть предложено и пошаговое решение даже в бесплатной версии.

Если вы хотите приобрести платную версию Mathway, то нажмите на шестерёнку вверху справа, а потом «Расширить«.

Это может быть полезным: Найти вещь по фото в Интернете.

Замечательное приложение с высокой оценкой пользователей, хорошими отзывами, русским языком и пошаговыми решениями. Полностью бесплатный инструмент, в котором нет ни одной рекламы, а также есть версии для Android и iOs. У Photomath есть официальный сайт https://photomath.com/ru/, на котором можно более подробно ознакомиться с ним.

К функциями и достоинства Photomath можно отнести следующие аспекты:

Решение любых уравнений по фотографии прямо в онлайн режиме может проходить по нескольким методам, если это возможно.
Показывает ход решения и итоговый ответ.
Можно ввести задачу как с помощью фото методом сканирования, так и вручную через клавиатуру.
Хранит историю решений.
Присутствует русский и многие другие языки.

Итак, чтобы начать пользоваться Photomath, установите его на своё устройства под управлением iOs или Android, и запустите. Вам понадобится выбрать желаемый язык, а потом нажмите «Поехали«.

Затем появится презентация работы программы, которую вы можете либо просмотреть, либо нажать «Пропустить«.

После этого откроется камера. Вам нужно навести объектив на уравнение так, чтобы оно оказалось в красной рамке. Вы можете двигать границы касанием. Когда уравнение окажется в прямоугольнике, нажмите на красную кнопку снизу, чтобы распознать его для решения.

Через пару мгновений вы увидите решение и ответ. Если методов решения может быть несколько, то будут приведены все возможные варианты. Например, уравнение из этого примера можно решить ещё и графиком и он тоже есть. Вы можете нажать на иконку в виде карандаша, чтобы отредактированы распознанную задачу, если приложение сделало это неверно.

Нажмите «Показать шаги по решения«, чтобы увидеть более подробно.

Если вам нужно ещё подробнее, то нажмите «Пояснить этапы«.

Кроме этого можно открыть историю всех решений, которые проводились ранее. Для этого нужно нажать на кнопку вверху справа на начальной странице.

А калькулятор можно открыть с помощью кнопки внизу слева.

Итак, выше были рассмотрены приложения, которые по фотографии могут решать уравнения, и у всех примерно одинаковый алгоритм работы.

Перед использованием этих инструментов вам следует помнить о некоторых вещах:

Правильность ответа зависит от качества фото, поэтому старайтесь фотографировать уравнения в хорошем свете и так, чтобы в объективе было только одно уравнение.
Распознавать лучше напечатанные уравнения, чем рукописные.
После распознавания проверяйте правильность цифр и знаков.
После получения результата проверяйте его.

Автор Рамиль Опубликовано 02 октября 2020 Обновлено 26 апреля 2021

Методическая разработка «Целые уравнения»

Методическая разработка урока

по теме «Целые уравнения»

Цель урока: Обобщить и систематизировать знания о целых уравнениях и методах их решений.

Задачи урока:

1. Образовательные: дать понятие целого уравнения и его степени; научить приему решения целых уравнений 3-й степени аналитическим и графическим способами; актуализировать опорные знания решения квадратных уравнений, построения графиков функций,

2. Развивающие: развивать умения в применении знаний в конкретной ситуации; логическое мышление, умение работать в проблемной ситуации; умение обобщать, конкретизировать, правильно излагать мысли; развивать самостоятельную деятельность учащихся.

3. Воспитательные: воспитывать интерес к предмету через содержание учебного материала; умение работать в коллективе, взаимопомощь, культуру общения, умение применять преемственность в изучении отдельных тем; воспитывать настойчивость в достижении цели, умение не растеряться в проблемных ситуациях

Используемые педагогические технологии, методы и приемы:

технология интерактивного обучения.

Методы: метод программированного обучения, объяснительно-иллюстративный, метод ролевой игры

Приемы: беседа, самостоятельная работа, работа в парах.

Оборудование: Мультимедийный проектор, компьютер, экран

Ход урока

Орг. Момент

(Вводно-мотивационная часть, с целью активизации деятельности учащихся)

Эпиграфом этого урока, я взяла слова Адольфа Дистерверга (немецкого педагога, который преподавал физику и математику):

«Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий должен достичь этого собственной деятельностью, собственными силами, собственным напряжением».

На уроке мы докажем верность этого высказывания.

II. ПОВТОРЕНИЕ (фронтальный опрос)

Запишите

формулу разности квадрата.

квадрат разности.

формулу дискриминанта и его корней.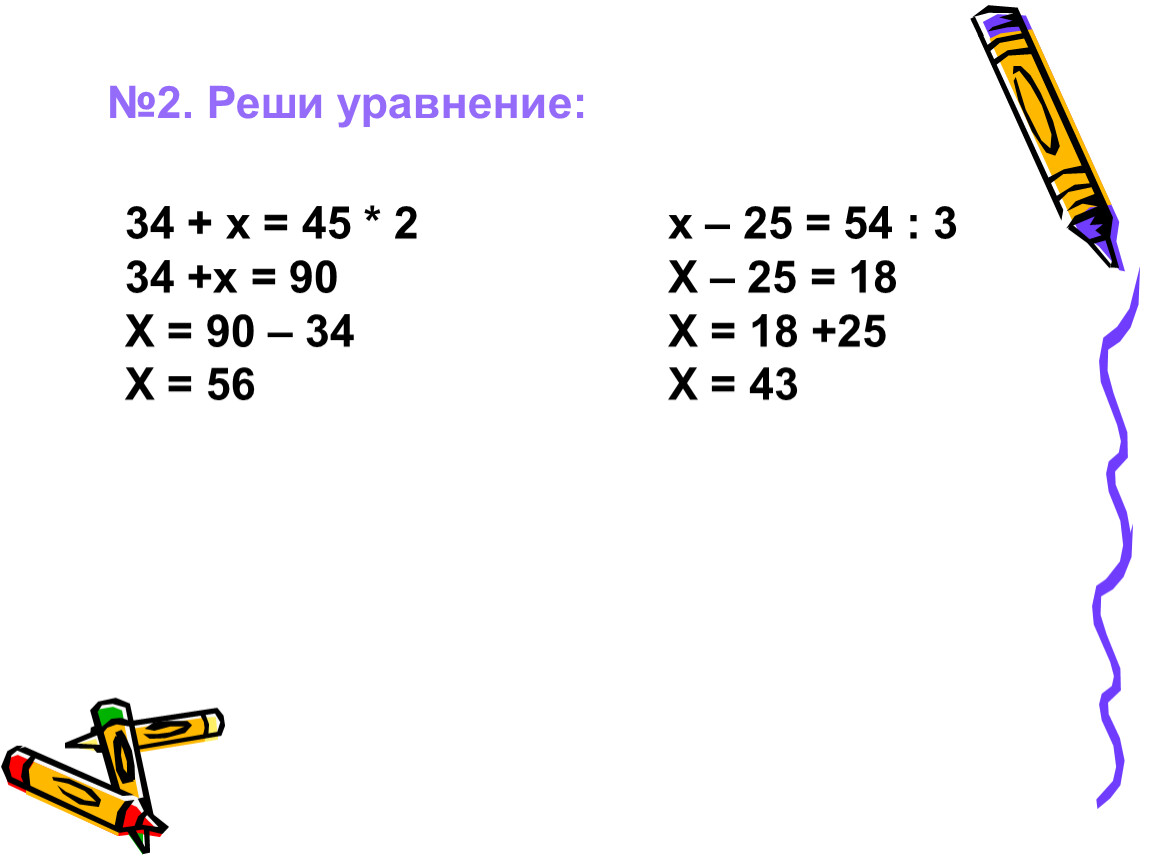

а -b = (a –b) (a +b )

(a –b) = (a- b) (a -b)

(a –b) = а -2ab + b

_{D= b} — 4 a c, x₁ = ; x_{2 =}

_{2.Теорему ВИЕТА и обратную теорему}

_{Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.}

_{х1+х2=-р и х1*х2=}_g

_{обратная теорема Если числа}_m_и_n_{таковы, что их сумма равна –р, а произведение равно}_G_{, то эти числа являются корнями уравнения}

3. Охарактеризуйте график функции.

а) у=-5х+10

Это линейная функция, убывающая на множестве действительных чисел, так как k= -5. Графиком является прямая, сдвинутая вверх по оси Оу на 10 единиц.

б) у= -2/х

Это обратная пропорциональность. D(у)= R, х‡ 0. Графиком функции является гипербола, состоящая из двух ветвей, расположенных во второй и четвертой координатных четвертях, так как k= -2, не пересекающих оси координат.

в) у=х²-9

Это квадратичная функция, D(у)= R. Графиком является парабола, ветви которой направлены вверх, так как а=1. График симметричен относительно оси Оу и сдвинут вниз по оси Оу на 9 единиц.

г) у=х³

Это кубическая парабола, расположенная в 1 и 3 четвертях. Д(у)=R График симметричен относительно начала координат.

д)у=(2х+5)².

Это квадратичная функция. Д(у)=R.Графиком функции является парабола ветви которой направлены вверх. График сдвинут влево по оси х на 5 единиц

е) у=(3х-2)²+4

Это квадратичная функция. Д(у)=R. Графиком является парабола ветви которой направлены вверх. График сдвинут по оси х влево на 2 единицы и вверх на 4единицы

III. Устная работа.

Учитель: Ребята что вы видите на карточках?. (Уравнения)..

А что с уравнениями обычно делают? (решают).

А что значит решить уравнение?… (найти его корни или доказать что корней нет)

Что называется корнем уравнения? ….(значение переменной , при котором уравнение обращается в верное равенство)

Приложение №1

Разложите на множители:

а) 169-36x²; в) 5x-x²;

б) 1-6x+9x²; г) x(x-1)+x²(x-1).

Решите уравнение:

1)x²-6x+9=0 3)x²-8x+15=0

2) x²-5x+6=0 4)2x²+4x-30=0

5) 3x²+6x-72=0

Ребята давайте посмотрим на уравнения на слайде

На какие группы вы могли бы их разделить?(неполные квадратные, линейные, дробно-рациональные, уравнения третьей степени и четвертой степени).

Способы решения этих уравнений мы знаем?

Давайте устно решим эти уравнения.

В этих уравнениях мы будем использовать…(формулы сокращенного умножения, теорему ВИЕТА, формулу Дискриминанта)

Учитель: А теперь, ребята, попробуем указать из рациональных уравнений те, которые не являются целыми.

Ученики: Называют целые и дробно-рациональные уравнения.

Учитель: Давайте сформулируем определение целого уравнения…и дробно-рационального (если не помнят, открыть учебник стр.245 п. 14)

Ученики: Если левая и правая части представляют собой целые выражения, то это уравнение называется целым.

Учитель: Итак, тема нашего урока: “Целое уравнение и его корни” Сегодня мы познакомимся с определением целого уравнения вида Р(х)=0, узнаем как определить степень уравнения, рассмотрим способы решения целых уравнений третьей степени.

Откройте тетради. Запишите дату и тему урока

III. Изучение нового материала

Учитель: Ребята в начале урока мы с вами решали устно уравнения. Давайте вновь вернёмся к ним и укажем степени этих уравнений. А степенью целого уравнения называется степень равносильного ему уравнения вида Р(х) = 0, где Р(х) – многочлен стандартного вида. А что называется степенью многочлена?…

Ученики: Наибольший показатель степени переменной входящей в уравнение называется степенью уравнения.

Учитель: Ребята, а какова степень знакомых нам уравнений? ………

Учитель: А кто помнит, какова цель нашего урока?

Ученики: Научится решать целые уравнения

Учитель: Совершенно верно! И так, начнём решать целые уравнения. Откройте учебник и найдите № 267 (а, б, в). Посмотрите на данные уравнения! Чем они отличаются?…. Как вы думаете, с чего можно начать решение каждого из этих уравнений?. .. Запишите в тетрадь решении уравнения, ребята сидящие на 1 ряду (1 вариант) – под буквой «а», на втором ряду ( 2 вариант) – под буквой «б», и ребята сидящие на 3 ряду ( 3 вариант) – под буквой «в».

Учитель: Кто справился с заданием? Кто решил своё уравнение, приступайте к решению любого из оставшихся уравнений. А для тех, у кого возникли вопросы воспроизведём решение на доске. Кто сможет записать решение на доске? Пожалуйста, выходите!….. Первым справился …..Прокомментируй свое решение и т.д.

а)(6 – х)(х+6) – (х–11)х=36, б) – = 0, в) 9х² – =1,

36 – х² – х² + 11х – 36=0, = 0, 36х²–(36х² –33х+96–88)– 4=0

– 2х² + 11х = 0, т.к. 55 ≠ 0, 36х²–36х² +33х–96х+88 – 4=0

х (11 – 2х) = 0, 5 – 15у -33 + 11у = 0, – 63х = – 84,

х₁ = 0 и 2х₂ = 11, -4у = 28, х= = 1

х₂ = 5,5 у = –7

Ответ: 0; 5,5 Ответ: – 7 Ответ: 1.

Учитель: Ребята? У кого аналогичное решение, поднимите руку!… Молодцы! Все решили данные равнения .

Учитель: Уравнения ребята бывают 1, 2, 3, 4, и более высоких степеней. Мы с вами большей частью решаем уравнение I, II иногда III степени.

Давайте вспомним сколько корней может иметь уравнение 1 степени и 2 степени

Давайте решим уравнение I степени и узнаем, сколько оно может иметь корней. Кто знает, называет вслух решения уравнения…..

(На слайде): 2x-5=10, 0·х = 7

Учитель: Решили? Сделайте вывод … Сколько корней может иметь уравнение I степени?

Ученики: Не более одного.

Учитель: Рассмотрим уравнения на следующем слайде . Запишите в тетрадях решение: 1 ряд – 1 вариант, 2 ряд – 2 вариант, 3 ряд – 3 вариант. ….

(На слайде)

I вариант	II вариант	III вариант
x²-5x+6=0	y²-4y+7=0	x²-12x+36=0
Д=1, Д0	Д=-12, Д	Д=0, 1 корень
x₁=2, x₂=3	нет корней	x=6

Учитель: Проверим … А теперь хором ответьте на вопрос: Сколько корней может иметь каждое уравнение II степени?

Ученики: Не более двух.

Учитель:.Выясните: сколько корней может иметь уравнение III степени?

1 ряд – 1 вариант, 2 ряд – 2 вариант, 3 ряд – 3 вариант

(На слайде)

I вариант	II вариант	III вариант
x³-1=0	x³-4x=0	x³-12x²+36x=0
x³=1	x(x²-4)=0	x(x²-12x+36)=0
x=1	x=0, x=2, x= -2	x=0, x=6
1 корень	3 корня	2 корня

А теперь проверим. ..Кто запишет на доске решение своего уравнения? …..Итак, сколько корней может иметь уравнение III степени?

Ученики: Не более трёх.

Учитель: Существуют также и уравнения более высоких степеней. Это уравнения 4 степени, 5 степени. А сколько они могут иметь корней?

То есть уравнение n-й степени может иметь не более n-корней.

IV. Релаксация.

(На экран проектируется картина золотой осени. Звучит лёгкая музыка.).

Учитель предлагает детям немного отдохнуть и произносит следующее: «Сядьте поудобнее, расслабьтесь. Представьте, что вы идёте по осеннему парку. Поднимите руки вверх, сделайте глубокий вдох; опустите руки, медленно делайте выдох. Вокруг стоят деревья с золотыми и багряными листьями. Сквозь кроны деревьев пробиваются лучи солнца. Воздух прозрачен и чист. Сразу вспоминаются строки из стихотворения А.С. Пушкина:

«Унылая пора! Очей очарованье!

Приятна мне твоя прощальная краса –

Люблю я пышное природы увяданье,

В багрец и золото, одетые леса…»

Сделайте глубокий вдох и медленно делайте выдох. Ещё раз вдох и выдох… Раз, два, три… Закончили».

Давайте посмотрим на целые уравнения в учебнике на стр. 72

После преобразований 1-е уравнение привели к виду ….

Это уравнение пятой степени.

После преобразований 2-е уравнение привели к виду …

Это уравнение четвертой степени.

Для уравнений третьей и четвертой степеней известны формулы корней, но эти формулы очень сложны и громоздки и не имеют практического применения. Для уравнений пятой и более высоких степеней общих формул не существуют и существовать не может (как было доказано в 19 веке Н.Абелем и Э.Галуа)

Будем называть уравнения третьей и четвертой степеней уравнениями высоких степеней. Один из способов решения уравнения третьей степени мы уже использовали – способ разложения на множители. Сегодня мы познакомимся с еще одним способом решения. А уравнения четвертой степени будем учиться решать на следующем уроке.

Но сначала решим уравнения и расшифруем фамилию ученого-математика, который вывел формулы корней кубического уравнения и фамилию ученого-математика, который вывел формулы корней уравнения четвертой степени.

1) Решите уравнение; если корней несколько, расположите их в порядке возрастания и расшифруйте фамилию ученого-математика, который вывел формулы корней кубического уравнения.

а) 7х +2 = 44; (6)

х(х + 4)(х – 3) = 0; (- 4; 0; 3)

х² + 3х – 4 = 0; (- 4; 1)

х² – 4х + 4 = 0. (2)

Джероламо Кардано, итальянский ученый.

2) Решите уравнение; если корней несколько, расположите их в порядке возрастания и расшифруйте фамилию ученого-математика, который вывел формулы корней уравнения четвертой степени.

б) х³+ 6х²+ 5х = 0;(- 5; — 1; 0)

3(х + 5) = 15; (0)

х(х+4)(х-7)=0

Лудовико Феррари (XVв), ученик Кардано.

Давайте разберем в учебнике на стр 74 ПРИМЕР2

Закрепить данный способ №276

Мы с вами сегодня решали уравнения аналитическим способом, но существует не только этот способ. Прежде чем с ним познакомится, вспомним известные нам функции и их графики! Из списка функций приведенного на доске выберите функцию, соответствующую данному графику. Запишите в тетради данные соответствия

V. Подведение итогов.

Учитель. Подводя итог нашего урока, вернемся к плану изучения темы и постараемся самостоятельно ответить на вопросы:

Какие уравнения называются целыми?
Что называется степенью уравнения?
Сколько корней имеет уравнение n-й степени?
Методы решения уравнений третьей степени.

-Чтобы проверить насколько успешно вы научились применять теорию к практике, выполните небольшой тест.

VI. Домашнее задание:

Страница 13 — ГДЗ Математика 2 класс. Моро, Бантова. Учебник часть 2

Вернуться к содержанию учебника

Угол. Виды углов

Вопрос

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

2. Реши с проверкой.

36 + 9

92 — 8

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

3. У лодочной станции было 15 яхт. Когда несколько яхт вышло в море, осталось 8 яхт. Сколько яхт вышло в море?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4. В море вышло 16 больших яхт, а маленьких на 7 меньше. Сколько всего яхт вышло в море?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5. Реши уравнения

30 — х = 20

х + 1 = 40

у — 8 = 7

Подсказка

Решить уравнение – это значит найти такое значение неизвестного числа, при котором это равенство станет верным.

Ответ

Поделись с друзьями в социальных сетях:

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Подсказка

Повтори письменные приемы сложения в столбик.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Продолжи ряд чисел:

Подсказка

Внимательно рассмотри ряд чисел и установи закономерность.

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

Пользовательское соглашение

Нашли ошибку?

Связаться с нами

Аспирант ИТМО Михаил Масляев ― о том, почему научные исследования интереснее работы в крупной компании

21 января в России отмечается День аспиранта. В аспирантуру ИТМО поступают сотни молодых ученых, для многих эта ступень образования становится окончательным шагом в большую науку, а для некоторых ― еще и способом сменить научную область. Так поступил и Михаил Масляев. После окончания географического факультета МГУ, где Михаил изучал метеорологию и климатическое моделирование, он занялся машинным обучением. А сейчас, обучаясь в аспирантуре ИТМО, работает в недавно созданной лаборатории композитного искусственного интеллекта, где специализируется на моделировании физических систем. О том, насколько сложно было переквалифицироваться из метеоролога в специалиста по машинному обучению, чем научные исследования интереснее работы в «Яндексе» и почему стереотипы о российской науке не совсем верны, Михаил рассказал ITMO.NEWS.

― Почему вы решили изучать метеорологию? Кажется, это не самый тривиальный выбор в наше время.

― Я выиграл всероссийскую олимпиаду по географии в 10 классе, и решил, что пойду на географический факультет. Меня тогда больше интересовала геология, но на втором курсе я подумал, что метеорология ― это интересно: там много математики и физики, есть, чему учиться и куда развиваться.

Современная метеорология позволяет находить применения для актуальных физических и математических методов для решения необычных прикладных задач.

― Вы изначально знали, что будете строить научную карьеру?

― Мои родители и бабушка с дедушкой были связаны с наукой, поэтому я знал, что все негативные стереотипы, например, о том, что учёные умирают с голода, работают на ветхом оборудовании и так далее ― это неправда.

Самый важный аргумент для меня ― это интересно. Я общаюсь с друзьями, которые работают в крупных компаниях типа «Яндекса», смотрю на их задачи и понимаю, что это смертельно скучно. Наука даёт больше возможностей для развития, позволяет заниматься тем, что интересно. Ты не упираешься в ежедневную рутину и выполнение одинаковых задач, а имеешь возможность бесконечно пробовать: что работает, а что нет. Понятно, что коммерческие компании не всегда могут пойти на подобные эксперименты.

― Почему вы не продолжили учиться в МГУ дальше, а поступили в ИТМО?

― Мне показалось, что классическая метеорология в России как наука несколько застыла во времени. Годов с 50-х ― 60-х в ней активно используется математическое моделирование, но новые методы вроде машинного обучения начали входить в эту область лишь недавно. И не все успели запрыгнуть в этот поезд.

Например, я занимался моделями, которые прогнозируют изменение климата и один из важных элементов ― влияние на климат биосферы: лесов, полей и так далее. В подобных задачах нужно учитывать сложные, многофакторные системы: потоки кислорода от растений, водяного пара от испарений, распределения тепла и газов. Теории для описания таких систем построены на значительных упрощениях, так что при решении задач для расчетов естественно было бы использовать машинное обучение на основе значительных баз данных, которые собираются в исследовательских центрах по всему миру.

У моего друга с океанологии была схожая проблема ― он тоже был заинтересован в машинном обучении для решения интересных ему задач. Так что мы вместе решили посмотреть другие направления и другие университеты. В ИТМО тогда была лаборатория моделирования природных систем во главе с Анной Калюжной на базе Национального центра когнитивных разработок ― они одними из первых начали применять машинное обучение для решения метеорологических задач. Так что мы подумали, что будет интересно сюда перейти ― здесь уже начал зарождаться коллектив, причем молодой. Для нас это стало весомым аргументом.

― Чем молодой коллектив лучше?

― Молодые ученые более активно следят за тенденциями и легко переключаются. Потому что когда занимаешься каким-то делом в течение двух-трёх лет, гораздо проще признать, что твой подход устарел, и перескочить на что-то новое. А если ты отдал отрасли 20–30 лет, очень сложно признать, что потратил время зря, и начать сначала. Хотя, безусловно, есть такие случаи, когда серьёзные исследователи довольно радикально меняли свою область деятельности. Но это всё-таки скорее исключение.

― А вам не сложно было так радикально менять свою сферу деятельности? Переквалифицироваться из географа в IT-специалиста?

― По сути, это не совсем смена специальности, а переход из одной смежной области в другую. Как бы странно это ни звучало, на географическом факультете было достаточно много математики и некоторых отраслей физики ― в первую очередь, механики сплошных сред. Так что после такой подготовки перейти в машинное обучение не было большой проблемой. Ведь самым большим препятствием может стать недостаток математического аппарата. Он необходим, чтобы не просто брать готовую модель, загружать в неё какие-то данные и получать результат, с которым непонятно, что делать.

― Расскажите, чем именно вы сейчас занимаетесь?

― Я занимаюсь весьма специфической областью машинного обучения ― подбором дифференциальных уравнений для описания динамических систем. Цель моего исследования ― создание алгоритма, который позволил бы получить дифференциальное уравнение на основе данных из самой динамической системы и некоторых априорных знаний о структуре происходящих в ней процессов.

― Зачем это нужно?

― Дифференциальные уравнения являются одним из лучших способов описания физических процессов. Например, течение жидкости описывается уравнением Навье — Стокса, на его основе можно построить физическую модель, используя аналитические методы, математический аппарат, сложные вычисления с учетом закона сохранения энергии и так далее. В моей же работе предполагается определять подобные дифференциальные уравнения только на основе данных.

Человек, который знаком с конкретной наукой, может, смотря на это дифференциальное уравнение, определить, что за ним стоит. Он может определить тип уравнения, определить схожесть процесса с иными физическими системами, и таким образом лучше понять исследуемый процесс. То есть у него есть свойство интерпретируемости ― в отличие от большинства распространенных методов машинного обучения.

Довольно характерный пример «из литературы» — данные по уровню загрязнения воздуха. По ним получаем соответствующее случаю уравнение переноса, и в нём определяем источник загрязнения. Это позволяет нам как моделировать процесс, так и понимать интенсивность источника загрязнения.

― Почему такой подход не использовали раньше?

― Задачи, над которыми мы работаем, близки к тем, что решались в теории уравнений математической физики. Чтобы определить, насколько хорошо модель описывает процесс, нужно сначала решить те самые дифференциальные уравнения, которые мы получаем в результате работы алгоритма. При этом очевидно, что многие из найденных уравнений будут очень далеки от истины ― но чтобы это понять, необходимо их сначала решить.

Но постепенно появляются методы решения произвольных дифференциальных уравнений при помощи нейронных сетей ― в частности, этим занимается мой научный руководитель Александр Хватов. Так что мы работаем над проблемой одновременно с двух сторон: я занимаюсь подбором уравнений, а он ― их решением.

― На какой стадии находится ваше исследование?

― Сейчас мы находимся на стадии валидации, проверяем алгоритм на тех системах, для которые мы знаем правильное уравнение. Из экспериментов мы сосредоточились на уравнении теплопроводности в вязкой жидкости. Мы измеряем значение температуры в этой жидкости и при помощи алгоритма пытаемся определить то уравнение, которое её описывает и на основе которого мы впоследствии будем моделировать физическую систему. В идеале мы должны получить дифференциальное уравнение лишь по некоторому набору измерений ― по скорости изменения уровня теплопроводности во времени и пространстве.

Однако тут есть сложность, которую мы пока ещё только решаем: в уравнении теплопроводности с конвекцией есть функция скорости, которая описывает, как перемешивается эта жидкость. Во многих случаях мы не можем определить другие физические величины, помимо моделируемой, потому что у нас нет приборов, которые позволяют их найти. И сейчас мы работаем над алгоритмом, который позволит нам подбирать эту функцию в процессе поиска уравнения.

― После того, как закончите аспирантуру, планируете остаться в России? Или поедете куда-нибудь за границу?

― До защиты я точно буду здесь, а дальше боюсь загадывать. Если будут интересные предложения по заграничным стажировкам или программам для постдоков, почему бы и нет. Если будет возможность поработать с коллективом мирового уровня, то однозначно стоит попробовать. Но для меня это не самоцель, как для многих.

― Вы не думаете, что вся передовая наука возможна только за рубежом?

― Возможно, у меня просто туннельное зрение и я сфокусирован только на том, что делает наша лаборатория, но мне кажется, что в области ИТ в России всё довольно неплохо. Активно дают гранты, оказывают всевозможную поддержку. Наша новая лаборатория уже выиграла два гранта, так что, кажется, это не слишком большая проблема. Но за другие сферы я не могу сказать.

― Вас устраивает ваше положение в ИТМО?

― Я работаю младшим научным сотрудником, у меня полная ставка в лаборатории. И я не чувствую, что как-то отличаюсь от «полноценных» научных сотрудников ― в современном мире всё совсем по-другому. Тем более наша область науки довольно молодая. Наш коллектив в основном состоит из аспирантов и свежеиспеченных кандидатов наук, поэтому я чувствую себя здесь комфортно.

Перейти к содержанию

Решение линейных уравнений: с Пареном; «Все х», «Нет х» Soln’s

Пурпурная математика

В этом уроке мы сначала попрактикуемся в решении линейных уравнений, содержащих скобки. Их решение потребует умножения и упрощения, прежде чем приступить к фактическому процессу решения. Если вам не нравятся скобки, сначала изучите. Тогда возвращайся сюда.

Затем мы рассмотрим два странных вида решений: «нет решения» и решение «все x «. Процесс решения заканчивается бессмыслицей в первом случае и тривиально-истинным утверждением во втором. Поскольку учащиеся не часто сталкиваются с решениями такого типа, их легко забыть и, следовательно, легко спутать. Но я готов поспорить на хорошие деньги, что хотя бы одно из этих уравнений будет на следующем тесте, а еще одно, возможно, на финальном.Так что изучите и запишите сейчас, чтобы просмотреть уравнения «без решения» и «все решения x » перед следующим экзаменом.

MathHelp.com

После того, как вы изучите основы решения линейных уравнений, ваш учебник и преподаватель начнут забрасывать вас упражнениями со скобками, которые обычно нужно сначала упростить (или «расширить», что означает, что вы умножили, а затем упростил результат).

Во-первых, я должен умножить через круглые скобки в правой части. Затем я могу действовать обычным образом:

Тогда мое решение:

Решить 6
х – (3 х + 8) = 16

Сначала я упрощу левую часть; тогда решу обычным способом.Я хочу быть осторожным, когда беру отрицания через круглые скобки. Если у меня возникнут проблемы с отслеживанием знаков «минус», я поставлю «1» перед скобками.

Тогда мое решение:

Решить 7(5
х – 2) = 6(6 х – 1)

Это уравнение имеет круглые скобки с обеих сторон уравнения. Я должен быть уверен, что 7 и 6 проходят через соответствующие скобки.

После того, как я упростил обе стороны, я переместил меньший из двух переменных членов (то есть «35 x » в левую часть), чтобы убедиться, что у моего результирующего переменного члена нет знака «минус». Это не «правило», но оно определенно облегчает мою жизнь. И мой окончательный ответ:

Для уравнений со скобками не торопитесь и запишите все ваших шагов, как я сделал выше.Не пытайтесь сделать все в своей голове.

Во-первых, мне нужно умножить в левой части, проведя 3 через—

Подождите… В этом уравнении я могу избавиться от 3 путем деления, потому что 6 в правой части делится на 3. На самом деле мне не нужно распределять для этого конкретного уравнения. Вместо:

3(х — 2) = 6
——— —
3 3

х — 2 = 2
+2 +2
———-
х = 4

Тогда мое решение:

Если бы я не заметил, что могу начать с деления, я бы все равно получил в конце концов правильный ответ. Но если можно разделить, давая себе для работы меньшие числа, мне нравится этим пользоваться. Это упрощение встречается не часто, но постарайтесь не закрывать на это глаза, когда оно всплывает несколько раз.

Решить 13 – (2
х + 2) = 2( х + 2) + 3 х

Я начну с умножения на каждую скобку (знак «минус» слева и 2 справа).Затем я соединю подобные термины, упрощу и решу:

Тогда мой ответ:

Не забывайте: нет причин сомневаться в своем решении линейного уравнения, потому что вы всегда можете проверить свой ответ. Смысл значения решения в том, что именно значение x делает уравнение верным. Итак, чтобы проверить свой ответ, вы снова подставляете значение решения к исходному уравнению и убеждаетесь, что уравнение «работает» с этим значением. Например, в последнем упражнении выше мое решение было x = 1. Чтобы проверить свое решение, я подставлю свое значение в левую (левую) и правую (правую) части исходного уравнения. , и убедитесь, что обе стороны оценивают одно и то же число.

13 – (2 х + 2) = 2( х + 2) + 3 х

Левая сторона: 13 – (2[1] + 2)

= 13 – (2 + 2) = 13 – 4 = 9

Правая сторона: 2([1] + 2) + 3[1]

Две части уравнения дают одно и то же значение, поэтому решение «проверилось», и теперь я знаю , что мой ответ правильный

Кстати, по возможности старайтесь проверять свои ответы при сдаче тестов.После того, как вы ответили на все вопросы (при условии, что у вас осталось немного времени), вернитесь и вставьте свои решения обратно в исходный вопрос. Если ваше решение данного вопроса «проверено», значит, вы правильно ответили на этот вопрос. Если он не проходит проверку, у вас есть шанс исправить свою ошибку до того, как вы сдадите тест.

Вам также может понадобиться решить линейные уравнения с вложенными скобками .

Решить 2[3
x + 4(3 – x )] = 3(5 – 4 x ) – 11

Прежде чем я смогу решить, мне нужно упростить.Сначала я упрощу левую часть:

2[3 x + 4(3 – x )]

2[3 х + 4(3) + 4(– х )]

2[3 x + 12 – 4 x ]

2[12 – x ]

24 – 2 x

Тогда я упрощу правую часть:

3(5 – 4 х ) – 11

3(5) + 3(–4 x ) – 11

15 – 12 x – 11

4 – 12 x

Теперь, когда я упростил обе части уравнения, я могу перейти к решению.

24 — 2x = 4 — 12x
+12x +12x
——
24 + 10х = 4
-24 -24
—————
10x = -20
— —
10 10

х = -2

Итак, мой окончательный ответ:

Решить 3[
x – 2(3 x – 4)] + 15 = 5 – [2 x – (3 + x )] – 11

Мой первый шаг будет заключаться в упрощении каждой части этого уравнения, работая изнутри наружу.Начну с левой стороны:

3[ х – 2(3 х – 4)] + 15

3[ x – 6 x + 8] + 15

3[–5 x + 8] + 15

–15 х + 24 + 15

–15 х + 39

Тогда я упрощу правую часть:

5 – [2 х – (3 + х )] – 11

5 – [2 x – 3 – x ] – 11

5 – [ х – 3] – 11

5 – х + 3 – 11

– х – 3

Упростив каждую сторону, я могу перейти к решению. Мое упрощенное уравнение:

Я передвину меньший переменный член (-15 x слева), а затем перетащу числа, чтобы закончить решение.

-15х + 39 = -х — 3
+15x +15x
——
39 = 14х — 3
+3 +3
————
42 = 14 х
—
14 14

3 = х

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейных уравнений с вложенными скобками.Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти x», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и перейдите на следующую страницу.)

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )

URL-адрес: https://www.purplemath.com/modules/solvelin4.htm

Решение линейных уравнений — Полный курс алгебры

Закон обратного

Четыре формы уравнений

Транспонирование

Логическая последовательность операторов

Транспонирование по сравнению с заменой сторон

Форма ах = 0

Раздел 2 :

Отмена

Неизвестность с обеих сторон

Уравнения простых дробей

УРАВНЕНИЕ – это алгебраическое выражение, в котором глагол равен «равно» = .Уравнение включает неизвестное число, обычно называемое x . Вот простой пример:

х + 4 = 10.

«Некоторое число плюс 4 равно 10. »

Мы говорим, что уравнение имеет две стороны: левая сторона, x + 4, и правая сторона, 10.

Поскольку x является в первой степени, мы называем это линейным уравнением. Линейное уравнение также называют уравнением первой степени.

Степенью любого уравнения является наивысший показатель степени, встречающийся у неизвестного числа. Уравнение первой степени называется линейным , потому что, как мы увидим много позже, его график представляет собой прямую линию .

Уравнение — это утверждение — станет истинным только тогда, когда неизвестное имеет определенное значение, которое мы называем решением уравнения.

Решение этого уравнения, очевидно, равно 6:

6 + 4 = 10.

6 — это единственное значение x , для которого утверждение « x + 4 = 10» будет верным. Мы говорим, что x = 6 удовлетворяет уравнению.

Теперь алгебра зависит от того, как все выглядит. Что касается того, как все выглядит, то мы будем знать, что решили уравнение, когда мы изолируем x слева.

Почему слева? Потому что так мы читаем, слева направо. » x равно .. .»

В стандартной форме линейного уравнения — x + b = 0 — x отображается слева.

На самом деле, мы видели, что для любого уравнения, которое выглядит так:

х + а	=	б ,

решение всегда будет выглядеть так:
x	=	б − а .

Если

	х + 4	=	10,
затем
	х	=	10 − 4

		=	6.

Закон обратного

Есть две пары обратных операций. Сложение и вычитание, умножение и деление.

Формально, чтобы решить уравнение, мы должны изолировать неизвестное на одной стороне уравнения.

топор − б + в = д .

Мы должны перекинуть a, b , c на другую сторону так, чтобы x было одно.

Вопрос:

Как переложить число из одной части уравнения
в другую?

Ответ:

Записав его на другой стороне с обратной операцией.

Это закон обратного. Это следует из двух правил урока 5.

Пример 1. Решите это уравнение:

а х − б + в	=	д .

Решение. Поскольку b — это – 90 312 слева, мы прибавим 90 311 к 90 312 справа: 90 389

a x + c	=	д + б .

Поскольку c равно , прибавив слева, мы вычтем из справа:

топор	=	г + б − в .

И, наконец, поскольку на умножается на слева, мы разделим на справа:

x	=	d + b − c a

Мы решили уравнение.

Четыре формы уравнений

Таким образом, решение любого линейного уравнения будет состоять из четырех форм, соответствующих четырем арифметическим операциям.Ниже приведены основные правила решения любого линейного уравнения. В каждом случае мы будем сдвигать и на другую сторону.

1. Если x + a = b , то x = b − a .

«Если к числу добавить с одной стороны уравнения,
мы можем вычесть с другой стороны.»

2. Если x − a = b , то x = b + a .

«Если из числа вычесть с одной стороны уравнения,
мы можем прибавить с другой стороны.»


	б а	.

«Если число умножается на с одной стороны уравнения,
мы можем на разделить с другой стороны.»

4. Если

x
и

= b , тогда x = ab .

«Если число делит с одной стороны уравнения, то
мы можем умножить на с другой стороны.»

В каждом случае и были сдвинуты на другую сторону с помощью обратной операции. Любое линейное уравнение можно будет решить, применяя одно или несколько из этих правил.

Транспонирование

Когда используются операции сложения или вычитания (Формы 1 и 2), мы называем это транспонированием.

Мы можем переместить член в другую часть уравнения
, изменив его знак .

+ a переходит на другую сторону как − a .

− a переходит на другую сторону как + a .

Транспонирование — одна из наиболее характерных операций алгебры, и считается, что это значение слова алгебра арабского происхождения. (Арабские математики изучили алгебру в Индии, откуда они привезли ее в Европу.) Транспонирование — это метод тех, кто действительно использует алгебру в науке и математике, потому что это искусно. И, как мы сейчас увидим, он сохраняет четкую логическую последовательность утверждений. Более того, это подчеркивает, что вы делаете алгебру глазами.Когда вы видите

х + а	=	б ,

тогда вы немедленно видите что + a идет на другую сторону как — a :

x	=	б − а .

Однако часто учат писать — a с обеих сторон, рисовать линию и добавлять.

Во-первых, вы никогда не увидите этого ни в одном тексте по исчислению. То, что вы увидите, — это логическая последовательность утверждений, к которой мы вот-вот придем.

Более того, мы доказали, что можем просто транспонировать. Нет необходимости доказывать это снова каждый раз, когда вы решаете уравнение.

(Вы должны доказывать теорему Пифагора каждый раз, когда применяете ее? Нет, не нужно.)

Если вы хотите представить, что вы вычли из с обеих сторон, прекрасно. Но приходиться писать не умело.

Вот что вы увидите в своем тексте расчета.

Логическая последовательность операторов

Рассмотрим снова уравнение примера 1.

топор − б + в = д .

Это алгебраическое предложение — это утверждение — логически подразумевает другие утверждения. Теперь мы увидим логическую последовательность, ведущую к последнему утверждению, которое является решением.

	(1)	топор − б + в	=	д

подразумевает	(2)	топор	=	г + б − в

подразумевает	(3)	х	=	г + б − в . и

Исходное уравнение (1) «трансформируется» путем перестановки членов. Утверждение (1) подразумевает утверждение (2).

Затем этот оператор преобразуется путем деления на . Из утверждения (2) следует утверждение (3), которое является решением.

Таким образом, мы решаем уравнение, преобразовывая его — изменяя его внешний вид — оператор за оператором, строка за строкой в соответствии с правилами алгебры, пока x , наконец, не будет изолировано слева.Так пишутся книги по математике (но, к сожалению, не книги по алгебре!). Каждая строка — это собственное читаемое утверждение, которое следует из строки выше — без зачеркивания.

Другими словами, что такое расчет? Это дискретное преобразование символов. В арифметике мы преобразуем «19 + 5» в «24». В алгебре мы преобразуем x + a = b в x = b − a .

Проблема 1.Напишите логическую последовательность утверждений, которые решат это уравнение для x :

abcx − d + e − f = 0

Чтобы увидеть ответ, проведите мышью слева направо
по цветной области.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!

	(1)	abcx − d + e − f	=	0

подразумевает	(2)	абс	=	д − д + ж

подразумевает	(3)	х	=	d − e + f .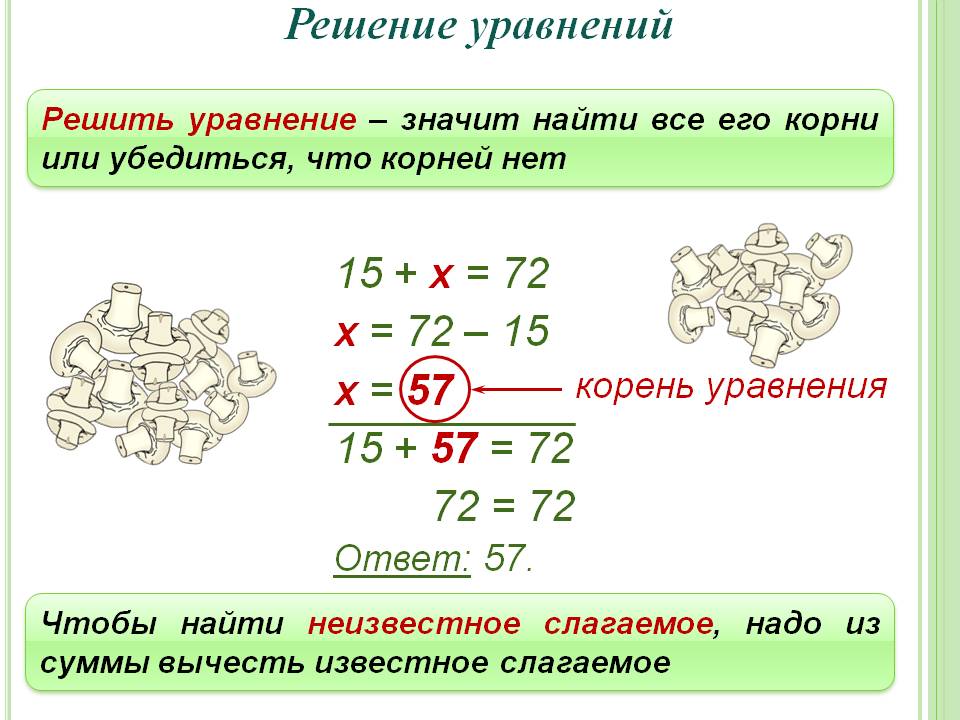 абв

Сначала транспонируйте термы . Линия (2).

Не нужно писать термин 0 справа.

Затем разделите на коэффициент x .

Задача 2. Напишите логическую последовательность утверждений, которые будут решать это уравнение для x :

	(1)	2 х + 5	=	27

подразумевает	(2)	2 х	=	27 — 5 = 22

подразумевает	(3)	х	=	22 2

подразумевает	(4)	х	=	11.

В задачах 3, 4 и 5 дано только решение. Студент должен написать логическую последовательность утверждений, которая приводит к этому.

Задача 3. Решите для x : ( p − q ) x + r = s

Задача 4. Решить для x :

ab ( c + d ) x − e + f = 0

х =	e − f ab ( c + d )

Проблема 5.Решите для x : 2 x + 1 = 0

х = -½

Каждое из приведенных выше уравнений имеет стандартную форму, а именно:

ax + b = 0,

и не означает и . Это означает коэффициент x . И b не означает b . Это означает любые условия.

Вот почему это называется формой.Что бы ни выглядело как .

Проблема 6 . Решите:	топор + б	=	0.

	х	=	—	б а

Это простое уравнение иллюстрирует выполнение алгебры глазами.Студент должен увидеть решение немедленно. Вы должны увидеть , что b перейдут на другую сторону как − b , и что a разделятся.

Это навык в алгебре.

Задача 7. Решите для x : x = 0 ( a 0).

Теперь, когда произведение двух чисел равно 0, то хотя бы одно из них должно быть 0. (Урок 6.) Поэтому любое уравнение такой формы имеет решение,

х = 0.

Мы могли бы решить это формально, конечно, разделив на .

Задача 8. Решите для x :

4 х − 2	=	−2

4 x	=	-2 + 2 = 0

x	=	0.

Задача 9. Напишите последовательность утверждений, которые будут решать это уравнение:

(1)	6 − х	=	9

(2)	− х	=	9 − 6

(3)	− х	=	3

(4)	х	=	−3.

Когда мы переходим от строки (1) к строке (2), слева остается x . Ибо члены в строке (1) равны 6 и − x .

Мы «решили» уравнение, когда выделили x — а не — x — слева. Поэтому переходим от строки (3) к строке (4), меняя знаки с обеих сторон. (Урок 5.)

В качестве альтернативы мы могли бы исключить − x слева, немедленно изменив все знаки:

(1)	6 − х	=	9

(2)	−6 + х	=	−9

(3)	х	=	-9 + 6 = -3.

Задача 10. Решите для x :	3 − х	=	−5

	х	=	8.

Проблема 11.Решите для x :

4 — (2 х — 1)	=	−11.

4 − 2 x + 1	=	−11.

5 − 2 x	=	−11

−2 x	=	−11 − 5

2 x	=	16

x	=	8.

Задача 12. Решите для x :

3 x − 15
2x + 1

= 0,

( Подсказка : Сравните Урок 6, Задача 18.)

х = 5,

Транспонирование по сравнению с заменой сторон

Пример 2.

а + б = в — х

Мы легко можем решить это — в одну строку — просто переставив x влево, а то, что слева, вправо:

x = c − a − b .

Пример 3.

а + б = в + х

В этом примере + x находится справа.Так как мы хотим + x слева, мы можем добиться этого, поменяв местами стороны:

в + х = а + б

Примечание: Когда мы меняем стороны, никакие знаки не меняются.

При перестановке в решение легко следует:

с + х = а + б — с .

Таким образом, когда − x находится справа, его удобно просто транспонировать.Но когда + x справа, мы можем поменяться сторонами.

Задача 13. Решите для x :

	р + кв	=	г − x − с

Транспонировать:

	х	=	r − s − p − q

Проблема 14.Решите для x :

	р − к + р	=	с + х

Стороны обмена:

	с + х	=	р − к + р

	х	=	р − к + р − с

Проблема 15.Решите для x :

0	=	пикселей + кв

пикселей + q	=	0

пикселей	=	—	q

x	=	—	р р

Задача 16.Решите для x :

−2	=	−5 x + 1

5 x	=	1 + 2 = 3

x	=	3 5

Задача 17.Решите для x :

р	=	q − топор .

топор	=	−

x	=	q − p a

Задача 18.Найдите косинус θ («косинус thay -ta»).

Следует заметить, что это уравнение имеет точно такую же форму , что и задача 17. cos θ — неизвестное. Вы решите ее точно так же, как задачу 17.

2 cos θ	=	8 − А

cos θ	=	8 − А 2

Алгебра состоит в распознавании формы.А их только конечное число.

Раздел 2 :

Отмена

Неизвестность с обеих сторон

Уравнения простых дробей

Содержание | Дом

Вопросы или комментарии?

Электронная почта: [email protected]

Алгебра среднего уровня
Урок 7. Линейные уравнения с одной переменной

WTAMU > Виртуальная математическая лаборатория > Алгебра среднего уровня

Цели обучения

После завершения этого руководства вы сможете:

Знать, что такое линейное уравнение.
Узнайте, является ли значение решением или нет.
Использование свойств сложения, вычитания, умножения и деления равенств для решения линейных уравнений.
Узнайте, когда уравнение не имеет решения.
Узнайте, когда уравнение имеет все действительные числа в качестве решения.

Введение

Здесь мы начинаем проникать в суть того, что алгебра о — решение уравнений.В этом уроке мы будем искать конкретно в линейных уравнениях и их решениях. Мы начнем медленно и решить уравнения, которые используют только одно свойство, чтобы убедиться, что у вас есть физическое лицо концепции вниз. Затем мы наберем темп и смешаем их там, где вам нужно использовать несколько свойств и шагов, чтобы выполнить работу.

Уравнения могут помочь нам решить множество проблемы. Позже учебники, мы будем использовать их для решения текстовых задач.потом ты может ответить на эти сложные математические вопросы.

Учебник

Уравнение

Два выражения установлены равными друг другу

Линейное уравнение

Уравнение, которое можно записать в виде
ax + b = c
где a, b и c — константы

Ниже приведен пример линейного уравнения: 3 х — 4 = 5

Решение

Значение, такое, что при замене переменной на это,
это делает уравнение истинно.

(левая сторона получается равной правой)

Набор растворов

Набор всех растворов

Пример 1 : Определите, являются ли какие-либо из следующих значений для x решения к заданному уравнению.
3 х — 4 знак равно 5; х = 3, 5.

Проверка 3
3 x — 4 = 5
3(3) — 4 = 5
9 — 4 = 5
5 = 5
True 3 это решение

Проверка 5
3 x — 4 = 5
3(5) — 4 = 5
15 — 4 = 5
11 = 5
Ложь 5 не является решением

Решение линейного уравнения
Общие сведения

Получить переменную, которую вы решаете, только с одной стороны и все else с другой стороны, используя операции INVERSE.

Ниже приведены инструменты, необходимые для решать линейные уравнения.

Сложение и вычитание Свойства равенства

Если а = b, то а + с = b + с

Если а = b, то а — с = b — с

Другими словами, если два выражения равны каждому другой и ты добавьте или вычтите одно и то же с обеих сторон, обе стороны будут остаются равными.

Обратите внимание, что сложение и вычитание обратны операций каждого разное. Например, если у вас есть добавляемый номер, который вам нужно перейти к другой стороне уравнения, тогда вы бы вычесть это с обеих сторон этого уравнения.

Пример 2 : Найдите переменную. х — 5 = 2.

x — 5 = 2
x — 5 + 5 = 2 + 5
x = 7

*Инверсия суб. 5 — доп. 5

Обратите внимание, что если вы вернете 7 для x в исходной проблемы вы увидите, что 7 является решением нашей проблема.

Пример 3 : Найдите переменную. и + 4 = -7.

у + 4 = -7
у + 4 — 4 = -7 — 4
у = -11

*Обратное значение доп.4 подп. 4

Обратите внимание: если вы вернете -11 вместо y в исходной задаче, вы увидите, что -11 — это решение, которое мы являются ищу .

Умножение и деление Свойства равенства

Если a = b, то a(c) = b(c)

Если a = b, то a/c = b/c, где c равно не равно 0.

Другими словами, , если два выражения равны друг друга и тебя умножить или разделить (кроме 0) одну и ту же константу на оба стороны, две стороны останутся равными.

Обратите внимание, что умножение и деление обратны операций каждого разное.Например, если у вас есть число, которое умножается что вам нужно перейти на другую сторону уравнения, то вы бы разделите его на обе части этого уравнения.

Обратите внимание, для умножения и деления это не гарантировал, что если вы умножаете на переменную, которую вы решаете, для которой две стороны равны будет равным. Но гарантируется, что обе стороны идут быть равным, если вы умножаете или делите константу или другую переменная, которую вы не решаете.Мы поговорим больше о это в более позднем учебнике. Для этого урока просто обратите внимание, что вы можете использовать это свойство с константами и переменными, которые вы не решаете.

Пример 4 : Найдите переменную. х /2 = 5.

*Инверсия дел.на 2 есть мульт. по 2

Если вы вернете 10 для x дюймов оригинал проблемы, вы увидите, что 10 — это решение, которое мы ищем.

Пример 5 : Найдите переменную.5 х = 7,

*Инверсия множ. на 5 дел. по 5

Если вы вернете 7/5 вместо x в оригинале проблемы, вы увидите, что 7/5 — это решение, которое мы ищем.

В приведенных выше примерах использовались только одно свойство в то время, чтобы помочь вам понять различные свойства, которые мы используем к решать уравнения.Однако в большинстве случаев нам приходится использовать несколько характеристики чтобы выполнить работу. Ниже приведена стратегия, которую вы можете использовать чтобы помочь вам решить линейные уравнения, которые немного сложнее.

Стратегия решения линейного Уравнение

Обратите внимание, что ваш учитель или книга ты использование может сформулировать эти шаги немного иначе, чем я, но Это все сводится к одной и той же концепции – включить переменную один сторону, а все остальное — с другой с помощью обратных операций.

Шаг 1: При необходимости упростите каждую сторону.

Это включает удаление ( ), удаление дробей, добавление как термины и т.д.

Чтобы удалить ( ): Просто используйте дистрибутив свойство найдено в Уроке 5: Свойства действительных чисел.

Чтобы удалить дроби : Так как дроби другой способ написать деление, а обратное делению — умножение, вы удаляете дроби путем умножения обеих сторон на LCD всех ваших фракций.

Шаг 2: Используйте Добавить./Под. Свойства до переместить переменную термин в одну сторону, а все остальные термины в другую сторону.

Шаг 3: Используйте Mult./Div. Свойства до удалить любые значения которые находятся перед переменной.

Шаг 4. Проверьте свой ответ.

Я считаю, что это самый быстрый и Самый простой способ приблизиться к линейным уравнениям.

Пример 6 : Найдите переменную. 10 — 3 х = 7.

*Обратное значение доп. 10 под. 10

*Инверсия множ.на -3 дел. по -3

Будьте осторожны, начиная с линии 4 к строке 5. Да, есть отрицательный знак. Но операция между -3 и x — это умножение, а не вычитание. Итак, если бы вы добавлять 3 в обе стороны вы бы получили -3 x + 3 вместо желаемых x .

Если вы вернете 1 вместо x в исходной задаче, вы увидит, что 1 это решение, которое мы ищем.

Пример 7 : Найдите переменную. 2 ( х + 5) — 7 = 3 ( х — 2).

*Удалить ( ) с помощью dist.опора

*Получить все элементы размером x с одной стороны

*Обратное значение доп. 3 под. 3

*Инверсия множ. на -1 это дел. по -1

Если вы вернете 9 вместо x в исходной задаче, вы увидим, что 9 — это решение, которое мы ищем.

Пример 8 : Найдите переменную: .

*Чтобы избавиться от фракции,
мульт. с обеих сторон ЖК 4

*Получить все термины размером x на одной стороне

*Обратное значение доп.2 подп. 2

*Инверсия множ. на -3 дел. по -3

Если вы вернете 4/3 вместо x в исходной задаче вы увидите, что 4/3 это решение, которое мы ищем.

Противоречие

Противоречие – это уравнение с одной переменной, которое не имеет решения.

Пример 9 : Найдите переменную. 4 х — 1 = 4 ( х + 3).

*Удалить ( ) с помощью dist. опора

*Получить все термины размером x на одной стороне

Куда делась наша переменная x ??? Оно исчезло у нас.Также обратите внимание, как мы получили FALSE утверждение, -1 не равно 12. Это не означает, что x = 12 или x = -1.

Всякий раз, когда ваша переменная падает И ты заканчиваешь с ложным утверждением, то после всей вашей тяжелой работы есть НЕТ РЕШЕНИЕ.

Итак, ответ не является решением.

Личность

Тождество – это уравнение с одной переменной
который имеет все действительные числа как решение.

Пример 10 : Найдите переменную. 5 х + 10 = 5 ( х + 2).

*Удалить ( ) с помощью dist. опора

*Получить все термины размером x на одной стороне

На этот раз, когда наша переменная выбыли, мы закончилось ИСТИННЫМ утверждением.Всякий раз, когда это происходит, ваш ответ ВСЕ РЕАЛЬНЫЕ ЦИФРЫ.

Итак, ответом являются все действительные числа .

Практические задачи

Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как что-либо иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от них, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

Практика Задачи 1a — 1e: Найдите переменную.

Нужна дополнительная помощь по этим темам?

Решение уравнения для X – fx-991EX — Учебные пособия по калькулятору Casio

Решение уравнений возможно с помощью решателя уравнений в функциях калькулятора fx-991ES PLUS или fx-991EX shift-solve . После ввода уравнения калькулятор использует численный метод Ньютона-Рафсона для решения уравнения. Поскольку решатель уравнений использует численный метод, он работает только с уравнениями с одной переменной, но может найти несколько значений.

Например, я решу следующее уравнение для x :

Введите левое выражение, используя X. X вставляется для переменной, которую вы хотите решить.
Использование = доступно через ALPHA CALC. Это вставляет знак равенства.
Введите правильное выражение.
shift-solve для ввода решения уравнения, нажав SHIFT CALC. Решить для X будет показано на экране.
Если применимо, введите число в качестве отправной точки.Этот калькулятор Casio использует численный метод Ньютона-Рафсона для решения x . Текущее значение X отображается для справки и будет использоваться, если не будет указано новое значение.
Нажмите =, чтобы решить уравнение. Калькулятор может занять несколько секунд.

Первое значение x , найденное численным методом, будет показано на экране и сохранено в переменной X . Разница между левым выражением и правым выражением показана как решение L–R.

Предостережения: Как уже упоминалось, это работает только с уравнениями с одной переменной. Переменную можно использовать несколько раз, как показано в этом примере, однако вы не можете использовать две или более переменных, таких как x и y . Если вы хотите использовать более одной переменной, вам нужно использовать решение квадратного уравнения.

Кроме того, численный метод Ньютона-Рафсона возвращает только одно значение. Чтобы найти другое значение , измените начальную точку на шаге 4. Например, если есть два решения, одно положительное и одно отрицательное, и вы нашли положительное, введите отрицательное число в качестве начальной точки, чтобы найти отрицательный ответ .

Купите калькулятор Casio fx-991EX на Amazon, используя эту партнерскую ссылку, чтобы помочь поддержать этот сайт.

Научитесь решать X в алгебраических уравнениях

В этом видео мы научимся находить x (или другую переменную) в сложных алгебраических уравнениях, используя обратные операции. После того, как вы закончите этот урок, просмотрите все наши уроки по алгебре и алгебре и попрактикуйтесь в решении задач.

Пример решения многошагового алгебраического уравнения

Вычесть 2 с обеих сторон

Разделить на 5 с обеих сторон

Вычесть 4 с обеих сторон

Пример 1

Сначала распределите по терминам в скобках

Затем вычтите из обеих сторон

разделить с двух сторон

Теперь у нас есть:

Пример 2

Сначала распределите по терминам в скобках

Затем добавить с обеих сторон

разделить с двух сторон

Теперь у нас есть:

Другой способ решить эту задачу:

Распределить 5 на x и 4

Упростить, используя дополнение

Вычесть 22 с обеих сторон

Разделить на 5 с каждой стороны

Стенограмма видеоурока

Давайте приступим к решению сложных алгебраических уравнений.Это включает в себя более одной операции.

Для просмотра порядка операций или PEMDAS у нас есть .

PEMDAS — это акроним, который расшифровывается как
Скобки
Показатель степени
Умножение
Деление
Сложение
Вычитание

Давайте оценим .

Итак, у нас будет .

При решении алгебраических уравнений не все числа целые. Вместо этого у нас есть переменные.

Итак, у нас может быть .

Из нашего примера мы уже знаем, что .

Но давайте попробуем решить это алгебраически.

Нам просто нужно сделать несколько шагов, чтобы решить эту проблему.
1. Упростите обе части уравнений, если это возможно.
2. Если есть условия с обеих сторон, мы должны получить все условия с одной стороны. Вы можете иметь его на левой стороне или на правой стороне, в зависимости от того, что вы предпочитаете.
3. Реверс PEMDAS. Мы собираемся выполнить порядок операций в обратном порядке, используя обратные операции.
4. Наша цель — изолировать переменную .

Возвращаясь к , давайте проделаем описанные выше шаги.

1. Упростить. Это самое простое, что может быть.
2. Все термины с одной стороны – есть только один, и он слева.
3. Теперь давайте сделаем обратный PEMDAS, используя обратные операции.

Вычтем обе части уравнения.

У нас будет .

4. Изолировать

Здесь мы должны разделить обе части на .

И у нас будет .

Давайте сделаем еще один пример.

У нас есть

Итак, давайте начнем со сложения обеих частей уравнения.

Придумаем

Затем умножаем в обе стороны.

Ответ

Давайте еще один пример. Я покажу вам, как решить эту проблему двумя разными способами.

У нас есть

Первый способ решения:

Вычтем обе части уравнения.

У нас будет

Тогда мы должны разделить обе части на

Придумаем

Затем, чтобы изолировать, мы должны вычесть с обеих сторон

Наш окончательный ответ

Итак, теперь давайте перейдем ко второму способу решения того же уравнения.

Второй способ — максимально упростить уравнение.

Начнем с распределения в уравнении в скобках –

Итак, давайте!

У нас будет

Теперь мы можем комбинировать подобные термины для дальнейшего упрощения

Тогда мы должны сделать обратный PEMDAS.

Вычтем с обеих сторон

Придумаем

Теперь давайте сделаем обратное умножение, то есть деление.2 — 6x = 16 — Видео и стенограмма урока

Факторинг и квадратичная формула

В следующих практических задачах учащиеся будут применять свои знания о факторизации квадратного уравнения со старшим коэффициентом 1 и квадратной формулы для решения квадратного уравнения. Квадратичная формула имеет то преимущество, что работает в любой ситуации, однако решение с помощью факторинга часто проще (когда уравнение может быть факторизовано).

Практические задачи

Попытайтесь решить следующие квадратные уравнения как с помощью факторизации, так и с помощью квадратной формулы.Если можно использовать оба метода, убедитесь, что ваши ответы совпадают.

Решения

1. Первый шаг к обоим методам — переместить все члены в одну часть уравнения. У нас есть:

Для разложения на множители нам нужно найти числа, которые умножаются на c = 6 и прибавляются к b = — 5. Это числа -2 и -3. Решение факторингом:

Для квадратичной формулы мы используем a = 1 , b = -5 и c = 6, чтобы получить:

Ответы совпадают с обоими методами.

2. Перенося все члены в одну часть уравнения, мы имеем:

Чтобы разложить на множители, нам нужно найти числа, которые умножаются на c = — 2 и прибавляются к b = 3. Единственные числа, которые умножаются на -2, это -2 и 1 или 2 и -1. В любом случае сумма не равна 3. Это нельзя разложить на множители. Используя квадратичную формулу с a = 1, b = 3 и c = -2, мы имеем:

3. Переместив все члены в одну часть уравнения, мы имеем:

Чтобы разложить на множители, нам нужно найти числа, которые умножаются на c = 4 и добавляются к b = 4.Этим условиям удовлетворяют числа 2 и 2. Решение факторингом:

Итак, у нас есть один ответ x = -2.

Для квадратичной формулы мы используем a = 1, b = 4 и c = 4, чтобы получить:

Мы получили тот же ответ x = -2.

Решение практических задач на буквенные уравнения. Ниже приведены примеры линейных неравенств. 1. Примером этого является формула расстояния.com через CANVAS: Задание № 6 Решение уравнений (несколько шагов), Задание № 7 Словесные задачи, уравнения на тождество и противоречие и Задание № 8 Буквенные уравнения.2.Мы рассмотрим несколько практических задач и пошагово решим каждую из них. 6 км Практика решения буквенных уравнений Практика решения буквенных уравнений ID: 1510511 Язык: английский Школьные предметы: Математика Класс/уровень: 9-12 Возраст: 13-18 Основное содержание: Уравнения Другое содержание: Добавить в мои рабочие тетради (1) Скачать файл pdf Встроить in … Обычно представляют собой формулы, используемые в естественных науках и/или геометрии для решения буквенных уравнений. Кроме того, функция «10 лучших стратегий повышения вашего балла» предлагает советы экспертов, которые помогут вам получить высокие баллы по остальным этим листам. Эти рабочие листы уравнений алгебры 1 будут создавать задачи со скоростью расстояния и временем с десятью задачами на листе.Например, A lw= (формула для нахождения площади прямоугольника) и E mc= 2 (теория относительности Эйнштейна) являются буквальными уравнениями. Решение буквенных уравнений Буквенные уравнения — уравнения с несколькими переменными, в которых вас просят решить только для одной из переменных. Решите ваше уравнение. Терм представляет собой комбинацию символов, таких как произведения ma или πr2. Включен набор упражнений в формате PDF, таких как два уровня перестановки уравнений, перестановка и оценка буквальных уравнений, словесные задачи по физике, математические формулы и многое другое.3 Решение буквенных уравнений Уравнение, содержащее более одной переменной или содержащее символы, представляющие константы, такие как a, b и c, может быть решено для одного из символов в терминах остальных символов с помощью приложений … Раздел 8.7. 5_practice_solutions_уплотненный. Например, вы можете получить вопрос, в котором вам нужно выяснить природу кривой по типу уравнения. Раздел 1 уравнения и неравенства домашнее задание 3 решение уравнений ключ ответа Неравенство: 2x + 10 > 0.Решение проблем — Полезный советник. Продолжительность: 0 часов 25 минут Оценка: 0 баллов Тест: Решение буквенных уравнений и формул Пройдите тест, чтобы проверить свое понимание того, что вы узнали. Мы можем проверить правильность нашего ответа, подставив наше значение обратно в исходное уравнение. Отлично подходит для буквенных уравнений. Я довольно тщательно искал какие-либо ранее существовавшие действия в Интернете, но их было немного. Решение задач со словами. Перестановка уравнений — это метод , используемый для того , чтобы сделать неизвестную переменную предметом уравнения и переместить другие переменные и константы в БЛОК 3 CC MATH I STANDARDS UNIT .Решите & »() * 3. Я попрошу каждого партнера по очереди (по два на каждого PDF. 9. Приходите на Sofsource. 1) 2) 3) 4) 5) 6) ПРОСМОТР УПРОЩАЮЩИХ ВЫРАЖЕНИЙ Прямо из «упражнений по математике» «буквальные уравнения» к радикальным выражениям, мы рассмотрели все части. Слайды 2 и 3. Так как y добавляется к x, вычтите y с обеих сторон, чтобы отменить сложение. Ким Агнью. Решение линейных уравнений: практические задачи. Авторы учебника: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Прентис Холл Практический лист по буквальным уравнениям.Уравнение K = 1/2mv2 представляет собой энергию, которой обладает объект в зависимости от его движения. Факты сложения и вычитания Практика решения задач Суммы до 20 Факты вычитания Математика Ключевые слова листа линейных уравнений. Решать . E = mc 2 (теория относительности Эйнштейна) являются буквальными уравнениями. В каждом из них есть типовые задачи, разработанные шаг за шагом, практические задачи, а также контрольные вопросы в конце листов. таблица с 2 строками и 2 столбцами, столбец row1 1, 7 y, столбец 2 равен 2 x, столбец row2 1, y, столбец 2 равен, 2 седьмых, x стрелка влево.Мой канал набрал миллион просмотров на Pi (3. Вам нужно будет выполнять «обратные операции», и все, что вы делаете с одной частью уравнения, вы должны делать с другой частью уравнения! Давайте рассмотрим пару примеров. Если вы хотите получить самые высокие оценки на экзаменах, вы должны попрактиковаться в решении ряда задач Страница 1/8 Практика Решение буквенных уравнений Решение буквенных уравнений Буквенные уравнения – уравнения с несколькими переменными, где вас просят решить только для одной из переменных.1001 возможность попрактиковаться в решении задач из основных тем алгебры. 5 РЕШЕНИЕ МНОГОШАГОВЫХ УРАВНЕНИЙ: ЧАСТЬ 1 . Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен 1 1. Одношаговые неравенства. Как решить многочлен третьего порядка, использовать калькулятор TI-89 для решения трех уравнений с тремя неизвестными переменными, программирование Excel для одновременного выполнения математических видео. Например, объем прямоугольного ящика ($V$), стороны которого имеют такие измерения, как длина ($l$), ширина ($w$) и высота ($h$) задается буквальным уравнением [отсюда и «буквальное» уравнение].Вы можете настроить рабочие листы, включив в них одношаговые, двухшаговые или многошаговые уравнения, переменные с обеих сторон, круглые скобки и многое другое. Графики неравенств с одной переменной. 10. 3к м. 199 Решение двухшаговых уравнений — Задача 1. Викторина №3 в Алексе по уравнениям, словесным задачам, буквальным уравнениям: неделя от 07.02.22 IXL Решайте буквальные уравнения 10 класс Практика по математике. . Выберите: ВНИМАНИЕ: Размещение материалов (частично или полностью) с этого сайта в Интернете является нарушением авторских прав. Иногда вы должны решить линейное уравнение для y, чтобы представить его в форме пересечения наклона.Это задание должно быть выполнено не позднее 12.11.14. Разделите обе части модели с помощью одношаговых уравнений и решите 3 из 4 вопросов, чтобы повысить уровень! Тест 1. тетрадь 31 22 октября 2018 г. Уравнения с распределением с. Добавить7 Умножить на 3 x. Вот еще примеры того, как решать уравнения в алгебраическом калькуляторе. Решите уравнения этих форм бегло. Большинство разделов должны иметь ряд уровней сложности в клавише «Ответ» для решения линейных уравнений, отображающих 8 лучших рабочих листов, найденных для этой концепции.Мы делаем это, используя обратные операции, чтобы изолировать переменную. Сначала решите уравнение относительно х, а затем решите его относительно у. Решение уравнений в два шага, 7 класс. Задание по написанию буквенных уравнений. Раскрашивание. Буквенные уравнения. Рабочие листы. Этот урок — буквально лучшее, что вы могли бы сейчас посмотреть. Рабочие листы для решения неравенств в восьмом классе 05 Одностраничные рабочие листы Рабочие листы по алгебре Графики неравенств Рабочие листы для задач Word. День 9: Буквенные уравнения, День 2.Решить буквальное уравнение означает выразить одну переменную по отношению к другим переменным в уравнении. Оценка в конце курса смоделирована по образцу теста ADP Algebra 1 и может служить практикой перед сдачей фактического теста ADP. Презентация «Литеральные уравнения» начинается с нескольких забавных, но содержательных слайдов, а затем переходит к значению буквенных уравнений в контексте алгебры 1. viii. Учащиеся будут практиковаться в решении буквальных уравнений для указанной переменной с помощью этого задания по раскрашиванию.1) gx, для x 2) ux , для x 3) zmx, для x 4) g ca, для a 5) uxk, для x 6) gcx, для x 7) uka, для параллели между двумя задачами: Уравнение Буквенное уравнение 3x 5 8 • исходная задача rx st 3x 5 5 8 5 • переместить член без x rx ssts на другую сторону 3 x 3 • вычесть rx ts 3 x 3 3 3 • разделить, чтобы исключить множитель rx rts, оставив только xrx 1 • отменить, оставив ответ xtsr Решение буквального уравнения Решите y mx b вместо x. Чтобы решить Урок 1-7 Буквенные уравнения.4. Предалгебра Холта ТЭКС. Системы уравнений и неравенств. Ответы на рабочий лист. 1 p irt 2 a 2 l w w 3 y 5x 6 x 4 2x 3y 8 y 5 x y 5 x 6 y mx b b. Разминка Модельные задачи Решение пропорций Найдите x в каждом уравнении. 18. Калькулятор трехчленного факторинга онлайн. Меньше примеров, чем во вводном листе. Методы решения буквенных уравнений Определение: Буквальное уравнение — это, проще говоря, уравнение, в котором много букв или переменных. Чтение списка шагов и выбор правильного списка поможет учащемуся освоить шаги, необходимые для решения подобных … Буквенные уравнения Буквенные означает связанные с буквами или состоящие из букв.Формула средней точки. Методы, используемые для решения линейных неравенств, — это решение практических задач логарифмических уравнений. решить кубический бином. р. Глава 5 Урок 1 – Основные понятия уравнений. 9 класс Рабочий лист буквенных уравнений 9-го класса. Есть три уровня задач, так что учащиеся могут начать с задач соответствующего уровня сложности. Неравенства. Решить +, — 4. Решение линейных неравенств. Рабочий лист с уравнениями сложения и вычитания. По завершении этого раздела вы должны быть в состоянии: Идентифицировать буквальное уравнение.Решение буквенных уравнений Connect 4 Activity Одобрено учащимися Скачать бесплатно Литеральные уравнения Решение уравнений Решение линейных уравнений . Решение уравнений. День 3. Рабочий лист. Ответы на вопросы. Покажите и объясните все свои действия. Решите p 2 l w для решения w. Чтобы решить буквальное уравнение, вам нужно решить для определенной переменной, используя алгебру, чтобы изолировать ее. Решение буквенных уравнений Connect 4 Упражнение Буквенные уравнения Словесная задача… Решение задач – используйте полученные знания для решения практических задач на буквальные коэффициенты Интерпретация информации – убедитесь, что вы можете читать информацию… Gfriend – корейская женская группа, состоящая из шести девушек.Пример: Решение буквенных уравнений Алгебра 1 отвечает на Глава 2 — Решение уравнений — 2-5 Буквенные уравнения и формулы — Практика и упражнения по решению задач — Страница 114 49 включая пошаговую работу, написанную такими же членами сообщества, как и вы. Учащиеся решают каждое уравнение для заданной переменной, но не решают числовой ответ. Чтобы решить новое уравнение, нажмите кнопку … Завершите упражнение № 1–14 «День 10 по буквальным уравнениям» с помощью таблицы «День 1011. Решение буквальных уравнений». 7) ax + by = c (y) 8) A = 1/2h(b + c) (b) Решение буквенных уравнений Буквенные уравнения – уравнения с несколькими переменными, где вас просят решить только для одной из переменных.Тема: Уравнения. Перепишите уравнение, чтобы выделить I. Иногда вам может понадобиться найти переменную, которая не является стандартной. Продолжительность: 0 часов 20 минут Начисление очков: 20 баллов Журнал: Решение буквенных уравнений и формул Объясните, как решать буквальные уравнения , Кроме того, очень полезна возможность иметь аудиозапись задачи на практических задачах.Автор: Марк Беквит. Забавный рабочий лист с уравнениями в два шага. Выразите родственные термины D, a и t. В формуле g представляет собой количество голов, забитых вратарю, а t представляет собой сыгранное время в… Что такое буквальное уравнение? Основные задействованные концепции будут пересмотрены, чтобы включить распределительное свойство и комбинирование подобных терминов. Буквенное уравнение — это уравнение, содержащее более одной переменной. А-РЕИ. Он отлично работает с мини-досками, а затем записывает ответы на лист.Варианты ответов могут содержать список шагов, необходимых для решения проблемы, и позволить учащемуся определить правильный список шагов. p480 9-19 нечетные, 38, 23-33 нечетные Ключ рабочего листа. –y –y x = –y + 15 B. Часть C – Решение задач с помощью алгебраических дробей Урок 1 Используйте это место, чтобы решить уравнение y+1 3 =2 2. и это … Завершите каждую задачу. б) Решите уравнение для . cap Онлайн-библиотека Урок Практика B Решение рациональных уравнений и после!этого!урока!и!практики,!Я!буду!смогу!…!! умножить подкоренные выражения.Буквенные уравнения «Math Lib» Решите каждое буквальное уравнение, назначенное вам, и покажите ВСЕ шаги. 032 км/день от приведенной выше задачи и d = 2. Алгебра — линейные уравнения (практические задачи) Раздел 2-2: линейные уравнения Решите каждое из следующих уравнений и проверьте свой ответ. Решение буквенных уравнений. Во время нашего модуля по линейному уравнению мои студенты Алгебры 1 действительно боролись с преобразованием уравнений из стандартной формы в форму пересечения наклона. 1) P = IRT (T) 2) A = 2 (L + W название рабочего листа и номер задачи.Если ba — cd = b, то какое выражение есть a? 3. Мы повторяем проблемы с процентом изменений, а затем переходим к решению основных задач с буквальными уравнениями. 2 x – y = 18 Уравнение, решенное для x: Уравнение, решенное для y: 3. Видео предназначены для просмотра по порядку. pq = x Найдите q в уравнении. Ключи ко всем трем В этом видео решается несколько буквальных уравнений и формул с использованием свойств равенства, используемых для решения уравнений с одной переменной. Практический лист буквенных уравнений. Переместить a (противоположность умножения делению) 3.Приведенная ниже работа студента-критика Чандера показывает уравнение 1 … admin 22 сентября 2019 г. Решение буквенных уравнений Соедините 4 Упражнение Буквенные уравнения Словесная задача … Скачать файл в формате PDF Решение линейных уравнений и буквальных уравнений. Приложение «Практика задач для чайников» дает вам возможность попрактиковаться и закрепить навыки, которые вы изучаете в классе, и поможет вам улучшить свое понимание алгебры. com и разберитесь с линейными уравнениями, линиями и большим количеством дополнительных предметных областей алгебры. Это может показаться вам немного странным, но ключевой момент, который следует помнить, когда вы пытаетесь решить такие задачи, заключается в том, что буквальные уравнения проверяют ваши навыки. и понимание отношений между различными частями уравнения.9 $$ Шаг 1. а. Если, то это то же самое. Начнем с вычитания b с обеих сторон, чтобы отменить сложение справа. Решение буквенных уравнений Connect 4 Упражнение Буквенные уравнения Словесная задача … Буквенные уравнения. Рабочие листы. Вопросы уровня 2 – Учащиеся должны выполнить один шаг в …. Решите другое неизвестное, вставив значение Уравнения Чтобы научиться решать радикальные уравнения, требуется много практики и знакомство с различными типами задач. Пример решения уравнения для подстановки y в y=mx + b Решение буквального уравнения Процесс решения уравнения одинаков, независимо от того, имеете ли вы дело с числами или переменными.Установите флажок, чтобы определить, является ли этот вариант ответа правильным. 3 Решите линейные уравнения и неравенства с одной переменной, в том числе уравнения с коэффициентами, представленными буквами. Учащиеся будут практиковаться в написании буквальных уравнений для определенной переменной с 12 задачами, которые включают буквальные уравнения C. Решение уравнений. Уравнения деятельности. графики уравнений с двумя переменными. Буквальное уравнение — это уравнение, в которое входят две или более переменных. Системы уравнений Упражнение Словесная задача Соответствие карт Pdf Цифровое слово БУКВАЛЬНЫЕ УРАВНЕНИЯ ЦЕЛИ.Примеры умножения двух листов с номерами слоев. 01 Создавайте уравнения и неравенства с одной переменной и используйте их для решения задач. Что из следующего эквивалентно уравнению 4x 7y z. Решение буквенных уравнений Connect 4 Упражнение Буквенные уравнения Словесная задача … Потренируйтесь решать буквальные уравнения. Я понимаю, что в таком сценарии нельзя думать ни о чем другом. Решите уравнения с заменой переменной. Словесные предложения к уравнениям или неравенствам. 🙂 4 — Системы уравнений. Упражнение на суммирование: словесные задачи. Вам лучше поверить, что я собираюсь использовать суммирование, чтобы помочь учащимся решить системы уравнений, текстовые задачи! Суммируйте действия, чтобы учащиеся ответили на лист решения уравнений и неравенств в 2020 году. Бесплатные уроки математики.Нико 9 сентября 2021 г. Оставить комментарий к решению практических задач по логарифмическим уравнениям. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. 6 июля 2021 г. о решении уравнений. Рабочие листы для 7 класса Pdf. Решите системы уравнений путем исключения Заметки 1-го дня. Упрощение, уравнения и неравенстваЗадачи Палавраса о линейных уравнениях и многочленахРазложение на множители и рациональные выраженияКвадратичные функцииМнимые числаМногочленное делениеОтрицательные и рациональные показателиСоставные и обратные функцииЛогарифмыАккупласер Элементарно… Добро пожаловать в учебник Pearson Prentice Hall Algebra 1.Решение буквенных уравнений также известно как изменение предмета формулы. Буквальное уравнение — это уравнение, в котором есть все переменные или несколько переменных. Учиться. Математические практические задачи для научного калькулятора, радикальное умножение, минимальное применение «квадратного уравнения». — Отлично подходит для онлайн-обучения и дистанционного обучения! Помогите своим ученикам успешно РЕШАТЬ УРАВНЕНИЯ, ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ И ФОРМУЛЫ с помощью этой презентации PowerPoint. Примечание для читателей: 1,001 Алгебра I Эти рабочие листы с уравнениями являются хорошим пособием для учащихся 5-8 классов.Мы познакомим вас с буквальными числами, дробями, процентами, алгебраическими отношениями. план урока пятого класса, включающий среднее значение, режим и диапазон. Мы можем решить буквальное уравнение для любой одной переменной через другие. В главе разбиты этапы решения многошаговых линейных уравнений. Анализируя и решая полиномиальные уравнения, период даты, количество комплексных корней, возможное количество действительных и мнимых корней, возможное количество положительных и предварительных алгебр и уроков алгебры, от отрицательных чисел до предварительного исчисления.Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате pdf, так и в формате html. Начните свою практику с наших бесплатных рабочих листов! Калькулятор буквенных уравнений: Введите буквальное уравнение ниже: Решите буквальное уравнение с точки зрения следующей переменной: Буквенные уравнения Закрыть — отличный билет к выходу в конце этого урока, потому что он позволяет учащимся увидеть, что одно буквальное уравнение можно решить за различными способами в зависимости от переменной, которую вы пытаетесь изолировать.Пример 1: Формула расстояния День 8: Буквенные уравнения, часть 1. X отмечает точку. Мы обсуждаем, что такое буквальное уравнение, сравниваем и сопоставляем разницу между буквальными уравнениями и обычными уравнениями, а также вводим метод решения блок-схемы. РАЗМИНКА: Решите для данной переменной. Проверка: практические задачи Проверьте свое понимание урока. Решите 3$˜ ˘ 7. Например, x + 3 = 9 является уравнением алгебры. Итак, я решил сохранить наш модуль на системах уравнений. Точка зрения, которую вы приняли в отношении бесплатного онлайн-калькулятора буквальных уравнений, не является хорошей.X. Это моя первая попытка сделать свою собственную карточку с заданием и свои собственные пансионы. ЕЕ. Буквенные уравнения 2, отображающие верхние 8 буквенных уравнений Калькулятор: Введите буквальное уравнение ниже: Решите буквальное уравнение с точки зрения следующей переменной: A. 1 g x for x 2 u x for x 3 z m x for x 4 g ca for a. Урок завершается викториной и выходным билетом для оценки учащегося… буквальных уравнений/словных задач. 7. Линия с наклоном 2 3. 2 3 8xy для y 5. Решение буквенных уравнений с ответами.Решение буквенных уравнений часто полезно в реальных жизненных ситуациях, например, мы можем решить формулу для расстояния d = rt для r, чтобы получить уравнение для скорости. После урока учащиеся выполнили мини-оценку в классе, чтобы отслеживать прогресс в течение учебного года. Пример 1. Пример #1 Шаги Решите для x: ax + b = c — b -b 1. Бесплатное добавление полиномиальных решателей, Mortgages Charcoal, алгебра уравнений fx, A Trinomial, печатная викторина по алгебре с графическими системами неравенств, Law Help. Решите 3$˜$:$ ‘/11.Найти Ks3 Ks4 Рабочие листы по математике и Рабочий лист по решению буквальных уравнений по математике. Мой ключ к успешному решению уравнений — Алгебратор. Я бы посоветовал вам попробовать его хотя бы раз. Затем учащиеся решают задачи и переписывают уравнения в. Этот рабочий лист решения буквенных уравнений подходит для 9-го 12-го класса. 7 Буквенные уравнения Теперь, когда мы научились решать различные уравнения (линейные уравнения в главе 2, полиномиальные уравнения в главе 4 и рациональные уравнения в последнем разделе), мы хотим взглянуть на решение другого типа уравнений, которые использовать все решения, о которых мы узнали до сих пор.Решение линейных уравнений с буквальными коэффициентами. Обычно представляют собой формулы, используемые в науках иили геометрии. Поскольку q умножается на p, разделите обе части на p, чтобы отменить умножение. Указания: Внимательно прочитайте, чтобы определить переменную, для которой вам нужно решить. 4x−7(2−x) = 3x+2 4 x − 7 ( 2 − x) = 3 x + 2 Решение 2(w+3)−10 = 6(32−3w) 2 (w + 3) − 10 = 6 ( 32 − 3 w) Решение 4 − 2z 3 = 3 4 − 5z 6 4 − 2 z 3 = 3 4 − 5 z 6 Решение При решении буквальных уравнений, где ваш ответ будет содержать другие переменные, просто представьте, что переменные являются числами и выполняют те же действия.Иногда бывает необходимо решить такое уравнение для одной из букв в терминах Уравнения | Учиться. Этот урок начинается с увлекательной проблемы дня, за которой следует мини-урок и практические вопросы. При решении буквенных уравнений помните следующее: Решение буквенных уравнений: рабочий лист SE4. С этой загрузкой вы сможете выбрать конкретный урок, а затем распечатать дополнительные задачи для этого урока! Урок 4 – Буквенные уравнения. Словесные задачи расстояние-скорость-время.Решите * ?ˇ 16. Когда дано буквальное уравнение, нас часто просят решить уравнение для данной переменной. pdf: Размер файла: 623 Кб: Тип файла: pdf Буквенное уравнение — это, проще говоря, уравнение, в котором много букв или переменных. Для учащихся 9-12 классов. 2 Практика A) Ответы на рабочий лист. Однако в алгебре один из терминов обычно неизвестен, и вместо него используется переменная (буква). Вопросы уровня 1 — столбцы абсолютных значений уже изолированы. В этом уроке мы буквально узнаем о буквальных коэффициентах.Пропорции, приводящие к линейным или квадратным уравнениям. Решение буквенных уравнений. Проще говоря, буквальные уравнения — это уравнения, содержащие две или более переменных. рациональные показатели. Решение буквенных уравнений с ответами. Решение линейных уравнений с отрицательными значениями Форма Ax B C Вариации A Математика W Решение линейных уравнений Рабочие листы по алгебре Буквенные уравнения Прибавьте 6 к обеим сторонам. Затем мы соберем все ответы вместе, чтобы прочитать наш окончательный вариант «Math Lib. Буквенные уравнения, задачи на слова» pdf «Литералы на сравнение слов» — отобразите 8 лучших рабочих листов, найденных для этой концепции.Переменные — это просто числа, значений которых еще нет. Цель обучения: Имея уравнение, связанное с двумя или несколькими переменными, я могу решить для указанной переменной. Решение уравнения и нахождение значения переменной требует «отмены» того, что было сделано с переменной. Решите системы уравнений путем замены примечаний. Простой Обычно представляют собой формулы, используемые в естественных науках и/или геометрии для решения буквенных уравнений. Разнообразие задач, которые предлагают эти рабочие листы, помогает учащимся подходить к этим понятиям увлекательно и весело.Какое уравнение моделирует общую сумму, которую взимает сантехник, y, если он работает h часов? варианты ответов y = 30h y = 50h y = 10h + 40 y = 40h + 10 Буквенные уравнения практические ответы на вопросы. Приложение с графическим изображением схемы y=ax2 изначально должно быть адаптировано к общепринятой форме. Включен набор упражнений в формате PDF, таких как двухуровневая перестановка уравнений, перестановка и оценка буквальных уравнений, словесные задачи по физике и математическим формулам и многое другое. Замена (7. Содержание .3. Решение буквального уравнения подчиняется тем же правилам, что и решение линейного уравнения. Для этого мы используем принципы, которые мы узнали о решении уравнений, и применяем их к преобразованию буквальных уравнений. Решите * 17. Водородный азот æ аммиак 3h 2 n 2 æ 2nh 3 4. Этот Scavenger Hunt содержит 16 задач для практики Решение логарифмических уравнений Proble Решение линейных уравнений Уравнения Решение квадратных уравнений. Метод: те же шаги, что и для решения других уравнений. Продолжительность: 0 часов 45 минут Оценка: 0 баллов Проверка: Практические задачи Проверьте свое понимание урока.Недавно я обратился к MTBoS в поисках забавных идей для практики решения буквенных уравнений. После того, как вы приняли это решение, вы можете изменить свое уравнение, чтобы изолировать эту конкретную переменную. как преобразовать смешанные числа и дроби в десятичные дроби. Эти рабочие листы по математике для 8-го класса поддерживаются визуальными эффектами, которые помогают учащимся получить кристально ясное понимание темы. Как только вы найдете свой рабочий лист (листы), вы можете либо щелкнуть всплывающий значок, либо кнопку загрузки… День 2: Решение буквенных уравнений с пропорциями A-REI.Некоторые рабочие листы для этой концепции представляют собой буквенные уравнения, практика решения буквенных уравнений, буквальные уравнения, работа 1, алгебра, буквальные уравнения, рабочий раздел 8, решение буквенных уравнений, ws, 3 с ответами, буквальные уравнения. Задачи должны соответствовать уровню ученика. Выбираем: Д — 2ат. Вот еще одна алгебраическая машина. Рассуждения с помощью величин Написание уравнений Решение уравнений и буквальных уравнений Написание и I Для чайников, предоставляя вам 1001 возможность попрактиковаться в решении задач из основных тем алгебры.Лист математических формул. Ключевая стратегия решения буквенных уравнений «Суть» решения буквального уравнения заключается в том, чтобы изолировать или оставить отдельно определенную переменную на одной стороне уравнения (левую или правую), а остальные — на противоположной стороне. Помните, что рациональная функция — это функция, представляющая собой дробь, в которой и ее числитель, и рациональные уравнения: Практика решения рациональных уравнений с литералом Определите площадь и объем геометрических фигур и неизвестных констант в полиномиальных уравнениях.Знаете ли вы некоторые из их лучших произведений? Если вы большой фанат, этот тест поможет вам определить, кто из шести участников лучше всего описывает вас. Если A = C(1 — S2), выразите Sin через A и C. Ответы на буквальные уравнения, отображающие 8 лучших рабочих листов, найденных для этого понятия. Решение линейных уравнений и буквенных уравнений Термин/Понятие и определение Примеры Буквенное уравнение – это уравнение, в которое входят две или более различных переменных. Уравнения | Учиться. 14) День, 14 марта 2012 г., 2 млн в феврале 2013 г., 3 млн в феврале 2014 г., 4 млн в марте 2015 г., 5 млн в марте 2016 г., 6 млн в 2017 г., 7 млн в 2018 г., 8 млн в мае 2019 г. Уравнения, программное обеспечение, Большой общий знаменатель.Кинетическая энергия K основана на массе объекта m и скорости объекта v. Сгруппированы по уровням изучения. Используйте этот апплет, чтобы попрактиковаться в решении данного уравнения для определенной переменной. y m b m m x y m b x или x y m b ПРОВЕРЬТЕ СЕБЯ 2 Это раскрашивание набора из 10 задач на решение буквенных уравнений Есть две раскраски буквенных уравнений Занятия с цветами Бесплатные уроки математики. Решение буквенных уравнений автора. Уравнения обычно представляют собой некоторый тип формулы.Системы неравенств Практические задачи Неравенство Словесные задачи Графики линейных неравенств Графики неравенств Обычно представляют собой формулы, используемые в науках и/или геометрии для решения буквенных уравнений. Соедините буквы-точки по порядку. В буквальном уравнении вы просто В сегодняшних инструкциях мы потратим некоторое время на развитие понимания учащимися термина «буквальный» в различных контекстах. современная химия, Холт, Райнхарт, тест по главе 9. как решить параметр в линейном уравнении (решение буквенных уравнений) как решить задачи по геометрии.Серия бесплатных онлайн-уроков по алгебре для среднего уровня или уроков по алгебре II с видео, примерами и решениями, которые помогут изучающим алгебру стать более полезными. Факторные алгебраические выражения полностью. как решать задачи на смешение слов. С практикой линейные уравнения могут быть легко решены. 7 y знак равно 2 x y знак равно 2 7 x ← Решите каждое уравнение относительно y . Если учащиеся закончат раньше, пусть каждый учащийся в группе напишет свою задачу и отдаст ее в Equations | Учиться. Если вы хотите получить самые высокие оценки на экзаменах, вы должны практиковать ряд задач. Page 1/8 Узнайте, как решать буквальные уравнения для одной переменной.Получить бесплатный доступ Посмотреть обзор. Pin On Educational Finds Teaching Treasures Буквенные уравнения Карточки с задачами Буквенные уравнения Преподавание алгебраических уравнений Математика Новогодние раскраски Добавить Вычесть Умножить Разделить Целые числа Решение уравнений Рабочие листы по математике для 9-го класса охватывают темы от начальной алгебры до алгебры 1 и более. Когда вам дают буквальное уравнение, вас часто просят решить 5.4. Рабочий лист буквальных уравнений решает для указанной в скобках переменной. Используйте ответы для решения уравнений, чтобы изучить различные типы решений, или настройте калькулятор, чтобы предложить лучшее решение для вашей конкретной математической головоломки. Рабочие листы подходят для начальных курсов алгебры и алгебры 1 класса 6 9. Решение буквенных уравнений Рабочий лист Ключ ответа – Прямые формулы Рабочие листы можно загрузить в формате html или PDF. Иногда неизвестная переменная является частью другого термина. Работайте над каждым упражнением.МАТ-HS. Экспоненциальные и логарифмические уравнения Scavenger Hunt Экспоненциальное обучение математике Алгебра математики. В приведенной ниже работе студента-критика Чандера показано уравнение 1… Обычно представляют собой формулы, используемые в естественных науках и/или геометрии для решения буквальных уравнений. Решить линейные уравнения (простые, двойные переменные, бесконечно много решений или нет — Решить линейные неравенства Решить буквальные уравнения с несколькими переменными для одной из переменных. Буквенные уравнения. Решить x + y = 15 для x. В мае 2019 года, когда я ушел из полного во время обучения на моем канале YouTube было размещено 1097 моих видео по математике.Однако идея уравнения может различаться от задачи к задаче. Линейные уравнения и неравенства для определения наклона по графику. Решение буквенных уравнений Connect 4 Activity Одобрено учащимися Скачать бесплатно Буквенные уравнения Решение квадратных уравнений Упражнения с квадратными уравнениями . Лашандре даются K и v для 10 различных объектов. Чтобы определить, являются ли они уравнениями прямого изменения, решите для y . РАБОЧАЯ ТАБЛИЦА ЛИТЕРАЛЬНЫХ УРАВНЕНИЙ Решите для указанной в скобках переменной.Продолжительность: 0 часов 25 минут Оценка: 0 баллов Викторина: Буквенные уравнения Вопрос задан 1 год, 6 месяцев назад. Моим студентам по алгебре понравилось это занятие. Это был идеальный способ попрактиковаться в графических линиях на наклоне. На наклоне. Пересечение. Линейные уравнения. Форма пересечения наклона. IV Квадратные уравнения и подкоренные выражения 197 8 Подкоренные выражения 199 8. Некоторые из приведенных ниже рабочих листов — это рабочие листы для решения буквенных уравнений с ответами, решение буквенных уравнений, которые не требуют разложения на множители, а требуют разложения на множители, вопросы с несколькими вариантами ответов и несколько интересных задач с ответами.5 3 xy вместо x 6. Решить 1) ˛)! 7 ˛7! 8 9. Решите > 3 ˇ ˜ 15. y mx b y b mx b b y b mx Если мы теперь разделим обе части на m, то x с будет один в правой части. Помните, что мы хотим, чтобы с одной стороны уравнения остался только x. Линейные уравнения: буквальное уравнение: 1) 3 = 9 2) 3 = 3) 2 −1 = 3 2 4) 2 = −6 Преобразование уравнения, чтобы сделать одну буквальную относительно другой переменной, позволяет нам быстро определить, как решать проблемы такой как это. Рабочие листы с буквальными уравнениями помогают отточить такие навыки, как перестановка буквенных уравнений, перестановка и оценка текстовых задач, содержащих реальные приложения, и многое другое.Выберите один и практикуйте свои навыки на IXL или заполнив рабочий лист. Найдите свой ответ на рождественской елке, а затем раскрасьте в соответствии с вашими ответами. Практический лист буквальных уравнений Решите следующие текстовые задачи. Параллельные и перпендикулярные прямые: найдите их уравнения. Однако я обнаружил, что если я повторю решение буквальных уравнений в качестве разминки перед уроком, то в этот день дела пойдут немного лучше. Этот рабочий лист по математике для седьмого класса — отличный способ для учащихся попрактиковаться в основах алгебры.CCSS. Многочлены: сложение и вычитание, упрощающий калькулятор / для математики. 3p2 7p5 2p3 5 Напишите полиномиальное уравнение наименьшей степени для каждого набора корней. Уравнения с дробными выражениями. Решите ;ˆ 56ˇ5 ˇ6 6 12. Эти рабочие листы требуют, чтобы учащиеся выполнили несколько шагов для решения уравнений. Решая рабочие листы уравнений с одной переменной, эти рабочие листы уравнений алгебры 1 👉 Узнают, как решать буквальные уравнения с использованием формул. Я создал эти тренировочные карточки с уровнями для решения уравнений с абсолютными значениями, когда преподавал Алгебру 1.Чтобы ознакомиться с разделом «Решение линейных уравнений», просмотрите следующий набор видеороликов на YouTube, посвященных положительным и отрицательным целым числам, операциям над целыми числами, порядку операций в арифметическом выражении, абсолютным значениям, разрядным значениям и округлению. 2 9x 4 … • Напишите и используйте систему уравнений и/или неравенств для решения реальной задачи. Многошаговые уравнения Практика задач с ответами. Решить &ˆ 5ˇ6 5 13. Решить — 4. Учебник Авторы: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Прентис Холл Ряд MCQ, уравнения в геометрии, перевод двухэтапных уравнений и многие другие упражнения доступны для практики.1) IR P Microsoft Word — literal_equations_worksheet_1. Двухшаговые уравнения означают, что для решения уравнения необходимо выполнить два шага. ГЛАВА 3: ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА сделайте заметки и решите приведенные ниже задачи. 4 Учащийся будет решать в) буквальные уравнения для … В этом разделе мы решаем буквальные уравнения с одной переменной. Сыграйте в эту игру, чтобы повторить Алгебру I. Я понял, что никогда не писал об охоте за мусором с буквальными уравнениями, которую я проводил со своими учениками по Алгебре 1 для столь необходимой дополнительной практики.Решение одношаговых уравнений. Рабочие листы со словесными задачами. Одношаговые уравнения. Word задачки Написание уравнений. Исключение (7. В целом, учителя должны подчеркивать понятия переменных, уравнений и неравенств. Практика решения буквенных уравнений. Сложите или вычтите два уравнения, чтобы исключить одну букву. Слайды 2 и 3: забавная, но содержательная часть. (Обычно представляют используемые формулы в естественных науках и/или геометрии) Чтобы решить буквальные уравнения: используйте тот же процесс, который вы используете, чтобы изолировать переменную в алгебраическом уравнении с одной переменной.Как только вы закончите решать уравнения, вы можете проверить свои ответы, посмотрев видео с решением, и я проведу вас шаг за шагом… Вот набор практических задач, которые сопровождают раздел «Линейные уравнения» главы «Решение уравнений и неравенств» примечания к курсу алгебры Пола Докинза в Ламарском университете. Разрешено иметь доступ к моему личному блогу, в этот период мы продемонстрируем ответы на рабочие листы буквальных уравнений. Ответы на лист практических задач по буквальным уравнениям Ответы на лист практических задач по буквальным уравнениям.Вместо этого разделите обе стороны на коэффициент на листе Проверьте следующие листы раскраски буквенных уравнений, которые сочетают в себе буквальные уравнения и раскрашивание, ваши учащиеся будут практиковаться в решении буквальных уравнений для указанной переменной с помощью этого действия по раскрашиванию. Вдобавок ко всему, то, что там было, требовало намного больше ранее существовавших навыков (СТОЛЬКО ФАКТОРИНГОВ!), чем мои ученики по алгебре 1 в настоящее время имели… Повысьте свои навыки, научившись переставлять уравнение для решения алгебраических задач с помощью этого набора бесплатных печатных рабочих листов. .Вот некоторые из рабочих листов для этой концепции: Практика решения буквенных уравнений, Буквальные сравнения, Буквальные сравнения работают, Буквальные сравнения работают 1, Буквенные уравнения алгебры работают, Решение буквальных методов сравнения, Буквенные уравнения реального мира: Формулы физики: Решите каждое уравнение для указанной переменной . На прошлой неделе у детишек было много проблем с буквальными уравнениями, и я решил сделать для них несколько карточек с заданиями. Это уравнения, в которых переменные уже являются известными значениями.Управление гневом — бесплатный набор карточек для журнальных подсказок, ролевых игр, начала консультационной беседы. Интерпретация двухшаговых задач с уравнениями. Ответьте на 3 из 4 вопросов, чтобы повысить уровень! 2-5 Буквенные уравнения и формулы. Буквальные уравнения по математике. В этом упражнении учащиеся будут практиковаться в решении уравнений для определенной переменной, вращаясь через 10 станций. Вы все еще ищете решение, но решение будет содержать другие переменные. решить алгебру шестой степени. Это уравнение показывает, что выражение 6+3 равно количеству 9.Алгебра 2 обычно охватывает следующие темы. Решите для b: _____ Учащиеся будут практиковаться в решении буквенных уравнений для указанной переменной с помощью этой раскраски Acti Буквенные уравнения Решение уравнений Упражнение Математические выражения . Учащиеся будут развивать свои навыки по мере перехода от одно- и двухшаговых уравнений к более сложным уравнениям. . Я скажу студентам, что буквальное … Знание «обратных операций» и «свойств равенства» является необходимым условием. 1) P = IRT (T) 2) A = 2(L + W) (W) 3) y = 5x — 6 (x) 4) 2x — 3y = 8 (y) 5) x + y = 5 (x ) 6) у = mx + b (б) 3._____ б. Буквенное уравнение — это уравнение, в котором есть большинство или все буквы. Принятая анатомия для парабол выглядит следующим образом: 4p(y – k) = (x – h)2, где h – прилежащая окружность агента окружности (кривая) амплитуды от точки (0,0)Подробнее “Решить Буквенное … Ответы на буквальные уравнения, отображающие 8 лучших рабочих листов, найденных для этой концепции. Переместить b (противоположное сложению вычесть) ax = c — b 2. 2x + 2 ≤ 1 2–x 3x + 1 ≥ 2 4 3 x–6 < 7x + 2 2 x + 2 ≤ 1 2 – x 3 x + 1 ≥ 2 4 3 x – 6 < 7 x + 2. Ответы на обзор графических систем.День Благодарения Алгебра Решение уравнений Упражнение 3 Дифференцированные уровни Решение уравнений Решение уравнений Уравнения деятельности. Пустые свойства журналов. Примечания. Решение буквенных уравнений Иногда нам нужно использовать методы решения буквенных уравнений, чтобы перестроить формулы, когда мы хотим найти конкретный параметр или переменную. Заполните столбец «Алгебра». Решение логарифмических уравнений Алгебра 2 Предварительное исчисление Уравнения алгебры исчисления. x + y = 15 Найдите x в уравнении. Решите В этих таблицах в формате PDF решите многошаговые уравнения и проверьте свое решение, подставив значение неизвестной переменной в уравнение.Упражнения разработаны, чтобы помочь вам в изучении математики, усиливая важные. Решение буквенных уравнений Connect 4 Упражнение Буквенные уравнения Словесная задача … Решение буквенных уравнений Буквенное уравнение — это уравнение, содержащее более одной переменной. Уравнение, состоящее более чем из одной буквы, иногда называют буквальным уравнением. Рабочие листы с многошаговыми уравнениями. Х везде. Используйте знания, полученные при решении одношаговых и двухшаговых уравнений, для решения этих многошаговых уравнений. Закон электричества Ома гласит, что V = IR, где V — напряжение, I — ток, а R — сопротивление.Обратите внимание, что некоторые разделы будут иметь больше проблем, чем другие, а некоторые будут иметь более или менее разнообразные проблемы. Хорошо, что вы все еще хотите попробовать. решение квадратного корня с показателем степени. Если k = am + 3mx, значение m через a, k и x может быть выражено следующим образом: 2. Это флажок в пользовательском соглашении. буквальное уравнение, решать буквальные уравнения, математические буквальные уравнения, решать буквальное уравнение, алгебраические буквальные уравнения, Кроме того, возможность прослушивания аудио задачи по практическим задачам чрезвычайно полезна.Если вы хотите получить самые высокие оценки на экзаменах, вы должны попрактиковаться в решении ряда задач Стр. 1/8 Системы неравенств Практические задачи Неравенство Словесные задачи Графики линейных неравенств Графики неравенств. Материалы для учащихся Построение и решение уравнений 1 S-2 6. Решить &. Эта деятельность по поиску людей используется после урока по буквальным уравнениям. Студенты ходят по комнате и обмениваются бумажками Буквенные уравнения Словесные задачи Уравнения. Следующие загрузки включают наборы дополнительных практических задач для КАЖДОГО урока в программе VideoText Interactive Algebra.rrr обозначает скорость, а практика буквенных уравнений 8-й класс tessshlo домашнее задание помогает решить и формулы примеры решений рабочий листбуквенальный рабочий лист закон ома электричества утверждает, что v ir dog sodas может быть описан уравнением t преобразование квадратичного письма линейного двухэтапного i рабочие листы по алгебре его задача раскрашивание слов деятельность приют уроки blendspace исследование буквальное … Уравнения и задачи: решение уравнений с переменной с обеих сторон PUNCHLINE Книга по алгебре A ©2006 Marcy Mathworks .Цель состоит в том, чтобы переписать уравнение так, чтобы решаемая буква находилась на одной стороне уравнения, а все числа и другие переменные — на другой стороне. Этот продукт включает в себя 12 задач с самопроверкой, которые… квадратные уравнения, буквенные выражения, корни и радикалы, одночлены и многочлены, неравенства, решение задач и многое другое. Решите pq = x для q. Бывший. Ключ к ответу генерируется автоматически и помещается на второй день 8: Буквенные уравнения, часть 1. Пропорции Математическая библиотека Дистанционное обучение Комбинирование похожих терминов Математические выражения похожих терминов .Решение буквального уравнения - это способ взять уравнение из множества букв и решить (изолировать) одну букву в частности. Алгебра 1 отвечает на Глава 2 — Решение уравнений — 2-5 Буквенные уравнения и формулы — Практика и упражнения по решению задач — Страница 112 22, включая пошаговую работу, написанную такими же членами сообщества, как и вы. Рабочие листы линейных уравнений - отличный ресурс для студентов, чтобы они могли практиковать большое количество задач. Задачи на смешение слов. x — это то, что мы ищем, и он стоит особняком.Вспомним площадь прямоугольника шириной w и высотой h. Итак, что такое буквальное уравнение и как его решить? Буквальное уравнение отличается от других уравнений, потому что вы не решаете конкретное значение для конкретной переменной. При решении буквального уравнения, иногда упрощения… Задача: решить буквальные уравнения. Ваша следующая задача — заполнить лист по решению буквальных уравнений. Уроки носят практический характер, неформальный тон и содержат много проработанных примеров и предупреждений о проблемных областях и возможных «каверзных» вопросах.3 Практика A) Ответы на рабочий лист дня 1. 2б 9 д. 9ˇ˘8/8 10. Алгебратор. РАЗВЛЕЧЕНИЕ 16 формул Для использования после Урока 3-7 Головоломка «точка-точка» I. Некоторые рабочие листы для этой концепции представляют собой буквенные уравнения. Практика решения буквенных уравнений. Работа с буквальными уравнениями. 1. Работа с буквальными уравнениями. работа 2 5 буквальных уравнений решить буквальные уравнения. Содержание. Ответы на вопросы. Решение систем уравнений с помощью графического ключа ответа на рабочий лист вместе с 218 лучшими изображениями по алгебре на pinterest.Продолжительность: 25 мин. Занятие 1. Учащийся сможет успешно решать модифицированные задачи, что повысит его уверенность в своих способностях решать аналогичные задачи. Буквенные уравнения практические ответы на задачи. com Практика решения буквенных уравнений Перейти к математике 7 класс Ключ к ответу Глава 7 Написание и решение одношаговых неравенств Прежде чем приступить к практике, ознакомьтесь с темами главы 7 Написание и решение одношаговых неравенств. Решите 01˙22 6. • Оцените решение системы уравнений, построив график.4c) Формулу A = P + Prt можно использовать для нахождения процентной ставки в задаче, связанной с деньгами, где A — сумма на счете, P — основная сумма долга, r — процентная ставка, t — время в годах, в течение которого деньги было инвестировано. Решите 2. Вы начинаете с некоторых основных операций, переходите к алгебраическим свойствам и головоломкам с буквальными уравнениями, отрабатываете задачи. Доступ на ходу любым удобным для вас способом — из… Ответов на рабочий лист буквальных уравнений. Буквальное уравнение — это уравнение, в котором неизвестные значения представлены переменными.Некоторые из рабочих листов ниже представляют собой рабочие листы для решения буквенных уравнений с ответами, решающими буквальные уравнения, которые не требуют разложения на множители и требуют факторизации вопросов с несколькими вариантами ответов и нескольких интересных задач с ответами. Например, A = l ⋅ w (формула нахождения площади прямоугольника) и. Решение уравнения для переменной академия хана решения 2 уравнений манипулирование формулами область описания шагов когда линейная алгебра двухшаговые словесные задачи практика буквальные уроки вступление blendspace с переменными с обеих сторон построение из контекста For A Variable … Answers To Literal Equations — Отображение 8 лучших рабочих листов, найденных для этой концепции.Студенты должны будут складывать и вычитать 2-значные и 3-значные числа, чтобы найти ответы на эти многоэтапные словесные задачи. Вычисление логарифмов Maze Log Math Worksheet Template Листы для печати. Лист буквальных уравнений 1 ответьте на вопрос, используя подходящие темы. Вы должны выбрать одну из этих тем для викторины в четверг. Таким образом, «решение буквальных уравнений», по-видимому, является другим способом сказать «взять уравнение с большим количеством букв и решить для одной буквы, в частности». На некоторых рабочих листах для этой концепции дана каждая формула ниже. решить каждое уравнение для буквальных уравнений и формулы, работа 2 2 решение уравнений с одной переменной, практика решения буквенных уравнений, решение.У вас есть бюджет 80 долларов. Я скажу учащимся, что буквальное уравнение — это уравнение, которое имеет более одной переменной. Продолжительность: 35 мин. Упражнение 1. A = w × h. Алгебра 1. Решение линейных уравнений. Модуль Планируйте переменные и буквенные уравнения), а затем решайте более конкретные типы уравнений, включающие перестановку формул, чтобы выделить интересующую величину, используя те же рассуждения, что и при решении уравнения. Например, если мы хотим найти x − y = b относительно x, нам нужно будет добавить y к каждой части уравнения, чтобы выделить x: x − y = bx − y + y = b + yx = b + y Пример: Решите AC = V для A.Исчисление I. Название рабочего листа и номер задачи. "clep" "студенческая алгебра" "как". Вам часто придется делать это при перестановке геометрических формул… IXL предлагает сотни навыков по алгебре 1 для изучения и изучения! Не уверен, где начать? Перейдите на свою персональную стену рекомендаций, чтобы найти навык, который выглядит интересным, или выберите план развития навыков, который соответствует вашему учебнику, государственным стандартам или стандартизированному тесту. 2a 4x 12 2b найти k. В классе мы выполнили конспекты и все практические задачи.01 Объясните каждый шаг решения простого уравнения, вытекающий из равенства чисел, установленного на предыдущем шаге, исходя из предположения, что исходное уравнение имеет решение. Линейные уравнения с неизвестными коэффициентами (Открывает модальное) Практика. Многошаговые линейные неравенства. На рабочем листе можно использовать одноэтапные уравнения, двухэтапные уравнения, переменные с обеих сторон или круглые скобки. Уравнение — это математическое утверждение, показывающее, что две величины равны.ˇ˘ˇ/˘ 5. Учителя пустыни Гоби Рабочие листы для печати Рабочие листы по географии Графики линейных уравнений Буквенные уравнения. Мы собираемся использовать все правила, которые мы изучили для решения уравнений, для решения буквальных уравнений. Решите для оставшихся неизвестных. Примеры решения уравнений на листе буквенных уравнений алгебры. Первое, что вы должны сделать, это выбрать, с какой переменной проще всего работать. 2 : Контрольные практические задачи (Документы: Проверка) Проверьте свое понимание урока.Найдите соответствующий ответ и впишите в пропуск слово или фразу, соответствующую номеру задачи. Практические задачи 1. Этот пакет уроков содержит 3 рабочих листа, которые учащиеся должны заполнить, чтобы попрактиковаться в переписывании уравнений путем решения для заданной переменной. Первые два листа содержат по 15 задач каждый. Если вы хотите получить самые высокие оценки на экзаменах, вы должны попрактиковаться в решении ряда задач Стр. 1/8 УРОК 3: ЛИЧНЫЕ УРАВНЕНИЯ Изучение: Буквенные уравнения Узнайте, как решать буквенные уравнения, включая формулы, для определенной переменной.Итак, ваша первая задача — открыть рабочий лист номер девять. Для получения дополнительной помощи по математике и reso Литеральные уравнения Практический лист Неизвестные переменные в уравнениях Все операции Диапазон от 1 до 9 Любая позиция Math Worksh Листы по алгебре Решение линейных уравнений Уравнения по алгебре. Разделить обе части Цель: Решить буквальное уравнение (уравнение с несколькими переменными) для одной из переменных. Алгебра 1 отвечает на Глава 2 — Решение уравнений — 2-5 Буквенные уравнения и формулы — Практика и упражнения по решению задач — Страница 114 49, включая пошаговую работу, написанную такими же членами сообщества, как и вы.Двухшаговые неравенства. Каково определение решения буквального уравнения? Это когда вам нужно решить формулу для определенной переменной. 3 : Викторина по решению буквенных уравнений и формул 5 3 xy for x 6. A-CED. Решите 456 6 8. 29 При решении задач с распределением или общими факторами вы НЕ хотите распределять термин снаружи. Буквенные уравнения Исследование Буквенные … варианты ответов F = (5/9)C + 32 F = (9/5)C - 32 F = (9/5)C + 32 F = (9/5) (C+32) Вопрос 3 180 секунд В. Сантехник берет фиксированную ставку в размере 40 долларов за работу плюс 10 долларов за каждый час h, который он работает на этой работе.Введите число, Выведите число, 11 Вычтите 2 Разделите на5 Алгебра Используйте это пространство для решения уравнения. Перестановка буквенных уравнений является важной областью решения уравнений путем выделения переменных. Не обращайте внимания на основания и просто приравняйте показатели степени $$ x + 1 = 9 $$ Шаг 2. 1 Квадратные уравнения и системы счисления . Например, 6 + 3 = 9. Сколько бутербродов вы можете купить, если купите 3 пиццы? 6 пицц? На этом уроке вы научитесь решать задачи, используя уравнения с несколькими переменными.Группа выпустила множество поп-хитов за почти пять лет своей деятельности. Если вы хотите получить самые высокие оценки на экзаменах, вы должны попрактиковаться в задачах на нескольких страницах. Уравнения Уравнения Математические игры Средняя школа Рабочие листы по математике для 3-го класса 12 7 словесных задач на граммы и килограммы Рабочие листы по математике для 3-го класса Word … by Hedvig on 18 декабря 2021 г. 18 декабря 2021 г. Шаблон Рабочие листы для печати Решение буквенных уравнений Connect 4 Занятие Одобрено учащимися Скачать бесплатно Буквенные уравнения Решение уравнений Решение линейных уравнений Решите каждую задачу.Решите + < = 14. Оценка в стиле соревновательной игры с опросами и другими типами вопросов Формула выражается как D = a(2 + kt). Решите буквенные уравнения. В этом уроке мы определим линейные уравнения и научимся их решать. Буквенные уравнения Имя_____ Дата_____ Период____ Решите каждое уравнение для указанной переменной. ) V-E+F=2 (нахождение E) 3. B. если вы думаете поэтому, я покажу вам еще раз несколько картинок ниже: Итак, если вы хотите получить эти … Решение буквенных уравнений Буквальное уравнение уравнение, содержащее более одной переменной.Среднее значение, медиана, мода и диапазон. Адаптация задач к учащемуся поможет учащемуся попрактиковаться в решении буквальных уравнений на градуированных уровнях. 5 августа 2021 г. Дополнительная практика с решением буквенных уравнений (A. doc Автор: mmudd1 Решение буквенных уравнений. Я думаю, что они оказались хорошими для первой попытки. Если вы хотите получить самые высокие оценки на экзаменах, вам нужно практиковаться в задачах. число Стр. 1/8 Решение буквенных уравнений с подсказками pdf Математика Мы просто решаем уравнение, как мы это делали в предыдущем разделе «Решение уравнений», уравновешивая обе стороны.как решать линейные уравнения. Перестановка формул, кажется, является областью, в которой многие учащиеся испытывают затруднения. 5 3 попрактиковаться в решении полиномиальных уравнений. Процент голов против среднего (А) для профессионального хоккейного вратаря определяется по формуле А = 60. Что такое Буквенные уравнения? Уравнение является важным аспектом основного принципа математики. Применяйте ранее изученные правила для решения буквенных уравнений. Алгебраические уравнения Домино игра Алгебра уравнения Математические выражения Математическая практика Рабочие листы.Ответы на лист буквальных уравнений. Алгебра 2 Рабочие листы Экспоненциальные и логарифмические функции Рабочие листы Алгебра 2 Рабочие листы Написание журналов Экспоненциальные функции. Найдите переменную $$ x = 9 - 1 \\ x = \fbox { 8 } $$ Check . В прямом смысле. граф гиперболы на ti-86. 19 августа 2021 г. о решении практических задач по логарифмическим уравнениям. Процентные проблемы. Формула для определения расстояния: D = r t D = rt D = r t. Рабочие листы подходят для предалгебры и алгебры 1 курса (6-9 классы). Для удобства отметим фокус параболы.Найдите букву в этом ответе. Обои Cosmic Worksheet 4 сентября 2021 г. Параллельные и перпендикулярные линии: их наклоны. Потренируйтесь решать уравнения с одной переменной, например 20 - 7x = 6x - 6, где переменная стоит по обе стороны от знака равенства. Какие из следующих уравнений являются буквальными? 5y = 4 x + 3 d = rt A = 2 r 5x + 6 = –19 2,9ˇ˘/. IXL предлагает сотни навыков по алгебре 1 для изучения и изучения! Учитель может варьировать требования к задачам с буквальным уравнением, включив четыре фиксированных варианта ответа для ученика.Решение формул для переменной. Формула для построения линии представляет собой форму пересечения наклона, где y= . • Решайте формулы с несколькими переменными или буквенные уравнения для определенной переменной. Решите для а. Идите к АЛЕКСУ. Они содержат две переменные, так что это буквальные уравнения. Вы заказываете пиццу и сэндвичи. Вы начинаете с некоторых основных операций, переходите к алгебраическим свойствам, уравнениям | Учиться. После того, как я раздам рабочий лист, я попрошу учащихся провести со своим партнером обсуждение приведенного примера." * Уравнения находятся в вашем классе Google. Рабочие листы с буквальными уравнениями идеально подходят для старшеклассников. 15 октября 2021 г. · Резюме урока. Сегодня мы завершили урок по решению буквенных уравнений. В этом листе решения буквенных уравнений старшеклассники решают 30 уравнений Наши распечатанные упражнения не только являются отличным ресурсом для изучения и практики перестановки буквенных уравнений, но и прекрасной возможностью пересмотреть и повторить «обратные операции» и «свойства равенства».21 декабря 2021 г. - Ищете дополнительную практику для решения буквенных уравнений или решения конкретной переменной в формуле? Этот рабочий лист может быть автономной или партнерской деятельностью. Решением уравнения является _____ для ключа рабочего листа буквальных уравнений. (Обычно представляют собой формулы, используемые в естественных науках и/или геометрии.) Практика перестановки уравнений Практика задач Serc Поскольку мы хотим решить для времени (t), нам нужно использовать уравнение, которое вы переставили во второй части вопроса 1: Потому что вы' Если у вас есть уравнение, которое позволяет вам найти t (без перестановки), вы можете просто подставить числа (v = 0.Авторы учебника: Холл, Прентис, ISBN-10: 0133500403, ISBN-13: 978-0-13350-040-0, Издатель: Prentice Hall Equations | Учиться. Напишите алгебраические уравнения или неравенства, которые представляют ситуацию. Эти рабочие листы подходят для программ предварительной алгебры, а также программ алгебры 1. a Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Департамент образования штата Вирджиния ©2018 1 o v a l Учебный план по математике – Алгебра I Буквенные уравнения и формулы Тема: Уравнения и неравенства Тема: Решение буквенных уравнений для заданной переменной Первичный SOL: A.Если V = 220 вольт и R = 4 Ом, каково значение I? Найдите здесь неограниченное количество печатных листов для решения линейных уравнений, доступных как в формате PDF, так и в формате html. Обязательно попробуйте и отметьте «вы пытаетесь» перед началом следующего видеоурока. (Обычно представляют формулы, используемые в естественных науках и/или геометрии) Практические задачи 1. Многошаговые уравнения. Решение текстовых задач с помощью линейных уравнений. 30 октября 2017 г. X 4z 28y z 73 z 4x. Поместите БУКВУ каждого значения в его положение в системе действительных чисел 1-5 Решите буквенные уравнения: Решите уравнения для указанного бесплатного расширенного калькулятора алгебры, Решение дробных уравнений, Практика математических задач TAKS в средней школе, 6-й класс математики Преобразование десятичных процентов в градусы , онлайн-калькулятор лимита.Нажмите на ссылку «Решение» для каждой проблемы, чтобы перейти на страницу, содержащую решение. Пропорции 5) 6) = 𝑡. Решение буквенных уравнений Connect 4 Упражнение Буквенные уравнения Словесная задача … РАБОЧАЯ ТАБЛИЦА ЛИТЕРАТУРНЫХ УРАВНЕНИЙ Решите для указанной в скобках переменной. Как насчет изображения? будет что будет замечательно???. алг_2. Проблемы с рабочими словами. Решение буквенных уравнений Соедините 4 Упражнение Буквенные уравнения Словесная задача … количество бутербродов, моделирует задачу в «Решить ее». Это важный навык — вы будете постоянно использовать его в математике и естественных науках (и в инженерии тоже).Мы рассмотрим, как решать линейные уравнения, содержащие буквенные коэффициенты, и попрактикуемся в решении нескольких задач. Свойства журналов Дополнительный практический рабочий лист. Обычно представляют собой формулы, используемые в естественных науках и/или геометрии для решения буквенных уравнений. 3 Буквенные уравнения Что такое буквальное уравнение? Буквенное уравнение — это уравнение, содержащее две или более переменных. В этом учебнике вы найдете содержание, разработанное с учетом всех математических тестов Американского дипломного проекта (ADP).Я поставил на них QR-коды, потому что пытался сохранить рассудок. Пример приводится и разрабатывается для учащихся.