Решение рациональных уравнений сложного вида в 9-м классе
Цели:
- Обобщить и углубить знания обучающихся по данной теме;
- Научить использовать различные методы решения: метод разложения на множители – группировки, метод замены переменной – подстановки для подведения рациональных уравнений сложного вида к более простому;
- Познакомить с различными видами рациональных уравнений: симметрических, частного случая возвратных уравнений и с методом их решения;
- Побуждать ребят к взаимоконтролю, самоконтролю и самоанализу при выполнении заданий;
- Оказывать взаимовыручку, поддержку со стороны одноклассников – ассистентов.
- Добиваться получения новых знаний через самостоятельное выполнение заданий с последующей взаимопроверкой.
Оборудование: доска раздвижная, листы – задания для устного счета, компьютер, экран.
Время: 90 минут – 2 урока.
Приложение 1
Ход урока
1. Проверка домашнего задания (5 минут).
На доске (на обратной стороне) заранее на перемене учащимися записаны решения. Ученики меняются тетрадями друг с другом по парте и после проверки ставят оценки “5” – нет ошибок; “4” – 1 -2 ошибки; “3” – 3-4 ошибки, а более – “ 2”.
2. Устный тест – повторение:
На парте лежат карточки с решениями и ответы к ним, выбрать правильный ответ и объяснить почему?
| задания / ответы | 1 | 2 | 3 | 4 |
| (х-3) (х+7)=0 | 3; 7 | 3; -7 | -3;7 | -3;-7 |
| х2– 6х + 5 = 0 | 5;1 | 2;3 | -5;-1 | -2; -3 |
| х2– 25 = 0 | 0;5 | 1;25 | -5;5 | Нет решения |
| х2 + 4х + 7 = 0 | 3,5; 2 | Нет решения | 2+; 2- | 1; 2,5 |
| 3(1-х)+2 = 5 – 3х | Нет решения | 3;1 | Множество корней | 0;5 |
Правильные ответы: 1 задание – 2; 2 зад. – 3; 3 зад. – 3; 4 зад. – 2; 5 зад. – 3.
Новая тема.
Учитель: Под рациональным уравнением принято понимать уравнение, которое может быть записано в виде: аnxn + an-1xn-1 + … a2x2+ a1x + a0 =0, где an, an-1, …a0 – заданные числа, а х – неизвестное. Простейшие рациональные уравнения мы решаем с помощью четырех основных методов.
(Метод перехода от равенства, связывающего функции, к равенству, связывающему аргументы; метод замены переменной; метод разложения на множители – группировки; функционально – графический метод).
Мы научились решать рациональные уравнения второй степени, а третьей, четвертой?
А каким методом вы решите уравнение вида a) х3 – 8 + х – 2 = 0?
Подсказка: желательно подвести к произведению многочленов.
Да, верно, используем метод разложения на множители – группировки. Группируем слагаемые, применим формулы сокращенного умножения и получим произведение нескольких множителей – многочленов в левой части уравнения, а в правой – нуль.
(Вызывается ученик сильный в математике, а если нет, то показывает учитель ход решения).
б) А при таком уравнении х3 – 3х + 2 = 0 можно использовать метод группировки?
Решение.
Перепишем уравнение, записав , получим , а теперь сгруппируем (х
Ответ: х1 = х3 = 1; х2 = -2.
Учитель: Вспомним, при решении биквадратных уравнений какой метод мы использовали? Самый распространенный из всех методов – да, метод замены переменной – метод подстановки. Искусство производить замену переменных заключается в том, чтобы увидеть, какая замена будет более рациональна и быстрее приведет к успеху. На сегодняшнем уроке мы это и рассмотрим.
Разберем решение данного уравнения:
Решение.
Освободимся от знаменателя, t2 + 4t + 3 = 0, где t ? 0.
Отсюда t1 = – 3; t2 = -1.
Дорешать самостоятельно, дальнейшее решение проецируется на экран.
По формуле решаем второе уравнение =
= = = = =
Ответ: х1 = -5, х2 = 1, х3 = , х4 = .
Учитель: Рассмотрим уравнение вида
г) (х2 + 10х )2 + (х2 + 5)2 = 157.
Метод замены переменной легко увидеть, если воспользоваться формулой квадрата суммы для второй скобки. (х2 + 10х )2 + (х2 +10х + 25) = 157; (Далее решает ученик у доски, а остальные – самостоятельно).
Решение.
Пусть тогда получим
х2 + 10х = 11 или х2 + 10х = -12. Решая эти уравнения, получим
Ответ: {-11; 1; -5 }. +
Учитель: Рассмотрим уравнение вида
Решение.
Найдем равенство сумм пар чисел -7 + 2 = -1 – 4,
Перемножим между собой первую и третью, вторую и четвертую скобки, получим (х2 – 5х – 14) ((х2 – 5х + 4) – 40.
Введем замену: х2 – 5х – 14 = t, где t – любое число, получим t(t + 18) = 40, t2 + 18t – 40 = 0.
(Работает учитель, показывая ход решения или ученик с помощью учителя).
Решим данное уравнение по т. Виета
где t1 = – 20, t2 = 2.
Решим систему уравнений
Ответ: х1 = 2, х2 = 3, х3 = х4 =
Решить самостоятельно
Проверка решения данного уравнения с помощью проекции решения на экране.
Решение.
+1 + 4 = + 2+ 3. Данное условие равенства выполняется, поэтому раскроем скобки, группируя первый множитель с последним и второй с третьим.
Тогда данное уравнение примет вид: (х2 + 5х + 4) (х2 + 5х +6) = 24.
Полагая х2 + 5х = t, получим квадратное уравнение (t +4)(t +6) = 24,
решая его t2+ 10t =0, t(t + 10) =0, найдем корни t1 =0, t2= -10.
Затем решаем уравнения
Учитель: Уравнения вида а0хn + a1xn-1 + … + akxk + … + a1x + a0 = 0, где коэффициенты членов, равно от стоящих от концов, равны между собой, называют симметрическими уравнениями.
Симметрические уравнения обладают следующими свойствами:
1. Симметрическое уравнение нечетной степени имеет корень х = -1, в чем можно убедиться непосредственной подстановкой;
2. Уравнение четной степени 2n решаются с помощью подстановки
V = x + сводится к уравнению степени n.
Решим уравнение.
Решение.
Данное уравнение симметрическое, так как коэффициенты равно отстоящих от концов, равны между собой. Степень уравнения нечетная равная 5, поэтому корень данного уравнения х = – 1.
Пусть Разделим левую часть уравнения на х + 1 и получим симметрическое уравнение четвертой степени:
Разделим обе части уравнения на х2: 2х2 + 3х – 16 + 3• + 2• 1/х2 = 0, и сгруппируем члены уравнения: 2(х2 + 1/х2) + 3 (1 + ) – 16 = 0.
Используем метод замены переменной при t = x + , возведем в квадрат обе части уравнения, получим t2 = (x + )2 = x2 + 2• x • + 1/x2, тогда x2 + 1/x2 = t2 – 2, и после преобразований получим квадратное уравнение 2 t2 + 3t – 20 = 0. Находим корни t = = = t 1 = , t2 = -4. Таким образом , исходное уравнение четвертой степени равносильно совокупности уравнений x + и x + = -4.
Решив данные уравнения, получим еще четыре корня исходного уравнения.
Ответ: х1 = -1, х2 = -2+, х3 = -2 – , х4 = 2, х5 = .
Учитель: Прошу вас, ребята, решить самостоятельно с последующей проверкой симметрическое уравнение четвертой степени. А почему оно симметрическое?
з) 2х4 + 3х3 – 16 х2 + 3х + 2 = 0.
Решение.
Разделим обе части уравнения на х2, получим 2х2 + 3х – 16 + + 2/х2 =0.
Сгруппируем (2х2+ 2/х2) + (3х+ ) – 16 = 0, 2(х2+12/х2) + 3(х+ ) – 16 =0.
Введем метод замены переменной, обозначим х+ = t,
возведем в квадрат обе части равенства, получим t
Ответ: х1 = , х2 = -2+, х3 = -2 – , х4 = 2.
Учитель: Мы рассмотрели симметрические уравнения, являющиеся частным случаем возвратных уравнений. Следовательно, и ход их решения будет похожим, но более подробно мы познакомимся с возвратными уравнениями и рассмотрим более подробно ход решения на следующем занятии. А сейчас,
я вам предложу домашнее задание на два варианта для самостоятельного решения. Дополнительно даны ответы ко всем уравнениям. Не сможете справиться, рассмотрим на уроке. а кто-то хочет больше решить, с довольствием приветствую вас.
Домашнее задание:
Вариант 1. Вариант 2. а) (х2 – 6х)2 -2(х – 3)2 = 81;
б) х3 + х + 2 = 0;
в) 6х4 – 35 х3 + 62 х2 – 35х + 6 = 0;
г) (х –1)(х+2)(х-3)(х+4) = 144;
д) (х2 + х + 1)(х2 + х + 2) = 12;а) (х2 – 8х)2 + 3(х – 4)2 = 76;
б) х3 + 3х2 + 2х = 0.
в) 5х4 – 12х3 + 14х2 – 12х + 5 = 0.
г) (х-1)(х-2)(х-3)(х-4) = 15.
д) (3х +2)4 – 13(3х + 2)2 + 36 = 0.
Выберите ответы, выполняя домашнее задание.
| А | В. 1. | С { -2; -1; 0}. | Д { -2; 1}. | Б{0; 1}. |
Учитель: Подведем итог нашей темы. Уравнения третьей и четвертой степени решались в общем случае методом замены переменной, в который заключается в том, что для решения уравнения вида f(x) =0 вводят переменную t = g(x) и выражают f(x)через t, получая новое уравнение w(t) = 0. Решая затем уравнение w(t)= 0, находят его корни {t1, t2, … tn}. После чего получают совокупность n – уравнений g(x) = t1, g(x) = t2, … g(x) = tn, из которых находят корни исходного уравнения.
Урок-зачет в 9-м классе «Целые уравнения»
Цели урока:
1) Воспитывать трудолюбие, терпение, прилежание, внимательность, настойчивость в преодолении трудностей;
2) Учиться принимать и оказывать помощь и поддержку товарищей;
3) Отработать навык решения целых уравнений, начиная с линейного вида и заканчивая уравнениями олимпиадного текста;
4) Учиться уважать труд младших и старших учеников твоего учителя
При подготовке к уроку проведена следующая работа:
- Подобран материал четырех вариантов заданий, аналогичных экзаменационным разного уровня сложности: линейных уравнений, квадратных, биквадратных, уравнений с заменой переменных, уравнений с применением в решении теоремы Безу и следствий из нее.
- Приглашены гости: родители и учителя математики.
- Выполнена презентация наиболее сложных типов целых уравнений.
- Ученикам 10а класса получены ответы к вариантам, приготовлены индивидуальные карточки с заданиями для всех 27 учеников 9а класса. Для проверки работ ответы вариантов внесены в таблицу, за каждый вариант отвечает один старшеклассник, он вводит сводную ведомость оценки (нормы оценок обговорены с учителем заранее). Еще потребуются два старшеклассника для сбора заданий у ребят.
- Учениками 7в и 7г классов приготовлена веселая песня на мотив песни «Коммунальная квартира». (Приложение 1)
- Перед исполнением песни ученик 7г класса читает стихотворение «Баллада о математике».
Этот небольшой концерт для девятиклассников прозвучит после сдачи зачета; во время подведения общих итоговых оценок урока.
Презентация.
Приложение 2.
Начало урока.
На экране высвечивается тема урока и его цели. Проводится устная разминка всех учеников по заготовленному тексту на доске. В это же время трое учеников решают квадратные уравнения.
1.
2х2-9х-35=0
Д = 361
х1 = -2,5; х2 = 7
Ответ: -2,5; 7
2.
х2+2х-8=0
Д 1 = 9
х1 = -4; х2 = 2
Ответ: -4; 2
Подобрать корни по формулам Виета:
а) х2+7х+10=0
б) х2-5х-6=0
в) х2-10х+21=0
г) х2+5х+10=0
Решения ученики проводят (1) и (2) подробно, применяя формулы Д, Д1 и формулу корней. Третий ученик напоминает формулы Виета, особо отмечая что Д > 0, иначе нет корней (г).
Вместе с учителем (за время подготовки) решения тремя учениками на доске) другие ребята устно проверяют себя в решении таких уравнений:
а) 3х = 2
б) -7х+5=0
в) 2(х-8)-5х = 11
г)
д) х2-9=0
е) 5х-7х2=0
После проверки решения с доски ребята в рабочих тетрадях отмечают тему урока и записывают решения целых уравнений с помощью теорем Безу и следствий из нее.
а) 2х3+3х2-23х-12 = 0
Решение у доски ведет сильный ученик.
б) -3х3+10х2+27х-10 = 0
3х3-10х2-27х+10 = 0
Решение у доски ведет сильный ученик.
При решении применялись теоремы:
Остаток при делении многочлена на двучлен (х-а) равен значению делимого многочлена при х = а.
Многочлен делится на двучлен (х-а) тогда, и только тогда, если а является корнем данного многочлена.
Если а — корень многочлена f(х), то f(а) = 0, следовательно f(х) = (х-а) * q(х), где q(х) - многочлен, степень которого на 1 меньше степени многочлена f(х).
Навыки решения целых уравнений с применением теоремы Безу и ее следствий ребята приобрели на занятиях элективного курса «Избранные вопросы математики».
Поскольку самым сложным для учеников является деление многочленов, пробуем еще раз делить многочлен на многочлен.
в) х4 + 2х3-2х2-5х-2 = 0
По следствию из теоремы Безу если f(х) = х4 + 2х3-2х2-5х-2 (коэффициент при «старшем» одночлене равен 1), тогда все рациональные корни многочлена являются целыми числами и являются делителями свободного члена, т.е. числа -2.
F(-2) = 0=> -2 — корень; f(-1) = 0=> -1 — корень.
Тогда f(х) делится на (х+2)(х+1) = х2+3х+2
Записи в тетрадях на этом заканчиваются.
Далее идет презентация решения целых уравнений.
1-й ученик. Применение теорем о корне многочлена и о целых корнях целого уравнения.
x3 — 8х2+13х-2=0
Целые корни уравнения являются делителями числа -2.
3-й ученик. Введение новой переменной.
(х2 — 2х — 5)2 — 2 * (х2 — 2х — 5) — 3 = 0
Пусть х2 — 2х — 5 = а, тогда
а2 — 2а — 3 = 0
а = 3 или а = -1 (по формулам Виета)
х2 — 2х — 5 = 3 или х2 — 2х — 5 = -1
х2 — 2х — 8 = 0 или х2 — 2х — 4 = 0
х = 4 или х = -2 Д = 5
(по формулам Виета) х = 1
Ответ: 4;-2; 1
2) (2х2 + 7х — 8) * (2х2 + 7х — 3) — 6 = 0
Пусть 2х2 + 7х = t, тогда
(t — 8) * ( t — 3) — 6 = 0
t2 — 11t + 18 = 0(по формулам Виета)
t = 9 или t = 2
2х2 + 7х = 9 или 2х2 + 7х = 2
2х2 + 7х — 9 = 0 2х2 + 7х — 2 = 0
Д=121 Д=65
х = -4,5 или х = 1 х=
Ответ: -4,5; 1;
4-й ученик. Применение разложения на множители.
1) 5х3 — 19х2 — 38х + 40 = 0
(5х3 + 40) — (19х2 + 38х) = 0
5 · (х3 + 8) — 19х * (х + 2) = 0
5· (х + 2) * (х2 — 2х +4) — 19х * (х + 2) = 0
(х + 2) * (5 * (х2 — 2х +4) — 19х) = 0
(х + 2) * (5х2 — 10х + 20 — 19х) = 0
(х + 2) * (5х2 — 29х + 20) = 0
х + 2 = 0 или 5х2 — 29х + 20 = 0
х = -2 Д = 841 — 4 * 5 * 20 = 441
х = 5 или = 0,8
Ответ: -2; 5; 0,8
2) 9х3 — 18х2 — х + 2 = 0
9х2 * (х — 2) — (х — 2) = 0
(х — 2) (9х2 — 1) = 0
(х — 2) (3х-1) (3х+1) =0
х1 = 2 х2 = х3 =
Ответ: 2;
Во время презентации подключались к работе ученики к обсуждению по вопросам: типичные ошибки при введении новой переменной, метод группировки и формулы сокращенного умножения при разложении на множители, подбор корней по формулам Виета.
5. На втором уроке ученики включены в работу по решению целых уравнений. Каждое уравнение уже записано на отдельном листе, на этом же листе ученик выполняет решение. Как только решение одно из заданий — поднимает руку, «курьер» - десятиклассник забирает решение на проверку в комиссию десятиклассников. Оценка оглашается и заносится в ведомость. За консультацией можно обратиться к учителю, если решение зашло в тупик, оценка при этом снижается (на полях делается замечание).
Работа рассчитана на 30минут. Приложение 2
Дополнительно на доске:
I вариант
х4-6х3-2х2-30х+25=0
Ответ: -5;1;-1;
II вариант
х4+3х3+х2-3х-2=0
Ответ: 1; -1; -2
6. Ученики 10 класса проверяли по ходу решения варианты заданий. Если часть работы не выполнена, то оценка за отсутствующие задания 0. Итоговая оценка идет как среднее арифметическое, заносится в ведомость, если есть возможность, высвечивается на экране в конце урока.
Пока подводятся итоги, ученики 7 классов выступают с концертом 5-6 минут. При наличии времени слово можно дать родителям, либо детям.
Урок заканчивается озвучиванием итоговых оценок.
Решение задач по темам «Уравнение окружности» и «Уравнение прямой». Более сложные случаи
Тема урока: «Решение задач по темам «Уравнение окружности» и «Уравнение прямой». Более сложные случаи». Здесь мы будем решать задачи на уравнение прямой и уравнение окружности, но рассмотрим более сложные задачи.
Напомним основные опорные факты по теме урока.
1. Уравнение окружности: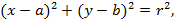 Q(a; b) – центр, r – радиус.
Q(a; b) – центр, r – радиус.
2.  уравнение прямой.
уравнение прямой.
3. Длина отрезка 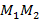 (рис. 1):
(рис. 1):
Рис. 1. Длина отрезка
Задача 1.
Даны две точки А и В. Найдите множество всех точек, для каждой из которых расстояние от точки А в 2 раза больше расстояния от точки В, если длина АВ=3.
Это задача на нахождение геометрического места точек (ГМТ).
Решение:
Введем прямоугольную систему координат так, чтобы точка А была началом координат, а точка В лежала на оси Ох, и определим координаты данных нам точек (рис. 2):

Рис. 2. Иллюстрация к задаче

а) Сначала рассмотрим частную задачу. Пусть искомые точки лежат на прямой АВ, тогда (рис. 3):

Рис. 3. Иллюстрация к задаче

Точка  делит отрезок АВ в заданном отношении внутренним образом.
делит отрезок АВ в заданном отношении внутренним образом.

Точка  делит отрезок АВ в заданном отношении внешним образом.
делит отрезок АВ в заданном отношении внешним образом.
Частная задача решена.
б) Рассмотрим общий случай, когда точка М – любая точка координатной плоскости, пусть ее координаты M(x;y) (рис. 4).

Рис. 4. Иллюстрация к задаче
По условию:



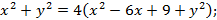


Выделяем полный квадрат:
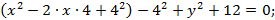

Мы получили уравнение окружности, значит искомое ГМТ – окружность с центром в точке C(4; 0) радиуса 2 (рис. 5):
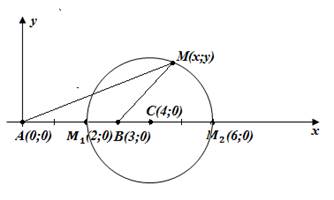
Рис. 5. Иллюстрация к задаче
Ответ: 
Задача 2.
Даны две точки А и В. Найдите множество всех точек M, для каждой из которых  , если АВ=4.
, если АВ=4.
Решение:
Вводим удобную систему координат и определяем координаты нужных нам точек (рис. 6):
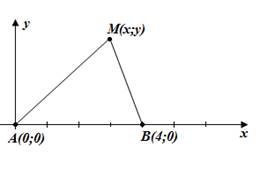
Рис. 6. Иллюстрация к задаче

Нужные нам расстояния 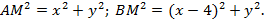
По условию  , тогда
, тогда
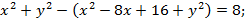
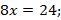
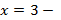 вертикальная прямая (рис. 7).
вертикальная прямая (рис. 7).
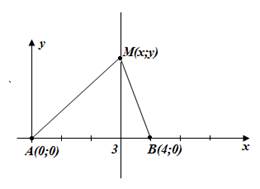
Рис. 7. Иллюстрация к задаче
Ответ: 
Задача 3.
Как известно, через три точки, не лежащие на одной прямой, проходит окружность и при том только одна.
Напишите уравнение окружности, проходящей через три данные точки: 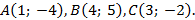
Решение:
Запишем уравнение окружности:
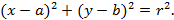
Окружность проходит через три точки, поэтому координаты каждой из них удовлетворяют уравнению окружности. Подставим координаты данных точек в уравнение окружности и получим систему:

Вычтем из уравнения (1) уравнение (2), а затем из уравнения (1) уравнение (3). Получим систему:
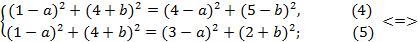


Найдем  из уравнения (1) исходной системы:
из уравнения (1) исходной системы:


Ответ:

Рассмотрим шуточную задачу.
Задача 4.
Вокруг земного шара по экватору натянули веревку длиной l. Если длину этой веревки увеличить на 1 м, то пролезет ли под ней мышь?
Дано: l;  м.
м.
Найти: АВ (рис. 8).

Рис. 8. Иллюстрация к задаче
Решение:


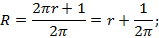


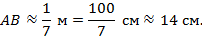
Ответ: да, мышь пролезет.
Итак, мы рассмотрели решение более сложных задач на уравнение окружности и уравнение прямой. С этими уравнениями далее мы будем встречаться неоднократно.
Список литературы
- Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
- Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- E-science.ru (Источник).
- E-science.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010., №№ 982, 985, 1002(б).
Урок математики по теме «Решение целых уравнений». 9-й класс
Цели урока:
Образовательные: учащиеся должны знать понятия целого уравнения, степени уравнения, способы разложения на множители, уметь решать уравнения способом разложения на множители.
Развивающие: развитие логического мышления, умения обобщать, делать выводы; развитие внимания, памяти, овладение основными общенаучными методами познания (анализ, синтез)
Воспитательные: формирование научного мировоззрения, интереса к математике, к истории математики, воспитание эстетического вкуса, самостоятельности, активности, развитие культуры речи.
Ход урока
I. Организационное начало. Приветствие. Посадка.
– Открыть тетради. Записать число, “Классная работа”, Тема: Решение целых уравнений.
На доске:
ДАТА:………………………
Решение целых уравнений. “ВЕЛИКОЕ ИСКУССТВО”
Д. Кардано.
Упражнения для устных заданий Ключ для отгадки слов
| 0 | -1 | 1 | -2 | 2 |
| Й | А | Н | Ф | Я |
| -3 | 3 | -4 | 4 | -5 |
| О | Т | Х | М | И |
| 5 | -6 | 6 | 7 | 8 |
| Л | Д | Р | Е | З |
II. Проверка знаний, усвоенных на прошлом уроке (фронтальная работа с использованием упражнений на доске).
Задание:
- Выписать в тетрадь номера тех уравнений, которые являются целыми (спросить 4-5 человек выборочно)
- Дать определение целого уравнения.
- Определить степень целых уравнений (учитель указкой показывает уравнение, учащиеся одновременно показывают на пальцах степень этого уравнения)
- Что называется степенью уравнения? (учащиеся дают определение)
III. Решение квадратных и линейных уравнений
(повторение способов их решений – задание по рядам)С помощью таблицы (ключа к разгадке), которая написана на доске, прочитать слова.
| Решить уравнения: | (должно получиться) |
| 1) (х+3)(x+2)=0 2) 12x+4=8x-20 3) x2-1=0 4) x2-4x+3=0 5) x(2+x)=x2-10 6) (x+2)(x+6)=0 Корни выписать в порядке возрастания каждое число один раз. |
-6 -5 -3 -2 -1 1 3 Д И О Ф А Н Т |
| Решить уравнения: | (должно получиться) |
| 1) (2x-8)(x+1)x=0 2) x2-3x-4=0 3) x(-x-1)+5=3(x-1)-2x 4) x/2+2/3=1+x/3 5) x(5-x)=-x2+4x+4 Корни выписать в порядке возрастания каждое число один раз. |
-4 -1 0 2 4 Х А Й Я М |
| Решить уравнения: | (должно получиться) |
| 1) ( x+1)(x-5)=0 2) x2+7x+12=0 3) 7(x-1)+7=6x+6 4) (2x-14)(х-8)=0 5) (3х-12)(x2+5)=0 6) x2+10х+25=0 Корни выписать в порядке их нахождения |
-1 5 -4 -3 6 7 8 4 -5 А Л Х О Р Е З М И |
- ДИОФАНТ
- АЛ-ХОРЕЗМИ
- ХАЙЯМ
IV. Изучение нового материала и первичное закрепление
.Три ученика делают сообщения об этих математиках.
1-ый ученик:
ДИОФАНТ.
Диофант жил в третьем веке нашей эры. Он написал
труд “Арифметика”. Уцелели только шесть книг
оригинала. Общее их число неизвестно. У Диофанта
впервые встречается систематическое
использование алгебраических символов.
Еще древние египтяне для удобства рассуждений
придумали специальное слово, обозначавшее
неизвестное, но не было никаких знаков: минус,
плюс, равенство. Диофант первый сделал шаг в этом
направлении, Во времена Диофанта языком науки
был греческий. Но греки еще не знали цифр. И они
первые девять цифр обозначили буквами
греческого алфавита с черточкой наверху,
следующие десять букв – десятки 10,20,…90.
Последняя буква в алфавите не имела числового
значения – это сигма концевая. Ею стали
обозначать неизвестное число, т.е. по-нашему “х”.
Придумал Диофант и два основных приема решения
уравнений – перенос неизвестных в одну сторону и
приведение подобных слагаемых.
Учитель:
Рассмотрим две задачи Диофанта. (1-ая была высечена на надгробии, 2-ая из его книги “Арифметика”)
Задача № 1
Путник! Здесь прах погребен Диофанта,
И числа поведать могут, о чудо, сколь долг был век его жизни.
Часть шестую его представляло счастливое детство.
Двенадцатая часть протекла еще жизни —
Пухом покрылся тогда подбородок.
Седьмую в бездетном браке провел Диофант.
Прошло пятилетье.
Он был осчастливлен рождением прекрасного первенца сына,
Коему рок половину лишь жизни счастливой и светлой
Дал на земле по сравненью с отцом.
И в печали глубокой старец земного удела конец воспринял,
Переживши года четыре с тех пор, как сына лишился.
Скажи, скольких лет жизни достигнув,
Смерть воспринял Диофант?
Задача №2
Найдите три числа так, чтобы наибольшее превосходило среднее на одну треть наименьшего, среднее было больше наименьшего на одну треть наибольшего, наименьшее на 10 больше одной трети среднего.
2-ой ученик:
АЛ-ХОРЕЗМИ
На Ближнем Востоке в 7-8 веках новой эры халифы
покровительствовали астрономии и математике.
Ал-Мамун соорудил в Багдаде “Дом мудрости” с
библиотекой и обсерваторией. В это время и
написал свой труд математик Мухаммед ибн Муса ал
– Хорезми, в котором рассматривал решения
уравнений: “Китаб аль-джебр валь мукабала”. На
русском языке перевод звучит как “Книга о
восстановлении и противоположение”. Слово
“аль-джебр” переводчик не стал переводить и
написал латинскими буквами “algebr”. С тех пор
алгебра – это наука об уравнениях.
5х-9=12-2х
аль-джебр: 5х+2х=12+9
Любопытен факт, что в средние века алгебраистами
называли не математиков, а хирургов-костоправов,
которые умели делать “аль-джебр”, т.е.
восстановление при вывихах и переломах. Об одном
таком алгебраисте писал Сервантес в своем романе
о Дон-Кихоте. Современные переводчики слово
алгебраист переводят как хирург, а в старых
изданиях так и было записано – алгебраист.
3-ий ученик:
ОМАР ХАЙЯМ.
Омар Хайям жил с 1048 г. по 1123 г. в Северной Персии.
Это был универсальный гений. Большинству людей
он известен как поэт, автор блестящих по
остроумию и изяществу коротких в 4 строки
стихотворений “рубаи”. Вот одно из них:
Чтоб мудро жизнь прожить, знать надобно немало
Два важных правила запомни для начала:
Ты лучше голодай, чем, что попало есть,
И лучше будь один, чем вместе с кем попало.
Он был астрономом, философом, математиком. Но не
везло ему с признанием. Обсерватория была
закрыта еще при его жизни. Точный, созданный им
календарь заменен на старый, традиционный.
В математическом “Трактате о доказательствах
алгебры” он рассмотрел все возможные виды
уравнений III степени и их геометрические решения.
Лишь спустя 4 века итальянскими учеными Никколо Тарталья и Джероламо Кардано был открыт алгебраический способ решения уравнений III степени. Никколо Тарталья был учителем в г. Верона. Джероламо Кардано – выдающимся врачом, математиком и механиком. Формулы корней очень сложны, а для уравнений V степени и выше формул для корней нет. Норвежец Нильс Хенрик Абель доказал, что с помощью арифметических действий и извлечения корня нельзя получить корни даже такого сравнительно простого уравнения как х5+х-1=0. К сожалению, Абель умер от туберкулеза совсем молодым. Ему было всего 26 лет. Но студенты всех университетов мира изучают теоремы Абеля, формулы Абеля. Трагична судьба другого математика – Эвариста Галуа. Он погиб на дуэли в 21 год. Но его исследования в теории уравнений служат основой всей современной алгебры.
Многие уравнения решаются специальными методами. Основные из них это:
| РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ | ВВЕДЕНИЕ НОВОЙ ПЕРЕМЕННОЙ |
Решить разложением на множители:
(на доске)
1.х2-5х=0
2.81х2-25=0
3.х3-2х2=0
4.х3+4х=0
5.х3-3х2-4х=0
6.х(х-1)-8(х-1)=0
7.х4+х3-5х2-5х=0
8.(х2+2х)2-(х+1)2=0
9.х3+2х2-3=0
10.(х2-х)2-(3х+8)2=0
Второй способ – введение новой переменной – рассмотрим на следующем уроке.
V. Подведение итогов
.Сегодня мы узнали многое об истории развития алгебры, о способах решения уравнений, повторили способы разложения многочлена на множители. Умение решать уравнения считалось искусством. Ф. Виет не употреблял слово “алгебра”. Он говорил – “аналитическое искусство”. И книга Джероламо Кардано о способах решения уравнений называется “Великое искусство”.
И сегодня на уроке мы прикоснулись к этому “великому искусству”.
(Учитель предлагает учащимся список литературы по истории математики.)
Список литературы по истории математики:
- Выгодский М.Я. Арифметика и алгебра в древнем мире. – М: Наука. 1967.
- Гнеденко Б.В. Очерки по истории математики в России. М.: Гостехиздат. 1946.
- Дальма А. Эварист Галуа, революционер и математик. М. Наука. 1984.
- Еленьский Щ. По следам Пифагора. М.: Детгиз. 1961.
- Инфельд Л. Эварист Галуа.– М.: “Молодая гвардия”. 1960.
- Никифоровский В.А. Из истории алгебры 16-17 веков. М.: Наука. 1979.
- Оре О. Замечательный математик Нильс Хенрик Абель. М., Физматгиз, 1961.
- Пичурин Л.Ф. За страницами учебника алгебры. М.: Просвещение. 1990.
- Стройк Д.Я. Краткий очерк истории математики. М.: Наука. 1984.
- Честяков В.Д. Знаменитые задачи древности. М.: Учпедгиз.1963.
Урок для 9 класса обобщающий по теме «Уравнения»
Технологическая карта урока
Предмет Математика
Класс: 9 клас
Тема урока: обобщающий урок по теме «Уравнения» в рамках подготовки к ОГЭ по математике
Тип урока: обобщение и систематизации знаний
Цель урока:
Обобщить и систематизировать знания по теме «Решение различных видов уравнений»
Отработать применение способов решения уравнений
Повторить теоретический материал по теме
Развитие логического мышления, памяти, внимания, умения сравнивать и обобщать
Вид урока: урок- консультация
Планируемые результаты: знать определение понятия уравнения, корня уравнения, что такое решить уравнение. Знать и уметь различать различные типы уравнений, решать уравнения различных типов по алгоритму.
УУД :
Личностные: действие смыслообразования, личностное самоопределение
Регулятивные: целеполагание как постановка учебной задачи, планирование, коррекция
Познавательные: умение структурировать знания, контроль и оценка процесса и результата деятельности, анализ, синтез
Коммуникативные: речевая деятельность, обмен знаниями между одноклассниками
Основные понятия: уравнения, алгоритм, типы уравнений, правила решения уравнений
Оборудование: проектор, презентация, дидактический материал (таблица и самостоятельная работа) в приложениях 1,2,3, конспект урока в приложении 4
Формы работы: групповая работа, работа в парах, индивидуальная работа, работа в тетрадях
Задачи этапа
Деятельность учителя
Деятельность ученика
УУД
личностные
регулятивные
познавательные
коммуникативные
1.
Организационный. Формулирование темы урока и целеполагание
Создать благоприятный психологический настрой на работу. Сформулировать тему и цели урока
Эпиграф к уроку «Математику нельзя изучать наблюдая, как это делает сосед» Л.Нивен
Приветствие.
Проверка готовности к уроку. Четко сформулировать цели урока, исходя из высказывания Эйнштейна о себе «Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Включаются в деловой ритм урока. Исходя из высказывания формулируют тему, цели урока.
формирование учебной мотивации
целеполагание.
положительная мотивация к изучению предметного материала
планирование сотрудничества с учителем и сверстниками
2.
Актуализация знаний
Актуализация опорных знаний.
Фронтальный опрос.
Ведет беседу об уравнении, корнях, степени уравнения, что такое решение уравнения. Алгоритмы решения различных видов уравнений. Предлагает заполнить обобщающую таблицу каждому ученику. Далее предлагает распределить уравнения по рассмотренным видам.
Называют определение уравнения, корня уравнения, как решаются уравнения, какие виды уравнений изучили с 5 по 9 класс. Применяют теоретический материал на практике. Заполняют предложенную таблицу по распределению уравнений из списка по видам (Приложение 1 и 2 ). Далее внизу таблицы есть десять примеров уравнений, которые необходимо распределить по видам без их решения
самооопределение
умение выполнять учебное действие в соответствии с целью
Анализируя и сравнивая предлагаемые задания, извлекают необходимую информацию
Выражают свои мысли с достаточной полнотой и точностью, используют чужие высказывания для обоснования своего суждения
4.
Закрепление полученных знаний на практике.
Обеспечение осмысления изученного материала. Заполнение таблицы алгоритмов решения различных видов уравнений
Выявление недостатков в знаниях.
Предлагает решить уравнения в общем виде по алгоритму для повторения изученного ранее материала и обобщения всех знаний по данной теме.
Организует проверку работы.
Решают уравнения. В общем виде в таблице. (составляют опорный универсальный конспект)
Ученики работают у доски.
Проверяют свою работу и работу ученика у доски.
смыслообразование
оценка своего вклада в работу
выбор наиболее эффективных способов решения уравнения
выражение своих мыслей,
аргументация своего мнения
5.
Самостоятельная работа по закреплению изученного
Выявление качества и уровня овладения знаний и способов действий, обеспечение их коррекции
Предлагает решить задание самостоятельной работы, состоящей из 4 модулей. В первом модуле надо решить три уравнения по выбору, во втором тоже три, в третьем и четвертом модуле по одному уравнению.
Решение самостоятельной работы по предложенному учителем плану ( Приложение 3).
Далее идет обмен листочками с самостоятельной работой и взаимопроверка по ответам на слайде и оценивание одноклассников. Потом учащиеся оценивают себя сами и сдают работу учителю.
смыслообразование
Проявляет познавательную инициативу. Контролируют свои действия
Учатся применять полученные знания в процессе индивидуальной работы
Осознают применяемый алгоритм с достаточной полнотой
6.
Домашнее задание.
Обеспечение понимания заданий из учебника.
Решить 10 уравнений, которые распределили по видам
Обсуждение трудных этапов выполнения задания.
смыслообразование
целеполагание, контроль, оценка, коррекция
смысловое чтение
умение слушать и понимать других
7.
Подведение итогов урока.
Рефлексия.
Мотивация собственной деятельности.
Подведение итогов урока. Самооценка в соответствии с целями урока. Организую обсуждение: Каковы были цели урока? Выполнили ли поставленные цели? Что вызвало трудность? Что запомнилось? На листочки с самостоятельной работой наклеивается один из стикеров:
Красный- ничего не понятно,
Желтый- надо еще поработать,
Зеленый- мне все понятно, я теперь могу решить любое уравнение.
Делают выводы по уроку, достигли поставленные цели или нет. Оценивают умения при помощи разноцветных стикеров.
личностное самоопределение
Проводят самооценку
Проводят рефлексию способов и условий своих действий
Планируют сотрудничество, используют критерии для обоснования своих суждений
Приложение 1
Фамилия Имя, класс: __________________________________________________
А)Б)
В)
2
Квадратное уравнение
А)
Б)
В)
Г)
3
Дробно- рациональное уравнение
А)
Б)
4
Биквадратное уравнение
3х+5=-4х-8
х2+6х=0
0,3х+2,5=2,6
2х2 -8=0
х4+2х2-8=0
4х2=0
3х2+2х-5=0
 +
+ =
=
 —
— =5
=5 =
= 
Приложение 2
 + b=c
+ b=cах+в=сх+d

ах+в=с

 +c=d
+c=dax4+bx2+c=0


 +
+  = c
= c
Приложение 3
Самостоятельная работа
Фамилия Имя : ____________________________________________________
x+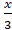 =
= 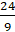
6+5x=2x+9
7+3(2x+1)=4
-6x-4(9-7x)=-5x+45
Квадратные уравнения
3x2-27=0
3x2-8x+5=0
x2-8x=0
2x2+8x+32=0
Дробно- рациональные уравнения
 =
= 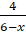
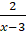 = -x
= -x
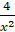 +
+ 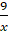 = -5
= -5
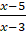 +
+ 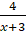 +
+ 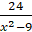 =0
=0
Биквадратные уравнения
2x4-19x2+9=0
x4-7x2+12=0
3x4-13x2+4=0
6(x-1)4+(x-1)2-1=0
Приложение 4
Сценарий урока
На доске эпиграф к уроку: «Математике нельзя изучать наблюдая, как это делает сосед» Л.Нивен
Организационный момент (2 минуты). Здороваюсь с детьми, домашнее задание собираю.
Формулирование темы урока (5 минут)
Послушайте высказывание Альберта Эйнштейна про себя и попробуйте определить тему урока «Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». ( формулируем тему урока, пишем в тетради). Обобщение и систематизация знаний по теме «Уравнения»
Целеполагание: (2 минуты). Какие цели можно поставить к нашему уроку, исходя из темы?
(обобщить и систематизировать знания по теме «Решение различных видов уравнений»
отработать применение способов решения уравнений
повторить теоретический материал по теме)
Актуализация знаний ( фронтальный опрос) (15 минут)
Что такое уравнение
Что значит решить уравнение
Что такое корень уравнения
Повторим виды уравнений и алгоритмы их решения. У вас на столах лежат таблицы, давайте вспомним все основные виды уравнений и как их решать. С уравнениями мы дружим с начальной школы, они постоянно на протяжении всего курса изучения математики все более усложнялись. Скоро нам сдавать огэ и при решении варианта тоже используются уравнения, это задания 6 и 21. Давайте вместе заполним таблицу.
Фамилия Имя, класс: __________________________________________________
ax=c-b
x=(c-b)/a
Ответ:
Б) ах+в=сх+d
ax-cx=d-b
x(a-c)=d-b
x=(d-b)/(a-c)
В) 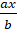 +c=d (умножим все части уравнения на b)
+c=d (умножим все части уравнения на b)
ax+cb=db
ax=db-cb
x=(db-cb)/a
2
Квадратное уравнение
А)полное квадратное уравнение
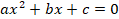
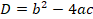
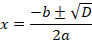
Б)неполное первого типа
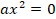
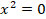
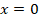
В)неполное второго типа
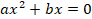
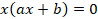
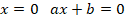
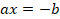

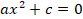
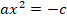
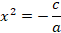
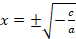 ,
,
при с<0
3
Дробно-рациональное уравнение
А)приводимое к линейному
 + b=c (находим ОДЗ, умножаем все части на общий знаменатель, решаем полученное уравнение)
+ b=c (находим ОДЗ, умножаем все части на общий знаменатель, решаем полученное уравнение)
x≠0 a+bx=cx
cx-bx=a
x(c-b)=a
x=a/(c-b)
Б) приводимое к квадратному
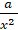 +
+  = c ОДЗ x≠0
= c ОДЗ x≠0
a +bx=c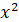
c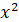 -bx-c=0и решаем квадратное уравнение.
-bx-c=0и решаем квадратное уравнение.
4
Биквадратное уравнение
ax4+bx2+c=0
делаем замену переменной x2=y и решаем полученное квадратное уравнение ay2+by+c=0 по алгоритму. Далее делаем обратную замену и получаем нужные корни.
3х+5=-4х-8
х2+6х=0
0,3х+2,5=2,6
2х2 -8=0
х4+2х2-8=0
4х2=0
3х2+2х-5=0
 +
+ =
=
 —
— =5
=5 =
= 
Предложены 10 уравнений, необходимо найти соответствие уравнения с видом и записать в последний столбик, просто записать.
Закрепление материала (15 минут). Теперь проведем работу в парах. Подпишите второй листочек у вас на партах и задание следующее: в самостоятельной работе 4 модуля, в каждом модуле по 4 задачи. Вам необходимо в первых двух модулях решить на выбор по три уравнения, в третьем модуле два , а в четвертом одно уравнение. Все решения подробно записать в соответствии со всеми правилами решения уравнений. Задачи выбираете сами.
Самостоятельная работа
Фамилия Имя : ____________________________________________________
x+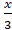 =
= 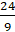
6+5x=2x+9
7+3(2x+1)=4
-6x-4(9-7x)=-5x+45
Квадратные уравнения
3x2-27=0
3x2-8x+5=0
x2-8x=0
2x2+8x+32=0
Дробно- рациональные уравнения
 =
= 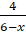
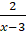 = -x
= -x
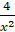 +
+  = -5
= -5
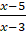 +
+ 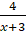 +
+ 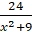 =0
=0
Биквадратные уравнения
2x4-19x2+9=0
x4-7x2+12=0
3x4-13x2+4=0
6(x-1)4+(x-1)2-1=0
Проверяем ответы со слайда и необходимо вам самим себя оценить, насколько хорошо вы усвоили данную тему.
Подведение итогов. Рефлексия (2 минуты). Наш урок подходит к концу. Вспомним цели урока. Достигли мы их или нет. Листочки с самостоятельной работой сдаем мне и на него наклеиваем один из стикеров:
Красный- я ничего не понял
Желтый- надо еще потренироваться
Зеленый- мне все понятно, теперь смогу решить любое уравнение.
Домашнее задание. Решить все уравнения из таблицы, которые записали в последнем столбике. На следующем уроке рассмотрим основные методы решения уравнений повышенной сложности.
Спасибо за урок
Урок по теме «Решение уравнений» 9 класс
9 класс
Урок по теме: «Решение уравнений».
Технологии обучения: информационно-коммуникационная, тестовая, развивающая.
Цель урока: Создание условий для представления учащимися целостной картины темы «Решение уравнений».
Образовательные задачи:
━ повторить виды уравнений и способы их решения;
━ способствовать восполнению существующих пробелов в знаниях учащихся
━ помочь учащимся систематизировать знания по данной теме.
Развивающие задачи:
━ развивать мыслительную деятельность;
━ развивать информационную компетенцию учащихся;
━способствовать проявлению познавательной активности учащихся.
Воспитательные задачи:
━ воспитывать культуру умственного труда;
━ воспитывать культуру речи.
Оборудование:
━1 персональный компьютер;
━ мультимедийный проектор;
━ экран;
━ задания с тестами и бланки ответов.
Актуальность выбранной формы и типа проведения урока.
Практика показывает, что учащиеся успешно решая отдельные виды уравнений по изучаемой теме, к концу 9 класса не имеют целостной картины изученных уравнений, не умеют систематизировать уравнения по видам и находить способы их решения.
Обобщающее повторение активизирует мыслительную деятельность учащихся, развивает их математические способности, даёт возможность систематизировать изученный материал.
Эффективность проведения обобщающего повторения зависит от организации деятельности учащихся на уроке.
На данном уроке сначала повторяется теоретический материал, а обобщение основных теоретических сведений проходит в виде устного теста, что позволяет интенсифицировать процесс повторения материала учащимися, способствует наглядному и быстрому доступу к информации. Проводится обучающая самостоятельная работа с последующим обсуждением. Проверка знаний проходит в виде самостоятельного решения теста на два варианта.
Обучающе-контролирующий вид работы позволяет оперативно выявить уровень знаний учащихся по данной теме.
Ход урока
Приветствует учащихся, отмечает отсутствующих.
Приветствуют учителя.
2.Мотивационно-ориентированный.
Цель: организация целенаправленной работы учащихся.
Включает презентацию.
«Сегодняшний урок – урок завершающий повторение темы «Решение уравнений». Сегодня не только урок повторения, но и систематизации знаний по данной теме.»
«Какие уравнения вы умеете решать?
Какими могут быть квадратные уравнения?
…линейные, квадратные, дробно-рациональные.
…полными, неполными, приведёнными.
Повторим решение линейных уравнений.
Сколько корней может иметь линейное уравнение ax = -b?»
4.Закрепление теоретического материала на примерах
«Решите устно линейные уравнения.
Сейчас вы решали простейшие линейные уравнения, среди них были уравнения с модулем. Решите письменно более сложные уравнения, содержащие модуль».
Если а≠0, то x=,
Если а=0, b=0, то xϵR
Если a=0, b≠0,то нет корней.
Ученики решают устно и дают ответы
5.Решение уравнений письменно
Учитель, проходя по рядам, наблюдает за работой учащихся (3-4 минуты)
Вызывает к доске по одному ученику от каждого варианта
Решают самостоятельно в тетрадях на два варианта.
Два ученика решают у доски, остальные проверяют свои решения.
6. Повторение решения квадратного уравнения (в форме фронтального опроса)
«Какой вид имеет квадратное уравнение?
Как решают квадратные уравнения?
Какой вид имеет неполное квадратное уравнение?
Как решают уравнения вида
аx2+bx=0?
Как решают уравнения вида
аx2+c=0?
Какое квадратное уравнение называется приведённым?
Какой вид имеет приведённое квадратное уравнение?
Как можно решить приведённое квадратное уравнение, не используя формулу корней квадратного уравнения?
Сформулируйте теорему Виета для приведённого квадратного уравнения.
Вспомните формулу разложения квадратного трёхчлена на множители. Она будет нужна нам для решения уравнений».
7.Закрепление теоретического материала на примерах
ax2+bx+c=0, а≠0
Используя формулу корней квадратного уравнения:
x=-b±b2-4ac2a
ax2+bx=0; ax2+c=0, a≠0
используя разложение на множители
выражаем x2, находим x.
, ac<0
Ученик даёт определение приведённого квадратного уравнения.
x2+px+q=0
используя теорему Виета.
Ученик формулирует теорему Виета.
ax2+bx+c=a(x-x1)(x-x2), x1, x2-корни квадратного трёхчлена
« Применив повторенный теоретический материал, решите тест «Верно-неверно».
Решив тест, вы получите слово, которое часто используете на уроках алгебры».
(учитель проводит фронтальный опрос по вопросам теста)
Отвечают на вопросы теста.
«Выполнив все задания, вы получили слово «Дискриминант».
Что оно означает в переводе с латинского языка?
Что различают с помощью дискриминанта?»
…означает слово «различитель».
…количество корней квадратного уравнения.
Если D>0, то уравнение имеет 2 корня,
Если D=0, то-1 корень,
Если D<0, то уравнение не имеет корней.
8. Гимнастика для глаз
9.Письменное решение квадратного уравнения с параметром в тетрадях
«Используя определение квадратного уравнения и условия зависимости количества корней квадратного уравнения от дискриминанта, решите квадратное уравнение с параметром».
После записи учениками в тетради уравнения, учитель выключает проектор.
Вызывает двух учеников к доске для проверки решения 1ого и 2ого случаев условия существования одного корня.
Выполняют обучающую самостоятельную работу в парах, консультируясь друг с другом. (5-7 минут)
Два ученика решают у доски, остальные ученики проверяют свои решения, задают вопросы, уточняя сложные моменты.
10. Решение дробно-рациональных уравнений
«Вспомните, как решить дробно-рациональное уравнение, имеющее вид: дробь равна нулю?»
Ученик формулирует условие равенства дроби нулю.
Включает презентацию.
«Решите устно дробно-рациональные уравнения»
Решают устно.
11.Домашнее задание:
№1154(г), №1155(г,е), №1161(в)
— задания из учебника на повторение решения уравнений с модулем и дробно-рациональных уравнений.
Учитель выключает проектор.
Записывают задания в дневники.
12. Самостоятельная работа в форме теста.
Учитель раздаёт задание теста, напечатанное на листах.
Решают тест , состоящий из 17 уравнений на бланках для ответов, записывая для себя ответы на черновиках. (13 минут).
13. Коррекция знаний
Учитель собирает бланки ответов.
Включает проектор ,для проверки ответов.
После окончания обсуждения решения уравнений, учитель выключает проектор.
Проверяют ответы, задают интересующие их вопросы.
13.Подведение итога урока.
Цель: формировать умение анализировать собственную деятельность.
Задаёт вопросы, побуждая учащихся к анализу своей деятельности на уроке:
1.Чем данный урок был полезен для вас?
2. Какие пробелы в знаниях помог восполнить?
3. Что нового открыли для себя на уроке?
Благодарит за работу на уроке.
Урок алгебры по теме «Уравнения, приводимые к квадратным». 9-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Образовательные: повторить способы решения уравнений, приводимых к квадратным, способствовать выработке навыка решения уравнений с помощью введения вспомогательной переменной, проверить усвоение темы на базовом уровне, обучать умению работать с тестовыми заданиями.
- Развивающие: развивать и совершенствовать умения применять имеющиеся знания в конкретной ситуации, развивать умение сравнивать, обобщать, правильно формулировать и излагать мысли, развивать память, логическое мышление, интерес к предмету через содержание учебного материала.
- Воспитательные:продолжать воспитывать навыки самоконтроля и взаимоконтроля, воспитывать у учащихся аккуратность, культуру общения, воспитывать такие качества характера, как чувство ответственности, настойчивости в достижении цели, умения не растеряться в проблемной ситуации, взаимоуважение.
Оборудование: проектор, экран, карточки с заданием, карточки с контролирующим тестом и карточки «Математический тренажер».
ХОД УРОКА
1. Организационный момент
– Сегодня мы будем решать уравнения третьей и четвертой степеней. В решение таких уравнений большой вклад внесли итальянские математики ХVI в.
Слайд 2. Выступление ученицы с исторической справкой.
Спицион Даль Ферро (1465-1526) и его ученик Фиори.
Н. Тарталья (ок. 1499-1557).
Дж. Кардано (1501-1576) и его ученик Л. Феррари.
Р. Бомбели (ок. 1530-1572).
12 февраля 1535 г. между Фиори и Н. Тартальей
состоялся научный поединок, на котором Тарталья
одержал блестящую победу. Он за два часа решил 30
задач, предложенных Фиори, а сам Фиори не решил ни
одной.
Учитель. Итак, Тарталья за 2 часа решил 30 задач. Мы проведём математический турнир и узнаем, сколько уравнений сможете решить вы за 40 минут? Какие способы решения уравнений при этом изберёте?
2. Устная работа
Слайды 3-4
1. Какие из чисел: – 3; – 2; – 1; 0; 1; 2; 3; являются корнями уравнений:
а) y3 – y = 0; (0; 1; –1)
б) y3 – 4y = 0; (0; 2 и – 2)
в) y3 + 9y = 0. (0;)
2. Сколько решений может иметь уравнение третьей степени?
3. Как проверить, является ли число корнем уравнения?
4. Каким способом вы решали бы уравнения первого задания?
5. Проверьте решение уравнения:
x3 – 5x2 + 16x – 80 = 0
x2 (x – 5) + 16(x – 5) = 0
(x – 5)( x2 + 16) = 0
(x – 5)(x – 4)(x + 4) = 0
Ответ: 5; – 4; 4.
Итак, мы повторили, что называется корнем уравнения, нашли ошибку в решении уравнения, вспомнили способ решения уравнения разложением на множители.
Отметьте в оценочной карточке, сколько
уравнений вы решили на первом этапе урока.
Переходим ко второму этапу
3. Практическая часть урока
1. Математический тренажёр в парах
| Карточка №1 Решите уравнения. 1. (х + 2)(х – 5) = 0 |
Карточка №1 (Ответы)
1. – 2 и 5 |
– Пары, поменяйтесь карточками.
– Проверьте друг у друга. (Ответы на экране).
Слайд 5
– Исправьте ошибки.
– Поблагодарите друг друга.
2. Работа у доски и в тетрадях. Решение уравнения по цепочке. Слайд 6
| 9х3 – 18х2 – x + 2 = 0 (9х3 – 18х2) – (x – 2) = 0 9х2(x – 2) – (x – 2) = 0 (x – 2)(9х2 – 1) = 0 x – 2 = 0 или 9х2 – 1 = 0 |
|
| x = 2 | 9х2 = 1 x1 = – x2 = |
Ответ: – ; ; 2.
3. Работа с карточками: Слайды 7-9
| 1. Какое уравнение называется
биквадратным? (Уравнения вида ах4+ bx2+
c = 0, где а ? 0, являющиеся квадратными относительно
х2, называются биквадратными уравнениями)
Как его решить? x4 – 5x2 + 4 = 0 x2 = 4 x2
= 1 Ответ: + 2; + 1. |
3. (x2 + 2x)2 – 2(x2 + 2x) – 3 = 0 Пусть x2 + 2x = t. Получим квадратное уравнение с переменной t. t2 – 2t – 3 = 0 x = – 1 x1 = – 3 Ответ: – 3; – 1; 1 (по т. Виета) |
| 2. (x2 – x + 1)( x2 – x – 7) = 65 Какой способ наиболее рационально здесь использовать? Пусть x2 – x = t, x1 = – 3; x2 = 4 корней нет Ответ: – 3; 4. |
№221 в. (x2 + x)(x2 + x – 5) = 84 t(t – 5) = 84 |
Сосчитайте количество верно решённых уравнений, занесите в таблицу.
4. Контролирующая часть урока
Тест
Вариант 1
Часть 1
1. Какое из уравнений имеет корни, равные – 1; 3; – 3?
А. (x – 1)(x2 – 9) = 0
Б. (x + 1)(x2 – 9) = 0
В. (x + 1)(x2 + 9) = 0
Г. (x – 1)(x2 + 9) = 0
2. Найдите корни уравнения (2x – 3)(x + 4) = 0.
А. 1,5 и – 4
Б. – 1,5 и 4
В. 1,5 и 4
Г. – 1,5 и – 4
3. Решите уравнение: 5 x2 = 25x
Ответ:________________________________
Часть 2
4. Закончи фразу: «Произведение корней уравнения x4 – 2x2 – 8 = 0 равно числу …»
А. – 8
Б. – 4
В. – 2
Г. 0
5. Решите уравнение ( решение и ответы оформите на отельном листе)
(x2 + 4x)(x2 + 4x – 17) = – 60
Верно выполненные задания:
части 1 оцениваются в 0,5 балла;
части 2: 1 – в 2 балла; 2 – в 4 балла
Критерии оценки:
Оценка «3» – 1,5 балла;
Оценка «4» – 3,5 балла;
Оценка «5» – 7,5 балла.
Вариант 2
Часть 1
1. Какое из уравнений имеет корни, равные – 2; 5 – 5?
А. (x – 2)(x2 – 25) = 0
Б. (x + 2)( x2 + 25) = 0
В. (x + 2)( x2 – 25) = 0
Г. (x – 2)( x2 + 25) = 0
2. Найдите корни уравнения (2x + 7)(x – 4) = 0.
А. 3,5 и – 4
Б. – 3,5 и – 4
В. 3,5 и 4
Г. – 3,5 и 4
3. Решите уравнение: 3x – x2 = 0
Ответ:________________________________
Часть 2
4. Закончи фразу: «Произведение корней уравнения x4 – 8x2 – 9 = 0 равно числу …»
А. – 1
Б. – 9
В. 9
Г. – 8
5. Решите уравнение ( решение и ответы оформите на отельном листе)
(x2 – 5x)(x2 – 5x + 10) + 24 = 0
Верно выполненные задания:
части 1 оцениваются в 0,5 балла;
части 2: 1 – в 2 балла; 2 – в 4 балла
Критерии оценки:
Оценка «3» – 1,5 балла;
Оценка «4» – 3,5 балла;
Оценка «5» – 7,5 балла.
Слайд 10
Дополнительное задание
Решите уравнение итальянских математиков:
(3x2 + x – 4) + 3x2 + x = 4 .
Решите уравнение: х3 – х2 – 4(x – 1)2 = 0
x2(x – 1) – 4(x – 1)2 = 0
(x – 1)( x2 – 4(x – 1)) = 0
x – 1 = 0 или (x2 – 4(x – 1)) = 0
x = 1 x2 – 4x + 4 = 0
(x – 2)2 = 0
x = 2
Ответ: 1; 2.
Слайд 11
Ответы к тесту
| № варианта | Часть 1 |
Часть 2 |
||||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | Б | А | 0 и 5 | Б | – 5; 1; 2; – 6. | |
| 2 | В | Г | 0 и 3 | Б | 1; 2; 3; 4. | |
Поменяйтесь тестами.
Проверьте друг у друга. (Ответы на экране).
Исправьте ошибки.
Поставьте оценки.
Поблагодарите друг друга.
Занесите количество верных уравнений в оценочную таблицу.
Слайд 12
5. Итог урока. Оценки
– Сколько уравнений решили сегодня на уроке? Какие способы решения вы применяли?
Слайд 13
Критерии оценок за работу на уроке: «5» – за 21-23 правильно решенных уравнений, «4» – 19-20 уравнений, «3» – 16 -18 уравнений.
Победители турнира:
Слайд 14
6. Домашнее задание
№
Слайд № 15
Оценочная таблица
Предмет__________________Ф.И. ученика_______________________
Этапы урока |
Первый (устная работа) |
Второй |
Третий (тестовый контроль) |
(Дополнительные задания) |
Итог | |
Математический тренажер |
Практическая часть |
|||||
| Количество верно выполненных заданий | ||||||
Список литературы:
- Лапшина И. В. Сборник тестов по курсу алгебры. 9 класс. Пособие для учителя. Ярославль, 2009.
- Кузнецова Л.В., Суворова С.Б., Буговинова Е.А. Сборник заданий для подготовки к итоговой аттестации в 9 классе. М.: Просвещение, 2010.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К. И., Суворова С.Б. Алгебра 9 класс. М.: Просвещение, 2010.
- http://www.ankolpakov.ru/2010/10/11/ob-algebraicheskom-uravnenii-3-j-stepeni-i-formulax-ego-kornej/
 +
+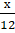 =
=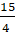
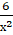 —
— =5
=5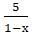 =
= 
 + b=c
+ b=c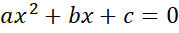
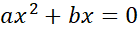
 +c=d
+c=d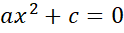
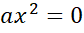
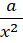 +
+  = c
= c