Уравнения касательной: Касательная к графику ункции: уравнение касательной

Posted on by alexxlab

Содержание

Касательная к графику ункции: уравнение касательной

 

Рассмотрим следующий рисунок:

На нем изображена некоторая функция y = f(x), которая дифференцируема в точке a. Отмечена точка М с координатами (а; f(a)). Через произвольную точку Р(a + ∆x; f(a + ∆x)) графика проведена секущая МР.

Если теперь точку Р сдвигать по графику к точке М, то прямая МР будет поворачиваться вокруг точки М. При этом ∆х будет стремиться к нулю. Отсюда можно сформулировать определение касательной к графику функции.

Касательная к графику функции

Касательная к графику функции есть предельное положение секущей при стремлении приращения аргумента к нулю. Следует понимать, что существование производной функции f в точке х0, означает, что в этой точке графика существует касательная к нему.

При этом угловой коэффициент касательной будет равен производной этой функции в этой точке f’(x0). В этом заключается геометрический смысл производной.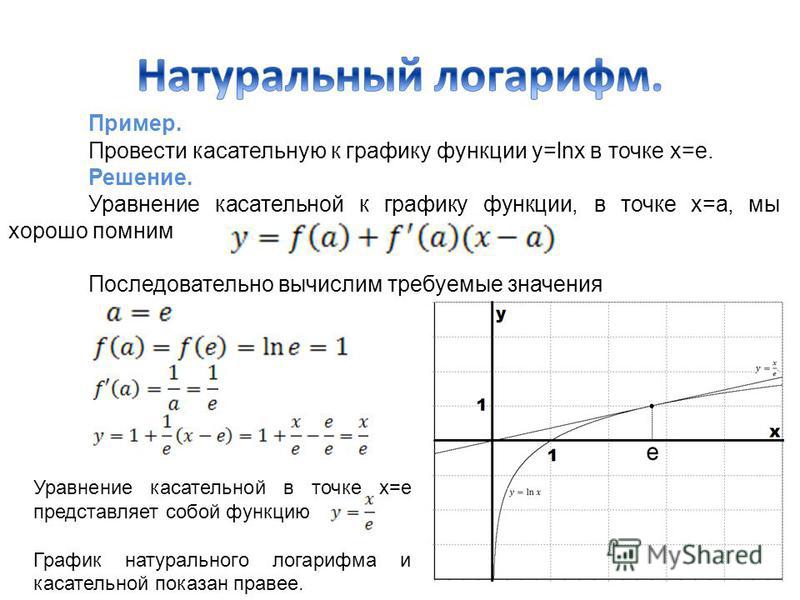 Касательная к графику дифференцируемой в точке х0 функции f — это некоторая прямая, проходящая через точку (x0;f(x0)) и имеющая угловой коэффициент f’(x0).

Уравнение касательной

Попытаемся получить уравнение касательной к графику некоторой функции f в точке А(x0; f(x0)). Уравнение прямой с угловым коэффициентом k имеет следующий вид:

y = k*x + b.

Так как у нас угловой коэффициент равен производной f’(x0), то уравнение примет следующий вид: y = f’(x0)*x + b.

Теперь вычислим значение b. Для этого используем тот факт, что функция проходит через точку А.

f(x0) = f’(x0)*x0 + b, отсюда выражаем b и получим b = f(x0) – f’(x0)*x0.

Подставляем полученное значение в уравнение касательной:

y = f’(x0)*x + b = f’(x0)*x + f(x0) – f’(x0)*x0 = f(x0) + f’(x0)*(x — x0).

y = f(x0) + f’(x0)*(x — x0).

Рассмотрим следующий пример: найти уравнение касательной к графику функции f(x) = x3 – 2*x2 + 1 в точке х = 2.

1. х0 = 2.

2. f(x0) = f(2) = 22 — 2*22 + 1 = 1.

3. f’(x) = 3*x2 – 4*x.

4. f’(x0) = f’(2) = 3*22 – 4*2 = 4.

5. Подставим полученные значения в формулу касательной, получим: y = 1 + 4*(x — 2). Раскрыв скобки и приведя подобные слагаемые получим: y = 4*x — 7.

Ответ: y = 4*x — 7.

Общая схема составления уравнения касательной к графику функции y = f(x):

1. Определить х0.

2. Вычислить f(x0).

3. Вычислить f’(x)

4. Вычислить f’(x0)

5. Подставить полученные значения в уравнение касательной y= f(x0) + f’(x0)*(x — x0).

Нужна помощь в учебе?



Предыдущая тема: Применения непрерывности: метод интервалов и примеры
Следующая тема:&nbsp&nbsp&nbspКритические точки функции: максимумы и минимумы

Уравнение касательной к графику функции

Вопросы занятия:

·     рассмотреть касательную к графику функции в точке;

·     вывести уравнение касательной к графику функции в общем виде.

Материал урока.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Упражнение.

Итак, мы с вами научились находить производные различных функций. На предыдущих уроках мы говорили, что умение находить производные – помогает в решении разных задач. На сегодняшнем уроке мы разберём, как с помощью производных можно составить уравнение касательной к графику функции и примеры применения производной к приближенным вычислениям.

Давайте сформулируем задачу.

Напомним, что если в некоторой точке к графику функции можно провести касательную, то функция дифференцируема в этой точке и f'(

a) существует.

Касательная – это прямая, значит, общее уравнение касательной можно записать в виде y = kx + m. Наша задача сводится к нахождению коэффициентов k и m.

Рассмотрим несколько примеров.

Пример.

Рассмотрим ещё один пример.

Пример.

Решая примеры, мы выполняли практически одни и те же действия. Давайте теперь попробуем сформулировать алгоритм составления уравнения касательной к графику функции y = f(x).

Уравнение касательной имеет ещё одно применение: с его помощью можно выполнять приближенные вычисления.

Рассмотрим общий приём.

Рассмотрим это на примере.

Пример.

Рассмотрим ещё один пример.

Пример.

Итак, давайте ещё раз выделим суть теории приближенных вычислений. Сложная кривая в окрестности точки x0 заменяется прямой (касательной к графику функции) и если приращения аргумента не велики, то для каждой функции можно вывести соответствующую формулу, по которой осуществляются приближенные вычисления.

Касательная плоскость и нормаль к явно заданной поверхности.

Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.

Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$

Уравнение нормали $$\frac{x-x_0}{F_x'(x_0, y_0, z_0)}=\frac{y-y_0}{F_y'(x_0, y_0, z_0)}=\frac{z-z_0}{F_z'(x_0, y_0, z_0)}.$$

В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.$$

Примеры:

7. 229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=\sin x\cos y$ в точке $(\pi/4, \pi/4, \pi/4).$

Решение.

Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.$$

Находим частные производные:

$z’_x=(\sin x\cos y)’_x=\cos x\cos y;$

$z’_x(\pi/4, \pi/4)=\cos \frac{\pi}{4}\cos \frac{\pi}{4}=\frac{1}{\sqrt 2}\cdot\frac{1}{\sqrt 2}=\frac{1}{2};$ 

$z’_y=(\sin x\cos y)’_y=-\sin x\sin y;$

$z’_y(\pi/4, \pi/4)=-\sin \frac{\pi}{4}\sin \frac{\pi}{4}=-\frac{1}{\sqrt 2}\cdot\frac{1}{\sqrt 2}=-\frac{1}{2};$

Таким образом, уравнение касательной плоскости: $$z-\frac{\pi}{4}=\frac{1}{2}(x-\frac{\pi}{4})-\frac{1}{2}(y-\frac{\pi}{4})\Rightarrow$$ $$\frac{1}{2}x -\frac{1}{2}y-z+\frac{\pi}{4}=0.$$ 

Уравнение нормали: $$\frac{x-\frac{\pi}{4}}{\frac{1}{2}}=\frac{y-\frac{\pi}{4}}{-\frac{1}{2}}=\frac{z-\frac{\pi}{4}}{-1}. 2-2x+6y=4$ найти уравнение нормали, параллельной прямой $\frac{x+2}{1}=\frac{y}{3}=\frac{z+1}{4}.$

 

 

Итоговый урок по теме «Уравнение касательной» – Документ 1 – УчМет

Ковалева Елена Ивановна

Учитель 1 категории

МБОУ СОШ№5 г.Рославль, Смоленская область

Учебник Алгебра и начала анализа. 10кл. В 2 ч. (профильный уровень)  Мордкович А.Г., Семенов П.В.

ПЛАН-КОНСПЕК УРОКА
Итоговый урок по теме «Уравнение касательной»

10 класс

Цель урока:

  • систематизировать и обобщить сведения, полученные учащимися на предыдущем уроке;

  • расширить представления учащихся о теме;

  • дополнить и обобщить представления учащихся о применении данной темы в жизни;

  • познакомить с историей данного вопроса.

9. Задачи:

  1. — обучающие

    : научиться распознавать сложные функции, знать правила дифференцирования, уметь применять формулу производной сложной функции при решении задач; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером.

  2. -развивающие развивать познавательные интересы через применение информационных технологий.

  3. -воспитательные воспитывать адаптивность к современным условиям обучения.

Тип урока урок закрепления изучаемого материала и выработки практических умений и навыков

Формы работы учащихся самостоятельная, индивидуальная, фронтальная работа.

Необходимое техническое оборудование компьютер, проектор, экран, презентация для сопровождения занятия, раздаточный материал для учащихся.

I. Организационный момент (0.5 мин.).

II. Постановка целей урока. Мотивация учащихся ( 2 мин). (слайд 1)

III. Обобщение знаний учащихся по теме «Производная. Уравнение касательной»(15 мин)(слайд 2)

Учитель приветствует учащихся и объявляет цель урока и план, используя презентационное сопровождение. Зачитывается эпиграф к уроку.

Учитель. Сегодня на уроке мы обобщим и закрепим идею геометрического смысла производной, сформируем начальное представление о приложениях производной в математике и истории их развития, «откроем» зависимость между свойствами монотонности функции, экстремумами и значениями производной; эпиграфом к уроку служат слова французского философа-материалиста Дени Дидро (1713 – 1784) – современника Декарта, Лейбница, личного библиотекаря Екатерины Великой.

«Начинать исследования можно по-разному… Все равно начало почти всегда оказывается весьма несовершенной, нередко безуспешной попыткой.

Есть истины, как страны, наиболее удобный путь, к которым становится известным лишь после того, как мы испробуем все пути. Кому-то приходится, рискуя собой, сходить с проторенной дороги, чтобы указать другим правильный путь… На пути к истине мы почти всегда обречены, совершать ошибки» (Дени Дидро)

Сегодня мы закрепим материал на тему «Уравнение касательной» решением ключевых или опорных задач, проверим усвоение техники нахождения производной и исследуем связь уравнения касательной с исследованием свойств графика функции , что в дальнейшем нам даст аппарат для построения практически графика любой функции и нахождения ее свойств. Приведет к решению задач на оптимизацию, те нахождения наибольшего и наименьшего значения некоторого конкретного тела, …

Итак, для проверки техники вычисления производной приглашаются учащиеся к компьютерам ( тесты на два варианта)

На местах ребята обсуждают предложенные незавершенные предложения ( слайды 3-4)

1.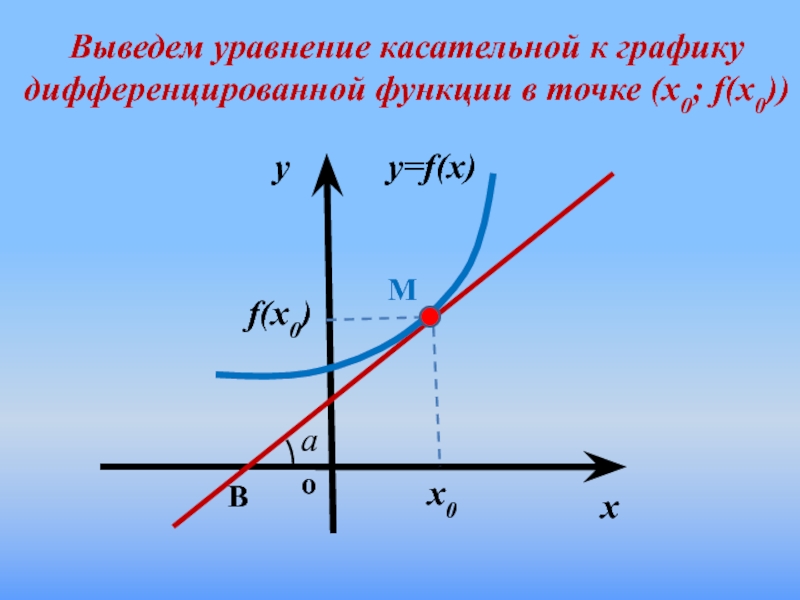 В чем состоит геометрический смысл производной?

2.В любой ли точке можно построить касательную?

3.Какая функция называется дифференцируемой в точке?

4.Касательная наклонена к под тупым углом к положительному направлению оси Ох ….

5.Кастельная наклонена под острым углом к оси ох…

6.Касательная наклонена под прямым углом к положительному направлению оси Ох…

7.Касательная параллельна оси Ох, следовательно…

8. Что называется секущей для графика функции y=f(x)?

9. Какая прямая называется касательной к графику функции?

10. Какая из отмеченных точек является точкой касания?

11. Записать уравнение касательной к графику функции в заданной точке в общем виде. 12. Чему равен угол наклона касательной к графику функции в заданной точке? 6. Как найти угловой коэффициент касательной?

13.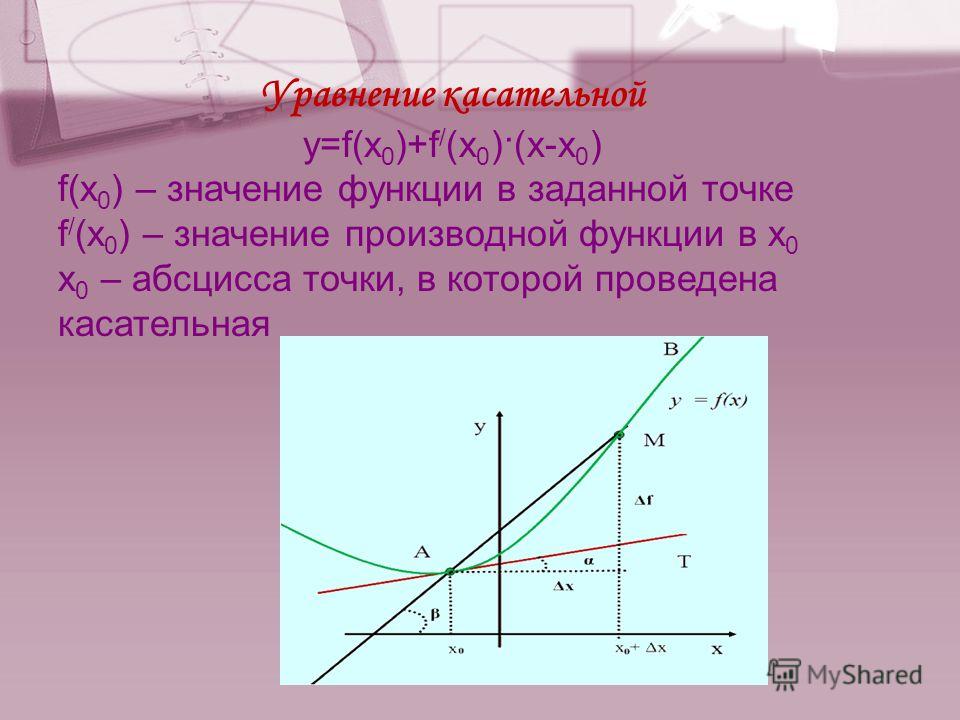 Известно, что угловой коэффициент касательной к графику функции в точке с абсциссой хо, равен 0,6. Чему равно значение производной в этой точке?

14. Касательная к графику функции f(x) в точке с абсциссой хо образует с положительным направлением оси ох угол 45о. Найти f/(xo).

Затем обсуждаем решение ключевых задач. (слайд 5)

  • Задание из предложенных ключевых задач составить свою задачу.

  • после обсуждения, решенных у доски задач , учащимся предлагается составить алгоритм решения из ключевых задач.

Учитель. Математический анализ, ядро которого составляют дифференциальное и интегральное исчисления, — самая тонкая область всей математики. Раздел математики, в котором изучаются производные и их применения к исследованию функций, называется дифференциальным исчислением, а раздел математики, в котором изучается операция интегрирования функции, то есть восстановления функции по её производной, называется интегральным исчислением.

Немного истории ( небольшое сообщение ученицы) (слайды 6-10)

Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия.

Большой вклад в развитие дифференциального исчисления внесли:

Архимед, который задолго до этого решил задачу на построение касательной к спирали, сумел найти максимум функции f(x) = х2 (а — х),

Пьер Ферма (1601 -1665), математическое определение производной, которого было принято всеми математиками, успешно применявшими в своём методе нахождения экстремумов многочленов задачи о построениях касательных к кривым,

Готфрид Вильгельм Лейбниц (1646 -1716), который установил геометрический смысл производной, как тангенс угла наклона касательной. «Штрихи к портрету» Готфрида Лейбница : в своей работе «Новый метод максимумов и минимумов», используя геометрическое истолкование, он кратко разъясняет признаки возрастания и убывания, максимума и минимума, выпуклости и вогнутости (следовательно, и достаточные условия экстремума для простейшего случая), а также точки перегиба. Его знаменитая фраза: «Без настоящих единиц не может быть и множества». С ним связаны имена выдающихся личностей, термины и понятия: Эпоха Просвещения, Петр I, Россия, Ньютон, рококо, арифмометр, кратер на Луне, подводная лодка, «Философский век». Подумайте над этим дома.

V I. Решение задач с практическим содержанием ( слайд 11)

Учитель . Обсуждая успехи своего ученика, учитель математики так отозвался о нем: «Он очень мало знает, но у него положительная производная». Все поняли, что хотел сказать учитель: скорость приращения знаний у ученика положительна, а это есть залог того, что его знания возрастут. Подумайте, как вы могли бы охарактеризовать три кривые роста знаний.

Ответ:I -ого знания не растут т.к. производная в каждой точке прямой равна нулю, знания II-го растут быстрее, чем III-го т.к. угол наклона касательных будет больше, а следовательно и больше производная, потому что тангенс функция возрастающая. (слайд 10-анимированный , в музыкальном сопровождении)

У вас на столах график некоторой функции, проведите в указанных точках схематично касательные и охарактеризуйте данную функцию у учетом изученного в 10 и 9-ом классах.

А теперь послушайте музыку, которая сейчас помогала исследованию В чем связь? ( слайд12) Почему именно музыку и график функции мы сегодня связываем?

Не всякую музыку можно слушать легко, для восприятия необходимо произвести усилия, вслушаться , представить действие , проникнуться настроением, поймать мысль композитора.

«Здесь мало увидеть,


Здесь нужно всмотреться,

Здесь мало услышать,


Здесь вслушаться нужно,» Н.Рыленков «Все в тающей дымке»

А может быть и с графиком , его надо не только увидеть, но в него надо всмотреться, почувствовать всю гармонию мелодии графика.

Такую мелодию нам предложит Семченкова Настя( на гитаре попыталась проиграть мелодию, повторяющую предложенный график).

А теперь попробуйте сами. Звучит вальс из балета «Лебединое озеро»

П.И.Чайковского.

Учитель. Ребята, а зачем нужно изучать данную тему.

Выберем ответы из левого столбца:

  • чтобы успешно закончить школу,

  • чтобы хорошо учиться в Вузе,

  • чтобы в работе сделать карьеру,

  • чтобы не обманули в магазине,

  • чтобы в финансовых операциях получать максимальную прибыль,

  • чтобы решать нестандартные задачи

                   

Нужна ли производная для будущей профессии?

Российский математик 19века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».

С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:

  • Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

  • Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;

  • Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

Вам предложены задачи из жизни, необходимо применить для решения свойства касательной.

1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста? (слайд13-анимированный –этапы рассуждений)

2.Вертикальный разрез теплицы имеет форму пятиугольника ABCDE, в котором FT=8м, AB=DE=1м. Из точки Р, расположенной на высоте 2м, подается горизонтально вытекающая струя воды, которая при максимальном напоре достигает точки Е(илиА). Какую высоту h нужно придать центральной части теплицы , если желательно, чтобы струя воды( она имеет форму параболы с вершиной в точке Р) не достигла крыши теплицы?

Во многих приложениях встречается понятие касания кривых между собой. Кривые называются касающимися ,если они имеют в этой точке общую касательную.

3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0

4.Покажите, что кривые у=4х2+2х-8 и у=-х3-х+10 касаются в точке А(3;34). Будут ли они касаться в точке В(2;-4)

5. При каких соотношениях парабола ах2+вх+с-0 касается оси Ох?

6. Найдите те значения х, при которых касательные в соответствующих точках параллельны между собой. При каком значении а кривые будут касаться друг друга?

Вам было предложено дома решить не менее творческую задачу: составления алгоритма решения нестандартной задачи , по теме «Уравнение касательной»

Обсуждаем данные алгоритмы.

Как вы уже заметили, что в данных алгоритмах повторяющиеся блоки, перечислите их: составление уравнения касательной в точке; нахождения точки касания по углу наклона касательной к положительному направлению оси Ох, по известному угловому коэффициенту, который может быть известен по условию параллельности прямых ,описанию условия нахождения точек касания

А теперь перейдем к выполнению практической работы , при выполнении которой вы должны применить все на практике. (Приложение1)

V. Постановка дифференцированного домашнего задания

Учитель раздает карточки с вариантами заданий (4 варианта) , которые содержат обязательную и необязательную части домашнего задания, делает соответствующие пояснения о том, что результаты будут необходимы на следующем уроке.

VI. Итог урока.

Учитель предлагает обобщить учащимся свои исследования, демонстрирует на слайдах результаты подведения итогов и дальнейший план изучения темы. На экране непрерывно идут титрами новые математические понятия: необходимое условие, достаточное условие, необходимое и достаточное условие.

Учащиеся высказывают свое мнение, подводят общий итог исследованию

Список используемой литературы

  1. Алгебра и начала анализа. 10 класс. В 2 ч. Ч.1. Учебник (профильный уровень) / А. Г. Мордкович, П. В. Семенов. – 4-е изд., доп. – М.: Мнемозина, 2007.

  2. Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений
    /А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.; Под ред. А.Н.Колмогорова-
    10-е изд.- М..: Просвещение,2000. – стр. 160-166

  3. Единый государственный экзамен: Математика: Контрол. измерит. материалы
    /Л.О.Денищева, Е.М.Бойченко, Ю.А.Глазков и.др.; М-во образования Рос.
    Федерации.- М.: Просвещение, 2003.

  4. Производная и её применение: Дидакт. матер, по курсу алгебры и начал анализа
    для 10-11 кл.ср.шк./Под ред. М.И.Башмакова — СПб, Свет, 1995.

  5. Клайн М. Математика. Утрата определённости: Пер. с англ./ Под ред. С предисл. И
    примеч. И.М.Яглома.- М.: Мир, 1984.

  6. Степанова М.В. Учебно-исследовательская деятельность школьников в профильном обучении: учебно-методическое пособие для учителя/ Под ред. А.П.Тряпининой. – СПб.: КАРО, 2005.

  7. Маркова В. Что такое исследовательская деятельность школьников / Математика (приложение к 1 сентября), №12, 2007.

Интернет – источники

Музыка «Балет «Лебединое озеро» — Вальс A-dur, акт 1» — (Пётр Ильич Чайковский)http://www.rusmusic.su/instrumental.php

Дени Дидро

http://books.atheism.ru/gallery/Diderot/

Екатерина Великая

http://mail.spb.fio.ru/archive/group15/c3wu3/pagehistory1.htm

Лейбниц

http://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%2C_%D0%93%D0%BE%D1%82%D1%84%D1%80%D0%B8%D0%B4_%D0%92%D0%B8%D0%BB%D1%8C%D0%B3%D0%B5%D0%BB%D1%8C%D0%BC

Ньютон

http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA

Архимед

http://ru. wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4

Лагранж

http://ru.wikipedia.org/wiki/%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%2C_%D0%96%D0%BE%D0%B7%D0%B5%D1%84_%D0%9B%D1%83%D0%B8

Ферма

http://ru.wikipedia.org/wiki/%D0%A4%D0%B5%D1%80%D0%BC%D0%B0%2C_%D0%9F%D1%8C%D0%B5%D1%80

Ньютон

http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA

Приложения к плану-конспекту урока

Итоговый урок по теме «Уравнение касательной»

Приложение 1

Геометрическое приложение производной

1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста?

2. Вертикальный разрез теплицы имеет форму пятиугольника ABCDE, в котором FT=8м, AB=DE=1м. Из точки Р , расположенной на высоте 2м, подается горизонтально вытекающая струя воды, которая при максимальном напоре достигает точки Е (или А ). Какую высоту h нужно придать центральной части теплицы, если желательно, чтобы струя воды ( она имеет форму параболы с вершиной в точке Р) не достигла крыши теплицы?

C

Р

В D

А Е

  • Во многих приложениях встречается понятие касания кривых между собой. Кривые называются касающимися , если они имеют в этой точке общую касательную.

3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0

4. Покажите, что кривые у=4х2+2х-8 и у=-х3-х+10 касаются в точке А (3;34). Будут ли они касаться в точке В (2;-4)

5. При каких соотношениях парабола ах2+вх+с-0 касается оси О х?

Приложение 2

Вариант 2

А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0

А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой

А5.3Угловой коэффициент касательной, проведенной к параболе
y = x – 2x в ее точке (x0; y0), равен 4. Напишите уравнение этой касательной.

A)  y = 4x — 4        B)  y = 4x + 9        C)  y = 4x + 4      D)  y = 4x — 5      E)  y = 4x — 9

А5.4 В какой точке касательная, проведенная к графику функции y = x — 2x + 1,

параллельна прямой y = -4(x + 1)?    
A)   (-1;)   B)   (-1; 4)   C)   (1;)  D)    (1; 4)   E)    (0; 4)

А5.5.В каких точках касательная к графику функции образует с осью Ох угол в 450?

А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108

А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х)

в точке с абсциссой х0

А5. 8.

Вариант 3

А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0

А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой

А5.3 Угловой коэффициент касательной, проведенной к графику функции y =   ,в точке (x0, y0) равен . Найдите x0, y0.
A)          B)          C)          D)  —        E) 

А5.4.В каких точках касательная к графику функции образует с осью Ох угол в 450?

А5.5. При каких значениях  x  касательная к графику функции y = 2x + 3x — 6x 

параллельна прямой y = 6x + 1 ?

A)      -2  и  3   B)      1  и  3   C)      -2  и  1 D)      2  и  -1   E)      -1  и  3

А5.6.В точке А(5;0) проведена касательная к графику функции .Найти длину отрезка касательной, заключенного между осями координат.

А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х)

в точке с абсциссой х0

А5.8. В какой точке нужно провести касательную к графику функции , чтобы она пересекла ось ординат в точке (0;6) ?

Вариант 4

А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0

А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой

А5.3. Угловой коэффициент касательной, проведенной к параболе
y = x – 2x в ее точке (x0; y0), равен 4. Напишите уравнение этой касательной.

A)  y = 4x — 4        B)  y = 4x + 9        C)  y = 4x + 4      D)  y = 4x — 5        E)  y = 4x — 9

А5.4. Какая из прямых параллельна касательной к кривой y = 4 – x в точке x0 = 2?
A)  y = 4 – 4x        B)  y = 2x + 8        C)  y = x + 8     D)  y = 4x + 8        E)  y = 8 – 4x

А5.5.В каких точках касательная к графику функции образует с осью Ох угол в 1350?

А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108

А5.7.Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х)

в точке с абсциссой х0

А5.8.Касательные, проведенные к графику функции в точках с абсциссами х1 и х2 параллельны. Известно, что х1 =. Найдите отношение

Приложение 3

Презентация — Уравнение касательной

Слайды и текст этой онлайн презентации

Слайд 1

10 КЛАСС
Уравнение касательной
ТЕМА УРОКА:

Слайд 2

ЦЕЛИ УРОКА:
1. Уточнить понятие касательной к графику функции.
2. Вывести уравнение касательной.
3. Создать алгоритм составления уравнения касательной к графику функции y=f(x).
4. Начать отрабатывать умения и навыки в составлении уравнения касательной в различных математических ситуациях.

Слайд 3

С f(x)=√(3-2x) f'(1)=?
Я f(x)=5/³√(3x+2) f’ (-1/3)=?
Ю f(x)=12/√(3x²+1) f’ (1)=?
Ф f(x)= 4√(3-2x²) f’ (-1)=?
К f(x)=2ctg2x f’ (-π/4)=?
И f(x)=4/(2-cos3x) f’ (- π /6)=?
Л f(x)= tg x f’ (π /6)=?
1 4/3 9 -4 -1 -3 5
РАСШИФРУЙТЕ, КАК ИСААК НЬЮТОН НАЗВАЛ ПРОИЗВОДНУЮ ФУНКЦИЮ

Слайд 4

ОТВЕТ :
ФЛЮКСИЯ

Слайд 5

Слайд 6

Понятие «производная» возникло в связи с необходимостью решения ряда задач физики, механики и математики.
Честь открытия основных законов математического анализа принадлежит английскому ученому Ньютону и немецкому математику Лейбницу.
Лейбниц рассматривал задачу о проведении касательной к произвольной кривой.

Слайд 7

2) y=3/x + 6√x 2) y=3/x + 6√x 2) y=3/x + 6√x
3/x²+3/√ x -3/x²+6/√ x -3/x²+ 3/√ x
ТЕСТ: НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ
4) y=x³+4×100 4) y=x³+4×100 4) y=x³+4×100
3x²+400×99 3×3+4×99 x3+4×99
5) y=7tgx+sinx 5) y=7tgx+sinx 5) y=7tgx+sinx
1/cos2x+cosx 7/cos2x+cosx 7/cos2x-cosx
6) y=√x*sinx 6) y=√x*sinx 6) y=√x*sinx
Sinx/(2 √x)+ √x cos x 2sin x cosx
7) y=x/(x2+1) 7) y=x/(x2+1) 7) y=x/(x2+1)
1-x2 x2 +1 (1-x2)/(x2+1) 2
10) y=cos(5x+π/3) 10) y=cos(5x+π/3) 10) y=cos(5x+π/3)
5sin(5x+ π/3) sin(5x+ π/3) -5sin(5x+ π/3)
9) y= √ (15-8x) 9) y= √ (15-8x) 9) y= √ (15-8x)
7/ √(15-8x) 3/ √(15-8x) -4/ (√15-8x)
1) y=2x-7 1) y=2x-7 1) y=2x-7
x²-7 2 2x
8) y=(5x+2)9 8) y=(5x+2)9 8) y=(5x+2)9
2(5x+2)8 45(5x+2)8 3(5x+2)8
3) y=cos x+2x 3) y=cos x+2x 3) y=cos x+2x
Sinx+2 -Sinx+2 -Sinx+2x
3) y=cos x+2x 3) y=cos x+2x 3) y=cos x+2x
Sinx+2 -Sinx+2 -Sinx+2x

Слайд 8

ОТВЕТЫ:
1) 2 2) 3 3) 2 4) 1 5) 2 6) 1 7) 3 8) 2 9) 3 10) 3

Слайд 9

ДАВАЙТЕ ОБСУДИМ ПОНЯТИЕ КАСАТЕЛЬНОЙ. СОГЛАСНЫ ЛИ ВЫ С УТВЕРЖДЕНИЕМ: »КАСАТЕЛЬНАЯ — ЭТО ПРЯМАЯ, ИМЕЮЩАЯ С ДАННОЙ КРИВОЙ ЕДИНСТВЕННУЮ ОБЩУЮ ТОЧКУ»? 1) ДА 2) НЕТ

Слайд 10

Слайд 11

Слайд 12

ПОЧЕМУ УГЛОВОЙ КОЭФФИЦИЕНТ КАСАТЕЛЬНОЙ РАВЕН ПРОИЗВОДНОЙ?

Слайд 13

АЛГОРИТМ СОСТАВЛЕНИЯ УРАВНЕНИЯ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ У=f(x)
1. Обозначить абсциссу точки касания буквой а. 2. Вычислить f(a). 3. Найти f ‘ (x) и вычислить f ‘(a). 4. Подставить найденные числа а, f(a), f ‘(a) в формулу y = f(a) + f ‘(a) * (x-a)

Слайд 14

ЗАКРЕПЛЕНИЕ
№ 828
Дополнительно:
2. Составить уравнение касательной к графику функции f(x)=х2-3х+5 в точке с абсциссой а=-1.
3. Составить уравнение касательной, проходящей через точку пересечения касательной графика функции f(x)=(3-x)/(x+1) с прямой у=1.
4. № 831 (а)
1. Устная работа : №809.

Слайд 15

ЗАДАНИЯ С ЕГЭ: (НА ДОМ)
А. КАСАТЕЛЬНАЯ, ПРОВЕДЕННАЯ К ГРАФИКУ ФУНКЦИИ У=Х³-Х В ТОЧКЕ С АБСЦИССОЙ Х=0, ПАРАЛЛЕЛЬНА ПРЯМОЙ: 1) У=7-Х 2) У=Х-7 3) У=2Х-7 4) У=√3*Х+7 А. ДЛЯ ФУНКЦИИ У=4Х-Х² КАСАТЕЛЬНАЯ, ПАРАЛЛЕЛЬНАЯ ОСИ АБСЦИСС, ПРОВЕДЕНА ЧЕРЕЗ ТОЧКУ КАСАНИЯ: 1) (0;0) 2) (4;0) 3) (2;4) 4) (-1;-5) А. УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ f(x)= 2х²-3х-1, ПРОВЕДЕННОЙ В ТОЧКЕ С АБСЦИССОЙ Х0=1, ИМЕЕТ ВИД: 1)У=Х-3 2) У=Х-1 3) У=-2Х+3 4) 6У=-11Х-1 А. УРАВНЕНИЕ КАСАТЕЛЬНОЙ, ПРОВЕДЕННОЙ К ГРАФИКУ ФУНКЦИИ f (х)= 3х²-2х+5 В ТОЧКЕ А(2;13): 1) У=76Х-502 2) У=10Х-7 3) У=10Х+33 4) У=76Х-139 А. НАЙТИ ТАНГЕНС УГЛА НАКЛОНА КАСАТЕЛЬНОЙ, ПРОВЕДЕННОЙ К ГРАФИКУ ФУНКЦИИ У= 3Х²-5Х В ТОЧКЕ С АБСЦИССОЙ Х0=2. 1) 0,83 2) 2 3)3 4) 7

10 класс. Алгебра. Производная. Уравнение касательной к графику функции. — Уравнение касательной к графику функции.

Комментарии преподавателя

Урав­не­ние ка­са­тель­ной к гра­фи­ку функ­ции

На преды­ду­щих за­ня­ти­ях были рас­смот­ре­ны за­да­чи на тех­ни­ку диф­фе­рен­ци­ро­ва­ния. Это очень важ­ные за­да­чи, и на­хож­де­ние про­из­вод­ных необ­хо­ди­мо в раз­ных за­да­чах, в том числе и в со­став­ле­нии урав­не­ния ка­са­тель­ной.

 По­стро­им кри­вую  (см. рис.1).

 

Рис. 1. Гра­фик функ­ции .

За­фик­си­ру­ем точку . Если , то зна­че­ние функ­ции равно . Зна­чит, имеем точку с ко­ор­ди­на­та­ми (.

За­да­ча: со­ста­вить урав­не­ние ка­са­тель­ной. Более стро­гая фор­му­ли­ров­ка – на­пи­сать урав­не­ние ка­са­тель­ной к функ­ции  в точке с абс­цис­сой , в ко­то­рой  — су­ще­ству­ет.

Урав­не­ние ка­са­тель­ной – это пря­мая,  ко­то­рая за­да­ет­ся фор­му­лой  

Любая пря­мая, в том числе и ка­са­тель­ная, опре­де­ля­ет­ся двумя чис­ла­ми: и . Ис­хо­дя из гео­мет­ри­че­ско­го смыс­ла про­из­вод­ной  (тан­генс угла на­кло­на ка­са­тель­ной) – это есть уг­ло­вой ко­эф­фи­ци­ент .

Па­ра­метр  най­дем из усло­вия, что ка­са­тель­ная про­хо­дит через точку (, то есть  . 

 .

Стало быть  .

За­пи­шем урав­не­ние ка­са­тель­ной

.

Или, .

По­лу­чи­ли урав­не­ние ка­са­тель­ной к кри­вой  в точке с абс­цис­сой .

Смысл каж­до­го эле­мен­та, ко­то­рый вхо­дит в урав­не­ние ка­са­тель­ной.

1) ( – точка ка­са­ния ка­са­тель­ной и гра­фи­ка функ­ции.

2)  — уг­ло­вой ко­эф­фи­ци­ент ка­са­тель­ной к гра­фи­ку функ­ции.

3)  – про­из­воль­ная точка на ка­са­тель­ной.

Очень много задач, когда за­да­на точка, ко­то­рая не лежит на гра­фи­ке функ­ции, и через нее надо про­ве­сти ка­са­тель­ную к дан­ной функ­ции. Надо четко по­ни­мать, что   – это про­из­воль­ная точка на ка­са­тель­ной.

Итак, по­лу­чи­ли урав­не­ние ка­са­тель­ной, про­ана­ли­зи­ро­ва­ли смысл каж­до­го эле­мен­та этой ка­са­тель­ной, и те­перь при­ве­дем при­мер, и на нем из­ло­жим ме­то­ди­ку по­стро­е­ния ка­са­тель­ной.

За­да­ча.

К кри­вой  в точке с абс­цис­сой  про­ве­сти ка­са­тель­ную. Про­ил­лю­стри­ру­ем поиск ка­са­тель­ной на ри­сун­ке (см. рис.2).

 

Рис. 2. Ка­са­тель­ная к гра­фи­ку функ­ции .

За­фик­си­ру­ем точку . Зна­че­ние функ­ции в этой точке  равно 1.

Ал­го­ритм со­став­ле­ния урав­не­ния ка­са­тель­ной к гра­фи­ку функ­ции:

1)  Найти  и точку ка­са­ния. 

 — дано.Точка ка­са­ния: (;.

2) Найти про­из­вод­ную в любой точке .

.

3) Найти зна­че­ние про­из­вод­ной в точке с абс­цис­сой .

 .

4) Вы­пи­сать и про­ана­ли­зи­ро­вать урав­не­ние ка­са­тель­ной.

.

Упро­ща­ем и по­лу­ча­ем:  .

Ответ: .

За­да­ча 1.

Пусть дано урав­не­ние ка­са­тель­ной .

Най­ди­те точки пе­ре­се­че­ния ка­са­тель­ной с осями ко­ор­ди­нат.

Если , то .  – это пер­вая точка.

Если , то  .  — вто­рая точка.

Итак, пер­вая точка – это точка  с ко­ор­ди­на­та­ми . Вто­рая точка – точка пе­ре­се­че­ния с осью  , точка  с ко­ор­ди­на­та­ми  (см. рис.3).

Рис.3. Точки пе­ре­се­че­ния ка­са­тель­ной к гра­фи­ку функ­ции  с осями ко­ор­ди­нат. За­да­ча 2.

Найти длину от­рез­ка ка­са­тель­ной, ко­то­рая от­се­ка­ет­ся осями ко­ор­ди­нат, то есть надо найти длину от­рез­ка .

Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник (Рис. 3). Длина ка­те­та  равна 1. Длина ка­те­та   . Длину от­рез­ка  из пря­мо­уголь­но­го тре­уголь­ни­ка най­дем по тео­ре­ме Пи­фа­го­ра:

 

За­да­ча 3.

Найти пло­щадь тре­уголь­ни­ка, об­ра­зо­ван­но­го ка­са­тель­ной и осями ко­ор­ди­нат. Ясно, что это пло­щадь тре­уголь­ни­ка (Рис. 3) — пло­щадь тре­уголь­ни­ка, об­ра­зо­ван­но­го ка­са­тель­ной и осями ко­ор­ди­нат.

Сле­ду­ю­щая за­да­ча для са­мо­сто­я­тель­но­го ре­ше­ния.

Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в тре­уголь­ник . Ра­ди­ус окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка .

Рас­смот­рим при­мер.

Дана функ­ция . На­пи­сать урав­не­ние ка­са­тель­ной к дан­ной кри­вой в точке с дан­ной абс­цис­сой.

Рас­смот­рим гра­фи­че­скую ил­лю­стра­цию (см. рис.4).

Рис. 4. Ка­са­тель­ная к  гра­фи­ку функ­ции .

На­хож­де­ние точки ка­са­ния.

1.   Точка ка­са­ния имеет ко­ор­ди­на­ты .

2. Найти .

3. Найти 

И, по­след­нее дей­ствие, – на­пи­сать урав­не­ние ка­са­тель­ной.

4. .

 Упро­стим и по­лу­чим  .

За­ме­тим в точке  си­ну­со­и­да и ка­са­тель­ная со­при­ка­са­ют­ся. В рай­оне точки  си­ну­со­и­да и пря­мая почти не раз­ли­ча­ют­ся.

Итак, мы вы­ве­ли урав­не­ние ка­са­тель­ной. Рас­смот­ре­ли все эле­мен­ты этой ка­са­тель­ной. Вы­яс­ни­ли их смысл. Сфор­му­ли­ро­ва­ли одну из ме­то­дик на­хож­де­ния ка­са­тель­ных в кон­крет­ных функ­ци­ях, в кон­крет­ных точ­ках и ре­ши­ли неко­то­рые со­пут­ству­ю­щие за­да­чи.

ИСТОЧНИК

http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/uravnenie-kasatelnoy-k-grafiku-funktsii

http://v.5klass.net/zip/457286d0df8865f8084b5db13cbd6e95.zip

http://school.xvatit.com/index.php?title=%D3%F0%E0%E2%ED%E5%ED%E8%E5_%EA%E0%F1%E0%F2%E5%EB%FC%ED%EE%E9_%EA_%E3%F0%E0%F4%E8%EA%F3_%F4%F3%ED%EA%F6%E8%E8

http://itest.kz/lekciya_uglovoj_koehfficzient_kasatelnoj_i_ee_uravnenie_ru

http://www.postupivuz.ru/vopros/12822.htm

 

Определение формулы касательной к окружности


Общая формула окружности
Уравнение касательной в указанной точке

Касательная к окружности

Если не использовать понятие производной, и взять объяснение из учебников середины прошлого века, то «Касательная к окружности — это прямая пересекающая окружность в двух совпадающих точках»

Окружность на  плоскости может быть представлена  в виде нескольких исходных данных

1. В виде  координат центра окружности (x0,y0) и её радиуса R.

2. В виде общего уравнения 

 

В виде параметрического вида и в полярных координатах мы рассматривать не будем, так как там формулы тоже на базируются на  координатах центра окружности и радиусе. 

Наша задача, зная параметры  окружности  и точку принадлежащую этой окружности вычислить параметры касательной к этой окружности.

Эта задача, является частным решением более общего калькулятор касательная к кривой второго порядка

Итак, если окружность выражена формулой

Уравнение касательной к окружности  если нам известны параметры общего уравнения  таково:

Таким  образом, зная все коэффициенты,   мы очень легко найдем уравнение касательной в заданной точке.

ВАЖНО: При указании точки, она должна быть обязательно(!!) принадлежать окружности,
и не быть точкой в какой либо стороне. В противном случае, уравнение касательной будет неверным.

Примеры

Вычислить уравнение касательной в точке (13.8, 0) к окружности выраженной формулой

Запишем коэффиценты этой кривой, взглянув на общую формулу

 

 

 

Общая формула окружности
Уравнение касательной в указанной точке

 

Второй пример:

Через окружность с центром (8.71, -4) и радиусом 7 проходит касательная и касается в точке (4,-4)

Найти уравнение этой прямой.

Раз у нас заданы радиус и коордианты центтра то уравнение имеет вид

раскроем скобки, получим 

Общая формула окружности
Уравнение касательной в указанной точке

Отрисовав, полученные линии в GeoGebra мы убедимся что расчет произведен верно.

Формально, используя вышеупомянутую программу, касательную можно провести там проще и быстрее. Смотрите где и как проще.

Удачных расчетов!

  • Определить формулу окружности по трем точкам >>

Как найти уравнение касательной

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Уравнение касательной к кривой | Дифференциальное исчисление

Нарисуйте график \ (f \) с указанием всех пересечений и точек поворота. {2} — 4x + 3 = 0 \\ (х-3) (х-1) = 0 \\ х = 3 \ текст {или} х = 1 \\ \ text {Shape: «frown»} (a Найдите уравнения касательных к \ (f \) в точке:

  1. \ (y \) — точка пересечения \ (f \).
  2. поворотный момент \ (f \).
  3. точка, где \ (x = \ text {4,25} \).
  1. \ begin {align *} y _ {\ text {int}}: (0; -3) \\ m _ {\ text {касательная}} = f ‘(x) & = -2x + 4 \\ f ‘(0) & = — 2 (0) + 4 \\ \ поэтому m & = 4 \\ \ text {Касательная} y & = 4x + c \\ \ text {Through} (0; -3) \ поэтому y & = 4x-3 \ end {align *}
  2. \ begin {align *} \ text {Поворотный момент:} (2; 1) \\ m _ {\ text {касательная}} = f ‘(2) & = -2 (2) + 4 \\ & = 0 \\ \ text {Касательное уравнение} y & = 1 \ end {align *}
  3. \ begin {align *} \ text {If} x & = \ text {4,25} \\ f (\ text {4,25}) & = — \ text {4,25} ^ {2} +4 (\ text {4,25}) — 3 \\ & = — \ text {4,0625} \\ m _ {\ text {tangent}} \ text {at} x & = \ text {4,25} \\ m & = — 2 (\ text {4,25}) + 4 \\ & = — \ текст {4,5} \\ \ text {Касательная} y & = — \ text {4,5} x + c \\ \ text {Сквозь} (\ text {4,25}; — \ text {4,0625}) \\ — \ text {4,0625} & = — \ text {4,5} (\ text {4,25}) + c \\ \ поэтому c & = \ text {15,0625} \\ y & = — \ text {4,5} x + \ text {15,0625} \ end {align *}

Нарисуйте три касательных выше на вашем графике \ (f \).

Запишите все наблюдения о трех касательных к \ (f \).

Касательная в точке \ (y _ {\ text {int}} \) (синяя линия): градиент положительный, функция в этой точке увеличивается.

Касательная в точке поворота (зеленая линия): градиент равен нулю, касательная — горизонтальная линия, параллельная оси \ (x \).

Касательная в точке \ (x = \ text {4,25} \) (фиолетовая линия): градиент отрицательный, функция в этой точке убывает.

Как найти уравнения касательных и нормальных прямых

Краткий обзор

  • Чтобы найти уравнение прямой, вам нужна точка и наклон.2) = 12 $$

    Наклон касательной составляет $$ m = 12 $$.

    Шаг 3

    Найдите форму точки с уклоном прямой с уклоном $$ m = 12 $$, проходящей через точку $$ (2,8) $$.

    $$ \ begin {align *} y — y_1 & = m (x-x_1) \\ [6pt] у — 8 & = 12 (х-2) \ end {выровнять *} $$

    Отвечать

    $$ y — 8 = 12 (x-2) $$

    Для справки, вот график функции и касательная, которую мы только что нашли.2 — х $$. Найдите уравнение касательной с наклоном $$ m = -3 $$.

    Шаг 1

    Найдите производную.

    $$ f ‘(x) = 2x -1 $$

    Шаг 2

    Найдите $$ x $$ — значение, где $$ f ‘(x) $$ равно наклону.

    $$ \ begin {align *} f ‘(x) & = 2x -1 \\ [6pt] -3 & = 2x -1 \\ [6pt] -2 & = 2x \\ [6pt] х & = -1 \ end {выровнять *} $$

    Шаг 3

    Найдите точку на функции, где $$ x = -1 $$.2 — (-1) = 1 + 1 = 2 $$

    Дело в $$ (- 1, 2) $$.

    Шаг 4

    Найдите уравнение прямой, проходящей через точку $$ (- 1,2) $$ с наклоном $$ m = -3 $$.

    $$ \ begin {align *} y -y_1 & = m (x-x_1) \\ [6pt] y — 2 & = -3 (x — (-1)) \\ [6pt] у — 2 & = -3 (х + 1) \ end {выровнять *} $$

    Отвечать

    $$ у — 2 = -3 (х + 1) $$

    Для справки, вот график функции и касательная, которую мы только что нашли.2 & = 12 \\ [6pt] y & = \ pm \ sqrt {12} \\ [6pt] y & = \ pm \ sqrt {4 \ cdot 3} \\ [6pt] у & = \ pm2 \ sqrt 3 \ end {выровнять *} $$

    Поскольку в задаче говорится, что нас интересует $$ y> 0 $$, мы используем $$ y = 2 \ sqrt 3 $$.

    Точка касания — $$ (2, 2 \ sqrt 3) $$.

    Шаг 2

    Найдите уравнение для $$ \ frac {dy} {dx} $$.

    Поскольку уравнение определено неявно, мы используем неявное дифференцирование.

    $$ \ begin {align *} 2x + 2y \, \ frac {dy} {dx} & = 0 \\ [6pt] 2y \, \ frac {dy} {dx} & = -2x \\ [6pt] \ frac {dy} {dx} & = — \ frac {2x} {2y} \\ [6pt] \ frac {dy} {dx} & = — \ frac x y \ end {выровнять *} $$

    Шаг 3

    Найдите наклон касательной в точке касания.

    В точке $$ (2,2 \ sqrt 3) $$ наклон касательной составляет

    $$ \ begin {align *} \ frac {dy} {dx} \ bigg | _ {(\ blue {2}, \ red {2 \ sqrt 3})} & = — \ frac {\ blue 2} {\ red {2 \ sqrt 3}} \\ [6pt] & = — \ frac 1 {\ sqrt 3} \\ [6pt] & = — \ frac 1 {\ sqrt 3} \ cdot \ blue {\ frac {\ sqrt 3} {\ sqrt 3}} \\ [6pt] & = — \ frac {\ sqrt 3} 3 \ end {выровнять *} $$

    Наклон касательной равен $$ m = — \ frac {\ sqrt 3} 3 $$.

    Шаг 4

    Найдите уравнение касательной, проходящей через $$ (2,2 \ sqrt 3) $$ с наклоном $$ m = — \ frac {\ sqrt 3} 3 $$.

    В точке $$ (2,2 \ sqrt 3) $$ наклон касательной составляет

    $$ \ begin {align *} y — y_1 & = m (x-x_1) \\ [6pt] y — 2 \ sqrt 3 & = — \ frac {\ sqrt 3} 3 (x-2) \ end {выровнять *} $$

    Отвечать

    Уравнение касательной: $$ y — 2 \ sqrt 3 = — \ frac {\ sqrt 3} 3 (x-2) $$

    Для справки график кривой и найденная касательная линия показан ниже.

    Нормальные линии

    Предположим, у нас есть касательная к функции. Функция и касательная пересекаются в точке касания. Линия, проходящая через ту же точку, которая перпендикулярна касательной, называется нормальной линией .

    Напомним, что когда две прямые перпендикулярны, их наклоны обратно пропорциональны.Поскольку наклон касательной равен $$ m = f ‘(x) $$, наклон нормальной линии равен $$ m = — \ frac 1 {f’ (x)} $$.

    Пример 4

    Предположим, что $$ f (x) = \ cos x $$. Найдите уравнение прямой к функции в $$ x = \ frac \ pi 6 $$.

    Шаг 1

    Найдите точку на функции.

    $$ f \ left (\ frac \ pi 6 \ right) = \ cos \ frac \ pi 6 = \ frac {\ sqrt 3} 2 $$

    Это $$ \ left (\ frac \ pi 6, \ frac {\ sqrt 3} 2 \ right) $$.

    Шаг 2

    Найдите значение производной в $$ x = \ frac \ pi 6 $$.

    $$ f ‘(x) = — \ sin x \ longrightarrow f’ \ left (\ frac \ pi 6 \ right) = — \ sin \ frac \ pi 6 = — \ frac 1 2 $$

    Наклон касательной равен $$ m = — \ frac 1 2 $$. Поскольку мы ищем прямую, перпендикулярную касательной, мы хотим использовать $$ m = 2 $$.

    Шаг 3

    Найдите уравнение прямой, проходящей через точку $$ \ left (\ frac \ pi 6, \ frac {\ sqrt 3} 2 \ right) $$ с наклоном $$ m = 2 $$.

    $$ \ begin {align *} y -y_1 & = m (x-x_1) \\ [6pt] y — \ frac {\ sqrt 3} 2 & = 2 \ left (x — \ frac \ pi 6 \ right) \ end {выровнять *} $$

    Отвечать

    Линия, нормальная к функции в $$ x = \ frac \ pi 6 $$, это $$ y — \ frac {\ sqrt 3} 2 = 2 \ left (x — \ frac \ pi 6 \ right) $$.

    Для справки, вот график функции и нормальной линии, которую мы нашли.

    Продолжайте практиковать задачи

    Ошибка: Нажмите «Не робот», затем повторите попытку.

    Уравнение касательной линии: проблемы и решения — Matheno.com

    В этих задачах всегда указывается, что вы найдете касательную или нормальную (= перпендикулярную) линию в определенной точке функции. Назовем эту точку $ (x_0, y_0) $.

    Чтобы ответить на эти вопросы, вы почти всегда будете использовать форму линии «точка-уклон». Напомним, что если линия имеет наклон м и и содержит точку $ (x_0, y_0) $, то вы можете записать ее уравнение в виде:

    Форма линии «точка-уклон»:
    $$ \ bbox [желтый, 5px] {y — y_0 = m (x — x_0)} $$

    В постановке задачи обычно указывается точка $ (x_0, y_0) $, поэтому на самом деле эти проблемы сводятся к определению наклона м линии — о чем мы поговорим ниже.

    Вы будете использовать это уравнение снова и снова; запомните это, если вы этого еще не знаете.

    (Это просто вариант определения наклона: $ m = \ dfrac {y — y_0} {x — x_0}.) $

    I. Касательная линия к кривой

    Очень часто в начале Расчет Вам будет предложено найти уравнение для прямой , касательной к кривой в определенной точке. Мы называем эту точку $ (x_0, y_0) $.

    Чтобы найти уравнение линии, вам просто нужно помнить, что касательная линия к кривой имеет наклон, равный производной функции, вычисленной в интересующей точке:

    $$ \ bbox [желтый, 5px] {m_ \ text {касательная линия} = f ‘(x_0)} $$


    То есть найдите производную функции $ f’ (x) $, а затем вычислите ее как $ x = x_0 $.Это значение, $ f ‘(x_0), $ равно наклону касательной.

    Следовательно, мы можем записать уравнение для касательной в точке $ (x_0, y_0) $ как

    \ [\ bbox [10px, border: 2px сплошной синий] {
    \ begin {align *}
    y — y_0 & = m_ \ text {касательная} (x — x_0) \\ [8px] y — y_0 & = f ‘(x_0) (x — x_0)
    \ end {align *}} \]

    Если эти уравнения кажутся вам абстрактными, не волнуйтесь. Мы обещаем, что как только вы решите несколько проблем, процесс обретет смысл.

    II.Нормальная линия к кривой

    Иногда вместо этого вам будет предложено найти прямую нормальную к кривой. Это то же самое, что запросить линию , перпендикулярную кривой.

    Вы снова будете использовать форму линии «точка-уклон». Но теперь, чтобы вычислить наклон прямой, вспомним, что наклоны перпендикулярных прямых являются отрицательными величинами, обратными друг другу ($ m_2 = — \ dfrac {1} {m_1} $). Нам нужен наклон линии, перпендикулярной кривой в точке и, следовательно, перпендикулярной касательной к кривой в этой точке:

    \ [\ bbox [yellow, 5px] {
    \ begin {align *}
    m_ \ text {нормальная линия} & = \ frac {-1} {m_ \ text {касательная линия}} \\ [12px] & = \ frac {-1} {f ‘(x_0)}
    \ end {align *}} \]


    Следовательно, мы можем записать уравнение для нормальной линии в $ (x_0, y_0) $ как

    \ [\ bbox [10px, граница: сплошной синий 2px] {
    \ begin {align *}
    y — y_0 & = m_ \ text {нормальная линия} (x — x_0) \\ [8px] y — y_0 & = \ frac {-1} {f ‘(x_0)} (x — x_0)
    \ end {align *}} \]

    Мы рекомендуем , а не , пытаясь запомнить все приведенные выше формулы.Вместо этого запомните форму линии «точка-наклон», а затем используйте то, что вы знаете о производной, сообщающей вам наклон касательной в данной точке. Проблемы, приведенные ниже, иллюстрируют.

    Задача 1 иллюстрирует процесс объединения различных фрагментов информации для нахождения уравнения касательной.

    Задача 2 требует, чтобы вы нашли фрагменты информации перед тем, как собрать их воедино.

    [свернуть]

    AC Аппроксимация касательной линии

    Подраздел 1.8.1 Касательная линия

    Для функции \ (f \), дифференцируемой в точке \ (x = a \ text {,} \), мы знаем, что можем определить наклон касательной к \ (y = f (x) \) в точке \ ((a, f (a)) \) путем вычисления \ (f ‘(a) \ text {.} \) Уравнение результирующей касательной прямой дается в форме точечного уклона как

    \ begin {уравнение *} y — f (a) = f ‘(a) (x-a) \ \ \ text {или} \ \ y = f’ (a) (x-a) + f (a) \ text {.} \ end {уравнение *}

    Обратите внимание: в этом контексте существует большая разница между \ (f (a) \) и \ (f (x) \).Первая является константой, которая возникает в результате использования заданного фиксированного значения \ (a \ text {,} \), а вторая является общим выражением правила, определяющего функцию. То же самое верно для \ (f ‘(a) \) и \ (f’ (x) \ text {:} \), мы должны тщательно различать эти выражения. Каждый раз, когда мы находим касательную, нам нужно вычислить функцию и ее производную при фиксированном \ (a \) — значении.

    На рисунке 1.8.2 мы видим график функции \ (f \) и его касательную линию в точке \ ((a, f (a)) \ text {.} \) Обратите внимание, как при увеличении масштаба мы видим, что локальная линейность \ (f \) более четко выделяется. Функция и касательная к ней почти неотличимы вблизи. Локальную линейность также можно увидеть динамически в java-апплете по адресу http://gvsu.edu/s/6J.

    Рисунок 1.8.2. Функция \ (y = f (x) \) и ее касательная линия в точке \ ((a, f (a)) \ text {:} \) слева, на расстоянии и справа, вблизи. Справа мы помечаем функцию касательной линии \ (y = L (x) \) и замечаем, что для \ (x \) около \ (a \ text {,} \) \ (f (x) \ приблизительно L ( х) \ текст {.} \)

    Подраздел 1.8.2 Локальная линеаризация

    Небольшое изменение перспективы и обозначений позволит нам более точно обсудить, как касательная линия приближает \ (f \) около \ (x = a \ text {.} \). Решая для \ (y \ text {, } \) уравнение касательной можно записать как

    \ begin {уравнение *} y = f ‘(a) (x-a) + f (a) \ end {уравнение *}

    Эта строка сама является функцией \ (x \ text {.} \). Заменяя переменную \ (y \) выражением \ (L (x) \ text {,} \), мы называем

    \ begin {уравнение *} L (x) = f ‘(a) (x-a) + f (а) \ end {уравнение *}

    локальная линеаризация \ (f \) в точке \ ((a, f (a)) \ text {.} \) В этих обозначениях \ (L (x) \) — не что иное, как новое имя для касательной. Как мы видели выше, для \ (x \), близкого к \ (a \ text {,} \) \ (f (x) \ приблизительно L (x) \ text {.} \)

    Пример 1.8.3.

    Предположим, что функция \ (y = f (x) \) имеет аппроксимацию касательной, заданную формулой \ (L (x) = 3-2 (x-1) \) в точке \ ((1,3) \ text {,} \), но мы ничего не знаем о функции \ (f \ text {.} \) Чтобы оценить значение \ (f (x) \) для \ (x \) около 1, например \ (f (1.2) \ text {,} \) мы можем использовать тот факт, что \ (f (1.2) \ приблизительно L (1,2) \) и, следовательно,

    \ begin {уравнение *} f (1,2) \ приблизительно L (1,2) = 3–2 (1,2–1) = 3–2 (0,2) = 2,6 \ text {.} \ end {уравнение *}

    Подчеркнем, что \ (y = L (x) \) — это просто новое имя для функции касательной. Используя это новое обозначение и наше наблюдение, что \ (L (x) \ приблизительно f (x) \) для \ (x \) near \ (a \ text {,} \), мы можем записать

    \ begin {уравнение *} f (x) \ приблизительно f (a) + f ‘(a) (x-a) \ \ text {for} \ x \ \ text {near} \ a \ text {.} \ end {уравнение *}

    Мероприятие 1.8.2.

    Предположим, что известно, что для данной дифференцируемой функции \ (y = g (x) \ text {,} \) ее локальная линеаризация в точке, где \ (a = -1 \) задается выражением \ (L (x) = -2 + 3 (x + 1) \ text {.} \)

    1. Вычислить значения \ (L (-1) \) и \ (L ‘(- 1) \ text {.} \)

    2. Какими должны быть значения \ (g (-1) \) и \ (g ‘(- 1) \ text {?} \) Почему?

    3. Ожидаете ли вы, что значение \ (g (-1.03) \) будет больше или меньше значения \ (g (-1) \ text {?} \) Почему?

    4. Используйте локальную линеаризацию, чтобы оценить значение \ (g (-1.03) \ text {.} \)

    5. Предположим, что вы также знаете, что \ (g » (- 1) = 2 \ text {.} \) Что это говорит вам о графике \ (y = g (x) \) в точке \ (a = -1 \ text {?} \)

    6. Для \ (x \) около \ (- 1 \ text {,} \) нарисуйте график локальной линеаризации \ (y = L (x) \), а также возможный график \ (y = g ( x) \) по осям, указанным на рисунке 1.8.4.

    Рисунок 1.8.4. Оси для построения \ (y = L (x) \) и \ (y = g (x) \ text {.} \)

    Из действия 1.8.2 мы видим, что локальная линеаризация \ (y = L (x) \) является линейной функцией, которая имеет два важных значения с функцией \ (y = f (x) \), из которой она получена.В частности,

    • , поскольку \ (L (x) = f (a) + f ‘(a) (xa) \ text {,} \) следует, что \ (L (a) = f (a) \ text {;} \ ) и
    • , поскольку \ (L \) — линейная функция, ее производная — это наклон.

    Следовательно, \ (L ‘(x) = f’ (a) \) для каждого значения \ (x \ text {,} \) и, в частности, \ (L ‘(a) = f’ (a) \ text {.} \) Следовательно, мы видим, что \ (L \) — линейная функция, которая имеет то же значение и тот же наклон, что и функция \ (f \) в точке \ ((a, f (a)) \ text {.} \)

    Таким образом, если мы знаем линейное приближение \ (y = L (x) \) для функции, мы знаем значение исходной функции и ее наклон в точке касания.Однако остается неизвестным, как выглядит функция \ (f \) в точке касания. По сути, существует четыре возможности, как показано на рисунке 1.8.5.

    Рисунок 1.8.5. Четыре возможных графика для нелинейной дифференцируемой функции и то, как она может быть расположена относительно ее касательной в точке.

    Эти возможные формы являются результатом того факта, что существует три варианта значения второй производной: либо \ (f » (a) \ lt 0 \ text {,} \) \ (f » (a) = 0 \ text {,} \) или \ (f » (a) \ gt 0 \ text {.} \)

    • Если \ (f » (a) \ gt 0 \ text {,} \), то мы знаем, что график \ (f \) вогнут вверх, и мы видим первую возможность слева, где касательная линия лежит полностью ниже кривой.
    • Если \ (f » (a) \ lt 0 \ text {,} \), то \ (f \) вогнута вниз, а касательная линия проходит над кривой, как показано на втором рисунке.
    • Если \ (f » (a) = 0 \) и \ (f » \) изменит знак в \ (x = a \ text {,} \), вогнутость графика изменится, и мы увидим либо третья или четвертая цифра. 2 .
    • Пятый вариант (который не очень интересен) может возникнуть, если функция \ (f \) сама по себе линейна, так что \ (f (x) = L (x) \) для всех значений \ (x \ text { .} \)

    Возможно, что \ (f » (a) = 0 \), но \ (f » \) не меняет знак в \ (x = a \ text {,} \), и в этом случае график будет выглядеть вроде один из первых двух вариантов.

    Графики на рис. 1.8.5 подчеркивают еще одну важную вещь, которую мы можем узнать из вогнутости графика около точки касания: лежит ли касательная линия выше или ниже самой кривой.Это ключевой момент, потому что он сообщает нам, будут ли значения аппроксимации касательной линии слишком большими или слишком маленькими по сравнению с истинным значением \ (f \ text {.} \). Например, в первой ситуации на крайнем левом графике на рис. 1.8.5, где \ (f » (a)> 0 \ text {,} \), поскольку касательная линия опускается ниже кривой, мы знаем, что \ (L (x) \ le f (x) \) для все значения \ (x \) рядом с \ (a \ text {.} \)

    Мероприятие 1.8.3.

    Это действие касается функции \ (f (x) \), о которой известна следующая информация:

    • \ (f \) — дифференцируемая функция, определенная для каждого действительного числа \ (x \)

    • \ (\ Displaystyle f (2) = -1 \)

    • \ (y = f ‘(x) \) имеет график, показанный на рисунке 1.8,6

    Рисунок 1.8.6. В центре график \ (y = f ‘(x) \ text {;} \) слева, оси для построения \ (y = f (x) \ text {;} \) справа, оси для построения \ (y = f » (x) \ text {.} \)

    Ваша задача — определить как можно больше информации о \ (f \) (особенно около значения \ (a = 2 \)), отвечая на вопросы ниже.

    1. Найдите формулу аппроксимации касательной от \ (L (x) \ text {,} \) до \ (f \) в точке \ ((2, -1) \ text {.} \)

    2. Используйте приближение касательной, чтобы оценить значение \ (f (2.07) \ text {.} \) Покажите свою работу внимательно и ясно.

    3. Нарисуйте график \ (y = f » (x) \) в правой сетке на рис. 1.8.6; обозначьте это соответствующим образом.

    4. Наклон касательной к \ (y = f (x) \) увеличивается, уменьшается или не уменьшается, когда \ (x = 2 \ text {?} \) Объясните.

    5. Нарисуйте возможный график \ (y = f (x) \) рядом с \ (x = 2 \) в левой сетке на рисунке 1.8.6. Включите эскиз \ (y = L (x) \) (находится в части (а)). Объясните, откуда вы знаете, что график \ (y = f (x) \) выглядит так, как будто вы его нарисовали.

    6. Ваша оценка в (b) переоценивает или занижает истинное значение \ (f (2.07) \ text {?} \) Почему?

    Идея о том, что дифференцируемая функция выглядит линейной и может быть хорошо аппроксимирована линейной функцией, является важной идеей, которая находит широкое применение в исчислении. Например, аппроксимируя функцию с ее локальной линеаризацией, можно разработать эффективный алгоритм для оценки нулей функции. Локальная линейность также помогает нам лучше понять некоторые сложные ограничения.Например, мы видели, что предел

    \ begin {уравнение *} \ lim_ {x \ to 0} \ frac {\ sin (x)} {x} \ end {уравнение *}

    является неопределенным, потому что его числитель и знаменатель стремятся к 0. Хотя нет алгебры, которую мы могли бы сделать, чтобы упростить \ (\ frac {\ sin (x)} {x} \ text {,} \), это просто показать, что линеаризация \ (f (x) = \ sin (x) \) в точке \ ((0,0) \) задается выражением \ (L (x) = x \ text {.} \) Следовательно , для значений \ (x \) около 0, \ (\ sin (x) \ приблизительно x \ text {,} \) и, следовательно,

    \ begin {уравнение *} \ frac {\ sin (x)} {x} \ приблизительно \ frac {x} {x} = 1 \ text {,} \ end {уравнение *}

    , что делает правдоподобным тот факт, что

    \ begin {уравнение *} \ lim_ {x \ to 0} \ frac {\ sin (x)} {x} = 1 \ text {. 2 \)), вы можете ожидать, что частные производные могут быть использованы для определения касательной плоскости к графику поверхности \ (z = f (х, у) \).3 \) определяют плоскость, то две касательные к поверхности \ (z = f (x, y) \) в направлениях \ (x \) и \ (y \), описанные на рисунке 2.3.1, содержатся в касательная плоскость в этой точке, , если касательная плоскость существует в этой точке . Существование этих двух касательных линий само по себе не гарантирует существования касательной плоскости. Возможно, что если мы возьмем след поверхности в плоскости \ (x — y = 0 \) (которая составляет угол 45 ° с положительной осью \ (x \)), полученная кривая в этой плоскости может иметь касательную линию, которая не находится в плоскости, определяемой двумя другими касательными линиями, или она может вообще не иметь касательной в этой точке.К счастью, оказывается, что если \ (\ dfrac {∂f} {∂x} \) и \ (\ dfrac {∂f} {∂y} \) существуют в области вокруг точки \ ((a, b) \) и непрерывны в точке \ ((a, b) \), то касательная плоскость к поверхности \ (z = f (x, y) \) будет существовать в точке \ ((a, b, f (a, б)) \). В этом тексте эти условия будут выполняться всегда.

    Предположим, что нам нужно уравнение касательной плоскости \ (T \) к поверхности \ (z = f (x, y) \) в точке \ ((a, b, f (a, b)) \) . Пусть \ (L_x \) и \ (L_y \) — касательные линии к следам поверхности в плоскостях \ (y = b \) и \ (x = a \) соответственно (как на рисунке 2.3.2) и предположим, что условия существования \ (T \) выполняются. Тогда уравнение для \ (T \) равно

    \ [A (x− a) + B (y− b) + C (z — f (a, b)) = 0 \ label {Eq2.4} \]

    , где \ (n = (A, B, C) \) — вектор нормали к плоскости \ (T \). Поскольку \ (T \) содержит линии \ (L_x \) и \ (L_y \), то все, что нам нужно, это векторы \ (v_x \) и \ (v_y \), которые параллельны \ (L_x \ text {и} L_y \) соответственно, а затем пусть \ (n = v_x × v_y \).

    Рисунок 2.3.2: Касательная плоскость

    Поскольку наклон \ (L_x \) равен \ (\ dfrac {∂f} {∂x} (a, b) \), то вектор \ (v_x = (1,0, \ dfrac {∂f} {∂x} (a, b)) \) параллельно \ (L_x \) (поскольку \ (v_x \) лежит в \ (xz \) — плоскости и лежит на прямой с наклоном \ (\ dfrac {\ dfrac {∂f} {∂x} (a, b)} {1} = \ dfrac {∂f} {∂x} (a, b) \).См. Рисунок 2.3.3). Точно так же вектор \ (v_y = (0,1, \ dfrac {∂f} {∂y} (a, b)) \) параллелен \ (L_y \). Следовательно, вектор

    \ [\ textbf {n} = \ mathbf {v_x} × \ mathbf {v_y} = \ begin {vmatrix} \ textbf {i} & \ textbf {j} & \ textbf {k} \\ [4pt] 1 & 0 & \ dfrac {∂f} {∂x} (a, b) \\ [4pt] 0 & 1 & \ dfrac {∂f} {∂y} (a, b) \ end {vmatrix} = — \ dfrac {∂f} {∂x} (a, b) \ textbf {i} — \ dfrac {∂f} {∂y} (a, b) \ textbf {j} + \ textbf {k} \ nonumber \]

    нормально к растению \ (T \). Таким образом, уравнение \ (T \) равно

    \ [- \ dfrac {∂f} {∂x} (a, b) (xa) — \ dfrac {∂f} {∂y} (a, b) (yb) + zf (a, b) = 0 \ label {Eq2.2 \) имеем \ (\ dfrac {∂f} {∂x} = 2x \) и \ (\ dfrac {∂f} {∂y} = 2y \), поэтому уравнение касательной плоскости в точке \ ((1,2,5) \) равно

    \ [\ nonumber 2 (1) (x − 1) +2 (2) (y − 2) — z +5 = 0 \ text {, или} \]

    \ [\ nonumber 2x + 4y− z −5 = 0 \]

    Аналогичным образом можно показать, что если поверхность определяется неявно уравнением вида \ (F (x, y, z) = 0 \), то касательная плоскость к поверхности в точке \ ( (a, b, c) \) задается уравнением

    \ [\ dfrac {∂F} {∂x} (a, b, c) (x− a) + \ dfrac {∂F} {∂y} (a, b, c) (y− b) + \ dfrac {∂F} {∂z} (a, b, c) (z — c) = 0 \ label {Eq2.2 −9 \) имеем \ (\ dfrac {∂F} {∂x} = 2x \), \ (\ dfrac {∂F} {∂y} = 2y \) и \ (\ dfrac {∂F } {∂z} = 2z \), поэтому уравнение касательной плоскости в точке (2,2, −1) равно

    \ [\ nonumber 2 (2) (x − 2) +2 (2) (y − 2) +2 (−1) (z +1) = 0 \ text {, или} \]

    \ [\ nonumber 2x + 2y− z −9 = 0 \]

    Авторы и авторство

    Нахождение уравнения прямой, касательной к функции | Ретт Аллен | The Startup

    Нет особой причины для этого поста. Я просто собираюсь решить математическую задачу.Почему? Потому что я думаю, это весело. Вот в чем проблема.

    Найдите уравнение прямых, которые проходят через точку (-1, -4) и касаются функции f (x) = 3x².

    Вот и все. Это проблема. Вот план. Я собираюсь решить эту конкретную проблему, а затем покажу вам отличный способ сделать это с помощью Python (для удовольствия).

    Итак, давайте разберемся с вопросом. Во-первых, что это вообще значит? Что ж, будет линия, проходящая через точку (-1, -4) — это ясно.Но это также должно касаться функции. Касательная к функции линия «коснется» ее всего в одной точке. Наклон линии будет равен производной этой функции в точке, которой она касается.

    На всякий случай, если вы не помните деривативы, вот краткий обзор.

    Хорошо, а теперь набросок, чтобы мы «грокнули» все это. Вот функция, точка (-1, -4) и точка касания (которую мы еще не знаем).

    О, обратите внимание, что неизвестная точка функции имеет значение x, равное «x», и значение y, равное f (x).Теперь есть два способа найти наклон этой касательной. Первый способ — просто использовать определение уклона вместе с двумя нашими известными точками. Я собираюсь использовать букву «m» для наклона.

    Второй способ найти наклон — использовать производную функции. Я назову производную «f’ (x) ». Мы можем найти производную, используя правило мощности.

    Поскольку оба этих метода должны иметь одинаковый наклон, я могу установить их равными друг другу.

    Теперь мне просто нужно решить относительно x.Я умножу обе стороны на (x + 4), а затем перенесу все члены в одну сторону.

    Используя квадратное уравнение, я получаю ДВА ответа. Это:

    Ради удовольствия, позвольте мне построить точки функции, соответствующие этим двум значениям x.

    Ага. Выглядит хорошо. Если вы проведете прямую линию из точки (-1, -4), похоже, что она просто коснется функции в обеих этих точках. Теперь нам просто нужно уравнение для этой линии (ну, обеих линий). Здесь я могу использовать формулу угла наклона линии, чтобы получить следующее.Ой, погоди. Во-первых, мне нужно поместить значения x BACK в исходную функцию, чтобы получить значения y этих точек. Кроме того, мне нужно ввести это значение x, чтобы найти наклон. Делая это, СЕЙЧАС я получаю:

    Это выглядит безумно, но ТЕХНИЧЕСКИ, это уравнение линии. Я не собираюсь это упрощать. Я должен был выбрать лучшие ценности, чтобы дать более хороший ответ, — но жизнь не всегда хороша (я говорю с вами, 2020 год).

    Вы можете сделать то же самое для другого значения x и получить вторую строку.Но теперь по-другому.

    Путь Python

    Я просто хочу это сделать. Это будет весело. Я не буду вдаваться в подробности программы, поэтому позвольте мне дать вам обзор.

    • Сначала я просто построю график функции и точки (точно так же, как график выше, который также был создан на Python).
    • Затем я могу переместить точку вдоль кривой функции. Это означает, что у меня будет два очка.
    • С этими двумя точками я сделаю две вещи.Сначала вычислите наклон от фиксированной точки до точки на кривой. Во-вторых, найдите производную функции в этой точке (в данном случае я использую числовую производную, если вы не можете найти фактическую производную функции). Вот руководство по числовым производным с помощью Python.
    • Поскольку я не смотрю на КАЖДУЮ единственную точку функции (потому что она числовая), я собираюсь искать такие значения x, чтобы разница между наклоном и производной была очень маленькой (но не обязательно нулевой).
    • О, мне просто нужно было научиться создавать анимированные графики в VPython — теперь я знаю, как это делать.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *