Методы решения иррациональных уравнений

Я бы почувствовал настоящее
удовлетворение лишь в том случае,
если бы смог передать ученику гибкость ума,
которая дала бы ему в дальнейшем
возможность самостоятельно решать задачи.

У.У.Сойер.

Определение. Уравнение с одной переменной называют иррациональным, если хотя бы одна из функций или содержит переменную под знаком радикала.

При решении иррациональных уравнений необходимо установить область допустимых значений переменных, исходя из условия, что все радикалы, входящие в уравнение, должны быть арифметическими.

1. Метод пристального взгляда

Этот метод основан на следующем теоретическом положении: “Если функция возрастает в области определения и число входит в множество значений, то уравнение имеет единственное решение

.”

Для реализации метода, основанного на этом утверждении требуется:

а) Выделить функцию, которая фигурирует в уравнении.

b) Записать область определения данной функции.

c) Доказать ее монотонность в области определения.

d) Угадать корень уравнения.

t) Обосновать, что других корней нет.

f) Записать ответ.

Пример 1. .

Наличие радикалов четной степени говорит о том, что подкоренные выражения должны быть неотрицательными. Поэтому сначала найдем область допустимых значение переменной .

Очевидно, что левая часть уравнения не существует ни при одном значении неизвестного . Таким образом, вопрос о решении уравнения снимается – ведь нельзя же осуществить операцию сложения в левой части уравнения, так как не существует сама сумма. Каков же вывод? Уравнение не может иметь решений, так как левая часть не существует ни при одном значении неизвестного .

Пример 2.

Рассмотрим функцию .

Найдем область определения данной функции:

Данная функция является монотонно возрастающей.

Для эта функция будет принимать наименьшее значение при , а далее только возрастать.. Число 5 принадлежит области значения, следовательно, согласно утверждению .

Проверкой убеждаемся, что это действительный корень уравнения..

2. Метод возведения обеих частей уравнений в одну и ту же степень.

Теорема.

Если возвести обе части уравнения (1) в натуральную степень , то уравнение (2) является следствием уравнения (1).

Доказательство. Если выполняется числовое равенство , то по свойствам степени выполняется равенство , т.е. каждый корень уравнения (1) является и корнем уравнения (2), это значит, что уравнение (2) является следствием уравнения (1).

Если , то справедливо и обратная теорема. В этом случае уравнения (1) и (2) равносильны.

Если , равенство справедливо, если выполняется хотя бы одно из равенств и . Значит уравнения (1) и (2) в этом случае не равносильны. Поэтому, если в ходе решения иррационального уравнения приходилось возводить обе его части в степень с четным показателем, то могли появиться посторонние корни. Чтобы отделить их, проверки можно избежать, введя дополнительное требование . В этом случае уравнение равносильно системе . В системе отсутствует требование , обеспечивающее существование корня степени , т.к. оно было бы излишним в связи с равенством .

Пример 1.

,

,

.

Ответ:

Если в уравнение входят несколько радикалов, то их можно последовательно исключать с помощью возведения в квадрат, получая в итоге уравнение вида При этом полезно учитывать область допустимых значений исходного уравнения.

Пример 2. 

Ответ:

3. Решение уравнений с использованием замены переменной.

Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.

Пример1. 

Пусть тогда исходное уравнение примет вид:

, корни которого и Решая уравнение , получаем и

Ответ:

В следующих примерах используется более сложная замена переменной.

Пример 2

Перенесем в левую часть все члены уравнения и произведем дополнительные преобразования: .

Замена приводит уравнение к виду корнями которого являются и

Осталось решить совокупность двух уравнений:

Ответ:

4. Метод разложения на множители выражений, входящих в уравнение.

Теорема.

Уравнение , определенное на всей числовой оси, равносильно совокупности уравнений

Пример1.

При уравнение принимает вид: которое равносильно совокупности двух уравнений:

Ответ:

Выделить общий множитель часто бывает очень трудно. Иногда это удается сделать после дополнительных преобразований. В приведенном ниже примере для этого рассматриваются попарные разности подкоренных выражений.

Пример 2.

Если внимательно посмотреть на уравнение, то можно увидеть, что разности подкоренных выражений первого и третьего , а также второго и четвертого членов этого уравнения равны одной и той же величине

В таком случае далее следует воспользоваться тождеством:

Уравнение примет вид:

или

Корень уравнения т.е. число при подстановке в исходное уравнение дает верное равенство.

Уравнение не имеет решений, так как его левая часть положительна в своей области определения.

Ответ:

5. Метод выделения полных квадратов при решении иррациональных уравнений.

При решении некоторых иррациональных уравнений полезна формула

Пример 1.

Преобразуем уравнение следующим образом:

или

Обозначим и решим полученное уравнение

методом интервалов.

Разбирая отдельно случаи , находим,

что решениями последнего уравнения являются .

Возвращаясь к переменной , получаем неравенства

Ответ:

6. Метод оценки.

Этот способ применим в том случае, когда подкоренные выражения представляют собой квадратный трехчлен, не раскладывающийся на линейные множители. Поэтому целесообразно оценить левую и правую части уравнения.

Пример 1.

Оценим обе части уравнения:

,

,

Левая часть уравнения существует при всех значениях переменной , не меньших 5, а правая – при всех значениях, не больших 5, следовательно, уравнение будет иметь решение, если обе части уравнения одновременно равны 5, т. е. справедлива следующая система:

Корнем второго уравнения системы является число

Проверим, является ли это число корнем второго уравнения:

.

Ответ:

Пример 2.

Для всех имеем

Используя неравенство Коши, можем записать:

причем равенство достигается при и

Таким образом, -корень исходного уравнения.

Ответ:

7. Иррациональные уравнения, содержащие степени выше второй.

Если уравнение имеет вид то его можно решить , возводя обе части этого уравнения в степень . Полученное уравнение при нечетном равносильно данному уравнению, а при четном является нго следствием, аналогично рассмотренному выше случаю при

Пример 1

Возведем обе части уравнения в куб:

или

которое равносильно совокупности двух уравнений:

Ответ:

При решении иррациональных уравнений очень часто пользуются следующим приемом.

Если то

В последнем равенстве заменяют на и получают

Далее легко избавиться от кубической иррациональности , возводя обе части в куб.

Пример 2.

Здесь, очевидно,

Возведем в куб обе части уравнения, получим:

,

или

или

или

или

Проверка подтверждает, что это корень уравнения.

Ответ:

Замечание.

Замена в конкретном примере левой части на правую, вообще говоря , неправомерна –ведь нам неизвестно ни одно значение , при котором это уравнение превращается в верное числовое равенство. Возможно, таких решений нет вообще. Допуская в практических действиях такую замену, мы фактически расширяем возможное множество решений. Поэтому все найденные решения следует проверять и только те, которые превращают исходное уравнение в верное равенство, следует записать в ответ.

От того, что школьник решит лишний десяток задач, умнее и сообразительнее он не станет, Результат обучения оценивается не количеством сообщаемой информации, а качеством ее усвоения. Это качество будет выше, если на один и тот же пример посмотреть с разных сторон. Решение задач разными способами способствует развитию активного мышления учащихся. Хорошую почву для этого дает решение примеров разными способами.

Пример 3. Способ 1.

(1)

Возведем обе части уравнения в куб:

Группируя, получаем:

Используя равенство (1) имеем:

или

или

или

корни которого

Ответ:

Способ 2.

Иногда полезно ввести не одну вспомогательную переменную, а несколько, сводя исходное уравнение к системе уравнений.

Пусть Тогда

Таким образом справедлива следующая система:

Возвращаясь к переменной находим

Ответ:

В следующем примере введение вспомогательной переменной сводит исходное уравнение к однородному.

Пример 4.

Положим

Тогда исходное уравнение примет вид:

Поскольку при котором переменная обращается в нуль, не является решением исходного уравнения ( в чем можно убедиться подстановкой), делим обе части уравнения на

решая которое , находим:

Осталось решить уравнения и

Корнями этих уравнений являются числа

Ответ:

Пример 5.

Область допустимых значений задается неравенством

Преобразуем уравнение следующим образом:

Один корень этого уравнения

Для решения второго уравнения положим

и решим

Корни этого уравнения

Последний корень не принадлежит указанному промежутку, поэтому, решая уравнение , получим

Ответ :

urok.1sept.ru

учимся решать методом уединения корня

1 октября 2013

Иррациональное уравнение — это любое уравнение, содержащее функцию под знаком корня. Например:

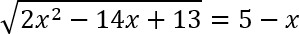
Такие уравнения всегда решаются в 3 шага:

1. Уединить корень. Другими словами, если слева от знака равенства помимо корня стоят другие числа или функции, все это надо перенести вправо, поменяв знак. Слева при этом должен остаться только радикал — без всяких коэффициентов.
2. 2. Возводим обе части уравнения в квадрат. При этом помним, что область значений корня — все неотрицательные числа. Следовательно, функция справа иррационального уравнения также должна быть неотрицательна: g(x) ≥ 0.
3. Третий шаг логично следует из второго: надо выполнить проверку. Дело в том, что на втором шаге у нас могли появиться лишние корни. И чтобы отсечь их, надо подставить полученные числа-кандидаты в исходное уравнение и проверить: действительно ли получается верное числовое равенство?

Решение иррационального уравнения

Разберемся с нашим иррациональным уравнением, данным в самом начале урока. Тут корень уже уединен: слева от знака равенства нет ничего, кроме корня. Возводим обе стороны в квадрат:

2x² − 14x + 13 = (5 − x)²
2x² − 14x + 13 = 25 − 10x + x²
x² − 4x − 12 = 0

Решаем полученное квадратное уравнение через дискриминант:

D = b² − 4ac = (−4)² − 4 · 1 · (−12) = 16 + 48 = 64
x₁ = 6; x₂ = −2

Осталось лишь подставить эти числа в исходное уравнение, т.е. выполнить проверку. Но и тут можно поступить грамотно, чтобы упростить итоговое решение.

Как упростить решение

Давайте подумаем: зачем вообще мы выполняем проверку в конце решения иррационального уравнения? Мы хотим убедиться, что при подстановке наших корней справа от знака равенства будет стоять неотрицательное число. Ведь мы уже точно знаем, что слева стоит именно неотрицательное число, потому что арифметический квадратный корень (из-за которого наше уравнение и носит название иррационального) по определению не может быть меньше нуля.

Следовательно, все, что нам надо проверить — это чтобы функция g(x) = 5 − x, которая стоит справа от знака равенства, была неотрицательной:

g(x) ≥ 0

Подставляем наши корни в эту функцию и получаем:

g(x₁) = g(6) = 5 − 6 = −1 < 0
g(x₂) = g(−2) = 5 − (−2) = 5 + 2 = 7 > 0

Из полученных значений следует, что корень x₁ = 6 нас не устраивает, поскольку при подстановке в правую часть исходного уравнения мы получаем отрицательное число. А вот корень x₂ = −2 нам вполне подходит, потому что:

1. Этот корень является решением квадратного уравнения, полученного в результате возведения обеих сторон иррационального уравнения в квадрат.
2. Правая сторона исходного иррационального уравнения при подстановке корня x₂ = −2 обращается в положительное число, т.е. область значений арифметического корня не нарушена.

Вот и весь алгоритм! Как видите, решать уравнения с радикалами не так уж и сложно. Главное — не забывать проверять полученные корни, иначе очень велика вероятность получить лишние ответы.

Смотрите также:

1. Как решать биквадратное уравнение
2. Как решать простейшие линейные уравнения? Рассмотрены все варианты: один корень, бесконечно много корней или корней нет вообще.
3. Сравнение дробей
4. Типичные задачи B12 с функциями
5. Четырехугольная пирамида: как найти координаты вершин
6. Задача B4: Цены на продукты в трех городах

www.berdov.com

Как решать уравнения с корнями | ЧтоКак.ру

Иногда в уравнениях встречается знак корня. Многим школьникам кажется, что решать такие уравнения «с корнями» или, правильнее выражаясь, иррациональные уравнения очень сложно, но это не так.

Инструкция

1

В отличие от других типов уравнений, например, квадратных или систем линейных уравнений, для решения уравнений с корнями, или точнее, иррациональных уравнений, не существует стандартного алгоритма. В каждом конкретном случае необходимо подобрать наиболее подходящий метод решения, исходя из «внешнего вида» и особенностей уравнения.Возведение частей уравнения в одинаковую степень.Чаще всего для решения уравнений с корнями (иррациональных уравнений) применяется возведение обеих частей уравнения в одну и ту же степень. Как правило, в степень, равную степени корня (в квадрат для корня квадратного, в куб для корня кубического). При этом следует иметь ввиду, что при возведении левой и правой части уравнения в четную степень у него могут появиться «лишние» корни. Поэтому, в этом случае следует проверять полученные корни путем подстановки их в уравнение. Особое внимание при решении уравнений с квадратными (четными) корнями следует уделить области допустимых значений переменной (ОДЗ). Иногда одной только оценки ОДЗ достаточно для решения или существенного «упрощения» уравнения.Пример. Решить уравнение:?(5х-16)=х-2Возводим обе части уравнения в квадрат:(?(5х-16))?=(х-2)?, откуда последовательно получаем:5х-16=х?-4х+4х?-4х+4-5х+16=0х?-9х+20=0Решая полученное квадратное уравнение, находим его корни:х=(9±?(81-4*1*20))/(2*1)х=(9±1)/2х1=4, х2=5Подставив оба найденных корня в исходное уравнение, получаем верное равенство. Следовательно оба числа являются решениями уравнения.

2

Метод введения новой переменной.Иногда найти корни «уравнения с корнями» (иррационального уравнения) удобнее методом введения новых переменных. Фактически, суть этого метода сводится просто к более компактной записи решения, т.е. вместо того, чтобы каждый раз писать громоздкое выражение, его заменяют условным обозначением.Пример. Решить уравнение: 2х+?х-3=0Можно решить данное уравнение и возведением обеих частей в квадрат. Однако, сами вычисления при этом будут выглядеть довольно-таки громоздко. При введении новой переменной процесс решения получится намного элегантнее:Введем новую переменную: у=?хПосле чего получаем обыкновенное квадратное уравнение:2у?+у-3=0, с переменной у.Решив полученное уравнение, находим два корня:у1=1 и у2=-3/2,подставляя найденные корни в выражение для новой переменной (у), получаем:?х=1 и ?х=-3/2.Так как значение квадратного корня не может быть отрицательным числом (если не затрагивать область комплексных чисел), то получаем единственное решение:х=1.

chtokak.ru

Уравнение. Корень уравнения

Уравнение – это равенство, которое справедливо не при любых значениях входящих в него букв, а только при некоторых. Так же можно сказать, что уравнение является равенством, содержащим неизвестные числа, обозначенные буквами.

Например, равенство 10 — x = 2 является уравнением, так как оно справедливо только при x = 8. Равенство x² = 49 это уравнение, справедливое при двух значениях x, а именно, при x = +7 и x = -7, так как (+7)² = 49 и (-7)² = 49.

Если вместо x подставить его значение, то уравнение превратится в тождество. Такие переменные, как x, которые только при определённых значениях обращают уравнение в тождество, называются неизвестными уравнения. Они обычно обозначаются последними буквами латинского алфавита x, y и z.

Любое уравнение имеет левую и правую части. Выражение, стоящее слева от знака =, называется левой частью уравнения, а стоящее справа – правой частью уравнения. Числа и алгебраические выражения, из которых состоит уравнение, называются членами уравнения:

Корни уравнения

Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство. Уравнение может иметь всего один корень, может иметь несколько корней или не иметь корней вообще.

Например, корнем уравнения

10 — x = 2

является число 8, а у уравнения

x² = 49

два корня – +7 и -7.

Решить уравнение – значит, найти все его корни или доказать, что их нет.

Виды уравнений

Кроме числовых уравнений, подобных приведённым выше, где все известные величины обозначены числами, существуют ещё буквенные уравнения, в которые кроме букв, обозначающих неизвестные, входят ещё буквы, обозначающие известные (или предполагаемые известные) величины.

Пример:

x — a = b + c
3x + c = 2a + 5

По числу неизвестных уравнения разделяются на уравнения с 1-м неизвестным, с 2-мя неизвестными, с 3-мя и более неизвестными.

Пример:

7x + 2 = 35 — 2x – уравнение с одним неизвестным,
3x + y = 8x — 2y – уравнение с двумя неизвестными.

naobumium.info

Найти корень уравнения? Это просто! :: SYL.ru

В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.

Что подразумевается под уравнением и его корнем?

Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.

Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.

Поиск всех возможных корней уравнения является его решением. То есть нужно выполнить ряд математических действий, которые его упрощают. А потом приводят к равенству, в котором содержится только неизвестная и какое-либо число.

В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.

Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.

О линейном уравнении

Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.

Алгоритм преобразований:

• перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
• разделить обе части получившегося равенства на коэффициент «а».

Общий вид решения такой:

х = -в/а.

Из него ясно, что ответом будет одно число. То есть всего один корень.

Квадратное уравнение

Его общий вид: а * х² + в * х + с = 0. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.

Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в² — 4 а * с. После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.

Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант

В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:

х_1,2 = (-в ± √Д) / (2 * а).

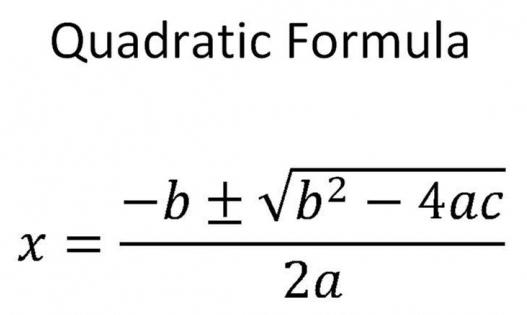
Здесь всегда получится два ответа. Это связано с тем, что в исходной формуле стоит знак «плюс/минус». Он существенно изменяет значение неизвестной.

При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:

х = (-в) / (2 * а).

При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.

Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.

Формулы для расчета корней квадратного уравнения, не использующие дискриминант

Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:

х² + в * х + с = 0.

Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:

х₁ + х₂ = -в
и
х₁ * х₂ = с.

Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.

К этому варианту всегда можно прийти от общего вида квадратного уравнения.

Достаточно только разделить все коэффициенты на «а».

Как быть, если нужно узнать наименьшее значение корня?

Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.

Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:

2 х⁵ + 2 х⁴ — 3 х³ — 3 х² + х + 1 = 0.

Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.

В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х⁴, во второй 3 х². Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.

После множителя (х + 1) будет стоять (2 х⁴ — 3 х² + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.

Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.

Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х² = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.

Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».

Нужно вернуться к введенному обозначению. х_1,2 = ± 1, х_3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.

В качестве заключения

Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.

Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.

Если х = -1, то получается такой же результат. Корень тоже подходящий.

Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.

Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.

Вывод: надо помнить о проверке и внимательно подходить к решению.

www.syl.ru

Что такое корень уравнения 🚩 Корень уравнения определение 🚩 Математика

В составе уравнения должны присутствовать два алгебраических выражения, равные между собой. Каждое из этих выражений содержит неизвестные. Неизвестные алгебраических выражений также называют переменными. Это связано с тем, что у каждой неизвестной может быть одно, два или неограниченное количество значений.

Например, в уравнении 5Х-14=6 значение у неизвестной Х только одно: Х=4.

Для сравнения возьмем уравнение У-Х=5. Здесь корней может быть найдено бесконечное количество. Значение неизвестной У будет меняться в зависимости от того, какое принято значение Х, и наоборот.

Определить все возможные значения переменных – значит найти корни уравнения. Для этого уравнение необходимо решить. Это осуществляется посредством математических действий, в результате которых алгебраические выражения, а вместе с ними и само уравнение, сокращаются до минимума. В результате либо определяется значение одной неизвестной, либо устанавливается взаимная зависимость двух переменных.

Чтобы проверить верность решения необходимо подставить в уравнение найденные корни и решить получившийся математический пример. В результате должно получиться равенство двух одинаковых чисел. Если равенства двух чисел не получилось, то уравнение решено неверно и, соответственно, корни не найдены.

Для примера возьмем уравнение с одной неизвестной: 2Х-4=8+Х.

Находим корень данного уравнения:

2Х-Х=8+4

Х=12

С найденным корнем решаем уравнение и получаем:

2*12-4=8+12

24-4=20

20=20

Уравнение решено верно.

Однако если принять за корень данного уравнения число 6, то получится следующее:

2*6-4=8+6

12-4=14

8=14

Уравнение решено неверно. Вывод: число 6 не является корнем данного уравнения.

Однако не всегда корни могут быть найдены. Уравнения, не имеющие корней, называются неразрешимыми. Так, например, не будет корней у уравнения Х2=-9, так как любое значение неизвестной Х, возведенное в квадрат, должно дать положительное число.

Таким образом, корень уравнения – это значение неизвестной, которое определяется путем решения данного уравнения.

www.kakprosto.ru

Квадратное уравнение с комплексными корнями

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Определение 1

Двучленным называется уравнение вида $x^{n} =A$.

Рассмотрим три случая:

• В случае если $A$ — это положительное действительное число, то корни уравнения находятся по формуле
\[x_{k} =\sqrt[{n}]{A} \cdot \left(\cos \frac{2k\pi }{n} +i\cdot \sin \frac{2k\pi }{n} \right),\, \, \, k=0,..,n-1.\]
• В случае если $A$ — это отрицательное действительное число, то корни уравнения находятся по формуле
\[x_{k} =\sqrt[{n}]{|A|} \cdot \left(\cos \frac{\pi +2k\pi }{n} +i\cdot \sin \frac{\pi +2k\pi }{n} \right),\, \, \, k=0,..,n-1.\]
• В случае если $A$ — это комплексное число, то корни уравнения находятся по формуле
\[x_{k} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.\]

Пример 1

Решить уравнение: $x^{3} =8$.

Решение:

Так как $A>0$, то $x_{k} =\sqrt[{3}]{8} \cdot \left(\cos \frac{2k\pi }{3} +i\cdot \sin \frac{2k\pi }{3} \right),\, \, \, k=0,..,2$.

При $k=0$ получаем $x_{0} =\sqrt[{3}]{8} \cdot \left(\cos 0+i\cdot \sin 0\right)=\sqrt[{3}]{8} =2$.

При $k=1$ получаем

\[x_{1} =\sqrt[{3}]{8} \cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)=\sqrt[{3}]{8} \cdot (-\frac{1}{2} +\frac{\sqrt{3} }{2} \cdot i)=2\cdot (-\frac{1}{2} +\frac{\sqrt{3} }{2} \cdot i)=-1+\sqrt{3} \cdot i.\]

При $k=2$ получаем

\[x_{2} =\sqrt[{3}]{8} \cdot \left(\cos \frac{4\pi }{3} +i\cdot \sin \frac{4\pi }{3} \right)=\sqrt[{3}]{8} \cdot (-\frac{1}{2} -\frac{\sqrt{3} }{2} \cdot i)=2\cdot (-\frac{1}{2} -\frac{\sqrt{3} }{2} \cdot i)=-1-\sqrt{3} \cdot i.\]

Пример 2

Решить уравнение: $x^{3} =1+i$.

Решение:

Так как $A$ — комплексное число, то

\[x_{k} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1,\, \, \, k=0,..,2.\]

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

\[r=\sqrt{1^{2} +1^{2} } =\sqrt{1+1} =\sqrt{2} \]

Вычислим аргумент исходного комплексного числа:

\[\varphi =\arg z=arctg\frac{1}{1} =arctg1=\frac{\pi }{4} \]

Подставим полученные значения и получим:

\[A=\sqrt{2} \cdot (\cos \frac{\pi }{4} +i\sin \frac{\pi }{4} )\]

Уравнение перепишем в виде:

\[x^{3} =\sqrt{2} \cdot (\cos \frac{\pi }{4} +i\sin \frac{\pi }{4} )\]

При $k=0$ получаем $x_{0} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4}{3} +i\cdot \sin \frac{\pi /4}{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)=\sqrt[{6}]{2} \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)$.

При $k=1$ получаем

\[\begin{array}{l} {x_{1} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+2\pi }{3} +i\cdot \sin \frac{\pi /4+2\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)} \end{array}\]

При $k=2$ получаем

\[\begin{array}{l} {x_{2} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+4\pi }{3} +i\cdot \sin \frac{\pi /4+4\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)} \end{array}\]

Определение 2

Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом

\[x_{1,2} =\frac{-b\pm \sqrt{D} }{2a} .\]

Примечание 1

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

Пример 3

Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.

Решение:

Вычислим дискриминант:

\[D=2^{2} -4\cdot 1\cdot 5=4-20=-16.\]

Так как $D \[x_{1,2} =\frac{-2\pm \sqrt{-16} }{2} =\frac{-2\pm i\cdot \sqrt{16} }{2} =\frac{-2\pm i\cdot 4}{2} =-1\pm 2i.\]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

Рис. 1

Примечание 2

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Определение 3

Комплексное число вида $\overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Примечание 3

Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.

Пример 4

Зная корни уравнения $x_{1,2} =1\pm 2i$, записать исходное уравнение.

Решение:

Запишем уравнение следующим образом:

\[(x-(1-2i))\cdot (x-(1+2i))=0.\]

Выполним умножение комплексных чисел

\[x^{2} -(1-2i)\cdot x-x\cdot (1+2i)+(1-2i)\cdot (1+2i)=0\]\[x^{2} -x+2i\cdot x-x-2i\cdot x+1-4i^{2} =0\] \[x^{2} -2x+1+4=0\] \[x^{2} -2x+5=0\]

Следовательно, $x^{2} -2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Пример 5

Решить уравнение: $z^{2} +(1-2i)\cdot z-(1+i)=0$ и изобразить корни на плоскости.

Решение:

Вычислим дискриминант:

\[D=(1-2i)^{2} +4\cdot 1\cdot (1+i)=1-4i+4i^{2} +4+4i=1-4+4=1.\]

Так как $D>0$, уравнение имеет два корня:

\[x_{1} =\frac{-(1-2i))-\sqrt{1} }{2} =\frac{-1+2i-1}{2} =\frac{-2+2i}{2} =-1+i.\] \[x_{2} =\frac{-(1-2i))+\sqrt{1} }{2} =\frac{-1+2i+1}{2} =\frac{2i}{2} =i.\]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

Рис. 2

Примечание 4

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

spravochnick.ru