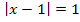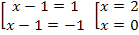Материал для подготовки к ЕГЭ (ГИА) по алгебре (10 класс) на тему: Уравнения_с_модулями
Занятие 1. Алгебраические уравнения с модулем.
(2 часа).
Теоретический материал.
Чтобы решить уравнение, содержащее переменную под знаком модуля, следует освободиться от знака модуля, воспользовавшись его определением:
х, если х0
= — х , если х
При решении таких уравнений обычно поступают следующим образом:
- находят те значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль;
- область допустимых значений переменной разбивается на промежутки, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак;
- на каждом из найденных промежутков решается уравнение без знака модуля.
Совокупность решений на указанных промежутках составляет решение исходного уравнения.
Пример 1. Решите уравнение: .
Решение.
Найдем те значения переменной, при которых выражение, стоящее под знаком модуля, обращаются в нуль: х – 2 = 0, х = 2.
— +
2 х
Рассмотрим решение уравнения на промежутках: х (2; ).
1. Если х , то 2 – х = 5; — х = 3; х = — 3; — 3
2. Если : х(2; ), то х – 2 = 5; х = 7; 7(2; ).
Ответ: — 3; 7.
Пример 2. Решите уравнение: = х + 2.
Решение.
В левой части уравнения стоит неотрицательное число, следовательно
х + 2 0., т.е. х — 2. Раскроем модуль с учетом, что х — 2, получим:
х + 2 = х +2, решением уравнения является любое число х .
Ответ: .
Пример 3. Решите уравнение: .
Решение.
Найдем те значения переменной, при которых выражения, стоящие
под знаком модуля, обращаются в нуль: 2х + 1+ 0; х = — 0,5; х – 4 =0; х = 4.
— — + — + +
— 0,5 4 х
Рассмотрим решение уравнения на промежутках: х(4;+).
1. Если х, то -2х – 1 = — х + 4; -х = 5; х = — 5;
— 5 .
2. Если х, то 2х + 1 = — х +4; 3х = 3; х = 1.
1 .
3. Если х(4; +), то 2х + 1 = х – 4; х = — 5;
— 5 (4; +).
Ответ: — 5; 1.
Пример 4. Решите уравнение: 0,6 = х 2 + 0,27.
Решение.
Найдем то значения переменной, при котором выражение, стоящее под знаком модуля, обращаются в нуль: х – 0,3 = 0; х = 0,3.
— +
0,3 х
1. Если х, то
0,6(0,3 – х) = х 2 + 0,27;
0,18 – 0,6х = х 2 + 0,27;
х 2 + 0,6х + 0,09 = 0;
D = 0,36 – 0,36 = 0;
х = — 0,3; — 0,3 .
2. Если х(0,3; +), то
0,6(х — 0,3) = х 2 + 0,27;
0,6 х – 0,18 = х 2 + 0,27;
х 2 – 0,6х + 0,45 = 0;
D = 0,36 – 1,8 = — 1,44, т.к. D
Ответ: — 0,3.
Пример 5. Решите уравнение: х2 + 4- 7х + 11 = 0.
Решение.
Найдем то значения переменной, при котором выражение, стоящее под знаком модуля, обращаются в нуль: х – 3 = 0; х = 3.
— +
3 х
1. Если х, то:
х2 – 4(х – 3) – 7х + 11 = 0;
х2 – 4х + 12 – 7х + 11 = 0;
х2 – 11х + 23 = 0;
D = 29;
х1,2 = ; х1 = ; ;
х2 = ; ;
2. Если х (3; , то:
х 2 + 4х — 12 – 7х + 11 = 0;
х2 — 3х – 1 = 0;
D =13;
х1,2 = ; х1 = ; (3; ,
х2 = ; (3; .
Ответ: ; .
Решите самостоятельно:
1. = -2. Ответ: пустое множество;
2. = 5. Ответ: — 7; 3.
3. = 11. Ответ: — 4; 7.
4. = х. Ответ: пустое множество.
5. = 5 – 4х. Ответ: 1.
6. = 4х – 3. Ответ: .
7. = — х – 2. Ответ: .
8. . Ответ: — 3,5; 3,5.
9. = + 2. Ответ: — 7; — 1.
10. . Ответ: -; 2.
.
nsportal.ru
План-конспект занятия по алгебре (10 класс) на тему: Решение уравнений с модулем и параметром
Пирогова Татьяна Николаевна г. Таганрог МОУ СОШ № 10.
Тема: «Решение уравнений с модулем и параметром»
10 класс, занятие элективного курса «Свойства функции».
План урока.
- Мотивация.
- Актуализация знаний.
- Решение линейного уравнения с модулем разными способами.
- Решение уравнений содержащих модуль под модулем.
- Исследовательская работа по определению зависимости количества корней уравнения
| |х| — а |= в от значений а и в.
- Решение уравнений с двумя модулями и параметром.
- Рефлексия.
Ход урока.
Мотивация. Как говорили древние философы «Мудрость – это любовь к знаниям, а любовь – это мера всех вещей». «Мера» на латинском языке — «modulus», от него и произошло слово «модуль». И сегодня мы с вами поработаем с уравнениями, содержащими модуль. Надеюсь, у нас все получится, и в конце урока мы с вами станем мудрее.
Актуализация знаний. Итак, вспомним, что мы уже знаем о модуле.
- Определение модуля. Модулем действительного числа – называется само число, если оно неотрицательно и противоположное ему число, если оно отрицательно.
- Геометрический смысл модуля. Модуль действительного числа а равен расстоянию от начала отсчета до точки с координатой а на числовой прямой.
–a 0 a
|–a| = |a| |a| x
- Геометрический смысл модуля разности величин. Модуль разности величин | а – в | — это расстояние между точками с координатами а и в на числовой прямой,
т.е. длина отрезка [а в]
1) Если a b 2) Если a > b
a b b a
S = b – a S = a – b
3) Если a = b, то S = a – b = b – a = 0
- Основные свойства модуля
- Модуль числа есть число неотрицательное, т.е. |x| ≥ 0 для любого x
- Модули противоположных чисел равны, т.е. |x| = |–x| для любого x
- Квадрат модуля равен квадрату подмодульного выражения, т.е.|x|2 =x2 для любого x
4. Модуль произведения двух чисел равен произведению модулей сомножителей, т.е.|a b| = |a| · |b|
5. Если знаменатель дроби отличен от нуля, то модуль дроби равен частному от деления модуля числителя на модуль знаменателя, т.е. при b ≠ 0
6. Для равенства любых чисел a и b справедливы неравенства:
| |a| – |b| | ≤ |a + b| ≤ |a| + |b|
| |a| – |b| | ≤ |a – b| ≤ |a| + |b|
- График модуля у = | х | — прямой угол с вершиной в начале координат, стороны которого являются биссектрисами 1 и 2 квадрантов.
- Как построить графики функций? у = |х –4|, у = |х +3|, у = |х –3|, у = |х| + 1,
- у = |х| – 3, у = |х| – 5, у = |х – 3| + 3, у = |х – 3| – 2, у = |х + 2| – 5. у = ||х| – а|
Пример. Решить уравнение .
Способ 1. Метод раскрытия модулей по промежуткам.
Способ 2. Непосредственное раскрытие модуля.
Если модуль числа равен 3, то это число 3 или -3.
Способ 3. Использование геометрического смысла модуля.
Необходимо найти на числовой оси такие значения х, которые удалены от 2 на расстояние, равное 3.
Способ 4. Возведение обеих частей уравнения в квадрат.
Здесь используется свойство модуля
2 |
х |
5 |
-1 |
2 |
3 |
3 |
и то, что обе части уравнения неотрицательные.
Способ 5. Графическое решение уравнения .
Обозначим . Построим графики функций и :
Абсциссы точек пересечения графиков дадут корни
-2 -1 0 1 2 3 |
1 |
-2 -1 0 1 2 3 4 5 |
-2 -1 0 1 2 3 |
1 |
-2 -1 0 1 2 3 4 5 |
и .
Самостоятельная работа
решите уравнения:
| х – 1| = 3 | х – 5| = 3 | х –3| = 3 | х + 3| = 3 | х + 5| = 3 | (-2; 4) (2; 8) (0; 6) (-6; 0) (-8;-2) |
А теперь добавьте в условия еще один модуль и решите уравнения:
| |х| – 1| = 3 | |х| –5| = 3 | |х| – 3| = 3 | |х| + 3| = 3 | |х| + 5| = 3 | () () (0) (нет корней) |
Итак, сколько корней может иметь уравнение вида | | х | – а |= в? От чего это зависит?
Исследовательская работа по теме
«Определение зависимости количества корней уравнения | | х | – а |= в от а и в»
Проведем работу по группам, с использованием аналитического, графического и геометрического способов решения.
Определим, при каких условиях данное уравнение имеет 1 корень, 2 корня, 3 корня, 4 корня и не имеет корней.
1 группа (по определению)
2 группа (используя геометрический смысл модуля)
3 группа (используя графики функций)
, а > 0 | , а | ||
1 группа | 2 группа | 3 группа | |
Нет корней | в в ≥ 0 в + а | в в ≥ 0 а + в | в в ≥ 0 в а |
ровно один корень | в > 0 и в + а = 0 | в > 0 и в + а = 0 | в > 0 и в = – а |
ровно два корня | в > 0 и в + а > 0 – в + а | в > 0 и в + а > 0 –в + а | в > 0 и в > | а |
|
ровно три корня | в > 0 и – в + а = 0 | в > 0 и – в + а = 0 | в > 0 и в = а |
ровно четыре корня | в > 0 и – в + а >0 | в > 0 и – в + а >0 | в > 0 и в а |
Сравните результаты, сделайте общий вывод и составьте общую схему.
Конечно, необязательно эту схему запоминать. Главное в проведенном нами исследовании было – увидеть эту зависимость, используя разные методы, и теперь повторить свои рассуждения при решении таких уравнений нам будет уже несложно.
Ведь решение задания с параметром всегда подразумевает некоторое исследование.
Решение уравнений с двумя модулями и параметром.
1. Найти значения р, при каждом из которых уравнение | |х| – р– 3| = 7 имеет ровно один корень.
Решение: | |х| – ( р + 3)| = 7
р+3= -7, р = -10. Или геометрически
р + 3–7 р + 3 р + 3+7 р + 3+7=0, р = -10
— 7 7 по схеме уравнение такого вида имеет ровно один корень, если в = – а, где в=7, а=р+3
2. Найти значения р, при каждом из которых уравнение | |х| – р– 6| = 11 имеет ровно два корня.
Решение: | |х| – ( р + 6)| = 11 геометрически
р + 6–11 р + 6 р + 6+11 р + 6-11р р + 6+11>0, р > -17
— 11 11
по схеме уравнение такого вида имеет ровно два корня, если в + а > 0 и – в + а где в=11, а=р+6. -17 р 5.
3. Найти значения р, при каждом из которых уравнение | |х| – 4р| = 5р–9 имеет ровно четыре корня.
Решение: по схеме уравнение такого вида имеет ровно четыре корня, если
0р–9 р, р > и р
т.е. 1 р 9.
Ответ: 1 р 9.
4. . Найти значения р, при каждом из которых уравнение | |х| – 2р| = 5р+2 не имеет корней. Решение: 5р+2 р+2 =0 и –2р>0, или 5р+2 >0 и 5р+2 р.
р р = –0,4, или р> – 0,4 и р . Ответ: р
5. При каких значениях параметра р уравнение | |х–4| – 3| + 2р= 0 имеет три корня. Найти эти корни.
Преобразуем уравнение к виду:
| |х–4| – 3|= – 2р.
По схеме уравнение такого вида имеет три корня,
если –2р=3>0,
т.е. р = –1,5.
||х–4|–3| = 3,
|х–4|=0, х = 4,
||х–4|=6, х = –2, х =10.
Ответ: при р= –1,5 уравнение имеет три корня: х1 = –2, х2 = 4, х3 =10.
Подведение итогов урока. Рефлексия.
Скажите, какие бы вы выделили главные слова урока? ( Модуль, параметр)
Что мы сегодня повторили? (Определение модуля, геометрический смысл модуля числа и разности чисел, свойства модуля, разные способы решения уравнений)
Что мы сегодня делали?
Что делали? — повторяли — решали — исследовали -обобщали -доказывали — строили | Модуль параметр | Что повторили? -определение — геометрический смысл — свойства — графики -уравнения — разные методы |
Домашнее задание.
nsportal.ru
Урок по алгебре (спецкурс) в 10 классе » Уравнения с модулем»
Учитель Кирилюк Н. А.
Предмет: Спецкурс по математике
Класс – 10-А Дата: 24.03 Урок №
Тема. Решение уравнений с модулем
Цель: обобщить и систематизировать знания о модуле, полученные ранее, познакомить со способами решения уравнеий, формировать умения и навыки решения уравнений с модуле.
развивать логическое мышление, математическую культуру речи и письма , вычислительные навыки;
воспитывать настойчивость, усердие, чувство уверенности в себе, умение работать в коллективе; интерес к изучаемому материалу;
формировать такие виды компетентностей: информационную, познавательную, коммуникативную, социальную.
Планируемые результаты обучения
Учащиеся приобретут следующие умения:
— личностные:
· Развитие инициативности, самостоятельности, навыков сотрудничества в разных видах деятельности;
· Развитие интереса к познанию нового.
— метапредметные:
— Развитие логического мышления;
· Развитие культуры грамотной математической речи;
— предметные:
— Умение выстраивать логическую цепочку рассуждений, аргументировать свои действия, выполнять доказательства.
Формирование УУД (универсальные учебные действия):
Регулятивные: осуществлять итоговый и пошаговый контроль результата; выстраивать алгоритм действий; корректировать деятельность: выделение и осознание того, что уже усвоено и что подлежит усвоению, осознание качества и уровня усвоения.
Личностные: определять новый уровень отношения к самому себе как субъекту деятельности; формировать способность к мобилизации сил и энергии, к волевому усилию
Познавательные
строить логические рассуждения, включающие установление причинно-следственных связей; строить речевые высказывания в устной и письменной форме; уметь осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий;
Коммуникативные организовывать и планировать учебное сотрудничество с учителем и одноклассниками; формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы
Тип модуля: содержательно — поисковый
Вид модуля: комбинированный
Оборудование: учебник, тетради, раздаточный материал
IV. Изучение нового материала и его первичное закрепление.Коллективная работа
30 мин.
V. Самостоятельная деятельность
Работа в парах, работа в группах
20 мин
VI. Домашнее завдание
5 мин
VII Итог урока. Рефлексия..
5 мин
Сценарий урока
II. Мотивация учебной деятельности учащихся . Самопостановка целей и задач на урок.
К. С. Станиславский любил рассказывать такую притчу: «Индийский магараджа считал умение сосредоточиться настолько важным, что решил назначить министром того, кто владеет им лучше других. Поэтому он предложил претенденту на эту должность пронести по стене вокруг города большой кувшин с молоком, не пролив ни капли. При этом слуги должны были его всячески отвлекать. Многие пытались пронести кувшин, но терпели неудачу. Только один человек сумел выполнить условие магараджи. «Ты слышал крики?» — спросили его потом. «Нет».— «Ты слышал звуки выстрелов?» — «Нет».— «Ты видел, как вокруг тебя плясали, смеялись, прыгали?» — «Нет. Я ничего не видел и не слышал. Я смотрел на молоко». О чём эта притча? Как вы считаете? (о внимании)
III . Актуализация опорных знаний учеников
1. Проверка домашнего задания(самопроверка). Коррекция знаний учащихся.
2. Повторение. Заполнение пропусков в таблице с теоретическими сведениями
Заполните пропуски в утверждениях:
Модуль произведения двух и более чисел равен________________________________________.
5.
Постоянный положительный множитель можно выносить ___________________________________
3. Устные упражнения
№ 1.Решить уравнения:
|x−3|=6
|x|=2,8
|2x−8|=4
|3−3x|=6
|10x+5|=−2
№ 2. Упростить выражение √(2a−6)2 если:
а) а−3≥0
б) a−3<0
IV. Изучение нового материала и его первичное закрепление.
1.Свойства модуля
1. |a| ≥ 0.
2. |a| ≥ a
3. (b≠0)
4. |a|=| —a|
5.
6. | a + b|≤| a|+|b|
7. | a+b|=|a|+|b|, когда ab≥0
8. | a+b|= a + b, когда a≥0, b≥0
9. |a – b| = |a|+|b|, когда ab≤0
10. |a|—|b|≥0, когда
2. Способы решения уравнений с модулем
Решения уравнений вида |f(x)|=b (b≥0)
| f(x)|=b
Пример 1.
|
Решение
=>
Ответ: ; 3; -1.
Решение уравнений с модулем по определению
Пример 2. Решим уравнение
Решение
=> =>
Ответ: -3; -2; 2; 3.
Решение уравнений вида |f(x)|=g(x)
|f(x)|=g(x) или |f(x)|=g(x)
Пример 3. Решим уравнение |3x+1|+x=9
|3x+1|=9-x => =>=>
Ответ:-5;2.
Решение уравнений вида |f(x)|=|g(x)|
|f(x)|=|g(x)| или |f(x)|=|g(x)|
Пример 4.
Решим уравнение |x+5|=|10+x
Решение
;
10x=-75
X=-7.5
Ответ: -7.5
Решение уравнений с модулем по общей схеме
1) Найти ОДЗ.
2)Найти нули всех функций в модуле.
3)Обозначить нули на ОДЗ и разбить ОДЗ на промежутки.
4)Найти решения в каждом промежутке и проверить, входит ли это решение в рассмотренный промежуток.
Пример 5. Решим уравнение |x-2|+|x-4|=3
Решение
1)ОДЗ: R.
2) x-2=0, x=2
x-4=0, x=4.
3)
x-2 — + +
x-4 — — +
4)Найдем решение в каждом промежутке и проверим, входит ли данное решение в данный промежуток:
a) x
б) x
в) x (4;+; x-2+x -4=3;
Ответ: 1.5; 4.5.
V. Самостоятельная деятельность.
1.Работа в парах.
1) |x+2|=3
2)|x+3|=2x-1
3) |x+1|-|2x-3|=1
4)|x+2|+|x+3|=x
5) |x+5|-|x-3|=8
6)|+3x+2|+4x+10=0
2. Работа в группах .
( по сборнику Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по алгебре и началам анализа для 11 класса. — Харьков, Гимназия, 2006., стр 7)
| || |||
№8 №8 №8
1,2,3 4,5,6 7,8,9
10,11,12 13,14,15 16,17,18
1.|x+4.2|=5.12.|3x-5|=4.8
3.||
10)-5x*-14=0
11)||-8x+4|-3|=7
12)|-3|x|+2|=1
4.|-x-1|=1
5.-|x|-2=0
6) x|x|+8x-7=0
13)|-2x|=3-2x
14) |x|+|x-4|=5
15)|x+1|+|x-3|=4
7) |x-4|+x=8
8) |x+3| —x=2
9) 2+|x-2|-1=0
16) |x|-|x-5|=6
17)|2x-3|-|x+2|=4x+5
18)|-4x+3|+|-5x+6|=1
3. Индивидуальные задания.
№ 1. | 8cos2x – cosx – 6 | + | 8cos2x – cosx – 3 | = 9.
№ 2. | 36x – 6x
+1 – 3| + | 36x – 6x+1 – 13 | = 16.VI. Домашнее задание
( по сборнику Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Сборник задач и заданий для тематического оценивания по алгебре и началам анализа для 11 класса. — Харьков, Гимназия, 2006.)
Стр.45 на выбор
1 группа №8 (1-4)
2 группа №8 (5-8)
3 группа №8 (9-11)
VII . Итог модуля. Рефлексия
.
Техника «рефлексивная мишень»
Участник ставит метки в сектора соответственно оценке результата: чем ближе к центру мишени, тем ближе к «5», на краях мишени оценка ближе к нулю. 
Урок по математике на тему «Решение уравнений с модулем» (10 класс)

Урок по теме: «Решение уравнений, содержащих знак абсолютной величины (модуля)»
Цель урока: Обобщение и систематизация знаний учащихся , развитие навыка решения уравнений и логического мышления учащихся.
Оборудование урока: таблица “Модуль”, плакаты с изображением уравнений содержащих переменную под знаком модуля и с графическим способом решения уравнений.
Ход урока.
I. Орг. момент
Сообщается план урока и почему именно эта тема выбрана.
II. Вступительное слово учителя.
Существенной характеристикой числа, как в действительной, так и в комплексной области является понятие его абсолютной величины (модуля).
Это понятие имеет широкое распространение в различных отделах физико-математических наук. Так, в математическом анализе одно из первых и фундаментальных понятий – понятие предела – в своем определении содержит понятие абсолютной величины числа. В теории приближенных вычислений первым, важнейшим понятием, является понятие абсолютной погрешности приближенного числа. В механике основным первоначальным понятием является понятие вектора, важнейшей характеристикой которого служит его абсолютная величина (модуль).
С понятием модуля (абсолютной величины) действительного числа учащиеся знакомятся еще в 6 классе. Однако в программах общеобразовательных школ и соответствующих учебниках в дальнейшем это понятие ни в теоретических материалах, ни в задачах и упражнениях почти не применяется. Возможность решения уравнений и неравенств, содержащих неизвестные под знаком модуля, имеют учащиеся классов или школ с углубленным изучением математики и некоторых других альтернативных школ, однако и в учебниках для этих школ задач подобного рода до обидного мало. В то же время на ЕГЭ задачи с модулем предлагаются все чаще и чаще.
.Изучение нового материала
Учитель: при решении уравнений, содержащих переменную под знаком модуля, чаще всего применяются следующих методы: 1) раскрытие модуля по определению, 2) возведение обоих частей в квадрат, 3) метод разбиения на промежутки, 4) графический метод.
Выступления учащихся:
Сообщение №1 «Некоторые способы решения уравнений с модулями».
Напомним сначала определение числа x:
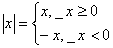
Приведем также основные свойства модуля, часто применяемых в решение задач:
|ab|=|a||b|;
|a|n=|an|;

|a|=0, если a=0
Поговорим о некоторых способах решения задач с модулем. Среди них один занимает самое главное место, так как он является самым общим, однако, иногда не самым рациональным. Заключается он в следующем.
Метод интервалов.
Предположим, что имеется уравнение или неравенство, в которое входят один или несколько модулей.
Первым делом нужно отделить критические точки. Под этим мы понимаем все значения переменной, при которых один из модулей обращается в нуль.
Нанесите полученное множество значений на ось данной переменной, например Ox. Прямая разобьется на несколько конечных и два бесконечных интервала. Каждый интервал соответствует знакопостоянству подмодульных выражений.
Рассмотреть столько случаев решения, сколько получилось интервалов. При этом освобождаться от модулей нужно, проверяя знак подмодульного выражения. Т.е. изменять его на противоположный, если выражение отрицательно и оставлять его прежним в противном случае. Важно не забыть, что частным ответом в каждом из полученных случаев является пересечение интервала и найденного решения.
Объединить полученные в каждом интервале ответы в один.
Рассмотрим подробнее этот метод на следующем примере.
|x + 2| + |x — 3| = 5
Нанесем на числовую прямую значение x, при котором x + 2 = 0 и значение x, при котором x – 3 = 0. Числовая прямая разобьется на промежутки (- ; -2), [-2; 3], (3; +
; -2), [-2; 3], (3; + ).
).

Решим уравнений на каждом из этих интервалов.
х
(- ; -2)
; -2)
[-2;3]
(3; + )
)
х+2
—
+ — +
+
x-3
—
— —
+
Рассмотрим первый промежуток, чтобы определить знак подмодульного выражения, возьмем контрольную точку x = 3, подставим ее в наше уравнение –3 + 2 < 0 и во второе -3 – 3 < 0. Аналогично рассмотрим знаки подмодульных выражений на втором и третьем промежутках.
Решим уравнение на каждом из этих промежутков, т.е. решим равносильную уравнению совокупность смешанных систем:
1)

–х – 2 – х + 3 = 5
–2х + 1 = 5
–2х = 4
х = –2
–2 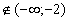

Не может быть корнем.
2)

х + 2 – х + 3 = 5
0х = 0 x любое число из [-2; 3].
3) 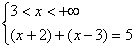
х + 2 + х – 3 = 5, x = 3
3 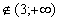 , не может быть корнем.
, не может быть корнем.
Вывод: Решение второй системы является объединением решений 3-х систем.
Ответ: x принадлежит [-2;3] или все значения сегмента [-2;3].
Сообщение №2 Графический метод.
Этот способ уже не столь универсален, но им нельзя пренебрегать, если он применим. Часто уравнение или неравенства с модулем содержит только линейные выражения относительно переменной. В этом случае существует очень простой рецепт построения графиков с модулями, что часто существенно облегчает решение задачи. Он базируется на простом замечании – графики таких выражений состоят из кусков линий, т.е. являются ломаными. Метод состоит в следующем:
Найти, как и раньше, все критические точки и нанести их на ось абсцисс. Найти непосредственно значения заданной функции в этих точках (это удобно делать с помощью отдельной таблицы) и нанести их на координатную плоскость.
В каждой из конечных интервалов, получаемых после разбиения критическими точками, график является прямой и может быть простым соединением нанесенных в предыдущем пункте точек на координатной плоскости.
Выбрать две удобные для вычисления точки, расположенные в левом и правом бесконечных интервалах и аналогично п.1 найти значения функций в них. Окончательно, соединяя построенный участок графика с оставшимися двумя точками, получим требуемый график.
Проиллюстрируем это на примере построения графика |x+2|+|x-3|=5. Построим график функции
у = |x + 2| + |x – 3| и y = 5
х + 2 = 0, x –3 = 0
x1 = –2 x2 = 3

Наносим на ось корни линейных функций стоящих под знаком модуля. На каждом из трех промежутков знаки этих линейных функций постоянны и мы можем избавиться от знака модуля.
если x < – 2, то y =-(x + 2) – (x – 3) = –2x + 1
если –2 < x < 3, то y = +(x + 2) – (x – 3) = x + 2 – x + 3 = 5
если x > 3, то y = +(x + 2) + (x – 3) = 2x – 1
При построении графика провести вертикальные прямые x = –2 и x = 3, которые разобьют плоскость на три части. В левой части надо провести прямую y=–2x + 1, в центральной полосе y = 5 и в правой y = 2x – 1: (для контроля надо следить, чтобы ломаная была непрерывной, т.е. чтобы значения в разделяющих точках изломах, вычисленные по соседним формулам совпали). В нашем случае при x — 2 значение функции y = –2x + 1 совпадает со значением y = 5, точно так же при x=3 совпадают значения функции y = 5 и y=2x – 1
Строим график 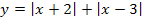
1) y = –2x + 1
х
-3
-4
у
7
9
2) у = 5
3) y = 2x – 1
х
4
5
у
7
9
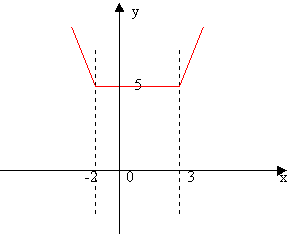
Графики 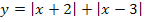 и y = 5 пересекаются на промежутке, если
и y = 5 пересекаются на промежутке, если 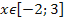 .
.
Ответ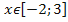
Сообщение №3 Раскрытие модуля по определению .
Решить уравнение 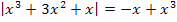
Решение. 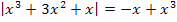
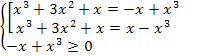 .
.
Проверим справедливость неравенства 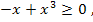 для найденных значений х:
для найденных значений х:
 верное неравенство, значит 0 – корень данного уравнения.
верное неравенство, значит 0 – корень данного уравнения. неверное неравенство, значит
неверное неравенство, значит  — посторонний корень.
— посторонний корень. верное неравенство, значит
верное неравенство, значит  – корень данного уравнения
– корень данного уравнения
Ответ:  ; 0.
; 0.
Решение уравнения, в котором под знаком модуля находится выражение содержащее модуль.
Решить уравнение 
Решение.
 .
.

 .
.
2)

Ответ: 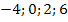 .
.
IV. Итоги урока.
Домашнее задание.
Всем учащимся даются задания для самостоятельного решения:
Записать в тетради решения уравнений вида:
1. |2x-3|=11
2. |2x-5|=5-4x
3. |4x-3|=4x-3
4. |x+2|+|x-3|=5
5. |x+1|-|x-2|+|3x+6|=5
infourok.ru
Урок по теме «Уравнение и неравенства с модулем». 10-й класс
Тип урока: урок совершенствования умений и навыков.
Цели урока:
Дидактическая: научить применять полученные знания при решении заданий повышенного уровня сложности, стимулировать учащихся к овладению рациональными приёмами и методами решения.
Развивающая: развивать логическое мышление, память познавательный интерес, вырабатывать умение анализировать и сравнивать.
Воспитательная: развивать аккуратность и трудолюбие, продолжить формирование навыков контроля и самоконтроля.
Ход урока
1. Организационный этап (1 минута).
2. Постановка цели (3 минуты).
Сегодня на уроке мы продолжим отрабатывать навыки решения уравнений и неравенств с модулем, используя как традиционные методы, так и нестандартные подходы.
3. Проверка домашнего задания (10 минут).
Если учащиеся не готовы показать все способы, то решение показывается на экране интерактивной доски. (Приложение 1)
Учитель вызывает по желанию 7-х человек к доске, параллельно проводит фронтальную беседу по теоретическим вопросам. (Приложение 2) Выставляет оценку за д/з.
На дом вам было предложено решить уравнения
|x – 6| = x2 – 5x + 9
|x2 + 4x + 3| = x + 3
|x – 6| = |x2 – 2x|
|x – 2| + |x – 1| = x – 8
и неравенства |x + 2| < 3 различными способами. Посмотрим ваше решение.
4. Выполнение упражнений (20 минут).
Многообразие приёмов решения задач с модулем подталкивает нас к выбору более рационального из них при решении конкретных уравнений или неравенств.
№ 1 (устно).
Учитель направляет на выбор рационального метода решения.
Учащиеся предлагают методы решения, один учащийся устно объясняет решение уравнения №1.
Решить уравнение |x2 – 6x – 7| = 7 + 6x – x2.
Решение (на основе аналитического определения модуля).
№2 Решить уравнение .
Учитель совместно с учащимися выбирает метод решения уравнения.
Следит за грамотным решением предложенного уравнения и одновременно проверяет индивидуальные решения уравнений у учащихся работающих на боковой доске по карточке, выставляет оценки за работу.
2 человека работают на боковой доске индивидуально (Приложение 3), остальные записывают в тетрадь решение уравнения №2.
Решение (применение геометрической интерпретации модуля).
На геометрическом языке: требуется найти точки с координатами х такие, что сумма расстояний от этих точек до точек с координатами -1 и 1 равна 2. Очевидно, что эти точки располагаются на отрезке [–1;1]
Ответ: [–1;1].
№3 Решите неравенство
Учитель направляет на выбор рационального метода решения.
Один ученик решает неравенство № 3. Остальные участвуют в выборе рационального метода решения неравенства. Записывают решение в тетрадь.
Решение (функционально графический метод).
Обе части неравенства определены на R. Левая часть неравенства принимает значения из отрезка [–1;1], а значения правой части составляют луч [1;∞]. Следовательно, исходное неравенство может иметь решение только, если выполняется система
Ответ: 0
№ 4 Найти все значения параметра b при которых уравнение ||x + 1| – 2| – 3 = b имеет ровно три различных корня.
Один ученик решает задание № 4 у доски. Три ученика работают по карточкам (Приложение 4), остальные записывают в тетрадь решение задания № 4.
Учитель следит за верностью рассуждений учащихся и одновременно проверяет решение заданий по карточкам, выставляет оценки за работу.
Решение (графический способ).
Рассмотрим функцию у = ||x + 1| – 2| – 3 и построим её график используя преобразования, содержащие модуль, а также параллельный перенос.
Графиком функции у = b является прямая параллельная оси х.
Очевидно, что исходное уравнение имеет ровно три различных корня при b=-1.
Ответ: b = -1.
№ 5 Решить неравенство
Один ученик решает у доски, остальные записывают решение неравенства №5 в тетради.
Учитель обсуждает совместно с учащимися метод решения неравенства, следит за грамотностью рассуждений учащихся и верной записью решения неравенства. Выставляет оценку за работу.
Решение (метод интервалов).
Решим уравнение f(x)=0. Получим:
5. Домашнее задание (3 минуты).
(Заранее приготовлен слайд на интерактивной доске.)
1) Решить неравенство ||2x – 1| – 3| > 3.
2) Найти все значения параметра b при которых уравнение |x – 3| + |x + 1| = b имеет ровно два различных корня.
3) Решить уравнение cosx = |cosx|(x + 1.5)2.
(Приложение №5)
Учитель поясняет домашнее задание, обращая внимание учащихся на то, что аналогичные задания были разобраны на уроке.
Первое неравенство можно решить методом интервалов, второе уравнение – графически, а третье-с помощью аналитического определения модуля, рассматривая три случая (подмодульное выражение больше нуля, равно нулю и меньше нуля ) отдельно.
6. Подведение итогов урока (3 минуты).
Решение уравнений и неравенств с модулем требует от учащихся глубоких теоретических знаний, умений применять их на практике, требует внимания трудолюбия, сообразительности. Наверное, поэтому такие задания и включены в материалы ЕГЭ.
Сегодня на уроке все очень хорошо поработали, 15 человек получили оценки. Молодцы ребята!
urok.1sept.ru
Презентация «Уравнения с модулем»

Уравнения с модулем
Способы решения
 0 -a, если а0, если а = 0 |a|= 2 «
0 -a, если а0, если а = 0 |a|= 2 «
Определения
- Модуль числа а – расстояние от точки с координатой а до ноля
- следствия
- 1. модуль числа неотрицателен (|a| ≥0)
а
-а
0
a, если а0
-a, если а
0, если а = 0
|a|=
2

Способы решения уравнений с модулями:
- 1. По определению модуля
- 2. Возведение обоих частей уравнения в квадрат
- 3. Замена переменной
- 4. Раскрытие модуля на промежутке знакопостоянства
- 5. Замена совокупностью систем
- 6. Важный частный случай
2

1. По определению модуля
|ƒ(x)| = a (а ≥0)
f(x) = a или f(x) = — a
Пример : |3x — 8| = 5
Решение:
3x — 8 = 5 или 3x — 8 = -5;
3x = 13, 3x = 3;
x = 13/3, x = 1.
Ответ: 13/3; 1.
2

Решить по определению модуля
1) |2x — 3| = 5
решение
решение
4) |11 – 2x 2 | = 3
2) |x 2 — 4x| = 5
решение
решение
2

По определению модуля № 1
|2x — 3| = 5
Решение
2x — 3 = 5 или 2x — 3 = -5
2x = 8 2x = -2
x = 4 x = -1
Ответ: -1;4
2

По определению модуля № 2
|x 2 + 4x| = 5
Решение
x 2 + 4x = 5 или x 2 + 4x = -5
x 2 + 4x — 5 = 0
Ответ: -5;1
x 2 + 4x + 5 = 0
D = 16 — 20= -4
D
x = -5
x = 1
2

По определению модуля № 3
Решение
|5x — 1| = 4
5x — 1 = 4 или 5x — 1 = -4
5x = 5 или 5x = -3
x =1 x =-3/5 = -0,6
Ответ: -0,6; 1
2

По определению модуля
По определению модуля № 4
решение
|11 — 2x 2 | = 3
11 — 2x 2 = 3 или 11 — 2x 2 = -3
2x 2 = 8 2x 2 = 14
x = 2 или x = -2 x = 7 x = — 7
Ответ: ; -2; 2;
2

2. Возведение обеих частей в квадрат
Пример |x — 3| = |x + 2|
Решение (x — 3) 2 = (x + 2) 2 *
(x — 3) 2 — (x + 2) 2 = 0
(x — 3 + x + 2)(x — 3 — x — 2) = 0
-5∙(2x – 1) = 0, то (2x – 1) = 0
x = 1/2
Ответ:0,5
*
При возведении обоих частей в квадрат данного уравнения равносильность не нарушается, т.к. модуль всегда неотрицательный, и |а| 2 = a 2
2

Решить возведением обеих частей в квадрат
|x — 4| = |x — 1|
|x + 5| = |2x — 5|
решение
решение
|x 2 – 5x| = |x 2 – x + 4|
|x 2 + 5x +11| = |2x + 1|
решение
решение
2

Решить возведением обеих частей в квадрат
|x — 4| = |x — 1|
(x — 4) 2 – (x — 1) 2 = 0
(x — 4 + x — 1)(x — 4 — x + 1) = 0
-3(2x — 5) = 0
2x — 5 = 0
x = 2,5
Ответ: 2,5
2
Вернуться назад

Решить возведением обеих частей в квадрат
|x + 5| = |2x — 5|
(x + 5) 2 — (2x — 5) 2 = 0
(x + 5 — 2x + 5)(x + 5 + 2x — 5) = 0
(-x + 10) · 3x = 0
-3x(x — 10) = 0
Ответ: 0;10
Вернутся назад
2

Решить возведением обеих частей в квадрат
|x 2 – 5x| = |x 2 – x + 4|
(x 2 — 5x) 2 = (x 2 — x + 4) 2
(x 2 — 5x) 2 — (x 2 — x + 4) 2 = 0
(2x 2 — 6x + 4)(-4x — 4) = 0
-8(x 2 — 3x + 2)(x + 1) = 0
(x — 2)(x — 1)(x + 1) = 0
Ответ: -1; 1; 2
Вернуться назад
2

Решить возведением обеих частей в квадрат
|x 2 + 5x + 11| = |2x + 1|
(x 2 + 5x + 11) 2 = (2x + 1) 2
(x 2 + 5x +11) 2 — (2x + 1) 2 = 0
(x 2 + 7x + 12)(x 2 + 3x +10) = 0
x 2 + 7x + 12 = 0 или x 2 + 3x +10 = 0
Ответ: -4; -3.
2

3.Замена переменной
Пример: x 2 — 7|x| — 8 = 0
Решение: t = |x| условие t ≥ 0
t 2 — 7t — 8 = 0
t 1 + t 2 = 7
t 1 · t 2 = -8
t 1 = -1 не удовлетворяет условию
t 2 = 8
|x| = 8
x = 8 x = -8
Ответ: 8; -8.
2

Решить заменой переменной
x 2 – 3|x| + 2 = 0
x 2 + 3|x| = 10
решение
решение
2

Решить заменой переменной
x 2 — 3|x| + 2 = 0
Решение
Пусть t = |x| , то t ≥ 0
t 2 — 3t + 2 = 0
t = 2 или t = 1.
Тогда:
1) |x| = 2 2) |x| = 1
x = 2 или x = -2; x = 1 или x = -1.
Ответ: -2;-1;1;2
2

Решить заменой переменной
x 2 + 3|x| = 10
Решение
x 2 + 3|x| — 10 = 0
Пусть t = |x| , t ≥ 0
t 2 + 3t – 10 = 0
t = 2 или t = -5 -5
Значит ,
|x|= 2
x = 2 или x = -2
Ответ: -2; 2.
2

4.Раскрытие модуля на промежутке знакопостоянства
- Универсальный способ
Пример: |x| + |x+1|=1
Найдем нули подмодульных выражений: 0; -1
Решение:
— — +
X
X+1
-1 0
— + +
Ответ: [-1;0].
2

Решить, используя раскрытие модуля на промежутках знакопостоянства
Раскрытие модуля на промежутке знакопостоянства
2) |x — 3| + 2|x + 1| = 4
1) |5 — x| + |x — 1| = 10
решение
3) |x — 1| + |2x — 3| = 2
решение
2

Раскрытие модуля на промежутках знакопостоянства № 1
Раскрытие модуля на промежутке знакопостоянства
|5 — x| + |x — 1| = 10
— + +
x — 1
5 — x
+ 1 + 5 —
Если x ≤ 1, то
5 — x –x + 1 = 10
— 2x + 6 = 10
— 2x = 10 – 6
-2x= 4
x = -2
Если 1
5 — x + x — 1 = 10
0x + 4 = 10
0x = 10 – 4
0x= 6
нет решений
Если x ≥ 5, то
-5 + x +x — 1 = 10
2x — 6 = 10
2x = 10 + 6
2x= 16
x = 8
Ответ: — 2 ; 8
2
 3, то x — 3 +2x + 2 = 4 3x — 1 = 4 3x = 4+1 3x= 5 x = 5/3 нет решений Ответ: — 1 2 «
3, то x — 3 +2x + 2 = 4 3x — 1 = 4 3x = 4+1 3x= 5 x = 5/3 нет решений Ответ: — 1 2 «
Раскрытие модуля на промежутках знакопостоянства № 2
|x — 3| + 2|x + 1| = 4
— + +
x + 1
x — 3
— -1 — 3 +
Если x ≤ -1, то
3 — x — 2x -2 = 4
— 3x + 1 = 4
— 3x = 4 – 1
-3x= 3
x = — 1
Если -1
3 – x + 2x + 2 = 4
x + 5 = 4
x = 4 – 5
x= -1
нет решений
Если x3, то
x — 3 +2x + 2 = 4
3x — 1 = 4
3x = 4+1
3x= 5
x = 5/3
нет решений
Ответ: — 1
2
 1,5, то x — 1 + 2x — 3 = 2 3x — 4 = 2 3x = 2 + 4 3x= 6 x = 2 Ответ: 2/3; 2 2 «
1,5, то x — 1 + 2x — 3 = 2 3x — 4 = 2 3x = 2 + 4 3x= 6 x = 2 Ответ: 2/3; 2 2 «
Раскрытие модуля на промежутках знакопостоянства № 3
|x — 1| + |2x — 3| = 2
— + +
x — 1
2x — 3
— 1 — 1,5 +
1. Если x ≤ 1, то
1 — x — 2x + 3 = 2
— 3x + 4 = 2
— 3x = 2 – 4
-3x= — 2
x = 2/3
2 . Если 1
x — 1 + 3 – 2x = 2
— x + 2 = 2
— x = 2 – 2
x= 0
нет решений
3 . Если x 1,5, то
x — 1 + 2x — 3 = 2
3x — 4 = 2
3x = 2 + 4
3x= 6
x = 2
Ответ: 2/3; 2
2

5.Замена совокупностью систем
|ƒ(x)| = g(х)
2

Замена совокупностью систем
Пример: |2x + 7| = 3x + 4
I способ
II способ
2
2

6. Важный частный случай
| f ( x ) | = — f ( x ), тогда f ( x ) ≤ 0
Пример: 7-4 x = |4 x -7|
Решение: т.к. |f ( x )| = -f( x ), то f( x )≤0
4 x — 7 ≤ 0
x ≤ 7/4 , 7/4 = 1,75
2

Удачи!
2
multiurok.ru
Этапы урока и их содержание | Время (мин) | Деятельность |
Сегодня на уроке мы продолжим отрабатывать навыки решения уравнений и неравенств с модулем, используя как традиционные методы, так и нестандартные подходы
На дом вам было предложено решить уравнения и неравенства различными способами. Посмотрим ваше решение
Многообразие приёмов решения задач с модулем подталкивает нас к выбору более рационального из них при решении конкретных уравнений или неравенств. № 1. (устно) Решить уравнение
Решение (на основе аналитического определения модуля). Т.к. , то х2 -6х-7-1. № 2 Решить уравнение Решение (применение геометрической интерпретации модуля). На геометрическом языке: требуется найти точки с координатами х такие, что сумма расстояний от этих точек до точек с координатами -1 и 1 равна 2. Очевидно, что эти точки располагаются на отрезке Ответ: . № 3 Решите неравенство cos x1+. Решение (функционально графический метод). Обе части неравенства определены на R. Левая часть неравенства принимает значения из отрезка , а значения правой части составляют луч . Следовательно, исходное неравенство может иметь решение только, если выполняется система х=0. Ответ: 0 № 4 Найти все значения параметра b при которых уравнениеимеет ровно три различных корня. Решение (графический способ). Рассмотрим функцию у = и построим её график используя преобразования, содержащие модуль, а также параллельный перенос. Графиком функции у =b является прямая параллельная оси х. Очевидно, что исходное уравнение имеет ровно три различных корня при b=-1. Ответ: b=-1. № 5 Решить неравенство . Решение (метод интервалов). Пусть f(x)= , тогда Df = (-∞;-1)(-1;2) (2;+∞). Решим уравнение f(x)=0. Получим: 2=х2-х-2 Осталось установить знак f(x) на промежутках: (-∞;-4), (-4;-1), (-1;2), (2;5), (5;+∞). Ответ: (-4;-1)(2;5).
(заранее приготовлен слайд на интерактивной доске) 1) Решить неравенство
2) Найти все значения параметра b при которых уравнение имеет ровно два различных корня. 3) Решить уравнение (приложение №5)
Решение уравнений и неравенств с модулем требует от учащихся глубоких теоретических знаний, умений применять их на практике, требует внимания трудолюбия, сообразительности. Наверное, поэтому такие задания и включены в материалы ЕГЭ. Сегодня на уроке все очень хорошо поработали, 15 человек получили оценки. Молодцы ребята! | 1 3 10 2 6 5 5 8 3 2 | Организационная сообщает тему урока, дату проведения, цель урока Если учащиеся не готовы показать все способы, то решение показывается на экране интерактивной доски,(приложение 1). Вызывает по желанию 7-х человек к доске, параллельно проводит фронтальную беседу по теоретическим вопросам (приложение 2) Выставляет оценку за д/з. Направляет на выбор рационального метода решения Совместно с учащимися выбирает метод решения уравнения. Следит за грамотным решением предложенного уравнения и одновременно проверяет индивидуальные решения уравнений у учащихся работающих на боковой доске по карточке, выставляет оценки за работу. Направляет на выбор рационального метода решения Следит за верностью рассуждений учащихся и одновременно проверяет решение заданий по карточкам, выставляет оценки за работу. Обсуждает совместно с учащимися метод решения неравенства, следит за грамотностью рассуждений учащихся и верной записью решения неравенства. Выставляет оценку за работу. Поясняет домашнее задание, обращая внимание учащихся на то, что аналогичные задания были разобраны на уроке. Первое неравенство можно решить методом интервалов, второе уравнение –графически, а третье-с помощью аналитического определения модуля, рассматривая три случая (подмодульное выражение больше нуля, равно нулю и меньше нуля ) отдельно. | Сообщают об отсутствующих записывают в тетради 7 учащихся работают у доски, остальные принимают активное участие в устном теоретическом опросе Предлагают методы решения, один учащийся устно объясняет решение уравнения №1. 2 человека работают на боковой доске индивидуально (приложение №3), остальные записывают в тетрадь решение уравнения №2. Один ученик решает неравенство № 3. Остальные участвуют в выборе рационального метода решения неравенства. Записывают решение в тетрадь. Один ученик решает задание № 4 у доски. Три ученика работают по карточкам (приложение №4), остальные записывают в тетрадь решение задания № 4. Один ученик решает у доски, остальные записывают решение неравенства №5 в тетради. Внимательно прослушав пояснение учителя, записывают домашнее задание. |
nsportal.ru
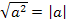
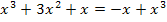
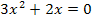
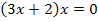
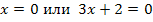

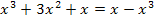
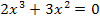
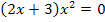
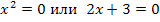
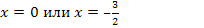
 верное неравенство, значит 0 – корень данного уравнения.
верное неравенство, значит 0 – корень данного уравнения.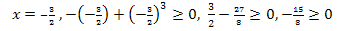 неверное неравенство, значит
неверное неравенство, значит 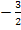 — посторонний корень.
— посторонний корень.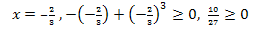 верное неравенство, значит
верное неравенство, значит 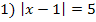
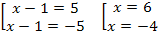 .
.