Задачи с параметрами из ЕГЭ
 Решение задач с параметрами требует наличия определенной математической культуры. С реше-нием задач с параметрами приходится сталкиваться не только в математике. Очень многие законы и закономерности из физики, эконо-мики и других областей описываются уравнениями и неравенствами с параметрами. Фактически, решая задачи по физике, химии, экономике и некоторым другим школьным дисциплинам, ученик имеет дело с параметрами. Решению задач с параметрами посвящено большое количество учебно-методической литературы. В данной статей приводятся лишь некоторые представления о том, как рассуждают при решении подобных заданий. С этой целью рассмотрены несколько примеров, большая часть которых взята из вариантов ЕГЭ по математике прошлых лет (задача C5).
Решение задач с параметрами требует наличия определенной математической культуры. С реше-нием задач с параметрами приходится сталкиваться не только в математике. Очень многие законы и закономерности из физики, эконо-мики и других областей описываются уравнениями и неравенствами с параметрами. Фактически, решая задачи по физике, химии, экономике и некоторым другим школьным дисциплинам, ученик имеет дело с параметрами. Решению задач с параметрами посвящено большое количество учебно-методической литературы. В данной статей приводятся лишь некоторые представления о том, как рассуждают при решении подобных заданий. С этой целью рассмотрены несколько примеров, большая часть которых взята из вариантов ЕГЭ по математике прошлых лет (задача C5).
Решение «типичных» задач с параметрами
Пример 1. При каких значениях корни уравнения
корни уравнения 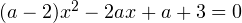 положительны?
положительны?Решение.
1) Начнем с рассмотрения случая, когда 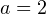 . Тогда уравнение принимает вид
. Тогда уравнение принимает вид 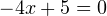 , откуда получаем, что
, откуда получаем, что 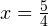 — положительный корень. Значит данное значение
— положительный корень. Значит данное значение  нам подходит. Запомнили.
нам подходит. Запомнили.
2) Теперь рассматриваем случай, когда 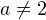 . Разделим обе части уравнения на
. Разделим обе части уравнения на 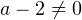 . В результате получаем следующее квадратное уравнение:
. В результате получаем следующее квадратное уравнение:
![Rendered by QuickLaTeX.com \[ x^2-\frac{2a}{a-2}x+\frac{a+3}{a-2}=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2a1a5696f7babf6e12fec10e43f71b72_l3.png)
Так как ветви соответствующей параболы направлены вверх, данное уравнение имеет два положительных корня в том случае, если эта парабола пересекает ось OY в точке, находящейся выше нуля (то есть значение соответствующей квадратичной функции при 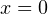 положительно), абсцисса вершины параболы положительна, а дискриминант квадратного уравнения неотрицателен. То есть имеет место следующая система:
положительно), абсцисса вершины параболы положительна, а дискриминант квадратного уравнения неотрицателен. То есть имеет место следующая система:
![Rendered by QuickLaTeX.com \[ \begin{cases} \frac{a+3}{a-2}>0 \\ \frac{a}{a-2}>0 \\ \frac{6-a}{(a-2)^2}\geqslant 0. \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6934153cefc4872fe1d3b7a0276d59a9_l3.png)
Решая данную систему неравенств, получаем промежуточный ответ: ![Rendered by QuickLaTeX.com a\in(-\mathcal{1};-3)\cup (2;6]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-780aef23813e74814c2cff6094848984_l3.png) .
.
3) Объединяем решения, полученные в предыдущих двух пунктах. В результате получаем окончательный ответ: ![Rendered by QuickLaTeX.com a\in(-\mathcal{1};-3)\cup [2;6]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9349b00263af091fa0f8e76c771ba917_l3.png) .
.
Задача для самостоятельного решения №1. Для каждого значения  решите уравнение
решите уравнение 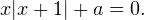
 уравнение
уравнение 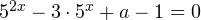 имеет единственный корень?
имеет единственный корень?Решение.
Используем следующую замену: 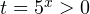 . Тогда первоначальное уравнение принимает вид:
. Тогда первоначальное уравнение принимает вид: 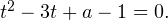 Полученное уравнение с параметром можно исследовать с помощью метода, использованного нами при решении предыдущего задания. Однако для разнообразия предлагаю воспользоваться здесь альтернативным подходом.
Полученное уравнение с параметром можно исследовать с помощью метода, использованного нами при решении предыдущего задания. Однако для разнообразия предлагаю воспользоваться здесь альтернативным подходом.
Исходное уравнение будет иметь единственный корень в том случае, если у данного уравнения будет один положительный корень либо два корня, один из которых положительный, другой — отрицательный или равный нулю.
1) Дискриминант уравнения равен: 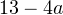 . Один корень это уравнение будет иметь в том случае, если полученный дискриминант окажется равным нулю, то есть при
. Один корень это уравнение будет иметь в том случае, если полученный дискриминант окажется равным нулю, то есть при 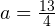 . При этом корень
. При этом корень 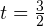 — положителен. Данное значение
— положителен. Данное значение  нам подходит. Запомнили.
нам подходит. Запомнили.
2) Рассматриваем случай, когда существует два корня, один из которых положителен, другой — неположителен. Условия, при которых эта ситуация реализуется, могут быть записаны следующим образом:
![Rendered by QuickLaTeX.com \[ \begin{cases} a<\frac{13}{4}, \\ \frac{3+\sqrt{13-4a}}{2}>0,\\ \frac{3-\sqrt{13-4a}}{2}\leqslant 0 \end{cases}\Leftrightarrow a\in(-\mathcal{1};1]. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-98af4f25194bca783bb29d3e4d38fbf4_l3.png)
Окончательно: ![Rendered by QuickLaTeX.com x\in(-\mathcal{1};1]\cup\left\{\frac{13}{4}\right\}](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bd73d27b23b94d9076ee8db00d438496_l3.png)
Задача для самостоятельного решения №2. Найдите все значения 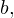 при которых уравнение
при которых уравнение  имеет единственное решение.
имеет единственное решение.
![Rendered by QuickLaTeX.com b\in\left[\frac{3}{4};+\mathcal{1}\rihgt].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c6a250a72ba0935a55f672a722541500_l3.png) Пример 3. При каких значениях параметра
Пример 3. При каких значениях параметра 
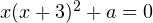 имеет ровно три корня?
имеет ровно три корня?Решение. Перепишем уравнение в виде: 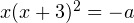 . Найдем промежутки возрастания и убывания функции
. Найдем промежутки возрастания и убывания функции 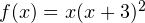 . Для этого найдем сперва ее производную:
. Для этого найдем сперва ее производную:
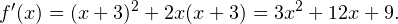
Нули производной равны 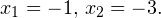
Производная принимает положительные значения на промежутке 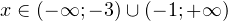 , на промежутке
, на промежутке 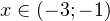 она принимает отрицательные значения. То есть в точке
она принимает отрицательные значения. То есть в точке 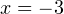 возрастание функции сменяется ее убыванием, то есть это точка максимума. Значение функции в этой точке:
возрастание функции сменяется ее убыванием, то есть это точка максимума. Значение функции в этой точке: 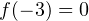 . Напротив, в точке
. Напротив, в точке 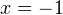 убывание функции сменяется ее возрастанием, то есть это точка минимума. Значение функции в этой точке:
убывание функции сменяется ее возрастанием, то есть это точка минимума. Значение функции в этой точке: 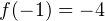 .
.
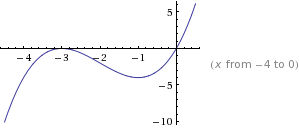
График данной функции
Следовательно, три решения исходное уравнение будет иметь в том случае, если прямая 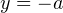 на координатной плоскости будет располагаться выше прямой
на координатной плоскости будет располагаться выше прямой  и ниже прямой
и ниже прямой 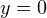 . Значит верно двойное неравенство:
. Значит верно двойное неравенство: 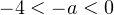 . Откуда получаем окончательный ответ:
. Откуда получаем окончательный ответ: 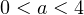 .
.
Задача для самостоятельного решения №3. Найдите все значения параметра 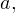 при которых уравнение
при которых уравнение 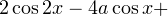
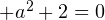 не имеет решений.
не имеет решений.
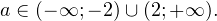
Не сходится с ответом?
Показать подсказкуПодсказка: преобразуйте выражение к виду: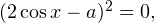 после чего используйте то, что
после чего используйте то, что 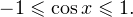
Решение задач с параметрами повышенной сложности
Пример 4. При каких уравнение
уравнение 
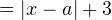 имеет ровно три корня?
имеет ровно три корня?Решение. Используем графический метод решения. График функции  отличается от параболы
отличается от параболы 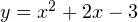 только тем, что отрицательная ее область зеркально отражается вверх относительно оси OX (ведь модуль не может принимать отрицательных значений).
только тем, что отрицательная ее область зеркально отражается вверх относительно оси OX (ведь модуль не может принимать отрицательных значений).
График функции  представляет собой всем известную «галочку», вершина которой смещена в точку
представляет собой всем известную «галочку», вершина которой смещена в точку 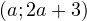 . В зависимости от значений параметра
. В зависимости от значений параметра  возможны следующие варианты взаимного расположения этих графиков на координатной плоскости:
возможны следующие варианты взаимного расположения этих графиков на координатной плоскости:
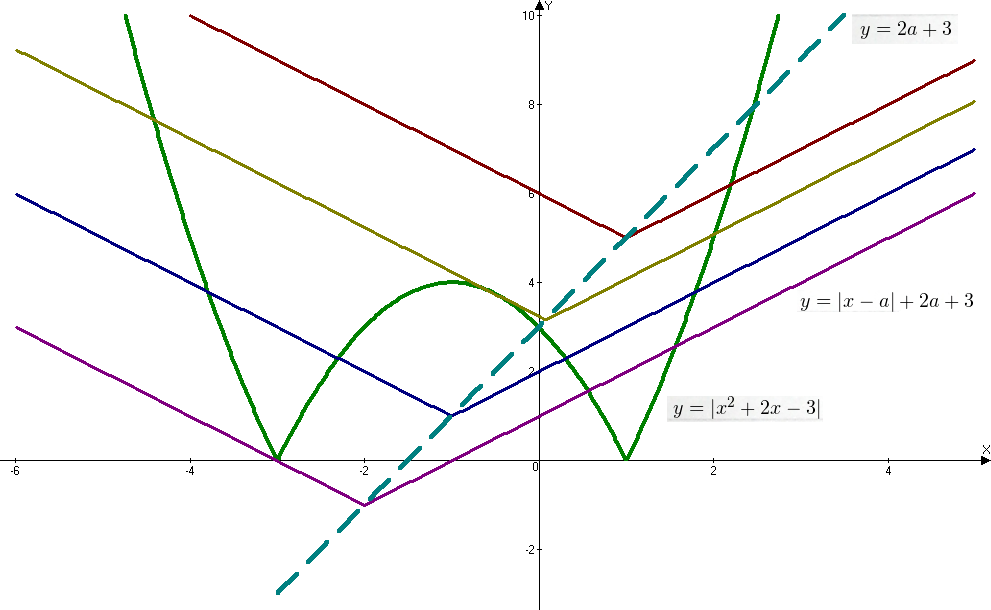
Взаимное расположение графиков соответствующих функций при разных значениях параметра
Видно, что три решения уравнение будет в случае фиолетовой и бежевой «галочки». Первый случай выполняется при условии выполнения равенства 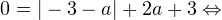
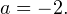 Во втором случае оба модуля раскрываются со отрицательным знаком. В результате приходим к уравнению
Во втором случае оба модуля раскрываются со отрицательным знаком. В результате приходим к уравнению  . Его дискриминант должен быть равен нулю, чтобы получилось одно пересечение (касание). То есть оказывается, что
. Его дискриминант должен быть равен нулю, чтобы получилось одно пересечение (касание). То есть оказывается, что 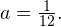
Ответ: 
Задача для самостоятельного решения №4. При каких  уравнение
уравнение  имеет ровно три корня?
имеет ровно три корня?
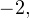
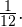 Пример 5. Найдите все значения параметра
Пример 5. Найдите все значения параметра  , при каждом из которых система уравнений
, при каждом из которых система уравнений ![Rendered by QuickLaTeX.com \[ \begin{cases} x^2+y^2 = 2a, \\ 2xy=2a-1 \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-19bcb1b0bbf7da3b9b3b483c3601a6b1_l3.png)
имеет ровно два решения.
Решение. Вместо 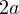 во втором уравнении подставляем
во втором уравнении подставляем  из первого, тогда второе уравнение системы принимает вид:
из первого, тогда второе уравнение системы принимает вид:
![Rendered by QuickLaTeX.com \[ 2xy = x^2+y^2-1\Leftrightarrow (x-y)^2 = 1\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0be853f08f75ce8659d1b8be0651b50d_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l} x-y = 1, \\ x-y = -1 \end{array}\right.\Leftrightarrow\left[\begin{array}{l} x = y+1, \\ x = y-1. \end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7baab013763d9081b322618d36927975_l3.png)
Обращаем внимание на то, что каждому найденному значению 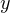 будет соответствовать единственное значение
будет соответствовать единственное значение 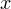 , такая пара
, такая пара 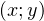 будет одним решением системы. Подставляя полученные выражения во второе уравнение системы, получаем два квадратичных уравнения:
будет одним решением системы. Подставляя полученные выражения во второе уравнение системы, получаем два квадратичных уравнения:  и
и 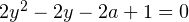 . Дискриминант и того, и другого равен
. Дискриминант и того, и другого равен  .
.
Нам нужно, чтобы у каждого из этих уравнений было по одному решению, тогда у исходной системы их будет два. Это условие выполняется в том случае, когда полученный дискриминант равен нулю. Итак, окончательный ответ: 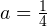 .
.
Задача для самостоятельного решения №5. Найдите все значения параметра  , при каждом из которых неравенство
, при каждом из которых неравенство 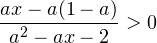 выполнено для любых значений переменной
выполнено для любых значений переменной 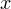 из отрезка
из отрезка ![Rendered by QuickLaTeX.com [-1;1]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-49a8582dba45ab841f7ccf7722200883_l3.png) .
.
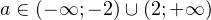 Пример 6. Найти все значения параметра
Пример 6. Найти все значения параметра  , при которых система
, при которых система ![Rendered by QuickLaTeX.com \[ \begin{cases}\log_a y = (x^2-2x)^2, \\ x^2+y=2x\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-cf533a649e0f501157e2e7f6bef06260_l3.png)
имеет ровно два решения.
Решение. Преобразуем систему к следующему виду:
![Rendered by QuickLaTeX.com \[ \begin{cases} \log_a y = (2x-x^2)^2, \\ y = 2x-x^2. \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-08384ad6d4c0cc861cd8be0a7fd58f01_l3.png)
Поскольку параметр  находится в основании логарифма, на него накладываются следующие ограничения:
находится в основании логарифма, на него накладываются следующие ограничения: 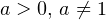 . Поскольку переменная
. Поскольку переменная 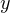 стоит под знаком логарифма, на нее накладывается следующее ограничение:
стоит под знаком логарифма, на нее накладывается следующее ограничение: 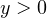 .
.
Скомбинировав оба уравнения системы, переходим к уравнению: 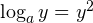 . В зависимости от того, какие значения принимает параметр
. В зависимости от того, какие значения принимает параметр  , возможны два случая:
, возможны два случая:
1) Пусть 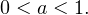 В этом случае функция
В этом случае функция 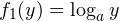 убывает в области допустимых значений, а функция
убывает в области допустимых значений, а функция 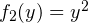 возрастает в той же области. Вспомнив внешний вид графиков соответствующих функций (кто не помним, может ознакомиться с этой статьей), осознаем, что корень у уравнения один, при этом он меньше 1. Второе уравнение системы и вся система в целом имеют, следовательно, два решения в силу того, что дискриминант уравнения
возрастает в той же области. Вспомнив внешний вид графиков соответствующих функций (кто не помним, может ознакомиться с этой статьей), осознаем, что корень у уравнения один, при этом он меньше 1. Второе уравнение системы и вся система в целом имеют, следовательно, два решения в силу того, что дискриминант уравнения 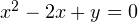 при
при 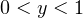 положителен. Рассматриваемый случай нам полностью подходит.
положителен. Рассматриваемый случай нам полностью подходит.
2) Пусть теперь 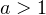 . В этом случае функция
. В этом случае функция  возрастает на области допустимых значений, и функция
возрастает на области допустимых значений, и функция  возрастает в этой области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что пересечься в одной точке они могут только в случае касания друг друга. Однако, касание это может произойти лишь в точке, абсцисса которой больше 1. Второе уравнение системы и вся система в целом, следовательно, иметь решений не будут в силу того, что дискриминант уравнения
возрастает в этой области. Вспомнив внешний вид графиков соответствующих функций, осознаем, что пересечься в одной точке они могут только в случае касания друг друга. Однако, касание это может произойти лишь в точке, абсцисса которой больше 1. Второе уравнение системы и вся система в целом, следовательно, иметь решений не будут в силу того, что дискриминант уравнения 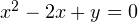 при
при  отрицателен.
отрицателен.
Итак, окончательный ответ: 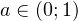 .
.
Задача для самостоятельного решения №6. Для каждого допустимого значения  решите неравенство
решите неравенство 
 и найдите, при каких значениях
и найдите, при каких значениях  множество решений неравенства представляет собой промежуток длины
множество решений неравенства представляет собой промежуток длины 
 , при каждом из которых уравнение
, при каждом из которых уравнение 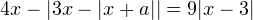 имеет два корня.
имеет два корня.Решение. Перепишем уравнение в виде:
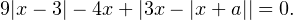
Рассмотрим функцию:
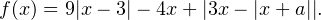
При 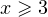 первый модуль раскрывается со знаком плюс, и функция принимает вид:
первый модуль раскрывается со знаком плюс, и функция принимает вид: 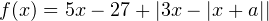 . Очевидно, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом
. Очевидно, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом  , то есть эта функция на данном промежутке возрастает.
, то есть эта функция на данном промежутке возрастает.
Рассмотрим теперь промежуток, на котором 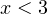 . В этом случае первый модуль раскрывается с минусом и функция принимает следующий вид:
. В этом случае первый модуль раскрывается с минусом и функция принимает следующий вид: 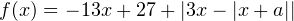 . Также легко видеть, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом
. Также легко видеть, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом 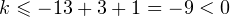 , то есть на этом промежутке функция убывает.
, то есть на этом промежутке функция убывает.
Итак, мы получили, что 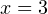 — точка минимума данной функции. А это означает, что для того, чтобы график данной функции пересекал ось OX в двух точках (то есть у исходного уравнения уравнения было два решения), значение функции в точке минимума должно быть меньше нуля. То есть имеет место неравенство:
— точка минимума данной функции. А это означает, что для того, чтобы график данной функции пересекал ось OX в двух точках (то есть у исходного уравнения уравнения было два решения), значение функции в точке минимума должно быть меньше нуля. То есть имеет место неравенство: 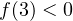 .
.
После несложных преобразований получаем окончательный ответ: 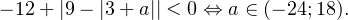
Задача для самостоятельного решения №7. При каких значениях 
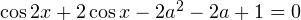 имеет ровно одно решение на промежутке
имеет ровно одно решение на промежутке 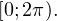 Показать ответОтвет:
Показать ответОтвет: 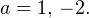
Не сходится с ответом?
Показать подсказкуВсе равно не получается?
Показать решение Пример 8. Найдите все положительные значения , при каждом из которых система:
, при каждом из которых система: ![Rendered by QuickLaTeX.com \[ \begin{cases} a^{2x-y-1} = x+3y-7, \\ 4y-x = 6 \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bcb8004114c8ecf2f82435ab63160cd4_l3.png)
имеет ровно два решения.
Решение.
Выразим 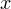 из второго уравнения и подставим в первое, получаем:
из второго уравнения и подставим в первое, получаем:
![Rendered by QuickLaTeX.com \[ \begin{cases} a^{2x-y-1} = x+3y-7, \\ x=4y-6\end{cases}\Leftrightarrow \begin{cases} a^{7y-13} = 7y-13, \\ x=4y-6. \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a391071ab6052177cb952a521cfa1e32_l3.png)
Для того, чтобы данная система имела два решения, необходимо, чтобы два решения имело первое уравнение этой системы. Нас интересуют только 
1) При 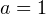 получаем линейное уравнение:
получаем линейное уравнение:  которое имеет одно решение. Этот случай не подходит.
которое имеет одно решение. Этот случай не подходит.
2) Рассматриваем случай, когда 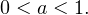 Уравнение принимает вид:
Уравнение принимает вид:  . Его правая часть представляет из себя возрастающую функцию, левая — убывающую. Это означает, что если у такого уравнения есть решение, то оно единственное. Этот случай нам не подходит.
. Его правая часть представляет из себя возрастающую функцию, левая — убывающую. Это означает, что если у такого уравнения есть решение, то оно единственное. Этот случай нам не подходит.
3) Теперь рассмотрим случай, когда 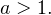 В зависимости от конкретного значения параметра
В зависимости от конкретного значения параметра  уравнение вида
уравнение вида 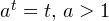 может не иметь решений (нет точек пересечения соответствующих графиков), иметь одно решение (прямая касается экспоненты), иметь два решения (две точки пересечения). Нам подходит последний случай.
может не иметь решений (нет точек пересечения соответствующих графиков), иметь одно решение (прямая касается экспоненты), иметь два решения (две точки пересечения). Нам подходит последний случай.
Разберемся со случаем, когда прямая касается экспоненты. Пусть  — абсцисса точки касания. В этой точке производная к экспоненте равняется единице (тангенс угла наклона касательной), кроме того значения обоих функций совпадают, то есть имеет место система:
— абсцисса точки касания. В этой точке производная к экспоненте равняется единице (тангенс угла наклона касательной), кроме того значения обоих функций совпадают, то есть имеет место система:
![Rendered by QuickLaTeX.com \[ \begin{cases} a^{\tau}\ln a = 1, \\ a^{\tau} = \tau \end{cases}\Leftrightarrow \begin{cases} a^{\tau} = \frac{1}{\ln a}, \\ a^{\tau} = \tau \end{cases}\Leftrightarrow \tau = \frac{1}{\ln a}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d8d685c10070cb1cf3f9917150102cc0_l3.png)
![Rendered by QuickLaTeX.com \[ a^{\frac{1}{\ln a}}\ln a = 1\Leftrightarrow a^{\log_a e} =\frac{1}{\ln a}\Leftrightarrow a = e^{\frac{1}{e}}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-22cf2c53305f8dada4380d16d30dc8dd_l3.png)
Если значение параметра окажется меньше, точек пересечения прямой и экспоненты уже будет две. Итак, окончательный ответ: 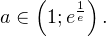
Задача для самостоятельного решения №8. Найти все значения 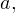 при каждом из которых наименьшее значение функции
при каждом из которых наименьшее значение функции 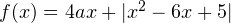 больше, чем
больше, чем 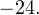
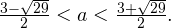
На сегодня на этом все. Следите за обновлениями, учите математику, задавайте свои вопросы в комментариях. Удачи вам! А напоследок случай из жизни Сократа о значимости некоторых параметров.
Репетитор по математике на Юго-Западной
Сергей Валерьевич
Прохожий спросил философа Сократа:
— Сколько часов пути до города?
Сократ ответил:
— Иди…
Путник пошел, и, когда он прошел двадцать шагов, Сократ крикнул:
— Два часа!
— Что же ты мне сразу не сказал? — возмутился тот.
— А откуда я знал, с какой скоростью ты будешь идти?!
уравнения и неравенства с параметром
Существует ровно три генеральных метода решения задач 18:
- Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;
- Графический метод — привлечение чертежа. Во многих задачах 18 достаточно начертить графики функций — и решение становится очевидным;
- Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.
Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.
Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)
- Глава 1.
- Графический подход
- § 1.
- Вебинар по задачам 18: модуль и окружности

- § 2.
- Как решать задачу 18: графический подход

- § 3.
- Задача 18: две окружности и модуль

- § 4.
- Задача 18: пересечение графиков окружности и модуля

- § 5.
- Новая задача 18 из пробного ЕГЭ — наглядный пример того, как эффективно работает графическое решение задач с параметром.

- Глава 2.
- Аналитический подход
- § 1.
- Задачи 18: Аналитическое решение

- § 2.
- Окружность и модуль: задачи 18 с двумя параметрами

- § 3.
- Аналитическое решение задачи 18 с перебором различных вариантов

- Глава 3.
- Нестандартные приемы
- § 1.
- Задача 18: метод симметричных корней

- § 2.
- Как увидеть симметрию корней в задаче 18?

- § 3.
- Метод мажорант в задаче 18

- § 4.
- Графическое решение сложных задач 18 с модулем

- § 5.
- Задание 18: Симметрия корней в системе уравнений

- § 6.
- Анализ знаков квадратного трёхчлена в сложных задачах 18

- § 7.
- Применение производной для отыскания точек пересечения графиков

- § 8.
- Продвинутый метод симметричных корней

- § 9.
- Новая задача 18 с графическим решением

Что такое параметр? Простые задачи с параметрами
Одна из сложных задач Профильного ЕГЭ по математике — задача с параметрами. В ЕГЭ 2020 года это №18. И даже в вариантах ОГЭ они есть. Что же означает это слово —
Толковый словарь (в который полезно время от времени заглядывать) дает ответ: «Параметр — это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса».
Хорошо, параметр — это какая-либо характеристика, свойство системы или процесса.
Вот, например, ракета выводит космический аппарат в околоземное пространство. Как вы думаете — какие параметры влияют на его полет?
Если корабль запустить с первой космической скоростью, приближенно равной 7,9 км/с, он выйдет на круговую орбиту.
Вторая космическая скорость, приближенно равная 11,2 км/с, позволяет космическому кораблю преодолеть поле тяжести Земли. Третья космическая скорость, приближенно равная 16,7 км/с, дает возможность преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.
А если скорость меньше первой космической? Значит, тонны металла, топлива и дорогостоящей аппаратуры рухнут на землю, сопровождаемые репликой растерянного комментатора: «Кажется, что-то пошло не так».
Скорость космического корабля можно — параметр, от которого зависит его дальнейшая траектория и судьба. Конечно, это не единственный параметр. В реальных задачах науки и техники, задействованы уравнения, включающие функции многих переменных и параметров, а также производные этих функций.
1. Теперь пример из школьной математики.
Все мы помним, что такое квадратное уравнение. Это уравнение вида , где коэффициент а не равен нулю.
Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.
Дискриминант квадратного уравнения:
Если  , квадратное уравнение имеет два корня: и
, квадратное уравнение имеет два корня: и
Если , квадратное уравнение имеет единственный корень
Если  , квадратное уравнение не имеет действительных корней. Рассмотрим уравнение . Его дискриминант равен Если
, квадратное уравнение не имеет действительных корней. Рассмотрим уравнение . Его дискриминант равен Если  , то есть
, то есть  , это квадратное уравнение имеет два корня.
, это квадратное уравнение имеет два корня.
Если при , уравнение имеет единственный корень.
Если  , то есть с > 1, корней нет.
, то есть с > 1, корней нет.
В нашем уравнении с — параметр, величина, которая принимать любые значения. Но от этого параметра с зависит количество корней данного уравнения.
Для того чтобы уверенно решать задачи с параметрами, необходимо отличное знание и алгебры, и планиметрии.
И еще две простые задачи с параметром.
2. Найдите значение параметра p, при котором уравнение имеет 2 различных корня.
Квадратное уравнение имеет два различных корня, когда  .
.
Найдем дискриминант уравнения
В нем
Т.к.  , получим:
, получим:

Вспомним, как решаются квадратичные неравенства (вы проходили это в 9 классе).
Найдем корни квадратного уравнения . Это и
Разложим левую часть неравенства на множители:
Значит,

Рисуем параболу с ветвями вверх. Она пересекает ось р в точках и

Записываем ответ:
3. При каких значениях параметра k система уравнений не имеет решений?
Оба уравнения системы — линейные. График линейного уравнения — прямая. Запишем уравнения системы в привычном для нас виде, выразив у через х:
Первое уравнение задает прямую с угловым коэффициентом . Второе уравнение — прямую с угловым коэффициентом -2.
Система уравнений не имеет решений, если эти прямые не пересекаются, то есть параллельны. Это значит, что и .
Действительно, в этом случае первое уравнение задает прямую , а второе — параллельную ей прямую
Ответ: 10
Читаем дальше:
Графический метод решения задач с параметрами.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Как подготовиться к решению задач с параметром на ЕГЭ
Задание № 18 варианта КИМ ЕГЭ по математике профильного уровня
Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.
Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.
«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.
Чему нужно научиться, решая задачи с параметром
В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.
Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т.д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.
Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.
Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме:
Следующая тема курса – графические методы решения задач с параметром
Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости (x; y) или в плоскости (x; a). Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т.д.), эти свойства и приемы их использования тоже нужно знать.
На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.
В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.
Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.
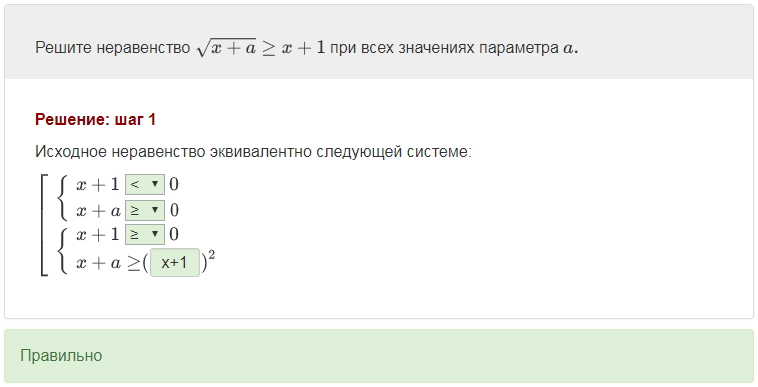
Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
- Купить доступ к этой задаче в составе экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
«Подготовка к ЕГЭ :Задачи с параметрами»
Доклад на ГМО учителя математики МБОУ СОШ №9
Молчановой Елены Владимировны
«Подготовка к ЕГЭ по математике: задачи с параметрами ».
Поскольку в школьных учебниках нет определения параметра, я предлагаю взять за основу следующий его простейший вариант.
Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Что означает «решить задачу с параметром»?
Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.
Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.
Более прозрачное понимание того, что означает решить задачу с параметром, у читателя сформируется после ознакомления с примерами решения задач на последующих страницах.
Какие основные типы задач с параметрами?
Тип 1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.
Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успех и при решении задач всех других основных типов.
Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).
Обращаю внимание на то, что при решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда прямое решение в соответствии с типом 1 является единственным разумным путем получения ответа при решении задачи типа 2.
Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).
Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.
Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Например, найти значения параметра, при которых:
1) уравнение выполняется для любого значения переменной из заданного промежутка;
2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.
Комментарий. Многообразие задач с параметром охватывает весь курс школьной математики (и алгебры, и геометрии), но подавляющая часть из них на выпускных и вступительных экзаменах относится к одному из четырех перечисленных типов, которые по этой причине названы основными.
Наиболее массовый класс задач с параметром — задачи с одной неизвестной и одним параметром. Следующий пункт указывает основные способы решения задач именно этого класса.
Каковы основные способы (методы) решения задач с параметром?
Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.
Комментарий. Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Комментарий. Исключительная наглядность и красота графического способа решения задач с параметром настолько увлекает изучающих тему «Задачи с параметром», что они начинают игнорировать другие способы решения, забывая общеизвестный факт: для любого класса задач их авторы могут сформулировать такую, которая блестяще решается данным способом и с колоссальными трудностями остальными способами. Поэтому на начальной стадии изучения опасно начинать с графических приемов решения задач с параметром.
Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
Перейду теперь к демонстрации указанных способов решения задач с параметром, так как это мой любимый метод решения заданий данного типа.
Проанализировав все задания с параметрами, решаемыми графическим методом, я знакомство с параметрами начинаю с заданий ЕГЭ В7 2002 года :
При каком целом значении к уравнение 45х – 3х2 – х3 + 3к = 0 имеет ровно два корня ?
Эти задания позволяют, во первых, вспомнить как строить графики с использованием производной, а во-вторых, объяснить смысл прямой у = к.
На последующих занятиях я пользуюсь подборкой легких и средних по уровню конкурсных задач с параметрами для подготовки к ЕГЭ, уравнений с модулем. Эти задания можно рекомендовать учителям по математике в качестве стартового комплекта упражнений для обучения работе с параметром, заключенным под знак модуля. Большинство номеров решаются графическим способом и предоставляют учителю готовый план урока (или двух уроков) с сильным учеником. Начальная подготовка к ЕГЭ по математике на упражнениях, близких по сложности к реальным номерам С5. Многие из предложенных заданий взяты из материалов для подготовки к ЕГЭ 2009 года, а некоторые – из интернета из опыта коллег.
1) Укажите все значения параметра p, при которых уравнение  имеет 4 корня?
имеет 4 корня?
Ответ: 
2) При каких значениях параметра а уравнение  не имеет решений?
не имеет решений?
Ответ: 
3) Найдите все значения а, при каждом из которых уравнение  имеет ровно 3 корня?
имеет ровно 3 корня?
Ответ: а=2
4) При каких значениях параметра b уравнение  имеет единственное решение? Ответ:
имеет единственное решение? Ответ: ![b \in (-\infty;-1] \cup {0} \cup (1;+ \infty)](/800/600/https/ds02.infourok.ru/uploads/ex/0af4/00051403-30a8b822/hello_html_676a2c2.gif)
5) Найдите все значения m, при которых уравнение  не имеет решений.
не имеет решений.
Ответ: ![m \in [-2;0,25]](/800/600/https/ds02.infourok.ru/uploads/ex/0af4/00051403-30a8b822/hello_html_m60671455.gif)
6) Найдите все значения а, при которых уравнение  имеет ровно 3 различных корня. (Если значений а более одного, то в ответе запишите их сумму.)
имеет ровно 3 различных корня. (Если значений а более одного, то в ответе запишите их сумму.)
Ответ: 3
7) При каких значениях b уравнение  имеет ровно 2 решения?
имеет ровно 2 решения?
Ответ: 
8) Укажите такие параметры k, при которых уравнение  имеет не менее двух решений.
имеет не менее двух решений.
Ответ: ![k \in [-2;1]](/800/600/https/ds02.infourok.ru/uploads/ex/0af4/00051403-30a8b822/hello_html_51a95238.gif)
9) При каких значениях параметра p уравнение ![k \in [-2;1]](/800/600/https/ds02.infourok.ru/uploads/ex/0af4/00051403-30a8b822/hello_html_m34072ab7.gif) имеет только одно решение?
имеет только одно решение?
Ответ: ![p \in (-\infty;0] \cup (0,5; +\infty)](/800/600/https/ds02.infourok.ru/uploads/ex/0af4/00051403-30a8b822/hello_html_650f873.gif)
10) Найдите все значения а, при каждом из которых уравнение (х + 1) имеет ровно 2 корня? Если значений а окажется несколько, то в ответ запишите их сумму.
имеет ровно 2 корня? Если значений а окажется несколько, то в ответ запишите их сумму.
Ответ: — 3
11) Найдите все значения а, при которых уравнение  имеет ровно 3 корня? (Если значений а более одного, то в ответ запишите их сумму).
имеет ровно 3 корня? (Если значений а более одного, то в ответ запишите их сумму).
Ответ: 4
12) При каком наменьшем натуральном значении параметра а уравнение  –
–  = 11 имеет только положительные корни?
= 11 имеет только положительные корни?
Ответ: 19
13) Найдите все значения а, при каждом из которых уравнение  = 1 имеет ровно 3 корня? (Если значений а более одного, то в ответе запишите их сумму).
= 1 имеет ровно 3 корня? (Если значений а более одного, то в ответе запишите их сумму).
Ответ:- 3
14) Укажите такие значения параметра t, при которых уравнение  имеет 4 различных решения. Ответ:
имеет 4 различных решения. Ответ: 
15) Найдите такие параметры m, при которых уравнение  имеет два различных решения. Ответ:
имеет два различных решения. Ответ: 
16) При каких значениях параметра p уравнение  имеет ровно 3 экстремума? Ответ:
имеет ровно 3 экстремума? Ответ: 
17) Укажите все возможные параметры n, при которых функция  имеет ровно одну точку минимума. Ответ:
имеет ровно одну точку минимума. Ответ: 
Опубликованный комплект регулярно используется мной для работы со способным, но не самым сильным учеником, претендующим, тем не менее, на высокий балл ЕГЭ за счет решения номера С5. Подготовку такого ученика учитель проводит в несколько этапов, выделяя для тренировки отдельных навыков, необходимых для поиска и реализации длинных решений, отдельные уроки. Эта подборка подходит для стадии формирования представлений о плавающих рисунках в зависимости от параметра. Номера 16 и 17 составлены по образцу реального уравнения с параметром на ЕГЭ 2011г. Задачи выстроены в порядок возрастания их сложности.
Задание C5 по математике ЕГЭ 2012
Здесь мы имеем традиционную задачу с параметром, требующую умеренного владения материалом и применения нескольких свойств и теорем. Это задание является одним из самых сложных заданий Единого государственного экзамена по математике. Оно рассчитано, прежде всего, на тех, кто собирается продолжать образование в вузах с повышенными требованиями к математической подготовке абитуриентов. Для успешного решения задачи важно свободно оперировать изученными определениями, свойствами, теоремами, применять их в различных ситуациях, анализировать условие и находить возможные пути решения.
На сайте подготовки к ЕГЭ Александра Ларина с 11.05.2012 года были предложены тренировочные варианты №1 – 22 с заданиями уровня «С», С5 некоторых из них были аналогичны тем заданиям, которые были на реальном экзамене. Например, найдите все значения параметра а, при каждом из которых графики функций f(х) =  и g(х) = а(х + 5) + 2 не имеют общих точек?
и g(х) = а(х + 5) + 2 не имеют общих точек?
Разберем решение задания С5 из экзамена 2012 года.
Задание С5 из ЕГЭ-2012
При каких значениях параметра a уравнение  имеет не менее двух корней.
имеет не менее двух корней.
Решим эту задачу графически. Построим график левой части уравнения:  и график правой части:
и график правой части:  и сформулируем вопрос задачи так: при каких значениях параметра a графики функций
и сформулируем вопрос задачи так: при каких значениях параметра a графики функций  и
и  имеют две или более общих точки.
имеют две или более общих точки.
В левой части исходного уравнения параметр отсутствует, поэтому мы можем построить график функции  .
.
Будем строить это график с помощью линейных преобразований графика функции  :
:

1. Сдвинем график функции  на 3 единицы вниз вдоль оси OY, получим график функции
на 3 единицы вниз вдоль оси OY, получим график функции  :
:

2. Построим график функции  . Для этого часть графика функции
. Для этого часть графика функции  , расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:
, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:

Итак, график функции  имеет вид:
имеет вид:

График функции  представляет собой семейство прямых с переменным коэффициентом наклона, равным а, сдвинутых на 1 единицу вниз вдоль оси OY. То есть точка с координатами (0;1) представляет собой центр вращения этого семейства прямых:
представляет собой семейство прямых с переменным коэффициентом наклона, равным а, сдвинутых на 1 единицу вниз вдоль оси OY. То есть точка с координатами (0;1) представляет собой центр вращения этого семейства прямых:

Рассмотрим положения прямой  , в которых она имеет более одной точки пересечения с графиком функции
, в которых она имеет более одной точки пересечения с графиком функции  :
:

Прямые АВ и АС имеют две точки пересечения с графиком функции. Все прямые, расположенные между ними имеют 3 точки пересечения с графиком функции  .
.
Чтобы найти коэффициент наклона прямой АВ, найдем абсциссу точки В.
Точка В – это точка пересечения графика функции  с осью ОХ. В этой точке у=0. Получим уравнение:
с осью ОХ. В этой точке у=0. Получим уравнение:  , отсюда
, отсюда  . Коэффициент а наклона прямой АВ равен тангенсу угла BAD треугольника ABD и равен
. Коэффициент а наклона прямой АВ равен тангенсу угла BAD треугольника ABD и равен 
Найдем коэффициент наклона прямой АС. Точка С – это точка, в которой прямая  касается графика функции
касается графика функции  (точка С принадлежит части графика функции
(точка С принадлежит части графика функции  , отображенной симметрично относительно оси ОХ). То есть это точка, в которой графики функции
, отображенной симметрично относительно оси ОХ). То есть это точка, в которой графики функции  и
и  имеют одну общую точку.
имеют одну общую точку.
Теперь нам нужно найти значение параметра а, при котором уравнение  имеет одно решение.
имеет одно решение.
Умножим обе части уравнения на х и перенесем все слагаемые влево. Получим квадратное уравнение  Это уравнение имеет единственный корень, если дискриминант равен нулю.
Это уравнение имеет единственный корень, если дискриминант равен нулю.
 ,
, 
Таким образом,
уравнение  имеет два решения, если
имеет два решения, если  или
или 
Уравнение имеет три решения, если 
Несколько советов при обучении решению задач с параметрами (тезисы коллег):
1) Для обучения решению сложных задач на модули графическим образом желательно провести хотя бы один урок на подготовку к выполнению необходимых построений. Нужно разобрать темы «построение графика функции», «построение множества точек, заданных уравнением с двумя переменными».
2) Перед тем, как приступить к задачам С5 хорошенько подумайте, стоит ли тратить время и силы на задания, успех в выполнении которых зависит в первую очередь от количества решенного математического материала без параметра. Ученик должен иметь отличную подготовку по уравнениям с одной переменной и уметь представлять себе весь процесс их решения от начала до самого конца. Если таких навыков нет — не тратье лишнее время на профильную подготовку к ЕГЭ. Уделите лучше время простой математике, без параметров.
3) Никогда не задавайте ученику того, что не было разобрано на занятии и предостерегайте его от потерь случаев. Параметры — коварная тема! Очень легко запутаться в многообразии случаев и какой-нибудь из них упустить.


