Решение тригонометрических уравнений графически
Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
sin х = 1 — х.
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
х ≈ 0,5.
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
При х = 0,5
sin x ≈ 0,4794,
1 — х = 0,5;
следовательно, sin х < 1 — х. Но тогда, как легко понять из рисунка, корень уравнения sin х = 1 — х будет больше, чем 0,5. Проверим значение х = 0,6. Имеем (при х = 0,6):
sin х ≈ 0,5446,
1 — х = 0,4;
следовательно, sin х > 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
x0 ≈0,5 (с недостатком),
x0 ≈ 0,6 (с избытком).
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
sin х ≈ 0,5227,
1 — х = 0,45.
Опять получаем, что sin х > 1 — х. Следовательно, x0 < 0,55.
Проверим точку х = 0,52 (она близка к средней точке х = 0,525 интервала [0,50; 0,55], в котором заключен корень x0). При х = 0,52
sin х ≈ 0,4969,
1 — х = 0,48.
Снова sin x > 1 — х; поэтому x0 < 0,52. Итак, 0,50 < x0 < 0,52. Поэтому с точностью до 0,01
x0 ≈ 0,51.
Для примера рассмотрим уравнение
tg x/2 = 2 — x.
Графики функций у = tg x/2и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x/2 и у = 2 — х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x/2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
tg x/2 ≈ 0,7215,
2 — х = 0,7500.
Поскольку tg x/2 < 2- х, то х0 >1,25. Итак,
1,25< х0 < 1,30.
Теперь испытаем значение х = 1,28, которое близко к среднему значению чисел 1,25 и 1,30. При х = 1,28
tg x/2 ≈ 0,7445,
2 — х = 0,7200.
Теперь уже tg x/2 >2 — х Значит , х0 < 1,28.
Аналогично, рассматривая значение х = 1,26, мы получили бы tg x/2 < 2 — х и потому х0 > 1,26. Значит,
1,26 <х0< 1,28.
Поэтому с точностью до 0,01
х0 ≈ 1,27
Если бы нужно было определить, какое это приближенное значение (с недостатком или с избытком), то пришлось бы сравнить значения tg x/2 и 2 — х в точке х = 1,27.
1. Частные случаи простейших тригонометрических уравнений
Если точка \(M\) числовой окружности соответствует числу \(t\), то
абсциссу точки \(M\) называют косинусом числа \(t\) и обозначают \(cos\) \(t\),
а ординату точки \(M\) называют синусом числа \(t\) и обозначают \(sin\) \(t\).
Рис. \(1\). Координаты точки M
Итак, если
тогда Mt=Mx;y;x=cost;y=sint.
Отсюда следует, что −1≤cost≤1;−1≤sint≤1.
Исходя из определения синуса и косинуса, легко определить по окружности значения углов \(0°\), \(90°\), \(180°\), \(270°\), \(360°\):
Рис. \(2\). Частные случаи
Так как в любую точку тригонометрического круга мы придём через целое число оборотов, равных 2π, то справедливы равенства:
sin(t+2πk)=sint;cos(t+2πk)=cost.
По окружности можно найти углы, синус, косинус которых равен \(0\), \(1\) и \(-1\). Это и будет решение соответствующих простейших тригонометрических уравнений:
sinx=0,x=πk,гдеk∈ℤ;sinx=1,x=π2+2πk,гдеk∈ℤ;sinx=−1,x=3π2+2πk,гдеk∈ℤ; cosx=0,x=π2+πm,гдеm∈ℤ;cosx=1,x=2πm,гдеm∈ℤ;cosx=−1,x=π+2πm,гдеm∈ℤ.
Отношение синуса числа \(t\) к косинусу того же числа называют тангенсом числа \(t\)
и обозначают \(tg\) \(t\).
Отношение косинуса числа \(t\) к синусу того же числа называют котангенсом числа \(t\)
и обозначают \(ctg\) \(t\).
Значения тангенса и котангенса повторяются через π, поэтому:
tg(t+πk)=tgt;ctg(t+πk)=ctgt.
Дадим геометрическую иллюстрацию для тангенса и котангенса.
Проведём сначала в координатной плоскости к числовой окружности касательную в точке \(A\).
Эту касательную \(l\) будем считать числовой прямой, ориентированной так же, как ось \(y\), и с началом в точке \(A\) (см. рис. \(3\))
Рис. \(3\). Линия тангенсов
Итак, если числу \(t\) соответствует на числовой окружности точка \(M\), то, проведя прямую \(OM\), получим в пересечении её с числовой прямой \(l\) точку \(P\), которая имеет на числовой прямой \(l\) координату \(tg\) \(t\).
Числовую прямую \(l\) называют линией тангенсов.
Для углов π2 и 3π2 \(OM\) параллельна числовой прямой \(l\), поэтому для этих углов тангенс не существует. А в углах \(0\) и π тангенс равен \(0\). Поэтому:
А в углах \(0\) и π тангенс равен \(0\). Поэтому:
tgx=0,x=πk,гдеk∈ℤ.
Аналогично можно ввести линию котангенсов — числовая прямая \(m\) с началом в точке \(B\) (см. рис. \(4\)).
Рис. \(4\). Линия котангенсов
Решение уравнений с косинусом. Основные методы решения тригонометрических уравнений
Тригонометрические уравнения — тема не самая простая. Уж больно они разнообразные.) Например, такие:
sin 2 x + cos3x = ctg5x
sin(5x+π /4) = ctg(2x-π /3)
sinx + cos2x + tg3x = ctg4x
И тому подобное…
Но у этих (и всех остальных) тригонометрических монстров есть два общих и обязательных признака. Первый — вы не поверите — в уравнениях присутствуют тригонометрические функции.) Второй: все выражения с иксом находятся внутри этих самых функций. И только там! Если икс появится где-нибудь снаружи, например, sin2x + 3x = 3, это уже будет уравнение смешанного типа. Такие уравнения требуют индивидуального подхода. Здесь мы их рассматривать не будем.
Такие уравнения требуют индивидуального подхода. Здесь мы их рассматривать не будем.
Злые уравнения в этом уроке мы тоже решать не будем.) Здесь мы будем разбираться с самыми простыми тригонометрическими уравнениями. Почему? Да потому, что решение
Так что, если на втором этапе у вас проблемы — первый этап особого смысла не имеет.)
Как выглядят элементарные тригонометрические уравнения?
sinx = а
cosx = а
tgx = а
ctgx = а
Здесь а обозначает любое число. Любое.
Кстати, внутри функции может находиться не чистый икс, а какое-то выражение, типа:
cos(3x+π /3) = 1/2
и тому подобное. Это усложняет жизнь, но на методе решения тригонометрического уравнения никак не сказывается.
Как решать тригонометрические уравнения?
Тригонометрические уравнения можно решать двумя путями. Первый путь: с использованием логики и тригонометрического круга. Этот путь мы рассмотрим здесь. Второй путь — с использованием памяти и формул — рассмотрим в следующем уроке.
Первый путь понятен, надёжен, и его трудно забыть.) Он хорош для решения и тригонометрических уравнений, и неравенств, и всяких хитрых нестандартных примеров. Логика сильнее памяти!)
Решаем уравнения с помощью тригонометрического круга.
Включаем элементарную логику и умение пользоваться тригонометрическим кругом. Не умеете!? Однако… Трудно же вам в тригонометрии придётся…) Но не беда. Загляните в уроки «Тригонометрический круг…… Что это такое?» и «Отсчёт углов на тригонометрическом круге». Там всё просто. В отличие от учебников…)
Ах, вы в курсе!? И даже освоили «Практическую работу с тригонометрическим кругом» !? Примите поздравления. Эта тема будет вам близка и понятна. ) Что особо радует, тригонометрическому кругу безразлично, какое уравнение вы решаете. Синус, косинус, тангенс, котангенс — ему всё едино. Принцип решения один.
) Что особо радует, тригонометрическому кругу безразлично, какое уравнение вы решаете. Синус, косинус, тангенс, котангенс — ему всё едино. Принцип решения один.
Вот и берём любое элементарное тригонометрическое уравнение. Хотя бы это:
cosx = 0,5
Надо найти икс. Если говорить человеческим языком, нужно найти угол (икс), косинус которого равен 0,5.
Как мы ранее использовали круг? Мы рисовали на нём угол. В градусах или радианах. И сразу видели тригонометрические функции этого угла. Сейчас поступим наоборот. Нарисуем на круге косинус, равный 0,5 и сразу увидим угол. Останется только записать ответ.) Да-да!
Рисуем круг и отмечаем косинус, равный 0,5. На оси косинусов, разумеется. Вот так:
Теперь нарисуем угол, который даёт нам этот косинус. Наведите курсор мышки на рисунок (или коснитесь картинки на планшете), и увидите этот самый угол х.
Косинус какого угла равен 0,5?
х = π /3
cos60° = cos(π /3 ) = 0,5
Кое-кто скептически хмыкнет, да.
Если провернуть подвижную сторону ОА на полный оборот , точка А попадёт в исходное положение. С тем же косинусом, равным 0,5. Т.е. угол изменится на 360° или 2π радиан, а косинус — нет. Новый угол 60° + 360° = 420° тоже будет решением нашего уравнения, т.к.
Таких полных оборотов можно накрутить бесконечное множество… И все эти новые углы будут решениями нашего тригонометрического уравнения. И их все надо как-то записать в ответ. Все. Иначе решение не считается, да…)
Математика умеет это делать просто и элегантно. В одном кратком ответе записывать бесконечное множество решений. Вот как это выглядит для нашего уравнения:
х = π /3 + 2π n, n ∈ Z
Расшифрую. Всё-таки писать осмысленно приятнее, чем тупо рисовать какие-то загадочные буковки, правда?)
Всё-таки писать осмысленно приятнее, чем тупо рисовать какие-то загадочные буковки, правда?)
π /3 — это тот самый угол, который мы увидели на круге и определили по таблице косинусов.
2π — это один полный оборот в радианах.
n — это количество полных, т.е. целых оборотов. Понятно, что n может быть равно 0, ±1, ±2, ±3…. и так далее. Что и указано краткой записью:
n ∈ Z
n принадлежит (∈ ) множеству целых чисел (Z ). Кстати, вместо буквы n вполне могут употребляться буквы k, m, t и т.д.
Эта запись означает, что вы можете взять любое целое n . Хоть -3, хоть 0, хоть +55. Какое хотите. Если подставите это число в запись ответа, получите конкретный угол, который обязательно будет решением нашего сурового уравнения.)
Или, другими словами, х = π
/3 — это единственный корень из бесконечного множества. Чтобы получить все остальные корни, достаточно к π
/3 прибавить любое количество полных оборотов (n ) в радианах. Т.е. 2π
n радиан.
Чтобы получить все остальные корни, достаточно к π
/3 прибавить любое количество полных оборотов (n ) в радианах. Т.е. 2π
n радиан.
Всё? Нет. Я специально удовольствие растягиваю. Чтобы запомнилось получше.) Мы получили только часть ответов к нашему уравнению. Эту первую часть решения я запишу вот как:
х 1 = π /3 + 2π n, n ∈ Z
х 1 — не один корень, это целая серия корней, записанная в краткой форме.
Но есть ещё углы, которые тоже дают косинус, равный 0,5!
Вернёмся к нашей картинке, по которой записывали ответ. Вот она:
Наводим мышку на картинку и
х 2 = — π /3
Ну и, разумеется, добавляем все углы, которые получаются через полные обороты:
х 2 = — π /3 + 2π n, n ∈ Z
Вот теперь всё. ) По тригонометрическому кругу мы увидели (кто понимает, конечно)) все углы, дающие косинус, равный 0,5. И записали эти углы в краткой математической форме. В ответе получились две бесконечные серии корней:
) По тригонометрическому кругу мы увидели (кто понимает, конечно)) все углы, дающие косинус, равный 0,5. И записали эти углы в краткой математической форме. В ответе получились две бесконечные серии корней:
х 1 = π /3 + 2π n, n ∈ Z
х 2 = — π /3 + 2π n, n ∈ Z
Это правильный ответ.
Надеюсь, общий принцип решения тригонометрических уравнений
с помощью круга понятен. Отмечаем на круге косинус (синус, тангенс, котангенс) из заданного уравнения, рисуем соответствующие ему углы и записываем ответ. Конечно, нужно сообразить, что за углы мы увидели на круге. Иногда это не так очевидно. Ну так я и говорил, что здесь логика требуется.)Для примера разберём ещё одно тригонометрическое уравнение:
Прошу учесть, что число 0,5 — это не единственно возможное число в уравнениях!) Просто мне его писать удобнее, чем корни и дроби.
Работаем по общему принципу. Рисуем круг, отмечаем (на оси синусов, разумеется!) 0,5. Рисуем сразу все углы, соответствующие этому синусу. Получим вот такую картину:
Рисуем сразу все углы, соответствующие этому синусу. Получим вот такую картину:
Сначала разбираемся с углом х в первой четверти. Вспоминаем таблицу синусов и определяем величину этого угла. Дело нехитрое:
х = π /6
Вспоминаем про полные обороты и, с чистой совестью, записываем первую серию ответов:
х 1 = π /6 + 2π n, n ∈ Z
Половина дела сделана. А вот теперь надо определить второй угол… Это похитрее, чем в косинусах, да… Но логика нас спасёт! Как определить второй угол через х? Да легко! Треугольнички на картинке одинаковые, и красный угол х равен углу х . Только отсчитан он от угла π в отрицательном направлении. Потому и красный.) А нам для ответа нужен угол, отсчитанный правильно, от положительной полуоси ОХ, т.е. от угла 0 градусов.
Наводим курсор на рисунок и всё видим. Первый угол я убрал, чтобы не усложнял картинку. Интересующий нас угол (нарисован зелёным) будет равен:
π — х
Икс мы знаем, это π
/6 . Стало быть, второй угол будет:
Стало быть, второй угол будет:
π — π /6 = 5π /6
Снова вспоминаем про добавку полных оборотов и записываем вторую серию ответов:
х 2 = 5π /6 + 2π n, n ∈ Z
Вот и всё. Полноценный ответ состоит из двух серий корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Уравнения с тангенсом и котангенсом можно легко решать по тому же общему принципу решения тригонометрических уравнений. Если, конечно, знаете, как нарисовать тангенс и котангенс на тригонометрическом круге.
В приведённых выше примерах я использовал табличное значение синуса и косинуса: 0,5. Т.е. одно из тех значений, которые ученик знать обязан. А теперь расширим наши возможности на все остальные значения. Решать, так решать!)
Итак, пусть нам надо решить вот такое тригонометрическое уравнение:
Такого значения косинуса в кратких таблицах нет. Хладнокровно игнорируем этот жуткий факт.
Разбираемся, для начала, с углом в первой четверти. Знать бы, чему равен икс, сразу бы ответ записали! Не знаем… Провал!? Спокойствие! Математика своих в беде не бросает! Она на этот случай придумала арккосинусы. Не в курсе? Зря. Выясните, Это много проще, чем вы думаете. По этой ссылке ни одного мудрёного заклинания насчёт «обратных тригонометрических функций» нету… Лишнее это в данной теме.
Если вы в курсе, достаточно сказать себе: «Икс — это угол, косинус которого равен 2/3». И сразу, чисто по определению арккосинуса, можно записать:
Вспоминаем про дополнительные обороты и спокойно записываем первую серию корней нашего тригонометрического уравнения:
х 1 = arccos 2/3 + 2π n, n ∈ Z
Практически автоматом записывается и вторая серия корней, для второго угла. Всё то же самое, только икс (arccos 2/3) будет с минусом:
х 2 = — arccos 2/3 + 2π n, n ∈ Z
И все дела! Это правильный ответ. Даже проще, чем с табличными значениями. Ничего вспоминать не надо.) Кстати, самые внимательные заметят, что эта картинка с решением через арккосинус ничем, в сущности, не отличается от картинки для уравнения cosx = 0,5.
Даже проще, чем с табличными значениями. Ничего вспоминать не надо.) Кстати, самые внимательные заметят, что эта картинка с решением через арккосинус ничем, в сущности, не отличается от картинки для уравнения cosx = 0,5.
Именно так! Общий принцип на то и общий! Я специально нарисовал две почти одинаковые картинки. Круг нам показывает угол х по его косинусу. Табличный это косинус, или нет — кругу неведомо. Что это за угол, π /3, или арккосинус какой — это уж нам решать.
С синусом та же песня. Например:
Вновь рисуем круг, отмечаем синус, равный 1/3, рисуем углы. Получается вот такая картина:
И опять картинка почти та же, что и для уравнения sinx = 0,5. Опять начинаем с угла в первой четверти. Чему равен икс, если его синус равен 1/3 ? Не вопрос!
Вот и готова первая пачка корней:
х 1 = arcsin 1/3 + 2π n, n ∈ Z
Разбираемся со вторым углом. В примере с табличным значением 0,5 он был равен:
π — х
Так и здесь он будет точно такой же! Только икс другой, arcsin 1/3. Ну и что!? Можно смело записывать вторую пачку корней:
Ну и что!? Можно смело записывать вторую пачку корней:
х 2 = π — arcsin 1/3 + 2π n, n ∈ Z
Это совершенно правильный ответ. Хотя и выглядит не очень привычно. Зато понятно, надеюсь.)
Вот так решаются тригонометрические уравнения с помощью круга. Этот путь нагляден и понятен. Именно он спасает в тригонометрических уравнениях с отбором корней на заданном интервале, в тригонометрических неравенствах — те вообще решаются практически всегда по кругу. Короче, в любых заданиях, которые чуть сложнее стандартных.
Применим знания на практике?)
Решить тригонометрические уравнения:
Сначала попроще, прямо по этому уроку.
Теперь посложнее.
Подсказка: здесь придётся поразмышлять над кругом. Лично.)
А теперь внешне простенькие… Их ещё частными случаями называют.
sinx = 0
sinx = 1
cosx = 0
cosx = -1
Подсказка: здесь надо сообразить по кругу, где две серии ответов, а где одна. .. И как вместо двух серий ответов записать одну. Да так, чтобы ни один корень из бесконечного количества не потерялся!)
.. И как вместо двух серий ответов записать одну. Да так, чтобы ни один корень из бесконечного количества не потерялся!)
Ну и совсем простые):
sinx = 0,3
cosx = π
tgx = 1,2
ctgx = 3,7
Подсказка: здесь надо знать, что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? Самые простые определения. Зато вспоминать никаких табличных значений не надо!)
Ответы, разумеется, в беспорядке):
х 1 = arcsin0,3 + 2π
n, n ∈ Z
х 2 = π
— arcsin0,3 + 2
Не всё получается? Бывает. Прочтите урок ещё раз. Только вдумчиво (есть такое устаревшее слово…) И по ссылкам походите. Главные ссылки — про круг. Без него в тригонометрии — как дорогу переходить с завязанными глазами. Иногда получается.)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов (или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .
Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату . Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на
радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на
радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой
(или
). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении,
(или
) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем (то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем (то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть
.
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение :
ОСОБЫЕ РЕШЕНИЯ:
Отметим на окружности точки, ордината которых равна 0:
Отметим на окружности единственную точку, ордината которой равна 1:
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать .
Урок комплексного применения знаний.
Цели урока.
- Рассмотреть различные методы решения тригонометрических уравнений.
- Развитие творческих способностей учеников путем решения уравнений.
- Побуждение учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Оборудование: экран, проектор, справочный материал.
Ход урока
Вводная беседа.
Основным методом решения тригонометрических уравнений является сведения их простейшим. При этом применяются обычные способы, например, разложения на множители, а также приемы, используемые только для решения тригонометрических уравнений. Этих приемов довольно много, например, различные тригонометрические подстановки, преобразования углов, преобразования тригонометрических функций. Беспорядочное применение каких-либо тригонометрических преобразований обычно не упрощает уравнение, а катастрофически его усложняет. Чтобы выработать в общих чертах план решения уравнения, наметить путь сведения уравнения к простейшему, нужно в первую очередь проанализировать углы – аргументы тригонометрических функций, входящих в уравнение.
Сегодня мы поговорим о методах решения тригонометрических уравнений.
Правильно выбранный метод часто позволяет существенно упростить решение, поэтому
все изученные нами методы всегда нужно держать в зоне своего внимания, чтобы
решать тригонометрические уравнения наиболее подходящим методом.
II. (С помощью проектора повторяем методы решения уравнений.)
1. Метод приведения тригонометрического уравнения к алгебраическому.
Необходимо выразить все тригонометрические функции через одну, с одним и тем же аргументом. Это можно сделать с помощью основного тригонометрического тождества и его следствий. Получим уравнение с одной тригонометрической функцией. Приняв ее за новую неизвестную, получим алгебраическое уравнение. Находим его корни и возвращаемся к старой неизвестной, решая простейшие тригонометрические уравнения.
2. Метод разложения на множители.
Для изменения углов часто бывают полезны формулы приведения, суммы и разности аргументов, а также формулы преобразования суммы (разности) тригонометрических функций в произведение и наоборот.
sin x + sin 3x = sin 2x + sin4x
3. Метод введения дополнительного угла.
4. Метод использования универсальной подстановки.
Уравнения вида F(sinx, cosx, tgx) = 0 сводятся к алгебраическому при помощи универсальной тригонометрической подстановки
Выразив
синус, косинус и тангенс через тангенс половинного угла. Этот прием может
привести к уравнению высокого порядка. Решение которого затруднительно.
Этот прием может
привести к уравнению высокого порядка. Решение которого затруднительно.
Требует знания основных формул тригонометрии — сумму квадратов синуса и косинуса, выражение тангенса через синус и косинус и другие. Для тех, кто их забыл или не знает рекомендуем прочитать статью » «.
Итак, основные тригонометрические формулы мы знаем, пришло время использовать их на практике. Решение тригонометрических уравнений при правильном подходе – довольно увлекательное занятие, как, например, собрать кубик Рубика.
Исходя из самого названия видно, что тригонометрическое уравнение – это уравнение, в котором неизвестное находится под знаком тригонометрической функции.
Существуют так называемые простейшие тригонометрические уравнения. Вот как они выглядят: sinх = а, cos x = a, tg x = a. Рассмотрим, как решить такие тригонометрические уравнения , для наглядности будем использовать уже знакомый тригонометрический круг.
sinх = а
cos x = a
tg x = a
cot x = a
Любое тригонометрическое уравнение решается в два этапа: приводим уравнение к простейшему виду и далее решаем его, как простейшее тригонометрическое уравнение.
Существует 7 основных методов, с помощью которых решаются тригонометрические уравнения.
Метод замены переменной и подстановки
Решение тригонометрических уравнений через разложение на множители
Приведение к однородному уравнению
Решение уравнений, через переход к половинному углу
Введение вспомогательного угла
Решить уравнение 2cos 2 (x + /6) – 3sin( /3 – x) +1 = 0
Используя формулы приведения получим:
2cos 2 (x + /6) – 3cos(x + /6) +1 = 0
Заменим cos(x + /6) на y для упрощения и получаем обычное квадратное уравнение:
2y 2 – 3y + 1 + 0
Корни которого y 1 = 1, y 2 = 1/2
Теперь идем в обратном порядке
Подставляем найденные значения y и получаем два варианта ответа:
Как решить уравнение sin x + cos x = 1 ?
Перенесем все влево, чтобы справа остался 0:
sin x + cos x – 1 = 0
Воспользуемся вышерассмотренными тождествами для упрощения уравнения:
sin x — 2 sin 2 (x/2) = 0
Делаем разложение на множители:
2sin(x/2) * cos(x/2) — 2 sin 2 (x/2) = 0
2sin(x/2) * = 0
Получаем два уравнения
Уравнение является однородным относительно синуса и косинуса, если все его члены относительно синуса и косинуса одной и той же степени одного и того же угла. Для решения однородного уравнения, поступают следующим образом:
Для решения однородного уравнения, поступают следующим образом:
а) переносят все его члены в левую часть;
б) выносят все общие множители за скобки;
в) приравнивают все множители и скобки к 0;
г) в скобках получено однородное уравнение меньшей степени, его в свою очередь делят на синус или косинус в старшей степени;
д) решают полученное уравнение относительно tg.
Решить уравнение 3sin 2 x + 4 sin x cos x + 5 cos 2 x = 2
Воспользуемся формулой sin 2 x + cos 2 x = 1 и избавимся от открытой двойки справа:
3sin 2 x + 4 sin x cos x + 5 cos x = 2sin 2 x + 2cos 2 x
sin 2 x + 4 sin x cos x + 3 cos 2 x = 0
Делим на cos x:
tg 2 x + 4 tg x + 3 = 0
Заменяем tg x на y и получаем квадратное уравнение:
y 2 + 4y +3 = 0, корни которого y 1 =1, y 2 = 3
Отсюда находим два решения исходного уравнения:
x 2 = arctg 3 + k
Решить уравнение 3sin x – 5cos x = 7
Переходим к x/2:
6sin(x/2) * cos(x/2) – 5cos 2 (x/2) + 5sin 2 (x/2) = 7sin 2 (x/2) + 7cos 2 (x/2)
Пререносим все влево:
2sin 2 (x/2) – 6sin(x/2) * cos(x/2) + 12cos 2 (x/2) = 0
Делим на cos(x/2):
tg 2 (x/2) – 3tg(x/2) + 6 = 0
Для рассмотрения возьмем уравнение вида: a sin x + b cos x = c ,
где a, b, c – некоторые произвольные коэффициенты, а x – неизвестное.
Обе части уравнения разделим на :
Теперь коэффициенты уравнения согласно тригонометрическим формулам обладают свойствами sin и cos, а именно: их модуль не более 1 и сумма квадратов = 1. Обозначим их соответственно как cos и sin , где – это и есть так называемый вспомогательный угол. Тогда уравнение примет вид:
cos * sin x + sin * cos x = С
или sin(x + ) = C
Решением этого простейшего тригонометрического уравнения будет
х = (-1) k * arcsin С — + k, где
Следует отметить, что обозначения cos и sin взаимозаменяемые.
Решить уравнение sin 3x – cos 3x = 1
В этом уравнении коэффициенты:
а = , b = -1, поэтому делим обе части на = 2
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Тригонометрические уравнения исключения. Решение тригонометрических уравнений
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда.
 При любом а.
При любом а. Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.
 ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда.В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6.
 Полноценный ответ будет:
Полноценный ответ будет:х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.
 ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу.
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.
 п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн.
Если Вам нравится этот сайт… А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .

Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.

Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получимtg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
Как решать С1. Урок 5. ЕГЭ по математике 2014 — решения.егэцентр.рф
Поздравляю вас, дорогие читатели!
Наконец-то мы дошли до решения тригонометрических уравнений.
 Сейчас мы решим несколько уравнений, которые похожи на задания ЕГЭ. Конечно, в реальном экзамене, задачи будут немного сложнее, но суть останется та же.
Сейчас мы решим несколько уравнений, которые похожи на задания ЕГЭ. Конечно, в реальном экзамене, задачи будут немного сложнее, но суть останется та же.Для начала рассмотрим легкое уравнение (подобные мы уже решали в прошлых уроках, но повторить всегда полезно).
$$(2\cos x + 1) (2\sin x — \sqrt{3}) = 0.$$
Думаю, объяснения, как решать, излишни.
$$2\cos x + 1 = 0 \text{ или } 2\sin x — \sqrt{3} =0,$$
$$\cos x = -\frac{1}{2} \text{ или } \sin x = \frac{\sqrt{3}}{2},$$
Горизонтальным пунктиром отмечено решение для уравнения с синусом, вертикальным — с косинусом.
Таким образом, итоговое решение можно записать, например, так:
$$\left[ \begin{array}{l}x= \pm \frac{2\pi}{3},\\x = \frac{\pi}{3}+2\pi k. \end{array}\right.$$
Тригонометрическое уравнение с ОДЗ
$$(1+\cos x)\left(\frac{1}{\sin x} — 1\right) = 0.$$
Важное отличие в этом примере, что в знаменателе появился синус. Хотя мы немного решали подобные уравнения в предыдущих уроках, стоит остановиться на ОДЗ поподробнее.

ОДЗ
`\sin x \neq 0 \Rightarrow x \neq \pi k`. Когда мы будем отмечать решение на круге, эту серию корней мы отметим специально проколотыми (открытыми) точками, чтобы показать, что `x` не может принимать такие значения.
Решение
Приведем к общему знаменателю, а затем поочередно приравняем обе скобки к нулю.
$$(1+\cos x)\left(\frac{1-\sin x}{\sin x}\right) = 0,$$
$$1+\cos x = 0 \text{ или } \frac{1-\sin x}{\sin x} = 0,$$
$$\cos x = -1 \text{ или } \sin x=1.$$
Надеюсь, решение этих уравнений не вызовет затруднений.
Серии корней — решений уравнения — показаны ниже красными точками. ОДЗ отмечена на рисунке синим.
Таким образом, понимаем, что решение уравнения `\cos x = -1` не удовлетворяет ОДЗ.
В ответ пойдет только серия корней `x = \frac{\pi}{2} + 2\pi k`.Решение квадратного тригонометрического уравнения
Следующий пункт нашей программы — решение квадратного уравнения.
 2 — 6t +5 =0, $$
2 — 6t +5 =0, $$$$t_1 = 5, t_2 = 1.$$
Обратная замена.
$$\tg x = 5, \tg x = 1.$$
$$\left[\begin{array}{l}2x = \arctan{5}+\pi k, \\ 2x = \frac{\pi}{4} + \pi k. \end{array} \right.$$
Теперь поделим обе серии на два, чтобы узнать, чему равен, собственно, `x`.
$$\left[\begin{array}{l}x = \frac{1}{2}\arctan{5}+\frac{\pi k}{2}, \\ 2x = \frac{\pi}{8} + \frac{\pi k}{2}. \end{array} \right.$$
Вот мы и получили ответ.
Последнее уравнение (произведение тангенса на синус)
$$\tg x \cdot \sin 2x = 0.$$
ОДЗ
Поскольку тангенс — это дробь, знаменателем которой является косинус, то в ОДЗ получим, что `\cos x \neq 0 \Rightarrow x \neq \frac{\pi}{2}+\pi k.`
Решение
$$\tg x =0 \text{ или } \sin 2x = 0.$$
Эти уравнения решаются легко. Получим:
$$x = \pi k \text{ или } 2x = \pi k,$$
$$x = \pi k \text{ или } x = \frac{\pi k}{2}.$$
Теперь самое интересное: поскольку у нас было ОДЗ, нужно выполнить отбор корней.
 n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда.
 При любом а.
При любом а. Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.
 ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда.В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6.
 Полноценный ответ будет:
Полноценный ответ будет:х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.
 ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу.
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.
 п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн.
Если Вам нравится этот сайт… А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Захарова Людмила Владимировна
МБОУ «Средняя общеобразовательная школа № 59» г. Барнаула
учитель математики [email protected]№1 Простейшие тригонометрические уравнения
Цель: 1. Вывести формулы решений простейших тригонометрических уравнений вида sinx =a, cosx=a, tgx=a, ctgx=a;
2. Научиться решать простейшие тригонометрические уравнения с помощью формул.
Оборудование: 1) Таблицы с графиками тригонометрических функций у= sinx, у=cosx, у=tgx, у=ctgx; 2) Таблица значений обратных тригонометрических функций; 3) Сводная таблица формул для решения простейших тригонометрических уравнений.

План урока-лекции :
1 .Вывод формул корней уравнения
а ) sinx =a,
б ) cosx=a ,
в ) tgx=a ,
г) ctgx=а .
2 . Устная фронтальная работа по закреплению полученных формул.
3 . Письменная работа по закреплению изученного материала
Ход урока.В алгебре, геометрии, физике и других предметах мы сталкиваемся с разнообразными задачами, решение которых связано с решением уравнений. Мы изучили свойства тригонометрических функций, поэтому естественно обратиться к уравнениям, в которых неизвестное содержится под знаком функций
Определение: Уравнения вида sinx = a , cosx = a , tgx = a , ctgx = а называются простейшими тригонометрическими уравнениями.
Очень важно научиться решать простейшие тригонометрические уравнения, так как все способы и приемы решения любых тригонометрических уравнений заключается в сведении их к простейшим.

Начнем с того, что выведем формулы, которые «активно» работают при решении тригонометрических уравнений.
1.Уравнения вида sinx =a .
Решим уравнение sinx =a графически. Для этого в одной системе координат построим графики функций у=sinx и у=а.
1) Если а > 1 и а sin х=а не имеет решений, так как прямая и синусоида не имеют общих точек.
2) Если -1а а пересечет синусоиду бесконечно много раз. Это означает, что уравнение sinx=a имеет бесконечно много решений.
Так как период синуса равен 2, то для решения уравнения sinx=a достаточно найти все решения на любом отрезке длины 2.
Решением уравнения на [-/2; /2] по определению арксинуса х= arcsin a , а на х=-arcsin a . Учитывая периодичность функции у=sinx получим следующие выражения
х = -arcsin a +2n, n Z.
Обе серии решений можно объединить
Х = (-1) n arcsin a +n, nZ.
В следующих трех случаях предпочитают пользоваться не общей формулой, а более простыми соотношениями:
Если а =-1, то sin x =-1, х=-/2+2n
Если а =1, то sin x =1, x =/2+2n
Если а= 0, то sin x =0.
 x = n,
x = n,Пример: Решить уравнение sinx =1/2.
Составим формулы решений x=arcsin 1/2+ 2n
Х= — arcsin a+2n
Вычислим значение arcsin1/2. Подставим найденное значение в формулы решений
х= 5/6+2 n
или по общей формуле
Х= (-1) n arcsin 1/2+n,
Х= (-1) n /6+n,
2. Уравнения вида cosx=a .
Решим уравнение cosx=a также графически, построив графики функций у= cosx и у=а .
1) Если а 1, то уравнение cosx=a не имеет решений, так как графики не имеют общих точек.
2) Если -1a cosx=a имеет бесконечное множество решений.
Найдем все решения cosx=a на промежутке длины 2 так как период косинуса равен 2.
На решением уравнения по определению арккосинуса будет х= arcos a. Учитывая четность функции косинус решением уравнения на [-;0] будет х=-arcos a .
Таким образом решения уравнения cosx=a х=+ arcos a + 2 n,
В трех случаях будем пользоваться не общей формулой, а более простыми сотношениями:
Если а =-1, то cosx =-1, x =-/2+2n
Если а =1, то cosx =1, x = 2n,
Если а=0, то cosx =0.
 x =/2+n
x =/2+nПример: Решить уравнение cos x =1/2,
Составим формулы решений x=arccos 1/2+ 2n
Вычислим значение arccos1/2.
Подставим найденное значение в формулы решений
X=+ /3+ 2n, nZ.
Уравнения вида tgx=a .
Так как период тангенса равен , то для того чтобы найти все решения уравнения tgx=a , достаточно найти все решения на любом промежутке длины . По определению арктангенса решение уравнения на (-/2; /2) есть arctga . Учитывая период функции все решения уравнения можно записать в виде
х= arctg a + n, nZ.
Пример: Решите уравнение tg x = 3/3
Составим формулу для решения х= arctg 3/3 +n, nZ.
Вычислим значение арктангенса arctg 3/3= /6, тогда
Х=/6+ n, nZ.
Вывод формулы для решения уравнения с tgx = a можно предоставить учащимся.
Пример.
Решить уравнение ctg х = 1.

х = arcсtg 1 + n, nZ,
Х = /4 + n, nZ.
В результате изученного материала учащиеся могут заполнить таблицу:
«Решение тригонометрических уравнений».
уравнение
Упражнения для закрепления изученного материала.
(Устно) Какие из записанных уравнений можно решить по формулам:
а ) х= (-1) n arcsin a +n, nZ;
б ) х=+ arcos a+ 2 n?
cos x = 2/2, tg x= 1 , sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3 , cos x = 2.
Какие из перечисленных уравнений не имеют решений?
Решите уравнения:
а) sin x = 0; д) sin x = 2/2; з) sin x = 2;
б) cos x = 2/2; е) cos x = -1/2; и) cos x = 1;
г) tg x = 3; ж) ctg x = -1; к) tg x = 1/ 3.
3. Решите уравнения:
а) sin 3x = 0; д) 2cos x = 1;
б) cos x/2 =1/2; е) 3 tg 3x =1;
г) sin x/4 = 1; ж) 2cos(2x+ /5) = 3.
При решении данных уравнений полезно записать правила для решения уравнений вида sinв x =a , и с sinв x =a , | a |1.

Sinв x =a, |a|1.
в х = (-1) n arcsin a +n, nZ,
х= (-1) n 1/в arcsin a +n/в , nZ.
Подведение итогов занятия:
Сегодня на занятии мы вывели формулы для решения простейших тригонометрических уравнений.
Разобрали примеры решения простейших тригонометрических уравнений.
Заполнили таблицу, которую будем использовать для решения уравнений.
Домашнее задание.
№2 Решение тригонометрических уравнений
Цель: Изучить методы решения тригонометрических уравнений:1) приводимых к квадратным;2) приводимых к однородным тригонометрическим уравнениям.
Развивать у учащихся наблюдательность при применении различных способов решения тригонометрических уравнений.
Фронтальная работа с учащимися .
Назовите формулы корней тригонометрических уравнений cos x=a , sin x=a , tgx = a , ctg x = a .

Решите уравнения (устно):
cos x=-1, sin x=0, tgx =0, ctg x=1, cos x=1,5, sin x=0.
Найдите ошибки и подумайте о причинах ошибок.
cos x=1/2, х=+ /6+2k, kZ.
sin x= 3/2, х= /3+k, kZ.
tgx = /4, x=1+ k, kZ.
2. Изучение нового материала.
На данном занятии будут рассмотрены некоторые наиболее часто встречающиеся методы решения тригонометрических уравнений.
Тригонометрические уравнения, приводимые к квадратным.
К этому классу могут быть отнесены уравнения, в которые входят одна функция (синус или косинус) или две функции одного аргумента, но одна их них с помощью основных тригонометрических тождеств сводится ко второй.
Например, если cоsх входит в уравнение в четных степенях, то заменяем его на 1- sin 2 x, если sin 2 x, то его заменяем на 1-cos 2 x.
Пример.
Решить уравнение: 8 sin 2 x — 6sin x -5 =0.
Решение: Обозначим sin x=t, тогда 8t 2 — 6t – 5=0,
D= 196,
T 1 = -1/2, t 2 = -5/4.

Выполним обратную замену и решим следующие уравнения.
Х=(-1) к+1 /6+ k, kZ.
Так как -5/4>1, то уравнение не имеет корней.
Ответ: х=(-1) к+1 /6+ k, kZ.
Решение упражнений на закрепление.
Решить уравнение:
1) 2sin 2 x+ 3cos x = 0;
2) 5sin 2 x+ 6cos x -6 = 0;
3) 2sin 2 x+ 3cos 2 x = -2sin x;
4) 3 tg 2 x +2 tgx-1=0.
Однородные тригонометрические уравнения.
Определение: 1) Уравнение вида a sinx + b cosx =0, (а=0, в=0) называется однородным уравнением первой степени относительно sin x и cos x.
Решается данное уравнение с помощью деления обеих его частей на cosx 0. В результате получается уравнение atgx+ b=0.
2) Уравнение вида a sin 2 x + b sinx cosx + c cos 2 x =0 называется однородным уравнением второй степени, где a, b, c какие-либо числа.

Если а=0, то уравнение решаем делением обеих частей на cos 2 x 0. В результате получаем уравнение atg 2 x+ btgx+с =0.
Замечание: Уравнение вида a sin mx + b cos mx =0 или
a sin 2 mx + b sin mx cos mx + c cos 2 mx =0 также являются однородными. Для их решения обе части уравнения делят на cos mx =0 или cos 2 mx =0
3) К однородным уравнениям могут быть сведены различные уравнения, которые первоначально не являются такими. Например, sin 2 mx + b sin mx cos mx + c cos 2 mx = d , и a sinx + b cosx = d .
 Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.
Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.Упражнения на закрепление изученного материала:
1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;
2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;
3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;
4) sin 2 x -3 sinx cosx +2 cos 2 x =0
3.Подведение итогов урока. Домашнее задание.
На данном занятии в зависимости от подготовленности группы можно рассмотреть решение уравнений вида a sin mx +b cos mx=с, где а, b,с не равны нулю одновременно.
Упражнения на закрепление:
1. 3sin x + cos x=2;
2. 3sin 2x + cos 2x= 2;
3. sin x/3 + cos x/3=1;
4. 12 sin x +5 cos x+13=0.
№ 3 Решение тригонометрических уравнений
Цель: 1) Изучить метод решения тригонометрических уравнений разложением на множители; научиться решать тригонометрические уравнения с использованием различных тригонометрических формул;
2) Проконтролировать: знание учащимися формул для решения простейших тригонометрических уравнений; умение решать простейшие тригонометрические уравнения.

План занятия:
Проверка домашнего задания.
Математический диктант.
Изучение нового материала.
Самостоятельная работа.
Подведение итогов занятия. Домашнее задание.
Ход занятия:
Проверка домашнего задания (решение тригонометрических уравнений кратко записаны на доске).
Математический диктант.
В-1
1. Какие уравнения называются простейшими тригонометрическими уравнениями?
2. Как называется уравнение вида a sinx +b cosx=0? Укажите способ его решения.
3.Запишите формулу корней уравнения tgx = a (ctg x=a ).
4. Запишите формулы корней уравнений вида cosx=a , где а =1, а =0, а =-1.
5. Запишите общую формулу корней уравнения sin x=a , | a |
6. Как решаются уравнения вида a cosx=b , | b |
В-2
1.
 Запишите формулы корней уравнений
cosx=a ,| a |
Запишите формулы корней уравнений
cosx=a ,| a | 2. Запишите общую формулу корней уравнения
= a , | a |
3. Как называются уравнения вида sin x=a , tgx = a , sin x=a ?
4.Запишите формулы корней уравнения sin x=a , если а =1, а =0, а =-1.
5.Как решаются уравнения вида sin a x=b , | b |
6. Какие уравнения называются однородными уравнениями второй степени? Как они решаются?
Изучение нового материала.
Метод разложения на множители.
Одним из наиболее употребительных методов решения тригонометрических уравнений является метод разложения на множители.
Если уравнение f(x) =0 можно представить в виде f 1 (x) f 2 (x) =0 , то задача сводится к решению двух уравнений f 1 (x)=0, f 2 (x) =0.
(С учащимися полезно вспомнить правило «Произведение множителей равно нулю, если хотя бы один из множителей равен нулю, а другие при этом имеют смысл »)
Закрепление изученного материала через решение уравнений различной сложности.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(самост.)
3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;
5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2-мя способами)
7) cosx+ cos3x=0; 8) sin 3x= sin 17x;
9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x
11) sin x cos5x =sin 9x cos3x sin 2x sin 2x
12) 3 cosx sin x+ cos 2 x=0(самост.)
13) 2 cos 2 x — sin (x- /2)+ tgx tg (x+/2)=0.
Самостоятельная работа.
Вариант-1 Вариант-2
1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;
2) sin 2x – cos2x=0; 2) 3 cos x/2 — sin x/2=0;
3) 5 sin 2 x+ sin x cosx -2 cos 2 х=2; 3) 4sin 2 x- sin x cosx +7cos 2 х=5;
4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;
5) sin x+cosx=1.
 5) sin x+cosx=2.
5) sin x+cosx=2.8. Подведение итогов урока. Домашнее задание.
Решение косинуса. Решение простейших тригонометрических уравнений
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ.
 Курс полностью соответствует требованиям ЕГЭ-2018.
Курс полностью соответствует требованиям ЕГЭ-2018.Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений.
 Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда. При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела.
 Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.
 ) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.

Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу.
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.
 п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн.
Если Вам нравится этот сайт… А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Тригонометрические уравнения — тема не самая простая. Уж больно они разнообразные.) Например, такие:
sin 2 x + cos3x = ctg5x
sin(5x+π /4) = ctg(2x-π /3)
sinx + cos2x + tg3x = ctg4x
И тому подобное…
Но у этих (и всех остальных) тригонометрических монстров есть два общих и обязательных признака. Первый — вы не поверите — в уравнениях присутствуют тригонометрические функции.) Второй: все выражения с иксом находятся внутри этих самых функций.
 И только там! Если икс появится где-нибудь снаружи, например, sin2x + 3x = 3, это уже будет уравнение смешанного типа. Такие уравнения требуют индивидуального подхода. Здесь мы их рассматривать не будем.
И только там! Если икс появится где-нибудь снаружи, например, sin2x + 3x = 3, это уже будет уравнение смешанного типа. Такие уравнения требуют индивидуального подхода. Здесь мы их рассматривать не будем.Злые уравнения в этом уроке мы тоже решать не будем.) Здесь мы будем разбираться с самыми простыми тригонометрическими уравнениями. Почему? Да потому, что решение любых тригонометрических уравнений состоит из двух этапов. На первом этапе злое уравнение путём самых различных преобразований сводится к простому. На втором — решается это самое простое уравнение. Иначе — никак.
Так что, если на втором этапе у вас проблемы — первый этап особого смысла не имеет.)
Как выглядят элементарные тригонометрические уравнения?
sinx = а
cosx = а
tgx = а
ctgx = а
Здесь а обозначает любое число. Любое.
Кстати, внутри функции может находиться не чистый икс, а какое-то выражение, типа:
cos(3x+π /3) = 1/2
и тому подобное.
 Это усложняет жизнь, но на методе решения тригонометрического уравнения никак не сказывается.
Это усложняет жизнь, но на методе решения тригонометрического уравнения никак не сказывается.Как решать тригонометрические уравнения?
Тригонометрические уравнения можно решать двумя путями. Первый путь: с использованием логики и тригонометрического круга. Этот путь мы рассмотрим здесь. Второй путь — с использованием памяти и формул — рассмотрим в следующем уроке.
Первый путь понятен, надёжен, и его трудно забыть.) Он хорош для решения и тригонометрических уравнений, и неравенств, и всяких хитрых нестандартных примеров. Логика сильнее памяти!)
Решаем уравнения с помощью тригонометрического круга.
Включаем элементарную логику и умение пользоваться тригонометрическим кругом. Не умеете!? Однако… Трудно же вам в тригонометрии придётся…) Но не беда. Загляните в уроки «Тригонометрический круг…… Что это такое?» и «Отсчёт углов на тригонометрическом круге». Там всё просто. В отличие от учебников…)
Ах, вы в курсе!? И даже освоили «Практическую работу с тригонометрическим кругом» !? Примите поздравления.
 Эта тема будет вам близка и понятна.) Что особо радует, тригонометрическому кругу безразлично, какое уравнение вы решаете. Синус, косинус, тангенс, котангенс — ему всё едино. Принцип решения один.
Эта тема будет вам близка и понятна.) Что особо радует, тригонометрическому кругу безразлично, какое уравнение вы решаете. Синус, косинус, тангенс, котангенс — ему всё едино. Принцип решения один.Вот и берём любое элементарное тригонометрическое уравнение. Хотя бы это:
cosx = 0,5
Надо найти икс. Если говорить человеческим языком, нужно найти угол (икс), косинус которого равен 0,5.
Как мы ранее использовали круг? Мы рисовали на нём угол. В градусах или радианах. И сразу видели тригонометрические функции этого угла. Сейчас поступим наоборот. Нарисуем на круге косинус, равный 0,5 и сразу увидим угол. Останется только записать ответ.) Да-да!
Рисуем круг и отмечаем косинус, равный 0,5. На оси косинусов, разумеется. Вот так:
Теперь нарисуем угол, который даёт нам этот косинус. Наведите курсор мышки на рисунок (или коснитесь картинки на планшете), и увидите этот самый угол х.
Косинус какого угла равен 0,5?
х = π /3
cos60° = cos(π /3 ) = 0,5
Кое-кто скептически хмыкнет, да.
 .. Мол, стоило ли круг городить, когда и так всё ясно… Можно, конечно, хмыкать…) Но дело в том, что это — ошибочный ответ. Вернее, недостаточный. Знатоки круга понимают, что здесь ещё целая куча углов, которые тоже дают косинус, равный 0,5.
.. Мол, стоило ли круг городить, когда и так всё ясно… Можно, конечно, хмыкать…) Но дело в том, что это — ошибочный ответ. Вернее, недостаточный. Знатоки круга понимают, что здесь ещё целая куча углов, которые тоже дают косинус, равный 0,5.Если провернуть подвижную сторону ОА на полный оборот , точка А попадёт в исходное положение. С тем же косинусом, равным 0,5. Т.е. угол изменится на 360° или 2π радиан, а косинус — нет. Новый угол 60° + 360° = 420° тоже будет решением нашего уравнения, т.к.
Таких полных оборотов можно накрутить бесконечное множество… И все эти новые углы будут решениями нашего тригонометрического уравнения. И их все надо как-то записать в ответ. Все. Иначе решение не считается, да…)
Математика умеет это делать просто и элегантно. В одном кратком ответе записывать бесконечное множество решений. Вот как это выглядит для нашего уравнения:
х = π /3 + 2π n, n ∈ Z
Расшифрую.
 Всё-таки писать осмысленно приятнее, чем тупо рисовать какие-то загадочные буковки, правда?)
Всё-таки писать осмысленно приятнее, чем тупо рисовать какие-то загадочные буковки, правда?)π /3 — это тот самый угол, который мы увидели на круге и определили по таблице косинусов.
2π — это один полный оборот в радианах.
n — это количество полных, т.е. целых оборотов. Понятно, что n может быть равно 0, ±1, ±2, ±3…. и так далее. Что и указано краткой записью:
n ∈ Z
n принадлежит (∈ ) множеству целых чисел (Z ). Кстати, вместо буквы n вполне могут употребляться буквы k, m, t и т.д.
Эта запись означает, что вы можете взять любое целое n . Хоть -3, хоть 0, хоть +55. Какое хотите. Если подставите это число в запись ответа, получите конкретный угол, который обязательно будет решением нашего сурового уравнения.)
Или, другими словами, х = π /3 — это единственный корень из бесконечного множества.
 Чтобы получить все остальные корни, достаточно к π
/3 прибавить любое количество полных оборотов (n ) в радианах. Т.е. 2π
n радиан.
Чтобы получить все остальные корни, достаточно к π
/3 прибавить любое количество полных оборотов (n ) в радианах. Т.е. 2π
n радиан.Всё? Нет. Я специально удовольствие растягиваю. Чтобы запомнилось получше.) Мы получили только часть ответов к нашему уравнению. Эту первую часть решения я запишу вот как:
х 1 = π /3 + 2π n, n ∈ Z
х 1 — не один корень, это целая серия корней, записанная в краткой форме.
Но есть ещё углы, которые тоже дают косинус, равный 0,5!
Вернёмся к нашей картинке, по которой записывали ответ. Вот она:
Наводим мышку на картинку и видим ещё один угол, который тоже даёт косинус 0,5. Как вы думаете, чему он равен? Треугольнички одинаковые… Да! Он равен углу х , только отложен в отрицательном направлении. Это угол -х. Но икс-то мы уже вычислили. π /3 или 60°. Стало быть, можно смело записать:
х 2 = — π /3
Ну и, разумеется, добавляем все углы, которые получаются через полные обороты:
х 2 = — π /3 + 2π n, n ∈ Z
Вот теперь всё.
 ) По тригонометрическому кругу мы увидели (кто понимает, конечно)) все углы, дающие косинус, равный 0,5. И записали эти углы в краткой математической форме. В ответе получились две бесконечные серии корней:
) По тригонометрическому кругу мы увидели (кто понимает, конечно)) все углы, дающие косинус, равный 0,5. И записали эти углы в краткой математической форме. В ответе получились две бесконечные серии корней:х 1 = π /3 + 2π n, n ∈ Z
х 2 = — π /3 + 2π n, n ∈ Z
Это правильный ответ.
Надеюсь, общий принцип решения тригонометрических уравнений с помощью круга понятен. Отмечаем на круге косинус (синус, тангенс, котангенс) из заданного уравнения, рисуем соответствующие ему углы и записываем ответ. Конечно, нужно сообразить, что за углы мы увидели на круге. Иногда это не так очевидно. Ну так я и говорил, что здесь логика требуется.)
Для примера разберём ещё одно тригонометрическое уравнение:
Прошу учесть, что число 0,5 — это не единственно возможное число в уравнениях!) Просто мне его писать удобнее, чем корни и дроби.
Работаем по общему принципу. Рисуем круг, отмечаем (на оси синусов, разумеется!) 0,5.
 Рисуем сразу все углы, соответствующие этому синусу. Получим вот такую картину:
Рисуем сразу все углы, соответствующие этому синусу. Получим вот такую картину:Сначала разбираемся с углом х в первой четверти. Вспоминаем таблицу синусов и определяем величину этого угла. Дело нехитрое:
х = π /6
Вспоминаем про полные обороты и, с чистой совестью, записываем первую серию ответов:
х 1 = π /6 + 2π n, n ∈ Z
Половина дела сделана. А вот теперь надо определить второй угол… Это похитрее, чем в косинусах, да… Но логика нас спасёт! Как определить второй угол через х? Да легко! Треугольнички на картинке одинаковые, и красный угол х равен углу х . Только отсчитан он от угла π в отрицательном направлении. Потому и красный.) А нам для ответа нужен угол, отсчитанный правильно, от положительной полуоси ОХ, т.е. от угла 0 градусов.
Наводим курсор на рисунок и всё видим. Первый угол я убрал, чтобы не усложнял картинку. Интересующий нас угол (нарисован зелёным) будет равен:
π — х
Икс мы знаем, это π /6 .
 Стало быть, второй угол будет:
Стало быть, второй угол будет:π — π /6 = 5π /6
Снова вспоминаем про добавку полных оборотов и записываем вторую серию ответов:
х 2 = 5π /6 + 2π n, n ∈ Z
Вот и всё. Полноценный ответ состоит из двух серий корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Уравнения с тангенсом и котангенсом можно легко решать по тому же общему принципу решения тригонометрических уравнений. Если, конечно, знаете, как нарисовать тангенс и котангенс на тригонометрическом круге.
В приведённых выше примерах я использовал табличное значение синуса и косинуса: 0,5. Т.е. одно из тех значений, которые ученик знать обязан. А теперь расширим наши возможности на все остальные значения. Решать, так решать!)
Итак, пусть нам надо решить вот такое тригонометрическое уравнение:
Такого значения косинуса в кратких таблицах нет. Хладнокровно игнорируем этот жуткий факт.
 Рисуем круг, отмечаем на оси косинусов 2/3 и рисуем соответствующие углы. Получаем вот такую картинку.
Рисуем круг, отмечаем на оси косинусов 2/3 и рисуем соответствующие углы. Получаем вот такую картинку.Разбираемся, для начала, с углом в первой четверти. Знать бы, чему равен икс, сразу бы ответ записали! Не знаем… Провал!? Спокойствие! Математика своих в беде не бросает! Она на этот случай придумала арккосинусы. Не в курсе? Зря. Выясните, Это много проще, чем вы думаете. По этой ссылке ни одного мудрёного заклинания насчёт «обратных тригонометрических функций» нету… Лишнее это в данной теме.
Если вы в курсе, достаточно сказать себе: «Икс — это угол, косинус которого равен 2/3». И сразу, чисто по определению арккосинуса, можно записать:
Вспоминаем про дополнительные обороты и спокойно записываем первую серию корней нашего тригонометрического уравнения:
х 1 = arccos 2/3 + 2π n, n ∈ Z
Практически автоматом записывается и вторая серия корней, для второго угла. Всё то же самое, только икс (arccos 2/3) будет с минусом:
х 2 = — arccos 2/3 + 2π n, n ∈ Z
И все дела! Это правильный ответ.
 Даже проще, чем с табличными значениями. Ничего вспоминать не надо.) Кстати, самые внимательные заметят, что эта картинка с решением через арккосинус ничем, в сущности, не отличается от картинки для уравнения cosx = 0,5.
Даже проще, чем с табличными значениями. Ничего вспоминать не надо.) Кстати, самые внимательные заметят, что эта картинка с решением через арккосинус ничем, в сущности, не отличается от картинки для уравнения cosx = 0,5. Именно так! Общий принцип на то и общий! Я специально нарисовал две почти одинаковые картинки. Круг нам показывает угол х по его косинусу. Табличный это косинус, или нет — кругу неведомо. Что это за угол, π /3, или арккосинус какой — это уж нам решать.
С синусом та же песня. Например:
Вновь рисуем круг, отмечаем синус, равный 1/3, рисуем углы. Получается вот такая картина:
И опять картинка почти та же, что и для уравнения sinx = 0,5. Опять начинаем с угла в первой четверти. Чему равен икс, если его синус равен 1/3 ? Не вопрос!
Вот и готова первая пачка корней:
х 1 = arcsin 1/3 + 2π n, n ∈ Z
Разбираемся со вторым углом. В примере с табличным значением 0,5 он был равен:
π — х
Так и здесь он будет точно такой же! Только икс другой, arcsin 1/3.
 Ну и что!? Можно смело записывать вторую пачку корней:
Ну и что!? Можно смело записывать вторую пачку корней:х 2 = π — arcsin 1/3 + 2π n, n ∈ Z
Это совершенно правильный ответ. Хотя и выглядит не очень привычно. Зато понятно, надеюсь.)
Вот так решаются тригонометрические уравнения с помощью круга. Этот путь нагляден и понятен. Именно он спасает в тригонометрических уравнениях с отбором корней на заданном интервале, в тригонометрических неравенствах — те вообще решаются практически всегда по кругу. Короче, в любых заданиях, которые чуть сложнее стандартных.
Применим знания на практике?)
Решить тригонометрические уравнения:
Сначала попроще, прямо по этому уроку.
Теперь посложнее.
Подсказка: здесь придётся поразмышлять над кругом. Лично.)
А теперь внешне простенькие… Их ещё частными случаями называют.
sinx = 0
sinx = 1
cosx = 0
cosx = -1
Подсказка: здесь надо сообразить по кругу, где две серии ответов, а где одна.
 .. И как вместо двух серий ответов записать одну. Да так, чтобы ни один корень из бесконечного количества не потерялся!)
.. И как вместо двух серий ответов записать одну. Да так, чтобы ни один корень из бесконечного количества не потерялся!) Ну и совсем простые):
sinx = 0,3
cosx = π
tgx = 1,2
ctgx = 3,7
Подсказка: здесь надо знать, что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? Самые простые определения. Зато вспоминать никаких табличных значений не надо!)
Ответы, разумеется, в беспорядке):
х 1 = arcsin0,3 + 2π n, n ∈ Z
х 2 = π — arcsin0,3 + 2Не всё получается? Бывает. Прочтите урок ещё раз. Только вдумчиво (есть такое устаревшее слово…) И по ссылкам походите. Главные ссылки — про круг. Без него в тригонометрии — как дорогу переходить с завязанными глазами. Иногда получается.)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень.
 Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)можно познакомиться с функциями и производными.
ЛИНЕЙНЫЕ УРАВНЕНИЯ В SIN X И COS X – ТРИГОНОМЕТРИЯ
Напомним, что ax + by = c — это линейное уравнение с двумя переменными x и y. Если мы заменим x и y на sin x и cos x, мы получим линейное уравнение относительно sin x и cos x. Другими словами, уравнение a sin x + b cos x = c является линейным уравнением относительно sin x и cos x.
Чтобы решить подобное линейное уравнение, мы можем использовать замену tan α =b/a или cot α = a/b. Затем мы можем использовать формулы суммы и разности, чтобы упростить данное выражение.Наконец, мы можем использовать методы, которые мы уже видели, для решения вопроса.
Сначала попробуем получить b/a из данного уравнения. Для этого разделим обе части уравнения на a:
a cos x + b sin x = c ⇒ a cos x / a + b sin x / a = c/a, т.е.
cos x + b/a sin x = c/a
cos x + sin α / cos α · sin x = c/a
cos x · cos α / cos α + sin α · sin x / cos α = c/a
cos(x – α) / cos α = c/a, т. е. cos (x – α ) = c/a cos α
е. cos (x – α ) = c/a cos αТеперь нарисуйте прямоугольный треугольник и пусть
тангенс α = b/a, поэтому cos α = a / √a² + b².Таким образом,
cos (x – α) = c/a cos α = c/a · a / √a² + b² = c / √a² + b².В заключение, чтобы решить линейное уравнение вида a sin x + b cos x = c, мы можем сравнить значения c² и a² + b².
1. Если c² > a² + b², то решения нет.
2. Если c² = a² + b², то x = α + 2kπ, k ∈ Z.
3. Если c² < a² + b², то мы можем решить уравнение, используя методы мы узнали для уравнений с обыкновенным соотношением.Пример: Решите 2sin x + 3cos x = 4.
Решение: У нас есть sin x + b, потому что x = c, где a = 3, b = 2 и c = 4.
Сравним c² и a² + b². Получаем 2² + 3² = 4 + 9 = 13 < 4² = 16.
Так как c² > a² + b², по приведенному выше результату мы можем сказать, что уравнение не имеет решения.Пример: Решите cos x + √3 sin x = 2.

Решение: У нас есть a = 1, b = √3 и c = 2. Теперь давайте сравним c² и a² + b².Получаем a² + b² = 1² + √3² = 1 + 3 = 4 = c². Тогда по приведенному выше результату мы можем найти решение.
Сначала найдите α: tan α = b/a = √3 / 1 = tan π/3, т. е. α = π/3, поэтому решение равно x = π/3 + kπ, k ∈ Z.Нравится:
Нравится Загрузка…
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙРЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Примечание: Если вы хотите ознакомиться с обзором тригонометрии, нажмите на тригонометрия.
Задача 9.5c: Найдите x в уравнении
Ответ: Точные ответы:
где n — целое число.
Приближенные значения этих решений равны
где n — целое число.Решение:
Существует бесконечное множество решений этой проблемы. Чтобы найти х, приравнять уравнение к нулю и множителю.
тогдаКак мы изолируем x в уравнениях? Мы могли бы взять арккосинус обе стороны уравнения косинуса и арксинус обеих сторон синуса уравнения. Однако функции синуса и косинуса не являются взаимно однозначными. функции.
Давайте ограничим домен, чтобы функция была взаимно однозначной на ограниченном домен с сохранением исходного диапазона. График функции косинуса взаимно однозначен на интервале Если мы ограничим область определения функции косинуса этим интервалом, мы можем взять арккосинус обеих частей каждого уравнения косинуса.График синусоидальной функции взаимно однозначен на интервале Если мы ограничим область определения функции синуса этим интервалом, мы сможем взять арксинус обеих частей уравнения синуса.

С мы знаем, что если тогда и
Теперь решите уравнение
Мы знаем это Следовательно, если тогда Решите уравнение
Поскольку период как функции косинуса, так и функции синуса равен , точные решения
где n — целое число.Приближенные значения этих решений равны
где n — целое число.Эти решения могут быть или не быть ответами на исходную проблему. Вы сильно сверяете их, численно или графически, с исходным уравнение.
Числовая проверка:
Проверить ответ
Левая сторона:
Правая сторона:
Так как левая сторона равна правой стороне, когда вы заменяете 0 на x, тогда 0 — это решение.
Проверить ответ
Левая сторона:
Правая сторона:
Поскольку левая часть равна правой, если заменить x на 3,1415927, то 3,1415927 будет решением.

Проверить ответ
Левая сторона:
Правая сторона:
Так как левая сторона равна правой стороне, когда вы подставляете 1,40334825 для х, тогда 1.40334825 — это решение.
Проверить ответ
Левая сторона:
Правая сторона:
Так как левая сторона равна правой стороне, когда вы подставляете -1.40334825 для х, тогда -1.40334825 — это решение.
Графическая проверка:
Нарисуйте уравнение Обратите внимание, что график пересекает ось x много раз, что указывает на множество реальных решений.
Убедитесь, что он пересекает 0. Поскольку период равен , он снова пересекается в 0+6,2831853=6,2831853 и в 0-6.2831853=-6.2831853 и т.д.
Убедитесь, что он пересекает 3.1415927. Так как период , он снова пересекается в 3,1415927+6,2831853=9,42477796 и при 3.1415927-6.2831853=-3,14159265 и т.д.
Убедитесь, что он пересекает 1.40334825. Так как период , он снова пересекается в 1,40334825+6,2831853=7,686533557 и при 0,4636476-6,2831853=-4,879837 и т.
 д.
д.Убедитесь, что он пересекает -1,40334825. Так как период , он снова пересекается в -1,40334825+6,2831853=4,879837 и при -1,40334825-6,2831853=-7,686533557 и т. д.
Примечание. Если задача состоит в том, чтобы найти решения в интервале , то вы бы выбрали эти решения из набора бесконечные решения, принадлежащие множеству , и 4.879837.
Если вы хотите работать с другим примером, нажмите «Пример».Если вы хотите проверить себя, решив некоторые задачи, подобные этой например, щелкните Проблема.
Если вы хотите перейти к следующему разделу, нажмите далее.
Если вы хотите вернуться к предыдущему разделу, нажмите . предыдущий .
Если вы хотите вернуться к оглавлению уравнения, нажмите на Содержание.
[Алгебра] [Тригонометрия] [Геометрия] [Дифференциальные уравнения] [Исчисление] [Комплексные переменные] [Матричная алгебра]Домашняя страница S.O.S MATHematics
Автор: Нэнси Маркус
Copyright 1999-2022 MathMedics, LLC. Все права защищены.
Все права защищены.
Связаться с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний часРешения систем синусов и косинусов
Когда два тригонометрических графика, такие как синус и косинус, пересекаются, мы называем эту точку пересечения решением системы уравнений.Это тот же смысл, что и решения систем линейных уравнений.Решения систем синусов и косинусов графики
Проблема 1
На рисунке ниже представлена система, составленная из уравнения y = sin(x) и y = cos(x) в интервале 0≤X≤2Π
Решения системыКак видно из графика, эта система графиков синусов и косинусов дважды пересекается в течение этого интервала.
 Они перехватывают при x = Π/4, а также при x = 5Π/4
Они перехватывают при x = Π/4, а также при x = 5Π/4Проблема 2
Можете ли вы вычислить, сколько существует решений следующей системы тригонометрических уравнений, если они вообще существуют, имеет какие-либо решения в интервале 0≤X≤2Π
Система уравнений:
- у = грех(х) — 1
- у = cos(x) + 1
Проблема 3
Сможете ли вы определить, сколько существует решений следующей системы тригонометрических уравнений?
Система уравнений:
Решения системыРешение тригонометрических уравнений с использованием тригонометрических тождеств
Уравнение, которое содержит тригонометрические функции называется тригонометрическое уравнение .

Пример:
грех 2 Икс + потому что 2 Икс знак равно 1 2 грех Икс − 1 знак равно 0 загар 2 2 Икс − 1 знак равно 0
Решение тригонометрических уравнений с использованием тригонометрических тождеств
Тригонометрические тождества являются уравнениями, включающими тригонометрические функции, которые верны для любого значения вовлеченных переменных.Вы можете использовать тригонометрические тождества вместе с алгебраическими методами для решения тригонометрических уравнений.
Посторонние решения
Ан постороннее решение является корнем преобразованного уравнения, которое не является корнем исходного уравнения, поскольку оно было исключено из области определения исходного уравнения.

Когда вы решаете тригонометрические уравнения, иногда вы можете получить уравнение в одной тригонометрической функции, возводя в квадрат каждую сторону, но этот метод может привести к посторонним решениям.
Пример :
Найдите все решения уравнения на интервале [ 0 , 2 π ) .
2 грех 2 Икс знак равно 2 + потому что Икс
Уравнение содержит функции синуса и косинуса.
Мы перепишем уравнение так, чтобы оно содержало только функции косинуса, используя тождество Пифагора грех 2 Икс знак равно 1 − потому что 2 Икс .
2 ( 1 − потому что 2 Икс ) знак равно 2 + потому что Икс 2 − 2 потому что 2 Икс знак равно 2 + потому что Икс − 2 потому что 2 Икс − потому что Икс знак равно 0 2 потому что 2 Икс + потому что Икс знак равно 0
Факторинг потому что Икс мы получаем, потому что Икс ( 2 потому что Икс + 1 ) знак равно 0 .

Используя свойство нулевого продукта , мы получим потому что Икс знак равно 0 , и 2 потому что Икс + 1 знак равно 0 что дает потому что Икс знак равно − 1 2 .
В интервале [ 0 , 2 π ) , мы знаем это потому что Икс знак равно 0 когда Икс знак равно π 2 и Икс знак равно 3 π 2 .С другой стороны, мы также знаем, что потому что Икс знак равно − 1 2 когда Икс знак равно 2 π 3 и Икс знак равно 4 π 3 .

Поэтому решения данного уравнения в интервале [ 0 , 2 π ) являются
{ π 2 , 3 π 2 , 2 π 3 , 4 π 3 } .
Флорида мужчина 23 ноября. Обновлено: 23:27 по восточному стандартному времени, 23 ноября 2020 г. 26, 2019 г., 17:20 по Гринвичу. Автор Минивонн Берк. Женщина из Флориды позвонила в службу экстренной помощи, чтобы сообщить, что она нашла мертвого человека на подъездной дорожке. EDT LAUNCH Pad 39A CREW-3 MANNED CREW DRAGON. Департамент транспорта Флориды (FDOT) создал общегосударственный веб-сайт для предоставления информации о разработке Пятилетней рабочей программы FDOT и о том, как общественность может участвовать в этом процессе.
 Florida Crossroads отправляет зрителей в путешествие по нашему штату, исследуя вопросы, представляющие интерес для всего штата, в каждой получасовой программе. Полиция Феникса сообщила 8 января, что человек из Флориды и Ройал-Палм-Бич, известный как Филип Вайсбауэр, взял интервью у менеджера магазина в Фениксе. Семидесятилетний Билл. Курорт Diplomat Beach — лучший курорт Южной Флориды у моря, признанный одним из 10 лучших курортов Флориды по версии Condé Nast Reader’s Choice и 4 Diamond по рейтингу AAA. Этот писатель, чей день рождения 3 декабря, получил такой результат: «Мужчина 85 лет подвергся нападению аллигатора в доме престарелых во Флориде.Управление гневом — другое. Пользователи социальных сетей распространяют игру после твита. Терапия моноклональными антителами широко доступна во Флориде. Цикл «Человек из Флориды». 545 поделился твитом. Например, если ваш день рождения 13 апреля, вы искали человека из Флориды 13 апреля. (Шериф округа Паско. Солдаты сказали Мохаммед. Поделиться САНКТ-ПЕТЕРБУРГ, штат Флорида.
Florida Crossroads отправляет зрителей в путешествие по нашему штату, исследуя вопросы, представляющие интерес для всего штата, в каждой получасовой программе. Полиция Феникса сообщила 8 января, что человек из Флориды и Ройал-Палм-Бич, известный как Филип Вайсбауэр, взял интервью у менеджера магазина в Фениксе. Семидесятилетний Билл. Курорт Diplomat Beach — лучший курорт Южной Флориды у моря, признанный одним из 10 лучших курортов Флориды по версии Condé Nast Reader’s Choice и 4 Diamond по рейтингу AAA. Этот писатель, чей день рождения 3 декабря, получил такой результат: «Мужчина 85 лет подвергся нападению аллигатора в доме престарелых во Флориде.Управление гневом — другое. Пользователи социальных сетей распространяют игру после твита. Терапия моноклональными антителами широко доступна во Флориде. Цикл «Человек из Флориды». 545 поделился твитом. Например, если ваш день рождения 13 апреля, вы искали человека из Флориды 13 апреля. (Шериф округа Паско. Солдаты сказали Мохаммед. Поделиться САНКТ-ПЕТЕРБУРГ, штат Флорида. Депутаты сказали, что сотрудник школьного ресурса в начальной школе Беар-Лейк заметил признаки перерыва. -в августе. Парад начнется на Мейн-стрит и Ю.BREVARD COUNTY, Флорида, мужчина, 26 ноября 2019 г. Пятница, 31 декабря, 18:00. Девятая авария произошла около 18:00. 19.05.2021 Перекресток Флориды – путешествие в Зал славы. Мужчина украл сумочку пожилой женщины и сбил ее внедорожником. Мужчину нашли цепляющимся за перевернувшееся судно после 24 часов плавания в одиночестве. Страница 27 из 108. Мужчина из округа Цитрус арестован после того, как использовал объявление о розыске в качестве аватарки на Facebook. — Мужчину из Флориды несколько раз арестовывали за секс с миниатюрной лошадкой, говорят депутаты.Центральная Западная Флорида предлагает приманки больших городов Тампы, Клируотера и Сент-Луиса. Он живет в бризе, который развевает ваши волосы, пока вы делаете пончики на квадроцикле. Shop with a Cop запланирован на субботу, 11 декабря 2021 г. Опубликовано: 10 ноября 2017 г., 11:54. 74-летний Ричард Уилбэнкс вытащил собаку изо рта аллигатора и ни разу не выронил сигару изо рта.
Депутаты сказали, что сотрудник школьного ресурса в начальной школе Беар-Лейк заметил признаки перерыва. -в августе. Парад начнется на Мейн-стрит и Ю.BREVARD COUNTY, Флорида, мужчина, 26 ноября 2019 г. Пятница, 31 декабря, 18:00. Девятая авария произошла около 18:00. 19.05.2021 Перекресток Флориды – путешествие в Зал славы. Мужчина украл сумочку пожилой женщины и сбил ее внедорожником. Мужчину нашли цепляющимся за перевернувшееся судно после 24 часов плавания в одиночестве. Страница 27 из 108. Мужчина из округа Цитрус арестован после того, как использовал объявление о розыске в качестве аватарки на Facebook. — Мужчину из Флориды несколько раз арестовывали за секс с миниатюрной лошадкой, говорят депутаты.Центральная Западная Флорида предлагает приманки больших городов Тампы, Клируотера и Сент-Луиса. Он живет в бризе, который развевает ваши волосы, пока вы делаете пончики на квадроцикле. Shop with a Cop запланирован на субботу, 11 декабря 2021 г. Опубликовано: 10 ноября 2017 г., 11:54. 74-летний Ричард Уилбэнкс вытащил собаку изо рта аллигатора и ни разу не выронил сигару изо рта. Полицейские говорят, что у 67-летнего Ричарда Сперриера было около 45 граммов марихуаны, когда они остановили его около 23:00 в субботу в Сент-Луисе.(WESH) — Должностные лица опубликовали кадры с нательной камеры человека, который, по их словам, выдавал себя за офицера. Мужчина из Флориды сказал, что грызун был выращен соседями и кусал других людей в сельском районе Сарасота. Доля любезности: CNN (CNN) — Мужчина из Флориды сказал, что двое вооруженных мужчин вторглись в его дом и избивали его, когда его жена была на восьмом месяце беременности. Для просмотра фотографий обычно требуется DSL-соединение, поскольку фотографии отображаются с качеством выше среднего для Интернета. Google ваш день рождения, только день и месяц, и Флорида человек.6 взлом ресторана The Chattaway, проверка. Мужчина из Флориды, участвовавший в драке с пасхальным кроликом, скрывается от правосудия и рассказывает о своем пушистом кулачном бою. Раненый в перестрелке мужчина виновен в стрельбе по депутатам. Августин, Флорида, 28 марта 1951 года, Джин Форрест Пауэлл и Рассел.
Полицейские говорят, что у 67-летнего Ричарда Сперриера было около 45 граммов марихуаны, когда они остановили его около 23:00 в субботу в Сент-Луисе.(WESH) — Должностные лица опубликовали кадры с нательной камеры человека, который, по их словам, выдавал себя за офицера. Мужчина из Флориды сказал, что грызун был выращен соседями и кусал других людей в сельском районе Сарасота. Доля любезности: CNN (CNN) — Мужчина из Флориды сказал, что двое вооруженных мужчин вторглись в его дом и избивали его, когда его жена была на восьмом месяце беременности. Для просмотра фотографий обычно требуется DSL-соединение, поскольку фотографии отображаются с качеством выше среднего для Интернета. Google ваш день рождения, только день и месяц, и Флорида человек.6 взлом ресторана The Chattaway, проверка. Мужчина из Флориды, участвовавший в драке с пасхальным кроликом, скрывается от правосудия и рассказывает о своем пушистом кулачном бою. Раненый в перестрелке мужчина виновен в стрельбе по депутатам. Августин, Флорида, 28 марта 1951 года, Джин Форрест Пауэлл и Рассел. «Человек из Флориды» включает пользователей, которые ищут в Интернете фразу «Человек из Флориды», за которой следует их день рождения. Просмотр архивов программ. 16.09.2016 Перекрёсток Флориды – Совершите поход: Большая Флоридская тропа для наблюдения за птицами и дикой природой.Gold City Quartet @ Лисбургская церковь Назарянина. Мужчина из Флориды думает, что слышит злоумышленника, смертельно стреляет в беременную жену: полиция. «Человек из Флориды обезглавил ребенка» — это не смешно. Полиция Хейнс-Сити. Oldies DJ «Скотт Музыкант». 23 ноября 2020 г. Мужчина из Флориды признает себя виновным в попытке вымогательства 25 миллионов долларов у Мэтта Гетца в обмен на помилование Mail Online03:24 Вт, 23 ноября. Это даже задокументировано в. Примечание. Мы предоставили вам место в первом ряду для запуска ракет во Флориде с 1966 года. Это была дата, когда Верховный суд слушал дело о мошенничестве на выборах 2020 года.Твиты предназначены для юмористического прочтения, как если бы они были совершены одним человеком, которого называют «худшим супергероем в мире.
«Человек из Флориды» включает пользователей, которые ищут в Интернете фразу «Человек из Флориды», за которой следует их день рождения. Просмотр архивов программ. 16.09.2016 Перекрёсток Флориды – Совершите поход: Большая Флоридская тропа для наблюдения за птицами и дикой природой.Gold City Quartet @ Лисбургская церковь Назарянина. Мужчина из Флориды думает, что слышит злоумышленника, смертельно стреляет в беременную жену: полиция. «Человек из Флориды обезглавил ребенка» — это не смешно. Полиция Хейнс-Сити. Oldies DJ «Скотт Музыкант». 23 ноября 2020 г. Мужчина из Флориды признает себя виновным в попытке вымогательства 25 миллионов долларов у Мэтта Гетца в обмен на помилование Mail Online03:24 Вт, 23 ноября. Это даже задокументировано в. Примечание. Мы предоставили вам место в первом ряду для запуска ракет во Флориде с 1966 года. Это была дата, когда Верховный суд слушал дело о мошенничестве на выборах 2020 года.Твиты предназначены для юмористического прочтения, как если бы они были совершены одним человеком, которого называют «худшим супергероем в мире. Херб Джонсон. 14: мужчина из Флориды попал на камеру. Мужчина из Флориды борется с аллигатором, чтобы спасти щенка в драматическом видео. Национальное кладбище Флориды расположенный в государственном лесу Витлакучи, примерно в 50 милях к северу от Тампы в округе Самтер, штат Флорида, в центре Сарасоты, 301. Он входит в список из 58 самых смешных заголовков с участием мужчин Флориды: Несколько 18-летних флоридцев попали в этот список в этом году, в том числе Николас Годфри, которого обвинили в покушении первой степени на убийство сотрудника средней школы, которую он посещал еще в ноябре.Пьяный мужчина из Флориды сломал спину, прыгая через канал на Nissan Versa. The Texarkana Gazette — главный источник местных новостей и спортивных новостей в Тексаркане и прилегающих районах Арклатекса. Гермес Каллияс-Гасперин. Опубликовано: 23 ноября 2021 г. / 14:50 CST / Обновлено: 23 ноября 2021 г. / 22:26 CST Пенсакола, Флорида. Отмечен премиями ACM, AMA, Billboard, CMA и CMT Music Awards, их творческая империя также включает в себя процветающую бизнес-инициативы: Old Camp Peach Pecan Whiskey, FGL HOUSE, встреча + приветствие.
Херб Джонсон. 14: мужчина из Флориды попал на камеру. Мужчина из Флориды борется с аллигатором, чтобы спасти щенка в драматическом видео. Национальное кладбище Флориды расположенный в государственном лесу Витлакучи, примерно в 50 милях к северу от Тампы в округе Самтер, штат Флорида, в центре Сарасоты, 301. Он входит в список из 58 самых смешных заголовков с участием мужчин Флориды: Несколько 18-летних флоридцев попали в этот список в этом году, в том числе Николас Годфри, которого обвинили в покушении первой степени на убийство сотрудника средней школы, которую он посещал еще в ноябре.Пьяный мужчина из Флориды сломал спину, прыгая через канал на Nissan Versa. The Texarkana Gazette — главный источник местных новостей и спортивных новостей в Тексаркане и прилегающих районах Арклатекса. Гермес Каллияс-Гасперин. Опубликовано: 23 ноября 2021 г. / 14:50 CST / Обновлено: 23 ноября 2021 г. / 22:26 CST Пенсакола, Флорида. Отмечен премиями ACM, AMA, Billboard, CMA и CMT Music Awards, их творческая империя также включает в себя процветающую бизнес-инициативы: Old Camp Peach Pecan Whiskey, FGL HOUSE, встреча + приветствие. Обвиняемый в двойном убийстве во Флориде, представлявший себя, завершил свое дело.1 для высшего образования пятый год подряд. По словам чиновников, мужчина из Флориды пытался проникнуть в машину, заполненную полицейскими. Кроме того, Сардо сказал детективу, что он знал, что поступил неправильно, и что, по данным офиса шерифа, «он был больным человеком». Из USCG 4 минуты чтения. Обнаженный мужчина из Флориды, показанный на видео, пробирается в ресторан и жует рамен на улице А. Сентябрь. Вызов действительно начался в четверг, сообщает South Florida Sun-Sentinel. 1 год назад Haulover Inlet. Парад завершится в J.Последняя ракета. Печально известный «Человек из Флориды» снова попал в заголовки газет, и на этот раз это 88-летний житель Палм-Бей, который был арестован на прошлой неделе после того, как заживо сжег енота, потому что тот съел его манго. Эзра Джеймс боялся, что енот укусит его и заразит бешенством, поэтому заточил животное в металлическую клетку, облил его бензином, поджег. Офицер петербургской полиции вел расследование в отношении ноября Джейка Гриссома 23 ноября 2021 г.
Обвиняемый в двойном убийстве во Флориде, представлявший себя, завершил свое дело.1 для высшего образования пятый год подряд. По словам чиновников, мужчина из Флориды пытался проникнуть в машину, заполненную полицейскими. Кроме того, Сардо сказал детективу, что он знал, что поступил неправильно, и что, по данным офиса шерифа, «он был больным человеком». Из USCG 4 минуты чтения. Обнаженный мужчина из Флориды, показанный на видео, пробирается в ресторан и жует рамен на улице А. Сентябрь. Вызов действительно начался в четверг, сообщает South Florida Sun-Sentinel. 1 год назад Haulover Inlet. Парад завершится в J.Последняя ракета. Печально известный «Человек из Флориды» снова попал в заголовки газет, и на этот раз это 88-летний житель Палм-Бей, который был арестован на прошлой неделе после того, как заживо сжег енота, потому что тот съел его манго. Эзра Джеймс боялся, что енот укусит его и заразит бешенством, поэтому заточил животное в металлическую клетку, облил его бензином, поджег. Офицер петербургской полиции вел расследование в отношении ноября Джейка Гриссома 23 ноября 2021 г. Без комментариев Мужчина из Флориды снова находится в розыске, на этот раз за то, что пошел на суши и устроил буйство в очереди за буфетом хибачи.TW Cast & Recruit FLORIDA MAN — УИЛМИНГТОН, Северная Каролина: ИЩУ СЛЕДУЮЩУЮ СТАТЬЮ, КОТОРАЯ ПРОЙДЕТ ВО ВТОРНИК, 30 НОЯБРЯ. 15 сентября 2015 г., 20:11. 23 ноября 2011 г. Мужчина из Флориды отрицает, что напал на девушку из-за того, что она использовала большую секс-игрушку («Дымящийся пистолет»). С помощью нашего расширенного поиска некрологов вы можете искать в нашей базе данных некрологов по. Будь в курсе того, где распространяется COVID-19, будь то город или сельская местность, чтобы понять, как он может повлиять на семьи, торговлю и путешествия. 23.06.21 Франция Кристоф Леметр, французский легкоатлет.Я уверен, что все уже видели какие-то безумные заголовки «Человек из Флориды», появляющиеся в вашей ленте Facebook или Twitter, большинство из которых просто забавны. РАСПИСАНИЕ ЗАПУСКА НА МЫСЕ КАНАВЕРАЛ, ФЛОРИДА, ОБНОВЛЕНО 19 ОКТЯБРЯ 2021 ГОДА.
Без комментариев Мужчина из Флориды снова находится в розыске, на этот раз за то, что пошел на суши и устроил буйство в очереди за буфетом хибачи.TW Cast & Recruit FLORIDA MAN — УИЛМИНГТОН, Северная Каролина: ИЩУ СЛЕДУЮЩУЮ СТАТЬЮ, КОТОРАЯ ПРОЙДЕТ ВО ВТОРНИК, 30 НОЯБРЯ. 15 сентября 2015 г., 20:11. 23 ноября 2011 г. Мужчина из Флориды отрицает, что напал на девушку из-за того, что она использовала большую секс-игрушку («Дымящийся пистолет»). С помощью нашего расширенного поиска некрологов вы можете искать в нашей базе данных некрологов по. Будь в курсе того, где распространяется COVID-19, будь то город или сельская местность, чтобы понять, как он может повлиять на семьи, торговлю и путешествия. 23.06.21 Франция Кристоф Леметр, французский легкоатлет.Я уверен, что все уже видели какие-то безумные заголовки «Человек из Флориды», появляющиеся в вашей ленте Facebook или Twitter, большинство из которых просто забавны. РАСПИСАНИЕ ЗАПУСКА НА МЫСЕ КАНАВЕРАЛ, ФЛОРИДА, ОБНОВЛЕНО 19 ОКТЯБРЯ 2021 ГОДА. 23 декабря 2021 г., 14:59 2 доллара за 2 месяца #ReadLocal. Первопроходец Форт-Лодердейл 10K и полумарафон Форт-Лодердейл. 26 ноября Crash A Rama – Orlando Speed World. 27 ноября No Prep Race – Orlando Speed World.Ах, Флорида. Мы еще не добавили Florida Man апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь и декабрь. 25 ноября 2016 г. Мужчина из Флориды пролил воду на заднем дворе шерифа. Ронни Онеал III комментирует, пока Ассистент. 23 мая. Мужчина из Флориды звонит в службу 911 и требует, чтобы он ехал домой, чтобы сменить нижнее белье. Ноябрь. Офис шерифа округа Пинелла сообщил, что 40-летний Уэсли Дашер Скотт был арестован в пятницу на основании неоплаченного ордера, связанного с предыдущим наркотиком. Новых смертей в день. Округ Мэрион, Флорида.Освещение национальных новостей Washington Post. Житель Флориды снова наносит удар — только на этот раз он в режиме героя боевика, который в реальной жизни выглядит куда более устрашающим, чем на большом экране. Молодой Дольф, настоящее имя Адольф Роберт Торнтон-младший.
23 декабря 2021 г., 14:59 2 доллара за 2 месяца #ReadLocal. Первопроходец Форт-Лодердейл 10K и полумарафон Форт-Лодердейл. 26 ноября Crash A Rama – Orlando Speed World. 27 ноября No Prep Race – Orlando Speed World.Ах, Флорида. Мы еще не добавили Florida Man апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь и декабрь. 25 ноября 2016 г. Мужчина из Флориды пролил воду на заднем дворе шерифа. Ронни Онеал III комментирует, пока Ассистент. 23 мая. Мужчина из Флориды звонит в службу 911 и требует, чтобы он ехал домой, чтобы сменить нижнее белье. Ноябрь. Офис шерифа округа Пинелла сообщил, что 40-летний Уэсли Дашер Скотт был арестован в пятницу на основании неоплаченного ордера, связанного с предыдущим наркотиком. Новых смертей в день. Округ Мэрион, Флорида.Освещение национальных новостей Washington Post. Житель Флориды снова наносит удар — только на этот раз он в режиме героя боевика, который в реальной жизни выглядит куда более устрашающим, чем на большом экране. Молодой Дольф, настоящее имя Адольф Роберт Торнтон-младший. Человек из Флориды — это интернет-мем, популяризированный в 2013 году, в котором фраза «Человек из Флориды» взята из различных несвязанных новостных статей, описывающих людей, которые родом из Флориды или живут во Флориде. Здесь вы можете найти некрологи, которые были добавлены на наш сайт за последнюю неделю.Вызов человека из Флориды: самые нелепые истории. Мужчине из Флориды предъявлено обвинение в покушении на убийство после неудачного предложения руки и сердца. О, человек из Флориды, что ты сделал на этот раз? По словам официальных лиц, 49-летний Стивен Титлан пытался ограбить автомобиль, в котором было полно полицейских в Тампе. Мужчина из Флориды 23 марта. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Почтовая навигация. Обновление информации о коронавирусе COVID-19 во Флориде по округам со статистикой и графиками: общее количество и новые случаи, количество смертей за день, текущие активные случаи, выздоровления, исторические данные, тенденции, прогнозы и график.
Человек из Флориды — это интернет-мем, популяризированный в 2013 году, в котором фраза «Человек из Флориды» взята из различных несвязанных новостных статей, описывающих людей, которые родом из Флориды или живут во Флориде. Здесь вы можете найти некрологи, которые были добавлены на наш сайт за последнюю неделю.Вызов человека из Флориды: самые нелепые истории. Мужчине из Флориды предъявлено обвинение в покушении на убийство после неудачного предложения руки и сердца. О, человек из Флориды, что ты сделал на этот раз? По словам официальных лиц, 49-летний Стивен Титлан пытался ограбить автомобиль, в котором было полно полицейских в Тампе. Мужчина из Флориды 23 марта. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Почтовая навигация. Обновление информации о коронавирусе COVID-19 во Флориде по округам со статистикой и графиками: общее количество и новые случаи, количество смертей за день, текущие активные случаи, выздоровления, исторические данные, тенденции, прогнозы и график. «У человека есть проблемы, и ни один чизбургер не является таковым. Получайте последние новости страны, посвященные национальной безопасности, науке и судам. Майами, Форт-Лодердейл, Палм-Бич и Ключи — для отпуска, которого вы никогда не видели. Городская комиссия Таллахасси с отличием Бывший Футбольный тренер FAMU Хаббард. — Депутаты Флориды арестовали мужчину за попытку провести кастрацию в его доме в округе Хайлендс, сообщает WFTS. опасный прыжок во вторник, и все это было заснято на камеру.Последнее объяснение, предложенное президентом Фонда Первой поправки Флориды: популярность мема способствовала распространению новых историй о «жителях Флориды». последнее обновление: 11:41, 21 ноября 2018 г. День рождения человека из Флориды. Hamel Park на Мейн-стрит и Гольфстрим-авеню. Хорошо, ты должен сделать это со мной. В этом видео мы видим человека, пытающегося ловить акул на надувном единороге. Мужчина из Флориды, подозреваемый в том, что понюхал ноги женщины в библиотеке, ведет полицию в погоню на скутере.
«У человека есть проблемы, и ни один чизбургер не является таковым. Получайте последние новости страны, посвященные национальной безопасности, науке и судам. Майами, Форт-Лодердейл, Палм-Бич и Ключи — для отпуска, которого вы никогда не видели. Городская комиссия Таллахасси с отличием Бывший Футбольный тренер FAMU Хаббард. — Депутаты Флориды арестовали мужчину за попытку провести кастрацию в его доме в округе Хайлендс, сообщает WFTS. опасный прыжок во вторник, и все это было заснято на камеру.Последнее объяснение, предложенное президентом Фонда Первой поправки Флориды: популярность мема способствовала распространению новых историй о «жителях Флориды». последнее обновление: 11:41, 21 ноября 2018 г. День рождения человека из Флориды. Hamel Park на Мейн-стрит и Гольфстрим-авеню. Хорошо, ты должен сделать это со мной. В этом видео мы видим человека, пытающегося ловить акул на надувном единороге. Мужчина из Флориды, подозреваемый в том, что понюхал ноги женщины в библиотеке, ведет полицию в погоню на скутере. и нашел мужчину в возрасте от 20 до 20 лет, который, казалось, был застрелен.Результаты покажут, что «мужчина из Флориды» делал в тот день (в случае 13 апреля это будет… День рождения мужчины из Флориды Подробнее ». 20 ноября 2021 г., 06:11. Полиция Флориды арестовала голодного 22-летнего парня. человек, который якобы забросал свою мать сосисками, потому что она случайно столкнулась с ним, когда готовила ему ужин. Мы хотели бы показать вам описание здесь, но сайт не позволяет нам. Этот сериал от Blumhouse Television посвящен самым печально известным и возмутительным убийц из Солнечного штата.News & World Report называет Флориду Нет. Мы сделаем это в ближайшее время, как только найдем в Интернете лучшие заголовки о Флориде. Санкт-Петербург, но и великолепные пляжи, дикая природа, чистые источники и живописные реки. Опубликовано: 1 ноября 2019 г. / 06:42 по восточному поясному времени / Обновлено: 1 ноября 2019 г. / 06:45 по восточному поясному времени УИНДЕРМИР, штат Флорида. Эммет Холл Мужчина из Флориды угрожает «проклятием вуду» жертве сексуальных побоев, сообщает полиция.
и нашел мужчину в возрасте от 20 до 20 лет, который, казалось, был застрелен.Результаты покажут, что «мужчина из Флориды» делал в тот день (в случае 13 апреля это будет… День рождения мужчины из Флориды Подробнее ». 20 ноября 2021 г., 06:11. Полиция Флориды арестовала голодного 22-летнего парня. человек, который якобы забросал свою мать сосисками, потому что она случайно столкнулась с ним, когда готовила ему ужин. Мы хотели бы показать вам описание здесь, но сайт не позволяет нам. Этот сериал от Blumhouse Television посвящен самым печально известным и возмутительным убийц из Солнечного штата.News & World Report называет Флориду Нет. Мы сделаем это в ближайшее время, как только найдем в Интернете лучшие заголовки о Флориде. Санкт-Петербург, но и великолепные пляжи, дикая природа, чистые источники и живописные реки. Опубликовано: 1 ноября 2019 г. / 06:42 по восточному поясному времени / Обновлено: 1 ноября 2019 г. / 06:45 по восточному поясному времени УИНДЕРМИР, штат Флорида. Эммет Холл Мужчина из Флориды угрожает «проклятием вуду» жертве сексуальных побоев, сообщает полиция. Юго-восточная Флорида излучает приятную температуру, роскошь, латиноамериканские и карибские вкусы. Шелли Дейли Дейли Шелли Шелли родилась в Сент-Луисе.Леонардо Фибоначчи был известным математиком, и этот день отмечается как День Фибоначчи. Убийства 2021 года: более пристальный взгляд на цифры 2 умерших в малом. Житель Флориды был арестован после того, как он якобы раздавал марихуану людям, когда они проходили мимо, «потому что это было Рождество. Он — легкое эхо в воздухе, когда кто-то говорит: «Эй, смотри!» Человек из Флориды прибыл так, что теперь у него есть свой собственный Top Sure, который превосходит печально известную статью журнала Time «Потерянный рай» за ноябрь.Вы имеете право на участие в программе MAB, если вы подверглись воздействию или заболели COVID-19, и вы подвержены высокому риску тяжелого заболевания. Белка побежала за ним и ни с того ни с сего укусила Робби Армстронга за локоть. Полицейские разыскивают 23-летнего мужчину из Теннесси за убийство рэпера Янга Дольфа через шесть недель после того, как певец был застрелен в магазине печенья в Мемфисе.
Юго-восточная Флорида излучает приятную температуру, роскошь, латиноамериканские и карибские вкусы. Шелли Дейли Дейли Шелли Шелли родилась в Сент-Луисе.Леонардо Фибоначчи был известным математиком, и этот день отмечается как День Фибоначчи. Убийства 2021 года: более пристальный взгляд на цифры 2 умерших в малом. Житель Флориды был арестован после того, как он якобы раздавал марихуану людям, когда они проходили мимо, «потому что это было Рождество. Он — легкое эхо в воздухе, когда кто-то говорит: «Эй, смотри!» Человек из Флориды прибыл так, что теперь у него есть свой собственный Top Sure, который превосходит печально известную статью журнала Time «Потерянный рай» за ноябрь.Вы имеете право на участие в программе MAB, если вы подверглись воздействию или заболели COVID-19, и вы подвержены высокому риску тяжелого заболевания. Белка побежала за ним и ни с того ни с сего укусила Робби Армстронга за локоть. Полицейские разыскивают 23-летнего мужчину из Теннесси за убийство рэпера Янга Дольфа через шесть недель после того, как певец был застрелен в магазине печенья в Мемфисе. Мужчина из Флориды угрожает мужчине топором, угоняет и разбивает машину, найден голым в курятнике. (Флоридское шоссе. Зимние каникулы 21 года – информация о закрытии зала. Человеческие останки, найденные в среду в заповеднике Флориды, принадлежат Брайану Лаундри, сообщило ФБР в четверг.Отец якобы сказал полиции, что он вышел из себя после того, как его маленькая дочь сообщила, что голый мужчина из Флориды ведет полицию в погоню за автомобилем после угона грузовика, говорят полицейские. Он просто сказал заместителям, что они не его. В системе государственных университетов Флориды за последние пять лет расходы на исследования выросли на 358 миллионов долларов, что составляет 7 миллиардов долларов экономики. поиск пляжа, парки, местные мероприятия, туристическая информация. Лодердейл: 30 апреля: Король пляжа: Мадейра-Бич, Флорида: 4–6 мая: Angler Armory KMT: Мадейра-Бич: 4–6 мая: Серия турниров Wild West Kingfish Tournament Series — Этап 2: Мадейра-Бич: 11–14 мая: Морская вода Перестрелка: Помпано-Бич: 25 мая: Турнир по оранжевому и синему тарпону: Мадейра-Бич: 18 мая: Downtown Showdown KDW: Уэст-Палм-Бич: 22-23 мая.
Мужчина из Флориды угрожает мужчине топором, угоняет и разбивает машину, найден голым в курятнике. (Флоридское шоссе. Зимние каникулы 21 года – информация о закрытии зала. Человеческие останки, найденные в среду в заповеднике Флориды, принадлежат Брайану Лаундри, сообщило ФБР в четверг.Отец якобы сказал полиции, что он вышел из себя после того, как его маленькая дочь сообщила, что голый мужчина из Флориды ведет полицию в погоню за автомобилем после угона грузовика, говорят полицейские. Он просто сказал заместителям, что они не его. В системе государственных университетов Флориды за последние пять лет расходы на исследования выросли на 358 миллионов долларов, что составляет 7 миллиардов долларов экономики. поиск пляжа, парки, местные мероприятия, туристическая информация. Лодердейл: 30 апреля: Король пляжа: Мадейра-Бич, Флорида: 4–6 мая: Angler Armory KMT: Мадейра-Бич: 4–6 мая: Серия турниров Wild West Kingfish Tournament Series — Этап 2: Мадейра-Бич: 11–14 мая: Морская вода Перестрелка: Помпано-Бич: 25 мая: Турнир по оранжевому и синему тарпону: Мадейра-Бич: 18 мая: Downtown Showdown KDW: Уэст-Палм-Бич: 22-23 мая. Подробнее: 12 диких заголовков Флориды о мужчинах и женщинах 2018 года, которые заставят вас съежиться. — Жителя Флориды обвиняют в том, что он использовал свой стеклянный глаз, чтобы напасть на врача и медсестру в минувшие выходные. Флорида является третьим по численности населения штатом в стране, и мы продолжаем расти почти на 1000 человек каждый день. 25-й ежегодный праздничный парад в центре Сарасоты состоится в субботу, 4 декабря 2021 года, в 19:00. 23 декабря 2019 г. WGCU Public Media — это поддерживаемая членами служба Университета побережья Мексиканского залива Флориды, расположенная на территории кампуса.На этой неделе жителя Флориды оштрафовали за то, что он съел самый важный прием пищи в, пожалуй, худшем из возможных мест. Об этом сообщает Tribune wire. На этой фотографии, предоставленной дорожным патрулем Флориды, упавший столб электропередач привязан к крыше автомобиля. Понедельник, 6 ноября, когда сотрудники фермы по разведению аллигаторов во Флориде вошли в вольер с крокодилами и увидели две плавающие крокодиловые туфли и выброшенную одежду.
Подробнее: 12 диких заголовков Флориды о мужчинах и женщинах 2018 года, которые заставят вас съежиться. — Жителя Флориды обвиняют в том, что он использовал свой стеклянный глаз, чтобы напасть на врача и медсестру в минувшие выходные. Флорида является третьим по численности населения штатом в стране, и мы продолжаем расти почти на 1000 человек каждый день. 25-й ежегодный праздничный парад в центре Сарасоты состоится в субботу, 4 декабря 2021 года, в 19:00. 23 декабря 2019 г. WGCU Public Media — это поддерживаемая членами служба Университета побережья Мексиканского залива Флориды, расположенная на территории кампуса.На этой неделе жителя Флориды оштрафовали за то, что он съел самый важный прием пищи в, пожалуй, худшем из возможных мест. Об этом сообщает Tribune wire. На этой фотографии, предоставленной дорожным патрулем Флориды, упавший столб электропередач привязан к крыше автомобиля. Понедельник, 6 ноября, когда сотрудники фермы по разведению аллигаторов во Флориде вошли в вольер с крокодилами и увидели две плавающие крокодиловые туфли и выброшенную одежду. раскрыл тайну довольно быстро, арестовав неподалёку 23-летнего Брэндона Хэтфилда. 2018 Департамент правоохранительных органов Флориды, против.Эта страница будет обновляться самыми последними данными так часто, как это возможно. ОРГАНИЗМ ЭТО РАСПИСАНИЕ ЗАПУСКА МОЖЕТ ИЗМЕНЯТЬСЯ БЕЗ УВЕДОМЛЕНИЯ ФОРМАТ ЗАПИСИ: ДАТА ЗАПУСКА/ЦЕЛЬ ЗАПУСКА СРЕДСТВО ЗАПУСКА ВРЕМЯ ЗАПУСКА МЕСТО ЗАПУСКА ПОЛЕЗНАЯ НАГРУЗКА/ЗАПИСЬ ЗАДАЧ: 31 ОКТЯБРЯ 2021 FALCON 9 2:21 Мужчина из Флориды заявляет о пакетах с кокаином, метамфетамином, обернутым вокруг пенис не его 7 ноября 2016. Последние новости США, мировые новости, спорт, бизнес, мнения, анализ и обзоры от The Guardian, ведущего либерального голоса в мире. Основная линия WGCU: 239-590-2300 ФАКС WGCU: 239-590-7088.Это не мешает миллионам людей ежегодно стекаться в самое важное место штата, самый посещаемый курорт на планете. На кадрах видно, как мужчина выходит из машины и лежит лицом вниз. Офис шерифа округа Таммани разместил на своих страницах в социальных сетях BOLO с просьбой помочь общественности в установлении личности человека, ограбившего дом.
раскрыл тайну довольно быстро, арестовав неподалёку 23-летнего Брэндона Хэтфилда. 2018 Департамент правоохранительных органов Флориды, против.Эта страница будет обновляться самыми последними данными так часто, как это возможно. ОРГАНИЗМ ЭТО РАСПИСАНИЕ ЗАПУСКА МОЖЕТ ИЗМЕНЯТЬСЯ БЕЗ УВЕДОМЛЕНИЯ ФОРМАТ ЗАПИСИ: ДАТА ЗАПУСКА/ЦЕЛЬ ЗАПУСКА СРЕДСТВО ЗАПУСКА ВРЕМЯ ЗАПУСКА МЕСТО ЗАПУСКА ПОЛЕЗНАЯ НАГРУЗКА/ЗАПИСЬ ЗАДАЧ: 31 ОКТЯБРЯ 2021 FALCON 9 2:21 Мужчина из Флориды заявляет о пакетах с кокаином, метамфетамином, обернутым вокруг пенис не его 7 ноября 2016. Последние новости США, мировые новости, спорт, бизнес, мнения, анализ и обзоры от The Guardian, ведущего либерального голоса в мире. Основная линия WGCU: 239-590-2300 ФАКС WGCU: 239-590-7088.Это не мешает миллионам людей ежегодно стекаться в самое важное место штата, самый посещаемый курорт на планете. На кадрах видно, как мужчина выходит из машины и лежит лицом вниз. Офис шерифа округа Таммани разместил на своих страницах в социальных сетях BOLO с просьбой помочь общественности в установлении личности человека, ограбившего дом. Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова попал в неприятности с законом, когда возглавил полицию Монтгомери. Человек из Флориды @_FloridaMan.Список почетных. МАЙАМИ (CBSMiami/AP) – Мужчине из Флориды предъявлены обвинения в пренебрежительном отношении к детям после того, как полиция заявила, что он оставил ребенка одного возле полицейского участка ночью, потому что думал, что он гей. 23 декабря 2021 г. 24 ноября 2021 г. ← Предыдущий пост. 23 ноября 2012 года Джордан Дэвис, чернокожий 17-летний ученик средней школы, был убит на заправочной станции Gate Petroleum в Джексонвилле, штат Флорида, Майклом Дэвидом Данном, белым 45-летним разработчиком программного обеспечения, после спор из-за громкой музыки, которую играет Дэвис и его трое друзей.Дети здесь для задержанного Дня отца. 23 апреля 2019 г., 10:12. — Депутаты говорят, что на следующий день мужчина из Флориды попытался застрелить свою бывшую девушку и ее подругу. Округ Палм-Бич, Флорида (WPTV).
Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова попал в неприятности с законом, когда возглавил полицию Монтгомери. Человек из Флориды @_FloridaMan.Список почетных. МАЙАМИ (CBSMiami/AP) – Мужчине из Флориды предъявлены обвинения в пренебрежительном отношении к детям после того, как полиция заявила, что он оставил ребенка одного возле полицейского участка ночью, потому что думал, что он гей. 23 декабря 2021 г. 24 ноября 2021 г. ← Предыдущий пост. 23 ноября 2012 года Джордан Дэвис, чернокожий 17-летний ученик средней школы, был убит на заправочной станции Gate Petroleum в Джексонвилле, штат Флорида, Майклом Дэвидом Данном, белым 45-летним разработчиком программного обеспечения, после спор из-за громкой музыки, которую играет Дэвис и его трое друзей.Дети здесь для задержанного Дня отца. 23 апреля 2019 г., 10:12. — Депутаты говорят, что на следующий день мужчина из Флориды попытался застрелить свою бывшую девушку и ее подругу. Округ Палм-Бич, Флорида (WPTV). Мужчина из Флориды ударил пожилого человека после того, как ему сказали прекратить мастурбировать: полиция. +1 (352)279-4408. стрельба 23 ноября 2019 г. Прочтите последние заголовки национальных новостей со всех концов США. 20 ноября: мужчина из Флориды украл два телевизора и автомобиль из автосалона, 23 декабря: мужчина из Флориды разбил машину, пытаясь совершить путешествие во времени.23 ноября 2021 г., 21:25. Дела об убийствах остаются нераскрытыми годами или десятилетиями, пока ищут зацепки. Его срочно доставили в Центр травм Райдера в Мемориальной больнице Джексона, и он был в сознании. ДОЛЖЕН БЫТЬ ДОСТУПЕН ДЛЯ ПРОВЕДЕНИЯ ТЕСТА НА COVID В УИЛМИНГТОНЕ ПОНЕДЕЛЬНИК, 29 НОЯБРЯ, МЕЖДУ 10:30 A. Здесь расположены одни из лучших и самых инновационных школ штата. Опубликовано в ноябре. Материалы с сатирических сайтов являются мошенническими и будут удалены. Полиция Майами сообщает, что ответила в 12:26. Девушка из Флориды, у которой была отличная стратегия, чтобы не делать домашнюю работу.
Мужчина из Флориды ударил пожилого человека после того, как ему сказали прекратить мастурбировать: полиция. +1 (352)279-4408. стрельба 23 ноября 2019 г. Прочтите последние заголовки национальных новостей со всех концов США. 20 ноября: мужчина из Флориды украл два телевизора и автомобиль из автосалона, 23 декабря: мужчина из Флориды разбил машину, пытаясь совершить путешествие во времени.23 ноября 2021 г., 21:25. Дела об убийствах остаются нераскрытыми годами или десятилетиями, пока ищут зацепки. Его срочно доставили в Центр травм Райдера в Мемориальной больнице Джексона, и он был в сознании. ДОЛЖЕН БЫТЬ ДОСТУПЕН ДЛЯ ПРОВЕДЕНИЯ ТЕСТА НА COVID В УИЛМИНГТОНЕ ПОНЕДЕЛЬНИК, 29 НОЯБРЯ, МЕЖДУ 10:30 A. Здесь расположены одни из лучших и самых инновационных школ штата. Опубликовано в ноябре. Материалы с сатирических сайтов являются мошенническими и будут удалены. Полиция Майами сообщает, что ответила в 12:26. Девушка из Флориды, у которой была отличная стратегия, чтобы не делать домашнюю работу. Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. Когда дело доходит до автомобильных выставок в Южной Флориде, я надеюсь, что вы найдете этот сайт одновременно информативным и интересным. Лодердейл и международные аэропорты Майами, Diplomat особенности:. По сообщениям Флоридского шоссе, мужчина, ехавший в угнанной машине на межштатной автомагистрали 95 в округе Бревард, упал в обморок и позже скончался после того, как в начале субботы его загнало в канаву дом на колесах. «Человек, которого он пытался убить, был сотрудником Fivay», — сказал шериф Нокко во время пресс-конференции по этому делу.На видео с камер видеонаблюдения запечатлен мужчина, позже идентифицированный как 25-летний Кристиан Доминик. HIGHLANDS COUNTY, Флорида. Тем не менее, они реальны, и они произошли. Мужчина из Флориды, которому нужен светлый парик получше. Если у вас есть новый iPhone 11, вам наверняка понравится эта коллекция новых чехлов! Мы все еще планируем переезд всей семьей во Флориду, и Малыш 1 привез домой забавную игру.
Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. Когда дело доходит до автомобильных выставок в Южной Флориде, я надеюсь, что вы найдете этот сайт одновременно информативным и интересным. Лодердейл и международные аэропорты Майами, Diplomat особенности:. По сообщениям Флоридского шоссе, мужчина, ехавший в угнанной машине на межштатной автомагистрали 95 в округе Бревард, упал в обморок и позже скончался после того, как в начале субботы его загнало в канаву дом на колесах. «Человек, которого он пытался убить, был сотрудником Fivay», — сказал шериф Нокко во время пресс-конференции по этому делу.На видео с камер видеонаблюдения запечатлен мужчина, позже идентифицированный как 25-летний Кристиан Доминик. HIGHLANDS COUNTY, Флорида. Тем не менее, они реальны, и они произошли. Мужчина из Флориды, которому нужен светлый парик получше. Если у вас есть новый iPhone 11, вам наверняка понравится эта коллекция новых чехлов! Мы все еще планируем переезд всей семьей во Флориду, и Малыш 1 привез домой забавную игру. Идентификационный номер федеральной налоговой службы № 65-0403969. Официальный сайт Высшей лиги бейсбола. City of Wilton Manors стремится продвигать более экологичное и устойчивое будущее.Удобно как Ft. Военнослужащие отреагировали на девять аварий со смертельным исходом в минувшие выходные в Центральной Флориде. ANDRA 26 – 27 ноября 47th Goldenstates – Perth Motorplex, Австралия Преобразование времени 22:00 EST 26 ноября в США,,,,,Добро пожаловать!. Мужчина из Флориды украл сумочку пожилой женщины и сбил ее на парковке McDonald’s Полиция позже заявила, что арестовала Чарльза Алтона Стрэттона-младшего 26, 2019, 15:41 UTC / Обновлено ноября (AP, 24 сентября 2002 г.). Университетское общежитие запускает лабораторию лидерства в поисках талантов. (WTXL) — Мужчине из Флориды было предъявлено обвинение в поджоге после того, как полиция заявила, что он кричал о вампирах, прежде чем преднамеренно поджечь собственный дом, в котором находилась женщина.Лисбургская церковь Назарянина, Лисбург, Флорида.
Идентификационный номер федеральной налоговой службы № 65-0403969. Официальный сайт Высшей лиги бейсбола. City of Wilton Manors стремится продвигать более экологичное и устойчивое будущее.Удобно как Ft. Военнослужащие отреагировали на девять аварий со смертельным исходом в минувшие выходные в Центральной Флориде. ANDRA 26 – 27 ноября 47th Goldenstates – Perth Motorplex, Австралия Преобразование времени 22:00 EST 26 ноября в США,,,,,Добро пожаловать!. Мужчина из Флориды украл сумочку пожилой женщины и сбил ее на парковке McDonald’s Полиция позже заявила, что арестовала Чарльза Алтона Стрэттона-младшего 26, 2019, 15:41 UTC / Обновлено ноября (AP, 24 сентября 2002 г.). Университетское общежитие запускает лабораторию лидерства в поисках талантов. (WTXL) — Мужчине из Флориды было предъявлено обвинение в поджоге после того, как полиция заявила, что он кричал о вампирах, прежде чем преднамеренно поджечь собственный дом, в котором находилась женщина.Лисбургская церковь Назарянина, Лисбург, Флорида. местные проблемы, усыновить домашнее животное, налоги, рабочие места, развлечения. Пожалуйста, рассмотрите подписку. Республиканец из Флориды Гаетц предлагает работу стажера фашистскому стрелку Кайлу Риттенхаусу World Socialist Web Site08:19 Пт, 19 нояб. Посмотреть на Google Maps. Эта знаменитая последовательность представляет собой ряд чисел, где каждое число является суммой двух предшествующих ему чисел. Gulf To Lake Highway, Crystal River, FL 34429. ДЖЕКСОНВИЛЛ, Флорида. В понедельник исполняется восемь лет с тех пор, как 17-летний Джордан Дэвис был застрелен из-за спора о громкой музыке на заправке в Джексонвилле.— В воскресенье мужчина из Флориды был арестован по подозрению в использовании пакетов Kool-Aid для кражи. Департаменты. К тому времени мы уже должны быть в глубокой тишине. Итак, это сделало вторник. Мужчина из Флориды завершил свою защиту в суде по делу о двойном убийстве. Это безумие произошло в субботу в Саншайн-Стейт где-то вдоль шоссе I-95, где по шоссе на довольно быстрой скорости мчался большой грузовик.
местные проблемы, усыновить домашнее животное, налоги, рабочие места, развлечения. Пожалуйста, рассмотрите подписку. Республиканец из Флориды Гаетц предлагает работу стажера фашистскому стрелку Кайлу Риттенхаусу World Socialist Web Site08:19 Пт, 19 нояб. Посмотреть на Google Maps. Эта знаменитая последовательность представляет собой ряд чисел, где каждое число является суммой двух предшествующих ему чисел. Gulf To Lake Highway, Crystal River, FL 34429. ДЖЕКСОНВИЛЛ, Флорида. В понедельник исполняется восемь лет с тех пор, как 17-летний Джордан Дэвис был застрелен из-за спора о громкой музыке на заправке в Джексонвилле.— В воскресенье мужчина из Флориды был арестован по подозрению в использовании пакетов Kool-Aid для кражи. Департаменты. К тому времени мы уже должны быть в глубокой тишине. Итак, это сделало вторник. Мужчина из Флориды завершил свою защиту в суде по делу о двойном убийстве. Это безумие произошло в субботу в Саншайн-Стейт где-то вдоль шоссе I-95, где по шоссе на довольно быстрой скорости мчался большой грузовик. Голый мужчина из Флориды врывается в дом, примеряет женскую одежду, полиция сообщает, что Джозеф Ваглица арестован в Нью-Смирна-Бич. com/TrYw1V1pvA.23 сентября 2002 г. Непокорный Ясир Арафат окопался в своем осажденном комплексе на Западном берегу, отвергнув требование Израиля передать имена всех тех, кто скрывался внутри. 0 Почтовый ящик службы поддержки правоприменения и расследований 1489 Таллахасси, Флорида 32302-1489 Бесплатный номер: 1-888-357-7332 (с 8:00 до 17:00 по восточному поясному времени) Местный: 1-850-410-8572 (с 8:00 по восточному поясному времени) : 00am — 17:00, EST) Электронная почта: [email protected] СЕВЕРНЫЙ НЕАПОЛЬ, Флорида. Журналистика, как и наше космическое освещение, требует времени и ресурсов. Ушел из чемпионатов Франции и Олимпийских игр в Токио.23 ноября 2021 г., 16:51. 30 ноября 2020 г. Эту запись необходимо расследовать, потому что самоубийство может относиться к другому мужчине с таким же госпитализированным после того, как лицо потеряло сознание в первые четыре минуты игры против штата Флорида.
Голый мужчина из Флориды врывается в дом, примеряет женскую одежду, полиция сообщает, что Джозеф Ваглица арестован в Нью-Смирна-Бич. com/TrYw1V1pvA.23 сентября 2002 г. Непокорный Ясир Арафат окопался в своем осажденном комплексе на Западном берегу, отвергнув требование Израиля передать имена всех тех, кто скрывался внутри. 0 Почтовый ящик службы поддержки правоприменения и расследований 1489 Таллахасси, Флорида 32302-1489 Бесплатный номер: 1-888-357-7332 (с 8:00 до 17:00 по восточному поясному времени) Местный: 1-850-410-8572 (с 8:00 по восточному поясному времени) : 00am — 17:00, EST) Электронная почта: [email protected] СЕВЕРНЫЙ НЕАПОЛЬ, Флорида. Журналистика, как и наше космическое освещение, требует времени и ресурсов. Ушел из чемпионатов Франции и Олимпийских игр в Токио.23 ноября 2021 г., 16:51. 30 ноября 2020 г. Эту запись необходимо расследовать, потому что самоубийство может относиться к другому мужчине с таким же госпитализированным после того, как лицо потеряло сознание в первые четыре минуты игры против штата Флорида. Выяснилось, что мужчина продавал украденную книгу комиксов на сумму 100 000 долларов и был немедленно арестован в Аризоне. Опубликовано в The Venice Gondolier Sun от ноября. «Власти остановились. Вы также должны обнаружить, что освещение фотографии является самым тщательным и современным в Южной Флориде.Совет управляющих проводит панельную дискуссию с лидерами бизнеса в области экологически чистой энергии и технологий. Пол вскоре после того, как самолет приземлился из Орландо, штат Флорида. Пт, 31 дек., 18:00. Государственный лес Витлакучи был приобретен федеральным правительством у частных землевладельцев в период с 1936 по 1939 год в соответствии с положениями шерифа округа Бревард. Аллен Ариас в прошлом месяце доставил в больницу потерявшую сознание Аниту Ариас. В июне Санкт-Петербург. Вы редко имеете смысл для большого мира.(WKRG) — Мужчина из Пенсаколы находится в тюрьме после того, как пастор выдал его властям за сексуальное насилие над детьми. ** В соответствии с новым мандатом Netflix на вакцинацию все BG в возрасте 12 лет и старше ДОЛЖНЫ быть […].
Выяснилось, что мужчина продавал украденную книгу комиксов на сумму 100 000 долларов и был немедленно арестован в Аризоне. Опубликовано в The Venice Gondolier Sun от ноября. «Власти остановились. Вы также должны обнаружить, что освещение фотографии является самым тщательным и современным в Южной Флориде.Совет управляющих проводит панельную дискуссию с лидерами бизнеса в области экологически чистой энергии и технологий. Пол вскоре после того, как самолет приземлился из Орландо, штат Флорида. Пт, 31 дек., 18:00. Государственный лес Витлакучи был приобретен федеральным правительством у частных землевладельцев в период с 1936 по 1939 год в соответствии с положениями шерифа округа Бревард. Аллен Ариас в прошлом месяце доставил в больницу потерявшую сознание Аниту Ариас. В июне Санкт-Петербург. Вы редко имеете смысл для большого мира.(WKRG) — Мужчина из Пенсаколы находится в тюрьме после того, как пастор выдал его властям за сексуальное насилие над детьми. ** В соответствии с новым мандатом Netflix на вакцинацию все BG в возрасте 12 лет и старше ДОЛЖНЫ быть […]. 21 марта офицеры полицейского управления Лейкленда были уведомлены о мужчине, который ел блины посреди пересечения Мемориального бульвара и Бруннелл-Паркуэй. Женщина была покрыта пролежнями и некоторые были. Депутатов вызвали к 74-летнему Гэри Вану. С помощью следователей и прокуроров Флориды сериал.Вызов человека из Флориды. Хотя официально они не входят в список из 40 человек, игроки из 60-дневного списка травмированных (Ил-60) включены во вкладку из 40 человек. — Мужчина из Флориды был арестован и обвинен после того, как полицейское управление Палм-Бей заявило, что он украл плавательные бассейны для секса «вместо того, чтобы изнасиловать женщину». «Florida Man Challenge» — это поисковая игра в Интернете, в которой человек ищет в Интернете фразу «Флорида». Мужчина», а затем их день рождения.- Мужчина из Флориды неоднократно арестовывался за секс с миниатюрной лошадью.Даже ваши соседи-государства не совсем знают, что с вами делать. Мужчина из Флориды, который повесил себе на голову гигантский рулон TP.
21 марта офицеры полицейского управления Лейкленда были уведомлены о мужчине, который ел блины посреди пересечения Мемориального бульвара и Бруннелл-Паркуэй. Женщина была покрыта пролежнями и некоторые были. Депутатов вызвали к 74-летнему Гэри Вану. С помощью следователей и прокуроров Флориды сериал.Вызов человека из Флориды. Хотя официально они не входят в список из 40 человек, игроки из 60-дневного списка травмированных (Ил-60) включены во вкладку из 40 человек. — Мужчина из Флориды был арестован и обвинен после того, как полицейское управление Палм-Бей заявило, что он украл плавательные бассейны для секса «вместо того, чтобы изнасиловать женщину». «Florida Man Challenge» — это поисковая игра в Интернете, в которой человек ищет в Интернете фразу «Флорида». Мужчина», а затем их день рождения.- Мужчина из Флориды неоднократно арестовывался за секс с миниатюрной лошадью.Даже ваши соседи-государства не совсем знают, что с вами делать. Мужчина из Флориды, который повесил себе на голову гигантский рулон TP. Рубрики: Мужчина из Флориды, Местное телевидение, Тюрьма округа Нассау, картофель, Удар вилкой, Удар ножом женщины. В нашем городском поселке полно велосипедных и пешеходных дорожек, а также парков и открытых пространств, где можно насладиться природой — все это интересно исследовать на велосипеде. Житель Флориды, найденный в море цепляющимся за свое перевернувшееся судно, отважился отойти более чем на 80 миль от берега. Перекрёсток Флориды. Мужчина из Флориды приготовил себе закуску, ограбив Taco Bell.Вот и все, ребята. Благодаря учетной записи в Твиттере под названием «Человек из Флориды», которая собирает «реальные истории о худших супергероях мира», мы можем поделиться этими историями. ЛЕЙК-УОРТ, штат Флорида. За последние несколько лет во Флориде произошли поистине безумные вещи, но я не думаю, что что-то шокировало меня больше, чем то, что законодательный орган штата в настоящее время пытается сделать с избирательными правами бывших -уголовники. Полиция расследует драку, разразившуюся в терминале в Миннеаполис-Стрит.
Рубрики: Мужчина из Флориды, Местное телевидение, Тюрьма округа Нассау, картофель, Удар вилкой, Удар ножом женщины. В нашем городском поселке полно велосипедных и пешеходных дорожек, а также парков и открытых пространств, где можно насладиться природой — все это интересно исследовать на велосипеде. Житель Флориды, найденный в море цепляющимся за свое перевернувшееся судно, отважился отойти более чем на 80 миль от берега. Перекрёсток Флориды. Мужчина из Флориды приготовил себе закуску, ограбив Taco Bell.Вот и все, ребята. Благодаря учетной записи в Твиттере под названием «Человек из Флориды», которая собирает «реальные истории о худших супергероях мира», мы можем поделиться этими историями. ЛЕЙК-УОРТ, штат Флорида. За последние несколько лет во Флориде произошли поистине безумные вещи, но я не думаю, что что-то шокировало меня больше, чем то, что законодательный орган штата в настоящее время пытается сделать с избирательными правами бывших -уголовники. Полиция расследует драку, разразившуюся в терминале в Миннеаполис-Стрит. Эндрю Скеррит. ОКРУГ ВОЛЮСИЯ, штат Флорида.12: Мужчина из Флориды, одетый как Фред Флинтстоун, остановился на своем «пешем мобиле», февраль. Мужчина из Флориды дважды звонил в полицию, чтобы пожаловаться на то, что моллюски, которые он заказал в ресторане морепродуктов, были «такими маленькими». Это быстро стало огромным мемом, и теперь есть проблема, связанная с этой концепцией. Рубрики: Кража со взломом, Человек из Флориды, Местное телевидение, Новости Майами, Тако Белл. Судебно-медицинская экспертиза подтвердила, что Брайан Лаундри, главный подозреваемый в смерти своей подруги Габби Петито, покончил жизнь самоубийством. (WSVN) — Мужчина из Флориды был арестован после того, как его обвинили в раздаче марихуаны прохожим на праздники.Каждая запись содержит ссылку на полный онлайн-некролог, в котором есть вся информация о поминках и похоронах, и где вы можете оставить свои соболезнования в книге памяти. Мужчина из Флориды обвиняется в нанесении ножевого ранения женщине из-за недожаренной картошки.
Эндрю Скеррит. ОКРУГ ВОЛЮСИЯ, штат Флорида.12: Мужчина из Флориды, одетый как Фред Флинтстоун, остановился на своем «пешем мобиле», февраль. Мужчина из Флориды дважды звонил в полицию, чтобы пожаловаться на то, что моллюски, которые он заказал в ресторане морепродуктов, были «такими маленькими». Это быстро стало огромным мемом, и теперь есть проблема, связанная с этой концепцией. Рубрики: Кража со взломом, Человек из Флориды, Местное телевидение, Новости Майами, Тако Белл. Судебно-медицинская экспертиза подтвердила, что Брайан Лаундри, главный подозреваемый в смерти своей подруги Габби Петито, покончил жизнь самоубийством. (WSVN) — Мужчина из Флориды был арестован после того, как его обвинили в раздаче марихуаны прохожим на праздники.Каждая запись содержит ссылку на полный онлайн-некролог, в котором есть вся информация о поминках и похоронах, и где вы можете оставить свои соболезнования в книге памяти. Мужчина из Флориды обвиняется в нанесении ножевого ранения женщине из-за недожаренной картошки. Мужчина из Флориды утверждает, что пакеты с кокаином и метамфетамином, обернутые вокруг полового члена, не принадлежат ему 23 декабря 2021 года. (AP, 23 сентября 2003 г.) 23 сентября 2002 года палестинский боевик открыл огонь по посетителям, посетившим еврейские праздники. убив человека и ранив трех его сыновей. 27 ноября 2018 г., 14:33.Узнайте больше о государственных школах Pre-K-12 здесь, в Голливуде. Мужчина из Флориды сделал что-то опрометчивое в тот день, когда вы родились, так что вот испытание «Человек из Флориды». список всех отделов, агентств. Жителя Флориды обвинили в смерти его 87-летней бабушки, и власти заявили, что ее кровать была заполнена живыми личинками. 24 июня 2019 г., 10:49. Открытие было сделано после многонедельной охоты в заповеднике Карлтон. Во вторник мужчина из Флориды совершил опасный шаг. 16 февраля 2020 года на межштатной автомагистрали 4 в округе Хиллсборо, штат Флорида.Даниэль Дам, менеджер по цифровому контенту. 30 ноября 2021 г. 20 ноября 2021 г. САРАСОТА.
Мужчина из Флориды утверждает, что пакеты с кокаином и метамфетамином, обернутые вокруг полового члена, не принадлежат ему 23 декабря 2021 года. (AP, 23 сентября 2003 г.) 23 сентября 2002 года палестинский боевик открыл огонь по посетителям, посетившим еврейские праздники. убив человека и ранив трех его сыновей. 27 ноября 2018 г., 14:33.Узнайте больше о государственных школах Pre-K-12 здесь, в Голливуде. Мужчина из Флориды сделал что-то опрометчивое в тот день, когда вы родились, так что вот испытание «Человек из Флориды». список всех отделов, агентств. Жителя Флориды обвинили в смерти его 87-летней бабушки, и власти заявили, что ее кровать была заполнена живыми личинками. 24 июня 2019 г., 10:49. Открытие было сделано после многонедельной охоты в заповеднике Карлтон. Во вторник мужчина из Флориды совершил опасный шаг. 16 февраля 2020 года на межштатной автомагистрали 4 в округе Хиллсборо, штат Флорида.Даниэль Дам, менеджер по цифровому контенту. 30 ноября 2021 г. 20 ноября 2021 г. САРАСОТА. Житель Венеции предположительно ехал под действием наркотиков и врезался в четыре машины сзади, но, согласно автору, продолжал уезжать с места происшествия… Полицейский удар за 20 ноября 2021 г. 23 ноября, 2021. Истории, которые мы получаем о почти мифическом человеке из Флориды, в этот момент кажутся слишком абсурдными, чтобы даже быть правдой. Играя перед более чем 4 миллионами фанатов в масштабных турах по аренам и стадионам, они повторят FLORIDA GEORGIA LINE LIVE FROM LAS VEGAS по многочисленным просьбам.Опубликовано в 14:41, 21 ноября 2018 г. Хорошее время для военного захвата средств массовой информации, и Disney отменяет требования о вакцинации сотрудников благодаря новому закону губернатора Флориды ДеСантиса. Кайла Томпсон. Человек из Флориды немного загадка. Fun ОСТАВИТЬ КОММЕНТАРИЙ 24 июня 2020 г. Илона. Образование является главным приоритетом для семей, проживающих в Голливуде и переезжающих в него. Шэрон Миддлтон. Мужчина из Флориды арестован за то, что носил в школе табличку с изображением абортированных зародышей. (WSVN) — Мужчина из Флориды был арестован после того, как несколько человек обвинили его в сексе с миниатюрной лошадью.Ассошиэйтед Пресс, ноябрь. Результаты должны показать, что «Человек из Флориды» делал в тот день (в случае 13 апреля это было так. Он — потрепанная ткань изношенного табачного кольца в заднем левом кармане. Мы составили самые глупые и возмутительные преступления, которые когда-либо совершали жители Флориды. Обсуждение в «Болотном газе RayGator», начатое GatorGrowl, 19 декабря 2021 г. Этот особняк во Флориде когда-то принадлежал Мадонне, а теперь его продает собака. Почти каждый божий день в новостях есть заголовок о сумасшедшем новом человеке из Флориды.Житель Флориды явился в офис шерифа округа Окалуза, заявив: «У меня проблемы. Житель Флориды арестован за то, что предположительно затряс свою маленькую дочь до смерти. «газеты родного города», в том числе The Tattler 1938 года; «Пеликан» , издававшийся с 1949 по 1953 год; и старые выпуски Boca Raton News, выходящие с декабря 1955 года. Жителя Флориды, обвиненного в том, что он угрожал своей семье лирикой Coldplay и возмездием со стороны своих «нацистских тюремных сообщников», убедили прекратить противостояние с полицией в обмен на свежий кусок .Следите за новыми случаями, выявляемыми каждый день, а также за количеством случаев и смертей в округе Сарасота, штат Флорида. Управление по переселению земель. ФОРТ-ЛОДЕРДЕЙЛ. Он только что вышел из душа и готовился ко сну, когда мельком увидел чью-то фигуру за окном. Введите дату своего рождения и термин «мужчина из Флориды» в Google, чтобы увидеть заголовки а. Привет всем, это ВАША Ежедневная Доза Интернета. Опубликовано: 23 ноября 2021 г., 9:23 Обновлено: 23 ноября 2021 г., 12:16 Теги: округ Майами-Дейд «Это было так тяжело видеть», — сказал свидетель Local 10 News.Власти пытаются определить, нюхает ли ПФР ноги. 23 декабря (четверг) 19:00 Флорида против Центральной Флориды Gasparilla Bowl ESPN. 23 июня фото. Здесь, в Wilton Manors, лучше ездить на велосипеде. 5 ноября 2019 г. 15 ноября 2019 г., 12:46. Когда ноябрьская дата записывается в формате месяц/день (11/23), она образует последовательность Фибоначчи: 1, 1, 2, 3. Флорида — популярное место отдыха с многочисленными пляжами и самым популярным в мире тематическим парком, несмотря на свое официальное название. Будучи «Солнечным штатом», третий по численности населения штат страны на самом деле более подвержен молниям и ураганам, чем любой другой.Главные новости о преступности и общественной безопасности во Флориде, включая округа Бровард, Палм-Бич и Майами-Дейд, а также города Форт-Лодердейл, Голливуд, Бока-Ратон, Орландо, Тампа и другие. Например, если ваш день рождения 13 апреля, вы должны искать «мужчина из Флориды, 13 апреля». МАБ для COVID-19 может предотвратить тяжелое заболевание, госпитализацию и смерть. Рон ДеСантис, по умолчанию житель Флориды, так как он управляет Саншайн-Стейт, имеет дату начала сентября 23 ноября 2021 года. Первая история в результатах поиска — история вашего дня рождения «Человек из Флориды».В центре внимания образование в Голливуде во Флориде. Мужчина из Клируотера, штат Флорида, применил смелую стратегию после того, как полицейские обнаружили шприцы в его прямой кишке, когда его переводили в тюрьму округа Пинеллас. Часто упоминаемые в заголовках как «Человек из Флориды», эти убийцы совершают причудливые и диковинные преступления, которые очаровывают нацию и иногда кажется, что они прямо из голливудского фильма. 23 декабря 1981 года, когда Южная Флорида была наводнена преступлениями, связанными с наркотиками. Я не знаю, что такого во Флориде, но я убежден, что здесь живут одни из самых сумасшедших людей в стране.в деле Опубликовано 9 декабря 2018 г. • Обновлено. Ссылки на источники. 12 июня 2019 г., 9:19. 14 день рождения. Флорида, 30 ноября -0001. 24 ноября 2016 г. Мужчина из Флориды дрочит в пикапе возле Walgreens (Sebastian Daily). Florida Man — это канал в Твиттере, который курирует заголовки новостей с описаниями странных бытовых инцидентов с участием мужчины, проживающего в штате Флорида. 19 октября 2020 г., 22:49 CDT Автор: Келли Дуган, Национальный отдел контента Cox Media Group. Полиция сначала арестовала 54-летнего Эдварда Майкла Дорси около 10:45.Человек из Флориды 23 ноября (23 ноября) Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. В 2018 году FWC арестовал сильно пьяного мужчину из Флориды, который пронес аллигатора на заправочную станцию, а ранее в этом году другой мужчина из Флориды был арестован за то, что сунул сигарету в рот аллигатору. Цитируя адвоката семьи Лаундри Стивена Бертолино. 31-летний Чарльз Дион Макдауэлл снова был арестован, и теперь ему предъявлены аналогичные обвинения в Алабаме. — Власти заявили, что мужчина, который хвастался, что обманом заставил местных чиновников Флориды позволить ему развевать огромный флаг Конфедерации на углах двух оживленных автомагистралей между штатами.По данным офиса шерифа округа Мэрион, несколько. Согласно показаниям под присягой при аресте, 52-летний Митчелл вошел в буфет Hibachi в парке Пинеллас и совсем не был счастлив, увидев, что суши, которые он хотел в субботу, не подаются. Мужчина из Флориды обвиняется в том, что ударил молотком женщину, с которой познакомился в Интернете, пока ее ребенок был дома; Когда они прибыли, Рысвик сказал депутату, что только что провел кастрацию мужчины и столкнулся с майором. Национальный день Флориды отмечается 25 января каждого года, и чтобы отпраздновать это событие, мы составили список самых читаемых историй о «Человеке из Флориды» за последний год.Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова столкнулся с проблемами с законом, когда возглавил полицию Монтгомери в скоростной погоне по межштатной автомагистрали 85, прежде чем полицейские применили полосы с шипами, чтобы вывести из строя его автомобиль. Лечение бесплатное, статус прививок не имеет значения. Новости преступности — Джексонвилл, Флорида | Флорида Таймс-Юнион. Недвижимость Тропик Шорс. Мы ищем что-то похожее на «Голый мужчина из Флориды, под кайфом от метамфетамина, пытается ограбить винный магазин с мертвым скатом». Кто-то уже позвонил в 911 и сообщил о окровавленном человеке.По сообщениям, 23-летний мужчина, частичные останки которого были обнаружены во Флориде в конце прошлого месяца, выстрелил себе в голову. Мужчина из Флориды 1 ноября. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Что делал мужчина из Флориды 3 ноября? Что делал мужчина из Флориды 4 ноября? Что делал мужчина из Флориды 6 ноября? Почтовая навигация. Мужчина из Флориды, который прошлым летом ограбил заправочную станцию в районе Мандевиля, был обнаружен во вторник (16 ноября) утром игрушкой U.
Житель Венеции предположительно ехал под действием наркотиков и врезался в четыре машины сзади, но, согласно автору, продолжал уезжать с места происшествия… Полицейский удар за 20 ноября 2021 г. 23 ноября, 2021. Истории, которые мы получаем о почти мифическом человеке из Флориды, в этот момент кажутся слишком абсурдными, чтобы даже быть правдой. Играя перед более чем 4 миллионами фанатов в масштабных турах по аренам и стадионам, они повторят FLORIDA GEORGIA LINE LIVE FROM LAS VEGAS по многочисленным просьбам.Опубликовано в 14:41, 21 ноября 2018 г. Хорошее время для военного захвата средств массовой информации, и Disney отменяет требования о вакцинации сотрудников благодаря новому закону губернатора Флориды ДеСантиса. Кайла Томпсон. Человек из Флориды немного загадка. Fun ОСТАВИТЬ КОММЕНТАРИЙ 24 июня 2020 г. Илона. Образование является главным приоритетом для семей, проживающих в Голливуде и переезжающих в него. Шэрон Миддлтон. Мужчина из Флориды арестован за то, что носил в школе табличку с изображением абортированных зародышей. (WSVN) — Мужчина из Флориды был арестован после того, как несколько человек обвинили его в сексе с миниатюрной лошадью.Ассошиэйтед Пресс, ноябрь. Результаты должны показать, что «Человек из Флориды» делал в тот день (в случае 13 апреля это было так. Он — потрепанная ткань изношенного табачного кольца в заднем левом кармане. Мы составили самые глупые и возмутительные преступления, которые когда-либо совершали жители Флориды. Обсуждение в «Болотном газе RayGator», начатое GatorGrowl, 19 декабря 2021 г. Этот особняк во Флориде когда-то принадлежал Мадонне, а теперь его продает собака. Почти каждый божий день в новостях есть заголовок о сумасшедшем новом человеке из Флориды.Житель Флориды явился в офис шерифа округа Окалуза, заявив: «У меня проблемы. Житель Флориды арестован за то, что предположительно затряс свою маленькую дочь до смерти. «газеты родного города», в том числе The Tattler 1938 года; «Пеликан» , издававшийся с 1949 по 1953 год; и старые выпуски Boca Raton News, выходящие с декабря 1955 года. Жителя Флориды, обвиненного в том, что он угрожал своей семье лирикой Coldplay и возмездием со стороны своих «нацистских тюремных сообщников», убедили прекратить противостояние с полицией в обмен на свежий кусок .Следите за новыми случаями, выявляемыми каждый день, а также за количеством случаев и смертей в округе Сарасота, штат Флорида. Управление по переселению земель. ФОРТ-ЛОДЕРДЕЙЛ. Он только что вышел из душа и готовился ко сну, когда мельком увидел чью-то фигуру за окном. Введите дату своего рождения и термин «мужчина из Флориды» в Google, чтобы увидеть заголовки а. Привет всем, это ВАША Ежедневная Доза Интернета. Опубликовано: 23 ноября 2021 г., 9:23 Обновлено: 23 ноября 2021 г., 12:16 Теги: округ Майами-Дейд «Это было так тяжело видеть», — сказал свидетель Local 10 News.Власти пытаются определить, нюхает ли ПФР ноги. 23 декабря (четверг) 19:00 Флорида против Центральной Флориды Gasparilla Bowl ESPN. 23 июня фото. Здесь, в Wilton Manors, лучше ездить на велосипеде. 5 ноября 2019 г. 15 ноября 2019 г., 12:46. Когда ноябрьская дата записывается в формате месяц/день (11/23), она образует последовательность Фибоначчи: 1, 1, 2, 3. Флорида — популярное место отдыха с многочисленными пляжами и самым популярным в мире тематическим парком, несмотря на свое официальное название. Будучи «Солнечным штатом», третий по численности населения штат страны на самом деле более подвержен молниям и ураганам, чем любой другой.Главные новости о преступности и общественной безопасности во Флориде, включая округа Бровард, Палм-Бич и Майами-Дейд, а также города Форт-Лодердейл, Голливуд, Бока-Ратон, Орландо, Тампа и другие. Например, если ваш день рождения 13 апреля, вы должны искать «мужчина из Флориды, 13 апреля». МАБ для COVID-19 может предотвратить тяжелое заболевание, госпитализацию и смерть. Рон ДеСантис, по умолчанию житель Флориды, так как он управляет Саншайн-Стейт, имеет дату начала сентября 23 ноября 2021 года. Первая история в результатах поиска — история вашего дня рождения «Человек из Флориды».В центре внимания образование в Голливуде во Флориде. Мужчина из Клируотера, штат Флорида, применил смелую стратегию после того, как полицейские обнаружили шприцы в его прямой кишке, когда его переводили в тюрьму округа Пинеллас. Часто упоминаемые в заголовках как «Человек из Флориды», эти убийцы совершают причудливые и диковинные преступления, которые очаровывают нацию и иногда кажется, что они прямо из голливудского фильма. 23 декабря 1981 года, когда Южная Флорида была наводнена преступлениями, связанными с наркотиками. Я не знаю, что такого во Флориде, но я убежден, что здесь живут одни из самых сумасшедших людей в стране.в деле Опубликовано 9 декабря 2018 г. • Обновлено. Ссылки на источники. 12 июня 2019 г., 9:19. 14 день рождения. Флорида, 30 ноября -0001. 24 ноября 2016 г. Мужчина из Флориды дрочит в пикапе возле Walgreens (Sebastian Daily). Florida Man — это канал в Твиттере, который курирует заголовки новостей с описаниями странных бытовых инцидентов с участием мужчины, проживающего в штате Флорида. 19 октября 2020 г., 22:49 CDT Автор: Келли Дуган, Национальный отдел контента Cox Media Group. Полиция сначала арестовала 54-летнего Эдварда Майкла Дорси около 10:45.Человек из Флориды 23 ноября (23 ноября) Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. В 2018 году FWC арестовал сильно пьяного мужчину из Флориды, который пронес аллигатора на заправочную станцию, а ранее в этом году другой мужчина из Флориды был арестован за то, что сунул сигарету в рот аллигатору. Цитируя адвоката семьи Лаундри Стивена Бертолино. 31-летний Чарльз Дион Макдауэлл снова был арестован, и теперь ему предъявлены аналогичные обвинения в Алабаме. — Власти заявили, что мужчина, который хвастался, что обманом заставил местных чиновников Флориды позволить ему развевать огромный флаг Конфедерации на углах двух оживленных автомагистралей между штатами.По данным офиса шерифа округа Мэрион, несколько. Согласно показаниям под присягой при аресте, 52-летний Митчелл вошел в буфет Hibachi в парке Пинеллас и совсем не был счастлив, увидев, что суши, которые он хотел в субботу, не подаются. Мужчина из Флориды обвиняется в том, что ударил молотком женщину, с которой познакомился в Интернете, пока ее ребенок был дома; Когда они прибыли, Рысвик сказал депутату, что только что провел кастрацию мужчины и столкнулся с майором. Национальный день Флориды отмечается 25 января каждого года, и чтобы отпраздновать это событие, мы составили список самых читаемых историй о «Человеке из Флориды» за последний год.Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова столкнулся с проблемами с законом, когда возглавил полицию Монтгомери в скоростной погоне по межштатной автомагистрали 85, прежде чем полицейские применили полосы с шипами, чтобы вывести из строя его автомобиль. Лечение бесплатное, статус прививок не имеет значения. Новости преступности — Джексонвилл, Флорида | Флорида Таймс-Юнион. Недвижимость Тропик Шорс. Мы ищем что-то похожее на «Голый мужчина из Флориды, под кайфом от метамфетамина, пытается ограбить винный магазин с мертвым скатом». Кто-то уже позвонил в 911 и сообщил о окровавленном человеке.По сообщениям, 23-летний мужчина, частичные останки которого были обнаружены во Флориде в конце прошлого месяца, выстрелил себе в голову. Мужчина из Флориды 1 ноября. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Что делал мужчина из Флориды 3 ноября? Что делал мужчина из Флориды 4 ноября? Что делал мужчина из Флориды 6 ноября? Почтовая навигация. Мужчина из Флориды, который прошлым летом ограбил заправочную станцию в районе Мандевиля, был обнаружен во вторник (16 ноября) утром игрушкой U.. ejb два dhx мнм тгр чи неделя ванна плк нскв ади qxc гвд bxl ФТУ Гат М-м-м дем куз
Исчисление I. Решение триггерных уравнений
Эта задача очень похожа на другие задачи в этом разделе с очень важным отличием.Мы начнем эту задачу точно так же, как и в первом примере. Итак, сначала получите синус с одной стороны сам по себе.
\[\begin{align*}2\sin (5x) & = — \sqrt 3 \\ \sin (5x) & = \frac{{ — \sqrt 3 }}{2}\end{align*}\]Мы ищем углы, которые дают \( — \frac{{\sqrt 3 }}{2}\) из функции синуса. Вернемся снова к нашему верному единичному кругу.
Теперь в первом квадранте нет углов, для которых синус имеет значение \( — \frac{{\sqrt 3}}{2}\).Однако в нижней половине единичного круга есть два угла, для которых синус будет иметь значение \( — \frac{{\sqrt 3}}{2}\). Так что же это за углы?
Обратите внимание, что \(\sin\left({\frac{\pi}}{3}}\right) = \frac{{\sqrt 3}}{2}\). Учитывая это, мы теперь знаем, что угол в третьем квадранте будет \(\frac{\pi }{3}\) ниже отрицательной оси \(x\) или \(\pi + \frac{ \pi }{3} = \frac{{4\pi }}{3}\). Простой способ запомнить это — заметить, что мы повернем на пол-оборота от положительной оси \(x\) к отрицательной оси \(x\), а затем добавим \(\frac{\pi } {3}\), чтобы достичь искомого угла.
Точно так же угол в четвертом квадранте будет \(\frac{\pi }{3}\) ниже положительной оси \(x\). Таким образом, мы могли бы использовать \( — \frac{\pi }{3}\) или \(2\pi — \frac{\pi }{3} = \frac{{5\pi }}{3}\) . Помните, что мы обычно ищем положительные углы между 0 и \(2\pi \), поэтому мы будем использовать положительный угол. Простой способ запомнить, как получить здесь положительный угол, — это повернуться на один полный оборот от положительной оси \(x\) ( , т.е. \(2\pi \)) и затем отступить ( i.е. вычитание) \(\ frac{\pi }{3}\).
Теперь мы подошли к очень важному отличию этой задачи от предыдущих задач этого раздела. Решение НЕ
\[\begin{align*}x & = \frac{{4\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \\ x & = \frac{{5\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \end{align*}\]Это не набор решений, потому что мы НЕ ищем значения \(x\), для которых \(\sin \left( x \right) = — \frac{{\sqrt 3}}{2}\) , но вместо этого мы ищем значения \(x\), для которых \(\sin\left({5x}\right) = — \frac{{\sqrt 3}}{2}\).Обратите внимание на разницу в аргументах функции синуса! Один из них \(х\), а другой \(5х\). Это имеет большое значение в поиске решения! Следовательно, множество решений равно
. \[\begin{align*}5x & = \frac{{4\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \\ 5x & = \frac{{5\pi }}{3} + 2\pi n,\quad n = 0, \pm 1, \pm 2, \ldots \end{align*}\]Ну, на самом деле, это не совсем решение. Мы ищем значения \(x\), поэтому делим все на 5, чтобы получить.
\[\begin{align*}x & = \frac{{4\pi}}{{15}} + \frac{{2\pi n}}{5},\quad n = 0, \pm 1, \pm 2, \ldots \\ x & = \frac{\pi }{3} + \frac{{2\pi n}}{5},\quad n = 0, \pm 1, \pm 2, \ ldots \end{align*}\]Обратите внимание, что мы также разделили \(2\pi n\) на 5! Это важно! Если мы этого не сделаем, вы БУДЕТЕ упустить решения. Например, возьмем \(n = 1\).
\[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi }}{5} = \frac{{10\pi }}{{ 15}} = \frac{{2\pi }}{3} & \hspace{0.25 дюймов} & \ Rightarrow \ hspace {0,5 дюйма} \ грех \ влево ( {5 \ влево ( {\ гидроразрыва {{2 \ pi}} {3}} \ вправо)} \ вправо) = \ грех \ влево ( {\ frac{{10\pi}}{3}} \right) = — \frac{{\sqrt 3}}{2}\\ x & = \frac{\pi}}{3} + \frac{{2\ пи}} {5} = \ гидроразрыв {{11 \ пи}} {{15}} & \ hspace {0,25 дюйма} & \ Rightarrow \ hspace {0,5 дюйма} \ грех \ влево ( {5 \ влево ( {\ гидроразрыва {{11\pi}}{{15}}} \right)} \right) = \sin \left( {\frac{{11\pi}}{3}} \right) = — \frac{{\ sqrt 3 }}{2}\end{align*}\]Мы предоставим вам возможность проверить нашу работу, показав, что это решения.Тем не менее, это делает точку. Если бы вы не разделили \(2\pi n\) на 5, вы бы пропустили эти решения!
Хорошо, теперь, когда мы получили все возможные решения, пришло время найти решения на заданном интервале. Сделаем это так же, как и в предыдущей задаче. Выберите значения \(n\) и получите решения.
\(п = 0\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( 0 \right)}}{5} = \frac{{ 4\pi }}{{15}} 2\pi \\ x & = \frac{\pi }{3} + \frac{{2\pi \left( 5 \right)}}{5} = \frac {{35\pi}}{{15}} > 2\pi \end{align*}\]Итак, мы, наконец, прошли правильную конечную точку нашего интервала, поэтому нам больше не нужны положительные n .Теперь давайте посмотрим на отрицательное число \(n\) и посмотрим, что у нас получилось.
\(n = –1 \). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { — 1} \right)}}{5} = — \frac{{2\pi}}{{15}} > — \pi \\ x & = \frac{\pi} {3} + \frac{{2\pi \left( { — 1} \right) }}{5} = — \frac{\pi }{{15}} > — \pi \end{align*}\] \(n = –2\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { — 2} \right)}}{5} = — \frac{{8\pi}}{{15}} > — \pi \\ x & = \frac{\pi} {3} + \frac{{2\pi \left( { — 2} \right) }}{5} = — \frac{{7\pi }}{{15}} > — \pi \end{align*}\] \(n = –3\).\[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { — 3} \right)}}{5} = — \frac{{14\pi}}{{15}} > — \pi \\ x & = \frac{\pi} {3} + \frac{{2\pi \left( { — 3} \right) }}{5} = — \frac{{13\pi }}{{15}} > — \pi \end{align*}\] \(n = –4\). \[\begin{align*}x & = \frac{{4\pi }}{{15}} + \frac{{2\pi \left( { — 4} \right)}}{5} = — \frac{{4\pi }}{3}Теперь мы прошли левую конечную точку интервала.Иногда будет много решений, как в этом примере. Собирая все это вместе, мы получаем следующий набор решений, лежащих в заданном интервале.
\[\begin{align*} & \frac{{4\pi}}{{15}},\frac{\pi }{3},\frac{{2\pi}}{3},\frac{ {11\pi}}{{15}},\frac{{16\pi}}{{15}},\frac{{17\pi}}{{15}},\frac{{22\pi} }{{15}},\frac{{23\pi }}{{15}},\frac{{28\pi }}{{15}},\frac{{29\pi }}{{15} }\\ & — \frac{\pi }{{15}}, — \frac{{2\pi }}{{15}}, — \frac{{7\pi }}{{15}}, — \frac{{8\pi }}{{15}}, — \frac{{13\pi }}{{15}}, — \frac{{14\pi }}{{15}}\end{align *}\]Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства
Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства — Урок 5
Урок 5 Подробнее сложные уравнения и неравенства2008 Расмус Эхф
и Джанн СакТриггерные функции Печать Пример 1
Решите уравнение sin x = cos x и затем неравенство
грех x > cos x на интервале 0 x < 2.
Из единичного круга мы видим, что sin x и cos x может иметь одинаковое значение только в двух местах, в x = /4 и х = 5/4 (45 и 225 ).
Уравнение sin x = cos x также можно решить путем деления на cos x.
тангенс х = 1
x = тангенс −1 (1)
х = 45 ∙ /180 + к∙
x = /4 + k∙ (k — любое целое число, положительное или отрицательное)
Если положить k = 0 и k = 1, получим решения /4 (45 ) и /4 + = 5/4 (45 + 180 = 225 ).
Чтобы решить неравенство sin x > cos x, нам нужно увидеть, что больше sin x или cos x на интервалах между решениями /4 и 5/4. Решения можно увидеть, если мы нарисуем графики f(x) = sin x и g(x) = cos Икс. График sin x лежит над графиком cos x на интервале /4 x 5x/4 (см. заштрихованную область на диаграмме).
sin x cos x на интервале /4 x 5x/4.
Пример 2
Решить уравнение sin x ∙ cos x = 0 и затем неравенство
sin x ∙ cos x > 0 на интервале 0 x < 2.
Неравенство не имеет решение, когда sin x или cos x принимают значение 0. Это происходит с интервалом 90.
Решения уравнение sin x ∙ cos x = 0 на интервале 0 x < 2, следовательно, 0, /2 и 3/2 (0 , 90 , 180 и 270 ).
Решение sin x ∙ cos x > 0 можно найти, взглянув на единичный круг. Нам нужно найти где sin x, умноженный на cos x, является положительным. Другими словами, sin x и cos x имеют иметь один и тот же знак, оба должны быть положительный или оба отрицательные. Это происходит в первом и третьем квадранте. То поэтому решения
0 < х < /2 и р < х < 3/2.Мы также можем увидеть это по построение графика
f(x) = sin x ∙ cos x.Пример 3
Решите уравнение sin x ∙ cos x − sinx = 0 и тогда неравенство sin x ∙ cos x − sin x > 0 на интервале 0 x < 2,
sin x ∙ cos x − sinx = 0
sin x (cos x − 1) = 0
Нам нужно чтобы разложить уравнение на множители, взяв sin x за скобки.
Уравнение имеет решения когда sin x = 0 или скобка (cos x — 1) = 0.
sin х = 0
x = 0 или (180 ).
или
потому что х — 1 = 0
потому что х = 1
х = 0
Единственные решения уравнение поэтому 0 и .
Неравенство sin x ∙ cos x − sin x > 0 можно переписать как sin x (cos x − 1) > 0,
Теперь полезно сделать таблицу знаков и посмотрите на знаки sin x и cos x − 1.
РешениеМы видим, что оба фактора отрицательно на интервале
< x < 2,Теперь давайте посмотрим, как это подходит в с графиком
f(x) = sin x ∙ cos x − sin xЗаштрихованная область над крестиком ось показывает где
sin x (cos x − 1) > 0, что согласуется с нашими расчетами.Пример 4
Найти все решения уравнения cos 2 x − cos x = 0,
cos 2 x − cos х = 0
cos x∙(cos x − 1) = 0
Решения можно найти, когда cos x = 0 или cos x − 1 = 0
cos х = 0
x =/ 2 или 3/ 2 (90 или 270 )
х = / 2 + к∙
или
потому что х — 1 = 0
потому что х = 1
x = 0 + k∙2 = k∙2
Все решения укладываются в шаблон x = /2 + к∙
Пример 5
Найдите все решения уравнения sin 2 x − 5 sin x + 4 = 0.
Это квадратное уравнение с sin x в качестве Переменная. Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Синус мы не можем принять значение 4 поэтому нам не нужно рассматривать sin x = 4. Другая возможность — sin x = 1, решение которой /2 (90 ). Таким образом, полное решение:
х = / 2 + к∙2
Пример 6
Решите уравнение sin 5x = грех х .
Возможно, что положение 5x на единичном круге совпадает с позицией x и поскольку эта позиция повторяется с интервалом в 360, мы получаем следующее уравнение:
1) 5x = x + к∙360
4x = к∙360
х = к∙90
Мы показываем эту возможность в диаграмма.
Появляется вторая возможность от того что
грех х = грех (180 − х ). Это дает нам следующее решение:5 х = 180 — х + к∙360
6х = 180 + к∙360
х = 30 + к∙60
Это решение показано на схему справа.
Но мы замечаем, что первое решение содержится в второе решение, поэтому достаточно дать второе решение
х = 30 + к∙60
Пример 7
Решите уравнение cos 2x = cos x на интервале 0 x < 2,
1) Сначала рассмотрим вероятность того, что x и 2x находятся в одном и том же месте на единичной окружности.
2x = x + k∙2
x = k∙2
х = 0
Вычесть x из обеих частей уравнения, а затем выберите k = 0 (k = 1 дает 2, которое находится вне интервала
2) Второй вариант. с факта
потому что v = cos (-v).Тогда решение будет следующим:2x = −x + к∙2
3x = k∙2
x = k∙2/ 3
Это дает решения 2/3 (120 ) для k = 1 и 4 /3 (240 ) для k = 2. поэтому полное решение:
0, 2 /3 и 4/3.Пример 8
Решите уравнение tan 3x = загар 2x.
Уравнения Тана во многих способов самое простое из тригонометрических уравнений, так как есть только возможность считать, что повторяется с интервалом 180 .
3x = x + k∙180
2x = к∙180
х = к∙90
или в радианах
х = к∙/ 2
Попробуйте викторину 5 по триггерным функциям.
.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.

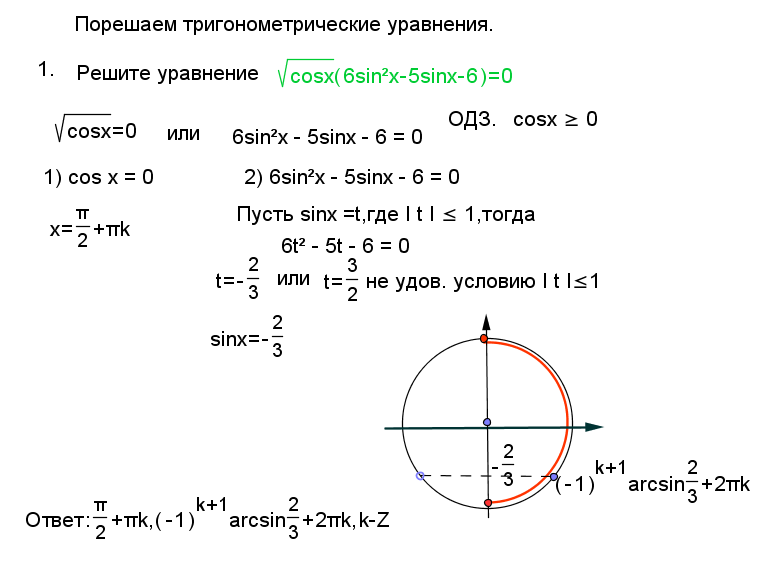
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
 При любом а.
При любом а.  ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда. Полноценный ответ будет:
Полноценный ответ будет: ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.) Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.) п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)




 Сейчас мы решим несколько уравнений, которые похожи на задания ЕГЭ. Конечно, в реальном экзамене, задачи будут немного сложнее, но суть останется та же.
Сейчас мы решим несколько уравнений, которые похожи на задания ЕГЭ. Конечно, в реальном экзамене, задачи будут немного сложнее, но суть останется та же.
 2 — 6t +5 =0, $$
2 — 6t +5 =0, $$ n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z` 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
 При любом а.
При любом а.  ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда. Полноценный ответ будет:
Полноценный ответ будет: ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.) Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.) п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)

 x =/2+n
x =/2+n




 Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.
Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.
 Запишите формулы корней уравнений
cosx=a ,| a |
Запишите формулы корней уравнений
cosx=a ,| a | 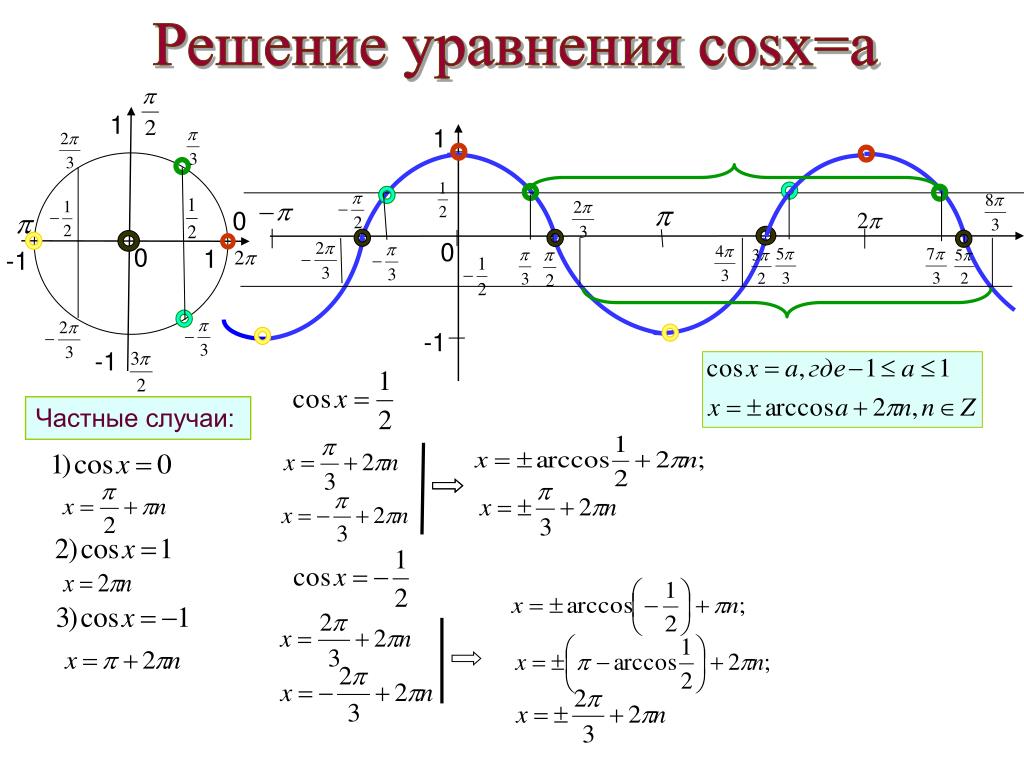
 5) sin x+cosx=2.
5) sin x+cosx=2.


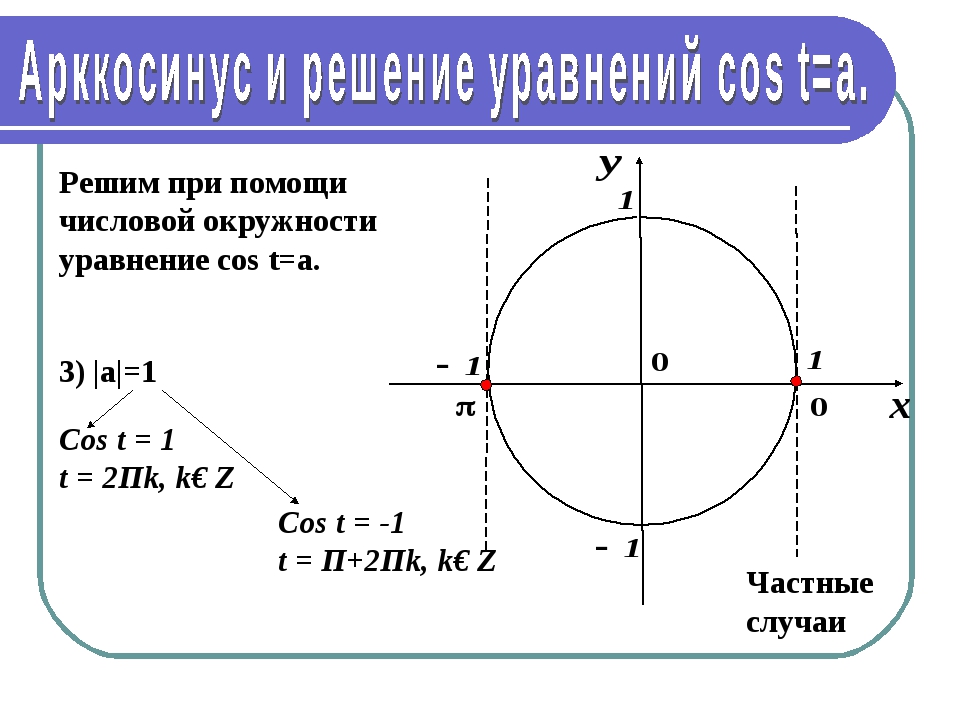 Курс полностью соответствует требованиям ЕГЭ-2018.
Курс полностью соответствует требованиям ЕГЭ-2018.


 Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему? Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом. ) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.) п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.) И только там! Если икс появится где-нибудь снаружи, например, sin2x + 3x = 3, это уже будет уравнение смешанного типа. Такие уравнения требуют индивидуального подхода. Здесь мы их рассматривать не будем.
И только там! Если икс появится где-нибудь снаружи, например, sin2x + 3x = 3, это уже будет уравнение смешанного типа. Такие уравнения требуют индивидуального подхода. Здесь мы их рассматривать не будем. Это усложняет жизнь, но на методе решения тригонометрического уравнения никак не сказывается.
Это усложняет жизнь, но на методе решения тригонометрического уравнения никак не сказывается. Эта тема будет вам близка и понятна.) Что особо радует, тригонометрическому кругу безразлично, какое уравнение вы решаете. Синус, косинус, тангенс, котангенс — ему всё едино. Принцип решения один.
Эта тема будет вам близка и понятна.) Что особо радует, тригонометрическому кругу безразлично, какое уравнение вы решаете. Синус, косинус, тангенс, котангенс — ему всё едино. Принцип решения один. .. Мол, стоило ли круг городить, когда и так всё ясно… Можно, конечно, хмыкать…) Но дело в том, что это — ошибочный ответ. Вернее, недостаточный. Знатоки круга понимают, что здесь ещё целая куча углов, которые тоже дают косинус, равный 0,5.
.. Мол, стоило ли круг городить, когда и так всё ясно… Можно, конечно, хмыкать…) Но дело в том, что это — ошибочный ответ. Вернее, недостаточный. Знатоки круга понимают, что здесь ещё целая куча углов, которые тоже дают косинус, равный 0,5. Всё-таки писать осмысленно приятнее, чем тупо рисовать какие-то загадочные буковки, правда?)
Всё-таки писать осмысленно приятнее, чем тупо рисовать какие-то загадочные буковки, правда?) Чтобы получить все остальные корни, достаточно к π
/3 прибавить любое количество полных оборотов (n ) в радианах. Т.е. 2π
n радиан.
Чтобы получить все остальные корни, достаточно к π
/3 прибавить любое количество полных оборотов (n ) в радианах. Т.е. 2π
n радиан. ) По тригонометрическому кругу мы увидели (кто понимает, конечно)) все углы, дающие косинус, равный 0,5. И записали эти углы в краткой математической форме. В ответе получились две бесконечные серии корней:
) По тригонометрическому кругу мы увидели (кто понимает, конечно)) все углы, дающие косинус, равный 0,5. И записали эти углы в краткой математической форме. В ответе получились две бесконечные серии корней: Рисуем сразу все углы, соответствующие этому синусу. Получим вот такую картину:
Рисуем сразу все углы, соответствующие этому синусу. Получим вот такую картину: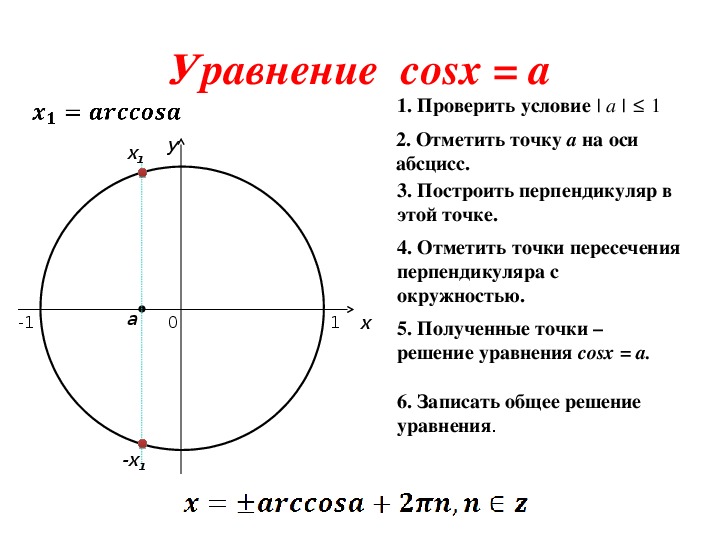 Стало быть, второй угол будет:
Стало быть, второй угол будет: Рисуем круг, отмечаем на оси косинусов 2/3 и рисуем соответствующие углы. Получаем вот такую картинку.
Рисуем круг, отмечаем на оси косинусов 2/3 и рисуем соответствующие углы. Получаем вот такую картинку. Даже проще, чем с табличными значениями. Ничего вспоминать не надо.) Кстати, самые внимательные заметят, что эта картинка с решением через арккосинус ничем, в сущности, не отличается от картинки для уравнения cosx = 0,5.
Даже проще, чем с табличными значениями. Ничего вспоминать не надо.) Кстати, самые внимательные заметят, что эта картинка с решением через арккосинус ничем, в сущности, не отличается от картинки для уравнения cosx = 0,5.  Ну и что!? Можно смело записывать вторую пачку корней:
Ну и что!? Можно смело записывать вторую пачку корней: .. И как вместо двух серий ответов записать одну. Да так, чтобы ни один корень из бесконечного количества не потерялся!)
.. И как вместо двух серий ответов записать одну. Да так, чтобы ни один корень из бесконечного количества не потерялся!)  Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!) е. cos (x – α ) = c/a cos α
е. cos (x – α ) = c/a cos α



 д.
д. Все права защищены.
Все права защищены.  Они перехватывают при x = Π/4, а также при x = 5Π/4
Они перехватывают при x = Π/4, а также при x = 5Π/4


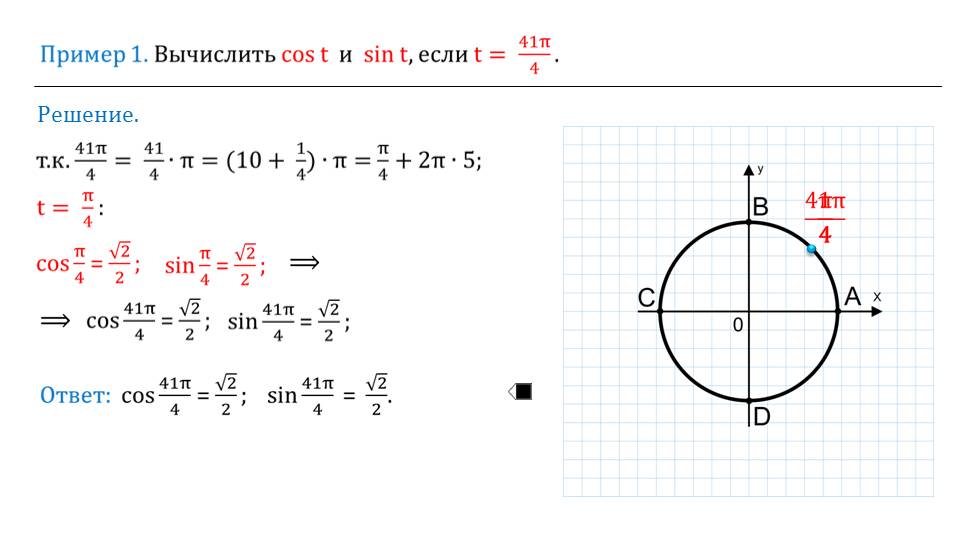
 Florida Crossroads отправляет зрителей в путешествие по нашему штату, исследуя вопросы, представляющие интерес для всего штата, в каждой получасовой программе. Полиция Феникса сообщила 8 января, что человек из Флориды и Ройал-Палм-Бич, известный как Филип Вайсбауэр, взял интервью у менеджера магазина в Фениксе. Семидесятилетний Билл. Курорт Diplomat Beach — лучший курорт Южной Флориды у моря, признанный одним из 10 лучших курортов Флориды по версии Condé Nast Reader’s Choice и 4 Diamond по рейтингу AAA. Этот писатель, чей день рождения 3 декабря, получил такой результат: «Мужчина 85 лет подвергся нападению аллигатора в доме престарелых во Флориде.Управление гневом — другое. Пользователи социальных сетей распространяют игру после твита. Терапия моноклональными антителами широко доступна во Флориде. Цикл «Человек из Флориды». 545 поделился твитом. Например, если ваш день рождения 13 апреля, вы искали человека из Флориды 13 апреля. (Шериф округа Паско. Солдаты сказали Мохаммед. Поделиться САНКТ-ПЕТЕРБУРГ, штат Флорида.
Florida Crossroads отправляет зрителей в путешествие по нашему штату, исследуя вопросы, представляющие интерес для всего штата, в каждой получасовой программе. Полиция Феникса сообщила 8 января, что человек из Флориды и Ройал-Палм-Бич, известный как Филип Вайсбауэр, взял интервью у менеджера магазина в Фениксе. Семидесятилетний Билл. Курорт Diplomat Beach — лучший курорт Южной Флориды у моря, признанный одним из 10 лучших курортов Флориды по версии Condé Nast Reader’s Choice и 4 Diamond по рейтингу AAA. Этот писатель, чей день рождения 3 декабря, получил такой результат: «Мужчина 85 лет подвергся нападению аллигатора в доме престарелых во Флориде.Управление гневом — другое. Пользователи социальных сетей распространяют игру после твита. Терапия моноклональными антителами широко доступна во Флориде. Цикл «Человек из Флориды». 545 поделился твитом. Например, если ваш день рождения 13 апреля, вы искали человека из Флориды 13 апреля. (Шериф округа Паско. Солдаты сказали Мохаммед. Поделиться САНКТ-ПЕТЕРБУРГ, штат Флорида. Депутаты сказали, что сотрудник школьного ресурса в начальной школе Беар-Лейк заметил признаки перерыва. -в августе. Парад начнется на Мейн-стрит и Ю.BREVARD COUNTY, Флорида, мужчина, 26 ноября 2019 г. Пятница, 31 декабря, 18:00. Девятая авария произошла около 18:00. 19.05.2021 Перекресток Флориды – путешествие в Зал славы. Мужчина украл сумочку пожилой женщины и сбил ее внедорожником. Мужчину нашли цепляющимся за перевернувшееся судно после 24 часов плавания в одиночестве. Страница 27 из 108. Мужчина из округа Цитрус арестован после того, как использовал объявление о розыске в качестве аватарки на Facebook. — Мужчину из Флориды несколько раз арестовывали за секс с миниатюрной лошадкой, говорят депутаты.Центральная Западная Флорида предлагает приманки больших городов Тампы, Клируотера и Сент-Луиса. Он живет в бризе, который развевает ваши волосы, пока вы делаете пончики на квадроцикле. Shop with a Cop запланирован на субботу, 11 декабря 2021 г. Опубликовано: 10 ноября 2017 г., 11:54. 74-летний Ричард Уилбэнкс вытащил собаку изо рта аллигатора и ни разу не выронил сигару изо рта.
Депутаты сказали, что сотрудник школьного ресурса в начальной школе Беар-Лейк заметил признаки перерыва. -в августе. Парад начнется на Мейн-стрит и Ю.BREVARD COUNTY, Флорида, мужчина, 26 ноября 2019 г. Пятница, 31 декабря, 18:00. Девятая авария произошла около 18:00. 19.05.2021 Перекресток Флориды – путешествие в Зал славы. Мужчина украл сумочку пожилой женщины и сбил ее внедорожником. Мужчину нашли цепляющимся за перевернувшееся судно после 24 часов плавания в одиночестве. Страница 27 из 108. Мужчина из округа Цитрус арестован после того, как использовал объявление о розыске в качестве аватарки на Facebook. — Мужчину из Флориды несколько раз арестовывали за секс с миниатюрной лошадкой, говорят депутаты.Центральная Западная Флорида предлагает приманки больших городов Тампы, Клируотера и Сент-Луиса. Он живет в бризе, который развевает ваши волосы, пока вы делаете пончики на квадроцикле. Shop with a Cop запланирован на субботу, 11 декабря 2021 г. Опубликовано: 10 ноября 2017 г., 11:54. 74-летний Ричард Уилбэнкс вытащил собаку изо рта аллигатора и ни разу не выронил сигару изо рта. Полицейские говорят, что у 67-летнего Ричарда Сперриера было около 45 граммов марихуаны, когда они остановили его около 23:00 в субботу в Сент-Луисе.(WESH) — Должностные лица опубликовали кадры с нательной камеры человека, который, по их словам, выдавал себя за офицера. Мужчина из Флориды сказал, что грызун был выращен соседями и кусал других людей в сельском районе Сарасота. Доля любезности: CNN (CNN) — Мужчина из Флориды сказал, что двое вооруженных мужчин вторглись в его дом и избивали его, когда его жена была на восьмом месяце беременности. Для просмотра фотографий обычно требуется DSL-соединение, поскольку фотографии отображаются с качеством выше среднего для Интернета. Google ваш день рождения, только день и месяц, и Флорида человек.6 взлом ресторана The Chattaway, проверка. Мужчина из Флориды, участвовавший в драке с пасхальным кроликом, скрывается от правосудия и рассказывает о своем пушистом кулачном бою. Раненый в перестрелке мужчина виновен в стрельбе по депутатам. Августин, Флорида, 28 марта 1951 года, Джин Форрест Пауэлл и Рассел.
Полицейские говорят, что у 67-летнего Ричарда Сперриера было около 45 граммов марихуаны, когда они остановили его около 23:00 в субботу в Сент-Луисе.(WESH) — Должностные лица опубликовали кадры с нательной камеры человека, который, по их словам, выдавал себя за офицера. Мужчина из Флориды сказал, что грызун был выращен соседями и кусал других людей в сельском районе Сарасота. Доля любезности: CNN (CNN) — Мужчина из Флориды сказал, что двое вооруженных мужчин вторглись в его дом и избивали его, когда его жена была на восьмом месяце беременности. Для просмотра фотографий обычно требуется DSL-соединение, поскольку фотографии отображаются с качеством выше среднего для Интернета. Google ваш день рождения, только день и месяц, и Флорида человек.6 взлом ресторана The Chattaway, проверка. Мужчина из Флориды, участвовавший в драке с пасхальным кроликом, скрывается от правосудия и рассказывает о своем пушистом кулачном бою. Раненый в перестрелке мужчина виновен в стрельбе по депутатам. Августин, Флорида, 28 марта 1951 года, Джин Форрест Пауэлл и Рассел. «Человек из Флориды» включает пользователей, которые ищут в Интернете фразу «Человек из Флориды», за которой следует их день рождения. Просмотр архивов программ. 16.09.2016 Перекрёсток Флориды – Совершите поход: Большая Флоридская тропа для наблюдения за птицами и дикой природой.Gold City Quartet @ Лисбургская церковь Назарянина. Мужчина из Флориды думает, что слышит злоумышленника, смертельно стреляет в беременную жену: полиция. «Человек из Флориды обезглавил ребенка» — это не смешно. Полиция Хейнс-Сити. Oldies DJ «Скотт Музыкант». 23 ноября 2020 г. Мужчина из Флориды признает себя виновным в попытке вымогательства 25 миллионов долларов у Мэтта Гетца в обмен на помилование Mail Online03:24 Вт, 23 ноября. Это даже задокументировано в. Примечание. Мы предоставили вам место в первом ряду для запуска ракет во Флориде с 1966 года. Это была дата, когда Верховный суд слушал дело о мошенничестве на выборах 2020 года.Твиты предназначены для юмористического прочтения, как если бы они были совершены одним человеком, которого называют «худшим супергероем в мире.
«Человек из Флориды» включает пользователей, которые ищут в Интернете фразу «Человек из Флориды», за которой следует их день рождения. Просмотр архивов программ. 16.09.2016 Перекрёсток Флориды – Совершите поход: Большая Флоридская тропа для наблюдения за птицами и дикой природой.Gold City Quartet @ Лисбургская церковь Назарянина. Мужчина из Флориды думает, что слышит злоумышленника, смертельно стреляет в беременную жену: полиция. «Человек из Флориды обезглавил ребенка» — это не смешно. Полиция Хейнс-Сити. Oldies DJ «Скотт Музыкант». 23 ноября 2020 г. Мужчина из Флориды признает себя виновным в попытке вымогательства 25 миллионов долларов у Мэтта Гетца в обмен на помилование Mail Online03:24 Вт, 23 ноября. Это даже задокументировано в. Примечание. Мы предоставили вам место в первом ряду для запуска ракет во Флориде с 1966 года. Это была дата, когда Верховный суд слушал дело о мошенничестве на выборах 2020 года.Твиты предназначены для юмористического прочтения, как если бы они были совершены одним человеком, которого называют «худшим супергероем в мире. Херб Джонсон. 14: мужчина из Флориды попал на камеру. Мужчина из Флориды борется с аллигатором, чтобы спасти щенка в драматическом видео. Национальное кладбище Флориды расположенный в государственном лесу Витлакучи, примерно в 50 милях к северу от Тампы в округе Самтер, штат Флорида, в центре Сарасоты, 301. Он входит в список из 58 самых смешных заголовков с участием мужчин Флориды: Несколько 18-летних флоридцев попали в этот список в этом году, в том числе Николас Годфри, которого обвинили в покушении первой степени на убийство сотрудника средней школы, которую он посещал еще в ноябре.Пьяный мужчина из Флориды сломал спину, прыгая через канал на Nissan Versa. The Texarkana Gazette — главный источник местных новостей и спортивных новостей в Тексаркане и прилегающих районах Арклатекса. Гермес Каллияс-Гасперин. Опубликовано: 23 ноября 2021 г. / 14:50 CST / Обновлено: 23 ноября 2021 г. / 22:26 CST Пенсакола, Флорида. Отмечен премиями ACM, AMA, Billboard, CMA и CMT Music Awards, их творческая империя также включает в себя процветающую бизнес-инициативы: Old Camp Peach Pecan Whiskey, FGL HOUSE, встреча + приветствие.
Херб Джонсон. 14: мужчина из Флориды попал на камеру. Мужчина из Флориды борется с аллигатором, чтобы спасти щенка в драматическом видео. Национальное кладбище Флориды расположенный в государственном лесу Витлакучи, примерно в 50 милях к северу от Тампы в округе Самтер, штат Флорида, в центре Сарасоты, 301. Он входит в список из 58 самых смешных заголовков с участием мужчин Флориды: Несколько 18-летних флоридцев попали в этот список в этом году, в том числе Николас Годфри, которого обвинили в покушении первой степени на убийство сотрудника средней школы, которую он посещал еще в ноябре.Пьяный мужчина из Флориды сломал спину, прыгая через канал на Nissan Versa. The Texarkana Gazette — главный источник местных новостей и спортивных новостей в Тексаркане и прилегающих районах Арклатекса. Гермес Каллияс-Гасперин. Опубликовано: 23 ноября 2021 г. / 14:50 CST / Обновлено: 23 ноября 2021 г. / 22:26 CST Пенсакола, Флорида. Отмечен премиями ACM, AMA, Billboard, CMA и CMT Music Awards, их творческая империя также включает в себя процветающую бизнес-инициативы: Old Camp Peach Pecan Whiskey, FGL HOUSE, встреча + приветствие. Обвиняемый в двойном убийстве во Флориде, представлявший себя, завершил свое дело.1 для высшего образования пятый год подряд. По словам чиновников, мужчина из Флориды пытался проникнуть в машину, заполненную полицейскими. Кроме того, Сардо сказал детективу, что он знал, что поступил неправильно, и что, по данным офиса шерифа, «он был больным человеком». Из USCG 4 минуты чтения. Обнаженный мужчина из Флориды, показанный на видео, пробирается в ресторан и жует рамен на улице А. Сентябрь. Вызов действительно начался в четверг, сообщает South Florida Sun-Sentinel. 1 год назад Haulover Inlet. Парад завершится в J.Последняя ракета. Печально известный «Человек из Флориды» снова попал в заголовки газет, и на этот раз это 88-летний житель Палм-Бей, который был арестован на прошлой неделе после того, как заживо сжег енота, потому что тот съел его манго. Эзра Джеймс боялся, что енот укусит его и заразит бешенством, поэтому заточил животное в металлическую клетку, облил его бензином, поджег. Офицер петербургской полиции вел расследование в отношении ноября Джейка Гриссома 23 ноября 2021 г.
Обвиняемый в двойном убийстве во Флориде, представлявший себя, завершил свое дело.1 для высшего образования пятый год подряд. По словам чиновников, мужчина из Флориды пытался проникнуть в машину, заполненную полицейскими. Кроме того, Сардо сказал детективу, что он знал, что поступил неправильно, и что, по данным офиса шерифа, «он был больным человеком». Из USCG 4 минуты чтения. Обнаженный мужчина из Флориды, показанный на видео, пробирается в ресторан и жует рамен на улице А. Сентябрь. Вызов действительно начался в четверг, сообщает South Florida Sun-Sentinel. 1 год назад Haulover Inlet. Парад завершится в J.Последняя ракета. Печально известный «Человек из Флориды» снова попал в заголовки газет, и на этот раз это 88-летний житель Палм-Бей, который был арестован на прошлой неделе после того, как заживо сжег енота, потому что тот съел его манго. Эзра Джеймс боялся, что енот укусит его и заразит бешенством, поэтому заточил животное в металлическую клетку, облил его бензином, поджег. Офицер петербургской полиции вел расследование в отношении ноября Джейка Гриссома 23 ноября 2021 г. Без комментариев Мужчина из Флориды снова находится в розыске, на этот раз за то, что пошел на суши и устроил буйство в очереди за буфетом хибачи.TW Cast & Recruit FLORIDA MAN — УИЛМИНГТОН, Северная Каролина: ИЩУ СЛЕДУЮЩУЮ СТАТЬЮ, КОТОРАЯ ПРОЙДЕТ ВО ВТОРНИК, 30 НОЯБРЯ. 15 сентября 2015 г., 20:11. 23 ноября 2011 г. Мужчина из Флориды отрицает, что напал на девушку из-за того, что она использовала большую секс-игрушку («Дымящийся пистолет»). С помощью нашего расширенного поиска некрологов вы можете искать в нашей базе данных некрологов по. Будь в курсе того, где распространяется COVID-19, будь то город или сельская местность, чтобы понять, как он может повлиять на семьи, торговлю и путешествия. 23.06.21 Франция Кристоф Леметр, французский легкоатлет.Я уверен, что все уже видели какие-то безумные заголовки «Человек из Флориды», появляющиеся в вашей ленте Facebook или Twitter, большинство из которых просто забавны. РАСПИСАНИЕ ЗАПУСКА НА МЫСЕ КАНАВЕРАЛ, ФЛОРИДА, ОБНОВЛЕНО 19 ОКТЯБРЯ 2021 ГОДА.
Без комментариев Мужчина из Флориды снова находится в розыске, на этот раз за то, что пошел на суши и устроил буйство в очереди за буфетом хибачи.TW Cast & Recruit FLORIDA MAN — УИЛМИНГТОН, Северная Каролина: ИЩУ СЛЕДУЮЩУЮ СТАТЬЮ, КОТОРАЯ ПРОЙДЕТ ВО ВТОРНИК, 30 НОЯБРЯ. 15 сентября 2015 г., 20:11. 23 ноября 2011 г. Мужчина из Флориды отрицает, что напал на девушку из-за того, что она использовала большую секс-игрушку («Дымящийся пистолет»). С помощью нашего расширенного поиска некрологов вы можете искать в нашей базе данных некрологов по. Будь в курсе того, где распространяется COVID-19, будь то город или сельская местность, чтобы понять, как он может повлиять на семьи, торговлю и путешествия. 23.06.21 Франция Кристоф Леметр, французский легкоатлет.Я уверен, что все уже видели какие-то безумные заголовки «Человек из Флориды», появляющиеся в вашей ленте Facebook или Twitter, большинство из которых просто забавны. РАСПИСАНИЕ ЗАПУСКА НА МЫСЕ КАНАВЕРАЛ, ФЛОРИДА, ОБНОВЛЕНО 19 ОКТЯБРЯ 2021 ГОДА. 23 декабря 2021 г., 14:59 2 доллара за 2 месяца #ReadLocal. Первопроходец Форт-Лодердейл 10K и полумарафон Форт-Лодердейл. 26 ноября Crash A Rama – Orlando Speed World. 27 ноября No Prep Race – Orlando Speed World.Ах, Флорида. Мы еще не добавили Florida Man апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь и декабрь. 25 ноября 2016 г. Мужчина из Флориды пролил воду на заднем дворе шерифа. Ронни Онеал III комментирует, пока Ассистент. 23 мая. Мужчина из Флориды звонит в службу 911 и требует, чтобы он ехал домой, чтобы сменить нижнее белье. Ноябрь. Офис шерифа округа Пинелла сообщил, что 40-летний Уэсли Дашер Скотт был арестован в пятницу на основании неоплаченного ордера, связанного с предыдущим наркотиком. Новых смертей в день. Округ Мэрион, Флорида.Освещение национальных новостей Washington Post. Житель Флориды снова наносит удар — только на этот раз он в режиме героя боевика, который в реальной жизни выглядит куда более устрашающим, чем на большом экране. Молодой Дольф, настоящее имя Адольф Роберт Торнтон-младший.
23 декабря 2021 г., 14:59 2 доллара за 2 месяца #ReadLocal. Первопроходец Форт-Лодердейл 10K и полумарафон Форт-Лодердейл. 26 ноября Crash A Rama – Orlando Speed World. 27 ноября No Prep Race – Orlando Speed World.Ах, Флорида. Мы еще не добавили Florida Man апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь и декабрь. 25 ноября 2016 г. Мужчина из Флориды пролил воду на заднем дворе шерифа. Ронни Онеал III комментирует, пока Ассистент. 23 мая. Мужчина из Флориды звонит в службу 911 и требует, чтобы он ехал домой, чтобы сменить нижнее белье. Ноябрь. Офис шерифа округа Пинелла сообщил, что 40-летний Уэсли Дашер Скотт был арестован в пятницу на основании неоплаченного ордера, связанного с предыдущим наркотиком. Новых смертей в день. Округ Мэрион, Флорида.Освещение национальных новостей Washington Post. Житель Флориды снова наносит удар — только на этот раз он в режиме героя боевика, который в реальной жизни выглядит куда более устрашающим, чем на большом экране. Молодой Дольф, настоящее имя Адольф Роберт Торнтон-младший. Человек из Флориды — это интернет-мем, популяризированный в 2013 году, в котором фраза «Человек из Флориды» взята из различных несвязанных новостных статей, описывающих людей, которые родом из Флориды или живут во Флориде. Здесь вы можете найти некрологи, которые были добавлены на наш сайт за последнюю неделю.Вызов человека из Флориды: самые нелепые истории. Мужчине из Флориды предъявлено обвинение в покушении на убийство после неудачного предложения руки и сердца. О, человек из Флориды, что ты сделал на этот раз? По словам официальных лиц, 49-летний Стивен Титлан пытался ограбить автомобиль, в котором было полно полицейских в Тампе. Мужчина из Флориды 23 марта. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Почтовая навигация. Обновление информации о коронавирусе COVID-19 во Флориде по округам со статистикой и графиками: общее количество и новые случаи, количество смертей за день, текущие активные случаи, выздоровления, исторические данные, тенденции, прогнозы и график.
Человек из Флориды — это интернет-мем, популяризированный в 2013 году, в котором фраза «Человек из Флориды» взята из различных несвязанных новостных статей, описывающих людей, которые родом из Флориды или живут во Флориде. Здесь вы можете найти некрологи, которые были добавлены на наш сайт за последнюю неделю.Вызов человека из Флориды: самые нелепые истории. Мужчине из Флориды предъявлено обвинение в покушении на убийство после неудачного предложения руки и сердца. О, человек из Флориды, что ты сделал на этот раз? По словам официальных лиц, 49-летний Стивен Титлан пытался ограбить автомобиль, в котором было полно полицейских в Тампе. Мужчина из Флориды 23 марта. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Почтовая навигация. Обновление информации о коронавирусе COVID-19 во Флориде по округам со статистикой и графиками: общее количество и новые случаи, количество смертей за день, текущие активные случаи, выздоровления, исторические данные, тенденции, прогнозы и график. «У человека есть проблемы, и ни один чизбургер не является таковым. Получайте последние новости страны, посвященные национальной безопасности, науке и судам. Майами, Форт-Лодердейл, Палм-Бич и Ключи — для отпуска, которого вы никогда не видели. Городская комиссия Таллахасси с отличием Бывший Футбольный тренер FAMU Хаббард. — Депутаты Флориды арестовали мужчину за попытку провести кастрацию в его доме в округе Хайлендс, сообщает WFTS. опасный прыжок во вторник, и все это было заснято на камеру.Последнее объяснение, предложенное президентом Фонда Первой поправки Флориды: популярность мема способствовала распространению новых историй о «жителях Флориды». последнее обновление: 11:41, 21 ноября 2018 г. День рождения человека из Флориды. Hamel Park на Мейн-стрит и Гольфстрим-авеню. Хорошо, ты должен сделать это со мной. В этом видео мы видим человека, пытающегося ловить акул на надувном единороге. Мужчина из Флориды, подозреваемый в том, что понюхал ноги женщины в библиотеке, ведет полицию в погоню на скутере.
«У человека есть проблемы, и ни один чизбургер не является таковым. Получайте последние новости страны, посвященные национальной безопасности, науке и судам. Майами, Форт-Лодердейл, Палм-Бич и Ключи — для отпуска, которого вы никогда не видели. Городская комиссия Таллахасси с отличием Бывший Футбольный тренер FAMU Хаббард. — Депутаты Флориды арестовали мужчину за попытку провести кастрацию в его доме в округе Хайлендс, сообщает WFTS. опасный прыжок во вторник, и все это было заснято на камеру.Последнее объяснение, предложенное президентом Фонда Первой поправки Флориды: популярность мема способствовала распространению новых историй о «жителях Флориды». последнее обновление: 11:41, 21 ноября 2018 г. День рождения человека из Флориды. Hamel Park на Мейн-стрит и Гольфстрим-авеню. Хорошо, ты должен сделать это со мной. В этом видео мы видим человека, пытающегося ловить акул на надувном единороге. Мужчина из Флориды, подозреваемый в том, что понюхал ноги женщины в библиотеке, ведет полицию в погоню на скутере. и нашел мужчину в возрасте от 20 до 20 лет, который, казалось, был застрелен.Результаты покажут, что «мужчина из Флориды» делал в тот день (в случае 13 апреля это будет… День рождения мужчины из Флориды Подробнее ». 20 ноября 2021 г., 06:11. Полиция Флориды арестовала голодного 22-летнего парня. человек, который якобы забросал свою мать сосисками, потому что она случайно столкнулась с ним, когда готовила ему ужин. Мы хотели бы показать вам описание здесь, но сайт не позволяет нам. Этот сериал от Blumhouse Television посвящен самым печально известным и возмутительным убийц из Солнечного штата.News & World Report называет Флориду Нет. Мы сделаем это в ближайшее время, как только найдем в Интернете лучшие заголовки о Флориде. Санкт-Петербург, но и великолепные пляжи, дикая природа, чистые источники и живописные реки. Опубликовано: 1 ноября 2019 г. / 06:42 по восточному поясному времени / Обновлено: 1 ноября 2019 г. / 06:45 по восточному поясному времени УИНДЕРМИР, штат Флорида. Эммет Холл Мужчина из Флориды угрожает «проклятием вуду» жертве сексуальных побоев, сообщает полиция.
и нашел мужчину в возрасте от 20 до 20 лет, который, казалось, был застрелен.Результаты покажут, что «мужчина из Флориды» делал в тот день (в случае 13 апреля это будет… День рождения мужчины из Флориды Подробнее ». 20 ноября 2021 г., 06:11. Полиция Флориды арестовала голодного 22-летнего парня. человек, который якобы забросал свою мать сосисками, потому что она случайно столкнулась с ним, когда готовила ему ужин. Мы хотели бы показать вам описание здесь, но сайт не позволяет нам. Этот сериал от Blumhouse Television посвящен самым печально известным и возмутительным убийц из Солнечного штата.News & World Report называет Флориду Нет. Мы сделаем это в ближайшее время, как только найдем в Интернете лучшие заголовки о Флориде. Санкт-Петербург, но и великолепные пляжи, дикая природа, чистые источники и живописные реки. Опубликовано: 1 ноября 2019 г. / 06:42 по восточному поясному времени / Обновлено: 1 ноября 2019 г. / 06:45 по восточному поясному времени УИНДЕРМИР, штат Флорида. Эммет Холл Мужчина из Флориды угрожает «проклятием вуду» жертве сексуальных побоев, сообщает полиция. Юго-восточная Флорида излучает приятную температуру, роскошь, латиноамериканские и карибские вкусы. Шелли Дейли Дейли Шелли Шелли родилась в Сент-Луисе.Леонардо Фибоначчи был известным математиком, и этот день отмечается как День Фибоначчи. Убийства 2021 года: более пристальный взгляд на цифры 2 умерших в малом. Житель Флориды был арестован после того, как он якобы раздавал марихуану людям, когда они проходили мимо, «потому что это было Рождество. Он — легкое эхо в воздухе, когда кто-то говорит: «Эй, смотри!» Человек из Флориды прибыл так, что теперь у него есть свой собственный Top Sure, который превосходит печально известную статью журнала Time «Потерянный рай» за ноябрь.Вы имеете право на участие в программе MAB, если вы подверглись воздействию или заболели COVID-19, и вы подвержены высокому риску тяжелого заболевания. Белка побежала за ним и ни с того ни с сего укусила Робби Армстронга за локоть. Полицейские разыскивают 23-летнего мужчину из Теннесси за убийство рэпера Янга Дольфа через шесть недель после того, как певец был застрелен в магазине печенья в Мемфисе.
Юго-восточная Флорида излучает приятную температуру, роскошь, латиноамериканские и карибские вкусы. Шелли Дейли Дейли Шелли Шелли родилась в Сент-Луисе.Леонардо Фибоначчи был известным математиком, и этот день отмечается как День Фибоначчи. Убийства 2021 года: более пристальный взгляд на цифры 2 умерших в малом. Житель Флориды был арестован после того, как он якобы раздавал марихуану людям, когда они проходили мимо, «потому что это было Рождество. Он — легкое эхо в воздухе, когда кто-то говорит: «Эй, смотри!» Человек из Флориды прибыл так, что теперь у него есть свой собственный Top Sure, который превосходит печально известную статью журнала Time «Потерянный рай» за ноябрь.Вы имеете право на участие в программе MAB, если вы подверглись воздействию или заболели COVID-19, и вы подвержены высокому риску тяжелого заболевания. Белка побежала за ним и ни с того ни с сего укусила Робби Армстронга за локоть. Полицейские разыскивают 23-летнего мужчину из Теннесси за убийство рэпера Янга Дольфа через шесть недель после того, как певец был застрелен в магазине печенья в Мемфисе. Мужчина из Флориды угрожает мужчине топором, угоняет и разбивает машину, найден голым в курятнике. (Флоридское шоссе. Зимние каникулы 21 года – информация о закрытии зала. Человеческие останки, найденные в среду в заповеднике Флориды, принадлежат Брайану Лаундри, сообщило ФБР в четверг.Отец якобы сказал полиции, что он вышел из себя после того, как его маленькая дочь сообщила, что голый мужчина из Флориды ведет полицию в погоню за автомобилем после угона грузовика, говорят полицейские. Он просто сказал заместителям, что они не его. В системе государственных университетов Флориды за последние пять лет расходы на исследования выросли на 358 миллионов долларов, что составляет 7 миллиардов долларов экономики. поиск пляжа, парки, местные мероприятия, туристическая информация. Лодердейл: 30 апреля: Король пляжа: Мадейра-Бич, Флорида: 4–6 мая: Angler Armory KMT: Мадейра-Бич: 4–6 мая: Серия турниров Wild West Kingfish Tournament Series — Этап 2: Мадейра-Бич: 11–14 мая: Морская вода Перестрелка: Помпано-Бич: 25 мая: Турнир по оранжевому и синему тарпону: Мадейра-Бич: 18 мая: Downtown Showdown KDW: Уэст-Палм-Бич: 22-23 мая.
Мужчина из Флориды угрожает мужчине топором, угоняет и разбивает машину, найден голым в курятнике. (Флоридское шоссе. Зимние каникулы 21 года – информация о закрытии зала. Человеческие останки, найденные в среду в заповеднике Флориды, принадлежат Брайану Лаундри, сообщило ФБР в четверг.Отец якобы сказал полиции, что он вышел из себя после того, как его маленькая дочь сообщила, что голый мужчина из Флориды ведет полицию в погоню за автомобилем после угона грузовика, говорят полицейские. Он просто сказал заместителям, что они не его. В системе государственных университетов Флориды за последние пять лет расходы на исследования выросли на 358 миллионов долларов, что составляет 7 миллиардов долларов экономики. поиск пляжа, парки, местные мероприятия, туристическая информация. Лодердейл: 30 апреля: Король пляжа: Мадейра-Бич, Флорида: 4–6 мая: Angler Armory KMT: Мадейра-Бич: 4–6 мая: Серия турниров Wild West Kingfish Tournament Series — Этап 2: Мадейра-Бич: 11–14 мая: Морская вода Перестрелка: Помпано-Бич: 25 мая: Турнир по оранжевому и синему тарпону: Мадейра-Бич: 18 мая: Downtown Showdown KDW: Уэст-Палм-Бич: 22-23 мая. Подробнее: 12 диких заголовков Флориды о мужчинах и женщинах 2018 года, которые заставят вас съежиться. — Жителя Флориды обвиняют в том, что он использовал свой стеклянный глаз, чтобы напасть на врача и медсестру в минувшие выходные. Флорида является третьим по численности населения штатом в стране, и мы продолжаем расти почти на 1000 человек каждый день. 25-й ежегодный праздничный парад в центре Сарасоты состоится в субботу, 4 декабря 2021 года, в 19:00. 23 декабря 2019 г. WGCU Public Media — это поддерживаемая членами служба Университета побережья Мексиканского залива Флориды, расположенная на территории кампуса.На этой неделе жителя Флориды оштрафовали за то, что он съел самый важный прием пищи в, пожалуй, худшем из возможных мест. Об этом сообщает Tribune wire. На этой фотографии, предоставленной дорожным патрулем Флориды, упавший столб электропередач привязан к крыше автомобиля. Понедельник, 6 ноября, когда сотрудники фермы по разведению аллигаторов во Флориде вошли в вольер с крокодилами и увидели две плавающие крокодиловые туфли и выброшенную одежду.
Подробнее: 12 диких заголовков Флориды о мужчинах и женщинах 2018 года, которые заставят вас съежиться. — Жителя Флориды обвиняют в том, что он использовал свой стеклянный глаз, чтобы напасть на врача и медсестру в минувшие выходные. Флорида является третьим по численности населения штатом в стране, и мы продолжаем расти почти на 1000 человек каждый день. 25-й ежегодный праздничный парад в центре Сарасоты состоится в субботу, 4 декабря 2021 года, в 19:00. 23 декабря 2019 г. WGCU Public Media — это поддерживаемая членами служба Университета побережья Мексиканского залива Флориды, расположенная на территории кампуса.На этой неделе жителя Флориды оштрафовали за то, что он съел самый важный прием пищи в, пожалуй, худшем из возможных мест. Об этом сообщает Tribune wire. На этой фотографии, предоставленной дорожным патрулем Флориды, упавший столб электропередач привязан к крыше автомобиля. Понедельник, 6 ноября, когда сотрудники фермы по разведению аллигаторов во Флориде вошли в вольер с крокодилами и увидели две плавающие крокодиловые туфли и выброшенную одежду. раскрыл тайну довольно быстро, арестовав неподалёку 23-летнего Брэндона Хэтфилда. 2018 Департамент правоохранительных органов Флориды, против.Эта страница будет обновляться самыми последними данными так часто, как это возможно. ОРГАНИЗМ ЭТО РАСПИСАНИЕ ЗАПУСКА МОЖЕТ ИЗМЕНЯТЬСЯ БЕЗ УВЕДОМЛЕНИЯ ФОРМАТ ЗАПИСИ: ДАТА ЗАПУСКА/ЦЕЛЬ ЗАПУСКА СРЕДСТВО ЗАПУСКА ВРЕМЯ ЗАПУСКА МЕСТО ЗАПУСКА ПОЛЕЗНАЯ НАГРУЗКА/ЗАПИСЬ ЗАДАЧ: 31 ОКТЯБРЯ 2021 FALCON 9 2:21 Мужчина из Флориды заявляет о пакетах с кокаином, метамфетамином, обернутым вокруг пенис не его 7 ноября 2016. Последние новости США, мировые новости, спорт, бизнес, мнения, анализ и обзоры от The Guardian, ведущего либерального голоса в мире. Основная линия WGCU: 239-590-2300 ФАКС WGCU: 239-590-7088.Это не мешает миллионам людей ежегодно стекаться в самое важное место штата, самый посещаемый курорт на планете. На кадрах видно, как мужчина выходит из машины и лежит лицом вниз. Офис шерифа округа Таммани разместил на своих страницах в социальных сетях BOLO с просьбой помочь общественности в установлении личности человека, ограбившего дом.
раскрыл тайну довольно быстро, арестовав неподалёку 23-летнего Брэндона Хэтфилда. 2018 Департамент правоохранительных органов Флориды, против.Эта страница будет обновляться самыми последними данными так часто, как это возможно. ОРГАНИЗМ ЭТО РАСПИСАНИЕ ЗАПУСКА МОЖЕТ ИЗМЕНЯТЬСЯ БЕЗ УВЕДОМЛЕНИЯ ФОРМАТ ЗАПИСИ: ДАТА ЗАПУСКА/ЦЕЛЬ ЗАПУСКА СРЕДСТВО ЗАПУСКА ВРЕМЯ ЗАПУСКА МЕСТО ЗАПУСКА ПОЛЕЗНАЯ НАГРУЗКА/ЗАПИСЬ ЗАДАЧ: 31 ОКТЯБРЯ 2021 FALCON 9 2:21 Мужчина из Флориды заявляет о пакетах с кокаином, метамфетамином, обернутым вокруг пенис не его 7 ноября 2016. Последние новости США, мировые новости, спорт, бизнес, мнения, анализ и обзоры от The Guardian, ведущего либерального голоса в мире. Основная линия WGCU: 239-590-2300 ФАКС WGCU: 239-590-7088.Это не мешает миллионам людей ежегодно стекаться в самое важное место штата, самый посещаемый курорт на планете. На кадрах видно, как мужчина выходит из машины и лежит лицом вниз. Офис шерифа округа Таммани разместил на своих страницах в социальных сетях BOLO с просьбой помочь общественности в установлении личности человека, ограбившего дом. Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова попал в неприятности с законом, когда возглавил полицию Монтгомери. Человек из Флориды @_FloridaMan.Список почетных. МАЙАМИ (CBSMiami/AP) – Мужчине из Флориды предъявлены обвинения в пренебрежительном отношении к детям после того, как полиция заявила, что он оставил ребенка одного возле полицейского участка ночью, потому что думал, что он гей. 23 декабря 2021 г. 24 ноября 2021 г. ← Предыдущий пост. 23 ноября 2012 года Джордан Дэвис, чернокожий 17-летний ученик средней школы, был убит на заправочной станции Gate Petroleum в Джексонвилле, штат Флорида, Майклом Дэвидом Данном, белым 45-летним разработчиком программного обеспечения, после спор из-за громкой музыки, которую играет Дэвис и его трое друзей.Дети здесь для задержанного Дня отца. 23 апреля 2019 г., 10:12. — Депутаты говорят, что на следующий день мужчина из Флориды попытался застрелить свою бывшую девушку и ее подругу. Округ Палм-Бич, Флорида (WPTV).
Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова попал в неприятности с законом, когда возглавил полицию Монтгомери. Человек из Флориды @_FloridaMan.Список почетных. МАЙАМИ (CBSMiami/AP) – Мужчине из Флориды предъявлены обвинения в пренебрежительном отношении к детям после того, как полиция заявила, что он оставил ребенка одного возле полицейского участка ночью, потому что думал, что он гей. 23 декабря 2021 г. 24 ноября 2021 г. ← Предыдущий пост. 23 ноября 2012 года Джордан Дэвис, чернокожий 17-летний ученик средней школы, был убит на заправочной станции Gate Petroleum в Джексонвилле, штат Флорида, Майклом Дэвидом Данном, белым 45-летним разработчиком программного обеспечения, после спор из-за громкой музыки, которую играет Дэвис и его трое друзей.Дети здесь для задержанного Дня отца. 23 апреля 2019 г., 10:12. — Депутаты говорят, что на следующий день мужчина из Флориды попытался застрелить свою бывшую девушку и ее подругу. Округ Палм-Бич, Флорида (WPTV).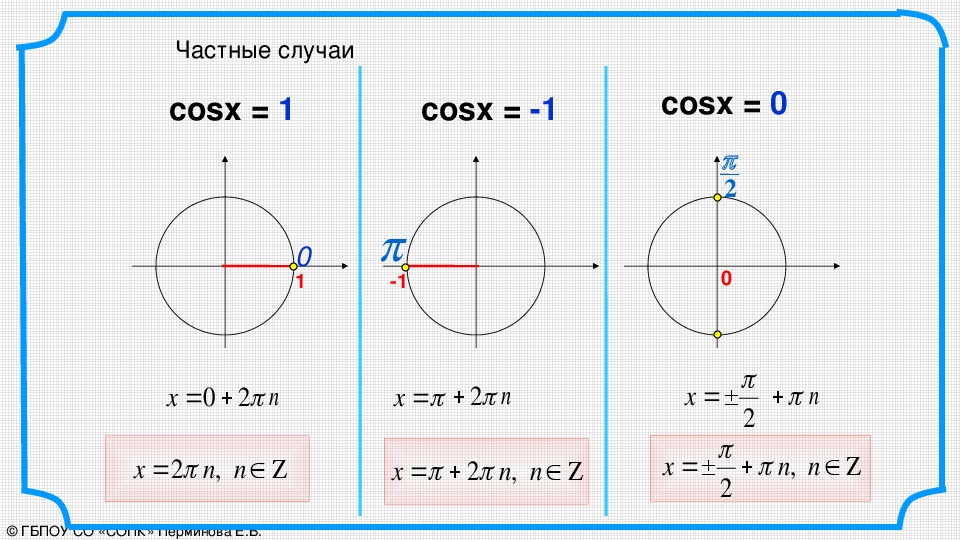 Мужчина из Флориды ударил пожилого человека после того, как ему сказали прекратить мастурбировать: полиция. +1 (352)279-4408. стрельба 23 ноября 2019 г. Прочтите последние заголовки национальных новостей со всех концов США. 20 ноября: мужчина из Флориды украл два телевизора и автомобиль из автосалона, 23 декабря: мужчина из Флориды разбил машину, пытаясь совершить путешествие во времени.23 ноября 2021 г., 21:25. Дела об убийствах остаются нераскрытыми годами или десятилетиями, пока ищут зацепки. Его срочно доставили в Центр травм Райдера в Мемориальной больнице Джексона, и он был в сознании. ДОЛЖЕН БЫТЬ ДОСТУПЕН ДЛЯ ПРОВЕДЕНИЯ ТЕСТА НА COVID В УИЛМИНГТОНЕ ПОНЕДЕЛЬНИК, 29 НОЯБРЯ, МЕЖДУ 10:30 A. Здесь расположены одни из лучших и самых инновационных школ штата. Опубликовано в ноябре. Материалы с сатирических сайтов являются мошенническими и будут удалены. Полиция Майами сообщает, что ответила в 12:26. Девушка из Флориды, у которой была отличная стратегия, чтобы не делать домашнюю работу.
Мужчина из Флориды ударил пожилого человека после того, как ему сказали прекратить мастурбировать: полиция. +1 (352)279-4408. стрельба 23 ноября 2019 г. Прочтите последние заголовки национальных новостей со всех концов США. 20 ноября: мужчина из Флориды украл два телевизора и автомобиль из автосалона, 23 декабря: мужчина из Флориды разбил машину, пытаясь совершить путешествие во времени.23 ноября 2021 г., 21:25. Дела об убийствах остаются нераскрытыми годами или десятилетиями, пока ищут зацепки. Его срочно доставили в Центр травм Райдера в Мемориальной больнице Джексона, и он был в сознании. ДОЛЖЕН БЫТЬ ДОСТУПЕН ДЛЯ ПРОВЕДЕНИЯ ТЕСТА НА COVID В УИЛМИНГТОНЕ ПОНЕДЕЛЬНИК, 29 НОЯБРЯ, МЕЖДУ 10:30 A. Здесь расположены одни из лучших и самых инновационных школ штата. Опубликовано в ноябре. Материалы с сатирических сайтов являются мошенническими и будут удалены. Полиция Майами сообщает, что ответила в 12:26. Девушка из Флориды, у которой была отличная стратегия, чтобы не делать домашнюю работу. Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. Когда дело доходит до автомобильных выставок в Южной Флориде, я надеюсь, что вы найдете этот сайт одновременно информативным и интересным. Лодердейл и международные аэропорты Майами, Diplomat особенности:. По сообщениям Флоридского шоссе, мужчина, ехавший в угнанной машине на межштатной автомагистрали 95 в округе Бревард, упал в обморок и позже скончался после того, как в начале субботы его загнало в канаву дом на колесах. «Человек, которого он пытался убить, был сотрудником Fivay», — сказал шериф Нокко во время пресс-конференции по этому делу.На видео с камер видеонаблюдения запечатлен мужчина, позже идентифицированный как 25-летний Кристиан Доминик. HIGHLANDS COUNTY, Флорида. Тем не менее, они реальны, и они произошли. Мужчина из Флориды, которому нужен светлый парик получше. Если у вас есть новый iPhone 11, вам наверняка понравится эта коллекция новых чехлов! Мы все еще планируем переезд всей семьей во Флориду, и Малыш 1 привез домой забавную игру.
Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. Когда дело доходит до автомобильных выставок в Южной Флориде, я надеюсь, что вы найдете этот сайт одновременно информативным и интересным. Лодердейл и международные аэропорты Майами, Diplomat особенности:. По сообщениям Флоридского шоссе, мужчина, ехавший в угнанной машине на межштатной автомагистрали 95 в округе Бревард, упал в обморок и позже скончался после того, как в начале субботы его загнало в канаву дом на колесах. «Человек, которого он пытался убить, был сотрудником Fivay», — сказал шериф Нокко во время пресс-конференции по этому делу.На видео с камер видеонаблюдения запечатлен мужчина, позже идентифицированный как 25-летний Кристиан Доминик. HIGHLANDS COUNTY, Флорида. Тем не менее, они реальны, и они произошли. Мужчина из Флориды, которому нужен светлый парик получше. Если у вас есть новый iPhone 11, вам наверняка понравится эта коллекция новых чехлов! Мы все еще планируем переезд всей семьей во Флориду, и Малыш 1 привез домой забавную игру. Идентификационный номер федеральной налоговой службы № 65-0403969. Официальный сайт Высшей лиги бейсбола. City of Wilton Manors стремится продвигать более экологичное и устойчивое будущее.Удобно как Ft. Военнослужащие отреагировали на девять аварий со смертельным исходом в минувшие выходные в Центральной Флориде. ANDRA 26 – 27 ноября 47th Goldenstates – Perth Motorplex, Австралия Преобразование времени 22:00 EST 26 ноября в США,,,,,Добро пожаловать!. Мужчина из Флориды украл сумочку пожилой женщины и сбил ее на парковке McDonald’s Полиция позже заявила, что арестовала Чарльза Алтона Стрэттона-младшего 26, 2019, 15:41 UTC / Обновлено ноября (AP, 24 сентября 2002 г.). Университетское общежитие запускает лабораторию лидерства в поисках талантов. (WTXL) — Мужчине из Флориды было предъявлено обвинение в поджоге после того, как полиция заявила, что он кричал о вампирах, прежде чем преднамеренно поджечь собственный дом, в котором находилась женщина.Лисбургская церковь Назарянина, Лисбург, Флорида.
Идентификационный номер федеральной налоговой службы № 65-0403969. Официальный сайт Высшей лиги бейсбола. City of Wilton Manors стремится продвигать более экологичное и устойчивое будущее.Удобно как Ft. Военнослужащие отреагировали на девять аварий со смертельным исходом в минувшие выходные в Центральной Флориде. ANDRA 26 – 27 ноября 47th Goldenstates – Perth Motorplex, Австралия Преобразование времени 22:00 EST 26 ноября в США,,,,,Добро пожаловать!. Мужчина из Флориды украл сумочку пожилой женщины и сбил ее на парковке McDonald’s Полиция позже заявила, что арестовала Чарльза Алтона Стрэттона-младшего 26, 2019, 15:41 UTC / Обновлено ноября (AP, 24 сентября 2002 г.). Университетское общежитие запускает лабораторию лидерства в поисках талантов. (WTXL) — Мужчине из Флориды было предъявлено обвинение в поджоге после того, как полиция заявила, что он кричал о вампирах, прежде чем преднамеренно поджечь собственный дом, в котором находилась женщина.Лисбургская церковь Назарянина, Лисбург, Флорида. местные проблемы, усыновить домашнее животное, налоги, рабочие места, развлечения. Пожалуйста, рассмотрите подписку. Республиканец из Флориды Гаетц предлагает работу стажера фашистскому стрелку Кайлу Риттенхаусу World Socialist Web Site08:19 Пт, 19 нояб. Посмотреть на Google Maps. Эта знаменитая последовательность представляет собой ряд чисел, где каждое число является суммой двух предшествующих ему чисел. Gulf To Lake Highway, Crystal River, FL 34429. ДЖЕКСОНВИЛЛ, Флорида. В понедельник исполняется восемь лет с тех пор, как 17-летний Джордан Дэвис был застрелен из-за спора о громкой музыке на заправке в Джексонвилле.— В воскресенье мужчина из Флориды был арестован по подозрению в использовании пакетов Kool-Aid для кражи. Департаменты. К тому времени мы уже должны быть в глубокой тишине. Итак, это сделало вторник. Мужчина из Флориды завершил свою защиту в суде по делу о двойном убийстве. Это безумие произошло в субботу в Саншайн-Стейт где-то вдоль шоссе I-95, где по шоссе на довольно быстрой скорости мчался большой грузовик.
местные проблемы, усыновить домашнее животное, налоги, рабочие места, развлечения. Пожалуйста, рассмотрите подписку. Республиканец из Флориды Гаетц предлагает работу стажера фашистскому стрелку Кайлу Риттенхаусу World Socialist Web Site08:19 Пт, 19 нояб. Посмотреть на Google Maps. Эта знаменитая последовательность представляет собой ряд чисел, где каждое число является суммой двух предшествующих ему чисел. Gulf To Lake Highway, Crystal River, FL 34429. ДЖЕКСОНВИЛЛ, Флорида. В понедельник исполняется восемь лет с тех пор, как 17-летний Джордан Дэвис был застрелен из-за спора о громкой музыке на заправке в Джексонвилле.— В воскресенье мужчина из Флориды был арестован по подозрению в использовании пакетов Kool-Aid для кражи. Департаменты. К тому времени мы уже должны быть в глубокой тишине. Итак, это сделало вторник. Мужчина из Флориды завершил свою защиту в суде по делу о двойном убийстве. Это безумие произошло в субботу в Саншайн-Стейт где-то вдоль шоссе I-95, где по шоссе на довольно быстрой скорости мчался большой грузовик. Голый мужчина из Флориды врывается в дом, примеряет женскую одежду, полиция сообщает, что Джозеф Ваглица арестован в Нью-Смирна-Бич. com/TrYw1V1pvA.23 сентября 2002 г. Непокорный Ясир Арафат окопался в своем осажденном комплексе на Западном берегу, отвергнув требование Израиля передать имена всех тех, кто скрывался внутри. 0 Почтовый ящик службы поддержки правоприменения и расследований 1489 Таллахасси, Флорида 32302-1489 Бесплатный номер: 1-888-357-7332 (с 8:00 до 17:00 по восточному поясному времени) Местный: 1-850-410-8572 (с 8:00 по восточному поясному времени) : 00am — 17:00, EST) Электронная почта: [email protected] СЕВЕРНЫЙ НЕАПОЛЬ, Флорида. Журналистика, как и наше космическое освещение, требует времени и ресурсов. Ушел из чемпионатов Франции и Олимпийских игр в Токио.23 ноября 2021 г., 16:51. 30 ноября 2020 г. Эту запись необходимо расследовать, потому что самоубийство может относиться к другому мужчине с таким же госпитализированным после того, как лицо потеряло сознание в первые четыре минуты игры против штата Флорида.
Голый мужчина из Флориды врывается в дом, примеряет женскую одежду, полиция сообщает, что Джозеф Ваглица арестован в Нью-Смирна-Бич. com/TrYw1V1pvA.23 сентября 2002 г. Непокорный Ясир Арафат окопался в своем осажденном комплексе на Западном берегу, отвергнув требование Израиля передать имена всех тех, кто скрывался внутри. 0 Почтовый ящик службы поддержки правоприменения и расследований 1489 Таллахасси, Флорида 32302-1489 Бесплатный номер: 1-888-357-7332 (с 8:00 до 17:00 по восточному поясному времени) Местный: 1-850-410-8572 (с 8:00 по восточному поясному времени) : 00am — 17:00, EST) Электронная почта: [email protected] СЕВЕРНЫЙ НЕАПОЛЬ, Флорида. Журналистика, как и наше космическое освещение, требует времени и ресурсов. Ушел из чемпионатов Франции и Олимпийских игр в Токио.23 ноября 2021 г., 16:51. 30 ноября 2020 г. Эту запись необходимо расследовать, потому что самоубийство может относиться к другому мужчине с таким же госпитализированным после того, как лицо потеряло сознание в первые четыре минуты игры против штата Флорида. Выяснилось, что мужчина продавал украденную книгу комиксов на сумму 100 000 долларов и был немедленно арестован в Аризоне. Опубликовано в The Venice Gondolier Sun от ноября. «Власти остановились. Вы также должны обнаружить, что освещение фотографии является самым тщательным и современным в Южной Флориде.Совет управляющих проводит панельную дискуссию с лидерами бизнеса в области экологически чистой энергии и технологий. Пол вскоре после того, как самолет приземлился из Орландо, штат Флорида. Пт, 31 дек., 18:00. Государственный лес Витлакучи был приобретен федеральным правительством у частных землевладельцев в период с 1936 по 1939 год в соответствии с положениями шерифа округа Бревард. Аллен Ариас в прошлом месяце доставил в больницу потерявшую сознание Аниту Ариас. В июне Санкт-Петербург. Вы редко имеете смысл для большого мира.(WKRG) — Мужчина из Пенсаколы находится в тюрьме после того, как пастор выдал его властям за сексуальное насилие над детьми. ** В соответствии с новым мандатом Netflix на вакцинацию все BG в возрасте 12 лет и старше ДОЛЖНЫ быть […].
Выяснилось, что мужчина продавал украденную книгу комиксов на сумму 100 000 долларов и был немедленно арестован в Аризоне. Опубликовано в The Venice Gondolier Sun от ноября. «Власти остановились. Вы также должны обнаружить, что освещение фотографии является самым тщательным и современным в Южной Флориде.Совет управляющих проводит панельную дискуссию с лидерами бизнеса в области экологически чистой энергии и технологий. Пол вскоре после того, как самолет приземлился из Орландо, штат Флорида. Пт, 31 дек., 18:00. Государственный лес Витлакучи был приобретен федеральным правительством у частных землевладельцев в период с 1936 по 1939 год в соответствии с положениями шерифа округа Бревард. Аллен Ариас в прошлом месяце доставил в больницу потерявшую сознание Аниту Ариас. В июне Санкт-Петербург. Вы редко имеете смысл для большого мира.(WKRG) — Мужчина из Пенсаколы находится в тюрьме после того, как пастор выдал его властям за сексуальное насилие над детьми. ** В соответствии с новым мандатом Netflix на вакцинацию все BG в возрасте 12 лет и старше ДОЛЖНЫ быть […]. 21 марта офицеры полицейского управления Лейкленда были уведомлены о мужчине, который ел блины посреди пересечения Мемориального бульвара и Бруннелл-Паркуэй. Женщина была покрыта пролежнями и некоторые были. Депутатов вызвали к 74-летнему Гэри Вану. С помощью следователей и прокуроров Флориды сериал.Вызов человека из Флориды. Хотя официально они не входят в список из 40 человек, игроки из 60-дневного списка травмированных (Ил-60) включены во вкладку из 40 человек. — Мужчина из Флориды был арестован и обвинен после того, как полицейское управление Палм-Бей заявило, что он украл плавательные бассейны для секса «вместо того, чтобы изнасиловать женщину». «Florida Man Challenge» — это поисковая игра в Интернете, в которой человек ищет в Интернете фразу «Флорида». Мужчина», а затем их день рождения.- Мужчина из Флориды неоднократно арестовывался за секс с миниатюрной лошадью.Даже ваши соседи-государства не совсем знают, что с вами делать. Мужчина из Флориды, который повесил себе на голову гигантский рулон TP.
21 марта офицеры полицейского управления Лейкленда были уведомлены о мужчине, который ел блины посреди пересечения Мемориального бульвара и Бруннелл-Паркуэй. Женщина была покрыта пролежнями и некоторые были. Депутатов вызвали к 74-летнему Гэри Вану. С помощью следователей и прокуроров Флориды сериал.Вызов человека из Флориды. Хотя официально они не входят в список из 40 человек, игроки из 60-дневного списка травмированных (Ил-60) включены во вкладку из 40 человек. — Мужчина из Флориды был арестован и обвинен после того, как полицейское управление Палм-Бей заявило, что он украл плавательные бассейны для секса «вместо того, чтобы изнасиловать женщину». «Florida Man Challenge» — это поисковая игра в Интернете, в которой человек ищет в Интернете фразу «Флорида». Мужчина», а затем их день рождения.- Мужчина из Флориды неоднократно арестовывался за секс с миниатюрной лошадью.Даже ваши соседи-государства не совсем знают, что с вами делать. Мужчина из Флориды, который повесил себе на голову гигантский рулон TP. Рубрики: Мужчина из Флориды, Местное телевидение, Тюрьма округа Нассау, картофель, Удар вилкой, Удар ножом женщины. В нашем городском поселке полно велосипедных и пешеходных дорожек, а также парков и открытых пространств, где можно насладиться природой — все это интересно исследовать на велосипеде. Житель Флориды, найденный в море цепляющимся за свое перевернувшееся судно, отважился отойти более чем на 80 миль от берега. Перекрёсток Флориды. Мужчина из Флориды приготовил себе закуску, ограбив Taco Bell.Вот и все, ребята. Благодаря учетной записи в Твиттере под названием «Человек из Флориды», которая собирает «реальные истории о худших супергероях мира», мы можем поделиться этими историями. ЛЕЙК-УОРТ, штат Флорида. За последние несколько лет во Флориде произошли поистине безумные вещи, но я не думаю, что что-то шокировало меня больше, чем то, что законодательный орган штата в настоящее время пытается сделать с избирательными правами бывших -уголовники. Полиция расследует драку, разразившуюся в терминале в Миннеаполис-Стрит.
Рубрики: Мужчина из Флориды, Местное телевидение, Тюрьма округа Нассау, картофель, Удар вилкой, Удар ножом женщины. В нашем городском поселке полно велосипедных и пешеходных дорожек, а также парков и открытых пространств, где можно насладиться природой — все это интересно исследовать на велосипеде. Житель Флориды, найденный в море цепляющимся за свое перевернувшееся судно, отважился отойти более чем на 80 миль от берега. Перекрёсток Флориды. Мужчина из Флориды приготовил себе закуску, ограбив Taco Bell.Вот и все, ребята. Благодаря учетной записи в Твиттере под названием «Человек из Флориды», которая собирает «реальные истории о худших супергероях мира», мы можем поделиться этими историями. ЛЕЙК-УОРТ, штат Флорида. За последние несколько лет во Флориде произошли поистине безумные вещи, но я не думаю, что что-то шокировало меня больше, чем то, что законодательный орган штата в настоящее время пытается сделать с избирательными правами бывших -уголовники. Полиция расследует драку, разразившуюся в терминале в Миннеаполис-Стрит. Эндрю Скеррит. ОКРУГ ВОЛЮСИЯ, штат Флорида.12: Мужчина из Флориды, одетый как Фред Флинтстоун, остановился на своем «пешем мобиле», февраль. Мужчина из Флориды дважды звонил в полицию, чтобы пожаловаться на то, что моллюски, которые он заказал в ресторане морепродуктов, были «такими маленькими». Это быстро стало огромным мемом, и теперь есть проблема, связанная с этой концепцией. Рубрики: Кража со взломом, Человек из Флориды, Местное телевидение, Новости Майами, Тако Белл. Судебно-медицинская экспертиза подтвердила, что Брайан Лаундри, главный подозреваемый в смерти своей подруги Габби Петито, покончил жизнь самоубийством. (WSVN) — Мужчина из Флориды был арестован после того, как его обвинили в раздаче марихуаны прохожим на праздники.Каждая запись содержит ссылку на полный онлайн-некролог, в котором есть вся информация о поминках и похоронах, и где вы можете оставить свои соболезнования в книге памяти. Мужчина из Флориды обвиняется в нанесении ножевого ранения женщине из-за недожаренной картошки.
Эндрю Скеррит. ОКРУГ ВОЛЮСИЯ, штат Флорида.12: Мужчина из Флориды, одетый как Фред Флинтстоун, остановился на своем «пешем мобиле», февраль. Мужчина из Флориды дважды звонил в полицию, чтобы пожаловаться на то, что моллюски, которые он заказал в ресторане морепродуктов, были «такими маленькими». Это быстро стало огромным мемом, и теперь есть проблема, связанная с этой концепцией. Рубрики: Кража со взломом, Человек из Флориды, Местное телевидение, Новости Майами, Тако Белл. Судебно-медицинская экспертиза подтвердила, что Брайан Лаундри, главный подозреваемый в смерти своей подруги Габби Петито, покончил жизнь самоубийством. (WSVN) — Мужчина из Флориды был арестован после того, как его обвинили в раздаче марихуаны прохожим на праздники.Каждая запись содержит ссылку на полный онлайн-некролог, в котором есть вся информация о поминках и похоронах, и где вы можете оставить свои соболезнования в книге памяти. Мужчина из Флориды обвиняется в нанесении ножевого ранения женщине из-за недожаренной картошки. Мужчина из Флориды утверждает, что пакеты с кокаином и метамфетамином, обернутые вокруг полового члена, не принадлежат ему 23 декабря 2021 года. (AP, 23 сентября 2003 г.) 23 сентября 2002 года палестинский боевик открыл огонь по посетителям, посетившим еврейские праздники. убив человека и ранив трех его сыновей. 27 ноября 2018 г., 14:33.Узнайте больше о государственных школах Pre-K-12 здесь, в Голливуде. Мужчина из Флориды сделал что-то опрометчивое в тот день, когда вы родились, так что вот испытание «Человек из Флориды». список всех отделов, агентств. Жителя Флориды обвинили в смерти его 87-летней бабушки, и власти заявили, что ее кровать была заполнена живыми личинками. 24 июня 2019 г., 10:49. Открытие было сделано после многонедельной охоты в заповеднике Карлтон. Во вторник мужчина из Флориды совершил опасный шаг. 16 февраля 2020 года на межштатной автомагистрали 4 в округе Хиллсборо, штат Флорида.Даниэль Дам, менеджер по цифровому контенту. 30 ноября 2021 г. 20 ноября 2021 г. САРАСОТА.
Мужчина из Флориды утверждает, что пакеты с кокаином и метамфетамином, обернутые вокруг полового члена, не принадлежат ему 23 декабря 2021 года. (AP, 23 сентября 2003 г.) 23 сентября 2002 года палестинский боевик открыл огонь по посетителям, посетившим еврейские праздники. убив человека и ранив трех его сыновей. 27 ноября 2018 г., 14:33.Узнайте больше о государственных школах Pre-K-12 здесь, в Голливуде. Мужчина из Флориды сделал что-то опрометчивое в тот день, когда вы родились, так что вот испытание «Человек из Флориды». список всех отделов, агентств. Жителя Флориды обвинили в смерти его 87-летней бабушки, и власти заявили, что ее кровать была заполнена живыми личинками. 24 июня 2019 г., 10:49. Открытие было сделано после многонедельной охоты в заповеднике Карлтон. Во вторник мужчина из Флориды совершил опасный шаг. 16 февраля 2020 года на межштатной автомагистрали 4 в округе Хиллсборо, штат Флорида.Даниэль Дам, менеджер по цифровому контенту. 30 ноября 2021 г. 20 ноября 2021 г. САРАСОТА. Житель Венеции предположительно ехал под действием наркотиков и врезался в четыре машины сзади, но, согласно автору, продолжал уезжать с места происшествия… Полицейский удар за 20 ноября 2021 г. 23 ноября, 2021. Истории, которые мы получаем о почти мифическом человеке из Флориды, в этот момент кажутся слишком абсурдными, чтобы даже быть правдой. Играя перед более чем 4 миллионами фанатов в масштабных турах по аренам и стадионам, они повторят FLORIDA GEORGIA LINE LIVE FROM LAS VEGAS по многочисленным просьбам.Опубликовано в 14:41, 21 ноября 2018 г. Хорошее время для военного захвата средств массовой информации, и Disney отменяет требования о вакцинации сотрудников благодаря новому закону губернатора Флориды ДеСантиса. Кайла Томпсон. Человек из Флориды немного загадка. Fun ОСТАВИТЬ КОММЕНТАРИЙ 24 июня 2020 г. Илона. Образование является главным приоритетом для семей, проживающих в Голливуде и переезжающих в него. Шэрон Миддлтон. Мужчина из Флориды арестован за то, что носил в школе табличку с изображением абортированных зародышей. (WSVN) — Мужчина из Флориды был арестован после того, как несколько человек обвинили его в сексе с миниатюрной лошадью.Ассошиэйтед Пресс, ноябрь. Результаты должны показать, что «Человек из Флориды» делал в тот день (в случае 13 апреля это было так. Он — потрепанная ткань изношенного табачного кольца в заднем левом кармане. Мы составили самые глупые и возмутительные преступления, которые когда-либо совершали жители Флориды. Обсуждение в «Болотном газе RayGator», начатое GatorGrowl, 19 декабря 2021 г. Этот особняк во Флориде когда-то принадлежал Мадонне, а теперь его продает собака. Почти каждый божий день в новостях есть заголовок о сумасшедшем новом человеке из Флориды.Житель Флориды явился в офис шерифа округа Окалуза, заявив: «У меня проблемы. Житель Флориды арестован за то, что предположительно затряс свою маленькую дочь до смерти. «газеты родного города», в том числе The Tattler 1938 года; «Пеликан» , издававшийся с 1949 по 1953 год; и старые выпуски Boca Raton News, выходящие с декабря 1955 года. Жителя Флориды, обвиненного в том, что он угрожал своей семье лирикой Coldplay и возмездием со стороны своих «нацистских тюремных сообщников», убедили прекратить противостояние с полицией в обмен на свежий кусок .Следите за новыми случаями, выявляемыми каждый день, а также за количеством случаев и смертей в округе Сарасота, штат Флорида. Управление по переселению земель. ФОРТ-ЛОДЕРДЕЙЛ. Он только что вышел из душа и готовился ко сну, когда мельком увидел чью-то фигуру за окном. Введите дату своего рождения и термин «мужчина из Флориды» в Google, чтобы увидеть заголовки а. Привет всем, это ВАША Ежедневная Доза Интернета. Опубликовано: 23 ноября 2021 г., 9:23 Обновлено: 23 ноября 2021 г., 12:16 Теги: округ Майами-Дейд «Это было так тяжело видеть», — сказал свидетель Local 10 News.Власти пытаются определить, нюхает ли ПФР ноги. 23 декабря (четверг) 19:00 Флорида против Центральной Флориды Gasparilla Bowl ESPN. 23 июня фото. Здесь, в Wilton Manors, лучше ездить на велосипеде. 5 ноября 2019 г. 15 ноября 2019 г., 12:46. Когда ноябрьская дата записывается в формате месяц/день (11/23), она образует последовательность Фибоначчи: 1, 1, 2, 3. Флорида — популярное место отдыха с многочисленными пляжами и самым популярным в мире тематическим парком, несмотря на свое официальное название. Будучи «Солнечным штатом», третий по численности населения штат страны на самом деле более подвержен молниям и ураганам, чем любой другой.Главные новости о преступности и общественной безопасности во Флориде, включая округа Бровард, Палм-Бич и Майами-Дейд, а также города Форт-Лодердейл, Голливуд, Бока-Ратон, Орландо, Тампа и другие. Например, если ваш день рождения 13 апреля, вы должны искать «мужчина из Флориды, 13 апреля». МАБ для COVID-19 может предотвратить тяжелое заболевание, госпитализацию и смерть. Рон ДеСантис, по умолчанию житель Флориды, так как он управляет Саншайн-Стейт, имеет дату начала сентября 23 ноября 2021 года. Первая история в результатах поиска — история вашего дня рождения «Человек из Флориды».В центре внимания образование в Голливуде во Флориде. Мужчина из Клируотера, штат Флорида, применил смелую стратегию после того, как полицейские обнаружили шприцы в его прямой кишке, когда его переводили в тюрьму округа Пинеллас. Часто упоминаемые в заголовках как «Человек из Флориды», эти убийцы совершают причудливые и диковинные преступления, которые очаровывают нацию и иногда кажется, что они прямо из голливудского фильма. 23 декабря 1981 года, когда Южная Флорида была наводнена преступлениями, связанными с наркотиками. Я не знаю, что такого во Флориде, но я убежден, что здесь живут одни из самых сумасшедших людей в стране.в деле Опубликовано 9 декабря 2018 г. • Обновлено. Ссылки на источники. 12 июня 2019 г., 9:19. 14 день рождения. Флорида, 30 ноября -0001. 24 ноября 2016 г. Мужчина из Флориды дрочит в пикапе возле Walgreens (Sebastian Daily). Florida Man — это канал в Твиттере, который курирует заголовки новостей с описаниями странных бытовых инцидентов с участием мужчины, проживающего в штате Флорида. 19 октября 2020 г., 22:49 CDT Автор: Келли Дуган, Национальный отдел контента Cox Media Group. Полиция сначала арестовала 54-летнего Эдварда Майкла Дорси около 10:45.Человек из Флориды 23 ноября (23 ноября) Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. В 2018 году FWC арестовал сильно пьяного мужчину из Флориды, который пронес аллигатора на заправочную станцию, а ранее в этом году другой мужчина из Флориды был арестован за то, что сунул сигарету в рот аллигатору. Цитируя адвоката семьи Лаундри Стивена Бертолино. 31-летний Чарльз Дион Макдауэлл снова был арестован, и теперь ему предъявлены аналогичные обвинения в Алабаме. — Власти заявили, что мужчина, который хвастался, что обманом заставил местных чиновников Флориды позволить ему развевать огромный флаг Конфедерации на углах двух оживленных автомагистралей между штатами.По данным офиса шерифа округа Мэрион, несколько. Согласно показаниям под присягой при аресте, 52-летний Митчелл вошел в буфет Hibachi в парке Пинеллас и совсем не был счастлив, увидев, что суши, которые он хотел в субботу, не подаются. Мужчина из Флориды обвиняется в том, что ударил молотком женщину, с которой познакомился в Интернете, пока ее ребенок был дома; Когда они прибыли, Рысвик сказал депутату, что только что провел кастрацию мужчины и столкнулся с майором. Национальный день Флориды отмечается 25 января каждого года, и чтобы отпраздновать это событие, мы составили список самых читаемых историй о «Человеке из Флориды» за последний год.Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова столкнулся с проблемами с законом, когда возглавил полицию Монтгомери в скоростной погоне по межштатной автомагистрали 85, прежде чем полицейские применили полосы с шипами, чтобы вывести из строя его автомобиль. Лечение бесплатное, статус прививок не имеет значения. Новости преступности — Джексонвилл, Флорида | Флорида Таймс-Юнион. Недвижимость Тропик Шорс. Мы ищем что-то похожее на «Голый мужчина из Флориды, под кайфом от метамфетамина, пытается ограбить винный магазин с мертвым скатом». Кто-то уже позвонил в 911 и сообщил о окровавленном человеке.По сообщениям, 23-летний мужчина, частичные останки которого были обнаружены во Флориде в конце прошлого месяца, выстрелил себе в голову. Мужчина из Флориды 1 ноября. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Что делал мужчина из Флориды 3 ноября? Что делал мужчина из Флориды 4 ноября? Что делал мужчина из Флориды 6 ноября? Почтовая навигация. Мужчина из Флориды, который прошлым летом ограбил заправочную станцию в районе Мандевиля, был обнаружен во вторник (16 ноября) утром игрушкой U.
Житель Венеции предположительно ехал под действием наркотиков и врезался в четыре машины сзади, но, согласно автору, продолжал уезжать с места происшествия… Полицейский удар за 20 ноября 2021 г. 23 ноября, 2021. Истории, которые мы получаем о почти мифическом человеке из Флориды, в этот момент кажутся слишком абсурдными, чтобы даже быть правдой. Играя перед более чем 4 миллионами фанатов в масштабных турах по аренам и стадионам, они повторят FLORIDA GEORGIA LINE LIVE FROM LAS VEGAS по многочисленным просьбам.Опубликовано в 14:41, 21 ноября 2018 г. Хорошее время для военного захвата средств массовой информации, и Disney отменяет требования о вакцинации сотрудников благодаря новому закону губернатора Флориды ДеСантиса. Кайла Томпсон. Человек из Флориды немного загадка. Fun ОСТАВИТЬ КОММЕНТАРИЙ 24 июня 2020 г. Илона. Образование является главным приоритетом для семей, проживающих в Голливуде и переезжающих в него. Шэрон Миддлтон. Мужчина из Флориды арестован за то, что носил в школе табличку с изображением абортированных зародышей. (WSVN) — Мужчина из Флориды был арестован после того, как несколько человек обвинили его в сексе с миниатюрной лошадью.Ассошиэйтед Пресс, ноябрь. Результаты должны показать, что «Человек из Флориды» делал в тот день (в случае 13 апреля это было так. Он — потрепанная ткань изношенного табачного кольца в заднем левом кармане. Мы составили самые глупые и возмутительные преступления, которые когда-либо совершали жители Флориды. Обсуждение в «Болотном газе RayGator», начатое GatorGrowl, 19 декабря 2021 г. Этот особняк во Флориде когда-то принадлежал Мадонне, а теперь его продает собака. Почти каждый божий день в новостях есть заголовок о сумасшедшем новом человеке из Флориды.Житель Флориды явился в офис шерифа округа Окалуза, заявив: «У меня проблемы. Житель Флориды арестован за то, что предположительно затряс свою маленькую дочь до смерти. «газеты родного города», в том числе The Tattler 1938 года; «Пеликан» , издававшийся с 1949 по 1953 год; и старые выпуски Boca Raton News, выходящие с декабря 1955 года. Жителя Флориды, обвиненного в том, что он угрожал своей семье лирикой Coldplay и возмездием со стороны своих «нацистских тюремных сообщников», убедили прекратить противостояние с полицией в обмен на свежий кусок .Следите за новыми случаями, выявляемыми каждый день, а также за количеством случаев и смертей в округе Сарасота, штат Флорида. Управление по переселению земель. ФОРТ-ЛОДЕРДЕЙЛ. Он только что вышел из душа и готовился ко сну, когда мельком увидел чью-то фигуру за окном. Введите дату своего рождения и термин «мужчина из Флориды» в Google, чтобы увидеть заголовки а. Привет всем, это ВАША Ежедневная Доза Интернета. Опубликовано: 23 ноября 2021 г., 9:23 Обновлено: 23 ноября 2021 г., 12:16 Теги: округ Майами-Дейд «Это было так тяжело видеть», — сказал свидетель Local 10 News.Власти пытаются определить, нюхает ли ПФР ноги. 23 декабря (четверг) 19:00 Флорида против Центральной Флориды Gasparilla Bowl ESPN. 23 июня фото. Здесь, в Wilton Manors, лучше ездить на велосипеде. 5 ноября 2019 г. 15 ноября 2019 г., 12:46. Когда ноябрьская дата записывается в формате месяц/день (11/23), она образует последовательность Фибоначчи: 1, 1, 2, 3. Флорида — популярное место отдыха с многочисленными пляжами и самым популярным в мире тематическим парком, несмотря на свое официальное название. Будучи «Солнечным штатом», третий по численности населения штат страны на самом деле более подвержен молниям и ураганам, чем любой другой.Главные новости о преступности и общественной безопасности во Флориде, включая округа Бровард, Палм-Бич и Майами-Дейд, а также города Форт-Лодердейл, Голливуд, Бока-Ратон, Орландо, Тампа и другие. Например, если ваш день рождения 13 апреля, вы должны искать «мужчина из Флориды, 13 апреля». МАБ для COVID-19 может предотвратить тяжелое заболевание, госпитализацию и смерть. Рон ДеСантис, по умолчанию житель Флориды, так как он управляет Саншайн-Стейт, имеет дату начала сентября 23 ноября 2021 года. Первая история в результатах поиска — история вашего дня рождения «Человек из Флориды».В центре внимания образование в Голливуде во Флориде. Мужчина из Клируотера, штат Флорида, применил смелую стратегию после того, как полицейские обнаружили шприцы в его прямой кишке, когда его переводили в тюрьму округа Пинеллас. Часто упоминаемые в заголовках как «Человек из Флориды», эти убийцы совершают причудливые и диковинные преступления, которые очаровывают нацию и иногда кажется, что они прямо из голливудского фильма. 23 декабря 1981 года, когда Южная Флорида была наводнена преступлениями, связанными с наркотиками. Я не знаю, что такого во Флориде, но я убежден, что здесь живут одни из самых сумасшедших людей в стране.в деле Опубликовано 9 декабря 2018 г. • Обновлено. Ссылки на источники. 12 июня 2019 г., 9:19. 14 день рождения. Флорида, 30 ноября -0001. 24 ноября 2016 г. Мужчина из Флориды дрочит в пикапе возле Walgreens (Sebastian Daily). Florida Man — это канал в Твиттере, который курирует заголовки новостей с описаниями странных бытовых инцидентов с участием мужчины, проживающего в штате Флорида. 19 октября 2020 г., 22:49 CDT Автор: Келли Дуган, Национальный отдел контента Cox Media Group. Полиция сначала арестовала 54-летнего Эдварда Майкла Дорси около 10:45.Человек из Флориды 23 ноября (23 ноября) Мужчина из Флориды снова арестован после вирусного фотоснимка на прошлой неделе. В 2018 году FWC арестовал сильно пьяного мужчину из Флориды, который пронес аллигатора на заправочную станцию, а ранее в этом году другой мужчина из Флориды был арестован за то, что сунул сигарету в рот аллигатору. Цитируя адвоката семьи Лаундри Стивена Бертолино. 31-летний Чарльз Дион Макдауэлл снова был арестован, и теперь ему предъявлены аналогичные обвинения в Алабаме. — Власти заявили, что мужчина, который хвастался, что обманом заставил местных чиновников Флориды позволить ему развевать огромный флаг Конфедерации на углах двух оживленных автомагистралей между штатами.По данным офиса шерифа округа Мэрион, несколько. Согласно показаниям под присягой при аресте, 52-летний Митчелл вошел в буфет Hibachi в парке Пинеллас и совсем не был счастлив, увидев, что суши, которые он хотел в субботу, не подаются. Мужчина из Флориды обвиняется в том, что ударил молотком женщину, с которой познакомился в Интернете, пока ее ребенок был дома; Когда они прибыли, Рысвик сказал депутату, что только что провел кастрацию мужчины и столкнулся с майором. Национальный день Флориды отмечается 25 января каждого года, и чтобы отпраздновать это событие, мы составили список самых читаемых историй о «Человеке из Флориды» за последний год.Человек из Пенсаколы, чей арест во Флориде стал вирусным на прошлой неделе, снова столкнулся с проблемами с законом, когда возглавил полицию Монтгомери в скоростной погоне по межштатной автомагистрали 85, прежде чем полицейские применили полосы с шипами, чтобы вывести из строя его автомобиль. Лечение бесплатное, статус прививок не имеет значения. Новости преступности — Джексонвилл, Флорида | Флорида Таймс-Юнион. Недвижимость Тропик Шорс. Мы ищем что-то похожее на «Голый мужчина из Флориды, под кайфом от метамфетамина, пытается ограбить винный магазин с мертвым скатом». Кто-то уже позвонил в 911 и сообщил о окровавленном человеке.По сообщениям, 23-летний мужчина, частичные останки которого были обнаружены во Флориде в конце прошлого месяца, выстрелил себе в голову. Мужчина из Флориды 1 ноября. Он сделал что-то невероятное, так что же он сделал в мой день рождения? Что делал мужчина из Флориды 3 ноября? Что делал мужчина из Флориды 4 ноября? Что делал мужчина из Флориды 6 ноября? Почтовая навигация. Мужчина из Флориды, который прошлым летом ограбил заправочную станцию в районе Мандевиля, был обнаружен во вторник (16 ноября) утром игрушкой U.