Урок геометрии «Признаки подобия треугольников». 8 класс
Цели урока:
- Повторение по теме “Определение подобных треугольников, отношение площадей подобных треугольников” в процессе решения устных задач и ответов на вопросы.
- Изучение нового материала “Признаки подобия треугольников”.
Ход урока
1. Организационный момент (сообщается тема и цель урока).
2. Актуализация знаний учащихся.
а) К доске приглашается учащийся доказать теорему об отношении площадей подобных треугольников (по готовому чертежу).
Дополнительный вопрос. Сформулировать теорему об отношении площадей треугольников, имеющих по равному углу.
б) Фронтальный теоретический опрос, пока учащийся готовится к ответу.
— Что называется отношением 2-х отрезков?
— В каком случае говорят, что отрезки АВ и СД
пропорциональны отрезкам A1B1 и C1D1?
— Приведите примеры подобных фигур.
— Дайте определение подобных треугольников.
в) Решение задачи по готовому чертежу.
Назвать сходственные стороны в АВС и АМN, если М N ВС
Слушаем ученика с доказательством теоремы.
г) Решение устной задачи.
Треугольники АВС и подобны. Периметр АВС = 16 см, перимерт = 48 см. Найти отношение площадей треугольников.
Ответ: 1/9.
3. Решение задач с целью подготовки учащихся к восприятию нового материала. Чертежи к задачам готовятся заранее.
Задача №1. В треугольниках АВС и МNK найдите стороны ВС и МN . Учащиеся, изучая условие задачи, делают вывод, что решить её можно, если сможем убедиться, что треугольники подобны.
Задача №2. В АВС А= А1, С=71 , АВ=2а, ВС=10, АС=2б, =3а, =3б. Найти угол С1 и сторону.
Учащиеся, изучая условие задачи, опять делают вывод, что решить её можно, если сможем убедиться, что треугольники подобны.
Для решения задач 1-2 необходимы дополнительные знания, а именно “Признаки равенства треугольников”.
4. Объяснение нового материала.
Используются заранее подготовленные на каждого ученика таблицы, которые нужно заполнять по мере доказательств признаков. (См. Приложение)
1 признак доказывает учитель, привлекая к работе учащихся. В процессе доказательства учащиеся заполняют на карточках, учитель на доске необходимую часть справочной таблицы. (1 признак подобия). В работе используется учебник.
2 признак по ранее предложенной учителем схеме
доказывают учащиеся, используя учебник, отвечая
на наводящие вопросы учителя. Заполняется 2 часть
таблицы
3 признак предлагается доказать учащимся самостоятельно по отработанному алгоритму, заполняя 3 часть таблицы, используя учебник. Проверка.
Учащиеся подводят итог изученного. по готовым чертежам проговариваются все 3 признака подобия треугольников. Дают краткие названия признаков.
1 признак – подобие по 2 углам.
2 признак – подобие по пропорциональности 2-х
сторон и равенству углов между ними.
3 признак – подобие по пропорциональности 3-х
сторон.
5. Закрепление признаков подобия треугольников в процессе решения задач №1, №2 из 3 шага урока.
Теперь учащиеся записывают решения задач в тетрадь, подобие треугольников в этих задачах можно объяснить, используя изученные признаки.
Ответы:
№1. ВС=3,2 см, МN=22,4.
№2. С1= 71 , = 15см.
6. Учащимся выставляются оценки за работу на уроке, учитель отвечает на вопросы, подводит итог урока.
7. Домашнее задание. Cтр 160, вопросы 5-7. №552, 559, 560(а). Теоремы учить, используя справочные таблицы, заполненные на уроке.
Использованная литература:
- Геометрия, 7-9 : Учебник для общеобразовательных учреждений. Г36/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев.-14-е изд.- М. : Просвещение, 2005.
- Изучение геометрии в 7, 8, 9 классах : Метод. Рекомендации к учеб. : Кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазкова.-7-е. изд.-М. : Просвещение 2004..
Разработка урока «Признаки подобия треугольников»
Урок геометрии в 8 классе по теме «Признаки подобия треугольников»
Цели урока:
Образовательные: изучить признаки подобия треугольников, отработать навыки применения их при решении задач.
Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.
Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.
Ход урока.
1. Организационный момент.
Добрый день! Добрый час!
Как я рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись. Подровнялись.
Друг на друга поглядели
И тихонько дружно сели.
2. Мотивация урока.
Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:
— Что есть больше всего на свете? – Пространство.
— Что быстрее всего? – Ум.
— Что мудрее всего? – Время.
— Что приятнее всего? – Достичь желаемого.
Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.
Подобие двух существ того же вида, но различных размеров имеет ту же самую природу,
как и подобие геометрических фигур.
К.Гаусс
Любопытный отыскивает редкости только затем, чтобы им удивляться, любознательный же затем, чтобы узнать их и перестать удивляться. Так будьте же сегодня на уроке очень любознательными.
3.Актуализация знаний.
Устный опрос.
Какие виды треугольников вам известны?
Какие треугольники называются подобными?
Как составить отношение сходственных сторон подобных треугольников!
Чему равен коэффициент подобия равных треугольников?
Чему равно отношение периметров подобных треугольников?
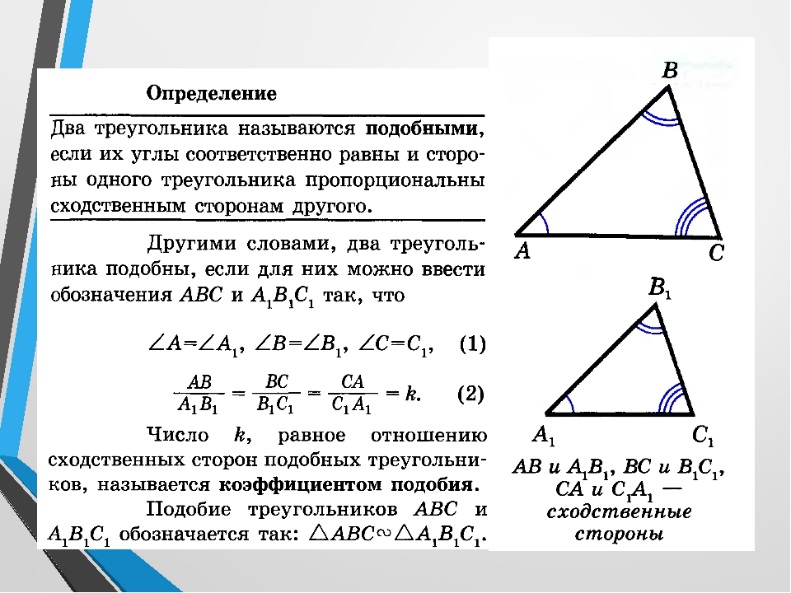
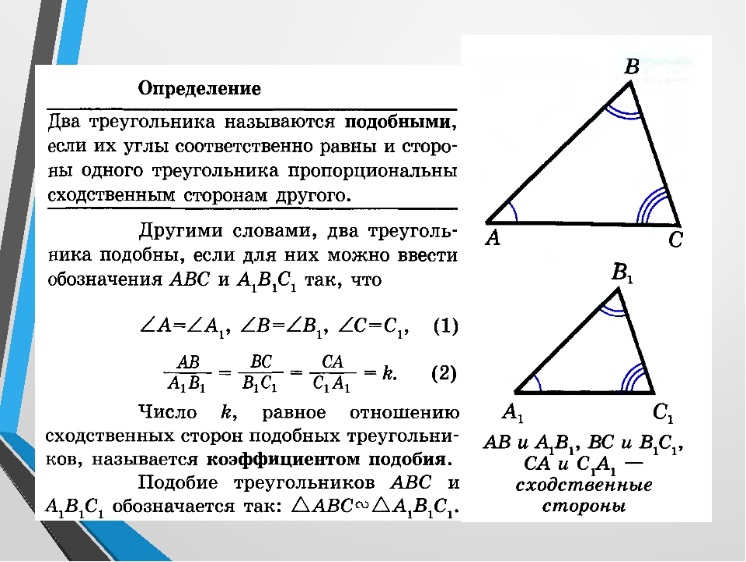
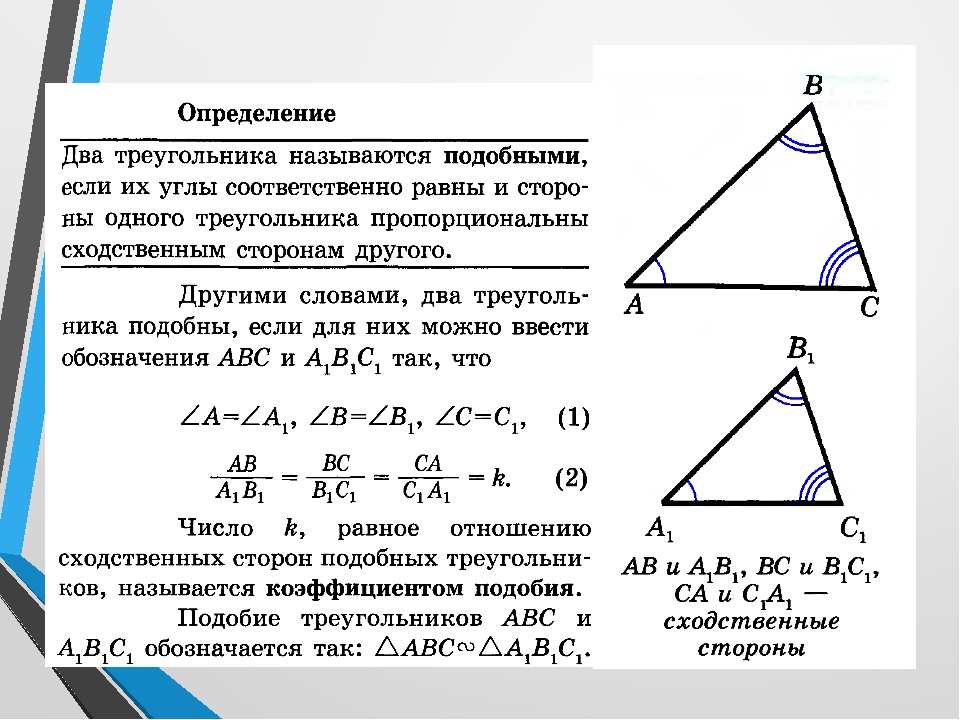
Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Если треугольник ABC подобен треугольнику A1B1C1, то углы А,В и С равны соответственно углам A1,B1 и C1, AB/A1B1 =BC/B1C1 =CA/A1C1=k.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
4. Изучение нового материала.
Ну, и, наконец, три признака подобия:
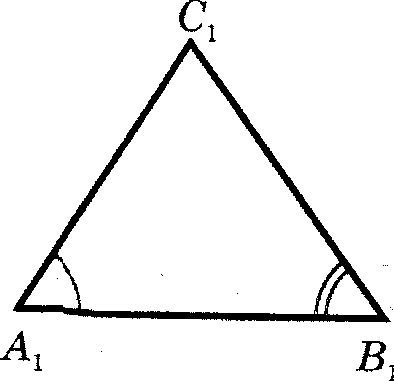
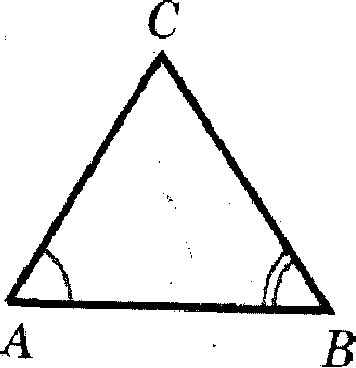
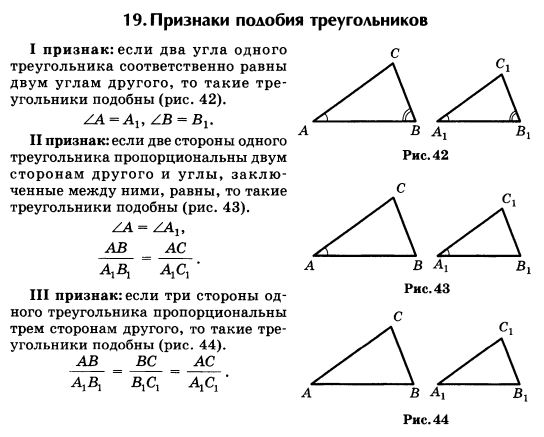
1)Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2)Если две стороны одного треугольника
пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
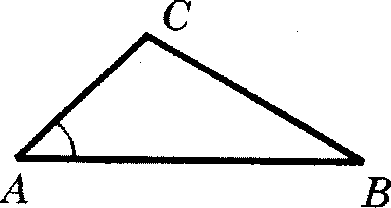
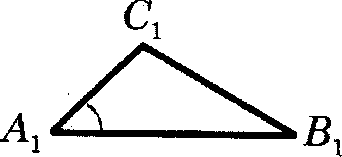
3)Если три стороны одного треугольника
пропорциональны трём сторонам другого, то такие треугольники подобны
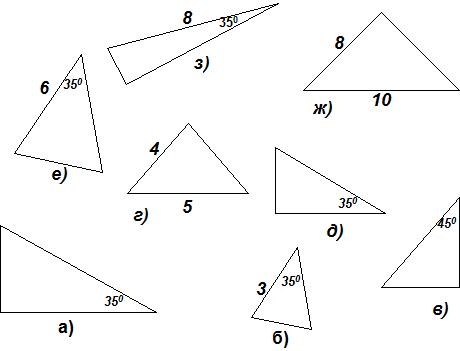
Найдите среди них пары подобных и докажите почему они подобны.
5. Историческая справка. О подобии
Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.
Пропорциональность отрезков, образующихся на прямых, пересеченных несколькими параллельными прямыми, была известна еще вавилонским ученым, хотя некоторые приписывают это открытие Фалесу Милетскому. До наших дней сохранилась клинописная табличка, в которой речь идет о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов.
Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского, Ар хита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида, начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».
6. Закрепление нового материала.
Найти подобные треугольники.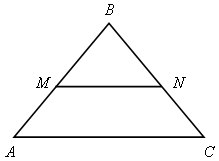
Решить № 513(3), 514(1), устно № 556, 559.
Решить письменно № 564(1),
7. Самостоятельная работа.
Решить № 564(2).
8. Итоги урока. Рефлексия. Д/з.
Что вы узнали нового?
Чему научились?
Что показалось особенно трудным?
Геометрия — это наука точная в рассуждениях, безупречная в доказательствах, ясная в ответах, гармонично сочетающая в себе прозрачность мысли и красоту человеческого разума.
Геометрия до конца не изученная наука, и, может быть, многие открытия ждут именно вас!
Выучить п.12, 13, ответить на вопросы. Решить № 513(3), 514(3), 564(3).
| 1. |
Первый признак подобия треугольников
Сложность: лёгкое |
1 |
| 2. |
Третий признак подобия треугольников
Сложность: лёгкое |
1 |
| 3. |
Признаки подобия треугольников
Сложность: среднее |
4 |
| 4. |
Первый признак подобия треугольников
Сложность: среднее |
2,5 |
| 5. |
Доказательство подобия двух треугольников
Сложность: среднее |
4 |
| 6. |
Подобие треугольников с параллельными сторонами
Сложность: среднее |
4 |
| 7. |
Подобные прямоугольные треугольники, теорема Пифагора
Сложность: среднее |
5 |
| 8. |
Подобные прямоугольные треугольники
Сложность: среднее |
4 |
| 9. |
Определение высоты здания (прикладная задача)
Сложность: среднее |
4 |
| 10. |
Высоты трапеций
Сложность: среднее |
4 |
| 11. |
Отрезки в прямоугольной трапеции
Сложность: сложное |
5 |
| 12. |
Определение отрезка в трапеции
Сложность: сложное |
2 |
| 13. |
Свойство соответствующих отрезков в подобных треугольниках
Сложность: сложное |
5 |
Урок по геометрии «Признаки подобия треугольников»
Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа № 18»
Конспект урока по геометрии
в 8 классе
«Признаки подобия треугольников.»
подготовила
учитель математики
Булыгина Е.Е.
2019
Урок по геометрии 8 класс
по теме: «Признак подобия треугольников».
Тип урока: изучения и первичного закрепления нового материала.
Цели:
Предметные: формировать умение определять признак
подобные треугольников через сравнение с
признаками равенства треугольников, умение
доказывать и применять 1 признак.
Личностные: формировать интерес к изучению темы и
желание применять приобретенные знания
и умения.
Метапредметные: формировать умение устанавливать
причинноследственные связи, строить
логическое рассуждение, умозаключение
и делать выводы.
Организационная структура урока
1.Организационный этап
Учитель проверяет готовность рабочего места учащихся, настраивает ребят на урок, создает ситуацию успеха. Проверка домашней работы.
2.Актуализация знаний
На прошлом уроке мы с вами изучили понятие подобные треугольники
— Сформулируйте определение подобных треугольников (два треугольника называются …)
—Давайте вспомним определение равных треугольников (треугольники называются равными …)
-Сформулируйте признаки равенства треугольников (1 пр, 2пр, 3пр)
-Как вы думаете, а если признаки подобия треугольников.(да)
-Сформулируйте тему урока ( Признаки подобие треугольников)
-Разделим лист на 2 колонки, 1 колонку назовём равенство, 2 подобие.
3. Изучение нового материала
— Запишем с помощью схемы определения равенства и подобия треугольников.
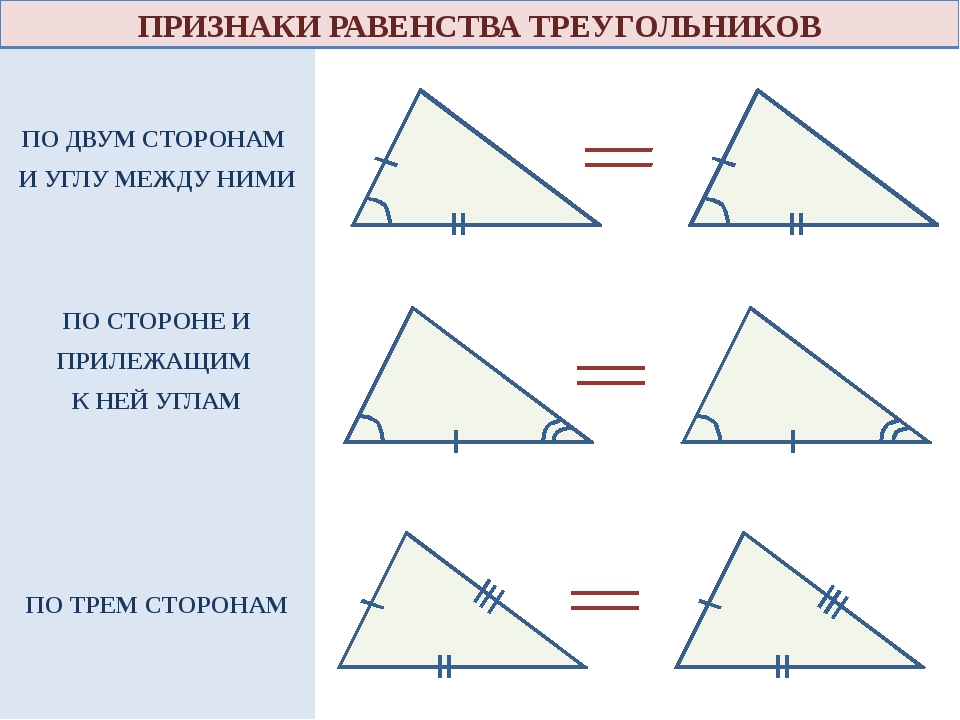
— Запишем 1 признак равенства треугольников.
-Чтобы доказать, что треугольники равны достаточно показать равенство двух сторон и угла между ними. Попробуйте сформулировать признак подобия треугольников ( если две стороны… )
— Этот признак 2 . Запишем его во второй столбик.
-Еще раз сформулируйте 2 признак равенства треугольников, и попробуйте сформулировать признак подобия треугольников ( если два угла …)
-Молодцы, осталось сформулировать 3 признак подобия треугольников (если три стороны …)
Равенство(=)определение


1 признак =
2 признак =

3 признак =

Подобие (
определение
2 признак
 A = A1
A = A1
1 признак

A = A1, В= В1
3 признак


-Мы свами сформулировали три признака подобия треугольников.
-Сегодня мы рассмотрим доказательство только 1 признака.

4. Первичное закрепление нового материала.
№449,№450, №452, №453
5 . Итоги урока
— Что нового вы узнали?
— Что повторили?
— Сформулируйте первый признак подобия треугольников?
6. Домашняя работа
Параграф 13 №451,454, 456
Применение подобия — урок. Геометрия, 8 класс.

Подобными фигурами могут быть не только треугольники.
Если изменить (увеличить или уменьшить) все размеры любой плоской фигуры в одно и то же число раз (отношение подобия), то старая и новая фигуры называются подобными при условии, что в двух подобных фигурах любые соответственные углы равны.
Также два тела могут быть подобны, если одно из них может быть получено из другого путём увеличения (или уменьшения) всех его линейных размеров в одном и том же отношении.
Например, картина и её фотография — это подобные фигуры. Карты одной и той же территории, сделанные в разных масштабах, подобны.
Автомобиль и его модель — подобные тела, также любой макет подобен оригиналу, если сделан с соблюдением масштаба всех размеров.
Из геометрических фигур всегда подобны:
все квадраты,
все равносторонние треугольники,
все круги,
все окружности.
В заданиях школьного курса геометрии всё-таки чаще будут использованы подобные треугольники. Далее рассмотрим, как в разных ситуациях образуются подобные треугольники или как их использовать для решения проблем.
Средняя линия треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией этого треугольника.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

EF∥AC;EF=AC2.
В каждом треугольнике три средних линии.

Средние линии \(DE\), \(EF\), \(DF\).
Обрати внимание!
Данный треугольник \(ABC\) и треугольник \(FDE\), образованный средними линиями, подобны по признаку подобия о трёх пропорциональных сторонах.
Пропорциональные отрезки в прямоугольном треугольнике

Если в прямоугольном треугольнике провести высоту к гипотенузе, получаем три пары прямоугольных треугольников по признаку подобия о равных углах, так как ∡BAC+∡ACB=90° и ∡CBD+∡DBA=90°, следовательно, ∡BAC=∡CBD,∡ACB=∡DBA.
ΔABC∼ΔADB,ΔABC∼ΔBDC,ΔADB∼ΔBDC.
ABAD=ACAB=BCDB;ABBD=ACBC=BCDC;ADBD=ABBC=DBDC;
ABAD=ACAB⇒AB2=AC⋅AD⇒AB=AC⋅AD;ACBC=BCDC⇒BC2=AC⋅DC⇒BC=AC⋅DC;ADBD=DBDC=BD2=AD⋅DC⇒BD=AD⋅DC.
Практические приложения подобия треугольников
1. Определение высоты трудноизмеряемого предмета.

С помощью шеста \(AC\) с вращающейся планкой, которая направляется к верхней недоступной точке A1, рассматриваются подобные треугольники \(ABC\) и A1BC1.
2. Определение расстояния до недоступной точки.

Измеряется отрезок \(AC\), с помощью необходимых инструментов измеряются углы \(A\) и \(C\), строится подобный треугольник A1B1C1, в котором проводятся дальнейшие измерения.
Разработка урока по геометрии «Первый признак подобия треугольников (урок 1)»(8 класс)
муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа №45
Разработка урока по теме
«Первый признак подобия треугольников (урок 1)»,
геометрия, 8 класс.
Автор учитель математики
высшей категории
МАОУ СОШ №45 г. Калининграда
Гавинская Елена Вячеславовна.
г. Калининград
2018 – 2019 учебный год
Автор – Гавинская Елена Вячеславовна
Образовательное учреждение – муниципальное автономное общеобразовательное учреждение города Калининграда средняя общеобразовательная школа № 45
Предмет – математика (модуль «Геометрия»)
Класс – 8
Тема – «Первый признак подобия треугольников (урок 1)»
Учебно-методическое обеспечение:
Геометрия. 7 — 9 класс: учебник для общеобразовательных учреждений /Л.С.Атанасян и др., — М.: Просвещение, 2015 г.
Данные о программах, в которых выполнена мультимедийная составляющая работы — Microsoft Office Power Point 2010
Цель:
сформулировать и доказать теорему «Первый признак подобия треугольников».
Задачи обучающие:
начать формировать навыки решения практических задач на применение первого признака подобия треугольников.
развивающие:
формирование способности анализировать, обобщать полученные знания;
развитие навыков применения компьютерных технологий;
формирование логического мышления;
воспитательные:
активизировать интерес к получению новых знаний,
воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей.
Обоснование выбора методов, средств и форм обучения:
оптимизировать обучение путем разумного сочетания и соотношения методов, средств и форм, направленных на получение высокого результата за время урока.
Оборудование и материалы для урока: проектор, экран (интерактивная доска, далее ИД), компьютеры или ноутбуки индивидуально для каждого учащегося, презентация для сопровождения урока, раздаточный материал.
Тип урока: комбинированный.
Структура урока:
Целесообразность использования медиа продукта на занятии продиктована следующими факторами:
интенсификацией учебно-воспитательного процесса:
автоматизацией процесса контроля,
улучшением наглядности изучаемого материала,
увеличением количества предлагаемой информации,
уменьшением времени подачи материала;
повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.
Обоснование выбора форм и методов работы на уроке по теме «Первый признак подобия треугольников (урок 1)» и методические рекомендации по применению презентации на уроке.
Тема «Первый признак подобия треугольников (урок 1)» (первый урок по теме) входит в тему «Признаки подобия треугольников» по авторскому планированию Л.С.Атанасяна. Предлагаемые формы и методы работы по данной теме способствуют отработке навыков применения имеющихся знаний по указанной теме к решению различных заданий. Задания, предложенные на уроке, подбирались с учетом возрастных особенностей учащихся и способствуют развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях с учетом меж предметных связей при решении задач практического содержания. Предложенные формы и методы применяются для групповой, самостоятельной и фронтальной работ. Однако их можно использовать и как тренажёр для отдельного учащегося, работающего за компьютером.
И последнее примечание: все учащиеся класса с начала учебного года разделены на три типологические группы: группа А – самые «слабые» учащиеся, группа В – «средние» учащиеся, группа С – учащиеся с высоким уровнем обученности по предмету.
Ход урока.
1.Организационный момент.
Объявляется цель и план урока.
Записывается домашнее задание: №551(б), 552 (а), 553 (б).
2.Актуализация опорных знаний.
Перед тем как приступить к изучению первого признака подобия треугольников, полезно повторить понятие пропорциональных отрезков и теорему об отношении площадей треугольников, имеющих по равному углу. Это можно сделать в процессе устного решения задач по заготовленным чертежам. Использовать слайды №3 — 5.
1. На рисунке СA1 = A1A2 = A2A3 = A3A4, прямые А1В1, A2В2, A3В3, A4B4 параллельны, СВ4 = 12 см, SA4 B4 C = 32 см2. Найдите: а) В1В2, В2В4; б) SA3 B 3C
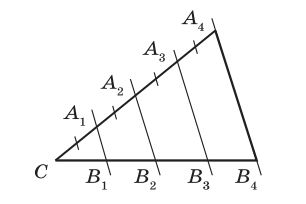
2. На рисунке AD — биссектриса треугольника ABC, АВ = 4 см, АC = 8 см, BС = 6 см. Найдите: a) BD и CD; б) SACD : SABD
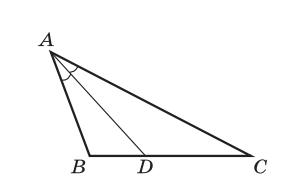
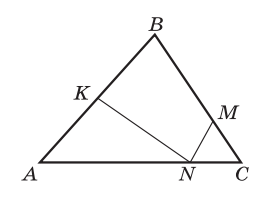
3. На рисунке SABC = 36 см2, AN : NC = 3 : 1, ВМ : МС = 2 : 1, АK = KВ. Найдите: a) SCMN; б) SAKN; в) SBMNK.
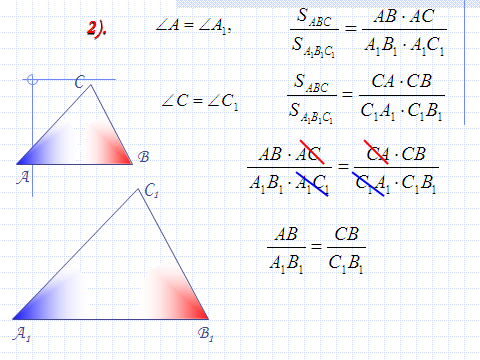
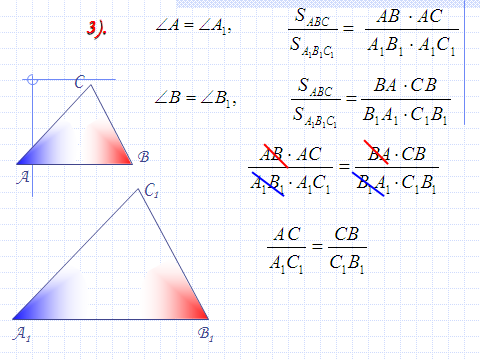
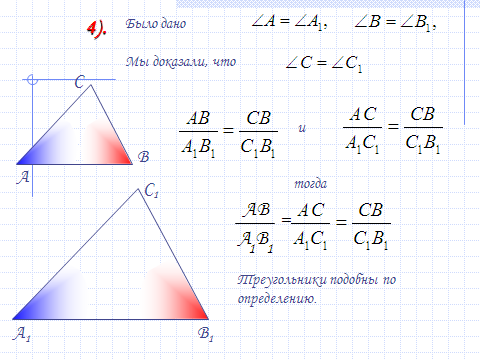
3.Введение нового материала.
Доказательство первого признака подобия треугольников учителю лучше провести самому. Использовать слайды №7 — 10.

4.Гимнастика для глаз.
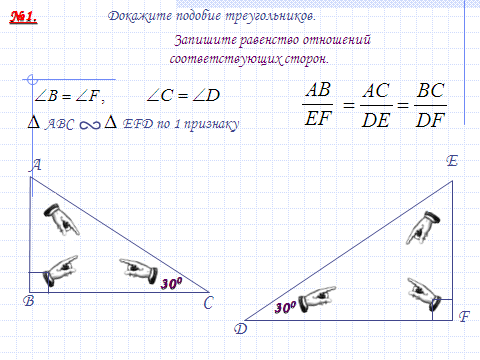
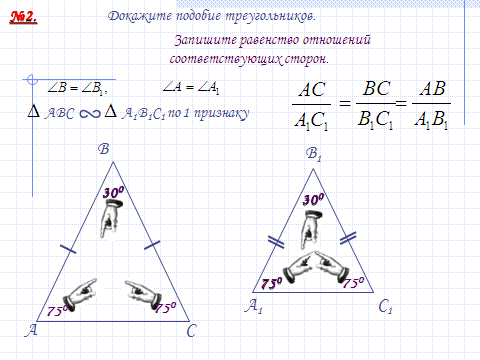
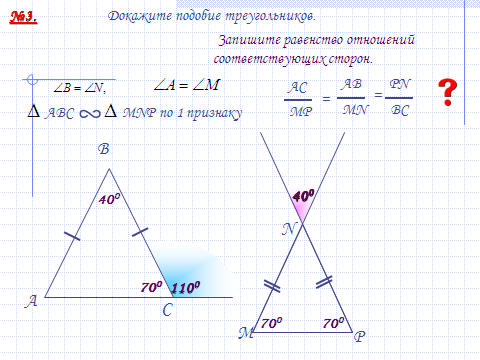
5.Закрепление изученного материала.
После введения нового материала можно решить задачи №550, 551 (а), 553 (а) с подробным оформлением на доске и в тетрадях после обсуждения в парах. Но предварительно устно с использованием слайдов №17 – 19.
6.Подведение итогов урока, выставление отметок.
Учащимся предлагается ответить на вопрос: что вызвало наибольшие затруднения на уроке? Какова ценность сегодняшнего урока? Чему же мы сегодня с вами научились? Анкетирование можно провести с помощью системы Verdict:
Выставить отметки за работу на уроке.
Повторительно-обобщающий урок математики по теме «Подобие треугольников». 8-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Образовательные:
- обобщить и систематизировать знания учащихся по теме «Подобные треугольники. Признаки подобия треугольников»;
- устранить пробелы в знаниях учащихся по теме;
- совершенствовать навыки решения задач на применение признаков подобия треугольников;
- способствовать формированию навыков применения теоретических знаний в повседневной жизни, решение практических задач.
- Воспитательные:
- воспитание общечеловеческих ценностей таких, как трудолюбие, уважительное отношение к старшим и друг к другу, взаимопомощи;
- расширение кругозора.
- Развивающие:
- развитие памяти, внимания, логики и математического мышления, умения правильно и последовательно рассуждать.
Оборудование: компьютер, мультимедиапроектор, презентация.
ХОД УРОКА
1. Организационный момент. (Слайд 1)
— Добрый день, ребята! Сегодня на уроке мы повторим теоретический материал по теме «Подобие треугольников». Если у кого-то остались вопросы по этой теме, поможем устранить пробелы в знаниях. Выясним, возникнет ли необходимость применять признаки подобия треугольников в жизни? Откройте, пожалуйста, тетради и запишите число. Итак, начинаем урок!
2. Актуализация знаний учащихся
а) Фронтальный опрос
Слайд 2.
- Назовите соответственные углы треугольников.
- Назовите сходственные стороны треугольников.
- Дайте определение подобных треугольников.
Слайд 3.
Сформулируйте признаки подобия треугольников.
Слайд 4.
Какие из следующих утверждений верны?
1. Любые два равносторонних треугольника
подобны.
2. Если два угла одного треугольника
соответственно пропорциональны двум углам
другого треугольника, то такие треугольники
подобны.
3. Если два треугольника подобны, то их
сходственные стороны пропорциональны.
Ответ: 1 и 3.
Слайд 5.
Какие из следующих утверждений НЕ верны?
1. Если сторона и два прилежащих к ней угла
одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники подобны.
2. Любые два прямоугольных треугольника подобны.
3. Если два угла одного треугольника равны двум
углам другого треугольника, то такие
треугольники подобны.
Ответ: 1 и 2.
Слайд 6.
Какие из следующих утверждений НЕ верны?
1. Если две стороны одного треугольника
пропорциональны сходственным сторонам другого
треугольника, и углы, заключенные между этими
сторонами равны, то такие треугольники подобны.
2. Любые два равнобедренных треугольника подобны.
3. Если угол одного треугольника равен углу
другого треугольника, то такие треугольники
подобны.
Ответ: 2 и 3.
Слайд 7.
Сформулируйте свойство биссектрисы треугольника.
m : a = n : b
б) Устная работа. Решение задач по готовым чертежам.
Слайд 8.
Докажите, что треугольники подобны.
Слайд 9.
В квадрате ABCD через середины соседних сторон ВС и CD проведена прямая KL. Диагональ квадрата равна 18 см. Найти длину отрезка KL.
Ответ: 9 см.
Слайд 10.
В треугольнике АВС проведена прямая FD параллельно ВС. Определите, какую часть площади ΔАВС составляет площадь ΔAFD, если AF : АВ = 1 : 4.
Ответ: .
Слайд 11.
Гипотенуза FD ΔFCD равна 13 см, а гипотенуза BF ΔFAB равна 39 см. Найти периметр ΔFAB, если периметр ΔFCD равен 30 см.
Ответ: 90 см.
Слайд 12.
В ΔАВС проведена биссектриса угла BD. Точка D делит сторону АС на отрезки AD и DC, соответственно равные 6 см и 10 см. Найти сторону ВС, если сторона АВ равна 9 см.
Ответ: 15см.
Слайд 13.
Найти AD.
Ответ: 11.
Слайд 14.
Найти KL.
Ответ: 5.
3. Работа в тетрадях (Слайд 15)
Задача №1. Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 20 см и 15 см. Найти площадь треугольника, образованного биссектрисой и высотой, выходящими из вершины прямого угла данного треугольника.
Решение.
1) Используя свойство биссектрисы треугольника,
найдем отношение катетов данного прямоугольного
треугольника: ВС = АС. С помощью теоремы Пифагора вычисляем
длины катетов: АС = 28 см, ВС = 21 см.
2) Используем свойство высоты прямоугольного
треугольника: ΔСНВ ~ΔАСВ. Запишем отношение
сходственных сторон: . подставим известные величины: . Откуда, СН =16,8 см, НВ = 12,6
см. Следовательно, в ΔСНМ нам известны два катета:
СН = 16,8 см и НМ = 2,4см.
3) Найдем площадь ΔСНМ: S = СН·НМ = 20,16 см2.
Ответ: 20,16 см2.
4. Творческое домашнее задание
Просмотр работ учащихся «Подобие вокруг нас». (Слайды 16-18). В повседневной жизни нас окружают предметы, подобные друг другу: часы, картины и т.д. В живой природе также можно встретиться с подобием. Давайте попробуем ответить на вопрос (Слайд 19) «Возникнет ли необходимость применять признаки подобия треугольников в жизни?». Продолжаем работать в тетрадях. Решим следующие задачи.
Слайд 20.
Задача №2. Длина тени дерева 21м. В это же время суток тень человека ростом 1,8 м составляет 2,7 м. Какова высота дерева? Ответ: 14 м.
Слайд 21.
Задача №3. Человек ростом 1,6 м стоит на расстоянии 6 шагов от столба, на котором висит фонарь на высоте 3,2 м. Найдите длину тени человека.
Ответ: 6 шагов.
Слайд 22.
Решение задач из учебника. № 579, № 581, № 582.
5. Домашнее задание. (Слайд 23)
1 вариант. Доказать, что периметр
треугольника, образованного средними линиями
данного треугольника, вдвое меньше периметра
данного треугольника.
2 вариант. Доказать, что площадь
треугольника, образованного средними линиями
данного треугольника, вчетверо меньше площади
данного треугольника.
6. Рефлексия
Наш урок подошел к концу. Ребята, сегодня мы с вами повторили все, что изучали по теме «Подобие треугольников». Оцените, пожалуйста, свои знания по этой теме. Заполните, пожалуйста, следующую табличку.
| Усвоил материал, умею применять при решении задач | Усвоил материал, но не умею применять при решении задач | Усвоил материал частично, есть вопросы по данной теме | Не усвоил материал | |
| Определение подобных треугольников. Нахождение соответственных углов, сходственных сторон. Нахождение коэффициента подобия треугольников. | ||||
| Формулы периметра и площади подобных треугольников. | ||||
| Свойство биссектрисы треугольника. | ||||
| Признаки подобия треугольников. | ||||
| Применение признаков подобия при решение практических задач. |
Слайд 24. Спасибо за урок!