Вертикальные и смежные углы
Геометрия – это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
 Смежные и вертикальные углы – это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Смежные и вертикальные углы – это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
 Острым называется угол, мера которого не превышает 90 градусов.
Острым называется угол, мера которого не превышает 90 градусов.Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Смежные углы
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение развернутого угла линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
 Вертикальные углы
Вертикальные углыУглы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении параллельных прямых произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
fb.ru
Вертикальные углы | Треугольники
Какие углы вертикальные? Каким свойством обладают вертикальные углы?
Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.
Определение.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
При пересечении двух прямых образуется две пары вертикальных углов:
∠1 и ∠2 — вертикальные углы
∠3 и ∠4 — вертикальные углы
Свойство вертикальных углов.
Вертикальные углы равны.
∠AOC =∠BOD
∠AOD =∠BOC
Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.
Задачи.
1) Сумма вертикальных углов равна 140º. Найти эти углы.
Решение:
Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.
Ответ: 70º, 70º.
2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.
Решение:
При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.
Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.
А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.
Ответ: 50º, 50º.
Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.
www.treugolniki.ru
Смежные и вертикальные углы
Урок 6
Смежные и вертикальные углы
Цели: ввести понятия смежных и вертикальных углов; рассмотреть их свойства; и показать, как применяются эти понятия при решении задач.
Наглядные пособия: таблицы «Смежные углы», «Вертикальные углы».
Ход урока
I. Анализ результатов самостоятельной работы.
II. Изучение нового материала. Решение задач.
1. Ввести понятие смежных углов и их свойства (сумма смежных углов равна 180°) с помощью таблицы «Смежные углы».
2. Выполнение практического задания № 55 (на доске и в тетрадях).
3. Устно решить задачи №№ 58, 59, 60, 63, 62 (по рис. 46).
4. Письменно решить задачу № 61 (в; г):
в) 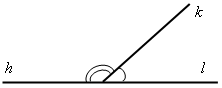
Дано: 
 kl – смежные;
kl – смежные; hk больше
hk больше  kl на 47°18′.
kl на 47°18′.
Найти:  hk и
hk и  kl.
kl.
Решение
Пусть 
 hk = х + 47°18′.
hk = х + 47°18′. По свойству о сумме смежных углов  kl +
kl +  hk =180°.
hk =180°.
х + х + 4718′ = 180°; 2х = 180° – 47°18′;
2х = 179°60′ – 47°18′; 2х = 132°42′; х = 66°21′.
 kl = 66°21′;
kl = 66°21′; 
Ответ: 113°39′ и 66°21′.
г) Пусть  kl = х, тогда
kl = х, тогда  hk = 3х.
hk = 3х.
х + 3х = 180°; 4х = 180°; х = 45°;  kl = 45°;
kl = 45°;  hk = 135°.
hk = 135°.
Ответ: 135° и 45°.
5. Понятие вертикальных углов можно ввести, выполняя следующее задание:
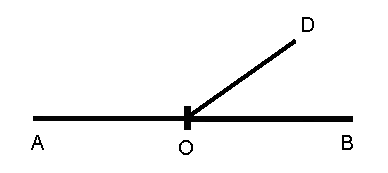
1) Начертите неразвернутый  АОВ и назовите лучи, являющиеся сторонами этого угла.
АОВ и назовите лучи, являющиеся сторонами этого угла.
2) Проведите луч ОС, являющийся продолжением луча ОА, и луч ОD, являющийся продолжением луча ОВ.
3) Запишите в тетради: углы АОВ и СОD называются вертикальными.
6. На таблице «Вертикальные углы» показать, что при пересечении двух прямых образуются две пары вертикальных углов с вершиной в точке пересечения этих прямых.
7. Определение вертикальных углов (рис. 41).
8. Обоснование того факта, что вертикальные углы равны, вначале можно провести на конкретном примере, записав его на доске и в тетрадях учащихся.
Задача. Прямые АВ и СD пересекаются в точке О так, что  АОD =
АОD =
= 35°. Найдите углы АОС и ВОС.
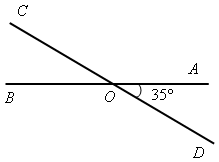
Решение
1) Углы АОD и АОС смежные, поэтому  ВОС = 180° – 35° = 145°.
ВОС = 180° – 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому  ВОС = 180° – 145° =
ВОС = 180° – 145° =
= 35°.
Значит,  ВОС =
ВОС =  АОD = 35°, причем эти углы являются вертикальными.
АОD = 35°, причем эти углы являются вертикальными.
Вопрос: верно ли утверждение, что любые вертикальные углы равны?
9. Самостоятельное доказательство учащимися свойства вертикальных углов (рис. 41) и запись этого доказательства в тетрадях.
10. Устно решить задачу № 65 (использовать таблицу «Вертикальные углы»).
11. Устно решить задачу № 67 по рисунку 47.
12. Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.
13. Выполнение практического задания № 57.
14. Беседа о построении прямых углов на местности (п. 13) с демонстрацией изготовленного учащимися экера.
III. Самостоятельная работа.
Вариант I
1. Один из смежных углов на 27° меньше другого. Найдите оба смежных угла.
2. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 226°.
Вариант II
1. Один из смежных углов в девять раз больше другого. Найдите оба смежных угла.
2. Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 81° больше другого.
IV. Итоги урока.
Домашнее задание: изучить пункты 11–13 из § 6; ответить на вопросы 17–21 на с. 26; выполнить практическое задание № 56; решить задачи №№ 61, 64, 65б.
infourok.ru
Конспект урока по геометрии» Смежные и вертикальные углы»
Тема урока: «Смежные и вертикальные углы»
Предмет: геометрия.
Класс:7.
Тип урока: введение и первичное закрепление новых знаний.
Цель урока: познакомить учащихся с понятиями смежных и вертикальных углов, рассмотреть их свойства, научить решать задачи на применение нового материала
Задачи:
обучающие: формирование знаний о вертикальных и смежных углах, навыков построения этих углов научить, умения вести исследование с опорой на алгоритм действий, анализировать полученные данные и делать выводы, умения решать задачи с использованием свойств смежных и вертикальных углов.
развивающие: развивать умение сравнивать, выявлять закономерности, обобщать; развивать логическое мышление и творческую сторону мыслительной деятельности, математически грамотную речь; через ИКТ повышать интерес к изучаемому предмету; развивать навыки работы по готовым чертежам; создавать условия для проявления познавательной деятельности учащихся; содействовать развитию математического кругозора, памяти, внимания.
воспитательные: способствовать совершенствованию навыков коллективной и групповой работы, умению ориентироваться при работе в группах, контролировать внимание на всех этапах урока, ответственности к учебному труду.
Тип урока: введение и первичное закрепление новых знаний.
Формы работы учащихся: индивидуальная, коллективная, работа в парах.
Необходимое техническое оборудование: учительский ноутбук (с выходом в Интернет), проектор, интерактивная доска, ноутбуки 11, дистанционная мышь для управления презентацией, меловая доска.
ХОД УРОКА
I. Актуализация знаний.
Сегодня мы повторим виды углов, их свойства и добавим к знаниям об углах ещё два вида. Чтобы не забыть старых знакомых, выполним устно задания
Назвать вид каждого угла и указать градусную меру.
2) Дано:  АОD = 8
АОD = 8 DОВ. Найти:
DОВ. Найти:  DОВ
DОВ
3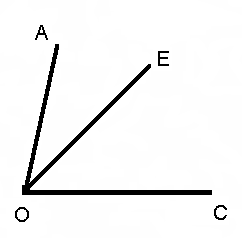 ) а)
) а)  АОЕ=300
АОЕ=300
 ЕОС=20°
ЕОС=20°
 AOC=?
AOC=?
б)  АОС=70°
АОС=70°
 АОЕ=50°
АОЕ=50°
 ЕОС=?
ЕОС=?
II. Изучение нового материала. Решение задач.
Решая 1 и 2 задачу, мы встретились с углами, которые носят название смежные и вертикальные. Это и есть тема нашего урока. Сегодня мы рассмотрим их определения и свойства.
Введение понятия «смежные углы».
1. Практическая работа. Построим прямую АD и отметим точку С, лежащую между точками А и D. Проведём луч СВ. Получились два угла: АСВ и ВСD. Такие углы принято называть смежными.
Попробуем сформулировать определение смежных углов, но сначала ответим на вопросы:
а) назовите стороны каждого из углов;
б) как связаны между собой стороны смежных углов?;
в) выделить особенности смежных углов (одна сторона общая, две другие являются продолжениями одна другой).
Обратить внимание на слово «смежные» — находящиеся рядом («межа»).
Далее прочитать определение смежных углов в учебнике, подчеркнув те условия, которые должны удовлетворять смежные углы.
2. Усвоение понятия смежных углов.
Найдите пары смежных углов и объясните, почему они смежные.
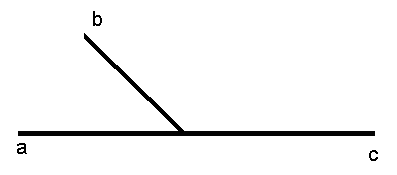
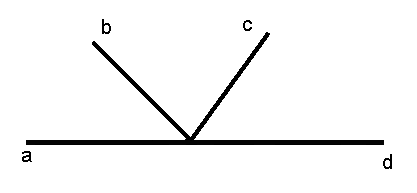
3. Сформулировать свойство смежных углов. (Предложить это сделать самим учащимся, вспомнив 3 задачу).
4. Закрепление понятия и свойства смежных углов.
Решить из учебника задачи № 55 (на доске и в тетрадях), № 59,60 — устно.
5. Введение понятия вертикальных углов.
Практическая работа:
1) проведите луч ОС, являющийся продолжением луча ОА и луч ОD, являющийся продолжением луча ОВ;
2) запишите в тетради: углы АОВ и СОD называются вертикальными.
Вопрос: Сколько пар вертикальных углов образуется при пересечении двух прямых?
Попробуем сформулировать определение вертикальных углов, ответив на вопросы:
1) назвать стороны каждого вертикального угла;
2) как связаны стороны вертикальных углов между собой?
3) выделить особенности вертикальных углов (1-я сторона 1-го угла является продолжением стороны второго, 2-я сторона 1-го угла является продолжением стороны второго).
Далее прочитать определение вертикальных углов в учебнике, подчеркнув те условия, которые должны удовлетворять вертикальные углы.
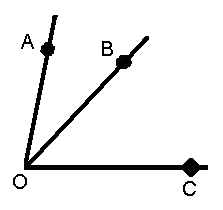
6. Усвоение понятия вертикальных углов.
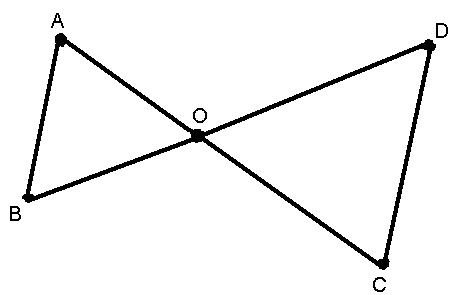
Указать пары вертикальных углов на рисунке и объяснить, почему они вертикальные.
7. Обоснование того факта, что вертикальные углы равны, вначале можно провести на конкретном примере:
Задача. Прямые АВ и СD пересекаются в точке О так, что угол АОD равен 350.
Найдите углы АОС и ВОС,
Задачу решить по готовому чертежу.
Вопрос: верно ли утверждение, что любые вертикальные углы равны?
Далее учащиеся самостоятельно разбирают доказательство свойства вертикальных углов по рис. 41 в учебнике и записывают в тетрадях.
8. На закрепление свойств вертикальных и смежных углов решить
№65 (а) устно, №66 (б; в) — письменно.
III. Тест. Итог урока.
1. Являются ли смежными углы
а)  DОС и
DОС и  DОЕ;
DОЕ;
б)  DОС и
DОС и  СОВ;
СОВ;
в)  DОЕ и
DОЕ и  АОВ?
АОВ?
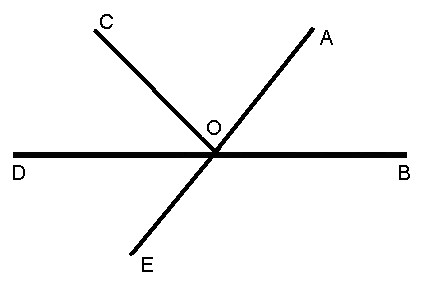
2. Являются ли вертикальными углы:
а)  DОЕ и
DОЕ и  СОА;
СОА;
б)  DОА и
DОА и  АОВ;
АОВ;
в)  АОВ и
АОВ и  DОЕ?
DОЕ?
Обсудить с детьми вопросы:
1) что нового вы узнали сегодня на уроке?
2) что было самое трудное на уроке?
3) что помогло с этой трудностью справиться?
IV. Домашнее задание. П. 11, №17, 18, №61 (а, б), 66 (а), 68.
infourok.ru