Равновесие тел. Виды равновесия
Виды равновесия тел
Различают:
- устойчивое равновесие
- неустойчивое равновесие
- безразличное равновесие
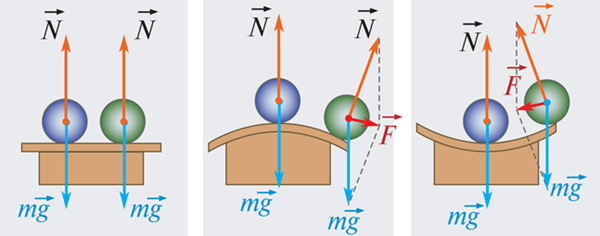
Это происходит, если при небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. Например, шарик, лежащий на дне сферического углубления (рис.1 а).
В данном случае при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Примером может служить шарик, находящийся в верхней точке выпуклой сферической поверхности (ри.1 б).
В этом случае при небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю. Например, шарик, лежащий на плоской поверхности (рис.1,в).
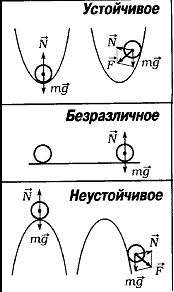
Рис.1. Различные типы равновесия тела на опоре: а) устойчивое равновесие; б) неустойчивое равновесие; в) безразличное равновесие.
Статическое и динамическое равновесие тел
Если в результате действия сил тело не получает ускорения, оно может находиться в состоянии покоя или двигаться равномерно прямолинейно. Поэтому можно говорить о статическом и динамическом равновесии.
В состоянии статического равновесия находится подвешенный на тросах фонарь, любое строительное сооружение. В качестве примера динамического равновесия можно рассматривать колесо, которое катится по плоской поверхности при отсутствии сил трения.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
| СТАТИКА. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ. | |
Статика — раздел механики, в котором рассматривается равновесие тел. Равновесие тел — состояние механической системы, в которой тела остаются неподвижными по отношению к выбранной системе отсчета. | |
Равновесие тел при отсутствии вращения (линии действия сил пересекаются в одной точке): Векторная сумма всех сил, действующих на тело, равна нулю(алгебраическая сумма проекций всех сил на любую ось равна нулю). |
|
Момент силы — равен произведению силы на плечо: Плечо силы — расстояние от оси вращения до линии действия силы. (обозначают буквами ℓ или d). Момент силы, вращающий тело против часовой стрелки, считают положительным, по часовой стрелке — отрицательным. |
|
Центр масс — точка, через которую должна проходить линия действия силы, чтобы под действием этой силы тело двигалось поступательно. Центр тяжести — точка приложения силы тяжести, действующей на тело. В однородном поле тяготения центр тяжести и центр масс совпадают. |
|
Рычаг (Архимед). Разновидности рычага: блок, ворот. Условие равновесия рычага: отношение сил обратно пропорционально отношению плеч этих сил. «Золотое правило механики»: выигрывая в силепроигрываешь в расстоянии. |
|
Равновесие тел при отсутствии вращения (линии действия сил не пересекаются в одной точке): 1. Векторная сумма всех сил, действующих на тело, равна нулю; 2. Алгебраическая сумма моментов всех сил, действующих на тело, относительно любой точки равна нулю. |
|
Т.е. |
|
ПАРА СИЛ: Момент пары: Пару нельзя уравновесить одной силой (равной величины)! Примеры: завинчивание гайки гаечным ключом, вращение рамки с током в магнитном поле и т.д. |
|
Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние. |
|
Безразличное: При малом отклонении тело остается в равновесии. | |
Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. | |
В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте. Все тела стремятся к минимуму потенциальной энергии. (Потенциальная яма). |
|
Равновесие тел на опоре: линия действия силы тяжести проходит через площадь опоры (Пизанская башня). Чем ниже центр тяжести, тем более устойчиво равновесие. |
|
Виды равновесия в физике, теория и онлайн калькуляторы
Если тело находится в состоянии равновесия, то сумма внешних сил, действующих на него равна нулю, равна нулю и сумма моментов этих сил относительно любой оси.
Виды равновесия. Устойчивое, неустойчивое и безразличное равновесие
Равновесие делят на: устойчивое, неустойчивое и безразличное.
ОпределениеРавновесие тела называют устойчивым, если при небольших смещениях, действующие на него силы, стремятся вернуть его снова в положение равновесия.
ОпределениеПоложение равновесия называют неустойчивым, если при малых смещениях силы, оказывающие воздействие на тело уводят его из положения равновесия еще больше.
Если при небольших смещениях из положения равновесия силы, действующие на тело и их моменты, уравновешиваются, как и прежде, то такое равновесие называют безразличным.
Классическим примером типов равновесия служит положение шарика на опорах различной формы. Рис. 1 (а) шарик находится в положении устойчивого равновесия. Рис.1 (б) равновесие тела неустойчивое. Рис.1 (в) положение тела безразличное.
Если тело имеет точку опоры (как шарик на рис.1), и равнодействующая всех сил, приложенных к телу, направлена к положению равновесия, то тело находится в устойчивом равновесии. В том случае, если равнодействующая направлена в сторону противоположную точке равновесия, то тело в неустойчивом равновесии. Если равнодействующая сил, приложенных к телу равна нулю, то равновесие безразличное.
Вид равновесия тела зависит от распределения его массы и положения этого тела относительно других тел.
Принцип минимума потенциальной энергии
В устойчивом положении равновесия центр тяжести занимает самое низкое положение в сравнении со всеми возможными соседними положениями тела. Устойчивому равновесию соответствует минимум потенциальной энергии тела относительно ее величин в соседних положениях этого же тела. Принцип минимума потенциальной энергии — это один из общих принципов устойчивости равновесия разных систем.
Данное свойство применяют для поиска положения равновесия и при исследовании характера равновесия.
График потенциальной энергии в зависимости от одной из координат центра тела, например, шарика (рис.1 (а)) является вогнутой кривой. Название такого графика — потенциальная яма. Нижняя точка графика $E_p\left(x\right)$ соответствует положению устойчивого равновесия. Для потенциальной энергии взаимодействия с Землей ${(E}_p=mgh)$, форма потенциальной ямы на графике повторяет форму чаши, в которой расположено тело. \textit{}
Вертикальная колонна стоящая свободно находится в положении устойчивого равновесия, так как при маленьких наклонах ее центр масс увеличивает свое расстояние от опоры (рис.2). Это происходит до того момента пока вертикальная проекция цента масс не выйдет за пределы площади опоры, что означает угол отклонения колонны от вертикали превысил максимальное значение. Получается, что область устойчивости находится в переделах от минимума потенциальной энергии (вертикальное положение) до ближайшего к нему максимума. Если колонна лежит горизонтально, то ее область устойчивости является более широкой, чем у вертикальной колонны.
www.webmath.ru
Условия равновесия тел
Равновесие тела
Тело находится в состоянии покоя (или движется равномерно и прямолинейно), если векторная сумма всех сил, действующих на него, равна нулю. Говорят, что силы уравновешивают друг друга. Когда мы имеем дело с телом определенной геометрической формы, при вычислении равнодействующей силы можно все силы прикладывать к центру масс тела.
Условие равновесия телЧтобы тело, которое не вращается, находилось в равновесии, необходимо, чтобы равнодействующая всех сил, действующий на него, была равна нулю.
F→=F1→+F2→+..+Fn→=0.

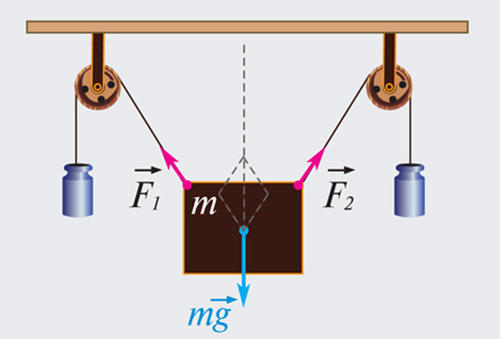
На рисунке выше изображено равновесие твердого тела. Брусок находится в состоянии равновесия под действием трех действующих не него сил. Линии действия сил F1→ и F2→ пересекаются в точке O. Точка приложения силы тяжести — центр масс тела C. Данные точки лежат на одной прямой, и при вычислении равнодействующей силы F1→, F2→ и mg→ приводятся к точке C.
Равновесие вращающегося тела. Правило моментов
Условия равенства нулю равнодействующей всех сил недостаточно, если тело может вращаться вокруг некоторой оси.
Плечом силы d называется длина перпендикуляра, проведенного от линии действия силы к точке ее приложения. Момент силы M — произведение плеча силы на ее модуль.
M=d·F.
Момент силы стремится повернуть тело вокруг оси. Те моменты, которые поворачивают тело против часовой стрелки, считаются положительными. Единица измерения момента силы в международной системе CИ — 1 Ньютонметр.
Определение. Правило моментовЕсли алгебраическая сумма всех моментов, приложенных к телу относительно неподвижной оси вращения, равна нулю, то тело находится в состоянии равновесия.
M1+M2+..+Mn=0

В общем случае для равновесия тел необходимо выполнение двух условий: равенство нулю равнодействующей силы и соблюдение правила моментов.
Безразличное, устойчивое и неустойчивое равновесие
В механике есть разные виды равновесия. Так, различают устойчивое и неустойчивое, а также безразличное равновесие.

Типичный пример безразличного равновесия — катящееся колесо (или шар), которое, если остановить его в любой точке, окажется в состоянии равновесия.
Устойчивое равновесие — такое равновесие тела, когда при его малых отклонениях возникают силы или моменты сил, которые стремятся вернуть тело в равновесное состояние.
Неустойчивое равновесие — состояние равновесия, при малом отклонении от которого силы и момент
zaochnik.com
Виды равновесия
Равновесие называют устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия. Это происходит, если при небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия.
Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия.
Равновесия называется безразличным, если при небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю.
Центр тяжести
Центром тяжестиназывается точка, через которую проходит равнодействующая сил тяжести при любом расположении тела.
Третий закон Ньютона
Тела действуют друг на друга с силами, вдоль одной прямой, равными по модулю и противоположными по направлению.Эти силы имеют одинаковую физическую природу; они приложены к разным телам и поэтому друг друга не компенсируют.
Сила упругости. Закон Гука
Сила упругостивозникает в результате деформации тела и направлена в сторону, противоположную деформации.
При малых по сравнению с размерами тел деформациях сила упругости прямо пропорциональна величине абсолютной деформации тела. В проекции на направление деформирования сила упругости равна
 ,
где
x– абсолютная деформация,k– коэффициент жесткости.
,
где
x– абсолютная деформация,k– коэффициент жесткости.
Этот закон был установлен экспериментально английским ученым Робертом Гуком и называется законом Гука:
Сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации.
Коэффициент пропорциональности в законе Гука называется жесткостью тела. Он зависит от формы и размеров тела и от материала, из которого оно изготовлено (уменьшается с увеличением длины и с уменьшением площади поперечного сечения – см. Молекулярную Физику).
В Си жесткость
выражается в ньютонах на метр: .
.
Упругая сила стремится восстановить форму тела, подвергнутого деформации, и приложена к телу, которое эту деформацию вызывает.
Природа силы упругости электромагнитная, т.к. сила упругости возникает в результате стремления электромагнитных сил, действующих между атомами вещества, вернуть атомы вещества в исходное положение при изменении их взаимного положения в результате деформации.
Упругая реакция опоры, нити, подвеса– пассивная сила, действующая всегда перпендикулярно поверхности опоры.
Сила трения. Коэффициент трения скольжения
Сила трениявозникает при соприкосновении поверхностей двух тел и всегда препятствует их взаимному перемещению.
Сила, возникающая на границе соприкосновения тел при отсутствии относительного движения называется силой трения покоя. Сила трения покоя – упругая сила, она равна по модуля внешней силе, направленной по касательной к поверхности соприкосновения тел, и противоположна ей по направлению.
При движении одного тела по поверхности другого возникает сила трения скольжения.
Сила трения имеет электромагнитную природу, т.к. возникает благодаря существованию сил взаимодействия между молекулами и атомами соприкасающихся тел – электромагнитных сил.
Сила трения скольжения прямо пропорциональна силе нормального давления (или упругой реакции опоры) и не зависит от площади поверхности соприкосновения тел {закон Кулона}:
 ,
где – коэффициент
трения.
,
где – коэффициент
трения.
Коэффициент трения зависит от рельефа поверхности и всегда меньше единицы: «сдвинуть легче, чем оторвать».
studfile.net
Равновесие тел. Виды равновесия. 10-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока: Изучить состояние равновесия тел, познакомиться с различными видами равновесия; выяснить условия, при которых тело находится в равновесии.
Задачи урока:
- Учебные: Изучить два условия равновесия, виды равновесия (устойчивое, неустойчивое, безразличное). Выяснить, при каких условиях тела более устойчивы.
- Развивающие: Способствовать развитию познавательного интереса к физике. Развитие навыков сравнивать, обобщать, выделять главное, делать выводы.
- Воспитательные: Воспитывать внимание, умения высказывать свою точку зрения и отстаивать её, развивать коммуникативные способности учащихся.
Тип урока: урок изучения нового материала с компьютерной поддержкой.
Оборудование:
- Диск «Движение и взаимодействие тел» из «Электронных уроков и тестов».
- Диск «Работа и мощность» из «Электронных уроков и тестов.
- Таблица «Условия равновесия».
- Призма наклоняющаяся с отвесом.
- Геометрические тела: цилиндр, куб, конус и т.д.
- Компьютер, мултимедиапроектор, интерактивная доска или экран.
- Презентация.
Ход урока
Сегодня на уроке мы узнаем, почему подъёмный кран не падает, почему игрушка «Ванька-встанька» всегда возвращается в исходное состояние, почему Пизанская башня не падает?
I. Повторение и актуализация знаний.
- Сформулировать первый закон Ньютона. О каком состоянии говорится в законе?
- На какой вопрос отвечает второй закон Ньютона? Формула и формулировка.
- На какой вопрос отвечает третий закон Ньютона? Формула и формулировка.
- Что называется равнодействующей силой? Как она находится?
- Из диска «Движение и взаимодействие тел» выполнить задание № 9 «Равнодействующая сил с разными направлениями» (правило сложения векторов (2, 3 упражнения)).
II. Изучение нового материала.
1. Что называется равновесием?
Равновесие – это состояние покоя.
2. Условия равновесия. (слайд 2)
а) Когда тело находится в покое? Из какого закона это следует?
Первое условие равновесия: Тело находится в равновесии, если геометрическая сумма внешних сил, приложенных к телу, равна нулю. ∑F = 0
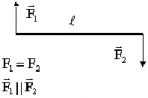
б) Пусть на доску действуют две равные силы, как показано на рисунке.
Будет ли она находиться в равновесии? (Нет, она будет поворачиваться)
В покое находится только центральная точка, а остальные движутся. Значит, чтобы тело находилось в равновесии, необходимо, чтобы сумма всех сил, действующих на каждый элемент равнялась 0.
Второе условие равновесия: Сумма моментов сил, действующих по часовой стрелке, должна равняться сумме моментов сил, действующих против часовой стрелки.
∑ Mпо часовой = ∑ Mпротив часовой
Момент силы: M = F L
L – плечо силы – кратчайшее расстояние от точки опоры до линии действия силы.
3. Центр тяжести тела и его нахождение. (слайд 4)
Центр тяжести тела – это точка, через которую проходит равнодействующая всех параллельных сил тяжести, действующих на отдельные элементы тела (при любом положении тела в пространстве).
Найти центр тяжести следующих фигур:
4. Виды равновесия.
а) (слайды 5–8)
Вывод: Равновесие устойчиво, если при малом отклонении от положения равновесия есть сила, стремящаяся вернуть его в это положение.
Устойчиво то положение, в котором его потенциальная энергия минимальна. (слайд 9)
б) Устойчивость тел, находящихся на точке опоры или на линии опоры. (слайды 10–17)
Вывод: Для устойчивости тела, находящегося на одной точке или линии опоры необходимо, чтобы центр тяжести находился ниже точки (линии) опоры.
в) Устойчивость тел, находящихся на плоской поверхности.
(слайд 18)
1) Поверхность опоры – это не всегда поверхность, которая соприкасается с телом (а та, которая ограниченна линиями, соединяющими ножки стола, треноги)
2) Разбор слайда из «Электронных уроков и тестов», диск «Работа и мощность», урок «Виды равновесия».
Рисунок 1.
- Чем различаются табуретки? (Площадью опоры)
- Какая из них более устойчивая? (С большей площадью)
- Чем различаются табуретки? (Расположением центра тяжести)
- Какая из них наиболее устойчива? (Укоторой центр тяжести ниже)
- Почему? (Т.к. её можно отклонить на больший угол без опрокидывания)
3) Опыт с призмой отклоняющейся
- Поставим на доску призму с отвесом и начнём её постепенно поднимать за один край. Что мы видим?
- Пока линия отвеса пересекает поверхность, ограниченную опорой, равновесие сохраняется. Но как только вертикаль, проходящая через центр тяжести, начнёт выходить за границы поверхности опоры, этажерка опрокидывается.
Разбор слайдов 19–22.
Выводы:
- Устойчиво то тело, у которого площадь опоры больше.
- Из двух тел одинаковой площади устойчиво то тело, у которого центр тяжести расположен ниже, т.к. его можно отклонить без опрокидывания на большой угол.
Разбор слайдов 23–25.
Какие корабли наиболее устойчивы? Почему? (У которых груз расположен в трюмах, а не на палубе)
Какие автомобили наиболее устойчивы? Почему? (Чтобы увеличить устойчивость машин на поворотах, полотно дороги наклоняют в сторону поворота.)
Выводы: Равновесие может быть устойчивым, неустойчивым, безразличным. Устойчивость тел тем больше, чем больше площадь опоры и ниже центр тяжести.
III. Применение знаний об устойчивости тел.
- Каким специальностям наиболее необходимы знания о равновесии тел?
- Проектировщикам и конструкторам различных сооружений (высотных зданий, мостов, телевизионных башен и т.д.)
- Цирковым артистам.
- Водителям и другим специалистам.
(слайды 28–30)
- Почему «Ванька-встанька» возвращается в положение равновесия при любом наклоне игрушки?
- Почему Пизанская башня стоит под наклоном и не падает?
- Каким образом сохраняют равновесие велосипедисты и мотоциклисты?
Выводы из урока:
- Существует три вида равновесия: устойчивое, неустойчивое, безразличное.
- Устойчиво положение тела, в котором его потенциальная энергия минимальна.
- Устойчивость тел на плоской поверхности тем больше, чем больше площадь опоры и ниже центр тяжести.
Домашнее задание: § 54–56 (Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский)
Использованные источники и литература:
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н.Сотский. Физика. 10 класс.
- Диафильм «Устойчивость» 1976 г. (отсканирован мною на плёночном сканере).
- Диск «Движение и взаимодействие тел» из «Электронных уроков и тестов».
- Диск «Работа и мощность» из «Электронных уроков и тестов».
urok.1sept.ru
Условия равновесия тел
Статикой называется раздел механики, изучающий условия равновесия тел.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

или 


|
Рисунок 1.14.1. Равновесие твердого тела под действием трех сил. При вычислении равнодействующей все силы приводятся к одной точке C |
На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил 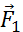 и
и  не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.
не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.
Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.
Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Произведение модуля силы 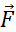 на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).
на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
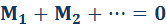
В Международной системе единиц (СИ) моменты сил измеряются в Ньютон—метрах (Н∙м).
|
Рисунок 1.14.2. Силы, действующие на рычаг, и их моменты. M1 = F1 · d1 > 0; M2 = – F2 · d2 < 0. При равновесии M1 + M2 = 0 |
В общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов сил.
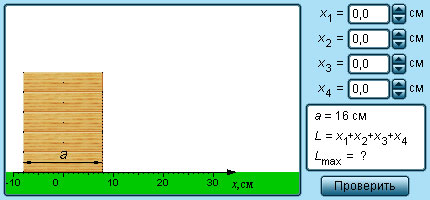 |
Модель. Равновесие брусков. |
Оба эти условия не являются достаточными для покоя.
|
Рисунок 1.14.3. Качение колеса по горизонтальной поверхности. Равнодействующая сила и момент сил равны нулю |
Катящееся по горизонтальной поверхности колесо – пример безразличного равновесия (рис. 1.14.3). Если колесо остановить в любой точке, оно окажется в равновесном состоянии. Наряду с безразличным равновесием в механике различают состояния устойчивого и неустойчивого равновесия.
Состояние равновесия называется устойчивым, если при малых отклонениях тела от этого состояния возникают силы или моменты сил, стремящиеся возвратить тело в равновесное состояние.
При малом отклонении тела из состояния неустойчивого равновесия возникают силы или моменты сил, стремящиеся удалить тело от положения равновесия.
Шар, лежащий на плоской горизонтальной поверхности, находится в состоянии безразличного равновесия. Шар, находящийся в верхней точке сферического выступа, – пример неустойчивого равновесия. Наконец, шар на дне сферического углубления находится в состоянии устойчивого равновесия (рис. 1.14.4).
|
Рисунок 1.14.4. Различные виды равновесия шара на опоре. (1) – безразличное равновесие, (2) – неустойчивое равновесие, (3) – устойчивое равновесие |
Для тела, имеющего неподвижную ось вращения, возможны все три вида равновесия. Безразличное равновесие возникает, когда ось вращения проходит через центр масс. При устойчивом и неустойчивом равновесии центр масс находится на вертикальной прямой, проходящей через ось вращения. При этом, если центр масс находится ниже оси вращения, состояние равновесия оказывается устойчивым. Если же центр масс расположен выше оси – состояние равновесия неустойчиво (рис. 1.14.5).
|
| Рисунок 1.14.5. Устойчивое (1) и неустойчивое (2) равновесие однородного круглого диска, закрепленного на оси O; точка C – центр массы диска; |
Особым случаем является равновесие тела на опоре. В этом случае упругая сила опоры приложена не к одной точке, а распределена по основанию тела. Тело находится в равновесии, если вертикальная линия, проведенная через центр масс тела, проходит через площадь опоры, т. е. внутри контура, образованного линиями, соединяющими точки опоры. Если же эта линия не пересекает площадь опоры, то тело опрокидывается. Интересным примером равновесия тела на опоре является падающая башня в итальянском городе Пиза (рис. 1.14.6), которую по преданию использовал Галилей при изучении законов свободного падения тел. Башня имеет форму цилиндра высотой 55 м и радиусом 7 м. Вершина башни отклонена от вертикали на 4,5 м.
Вертикальная линия, проведенная через центр масс башни, пересекает основание приблизительно в 2,3 м от его центра. Таким образом, башня находится в состоянии равновесия. Равновесие нарушится и башня упадет, когда отклонение ее вершины от вертикали достигнет 14 м. По-видимому, это произойдет очень нескоро.
|
Рисунок 1.14.6. Падающая Пизанская башня. Точка C – центр масс, точка O – центр основания башни, CC’ – вертикаль, проходящая через центр масс |
questions-physics.ru
 или
или 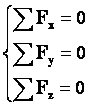


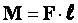

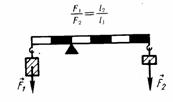
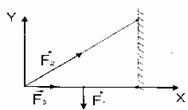
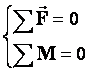



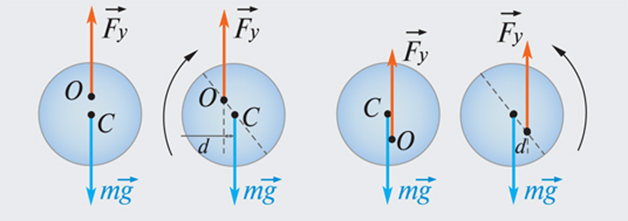
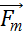 – сила тяжести;
– сила тяжести;  – упругая сила оси; d – плечо
– упругая сила оси; d – плечо