Механическое равновесие — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 сентября 2019; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 сентября 2019; проверки требуют 3 правки.

Механи́ческое равнове́сие — состояние механической системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и сумма моментов всех сил, приложенных к телу относительно любой произвольно взятой оси вращения, также равна нулю^[1].

В состоянии равновесия тело находится в покое (вектор скорости равен нулю) в выбранной системе отсчета либо движется равномерно прямолинейно или вращается без касательного ускорения.

В механике сплошной среды, где принимается гипотеза сплошности, такое определение неприменимо. К тому же данное определение ничего не говорит об одной из наиболее важных характеристик равновесия — его устойчивости. Поэтому более общее и распространённое определение механического равновесия звучит так:

Механическое равновесие — состояние системы, при котором её положение в конфигурационном пространстве находится в точке с нулевым градиентом потенциальной энергии.

Так как энергия и силы связаны фундаментальными зависимостями, это определение эквивалентно первому. Однако определение через энергию может быть расширено для того, чтобы получить информацию об устойчивости положения равновесия.

Различают три вида равновесия тел: устойчивое, неустойчивое и безразличное. Равновесие называется устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия. Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Равновесие называется безразличным, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил равна нулю

[1].

Приведём пример для системы с одной степенью свободы. В этом случае достаточным условием положения равновесия будет являться наличие локального экстремума потенциальной энергии в исследуемой точке. Как известно, условием локального экстремума дифференцируемой функции является равенство нулю её первой производной. Чтобы определить, когда эта точка является минимумом или максимумом, необходимо проанализировать её вторую производную. Устойчивость положения равновесия характеризуется следующими вариантами:

• неустойчивое равновесие;
• устойчивое равновесие;
• безразличное равновесие.

Неустойчивое равновесие[править | править код]

В случае, когда вторая производная отрицательна, потенциальная энергия системы находится в состоянии локального максимума. Это означает, что положение равновесия неустойчиво. Если система будет смещена на небольшое расстояние, то она продолжит своё движение за счёт сил, действующих на систему. Т. е. при выведении тела из равновесия оно не возвращается на исходную позицию.

Устойчивое равновесие[править | править код]

Вторая производная > 0: потенциальная энергия в состоянии локального минимума, положение равновесия устойчиво (см. Теорема Лагранжа об устойчивости равновесия). Если систему сместить на небольшое расстояние, она вернётся назад в состояние равновесия. Равновесие устойчиво, если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями. При таком равновесии выведенное из равновесия тело возвращается на первоначальное место.

Безразличное равновесие[править | править код]

Вторая производная = 0: в этой области энергия не варьируется, а положение равновесия является безразличным. Если система будет смещена на небольшое расстояние, она останется в новом положении. Если отклонить или сдвинуть тело оно останется в равновесии.

• Виды устойчивости
• 

  Неустойчивое равновесие

• 

  Устойчивое равновесие

• 

  Безразличное равновесие

Устойчивость в системах с большим числом степеней свободы[править | править код]

Если система имеет несколько степеней свободы, то может оказаться, что при отклонениях вдоль конкретного направления равновесие устойчиво, но если равновесие неустойчиво хотя бы в одном направлении, то оно неустойчиво и в целом. Простейшим примером такой ситуации является точка равновесия типа «седловина» или «перевал».

Равновесие системы с несколькими степенями свободы будет устойчивым только в том случае, если оно устойчиво по всем направлениям.

1. ↑ ^{1 2} Кабардин О. Ф. Физика. — М., Просвещение, 1985. — с. 32-36

Равновесие: определение, виды, примеры | Статья в журнале «Юный ученый»

 

1.               Цель проекта:

Изучение видов равновесия.

2.               Задачи:

Рассмотреть виды равновесия.

Выявить их отличия друг от друга.

Показать практическое применение описанных эффектов.

Опытным путём рассчитать зависимость вероятности падения хлеба маслом вниз от соотношения толщин хлеба и масла.

3.               Актуальность:

В природе всё пребывает в равновесии, нет предметов, у которых не было бы центра тяжести и зачастую его сложно определить.

Основная часть

4.               Теоретическая часть

Самая главная наука во вселенной — это физика. На физике, как на фундаменте, стоят все прочие науки. Физика — многогранна и сегодня речь пойдёт о механическом равновесии и его видах.

4.1.          Что такое равновесие

Что такое равновесие? Понятие равновесия — одно из самых универсальных в естественных науках.

Равновесие — это комплекс сил, которые действуя на одну систему, компенсируют друг друга и система не получает ускорение. А система— множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность, единство.

4.2.          Виды равновесия

Существует 3 вида равновесия: устойчивое, неустойчивое и безразличное.

Устойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, возвращается в прежнее положение.

Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.

Безразличное равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, не меняет своего положения (состояния).

 

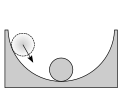
1 опыт: устойчивое равновесие: шарик неподвижно лежит на дне сферического углубления. При небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. Шарик возвращается в исходную точку.

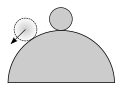
2 опыт: неустойчивое равновесие: шарик неподвижно лежит на вершине сферической поверхности. При небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия. Шарик не возвращается в исходную точку.

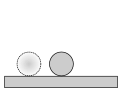
3 опыт: безразличное равновесие: шарик неподвижно лежит на плоской поверхности. При небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю. Шарик после перемещения не меняет своё положение.

4.3.          Применение принципов равновесия

Принципы устойчивого равновесия используются в строительстве зданий. Устойчивое равновесие корабля обеспечивает балласт в трюме.

Понятие устойчивости широко применяется в самолётостроении.

Устойчивость и управляемость летательного аппарата — взаимосвязанные свойства динамики полета.

Управляемость — свойство самолёта отвечать соответствующими линейными и угловыми перемещениями в пространстве на команды управления.

Устойчивость — свойство самолёта восстанавливать без вмешательства пилота кинематические параметры невозмущенного движения и возвращаться к исходному режиму полета после прекращения действия возмущений.

Устойчивое равновесие пассажирского самолёта обеспечивает верхнее расположение крыльев относительно фюзеляжа.

 

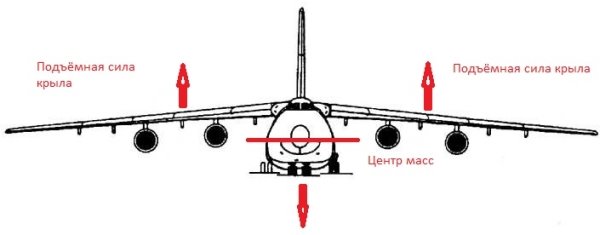
Неустойчивое равновесие применяется в строительстве военных самолётов.

 

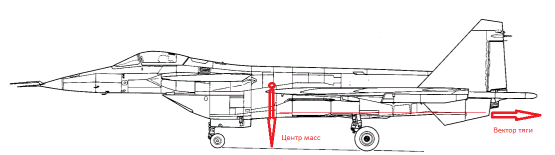
Для достижения сверх манёвренности нужно снизить устойчивость самолёта до нулевой или даже отрицательной — ввести его в состояние неустойчивого равновесия. Например, обеспечить взаимное расположение вектора тяги ниже центра масс. И нужно увеличить тягу двигателей настолько, чтобы она превышала вес самолёта. В таком случае говорят, что удельная тяга больше единицы.

При этом управлять им вручную, когда органы управления связаны напрямую с рулями, становится невозможно. Управление берёт на себя автоматика, а лётчик, грубо говоря, только приказывает ей, что делать. Такой принцип применяется в системах управления истребителей 5-го поколения.

А все самолёты на земле находятся в состоянии безразличного равновесия.

5.               Практическая часть

Физику многие боятся, как огня, считая трудной. Однако понимание зависит от способа изложения. Поехали?…

5.1.          Описание системы падающего бутерброда

Распространено убеждение, что бутерброд практически всегда падает маслом вниз. Это связано с равновесием.

Лучший способ исследования в смысле объективности — поставить эксперимент. Нужно ронять на пол бутерброды до тех пор, пока вы не придете к определенному выводу. Но это негигиенично, неэкономично и неэтично. Верный результат можно получить и с помощью мысленного эксперимента. Правда, при условии, что вы умеете доводить мысленный эксперимент до конца.

Для упрощения представим себе, что бутерброд, стоит на ребре. Предположим, что стол резко убрали. Как поведёт себя бутерброд?

Принимаем, что в самом бутерброде при его падении не возникает никаких сил, которые давали бы предпочтение одной из двух ситуаций или они бесконечно малы: трение воздуха о масло и о хлеб одинаково, ветра нет.

Ну а теперь перейдём к расчётам.

5.2.          Определение плотности хлеба и масла.

Для начала вычислим плотность масла и хлеба.

 

Размеры: 6×4,5×4см

Объём: 108 см3

Вес: 127 г

Плотность: 127 г/108 см3

ρ = 1,18 г/см3

 

 

Размеры: 7×9,5×10,5см

Объём: 698,3 см3

Вес: 318 г

Плотность: 318г / 698,3 см3

ρ = 0, 45 г/см3

5.3.          Расчет соотношения толщины хлеба и масла

Нарисуем схему бутерброда, стоящего на ребре.

 

Принимаем следующие обозначения:

М — толщина масла

Хл — толщина хлеба

М/2 — половина масла

М1 — расстояние от центра масс масла до центра масс бутерброда

Рм — сила, действующая на масло

Р — сила, действующая на бутерброд

Хл/2 — половина хлеба

Хл1 — расстояние от центра масс хлеба до центра масс бутерброда

Рхл — сила, действующая на хлеб

ЦМ — центр масс

Ц — центр бутерброда

Вычисляем силы, действующие на хлеб и масло:

Рм = m_м * g = ρ_м * V_м = ρ_м * S_бут * М

Рхл = ρ_хл * S_бут * Хл

Вычисляем силы, действующие на бутерброд:

М1 * Рм = Хл1 * Рхл

Хл1 + М1 = (Хл + М) / 2 =>

Хл1 * (ρ_хл * Хл + ρ_м * М)/ρ_м * М = (Хл + М)/2

Вычисляем расположение центра масс:

Хл1 = (Хл + М) * ρ_хл * М / 2*(ρ_хл * Хл + ρ_м * М)

Хл1 =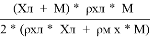

Цм = Хл1 + Хл/2

Цм = ((Хл + М) * ρ_хл * М)/ (2*(ρ_хл * Хл + ρ_м * М)) + Хл/2

Вычисляем расположение центра бутерброда:

Ц = (М+Хл)/2

Сравниваем расположение центра масс и центра бутерброда.

Условия падения бутерброда маслом вниз:

Цм>Ц

Данные и формулы заносим в таблицу Exel. Полученные результаты расчётов приведены в таблице 1.

 

Таблица 1

Толщина хлеба Хл			Толщина хлеба Хл			Толщина хлеба Хл
1	см		1,5	см		2	см
Толщина масла	Центр бутерброда	Центр масс	Толщина масла	Центр бутерброда	Центр масс	Толщина масла	Центр бутерброда	Центр масс
М	Ц,	Цм	М	Ц,	Цм	М	Ц,	Цм
см	см	см	см	см	см	см	см	см
0,1	0,55	0,61	0,1	0,8	0,87	0,1	1,05	1,12
0,2	0,6	0,71	0,2	0,85	0,97	0,2	1,1	1,23
0,3	0,65	0,79	0,3	0,9	1,06	0,3	1,15	1,32
0,4	0,7	0,86	0,4	0,95	1,14	0,4	1,2	1,41
0,5	0,75	0,93	0,5	1	1,22	0,5	1,25	1,49
0,6	0,8	0,99	0,6	1,05	1,29	0,6	1,3	1,57
0,7	0,85	1,05	0,7	1,1	1,36	0,7	1,35	1,65
0,8	0,9	1,11	0,8	1,15	1,42	0,8	1,4	1,72
0,9	0,95	1,17	0,9	1,2	1,48	0,9	1,45	1,78
1	1	1,22	1	1,25	1,55	1	1,5	1,85
1,1	1,05	1,28	1,1	1,3	1,61	1,1	1,55	1,92
1,2	1,1	1,33	1,2	1,35	1,66	1,2	1,6	1,98
1,3	1,15	1,39	1,3	1,4	1,72	1,3	1,65	2,04
1,4	1,2	1,44	1,4	1,45	1,78	1,4	1,7	2,10
1,5	1,25	1,50	1,5	1,5	1,84	1,5	1,75	2,16

 

Итак, делаем следующие выводы:

1.               Мы рассмотрели виды равновесия
2.               Показали практическое применение физических принципов равновесия на примере авиации.
3.               Вычислили и доказали, что плотность масла больше плотности хлеба.
4.               Провели расчёты устойчивости системы бутерброд — масло.
5.               Рассмотрели действующие на систему силы и определили, что при наших условиях бутерброд всегда должен падать маслом вниз.

Заключительная часть

Мы живём в удивительном мире, нам хочется понять то, что мы видим вокруг, ищем ответы на вопросы: почему деревья качаются, почему в дырках ничего нет, почему апельсины круглые, почему всё происходит так, а не иначе? Мы попытались приблизиться к пониманию того многообразия сил, которые действуют на тела, в том числе и на нас даже в состоянии покоя. Отличаясь по масштабам как от атомов, так и от звёзд мы раздвигаем горизонты исследований, чтобы охватить как очень маленькие, так и очень большие объекты.

Хочется закончить словами Стивена Хокинга: «И, если будут найдены ответы на все вопросы, это будет полным триумфом человеческого разума, ибо тогда нам станет понятен замысел Бога».

 

Литература:

 

1.               Сайт https://ru.wikipedia.org/
2.               Учебник физики 7–9 класс Пёрышкин А. В.
3.               Учебник математики 8 класс Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова
4.               Заочная физико-техническая школа ФИЗИКА «Векторы в физике»
5.               Я. И. Перельман Занимательная физика

Виды равновесия в физике, теория и онлайн калькуляторы

Если тело находится в состоянии равновесия, то сумма внешних сил, действующих на него равна нулю, равна нулю и сумма моментов этих сил относительно любой оси.

Виды равновесия. Устойчивое, неустойчивое и безразличное равновесие

Равновесие делят на: устойчивое, неустойчивое и безразличное.

Определение

Равновесие тела называют устойчивым, если при небольших смещениях, действующие на него силы, стремятся вернуть его снова в положение равновесия.

Определение

Положение равновесия называют неустойчивым, если при малых смещениях силы, оказывающие воздействие на тело уводят его из положения равновесия еще больше.

Если при небольших смещениях из положения равновесия силы, действующие на тело и их моменты, уравновешиваются, как и прежде, то такое равновесие называют безразличным.

Классическим примером типов равновесия служит положение шарика на опорах различной формы. Рис. 1 (а) шарик находится в положении устойчивого равновесия. Рис.1 (б) равновесие тела неустойчивое. Рис.1 (в) положение тела безразличное.

Если тело имеет точку опоры (как шарик на рис.1), и равнодействующая всех сил, приложенных к телу, направлена к положению равновесия, то тело находится в устойчивом равновесии. В том случае, если равнодействующая направлена в сторону противоположную точке равновесия, то тело в неустойчивом равновесии. Если равнодействующая сил, приложенных к телу равна нулю, то равновесие безразличное.

Вид равновесия тела зависит от распределения его массы и положения этого тела относительно других тел.

Принцип минимума потенциальной энергии

В устойчивом положении равновесия центр тяжести занимает самое низкое положение в сравнении со всеми возможными соседними положениями тела. Устойчивому равновесию соответствует минимум потенциальной энергии тела относительно ее величин в соседних положениях этого же тела. Принцип минимума потенциальной энергии — это один из общих принципов устойчивости равновесия разных систем.

Данное свойство применяют для поиска положения равновесия и при исследовании характера равновесия.

График потенциальной энергии в зависимости от одной из координат центра тела, например, шарика (рис.1 (а)) является вогнутой кривой. Название такого графика — потенциальная яма. Нижняя точка графика $E_p\left(x\right)$ соответствует положению устойчивого равновесия. Для потенциальной энергии взаимодействия с Землей ${(E}_p=mgh)$, форма потенциальной

Устойчивое равновесие в физике, теория и онлайн калькуляторы

Определение

Если тело находится в состоянии покоя относительно инерциальной системы отсчета, то считают, что оно находится в равновесии.

Условия равновесия изучает раздел физики, который называют статикой.

Условия равновесия тела

Первое условие равновесия можно сформулировать исходя, из второго закона Ньютона: тело может находиться в состоянии покоя в некоторой инерциальной системе отсчета только, если равнодействующая всех сил, приложенных к этому телу (материальной точке) равна нулю:

\[\sum\limits^N_{i=1}{{\overline{F}}_i=0\left(1\right).}\]

Выражение (1) называют необходимым условием равновесия тела.

Если тело не подходит под определение материальной точки, то первого условия равновесия недостаточно.

Если тело может вращаться около некоторой оси, то оно находится в состоянии равновесия, если сумма моментов всех действующих на него сил относительно любой оси вращения равна нулю:

\[\sum\limits^N_{i=1}{{\overline{M}}_i=0\left(2\right).}\]

Второе условие равновесия называют правилом моментов сил. $\ $\textit{}

Выше названные условия являются достаточными для того, чтобы тело считать находящимся в равновесии.

Виды равновесия

Равновесие можно разделить на: устойчивое, неустойчивое и безразличное.

Равновесие тела называют устойчивым, если при небольших смещениях, действующие на него силы, стремятся вернуть его снова в положение равновесия.

Положение равновесия называют неустойчивым, если при малых смещениях силы, оказывающие воздействие на тело уводят его из положения равновесия еще больше.

Если при небольших смещениях из положения равновесия силы, действующие на тело и их моменты, уравновешиваются, как и прежде, то такое равновесие называют безразличным.

В устойчивом положении равновесия центр тяжести занимает самое низкое положение в сравнении со всеми возможными соседними положениями тела.

1) Допустим, что тело может вращаться около закрепленной оси. Тело находится в положении равновесия, если ось проходит через центр масс тела (безразличное равновесие). Если центр тяжести тела находится ниже оси вращения, то положение равновесия тела будет устойчивым. Пусть ось вращения расположена ниже центра масс тела, то равновесие будет неустойчивым.

2) В том случае, если тело имеет точку опоры (например, шарик, лежащий на опоре), то тело находится в состоянии устойчивого равновесия, когда равнодействующая всех сил, приложенных к телу, направлена в сторону положения равновесия. Если равнодействующая равна нулю, то положение равновесия безразличное. Положение тела будет не устойчивым равновесием, если равнодействующая сил, приложенных к телу, направлена от положения равновесия.

3) Пусть тело имеет площадь опоры. Тогда его равновесие будет устойчивым, если вертикаль, проводимая через центр масс этого тела, пересечет площадь опоры.

Потенциальная энергия и устойчивое равновесие

Как было сказано тело может находиться в состоянии равновесия только, если равнодействующая всех сил, приложенных к телу, равна нулю. Следовательно, равновесию соответствует точка минимума (M) или максимума (N) потенциальной энергии ($E_p$), так как в этих точках сила становится равной нулю. Но, следует заметить, что точки максимума и минимума энергии не являются равноценными (рис.1).

Т. Виды равновесия — PhysBook

Виды равновесия

Рис. 1

Для того чтобы судить о поведении тела в реальных условиях, мало знать, что оно находится в равновесии. Надо еще оценить это равновесие. Различают устойчивое, неустойчивое и безразличное равновесие.

Равновесие тела называют устойчивым, если при отклонении от него возникают силы, возвращающие тело в положение равновесия (рис. 1, а, положение 2). В устойчивом равновесии центр тяжести тела занимает наинизшее из всех близких положений. Положение устойчивого равновесия связано с минимумом потенциальной энергии по отношению ко всем близким соседним положениям тела.

Равновесие тела называют неустойчивым, если при самом незначительном отклонении от него равнодействующая действующих на тело сил вызывает дальнейшее отклонение тела от положения равновесия (рис. 1, а, положение 1). В положении неустойчивого равновесия высота центра тяжести максимальна и потенциальная энергия максимальна по отношению к другим близким положениям тела.

Равновесие, при котором смещение тела в любом направлении не вызывает изменения действующих на него сил и равновесие тела сохраняется, называют безразличным (рис. 1, а, положение 3).

Безразличное равновесие связано с неизменной потенциальной энергией всех близких состояний, и высота центра тяжести одинакова во всех достаточно близких положениях.

Тело, имеющее ось вращения (например, однородная линейка, которая может вращаться вокруг оси, проходящей через точку О, изображенная на рисунке 1, б), находится в равновесии, если вертикальная прямая, проходящая через центр тяжести тела, проходит через ось вращения. Причем если центр тяжести С выше оси вращения (рис. 1, б; 1), то при любом отклонении от положения равновесия потенциальная энергия уменьшается и момент силы тяжести относительно оси О отклоняет тело дальше от положения равновесия. Это неустойчивое положение равновесия. Если центр тяжести находится ниже оси вращения (рис. 1, б; 2), то равновесие устойчивое. Если центр тяжести и ось вращения совпадают (рис. 1, б; 3), то положение равновесия безразличное.

Тело, имеющее площадь опоры, находится в равновесии, если вертикальная прямая, проходящая через центр тяжести тела не выходит за пределы площади опоры этого тела, т.е. за пределы контура образованного точками соприкосновения тела с опорой Равновесие в этом случае зависит не только от расстояния между центром тяжести и опорой (т.е. от его потенциальной энергии в гравитационном поле Земли), но и от расположения и размеров площади опоры этого тела.

На рисунке 1, в изображено тело, имеющее форму цилиндра. Если его наклонить на малый угол, то оно возвратится в исходное положение 1 или 2 Если же его отклонить на угол β (положение 3), то тело опрокинется. При заданной массе и площади опоры устойчивость тела тем выше, чем ниже расположен его центр тяжести, т.е. чем меньше угол между прямой, соединяющей центр тяжести тела и крайнюю точку соприкосновения площади опоры с горизонтальной плоскостью.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 85-87.

Равновесие тел в физике, теория и онлайн калькуляторы

Тело находится в состоянии равновесия, если оно покоится относительно некоторой инерциальной системы отсчета. Изучение условий равновесия тел имеет большое прикладное значение при создании зданий, сооружений, машин и механизмов.

Условия равновесия тел

Первое условие равновесия формулируется, из второго закона Ньютона: тело может находиться в состоянии покоя в некоторой инерциальной системе отсчета только, если равнодействующая всех сил, приложенных к этому телу (материальной точке) равна нулю. И так, первое условие равновесия записывается так:

\[\sum\limits^N_{i=1}{{\overline{F}}_i=0\left(1\right).}\]

Для нахождения тела в состоянии равновесия, необходимо равенство нулю равнодействующей, приложенных к телу сил.

Если тело нельзя считать материальной точкой, то первого условия равновесия будет недостаточно. Рассмотрим стержень на который действуют две равные по модулю, и противоположные по направлению силы (${\overline{F}}_1\ и{\ \overline{F}}_2\ $) рис.1. Данный стержень может вращаться около своей оси, следовательно, он не находится в состоянии равновесия.

Для формулировки второго условия равновесия используем такую физическую величину, как момент силы ($\overline{M}$):

\[\overline{M}=\overline{r}\times \overline{F\ }\left(2\right),\]

где $\overline{r}\times \overline{F\ }$ — векторное произведение; $\left|\overline{M}\right|=\left|\overline{r}\right|\cdot \left|\overline{F\ }\right|{\sin \widehat{\overline{r},\overline{F\ }}\ }$; $\widehat{\overline{r},\overline{F\ }}$ — угол между вектором силы и радиус-вектором ($\overline{r}$), который проведен от точки вращения к точке приложения силы. Направление вектора момента силы определяют по правилу правого винта (Правый винт вращают от вектора $\overline{r}\ $к вектору $\overline{F\ }$ по кратчайшему расстоянию, при этом поступательное движение винта указывает направление вектора момента силы).

Тело, которое имеет возможность вращаться вокруг неподвижной оси, находится в состоянии равновесия, если сумма моментов всех действующих на него сил относительно любой оси вращения равна нулю:

\[\sum\limits^N_{i=1}{{\overline{M}}_i=0\left(3\right).}\]

Второе условие равновесия называют правилом моментов сил. $\ $\textit{}

Виды равновесия тел

Равновесие можно разделить на: устойчивое, неустойчивое и безразличное.

Равновесие тела называют устойчивым, если при небольших смещениях, действующие на него силы, стремятся вернуть его снова в положение равновесия.

Положение равновесия называют неустойчивым, если при малых смещениях силы, оказывающие воздействие на тело уводят его из положения равновесия еще больше.

Если при небольших смещениях из положения равновесия силы, действующие на тело и их моменты, уравновешиваются, как и прежде, то такое равновесие называют безразличным.

В устойчивом положении равновесия центр тяжести занимает самое низкое положение в сравнении со всеми возможными соседними положениями тела. Устойчивому равновесию соответствует минимум потенциальной энергии тела относительно ее величин в соседних положениях этого же тела. Принцип минимума потенциальной энергии — это один из общих принципов устойчивости равновесия разных систем.

1) Допустим, что тело может вращаться около закрепленной оси. Тело находится в положении равновесия, если ось проходит через центр масс тела (безразличное равновесие). Если центр тяжести тела находится ниже оси вращения, то положение равновесия тела будет устойчивым. Пусть ось вращения расположена ниже центра масс тела, то ра

Равновесие тел

Все вы отлично знаете значение слова «равновесия». Например, в равновесии могут находиться весы, равновесие может держать едущий велосипедист или бегущий человек.

В физике под равновесием понимается состояние покоя. Например, дом и большинство его частей покоятся относительно Земли, несмотря на то, что этот дом находится под воздействием различных сил. Любое реальное тело деформируется под воздействием тех или иных сил. Если эти силы вызывают значительные деформации, такие, как растяжение пружины или изгиб металлической линейки, ни в коем случае нельзя считать, что эти тела находятся в равновесии. Если тело двигается и при этом существенно деформируется, то, по мере его движения, меняется его форма и, некоторые силы начинают действовать на данное тело по-разному. Кроме того, с изменением формы постоянно меняется модуль и направление внутренних сил. Вы можете себе представить, насколько сложно описать такое движение математически.

Однако, во многих случаях на практике эти деформации незначительны. В таких случаях мы можем говорить о равновесии абсолютно твердых тел, тем самым пренебрегая их деформацией.

Скажем, бревенчатый дом, находясь на Земле, разумеется, находится в состоянии равновесия.

Каждое бревно, балка или кусок шифера не двигаются относительно Земли. Хотя, если присмотреться, то можно обнаружить, что некоторые бревна деформировались под действием веса других бревен. Мы можем увидеть какие-то незначительные изменения формы бревен или досок. Но, как правило, этими изменениями можно пренебречь. Поэтому, дом можно считать абсолютно твердым телом, находящимся в равновесии.

Возьмем некое произвольное тело и выберем несколько произвольных элементов этого тела. На каждый элемент тела может действовать несколько внешних и несколько внутренних сил.

В данном примере мы будем рассматривать равнодействующие внешних сил и равнодействующие внутренних сил. Черными стрелочками обозначены равнодействующие некоторых сил, которые действуют извне на различные элементы тела. Оранжевыми стрелочками обозначены воздействия элементов тела друг на друга посредством внутренних сил. Но, как вы знаете, всякое действие имеет противодействие. Противодействие каждого элемента обозначено зелеными стрелочками. Так вот, если тело находится в состоянии покоя, то ускорение каждого элемента должно быть равно нулю. Следовательно, равнодействующая сила, действующая на каждый из элементов, равна нулю.

Таким образом, можно утверждать, что если равнодействующая сила внутренних и внешних сил, действующих на каждый элемент тела, равна нулю, то тело находится в равновесии.

Рассмотрим несколько простых примеров. На каждую точку припаркованной машины действует сила тяжести. Эту силу тяжести уравновешивает реакция опоры в тех точках, которые взаимодействуют с опорой. В точках, которые не соприкасаются с опорой, силу тяжести уравновешивает сила упругости, препятствующая деформации.

В действительности мы знаем, что если машину как следует нагрузить, то она немного просядет, но этой деформацией можно пренебречь, поскольку изменение формы машины весьма незначительно.

Также можно привести в пример лодку, находящуюся на воде. При мертвом штиле и выключенном моторе лодка будет находиться в равновесии. На каждую её точку будет действовать сила тяжести и сила Архимеда. Сумма этих сил будет равна нулю.

Раздел механики, изучающий равновесие и условия равновесия абсолютно твердых тел, называется статикой. В этом разделе мы будем считать все тела абсолютно твердыми и рассматривать случаи, когда эти тела находятся в состоянии покоя.

Необходимо отметить, что существует три вида равновесия: устойчивое, неустойчивое и безразличное.

Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.

Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.

Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.