Ядерная энергия — Википедия

Ядерная энергия (атомная энергия) — энергия, содержащаяся в атомных ядрах и выделяемая при ядерных реакциях и радиоактивном распаде.

В природе ядерная энергия выделяется в звёздах, а человеком применяется, в основном, в ядерном оружии и ядерной энергетике, в частности, на атомных электростанциях.

Открытие нейтрона в 1932 году (Джеймс Чедвик) можно считать началом современной ядерной физики.^[1]

Боровская модель атома представляет из себя положительно заряженное ядро, где сконцентрирована почти вся масса атома (оно состоит из нейтронов и протонов), в окружении нескольких оболочек из очень лёгких отрицательно заряженных частиц (электронов). Размер атома оказывается порядка ангстрема (10⁻¹⁰ м), в то время как размеры ядра составляют от одного до нескольких ферми (10⁻¹⁵ м), то есть ядро меньше атома в 100 000 раз.

Электрически нейтральные атомы содержат одинаковое число электронов и протонов. Химический элемент однозначно определяется числом протонов в ядре, это число называется атомным номером (

Z). Число нейтронов (N) в ядрах атомов данного элемента может варьироваться. Для малых Z это число у бета-стабильных ядер близко к числу протонов (N ≈ Z), но с увеличением Z, чтобы ядро оставалось стабильным, число нейтронов должно расти быстрее, чем Z. Атомы, которые отличаются только числом нейтронов в ядре, называются изотопами одного и того же элемента. Общее число нуклонов (то есть протонов и нейтронов) в ядре называется массовым числом A = Z + N.

Для названия изотопа обычно используется буквенное обозначение химического элемента с верхним индексом — атомной массой и (иногда) нижним индексом — атомным номером; например, изотоп уран-238 может быть записан в виде 92238U.{\displaystyle {}_{92}^{238}\mathrm {U} .}

Нуклоны, из которых состоят ядра, обладают относительно малой массой (около 1 а.е.м.), электрический заряд протона положителен, а нейтрон не заряжен. Поэтому, если учитывать только существование электромагнитных и гравитационных сил, ядро будет нестабильно (одноимённо заряженные частицы будут отталкиваться, разрушая ядро, а массы нуклонов недостаточно велики, чтобы гравитация могла противодействовать кулоновскому отталкиванию), что делало бы невозможным существование материи. Из очевидного факта существования материи вытекает, что в модель необходимо добавить третью силу, которую назвали сильным взаимодействием (строго говоря, между нуклонами в ядре действует главным образом не само сильное взаимодействие как таковое, а остаточные ядерные силы, обусловленные сильным взаимодействием). Эта сила должна, в частности, быть очень интенсивной, притягивающей на очень коротких расстояниях (на расстояниях порядка размеров ядра) и отталкивающей на ещё более коротких расстояниях (порядка размеров нуклона), центральной в определённом диапазоне расстояний, зависящей от спина и не зависящей от типа нуклона (нейтроны или протоны). В 1935 году Хидеки Юкава создал первую модель этой новой силы, постулировав существование новой частицы, пиона. Легчайший из мезонов он отвечает за бо́льшую часть потенциала между нуклонами на расстоянии порядка 1 фм. Потенциал Юкавы, который адекватно описывает взаимодействие двух частиц со спинами s1{\displaystyle s_{1}} и s2{\displaystyle s_{2}}, можно записать в виде:

V(r)=gπ2(mπc2)33(Mc2)2ℏ2[s1s2+S121+3Rr+3R2r2]e−rRrR.{\displaystyle V(r)={\frac {g_{\pi }^{2}(m_{\pi }c^{2})^{3}}{3(Mc^{2})^{2}{\hbar }^{2}}}\left[s_{1}s_{2}+S_{12}1+{\frac {3R}{r}}+{\frac {3R^{2}}{r^{2}}}\right]{\frac {e^{-{\frac {r}{R}}}}{\frac {r}{R}}}.}

Другие эксперименты, проводившиеся на ядрах, показали, что их форма должна быть приблизительно сферической с радиусом R=1,5⋅A1/3{\displaystyle R=1,5\cdot A^{1/3}} фм, где A — атомная масса, то есть количество нуклонов. Отсюда вытекает, что плотность ядер (и количество нуклонов на единицу объёма) постоянна. В самом деле, V∼R3∼A,{\displaystyle V\sim R^{3}\sim A,} то есть объём пропорционален А. Так как плотность рассчитывается путём деления массы на объём, ρ=AV=const.{\displaystyle \rho ={\frac {A}{V}}={\rm {{const}.}}} Это привело к описанию ядерной материи как несжимаемой жидкости и к появлению капельной модели ядра как фундаментальной модели, необходимой для описания деления ядер.

Энергия связи[править | править код]

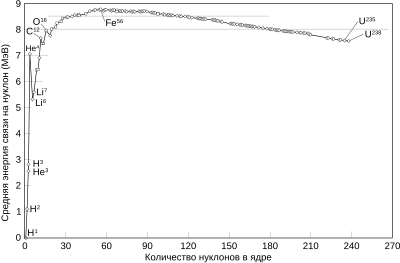Зависимость удельной энергии связи (то есть энергии связи, приходящейся на один нуклон) от числа нуклонов в ядре.

Хотя ядро состоит из нуклонов, однако масса ядра — это не просто сумма масс нуклонов. Энергия, которая удерживает вместе эти нуклоны, наблюдается как разница в массе ядра и массах составляющих его отдельных нуклонов, с точностью до коэффициента c², связывающего массу и энергию уравнением E=m⋅c2.{\displaystyle E=m\cdot c^{2}.} Таким образом, определив массу атома и массу его компонент, можно определить среднюю энергию на нуклон, удерживающую вместе различные ядра.

Из графика можно видеть, что очень лёгкие ядра имеют меньшую энергию связи на нуклон, чем ядра, которые немного тяжелее (в левой части графика). Это является причиной того, что в термоядерных реакциях (то есть при слиянии лёгких ядер) выделяется энергия. И наоборот, очень тяжёлые ядра в правой части графика имеют более низкую энергию связи на нуклон, чем ядра средней массы. В связи с этим деление тяжёлых ядер также энергетически выгодно (то есть происходит с выделением ядерной энергии). Следует отметить также, что при слиянии (в левой части) разница масс гораздо больше, чем при делении (в правой части).

Энергия, которая требуется, чтобы разделить полностью ядро на отдельные нуклоны, называется энергией связи E_с ядра. Удельная энергия связи (то есть энергия связи, приходящаяся на один нуклон, ε = E_с/A, где A — число нуклонов в ядре, или массовое число), неодинакова для разных химических элементов и даже для изотопов одного и того же химического элемента. Удельная энергия связи нуклона в ядре меняется в среднем в пределах от 1 МэВ у лёгких ядер (дейтерий) до 8,6 МэВ у ядер средней массы (с массовым числом А ≈ 100). У тяжёлых ядер (А ≈ 200) удельная энергия связи нуклона меньше, чем у ядер средней массы, приблизительно на 1 МэВ, так что их превращение в ядра среднего веса (деление на 2 части) сопровождается выделением энергии в количестве около 1 МэВ на нуклон, или около 200 МэВ на ядро. Превращение лёгких ядер в более тяжёлые ядра даёт ещё больший энергетический выигрыш в расчёте на нуклон. Так, например, реакция соединения ядер дейтерия и трития

1D2+1T3→2He4+0n1{\displaystyle \mathrm {{_{1}}D^{2}+{_{1}}T^{3}\rightarrow {_{2}}He^{4}+{_{0}}n^{1}} }

сопровождается выделением энергии 17,6 МэВ, то есть 3,5 МэВ на нуклон^[2].

Деление ядер[править | править код]

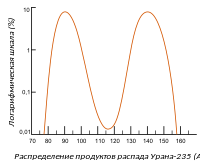Типичное распределение масс осколков деления. График представлен для урана-235.

Э. Ферми после открытия нейтрона провёл серию экспериментов, в которых различные ядра бомбардировались этими новыми частицами. В этих экспериментах обнаружено, что нейтроны низкой энергии часто поглощаются ядром с испусканием фотона (так называемый радиоактивный захват нейтрона).

Чтобы исследовать эту реакцию, эксперимент систематически повторялся для всех элементов периодической таблицы. В результате были обнаружены новые радиоактивные изотопы элементов, служивших мишенями. Однако при облучении урана был обнаружен ряд других, лёгких элементов. Лиза Мейтнер, Отто Ган и Фриц Штрассман смогли это объяснить, предположив, что ядро урана при захвате нейтрона разделится на две примерно равные массы. Действительно, в продуктах реакции был обнаружен барий с атомной массой около половины массы урана. Позже было обнаружено, что это деление происходило не во всех изотопах урана, но только в ²³⁵U. А ещё позже стало известно, что это деление может привести к множеству различных элементов, распределение которых по массе напоминает двойной горб верблюда.

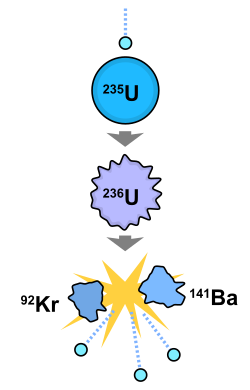Схема деления ²³⁵U. Низкоскоростной (тепловой) нейтрон, захваченный ядром урана, дестабилизирует его, и оно делится на две части, а также испускает 2-3 (в среднем 2,5) нейтрона деления.

При делении урана тепловым нейтроном возникает не только два более лёгких ядра (осколка деления), но также излучаются 2 или 3 (в среднем 2,5 для ²³⁵U) нейтрона, имеющие высокую кинетическую энергию. Для урана, как тяжёлого ядра, не выполняется соотношение N ≈ Z (равное число протонов и нейтронов), которое имеет место для более лёгких элементов, так что продукты деления нейтронно-избыточны. В результате эти продукты деления оказываются бета-радиоактивными: избыточные нейтроны ядра постепенно превращаются в протоны (с испусканием бета-частиц), а само ядро, сохраняя массовое число, движется по изобарической цепочке к ближайшему на ней бета-стабильному ядру. Деление ²³⁵U может произойти в более чем 40 вариантах, что порождает более 80 различных продуктов деления, которые, в свою очередь, распадаясь, формируют цепочки распада, так что в конечном счёте продукты деления урана включают около 200 нуклидов (непосредственно или как дочерние нуклиды).

Энергия, выделяющаяся при делении каждого ядра ²³⁵U, составляет в среднем около 200 МэВ. Минералы, используемые для добычи урана, содержат, как правило, около 1 г на кг урановой руды (настуран, например). Поскольку изотопное содержание ²³⁵U в природном уране всего 0,7 %, получаем, что на каждый килограмм добытой руды будет приходиться 1,8·10¹⁹ атомов ²³⁵U. Если все эти атомы ²³⁵U из 1 грамма урана поделятся, то выделится 3,6·10²⁷ эВ = 5,8·10⁸ Дж энергии. Для сравнения, при сжигании 1 кг угля наилучшего качества (антрацит) выделяется энергия около 4·10⁷ Дж энергии, то есть для получения ядерной энергии, содержащейся в 1 кг природного урана, необходимо сжечь более 10 тонн антрацита.

Появление 2,5 нейтронов на акт деления позволяет осуществить цепную реакцию, если из этих 2,5 нейтронов как минимум один сможет произвести новое деление ядра урана. Обычно испускаемые нейтроны не делят ядра урана сразу же, но сначала должны быть замедлены до тепловых скоростей (2200 м/с при

T=300 K). Замедление достигается наиболее эффективно с помощью окружающих атомов другого элемента с малым A, например водорода, углерода и т. п. материала, называемого замедлителем.

Некоторые другие ядра также могут делиться при захвате медленных нейтронов, например ²³³U или ²³⁹Pu. Однако возможно также деление быстрыми нейтронами (высокой энергии) таких ядер как ²³⁸U (его в 140 раз больше, чем ²³⁵U) или ²³²Th (его в земной коре в 400 раз больше, чем ²³⁵U).

Элементарная теория деления была создана Нильсом Бором и Дж. Уилером с использованием капельной модели ядра.

Деление ядер также может быть достигнуто с помощью быстрых альфа-частиц, протонов или дейтронов. Однако эти частицы, в отличие от нейтронов, должны иметь большую энергию для преодоления кулоновского барьера ядра.

Известны экзотермические ядерные реакции, высвобождающие ядерную энергию.

Обычно для получения ядерной энергии используют цепную ядерную реакцию деления ядер урана-235 или плутония, реже других тяжёлых ядер (уран-238, торий-232). Ядра делятся при попадании в них нейтрона, при этом получаются новые нейтроны и осколки деления. Нейтроны деления и осколки деления обладают большой кинетической энергией. В результате столкновений осколков с другими атомами эта кинетическая энергия быстро преобразуется в тепло.

Другим способом высвобождения ядерной энергии является термоядерный синтез. При этом два ядра лёгких элементов соединяются в одно тяжёлое. В природе такие процессы происходят на Солнце и в других звёздах, являясь основным источником их энергии.

Многие атомные ядра являются неустойчивыми. С течением времени часть таких ядер самопроизвольно превращаются в другие ядра, высвобождая энергию. Такое явление называют радиоактивным распадом.

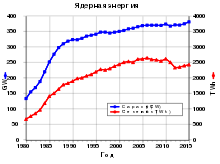Установленная мощность (синяя линия) и годовое производство энергии (красная линия) ядерными электростанциями с 1980 по 2012 гг.

Деление[править | править код]

В настоящее время из всех источников ядерной энергии наибольшее практическое применение имеет энергия, выделяющаяся при делении тяжёлых ядер. В условиях дефицита энергетических ресурсов ядерная энергетика на реакторах деления считается наиболее перспективной в ближайшие десятилетия. На атомных электрических станциях ядерная энергия используется для получения тепла, используемого для выработки электроэнергии и отопления. Ядерные силовые установки решили проблему судов с неограниченным районом плавания (атомные ледоколы, атомные подводные лодки, атомные авианосцы).

Энергия деления ядер урана или плутония применяется в ядерном и термоядерном оружии (как пускатель термоядерной реакции и как источник дополнительной энергии при делении ядер нейтронами, возникающими в термоядерных реакциях).

Существовали экспериментальные ядерные ракетные двигатели, но испытывались они исключительно на Земле и в контролируемых условиях, по причине опасности радиоактивного загрязнения в случае аварии.

Атомные электростанции в 2012 году производили 13 % мировой электроэнергии и 5,7 % общего мирового производства энергии^[3][4]. Согласно отчёту Международного агентства по атомной энергии (МАГАТЭ), на 2013 год насчитывается^[5]436 действующих ядерных энергетических (то есть производящих утилизируемую электрическую и/или тепловую энергию)^[6] реакторов в 31 стране мира^[7]. Кроме того, на разных стадиях сооружения находится ещё 73 энергетических ядерных реакторов в 15 странах^[5]. В настоящее время в мире имеется также около 140 действующих надводных кораблей и подводных лодок, использующих в общей сложности около 180 реакторов^[8][9][10]. Несколько ядерных реакторов были использованы в советских и американских космических аппаратах, часть из них всё ещё находится на орбите. Кроме того, в ряде приложений используется ядерная энергия, генерируемая в нереакторных источниках (например, в термоизотопных генераторах). При этом не прекращаются дебаты об использовании ядерной энергии^[11][12]. Противники ядерной энергетики (в частности, такие организации, как «Гринпис») считают, что использование ядерной энергии угрожает человечеству и окружающей среде^[13][14][15]. Защитники ядерной энергетики (МАГАТЭ, Всемирная ядерная ассоциация и т. д.), в свою очередь, утверждают^[16], что этот тип энергетики позволяет снизить выбросы парниковых газов в атмосферу и при нормальной эксплуатации несёт значительно меньше рисков для окружающей среды, чем другие типы энергогенерации^[17].

Термоядерный синтез[править | править код]

Энергия термоядерного синтеза применяется в водородной бомбе. Проблема управляемого термоядерного синтеза пока не решена, однако в случае решения этой проблемы он станет практически неограниченным источником дешёвой энергии.

Радиоактивный распад[править | править код]

Энергия, выделяемая при радиоактивном распаде, используется в долгоживущих источниках тепла и бета-гальванических элементах. Автоматические межпланетные станции типа «Пионер» и «Вояджер», а также марсоходы и другие межпланетные миссии используют радиоизотопные термоэлектрические генераторы. Изотопный источник тепла использовали советские лунные миссии «Луноход-1» и «Луноход-2».

1. ↑ Settle, Frank (2005), Nuclear Chemistry. Discovery of the Neutron (1932) Архивная копия от 5 июля 2009 на Wayback Machine  (недоступная ссылка с 22-05-2013 [2435 дней] — история, копия), General Chemistry Case Studies
2. ↑ Краткая энциклопедия «Атомная энергия», Государственное научное издательство «Большая советская энциклопедия», 1956 г.
3. ↑ Key World Energy Statistics 2012 (неопр.). — International Energy Agency, 2012.
4. ↑ World Nuclear Association. Another drop in nuclear generation Архивная копия от 1 ноября 2012 на Wayback Machine World Nuclear News, 05 May 2010.
5. ↑ ^{1 2} PRIS — Home
6. ↑ Кроме энергетических, существуют также исследовательские и некоторые другие ядерные реакторы.
7. ↑ World Nuclear Power Reactors 2007-08 and Uranium Requirements (неопр.). World Nuclear Association (9 июня 2008). Дата обращения 21 июня 2008. Архивировано 3 марта 2008 года.
8. ↑ What is Nuclear Power Plant — How Nuclear Power Plants work | What is Nuclear Power Reactor — Types of Nuclear Power Reactors — EngineersGarage (неопр.) (недоступная ссылка). Дата обращения 12 мая 2013. Архивировано 4 октября 2013 года.
9. ↑ Nuclear-Powered Ships | Nuclear Submarines
10. ↑ http://www.ewp.rpi.edu/hartford/~ernesto/F2010/EP2/Materials4Students/Misiaszek/NuclearMarinePropulsion.pdf Архивная копия от 26 февраля 2015 на Wayback Machine Naval Nuclear Propulsion, Magdi Ragheb. На 2001 год было построено 235 корабельных ядерных реакторов, часть из которых уже выведена из эксплуатации.
11. ↑ Union-Tribune Editorial Board. The nuclear controversy (неопр.) (недоступная ссылка). Union-Tribune (27 марта 2011). Дата обращения 28 сентября 2012. Архивировано 19 ноября 2011 года.
12. ↑ James J. MacKenzie. Review of The Nuclear Power Controversy by Arthur W. Murphy The Quarterly Review of Biology, Vol. 52, No. 4 (Dec., 1977), pp. 467—468.
13. ↑ Share. Nuclear Waste Pools in North Carolina (неопр.) (недоступная ссылка). Projectcensored.org. Дата обращения 24 августа 2010. Архивировано 19 октября 2017 года.
14. ↑ NC WARN » Nuclear Power
15. ↑ Sturgis, Sue Investigation: Revelations about Three Mile Island disaster raise doubts over nuclear plant safety (неопр.)
     (недоступная ссылка). Southernstudies.org. Дата обращения 24 августа 2010. Архивировано 9 февраля 2010 года.
16. ↑ U.S. Energy Legislation May Be ‘Renaissance’ for Nuclear Power.
17. ↑ PRIS — Reactor status reports — Operational & Long-Term Shutdown — By Country (неопр.). pris.iaea.org. Дата обращения 8 декабря 2019.

• Clarfield, Gerald H. and William M. Wiecek (1984). Nuclear America: Military and Civilian Nuclear Power in the United States 1940—1980, Harper & Row.
• Cooke, Stephanie (2009). In Mortal Hands: A Cautionary History of the Nuclear Age, Black Inc.
• Cravens, Gwyneth. Power to Save the World: the Truth about Nuclear Energy (англ.). — New York: Knopf (англ.)русск., 2007. — ISBN 0-307-26656-7.
• Elliott, David (2007). Nuclear or Not? Does Nuclear Power Have a Place in a Sustainable Energy Future?, Palgrave.
• Falk, Jim (1982).
  Global Fission: The Battle Over Nuclear Power, Oxford University Press.
• Ferguson, Charles D., (2007). Nuclear Energy: Balancing Benefits and Risks Council on Foreign Relations.
• Herbst, Alan M. and George W. Hopley (2007). Nuclear Energy Now: Why the Time has come for the World’s Most Misunderstood Energy Source, Wiley.
• Schneider, Mycle, Steve Thomas, Antony Froggatt, Doug Koplow (August 2009). The World Nuclear Industry Status Report, German Federal Ministry of Environment, Nature Conservation and Reactor Safety.
• Walker, J. Samuel (1992). Containing the Atom: Nuclear Regulation in a Changing Environment, 1993—1971, Berkeley: University of California Press.
• Walker, J. Samuel (2004). Three Mile Island: A Nuclear Crisis in Historical Perspective, Berkeley: University of California Press.
• Weart, Spencer R. The Rise of Nuclear Fear. Cambridge, MA: Harvard University Press, 2012. ISBN 0-674-05233-1

Международные соглашения[править | править код]

Гравитационная энергия — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 ноября 2016; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 ноября 2016; проверки требуют 5 правок.

Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением.

Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя).

Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии, постоянна. Для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.

Гравитационная энергия играет очень важную роль на заключительных этапах эволюции звёзд, при их превращении в нейтронные звёзды и сверхновые^[1].

Для двух тяготеющих точечных тел с массами M и m гравитационная энергия Ug{\displaystyle U_{g}} равна:

 Ug=−GMmR,{\displaystyle \ U_{g}=-G{Mm \over R},}

где:

 G{\displaystyle \ G} — гравитационная постоянная;

 R{\displaystyle \ R} — расстояние между центрами масс тел.

Этот результат получается из закона тяготения Ньютона, при условии, что для бесконечно удалённых тел гравитационная энергия равна 0. Выражение для гравитационной силы имеет вид

Fg=GMmR2,{\displaystyle F_{g}=G{Mm \over R^{2}},}

где:

Fg{\displaystyle F_{g}} — сила гравитационного взаимодействия

С другой стороны согласно определению потенциальной энергии

Fg=dUgdR.{\displaystyle F_{g}={\frac {dU_{g}}{dR}}.}

Тогда:

Ug=const−GMmR.{\displaystyle U_{g}=const-G{Mm \over R}.}

Константа в этом выражении может быть выбрана произвольно. Её обычно выбирают равной нулю, чтобы при r, стремящемуся к бесконечности, Ug{\displaystyle U_{g}} стремилось к нулю.

Этот же результат верен для малого тела, находящегося вблизи поверхности большого. В этом случае R можно считать равным h+RM{\displaystyle h+R_{M}}, где RM{\displaystyle R_{M}} — радиус тела массой M, а h — расстояние от центра тяжести тела массой m до поверхности тела массой M.

На поверхности тела M имеем:

Ug=−GMmRM,{\displaystyle U_{g}=-G{Mm \over R_{M}},}

Если размеры тела M{\displaystyle M} много больше размеров тела m{\displaystyle m}, то формулу гравитационной энергии можно переписать в следующем виде:

Ug=−GMmRM+h=−mGMRM11+h/RM≈−mGMRM(1−hRM)=mgh−mGMRM,{\displaystyle U_{g}=-G{Mm \over R_{M}+h}=-mG{\frac {M}{R_{M}}}{\frac {1}{1+h/R_{M}}}\approx -mG{\frac {M}{R_{M}}}\left(1-{\frac {h}{R_{M}}}\right)=mgh-m{\frac {GM}{R_{M}}},}

где величину g=GMRM2{\displaystyle g={\frac {GM}{R_{M}^{2}}}} называют ускорением свободного падения. При этом член mGMRM{\displaystyle m{\frac {GM}{R_{M}}}} не зависит от высоты поднятия тела над поверхностью и может быть исключён из выражения путём выбора соответствующей константы. Таким образом для малого тела, находящегося на поверхности большого тела справедлива следующая формула

Ug=mgh.{\displaystyle U_{g}=mgh.}

В частности, эта формула применяется для вычисления потенциальной энергии тел, находящихся вблизи поверхности Земли.

В общей теории относительности наряду с классическим отрицательным компонентом гравитационной энергии связи появляется положительная компонента, обусловленная гравитационным излучением, то есть полная энергия гравитирующей системы убывает во времени за счёт такого излучения.

Плотность энергии — Википедия

Материал из Википедии — свободной энциклопедии

Плотность энергии — количество энергии на единицу объёма.

При линейной деформации плотность энергии, запасаемая упругим телом, равна:

W=12τijεij=12cijklεijεkl{\displaystyle W={\frac {1}{2}}\tau _{ij}\varepsilon _{ij}={\frac {1}{2}}c_{ijkl}\varepsilon _{ij}\varepsilon _{kl}}

где εij{\displaystyle \varepsilon _{ij}} — тензор деформации, τij{\displaystyle \tau _{ij}} — тензор напряжений, cijkl{\displaystyle c_{ijkl}} — тензор упругости.

В простейшем случае (сжатие-растяжение) плотность упругой энергии равна

W=Eε22{\displaystyle W={\frac {E\varepsilon ^{2}}{2}}}

где ε{\displaystyle \varepsilon } — относительная деформация, E{\displaystyle E} — модуль Юнга.

Плотность энергии идеального газа может быть вычислена через давление, либо через молекулярную/молярную плотность и температуру:

W=1γ−1p=1γ−1nkT=1γ−1νRT=1γ−1ρMRT{\displaystyle W={\frac {1}{\gamma -1}}p={\frac {1}{\gamma -1}}nkT={\frac {1}{\gamma -1}}\nu RT={\frac {1}{\gamma -1}}{\frac {\rho }{M}}RT}

где:

γ{\displaystyle \gamma } — показатель адиабаты;

n{\displaystyle n} — число молекул в единице объёма;

k{\displaystyle k} — постоянная Больцмана;

T{\displaystyle T} — абсолютная температура;

ν{\displaystyle \nu } — молярная плотность;

R{\displaystyle R} — газовая постоянная;

ρ{\displaystyle \rho } — плотность;

M{\displaystyle M} — молярная масса.

Плотность энергии фотонного газа (равновесного излучения абсолютно чёрного тела), имеющего температуру T{\displaystyle T}, равно:

W=(π2k415c3ℏ3)T4=4cσT4{\displaystyle W=\left({\frac {\pi ^{2}k^{4}}{15c^{3}\hbar ^{3}}}\right)T^{4}={\frac {4}{c}}\sigma T^{4}}, где σ — постоянная Стефана — Больцмана.

Плотность энергии в электродинамике и теории относительности[править | править код]

В специальной теории относительности плотность энергии является tt{\displaystyle tt}-компонентой тензора энергии-импульса.

Плотность электромагнитной энергии[править | править код]

Плотность энергии электромагнитного поля может быть выражена через параметры электрического и магнитного полей.

В СИ: W=E⋅D2+B⋅h3{\displaystyle W={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}};

В СГС: W=E⋅D8π+B⋅H8π{\displaystyle W={\frac {\mathbf {E} \cdot \mathbf {D} }{8\pi }}+{\frac {\mathbf {B} \cdot \mathbf {H} }{8\pi }}}

В таблице приведена плотность энергии замкнутых систем, включая дополнительные внешние компоненты, такие как окислители или источники тепла, но исключая энергию покоя системы в конечном состоянии. 1 МДж ≈ 278 Вт·ч.

Плотность энергии

Название	Плотность энергии на единицу массы (МДж/кг)	Плотность энергии на единицу массы (Вт⋅ч/кг)	Плотность энергии на единицу объёма (МДж/л)	Практическая эффективность использования %
Аннигиляция материя + антиматерия	до 89 875 517 873,681 764 (точно) ≈ 9⋅1010	24 965 421 631 578,26(7) ≈ 25⋅1012		Зависит от вступающих в реакцию частиц, электроны и позитроны аннигилируют полностью, при аннигиляции барионов часть энергии в конечном счёте уносят нейтрино
Слияние ядер водорода	645 000 000	179 310 000 000	~1–10⋅1012 (в ядре Солнца)
Реакция дейтерий-тритий	337 000 000	93 686 000 000
Уран-235, используемый в ядерном оружии	88 250 000	24 533 500 000	1 681 000 000
Природный уран (99,3 % U-238, 0,7 % U-235) в реакторе на быстрых нейтронах	86 000 000	23 908 000 000		[50 %]
Тепловая энергия от α-распада плутония-238	2 200 000[1]	611 600 000	43 648 000
Кинетическая энергия спутника Земли на низкой орбите	33	9 167
Дизельное топливо в мощной дизельной электростанции (без учёта массы генератора)	20,1[2]	5 583		47 %
Бензин (без учёта массы генератора)	8,1—10,5[3][4]	2250—2917		19—24 %
Супермаховик	1,8	500		98%
Генератор на водородном топливном элементе, без учёта массы конструкции	12[5]	3000
Серебряно-цинковый аккумулятор	0,47[6]	130,6	1,8
Литий-ионный аккумулятор	0,46—0,72[7]	128—200	2
Ni-MH-аккумулятор формата AA ёмкостью 2000 мА·ч	0,33	92	1,24
Тяговый свинцово-кислотный аккумулятор	0,17[8]	47
Пусковой свинцово-кислотный аккумулятор	0,1368[9]	38	0,337
Накопители на сверхпроводящих магнитах			0,1
Ионистор	0,03[10]	6,17	0,032 (MAXWELL K2)
Керамический конденсатор			0,003[11]
Электролитический конденсатор	0,000 639	0,1775	0,00083
Плёночный конденсатор	0,000 180[12]	0,05	0,0025 (maxwell CM-3)
Гравитационный аккумулятор (груз 1 кг на высоте 1 м)	0,000 009 8	0,0027	0,0001 для свинца
Взведенная часовая пружина	0,0003	0,083	0,0006
Название	Плотность энергии на единицу массы (МДж/кг)	Плотность энергии на единицу массы (Вт⋅ч/кг)	Плотность энергии на единицу объёма (МДж/л)	Практическая эффективность использования %

Планковская энергия — Википедия

Материал из Википедии — свободной энциклопедии

Пла́нковская эне́ргия — физическая константа, численно равная планковской массе, умноженной на квадрат скорости света. В планковской системе единиц планковская энергия является единицей измерения энергии. Обозначается EP{\displaystyle E_{P}}.

Ep=mpc2=ℏc5G≈{\displaystyle E_{p}=m_{p}c^{2}={\sqrt {\frac {\hbar c^{5}}{G}}}\approx } 1,956⋅10⁹Дж ≈{\displaystyle \approx } 1,22⋅10²⁸эВ ≈{\displaystyle \approx } 543,3 кВт·ч ≈{\displaystyle \approx } 4,6718⋅10⁸кал.

Для сравнения, она превосходит примерно на восемь порядков максимальную измеренную энергию космических лучей и примерно на 6 % дульную энергию мощнейшего артиллерийского орудия в истории — 800-мм железнодорожной пушки Дора:

EDora=mv22≈7100∗72022≈{\displaystyle E_{Dora}={\frac {mv^{2}}{2}}\approx {\frac {7100*720^{2}}{2}}\approx } 1,840⋅10⁹Дж ≈{\displaystyle \approx } 511,11 кВт⋅ч

В планковскую эпоху, примерно 13,8 млрд лет назад, вещество Вселенной имело планковскую энергию, планковский радиус (10⁻³⁵ м), планковскую температуру (10³² К)^[1] и планковскую плотность (~10⁹⁷ кг/м³).

Для сигнала, путешествующего вокруг точечной гравитирующей массы, гравитационная задержка может быть вычислена по следующей формуле:

Δt=−2GMc3ln⁡(1−R⋅x).{\displaystyle \Delta t=-{\frac {2GM}{c^{3}}}\ln(1-\mathbf {R} \cdot \mathbf {x} ).} (1)

Здесь R{\displaystyle \mathbf {R} } — это единичный вектор, направленный от наблюдателя к источнику, а x{\displaystyle \mathbf {x} } — единичный вектор, направленный от наблюдателя к гравитирующей точке массы M.

Отсюда следует, что для того, чтобы вызвать задержку сигнала равную фиксированному и априори заданному промежутку времени τ{\displaystyle \tau }, требуется масса

M=−τc32ln(1−R⋅x)G.{\displaystyle M=-{\frac {\tau c^{3}}{2ln(1-\mathbf {R} \cdot \mathbf {x} )G}}.} (2)

Энергия, эквивалентная данной массе, равна:

E1(τ)=−τc52ln(1−R⋅x)G.{\displaystyle E_{1}(\tau )=-{\frac {\tau c^{5}}{2ln(1-\mathbf {R} \cdot \mathbf {x} )G}}.} (3)

С другой стороны энергия кванта ЭМ излучения с периодом τ{\displaystyle \tau } равна

E2(τ)=hτ=2πℏτ.{\displaystyle E_{2}(\tau )={\frac {h}{\tau }}={\frac {2\pi \hbar }{\tau }}.} (4)

Произведение этих 2 энергий, определяемых формулами (3) и (4) равно:

E1(τ)E2(τ)=−τc52ln(1−R⋅x)G2πℏτ=−2πℏc52ln(1−R⋅x)G=−πℏc5ln(1−R⋅x)G=−πEP2ln(1−R⋅x).{\displaystyle E_{1}(\tau )E_{2}(\tau )=-{\frac {\tau c^{5}}{2ln(1-\mathbf {R} \cdot \mathbf {x} )G}}{\frac {2\pi \hbar }{\tau }}=-{\frac {2\pi \hbar c^{5}}{2ln(1-\mathbf {R} \cdot \mathbf {x} )G}}=-{\frac {\pi \hbar c^{5}}{ln(1-\mathbf {R} \cdot \mathbf {x} )G}}=-{\frac {\pi E_{P}^{2}}{ln(1-\mathbf {R} \cdot \mathbf {x} )}}.} (5)

Таким образом, произведение энергии, эквивалентной массе, вызывающей задержку, равную τ{\displaystyle \tau }, и энергии фотона с периодом τ{\displaystyle \tau } не зависит от τ{\displaystyle \tau } и равно квадрату планковской энергии с точностью до безразмерного коэффициента : −πln(1−R⋅x){\displaystyle -{\frac {\pi }{ln(1-\mathbf {R} \cdot \mathbf {x} )}}}.

Соответственно, отношение этих 2 энергий равно

E1(τ)E2(τ)=−τ2c54Gπln(1−R⋅x)ℏ==τ24πln(1−R⋅x)tP2=−14πln(1−R⋅x)(τtP)2.{\displaystyle {\frac {E_{1}(\tau )}{E_{2}(\tau )}}=-{\frac {\tau ^{2}c^{5}}{4G\pi ln(1-\mathbf {R} \cdot \mathbf {x} )\hbar }}=={\frac {\tau ^{2}}{4\pi ln(1-\mathbf {R} \cdot \mathbf {x} )t_{P}^{2}}}=-{\frac {1}{4\pi ln(1-\mathbf {R} \cdot \mathbf {x} )}}({\frac {\tau }{t_{P}}})^{2}.} (6)

Где tP{\displaystyle t_{P}} — планковское время.

Энергия ионизации — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 марта 2013; проверки требуют 9 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 марта 2013; проверки требуют 9 правок.

Энергия ионизации — разновидность энергии связи или, как её иногда называют, первый ионизационный потенциал (I₁), представляет собой наименьшую энергию, необходимую для удаления электрона от свободного атома в его низшем энергетическом (основном) состоянии на бесконечность.^[1]

Энергия ионизации является одной из главных характеристик атома, от которой в значительной степени зависят природа и прочность образуемых атомом химических связей. От энергии ионизации атома существенно зависят также восстановительные свойства соответствующего простого вещества.

Для многоэлектронного атома существуют также понятия второго, третьего и т. д. ионизационных потенциалов, представляющих собой энергию удаления электрона от его свободных невозбуждённых катионов с зарядами +1, +2 и т. д. Эти ионизационные потенциалы, как правило, менее важны для характеристики химического элемента.^[2]

Энергия ионизации всегда имеет эндоэнергетическое значение (это понятно, так как, чтобы оторвать электрон от атома, требуется приложить энергию, — самопроизвольно это произойти не может).

На энергию ионизации атома наиболее существенное влияние оказывают следующие факторы:

1. эффективный заряд ядра, являющийся функцией числа электронов в атоме, экранирующих ядро и расположенных на более глубоко лежащих внутренних орбиталях;
2. радиальное расстояние от ядра до максимума зарядовой плотности наружного, наиболее слабо связанного с атомом и покидающего его при ионизации, электрона;
3. мера проникающей способности этого электрона;
4. межэлектронное отталкивание среди наружных (валентных) электронов.

На энергию ионизации оказывают влияние также и менее значительные факторы, такие как квантовомеханическое обменное взаимодействие, спиновая и зарядовая корреляция и др.

Энергии ионизации элементов измеряется в Электронвольт на 1 атом или в Джоуль на моль.^[3]

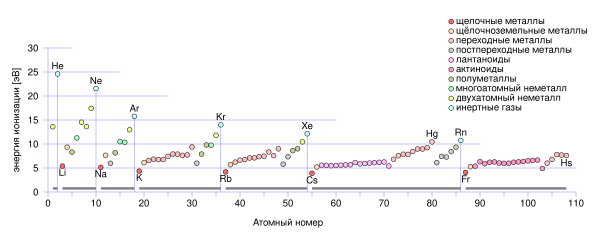Энергии ионизации элементов.

Энергия последовательной ионизации I_n (кДж/моль) атомов элементов третьего периода^[4]

Элемент	I1	I2	I3	I4	I5	I6	I7
Na	495,8	4564	—	—	—	—	—
Mg	737,7	1451	7730	—	—	—	—
Al	577,6	1817	2744	11600	—	—	—
Si	786,5	1577	3228	4350	16100	—	—
P	1011,8	1904	2910	4950	6270	21200	—
S	999,6	2253	3380	4565	6950	8490	27000
Cl	1251,2	2296	3850	5160	6560	9360	11000
Ar	1520,6	2666	3946	5770	7230	8780	12000

Сродство к электрону

Энергия — Википедия

Эне́ргия (др.-греч. ἐνέργεια — действие, деятельность, сила, мощь) — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в течение которого система будет являться замкнутой. Это утверждение носит название закона сохранения энергии.

С фундаментальной точки зрения, энергия представляет собой один из трёх (энергия, импульс, момент импульса) аддитивных интегралов движения (то есть сохраняющихся при движении величин), связанный, согласно теореме Нётер, с однородностью времени.

Слово «энергия» введено Аристотелем в трактате «Физика», однако там оно обозначало деятельность человека.

Используемые обозначения

Обычно обозначается символом Е — от лат. energīa (действие, деятельность, мощь).

Для обозначения тепловой энергии обычно используется символ Q — от англ. quantity of heat (количество теплоты).

Для обозначения внутренней энергии тела обычно используется символ U (происхождение символа подлежит уточнению).

В отдельных случаях может использоваться символ W — от англ. work (работа, труд), как способность выполнять работу.

История термина

Термин «энергия» происходит от греческого слова ἐνέργεια, которое впервые появилось в работах Аристотеля и обозначало действие или действительность (т.е. действительное осуществление действия в противоположность его возможности), праиндоевропейский корень werg обозначал работу или деятельность (ср. англ. work, нем. Werk) и в виде οργ/ουργ присутствует в таких греческих словах, как оргия или теургия и т.п.

Томас Юнг первым использовал понятие «энергия» в современном смысле слова

Лейбниц в своих трактатах 1686 и 1695 годов ввёл понятие «живой силы» (vis viva), которую он определил как произведение массы объекта и квадрата его скорости (в современной терминологии — кинетическая энергия, только удвоенная). Кроме того, Лейбниц верил в сохранение общей «живой силы». Для объяснения уменьшения скорости тел из-за трения, он предположил, что утраченная часть «живой силы» переходит к атомам.

Маркиза Эмили дю Шатле в книге «Учебник физики» (фр. Institutions de Physique, 1740), объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда.

В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия «живая сила»^[1]. Гаспар-Гюстав Кориолис раскрыл связь между работой и кинетической энергией в 1829 году. Уильям Томсон (будущий лорд Кельвин) впервые использовал термин «кинетическая энергия» не позже 1851 года, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».

Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.

Развитие паровых двигателей требовало от инженеров разработать понятия и формулы, которые позволили бы им описать механический и термический КПД своих систем. Инженеры (Сади Карно), физики (Джеймс Джоуль, Эмиль Клапейрон и Герман Гельмгольц), математики — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии»^[1]. Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия»^[1]. В 1881 году Уильям Томсон заявил перед слушателями^[2]:

Само слово энергия, хотя и было впервые употреблено в современном смысле доктором Томасом Юнгом приблизительно в начале этого века, только сейчас входит в употребление практически после того, как теория, которая дала определение энергии, … развилась от просто формулы математической динамики до принципа, пронизывающего всю природу и направляющего исследователя в области науки.

Оригинальный текст (англ.)

The very name energy, though first used in its present sense by Dr Thomas Young about the beginning of this century, has only come into use practically after the doctrine which defines it had … been raised from mere formula of mathematical dynamics to the position it now holds of a principle pervading all nature and guiding the investigator in the field of science.

В течение следующих тридцати лет эта новая наука имела несколько названий, например, «динамическая теория тепла» (англ. dynamical theory of heat) и «энергетика» (англ. energetics). В 1920-х годах общепринятым стало название «термодинамика» — наука о преобразовании энергии.

Особенности преобразования тепла и работы были показаны в первых двух законах термодинамики. Наука об энергии разделилась на множество различных областей, таких как биологическая термодинамика и термоэкономика (англ. thermoeconomics). Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе.

В 1918 году было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряжённой энергии. То есть энергия сохраняется, потому что законы физики не отличают разные моменты времени (см. Теорема Нётер, изотропия пространства).

В 1961 году выдающийся преподаватель физики и нобелевский лауреат, Ричард Фейнман в лекциях так выразился о концепции энергии^[3]:

Существует факт, или, если угодно, закон, управляющий всеми явлениями природы, всем, что было известно до сих пор. Исключений из этого закона не существует; насколько мы знаем, он абсолютно точен. Название его — сохранение энергии. Он утверждает, что существует определённая величина, называемая энергией, которая не меняется ни при каких превращениях, происходящих в природе. Само это утверждение весьма и весьма отвлечённо. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним.

Оригинальный текст (англ.)

There is a fact, or if you wish, a law, governing natural phenomena that are known to date. There is no known exception to this law—it is exact so far we know. The law is called conservation of energy; it states that there is a certain quantity, which we call energy that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity, which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.

Виды энергии

Механика различает потенциальную энергию (или, в более общем случае, энергию взаимодействия тел или их частей между собой или с внешними полями) и кинетическую энергию (энергия движения). Их сумма называется полной механической энергией.

Энергией обладают все виды полей. По этому признаку различают: электромагнитную (разделяемую иногда на электрическую и магнитную энергии), гравитационную (тяготения) и атомную (ядерную) энергии (также может быть разделена на энергию слабого и сильного взаимодействий).

Термодинамика рассматривает внутреннюю энергию и иные термодинамические потенциалы.

В химии рассматриваются такие величины, как энергия связи и энтальпия, имеющие размерность энергии, отнесённой к количеству вещества. См. также: химический потенциал.

Энергия взрыва иногда измеряется в тротиловом эквиваленте.

Кинетическая

Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в СИ — джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Потенциальная

Потенциальная энергия U(r→){\displaystyle U({\vec {r}})} — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[5].

Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Электромагнитная

Гравитационная

Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением. Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя). Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии постоянна, для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.

Ядерная

Ядерная энергия (атомная энергия) — это энергия, содержащаяся в атомных ядрах и выделяемая при ядерных реакциях.

Энергия связи — энергия, которая требуется, чтобы разделить ядро на отдельные нуклоны, называется энергией связи. Энергия связи, приходящаяся на один нуклон, неодинакова для разных химических элементов и, даже, изотопов одного и того же химического элемента.

Внутренняя

Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекул. Внутреннюю энергию тела нельзя измерить напрямую. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между её значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Химический потенциал

Химический потенциал μ{\displaystyle \mu } — один из термодинамических параметров системы, а именно энергия добавления одной частицы в систему без совершения работы.

Энергия взрыва

Взрыв — физический или/и химический быстропротекающий процесс с выделением значительной энергии в небольшом объёме за короткий промежуток времени, приводящий к ударным, вибрационным и тепловым воздействиям на окружающую среду и высокоскоростному расширению газов.

При химическом взрыве, кроме газов, могут образовываться и твёрдые высокодисперсные частицы, взвесь которых называют продуктами взрыва. Энергию взрыва иногда измеряют в тротиловом эквиваленте — мере энерговыделения высокоэнергетических событий, выраженной в количестве тринитротолуола (ТНТ), выделяющем при взрыве равное количество энергии.

Энергия вакуума

Энергия вакуума — энергия, равномерно распределённая в вакууме и вызывающая отталкивание между любыми материальными объектами во Вселенной с силой, прямо пропорциональной их массе и расстоянию между ними. Обладает крайне низкой плотностью.

Осмотическая энергия

Осмотическая энергия — работа, которую надо произвести, чтобы повысить концентрацию молекул или ионов в растворе.

Энергия и работа

Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах.

В специальной теории относительности

Энергия и масса

Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна

E=mc2,{\displaystyle E=mc^{2},}

где E{\displaystyle E} — энергия системы, m{\displaystyle m} — её масса, c{\displaystyle c} — скорость света в вакууме. Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.

Энергия тела, согласно законам классической механики, зависит от системы отсчета, то есть неодинакова для разных наблюдателей. Если тело движется со скоростью v относительно некоего наблюдателя, то для другого наблюдателя, движущегося с той же скоростью, оно будет казаться неподвижным. Соответственно, для первого наблюдателя кинетическая энергия тела будет равна, mv2/2{\displaystyle mv^{2}/2}, где m{\displaystyle m} — масса тела, а для другого наблюдателя — нулю.

Эта зависимость энергии от системы отсчета сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчета к другой используется сложная математическая конструкция — тензор энергии-импульса.

Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:

E=mc21−v2/c2,{\displaystyle E={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}},}

где m{\displaystyle m} — инвариантная масса. В системе отсчета, связанной с телом, его скорость равна нулю, а энергия, которую называют энергией покоя, выражается формулой:

E0=mc2.{\displaystyle E_{0}=mc^{2}.}

Это минимальная энергия, которую может иметь массивное тело. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна находит абсолютное значение этой постоянной.

Энергия и импульс

Специальная теория относительности рассматривает энергию как компоненту 4-импульса (4-вектора энергии-импульса), в который наравне с энергией входят три пространственные компоненты импульса. Таким образом энергия и импульс оказываются связанными и оказывают взаимное влияние друг на друга при переходе из одной системы отсчёта в другую.

В квантовой механике

В квантовой механике энергия E{\displaystyle E} свободной частицы связана с круговой частотой ω{\displaystyle \omega } соответствующей волны де Бройля соотношением E=ℏω{\displaystyle E=\hbar \omega }, где ℏ{\displaystyle \hbar } — постоянная Планка. ^[6][7] Это уравнение является математическим выражением принципа корпускулярно-волнового дуализма волн и частиц для случая энергии.^[8] В квантовой механике энергия двойственна времени. В частности, в силу фундаментальных причин принципиально невозможно измерить абсолютно точно энергию системы в каком-либо процессе, время протекания которого конечно. При проведении серии измерений одного и того же процесса значения измеренной энергии будут флуктуировать, однако среднее значение всегда определяется законом сохранения энергии. Это приводит к тому, что иногда говорят, что в квантовой механике сохраняется средняя энергия.

В общей теории относительности

В общей теории относительности время не является однородным, поэтому возникают определённые проблемы при попытке введения понятия энергии. В частности, оказывается невозможным определить энергию гравитационного поля как тензор относительно общих преобразований координат.

Энергия и энтропия

Внутренняя энергия (или энергия хаотического движения молекул) является самым «деградированным» видом энергии — она не может превращаться в другие виды энергии без потерь (см.: энтропия).

Физическая размерность

В системе физических величин LMT энергия имеет размерность ML2T−2{\displaystyle ML^{2}T^{-2}}.

Соотношения между единицами энергии.

Единица	Эквивалент
	в Дж	в эрг	в межд. кал	в эВ
1 Дж	1	107	0,238846	0,624146·1019
1 эрг	10−7	1	2,38846·10−8	0,624146·1012
1 межд. Дж[9]	1,00020	1,00020·107	0,238891	0,624332·1019
1 кгс·м	9,80665	9,80665·107	2,34227	6,12078·1019
1 кВт·ч	3,60000·106	3,60000·1013	8,5985·105	2,24693·1025
1 л·атм	101,3278	1,013278·109	24,2017	63,24333·1019
1 межд. кал (calIT)	4,1868	4,1868·107	1	2,58287·1019
1 термохим. кал (калТХ)	4,18400	4,18400·107	0,99933	2,58143·1019
1 электронвольт (эВ)	1,60219·10−19	1,60219·10−12	3,92677·10−20	1

Источники энергии

Условно источники энергии можно поделить на два типа: невозобновляемые и постоянные. К первым относятся газ, нефть, уголь, уран и т. д. Технология получения и преобразования энергии из этих источников отработана, но, как правило, неэкологична, и многие из них истощаются. К постоянным источникам можно отнести энергию солнца, энергию, получаемую на ГЭС и т. д.

Невозобновляемые ресурсы энергии и их величина (Дж)^[10]

Вид ресурса	Запасы
Термоядерная энергия	3,6*1026
Ядерная энергия	2*1024
Химическая энергия нефти и газа	2*1023
Внутреннее тепло Земли	5*1020

Возобновляемые ресурсы энергии и их годовая величина (Дж)^[10]

Вид ресурса	Запасы
Солнечная энергия	2*1024
Энергия морских приливов	2,5*1023
Энергия ветра	6*1021
Энергия рек	6,5*1019

Потребление энергии

Существует довольно много форм энергии, большинство из которых^[11] так или иначе используются в энергетике и различных современных технологиях.

Темпы энергопотребления растут во всем мире, поэтому на современном этапе развития цивилизации наиболее актуальна проблема энергоэффективности и энергосбережения.

См. также

Примечания

1. ↑ ^{1 2 3} Смит, Кросби. The science of energy: a cultural history of energy physics in Victorian Britain. — The University of Chicago Press, 1998. — ISBN 0-226-76421-4.
2. ↑ Томсон, Уильям. Об источниках энергии, доступных человеку для совершения механических эффектов = On the sources of energy available to man for the production of mechanical effect. — BAAS Rep, 1881. С. 513
3. ↑ Richard Feynman. The Feynman Lectures on Physics. — США: Addison Wesley, 1964. — Vol. 1. — ISBN 0-201-02115-3.
4. ↑ Фейнман, Ричард. Фейнмановские лекции по физике = The Feynman Lectures on Physics. — Т. 1.
5. ↑ Ландау, Л. Д., Лифшиц, Е. М. Теоретическая физика. — 5-е изд. — М.: Физматлит, 2004. — Т. I. Механика. — 224 с. — ISBN 5-9221-0055-6.
6. ↑ Паули, 1947, с. 11.
7. ↑ Широков, 1972, с. 18.
8. ↑ Широков, 1972, с. 19.
9. ↑ Джоуль (единица энергии и работы) — статья из Большой советской энциклопедии. Г. Д. Бурдун. 
10. ↑ ^{1 2} Алексеев, 1978, с. 134.
11. ↑ http://profbeckman.narod.ru/InformLekc.files/Inf03.pdf

Литература

Ссылки

Обсуждение:Потенциальная энергия — Википедия

На вектор делить нельзя. В этом случае пишется квадрат модуля вектора в знаменателе и домножается на вектор в числителе. 158.250.29.169 07:37, 16 июня 2008 (UTC)АИ

«Из определения понятно, что величина потенциальной энергии — постоянна . Она отсчитывается от некой точки пространства, выбор которой определяется удобством дальнейших вычислений. Понятно также, что корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тел, но не от пути их перемещения.» — и все-то из такого непонятного определения понятно. По приведенному определению это какае-то работа, которую необходимо совершить против каких-то действующих сил. Из определения я только понял, что если я буду двигать объект против силы трения, то я буду совершать потенциальную энергию. 87.252.227.58 15:04, 6 января 2009 (UTC)

«Из определения понятно, что величина потенциальной энергии — постоянна» — чушь, удалил. 80.249.231.101 16:44, 11 января 2009 (UTC)

Чуть-чуть подправил. Тела не могут находиться в одной точке. Либо мы выбираем точки для всех тел, либо выбираем конфигурацию тел. Feodor Garbouzov 18:10, 18 января 2010 (UTC)

Делить вектор на вектор можно и нужно по тем же правилам, что и при перемножении. Например при вращательном движении точки по радиусу

V→R→=ω→{\displaystyle {\frac {\vec {V}}{\vec {R}}}={\vec {\omega }}}

ω→{\displaystyle {\vec {\omega }}} осевой вектор угловой скорости.

Если вращение против часовой стрелки, то поворачиваем V→{\displaystyle {\vec {V}}} в ближайшую сторону к R→{\displaystyle {\vec {R}}} получаем направление ω{\displaystyle \omega } вверх.

Какое то начальство запретило делить вектор на вектор, вот и приходится выкручиваться подчиненным, в формулах добавлять в числитель вектор, а в знаменатель его модуль.

Они думают, что так наукообразнее.—Михаил Певунов 19:12, 25 июля 2015 (UTC)

Не понял пассаж «Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле.» Кинетическая энергия пропорциональна квадрату скорости, которая, в свою очередь, тоже измеряется в некоторой системе отсчета, что предполагает наличие чего-то, кроме «одного отдельного тела» 88.81.253.146 16:18, 26 ноября 2010 (UTC)

• На данный момент [1] ответ на вопрос экзамена «Потенциальная энергия» написан на 2 (два) балла. В английской версии ответ написан гораздо лучше. Определением без лишних слов является формула: W=−ΔU{\displaystyle \,W=-\Delta U} , которой в русской статье нет. Что плохо, т.е. неудовлетворительно.
• В русской статье сказано, что пот. энергия — это способность тела совершать работу. Однако рассчитывается (читай, определяется) потенциальная энергия не так. Не через работу, которую тело совершает над чем-то (это вообще звучит некорректно!), а через работу W{\displaystyle \,W} заданной потенциальной СИЛЫ, которая действует на тело при перемещении его из точки 1 в точку 2. Для потенциальных сил (гравитационных, электростатических, сил упругости) эта работа не зависит от траектории перехода и определяется только координатами (или разностью координат) точек 1,2.
• Таким образом, работающим определением, по которому можно рассчитать потенциальную энергию (а не просто поговорить и разойтись) является примерно такое определение:

Потенциальной энергией U{\displaystyle \,U} тела (материальной точки), находящегося в поле действия заданной потенциальной силы F{\displaystyle \,F} , называется такая функция координат, при которой W=−ΔU{\displaystyle \,W=-\Delta U} ,

где W{\displaystyle \,W} — работа силы F{\displaystyle \,F} при перемещении тела из точки 1 в точку 2;

ΔU=U2−U1{\displaystyle \,\Delta U=U2-U1} — приращение потенциальной энергии при перемещении тела из 1 в 2.

Из математического анализа известно, что формула W=−ΔU{\displaystyle \,W=-\Delta U} эквивалентна формуле F=-grad(U). То есть, потенциальную энергию можно определить и прямо через потенциальную силу.

• Далее, неплохо привести примеры потенциальных сил и соответствующих им выражений для потенциальной энергии:

Fтяж=mg => U=mgh

Fгр=GmM/R^2 => U=-GmM/R

Fупр=kx => U=kx^2/2

Fкул=kqQ/R^2 => U=kqQ/R

Fэл=qE => U=-qEx (для однородного электрического поля, E вдоль x)

• Поскольку я в статьях подобной тематики не участвовал, предлагаю доработать эту статью заинтересованным (в физике) участникам. Тем более, что написано: Проект:Физика (Уровень III, Важность «высокая») Ler 16:44, 7 декабря 2010 (UTC)

  Согласен, статья написана по-детски. Требуется полная переработка. Пока руки просто не дошли. — Артём Коржиманов 18:01, 7 декабря 2010 (UTC)

Правка тоже написана не по взрослому. Потенциальная сила это у боксеров. Не каждый потенциально обладает нокаутирующим ударом. Из математического анализа уравнений потенциальной энергии известно, что определить потенциальную энергию через потенциальную силу невозможно. Гиря на столе и на шкафу давит на опоры с одинаковой силой. Требуется еще знать высоту до пола.

Fупр=kx => U=kx^2/2 Если известна Fупр, но неизвестна к и х, то что можно определить.—Михаил Певунов 19:43, 25 июля 2015 (UTC)

• С понятием пот энергии человек сталкивается в 7 (седьмом) классе средней школы. И вот, семиклассник, недопонявший в школе что есть потэнергия, открывает Википедию и читает: «Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил..» — Мляяяя!! Это кем и для кого написано?.. ИМХО это написано недучившимся студентом дабы повыеживаться перед девочками, какие он умные слова знает!..Pavel Suvorov (обс.) 10:50, 10 марта 2019 (UTC)

Потенциальная тепловая энергия[править код]

Понятия потенциальная тепловая энергия в статье не отражено, хотя оно просто определяется школьным курсом физики.

Берем один моль идеального газа объемом 22,14 литра, Т = 273^оК, давлением 1 кГ/см²

Берем цилиндр сечением поршня 100 см². Длина столба газа под поршнем будет 2,414 м

Нагреваем газ еще на 273^оК до Т = 546^оК.

Избыточное давление под поршнем 1 кГ/см² * 100 см² = 100 кГ.

Подпираем поршень пружиной, жесткостью к = 100 кГ/ метр, до усилия 100 кГ

Система находится в равновесии.Давление газа уравновешено пружиной.

Начинаем подогревать газ еще на 273^оК. Газ расширяясь сжимает пружину и потенциальная тепловая энергия газа, переходит в потенциальную энергию сжатия пружины.

Применяем уравнение Клайперона для газа E = PV = kT

ГАЗОВАЯ ПОСТОЯННАЯ (R), универсальная фнз. постоянная, входящая в ур-ние состояния 1 моля идеального газа: pv=RT (см. КЛАПЕЙРОНА УРАВНЕНИЕ), где р — давление, v — объём моля, Т — абс. темп-pa.

и механики для пружины E = kX²/2

Энергия одного моля газа, нагретого на 273^оК = к*273^оК

Энергия сжатой пружины 100 кГ/метр * (2,414 метр)²/2 = 291,37 КГм = 2858,34 Дж.

к = 2858,34 Дж./273^о = 10,47 Дж/1моль*1^оК

Литература: Учебник физики.—Михаил Певунов 07:50, 25 июля 2015 (UTC)