Формулы кинематики с пояснениями по физике / Блог / Справочник :: Бингоскул
Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.
Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S=v *t
- S — путь
- v — скорость
- t — время
Равномерное движение
x=x_0 + v*t
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
Равномерно ускоренное движение:
ускорениеa=\frac { v — v_0 } { t }
- a — ускорение
- v — скорость
- v0 — начальная скорость
- t — время
Равномерно ускоренное движение:
скоростьv=v_0 + at
- v — скорость
- v0 — начальная скорость
- a — ускорение
- t — время
Равномерно ускоренное движение:
путьS=vt + \frac { at^2 } { 2 }
- s — путь
- v — скорость
- t — время
- a — ускорение
Равномерно ускоренное движение:
координатаx=x_0 + vt + \frac { at^2 } { 2 }
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
- a — ускорение
Высота тела, брошенного вертикально вверх (вниз)
h=h_0 + v_ { 0 } t — \frac { gt^2 } { 2 }
- h — высота
- h0 — начальная высота
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v=v_0 — gt
- v — скорость
- v0 — начальная скорость
- g — ускорение свободного падения
- t — время
Скорость, ускорение, время
v=at
- v — скорость
- a — ускорение
- t — время
Скорость свободно падающего тела
v=gt
- v — скорость
- g — ускорение свободного падения
- t — время
Центростремительное ускорение
a=\frac { v^2 } { R }
- a — центростремительное ускорение
- v — скорость
- R — радиус
Угловая скорость
\omega=\frac { \phi } { t }
- ω — угловая скорость
- φ — угол
- t — время
Равномерное круговое движение
l=R\phi
- l — длина дуги окружности
- R — радиус
- φ — угол
Равномерное круговое движение: линейная скорость
v=R \omega
- v — линейная скорость
- R — радиус
- ω — угловая скорость
Период вращения
T=\frac { t } { N }
- T — период
- t — время
- N — число вращений
T=\frac { 2 \pi R } { v }
- T — период
- R — радиус
- v — линейная скорость
T=\frac { 2 \pi } { \omega }
- T — период
- ω — угловая скорость
Центростремительное ускорение
a=\frac { 4 \pi^ { 2 } R } { T^2 }
- a — центростремительное ускорение
- R — радиус
- T — период вращения
a=4 \pi^ { 2 } Rn^2
- a — центростремительное ускорение
- R — радиус
- n — частота вращения
Частота вращения
n=\frac { 1 } { T }
- n — частота вращения
- T — период вращения
Центростремительное ускорение
a=\omega ^ { 2 } R
- a — центростремительное ускорение
- ω — угловая скорость
- R — радиус
Дальность броска тела, брошенного под углом к горизонту
x=v_0t \cos(\alpha)
- x — координата (дальность)
- v0 — начальная скорость
- t — время
- α — угол
Высота подъема тела, брошенного под углом к горизонту
y=v_0t \sin (\alpha) — \frac { gt^2 } { 2 }
- y — координата (высота подъема )
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
- α — угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y=v_0* \sin (\alpha) — gt
- vy — вертикальная скорость
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
- t — время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max =\frac { v_0^2* \sin (\alpha)^ { 2 } } { 2g }
- hмакс — максимальная высота
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t=\frac { 2v_0 * \sin (\alpha) } { g }
- t — время
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x=x_0 + vt
- x — координата (дальность)
- x0 — начальная координата
- v — скорость
- t — время
Высота подъема тела, брошенного горизонтально
y=y_0 — \frac { gt^2 } { 2 }
- y — координата (высота подъема)
- y0 — начальная координата (высота)
- g — ускорение свободного падения
- t — время
Общее время движения тела, брошенного горизонтально
t_max=\sqrt { \frac { 2h } { g } }
- tмакс — максимальное время
- h — высота
- g — ускорение свободного падения
Смотри также:
Кинематика.
 Формулы Кинематика. Формулы
Формулы Кинематика. Формулы| Номер | Название формулы | Запись формулы | Примечание |
| (1) | Закон равноускоренного криволинейного движения | vS0 — модуль начальной скорости; aS — ускорение | |
| (2) | Скорость равномерного прямолинейного движения | ||
| (3) | Скорость | ||
| (4) | Ускорение | ||
| (5) | Касательное ускорение | dv = dl/dt, т.е. путевая скорость вдоль рассматриваемой траектории | |
| (6) | Нормальное ускорение | ||
| (7) | Скорость свободного падения тела | ||
| (8) | Время тела при свободном падении | ||
| (9) | Время при равномерном движении по окружности | ||
| (10) | Скорость равномерного движения по окружности | ||
| (11) | Угловая (мгновенная) скорость равномерного движения по окружности | Единица измерения угловой скорости — радианы в секунду | |
| (12) | Скорость равноускоренного движения по окружности | ||
| (13) | Угловая (мгновенная) скорость равноускоренного движения по окружности |
— версия для печати
- Определение
- Кинематикой называется раздел физики, занимающийся исследованием законов движения идеальных тел
- Пояснение
- Под чертой вверху буквы подразумевается знак вектора.

| Если у вас есть мысли или идеи по поводу данной таблицы или, например, вы считаете, что полезно было бы создать определенную вспомогательную памятку, то мы обязательно рассмотрим ваше предложение, которое можно изложить по ссылке (где вы также можете поделиться с нами любыми мыслями по поводу сайта scolaire.ru). Мы готовы устранить любые неудобства, связанные с использованием данной таблицы, или ей подобных, которые можно найти в разделе «Физика». |
© Школяр. Лингвистика (при поддержке «Ветвистого древа») 2009—2016
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест
Формулы по кинематике, динамике, законам сохранения, молекулярной физике, электричеству, магнетизму, оптике. Тест — курсы по физике Skip navigation- Элементы математики
- действия с векторами
- выражение неизвестной
- Физические величины
- Единицы измерения
- Постоянные величины в физике
- плотность вещества
- предел прочности, модуль Юнга
- скорость звука
- удельная теплота
- диэлектрическая проницаемость
- удельное сопротивление
- электрохимический эквивалент
- Формулы
- I.
 Механика
Механика - Кинематика
- равномерное движение
- относительность движения
- неравномерное движение
- равноускоренное движение
- ускорение свободного падения
- графики движения
- движение по окружности
- параболическое движение
- Динамика
- закон тяготения
- законы Ньютона
- силы в природе
- равнодействующая сила
- Законы сохранения
- импульс тела, импульс силы
- закон сохранения импульса
- работа и мощность
- кинетическая и потенциальная энергии
- закон сохранения энергии
- Статика
- плечо и момент силы
- условия равновесия
- центр тяжести, центр масс
- Колебания и волны
- колебательное движение
- гармонические колебания
- маятники
- превращение энергии при колебаниях
- упругие волны
- звуковые волны
- II.
 Молекулярная физика
Молекулярная физика - Молекулярная физика
- основные положения мкт
- давление
- основное уравнение мкт, температура
- уравнение идеального газа
- изопроцессы
- свойства жидкостей*
- свойства твердых тел
- Термодинамика
- работа, внутренняя энергия
- первый закон термодинамики
- второй закон термодинамики
- тепловые двигатели
- III. Основы электродинамики
- Электричество
- электрический заряд
- закон Кулона
- напряженность поля
- потенциал и работа поля
- диэлектрики, проводники
- электроемкость, конденсаторы
- энергия конденсатора
- Электрический ток
- электрический ток, сила и плотность
- закон Ома для участка цепи
- работа и мощность тока
- закон Ома для замкнутой цепи
- электрический ток в различных средах
- электрические явления
- Магнетизм
- магнитное поле
- сила Ампера
- сила Лоренца
- Электромагнетизм
- магнитный поток
- закон электромагнитной индукции
- самоиндукция, энергия поля
- электромагнитные колебания
- электромагнитные волны
- переменный ток
- трансформатор*
- IV.
 Оптика
Оптика - Волновая оптика
- свет как электромагнитные волны
- интерференция
- дифракция
- Геометрическая оптика
- законы распространения света
- линзы, оптические приборы
- V. Теория относительности
- Теория относительности
- постулаты теории относительности
- VI. Квантовая физика
- Световые кванты
- фотон
- фотоэффект
- квантовые постулаты Бора
- излучение и поглощение света
- Атомное ядро
- энергия связи ядра
- ядерные реакции
- закон радиоактивного распада
- элементарные частицы и их свойства
- Современная физика*
- физика элементарных частиц
- мир внутри атомного ядра
- время расщепляем на мгновения
- нанотехнологии и нанофизика
- вещество в экстремальных состояниях
основные формулы с пояснениями или определения по физике в 10 классе, какие законы динамики или механики для ЕГЭ
Описать можно все что угодно: картину в галерее, уличного хулигана в кабинете участкового и даже свои душевные переживания на приеме у психотерапевта.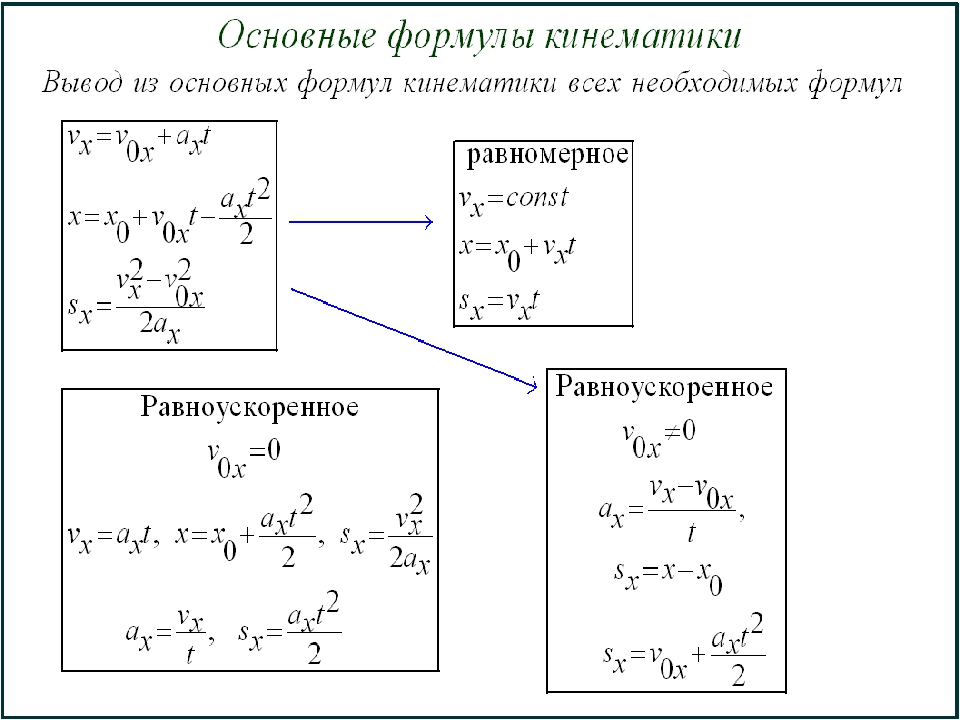 Достаточно вооружиться бумагой, ручкой и вперед.
Достаточно вооружиться бумагой, ручкой и вперед.
Но что необходимо, чтобы описать движение? На этот вопрос нам поможет ответить кинематика, раздел механики, который как раз и занимается описанием механического движения.
Физика простыми словами | Кинематика
Как описать движение?Давайте разберемся с терминологией и введем основные понятия, без которых нам никак не обойтись. Итак,
движением мы будем называть любое изменение положения тела в пространстве с течением времени.К слову сразу отметим, что время в физике принято мерить секундами, а само движущееся тело не всегда рассматривается целиком. Зачастую его размерами и формой можно пренебречь и рассматривать как точку, имеющую массу.
В механике вы можете услышать такие понятия как точечное тело или материальная точка. Так вот знайте, речь идет как раз об этом.
К примеру, какие бы габариты не имела ваша машина, если вы едете по трасе из Ростова в Москву, то она в любом случае очень мала в сравнении с расстоянием, а значит мы можем рассматривать её как материальную точку. А вот если, приехав в столицу нашей необъятной родины, вы ищете свободное место где припарковаться, то тут размерами и формой автомобиля пренебречь уже не получится.
А вот если, приехав в столицу нашей необъятной родины, вы ищете свободное место где припарковаться, то тут размерами и формой автомобиля пренебречь уже не получится.
Положение тела или материальной точки в пространстве рассматривается с помощью системы координат, за начало которой мы принимаем тело отсчета, относительно которого происходит движение. В зависимости от сложности этого движения мы можем иметь дело с одномерным, двухмерным, или трехмерным пространством.
Соответственно, наша система координат может иметь одну, две или три оси. Как правило трехмерные пространства в школьной физике практически не встречаются, поэтому мы ограничимся двухмерным с координатными осями х и у.
Чтобы определить координаты нашей материальной точки, необходимо построить её проекции на соответствующие координатные оси, опустив на них перпендикуляры.
Теперь если наблюдая за движущейся материальной точкой, построить линию, по которой она движется, мы получим траекторию движения. Измерив длину траектории можно определить пройденный
Измерив длину траектории можно определить пройденный
Так как единицей длинны в международной системе единиц был принят метр, то путь, пройденный телом, и длина вектора перемещения, или, как еще говорят, его модуль, так же будут измерятся в метрах. Отметим, что модуль перемещения всегда будет меньше, ну или в крайнем случае равен пути, но никак не больше.
Все просто, вектора кривыми не бывают, и перемещение не является исключением. А вот что касается траектории, то её мы можем гнуть как угодно.
Исходя из этого, можно выделить два вида механического движения: прямолинейное — когда траектория прямая линия и криволинейное — когда тело движется по кривой, ну, к примеру, параболе или окружности.
Прямолинейное движениеДавайте представим, что мы едем в автобусе, а для простоты будем считать, что траектория нашего движения — прямая линия.
v=s/t
Так как движение относительно, то относительной будет и скорость. К примеру, если наш автобус едет со скоростью v1, ну скажем, равной 20 м/с, а мы, находясь в автобусе, идем в направлении водителя со скоростью v2, равной 1 м/с, то наша скорость относительно дороги будет определятся как сумма двух этих скоростей. То есть 21 м/с.
v=v1+v2
Ну а если мы будем идти от водителя, то наша скорость относительно дороги будет уже равна 19 м/с. И казалось бы, ничего не поменялось, и значения скоростей v1 и v2 остались прежними, но изменилось направление нашего движения, а значит, чтобы найти скорость, с которой мы движемся относительно дороги, нам нужно вычесть v2 из v1 .
v=v1-v2
В рассмотренных примерах мы условно принимали движение как равномерное, то есть движение с постоянной скоростью. Но в реальности, автобус то и дело будет останавливаться на светофорах и остановках, а потом опять разгоняться. Обгонять неторопливых автолюбителей.
Но в реальности, автобус то и дело будет останавливаться на светофорах и остановках, а потом опять разгоняться. Обгонять неторопливых автолюбителей.
Да и у нас не получится ходить по нему с постоянной скоростью, тем более если ехать в час пик, когда автобус забит под завязку. В реальности движение будет неравномерным, и скорость будет постоянно меняться.
При неравномерном движении отношение всего пройденного пути ко времени называется средней скоростью.
vср=s/t
И хотя в некоторых случаях она бывает очень удобна, но все же не всегда приемлема при описании движения. Думаю, будет очень трудно доказать сотруднику гос автоинспекции, остановившему вас за превышение скорости, что ваша средняя скорость на всем пути была в пределах нормы.
Тут речь пойдет о мгновенной скорости, или скорости в какой-то определенный момент времени. Если посмотреть на спидометр движущегося автомобиля, то мы как раз её увидим.
И стоит нам по сильнее нажать на педаль газа, как в то же мгновение стрелка спидометра начинает ползти вверх, оповещая нас об изменении скорости.
И здесь необходимо ввести понятие ускорения, величины, которая будет характеризовать изменение скорости движения за какой то промежуток времени (t). Её принято обозначать маленькой буквой a и измерять в м/с2.
а=(V-V0)/t
Ускорение, так же как и скорость, величина векторная, а значит будет иметь свое направление. Причем, если направление вектора ускорения будет совпадать с направлением скорости, то скорость будет возрастать.
Такое движение называют ускоренным. И напротив, снижение скорости, при замедленном движении, будет свидетельствовать о том что вектора ускорения и скорости смотрят в разные стороны. Выразим скорость и перемещение для движения с ускорением:
Если объединить эти уравнения в одно, мы получим формулу разности квадратов скоростей :
Итак, мы ввели основные понятия и величины кинематики и вывели основные уравнения, связывающие их.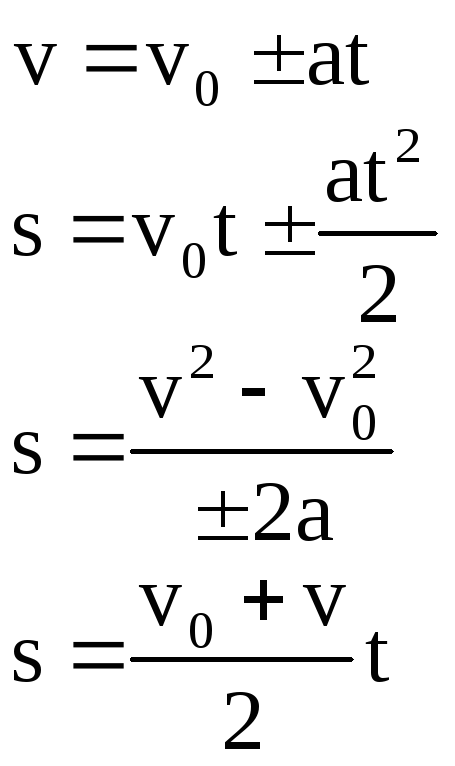 Но для простоты мы брали прямолинейное движение.
Но для простоты мы брали прямолинейное движение.
Если же говорить о движении по кривой, то нам придется уже рассматривать его в двухмерном или даже трехмерном пространстве.
Для этого необходимо будет построить проекции векторов скорости, перемещения и ускорения на соответствующие координатные оси, а при работе с проекциями мы опять получим уже знакомые уравнения для прямолинейного движения, которые примут следующий вид:
- Sx= V0x t +(axt2) /2
Sy= V0у t +(aуt2) /2
vx=v0x+axt
vy=v0y+ayt
Или для определения координат движущейся материальной точки:
- x= x 0 + V0x t +(axt2) /2
y= y 0 + V0у t +(aуt2) /2
Где х0, у0 — координаты начального положения точки в пространстве, а х, у — координаты её конечного положения.
Для описания движения в трехмерном пространстве у нас добавится третья ось z, и, соответственно, проекции скорости, ускорения и перемещения на эту ось.
Принцип разложения движения на простые составляющие лежит в основе многих устройств. Так первые компьютерные мыши были оснащены шариком, вращение которого приводило во вращение два перпендикулярно расположенных друг к другу колесика со специальными датчиками, они то и раскладывали сложные движения мыши на горизонтальные и вертикальные составляющие.
Стоило одному из этих колесиков покрыться толстым слоем грязи, как оно переставало вращаться, и указатель на экране начинал двигаться только по прямой, горизонтальной или вертикальной.
Современные оптические мыши лишены этого недостатка, так как в них шарик и колесики, заменены на лазерные датчики, но тем не менее принцип разложения движения они унаследовали от своих прародительниц.
Источник: https://physicsline.ru/teoriya/fizika-prostymi-slovami/fizika-prostymi-slovami-kinematika/
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
- Переходим к постоянному электрическому току:
- Далее добавляем формулы по теме: “Магнитное поле электрического тока”
- Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
- Ну и, конечно, куда же без электромагнитных колебаний:
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
Источник: https://NauchnieStati.ru/spravka/bolee-50-osnovnyh-formul-po-fizike/
Осн. формулы и метод. рекомендации по решению задач на кинематику МТ
Ближайшие темы будут посвящены решению задач на движение тел, без учета причин, вызвавших это движения, т.е. решению задач по кинематике.
Но для того, чтобы начать рассмотрение решений задач по данной теме, необходимо вспомнить основные формулы, связанные с этим разделом. Для удобства, сведём все формулы в таблицу.
Основные формулы равномерного прямолинейного движения
|
Формула |
Описание формулы |
|
Перемещение
тела за промежуток времени t, где –
скорость тела, sx, vx – проекции перемещения и скорость на ось Ох. |
|
|
Путь за промежуток времени t. |
|
|
Закон сложения скоростей в классической механике. |
|
|
Кинематическое уравнение равномерного движения, где х — координата тела в момент времени t, х0 — начальная координата тела. |
Основные формулы равноускоренного прямолинейного движения
|
Формула |
Описание формулы |
|
Скорость тела в момент времени t, где – ускорение тела, – скорость тела в начальный момент времени. |
|
|
Перемещение
тела за промежуток времени t. |
|
|
Кинематическое уравнение равноускоренного движения. |
Основные формулы движения тела по окружности с постоянной по модулю скоростью.
|
Формула |
Описание формулы |
|
Линейная скорость тела, где l — длина дуги окружности, пройденной телом за промежуток времени Δt. |
|
|
Угловая скорость тела, где Dj – угол поворота радиус-вектора движущегося по окружности тела за промежуток времени Dt. |
|
|
Связь
линейной скорости с угловой, где R — радиус
окружности. |
|
|
Период вращения, где N — число оборотов тела за промежуток времени Δt. |
|
|
Частота вращения. |
|
|
Связь между линейной скоростью, периодом вращения и частотой. |
|
|
Центростремительное ускорение. |
Известно, что для большей наглядности движение можно описывать с помощью графиков.
Давайте рассмотрим в сравнении графики для равномерного и равноускоренного движения.
Известно, что при равномерном движении скорость тела не
изменяется с течением времени. Поэтому графиком скорости, в этом случае, будет
прямая линия, параллельная оси времени. При равноускоренном движении тела,
неизменной величиной является ускорение. Поэтому графиком ускорения будет
являться также прямая линия, параллельная оси времени.
При равноускоренном движении тела,
неизменной величиной является ускорение. Поэтому графиком ускорения будет
являться также прямая линия, параллельная оси времени.
По графику скорости для равномерного движения, можно определить путь, пройденный телом за некоторый промежуток времени. Для этого достаточно определить площадь прямоугольника, образованного графиком скорости и осью времени.
Известно, что перемещение тела при равномерном движении линейно зависит от времени, поэтому графиком перемещения является прямая линия вида
y = kx.
Наклон же графика к оси времени зависит от модуля скорости. При равноускоренном движении линейно зависимой величиной является скорость тела. Поэтому графиком скорости является прямая линия вида
y = kx +b.
Используя график скорости для равноускоренного движения можно
определить перемещение тела за некоторый промежуток времени. Для этого
необходимо определить площадь прямоугольной трапеции или прямоугольного
треугольника, ограниченных графиком скорости и осью времени.
Для этого
необходимо определить площадь прямоугольной трапеции или прямоугольного
треугольника, ограниченных графиком скорости и осью времени.
График зависимости координаты от времени при равномерном движении, то есть график движения, представлен на рисунке ниже. По этому графику можно определить: координату тела в любой момент времени, путь, пройденный телом за некоторый промежуток времени, кратчайшее расстояние между телами в любой момент времени, а также момент и место встречи тел.
А графиком перемещения при равноускоренном движении является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения. Так, если проекция ускорения отрицательна, то возможны следующие три вида графика перемещения:
– когда проекция начальной скороститела равна нулю;
– когда проекция начальной скорости тела меньше нуля;
– когда проекция начальной скорости тела больше нуля.
Если проекция ускорения положительна, то здесь также возможны три случая:
– когда начальная скорость тела равна нулю;
– когда проекция начальной скорости больше нуля;
– когда проекция начальной скорости меньше нуля.
Методические рекомендации по решению задач на кинематику материальной точки
1) Сделать схематический рисунок, который лучше всего представить в виде траектории движущейся точки с изображением векторов перемещения, скорости и ускорения.
2) Выбрать систему отсчета (то есть тело отсчета, связанную с
ним систему координат и начало отсчета времени) на основании тщательного
анализа условия задачи. Рациональный выбор системы отсчета, как правило,
значительно упрощает решение задачи. При выборе положительных направлений
координатных осей необходимо руководствоваться направлением движения (то есть
направлением вектора скорости) или направлением вектора ускорения.
3) Составить на основании законов движения систему уравнений в векторном виде для всех тел, участвующих в движении. А затем в скалярной форме, спроецировав на координатные оси эти векторные уравнения движения. При записи этих уравнений не забыть привести в соответствие знаки проекций скорости и ускорения с направлением координатных осей. При необходимости дополнить систему уравнений соотношениями, составленными на основе данных задачи и конкретной ситуации, описанной в ней.
4) Решить полученную систему уравнений относительно искомых величин в общем виде, убедиться в соответствии единиц измерения и проделать числовые расчеты.
Следование этим простым рекомендациям позволит вам успешнее справляться с решением задач на кинематику материальной точки.
Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 2. Равномерное прямолинейное движение материальной точки
Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Траектория — линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni. htm.
htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:
Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.
Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:
Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.
Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
,
и перемещение:
.
Подставляя выражение для скорости, получим:
Если начальный момент времени t0 принять равным нулю, то скорость равна:
Выразим отсюда радиус-вектор :
Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
х=х0+vхt.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:
Его можно найти, зная модуль скорости
Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:
Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т.е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Дано: xо = — 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.
Решение: координату точки найдем по формуле:
х = х0 + 𝞾х t
Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = — 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
Дано:
Найти .
Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:
,
где — искомая величина.
Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины
Ответ: .
Механическое движение — определение, формулы, примеры
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Путь — вектор, проведенный из начальной точки пути в конечную [м].
Чтобы сразу практиковаться, приходите в современную школу для подростков Skysmart. Ученики занимаются на интерактивной платформе по индивидуальной программе, отслеживает прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю. |
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость → → → |
Средняя путевая скорость V ср. V ср.путевая — средняя путевая скорость [м/с] |
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения x(t) = x0 + vxt x(t) — искомая координата [м] |
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси x(t) = x0 — vxt x(t) — искомая координата [м] |
Графики
Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
В видео ниже разбираемся, как строить графики кинематических величин и зачем они нужны.
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, прямолинейное движение — это движение с ускорением по прямой линии. 2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Примеров механического движения в жизни — масса. Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.
Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.
Приходите на бесплатный вводный урок и начните заниматься физикой в удовольствие уже завтра!
Кинематические уравнения
Целью этого первого раздела «Класса физики» было исследование разнообразных средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени). В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов.Эти уравнения известны как кинематические уравнения.
Есть множество величин, связанных с движением объектов — смещение (и расстояние), скорость (и скорость), ускорение и время. Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м / с, на север в течение 12,0 секунд для смещения на север на 264 метра, то движение автомобиля полностью описано.И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения дают полное описание движения объекта. Однако не всегда такая полнота известна. Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны.Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна к заносу 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).
Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м / с, на север в течение 12,0 секунд для смещения на север на 264 метра, то движение автомобиля полностью описано.И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения дают полное описание движения объекта. Однако не всегда такая полнота известна. Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны.Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна к заносу 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).
БОЛЬШОЙ 4
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для предсказания неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением. Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение.Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно рассчитать значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация. Например, если известно значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений. Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался.Символ a обозначает ускорение объекта. А символ v обозначает скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, они могут использоваться для прогнозирования неизвестной информации о движении объекта, если известна другая информация. В следующей части Урока 6 мы исследуем процесс этого.
В следующей части Урока 6 мы исследуем процесс этого.
Формула кинематических уравнений
Кинематика — это исследование движущихся объектов и их взаимосвязей. Есть четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.
a) D = v i t + 1/2 при 2 b) (v i + v f ) / 2 = D / t
c) a = (v f — v i ) / t d) v f 2 = v i 2 + 2aD
D = смещение
a = ускорение
t = время
v f = конечная скорость
v i = начальная скорость
Формула кинематических уравнений.
1) Боб едет на велосипеде в магазин со скоростью 4 м / с, когда перед ним выбегает кошка. Он быстро тормозит до полной остановки, с ускорением — 2м / с 2 . Какое у него перемещение?
Какое у него перемещение?
Ответ: Поскольку Боб остановлен, конечная скорость v f = 0. Его начальная скорость v i = 4 м / с. Ускорение, a = -2 м / с 2 . Время не указано, поэтому используйте уравнение (d) для смещения D, потому что оно не зависит от времени.
v f 2 = v i 2 + 2aD
(0) 2 = (4 м / с) 2 +2 (- 2 м / с 2 ) D
0 = 16 м 2 / с 2 + (- 4 м / с 2 ) D
-16 м 2 / с 2 = (- 4 м / с 2 ) D
16 м 2 / с 2 = 4 м / с 2 ) D
(16 м 2 / с 2 ) / (4 м / с 2 ) = D
Водоизмещение полное 4 м.
2) Вы путешествуете с постоянной скоростью 11 м / с в течение 5 минут. Как далеко вы уехали?
Ответ: При постоянной скорости v i = v f = 11 м / с. Время t = 5 мин или t = (60 сек / мин x 5 мин) = 300 сек. Теперь используйте уравнение (b), чтобы найти смещение D.
Время t = 5 мин или t = (60 сек / мин x 5 мин) = 300 сек. Теперь используйте уравнение (b), чтобы найти смещение D.
(v i + v f ) / 2 = D / t
D = [(v i + v f ) / 2] t
D = [(11 м / с + 11 м / с) / 2] x 300 с
D = (22 м / с) / 2 x 300 с
D = 11 м / с x 300 с
D = 3300 м. Водоизмещение полное 3,300 м.
3) Каково ускорение автомобиля, который разгоняется с 11 до 40 м / с за 10 секунд?
Ответ: V i = 11 м / с. V f = 40 м / с. Время, t = 10 с. Используйте кинематическое уравнение c), чтобы найти ускорение.
a = (v f — v i ) / t
a = (40 м / с — 11 м / с) / 10 с
a = (29 м / с) / 10 с = 2,9 м / с 2
4) Если автомобиль разгоняется на 3.0 м / с 2 от полной остановки, сколько времени потребуется, чтобы проехать 3000 м?
Ответ: Ускорение a = 2,9 м / с 2 и перемещение D = 3000 м. Автомобиль был неподвижен, поэтому v i = 0. Используйте уравнение a), чтобы найти время.
Автомобиль был неподвижен, поэтому v i = 0. Используйте уравнение a), чтобы найти время.
D = v i t + 1/2 при 2
3000 м = 0т + 1/2 (3,0 м / с 2 ) т 2
3000 м = 1/2 (3,0 м / с 2 ) / т 2
3000 м / 1.5 м / с 2 = t 2
2000 с 2 = t 2
t = 44,72 сек
Уравнения движения | Движение в одном измерении
21.7 Уравнения движения (ESAHG)
В этом разделе мы рассмотрим третий способ описания движения. Мы рассмотрели описание движения с помощью слов и графиков. В этом разделе мы исследуем уравнения, которые можно использовать для описания движения.
Этот раздел посвящен решению задач, связанных с равноускоренным движением.{-1} $} \ text {в момент} t \\ \ vec {s} & = \ text {displacement} \ text {(m)} \ end {выровнять *}
Галилео Галилей из Пизы, Италия, первым определил правильный математический закон ускорения: общее пройденное расстояние, начиная с состояния покоя, пропорционально квадрату времени. Он также пришел к выводу, что объекты сохраняют свою скорость, если на них не действует сила — часто трение, опровергая принятую аристотелевскую гипотезу о том, что объекты «естественным образом» замедляются и останавливаются, если на них не действует сила.{2} + 2 \ vec {a} \ Delta \ vec {x} \ qquad (4)
\ end {выровнять *}
Он также пришел к выводу, что объекты сохраняют свою скорость, если на них не действует сила — часто трение, опровергая принятую аристотелевскую гипотезу о том, что объекты «естественным образом» замедляются и останавливаются, если на них не действует сила.{2} + 2 \ vec {a} \ Delta \ vec {x} \ qquad (4)
\ end {выровнять *}
Вопросы могут быть разными, но следующий метод ответа на них всегда будет работать. Используйте это при ответе на вопрос, связанный с движением с постоянным ускорением. Вам нужны любые три известные величины (\ ({\ vec {v}} _ {i} \), \ ({\ vec {v}} _ {f} \), \ (\ Delta \ vec {x} \) , \ (t \) или \ (\ vec {a} \)), чтобы иметь возможность вычислить четвертый.
Стратегия решения проблем:
Внимательно прочтите вопрос, чтобы определить указанные количества.Запишите их.
Определите используемое уравнение. Запишите !!!
Убедитесь, что все значения указаны в правильных единицах, и введите их в уравнение.
Конечная скорость : Найдите подходящее уравнение для расчета конечной скорости {- 2} $} \ text {Восток}
\ end {align *}
{- 2} $} \ text {Восток}
\ end {align *}Мы можем использовать уравнение 1 — помните, что теперь мы также знаем ускорение объекта.{-1} $} \) в \ (\ text {8} \) \ (\ text {s} \). Рассчитайте необходимое ускорение и общее расстояние, которое он прошел за это время.
Решение еще не доступно
Расширение: поиск уравнений движения (ESAHH)
Следующее не является частью учебной программы и может считаться дополнительной информацией.
Вывод уравнения 1
Согласно определению ускорения:
\ [\ vec {a} = \ frac {\ Delta \ vec {v}} {t} \]где \ (\ Delta \ vec {v} \) — изменение скорости, т.е.е. \ (\ Delta v = {\ vec {v}} _ {f} — {\ vec {v}} _ {i} \). Таким образом, мы имеем
\ begin {align *} \ vec {a} & = \ frac {{\ vec {v}} _ {f} — {\ vec {v}} _ {i}} {t} \\ {\ vec {v}} _ {f} & = {\ vec {v}} _ {i} + \ vec {a} t \ end {align *}Вывод уравнения 2
Мы видели, что смещение можно рассчитать по площади под графиком зависимости скорости от времени.
 Для равноускоренного движения наиболее сложный график зависимости скорости от времени, который мы можем получить, представляет собой прямую линию.Посмотрите на график ниже — он представляет объект с начальной скоростью \ ({\ vec {v}} _ {i} \) , разгоняющийся до конечной скорости \ ({\ vec {v}} _ { f} \) за общее время т .
Для равноускоренного движения наиболее сложный график зависимости скорости от времени, который мы можем получить, представляет собой прямую линию.Посмотрите на график ниже — он представляет объект с начальной скоростью \ ({\ vec {v}} _ {i} \) , разгоняющийся до конечной скорости \ ({\ vec {v}} _ { f} \) за общее время т .Чтобы вычислить окончательное смещение, мы должны вычислить площадь под графиком — это просто площадь прямоугольника, добавленная к площади треугольника. Эта часть графика заштрихована для ясности.
\ begin {align *} {\ text {Area}} _ {△} & = \ frac {1} {2} b \ times h \\ & = \ frac {1} {2} t \ times \ left ({v} _ {f} — {v} _ {i} \ right) \\ & = \ frac {1} {2} {v} _ {f} t — \ frac {1} {2} {v} _ {i} t \ конец {выравнивание *} \ begin {выравнивание *} {\ text {Area}} _ {\ square} & = l \ times b \\ & = t \ times {v} _ {i} \\ & = {v} _ {i} т \ конец {выравнивание *} \ begin {выравнивание *} \ text {Displacement} & = {\ text {Area}} _ {\ square} + {\ text {Area}} _ {△} \\ \ Delta \ vec {x} & = {v} _ {i} t + \ frac {1} {2} {v} _ {f} t — \ frac {1} {2} {v} _ {i} т \\ \ Delta \ vec {x} & = \ frac {\ left ({v} _ {i} + {v} _ {f} \ right)} {2} t \ end {align *}Вывод уравнения 3
Это уравнение просто выводится путем исключения конечной скорости \ ({v} _ {f} \) в уравнении 2.
 {- 1} $} \), когда водитель видит ребенка \ (\ text {50} \) \ (\ text {m} \) перед ним на дороге.{-2} $} \). Его время реакции на нажатие тормоза составляет \ (\ text {0,5} \) секунды. Будет ли грузовик сбить ребенка?
{- 1} $} \), когда водитель видит ребенка \ (\ text {50} \) \ (\ text {m} \) перед ним на дороге.{-2} $} \). Его время реакции на нажатие тормоза составляет \ (\ text {0,5} \) секунды. Будет ли грузовик сбить ребенка?Проанализировать проблему и определить, какая информация предоставляется
Полезно нарисовать временную шкалу, подобную этой:
Нам необходимо знать следующее:
Какое расстояние водитель преодолевает, прежде чем нажать на тормоз.
Как долго грузовик останавливается после нажатия на тормоз.
Общее расстояние, которое грузовик преодолевает до остановки.
Рассчитать расстояние \ (AB \)
Прежде чем водитель нажмет на тормоз, грузовик движется с постоянной скоростью. Ускорения нет, поэтому уравнения движения не используются.
\ begin {align *} v & = \ frac {D} {t} \\ 10 & = \ frac {D} {\ text {0,5}} \\ D & = \ текст {5} \ текст {м} \ end {выровнять *} Чтобы найти пройденное расстояние, мы используем:
Чтобы найти пройденное расстояние, мы используем:Грузовик преодолевает \ (\ text {5} \) \ (\ text {m} \) до того, как водитель нажмет на тормоз.{-2} $} \ right) t \\ т & = \ текст {8} \ текст {s} \ end {align *}
Рассчитать расстояние \ (BC \)
Для расстояния мы можем использовать Уравнение 2 или Уравнение 3. Мы будем использовать Уравнение 2:
\ begin {align *} \ Delta \ vec {x} & = \ frac {\ left ({\ vec {v}} _ {i} + {\ vec {v}} _ {f} \ right)} {2} t \\ \ Delta \ vec {x} & = \ frac {10 + 0} {2} \ left (8 \ right) \\ \ Delta \ vec {x} & = \ text {40} \ text {m} \ end {align *}Напишите окончательный ответ
Общее расстояние, которое преодолевает грузовик, составляет \ ({d} _ {AB} + {d} _ {BC} = \ text {5} + \ text {40} = \ text {45} \) метров.
 Ребенок находится на \ (\ text {50} \) метрах впереди. Грузовик не ударит ребенка.
Ребенок находится на \ (\ text {50} \) метрах впереди. Грузовик не ударит ребенка.Основы кинематики | Безграничная физика
Определение кинематики
Кинематика — это исследование движения точек, объектов и групп объектов без учета причин их движения.
Цели обучения
Определить кинематику
Основные выводы
Ключевые моменты
- Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов.
- Изучение кинематики можно абстрагировать в чисто математических выражениях.
- Кинематические уравнения могут использоваться для расчета различных аспектов движения, таких как скорость, ускорение, смещение и время.
Ключевые термины
- кинематика : Раздел механики, имеющий отношение к движущимся объектам, но не к задействованным силам.
Кинематика — это раздел классической механики, который описывает движение точек, объектов и систем групп объектов без ссылки на причины движения (т.
 е., силы). Изучение кинематики часто называют «геометрией движения».
е., силы). Изучение кинематики часто называют «геометрией движения».Объекты вращаются вокруг нас. Все, от теннисного матча до полета космического зонда над планетой Нептун, связано с движением. Когда вы отдыхаете, ваше сердце перемещает кровь по венам. Даже в неодушевленных предметах есть непрерывное движение в колебаниях атомов и молекул. Могут возникнуть интересные вопросы о движении: сколько времени потребуется космическому зонду, чтобы добраться до Марса? Куда приземлится футбольный мяч, если его бросить под определенным углом? Однако понимание движения также является ключом к пониманию других концепций физики.Например, понимание ускорения имеет решающее значение для изучения силы.
Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов, а также их дифференциальные свойства (такие как скорость и ускорение). Кинематика используется в астрофизике для описания движения небесных тел и систем; и в машиностроении, робототехнике и биомеханике для описания движения систем, состоящих из соединенных частей (таких как двигатель, роботизированная рука или скелет человеческого тела).

Формальное изучение физики начинается с кинематики. Слово «кинематика» происходит от греческого слова «kinesis», означающего движение, и связано с другими английскими словами, такими как «cinema» (фильмы) и «kinesiology» (изучение движения человека). Кинематический анализ — это процесс измерения кинематических величин, используемых для описания движения. Изучение кинематики можно абстрагировать в чисто математических выражениях, которые можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, смещение, время и траектория.
Кинематика траектории частицы : Кинематические уравнения могут использоваться для расчета траектории частиц или объектов. Физические величины, относящиеся к движению частицы, включают: массу m, положение r, скорость v, ускорение a.
Система отсчета и смещение
Чтобы описать движение объекта, необходимо указать его положение относительно удобной системы отсчета.
Цели обучения
Оценить смещение в системе координат.

Основные выводы
Ключевые моменты
- Выбор системы отсчета требует решения, где находится исходное положение объекта и какое направление будет считаться положительным.
- Допустимые системы отсчета могут отличаться друг от друга перемещением друг относительно друга.
- Рамки отсчета особенно важны при описании смещения объекта.
- Смещение — это изменение положения объекта относительно его системы отсчета.
Ключевые термины
- смещение : векторная величина, которая обозначает расстояние с направленным компонентом.
- рамка отсчета : система координат или набор осей, в пределах которых можно измерить положение, ориентацию и другие свойства объектов в ней.
Чтобы описать движение объекта, вы должны сначала описать его положение — где он находится в любой конкретный момент времени. Точнее, нужно указать его положение относительно удобной системы отсчета.
 Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Землю или от нее. Математически положение объекта обычно представлено переменной x .
Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Землю или от нее. Математически положение объекта обычно представлено переменной x .Кодовые ссылки
Есть два варианта, которые вы должны сделать, чтобы определить переменную положения x . Вы должны решить, где поставить x = 0 и какое направление будет положительным. Это называется выбором системы координат или выбором системы отсчета.Пока вы последовательны, любой фрейм одинаково действителен. Но вы не хотите менять систему координат во время расчета. Представьте, что вы сидите в поезде на станции и вдруг замечаете, что станция движется назад. Большинство людей сказали бы, что они просто не заметили, что поезд движется — только казался таким, как будто станция движется. Но это показывает, что существует третий произвольный выбор , связанный с выбором системы координат: действительные системы отсчета могут отличаться друг от друга, перемещаясь друг относительно друга.
 Может показаться странным использование системы координат, движущейся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.
Может показаться странным использование системы координат, движущейся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.СПРАВОЧНИКИ профессора Хьюма и профессора Дональда Айви из Университета Торонто
В этом классическом фильме профессора Хьюм и Айви умело иллюстрируют системы отсчета и различают фиксированные и движущиеся системы отсчета.
Frames of Reference (1960) Обучающий фильм : Frames of Reference — образовательный фильм 1960 года, созданный Комитетом по изучению физических наук. Фильм предназначен для показа на курсах физики в средней школе. В фильме профессора физики Университета Торонто Паттерсон Хьюм и Дональд Айви объясняют различие между инерциальной и неинтерциальной системами отсчета, демонстрируя эти концепции с помощью юмористических трюков с камерой.
 Например, фильм начинается с Доктора.Хьюм, который кажется перевернутым, обвиняет доктора Айви в том, что он перевернут. Только когда пара подбрасывает монету, становится очевидно, что доктор Айви — и камера — действительно перевернуты. Юмор фильма служит как для заинтересованности студентов, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих неожиданно непредсказуемые места в зоне просмотра. Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее творческие люди могут найти в прохожих.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик Престамон
Например, фильм начинается с Доктора.Хьюм, который кажется перевернутым, обвиняет доктора Айви в том, что он перевернут. Только когда пара подбрасывает монету, становится очевидно, что доктор Айви — и камера — действительно перевернуты. Юмор фильма служит как для заинтересованности студентов, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих неожиданно непредсказуемые места в зоне просмотра. Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее творческие люди могут найти в прохожих.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик ПрестамонРабочий объем
Смещение — это изменение положения объекта относительно его системы отсчета.
 Например, если автомобиль движется из дома в продуктовый магазин, его перемещение — это относительное расстояние продуктового магазина до системы отсчета или дома. Слово «смещение» означает, что объект переместился или был перемещен. Смещение — это изменение положения объекта, которое математически можно представить следующим образом:
Например, если автомобиль движется из дома в продуктовый магазин, его перемещение — это относительное расстояние продуктового магазина до системы отсчета или дома. Слово «смещение» означает, что объект переместился или был перемещен. Смещение — это изменение положения объекта, которое математически можно представить следующим образом:[латекс] \ Delta \ text {x} = \ text {x} _ \ text {f} — \ text {x} _0 [/ latex]
, где Δ x — смещение, x f — конечное положение, а x 0 — начальное положение.
показывает важность использования системы координат при описании перемещения пассажира в самолете.
Перемещение в системе ведения : Пассажир перемещается со своего места на заднюю часть самолета. Его расположение относительно самолета указано x. Смещение пассажира на -4,0 м относительно самолета показано стрелкой в направлении задней части самолета. Обратите внимание, что стрелка, обозначающая его перемещение, вдвое длиннее стрелки, обозначающей перемещение профессора (он перемещается вдвое дальше).

Введение в скаляры и векторы
Вектор — это любая величина, имеющая как величину, так и направление, тогда как скаляр имеет только величину.
Цели обучения
Определите разницу между скалярами и векторами
Основные выводы
Ключевые моменты
- Вектор — это любая величина, имеющая величину и направление.
- Скаляр — это любая величина, которая имеет величину, но не имеет направления.
- Смещение и скорость — это векторы, а расстояние и скорость — скаляры.
Ключевые термины
- скаляр : величина, имеющая величину, но не направление; сравнить вектор.
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
В чем разница между расстоянием и смещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Смещение — это пример векторной величины.
 Расстояние — это пример скалярной величины.Вектор — это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км / ч на восток и силу 500 ньютонов прямо вниз.
Расстояние — это пример скалярной величины.Вектор — это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км / ч на восток и силу 500 ньютонов прямо вниз.Скаляры и векторы : Г-н Андерсен объясняет различия между скалярными и векторными величинами. Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
В математике, физике и технике вектор — это геометрический объект, который имеет величину (или длину) и направление и может быть добавлен к другим векторам в соответствии с векторной алгеброй.Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-). Вектор часто представлен отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B, как показано на.

Векторное представление : Вектор часто представляется отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B.
Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не имеют определенного направления.В физике скаляр — это простая физическая величина, которая не изменяется при поворотах или перемещениях системы координат. Это любая величина, которая может быть выражена одним числом и имеет величину, но не направление. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, ограничение скорости 90 км / ч, рост человека 1,8 м и расстояние 2,0 м — все это скаляры или количества без указания направление. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура –20ºC.В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками. (Сравнение скаляров и векторов показано на рис.
 )
)Скаляры и векторы : Краткий список величин, которые являются либо скалярами, либо векторами.
Уравнения кинематики и постоянное ускорение
В своих «Диалогах двух новых наук» Галилей вывел взаимосвязь между пройденным расстоянием и временем, когда шары катились по наклонной плоскости.Это часто называют законом падающих тел. Интересно, что в доказательстве Галилея вместо алгебры, которую мы представим здесь, использовалась классическая евклидова геометрия (которая была бы незнакома современному изучающему геометрию из учебников). Учащиеся продвинутого уровня могут получить те же уравнения с помощью математического анализа.
Основа Закона падающих тел заключается в том, что по мере того, как мяч катится по рампе, он ускоряется. По мере увеличения его скорости увеличивается расстояние, которое он проходит за каждую единицу времени.Галилей определил это с помощью колокольчиков спускового механизма катящегося шарика.
Процитируем Галилея в переводе:
По сути, Галилей представил, что не только ускорение вниз по рампе из-за постоянной силы тяжести, но и что скорость увеличивается линейно с временем .
 Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.Основываясь на том, что вы уже узнали и что представил Галилей, у нас есть то, что мой учитель физики Гленн Глейзер любил называть пятью священными уравнениями кинематики для постоянного ускорения. В этих уравнениях v — скорость, x — положение, t — время и a — ускорение. Помните, что Δ означает изменение.
1. или Δx = v ср. Δt
2. или v f = v o + aΔt или Δv = aΔt
3.
4. Δx = v o Δt + ½ a Δt 2
5. v f 2 = v o 2 + 2aΔx
Первые два уравнения, которые мы видели раньше. Важно отметить, что в первом уравнении используется средняя скорость , тогда как во втором уравнении используется изменение между исходной и конечной скоростью . Связь между ними представлена в третьем уравнении, которое представляет собой просто закон средних чисел.Средняя скорость — это среднее значение исходной и конечной скорости.
Из этих трех основных определений мы можем вывести следующие два уравнения, используя либо геометрию, либо алгебру (или исчисление).
Используя алгебру, мы можем вывести уравнение №4.
Исходя из уравнения № 1
Δx = v ср. Δt
Затем мы подставляем определение средней скорости из уравнения №3.
Отсюда мы подставляем окончательную скорость, полученную в уравнении № 2
Затем мы распределяем член Δt и упрощаем, комбинируя члены v o .
Мы упрощаем оставшиеся два члена, чтобы получить
Стоит отметить, что происходит, когда исходная скорость v o, равна нулю. Это уравнение еще больше упрощается и становится
.Если мы предположим, что исходная позиция и время равны нулю, мы можем дополнительно уменьшить это до
Используя геометрию, мы можем исследовать область под кривой графика зависимости скорости от времени для движения с постоянным ускорением.
Если мы посмотрим на область под кривой, мы можем разбить ее на прямоугольник и треугольник. Красный прямоугольник — это вклад исходной скорости объекта. Смещение из-за ускорения представлено зеленым треугольником. Треугольник имеет ширину Δt и высоту aΔt, которые мы знаем из уравнения №2. Член ½ происходит от формулы площади треугольника.
Мы также можем использовать исчисление для вывода этого уравнения путем интегрирования удвоенного ускорения по времени.
Пятое священное уравнение может быть получено аналогичными заменами, и его оставят как домашнее задание.
Теперь давайте рассмотрим несколько примеров задач: Численное решение задач.
Пример 1
По легенде, Галилей уронил мяч из Пизанской башни. Если башня имеет высоту 55,9 м и пренебрегает сопротивлением воздуха, сколько времени потребуется свинцовому мячу, чтобы достичь земли?
Гивенс: a = g ≈ 10 м / с 2
Δx = 55.9 м
Неизвестно: t = ???
Уравнение, связывающее эти переменные, — это священное уравнение 4 th .
Δx = v o Δt + ½ a Δt 2
Как упоминалось ранее, поскольку начальная скорость равна нулю, уравнение упрощается.
Δx = v o Δt + ½ a Δt 2 = ½ a Δt 2
Поскольку мы хотим изолировать переменную для времени, мы пересекаем умножение, чтобы переместить ½ и член ускорения на другую сторону.
Затем извлекаем квадратный корень из обеих частей.
Это дает выражение для времени. Обратите внимание, что я вставил несколько дополнительных скобок, которые могут вам не понадобиться.
При подключении номеров это довольно просто то, что мы называем «подключи и забей». Однако с агрегатами нужно быть осторожным. Вы, наверное, догадались, что время будет измеряться в секундах. Однако у вас должна быть возможность отменить фактические единицы, чтобы получить время в секундах.
Пример 2
Койот падает со скалы высотой 25 метров. Как быстро койот падает, когда ударяется о землю? Если проблема койота
Дано x = 25 м
a = g ≈ 10 м / с 2
Неизвестно: v = ???
Эту проблему можно решить несколькими способами. Можно было использовать комбинацию или Священные уравнения №2 и №4. Или вы можете напрямую использовать уравнение № 5.
Использование v f 2 = v o 2 + 2aΔx
Это упрощается, поскольку исходная скорость v o, равна нулю.
Если извлечь квадратный корень из обеих частей уравнения
Обратите внимание, как вы извлекаете квадратный корень из единиц, чтобы получить м / с .
Мы оставим решение этой задачи с двумя уравнениями для домашней задачи.
Краткое изложение проблем построения графиков, наклона и площади под кривыми
Изучая графики положения, скорости и ускорения, вы сможете рисовать их как взаимозаменяемые.
Вчера в классе вы видели, что график объекта, ускоряющегося вниз по склону, выглядит следующим образом:
В этом примере мы используем программное обеспечение для анализа изображений.Это пример с мячом, катящимся с холма. Следует отметить, что график ускорения не показывает фактическую скорость, а показывает только то, как она меняется. Точно так же график скорости не дает вам фактического положения объекта, а только того, как он изменяется. Щелкнув по мячу и нажав кнопку трека, вы увидите график положения и скорости.
Здесь вы можете увидеть результаты построения графика движения. График положения представляет собой параболу, а график скорости — линейный.
Какие кинематические формулы?
Kinematic Equations: Целью этого первого раздела The Physics Classroom было исследование разнообразных средств, с помощью которых может быть описано движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени).
В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов. Эти уравнения известны как кинематические уравнения. Существует множество величин, связанных с движением объектов: смещение (и расстояние), скорость (и скорость), ускорение и время.
Что такое кинематические формулы?Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22.0 м / с, север в течение 12,0 секунд для смещения на север на 264 метра, затем движение автомобиля полностью описывается. И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины.
Эти два утверждения дают полное описание движения объекта. Однако не всегда такая полнота известна.Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете узнать, что ваша машина имеет скорость 22 м / с, восток, и способна к заносу 8,0 м / с 2 , запад.
Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений)
4 кинематических уравнения
Кинематика — это изучение движущихся объектов и их взаимосвязей.Есть четыре (4) кинематических уравнения, которые относятся к смещению D, скорости v, времени t и ускорению a.
a) D = v i t + 1/2 при 2 b) (v i + v f ) / 2 = D / t
c) a = (v f — v i ) / t d) v f 2 = v i 2 + 2aD
D = смещение
a = ускорение
t = время
v f = конечная скорость
v i = начальная скорость
Какие 3 кинематических уравнения?
Если мы знаем три из этих пяти кинематических переменных — Δ x, t, v 0, v, a \ Delta x, t, v_0, v, a Δx, t, v0, v, adelta, x, запятая , t, запятая, v, начальный индекс, 0, конечный индекс, запятая, v, запятая, a — для объекта с постоянным ускорением мы можем использовать кинематическую формулу , см. ниже, чтобы найти одну из неизвестных переменных .
Сколько существует кинематических уравнений?
Четыре кинематических уравнения , которые описывают движение объекта: В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта.
Для чего используются кинематические уравнения?
Кинематические уравнения можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, смещение и время.
Список кинематических уравнений
Кинематические формулы — это набор формул, которые относятся к пяти кинематическим переменным, перечисленным ниже.
Большой 1.
четырехъядерный v = v0 + at1
v = v0 + at1,
точка, пробел, v, равно, v, начальный индекс, 0, конечный индекс, плюс, a, t
Большой 2.
четырехугольник {\ Delta x} = (\ dfrac {v + v_0} {2}) t2
Δx = (2v + v0) t2,
точка, пробел, дельта, x, равно, левая скобка, начальная дробь, v, плюс, v, начальный нижний индекс, 0, конечный нижний индекс, деление на, 2, конечная дробь, правая скобка, t
Большой 3.2 + 2а \ Дельта x4.
v2 = v02 + 2aΔx4,
точка, пробел, v, начальный надстрочный индекс, 2, конечный надстрочный индекс, равно, v, начальный подстрочный индекс, 0, конечный подстрочный индекс, начальный надстрочный индекс, 2, конечный надстрочный индекс, плюс, 2, a, дельта, x
Поскольку кинематические формулы являются точными только в том случае, если ускорение является постоянным в течение рассматриваемого временного интервала, мы должны быть осторожны, чтобы не использовать их при изменении ускорения. Кроме того, кинематические формулы предполагают, что все переменные относятся к одному и тому же направлению: по горизонтали xxx, по вертикали yyy и т. Д.2} g = 9,81s2m g, равно, 9, точка, 81, начальная дробь, m, деленная на, s, начальный верхний индекс, 2, конечный верхний индекс, конечная дробь.
Это и странно, и удачно, если вдуматься. Это странно, поскольку это означает, что большой валун будет ускоряться вниз с тем же ускорением, что и небольшой камешек, и, если его уронить с той же высоты, он одновременно ударится о землю.
Это удачно, поскольку нам не нужно знать массу снаряда при решении кинематических формул, поскольку свободно летящий объект будет иметь такую же величину ускорения, g = 9.2} ay = −9,81s2m a, начальный индекс, y, конечный индекс, равно, минус, 9, точка, 81, начальная дробь, m, деленное на, s, начальный верхний индекс, 2, конечный верхний индекс, конечная дробь для снаряд, когда мы подставляем кинематические формулы.
Физика кинематических уравнений
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением.Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно рассчитать значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация.
Например, если значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля известны, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался. Символ обозначает ускорение объекта.А символ v обозначает скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем, как это сделать.
Читайте также: Формула линейной интерполяции
Основные кинематические уравнения
Кинематика — это исследование движения объектов без учета сил, вызывающих это движение. Эти знакомые уравнения позволяют студентам анализировать и предсказывать движение объектов, и студенты будут продолжать использовать эти уравнения на протяжении всего изучения физики. Твердое понимание этих уравнений и того, как их использовать для решения проблем, необходимо для успеха в физике.Эта статья представляет собой чисто математическое упражнение, предназначенное для быстрого обзора того, как уравнения кинематики выводятся с помощью алгебры.
Это упражнение ссылается на диаграмму на рис. 1, на которой ось x представляет время, а ось y представляет скорость. Диагональная линия представляет движение объекта, скорость которого изменяется с постоянной скоростью. Заштрихованная область (A 1 + A 2 ) представляет смещение объекта в течение интервала времени между t 1 и t 2 , в течение которого скорость объекта увеличилась с v 1 до v 2. .
В этом документе будут использоваться следующие переменные:
v = величина скорости объекта (метры в секунду, м / с)
v 1 = величина начальной скорости (метров на секунда, м / с) (в некоторых текстах это vi или v 0 )
v 2 = величина конечной скорости (метры в секунду, м / с) (в некоторых текстах это v f )
a = величина ускорения (в метрах в секунду в квадрате, м / с 2 )
с = вектор смещения, величина смещения — это расстояние,
с = │ s │ = d (векторы выделены жирным шрифтом; тот же символ, не выделенный жирным шрифтом, представляет величину вектора)
Δ указывает на изменение, например Δv = (v 2 –v 1 )
t = время
t 1 = начальное время
t 2 = Последний разEquations of Motion — The Physics Hypertextbook
Обсуждение
постоянное ускорение
Для точности этот раздел должен называться «Одномерные уравнения движения при постоянном ускорении».Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.
Учитывая, что мы живем в трехмерной вселенной, в которой единственная константа — это изменение, у вас может возникнуть соблазн сразу отказаться от этого раздела. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время — ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Об этом я могу сказать с абсолютной метафизической уверенностью.
Так что же тогда хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект двигался или будет двигаться по прямому пути с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать фактически одномерным, если существует только одна степень свободы для задействованных объектов.Дорога может изгибаться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы — свободу двигаться в одном или противоположном направлении. (Вы не можете ездить по дороге по диагонали и надеетесь остаться на ней надолго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.
Наша цель в этом разделе состоит в том, чтобы вывести новые уравнения, которые можно использовать для описания движения объекта в терминах его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ( т ). Есть три способа объединить их в пары: скорость-время, положение-время и скорость-положение. В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.
Поскольку мы имеем дело с движением по прямой линии, направление будет обозначаться знаком — положительные величины указывают в одну сторону, а отрицательные величины указывают в противоположную сторону.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, если одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.
скорость-время
Связь между скоростью и временем проста при равномерно ускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, когда ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиваться вдвое на эту величину в два раза быстрее. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы должны быть в состоянии увидеть уравнение уже мысленным взором.
Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начнем с определения ускорения.
Увеличьте ∆ v до v — v 0 и конденсируйте ∆ t до t .
Затем найдите v как функцию от t .
v = v 0 + при [1]
Это первое уравнение движения . Он записывается как полином — постоянный член ( v 0 ), за которым следует член первого порядка ( на ).Поскольку наивысший порядок равен 1, правильнее называть его линейной функцией .
Символ v 0 [vee naught] называется начальной скоростью или скоростью за время t = 0. Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшее определение было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос «Какая начальная скорость?» «Это зависит от обстоятельств». Это оказывается ответом на множество вопросов.
Обозначение v — это скорость через некоторое время t после начальной скорости. Его часто называют конечной скоростью , но это не делает его «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость обозначена символом v ? Если вы внимательно слушали, значит, вы должны были ожидать ответа. По-разному. Это может быть скорость метеора, когда он проходит мимо Луны, входит в атмосферу Земли или ударяется о поверхность Земли. Это также может быть скорость метеорита, находящегося на дне кратера. (В этом случае v = 0 м / с.) Является ли какое-либо из этих значений конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из дыры в земле и уехать вместе с ним.Это актуально? Наверное, нет, но это зависит от обстоятельств. Для такого рода вещей нет правил. Вы должны проанализировать текст задачи на предмет физических величин, а затем присвоить значение математическим символам.
Последняя часть этого уравнения на — это изменение скорости по сравнению с начальным значением. Напомним, что a — это скорость изменения скорости, а t — это время после некоторого начального события . Ставка раз время меняется. Учитывая, что объект ускоряется со скоростью 10 м / с 2 , через 5 с он будет двигаться на 50 м / с быстрее.Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…
15 м / с + 50 м / с = 65 м / с
время позиции
Смещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как и дольше). Иди дальше. Ускорение усугубляет эту простую ситуацию, поскольку скорость теперь также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит смешно. «Смещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.»Время удваивается, поэтому смещение пропорционально квадрату времени. Автомобиль, разгоняющийся в течение двух секунд, преодолеет в четыре раза больше расстояния, чем автомобиль, ускоряющийся всего за одну секунду (2 2 = 4). Автомобиль, ускоряющийся в течение трех секунды покрыли бы расстояние в девять раз большее (3 2 = 9).
Если бы это было так просто. Этот пример работает, только когда начальная скорость равна нулю. Смещение пропорционально квадрату времени, когда ускорение постоянное, а начальная скорость равна нулю.Истинное общее утверждение должно учитывать любую начальную скорость и то, как она менялась. Это приводит к ужасно запутанному утверждению соразмерности. Смещение прямо пропорционально времени и пропорционально квадрату времени, когда ускорение постоянно. Функция, которая является одновременно линейной и квадратной, называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Смещение является квадратичной функцией времени при постоянном ускорении
Формулировки пропорциональности полезны, но не столь общие, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой проблемы. Один из способов понять их — использовать алгебру.
Начнем с определения средней скорости.
Увеличьте ∆ с до с — с 0 и конденсируйте ∆ t до t .
Найдите позицию.
с = с 0 + vt [a]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона .Я предпочитаю второй вариант, поскольку правило может применяться к любой величине, которая изменяется с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже, Оксфорд, английским философом, математиком, логиком и калькулятором Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится на полпути между ее конечным и начальным значениями.
v = ½ ( v + v 0 ) [4]
Подставьте первое уравнение движения [1] в это уравнение [4] и упростите, чтобы исключить v .
v = ½ [( v 0 + при ) + v 0 ] v = ½ (2 v 0 + при )
v = v 0 + ½ at [b]
Теперь замените [b] на [a], чтобы исключить v [vee bar].
с = с 0 + ( v 0 + ½ при ) t
И, наконец, найдите s как функцию от t .
с = с 0 + v 0 t + ½ при 2 [2]
Это второе уравнение движения . Он записывается как полином — постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ при 2 ). ). Поскольку наивысший порядок равен 2, правильнее называть его квадратичным .
Символ s 0 [ess naught] часто рассматривается как начальная позиция . Обозначение s — это позиция через некоторое время t позже. Если хотите, можете называть это последней позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.
∆ с = v 0 t + ½ при 2 [2]
скорость-позиция
Первые два уравнения движения описывают одну кинематическую переменную как функцию времени.По сути…
- Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
- Смещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ т 2 ).
Объединение этих двух утверждений приводит к третьему, не зависящему от времени. При замене должно быть очевидно, что…
- Смещение пропорционально квадрату скорости при постоянном ускорении (∆ с ∝ v 2 ).
Это утверждение особенно важно для безопасности вождения. Когда вы вдвое увеличиваете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить. Увеличьте скорость втрое, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.
Концептуальное введение сделано. Пришло время вывести формальное уравнение.
метод 1
Объедините первые два уравнения вместе таким образом, чтобы исключить время как переменную. Самый простой способ сделать это — начать с первого уравнения движения…
v = v 0 + при [1]
решить на время…
, а затем подставим его во второе уравнение движения…
с = с 0 + v 0 t + ½ при 2 [2]
как это…
с = с 0 + с 0 ⎛
v — v 0 ⎞
+ ½ а ⎛
v — v 0 2
а а с — с 0 = vv 0 — v 0 2 + v 2 -2 vv 0 + v 0 2 а 2 а 2 a ( с — с 0 ) = 2 ( vv 0 — v 0 2 ) + ( v 2 — 2 vv 0 + v 0 2 ) 2 a ( с — с 0 ) = v 2 — v 0 2 Возведите объект в квадрат скорости, и все готово.
v 2 = v 0 2 + 2 a ( с — с 0 ) [3]
Это третье уравнение движения . Еще раз, символ s 0 [ess naught] — это начальная позиция , , а s, — это позиция через некоторое время с до . При желании вы можете написать уравнение, используя ∆ s — изменение положения в положении , смещение или расстояние в зависимости от ситуации.
v 2 = v 0 2 + 2 a ∆ s [3]
метод 2
Более сложный способ вывести это уравнение — начать со второго уравнения движения в этой форме…
∆ с = v 0 t + ½ при 2 [2]
и решите ее на время. Это непростая работа, поскольку уравнение квадратично. Переставьте термины так…
½ при 2 + v 0 t — ∆ с = 0
и сравните его с общей формой квадратичной.
топор 2 + bx + c = 0
Решения этого даются известным уравнением…
x = — b ± √ ( b 2 — 4 ac ) 2 а Замените символы в общем уравнении эквивалентными символами из нашего преобразованного второго уравнения движения…
т = — v 0 ± √ [ v 0 2 — 4 (½ a ) (∆ с )] 2 (½ a ) почисти немного…
т = — v 0 ± √ ( v 0 2 — 2 a ∆ s ) а , а затем подставьте его обратно в первое уравнение движения.
v = v 0 + при [1]
v = v 0 + a ⎛
— v 0 ± √ ( v 0 2 — 2 a ∆ s ) ⎞
а Stuff отменяется, и мы получаем это…
v = ± √ ( v 0 2 + 2 a ∆ с )
Выровняйте обе стороны, и все готово.
v 2 = v 0 2 + 2 a ∆ s [3]
Это было не так уж и плохо, не так ли?
исчисления выводов
Исчисление — это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение — это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорость-время. Если предположить, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].
а = дв = и dt = v — v 0 = при в = v 0 + at [1] Опять же, по определению, скорость — это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
в = DS = v dt DS = ( v 0 + при ) dt = т ⌠ ( v 0 + at ) dt 0 с — с 0 = v 0 t + ½ при 2 с = с 0 + v 0 t + ½ при 2 [2] В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Это произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…
Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Он также равен самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебра с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению ( dv dt ), и другую производную, равную обратной скорости ( dt ds ).
дв = дв 1 DS DS дв = дв дт DS DS дт дв = дв дт DS дт DS дв = а 1 DS в Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
= в дв = а DS = ½ ( v 2 — v 0 2 ) = a ( с — с 0 ) в 2 = v 0 2 + 2 a ( с — с 0 ) [3] Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.

 Механика
Механика Молекулярная физика
Молекулярная физика Оптика
Оптика



 путевая = S/t
путевая = S/t {- 2} $} \ text {Восток}
\ end {align *}
{- 2} $} \ text {Восток}
\ end {align *} Для равноускоренного движения наиболее сложный график зависимости скорости от времени, который мы можем получить, представляет собой прямую линию.Посмотрите на график ниже — он представляет объект с начальной скоростью \ ({\ vec {v}} _ {i} \) , разгоняющийся до конечной скорости \ ({\ vec {v}} _ { f} \) за общее время т .
Для равноускоренного движения наиболее сложный график зависимости скорости от времени, который мы можем получить, представляет собой прямую линию.Посмотрите на график ниже — он представляет объект с начальной скоростью \ ({\ vec {v}} _ {i} \) , разгоняющийся до конечной скорости \ ({\ vec {v}} _ { f} \) за общее время т .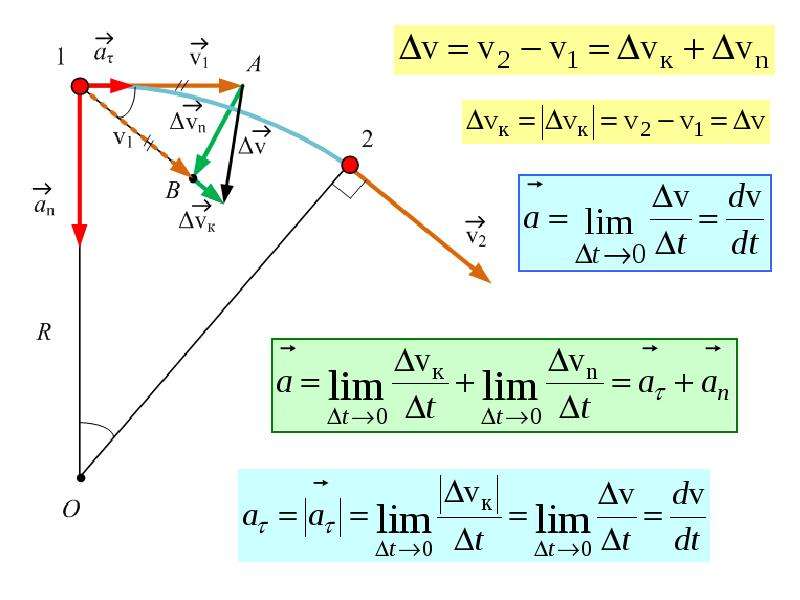 {- 1} $} \), когда водитель видит ребенка \ (\ text {50} \) \ (\ text {m} \) перед ним на дороге.{-2} $} \). Его время реакции на нажатие тормоза составляет \ (\ text {0,5} \) секунды. Будет ли грузовик сбить ребенка?
{- 1} $} \), когда водитель видит ребенка \ (\ text {50} \) \ (\ text {m} \) перед ним на дороге.{-2} $} \). Его время реакции на нажатие тормоза составляет \ (\ text {0,5} \) секунды. Будет ли грузовик сбить ребенка? Чтобы найти пройденное расстояние, мы используем:
Чтобы найти пройденное расстояние, мы используем: Ребенок находится на \ (\ text {50} \) метрах впереди. Грузовик не ударит ребенка.
Ребенок находится на \ (\ text {50} \) метрах впереди. Грузовик не ударит ребенка. е., силы). Изучение кинематики часто называют «геометрией движения».
е., силы). Изучение кинематики часто называют «геометрией движения».

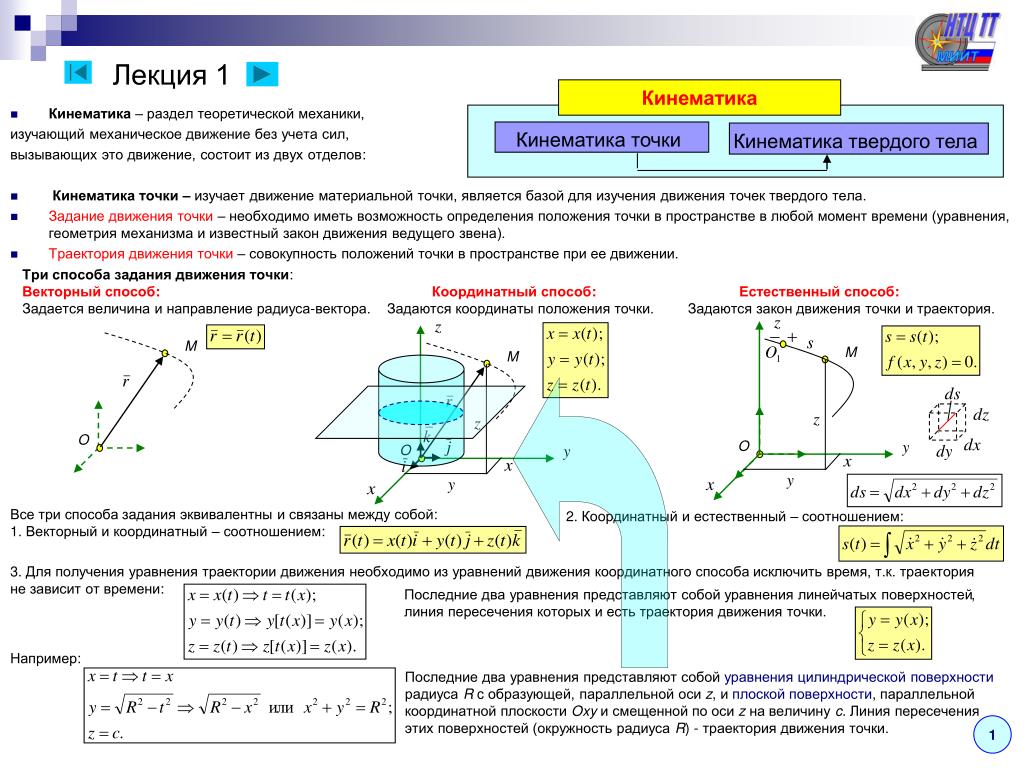 Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Землю или от нее. Математически положение объекта обычно представлено переменной x .
Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Землю или от нее. Математически положение объекта обычно представлено переменной x . Может показаться странным использование системы координат, движущейся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.
Может показаться странным использование системы координат, движущейся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.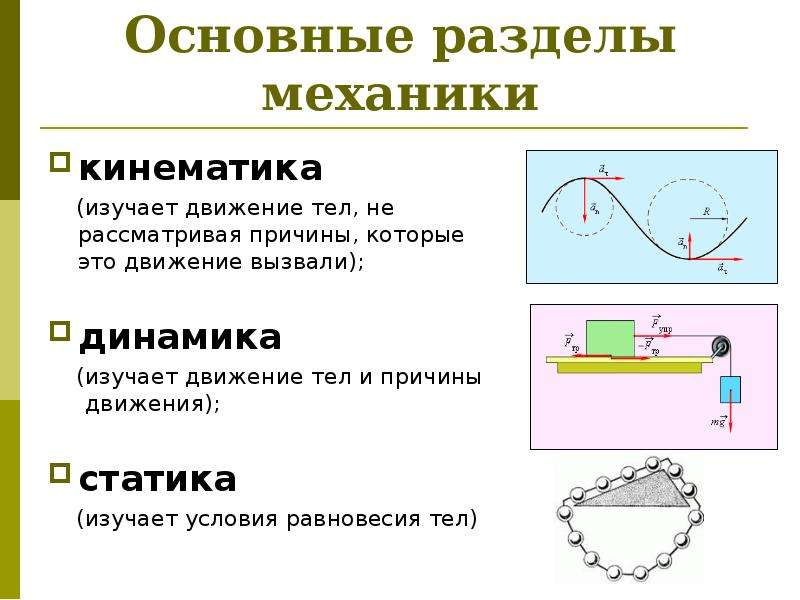 Например, фильм начинается с Доктора.Хьюм, который кажется перевернутым, обвиняет доктора Айви в том, что он перевернут. Только когда пара подбрасывает монету, становится очевидно, что доктор Айви — и камера — действительно перевернуты. Юмор фильма служит как для заинтересованности студентов, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих неожиданно непредсказуемые места в зоне просмотра. Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее творческие люди могут найти в прохожих.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик Престамон
Например, фильм начинается с Доктора.Хьюм, который кажется перевернутым, обвиняет доктора Айви в том, что он перевернут. Только когда пара подбрасывает монету, становится очевидно, что доктор Айви — и камера — действительно перевернуты. Юмор фильма служит как для заинтересованности студентов, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих неожиданно непредсказуемые места в зоне просмотра. Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее творческие люди могут найти в прохожих.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик Престамон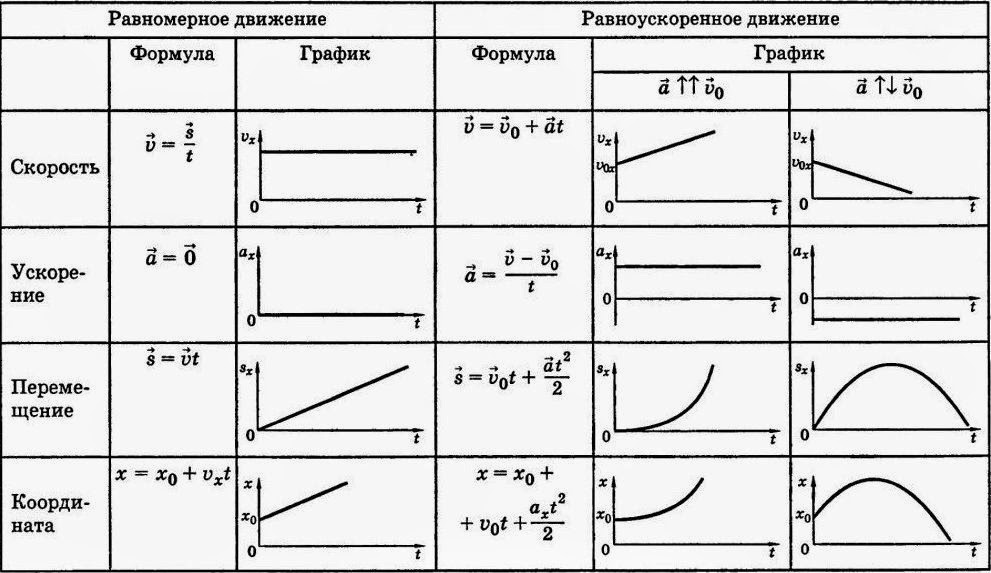
 Расстояние — это пример скалярной величины.Вектор — это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км / ч на восток и силу 500 ньютонов прямо вниз.
Расстояние — это пример скалярной величины.Вектор — это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км / ч на восток и силу 500 ньютонов прямо вниз.
 )
)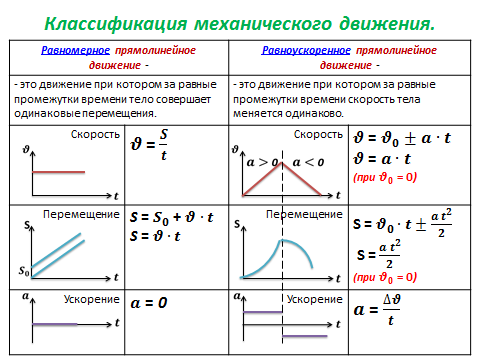 Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.