Правильный треугольник — Википедия

Материал из Википедии — свободной энциклопедии

Правильный треугольник.

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Правильный тетраэдр состоит из четырёх правильных треугольников.

Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.

• Радиус вписанной окружности правильного треугольника, выраженный через его сторону:

r=36a{\displaystyle r={\frac {\sqrt {3}}{6}}a}

• Радиус описанной окружности правильного треугольника, выраженный через его сторону:

R=33a{\displaystyle R={\frac {\sqrt {3}}{3}}a}

P=3a=33R=63r{\displaystyle P=3a=3{\sqrt {3}}R=6{\sqrt {3}}r}

h=m=l=32a{\displaystyle h=m=l={\frac {\sqrt {3}}{2}}a}

• Площадь правильного треугольника рассчитывается по формулам:

S=34a2=334R2=33r2=336P2{\displaystyle S={\frac {\sqrt {3}}{4}}a^{2}={\frac {3{\sqrt {3}}}{4}}R^{2}=3{\sqrt {3}}r^{2}={\frac {\sqrt {3}}{36}}P^{2}}

• Радиус описанной окружности равен двойному радиусу вписанной окружности:

R=2r{\displaystyle R=2r}

• Для равностороннего треугольника T группа движений (самосовмещений) плоскости, переводящих треугольник в себя, состоит из 6 элементов: трёх поворотов на углы 0, ^2π⁄₃ и ^4π⁄₃ вокруг точки O, а также трёх симметрий относительно трёх прямых, на которых лежат биссектрисы треугольника (последние являются также его высотами и медианами).
• На описанной окружности произвольного треугольника ABC{\displaystyle ABC} существуют ровно три точки такие, что их прямая Симсона касается окружности Эйлера треугольника ABC{\displaystyle ABC}, причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
• Равносторонний треугольник является одновременно и равноугольным треугольником, то есть у него равны все внутренние углы.
• Равносторонний треугольник является частными случаем равнобедренного треугольника, а именно: дважды равнобедренным треугольником.

Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.

Теоремы о равностороннем треугольнике или содержащие его[править | править код]

Многоугольники
Звёздчатые многоугольники
Паркеты на плоскости
Правильные многогранники и сферические паркеты
Многогранники Кеплера — Пуансо
Соты
Четырёхмерные многогранники	{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}

Треугольник Рёло — Википедия

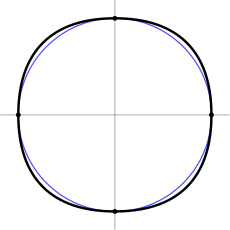
Построение треугольника Рёло

Треуго́льник Рёло́^{[* 1]} представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне^[1][2]. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.

Треугольник Рёло является простейшей после круга фигурой постоянной ширины^[1]. То есть если к треугольнику Рёло провести пару параллельных опорных прямых^{[* 2]}, то расстояние между ними не будет зависеть от выбранного направления^[3]. Это расстояние называется шириной треугольника Рёло.

Среди прочих фигур постоянной ширины треугольник Рёло выделяется рядом экстремальных свойств: наименьшей площадью

[1], наименьшим возможным углом при вершине^[4], наименьшей симметричностью относительно центра^[5]. Треугольник получил распространение в технике — на его основе были созданы кулачковые и грейферные механизмы, роторно-поршневой двигатель Ванкеля и даже дрели, позволяющие сверлить (фрезеровать) квадратные отверстия^[6].

Название фигуры происходит от фамилии немецкого механика Франца Рёло. Он, вероятно, был первым, кто исследовал свойства этого так называемого криволинейного треугольника; также он использовал его в своих механизмах^[7].

Рёло не является первооткрывателем этой фигуры, хотя он и подробно исследовал её. В частности, он рассматривал вопрос о том, сколько контактов (в кинематических парах) необходимо, чтобы предотвратить движение плоской фигуры, и на примере искривлённого треугольника, вписанного в квадрат, показал, что даже трёх контактов может быть недостаточно для того, чтобы фигура не вращалась

[8].

Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке^[9]. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции^[10], а также в Мадридском кодексе^[9].

Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами (угол между плоскостями этих меридианов равен 90°) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов^[11].

Ещё раньше, в XIII веке, создатели церкви Богоматери в Брюгге использовали треугольник Рёло в качестве формы для некоторых окон^[9].

Треугольник Рёло является плоской выпуклой геометрической фигурой^[12].

Основные геометрические характеристики[править | править код]

Если ширина треугольника Рёло равна a{\displaystyle a}, то его площадь равна^[13]

S=12(π−3)⋅a2,{\displaystyle S={{1} \over {2}}\left(\pi -{\sqrt {3}}\right)\cdot a^{2},}

периметр

p=πa,{\displaystyle p=\pi a,}

радиус вписанной окружности

r=(1−13)⋅a,{\displaystyle r=\left(1-{{1} \over {\sqrt {3}}}\right)\cdot a,}

а радиус описанной окружности

R=a3{\displaystyle R={{a} \over {\sqrt {3}}}}.

Симметрия[править | править код]

Треугольник Рёло обладает осевой симметрией. Он имеет три оси симметрии второго порядка, каждая из которых проходит через вершину треугольника и середину противоположной дуги, а также одну ось симметрии третьего порядка, перпендикулярную плоскости треугольника и проходящую через его центр^{[* 3]}. Таким образом, группа симметрий треугольника Рёло состоит из шести отображений (включая тождественное) и совпадает с группой D3{\displaystyle D_{3}} симметрий правильного треугольника.

Построение циркулем[править | править код]

Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей.

Свойства, общие для всех фигур постоянной ширины[править | править код]

Поскольку треугольник Рёло является фигурой постоянной ширины, он обладает всеми общими свойствами фигур этого класса. В частности,

• с каждой из своих опорных прямых треугольник Рёло имеет лишь по одной общей точке^[14];
• расстояние между двумя любыми точками треугольника Рёло ширины a{\displaystyle a} не может превышать a{\displaystyle a}^[15];
• отрезок, соединяющий точки касания двух параллельных опорных прямых к треугольнику Рёло, перпендикулярен к этим опорным прямым^[16];
• через любую точку границы треугольника Рёло проходит по крайней мере одна опорная прямая^[17];
• через каждую точку P{\displaystyle P} границы треугольника Рёло проходит объемлющая его окружность радиуса a{\displaystyle a}^{[* 4]}, причём опорная прямая, проведённая к треугольнику Рёло через точку P{\displaystyle P}, является касательной к этой окружности^[18];
• радиус окружности, имеющей не меньше трёх общих точек с границей треугольника Рёло ширины a{\displaystyle a}, не превышает a{\displaystyle a}^[19];
• по теореме Ханфрида Ленца^[de] о множествах постоянной ширины треугольник Рёло нельзя разделить на две фигуры, диаметр которых был бы меньше ширины самого треугольника^[20][21];
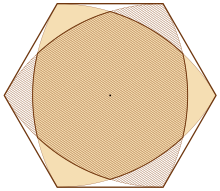
• треугольник Рёло, как и любую другую фигуру постоянной ширины, можно вписать в квадрат^[22], а также в правильный шестиугольник^[23];
• по теореме Барбье формула периметра треугольника Рёло справедлива для всех фигур постоянной ширины^[24][25][26].

Экстремальные свойства[править | править код]

Наименьшая площадь[править | править код]

Среди всех фигур постоянной ширины a{\displaystyle a} у треугольника Рёло наименьшая площадь^[1]. Это утверждение носит название теоремы Бляшке — Лебега^[27][28] (по фамилиям немецкого геометра Вильгельма Бляшке, опубликовавшего теорему в 1915 году^[29], и французского математика Анри Лебега, который сформулировал её в 1914 году^[30]). В разное время варианты её доказательства предлагали Мацусабуро Фудзивара (1927 и 1931 год)^[31][32], Антон Майер (1935 год)^[33], Гарольд Эгглстон (1952 год)^[34], Абрам Безикович (1963 год)^[35], Дональд Чакериан (1966 год)^[36], Эванс Харрелл (2002 год)^[37] и другие математики^[5].

Чтобы найти площадь треугольника Рёло, можно сложить площадь внутреннего равностороннего треугольника

S△=34⋅a2{\displaystyle S_{\triangle }={{\sqrt {3}} \over {4}}\cdot a^{2}}

и площадь трёх оставшихся одинаковых круговых сегментов, опирающихся на угол в 60°

Sseg=a22(π3−sin⁡π3)=(π6−34)⋅a2,{\displaystyle S_{seg}={{a^{2}} \over {2}}\left({{\pi } \over {3}}-\sin {{\pi } \over {3}}\right)={\left({{\pi } \over {6}}-{{\sqrt {3}} \over {4}}\right)\cdot a^{2}},}

то есть

Srt=S△+3Sseg=12(π−3)⋅a2=a2⋅0,70477…{\displaystyle S_{rt}=S_{\triangle }+3S_{seg}={{1} \over {2}}\left(\pi -{\sqrt {3}}\right)\cdot a^{2}=a^{2}\cdot 0{,}70477\ldots }^[38]

Фигура, обладающая противоположным экстремальным свойством — круг. Среди всех фигур данной постоянной ширины его площадь

S◯=a2⋅π4=a2⋅0,78539…{\displaystyle S_{\bigcirc }=a^{2}\cdot {{\pi } \over {4}}=a^{2}\cdot 0{,}78539\ldots }

максимальна^{[39][* 5]}. Площадь соответствующего треугольника Рёло меньше на ≈10,27 %. В этих пределах лежат площади всех остальных фигур данной постоянной ширины.

Наименьший угол[править | править код]

Через каждую вершину треугольника Рёло, в отличие от остальных его граничных точек, проходит не одна опорная прямая, а бесконечное множество опорных прямых. Пересекаясь в вершине, они образуют «пучок». Угол между крайними прямыми этого «пучка» называется углом при вершине. Для фигур постоянной ширины угол при вершинах не может быть меньше 120°. Единственная фигура постоянной ширины, имеющая углы, равные в точности 120° — это треугольник Рёло^[4].

Наименьшая центральная симметрия[править | править код]

Треугольник Рёло (бежевый) и его образ при центральной симметрии относительно своего центра (заштрихован). Наибольшая центрально-симметричная фигура, в нём содержащаяся (криволинейный шестиугольник), и наименьшая центрально-симметричная выпуклая, его содержащая (правильный шестиугольник) выделены жирной линией

Из всех фигур постоянной ширины треугольник Рёло обладает центральной симметрией в наименьшей степени^{[5][40][41][42][43]}. Существует несколько различных способов дать определение степени симметричности фигуры. Один из них — это мера Ковнера — Безиковича. В общем случае для выпуклой фигуры C{\displaystyle C} она равна

σ(C)=μ(A)μ(C),{\displaystyle \sigma (C)={{\mu (A)} \over {\mu (C)}},}

где μ{\displaystyle \mu } — площадь фигуры, A{\displaystyle A} — содержащаяся в C{\displaystyle C} центрально-симметричная выпуклая фигура максимальной площади. Для треугольника Рёло такой фигурой является шестиугольник с искривлёнными сторонами, представляющий собой пересечение этого треугольника Рёло со своим образом при центральной симметрии относительно своего центра^{[* 3]}. Мера Ковнера — Безиковича для треугольника Рёло равна

σ=6arccos⁡(5+3312)+3−11π−3=0,84034…{\displaystyle \sigma ={{6\arccos {\left({{5+{\sqrt {33}}} \over {12}}\right)}+{\sqrt {3}}-{\sqrt {11}}} \over {\pi -{\sqrt {3}}}}=0{,}84034\ldots }^[5][40]

Другой способ — это мера Эстерманна

τ(C)=μ(C)μ(B),{\displaystyle \tau (C)={{\mu (C)} \over {\mu (B)}},}

где B{\displaystyle B} — содержащая C{\displaystyle C} центрально-симметричная фигура минимальной площади. Для треугольника Рёло B{\displaystyle B} — это правильный шестиугольник, поэтому мера Эстерманна равна

τ=π−33=0,81379…{\displaystyle \tau ={{\pi -{\sqrt {3}}} \over {\sqrt {3}}}=0{,}81379\ldots }^[5][36]

Для центрально-симметричных фигур меры Ковнера — Безиковича и Эстерманна равны единице. Среди фигур постоянной ширины центральной симметрией обладает только круг^[25], который (вместе с треугольником Рёло) и ограничивает область возможных значений их симметричности.

Качение по квадрату[править | править код]

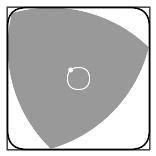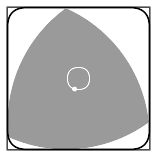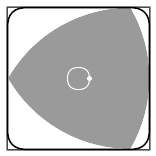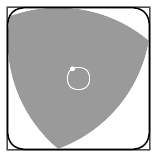
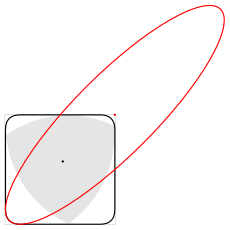
Любая фигура постоянной ширины вписана в квадрат со стороной, равной ширине фигуры, причём направление сторон квадрата может быть выбрано произвольно^{[22][* 6]}. Треугольник Рёло — не исключение, он вписан в квадрат и может вращаться в нём, постоянно касаясь всех четырёх сторон^[44].

Каждая вершина треугольника при его вращении «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах — там вершина описывает дугу эллипса. Центр этого эллипса расположен в противоположном углу квадрата, а его больша́я и малая оси повёрнуты на угол в 45° относительно сторон квадрата и равны

a⋅(3±1),{\displaystyle a\cdot \left({\sqrt {3}}\pm 1\right),}

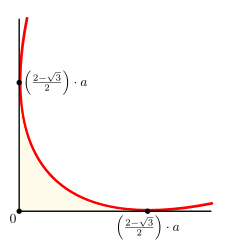
где a{\displaystyle a} — ширина треугольника^[45]. Каждый из четырёх эллипсов касается двух смежных сторон квадрата на расстоянии

a⋅(1−32)=a⋅0,13397…{\displaystyle a\cdot \left(1-{{\sqrt {3}} \over {2}}\right)=a\cdot 0{,}13397\ldots }

от угла^[38].

Эллипс (выделен красным цветом), очерчивающий один из углов фигуры (её граница выделена чёрным цветом), которую покрывает треугольник Рёло при вращении в квадрате	Угол покрываемой вращением фигуры. Подписаны точки касания сторон квадрата с эллипсом. Светло-жёлтым показан не затронутый вращением угол квадрата

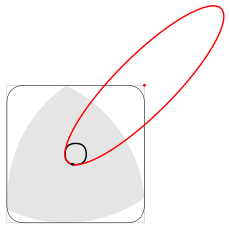
Центр треугольника Рёло при вращении движется по траектории, составленной из четырёх одинаковых дуг эллипсов. Центры этих эллипсов расположены в вершинах квадрата, а оси повёрнуты на угол в 45° относительно сторон квадрата и равны

a⋅(1±13){\displaystyle a\cdot \left(1\pm {{1} \over {\sqrt {3}}}\right)}^[45].

Иногда для механизмов, реализующих на практике такое вращение треугольника, в качестве траектории центра выбирают не склейку из четырёх дуг эллипсов, а близкую к ней окружность^[46].

Эллипс (выделен красным цветом), очерчивающий одну четвёртую кривой, по которой движется центр треугольника Рёло при вращении в квадрате	Траектория центра треугольника Рёло при вращении в квадрате. Выделены точки сопряжения четырёх дуг эллипсов. Для сравнения показана окружность (синим цветом), проходящая через эти же четыре точки

Площадь каждого из четырёх не затронутых вращением уголков равна

β=a2⋅(1−32−π24){\displaystyle \beta =a^{2}\cdot \left(1-{{\sqrt {3}} \over {2}}-{{\pi } \over {24}}\right)}^[47]

и, вычитая их из площади квадрата, можно получить площадь фигуры, которую образует треугольник Рёло при вращении в нём

a2−4β=a2⋅(23+π6−3)=a2⋅0,98770…{\displaystyle a^{2}-4\beta =a^{2}\cdot \left(2{\sqrt {3}}+{{\pi } \over {6}}-3\right)=a^{2}\cdot 0{,}98770\ldots }^[38][47][48]

Разница с площадью квадрата составляет ≈1,2 %, поэтому на основе треугольника Рёло создают свёрла, позволяющие получать почти квадратные отверстия^[45].

Сверление квадратных в сечении к оси фрезы отверстий[править | править код]

«Мы все слыхали о гаечных ключах, приспособленных для гаек с левой резьбой, завязанных в узел водопроводных трубах и бананах из чугуна. Мы считали подобные вещи смешными безделушками и отказывались даже верить, что они когда-нибудь встретятся нам в действительности. И вдруг появляется инструмент, позволяющий сверлить квадратные отверстия!»

рекламная листовка фирмы
Watts Brothers Tool Works^{[49][* 7]}

Фреза с сечением в виде треугольника Рёло и режущими лезвиями, совпадающими с его вершинами, позволяет получать почти квадратные отверстия. Отличие таких отверстий от квадрата в сечении состоит лишь в немного скруглённых углах^[50]. Другая особенность подобной фрезы заключается в том, что его ось при вращении не должна оставаться на месте, как это происходит в случае традиционных спиральных свёрл, а описывает в плоскости сечения кривую, состоящую из четырёх дуг эллипсов. Поэтому патрон, в котором зажата фреза, и крепление инструмента не должно препятствовать этому движению^[45].

Впервые реализовать подобную конструкцию крепления инструмента удалось Гарри Уаттсу, английскому инженеру, работавшему в США. Для этого он использовал направляющую пластину с отверстием в виде квадрата, в котором могло радиально перемещаться сверло, зажатое в «плавающем патроне»^[50]. Патенты на патрон^[51] и сверло^[52] были получены Уаттсом в 1917 году. Продажу новых дрелей осуществляла фирма Watts Brothers Tool Works^[en][53][54]. Ещё один патент США на похожее изобретение был выдан в 1978 году^[55].

Двигатель Ванкеля[править | править код]

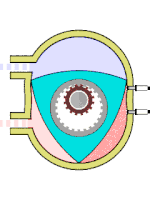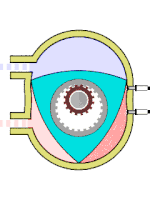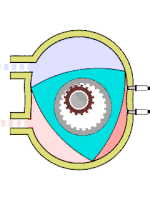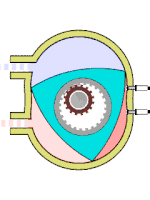Схема работы двигателя Ванкеля

Другой пример использования можно найти в двигателе Ванкеля: ротор этого двигателя выполнен в виде треугольника Рёло^[6]. Он вращается внутри камеры, поверхность которой выполнена по эпитрохоиде^[56]. Вал ротора жёстко соединён с зубчатым колесом, которое сцеплено с неподвижной шестернёй. Такой трёхгранный ротор обкатывается вокруг шестерни, всё время касаясь вершинами внутренних стенок двигателя и образуя три области переменного объёма, каждая из которых по очереди является камерой сгорания^[6]. Благодаря этому двигатель выполняет три полных рабочих цикла за один оборот.

Двигатель Ванкеля позволяет осуществить любой четырёхтактный термодинамический цикл без применения механизма газораспределения. Смесеобразование, зажигание, смазка, охлаждение и пуск в нём принципиально такие же, как у обычных поршневых двигателей внутреннего сгорания^[56].

Грейферный механизм[править | править код]

Рамочно-кулачковый грейферный механизм кинопроектора «Луч-2»

Ещё одно применение треугольника Рёло в механике — это грейферный механизм, осуществляющий покадровое перемещение плёнки в кинопроекторах. Грейфер проектора «Луч-2», например, основан на треугольнике Рёло, который вписан в рамку-квадрат и закреплён на двойном параллелограмме. Вращаясь вокруг вала привода, треугольник двигает рамку с расположенным на ней зубом. Зуб входит в перфорацию киноплёнки, протаскивает её на один кадр вниз и выходит обратно, поднимаясь затем к началу цикла. Его траектория тем ближе к квадрату, чем ближе к вершине треугольника закреплён вал (идеально квадратная траектория позволила бы проецировать кадр в течение ¾ цикла)^[6][57][58].

Существует и другая конструкция грейфера, также основанная на треугольнике Рёло. Как и в первом случае, рамка этого грейфера совершает возвратно-поступательное движение, однако её двигает не один, а два кулачка, работа которых синхронизирована с помощью зубчатой передачи^[28].

Крышки для люков[править | править код]

В форме треугольника Рёло можно изготавливать крышки для люков — благодаря постоянной ширине они не могут провалиться в люк^[59].

В Сан-Франциско, для системы рекуперирования воды^[en] корпуса люков имеют форму треугольника Рёло, но их крышки имеют форму равносторонних треугольников.

Кулачковый механизм[править | править код]

Внешние изображения
Кулачковые механизмы на основе треугольника Рёло
	Модели L01[60], L02[61] и L06[62] из коллекции механизмов Франца Рёло

Треугольник Рёло использовался в кулачковых механизмах некоторых паровых двигателей начала XIX века. В этих механизмах вращательное движение кривошипа поворачивает треугольник Рёло, прикреплённый к толкателю передаточными рычагами, что заставляет толкатель совершать возвратно-поступательное движение^[63]. По терминологии Рёло, это соединение образует «высшую» кинематическую пару, поскольку контакт звеньев происходит по линии, а не по поверхности^[64]. В подобных кулачковых механизмах толкатель при достижении крайнего правого или левого положения остаётся некоторое конечное время неподвижен^[63][10].

Треугольник Рёло ранее широко применялся в кулачковых механизмах швейных машин зигзагообразной строчки.

В качестве кулачка треугольник Рёло использовали немецкие часовые мастера в механизме наручных часов A. Lange & Söhne «Lange 31»^[65].

Каток[править | править код]

Для перемещения тяжёлых предметов на небольшие расстояния можно использовать не только колёсные, но и более простые конструкции, например, цилиндрические катки^[66]. Для этого груз нужно расположить на плоской подставке, установленной на катках, а затем толкать его. По мере освобождения задних катков их необходимо переносить и класть спереди^[67][66]. Такой способ транспортировки человечество использовало до изобретения колеса.

При этом перемещении важно, чтобы груз не двигался вверх и вниз, так как тряска потребует дополнительных усилий от толкающего^[67]. Для того, чтобы движение по каткам было прямолинейным, их сечение должно представлять собой фигуру постоянной ширины^[67][68]. Чаще всего сечением был круг, ведь катками служили обыкновенные брёвна. Однако сечение в виде треугольника Рёло будет ничуть не хуже^{[прояснить]} и позволит передвигать предметы столь же прямолинейно^[6][67].

Несмотря на то, что катки в форме треугольника Рёло позволяют плавно перемещать предметы, такая форма не подходит для изготовления колёс, поскольку треугольник Рёло не имеет фикс

Гиперболический треугольник — Википедия

В гиперболической геометрии гиперболический треугольник является треугольником на гиперболической плоскости. Он состоит из трёх отрезков, называемых сторонами или рёбрами, и трёх точек, называемых углами или вершинами.

Как и в евклидовом случае, три точки гиперболического пространства произвольной размерности всегда лежат в той же плоскости. Следовательно, планарные гиперболические треугольники также описывают треугольники, возможные в любых гиперболических пространствах высокой размерности.

Гиперболический треугольник состоит из трёх неколлинеарных точек и трёх отрезков между ними^[1].

Гиперболические треугольники имеют некоторые свойства, которые аналогичны свойствам треугольников в евклидовой геометрии:

Гиперболические треугольники имеют некоторые свойства, аналогичные свойствам треугольников на сферической или эллиптической геометрии:

• Два треугольника с той же суммой углов равны по площади.
• Существует верхняя граница для площади треугольников.
• Существует верхняя граница для радиуса вписанной окружности.
• Два треугольника конгруэнтны тогда и только тогда, когда они переходят друг в друга в результате конечного числа отражений относительно прямой.
• Два треугольника с равными соответствующими углами конгруэнтны (то есть все подобные треугольники конгруэнтны).

Гиперболические треугольники имеют некоторые свойства, которые противоположны свойствам треугольников в сферической или эллиптической геометрии:

• Сумма углов треугольника меньше 180°.
• Площадь треугольника пропорциональна дефициту его суммы углов (до 180°).

Гиперболические треугольники имеют также некоторые свойства, которых нет в других геометриях:

Треугольники с идеальными вершинами[править | править код]

Определение треугольника можно обобщить, если разрешить вершинам лежать на идеальной границе гиперплоскости, при этом стороны должны лежать внутри плоскости. Если пара сторон является асимптотически параллельными (то есть расстояние между ними стремится к нулю при стремлении к идеальной точке, но они не пересекаются), то они заканчиваются в идеальной вершине, представленной омега-точкой.

Говорят, что такая пара сторон образует нулевой угол.

Треугольник с нулевым углом невозможен в евклидовой геометрии для прямолинейных сторон, лежащих на разных прямых. Однако такие нулевые углы возможны для касающихся окружностей^[en].

Треугольник с одной идеальной вершиной называется омега-треугольником

.

Специальные виды треугольников с идеальными вершинами:

Треугольник параллельности[править | править код]

Треугольник, в котором одна вершина является идеальной точкой, один угол прямой — третий угол является углом параллельности для стороны между прямым углом и третьим углом.

Треугольник Швайкерта[править | править код]

Треугольник, в котором две вершины являются идеальными точками, а оставшийся угол является прямым. Это один из первых гиперболических треугольников (1818), который описал Фердинанд Карл Швайкерт.

Идеальный треугольник[править | править код]

Треугольник, в котором все вершины являются идеальными точками. Такой треугольник является самым большим из возможных треугольников в геометрии Лобачевского, поскольку имеет нулевую сумму углов.

Связи между углами и сторонами аналогичны связям между такими же объектами в сферической тригонометрии. Масштаб длины для сферической геометрии и геометрии Лобачевского можно, например, определить как длину стороны равностороннего треугольника с фиксированными углами.

Масштаб длины наиболее удобен, если длины измеряются в терминах абсолютной длины (специальной единицы длины, аналогичной отношению между расстояниями в сферической геометрии). Выбор масштаба длины делает формулы проще

[4].

В терминах модели Пуанкаре в верхней полуплоскости абсолютная длина соответствует инфинитезимальной метрике ds=|dz|Im⁡(z){\displaystyle ds={\frac {|dz|}{\operatorname {Im} (z)}}}, а в дисковой модели Пуанкаре соответствует ds=2|dz|1−|z|2{\displaystyle ds={\frac {2|dz|}{1-|z|^{2}}}}

В терминах (постоянной отрицательной) кривизны Гаусса K гиперболической плоскости единица абсолютной длины соответствует длине

R=1−K.{\displaystyle R={\frac {1}{\sqrt {-K}}}.}

В гиперболическом треугольнике сумма углов A, B, C (соответствующих противоположным сторонам с тем же буквами) строго меньше развёрнутого угла. Разница между мерой развёрнутого угла и суммой мер углов треугольника называется дефектом треугольника. Площадь гиперболического треугольника равна его дефекту, умноженному на квадрат R:

(π−A−B−C)R2.{\displaystyle (\pi -A-B-C)R^{2}{}{}.\!}

Эта теорема, впервые доказанная Иоганном Генрихом Ламбертом^[5], связана с теоремой Жирара в сферической геометрии.

Во всех формулах ниже стороны a, b и c должны быть измерены по абсолютной длине, единице, такой, что кривизна Гаусса K поверхности равна −1. Другими словами, величина R в вышестоящем параграфе должна быть принята равной 1.

Тригонометрические формулы для гиперболических треугольников зависят от гиперболических функций sh, ch, and th.

Тригонометрия прямоугольных треугольников[править | править код]

Если C обозначает прямой угол, то:

• Синус угла A равен гиперболическому синусу противоположной углу стороны A, делённому на гиперболический синус гипотенузы c.

sin⁡A=shashc.{\displaystyle \sin A={\frac {\mathrm {sh} \,a}{\,\mathrm {sh} \,c\,}}.\,}

• Косинус угла A равен гиперболическому тангенсу прилежащего катета b, делённому на гиперболический тангенс гипотенузы c.

cos⁡A=thbthc.{\displaystyle \cos A={\frac {\mathrm {th} \,b}{\,\mathrm {th} \,c\,}}.\,}

• Тангенс угла A равен гиперболическому тангенсу противоположного катета a, делённого на гиперболический синус прилежащего катета b.

tgA=thashb.{\displaystyle \mathrm {tg} \,A={\frac {\mathrm {th} \,a}{\,\mathrm {sh} \,b\,}}.}

• Гиперболический косинус прилежащего катета b угла A равен косинусу угла B, делённому на синус угла A.

ch(b)=cos⁡Bsin⁡A.{\displaystyle {\textrm {ch(b)}}={\frac {\cos B}{\sin A}}.}

• Гиперболический косинус гипотенузы c равен произведению гиперболических косинусов катетов a и b.

ch(c)=ch(a)ch(b).{\displaystyle {\textrm {ch(c)}}={\textrm {ch(a)}}{\textrm {ch(b)}}.}

• Гиперболический косинус гипотенузы H равен произведению косинусов углов, делённому на произведение их синусов^[6].

ch(H) =cos⁡Acos⁡Bsin⁡Asin⁡B=ctgActgB{\displaystyle ={\frac {\cos A\cos B}{\sin A\sin B}}=\mathrm {ctg} \,A\mathrm {ctg} \,B}

Отношения между углами[править | править код]

Верны следующие равенства^[7]:

cos⁡A=chasin⁡B{\displaystyle \cos A=\mathrm {ch} \,a\sin B}

sin⁡A=cos⁡Bchb{\displaystyle \sin A={\frac {\cos B}{\mathrm {ch} \,b}}}

tgA=cot⁡Bchc{\displaystyle \mathrm {tg} \,A={\frac {\cot B}{\mathrm {ch} \,c}}}

cos⁡B=chbsin⁡A{\displaystyle \cos B=\mathrm {ch} \,b\sin A}

chc=ctgActgB{\displaystyle \mathrm {ch} \,c=\mathrm {ctg} \,A\mathrm {ctg} \,B}

Площадь[править | править код]

Площадь прямоугольного треугольника равна:

Площадь =π2−∠A−∠B{\displaystyle ={\frac {\pi }{2}}-\angle A-\angle B}

а также

Area=2arctan⁡(th(a2)th(b2)){\displaystyle {\textrm {Area}}=2\arctan(\mathrm {th} \,({\frac {a}{2}})\mathrm {th} \,({\frac {b}{2}}))}^[8].

Угол параллельности[править | править код]

Экземпляр омега-треугольника с прямым углом даёт конфигурацию для проверки угла параллельности в треугольнике.

В случае, когда угол B = 0, a = c = ∞{\displaystyle \infty } и th(∞)=1{\displaystyle {\textrm {th}}(\infty )=1}, получаем cos⁡A=th(b).{\displaystyle \cos A={\textrm {th(b)}}.} (b = прилежащий катет)

Равносторонний треугольник[править | править код]

Тригонометрические формулы для прямоугольных треугольников дают также отношения между сторонами s и углами A равностороннего треугольника (треугольника, у которого все стороны имеют одинаковую длину и все углы равны):

cos⁡A=th22sth(s){\displaystyle \cos A={\frac {{\textrm {th}}{\frac {1}{2}}s}{{\textrm {th}}(s)}}}

ch22s=cos⁡(12A)sin⁡(A)=12sin⁡(12A){\displaystyle \mathrm {ch} \,{\frac {1}{2}}s={\frac {\cos({\frac {1}{2}}A)}{\sin(A)}}={\frac {1}{2\sin({\frac {1}{2}}A)}}}

Общая тригонометрия[править | править код]

Независимо от того, является C прямым углом или нет, выполняются следующие соотношения: Гиперболический закон косинусов^[en]:

chc=chachb−shashbcos⁡C,{\displaystyle \mathrm {ch} \,c=\mathrm {ch} \,a\mathrm {ch} \,b-\mathrm {sh} \,a\mathrm {sh} \,b\cos C,}

Двойственная закону теорема

cos⁡C=−cos⁡Acos⁡B+sin⁡Asin⁡Bchc,{\displaystyle \cos C=-\cos A\cos B+\sin A\sin B\mathrm {ch} \,c,}

Существует также закон синусов:

sin⁡Asha=sin⁡Bshb=sin⁡Cshc,{\displaystyle {\frac {\sin A}{\mathrm {sh} \,a}}={\frac {\sin B}{\mathrm {sh} \,b}}={\frac {\sin C}{\mathrm {sh} \,c}},}

и четырёхчленная формула:

cos⁡Ccha=shachb−sin⁡CctgB.{\displaystyle \cos C\mathrm {ch} \,a=\mathrm {sh} \,a\mathrm {ch} \,b-\sin C\mathrm {ctg} \,B.}

Для гиперболической тригонометрии:

1. ↑ Stothers, 2000.
2. ↑ Атанасян Л. С. Окружность // Геометрия Лобачевского / под ред. М. С. Стригуновой. — М.: БИНОМ. Лаборатория знаний, 2014. — С. 125—126. — 467 с. — ISBN 978-5-9963-2364-7.
3. ↑ Атанасян Л. С. Замечательные точки и прямые треугольника // Геометрия Лобачевского / под ред. М. С. Стригуновой. — М.: БИНОМ. Лаборатория знаний, 2014. — С. 166—167. — 467 с. — ISBN 978-5-9963-2364-7.
4. ↑ Needham, 1998, с. 270.
5. ↑ Ratcliffe, 2006, с. 99.
6. ↑ Martin, 1998, с. 433.
7. ↑ Smogorzhevski, 1982, с. 63.
8. ↑ Mathematics stackexchange, 2015.

Группа треугольника — Википедия

В математике группа треугольника — это группа, которая может быть представлена геометрически при помощи последовательных отражений относительно сторон треугольника. Треугольником может служить обычный евклидов треугольник, треугольник на сфере или гиперболический треугольник. Любая группа треугольника является группой симметрии паркета конгруэнтных треугольников в двумерном пространстве, на сфере или на плоскости Лобачевского (см. также статью об гиперболической плоскости ).

Пусть l, m, n — целые числа, большие либо равные 2. Группа треугольника Δ(l,m,n) является группой движений евклидового пространства, двумерной сферы, вещественной проективной плоскости или гиперболической плоскости, порождённой отражениями относительно сторон треугольника с углами π/l, π/m and π/n (измеряемые в радианах). Произведение отражений относительно двух смежных сторон является вращением на угол, равный удвоенному углу между этими сторонами, 2π/l, 2π/m и 2π/n. Таким образом, если отражения обозначить буквами a, b и c, а углы между сторонами в циклическом порядке, как указано выше, имеют место следующие соотношения:

1. a2=b2=c2=1{\displaystyle a^{2}=b^{2}=c^{2}=1}
2. (ab)l=(bc)n=(ca)m=1.{\displaystyle (ab)^{l}=(bc)^{n}=(ca)^{m}=1.}

Существует теорема, что все другие соотношения между a, b, c являются следствием этих соотношений и что Δ(l, m, n) является дискретной группой^[en] движений соответствующего пространства. Эта группа треугольника является группой отражений^[en], допускающей задание

Δ(l,m,n)=⟨a,b,c∣a2=b2=c2=(ab)l=(bc)n=(ca)m=1⟩.{\displaystyle \Delta (l,m,n)=\langle a,b,c\mid a^{2}=b^{2}=c^{2}=(ab)^{l}=(bc)^{n}=(ca)^{m}=1\rangle .}

Абстрактная группа с этим заданием является группой Коксетера с тремя генераторами.

Если заданы любые натуральные числа l, m, n > 1, в точности одна из классических двумерных геометрий (евклидова, сферическая или гиперболическая) допускает треугольник с углами (π/l, π/m, π/n) и пространство замощено отражениями этого треугольника. Сумма углов треугольника определяет тип геометрии по Формула Гаусса — Бонне: пространство евклидово, если сумма углов в точности равна π, сферическое, если превышает π и гиперболическое, если строго меньше π. Более того, любые два треугольника с заданными углами конгруэнтны. Каждая группа треугольника определяет замощение, которое обычно раскрашивается в два цвета, так что любые два соседних элемента мозаики имеют разные цвета.

В терминах чисел l, m, n > 1 существуют следующие возможности.

Евклидова плоскость[править | править код]

1l+1m+1n=1.{\displaystyle {\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}=1.}

Группа треугольника является бесконечной группой симметрии некоторого паркета (или мозаики) евклидовой плоскости треугольниками, углы которых в сумме дают π (или 180°). С точностью до перестановок, тройка (l, m, n) является одной из троек (2,3,6), (2,4,4), (3,3,3). Соответствующие группы треугольников являются представителями группы рисунков обоев^[en]*.

Сфера[править | править код]

1l+1m+1n>1.{\displaystyle {\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}>1.}

Группа треугольника является конечной группой симметрии паркета на единичной сфере из сферических треугольников, или треугольников Мёбиуса, сумма углов которых в сумме дают число, большее π. С точностью до перестановки тройки (l,m,n) имеют вид (2,3,3), (2,3,4), (2,3,5) или (2,2,n), n > 1. Сферические группы треугольников можно сопоставить с группами симметрий правильных многогранников в трёхмерном евклидовом пространстве: Δ(2,3,3) соответствует тетраэдру, Δ(2,3,4) соответствует как кубу, так и октаэдра (они имеют одну и ту же группу симметрии), Δ(2,3,5) соответствует как додекаэдру, так и икосаэдру. Группы Δ(2,2,n), n > 1, диэдрической симметрии можно рассматривать как группы симметрии семейства диэдров, которые образуются двумя одинаковыми правильными n-угольниками, соединёнными вместе, или, двойственно, осоэдром, который образован объединением n двуугольников.

Сферический паркет, соответствующий правильному многограннику, получается путём барицентрического подразделения многогранника и проекции полученных точек и прямых на описанную сферу. Для тетраэдра имеется четыре грани, и каждая грань является равносторонним треугольником, который делится на 6 меньших частей медианами, пересекающимися в центре. Получающаяся мозаика имеет 4 × 6=24 сферических треугольника (это сферический тетракисгексаэдр).

Эти группы конечны, что соответствует компактности сферы — площади дисков на сфере растут в терминах радиуса, но в конечном счёте покрывают всю сферу.

Треугольные замощения приведены ниже:

(2,2,2)	(2,2,3)	(2,2,4)	(2,2,5)	(2,2,6)	(2,2,n)
(2,3,3)		(2,3,4)		(2,3,5)

Сферические паркеты, соответствующие октаэдру и икосаэдру, а также диэдральным сферичесим мозаикам с чётным n, центрально симметричны. Поэтому каждая эта упаковка определяет паркет вещественной проективной плоскости, эллиптический паркет^[en]. Их группа симметрии является факторгруппой сферической группы треугольников по центральной симметрии (-I), которая является центральным элементом порядка 2. Поскольку проективная плоскость является моделью эллиптической геометрии, такие группы называются эллиптическими группами треугольника^[1].

Гиперболическая плоскость[править | править код]

1l+1m+1n<1.{\displaystyle {\frac {1}{l}}+{\frac {1}{m}}+{\frac {1}{n}}<1.}

Группа треугольника является бесконечной группой симметрии паркета на гиперболической плоскости из гиперболических треугольников, сумма углов которого меньше π. Все тройки, не перечисленные выше, представляют паркеты на гиперболической плоскости. Например, тройка (2,3,7) даёт группу треугольника (2,3,7). Существует бесконечно много таких групп. Ниже приведены паркеты, связанные с некоторыми малыми значениями.

Гиперболические группы треугольников являются примерами неевклидовых кристаллографических групп^[en] и обобщены в теории Громова гиперболических групп.

Обозначим через D(l,m,n) подгруппу с индексом 2 в Δ(l, m, n), сгенерированную словами чётной длины в генераторах. Такие подгруппы иногда называются «обычными» группами треугольников^[2] или группами фон Дика, по имени Вальтера фон Дика. Сферические, евклидовы и гиперболические треугольники соответствуют элементам группы, сохряняющей ориентацию треугольников. Проективные (эллиптические) треугольники нельзя интерпретировать таким образом, поскольку проективная плоскость не имеет ориентации, и в ней нет «сохранения ориентации». Отражения, однако, локально сохраняют ориентацию (и любое многообразие локально ориентируемо, поскольку локально евклидово).^[3]

Группы D(l,m,n) определяются следующим заданием:

D(l,m,n)=⟨x,y∣xl,ym,(xy)n⟩.{\displaystyle D(l,m,n)=\langle x,y\mid x^{l},y^{m},(xy)^{n}\rangle .}

В терминах генераторов это x = ab, y = ca, yx = cb. Геометрически три элемента x, y, xy соответствуют вращениям на 2π/l, 2π/m и 2π/n вокруг трёх вершин треугольника.

Заметим, что D(l,m,n) ≅ D(m,l,n) ≅ D(n,m,l), так что D(l,m,n) не зависит от порядка чисел l,m,n.

Гиперболическая группа фон Дика — это группа Фукса^[en], дискретная группа, состоящая из сохраняющих ориентацию изометрий гиперболической плоскости.

Группы треугольников сохраняют паркетную укладку треугольниками, а именно фундаментальную область для действия (треугольника, определённого прямыми отражения), называемого треугольником Мёбиуса, и задаются тройкой целых чисел (l,m,n), соответствующих треугольникам (2l,2m,2n) с общей вершиной. Существуют также паркеты, образованные треугольниками с наложением, которые соответствуют треугольникам Шварца с рациональными числами (l/a,m/b,n/c), где знаменатели взаимно просты с числителями. Это соответствует сторонам под углом aπ/l (соотв.), что соответствует вращению на of 2aπ/l (соотв.), которое имеет порядок l и потому идентично элементу абстрактной группы, но различается, когда представляется в виде отражений.

Например, треугольник Шварца (2 3 3) даёт на сфере паркет плотности^[en] 1, в то время как треугольник (2 3/2 3) даёт на сфере паркет с плотностью 3, но с той же самой абстрактной группой. Эти симметрии паркетов с наложением не считаются группами треугольников.

Группы треугольников датируются по меньшей мере представлением икосаэдральной группы^[en] как группы вращений треугольника (2,3,5) Гамильтоном в 1856 в его статье об икосианах^[4].

Группы треугольников возникают в арифметической геометрии^[en]. Модулярная группа, генерируемая двумя элементами, S и T, с соотношениями S² = (ST)³ = 1, является группой вращений треугольника (2,3,∞) и отображается во все группы треугольников (2,3,n) добавлением отношения Tⁿ = 1. Более обще, группа Гекке^[en] H_q, генерируемая двумя элементами, S и T, с соотношением S² = (ST)^q = 1 (нет отношения отдельно для T), является группой вращений треугольника (2,q,∞) и отображается во все группы треугольников (2,q,n) добавлением отношения Tⁿ = 1. Модулярная группа является группой Гекке H₃. В теории dessins d’enfants^[en] функция Белого позволяет получить замощение римановой поверхности, соответствующее некоторой группе треугольника.

Все 26 спорадических групп являются факторгруппами групп треугольника^[6], из которых 12 являются группами Гурвица (факторгруппа группы (2,3,7)).

• Gross, Jonathan L. & Tucker, Thomas W. (2001), «6.2.8 Triangle Groups», Topological graph theory, Courier Dover Publications, с. 279–281, ISBN 978-0-486-41741-7 
• Magnus, Wilhelm (1974), «II. Discontinuous groups and triangle tessellations», Noneuclidean tesselations and their groups, Academic Press, с. 52–106, ISBN 978-0-12-465450-1 
• Wilson, R. A. (2001), «The Monster is a Hurwitz group», Journal of Group Theory Т. 4 (4): 367–374, doi:10.1515/jgth.2001.027, <http://web.mat.bham.ac.uk/R.A.Wilson/pubs/MHurwitz.ps>. Проверено 24 декабря 2017.  Архивная копия от 5 марта 2012 на Wayback Machine
• Sir William Rowan Hamilton. Memorandum respecting a new System of Roots of Unity // Philosophical Magazine. — 1856. — Т. 12. — С. 446.

• Robert Dawson Некоторые сферические паркеты (Показано большое число интересных замощений сферы, большинство из которых не являются паркетами группы треугольников.)
• Elizabeth r chen triangle groups (2010) Обои на экран дисплея

Ортотреугольник — Википедия

Материал из Википедии — свободной энциклопедии

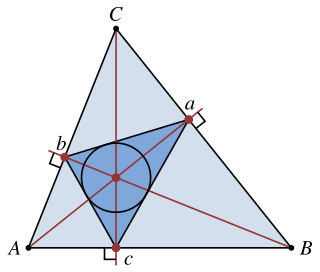
Ортотреуго́льник (ортоцентрический треугольник) — это треугольник Δabc, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) Δabc сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника Δabc.

• Задача Фаньяно. Ортоцентрический треугольник остроугольного треугольника АВС обладает наименьшим периметром из всех вписанных треугольников.
• Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).
• Если точки A₁, B₁ и C₁ на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что

∠BA1C1=∠CA1B1{\displaystyle \angle BA_{1}C_{1}=\angle CA_{1}B_{1}} , ∠CB1A1=∠AB1C1{\displaystyle \angle CB_{1}A_{1}=\angle AB_{1}C_{1}} и ∠AC1B1=∠BC1A1{\displaystyle \angle AC_{1}B_{1}=\angle BC_{1}A_{1}},

то A1B1C1{\displaystyle A_{1}B_{1}C_{1}} — ортотреугольник треугольника ABC.

• Если вокруг данного остроугольного треугольника описать окружность и в трех вершинах треугольника провести прямые, касательные к окружности, то пересечение этих прямых образует треугольник, который называют тангенциальным треугольником по отношению к данному треугольнику.

Свойства подобия родственных треугольников[править | править код]

• Исходный треугольник ΔABC{\displaystyle \Delta ABC} по отношению к ортотреугольнику является треугольником трех внешних биссектрис^[1].

Свойства параллельности (антипараллельности) сторон родственных треугольников[править | править код]

• Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
• Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
• Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
• Если точки касания вписанной в данный треугольник окружности соединены отрезками, то получится треугольник Жергонна. Пусть в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно, ортотреугольник треугольника Жергонна и исходный треугольник подобны.

Другие свойства[править | править код]

• Площадь ортотреугольника равна:

Sort=S(2abc)2(a2+b2−c2)(a2+c2−b2)(b2+c2−a2){\displaystyle S_{ort}={\frac {S}{(2abc)^{2}}}(a^{2}+b^{2}-c^{2})(a^{2}+c^{2}-b^{2})(b^{2}+c^{2}-a^{2})}

где S{\displaystyle S} — площадь треугольника ΔABC; a,b,c{\displaystyle a,b,c} — его соответствующие стороны.

• Окружность, описанная около ортотреугольника Δabc, для самого треугольника ΔABC является окружностью Эйлера (окружностью 9 точек), то есть одновременно проходит, через 3 основания медиан последнего. Заметим, что эти 3 основания медиан являются вершинами дополнительного треугольника для треугольника ΔABC.
• Радиусы окружности, описанной около данного треугольника ΔABC, проведенные через его вершины, перпендикулярны соответственным сторонам ортотреугольника Δabc (Зетель, следствие 2, § 66, с. 81).

• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 38-39. — ISBN 5-94057-170-0.
• Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. 153 с.

1. ↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100

Целочисленный треугольник — Википедия

Целочисленный треугольник — это треугольник, длины всех сторон которого выражаются целыми числами. Рациональный треугольник можно определить как треугольник, стороны которого являются рациональными числами. Любой рациональный треугольник можно привести к целочисленному (умножив все стороны на одно и то же число, наименьшее общее кратное знаменателей), так что нет существенной разницы между целочисленными и рациональными треугольниками. Заметим, однако, что существуют и другие определения «рационального треугольника». Так, в 1914 Кармайкл ^[1] использовал этот термин для обозначения того, что мы теперь называем героновым треугольником. Сомос (Somos)^[2] использует термин для треугольников, отношения сторон которого являются рациональными числами. Конвей и Гай^[3] определяют рациональный треугольник как треугольник с рациональными сторонами и углами (в градусах) — в этом случае рациональными будут только равносторонние треугольники с рациональными сторонами.

У целочисленных треугольников есть несколько общих свойств (см. первый раздел ниже). Все остальные разделы посвящены целочисленным треугольникам со специфичными свойствами.

Основные свойства целых треугольников[править | править код]

Целочисленные треугольники с заданным периметром[править | править код]

Любая тройка положительных чисел может стать сторонами треугольника, необходимо лишь удовлетворение неравенства треугольника — самая длинная сторона должна быть короче суммы двух других сторон. Каждая такая тройка задаёт единственный (с точностью до конгруэнтности) треугольник. Так что число целочисленных треугольников с периметром p равно числу разбиений p на три положительные части, удовлетворяющие неравенству треугольника. Эти числа являются ближайшими к ^p2⁄₄₈ для чётных p и к ^{(p + 3)2}⁄₄₈ для нечётных^[4][5]. Это также означает, что число целочисленных треугольников с чётным периметром p = 2n равно числу с нечётным периметром p = 2n — 3. Таким образом, нет треугольников с периметрами 1, 2 и 4, имеется по одному с периметрами 3, 5, 6 и 8, и по два с периметрами 7 и 10. Последовательность числа целочисленных треугольников с периметрами p, начиная с p = 1:

0, 0, 1, 0, 1, 1, 2, 1, 3, 2, 4, 3, 5, 4, 7, 5, 8, 7, 10, 8 … (последовательность A005044 в OEIS)

Целочисленные треугольники с заданной большей стороной[править | править код]

Число целочисленных треугольников (с точностью до конгруэнции^{[неизвестный термин]}) с заданной наибольшей стороной c равно числу троек (a, b, c), таких, что a + b > c и a ≤ b ≤ c. Это значение равно Ceiling[^(c + 1)⁄₂] * Floor[^(c + 1)⁄₂]^[4]. Для чётных c это равно удвоенному треугольному числу ^c⁄₂(^c⁄₂ + 1), а для нечётных c это равно квадрату ^(c + 1)2⁄₄. Это означает, что число целочисленных треугольников с наибольшей стороной c превышает число целочисленных треугольников с наибольшей стороной c−2 на c. Последовательность числа неконгруэнтных целочисленных треугольников с наибольшей стороной c, начиная с c = 1:

1, 2, 4, 6, 9, 12, 16, 20, 25, 30, 36, 42, 49, 56, 64, 72, 81, 90 … (последовательность A002620 в OEIS)

Число целочисленных треугольников (с точностью до конгруэнции) с данной наибольшей стороной c, вершины которого лежат на или внутри полуокружности диаметра c, равно числу троек (a, b, c), таких, что a + b > c , a² + b² ≤ c² и a ≤ b ≤ c. Это число совпадает с числом целочисленных треугольников с тупым или прямым углом с наибольшей стороной c. Последовательность числа таких треугольников, начинающаяся с c = 1:

0, 0, 1, 1, 3, 4, 5, 7, 10, 13, 15, 17, 22, 25, 30, 33, 38, 42, 48 … (последовательность A236384 в OEIS)

Разница между последними двумя последовательностями даёт число целочисленных треугольников с острыми углами (с точностью до конгруэнции) с наибольшей стороной c. Последовательность числа остроугольных треугольников, начиная с c = 1:

1, 2, 3, 5, 6, 8, 11, 13, 15, 17, 21, 25, 27, 31, 34, 39, 43, 48, 52 … (последовательность A247588 в OEIS)

Площадь целочисленного треугольника[править | править код]

По формуле Герона, если T — площадь треугольника, а длины сторон равны a, b и c, то

4T=(a+b+c)(a+b−c)(a−b+c)(−a+b+c).{\displaystyle 4T={\sqrt {(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}}.}

Поскольку все множители под знаком корня в правой части формулы являются целыми числами, все целочисленные треугольники должны иметь целочисленное значение величины 16T².

Углы целочисленного треугольника[править | править код]

По теореме косинусов любой угол целочисленного треугольника имеет рациональный косинус.

Если углы любого треугольника образуют арифметическую прогрессию, то один из его углов должен быть 60°.^[6] Для целочисленных треугольников оставшиеся углы должны также иметь рациональные косинусы и метод генерации таких треугольников приведён ниже. Однако, за исключением тривиального случая равностороннего треугольника, не существует целочисленных треугольников, углы которого образуют геометрическую или гармоническую прогрессию. Это потому, что углы должны быть рациональными углами вида ^πp⁄_q с рациональными 0 < ^p⁄_q < 1. Но все углы целочисленных треугольников должны иметь рациональные косинусы, а это может произойти только в случае, когда ^p⁄_q = ¹⁄₃ ^[7], то есть целочисленный треугольник является равносторонним.

Деление стороны высотой[править | править код]

Любая высота, опущенная из вершины на противоположную сторону или её продолжение, делит эту сторону (или продолжение) на отрезки рациональной длины.

Общая формула[править | править код]

Геронов треугольник — это треугольник с целочисленными сторонами и целочисленной площадью. Любой геронов треугольник имеет стороны, пропорциональные ^[8].

a=n(m2+k2){\displaystyle a=n(m^{2}+k^{2})},

b=m(n2+k2){\displaystyle b=m(n^{2}+k^{2})},

c=(m+n)(mn−k2){\displaystyle c=(m+n)(mn-k^{2})},

Полупериметр =mn(m+n){\displaystyle =mn(m+n)},

Площадь=mnk(m+n)(mn−k2){\displaystyle =mnk(m+n)(mn-k^{2})},

для целых m, n и k, удовлетворяющих условиям

gcd(m,n,k)=1{\displaystyle \gcd {(m,n,k)}=1},

mn>k2≥m2n/(2m+n){\displaystyle mn>k^{2}\geq m^{2}n/(2m+n)}

m≥n≥1{\displaystyle m\geq n\geq 1}.

Множитель пропорции для треугольников в общем случае является рациональным числом  pq{\displaystyle {\frac {p}{q}}} , где  q=gcd(a,b,c){\displaystyle q=\gcd {(a,b,c)}}  сокращает сгенерированный геронов треугольник к примитивному, а  p{\displaystyle p}  растягивает этот примитивный треугольник до требуемого размера.

Пифагоровы треугольники[править | править код]

Пифагоров треугольник — это прямоугольный геронов треугольник и его три стороны известны как пифагорова тройка^[9]. Все примитивные (не имеющие общего множителя) пифагоровы тройки (a,b,c){\displaystyle (a,b,c)} с гипотенузой c{\displaystyle c} можно получить с помощью формул

a=m2−n2{\displaystyle a=m^{2}-n^{2}},

b=2mn{\displaystyle b=2mn},

c=m2+n2{\displaystyle c=m^{2}+n^{2}},

Полупериметр=m(m+n){\displaystyle =m(m+n)},

Площадь=mn(m2−n2){\displaystyle =mn(m^{2}-n^{2})},

где m и n взаимно простые целые и одно из них чётно, при этом m > n.

Пифагоровы треугольники с целой высотой, опирающейся на гипотенузу[править | править код]

Ни в каком примитивном пифагоровом треугольнике высота, опирающуюся на гипотенузу, не выражается целым числом. Однако существуют непримитивные пифагоровы треугольники такого вида. Все пифагоровы треугольники с катетами a и b, гипотенузой c, и целой высотой d{\displaystyle d}, опущенной на гипотенузу, которые необходимо будут удовлетворять равенствам a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}} и 1a2+1b2=1d2{\displaystyle {\tfrac {1}{a^{2}}}+{\tfrac {1}{b^{2}}}={\tfrac {1}{d^{2}}}}, генерируются формулами^[10][11]

a=(m2−n2)(m2+n2){\displaystyle a=(m^{2}-n^{2})(m^{2}+n^{2})},

b=2mn(m2+n2){\displaystyle b=2mn(m^{2}+n^{2})},

c=(m2+n2)2{\displaystyle c=(m^{2}+n^{2})^{2}},

d=2mn(m2−n2){\displaystyle d=2mn(m^{2}-n^{2})},

Полупериметр==m(m+n)(m2+n2){\displaystyle =m(m+n)(m^{2}+n^{2})},

Площадь==mn(m2−n2)(m2+n2)2{\displaystyle =mn(m^{2}-n^{2})(m^{2}+n^{2})^{2}},

для взаимно простых чисел m, n с m > n.

Более того, из любого пифагорова треугольника с катетами x, y и гипотенузой z можно получить другой пифагоров треугольник с целой высотой d на гипотенузу c по формуле^[11]

(a,b,c,d)=(xz,yz,z2,xy).{\displaystyle (a,b,c,d)=(xz,yz,z^{2},xy).}

Героновы треугольники со сторонами в арифметической прогрессии[править | править код]

Треугольник с целочисленными сторонами и целочисленной площадью имеет стороны в арифметической прогрессии в том и только в том случае, когда^[12] стороны равны (b — d, b, b + d), где

b=2(m2+3n2)/g{\displaystyle b=2(m^{2}+3n^{2})/g},

d=(m2−3n2)/g{\displaystyle d=(m^{2}-3n^{2})/g},

и где g является наибольшим общим делителем чисел m2−3n2,{\displaystyle m^{2}-3n^{2},} 2mn{\displaystyle 2mn} и m2+3n2.{\displaystyle m^{2}+3n^{2}.}

Героновы треугольники с одним углом вдвое большим другого[править | править код]

Все героновы треугольники с B=2A генерируются ^[13] либо формулами

a=k2(s2+r2)24{\displaystyle a={\tfrac {k^{2}(s^{2}+r^{2})^{2}}{4}}},

b=k2(s4−r4)2{\displaystyle b={\tfrac {k^{2}(s^{4}-r^{4})}{2}}},

c=k2(3s4−10s2r2+3r4)4{\displaystyle c={\tfrac {k^{2}(3s^{4}-10s^{2}r^{2}+3r^{4})}{4}}},

Площадь=k2csr(s2−r2)2{\displaystyle ={\tfrac {k^{2}csr(s^{2}-r^{2})}{2}}},

с целыми k, s, r, такими, что s² > 3r², либо формулами

a=q2(u2+v2)24{\displaystyle a={\tfrac {q^{2}(u^{2}+v^{2})^{2}}{4}}},

b=q2uv(u2+v2){\displaystyle b=q^{2}uv(u^{2}+v^{2})},

c=q2(14u2v2−u4−v4)4{\displaystyle c={\tfrac {q^{2}(14u^{2}v^{2}-u^{4}-v^{4})}{4}}},

Площадь=q2cuv(v2−u2)2{\displaystyle ={\tfrac {q^{2}cuv(v^{2}-u^{2})}{2}}},

с целыми q, u, v, такими, что v > u и v² < (7+4√3)u².

Никакой геронов треугольник с B = 2A не является равнобедренным или прямоугольным.

Равнобедренные героновы треугольники[править | править код]

Все равнобедренные героновы треугольники получается умножением на рациональное число^[14] сторон

a=2(u2−v2){\displaystyle a=2(u^{2}-v^{2})},

b=u2+v2{\displaystyle b=u^{2}+v^{2}},

c=u2+v2{\displaystyle c=u^{2}+v^{2}},

для взаимно простых целых u и v с u>v.

Героновы треугольники как грани тетраэдра[править | править код]

Существуют тетраэдры, имеющие целочисленный объём и героновы треугольники в качестве граней. В качестве примера — тетраэдр с ребром 896, противоположным ребром 190, а оставшиеся два ребра по 1073. Две грани этого тетраэдра имеют площадь 436800, две другие — 47120, а объём равен 62092800^[15].

Свойства треугольников Герона[править | править код]

• Периметр геронова треугольника всегда является чётным числом^[16]. Таким образом, геронов треугольник имеет нечётное число сторон чётной длины^[17] и любой примитивный геронов треугольник имеет в точности одну чётную сторону.
• Полупериметр s геронова треугольника со сторонами a, b и c не может быть простым числом. Это видно из того, что s(s-a)(s-b)(s-c) должен быть полным квадратом и в случае простоты s один из множителей должен делиться на s, но это невозможно, поскольку все стороны меньше s.
• Площадь геронова треугольника всегда делится на 6^[16].
• Все высоты геронова треугольника являются рациональными числами^[2]. Это легко видеть из формулы площади треугольника. Поскольку геронов треугольник имеет целочисленные стороны и площадь, удвоенная площадь, делённая на основание, даст рациональное число. Некоторые героновы треугольники имеют три высоты, не являющиеся целыми числами, например, остроугольный треугольник (15, 34, 35) с площадью 252 и тупоугольный (5, 29, 30) с площадью 72. Любой геронов треугольник с одной или больше нецелочисленной высотой можно преобразовать в подобный геронов треугольник, умножив все стороны на наименьшее общее кратное знаменателей высот.
• Героновы треугольники, не имеющие целочисленной высоты (неразложимые и не пифагоровы), имеют стороны, делящиеся на простые вида 4k+1^[18]. Однако разложимые героновы треугольники должны иметь две стороны, являющиеся гипотенузами пифагоровых треугольников. Отсюда — все героновы треугольники, не являющиеся пифагоровыми, имеют по меньшей мере две стороны, делящиеся на простые вида 4k+1. Наконец, все героновы треугольники имеют по меньшей мере одну сторону, делящуюся на простое число вида 4k+1.
• Все отрезки перпендикуляров от середин сторон^[en] до другой стороны геронова треугольника являются рациональными числами — для любого треугольника они задаются формулами pa=2aTa2+b2−c2,{\displaystyle p_{a}={\tfrac {2aT}{a^{2}+b^{2}-c^{2}}},} pb=2bTa2+b2−c2,{\displaystyle p_{b}={\tfrac {2bT}{a^{2}+b^{2}-c^{2}}},} и pc=2cTa2−b2+c2{\displaystyle p_{c}={\tfrac {2cT}{a^{2}-b^{2}+c^{2}}}}, где стороны a ≥ b ≥ c и площадь равна T^[19], а в героновом треугольнике величины a, b, c и T являются целыми числами.
• Не существует равносторонних героновых треугольников^[2].
• Не существует героновых треугольников со сторонами 1 или 2^[20].
• Существует бесконечно много примитивных героновых треугольников со сторонами a при условии a > 2^[20].
• Не существует героновых треугольников со сторонами, образующими геометрическую прогрессию^[12].
• Если две стороны геронова треугольника имеют общий делитель, этот делитель должен быть суммой двух квадратов^[21].
• Любой угол геронова треугольника имеет рациональный синус. Это следует из формулы площади треугольника Площадь = (1/2)ab sin C, в которой площадь и стороны a и b являются целыми (и то же самое для других сторон).
• Не существует героновых треугольников, у которых внутренние углы образуют арифметическую прогрессию. Это следует из того, что в случае арифметической прогрессии углов один угол должен равняться 60°, а синус этого угла не рационален^[6].
• Любой квадрат, вписанный в геронов треугольник, имеет рациональные стороны — для любого треугольника вписанный квадрат на стороне длины a имеет стороны 2Taa2+2T{\displaystyle {\tfrac {2Ta}{a^{2}+2T}}}, где T — площадь треугольника^[22]. В героновом треугольнике и T, и a являются целыми числами.
• Любой геронов треугольник имеет рациональный радиус вписанной окружности — для любого треугольника этот радиус равен отношению площади к половине периметра, и обе эти величины в героновом треугольнике рациональны.
• Любой геронов треугольник имеет рациональный радиус описанной окружности — в общем случае радиус равен одной четвёртой произведения сторон, делённой на площадь. В героновом треугольнике стороны и площадь являются целыми числами.

Целочисленные треугольники на двумерной решётке[править | править код]

Двумерная решётка — это правильный массив изолированных точек, в которой при выборе одной точки в качестве начала координат (0, 0) все остальные точки будут иметь вид (x, y), где x и y пробегают по всем положительным и отрицательным целым числам. Треугольник на решётке — это любой треугольник, вершины которого являются точками решётки. По формуле Пика треугольник на решётке имеет рациональную площадь, которая либо является целым числом, либо имеет в знаменателе 2. Если треугольник на решётке имеет целые стороны, то он является героновым треугольником ^[17].

Более того, было показано, что все героновы треугольники можно нарисовать на решётке ^[23]. Следовательно, можно утверждать, что целочисленный треугольник является героновым тогда и только тогда, когда его можно нарисовать на решётке.

Целочисленные треугольники со специфичными свойствами углов[править | править код]

Целочисленные треугольники с рациональной биссектрисой[править | править код]

Семейство треугольников с целочисленными сторонами a,b,c{\displaystyle a,b,c} и рациональной биссектрисой d{\displaystyle d} угла A задаётся уравнениями^[24]

a=2(k2−m2){\displaystyle a=2(k^{2}-m^{2})},

b=(k−m)2{\displaystyle b=(k-m)^{2}},

c=(k+m)2{\displaystyle c=(k+m)^{2}},

d=2km(k2−m2)k2+m2{\displaystyle d={\tfrac {2km(k^{2}-m^{2})}{k^{2}+m^{2}}}},

с целыми k>m>0{\displaystyle k>m>0}.

Целочисленные треугольники с целыми n-делителями всех углов[править | править код]

Существуют треугольники, в которых три стороны и все три биссектрисы являются целыми числами ^[25].

Существуют треугольники, в которых три стороны и две трисектрисы каждого угла являются целыми числами^[25].

Однако для n>3 не существует треугольников с целочисленными сторонами, в котором (n-1) n-сектрис каждого угла являются целыми числами^[25].

Целочисленные треугольники с одним углом, имеющим рациональный косинус[править | править код]

Некоторые целочисленные треугольники с углом в верш

Треугольник (фильм, 2009) — Википедия

Материал из Википедии — свободной энциклопедии

«Треугольник» (англ. Triangle) — третий полнометражный кинофильм Кристофера Смита, мистический триллер производства Великобритании и Австралии. Главная героиня фильма (её роль исполняет Мелисса Джордж) оказывается вместе с друзьями на заброшенном лайнере, где узнает от незнакомки, о том, что ей нужно убить своих друзей, чтобы вернуться к сыну.

Мировая премьера фильма состоялась 27 августа 2009 года.

Джесс, молодая мать-одиночка, садится на яхту под названием «Треугольник», чтобы провести день в компании своего друга Грега и его четырёх друзей. Грег говорит другим, чтобы не приставали к Джесс — у неё ребёнок аутист. Через несколько часов после выхода в море яхта неожиданно оказывается в полном штиле, а затем терпит крушение во время начавшейся бури. Все, кроме Хизер, которая тонет во время шторма, остаются в живых. Дрейфуя на перевёрнутой яхте, Грег и компания видят огромный пассажирский лайнер, на который они переходят. Судно оказывается пустым, часы на борту остановились. Но они не одни на этом корабле — за ними кто-то неустанно следит… Джесс к тому же находит на корабле связку своих ключей, которые должны были остаться на яхте и утонуть во время шторма.

Разделившись, друзья по очереди гибнут — их убивает из ружья человек в маске и рабочей форме. В живых остаётся только Джесс, которой удается побороть убийцу. Перед прыжком за борт убийца женским голосом говорит Джесс, что скоро убитые вернутся, и она должна будет опять убить их всех, чтобы вернуться домой. Человек в робе падает за борт. Джесс видит, что лайнер приближается к перевернутой яхте, на которой были она и её друзья. Они опять заходят на борт, в том числе вторая «копия» Джесс. Скрытно следуя за компанией, Джесс понимает, что попала во временную петлю. Сначала она пытается спасти всех и не убивать своих друзей. Однако после нескольких попыток ей это не удаётся, к тому же она обнаруживает, что проживала попадание на лайнер уже десятки раз.

Наконец, Джесс решает убить всю группу, и расправляется с друзьями, надев робу и маску. Однако копия Джесс из новой группы сбрасывает её в море, как это сделала сама Джесс в первое появление на лайнере. Джесс просыпается на пляже, куда её вынесло из моря, и добирается до города. Заглянув в окно своего дома, она видит себя и своего сына Томми перед поездкой на яхте, то есть она попадает в прошлое. Джесс видит, что её копия кричит и раздражается на больного сына. Она убивает свою копию, кладёт труп в багажник машины и едет с сыном в порт, обещая ему никогда больше не обижать его. По дороге они попадают в аварию, в которой её сын погибает и убитая ей Джесс выпадает из багажника.

Увидев, что её сын погиб, она сразу же, не возвращаясь в дом, идет в порт к друзьям, и Грег говорит остальным, чтобы Джесс не доставали, так как её сын болен аутизмом.

Фильм получил положительные отзывы кинокритиков. На сайте Rotten Tomatoes на основе 38 рецензий фильм имеет рейтинг 82 %^[1].