Второй признак подобия треугольников / Подобные треугольники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Подобные треугольники
5. Второй признак подобия треугольников

Теорема

Доказательство

Дано: АВС и А₁В₁С₁,  А = А₁,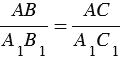

Доказать: АВС

А₁В₁С₁

Доказательство:

Рассмотрим АВС и А₁В₁С₁, у которых 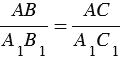и А = А₁:

Для доказательства теоремы, учитывая первый признак подобия треугольников, достаточно доказать, что 

В = В₁.

Рассмотрим АВС₂, у которого 1 = А₁, 2 = В₁.

АВС₂

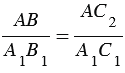А₁В₁С₁ по первому признаку подобия треугольников, поэтому . С другой стороны, по условию 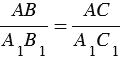. Из этих двух равенств получаем АС = АС₂.

АВС =АВС₂ по первому признаку равенства треугольников (АВ — общая сторона, АС = АС₂ и А =

1, поскольку А = А₁ и 1 = А₁). Отсюда следует, что В = 2, а так как 2 = В₁, то В = В₁. Теорема доказана.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Пропорциональные отрезки

Определение подобных треугольников

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Третий признак подобия треугольников

Средняя линия треугольника

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

О подобии произвольных фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Подобные треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 553, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 559, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 613, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 626*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 630, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 849, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 854, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Второй признак подобия треугольников

На прошлом уроке мы с вами познакомились с первым признаком подобия треугольников. Вспомним его.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Сегодня на уроке мы познакомимся со вторым признаком подобия треугольников.

Теорема (2-й признак подобия треугольников). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.

Доказательство:

, .

, , тогда  по 1-му признаку.

.

Тогда .

Рассмотрим  и .

, – общая, , значит, .

Следовательно, .

Что и требовалось доказать.

Посмотрите на следующие треугольники и найдите среди них подобные.

Каждый из треугольников имеет угол, равный 65º. Но только у треугольников а и б известны длины сторон, образующих этот угол. Проверим пропорциональны ли эти стороны. Составим отношение их длин ,  . Видим, что эти отношения равны, а значит, стороны пропорциональны. Таким образом, мы получили, что треугольники а и б подобны по двум сторонам и углу между ними, то есть по второму признаку.

Задача. На одной из сторон  отложены отрезки  и , равные соответственно  см и  см. На другой стороне этого же угла отложены отрезки  и , соответственно равные  см и  см. Подобны ли треугольники  и ?

Решение.

Рассмотрим  и .

 – общий,  

;

;

значит, .

Следовательно,  по 2-му признаку.

Ответ: треугольники подобны.

Задача. На рисунке ,  см,  см, а  см. Найдите  и .

Решение.

Рассмотрим  и .

 как вертикальные,

, , .

Получаем, что  по 2-му признаку, .

, ,  см,  см,  см,  (см).

Ответ:  см,  см.

Итак, сегодня на уроке мы познакомились со вторым признаком подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.

Также мы решили несколько задач на закрепление материала.

Урок 35. 2-й и 3-й признаки подобия треугольников

Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 35. Второй и третий признаки подобия треугольников. Вернуться к Списку уроков Тематического планирования.

---

 

Урок 35. Второй и третий признаки
подобия треугольников

Основные дидактические цели урока: рассмотреть второй и третий признаки подобия треугольников; показать применение второго и третьего признаков подобия треугольников при решении задач.

Ход урока

I. Организационный момент.

Мотивация к учебной деятельности. (Учитель сообщает тему урока, формулирует цели урока.)

II. Актуализация знаний учащихся

1. Работа в рабочих тетрадях.

Решить задачу № 57 (самостоятельно с последующим обсуждением решения).

Наводящие вопросы.

• Докажите, что ΔABF ~ ΔCDF.
• Чему равен коэффициент подобия треугольников ABF и CDF?
• Найдите отношение сторон BF и DF.
• Чему равно значение DF?

2. Решение задач по готовым чертежам (самостоятельно). (В тетрадях записать краткое решение.)

• 1) Дано: ∠N = ∠A, ВС = 12 см, MN = 6 см, CN = 4 см (рис. 7.27). Найти: АС.
• 2) Дано: ВС ⊥ АС, EF ⊥ AB, ВС = 12 см, EF = 6 см, АЕ = 10 см (рис. 7.28). Найти: АВ.
• 3) Дано: ∠3 = ∠1 + ∠2, CD = 4 см, ВС = 9 см (рис. 7.29). Найти: АС.

3. Обсуждение решений задач, с которыми не справилось большинство учащихся.

III. Работа по теме урока

1. Формулировка темы урока.

• Сформулируйте первый признак равенства треугольников.
• Существуют ли еще какие-либо признаки подобия треугольников?

2. Сформулировать другие признаки подобия треугольников (работа в группах).
3. Доказать второй и третий признаки подобия треугольников.

Второй признак подобия треугольников

Теорема: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

(Учащиеся записывают в тетрадях план-конспект доказательства теоремы.)

План-конспект доказательства теоремы

4. Составить план-конспект доказательства третьего признака подобия треугольников. (Учитель делит класс на группы. На обсуждение дается 5 мин. Далее заслушивают представителей групп, в обсуждении решения участвует весь класс.)

Третий признак подобия треугольников

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

План-конспект доказательства теоремы

IV. Закрепление изученного материала

1. Работа в рабочих тетрадях.

Решить задачи № 59, 60 (работа в парах). (Учитель контролирует работу менее подготовленных учащихся и по мере необходимости оказывает индивидуальную помощь.)

Задача № 59. Наводящие вопросы.

• Каким является ∠C для треугольников АВС и MNC?
• Чему равно отношение сторон, заключающих этот угол (АС : CN и ВС : СМ)?
• Что можно сказать о сторонах АС и ВС треугольника АВС и сторонах CN и СМ треугольника MNC?
• Какой признак подобия треугольников был применен при доказательстве подобия треугольников MNC и АВС?

Задача № 60. Наводящие вопросы.

• Чему равно отношение сторон MN и CD, МР и СЕ, NP и DE треугольников MNP и CD ЕР
• Что можно сказать о сторонах треугольников MNP и CDE?
• Укажите признак, на основании которого треугольники MNP и CDE подобны.

(Учащиеся, успешно справившиеся с решением задач, решают дополнительные задачи.)

2. Решить дополнительные задачи.

1) В треугольниках АВС и А₁В₁С₁, BE и В₁Е₁ — биссектрисы, ∠B = ∠B₁, АЕ : ЕС = А₁Е₁ : Е₁С₁. Докажите, что ΔАВЕ ~ ΔА₁В₁Е₁.

2) В треугольнике АВС АВ = 4, ВС = 6, АС = 7. Точка Е лежит на стороне АВ. Внутри треугольника взята точка М так, что МВ = 5,25, ME = 4,5, АЕ = 1. Прямая ВМ пересекает АС в точке Р. Докажите, что ΔАРВ равнобедренный.

V. Рефлексия учебной деятельности

1. Сформулируйте второй (третий) признак подобия треугольников.
2. Две стороны одного треугольника пропорциональны двум сторонам другого. В каком случае данные треугольники будут подобны?
3. Подобны ли равнобедренные треугольники, если у них углы между боковыми сторонами равны?
4. Подобны ли равнобедренные треугольники, если боковая сторона и основание одного из них пропорциональны боковой стороне и основанию другого?
5. Могут ли быть подобными прямоугольные треугольники, если катеты одного из них пропорциональны катетам другого?

Домашнее задание

1. П. 62, 63, вопросы 6, 7 (учебник, с. 158, 159).
2. Решить задачи № 559, 560 (б), 561.
3. Решить дополнительную задачу.

В треугольниках ABС и A₁B₁C₁, BD и B₁D₁ — медианы, ∠A = ∠A₁, ∠BDA = ∠В₁D₁A₁. Докажите, что треугольник BDC подобен треугольнику B₁D₁С₁.

 

---

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 35. Второй и третий признаки подобия треугольников.

Вернуться к Списку уроков Тематического планирования.

math-public:vtoroj_priznak_podobiya_treugolnikov [Президентский ФМЛ №239]

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Доказательство

Первый способ (без использования тригонометрии).

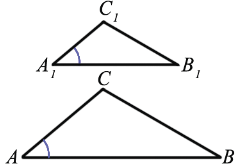
Рассмотрим два треугольника $ABC$ и $A_1B_1C_1$, у которых $\dfrac{AB}{A_1B_1}=\dfrac{AC}{A_1C_1}$ и $\angle A=\angle A_1$.

Докажем, что $\triangle ABC\sim\triangle A_1B_1C_1$.

Для этого, учитывая первый признак подобия треугольников, достаточно доказать, что $\angle B=\angle B_1$.

Рассмотрим треугольник $ABC_2$, у которого $\angle 1=\angle A_1$, $\angle 2=\angle B_1$.

Треугольники $ABC_2$ и $A_1B_1C_1$ подобны по первому признаку подобия треугольников, поэтому $\dfrac{AB}{A_1B_1}=\dfrac{AC_2}{A_1C_1}$.

C другой стороны, по условию $\dfrac{AB}{A_1B_1}=\dfrac{AC}{A_1C_1}$.

Из этих двух равенств получаем $AC=AC_2$.

Треугольники $ABC$ и $ABC_2$ равны по двум сторонам и углы между ними ($AB$ – общая, $AC=AC_2$ и $\angle A=\angle 1$, поскольку $\angle A=\angle A_1$ и $\angle 1=\angle A_1)$.

Отсюда следует, что $\angle B=\angle 2$, а так как $\angle 2=\angle B_1$, то $\angle B=\angle B_1$.

Второй способ (через тригонометрию).

Рассмотрим два треугольника $ABC$ и $A_1B_1C_1$ со сторонами $a, b, c$ и $a_1, b_1, c_1$ соответственно.

Пусть $\dfrac{a}{a_1}=\dfrac{b}{b_1}$ и $\angle C=\angle C_1$. Докажем, что тогда $\triangle ABC\sim\triangle A_1B_1C_1$.

Обозначим $k=\dfrac{a}{a_1}=\dfrac{b}{b_1}$.
Тогда $a=k\cdot a_1$, $b=k\cdot b_1$.

По теореме косинусов в треугольнике $ABC$: $$c^2=a^2+b^2-2ab\cos{C}=k^2a_1^2+k^2b_1^2-2ka_1kb_1\cos{C_1}=k^2(a_1^2+b_1^2-2a_1b_1\cos{C})=k^2c_1^2.$$

Следовательно, $c=kc_1$, то есть стороны треугольников $ABC$ и $A_1B_1C_1$ пропорциональны.

Тогда по третьему признаку $\triangle ABC\sim\triangle A_1B_1C_1$.

math-public/vtoroj_priznak_podobiya_treugolnikov.txt · Последние изменения: 2016/04/08 18:19 — labreslav

Третий признак подобия треугольников / Подобные треугольники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Подобные треугольники
5. Третий признак подобия треугольников

Теорема

Доказательство

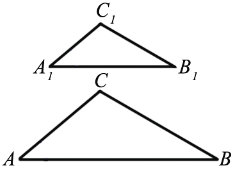
Дано: АВС и А₁В₁С₁,

Доказать: АВСА₁В₁С₁

Доказательство:

Рассмотрим АВС и А₁В₁С₁, у которых (1)

Для доказательства теоремы, учитывая второй признак подобия треугольников, достаточно доказать, что  А = А₁.

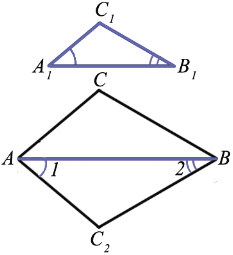
Рассмотрим АВС₂, у которого 1 = А₁, 2 = В₁.

АВС₂А₁В₁С₁ по первому признаку подобия треугольников, поэтому 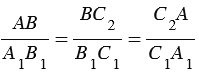(2).

Сравнивая равенства (1) и (2), получаем: ВС = ВС₂, СА =С₂А. АВС =АВС₂ по трем сторонам. Отсюда следует, что А = 1, а так как 1 = А₁, то А = А₁. Теорема доказана.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Пропорциональные отрезки

Определение подобных треугольников

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Средняя линия треугольника

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

О подобии произвольных фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Подобные треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 560, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 613, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 626*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Первый признак подобия треугольников

Вспомним, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

На одном из предыдущих уроков мы отмечали, что подобие треугольников можно установить, проверив только некоторые из равенств. И сейчас мы познакомимся с первым признаком подобия треугольником.

Теорема (1-й признак подобия треугольников). Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство.

, .

, , ,

, следовательно, .

Так как , то .

Так как , то .

, .

Так как , то .

, .

Следовательно, .

Выше мы доказали, что соответственные углы этих треугольников равны, а значит, они треугольники подобны.

Что и требовалось доказать.

Из доказанной теоремы следует, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному.

Давайте возьмём некоторый треугольник ABC и проведём прямую MN, параллельную стороне AC.

 как соотв. при  и секущей ,  

 как соотв. при  и секущей , 

следовательно,  по 1-му признаку.

Также из доказанного признака следует, что прямоугольные треугольники подобны по острому углу.

Действительно. Если у прямоугольных треугольников ABC и A₁B₁C₁ угол А равен углу А₁, то  по 1-му признаку.

А теперь давайте посмотрим на следующие треугольники и найдём среди них подобные.

Итак, треугольники а и в подобны по первому признаку, так как два угла одного треугольника соответственно равны двум углам другого треугольника.

Треугольники д и е являются подобными, так как они прямоугольные и у них острые углы равны.

И у нас остались треугольники б и г. Так как сумма углов треугольника равна ста восьмидесяти градусам, то несложно найти градусную меру третьего угла треугольника б. Она равна 40º. А тогда эти треугольники подобны по двум углам, то есть по первому признаку.

Задача. На стороне  параллелограмма отмечена точка . Прямые  и  пересекаются в точке . Найдите  и , если  см,  см,  см,  см.

Решение.

Рассмотрим  и .

 как вертикальные,  как внутр. накрест лежащие  при  и секущей . 

Значит,  по 1-му признаку.

, то есть .

, ,  (см).

 см.

, ,  (см).

Ответ:  см;  см.

Задача. На рисунке  см,  см,  см, а . Найдите .

Решение.

 

Рассмотрим  и .

 по условию задачи,  – общий.  

Значит,  по 1-му признаку.

, ,   (см).

Ответ:  см.

Итак, на уроке мы доказали первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Убедились, что прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному. А также, что прямоугольные треугольники подобны по острому углу.

Кроме этого решили задачи на закрепление нового материала.